State of Charge Estimation and Evaluation of Lithium Battery Using Kalman Filter Algorithms
Abstract
1. Introduction
2. Establishment of Battery Model
2.1. Subjects
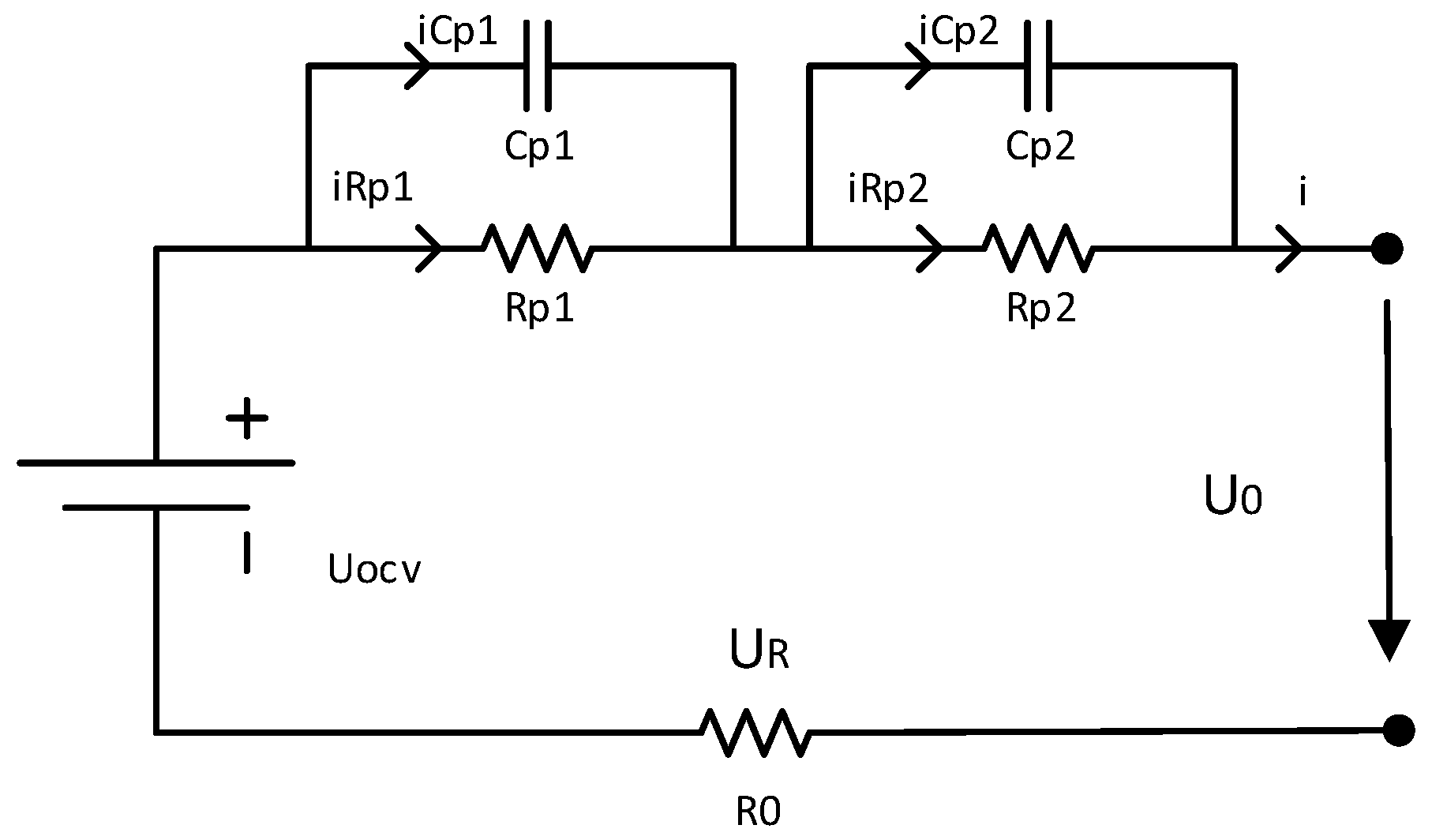
2.2. Model Structure
2.3. Introduction of Experimental Platform
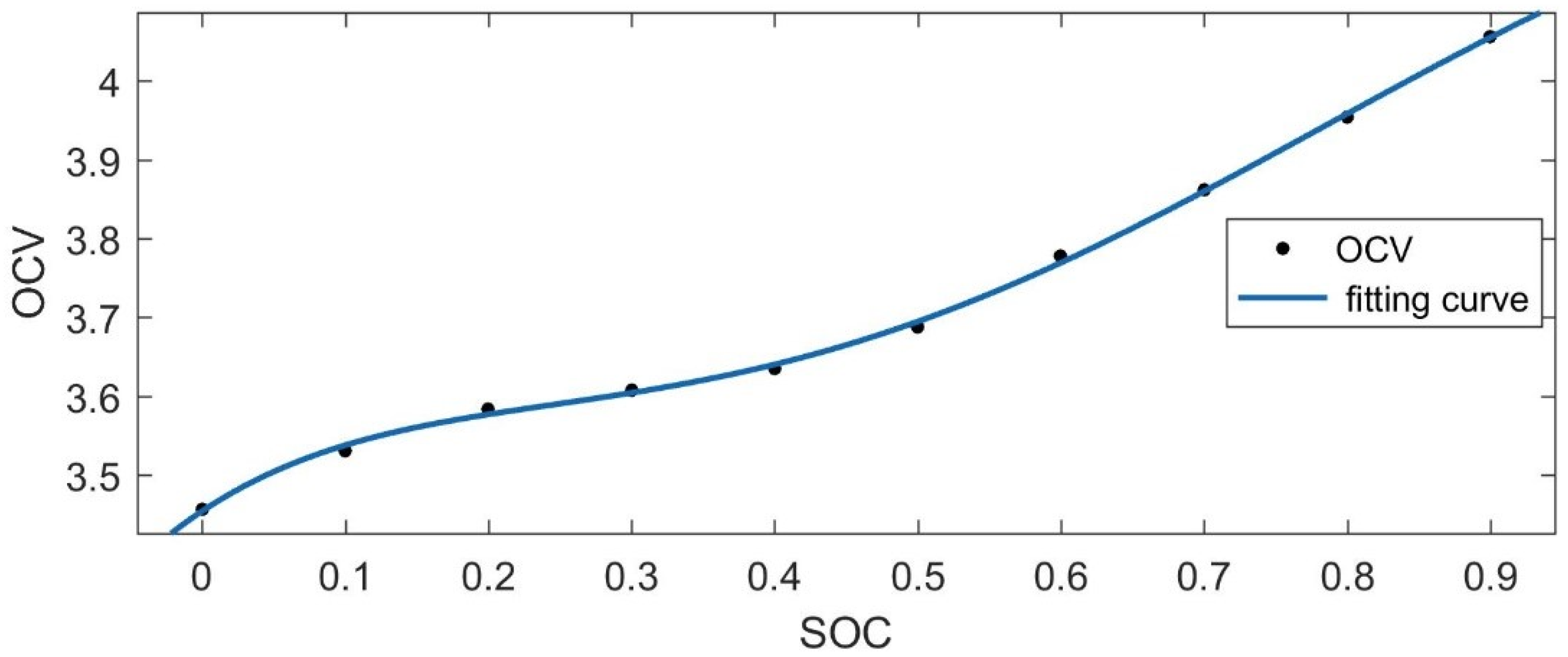
2.4. Measurement of the Relationship Curve between OCV and SOC
2.5. Identification of the Resistance-Capacitance Parameters of the Battery Model
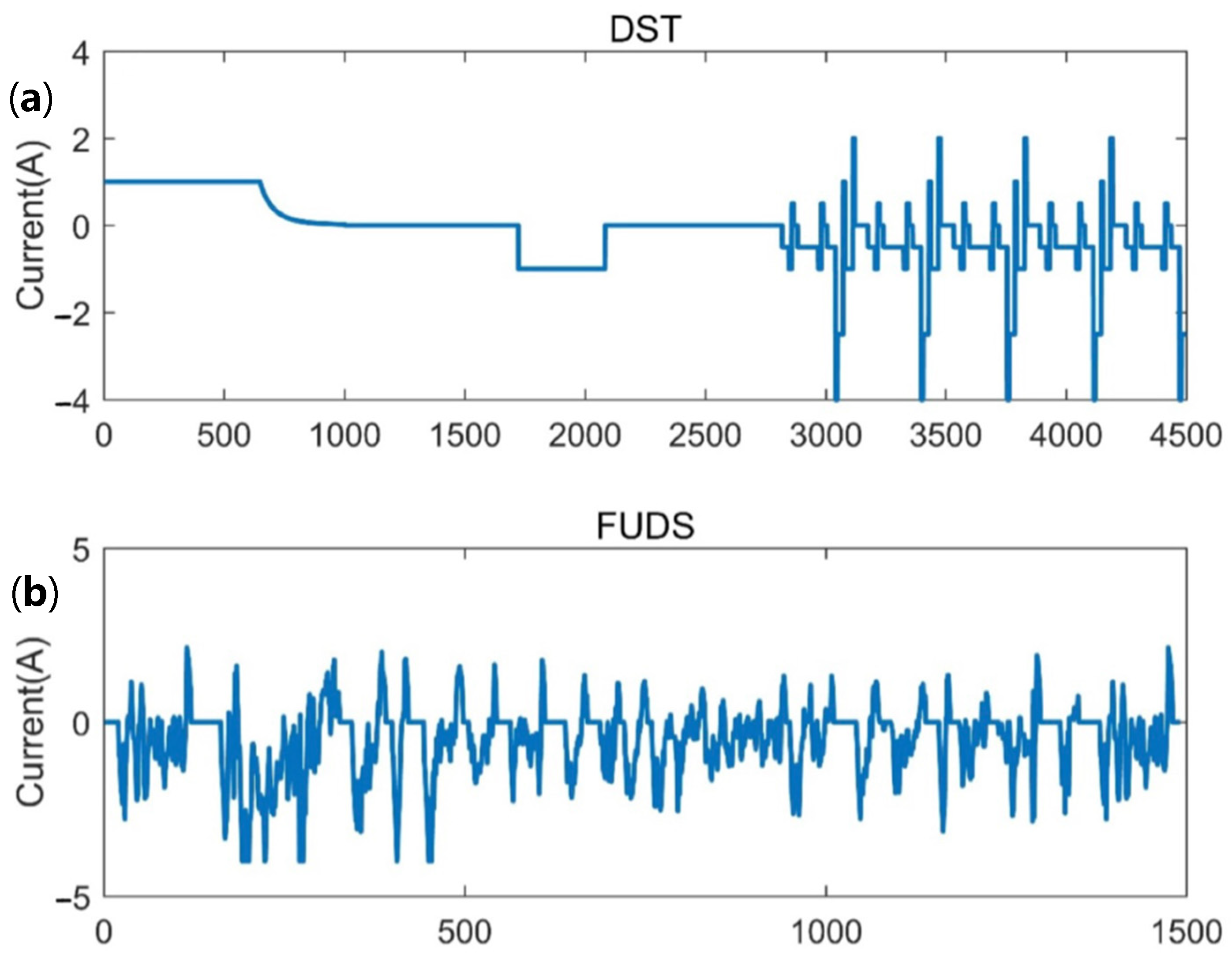
2.5.1. Model Parameter Identification Test
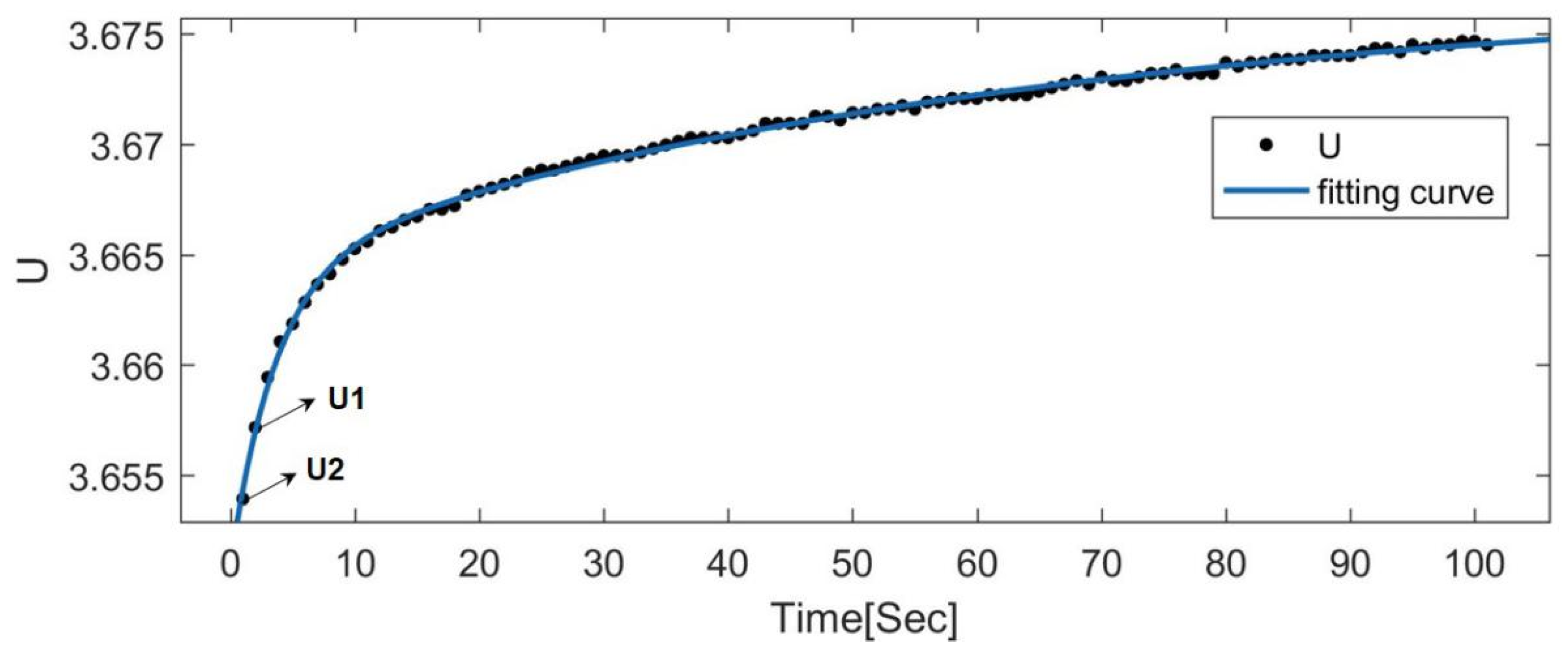
2.5.2. Model Parameter Identification Method
3. AUKF Algorithm for SOC Estimation
3.1. Algorithm Initialization
3.2. Prediction
3.2.1. Sigma Points (UT Transform) Are Generated at the k−1 Moment
3.2.2. Time Update
3.3. Survey Update
3.3.1. Generating Sigma Points at the k|k−1 Moment
3.3.2. Calculating the Predicted Output Voltage and Covariance
3.3.3. Modifying System State Estimation
3.4. Adjustment of Q and V
4. Experimental Results and Analysis
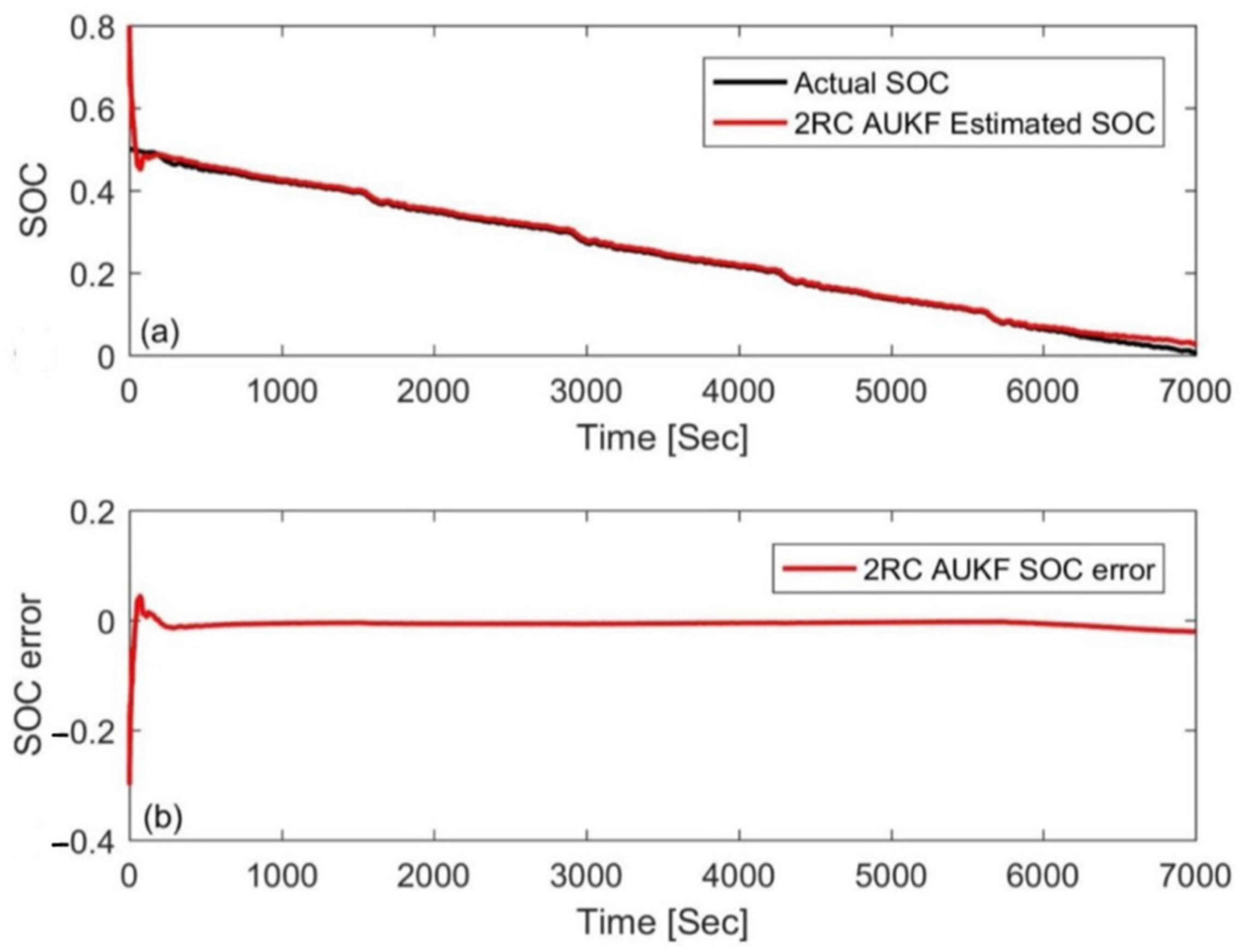
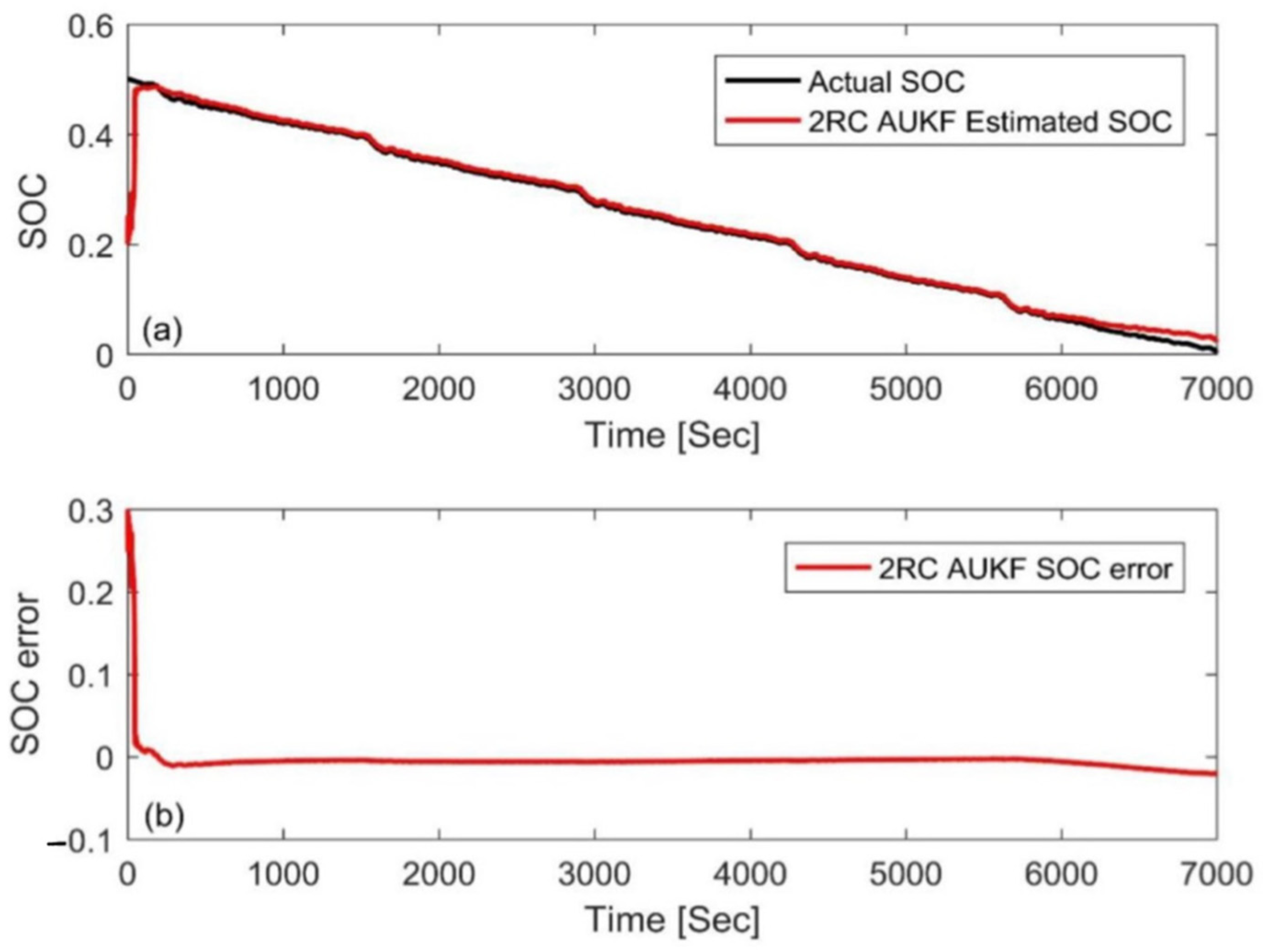
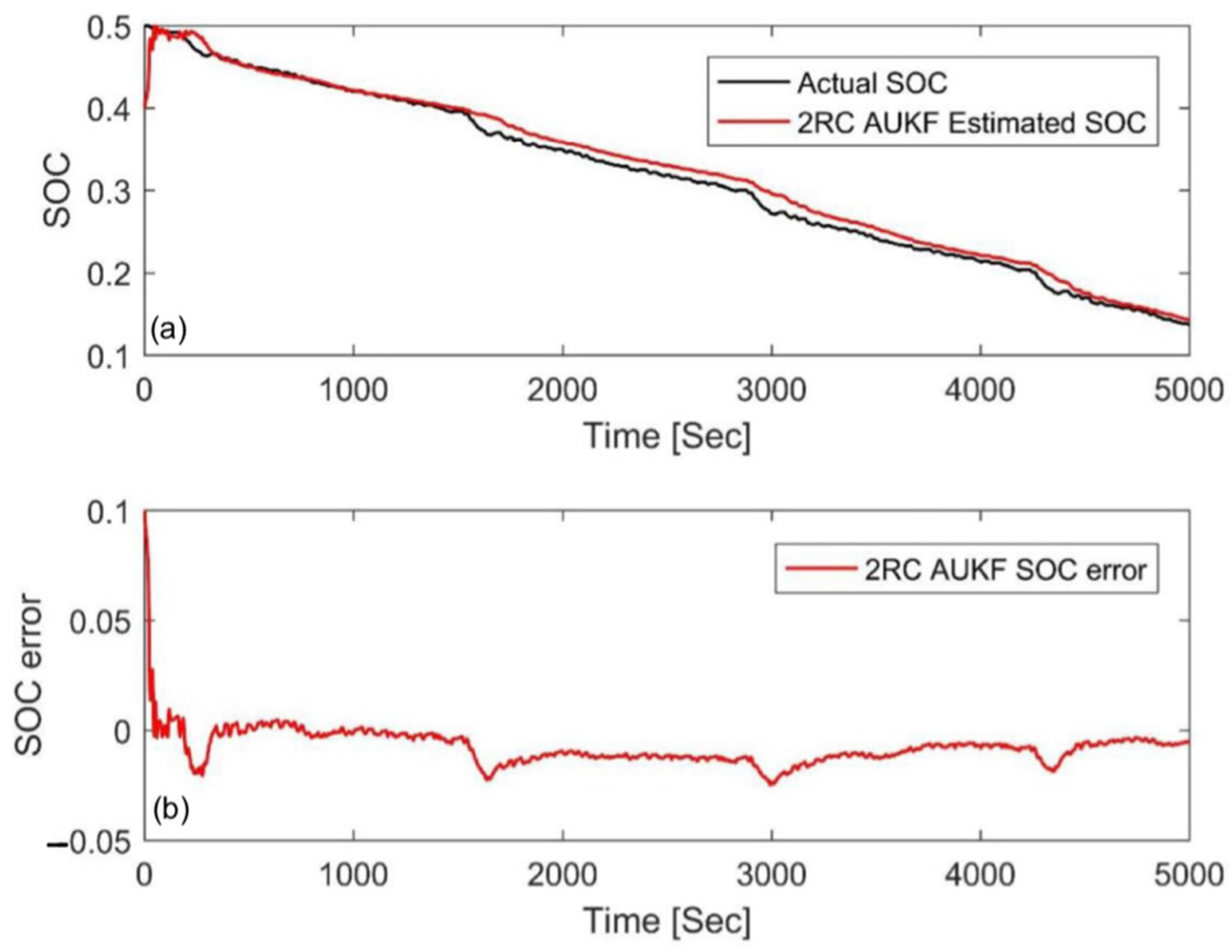
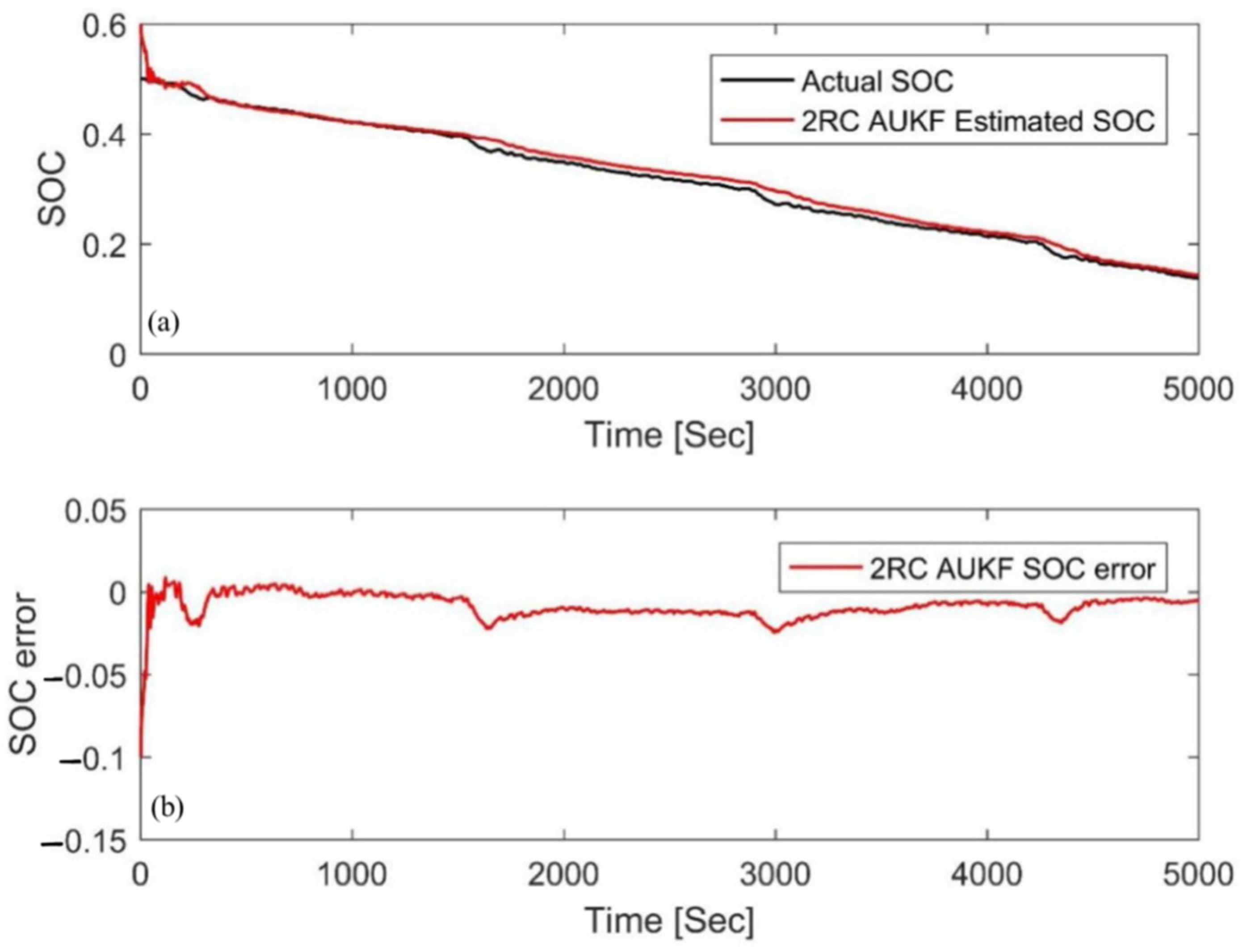
4.1. Simulation with Different Initial Errors
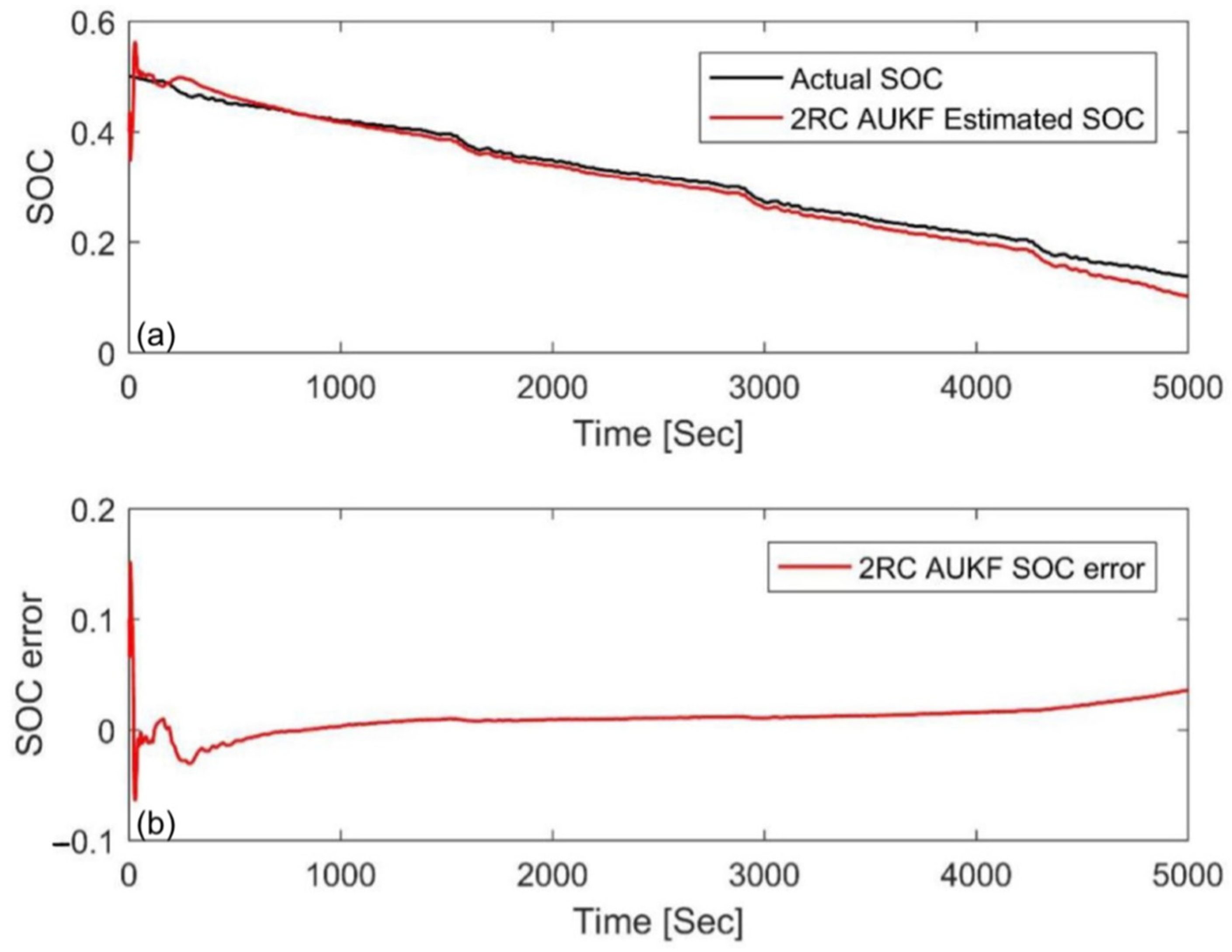
4.2. Simulation at Different Temperatures
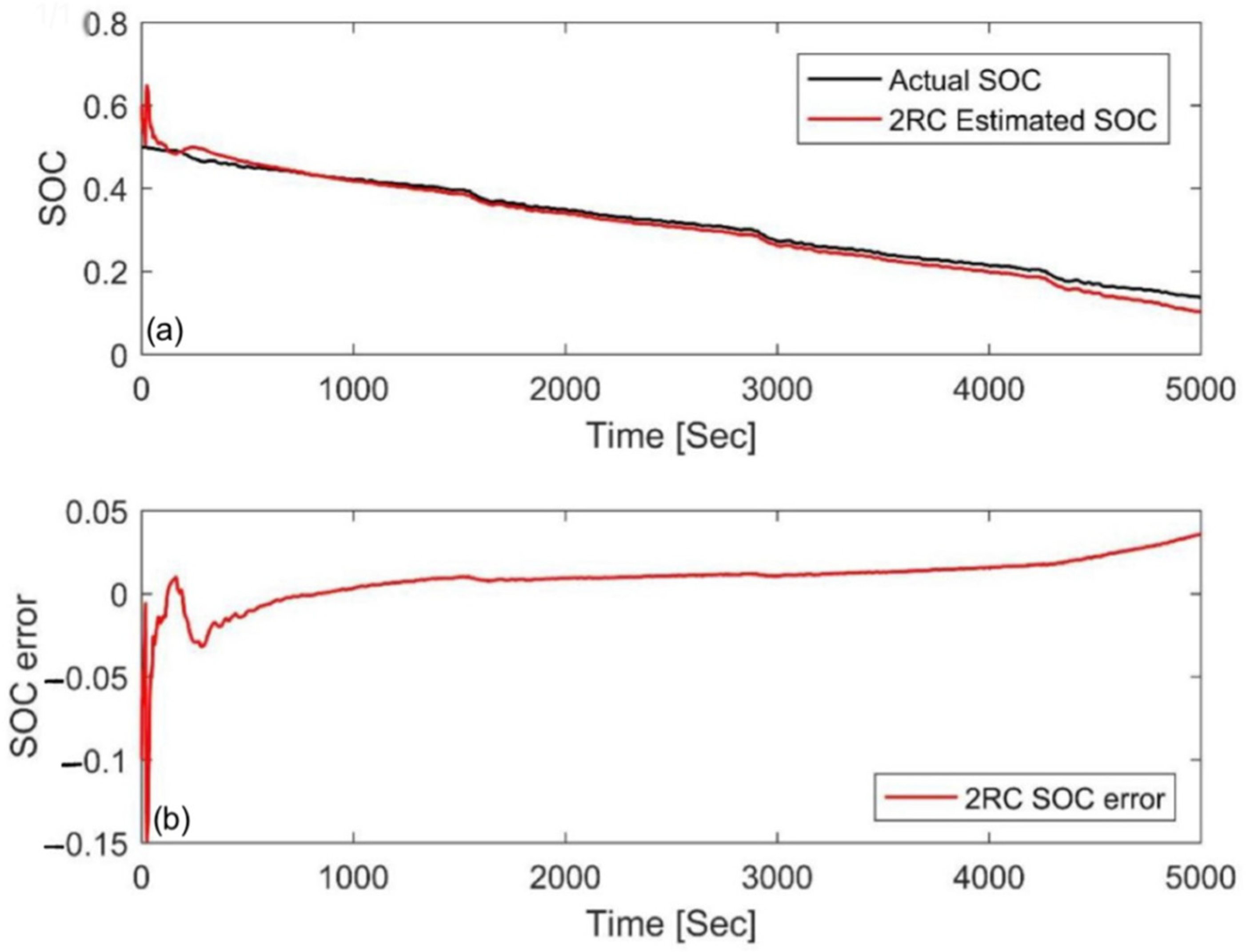
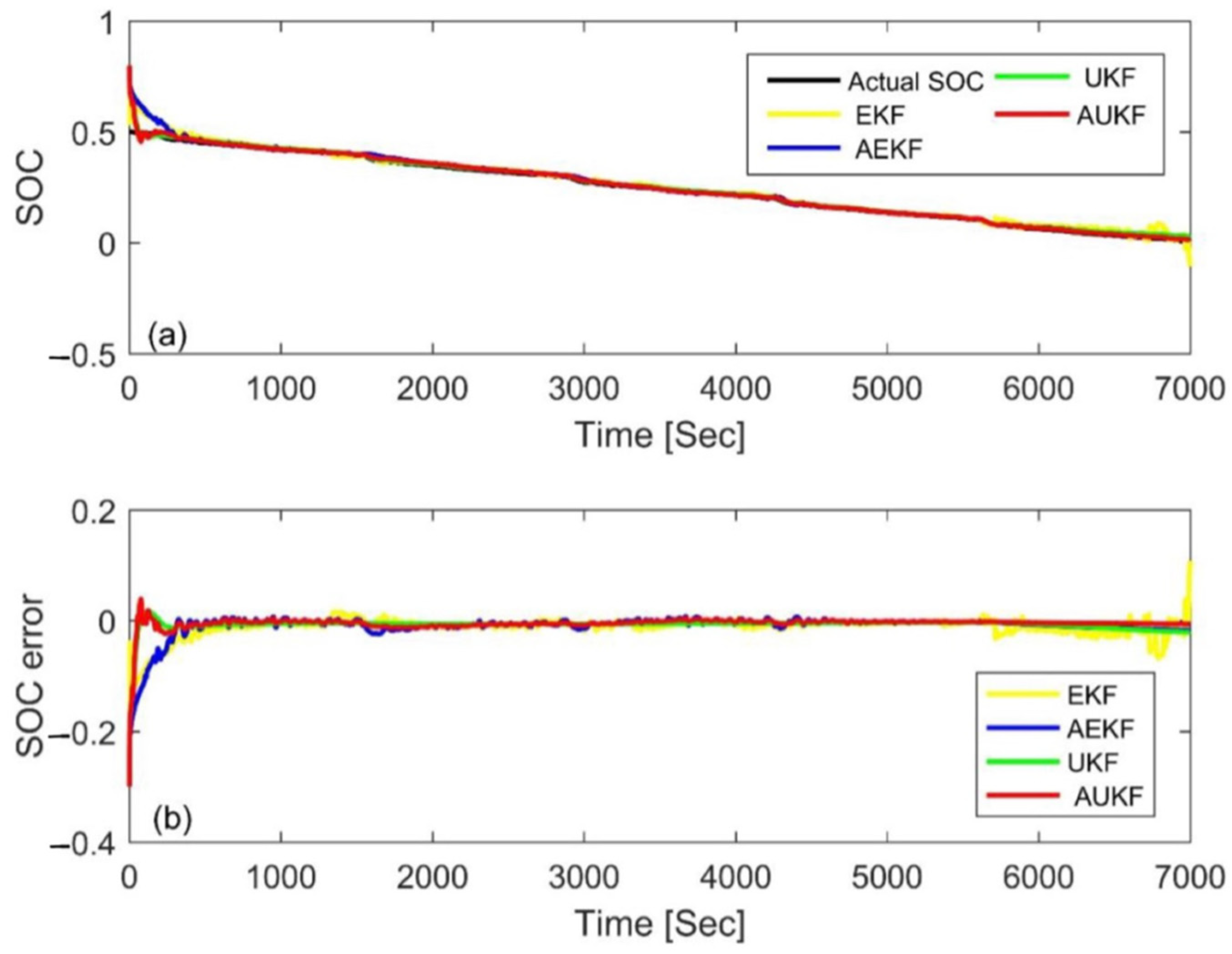
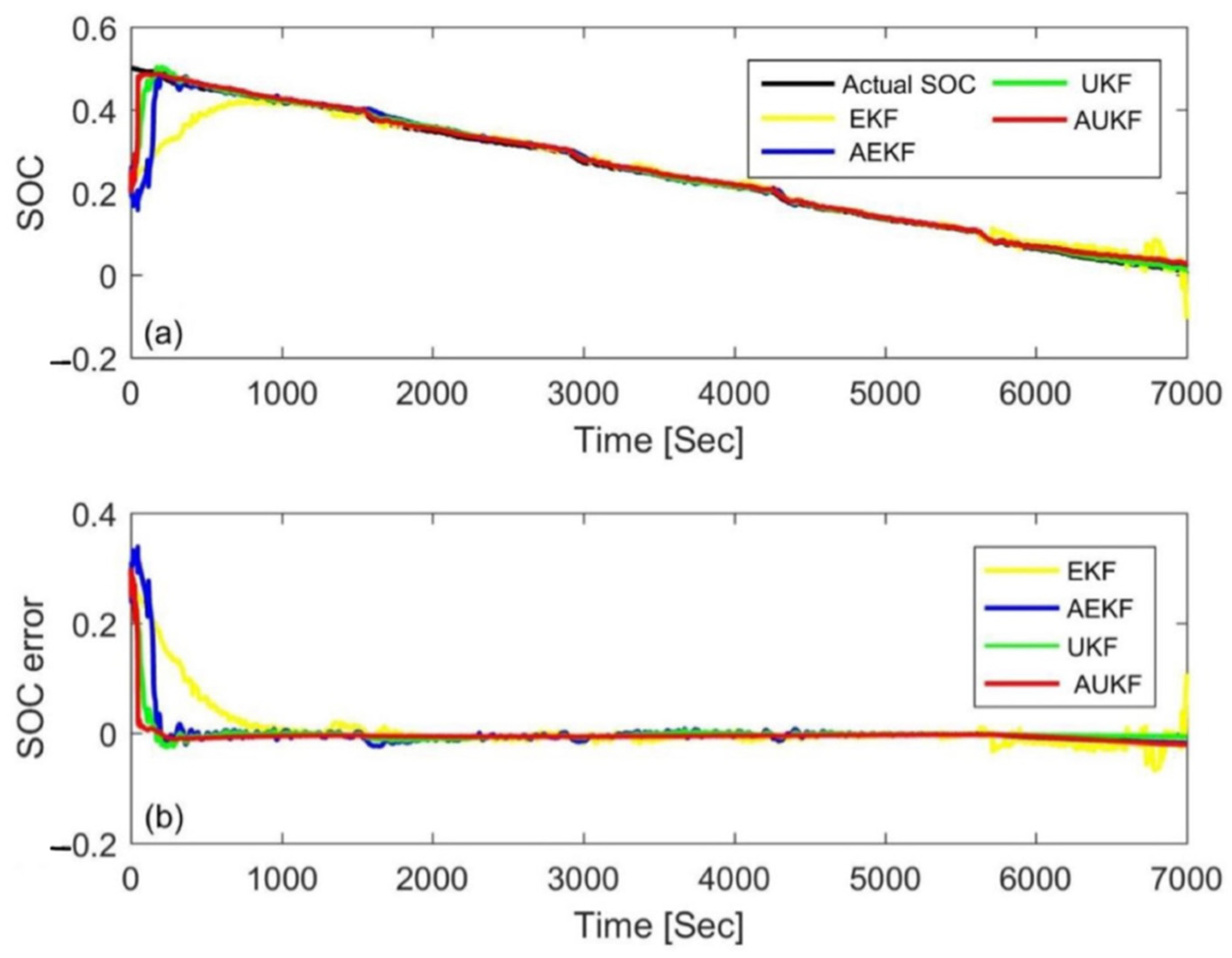
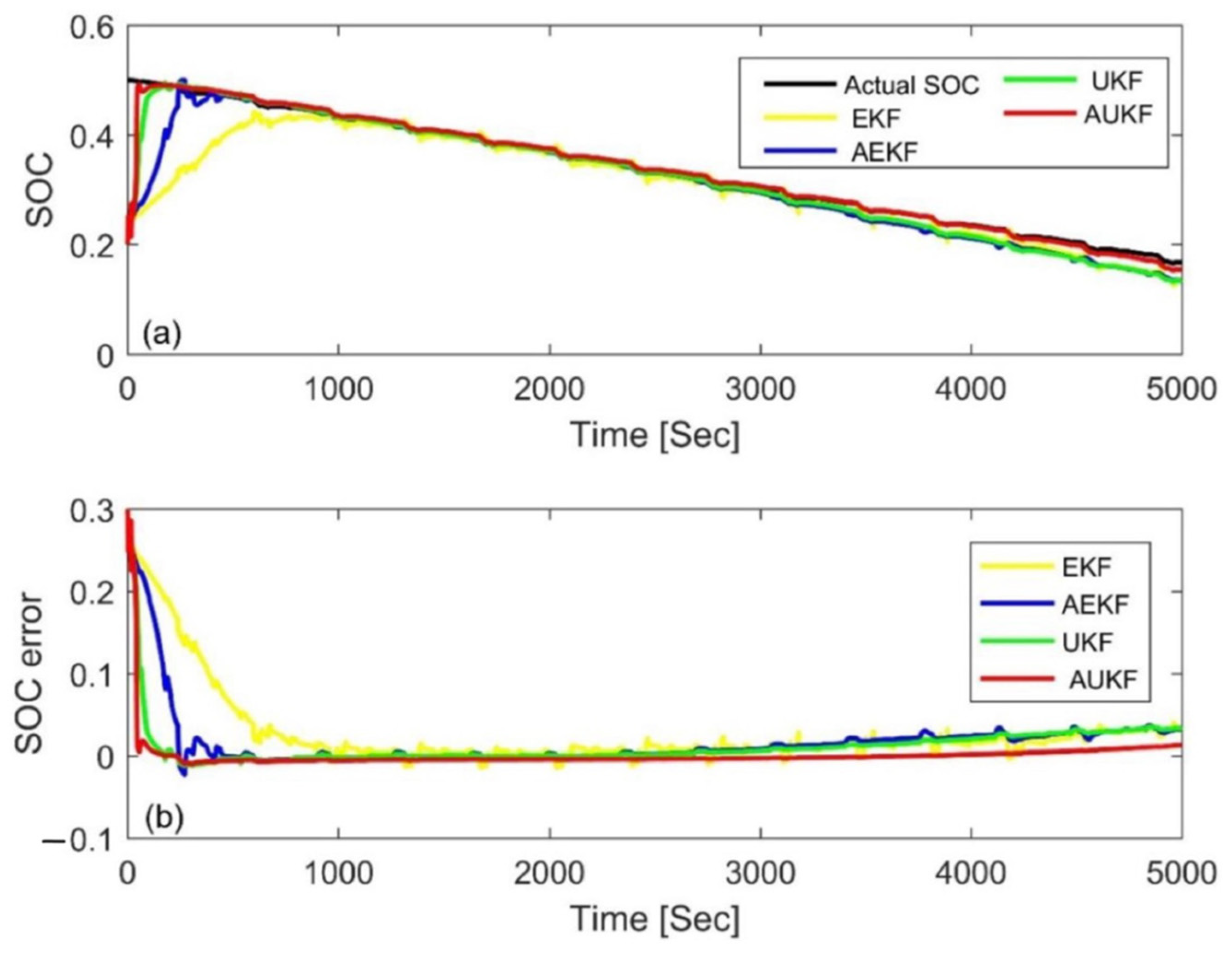
4.3. Simulation Comparison of Different Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.P.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H.O. SOC estimation for lithium-ion batteries: Review and future challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Cheng, K.W.E.; Divakar, B.; Wu, H.; Ding, K.; Ho, H.F. Battery-management system (BMS) and SOC development for electrical vehicles. IEEE Trans. Veh. Technol. 2010, 60, 76–88. [Google Scholar] [CrossRef]
- Luo, M.; Guo, Y.; Kang, J.; She, L.; Geng, Z. Ternary-material lithium-ion battery SOC estimation under various ambient temperature. Ionics 2018, 24, 1907–1917. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, X.; Li, G. State of charge estimation for pulse discharge of a LiFePO4 battery by a revised Ah counting. Electrochim. Acta 2015, 151, 63–71. [Google Scholar] [CrossRef]
- Chen, X.; Lei, H.; Xiong, R.; Shen, W.; Yang, R. A novel approach to reconstruct open circuit voltage for state of charge estimation of lithium ion batteries in electric vehicles. Appl. Energy 2019, 255, 113758. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; He, H.; Mu, H.; Wang, C. A novel method on estimating the degradation and state of charge of lithium-ion batteries used for electrical vehicles. Appl. Energy 2017, 207, 336–345. [Google Scholar] [CrossRef]
- Wang, J.; Xiong, R.; Li, L.; Fang, Y. A comparative analysis and validation for double-filters-based state of charge estimators using battery-in-the-loop approach. Appl. Energy 2018, 229, 648–659. [Google Scholar] [CrossRef]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Zahid, T.; Xu, K.; Li, W.; Li, C.; Li, H. State of charge estimation for electric vehicle power battery using advanced machine learning algorithm under diversified drive cycles. Energy 2018, 162, 871–882. [Google Scholar] [CrossRef]
- Qin, T.; Zeng, S.; Guo, J. Robust prognostics for state of health estimation of lithium-ion batteries based on an improved PSO-SVR model. Microelectron. Reliab. 2015, 55, 1280–1284. [Google Scholar] [CrossRef]
- Kang, L.; Zhao, X.; Ma, J. A new neural network model for the state-of-charge estimation in the battery degradation process. Appl. Energy 2014, 121, 20–27. [Google Scholar] [CrossRef]
- Xu, J.; Cao, B.; Chen, Z.; Zou, Z. An online state of charge estimation method with reduced prior battery testing information. Int. J. Electr. Power Energy Syst. 2014, 63, 178–184. [Google Scholar] [CrossRef]
- Liu, Z.; Dang, X.; Jing, B.; Ji, J. A novel model-based state of charge estimation for lithium-ion battery using adaptive robust iterative cubature Kalman filter. Electr. Power Syst. Res. 2019, 177, 105951. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Ye, M.; Guo, H.; Xiong, R.; Yu, Q. A double-scale and adaptive particle filter-based online parameter and state of charge estimation method for lithium-ion batteries. Energy 2018, 144, 789–799. [Google Scholar] [CrossRef]
- Xiong, R.; Yu, Q.; Wang, L.Y.; Lin, C. A novel method to obtain the open circuit voltage for the state of charge of lithium ion batteries in electric vehicles by using H infinity filter. Appl. Energy 2017, 207, 346–353. [Google Scholar] [CrossRef]
- Ma, Y.; Li, B.; Li, G.; Zhang, J.; Chen, H. A nonlinear observer approach of SOC estimation based on hysteresis model for lithium-ion battery. IEEE/CAA J. Autom. Sin. 2017, 4, 195–204. [Google Scholar] [CrossRef]
- Long, H.Y.; Zhu, C.Y.; Huang, B.B.; Piao, C.H.; Sun, Y.Q. Model parameters online identification and SOC joint estimation for Lithium-ion battery based on a composite algorithm. J. Electr. Eng. Technol. 2019, 14, 1485–1493. [Google Scholar] [CrossRef]
- Vasebi, A.; Bathaee, S.M.T.; Partovibakhsh, M. Predicting state of charge of lead-acid batteries for hybrid electric vehicles by extended Kalman filter. Energy Convers. Manag. 2008, 49, 75–82. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. A new extension of the Kalman filter to nonlinear systems. Proc. SPIE Int. Soc. Opt. Eng. 1999, 3068, 182–193. [Google Scholar]
- Santhanagopalan, S.; White, R.E. State of charge estimation using an unscented filter for high power lithium ion cells. Int. J. Energy Res. 2010, 34, 152–163. [Google Scholar] [CrossRef]
- Wu, Z.; Shang, M.; Shen, D.; Qi, S. SOC estimation for batteries using MS-AUKF and neural network. J. Renew. Sustain. Energy 2019, 11, 024103. [Google Scholar] [CrossRef]
- Renjian, F.; Shuai, Z.; Xiaodong, L. On-line estimation of dynamic state-of-charge for lead acid battery based on fuzzy logic. In Proceedings of the 2013 2nd International Conference on Measurement, Information and Control, Harbin, China, 16–18 August 2013. [Google Scholar]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-charge estimation of the lithium-ion battery using an adaptive extended Kalman filter based on an improved thevenin model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- Han, J.; Kim, D.; Sunwoo, M. State-of-charge estimation of lead-acid batteries using an adaptive extended Kalman filter. J. Power Sources 2009, 188, 606–612. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]
- Partovibakhsh, M.; Liu, G. An adaptive unscented Kalman filtering approach for online estimation of model parameters and state-of-charge of lithium-ion batteries for autonomous mobile robots. IEEE Trans. Control Syst. Technol. 2015, 23, 357–363. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, M.; Zhou, A.; Li, Y.; Li, S.; Fu, C.; Gong, C. State of charge estimation for lithium-ion batteries based on adaptive dual Kalman filter. Appl. Math. Model. 2020, 77, 1255–1272. [Google Scholar] [CrossRef]
- Rzepka, B.; Bischof, S.; Blank, T. Implementing an extended Kalman filter for SOC estimation of a Li-ion battery with hysteresis: A step-by-step guide. Energies 2021, 14, 3733. [Google Scholar] [CrossRef]
- Yang, S.; Zhou, S.; Hua, Y.; Zhou, X.; Liu, X.; Pan, Y.; Ling, H.; Wu, B. A parameter adaptive method for state of charge estimation of lithium-ion batteries with an improved extended Kalman filter. Sci. Rep. 2021, 11, 5805. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Lu, D.; Liu, Q.; Liu, L.; Zhao, X. State of charge estimation for LiFePO4 battery via dual extended Kalman filter and charging voltage curve. Electrochim. Acta 2019, 296, 1009–1017. [Google Scholar] [CrossRef]
- Wang, Q.; Kang, J.; Tan, Z.; Luo, M. An online method to simultaneously identify the parameters and estimate states for lithium ion batteries. Electrochim. Acta 2018, 289, 376–388. [Google Scholar] [CrossRef]
- Guo, F.; Hu, G.; Xiang, S.; Zhou, P.; Hong, R.; Xiong, N. A multi-scale parameter adaptive method for state of charge and parameter estimation of lithium-ion batteries using dual Kalman filters. Energy 2019, 178, 79–88. [Google Scholar] [CrossRef]
- Shrivastava, P.; Kok Soon, T.; Bin Idris, M.Y.I.; Mekhilef, S.; Adnan, S.B.R.S. Combined state of charge and state of energy estimation of lithium-ion battery using dual forgetting factor-Based adaptive extended Kalman filter for electric vehicle applications. IEEE Trans. Veh. Technol. 2021, 70, 1200–1215. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S.; Adnan, S.B.R.S. Model-based state of X estimation of lithium-ion battery for electric vehicle applications. Int. J. Energy Res. 2022, 46, 10704–10723. [Google Scholar] [CrossRef]
- Xing, J.; Wu, P. State of charge estimation of lithium-ion battery based on improved adaptive unscented Kalman filter. Sustainability 2021, 13, 5046. [Google Scholar] [CrossRef]
- Yang, W.; Wen, Y.; Pandžić, H.; Zhang, W. A multi-state control strategy for battery energy storage based on the state-of-charge and frequency disturbance conditions. Int. J. Electr. Power Energy Syst. 2022, 135, 107600. [Google Scholar] [CrossRef]
- Qian, C.; Xu, B.; Xia, Q.; Ren, Y.; Yang, D.; Wang, Z. A dual-input neural network for online state-of-charge estimation of the lithium-ion battery throughout its lifetime. Materials 2022, 15, 5933. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Liu, X.; Liu, Z. Model-based state of charge and peak power capability joint estimation of lithium-ion battery in plug-in hybrid electric vehicles. J. Power Sources 2013, 229, 159–169. [Google Scholar] [CrossRef]
- Quanshi, C.; Chengtao, L.J.A.T. Summarization of studies on performance models of batteries for electric vehicle. Automob. Technol. 2005, 3, 1–5. [Google Scholar]
- Xia, C.Y.; Zhang, S.; Sun, H.T. A strategy of estimating state of charge based on extended Kalman filter. Chin. J. Power Sources 2007, 31, 414. [Google Scholar]
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Appl. Energy 2016, 183, 513–525. [Google Scholar] [CrossRef]




| Types | Positive and Negative | Rated Voltage | Rated Capacity | Up/Down Cutoff Voltage | Maximum Current |
|---|---|---|---|---|---|
| 18,650 | LiNiMnCoO2/ Graphite | 3.6 V | 2.0 Ah | 2.5 V/4.2 V | 22 A (25 Celsius) |
| R0 (Ω) | Rp1 (Ω) | Cp1 (F) | Rp2 (Ω) | Cp2 (F) |
|---|---|---|---|---|
| 0.07898 | 0.009617 | 455.2766 | 0.012407 | 5573.927 |
| Initial Value | MAE | Convergence Rate (s) |
|---|---|---|
| 80% | 0.0054 | 49 |
| 20% | 0.0071 | 48 |
| Initial Value | MAE |
|---|---|
| 40% | 0.0132 |
| 60% | 0.0136 |
| Initial Value | MAE |
|---|---|
| 40% | 0.0091 |
| 60% | 0.0091 |
| Algorithm | Initial Value | MAE | Convergence Time |
|---|---|---|---|
| EKF | 80% | 0.0134 | 489 |
| EKF | 20% | 0.0212 | 725 |
| UKF | 80% | 0.0075 | 55 |
| UKF | 20% | 0.0081 | 140 |
| AEKF | 80% | 0.0101 | 303 |
| AEKF | 20% | 0.0123 | 169 |
| AUKF | 80% | 0.0054 | 49 |
| AUKF | 20% | 0.0071 | 48 |
| Algorithm | Initial Value | MAE | Convergence Time |
|---|---|---|---|
| EKF | 80% | 0.0183 | 519 |
| EKF | 20% | 0.0282 | 603 |
| UKF | 80% | 0.0124 | 103 |
| UKF | 20% | 0.0130 | 110 |
| AEKF | 80% | 0.0151 | 167 |
| AEKF | 20% | 0.0186 | 240 |
| AUKF | 80% | 0.0056 | 36 |
| AUKF | 20% | 0.0065 | 45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Hu, R.; Ma, Z.; Jiang, W. State of Charge Estimation and Evaluation of Lithium Battery Using Kalman Filter Algorithms. Materials 2022, 15, 8744. https://doi.org/10.3390/ma15248744
Hu L, Hu R, Ma Z, Jiang W. State of Charge Estimation and Evaluation of Lithium Battery Using Kalman Filter Algorithms. Materials. 2022; 15(24):8744. https://doi.org/10.3390/ma15248744
Chicago/Turabian StyleHu, Longzhou, Rong Hu, Zengsheng Ma, and Wenjuan Jiang. 2022. "State of Charge Estimation and Evaluation of Lithium Battery Using Kalman Filter Algorithms" Materials 15, no. 24: 8744. https://doi.org/10.3390/ma15248744
APA StyleHu, L., Hu, R., Ma, Z., & Jiang, W. (2022). State of Charge Estimation and Evaluation of Lithium Battery Using Kalman Filter Algorithms. Materials, 15(24), 8744. https://doi.org/10.3390/ma15248744







