Nonlocal Strain Gradient Theory for the Bending of Functionally Graded Porous Nanoplates
Abstract
1. Introduction
2. Basic Formulation
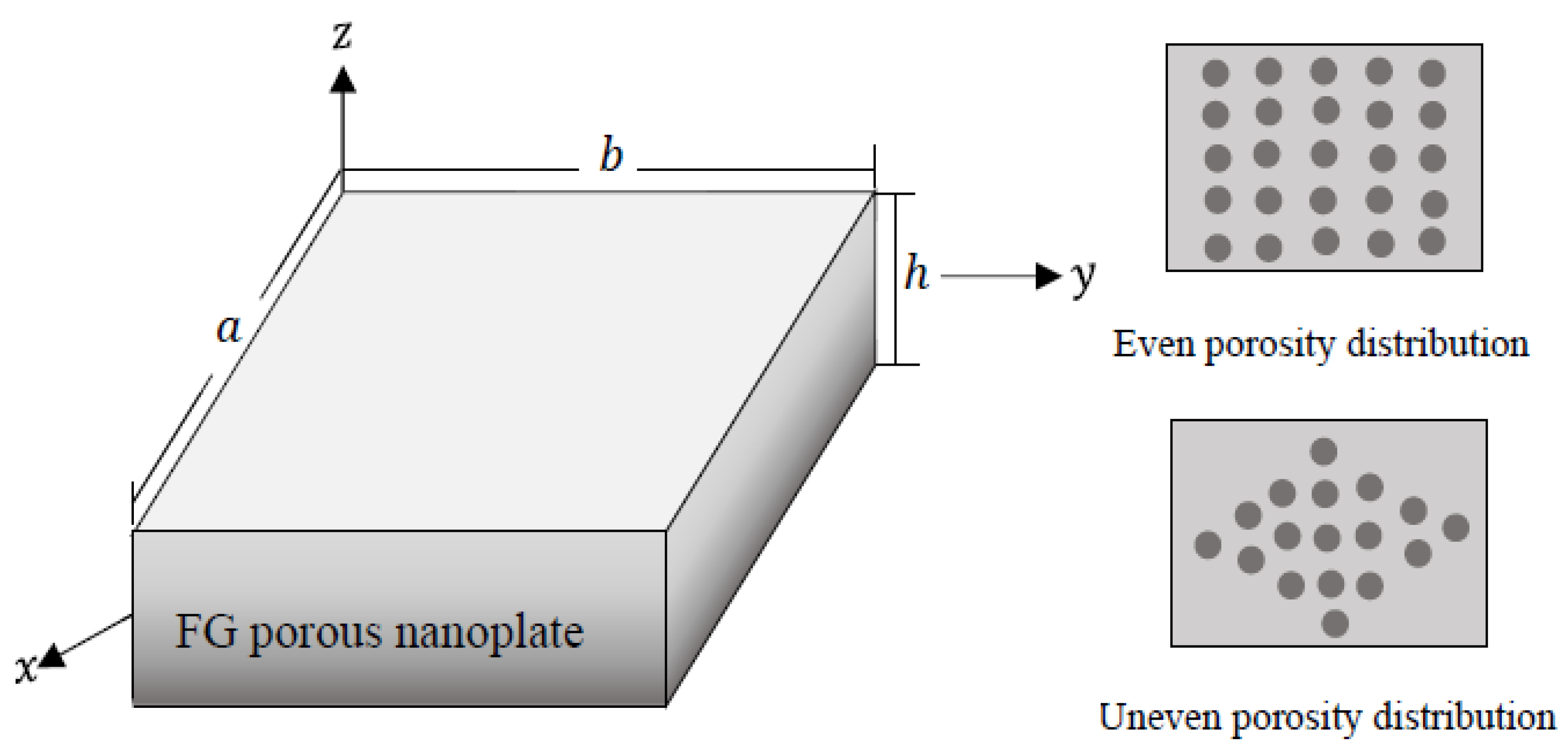
2.1. Material Properties of FG Porous Nanoplate
2.2. The Nonlocal Strain Gradient Theory for FG Porous Nanoplate
2.3. Displacement Model
3. Governing Equations
4. Closed-Form Solution
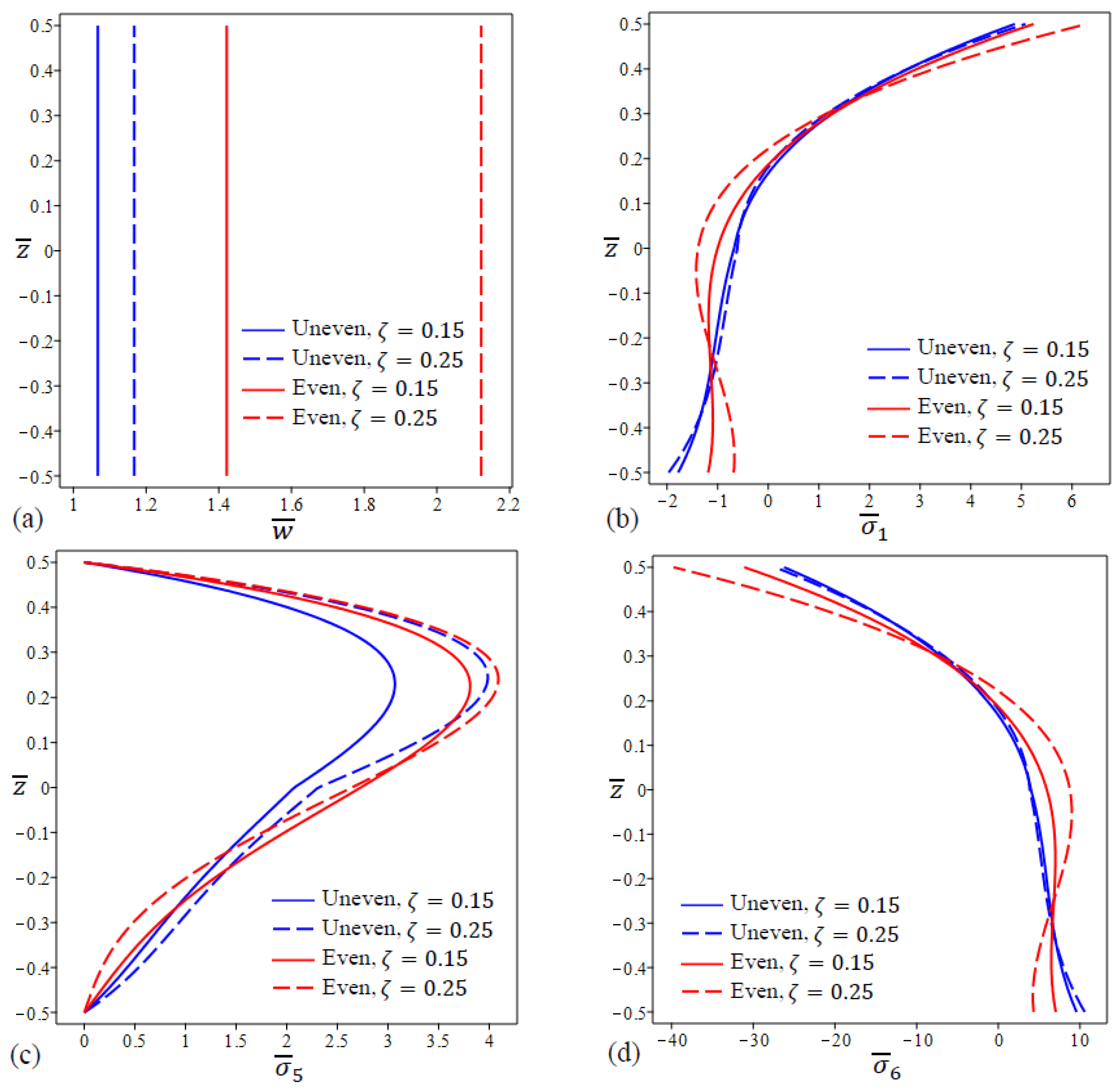
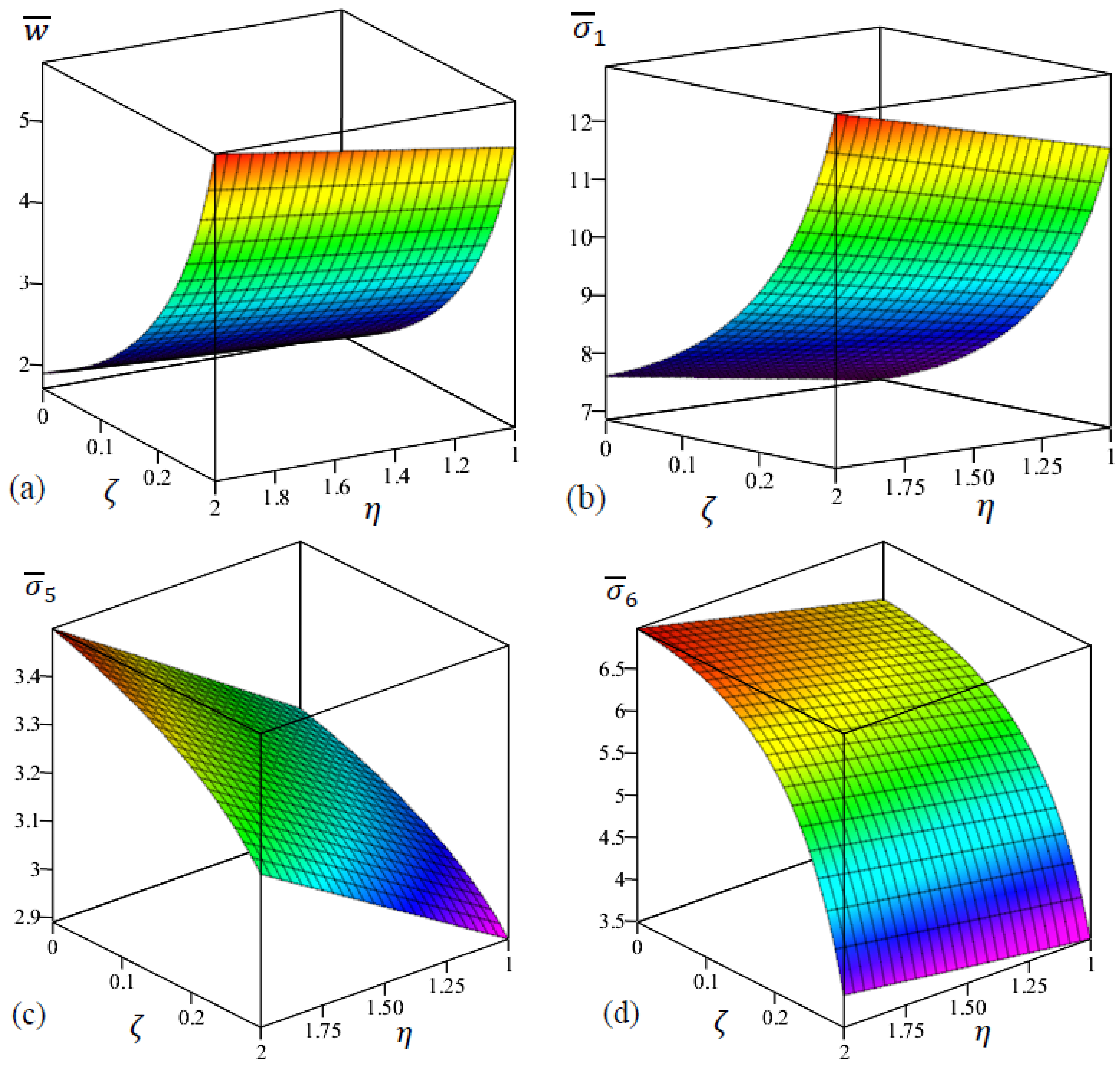
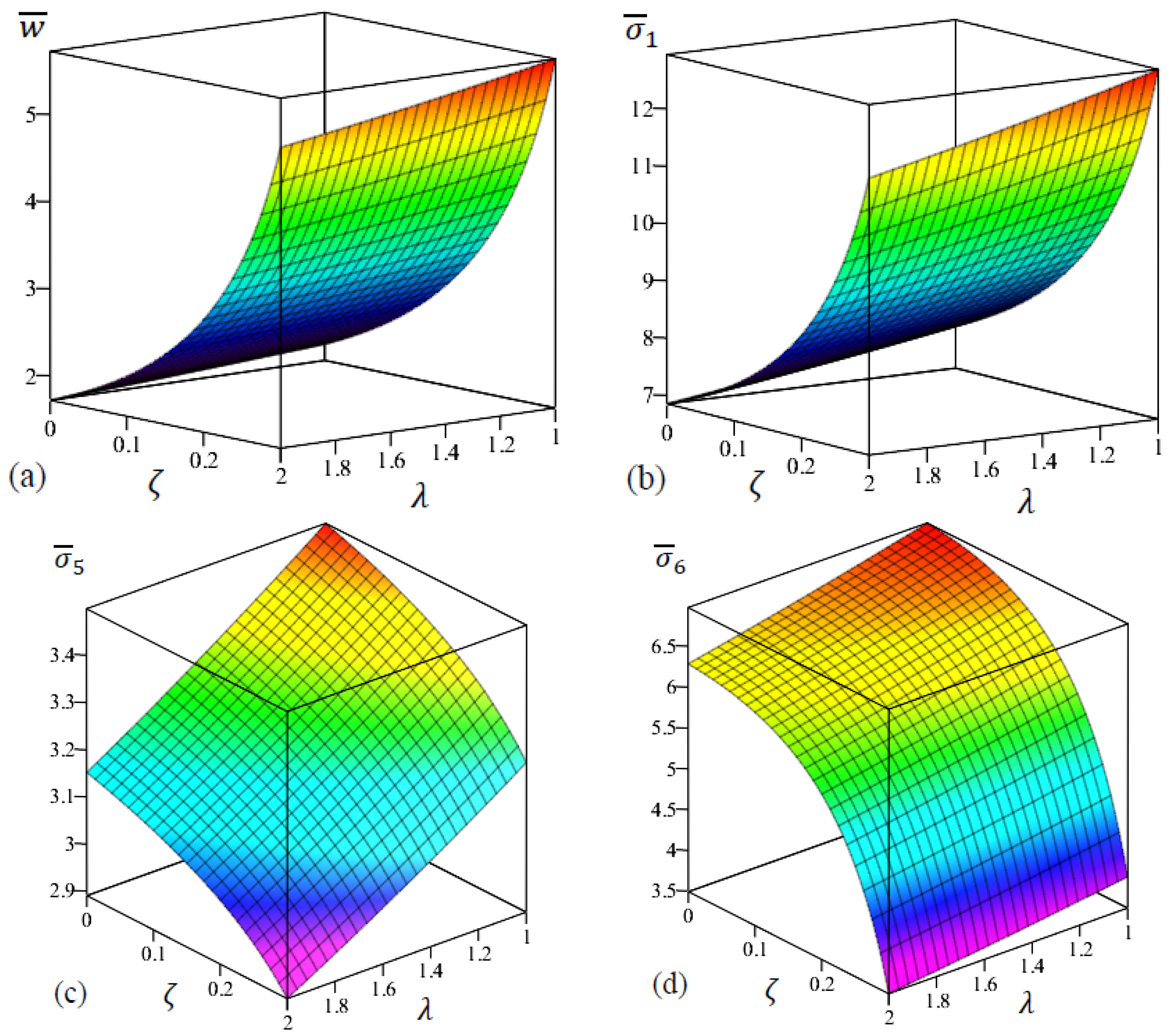
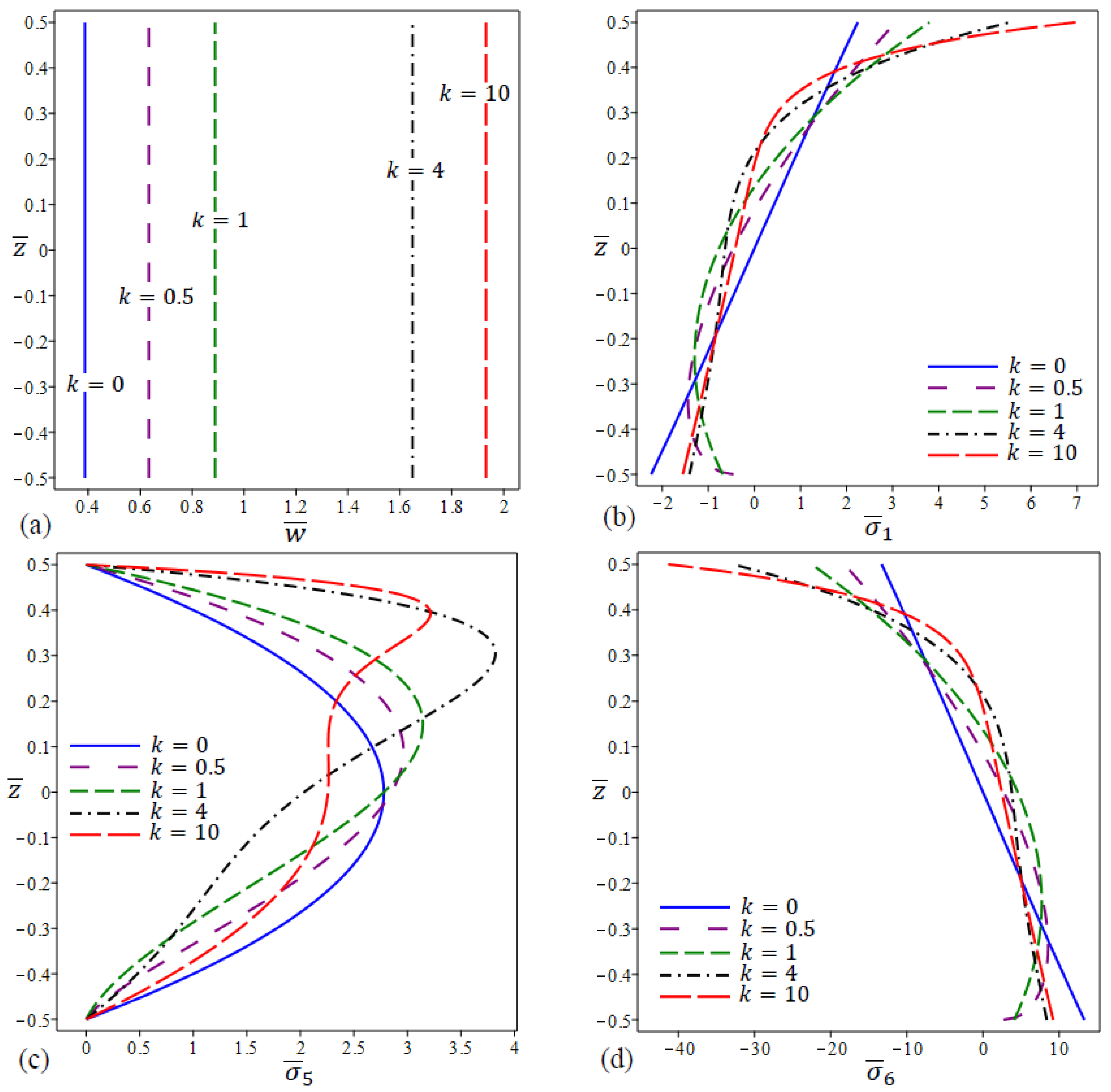
5. Results and Discussions
5.1. Verification Analysis
5.2. Parametric Analysis
6. Conclusions
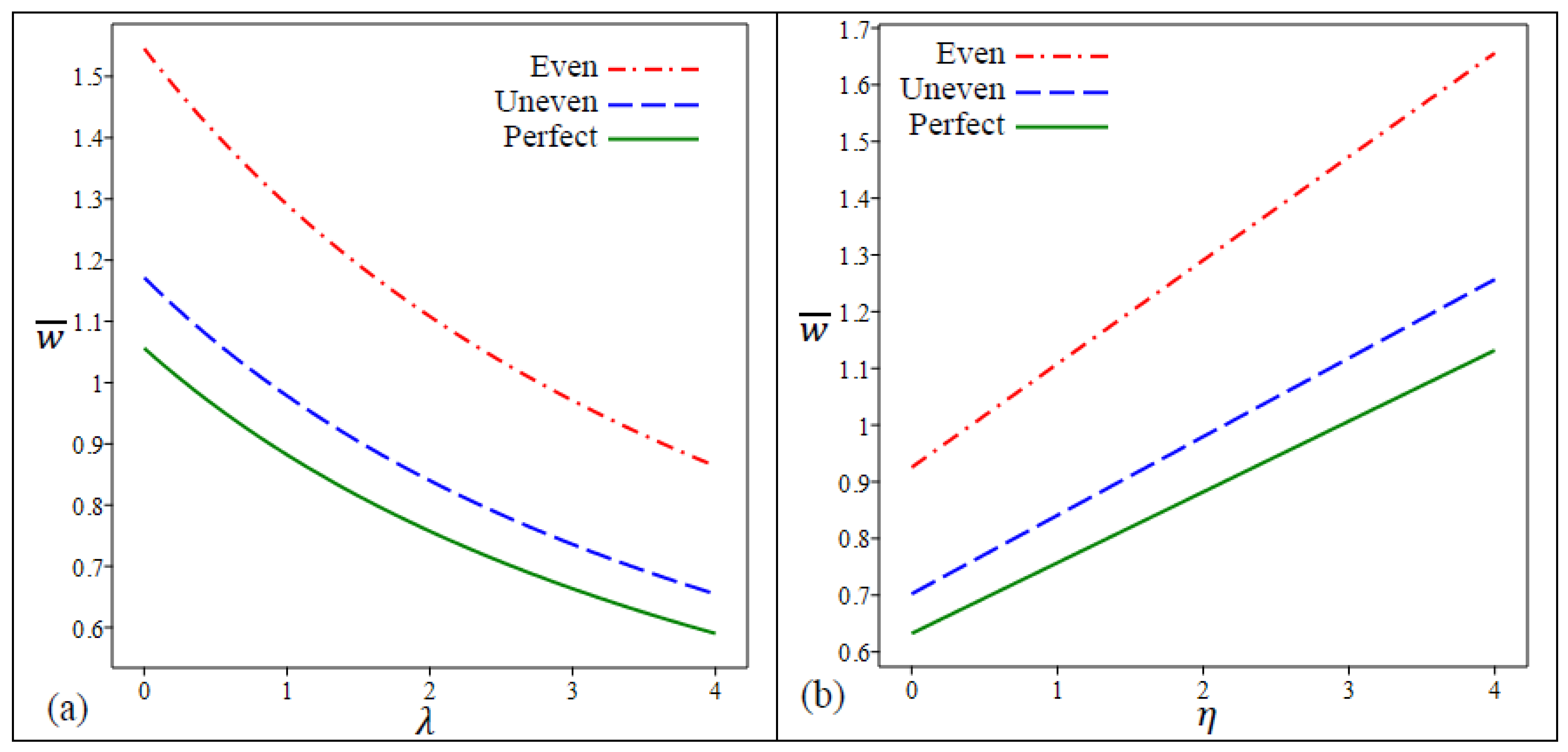
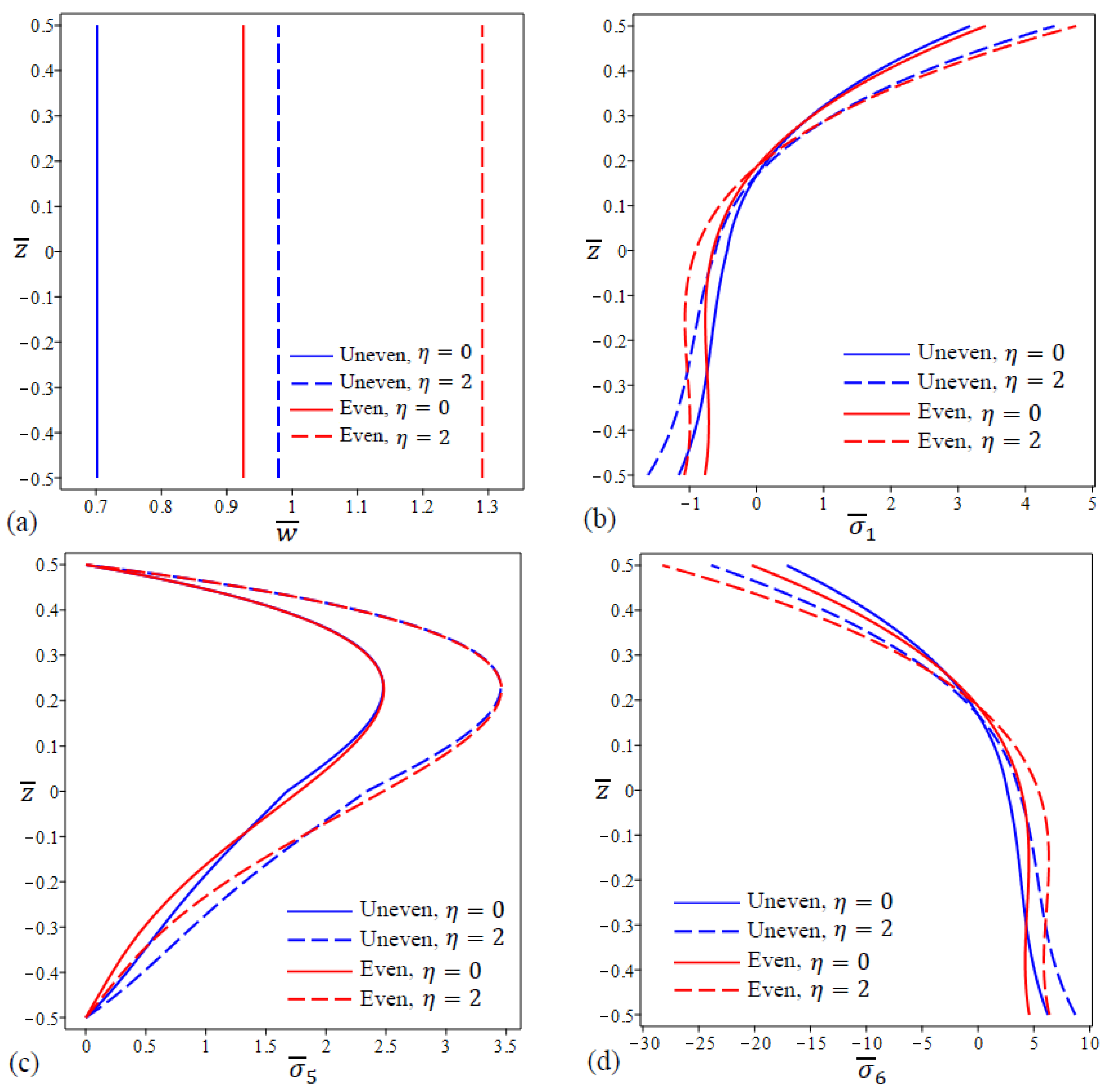
- The presence of a porosity factor has a significant impact on the static response of the FG nanoplate and FG nanoplates with unevenly distributed porosities deflect less than those with evenly distributed porosities;
- The impact of the nonlocal parameter on the central deflection and stresses is opposite to that of the response of strain gradient parameter under the same conditions;
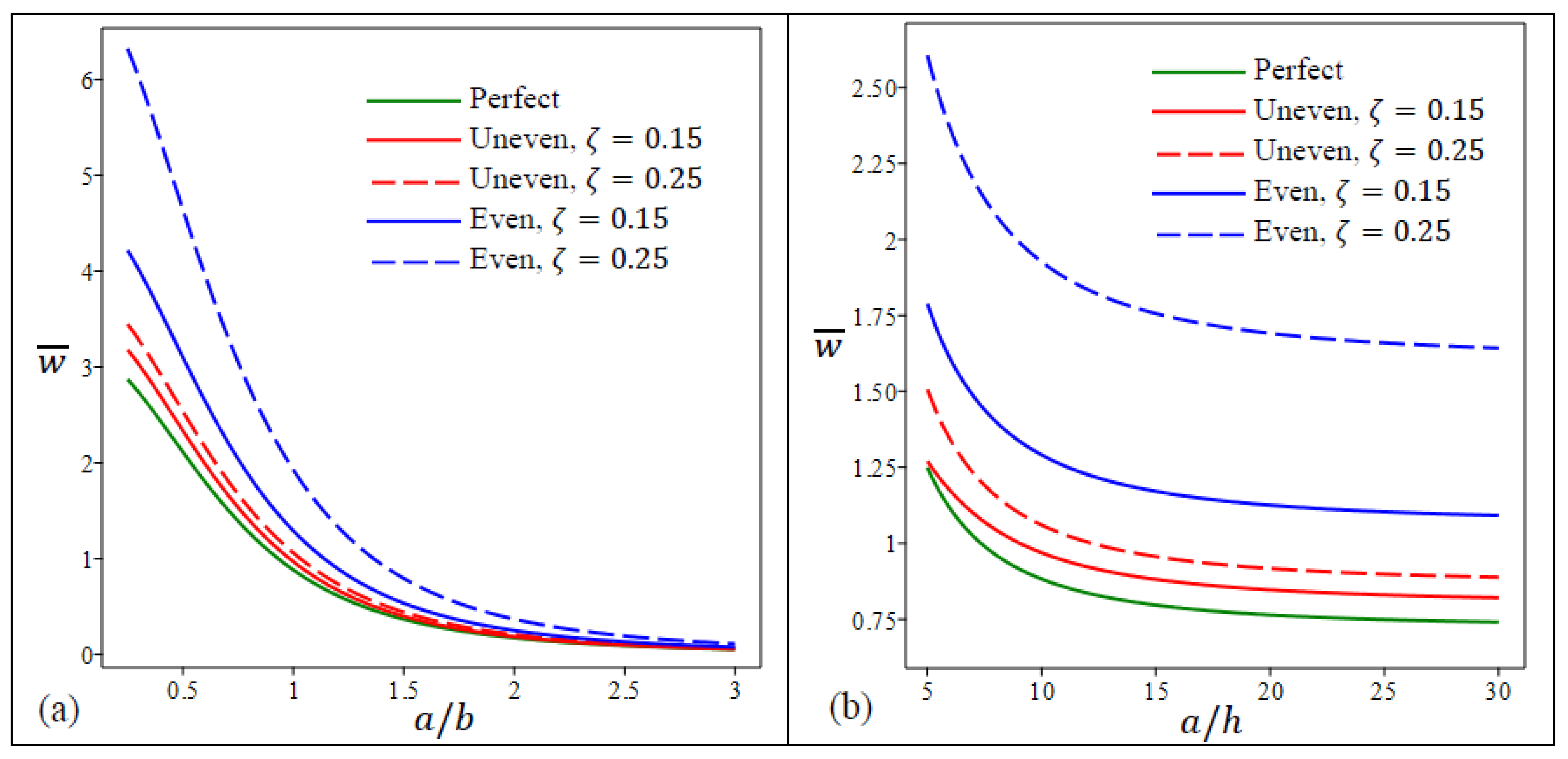
- The impact of aspect ratio on the central deflection is much larger than that of the side-to-thickness ratio ;
- The results in the tables and figures indicate that the decreasing in the length scale parameter increases the center deflection and stresses;
- The center deflection and stresses increase by the increase in the nonlocal parameter for all types of FG porous nanoplates. It implies that the nonlocal parameter may be capable of reducing the stiffness of FG porous nanoplates.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Thostenson, E.T.; Ren, Z.; Chou, T.W. Advances in the science and technology of carbon nanotubes and their composites: A review. Compos. Sci. Technol. 2011, 61, 1899912. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Nami, M.R.; Janghorban, M. Static analysis of rectangular nanoplates using trigonometric shear deformation theory based on nonlocal elasticity theory. Beilstein J. Nanotechnol. 2013, 4, 968–973. [Google Scholar] [CrossRef] [PubMed]
- Sobhy, M.; Radwan, A.F. A new quasi 3-D nonlocal hyperbolic plate theory for vibration and buckling of FGM nanoplates. Int. J. Appl. Mech. 2017, 9, 1750008. [Google Scholar] [CrossRef]
- Allahyari, E.; Asgari, M.; Pellicano, F. Nonlinear strain gradient analysis of nanoplates embedded in an elastic medium incorporating surface stress effects. Eur. Phys. J. Plus 2019, 134, 191. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Bending analysis of embedded carbon nanotubes resting on an elastic foundation using strain gradient theory. Acta Astronaut. 2016, 119, 1–12. [Google Scholar] [CrossRef]
- Rahmani, O.; Shokrnia, M.; Golmohammadi, H.; Hosseini, S.A.H. Dynamic response of a single-walled carbon nanotube under a moving harmonic load by considering modified nonlocal elasticity theory. Eur. Phys. J. Plus 2018, 133, 42. [Google Scholar] [CrossRef]
- Civalek, Ö.; Demir, C. A simple mathematical model of microtubules surrounded by an elastic matrix by nonlocal finite element method. Appl. Math. Comput. 2012, 89, 335–352. [Google Scholar] [CrossRef]
- Zenkour, A.M. A novel mixed nonlocal elasticity theory for thermoelastic vibration of nanoplates. Compos. Struct. 2018, 185, 821–833. [Google Scholar] [CrossRef]
- Hussainm, A.; Haider, Q.; Rehman, A.; Ahmad, H.; Baili, J.; Aljahdaly, N.H.; Hassan, A. A thermal conductivity model for hybrid heat and mass transfer investigation of single and multi-wall carbon nano-tubes flow induced by a spinning body. Case Stud. Therm. Eng. 2021, 28, 101449. [Google Scholar] [CrossRef]
- Tho, N.C.; Thanh, N.T.; Tho, T.D.; van Minh, P.; Hoa, L.K. Modelling of the flexoelectric effect on rotating nanobeams with geometrical imperfection. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 510. [Google Scholar] [CrossRef]
- Duc, D.H.; Thom, D.V.; Cong, P.H.; Minh, P.V.; Nguyen, N.X. Vibration and static buckling behavior of variable thickness flexoelectric nanoplates. Mech. Based Des. Struc. 2022, 1–29. [Google Scholar] [CrossRef]
- Thai, L.M.; Luat, D.T.; Phung, V.B.; Minh, P.V.; Thom, D.V. Finite element modeling of mechanical behaviors of piezoelectric nanoplates with flexoelectric effects. Arch. Appl. Mech. 2022, 92, 163–182. [Google Scholar] [CrossRef]
- Mahmure, A.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Free vibration of thin-walled composite shell structures reinforced with uniform and linear carbon nanotubes: Effect of the elastic foundation and nonlinearity. Nanomaterials 2021, 11, 2090. [Google Scholar] [CrossRef]
- Avey, M.; Sofiyev, A.H.; Kuruoglu, N. Influence of elastic foundations and thermal environments on the thermoelastic buckling of nanocomposite truncated conical shells. Acta Mech. 2022, 233, 685–700. [Google Scholar] [CrossRef]
- Avey, M.; Fantuzi, N.; Sofiyev, A.H. Mathematical modeling and analytical solution of thermoelastic stability problem of functionally graded nanocomposite cylinders within different theories. Mathematics 2022, 10, 1081. [Google Scholar] [CrossRef]
- Avey, M.; Fantuzi, N.; Sofiyev, A.H. On the solution of thermal buckling problem of moderately thick laminated conical shells containing carbon nanotube originating layers. Materials 2022, 15, 7427. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P. A nonlocal sinusoidal shear deformation beam theory with application to bending, buckling, and vibration of nanobeams. Int. J. Eng. Sci. 2012, 54, 58–66. [Google Scholar] [CrossRef]
- Lou, J.; He, L.; Du, J.; Wu, H. Buckling and post-buckling analyses of piezoelectric hybrid microplates subject to thermo–electro-mechanical loads based on the modified couple stress theory. Compos. Struct. 2016, 153, 332–344. [Google Scholar] [CrossRef]
- Barati, M.R.; Zenkour, A.M. A general bi-Helmholtz nonlocal strain-gradient elasticity for wave propagation in nanoporous graded double-nanobeam systems on elastic substrate. Compos. Struct. 2017, 168, 885–892. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.; Zhao, J. A unified size-dependent plate model based on nonlocal strain gradient theory including surface effects. Appl. Math. Model 2019, 68, 583–602. [Google Scholar] [CrossRef]
- Thanh, C.-L.; Tran, L.V.; Vu-Huu, T.; Nguyen-Xuan, H.; Abdel-Wahab, M. Size-dependent nonlinear analysis and damping responses of FG-CNTRC micro-plates. Comput. Meth. Appl. Mech. Eng. 2019, 353, 253–276. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Phadikar, J.K. Nonlocal elasticity theory for vibration of nanoplates. J. Sound Vib. 2009, 325, 206–223. [Google Scholar] [CrossRef]
- Aghababaei, R.; Reddy, J.N. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 2009, 326, 277–289. [Google Scholar] [CrossRef]
- Shen, Z.-B.; Tang, H.-L.; Li, D.-K.; Tang, G.-J. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Comput. Mater. Sci. 2012, 61, 200–205. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Shojaee, M. Free vibration of nanoplates based on a nonlocal two-variable refined plate theory. Compos. Struct. 2013, 95, 443–452. [Google Scholar] [CrossRef]
- Udupa, G.; Rao, S.S.; Gangadharan, K.V. Functionally graded composite materials: An overview. Proc. Mater. Sci. 2014, 5, 1291–1299. [Google Scholar] [CrossRef]
- Zhu, J.; Lai, Z.; Yin, Z.; Jeon, J.; Lee, S. Fabrication of ZrO2–NiCr functionally graded material by powder metallurgy. Mater. Chem. Phys. 2001, 68, 130–135. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R. Exact solution for free vibration of thick rectangular plates made of porous materials. Compos. Struct. 2015, 134, 1051–1060. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Free and forced vibrations of shear deformable functionally graded porous beams. Int. J. Mech. Sci. 2016, 108, 14–22. [Google Scholar] [CrossRef]
- Shafiei, N.; Mirjavadi, S.S.; MohaselAfshari, B.; Rabby, S.; Kazemi, M. Vibration of two-dimensional imperfect functionally graded (2D-FG) porous nano-/micro-beams. Comput. Methods Appl. Mech. Eng. 2017, 322, 615–632. [Google Scholar] [CrossRef]
- Arshid, E.; Khorshidvand, A.R. Free vibration analysis of saturated porous FG circular plates integrated with piezoelectric actuators via differential quadrature method. Thin-Walled Struct. 2018, 125, 220–233. [Google Scholar] [CrossRef]
- Akbas, S. Forced vibration analysis of functionally graded porous deep beams. Compos. Struct. 2018, 186, 293–302. [Google Scholar] [CrossRef]
- Wu, D.; Liu, A.; Huang, Y.; Huang, Y.; Pi, Y.; Gao, W. Dynamic analysis of functionally graded porous structures through finite element analysis. Eng. Struct. 2018, 165, 287–301. [Google Scholar] [CrossRef]
- Gao, K.; Li, R.; Yang, J. Dynamic characteristics of functionally graded porous beams with interval material properties. Eng. Struct. 2019, 197, 109441. [Google Scholar] [CrossRef]
- Liu, Y.; Suab, S.; Huang, H.; Lianga, Y. Thermal-mechanical coupling buckling analysis of porous functionally graded sandwich beams based on physical neutral plane. Compos. Eng. 2019, 168, 236–242. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Buckling and bending analyses of a novel functionally graded porous plate using Chebyshev-Ritz method. Arch. Civ. Mech. Eng. 2019, 19, 157–170. [Google Scholar] [CrossRef]
- Demirhan, P.A.; Taskin, V. Bending and free vibration analysis of Levy-type porous functionally graded plate using state space approach. Compos. Eng. 2019, 160, 661–676. [Google Scholar] [CrossRef]
- Kim, J.; Żur, K.K.; Reddy, J.N. Bending, free vibration, and buckling of modified couples stress-based functionally graded porous micro-plates. Compos. Struct. 2019, 209, 879–888. [Google Scholar] [CrossRef]
- Alghanmi, R.A.; Zenkour, A.M. Effect of porosity on the bending of functionally graded plates integrated with PFRC layer. Eur. Phys. J. Plus. 2021, 136, 142. [Google Scholar] [CrossRef]
- Phung-Van, P.; Thai, C.-H.; Nguyen-Xuan, H.; Abdel-Wahab, M. An isogeometric approach of static and free vibration analyses for porous FG nanoplates. Eur. J. Mech. Solids 2019, 78, 103851. [Google Scholar] [CrossRef]
- Phung-Van, P.; Thai, C.-H.; Nguyen-Xuan, H.; Abdel-Wahab, M. Porosity-dependent nonlinear transient responses of functionally graded nanoplates using isogeometric analysis. Compos. Eng. 2019, 164, 215–225. [Google Scholar] [CrossRef]
- Moradi-Dastjerdi, R.; Aghadavoudi, F. Static analysis of functionally graded nanocomposite sandwich plates reinforced by defected CNT. Compos. Struct. 2018, 200, 839–848. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Li, F.M.; Kishimoto, K. Thermal effects on vibration properties of double-layered nanoplates at small scales. Compos. Eng. 2011, 42, 1311–1317. [Google Scholar] [CrossRef]
- Simsek, M.; Yurtcu, H.H. Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Compos. Struct. 2013, 97, 378–386. [Google Scholar] [CrossRef]
- Aksencer, T.; Aydogdu, M. Levy type solution method for vibration and buckling of nanoplate susing nonlocal elasticity theory. Phys. Low-Dimens. Syst. Nanostruct. 2011, 43, 954–959. [Google Scholar] [CrossRef]
- Jomehzadeh, E.; Saidi, A.R. Levy type solution for free vibration analysis of a nano-plate considering the small scale effect. Recent Adv. Vib. Anal. 2011, 47–58. [Google Scholar] [CrossRef][Green Version]
- Alghanmi, R.A.; Zenkour, A.M. An electromechanical model for functionally graded porous plates attached to piezoelectric layer based on hyperbolic shear and normal deformation theory. Compos. Struct. 2021, 274, 114352. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Alghanmi, R.A. A refined quasi-3D theory for the bending of functionally graded porous sandwich plates resting on elastic foundations. Thin-Walled Struct. 2011, 181, 110047. [Google Scholar] [CrossRef]
- Daikh, A.A.; Zenkour, A.M. Effect of porosity on the bending analysis of various functionally graded sandwich plates. Mat. Res. Express. 2019, 6, 065703. [Google Scholar] [CrossRef]
- Askes, H.; Aifantis, E.C. Gradient elasticity and flexural wave dispersion in carbon nanotubes. Phys. Rev. 2009, 80, 195412. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Patel, H.G. A two variable refined plate theory for orthotropic plate analysis. Int. J. Solid. Struct. 2006, 43, 6783–6799. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. Analytical solution of a two variable refined plate theory for bending analysis of orthotropic Levy-type plates. Int. J. Mech. Sci. 2012, 54, 269–276. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar] [CrossRef]
- Sobhy, M. A comprehensive study on FGM nanoplates embedded in an elastic medium. Compos. Struct. 2015, 134, 966–980. [Google Scholar] [CrossRef]
- Hoa, L.K.; Vinh, P.V.; Duc, N.D.; Trung, N.T.; Son, L.T.; Thom, D.V. Bending and free vibration analyses of functionally graded material nanoplates via a novel nonlocal single variable shear deformation plate theory. Proc.-Inst. Mech. Eng. J. Mech. Eng. Sci. 2020, 235, 3641–3653. [Google Scholar] [CrossRef]

| Method | ||||||
|---|---|---|---|---|---|---|
| 0 | 0 | Sobhy [58] | 2.9603 | 19.9550 | 2.4618 | 10.7450 |
| Hoa et al. [59] | 2.9607 | 19.9433 | 2.3873 | 10.7387 | ||
| Present | 2.9606 | 19.9432 | 2.3857 | 10.7387 | ||
| 2 | Sobhy [58] | 5.2977 | 35.7108 | 4.4056 | 19.2289 | |
| Hoa et al. [59] | 5.2983 | 35.6900 | 4.2723 | 19.2177 | ||
| Present | 5.2981 | 35.6898 | 4.2694 | 19.2176 | ||
| 0.5 | 0 | Sobhy [58] | 5.4971 | 29.6544 | 2.4559 | 4.4493 |
| Hoa et al. [59] | 5.4816 | 29.3487 | 2.2354 | 4.4899 | ||
| Present | 5.4974 | 29.6351 | 2.3794 | 4.4474 | ||
| 2 | Sobhy [58] | 9.8374 | 53.0686 | 4.3950 | 7.9624 | |
| Hoa et al. [59] | 9.8096 | 52.5215 | 4.0003 | 8.0350 | ||
| Present | 9.8380 | 53.0340 | 4.2580 | 7.9589 |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 1 | 4 | 10 | |||
| 4 | 0 | Hoa et al. [59] | 3.7905 | 5.6097 | 7.1689 | 11.0892 | 13.5096 |
| Present | 3.7864 | 5.6546 | 7.2842 | 11.5987 | 13.9086 | ||
| 0.5 | Hoa et al. [59] | 3.9775 | 5.8866 | 7.5227 | 11.6364 | 14.1762 | |
| Present | 3.9732 | 5.9336 | 7.6437 | 12.1711 | 14.5949 | ||
| 1 | Hoa et al. [59] | 4.5387 | 6.7171 | 8.5840 | 13.2781 | 16.1762 | |
| Present | 4.5338 | 6.7708 | 8.7221 | 13.8881 | 16.6540 | ||
| 1.5 | Hoa et al. [59] | 5.4740 | 8.1012 | 10.3528 | 16.0142 | 19.5096 | |
| Present | 5.4680 | 8.1660 | 10.5194 | 16.7500 | 20.0858 | ||
| 10 | 0 | Hoa et al. [59] | 2.9607 | 4.5292 | 5.8701 | 8.7307 | 10.0194 |
| Present | 2.9606 | 4.5371 | 5.8895 | 8.8148 | 10.0870 | ||
| 0.5 | Hoa et al. [59] | 3.1068 | 4.7527 | 6.1598 | 9.1615 | 10.5139 | |
| Present | 3.1067 | 4.7610 | 6.1802 | 9.2498 | 10.5848 | ||
| 1 | Hoa et al. [59] | 3.5451 | 5.4233 | 7.0289 | 10.4540 | 11.9972 | |
| Present | 3.5450 | 5.4327 | 7.0521 | 10.5547 | 12.0781 | ||
| 1.5 | Hoa et al. [59] | 4.2756 | 6.5408 | 8.4773 | 12.6082 | 14.4694 | |
| Present | 4.2755 | 6.5522 | 8.5053 | 12.7297 | 14.5670 | ||
| 100 | 0 | Hoa et al. [59] | 2.8042 | 4.3255 | 5.6252 | 8.2859 | 9.3613 |
| Present | 2.8042 | 4.3255 | 5.6254 | 8.2868 | 9.3620 | ||
| 0.5 | Hoa et al. [59] | 2.9426 | 4.5389 | 5.9028 | 8.6948 | 9.8232 | |
| Present | 2.9426 | 4.5390 | 5.9030 | 8.6957 | 9.8239 | ||
| 1 | Hoa et al. [59] | 3.3577 | 5.1793 | 6.7356 | 9.9215 | 11.2091 | |
| Present | 3.3577 | 5.1794 | 6.7358 | 9.9225 | 11.2099 | ||
| 1.5 | Hoa et al. [59] | 4.0496 | 6.2466 | 8.1236 | 11.9660 | 13.5189 | |
| Present | 4.0496 | 6.2467 | 8.123939 | 11.9671 | 13.5199 | ||
| Perfect | Even | Uneven | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0.7573 | 1.1081 | 1.6539 | 0.8400 | 0.9098 |
| 1 | 0.6325 | 0.9254 | 1.3812 | 0.7015 | 0.7599 | |
| 2 | 0.5429 | 0.7944 | 1.1858 | 0.6023 | 0.6523 | |
| 4 | 0.4232 | 0.6192 | 0.9242 | 0.4694 | 0.5084 | |
| 1 | 0 | 0.9068 | 1.3268 | 1.9804 | 1.0058 | 1.0894 |
| 1 | 0.7573 | 1.1081 | 1.6539 | 0.8400 | 0.9098 | |
| 2 | 0.6501 | 0.9512 | 1.4198 | 0.7211 | 0.7811 | |
| 4 | 0.5067 | 0.7414 | 1.1066 | 0.5621 | 0.6088 | |
| 2 | 0 | 1.0563 | 1.5455 | 2.3068 | 1.1717 | 1.2690 |
| 1 | 0.8821 | 1.2907 | 1.9265 | 0.9785 | 1.0598 | |
| 2 | 0.7572 | 1.1081 | 1.6539 | 0.8400 | 0.9098 | |
| 4 | 0.5902 | 0.8636 | 1.2890 | 0.6547 | 0.7091 | |
| 4 | 0 | 1.3552 | 1.9830 | 2.9598 | 1.5033 | 1.6282 |
| 1 | 1.1318 | 1.6561 | 2.4718 | 1.2555 | 1.3598 | |
| 2 | 0.9716 | 1.4217 | 2.1220 | 1.0778 | 1.1674 | |
| 4 | 0.7573 | 1.1081 | 1.6539 | 0.8400 | 0.9098 | |
| Perfect | Even | Uneven | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 3.6067 | 4.0854 | 4.8992 | 3.8081 | 3.9583 |
| 1 | 3.0121 | 3.4119 | 4.0915 | 3.1803 | 3.3058 | |
| 2 | 2.5858 | 2.9290 | 3.5125 | 2.7302 | 2.8379 | |
| 4 | 2.0154 | 2.2829 | 2.7376 | 2.1279 | 2.2119 | |
| 1 | 0 | 4.3186 | 4.8918 | 5.8662 | 4.5597 | 4.7396 |
| 1 | 3.6067 | 4.0854 | 4.8992 | 3.8081 | 3.9583 | |
| 2 | 3.0963 | 3.5072 | 4.2058 | 3.2691 | 3.3981 | |
| 4 | 2.4132 | 2.7335 | 3.2780 | 2.5480 | 2.6485 | |
| 2 | 0 | 5.0306 | 5.6982 | 6.8333 | 5.3114 | 5.5210 |
| 1 | 4.2013 | 4.7588 | 5.7068 | 4.4358 | 4.6108 | |
| 2 | 3.6067 | 4.0854 | 4.8992 | 3.8081 | 3.9583 | |
| 4 | 2.8110 | 3.1841 | 3.8184 | 2.9680 | 3.0851 | |
| 4 | 0 | 6.4544 | 7.3110 | 8.7674 | 6.8148 | 7.0836 |
| 1 | 5.3904 | 6.1058 | 7.3221 | 5.6913 | 5.9159 | |
| 2 | 4.6275 | 5.2417 | 6.2858 | 4.8859 | 5.0787 | |
| 4 | 3.6067 | 4.0854 | 4.8992 | 3.8081 | 3.9583 | |
| Perfect | Even | Uneven | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 2.1857 | 2.1271 | 2.0595 | 1.9621 | 1.8000 |
| 1 | 1.8254 | 1.7765 | 1.7200 | 1.6386 | 1.5033 | |
| 2 | 1.5670 | 1.5251 | 1.4766 | 1.4067 | 1.2905 | |
| 4 | 1.2213 | 1.1886 | 1.1508 | 1.0964 | 1.0058 | |
| 1 | 0 | 2.6171 | 2.5470 | 2.4660 | 2.3494 | 2.1553 |
| 1 | 2.1857 | 2.1271 | 2.0595 | 1.9621 | 1.8000 | |
| 2 | 1.8763 | 1.8261 | 1.7680 | 1.6844 | 1.5453 | |
| 4 | 1.4624 | 1.4233 | 1.3780 | 1.3128 | 1.2044 | |
| 2 | 0 | 3.0485 | 2.9669 | 2.8726 | 2.7367 | 2.5106 |
| 1 | 2.5460 | 2.4778 | 2.3990 | 2.2855 | 2.0967 | |
| 2 | 2.1857 | 2.1271 | 2.0595 | 1.9621 | 1.8000 | |
| 4 | 1.7035 | 1.6579 | 1.6052 | 1.5292 | 1.4029 | |
| 4 | 0 | 3.9114 | 3.8067 | 3.6856 | 3.5113 | 3.2212 |
| 1 | 3.2666 | 3.1791 | 3.0780 | 2.9324 | 2.6902 | |
| 2 | 2.8043 | 2.7292 | 2.6424 | 2.5174 | 2.3094 | |
| 4 | 2.1857 | 2.1271 | 2.0595 | 1.9621 | 1.8000 | |
| Perfect | Even | Uneven | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 5.44216 | 5.10538 | 4.1978 | 5.4135 | 5.3822 |
| 1 | 4.5450 | 4.2637 | 3.5058 | 4.5211 | 4.4949 | |
| 2 | 3.9018 | 3.6603 | 3.0096 | 3.8812 | 3.8588 | |
| 4 | 3.0410 | 2.8529 | 2.3457 | 3.0250 | 3.0075 | |
| 1 | 0 | 6.5164 | 6.1131 | 5.0264 | 6.4821 | 6.4446 |
| 1 | 5.4421 | 5.1054 | 4.1978 | 5.4135 | 5.3822 | |
| 2 | 4.6720 | 4.3829 | 3.6037 | 4.6474 | 4.6205 | |
| 4 | 3.6413 | 3.4160 | 2.8087 | 3.6222 | 3.6018 | |
| 2 | 0 | 7.5906 | 7.1209 | 5.8550 | 7.5507 | 7.5070 |
| 1 | 6.3393 | 5.9470 | 4.8898 | 6.3059 | 6.2694 | |
| 2 | 5.4422 | 5.1054 | 4.1978 | 5.4135 | 5.3822 | |
| 4 | 4.2416 | 3.9791 | 3.2717 | 4.2193 | 4.1948 | |
| 4 | 0 | 9.7391 | 9.1364 | 7.5122 | 9.6878 | 9.6317 |
| 1 | 8.1336 | 7.6303 | 6.2738 | 8.0908 | 8.0439 | |
| 2 | 6.9825 | 6.5504 | 5.3859 | 6.9458 | 6.9055 | |
| 4 | 5.4422 | 5.1054 | 4.1978 | 5.4135 | 5.3822 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghanmi, R.A. Nonlocal Strain Gradient Theory for the Bending of Functionally Graded Porous Nanoplates. Materials 2022, 15, 8601. https://doi.org/10.3390/ma15238601
Alghanmi RA. Nonlocal Strain Gradient Theory for the Bending of Functionally Graded Porous Nanoplates. Materials. 2022; 15(23):8601. https://doi.org/10.3390/ma15238601
Chicago/Turabian StyleAlghanmi, Rabab A. 2022. "Nonlocal Strain Gradient Theory for the Bending of Functionally Graded Porous Nanoplates" Materials 15, no. 23: 8601. https://doi.org/10.3390/ma15238601
APA StyleAlghanmi, R. A. (2022). Nonlocal Strain Gradient Theory for the Bending of Functionally Graded Porous Nanoplates. Materials, 15(23), 8601. https://doi.org/10.3390/ma15238601






