Improvement of Mixed-Mode I/II Fracture Toughness Modeling Prediction Performance by Using a Multi-Fidelity Surrogate Model Based on Fracture Criteria
Abstract
:1. Introduction
2. Mixed-Mode I/II Fracture Toughness
3. Mixed-Mode I/II Fracture Toughness Prediction
3.1. Mixed-Mode I/II Fracture Criteria
3.1.1. Generalized Maximum Tangential Stress Criteria (GMTS)
3.1.2. Average Strain Energy Density Criteria (ASED)
3.1.3. Generalized Maximum Energy Release Rate Criteria (GMERR)
3.2. Artificial Intelligence Method
3.2.1. Concept of Multi-Fidelity Surrogate Model
3.2.2. Data Preparation and Model Performance Evaluation
3.2.3. Brief of Kriging Model
3.2.4. Brief of Multi-Fidelity Surrogate Model
4. Results and Discussions of the Artificial Intelligence Prediction Models
5. Conclusions
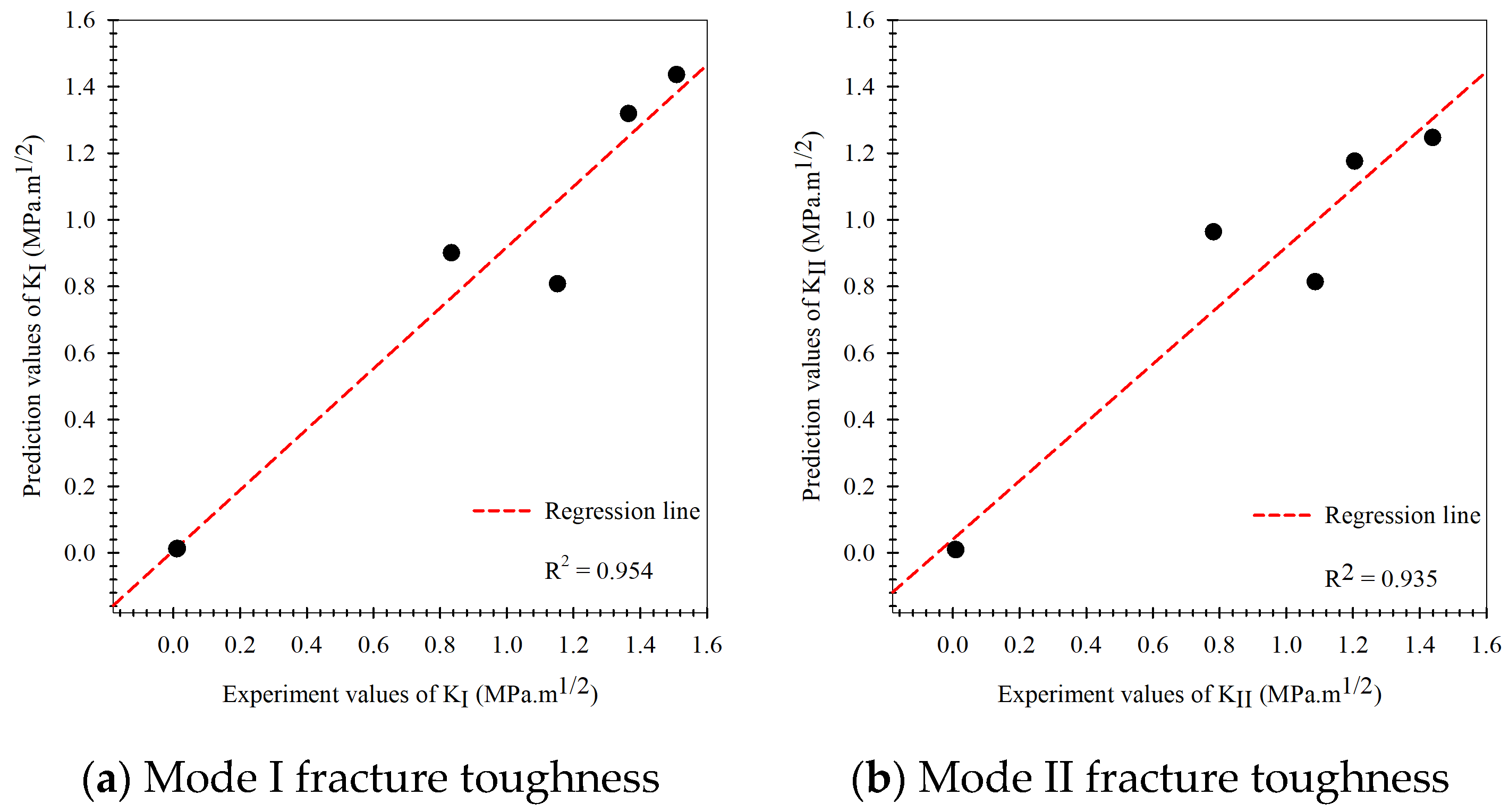
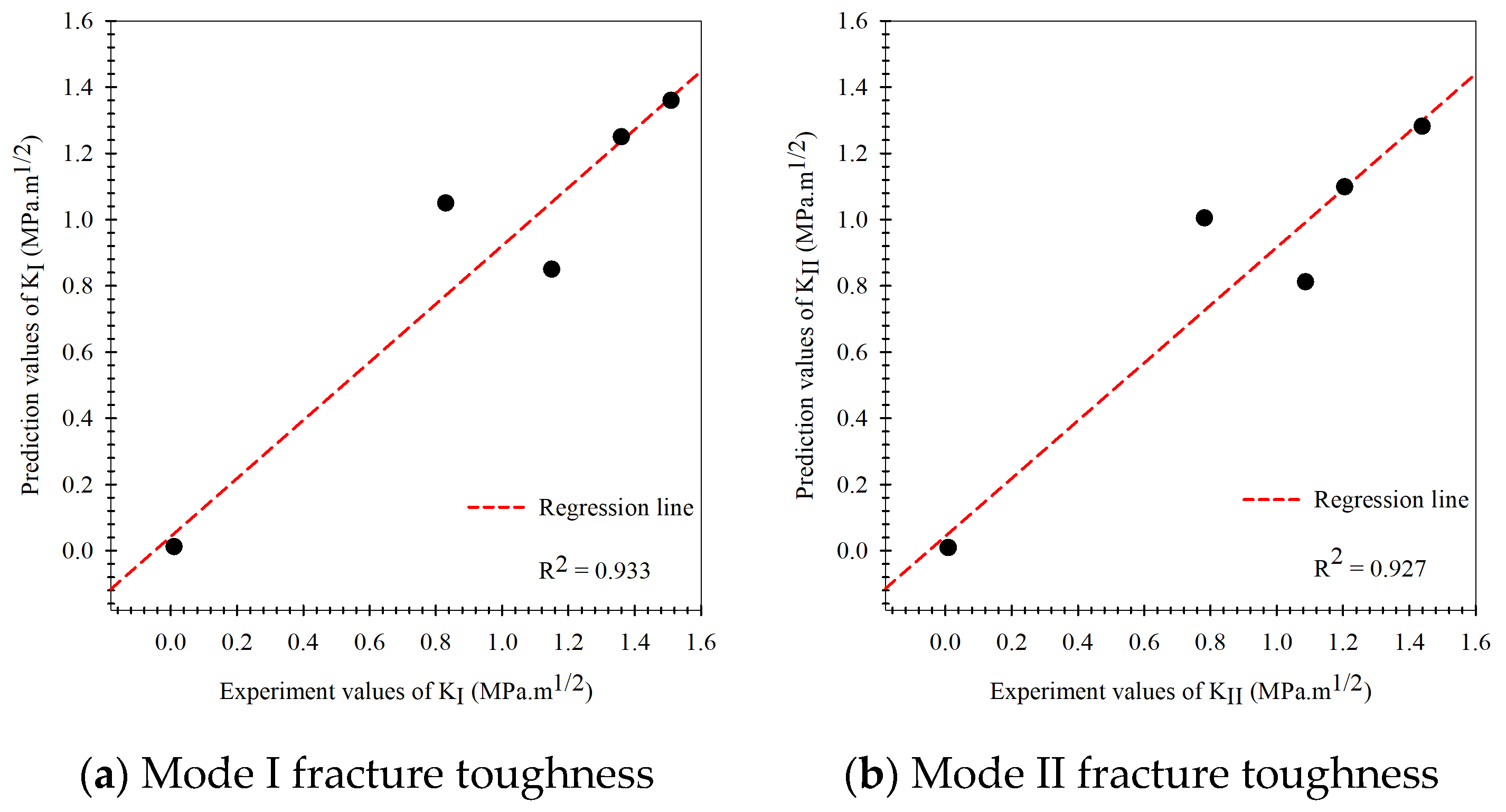
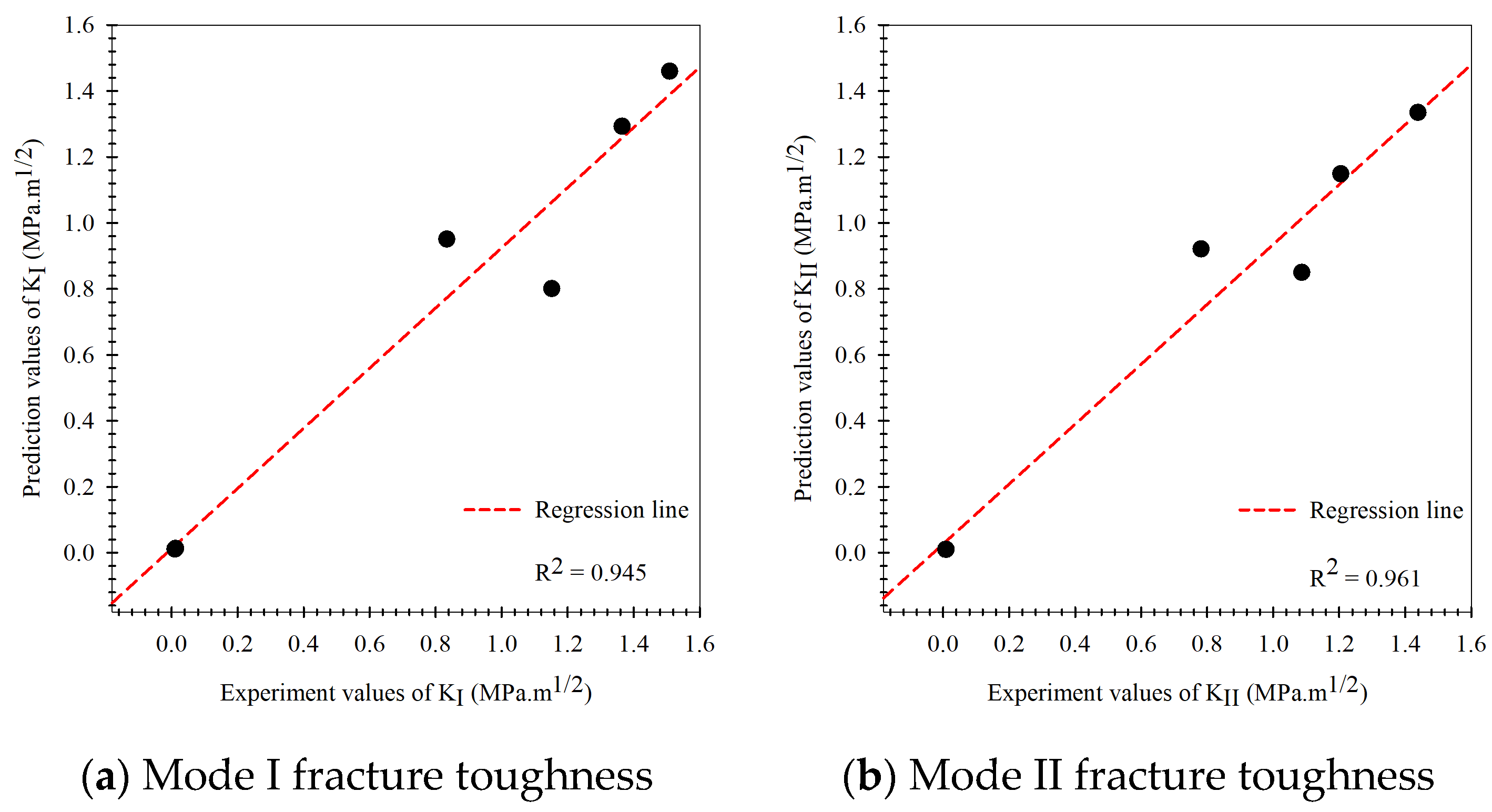
- As for the fracture criteria, the elementary fracture toughness prediction results are very close to the experimental results under pure mode loading since the fracture criteria equations rely on critical fracture toughness under pure load (, ), which was obtained from the experiment. For the predicted results at mixed-mode loading, the values were found to be rather inconsistent with the experimental results.
- As for the original Kriging model, the predicted fracture toughness was rather inaccurate compared to the experimental results in the modeling process. The model had values equal to 0.896 and 0.859, MAPE values equal to 16.70% and 14.79%, and the RMSE equal to 0.207 and 0.230 when considering modes I and II fracture toughness, respectively.
- The prediction performance of the multi-fidelity surrogate model, which is modeled on experimental data as well as the elementary prediction data obtained from the fracture criteria, was found to be higher than that of the original Kriging model or the fracture criteria. For the multi-fidelity surrogate model, the model’s performance depends on the fracture criteria used in the modeling process.
- The multi-fidelity surrogate model based on the GMTS criteria had , MAPE, and RMSE equal to 0.954, 12.41%, 0.147, and 0.935, 12.54%, 0.156 following the mode I and II loading while model based on the ASED had R2, MAPE, and RMSE equal to 0.933, 15.07%, 0.170 and 0.927, 12.25%, 0.164 and the model based on the MERR had , MAPE, and RMSE equal to 0.945, 12.23%, 0.155 and 0.961, 12.28%, 0.122, respectively.
- The multi-fidelity surrogate model based on the fracture criteria will ostensibly perform better than the original Kriging model, which solely relied on experimental data in the modeling process, in case the input factors to be predicted differ from the input factors used in the modeling process.
- The multi-fidelity models’ prediction performance indicated that they are very useful in situations where testing materials are difficult to obtain or prepare for in order to gather enough data to apply artificial intelligence techniques to the problem of fracture toughness. They also assist in reducing the costs associated with data acquisition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| Experiment data | |
| Average of experiment data | |
| Prediction data | |
| ASED | Average strain energy density fracture criteria |
| Initial crack length | |
| Young’s modulus | |
| Output of high-fidelity function | |
| Output of low-fidelity function | |
| Shear modulus | |
| GMTS | Generalized maximum tangential stress fracture criteria |
| GMERR | Generalized maximum energy release rate fracture criteria |
| High order term in the stress solution | |
| ICB | Inclination crack bending specimen |
| Critical mode I stress intensity factor | |
| Critical mode II stress intensity factor | |
| , | Mode I and mode II stress intensity factor |
| , | Mode I and mode I stress intensity factor from ASED criteria |
| , | Mode I and mode I stress intensity factor from GMTS criteria |
| , | Mode I and mode I stress intensity factor from GMERR criteria |
| Mode mix parameter | |
| MAPE | Mean absolute percentage error |
| Or-K | Original Kriging model |
| Maximum load applied | |
| Coefficient of determination | |
| Radius of control volume | |
| RMSE | Root means square error |
| Distance to the crack tip in polar coordinates | |
| Critical distance | |
| Span length of three-point bending | |
| Global model | |
| T-Stress | |
| Normalized form of T-stress | |
| Specimen width | |
| , | Mode I and mode II strain energy density |
| , | Mode I and mode II critical strain energy density |
| Input data of the artificial intelligence model | |
| , | Mode I, II dimensionless stress intensity factor |
| Inclined crack angle | |
| Local model | |
| Hyperparameter of Kriging model | |
| Initial crack growth angle | |
| , | Mode I and mode II Williams’ eigenvalues |
| Poisson’s ratio | |
| Gaussian distribution | |
| Tensile strength | |
| Tangential stresses at the crack tip | |
| Shear strength | |
| (, and ) | Hyperparameter of multi-fidelity surrogate model |
References
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Aliha, M.; Berto, F.; Bahmani, A.; Gallo, P. Mixed mode I/II fracture investigation of Perspex based on the averaged strain energy density criterion. Phys. Mesomech. 2017, 20, 149–156. [Google Scholar] [CrossRef]
- Mousavi, A.; Aliha, M.; Imani, D. Effects of biocompatible Nanofillers on mixed-mode I and II fracture toughness of PMMA base dentures. J. Mech. Behav. Biomed. Mater. 2020, 103, 103566. [Google Scholar] [CrossRef] [PubMed]
- Aliha, M.; Linul, E.; Bahmani, A.; Marsavina, L. Experimental and theoretical fracture toughness investigation of PUR foams under mixed mode I+ III loading. Polym. Test. 2018, 67, 75–83. [Google Scholar] [CrossRef]
- Poapongsakorn, P.; Wiangkham, A.; Aengchuan, P.; Noraphaiphipaksa, N.; Kanchanomai, C. Time-dependent fracture of epoxy resin under mixed-mode I/III loading. Theor. Appl. Fract. Mech. 2020, 106, 102445. [Google Scholar] [CrossRef]
- Zeinedini, A.; Moradi, M.; Taghibeigi, H.; Jamali, J. On the mixed mode I/II/III translaminar fracture toughness of cotton/epoxy laminated composites. Theor. Appl. Fract. Mech. 2020, 109, 102760. [Google Scholar] [CrossRef]
- Pan, X.; Huang, J.; Gan, Z.; Hua, W.; Dong, S. Investigation on mixed-mode II-III fracture of the sandstone by using eccentric cracked disk. Theor. Appl. Fract. Mech. 2021, 115, 103077. [Google Scholar] [CrossRef]
- Liu, G.; Jia, L.; Kong, B.; Guan, K. Artificial neural network application to study quantitative relationship between silicide and fracture toughness of Nb-Si alloys. Mater. Des. 2017, 129, 210–218. [Google Scholar] [CrossRef]
- Han, X.; Xiao, Q.; Cui, K.; Hu, X.; Chen, Q.; Li, C.; Qiu, Z. Predicting the fracture behavior of concrete using artificial intelligence approaches and closed-form solution. Theor. Appl. Fract. Mech. 2021, 112, 102892. [Google Scholar] [CrossRef]
- Wiangkham, A.; Ariyarit, A.; Aengchuan, P. Prediction of the influence of loading rate and sugarcane leaves concentration on fracture toughness of sugarcane leaves and epoxy composite using artificial intelligence. Theor. Appl. Fract. Mech. 2022, 117, 103188. [Google Scholar] [CrossRef]
- Amirdehi, H.F.; Aliha, M.; Moniri, A.; Torabi, A. Using the generalized maximum tangential stress criterion to predict mode II fracture of hot mix asphalt in terms of mode I results–A statistical analysis. Constr. Build. Mater. 2019, 213, 483–491. [Google Scholar] [CrossRef]
- Torabi, A.; Kalantari, M.; Aliha, M.; Ghoreishi, S. Pure mode II fracture analysis of dissimilar Al-Al and Al-Cu friction stir welded joints using the generalized MTS criterion. Theor. Appl. Fract. Mech. 2019, 104, 102369. [Google Scholar] [CrossRef]
- Torabi, A.R.; Berto, F.; Campagnolo, A.; Akbardoost, J. Averaged strain energy density criterion to predict ductile failure of U-notched Al 6061-T6 plates under mixed mode loading. Theor. Appl. Fract. Mech. 2017, 91, 86–93. [Google Scholar] [CrossRef]
- Moghaddam, M.R.; Ayatollahi, M.; Berto, F. Mixed mode fracture analysis using generalized averaged strain energy density criterion for linear elastic materials. Int. J. Solids Struct. 2017, 120, 137–145. [Google Scholar] [CrossRef]
- Hou, C.; Jin, X.; Fan, X.; Xu, R.; Wang, Z. A generalized maximum energy release rate criterion for mixed mode fracture analysis of brittle and quasi-brittle materials. Theor. Appl. Fract. Mech. 2019, 100, 78–85. [Google Scholar] [CrossRef]
- Ariyarit, A.; Sugiura, M.; Tanabe, Y.; Kanazaki, M. Hybrid surrogate-model-based multi-fidelity efficient global optimization applied to helicopter blade design. Eng. Optim. 2018, 50, 1016–1040. [Google Scholar] [CrossRef]
- Ding, F.; Kareem, A. A multi-fidelity shape optimization via surrogate modeling for civil structures. J. Wind Eng. Ind. Aerodyn. 2018, 178, 49–56. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, F.; Ji, T.; Zhu, Z.; Zheng, Y. Multi-fidelity deep neural network surrogate model for aerodynamic shape optimization. Comput. Methods Appl. Mech. Eng. 2021, 373, 113485. [Google Scholar] [CrossRef]
- Lu, P.; Xu, Z.; Chen, Y.; Zhou, Y. Prediction method of bridge static load test results based on Kriging model. Eng. Struct. 2020, 214, 110641. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Fan, D.; Song, J.; Yang, F. Application of kernel extreme learning machine and Kriging model in prediction of heavy metals removal by biochar. Bioresour. Technol. 2021, 329, 124876. [Google Scholar] [CrossRef]
- Jiang, Z.; Huang, X.; Chang, M.; Li, C.; Ge, Y. Thermal error prediction and reliability sensitivity analysis of motorized spindle based on Kriging model. Eng. Fail. Anal. 2021, 127, 105558. [Google Scholar] [CrossRef]
- Wiangkham, A.; Ariyarit, A.; Aengchuan, P. Prediction of the mixed mode I/II fracture toughness of PMMA by an artificial intelligence approach. Theor. Appl. Fract. Mech. 2021, 112, 102910. [Google Scholar] [CrossRef]
- Najjar, S.; Moghaddam, A.M.; Sahaf, A.; Yazdani, M.R.; Delarami, A. Evaluation of the mixed mode (I/II) fracture toughness of cement emulsified asphalt mortar (CRTS-II) using mixture design of experiments. Constr. Build. Mater. 2019, 225, 812–828. [Google Scholar] [CrossRef]
- Aminzadeh, A.; Fahimifar, A.; Nejati, M. On Brazilian disk test for mixed-mode I/II fracture toughness experiments of anisotropic rocks. Theor. Appl. Fract. Mech. 2019, 102, 222–238. [Google Scholar] [CrossRef]
- Wei, M.; Dai, F. Laboratory-scale mixed-mode I/II fracture tests on columnar saline ice. Theor. Appl. Fract. Mech. 2021, 114, 102982. [Google Scholar] [CrossRef]
- Aliha, M.; Shaker, S.; Keymanesh, M. Low temperature fracture toughness study for bitumen under mixed mode I+ II loading condition. Eng. Fract. Mech. 2019, 206, 297–309. [Google Scholar] [CrossRef]
- Courtin, S.; Gardin, C.; Bezine, G.; Hamouda, H.B.H. Advantages of the J-integral approach for calculating stress intensity factors when using the commercial finite element software ABAQUS. Eng. Fract. Mech. 2005, 72, 2174–2185. [Google Scholar] [CrossRef]
- Miarka, P.; Seitl, S.; Horňáková, M.; Lehner, P.; Konečný, P.; Sucharda, O.; Bílek, V. Influence of chlorides on the fracture toughness and fracture resistance under the mixed mode I/II of high-performance concrete. Theor. Appl. Fract. Mech. 2020, 110, 102812. [Google Scholar] [CrossRef]
- Lazzarin, P.; Zambardi, R. A finite-volume-energy based approach to predict the static and fatigue behavior of components with sharp V-shaped notches. Int. J. Fract. 2001, 112, 275–298. [Google Scholar] [CrossRef]
- Foti, P.; Ayatollahi, M.R.; Berto, F. Rapid strain energy density evaluation for V-notches under mode I loading conditions. Eng. Fail. Anal. 2020, 110, 104361. [Google Scholar] [CrossRef]
- Lewis, C.D. Industrial and Business Forecasting Methods: A Practical Guide to Exponential Smoothing and Curve Fitting; Butterworth-Heinemann: Oxford, UK, 1982. [Google Scholar]
- Hamdia, K.M.; Lahmer, T.; Nguyen-Thoi, T.; Rabczuk, T. Predicting the fracture toughness of PNCs: A stochastic approach based on ANN and ANFIS. Comput. Mater. Sci. 2015, 102, 304–313. [Google Scholar] [CrossRef]
- Qiao, L.; Liu, Y.; Zhu, J. Application of generalized regression neural network optimized by fruit fly optimization algorithm for fracture toughness in a pearlitic steel. Eng. Fract. Mech. 2020, 235, 107105. [Google Scholar] [CrossRef]
- Balcıoğlu, H.E.; Seçkin, A.Ç. Comparison of machine learning methods and finite element analysis on the fracture behavior of polymer composites. Arch. Appl. Mech. 2021, 91, 223–239. [Google Scholar] [CrossRef]
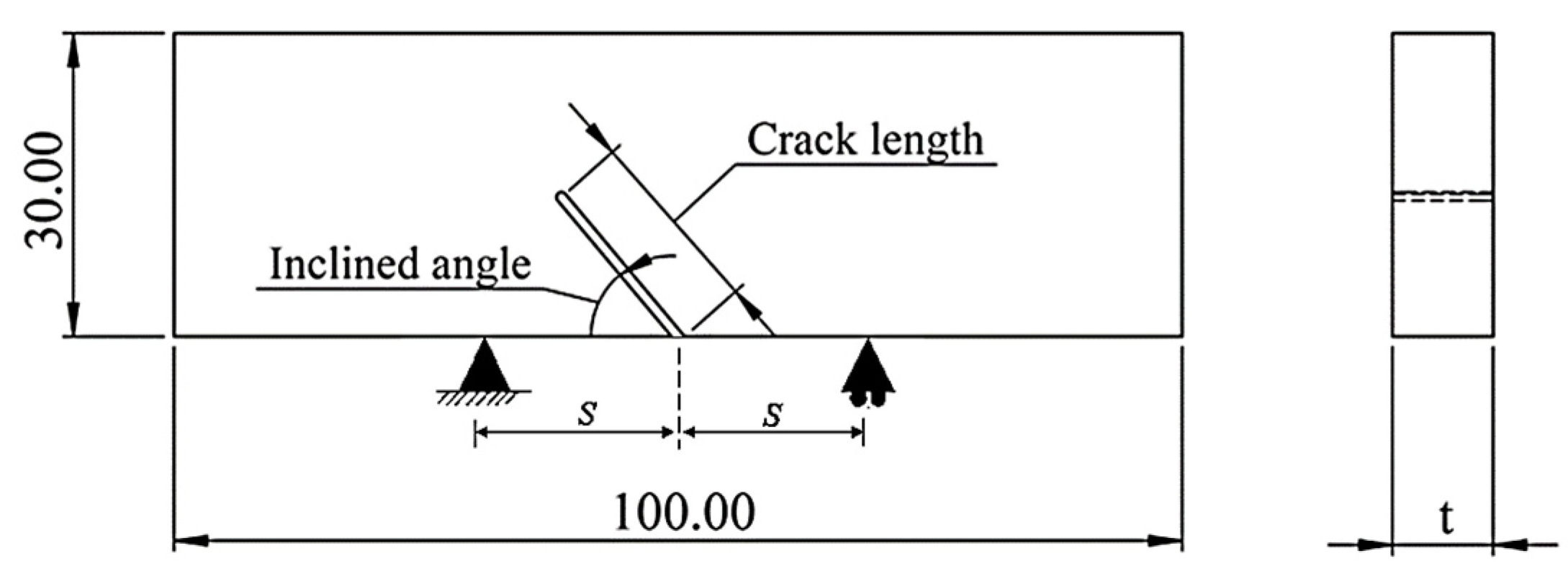
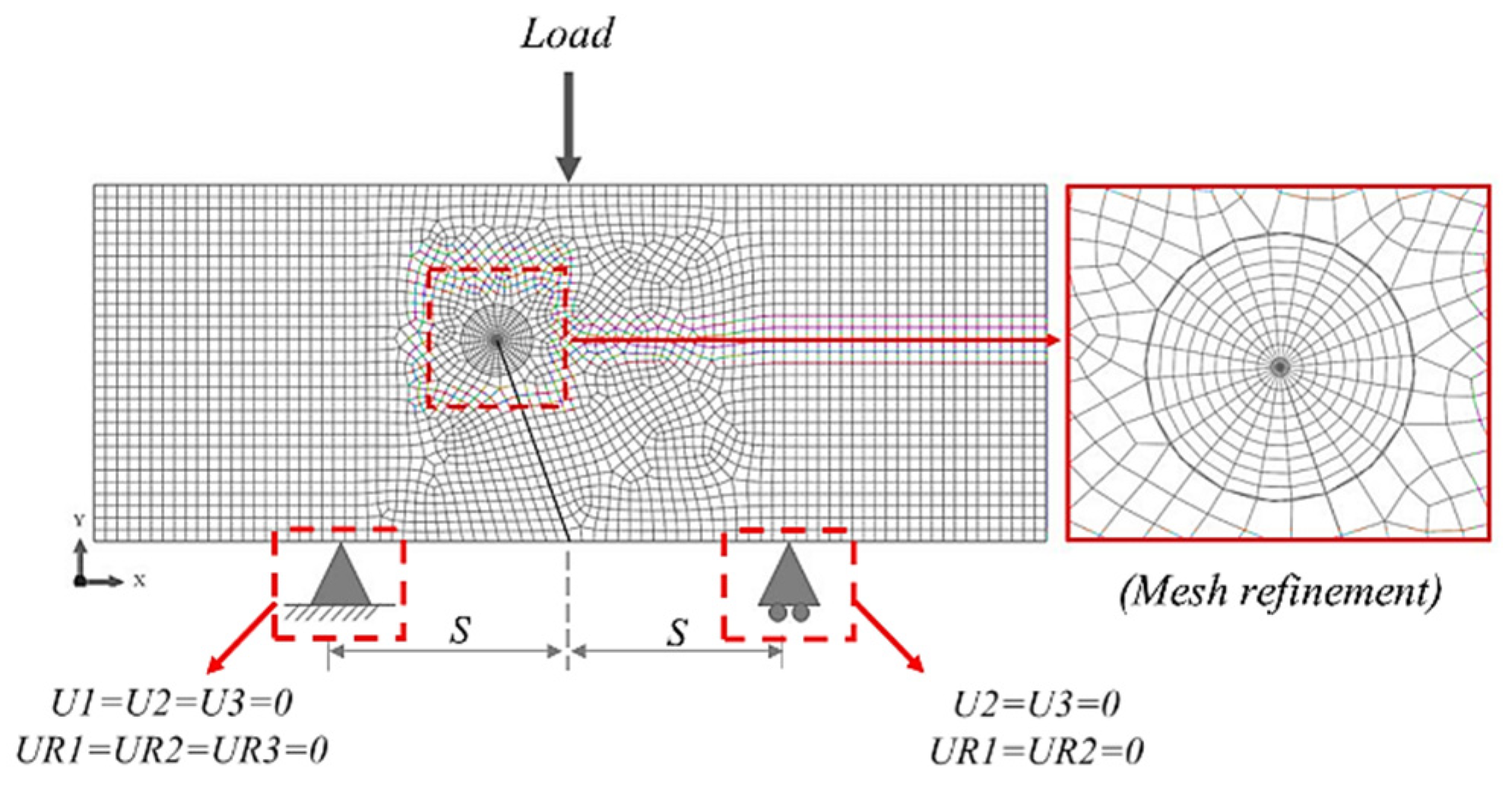



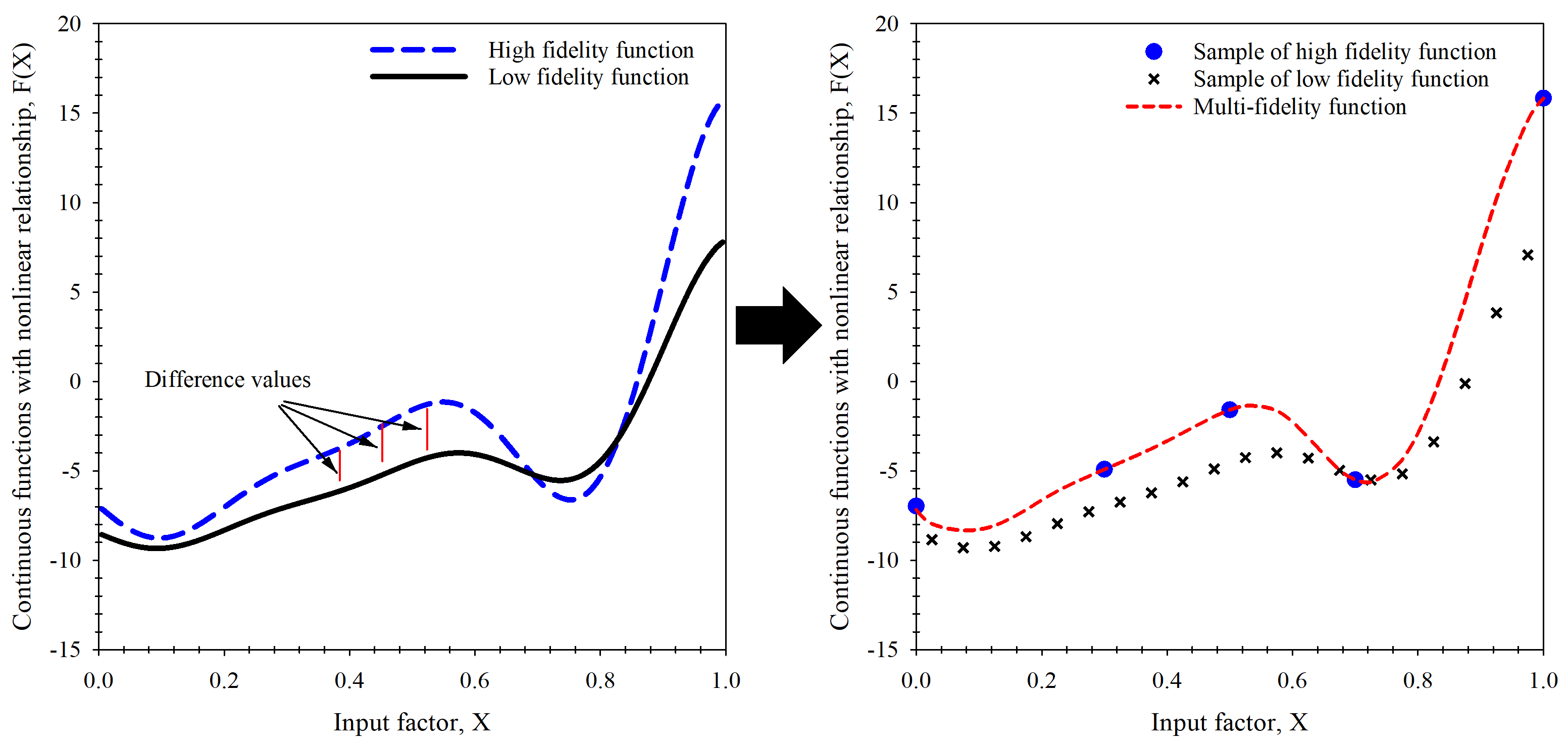

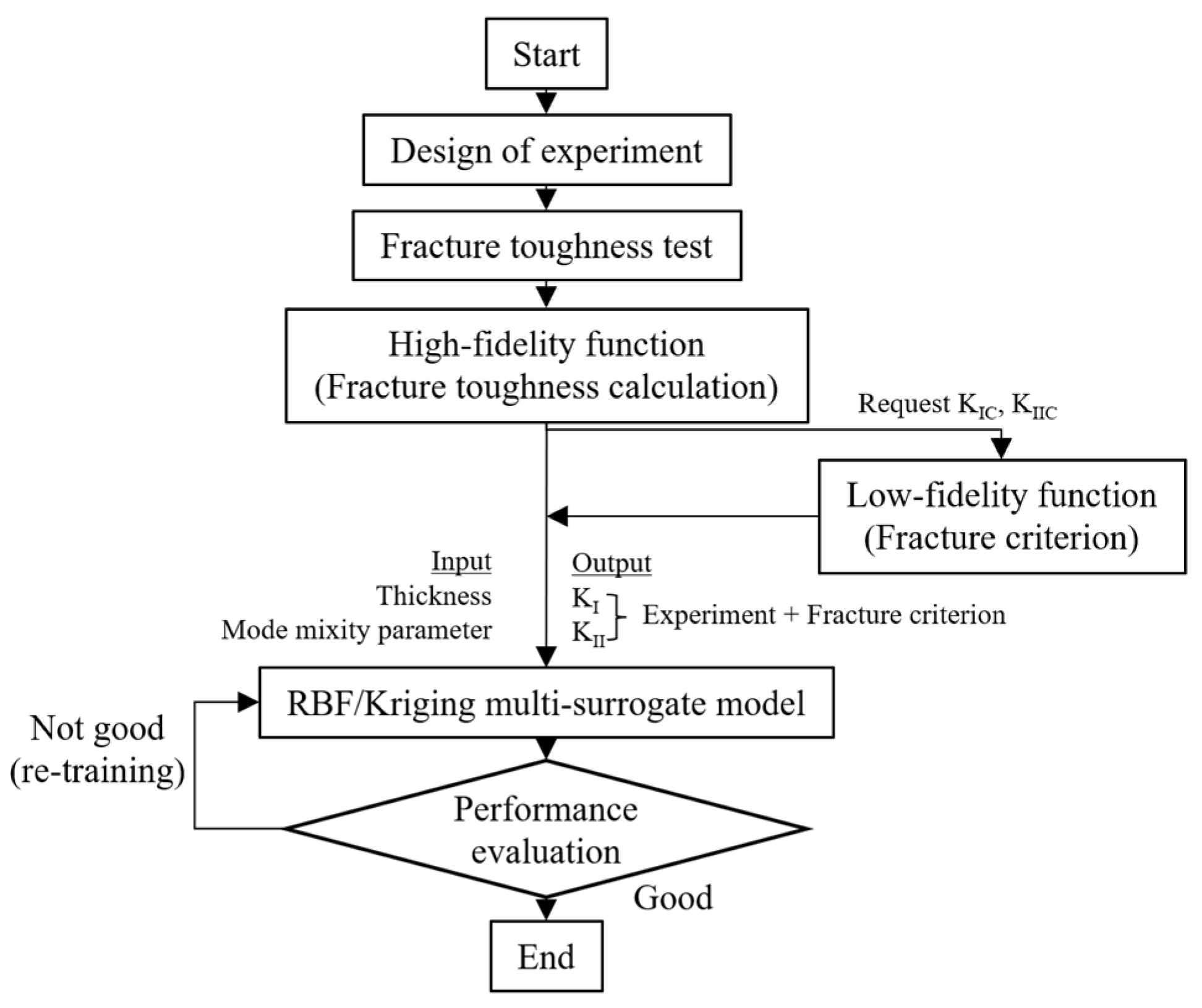

| Properties | Values |
|---|---|
| Tensile strength (MPa), | 70.00 ± 3.67 |
| Shear strength (MPa), | 43.00 ± 2.45 |
| Young’s modulus (GPa), | 2.95 ± 0.78 |
| Shear modulus (GPa), | 1.10 ± 0.14 |
| Poisson’s ratio, | 0.30 ± 0.02 |
| Thickness (mm) | Me | KI (MPa·m1/2) | KII (MPa·m1/2) | ||
|---|---|---|---|---|---|
| Average | SD | Average | SD | ||
| 5 | 1.0 | 1.509 | 0.052 | 0.009 | 0.002 |
| 5 | 0.5 | 0.854 | 0.041 | 0.825 | 0.039 |
| 5 | 0.0 | 0.012 | 0.001 | 1.439 | 0.110 |
| 10 | 1.0 | 1.365 | 0.080 | 0.008 | 0.002 |
| 10 | 0.5 | 1.152 | 0.039 | 1.107 | 0.036 |
| 10 | 0.0 | 0.010 | 0.001 | 1.205 | 0.042 |
| Factors | Experimental | Prediction Model | ||||
|---|---|---|---|---|---|---|
| Me | Thickness (mm) | KI (MPa·m1/2) | Or-K | GM-K | AS-K | ER-K |
| KI (MPa·m1/2) | KI (MPa·m1/2) | KI (MPa·m1/2) | KI (MPa·m1/2) | |||
| 0.5 | 5 | 0.887 | 0.834 | 0.845 | 0.844 | 0.844 |
| 0.3 | 7 | 0.993 | 0.851 | 0.981 | 0.989 | 0.999 |
| 0.8 | 8 | 0.321 | 0.210 | 0.361 | 0.372 | 0.355 |
| 0.5 | 9 | 1.175 | 1.151 | 1.160 | 1.181 | 1.165 |
| 0.0 | 10 | 0.010 | 0.015 | 0.007 | 0.006 | 0.007 |
| 0.5 | 10 | 1.081 | 1.151 | 1.155 | 1.151 | 1.151 |
| Factors | Experimental | Prediction Model | ||||
|---|---|---|---|---|---|---|
| Me | Thickness (mm) | KII (MPa·m1/2) | Or-K | GM-K | AS-K | ER-K |
| KII (MPa·m1/2) | KII (MPa·m1/2) | KII (MPa·m1/2) | KII (MPa·m1/2) | |||
| 0.5 | 5 | 0.854 | 0.782 | 0.785 | 0.782 | 0.784 |
| 0.3 | 7 | 0.657 | 0.789 | 0.631 | 0.682 | 0.647 |
| 0.8 | 8 | 1.253 | 0.989 | 1.204 | 1.292 | 1.206 |
| 0.5 | 9 | 1.168 | 1.087 | 1.190 | 1.201 | 1.185 |
| 0.0 | 10 | 1.190 | 1.204 | 1.208 | 1.205 | 1.209 |
| 0.5 | 10 | 1.073 | 1.087 | 1.080 | 1.079 | 1.070 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wiangkham, A.; Aengchuan, P.; Kasemsri, R.; Pichitkul, A.; Tantrairatn, S.; Ariyarit, A. Improvement of Mixed-Mode I/II Fracture Toughness Modeling Prediction Performance by Using a Multi-Fidelity Surrogate Model Based on Fracture Criteria. Materials 2022, 15, 8580. https://doi.org/10.3390/ma15238580
Wiangkham A, Aengchuan P, Kasemsri R, Pichitkul A, Tantrairatn S, Ariyarit A. Improvement of Mixed-Mode I/II Fracture Toughness Modeling Prediction Performance by Using a Multi-Fidelity Surrogate Model Based on Fracture Criteria. Materials. 2022; 15(23):8580. https://doi.org/10.3390/ma15238580
Chicago/Turabian StyleWiangkham, Attasit, Prasert Aengchuan, Rattanaporn Kasemsri, Auraluck Pichitkul, Suradet Tantrairatn, and Atthaphon Ariyarit. 2022. "Improvement of Mixed-Mode I/II Fracture Toughness Modeling Prediction Performance by Using a Multi-Fidelity Surrogate Model Based on Fracture Criteria" Materials 15, no. 23: 8580. https://doi.org/10.3390/ma15238580
APA StyleWiangkham, A., Aengchuan, P., Kasemsri, R., Pichitkul, A., Tantrairatn, S., & Ariyarit, A. (2022). Improvement of Mixed-Mode I/II Fracture Toughness Modeling Prediction Performance by Using a Multi-Fidelity Surrogate Model Based on Fracture Criteria. Materials, 15(23), 8580. https://doi.org/10.3390/ma15238580






