Thermal and Structural Characterization of a Titanium Carbide/Carbon Composite for Nuclear Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Production of the TiC samples
2.3. Dimensional and Morphological Characterization
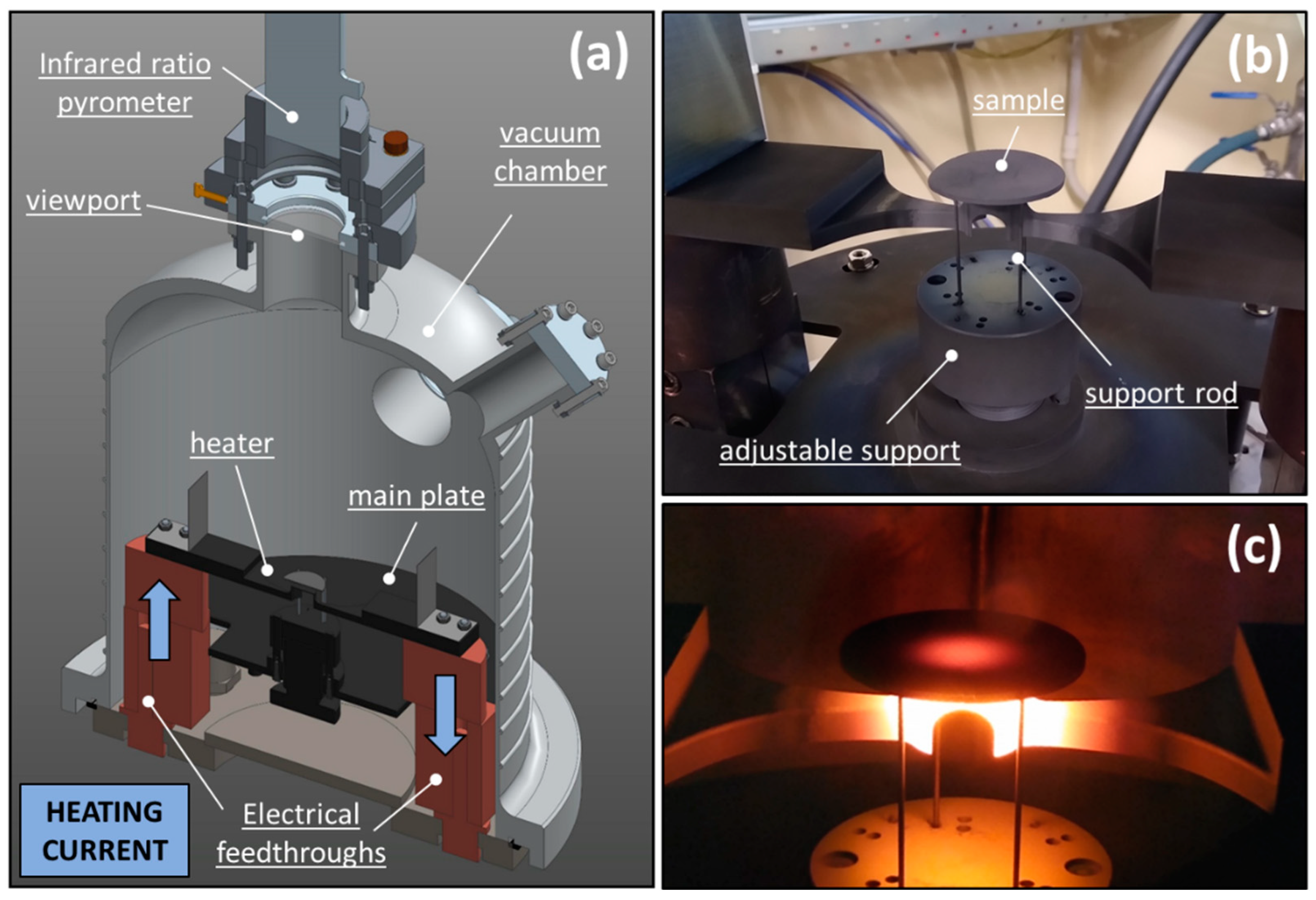
2.4. High-Temperature Thermal Characterization
2.5. Estimation of the Stress Limit through the Virtual Thermoelastic Parameter (VTP) Approach
3. Results
3.1. Production of the TiC Samples
3.2. Dimensional and Morphological Characterization
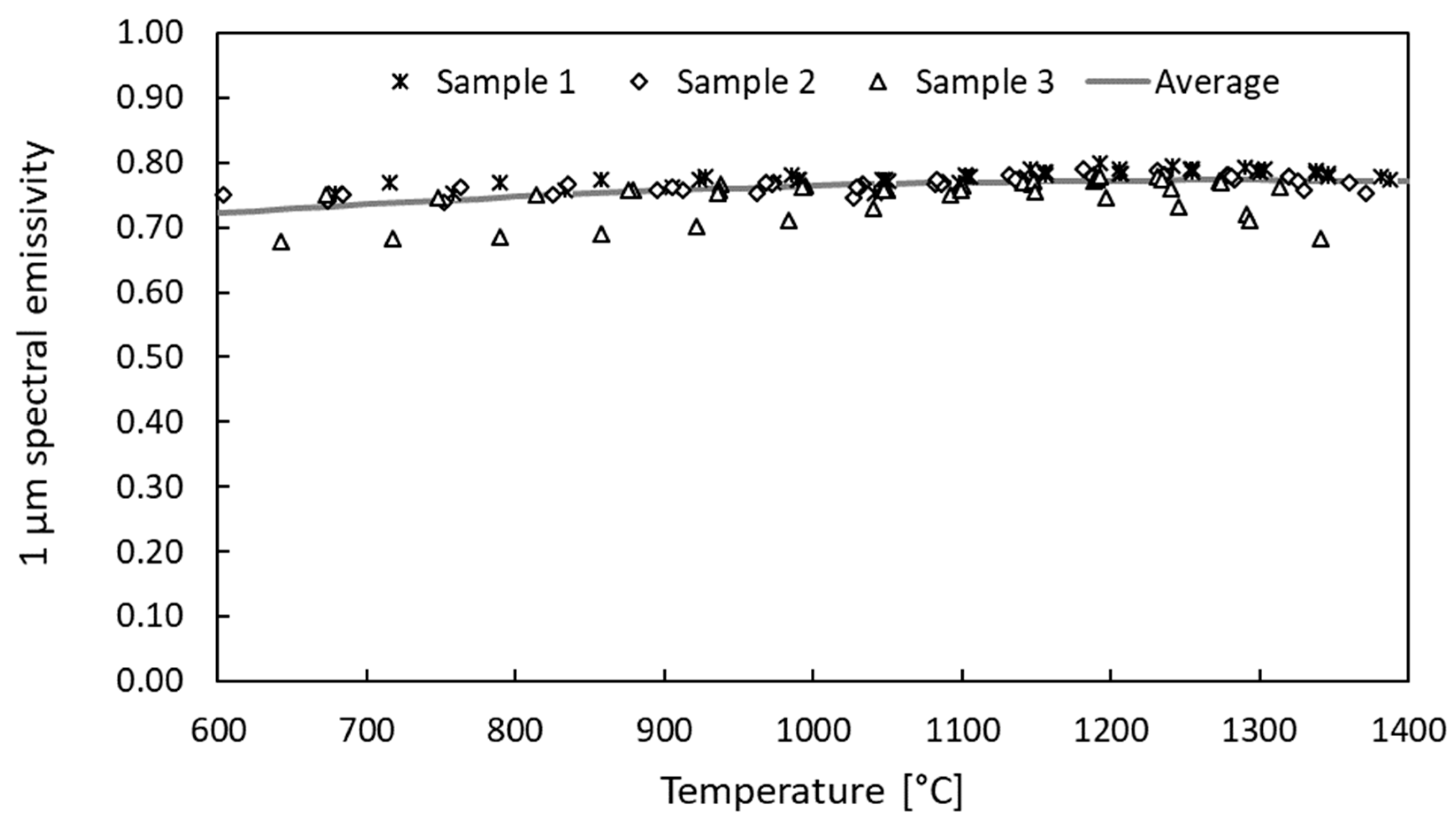
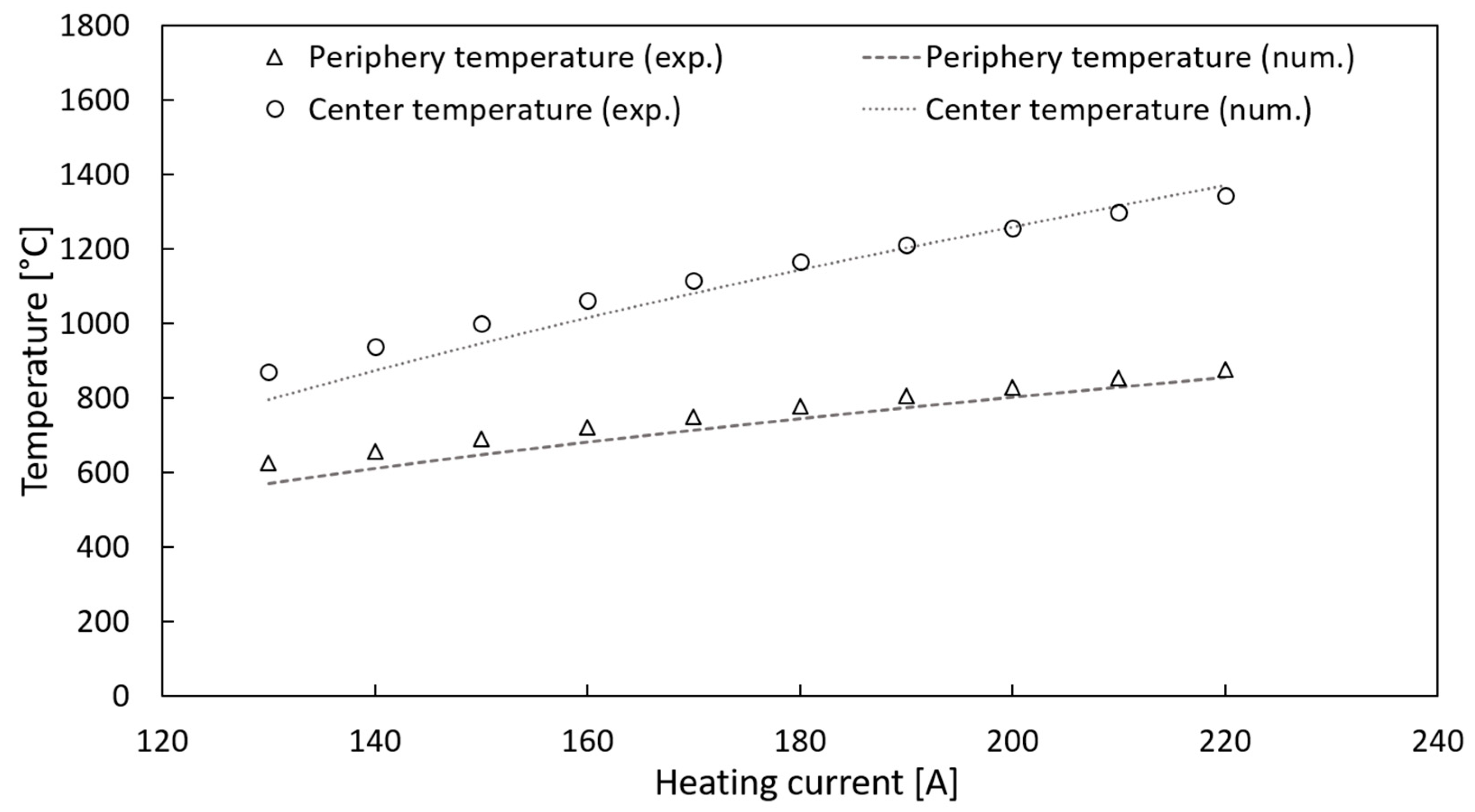
3.3. High-Temperature Thermal Characterization
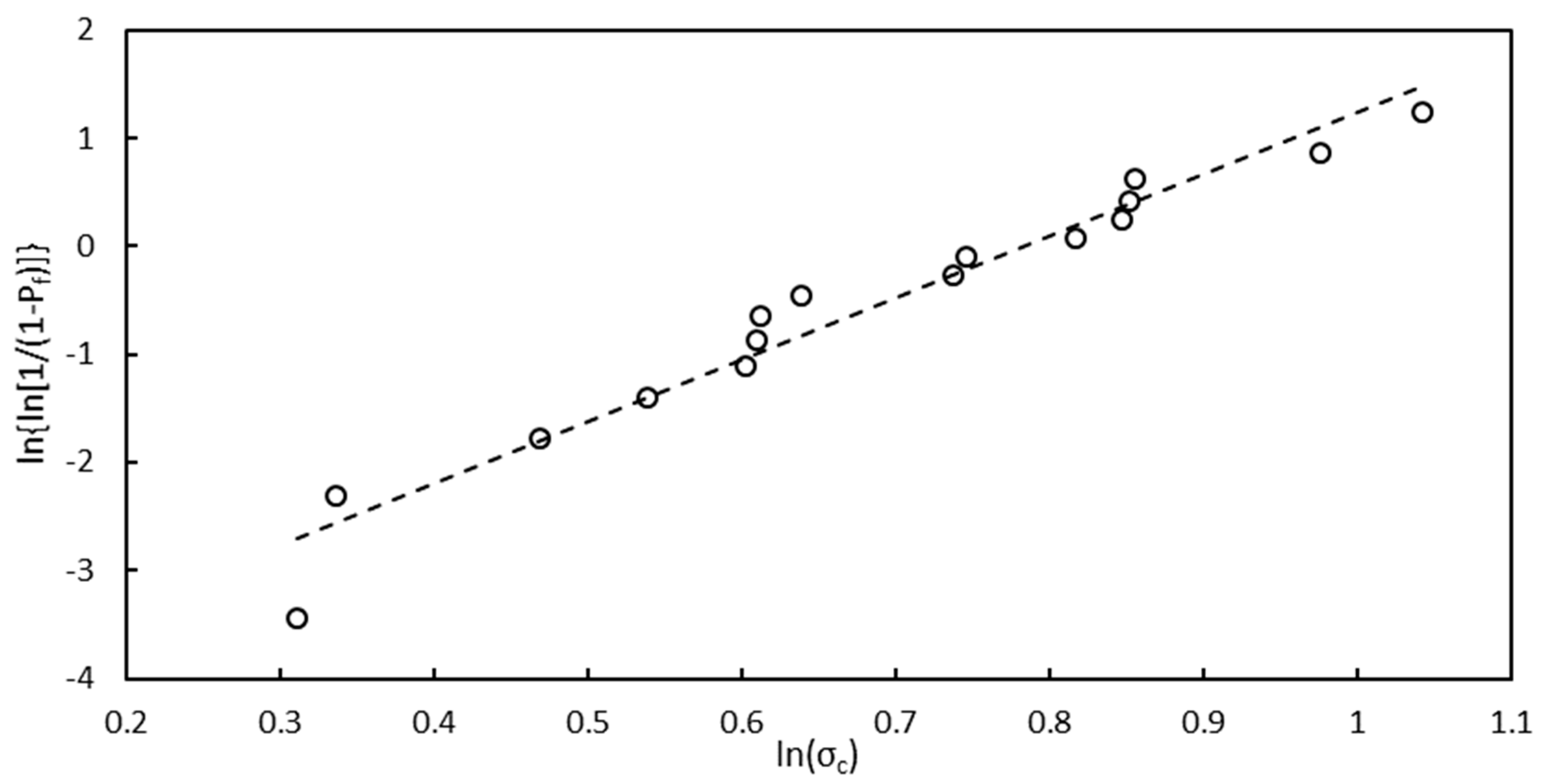
3.4. Estimation of the Stress Limit through the Virtual Thermoelastic Parameter (VTP) Approach
4. Discussion
5. Conclusions
Author Contributions
Funding

Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Catherall, R.; Andreazza, W.; Breitenfeldt, M.; Dorsival, A.; Focker, G.J.; Gharsa, T.P.; Giles, T.J.; Grenard, J.-L.; Locci, F.; Martins, P.; et al. The ISOLDE facility. J. Phys. G Nucl. Part. Phys. 2017, 44, 094002. [Google Scholar] [CrossRef]
- Bricault, P. Status report of the radioactive ion beam production at TRIUMF (invited). Rev. Sci. Instrum. 2006, 77, 03A710. [Google Scholar] [CrossRef]
- Radford, D.C.; Baktash, C.; Galindo-Uribarri, A.; Gross, C.J.; Lewis, T.A.; Mueller, P.E.; Hausladen, P.A.; Shapira, D.; Stracener, D.W.; Yu, C.-H.; et al. Physics with heavy neutron-rich RIBs at the HRIBF. In Exotic Nuclei and Atomic Masses; Springer: Berlin/Heidelberg, Germany, 2003; pp. 291–293. [Google Scholar] [CrossRef]
- Santos, F.D.O.; Himpe, P.; Lewitowicz, M.; Stefan, I.; Smirnova, N.; Achouri, N.L.; Angelique, J.C.; Angulo, C.; Axelsson, L.; Baiborodin, D.; et al. Study of 19Na at SPIRAL. Eur. Phys. J. A 2005, 24, 237–247. [Google Scholar] [CrossRef][Green Version]
- Azaiez, F.; Essabaa, S.; Ibrahim, F.; Verney, D. The ALTO Facility in Orsay. Nucl. Phys. News 2013, 23, 5–10. [Google Scholar] [CrossRef]
- Andrighetto, A.; Manzolaro, M.; Corradetti, S.; Scarpa, D.; Monetti, A.; Rossignoli, M.; Ballan, M.; Borgna, F.; D’Agostini, F.; Gramegna, F.; et al. Spes: An intense source of Neutron-Rich Radioactive Beams at Legnaro. J. Phys. Conf. Ser. 2018, 966, 012028. [Google Scholar] [CrossRef]
- Ramos, J.; Ballan, M.; Egoriti, L.; Houngbo, D.; Rothe, S.; Augusto, R.D.S.; Gottberg, A.; Dierckx, M.; Popescu, L.; Marzari, S.; et al. Design and tests for the new CERN-ISOLDE spallation source: An integrated tungsten converter surrounded by an annular UC target operated at 2000 °C. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2019, 463, 357–363. [Google Scholar] [CrossRef]
- Corradetti, S.; Andrighetto, A.; Manzolaro, M.; Scarpa, D.; Vasquez, J.; Rossignoli, M.; Monetti, A.; Calderolla, M.; Prete, G. Research and development on materials for the SPES target. EPJ Web Conf. 2014, 66, 11009. [Google Scholar] [CrossRef]
- Barbui, M.; Andrighetto, A.; Antonucci, C.; Biasetto, L.; Carturan, S.; Cervellera, F.; Cevolani, S.; Cinausero, M.; Colombo, P.; Dainelli, A.; et al. Calculations and first results obtained with a SiC prototype of the SPES direct target. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2008, 266, 4289–4293. [Google Scholar] [CrossRef]
- Carraz, L.; Haldorsen, I.; Ravn, H.; Skarestad, M.; Westgaard, L. Fast release of nuclear reaction products from refractory matrices. Nucl. Instrum. Methods 1978, 148, 217–230. [Google Scholar] [CrossRef]
- Hoff, P.; Jonsson, O.; Kugler, E.; Ravn, H. Release of nuclear reaction products from refractory compounds. Nucl. Instrum. Methods Phys. Res. 1984, 221, 313–329. [Google Scholar] [CrossRef]
- Hanemaayer, V.; Bricault, P.; Dombsky, M. Composite ceramic targets for high power proton irradiation. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2008, 266, 4334–4337. [Google Scholar] [CrossRef]
- Ashford, M.; Popescu, L.; Houngbo, D.; Dierckx, M.; Abderrahim, H.A. Exploratory study for the production of Sc beams at the ISOL facility of MYRRHA preliminary thermal investigations. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2019, 463, 244–247. [Google Scholar] [CrossRef]
- Galevsky, G.V.; Rudneva, V.V.; Garbuzova, A.K.; Valuev, D.V. Titanium Carbide: Nanotechnology, Properties, Application. IOP Conf. Ser. Mater. Sci. Eng. 2015, 91, 012017. [Google Scholar] [CrossRef]
- Tusseau-Nenez, S.; Roussière, B.; Barré-Boscher, N.; Gottberg, A.; Corradetti, S.; Andrighetto, A.; Mhamed, M.C.; Essabaa, S.; Franberg-Delahaye, H.; Grinyer, J.; et al. Characterization of uranium carbide target materials to produce neutron-rich radioactive beams. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2016, 370, 19–31. [Google Scholar] [CrossRef]
- Ramos, J.; Gottberg, A.; Augusto, R.; Mendonca, T.; Riisager, K.; Seiffert, C.; Bowen, P.; Senos, A.; Stora, T. Target nanomaterials at CERN-ISOLDE: Synthesis and release data. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2016, 376, 81–85. [Google Scholar] [CrossRef]
- Gottberg, A. Target materials for exotic ISOL beams. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2016, 376, 8–15. [Google Scholar] [CrossRef]
- Manzolaro, M.; Corradetti, S.; Ballan, M.; Salomoni, R.; Andrighetto, A.; Meneghetti, G. Thermal and Mechanical Characterization of Carbides for High Temperature Nuclear Applications. Materials 2021, 14, 2689. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.T.; Hoque, A.; Azmi, M.M.; Gafur, M.A.; Khan, R.A.; Hossain, M.K. Fe2O3 nanoparticles dispersed unsaturated polyester resin based nanocomposites: Effect of gamma radiation on mechanical properties. Radiat. Eff. Defects Solids 2019, 174, 480–493. [Google Scholar] [CrossRef]
- Rahman, M.; Hoque, A.; Gafur, M.; Khan, R.A.; Hossain, M.K. Study on the mechanical, electrical and optical properties of metal-oxide nanoparticles dispersed unsaturated polyester resin nanocomposites. Results Phys. 2019, 13, 102264. [Google Scholar] [CrossRef]
- Khan, S.; Hossain, M.K. Classification and properties of nanoparticles. In Nanoparticle-Based Polymer Composites; Woodhead Publishing: Sawston, UK, 2022; pp. 15–54. [Google Scholar] [CrossRef]
- Corradetti, S.; Carturan, S.; Andrighetto, A.; Mariotto, G.; Giarola, M.; Fabrizi, A.; Maddalena, A.; Biasetto, L. Graphene derived lanthanum carbide targets for the SPES ISOL facility. Ceram. Int. 2017, 43, 10824–10831. [Google Scholar] [CrossRef]
- Corradetti, S.; Carturan, S.; Maggioni, G.; Franchin, G.; Colombo, P.; Andrighetto, A. Nanocrystalline titanium carbide/carbon composites as irradiation targets for isotopes production. Ceram. Int. 2019, 46, 9596–9605. [Google Scholar] [CrossRef]
- Manzolaro, M.; Corradetti, S.; Andrighetto, A.; Ferrari, L. A steady-state high-temperature method for measuring thermal conductivity of refractory materials. Rev. Sci. Instrum. 2013, 84, 054902. [Google Scholar] [CrossRef] [PubMed]
- Bergman, T.L.; Bergman, T.L.; Incropera, F.P.; DeWitt, D.P.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; Wiley: Hoboken, NJ, USA, 2011; ISBN 047131272X. [Google Scholar]
- ASTM C1239-07; Standard Practice for Reporting Uniaxial Strength Data and Estimating Weibull Distribution Parameters for Advanced Ceramics. ASTM International: West Conshohocken, PA, USA. Available online: https://www.astm.org (accessed on 30 August 2022).
- Ma, Y.; Bao, C.; Song, S.; Lei, J. Effects of TiC addition on microstructures, mechanical properties and fracture behaviors of porous titanium carbide ceramics. Ceram. Int. 2018, 44, 19919–19925. [Google Scholar] [CrossRef]
- Storms, E.K.; Margrave, J.L. The Refractory; Elsevier Science: Amsterdam, The Netherlands, 2016; ISBN 9781483271774. [Google Scholar]
- Pierson, H.O. Handbook of Refractory Carbides & Nitrides: Properties, Characteristics, Processing and Application; Elsevier Science: Amsterdam, The Netherlands, 1996; ISBN 9780815517702. [Google Scholar]
- Zanini, A.; Corradetti, S.; Carturan, S.M.; Colombo, P.; Andrighetto, A.; Franchin, G. Sucrose-based sol-gel synthesis of microporous titanium carbide as target material for the production of radioisotopes. Microporous Mesoporous Mater. 2022, 337, 111917. [Google Scholar] [CrossRef]
- Corradetti, S.; Carturan, S.; Biasetto, L.; Andrighetto, A.; Colombo, P. Boron carbide as a target for the SPES project. J. Nucl. Mater. 2013, 432, 212–221. [Google Scholar] [CrossRef]
- Monetti, A.; Andrighetto, A.; Petrovich, C.; Manzolaro, M.; Corradetti, S.; Scarpa, D.; Rossetto, F.; Dominguez, F.M.; Vasquez, J.; Rossignoli, M.; et al. The RIB production target for the SPES project. Eur. Phys. J. A 2015, 51, 128. [Google Scholar] [CrossRef]
- Ramos, J.; Stora, T.; Senos, A.; Bowen, P. Thermal stability of nanometric TiC-carbon composites: Effects of carbon allotropes and Zr milling impurities. J. Eur. Ceram. Soc. 2018, 38, 4882–4891. [Google Scholar] [CrossRef]
- Corradetti, S.; Manzolaro, M.; Andrighetto, A.; Zanonato, P.; Tusseau-Nenez, S. Thermal conductivity and emissivity measurements of uranium carbides. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2015, 360, 46–53. [Google Scholar] [CrossRef]
- Corradetti, S.; Carturan, S.M.; Ballan, M.; Eloirdi, R.; Celdran, P.A.; Walter, O.; Staicu, D.; Blanco, O.D.; Andrighetto, A.; Biasetto, L. Effect of graphite and graphene oxide on thorium carbide microstructural and thermal properties. Sci. Rep. 2021, 11, 9058. [Google Scholar] [CrossRef]
- Silvestroni, L.; Corradetti, S.; Manzolaro, M.; Ballan, M.; Cesarotto, D.; Sciti, D.; Zoli, L. Novel SiC/C composite targets for the production of radioisotopes for nuclear applications. J. Eur. Ceram. Soc. 2022, 42, 6750–6756. [Google Scholar] [CrossRef]



| Young’s Modulus (E*) | Poisson’s Ratio (ν*) | Coefficient of Thermal Expansion (α*) |
|---|---|---|
| 3220 (MPa) [27] | 0.191 [28] | 7.4∙10−6 (1/°C) [29] |
| Before Thermal Treatment | After Thermal Treatment | |
|---|---|---|
| Diameter (mm) | 40.5 ± 0.2 | 36.6 ± 0.7 |
| Thickness (mm) | 1.56 ± 0.05 | 1.57 ± 0.06 |
| Average Mass before Thermal Treatment (g) | Average Mass after Thermal Treatment (g) | Average Mass Loss | Average Porosity |
|---|---|---|---|
| 3.97 ± 0.07 | 2.34 ± 0.12 | 41 ± 3% | 58 ± 3% |
| Sample Number | Sample Thickness (mm) | Sample Diameter (mm) | Heater-Sample Distance (mm) | Fracture Current Intensity (Ifract) (A) | Center Temperature at the Fracture (°C) |
|---|---|---|---|---|---|
| 1 | 1.53 | 35.95 | 3.11 | 165 | 752 |
| 2 | 1.51 | 36.06 | 3.11 | 150 | 892 |
| 3 | 1.58 | 35.95 | 3.11 | 160 | 999 |
| 4 | 1.61 | 36.34 | 4.77 | 160 | 966 |
| 5 | 1.61 | 36.08 | 3.11 | 170 | 1032 |
| 6 | 1.63 | 36.24 | 3.11 | 170 | 1040 |
| 7 | 1.62 | 35.87 | 3.11 | 190 | 1131 |
| 8 | 1.57 | 36.00 | 1.22 | 160 | 1369 |
| 9 | 1.55 | 36.07 | 1.22 | 120 | 814 |
| 10 | 1.63 | 36.17 | 1.85 | 140 | 917 |
| 11 | 1.62 | 36.24 | 1.85 | 140 | 874 |
| 12 | 1.58 | 36.07 | 3.11 | 140 | 874 |
| 13 | 1.62 | 36.02 | 3.11 | 160 | 960 |
| 14 | 1.55 | 35.81 | 1.22 | 150 | 951 |
| 15 | 1.62 | 36.17 | 1.22 | 120 | 795 |
| 16 | 1.65 | 36.12 | 1.85 | 140 | 851 |
| (/) (Lower Bound) | (/) (Average) | (/) (Upper Bound) | θ (MPa) (Lower Bound) | θ (MPa) (Average) | θ (MPa) (Upper Bound) | σ*LIMIT (MPa) | Temperature Range (°C) |
|---|---|---|---|---|---|---|---|
| 3.72 | 5.72 | 7.38 | 2.03 | 2.21 | 2.40 | 0.44 | 700 ÷ 1400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballan, M.; Corradetti, S.; Manzolaro, M.; Meneghetti, G.; Andrighetto, A. Thermal and Structural Characterization of a Titanium Carbide/Carbon Composite for Nuclear Applications. Materials 2022, 15, 8358. https://doi.org/10.3390/ma15238358
Ballan M, Corradetti S, Manzolaro M, Meneghetti G, Andrighetto A. Thermal and Structural Characterization of a Titanium Carbide/Carbon Composite for Nuclear Applications. Materials. 2022; 15(23):8358. https://doi.org/10.3390/ma15238358
Chicago/Turabian StyleBallan, Michele, Stefano Corradetti, Mattia Manzolaro, Giovanni Meneghetti, and Alberto Andrighetto. 2022. "Thermal and Structural Characterization of a Titanium Carbide/Carbon Composite for Nuclear Applications" Materials 15, no. 23: 8358. https://doi.org/10.3390/ma15238358
APA StyleBallan, M., Corradetti, S., Manzolaro, M., Meneghetti, G., & Andrighetto, A. (2022). Thermal and Structural Characterization of a Titanium Carbide/Carbon Composite for Nuclear Applications. Materials, 15(23), 8358. https://doi.org/10.3390/ma15238358







