Solubilization and Thermodynamic Analysis of Isotretinoin in Eleven Different Green Solvents at Different Temperatures
Abstract
1. Introduction
2. Materials and Methods
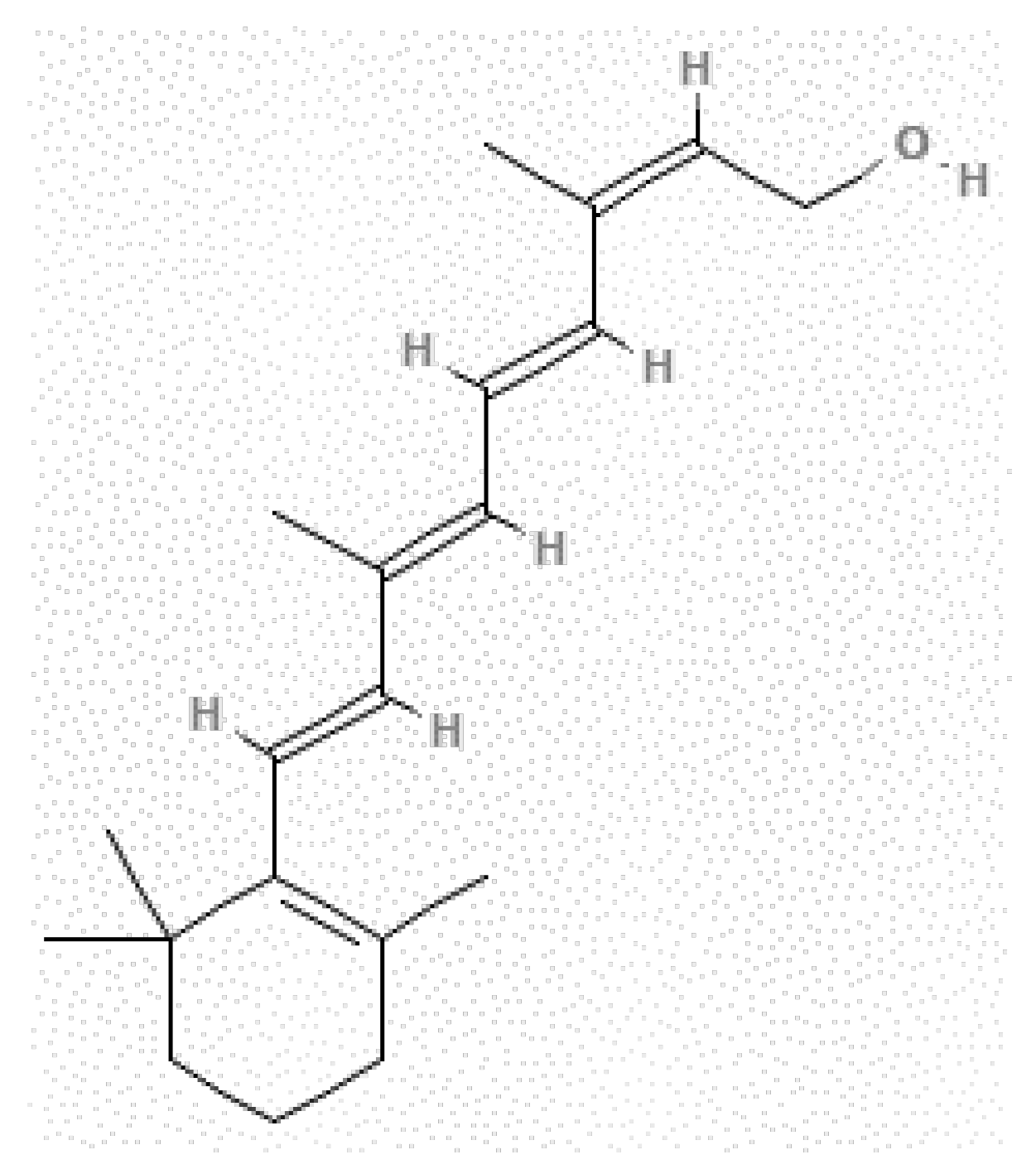
2.1. Materials
2.2. Analytical Methodology for Determination of ITN
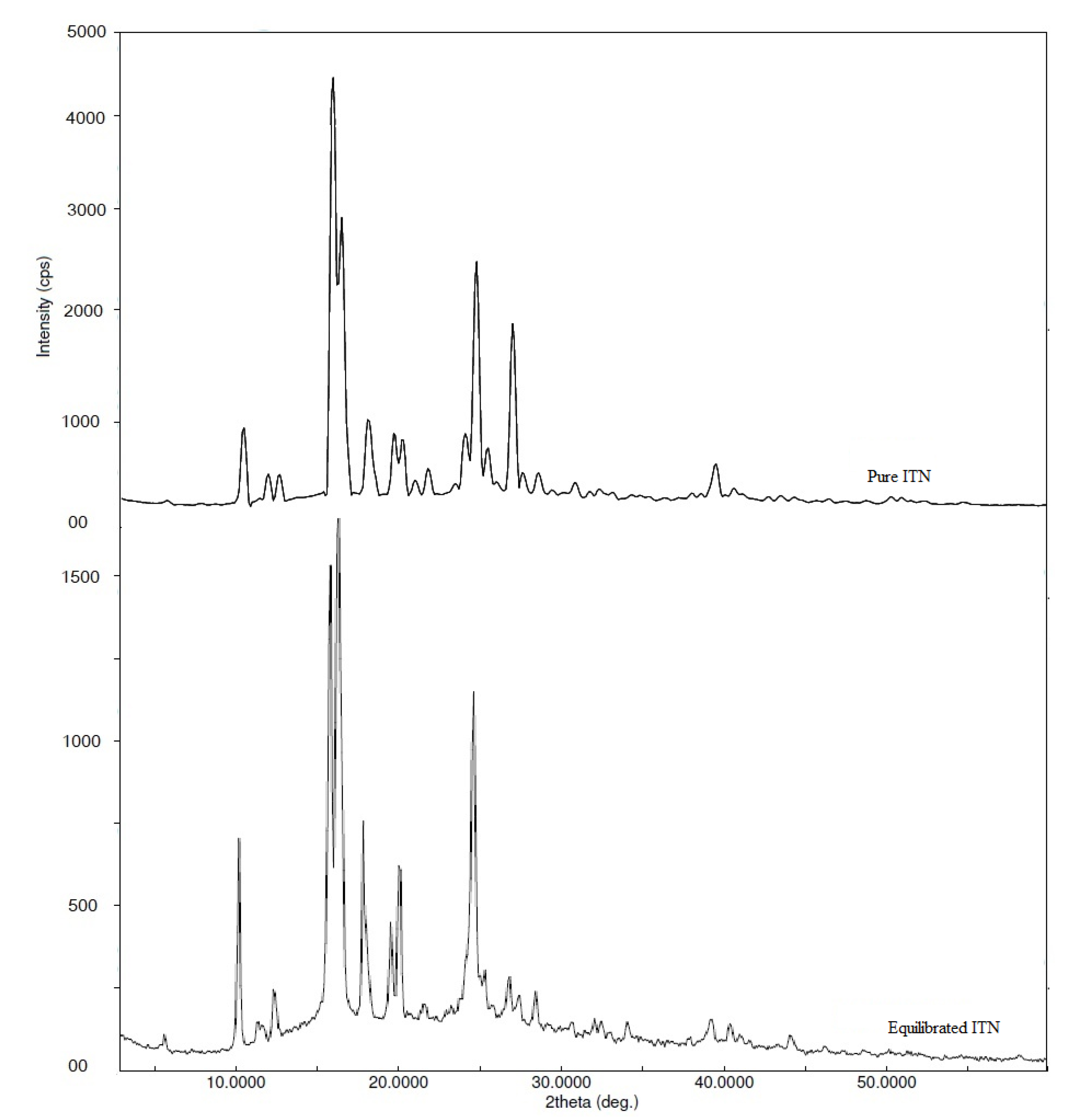
2.3. Characterization of Solid Phases of ITN
2.4. ITN Solubility Determination
2.5. Determination of Solubility Parameters
2.6. Ideal Solubility of ITN and Solute–Solvent Interactions
2.7. ITN Solubility Correlation Using Computational Models
2.8. Thermodynamic Analysis
2.9. Statistical Analysis
3. Results and Discussion
3.1. Characterization of Solid Phases of ITN
3.2. Measured Solubility of ITN
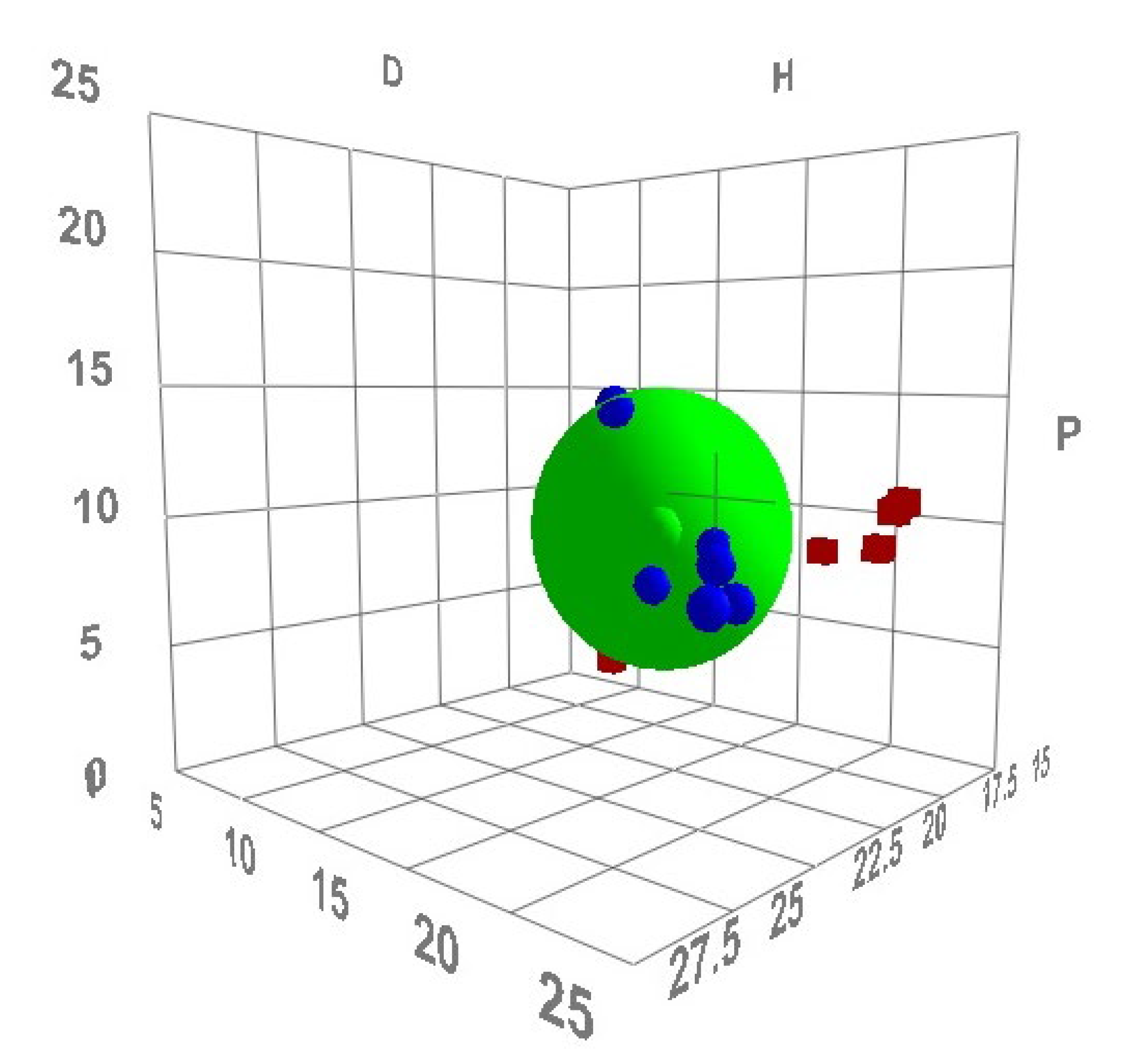
3.3. Determination of HSPs
3.4. Assessment of Solute–Solvent Interactions
3.5. ITN Solubility Correlation Using Computational Models
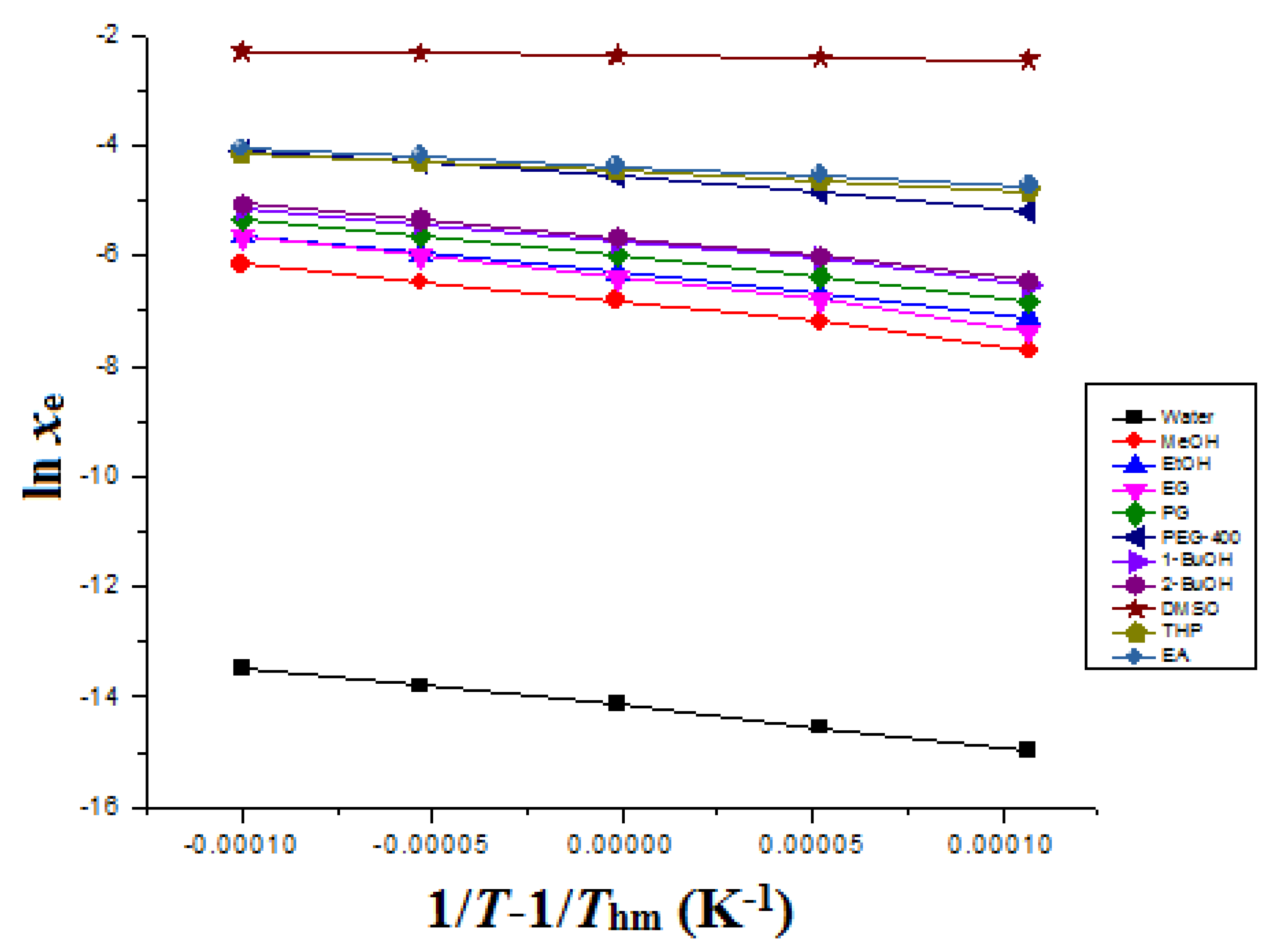
3.6. Apparent Thermodynamic Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berbenni, V.; Marini, A.; Bruni, G.; Cardini, A. Thermoanalytical and spectroscopic characterization of solid-state retinoic acid. Int. J. Pharm. 2001, 221, 123–141. [Google Scholar] [CrossRef]
- Ascenso, A.; Guedes, R.; Bernardino, R.; Diogo, H.; Carvalho, F.A.; Santos, N.C.; Silva, A.M.; Marques, H.C. Complexation and full characterization of the tretinoin and dimethyl-βeta-cyclodextrin complex. Aaps Pharmscitech 2011, 12, 553–563. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ghorab, M.M.; Babiker, M.E. Formulation and in-vitro evaluation of isotretinoin tablets. J. Chem. Pharm. Res. 2012, 4, 2817–2831. [Google Scholar]
- Muccio, D.D.; Brouillette, W.J.; Alam, M.; Vaezi, M.F.; Sani, B.P.; Venepally, P.; Reddy, L.; Li, E.; Norris, A.W.; Simpson-Herren, L.; et al. Conformationally defined 6-s-trans-retinoic acid analogs. 3. Structure–activity relationships for nuclear receptor binding, transcriptional activity, and cancer chemopreventive activity. J. Med. Chem. 1996, 39, 3625–3635. [Google Scholar] [CrossRef] [PubMed]
- Muccio, D.D.; Brouillette, W.J.; Breritman, T.R.; Taimi, M.; Emanuel, P.D.; Zhang, X.; Chen, G.; Sani, B.P.; Venepally, P.; Reddy, L.; et al. Conformationally defined retinoic acid analogues. 4. Potential new agents for acute promyelocytic and juvenile myelomonocytic leukemias. J. Med. Chem. 1998, 41, 1679–1687. [Google Scholar] [CrossRef] [PubMed]
- Levin, A.H.; Bos, M.E.; Zusi, F.C.; Nair, X.; Whiting, G.; Bouquin, P.; Tetrault, G.; Carrol, F.I. Evaluation of retinoids as therapeutic agents in dermatology. Pharm. Res. 1994, 11, 192–200. [Google Scholar]
- Anadolu, R.Y.; Sen, T.; Tarimci, N.; Birol, A.; Erdem, C. Improved efficacy and tolerability of retinoic acid in acne vulgaris: A new topical formulation with cyclodextrin complex psi. Eur. J. Acad. Dermatol. Venereol. 2004, 18, 416–421. [Google Scholar] [CrossRef]
- Loveday, S.M.; Singh, H. Recent advances in technologies for vitamin A protection in foods. Trends Food Sci. Technol. 2008, 19, 657–668. [Google Scholar] [CrossRef]
- Gollnick, H.; Zouboulis, C.C. Not all acne is acne vulgaris. Dtsch. Aerztebl. Int. 2014, 111, 301–312. [Google Scholar] [CrossRef]
- Espinosa, N.I.; Cohen, P.R. Acne vulgaris: A patient and physician’s experience. Dermatol. Ther. 2020, 10, 1–14. [Google Scholar] [CrossRef]
- Fallah, H.; Rademaker, M. Isotretenoin for acne vulgaris—An update on adverse effects and laboratory monitoring. J. Dermatol. Treat. 2022, 33, 2414–2424. [Google Scholar] [CrossRef]
- Alwhaibi, A.; Alenazi, M.; Almadi, B.; Alotaibi, A.; Alshehri, S.M.; Shakeel, F. A practical method for oral administration of pediatric oncology patient: A case study of neuroblastoma. J. Oncol. Pharm. Pract. 2022. [Google Scholar] [CrossRef]
- Tan, X.; Meltzer, N.; Lindebaum, S. Solid-state stability studies of 13-cis-retinoic acid and all-trans-retinoic acid using microcalorimetry and HPLC analysis. Pharm. Res. 1992, 9, 1203–1208. [Google Scholar] [CrossRef]
- Yap, K.L.; Liu, X.; Thenmozhiyal, J.C.; Ho, P.C. Characterization of the 13-cis-retinoic acid/cyclodextrin inclusion complexes by phase solubility, photostability, physicochemical and computational analysis. Eur. J. Pharm. Sci. 2005, 25, 49–56. [Google Scholar] [CrossRef]
- Dadmand, S.; Kamari, F.; Acree, W.E., Jr.; Jouyban, A. Solubility prediction of drugs in binary solvent mixtures at various temperatures using a minimum number of experimental data points. AAPS PharmSciTech. 2019, 20, E10. [Google Scholar] [CrossRef]
- Razaei, H.; Rahimpour, E.; Zhao, H.; Martinez, F.; Barzegar-Jalali, M.; Jouyban, A. Solubility of baclofen in some neat and mixed solvents at different temperatures. J. Mol. Liq. 2022, 347, E118352. [Google Scholar] [CrossRef]
- Shakeel, F.; Haq, N.; Alsarra, I.A. Equilibrium solubility determination, Hansen solubility parameters and solution thermodynamics of cabozantinib malate in different monosolvents of pharmaceutical importance. J. Mol. Liq. 2021, 324, E115146. [Google Scholar] [CrossRef]
- Ahad, A.; Shakeel, F.; Raish, M.; Ahmad, A.; Jardan, Y.A.B.; Al-Jenoobi, F.I.; Al-Mohizea, A.M. Thermodynamic solubility profile of temozolomide in different commonly used pharmaceutical solvents. Molecules 2022, 27, 1437. [Google Scholar] [CrossRef]
- Guimarãesa, C.A.; Mena, F.; Mena, B.; Quenca-Guillena, J.S.; Matos, J.D.R.; Mercuri, L.P.; Braz, A.B.; Rossetti, F.C.; Kedor-Hackmann, E.R.M.; Santoro, M.I.R.M. Comparative physical–chemical characterization of encapsulated lipid-based isotretinoin products assessed by particle size distribution and thermal behavior analyses. Thermochim. Acta 2010, 505, 73–78. [Google Scholar] [CrossRef]
- Patel, M.R.; Patel, R.B.; Parikh, J.R.; Patel, B.G. HPTLC method for estimation of isotretinoin in topical formulations, equilibrium solubility screening, and in vitro permeation study. J. Liq. Chromatogr. Relat. Technol. 2011, 34, 1783–1799. [Google Scholar] [CrossRef]
- Patel, M.R.; Patel, R.B.; Parikh, J.R.; Patel, B.G. Improving the isotretinoin photostability by incorporating in microemulsion matrix. ISRN Pharm. 2011, 2011, E838016. [Google Scholar] [CrossRef] [PubMed]
- Patel, M.R.; Patel, R.B.; Parikh, J.R.; Patel, B.G. Novel isotretinoin microemulsion-based gel for targeted topical therapy of acne: Formulation consideration, skin retention and skin irritation studies. Appl. Nanosci. 2016, 6, 539–553. [Google Scholar] [CrossRef]
- Chavda, H.; Patel, J.; Chavada, D.; Dave, S.; Patel, A.; Patel, C. Self-nanoemulsifying powder of isotretinoin: Preparation and characterization. J. Powder Technol. 2013, 2013, E108569. [Google Scholar] [CrossRef]
- Hosny, K.M.; Al Nahyah, K.S.; Alhakamy, N.A. Self-nanoemulsion loaded with a combination of isotretinoin, an antiacne drug, and quercetin: Preparation, optimization, and in vivo assessment. Pharmaceutics 2021, 13, E46. [Google Scholar]
- Alqarni, M.H.; Haq, N.; Alam, P.; Abdel-Kader, M.S.; Foudah, A.I.; Shakeel, F. Solubility data, Hansen solubility parameters and thermodynamic behavior of pterostilbene in some pure solvents and different (PEG-400 + water) cosolvent compositions. J. Mol. Liq. 2021, 331, E115700. [Google Scholar] [CrossRef]
- Ahad, A.; Shakeel, F.; Raish, M.; Al-Jenoobi, F.I.; Al-Mohizea, A.M. Solubility and thermodynamic analysis of antihypertensive agent nitrendipine in different pure solvents at the temperature range of 298.15 to 318.15 K. APPS PharmSciTech. 2017, 18, 2737–2743. [Google Scholar] [CrossRef]
- Higuchi, T.; Connors, K.A. Phase-solubility techniques. Adv. Anal. Chem. Instr. 1965, 4, 117–122. [Google Scholar]
- Ortiz, C.P.; Cardenas-Torres, R.E.; Martinez, F.; Delgado, D.R. Solubility of sulfamethazine in the binary mixture of acetonitrile + methanol from 278.15 to 318.15 K: Measurement, dissolution thermodynamics, preferential solvation, and correlation. Molecules 2021, 26, 7588. [Google Scholar] [CrossRef]
- Shen, J.; Liang, X.; Lei, H. Measurements, thermodynamic modeling, and a hydrogen bonding study on the solubilities of metoprolol succinate in organic solvents. Molecules 2018, 23, 2469. [Google Scholar] [CrossRef]
- Kitak, T.; Dumicic, A.; Planinsek, O.; Sibanc, R.; Srcic, S. Determination of solubility parameters of ibuprofen and ibuprofen lysinate. Molecules 2015, 20, 21549–21568. [Google Scholar] [CrossRef]
- Zhang, C.; Jouyban, A.; Zhao, H.; Farajtabar, A.; Acree, W.E., Jr. Equilibrium solubility, Hansen solubility parameter, dissolution thermodynamics, transfer property and preferential solvation of zonisamide in aqueous binary mixtures of ethanol, acetonitrile, isopropanol and N,N-dimethylformamide. J. Mol. Liq. 2021, 326, E115219. [Google Scholar] [CrossRef]
- He, H.; Wan, Y.; Sun, R.; Zhang, P.; Jiang, G.; Sha, J.; Li, Y.; Li, T.; Ren, B. Piperonylonitrile solubility in thirteen pure solvents: Correlation, Hansen solubility parameters solvent effect and thermodynamic analysis. J. Chem. Thermodyn. 2020, 150, E106191. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; te Nijenhuis, K. Properties of Polymers: Their Correlation with Chemical Structure, their Numerical Estimation and Prediction from Additive Group Contributions; Elsevier: Amsterdam The Netherlands; Tokyo, Japan, 2009; p. 189. [Google Scholar]
- Güner, A. The algorithmic calculations of solubility parameter for the determination of interactions in dextran/certain polar solvent systems. Eur. Polym. J. 2004, 40, 1587–1594. [Google Scholar] [CrossRef]
- Mohammad, M.A.; Alhalaweh, A.; Velaga, S.P. Hansen solubility parameter as a tool to predict cocrystal formation. Int. J. Pharm. 2011, 407, 63–71. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, H.; Farajtabar, A.; Zhu, P.; Jouyban, A.; Acree, W.E., Jr. Equilibrium solubility of amrinone in aqueous co-solvent solutions reconsidered: Quantitative molecular surface, inter/intra-molecular interactions and solvation thermodynamics analysis. J. Mol. Liq. 2022, 355, E118995. [Google Scholar] [CrossRef]
- Rios, M.D.D.I.; Ramos, E.H.; Canavaciolo, V.G.; Murillo, R.V.; Carrion, K.P.; de Cardenas, L.Z. Obtaining a fraction of sugarcane wax rich in policosanol by using ethanol as solvent: Results interpretation through Hansen’s solubility theory. ACS Omega 2022, 7, 27324–27333. [Google Scholar] [CrossRef]
- Benazzouz, A.; Moity, L.; Pierlot, C.; Sergent, M.; Molinier, V.; Aubry, J.-M. Selection of a greener set of solvents evenly spread in the Hansen space by space-filling design. Ind. Eng. Chem. Res. 2013, 52, 16585–16597. [Google Scholar] [CrossRef]
- Rios, M.D.D.I.; Ramos, E.H. Determination of the Hansen solubility parameters and hansen sphere radius with the aid of the solver add-in of microsoft excel. SN Appl. Sci. 2020, 2, E676. [Google Scholar] [CrossRef]
- Gharagheizi, F. New procedure to calculate the Hansen solubility parameters of polymers. J. Appl. Polym. Sci. 2007, 103, 31–36. [Google Scholar] [CrossRef]
- Greenhalgh, D.J.; Williams, A.C.; Timmins, P.; York, P. Solubility parameters as predictors of miscibility in solid dispersions. J. Pharm. Sci. 1999, 88, 1182–1190. [Google Scholar] [CrossRef]
- Tinjaca, D.A.; Martinez, F.; Almanza, O.A.; Jouyban, A.; Acree, W.E. Solubility, correlation, dissolution thermodynamics and preferential solvation of meloxicam in aqueous mixtures of 2-propanol. Pharm. Sci. 2022, 28, 130–144. [Google Scholar] [CrossRef]
- Hildebrand, J.H.; Prausnitz, J.M.; Scott, R.L. Regular and Related Solutions; Van Nostrand Reinhold: New York, NY, USA, 1970. [Google Scholar]
- Manrique, Y.J.; Pacheco, D.P.; Martínez, F. Thermodynamics of mixing and solvation of ibuprofen and naproxen in propylene glycol + water cosolvent mixtures. J. Sol. Chem. 2008, 37, 165–181. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, X.; Yu, Y.; Zhao, S.; Song, H.; Chen, A.; Shang, Z. Preparation and characterization of vanillin cross-linked chitosan microspheres of pterostilbene. Int. J. Polym. Anal. Charact. 2014, 19, 83–93. [Google Scholar] [CrossRef]
- Mohammadian, E.; Rahimpour, E.; Martinez, F.; Jouyban, A. Budesonide solubility in polyethylene glycol 400 + water at different temperatures: Experimental measurement and mathematical modelling. J. Mol. Liq. 2019, 274, 418–425. [Google Scholar] [CrossRef]
- Apelblat, A.; Manzurola, E. Solubilities of o-acetylsalicylic, 4-aminosalicylic, 3,5-dinitrosalicylic and p-toluic acid and magnesium-DL-aspartate in water from T = (278–348) K. J. Chem. Thermodyn. 1999, 31, 85–91. [Google Scholar] [CrossRef]
- Manzurola, E.; Apelblat, A. Solubilities of L-glutamic acid, 3-nitrobenzoic acid, acetylsalicylic, p-toluic acid, calcium-L-lactate, calcium gluconate, magnesium-DL-aspartate, and magnesium-L-lactate in water. J. Chem. Thermodyn. 2002, 34, 1127–1136. [Google Scholar] [CrossRef]
- Ksiazczak, A.; Moorthi, K.; Nagata, I. Solid-solid transition and solubility of even n-alkanes. Fluid Phase Equilib. 1994, 95, 15–29. [Google Scholar] [CrossRef]
- Tong, Y.; Wang, Z.; Yang, E.; Pan, B.; Jiang, J.; Dang, P.; Wei, H. Determination and correlation of solubility and solution thermodynamics of ethenzamide in different pure solvents. Fluid Phase Equilib. 2016, 427, 549–556. [Google Scholar] [CrossRef]
- Alyamani, M.; Alshehri, S.; Alam, P.; Wani, S.U.D.; Ghoneim, M.M.; Shakeel, F. Solubility and solution thermodynamics of raloxifene hydrochloride in various (DMSO + water) compositions. Alex. Eng. J. 2022, 61, 9119–9128. [Google Scholar] [CrossRef]
- Shakeel, F.; Alshehri, S. Solubilization, Hansen solubility parameters, solution thermodynamics and solvation behavior of flufenamic acid in (Carbitol + water) mixtures. Processes 2020, 8, 1224. [Google Scholar] [CrossRef]
- Krug, R.R.; Hunter, W.G.; Grieger, R.S. Enthalpy-entropy compensation. 2. Separation of the chemical from the statistic effect. J. Phys. Chem. 1976, 80, 2341–2351. [Google Scholar] [CrossRef]
- Holguín, A.R.; Rodríguez, G.A.; Cristancho, D.M.; Delgado, D.R.; Martínez, F. Solution thermodynamics of indomethacin in propylene glycol + water mixtures. Fluid Phase Equilib. 2012, 314, 134–139. [Google Scholar] [CrossRef]
- Shakeel, F.; Haq, N.; Radwan, A.A.; Alanazi, F.K.; Alsarra, I.A. Solubility and thermodynamic analysis of N′-(1-(N-(methyl)benzylaminomethyl)-2-oxoindolin-3-ylidene)-2-(benzyloxy) benzohydrazide in different neat solvents at different temperatures. J. Mol. Liq. 2016, 220, 108–112. [Google Scholar] [CrossRef]
- Haq, N.; Alghaith, A.F.; Alshehri, S.; Shakeel, F. Solubility and thermodynamic data of febuxostat in various mono solvents at different temperatures. Molecules 2022, 27, 4043. [Google Scholar] [CrossRef]
- Shakeel, F.; Haq, N.; Alsarra, I.; Alshehri, S. Solubility data, solubility parameters and thermodynamic behavior of an antiviral drug emtricitabine in different pure solvents: Molecular understanding of solubility and dissolution. Molecules 2021, 26, 746. [Google Scholar] [CrossRef]


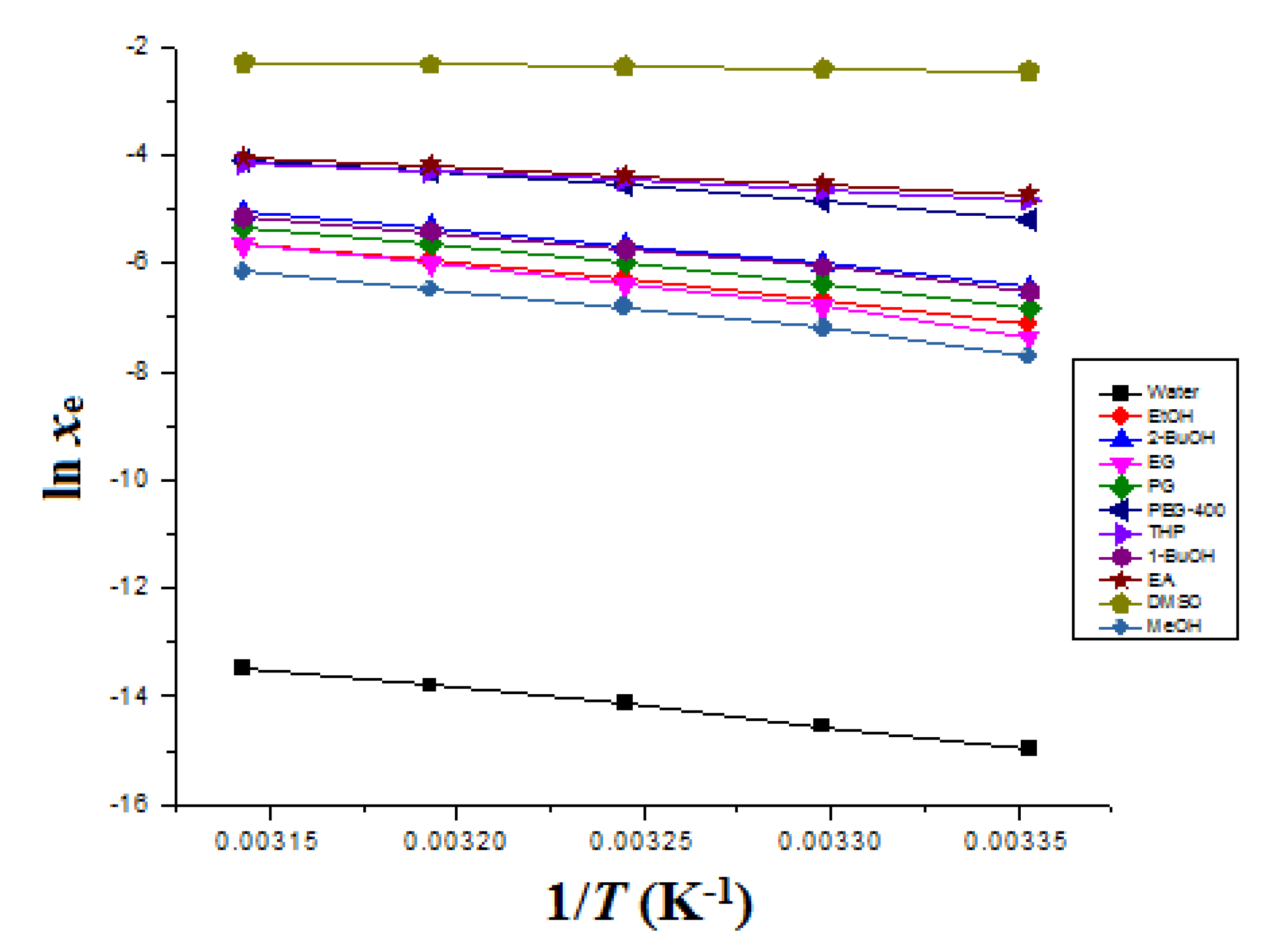
| GS | xe | ||||
|---|---|---|---|---|---|
| T = 298.2 K | T = 303.2 K | T = 308.2 K | T = 313.2 K | T = 318.2 K | |
| Water | 3.16 × 10−7 | 4.80 × 10−7 | 7.20 × 10−7 | 1.02 × 10−6 | 1.38 × 10−6 |
| MeOH | 4.45 × 10−4 | 7.45 × 10−4 | 1.09 × 10−3 | 1.54 × 10−3 | 2.10 × 10−3 |
| EG | 6.27 × 10−4 | 1.11 × 10−3 | 1.65 × 10−3 | 2.47 × 10−3 | 3.49 × 10−3 |
| EtOH | 8.06 × 10−4 | 1.24 × 10−3 | 1.83 × 10−3 | 2.59 × 10−3 | 3.51 × 10−3 |
| PG | 1.07 × 10−3 | 1.71 × 10−3 | 2.52 × 10−3 | 3.53 × 10−3 | 4.88 × 10−3 |
| 1-BuOH | 1.46 × 10−3 | 2.33 × 10−3 | 3.19 × 10−3 | 4.42 × 10−3 | 5.88 × 10−3 |
| 2-BuOH | 1.56 × 10−3 | 2.46 × 10−3 | 3.44 × 10−3 | 4.83 × 10−3 | 6.32 × 10−3 |
| PEG-400 | 5.56 × 10−3 | 7.92 × 10−3 | 1.06 × 10−2 | 1.33 × 10−2 | 1.66 × 10−2 |
| THP | 8.06 × 10−3 | 9.64 × 10−3 | 1.14 × 10−2 | 1.36 × 10−2 | 1.59 × 10−2 |
| EA | 8.82 × 10−3 | 1.07 × 10−2 | 1.25 × 10−2 | 1.52 × 10−2 | 1.73 × 10−2 |
| DMSO | 8.64 × 10−2 | 8.95 × 10−2 | 9.29 × 10−2 | 9.74 × 10−2 | 1.01 × 10−1 |
| xidl | 4.28 × 10−1 | 4.43 × 10−1 | 4.58 × 10−1 | 4.73 × 10−1 | 4.88 × 10−1 |
| Components | HSPs | Ra */MPa1/2 | ∆δδ/MPa1/2 | ∆δ */MPa1/2 | RED (Ra/R0) | |||
|---|---|---|---|---|---|---|---|---|
| δd/MPa1/2 | δp/MPa1/2 | δh/MPa1/2 | δ/MPa1/2 | |||||
| ITN | 17.60 | 2.60 | 7.50 | 19.30 | - | - | - | - |
| Water | 15.50 | 16.00 | 42.30 | 47.80 | 37.52 | 37.34 | 28.50 | 5.30 |
| MeOH | 17.40 | 10.60 | 22.40 | 30.30 | 16.91 | 16.91 | 11.00 | 1.94 |
| EG | 18.00 | 11.10 | 23.40 | 31.60 | 18.04 | 18.03 | 12.30 | 2.12 |
| EtOH | 16.20 | 8.40 | 17.60 | 25.40 | 11.97 | 11.73 | 6.10 | 1.23 |
| PG | 17.40 | 9.10 | 21.70 | 29.20 | 15.62 | 15.61 | 9.90 | 1.81 |
| 1-BuOH | 15.90 | 6.30 | 15.20 | 22.90 | 9.19 | 8.71 | 3.60 | 0.97 |
| 2-BuOH | 15.80 | 5.40 | 12.40 | 20.80 | 6.69 | 5.92 | 3.50 | 0.86 |
| PEG-400 | 14.60 | 7.50 | 9.40 | 18.90 | 7.97 | 6.05 | 0.40 | 0.99 |
| THP | 16.30 | 7.20 | 11.90 | 21.40 | 6.87 | 6.49 | 2.10 | 0.54 |
| EA | 15.70 | 5.60 | 7.00 | 18.10 | 4.86 | 3.58 | 1.20 | 0.97 |
| DMSO | 17.40 | 14.20 | 7.30 | 23.60 | 11.60 | 11.60 | 4.30 | 0.99 |
| GS | γi | ||||
|---|---|---|---|---|---|
| T = 298.2 K | T = 303.2 K | T = 308.2 K | T = 313.2 K | T = 318.2 K | |
| Water | 1,356,095 | 923,995.2 | 636,792.1 | 464,426.5 | 354,487.0 |
| MeOH | 961.7445 | 594.1927 | 417.5994 | 306.6269 | 232.0172 |
| EG | 682.7352 | 397.7430 | 277.6888 | 191.4309 | 139.6863 |
| EtOH | 531.2276 | 357.3747 | 249.5203 | 182.1199 | 139.1357 |
| PG | 399.4916 | 257.8128 | 181.3776 | 133.9927 | 101.0275 |
| 1-BuOH | 291.8713 | 189.5621 | 143.3259 | 107.0819 | 83.05753 |
| 2-BuOH | 273.9716 | 180.1061 | 133.1211 | 97.88820 | 77.29692 |
| PEG-400 | 77.06326 | 55.92912 | 42.94635 | 35.33440 | 29.40221 |
| THP | 53.15250 | 45.97158 | 39.92065 | 34.66999 | 30.56384 |
| EA | 48.58303 | 41.29086 | 36.62448 | 31.10461 | 28.22605 |
| DMSO | 4.957833 | 4.952277 | 4.930169 | 4.860074 | 4.820541 |
| GS | A | B | C | R2 | Overall RMSD (%) |
|---|---|---|---|---|---|
| Water | 869.29 | −46,552 | −127.80 | 0.9996 | |
| MeOH | 1593.1 | −79,662 | −234.08 | 0.9992 | |
| EG | 1573.8 | −79,404 | −230.79 | 0.9990 | |
| EtOH | 956.05 | −50,146 | −139.53 | 0.9998 | |
| PG | 1209.3 | −61,839 | −177.05 | 0.9995 | |
| 1-BuOH | 1229.9 | −62,257 | −180.37 | 0.9987 | 2.00 |
| 2-BuOH | 1302.4 | −65,672 | −191.07 | 0.9997 | |
| PEG-400 | 1196.9 | −59,554 | −175.93 | 0.9989 | |
| THP | 36.256 | −4654.6 | −4.4703 | 0.9999 | |
| EA | 304.76 | −16,944 | −44.348 | 0.9984 | |
| DMSO | −112.62 | 4405.3 | 16.743 | 0.9985 |
| GS | a | b | R2 | Overall RMSD (%) |
|---|---|---|---|---|
| Water | 8.6318 | −7030.1 | 0.9977 | |
| MeOH | 16.792 | −7290.0 | 0.9929 | |
| EG | 19.677 | −8047.2 | 0.9939 | |
| EtOH | 16.372 | −6997.2 | 0.9975 | |
| PG | 17.000 | −7094.9 | 0.9957 | |
| 1-BuOH | 15.287 | −6488.5 | 0.9939 | 3.56 |
| 2-BuOH | 15.703 | −6574.9 | 0.9945 | |
| PEG-400 | 12.166 | −5163.4 | 0.9919 | |
| THP | 6.1159 | −3261.4 | 0.9999 | |
| EA | 6.0950 | −3225.9 | 0.9972 | |
| DMSO | 0.11760 | −766.58 | 0.9952 |
| GS | λ | h | Overall RMSD (%) |
|---|---|---|---|
| Water | 8.89740 | 1192.10 | |
| MeOH | 0.311000 | 23,440.5 | |
| EG | 0.900600 | 8935.37 | |
| EtOH | 0.084900 | 82,417.0 | |
| PG | 0.327900 | 21,637.3 | |
| 1-BuOH | 0.045800 | 141,670 | 4.41 |
| 2-BuOH | 0.134700 | 48,959.9 | |
| PEG-400 | 0.239500 | 21,559.1 | |
| THP | 0.088400 | 36,893.6 | |
| EA | 0.030900 | 104,398 | |
| DMSO | 0.575800 | 1331.34 |
| GS | ΔsolH0/kJ mol−1 | ΔsolG0/kJ mol−1 | ΔsolS0/J mol−1 K−1 | R2 |
|---|---|---|---|---|
| Water | 58.52 | 36.33 | 72.03 | 0.9976 |
| MeOH | 60.68 | 17.59 | 139.8 | 0.9927 |
| EG | 66.90 | 16.50 | 163.8 | 0.9937 |
| EtOH | 58.25 | 16.24 | 136.3 | 0.9974 |
| PG | 59.06 | 15.44 | 141.6 | 0.9966 |
| 1-BuOH | 54.01 | 14.78 | 127.3 | 0.9937 |
| 2-BuOH | 54.90 | 14.61 | 130.7 | 0.9944 |
| PEG-400 | 42.98 | 11.76 | 101.3 | 0.9917 |
| THP | 27.15 | 11.44 | 50.97 | 0.9999 |
| EA | 26.85 | 11.20 | 50.79 | 0.9972 |
| DMSO | 6.382 | 6.071 | 1.009 | 0.9954 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakeel, F.; Haq, N.; Mahdi, W.A.; Alsarra, I.A.; Alshehri, S.; Alenazi, M.; Alwhaibi, A. Solubilization and Thermodynamic Analysis of Isotretinoin in Eleven Different Green Solvents at Different Temperatures. Materials 2022, 15, 8274. https://doi.org/10.3390/ma15228274
Shakeel F, Haq N, Mahdi WA, Alsarra IA, Alshehri S, Alenazi M, Alwhaibi A. Solubilization and Thermodynamic Analysis of Isotretinoin in Eleven Different Green Solvents at Different Temperatures. Materials. 2022; 15(22):8274. https://doi.org/10.3390/ma15228274
Chicago/Turabian StyleShakeel, Faiyaz, Nazrul Haq, Wael A. Mahdi, Ibrahim A. Alsarra, Sultan Alshehri, Miteb Alenazi, and Abdulrahman Alwhaibi. 2022. "Solubilization and Thermodynamic Analysis of Isotretinoin in Eleven Different Green Solvents at Different Temperatures" Materials 15, no. 22: 8274. https://doi.org/10.3390/ma15228274
APA StyleShakeel, F., Haq, N., Mahdi, W. A., Alsarra, I. A., Alshehri, S., Alenazi, M., & Alwhaibi, A. (2022). Solubilization and Thermodynamic Analysis of Isotretinoin in Eleven Different Green Solvents at Different Temperatures. Materials, 15(22), 8274. https://doi.org/10.3390/ma15228274









