Effect of Ball Burnishing Pressure on Surface Roughness by Low Plasticity Burnishing Inconel 718 Pre-Turned Surface
Abstract
1. Introduction
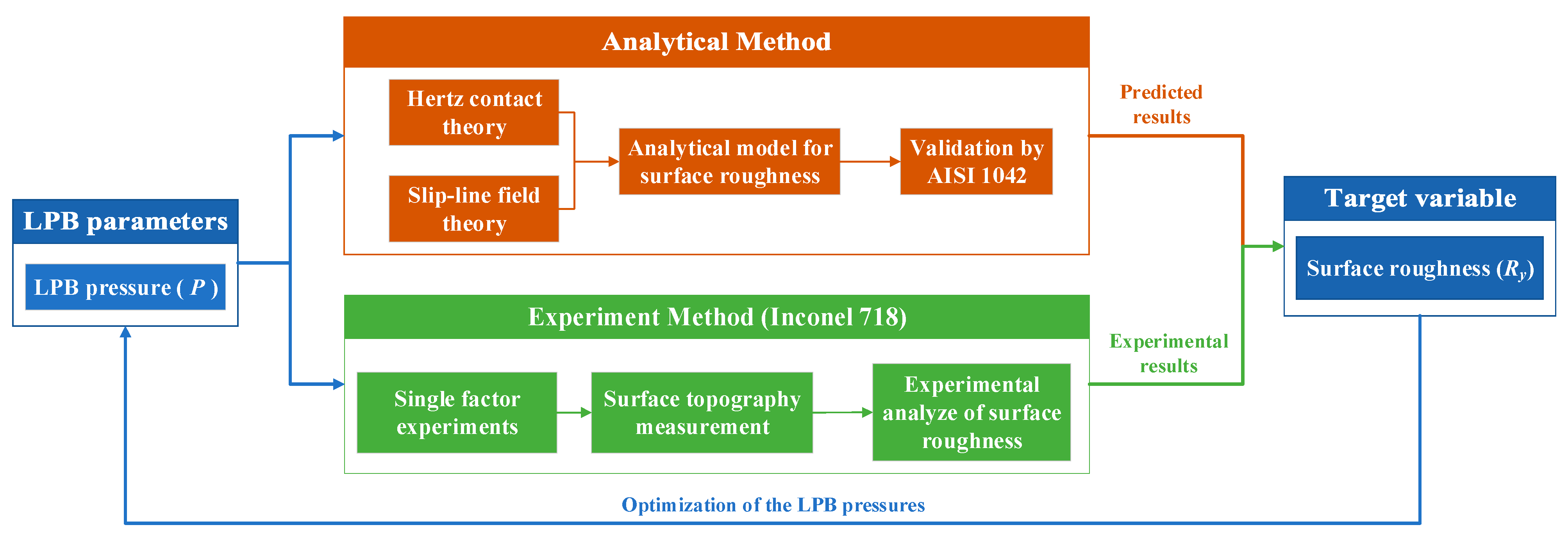
2. Theoretical Modeling of Low Plasticity Burnished Surface Roughness
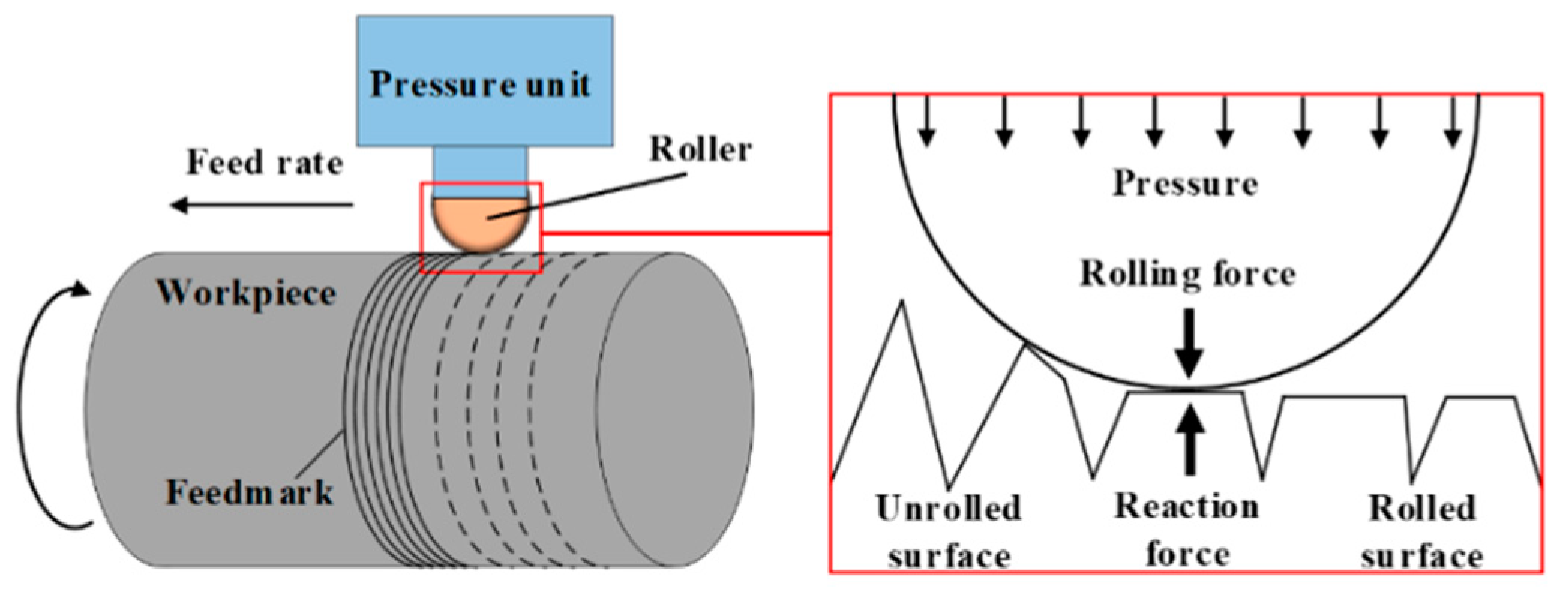
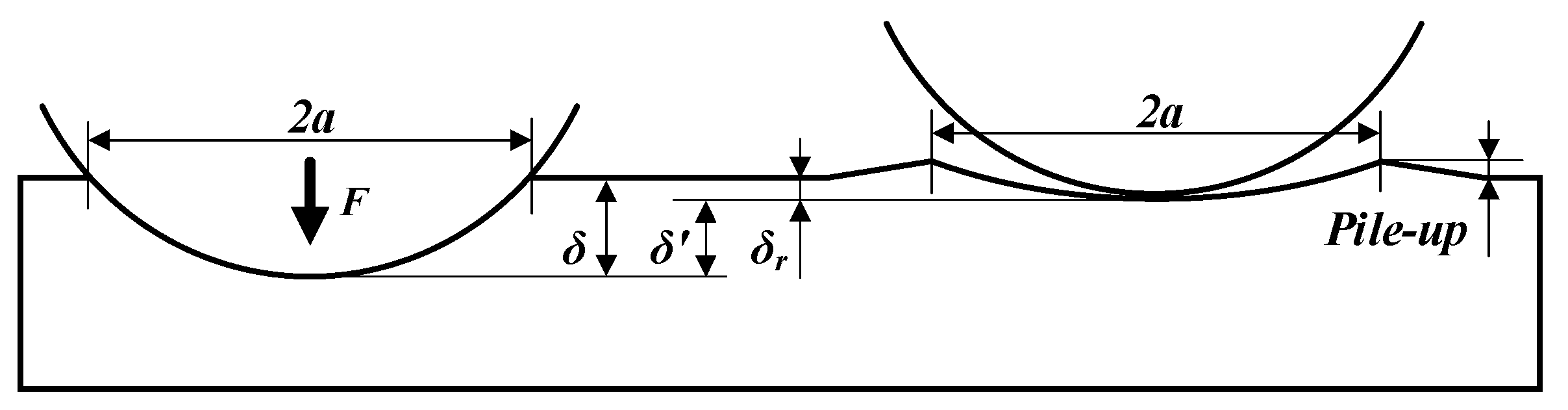
2.1. Surface Formation Mechanism of LPB
- (a)
- The turned surface roughness peaks are simplified to wedge shapes.
- (b)
- The roller is simplified as a line since the diameter of the roller is much larger than the surface roughness peak.
- (c)
- The plastic deformation of the surface wedge is larger compared to that of the elastic deformation. Therefore, the material of the surface roughness peak is assumed as the ideal rigid-plastic material and the roller rigid body.
- (d)
- The frictional coefficient between the ball and the workpiece is 10−5~5 × 10−3 [24]. Therefore, the surface is assumed to be frictionless to simplify the model derivation.
- (e)
- The surface is flat when the surface roughness reaches the minimum value.
- (f)
- The low boundary of surface roughness is not affected by the pile-up.
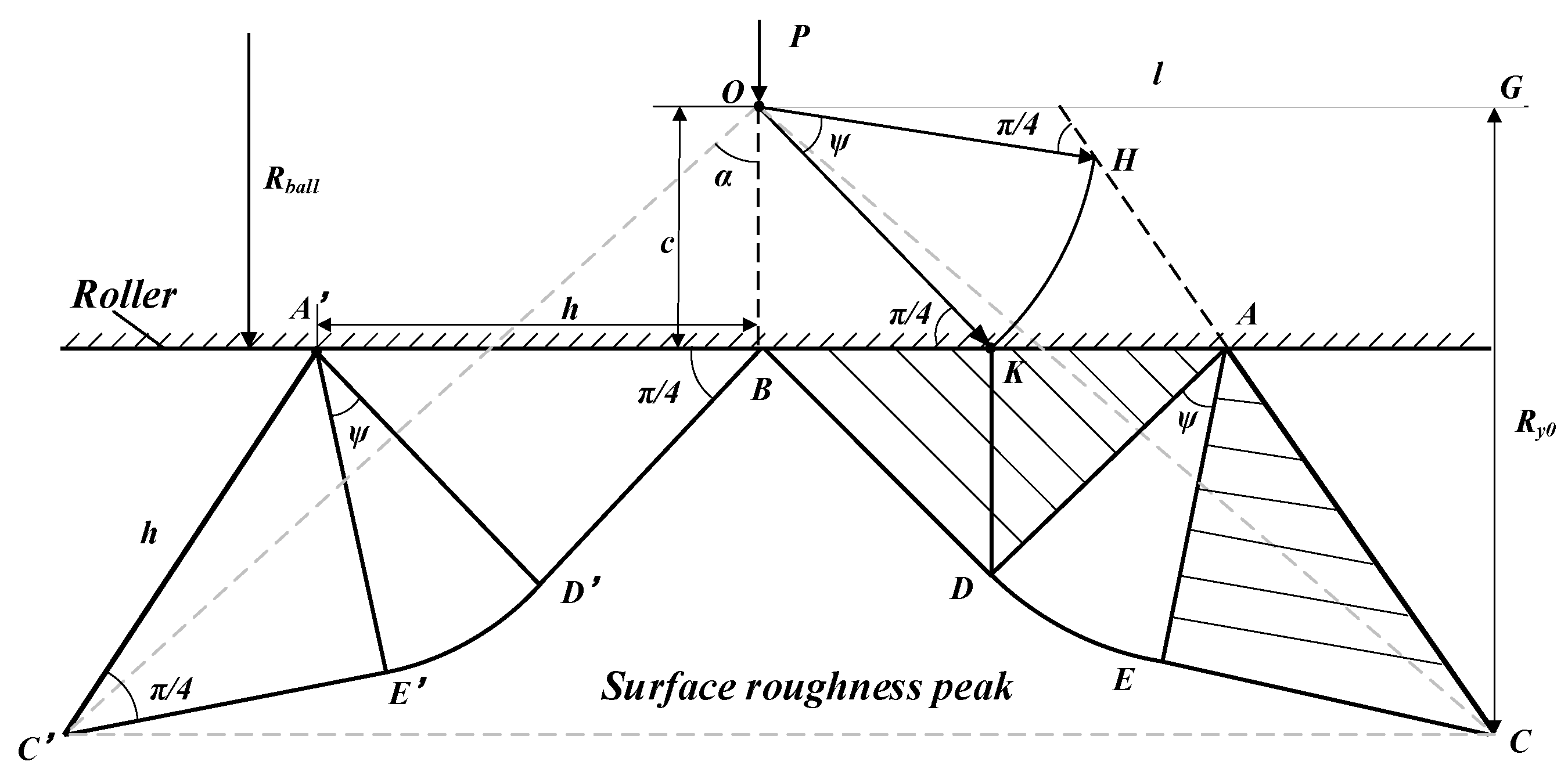
2.2. Modeling of Surface Roughness in SS
2.3. Modeling of Surface Roughness in IS
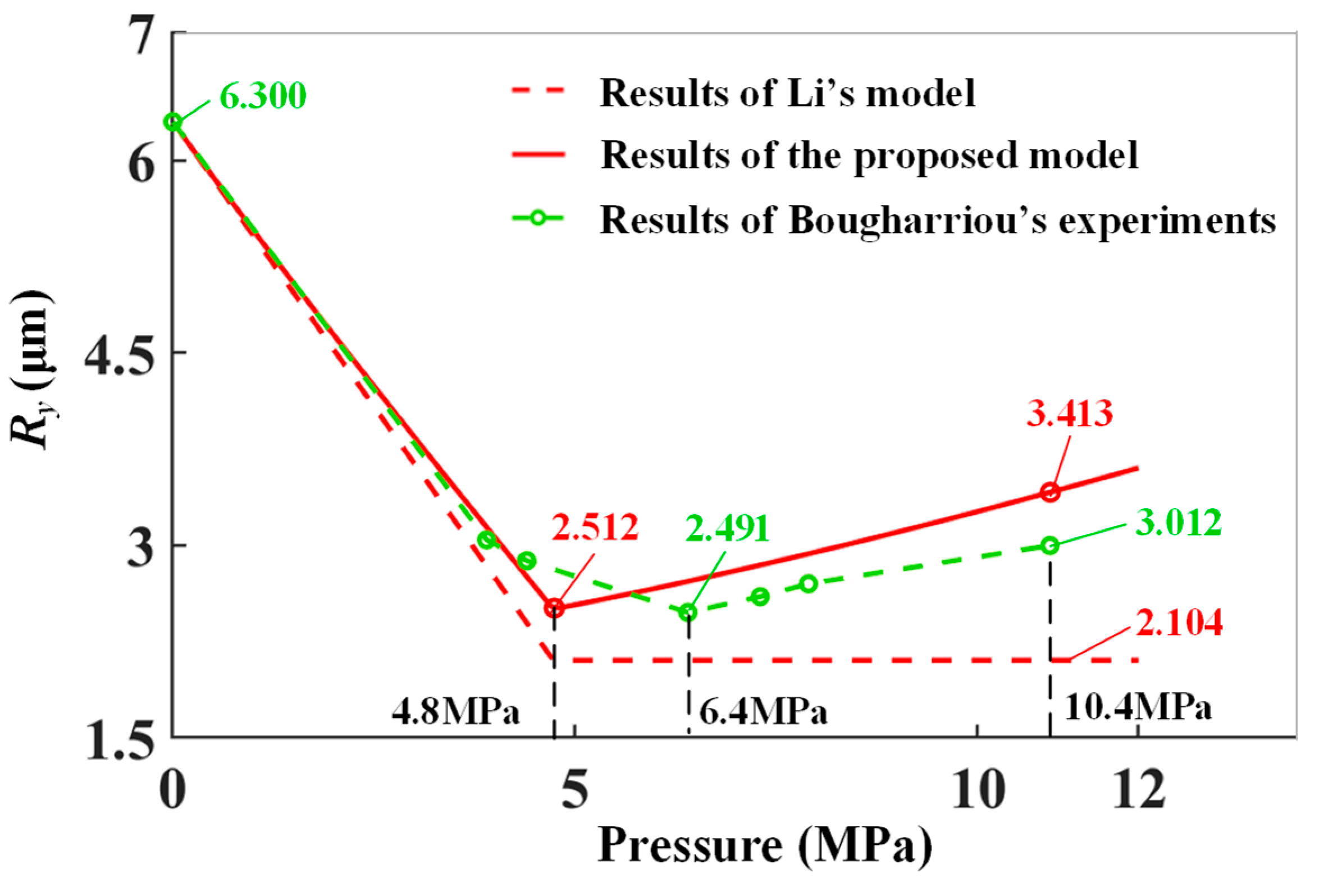
2.4. Validation of Proposed Model Prediction Results
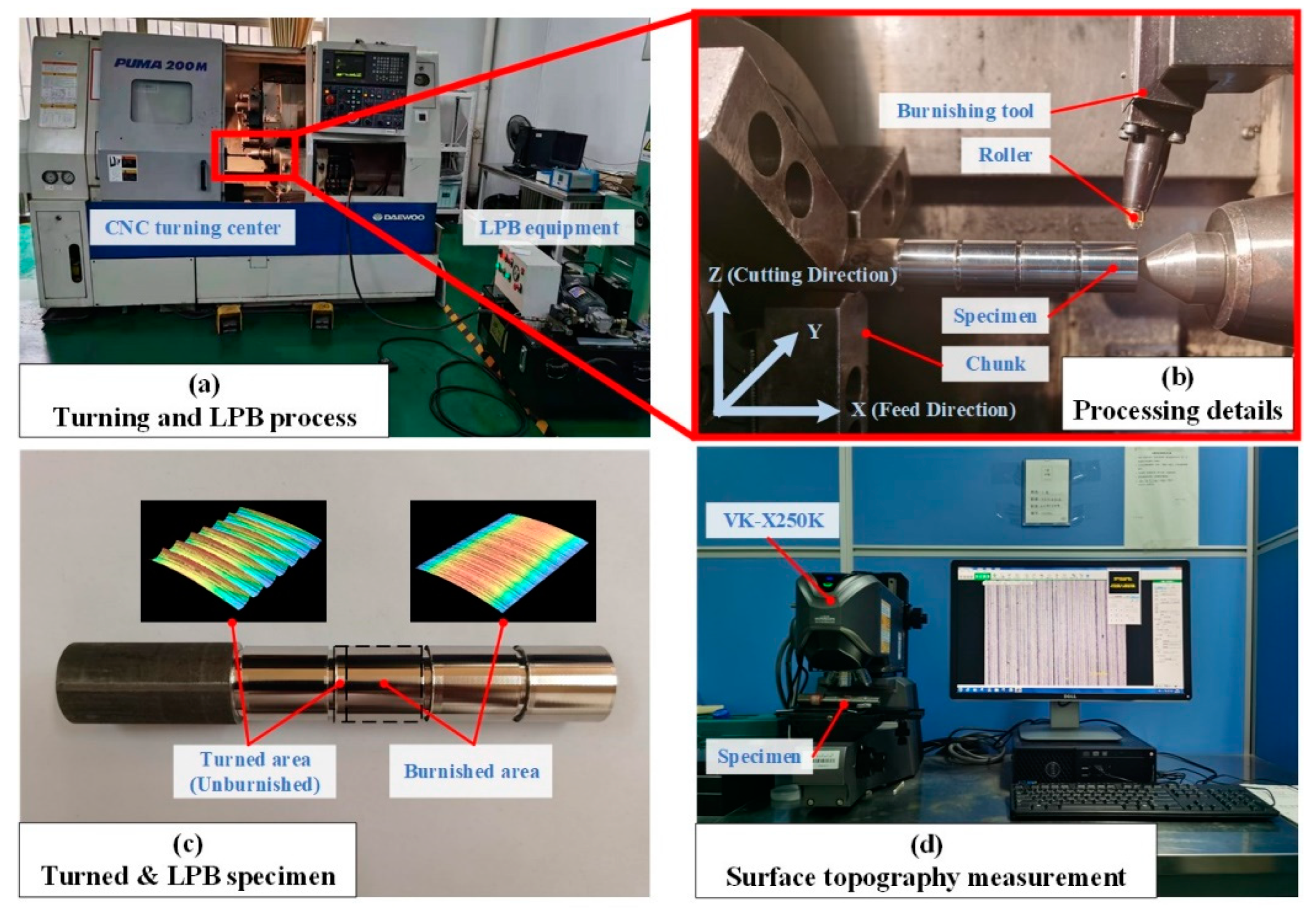
3. Experiments
3.1. Materials
3.2. Experimental Method
4. Results and Discussion
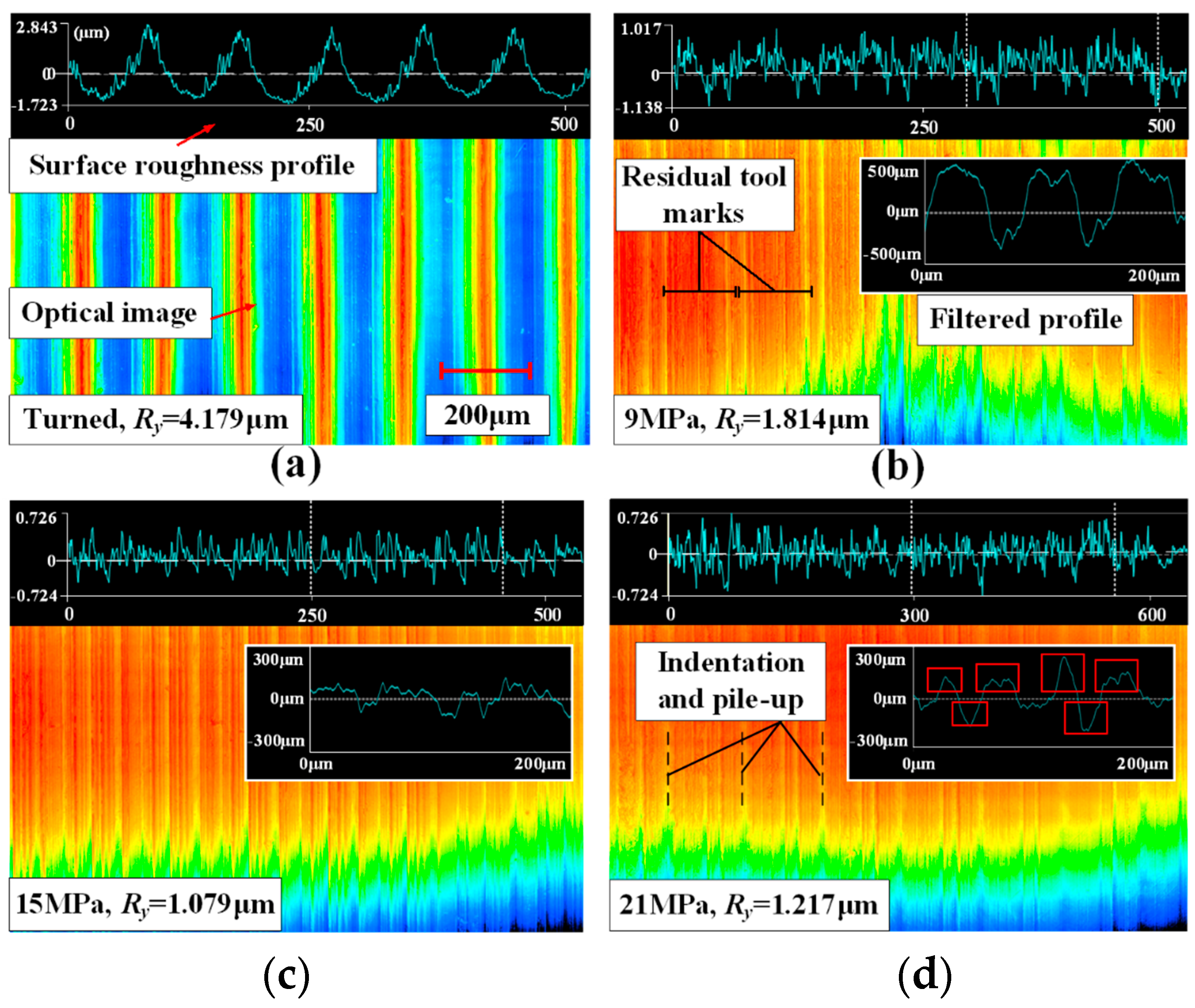
4.1. Experimental Results
4.2. Surface Roughness Prediction and the LPB Pressure Optimization for LPBed Inconel 718
5. Conclusions
- (1)
- The analytical prediction model for the LPBed surface roughness was proposed based on Hertz contact mechanics and slip-line field theory. The increment of the surface roughness in IS was attributed to the pile-up. Considering the deterioration, the proposed model could successfully predict surface roughness under excessive pressures.
- (2)
- The LPBed surface roughness of AISI 1042 was used to validate the proposed model. The predicted result of the minimum roughness was 2.512 μm (the error was 0.8%). Moreover, the surface roughness at 10.4 MPa was 3.413 μm (13.3%). According to the proposed model, the optimal LPB pressure corresponding to the minimum surface roughness was 4.8 MPa (25%). The results of Li’s model were 2.104 μm (15.5%), 2.104 μm (30.1%) and [4.8 MPa, +∞) (+∞%), respectively. Considering the pile-up, the proposed model could predict the surface roughness and the optimal pressures more accurately compared with the model of Li.
- (3)
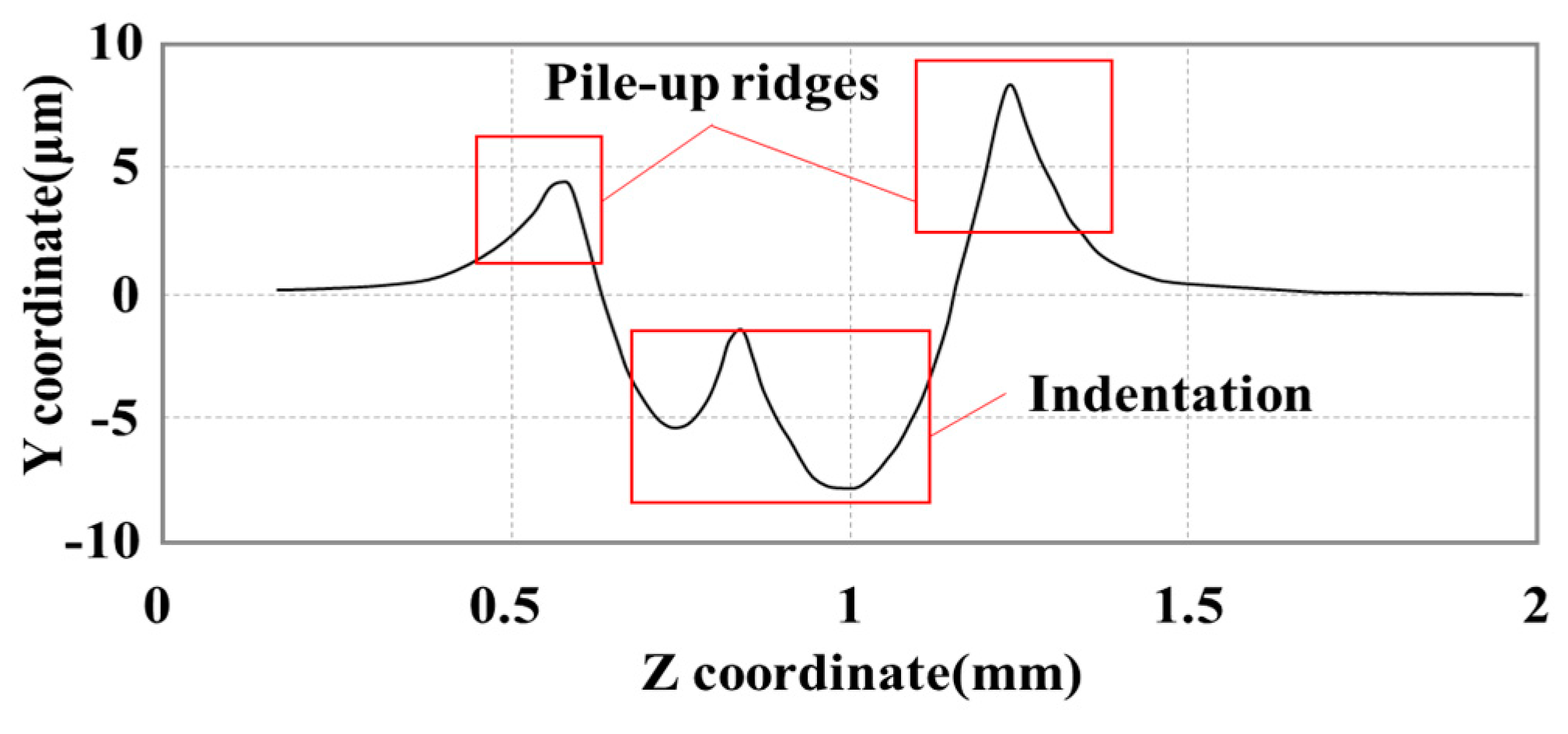
- The Inconel 718 was manufactured under different LPB pressures. The tool marks could be smoothed out by the LPB process. The minimum value of surface roughness was 1.079 μm. The surface roughness decreased by 72.9% compared with the turned surface roughness. However, the minimum surface roughness was limited. The surface roughness increased by 12.8% when the pressure reached 21 MPa. Pile-up and indentations observed under excessive pressures supported the deterioration of the surface roughness.
- (4)
- The proposed model was used to predict the surface roughness and the optimal interval of the LPB pressure. The error in the proposed results was less than 7%. The proposed model was more accurate than Li’s model (15.3%). The predicted optimal interval (12.2 MPa to 17.5 MPa) was consistent with the experimental one (12 MPa to 18 MPa). The proposed model could be used to predict the LPBed surface roughness of Inconel 718, and further conduct the LPB process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akhtar, W.; Sun, J.; Chen, W. Effect of Machining Parameters on Surface Integrity in High Speed Milling of Super Alloy GH4169/Inconel 718. Mater. Manuf. Processes 2016, 31, 620–627. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, X.; Ding, H. Tool Wear Characteristics in Machining of Nickel-Based Superalloys. Int. J. Mach. Tool. Manuf. 2013, 64, 60–77. [Google Scholar] [CrossRef]
- Caudill, J.; Schoop, J.; Jawahir, I.S. Correlation of Surface Integrity with Processing Parameters and Advanced Interface Cooling/Lubrication in Burnishing of Ti-6Al-4V Alloy. Adv. Mater. Process. Technol. 2019, 5, 53–66. [Google Scholar] [CrossRef]
- Wang, Z.; Jia, Y.; Zhang, X.; Fu, Y.; Zhang, C.; Tu, S. Effects of Different Mechanical Surface Enhancement Techniques on Surface Integrity and Fatigue Properties of Ti-6Al-4V: A Review. Crit. Rev. Solid State 2019, 44, 445–469. [Google Scholar] [CrossRef]
- Alshareef, A.J.; Marinescu, I.D.; Basudan, I.M.; Alqahtani, B.M.; Tharwan, M.Y. Ball-Burnishing Factors Affecting Residual Stress of AISI 8620 Steel. Int. J. Adv. Manuf. Technol. 2020, 107, 1387–1397. [Google Scholar] [CrossRef]
- Mohammadi, F.; Sedaghati, R.; Bonakdar, A. Finite Element Analysis and Design Optimization of Low Plasticity Burnishing Process. Int. J. Adv. Manuf. Technol. 2014, 70, 1337–1354. [Google Scholar] [CrossRef]
- Seemikeri, C.Y.; Mahagaonkar, S.B.; Brahmankar, P.K. The Influence of Surface Enhancement by Low Plasticity Burnishing on the Surface Integrity of Steels. Int. J. Surf. Sci. Eng. 2010, 4, 465–491. [Google Scholar] [CrossRef]
- Yuan, X.; Sun, Y.; Li, C.; Liu, W. Experimental Investigation into the Effect of Low Plasticity Burnishing Parameters on the Surface Integrity of TA2. Int. J. Adv. Manuf. Technol. 2017, 88, 1089–1099. [Google Scholar] [CrossRef]
- Revankar, G.D.; Shetty, R.; Rao, S.S.; Gaitonde, V.N. Wear Resistance Enhancement of Titanium Alloy (Ti-6Al-4V) by Ball Burnishing Process. J. Mater. Res. Technol. 2017, 6, 13–32. [Google Scholar] [CrossRef]
- John, M.R.S.; Suresh, P.; Raguraman, D.; Vinayagam, B.K. Surface Characteristics of Low Plasticity Burnishing for Different Materials Using Lathe. Arab. J. Sci. Eng. 2014, 39, 3209–3216. [Google Scholar] [CrossRef]
- Hassan, A.M. An Investigation into the Surface Characteristics of Burnished Cast Al-Cu Alloys. Int. J. Mach. Tool. Manu. 1997, 37, 813–821. [Google Scholar] [CrossRef]
- López De Lacalle, L.N.; Lamikiz, A.; Sánchez, J.A.; Arana, J.L. The Effect of Ball Burnishing on Heat-Treated Steel and Inconel 718 Milled Surfaces. Int. J. Adv. Manuf. Technol. 2007, 32, 958–968. [Google Scholar] [CrossRef]
- Mezlini, S.; Mzali, S.; Sghaier, S.; Braham, C.; Kapsa, P. Effect of a Combined Machining/Burnishing Tool on the Roughness and Mechanical Properties. Lubr. Sci. 2014, 26, 175–187. [Google Scholar] [CrossRef]
- Magalhães, F.C.; Abrão, A.M.; Denkena, B.; Breidenstein, B.; Mörke, T. Analytical Modeling of Surface Roughness, Hardness and Residual Stress Induced by Deep Rolling. J. Mater. Eng. Perform. 2017, 26, 876–884. [Google Scholar] [CrossRef]
- Bougharriou, A.; Saï, W.B.; Saï, K. Prediction of Surface Characteristics Obtained by Burnishing. Int. J. Adv. Manuf. Technol. 2010, 51, 205–215. [Google Scholar] [CrossRef]
- Balland, P.; Tabourot, L.; Degre, F.; Moreau, V. Mechanics of the Burnishing Process. Precis. Eng. 2013, 37, 129–134. [Google Scholar] [CrossRef]
- Öpöz, T.T.; Chen, X. Experimental Study on Single Grit Grinding of Inconel 718. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 713–726. [Google Scholar] [CrossRef]
- Dai, C.; Yu, T.; Ding, W.; Xu, J.; Yin, Z.; Li, H. Single Diamond Grain Cutting-Edges Morphology Effect on Grinding Mechanism of Inconel 718. Precis. Eng. 2019, 55, 119–126. [Google Scholar] [CrossRef]
- Zhang, T.; Bugtai, N.; Marinescu, I.D. Burnishing of Aerospace Alloy: A Theoretical-Experimental Approach. J. Manuf. Syst. 2015, 37, 472–478. [Google Scholar] [CrossRef]
- Bouzid, W.; Tsoumarev, O.; Sa, K. An Investigation of Surface Roughness of Burnished AISI 1042 Steel. Int. J. Adv. Manuf. Technol. 2004, 24, 120–125. [Google Scholar] [CrossRef]
- Korzynski, M. Modeling and Experimental Validation of the Force–Surface Roughness Relation for Smoothing Burnishing with a Spherical Tool. Int. J. Mach. Tool. Manu. 2007, 47, 1956–1964. [Google Scholar] [CrossRef]
- Li, F.L.; Xia, W.; Zhou, Z.Y.; Zhao, J.; Tang, Z.Q. Analytical Prediction and Experimental Verification of Surface Roughness During the Burnishing Process. Int. J. Mach. Tool. Manu. 2012, 62, 67–75. [Google Scholar] [CrossRef]
- Bougharriou, A.; Saï, K.; Bouzid, W. Finite Element Modelling of Burnishing Process. Mater. Technol. 2010, 25, 56–62. [Google Scholar] [CrossRef]
- Li, F.; Xia, W.; Zhou, Z. Finite Element Calculation of Residual Stress and Cold-Work Hardening Induced in Inconel 718 by Low Plasticity Burnishing. In Proceedings of the 2010 Third International Conference on Information and Computing, Wuxi, China, 4–6 June 2010. [Google Scholar]
- Hill, R. The Mathematical Theory of Plasticity; The Clarendon Press: Oxford, UK, 1950; pp. 213–226. [Google Scholar]
- Charfeddine, Y.; Youssef, S.; Sghaier, S.; Sghaier, J.; Hamdi, H. Study of the Simultaneous Grinding/Ball-burnishing of AISI 4140 Based on Finite Element Simulations and Experiments. Int. J. Mech. Sci. 2021, 192, 106097. [Google Scholar] [CrossRef]
- Hua, Y.; Liu, Z.; Wang, B.; Jiang, J. Residual Stress Regenerated on Low Plasticity Burnished Inconel 718 Surface After Initial Turning Process. J. Manuf. Sci. Eng.-T. Asme. 2019, 141, 121004. [Google Scholar] [CrossRef]
- Ogar, P.; Gorokhov, D.; Zhuk, A.; Kushnarev, V. Contact Geometry During Indentation of a Sphere into an Elastoplastic Half-Space. MATEC Web Conf. 2019, 298, 00093. [Google Scholar] [CrossRef][Green Version]
- Johnson, K.L.; Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987; pp. 90–95, 153–184. [Google Scholar]
- Black, A.J.; Kopalinsky, E.M.; Oxley, P.L.B. Analysis and Experimental Investigation of a Simplified Burnishing Process. Int. J. Mech. Sci. 1997, 39, 629–641. [Google Scholar] [CrossRef]
- Hua, Y.; Liu, Z.; Wang, B.; Hou, X. Surface Modification through Combination of Finish Turning with Low Plasticity Burnishing and its Effect on Fatigue Performance for Inconel 718. Surf. Coat. Technol. 2019, 375, 508–517. [Google Scholar] [CrossRef]


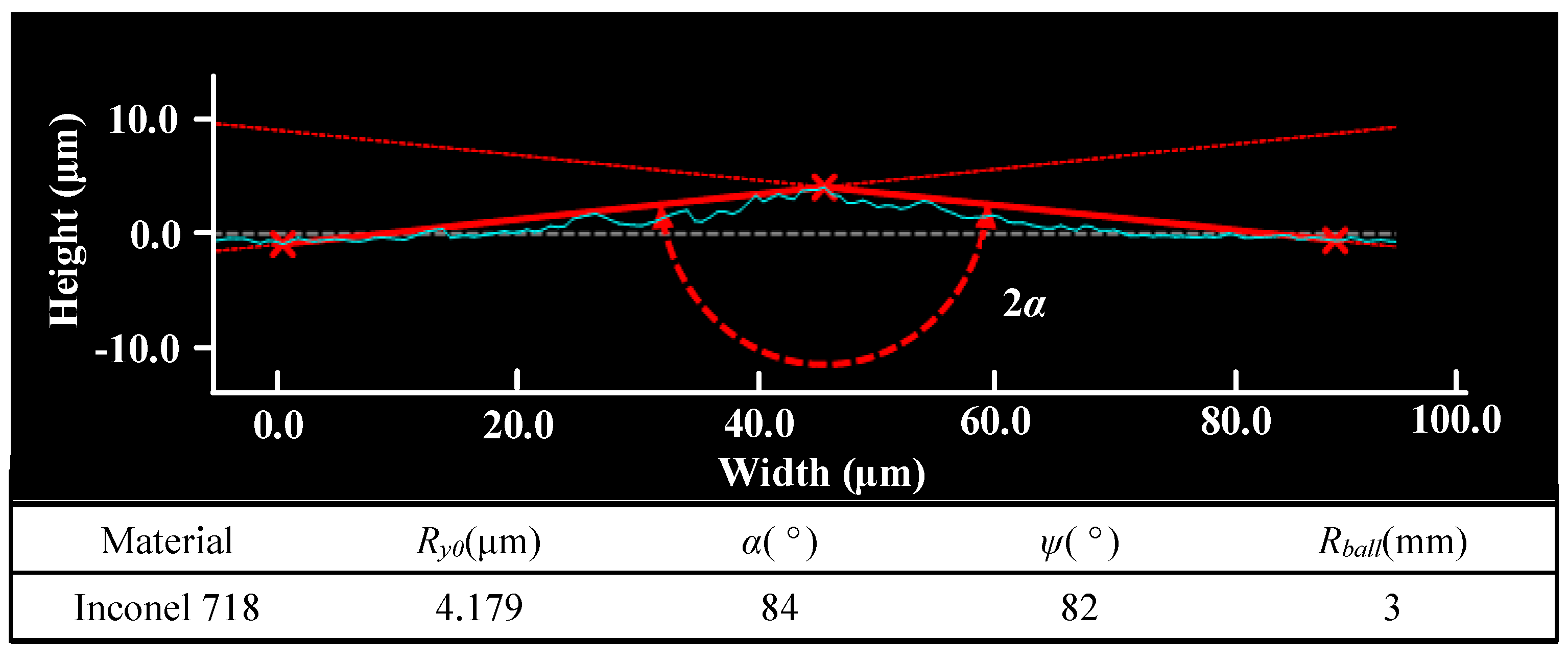

| Material | E (GPa) | ν | σs (MPa) | σb (MPa) | Ry0 (μm) | α (°) | Rball (mm) |
|---|---|---|---|---|---|---|---|
| AISI 1042 | 210 | 0.3 | 300 | 570 | 6.3 | 170.8 | 9 |
| Material | E (GPa) | ν | σs (MPa) | σb (MPa) |
|---|---|---|---|---|
| Inconel 718 | 205 | 0.3 | 1360.5 | 1502 |
| SiN (Roller) | 300 | 0.27 | - | - |
| Results | Ry,min (μm) | ERmin | Ry,21 (μm) | ER21 | Emax | IOP (MPa) |
|---|---|---|---|---|---|---|
| Prediction | 1.031 | 4.4% | 1.263 | 3.8% | 7.0% | [12.2, 17.5] |
| Experiment | 1.079 | - | 1.217 | - | [12, 18] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, P.; Liu, Z.; Yao, X.; Cai, Y. Effect of Ball Burnishing Pressure on Surface Roughness by Low Plasticity Burnishing Inconel 718 Pre-Turned Surface. Materials 2022, 15, 8067. https://doi.org/10.3390/ma15228067
Cui P, Liu Z, Yao X, Cai Y. Effect of Ball Burnishing Pressure on Surface Roughness by Low Plasticity Burnishing Inconel 718 Pre-Turned Surface. Materials. 2022; 15(22):8067. https://doi.org/10.3390/ma15228067
Chicago/Turabian StyleCui, Pengcheng, Zhanqiang Liu, Xinglin Yao, and Yukui Cai. 2022. "Effect of Ball Burnishing Pressure on Surface Roughness by Low Plasticity Burnishing Inconel 718 Pre-Turned Surface" Materials 15, no. 22: 8067. https://doi.org/10.3390/ma15228067
APA StyleCui, P., Liu, Z., Yao, X., & Cai, Y. (2022). Effect of Ball Burnishing Pressure on Surface Roughness by Low Plasticity Burnishing Inconel 718 Pre-Turned Surface. Materials, 15(22), 8067. https://doi.org/10.3390/ma15228067









