The Transmission Properties of One-Dimensional Photonic Crystals with Gradient Materials
Abstract
1. Introduction
2. Physical Model and Numerical Method
2.1. Physical Model
2.2. Numerical Method
3. Numerical Results and Discussions
3.1. Research of PBG
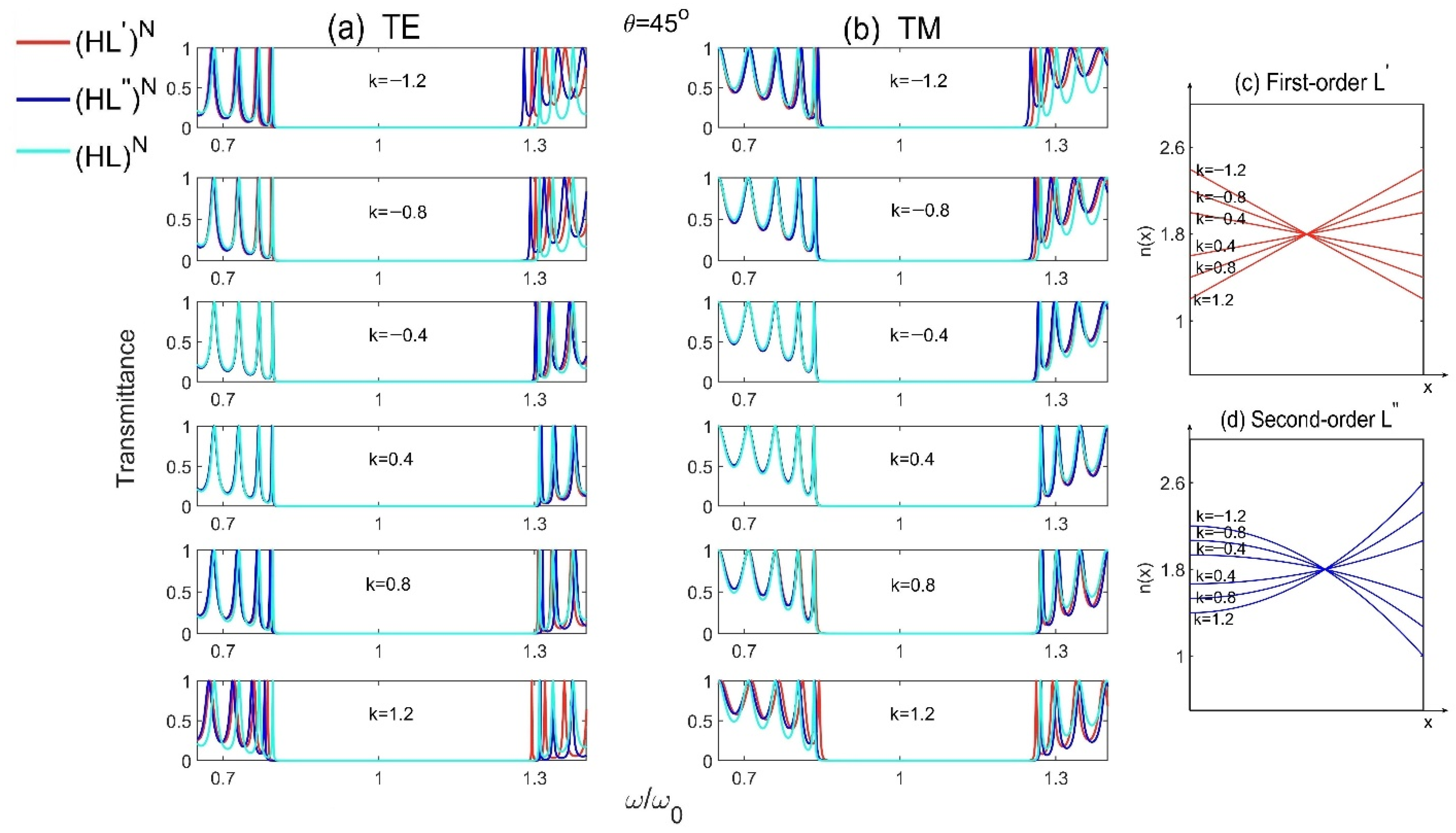
3.1.1. PBG Properties of Model 1 and Model 2
3.1.2. PBG Properties of Model 3 and Model 4
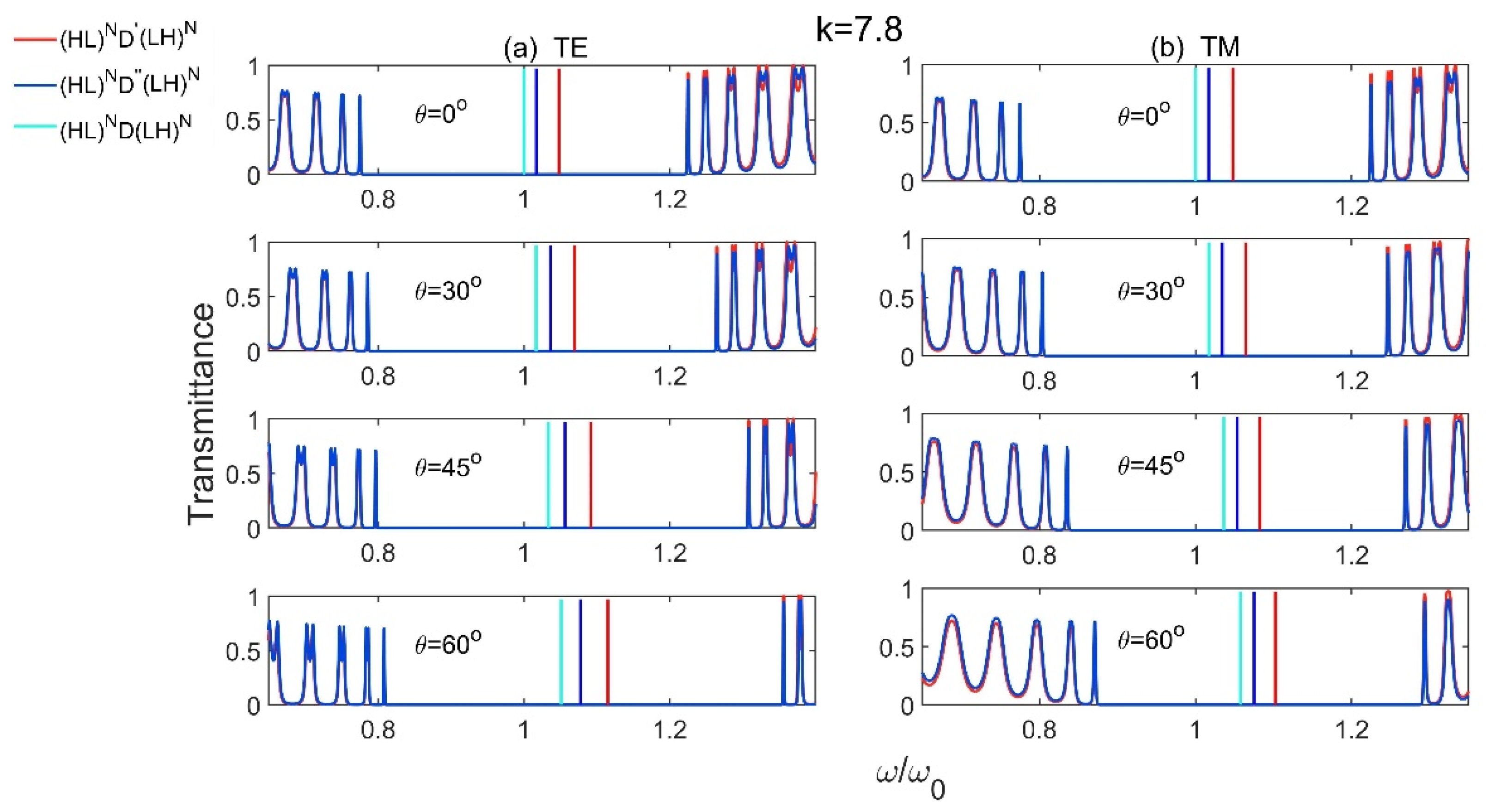
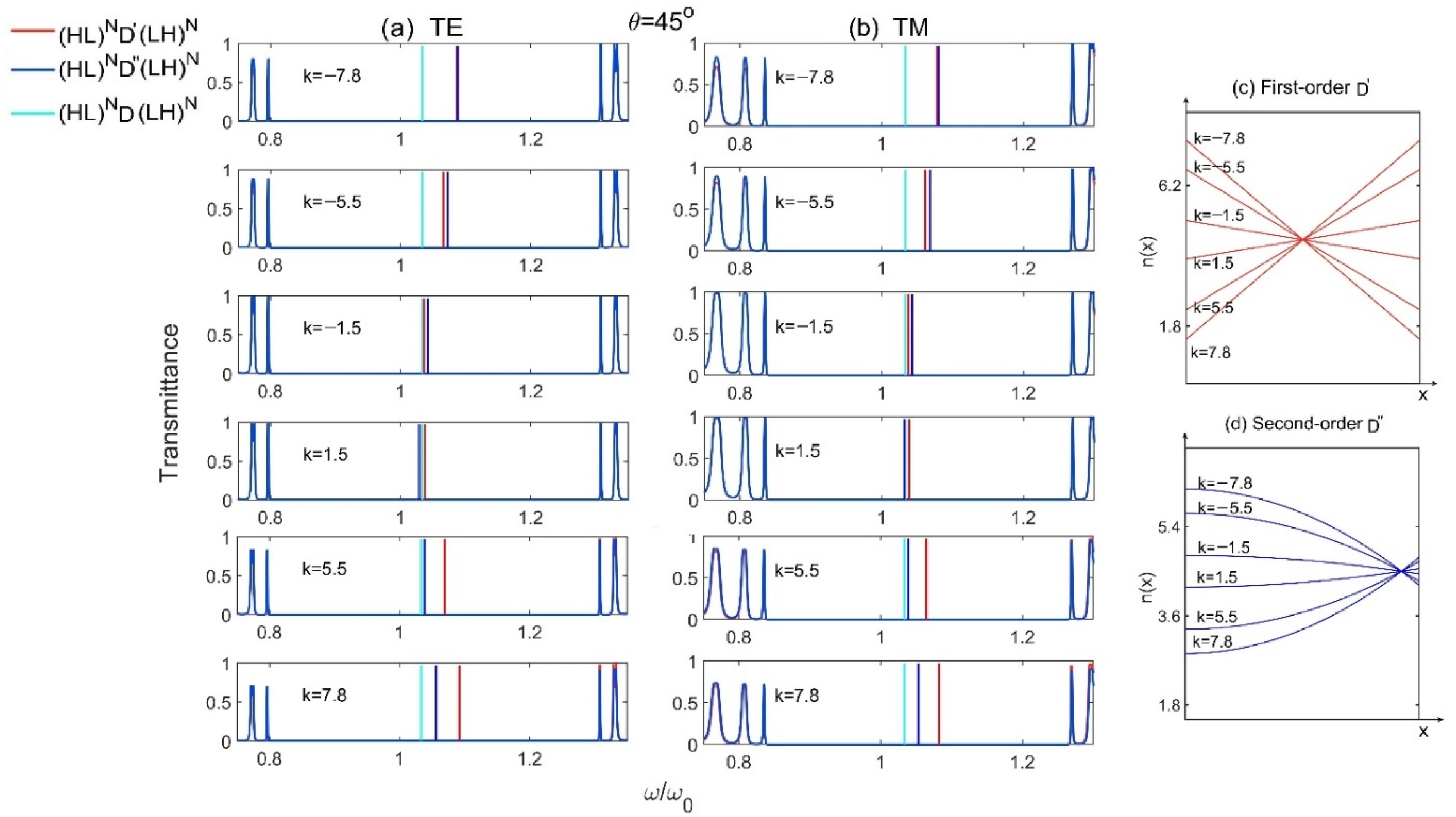
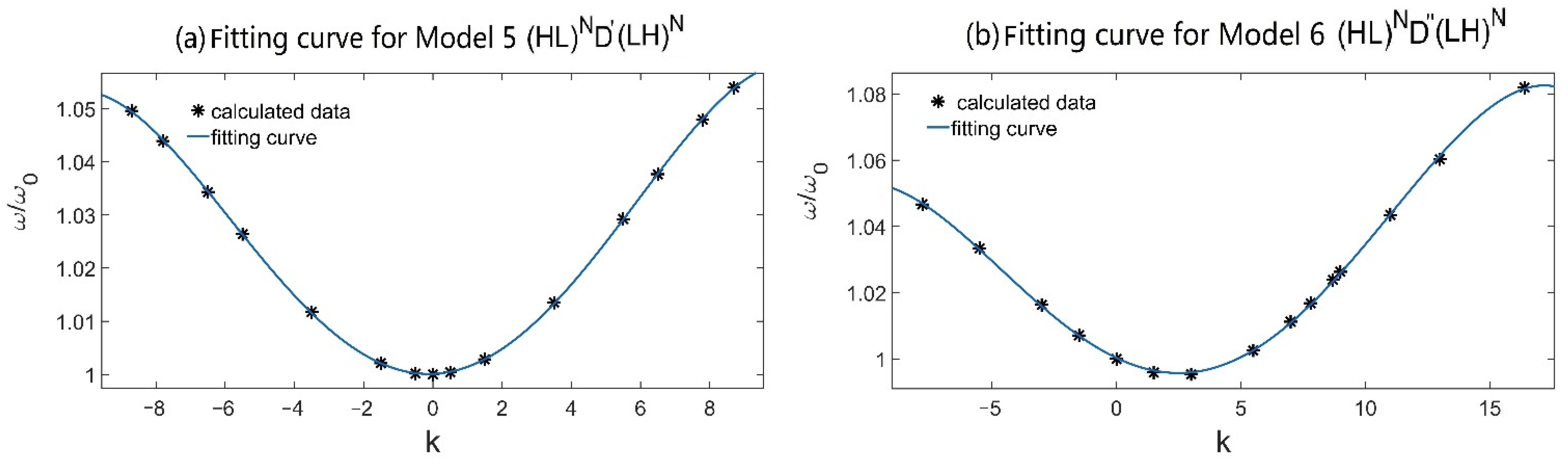
3.2. Research of Defect Mode in Model 5 and Model 6
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Joannopoulos, J.D.; Villeneuve, P.R.; Fan, S. Photonic crystals: Putting a new twist on light. Nature 1997, 386, 143–149. [Google Scholar] [CrossRef]
- Thylen, L.; Qiu, M.; Anand, S. Photonic crystals—A step towards integrated circuits for photonics. Chemphyschem 2004, 5, 1268–1283. [Google Scholar] [CrossRef] [PubMed]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Inoue, K.; Ohtaka, K. Photonic Crystals: Physics, Fabrication and Applications, 1st ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Kosaka, H.; Kawashima, T.; Tomita, A.; Notomi, M.; Tamamura, T.; Sato, T.; Kawakami, S. Self-collimating phenomena in photonic crystals. Appl. Phys. Lett. 1999, 74, 1212–1214. [Google Scholar] [CrossRef]
- Zalevsky, Z.; George, A.K.; Luan, F.; Bouwmans, G.; Dainese, P.; Cordeiro, C.; July, N. Photonic crystal in-fiber devices. Opt. Eng. 2005, 44, 125003. [Google Scholar] [CrossRef]
- Ayre, M.; Cambournac, C.; Khayam, O.; Benisty, H.; Stomeo, T.; Krauss, T.F. Photonic crystal waveguides for coarse-selectivity devices. Photonics Nanostruct.—Fundam. Appl. 2008, 6, 19–25. [Google Scholar] [CrossRef]
- Zhou, W.; Mackie, D.M.; Taysing-Lara, M.; Dang, G.; Newman, P.G.; Svensson, S. Novel reconfigurable semiconductor photonic crystal-MEMS device. Solid-State Electron. 2006, 50, 908–913. [Google Scholar] [CrossRef]
- Rajan, G.; Callaghan, D.; Semenova, Y.; Farrell, G. Photonic crystal fiber sensors for minimally invasive surgical devices. IEEE Trans. Biomed. Eng. 2012, 59, 332–338. [Google Scholar] [CrossRef]
- Ansari, N.; Tehranchi, M.M.; Ghanaatshoar, M. Characterization of defect modes in one-dimensional photonic crystals: An analytic approach. Phys. B 2009, 404, 1181–1186. [Google Scholar] [CrossRef]
- Kawai, N.K.N.; Wada, M.W.M.; Sakoda, K.S.K. Numerical analysis of localized defect modes in a photonic crystal: Two-dimensional triangular lattice with square rods. Jpn. J. Appl. Phys. 1998, 37, 4644. [Google Scholar] [CrossRef]
- Zhang, L.; Qiao, W.; Chen, L.; Wang, J.; Zhao, Y.; Wang, Q.; He, L. Double defect modes of one-dimensional dielectric photonic crystals containing a single negative material defect. Optik 2014, 125, 1354–1357. [Google Scholar] [CrossRef]
- Yang, D.Q.; Wang, C.; Ji, Y.F. Silicon on-chip 1D photonic crystal nanobeam bandstop filters for the parallel multiplexing of ultra-compact integrated sensor array. Opt. Express 2016, 24, 16267–16279. [Google Scholar] [CrossRef] [PubMed]
- Taha, T.A.; Mehaney, A.; Elsayed, H.A. Detection of heavy metals using one-dimensional gyroidal photonic crystals for effective water treatment. Mater. Chem. Phys. 2022, 285, 126125. [Google Scholar] [CrossRef]
- Alrowaili, Z.A.; Elsayed, H.A.; Ahmed, A.M.; Taha, T.A.; Mehaney, A. Simple, efficient and accurate method toward the monitoring of ethyl butanoate traces. Opt. Quantum Electron 2022, 54, 126. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Singh, K.S.; Ojha, S. Enhanced omni-directional reflection frequency range in Si-based one dimensional photonic crystal with defect. Optik 2011, 122, 910–913. [Google Scholar] [CrossRef]
- Deng, Z.; Su, Y.; Gong, W.; Wang, X.; Gong, R. Temperature characteristics of Ge/ZnS one-dimension photonic crystal for infrared camouflage. Opt. Mater. 2021, 121, 111564. [Google Scholar] [CrossRef]
- Moghadam, R.Z.; Ahmadvand, H. Optical and Mechanical Properties of ZnS/Ge0.1C0.9 Antireflection Coating on Ge Substrate. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 1491–1497. [Google Scholar] [CrossRef]
- Zhu, Q.; Jin, L.; Fu, Y. Graded index photonic crystals: A review. Ann. Der Phys. 2015, 527, 205–218. [Google Scholar] [CrossRef]
- Kurt, H.; Citrin, D.S. Graded index photonic crystals. Opt. Express 2007, 15, 1240–1253. [Google Scholar] [CrossRef]
- Singh, B.K.; Chaudhari, M.K.; Pandey, P.C. Photonic and Omnidirectional Band Gap Engineering in One-Dimensional Photonic Crystals Consisting of Linearly Graded Index Material. J. Light. Technol. 2016, 34, 2431–2438. [Google Scholar] [CrossRef]
- Singh, B.K.; Tiwari, S.; Chaudhari, M.K.; Pandey, P.C. Tunable photonic defect modes in one-dimensional photonic crystals containing exponentially and linearly graded index defect. Optik 2016, 127, 6452–6462. [Google Scholar] [CrossRef]
- Singh, B.K.; Bambole, V.; Rastogi, V.; Pandey, P.C. Multi-channel photonic bandgap engineering in hyperbolic graded index materials embedded one-dimensional photonic crystals. Opt. Laser Technol. 2020, 129, 106293. [Google Scholar] [CrossRef]
- Osting, B. Bragg structure and the first spectral gap. Appl. Math. Lett. 2012, 25, 1926–1930. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Al-ghezi, H.; Gnawali, R.; Banerjee, P.P.; Sun, L.; Slagle, J.; Evans, D. 2X2 anisotropic transfer matrix approach for optical propagation in uniaxial transmission filter structures. Opt. Express 2020, 28, 35761–35783. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Feng, N.; Wang, G.; Zheng, H. Reflection and transmission coefficients in multilayered fully anisotropic media solved by transfer matrix method with plane waves for predicting energy transmission course. IEEE Trans. Antennas Propag. 2021, 69, 4727–4736. [Google Scholar] [CrossRef]
- Giltner, D.M.; McGowan, R.W.; Lee, S.A. Theoretical and experimental study of the Bragg scattering of atoms from a standing light wave. Phys. Rev. A 1995, 52, 3966–3972. [Google Scholar] [CrossRef]
- Nilsen-Hofseth, S.; Romero-Rochin, V. Dispersion relation of guided-mode resonances and Bragg peaks in dielectric diffraction gratings. Phys. Rev. E 2001, 64, 036614. [Google Scholar] [CrossRef]

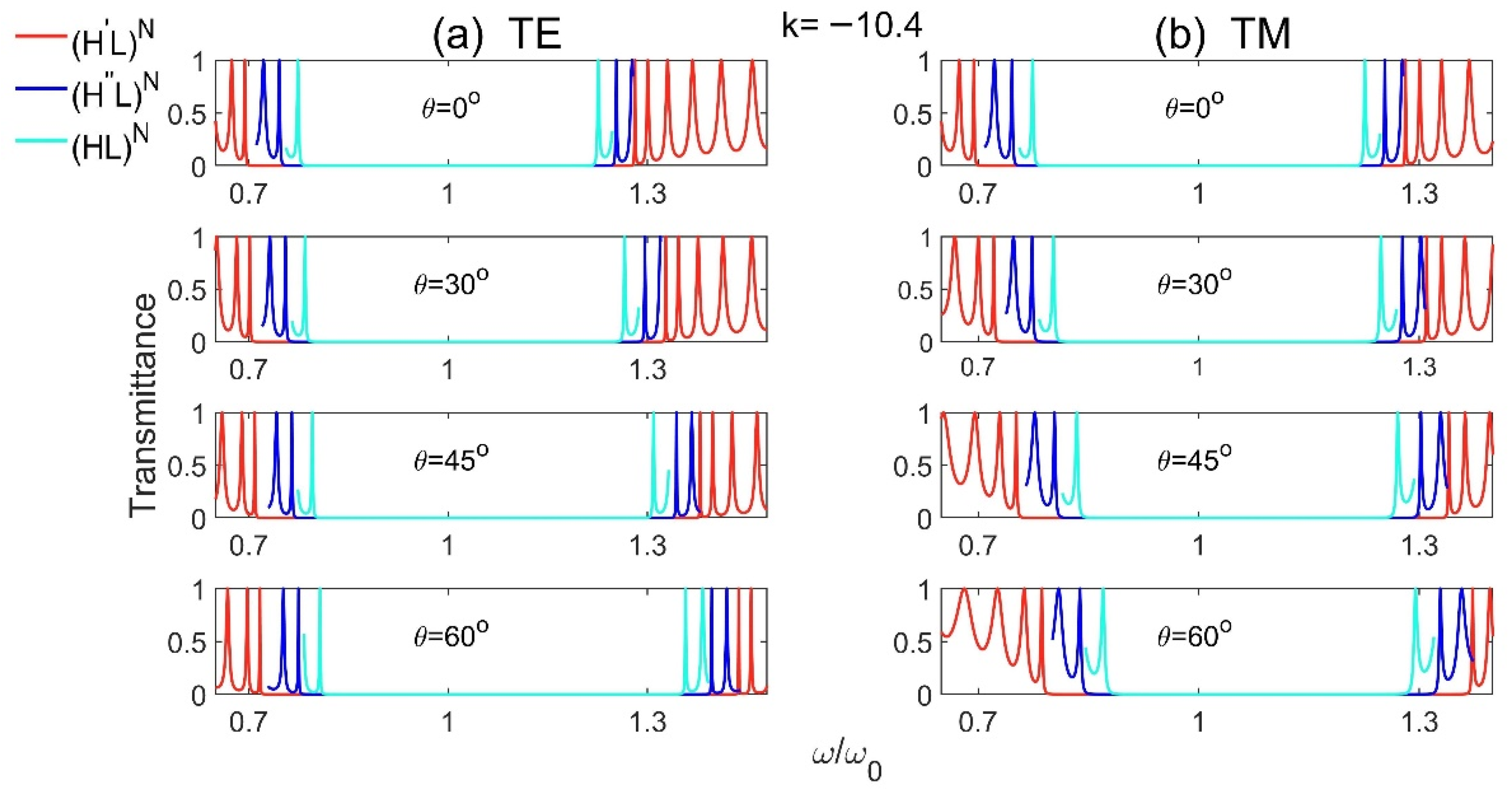


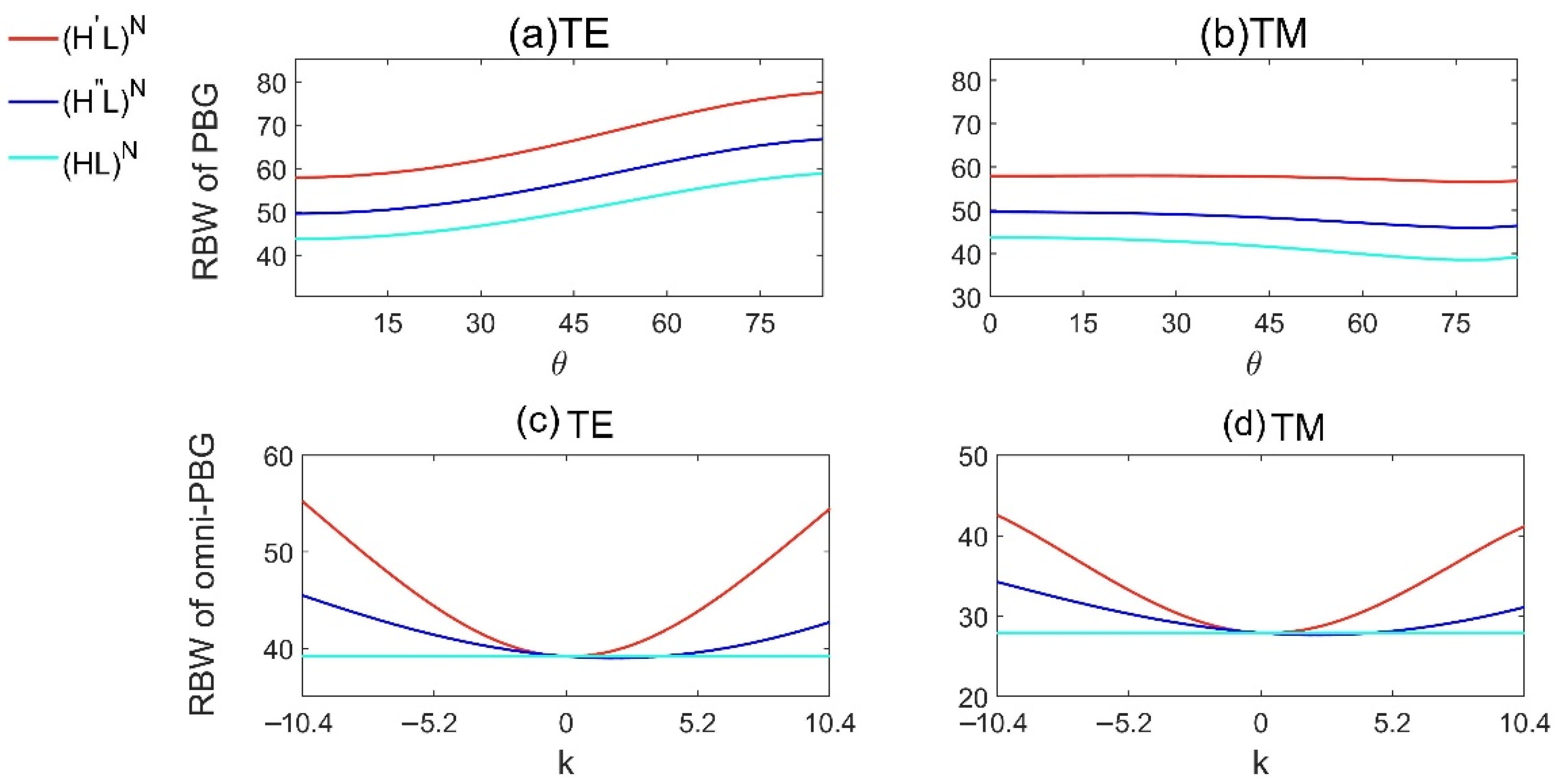
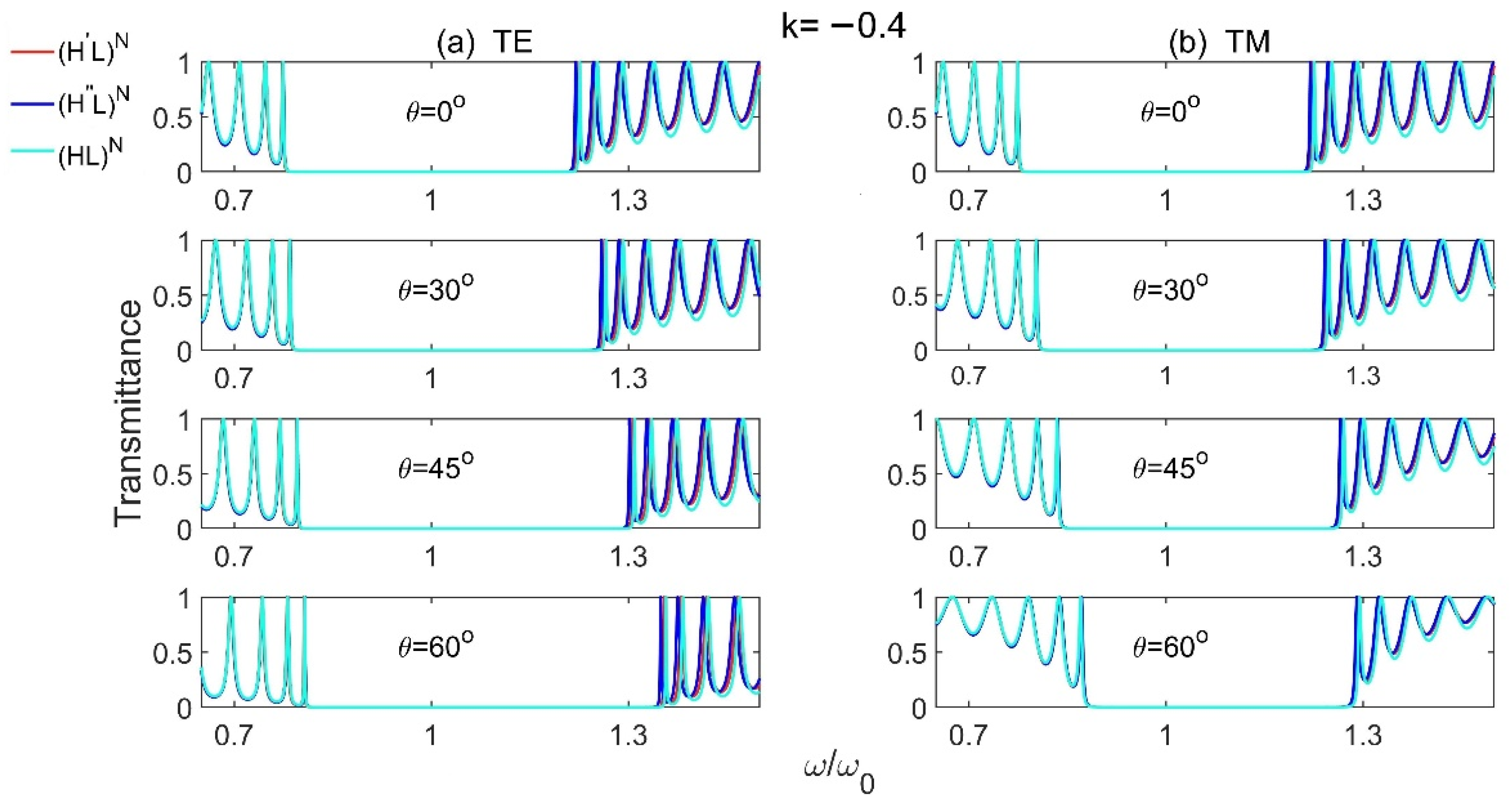
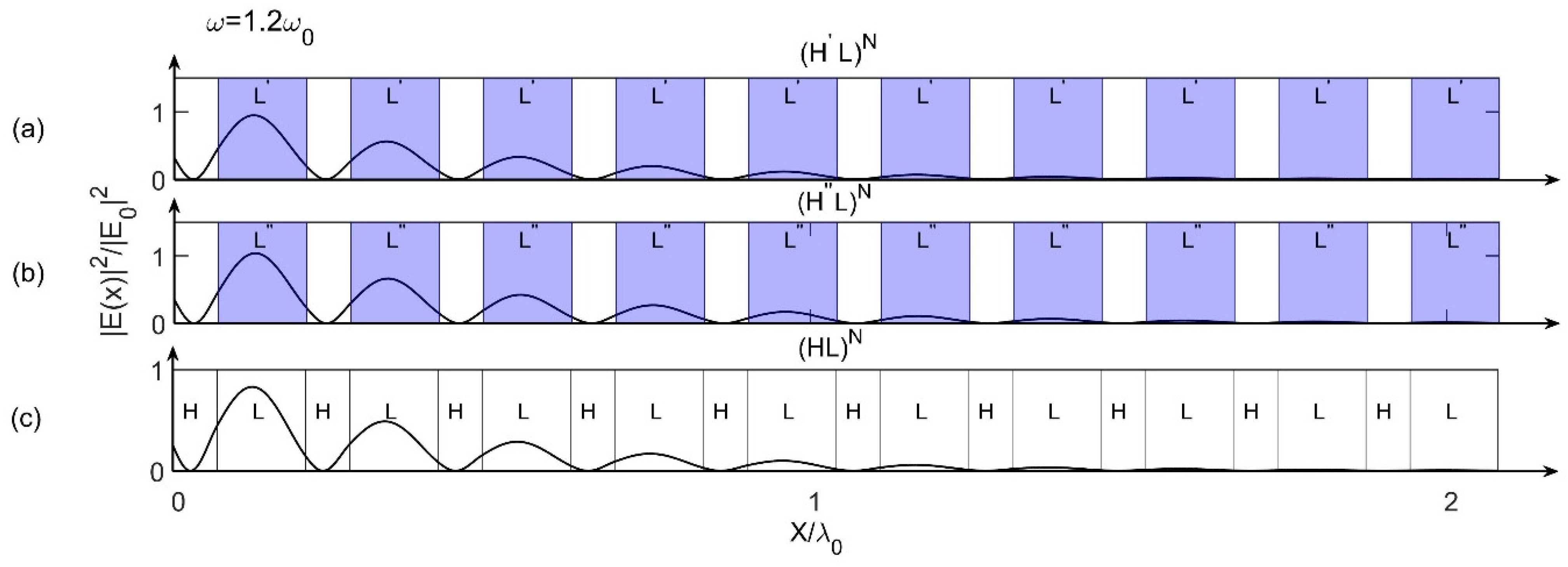
| TE | TM | ||||||
|---|---|---|---|---|---|---|---|
| 0° | 0.5792 | 0.4958 | 0.4370 | 0.5792 | 0.4958 | 0.4370 | |
| 30° | 0.6192 | 0.5307 | 0.4676 | 0.5796 | 0.4904 | 0.4279 | |
| 45° | 0.6645 | 0.5701 | 0.5020 | 0.5776 | 0.4824 | 0.4155 | |
| 60° | 0.7164 | 0.6152 | 0.5413 | 0.5723 | 0.4705 | 0.3988 | |
| Omni-PBG | 0.5533 | 0.4626 | 0.3992 | 0.4485 | 0.3650 | 0.2986 | |
| C-PBG | 0.4485 | 0.3650 | 0.2986 | The same as TE case | |||
| 0° | 0.4835 | 0.4583 | 0.4370 | 0.4835 | 0.4583 | 0.4370 | |
| 30° | 0.5173 | 0.4904 | 0.4676 | 0.4778 | 0.4505 | 0.4279 | |
| 45° | 0.5554 | 0.5268 | 0.5020 | 0.4694 | 0.4396 | 0.4155 | |
| 60° | 0.5989 | 0.5683 | 0.5413 | 0.4572 | 0.4247 | 0.3988 | |
| Omni-PBG | 0.4500 | 0.4220 | 0.3992 | 0.3532 | 0.3236 | 0.2986 | |
| C-PBG | 0.3532 | 0.3236 | 0.2986 | The same as TE case | |||
| 0° | 0.4491 | 0.4446 | 0.4370 | 0.4491 | 0.4446 | 0.4370 | |
| 30° | 0.4805 | 0.4757 | 0.4676 | 0.4409 | 0.4359 | 0.4279 | |
| 45° | 0.5158 | 0.5109 | 0.5020 | 0.4296 | 0.4240 | 0.4155 | |
| 60° | 0.5562 | 0.5510 | 0.5413 | 0.4140 | 0.4079 | 0.3988 | |
| Omni-PBG | 0.4125 | 0.4074 | 0.3992 | 0.3138 | 0.3078 | 0.2986 | |
| C-PBG | 0.3138 | 0.3078 | 0.2986 | The same as TE case | |||
| 0° | 0.4475 | 0.4352 | 0.4370 | 0.4475 | 0.4352 | 0.4370 | |
| 30° | 0.4788 | 0.4655 | 0.4676 | 0.4392 | 0.4260 | 0.4279 | |
| 45° | 0.5142 | 0.4996 | 0.5020 | 0.4280 | 0.4137 | 0.4155 | |
| 60° | 0.5546 | 0.5386 | 0.5413 | 0.4128 | 0.3972 | 0.3988 | |
| Omni-PBG | 0.4101 | 0.3971 | 0.3992 | 0.3088 | 0.2958 | 0.2986 | |
| C-PBG | 0.3088 | 0.2958 | 0.2986 | The same as TE case | |||
| 0° | 0.4808 | 0.4399 | 0.4370 | 0.4808 | 0.4399 | 0.4370 | |
| 30° | 0.5146 | 0.4705 | 0.4676 | 0.4751 | 0.4313 | 0.4279 | |
| 45° | 0.5528 | 0.5049 | 0.5020 | 0.4668 | 0.4197 | 0.4155 | |
| 60° | 0.5965 | 0.5443 | 0.5413 | 0.4552 | 0.4042 | 0.3988 | |
| Omni-PBG | 0.4460 | 0.4024 | 0.3992 | 0.3445 | 0.3004 | 0.2986 | |
| C-PBG | 0.3445 | 0.3004 | 0.2986 | The same as TE case | |||
| 0° | 0.5762 | 0.4677 | 0.4370 | 0.5762 | 0.4677 | 0.4370 | |
| 30° | 0.6165 | 0.5002 | 0.4676 | 0.5768 | 0.4617 | 0.4279 | |
| 45° | 0.6623 | 0.5368 | 0.5020 | 0.5753 | 0.4532 | 0.4155 | |
| 60° | 0.7148 | 0.5787 | 0.5413 | 0.5706 | 0.4415 | 0.3988 | |
| Omni-PBG | 0.5487 | 0.4327 | 0.3992 | 0.4375 | 0.3310 | 0.2986 | |
| C-PBG | 0.4375 | 0.3310 | 0.2986 | The same as TE case | |||
| TE | TM | ||||||
|---|---|---|---|---|---|---|---|
| 0° | 1.0439 | 1.0466 | 1 | 1.0439 | 1.0466 | 1 | |
| 30° | 1.0650 | 1.0672 | 1.0165 | 1.0603 | 1.0628 | 1.0171 | |
| 45° | 1.0869 | 1.0884 | 1.0335 | 1.0783 | 1.0805 | 1.0361 | |
| 60° | 1.1095 | 1.1102 | 1.0510 | 1.0982 | 1.1003 | 1.0576 | |
| 0° | 1.0264 | 1.0334 | 1 | 1.0264 | 1.0334 | 1 | |
| 30° | 1.0458 | 1.0528 | 1.0165 | 1.0432 | 1.0500 | 1.0171 | |
| 45° | 1.0658 | 1.0729 | 1.0335 | 1.0617 | 1.0683 | 1.0361 | |
| 60° | 1.0866 | 1.0937 | 1.0510 | 1.0824 | 1.0887 | 1.0576 | |
| 0° | 1.0021 | 1.0071 | 1 | 1.0021 | 1.0071 | 1 | |
| 30° | 1.0189 | 1.0242 | 1.0165 | 1.0192 | 1.0241 | 1.0171 | |
| 45° | 1.0361 | 1.0418 | 1.0335 | 1.0382 | 1.0430 | 1.0361 | |
| 60° | 1.0539 | 1.0599 | 1.0510 | 1.0596 | 1.0643 | 1.0576 | |
| 0° | 1.0028 | 0.9959 | 1 | 1.0028 | 0.9959 | 1 | |
| 30° | 1.0197 | 1.0122 | 1.0165 | 1.0199 | 1.0131 | 1.0171 | |
| 45° | 1.0370 | 1.0290 | 1.0335 | 1.0389 | 1.0322 | 1.0361 | |
| 60° | 1.0548 | 1.0463 | 1.0510 | 1.0603 | 1.0538 | 1.0576 | |
| 0° | 1.0292 | 1.0026 | 1 | 1.0292 | 1.0026 | 1 | |
| 30° | 1.0489 | 1.0201 | 1.0165 | 1.0461 | 1.0200 | 1.0171 | |
| 45° | 1.0692 | 1.0383 | 1.0335 | 1.0647 | 1.0392 | 1.0361 | |
| 60° | 1.0903 | 1.0571 | 1.0510 | 1.0854 | 1.0608 | 1.0576 | |
| 0° | 1.0479 | 1.0169 | 1 | 1.0479 | 1.0169 | 1 | |
| 30° | 1.0694 | 1.0362 | 1.0165 | 1.0644 | 1.0343 | 1.0171 | |
| 45° | 1.0918 | 1.0564 | 1.0335 | 1.0825 | 1.0536 | 1.0361 | |
| 60° | 1.1149 | 1.0774 | 1.0510 | 1.1025 | 1.0750 | 1.0576 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Lin, M.; Liang, Z.; Wang, Q.; Zheng, Y.; Ouyang, Z. The Transmission Properties of One-Dimensional Photonic Crystals with Gradient Materials. Materials 2022, 15, 8049. https://doi.org/10.3390/ma15228049
Fu L, Lin M, Liang Z, Wang Q, Zheng Y, Ouyang Z. The Transmission Properties of One-Dimensional Photonic Crystals with Gradient Materials. Materials. 2022; 15(22):8049. https://doi.org/10.3390/ma15228049
Chicago/Turabian StyleFu, Lixin, Mi Lin, Zixian Liang, Qiong Wang, Yaoxian Zheng, and Zhengbiao Ouyang. 2022. "The Transmission Properties of One-Dimensional Photonic Crystals with Gradient Materials" Materials 15, no. 22: 8049. https://doi.org/10.3390/ma15228049
APA StyleFu, L., Lin, M., Liang, Z., Wang, Q., Zheng, Y., & Ouyang, Z. (2022). The Transmission Properties of One-Dimensional Photonic Crystals with Gradient Materials. Materials, 15(22), 8049. https://doi.org/10.3390/ma15228049







