Simulation of Inclusion Particle Motion Behavior under Interfacial Tension in Continuous Casting Mold
Abstract
:1. Introduction
1.1. Inclusions in the Continuous Casting Mold
1.2. Inclusion Motion Characteristics
1.3. Background of the Research
2. Numerical Modeling
The Governing Equations
3. Numerical Details
4. Results and Discussion
Mold and Inclusion Characteristics
5. Conclusions
- A transient, two-dimensional model of a continuous casting mold was developed using Ansys Fluent software. Alumina inclusions in microalloyed steel were tracked under the condition of solidification at the boundary side. Further, the empirical relationship of interfacial tension was used to study the effects of temperature and surfactant concentration (sulfur) on inclusion motion near the solidifying boundary layer in the mold.
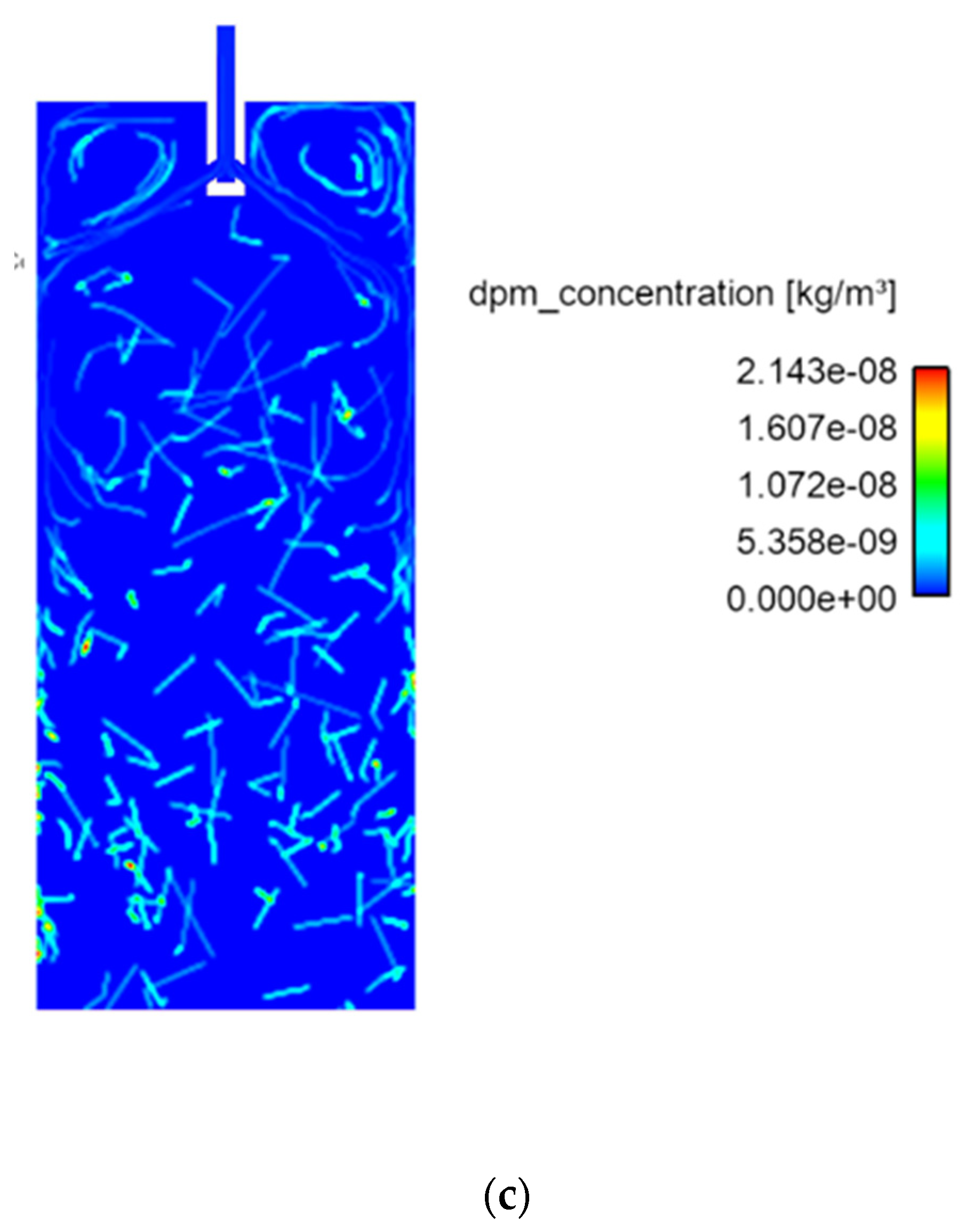
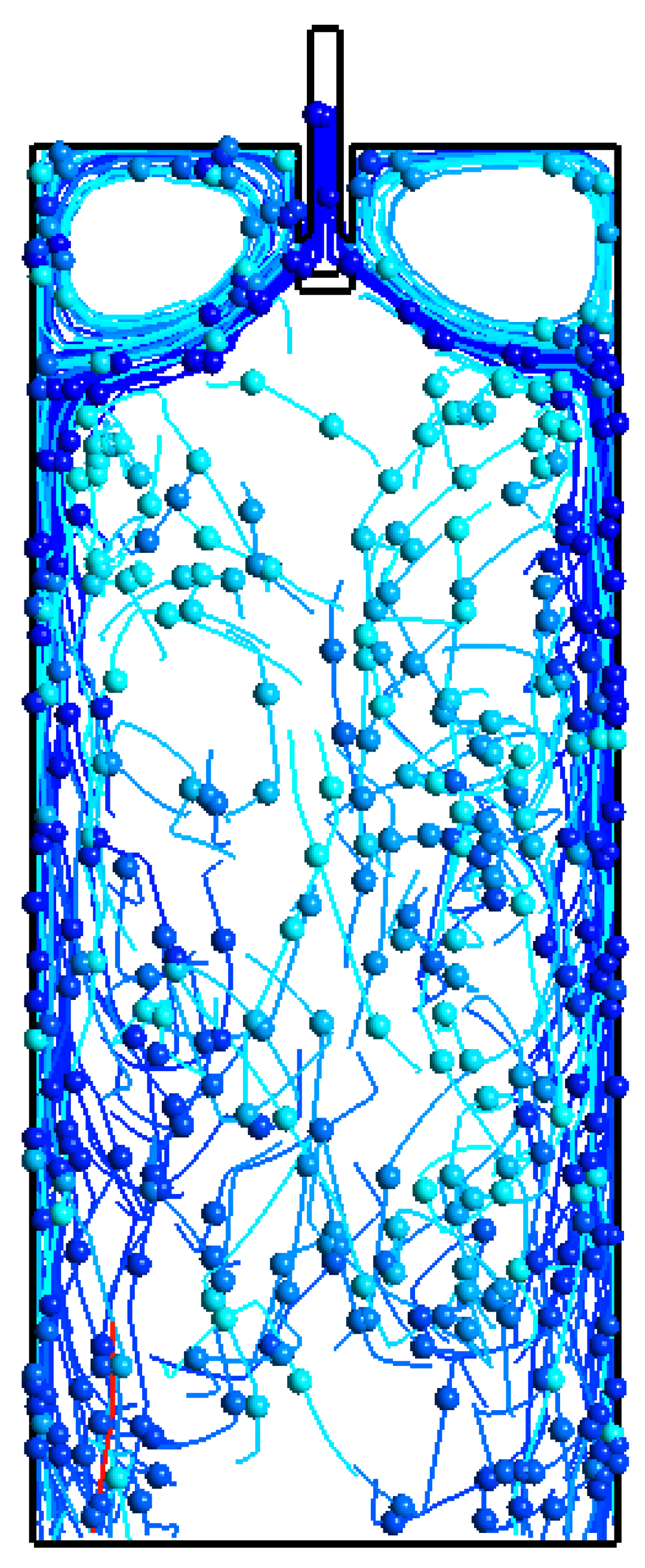
- The simulation findings indicate that the size of the inclusions and the inlet temperature have significant effects on the distribution of inclusions. It was also observed that a major part of the inclusion distribution was on the left and right sides of the mold, which are solidifying boundary layers. Further, the midzone of the mold had a lower concentration of inclusions. The inclusion motions were affected by several parameters, such as the velocity of the local zone, buoyancy force, natural convection, and interfacial tension.
- The inclusion diameter affected the inclusion distribution throughout the domain. Larger-sized inclusions had different distribution characteristics as compared to small (5-micron size) inclusions. It was found that larger inclusions were more evenly concentrated in the mold zone as compared to the smaller sizes. This implies that larger inclusions can be more influenced by the melt flow velocity and buoyancy forces.
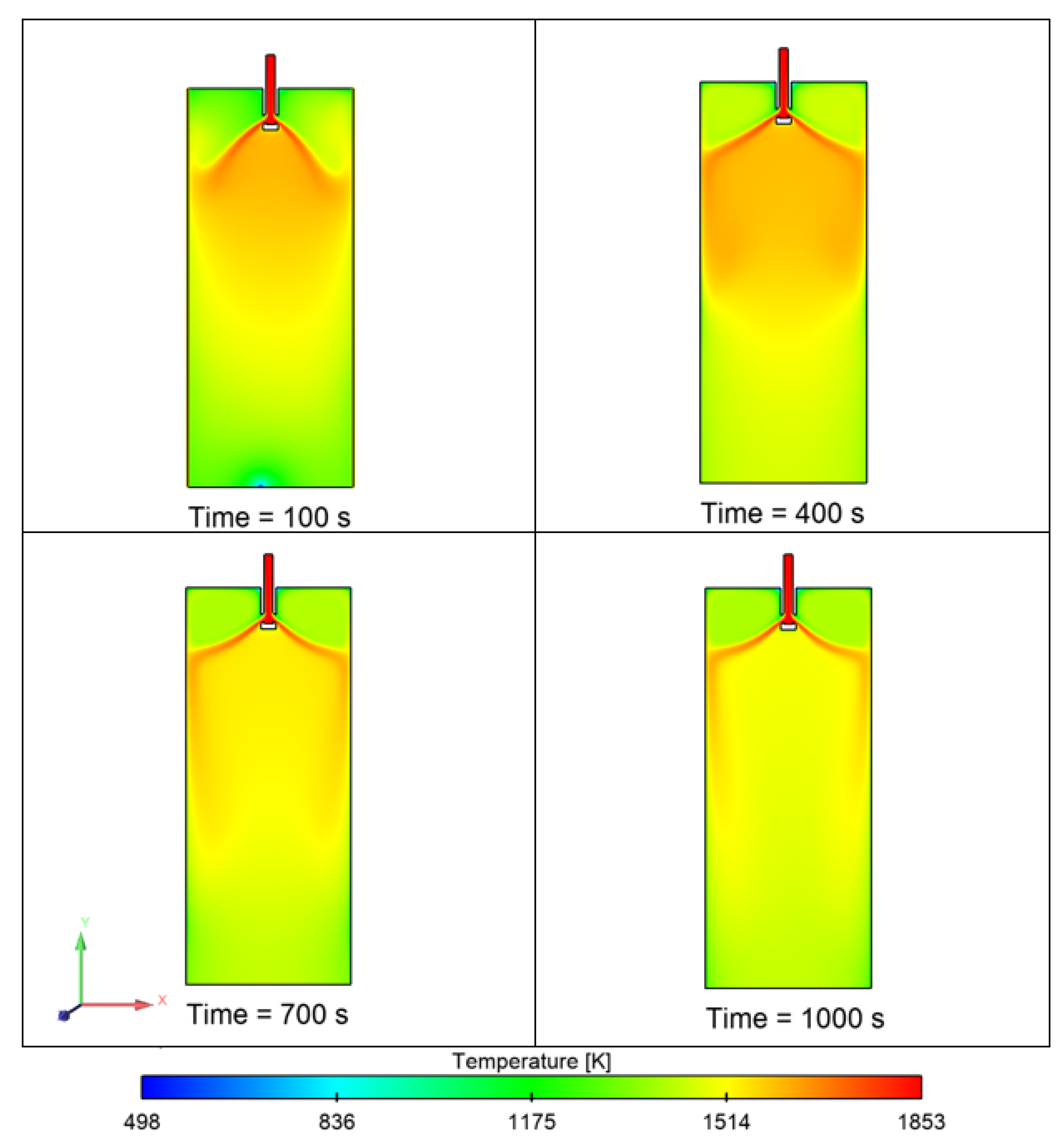
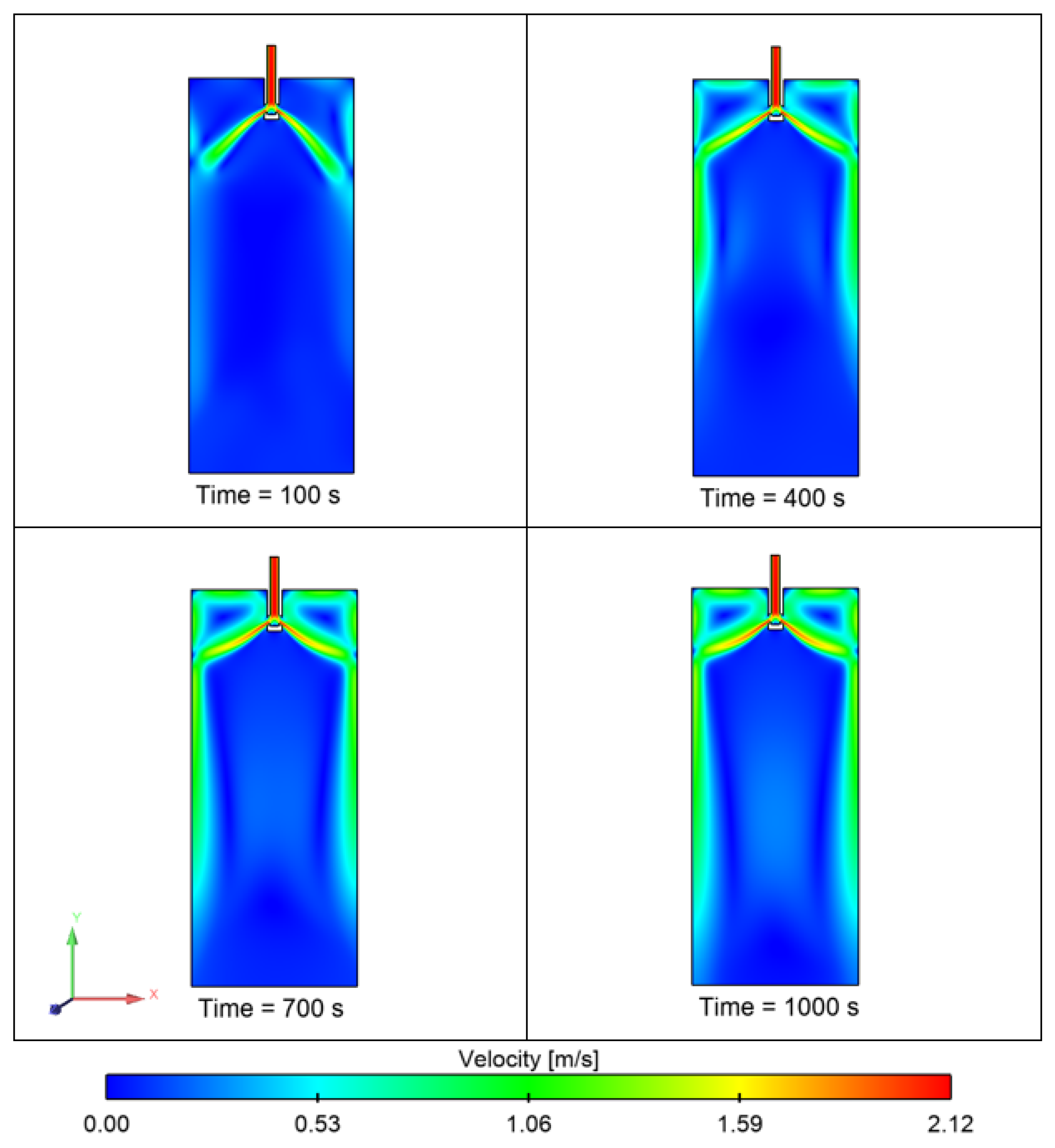
- The effect of temperature on the inclusion distribution was investigated to analyze the impact of natural convection and interfacial tension. It was noticed that the inclusion concentration was more evenly distributed in the mold as compared to lower-temperature conditions.
- The entrapment percentage of alumina inclusions was low over time when the interfacial tension equation was not used. However, the entrapment percentage varied in the case of sulfur mixing (using the empirical relationship in modeling). It was found that a 10 ppm sulfur concentration did not have much impact. However, we observed that there was a significant rise in the entrapment of alumina inclusions in the solidifying boundary layer at sulfur concentrations up to 70 ppm. Another important outcome was that the maximum entrapment of alumina inclusions occurred at 70 ppm, but the entrapment percentage was lower at 100 ppm sulfur.
- It was found that the removal percentage varied according to the sulfur concentration. The addition of sulfur at concentrations from 10 ppm to 70 ppm resulted in around a 4% increase in the removal of alumina inclusions (trapped in the solidifying shell), except for the 100-ppm case.
- The smaller-sized inclusion particles had a 25% higher chance of entrapment at the top level of the mold (slag layer). However, the larger-sized inclusion particles sustained their motion in the melt for a longer period, and their percentage entrapment was lower.
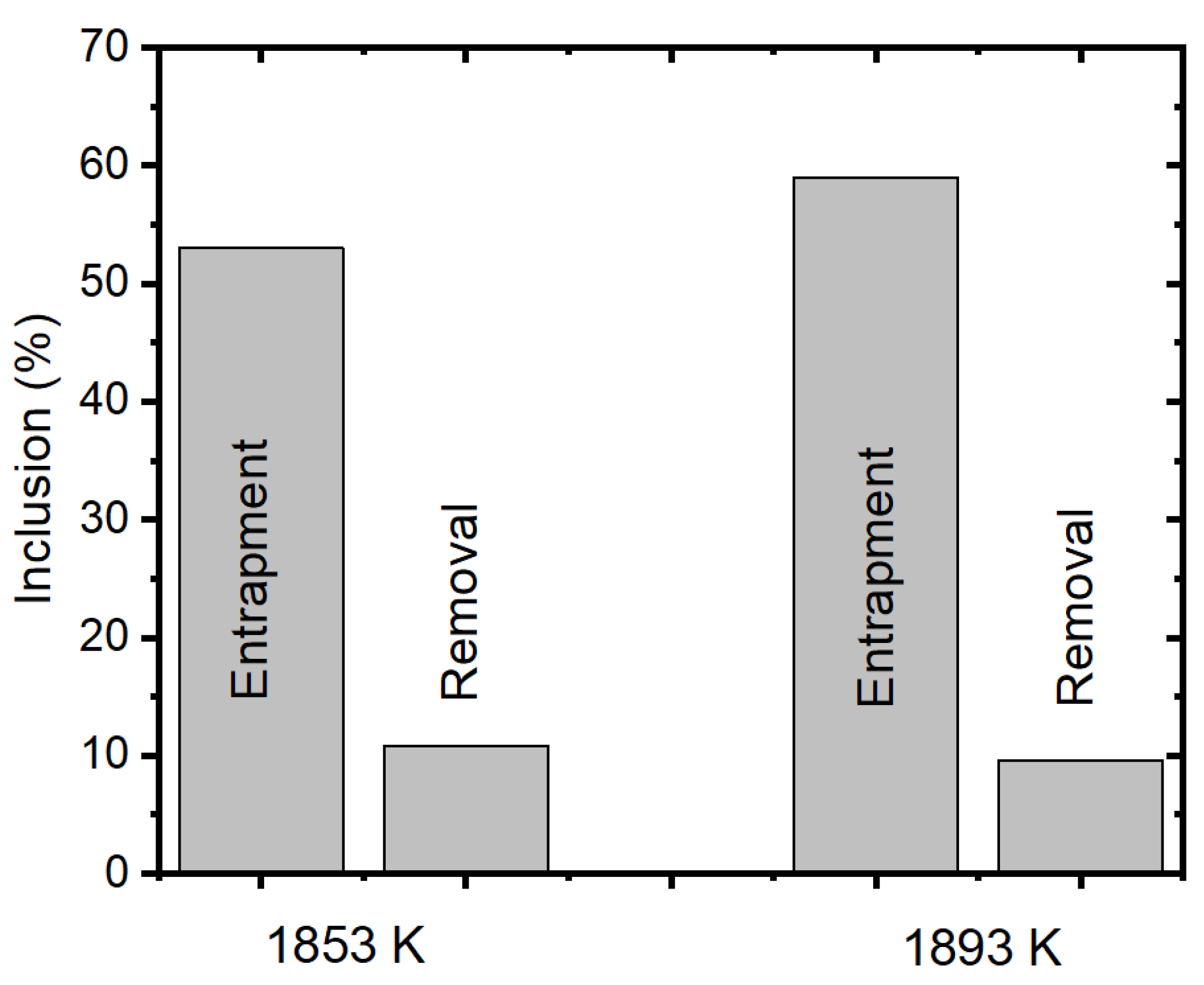
- It can be noted that the inclusion entrapment percentage increased as the inlet temperature was increased. The temperature at the inlet and top surface zone affected the surface tension and melt flow characteristics. Secondly, we also observed that the removal percentage did not vary significantly.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kovačič, M.; Župerl, U. Genetic programming in the steelmaking industry. Genet. Program. Evolvable Mach. 2020, 21, 99–128. [Google Scholar] [CrossRef]
- You, D.; Michelic, S.K.; Presoly, P.; Liu, J.; Bernhard, C. Modeling Inclusion Formation during Solidification of Steel: A Review. Metals 2017, 7, 460. [Google Scholar] [CrossRef] [Green Version]
- Qin, X.; Cheng, C.; Li, Y.; Zhang, C.; Zhang, J.; Jin, Y. A simulation study on the flow behavior of liquid steel in tundish with annular argon blowing in the upper nozzle. Metals 2019, 9, 225. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Yang, S.; Wang, F.; Li, J. Optimization on reducing slag entrapment in 150 × 1270 mm slab continuous casting mold. Materials 2019, 12, 1774. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merder, T.; Pieprzyca, J.; Warzecha, M.; Warzecha, P.; Hutny, A. Evolution of the numerical model describing the distribution of non-metallic inclusions in the tundish. Materials 2021, 14, 2229. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Yang, X.; Lai, C.; Tong, Z. Study on mns inclusion aggregation along continuous casting slab thickness of medium carbon structural steel. Metals 2022, 12, 56. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, Z.; Lv, M.; Li, X.; Song, B.; Fang, M. Evolution of Non-Metallic Inclusions in 27SiMn Steel. Metals 2022, 12, 718. [Google Scholar] [CrossRef]
- Tie, Z.; Tang, H.; Wang, K.; Miao, H.; Cai, S.; Xian, F.; Zhang, J. Effect of Flow Field Optimization of an Asymmetric Multi-Strand Tundish on the Quality Consistency of Cracking Con-Rod Steel. Materials 2022, 15, 3698. [Google Scholar] [CrossRef]
- Migas, P.; Ślęzak, M.; Karbowniczek, M.; Szczęch, S.; Hornik, A. Numerical Investigation of Outflow of Non-Metallic Inclusions during Steel Refining in the Ladle. Materials 2022, 15, 3039. [Google Scholar] [CrossRef]
- Jeong, J.; Park, D.; Shim, S.; Na, H.; Bae, G.; Seo, S.-J.; Lee, J. Interfacial tension between SPFH590 microalloyed steel and alumina. Metall. Mater. Trans. B 2019, 51, 690–696. [Google Scholar] [CrossRef]
- Jeong, J.; Park, D.; Shim, S.; Na, H.; Bae, G.; Seo, S.J.; Lee, J. Prediction of Behavior of Alumina Inclusion in Front of Solid–Liquid Interface in SPFH590 Steel. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2020, 51, 690–696. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, J.; Dong, Q.; Zhou, Q.H. Fluid flow and heat transfer with nail dipping method in mould during continuous casting process. Ironmak. Steelmak. 2019, 46, 855–864. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, J.; Dong, Q.; Zhou, Q.H. Challenges in Special Steel Making. Ironmak. Steelmak. 2019, 46, 855–864. [Google Scholar] [CrossRef]
- Siddiqui, M.I.H.; Maurya, A.; Ashraf, M.; Asiri, F. Modeling of Inclusion Motion Under Interfacial Tension in a Flash Welding Process. In Advanced Computational Methods in Mechanical and Materials Engineering; CRC Press: Boca Raton, FL, USA, 2021; pp. 91–110. [Google Scholar]
- Mukai, K.; Zeze, M. Motion of fine particles under interfacial tension gradient in relation to continuous casting process. Steel Res. 2003, 74, 131–138. [Google Scholar] [CrossRef]
- Wang, Z.; Mukai, K.; Lee, J. Behavior of fine bubbles in front of the solidifying interface. ISIJ Int. 1999, 39, 553–562. [Google Scholar] [CrossRef]
- Matsushita, T.; Mukai, K.; Zeze, M. Correspondence between surface tension estimated by a surface thermodynamic model and number of bubbles in the vicinity of the surface of steel products in continuous casting process. ISIJ Int. 2013, 53, 18–26. [Google Scholar] [CrossRef] [Green Version]
- Scheller, P.R.; Lee, J.; Yoshikwa, T.; Tanaka, T. Treatise on Process Metallurgy Volume 2: Process Phenomena. In Treatise on Process Metallurgy; Seetharaman, S., Ed.; Elsevier: Oxford, UK, 2013; Volume 2, pp. 119–139. [Google Scholar]
- Shibata, H.; Yin, H.; Yoshinaga, S.; Emi, T.; Suzuki, M. In Situ Observation of Engulfment and Pushing of Nonmetallic Inclusions in Steel Melt by Advancing Melt/Solid Interface. ISIJ Int. 1998, 38, 49–56. [Google Scholar] [CrossRef] [Green Version]
- Yin, H.; Emi, T. Marangoni flow at the gas/melt interface of steel. Metall. Mater. Trans. B 2003, 34, 483–493. [Google Scholar] [CrossRef]
- Thomas, B.G. Modeling of the continuous casting of steel—Past, present, and future. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2002, 33, 795–812. [Google Scholar] [CrossRef]
- Siddiqui, M.I.H.; Jha, P.K. Assessment of turbulence models for prediction of intermixed amount with free surface variation using CLSVOF method. ISIJ Int. 2014, 54, 2578–2587. [Google Scholar] [CrossRef]
- Mazumdar, D.; Evans, J.W. Modeling of Steelmaking Processes; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Sahai, Y.; Emi, T. Tundish Technology for Clean Steel Production; World Scientific: Singapore, 2008. [Google Scholar]
- Thomas, B.G. Review on Modeling and Simulation of Continuous Casting. Steel Res. Int. 2018, 89, 1700312. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, J.; Dong, Q.; Zhou, Q.H. Modelling on inclusion motion and entrapment during the full solidification in curved billet caster. Metals 2018, 5, 320. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Li, B. Effect of vertical length on asymmetric flow and inclusion transport in vertical-bending continuous caster. Powder Technol. 2018, 323, 403–415. [Google Scholar] [CrossRef]
- Siddiqui, M.I.H.; Geleta, D.D.; Bae, G.; Lee, J. Numerical Modeling of the Inclusion Behavior during AC Flash Butt Welding. ISIJ Int. 2020, 60, 2503–2511. [Google Scholar] [CrossRef]
- Fei, P.; Min, Y.; Liu, C.; Jiang, M. Effect of continuous casting speed on mold surface flow and the related near-surface distribution of non-metallic inclusions. Int. J. Miner. Metall. Mater. 2019, 46, 855–864. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, L. Determination for the Entrapment Criterion of Non-metallic Inclusions by the Solidification Front during Steel Centrifugal Continuous Casting. Ironmak. Steelmak. 2016, 46, 855–864. [Google Scholar] [CrossRef]
- Chen, W.; Ren, Y.; Zhang, L. Large Eddy Simulation on the Fluid Flow, Solidification and Entrapment of Inclusions in the Steel Along the Full Continuous Casting Slab Strand. JOM 2018, 46, 855–864. [Google Scholar] [CrossRef]
- Kölbl, N.; Harmuth, H. Automated break temperature determination of mould slags for the continuous casting of steel based on temperature-dependent viscosity data. Ironmak. Steelmak. 2020, 47, 899–902. [Google Scholar] [CrossRef]
- Chen, W.; Ren, Y.; Zhang, L.; Scheller, P.R. Numerical Simulation of Steel and Argon Gas Two-Phase Flow in Continuous Casting Using LES + VOF + DPM Model. Ironmak. Steelmak. 2019, 71, 1158–1168. [Google Scholar] [CrossRef]
- Chakraborty, S.; O’Malley, R.J.; Bartlett, L. Removal of Alumina Inclusions from Molten Steel by Ceramic Foam Filtration. Int. J. Met. 2021, 15, 1006–1020. [Google Scholar] [CrossRef]
- Mukai, K.; Zeze, M.; Morohoshi, T. Motion of fine particles under interfacial tension gradient in relation to solidification of steel. Mater. Sci. Forum 2006, 508, 211–220. [Google Scholar] [CrossRef]
- Iida, T.G. RIL: The Physical Properties of Liquid Metals; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Maurya, A.; Jha, P.K. Influence of electromagnetic stirrer position on fluid flow and solidification in continuous casting mold. Appl. Math. Model. 2017, 48, 736–748. [Google Scholar] [CrossRef]
- Cho, S.M.; Thomas, B.G.; Hwang, J.Y.; Bang, J.G.; Bae, I.S. Modeling of inclusion capture in a steel slab caster with vertical section and bending. Metals 2021, 11, 654. [Google Scholar] [CrossRef]
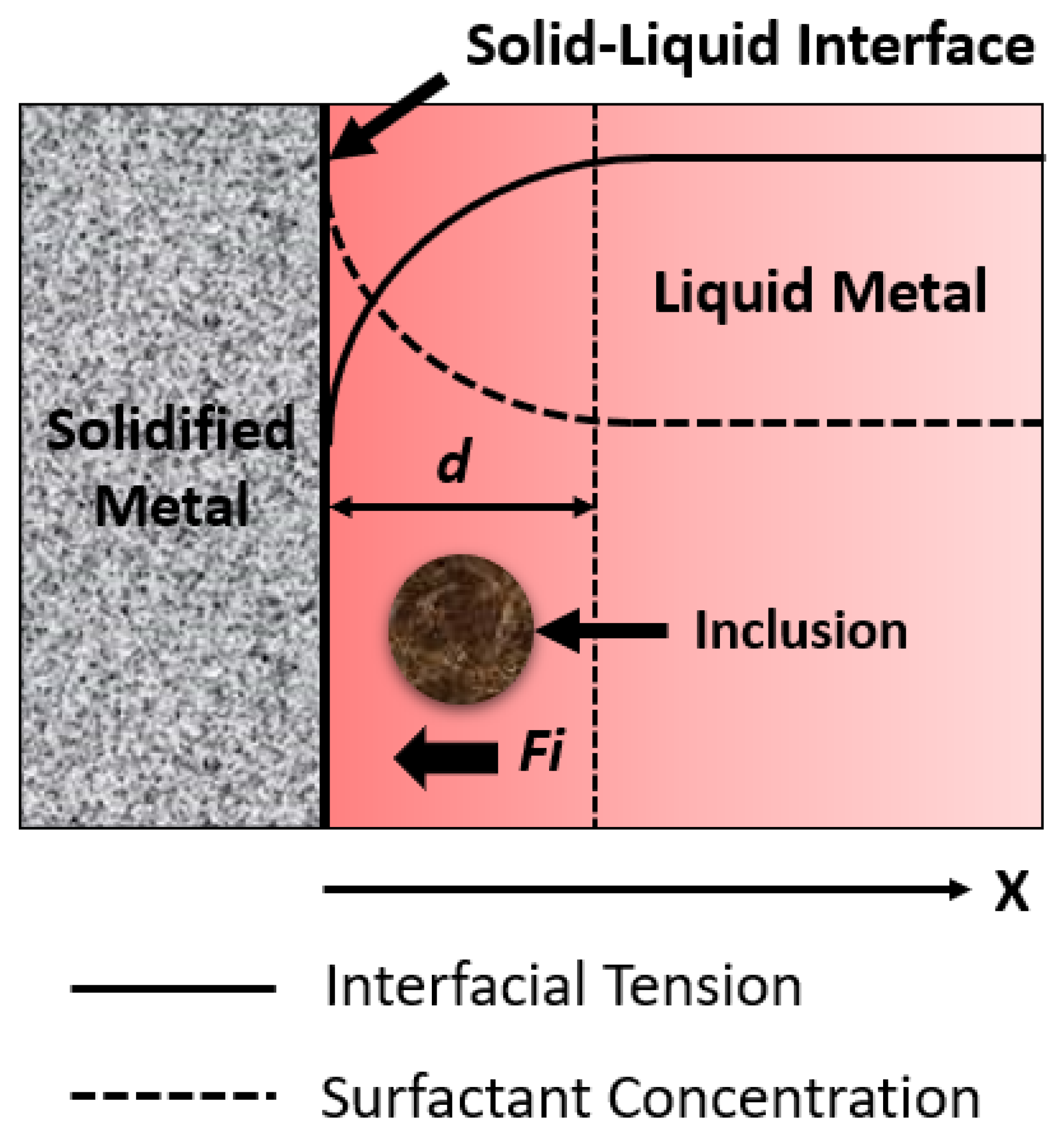

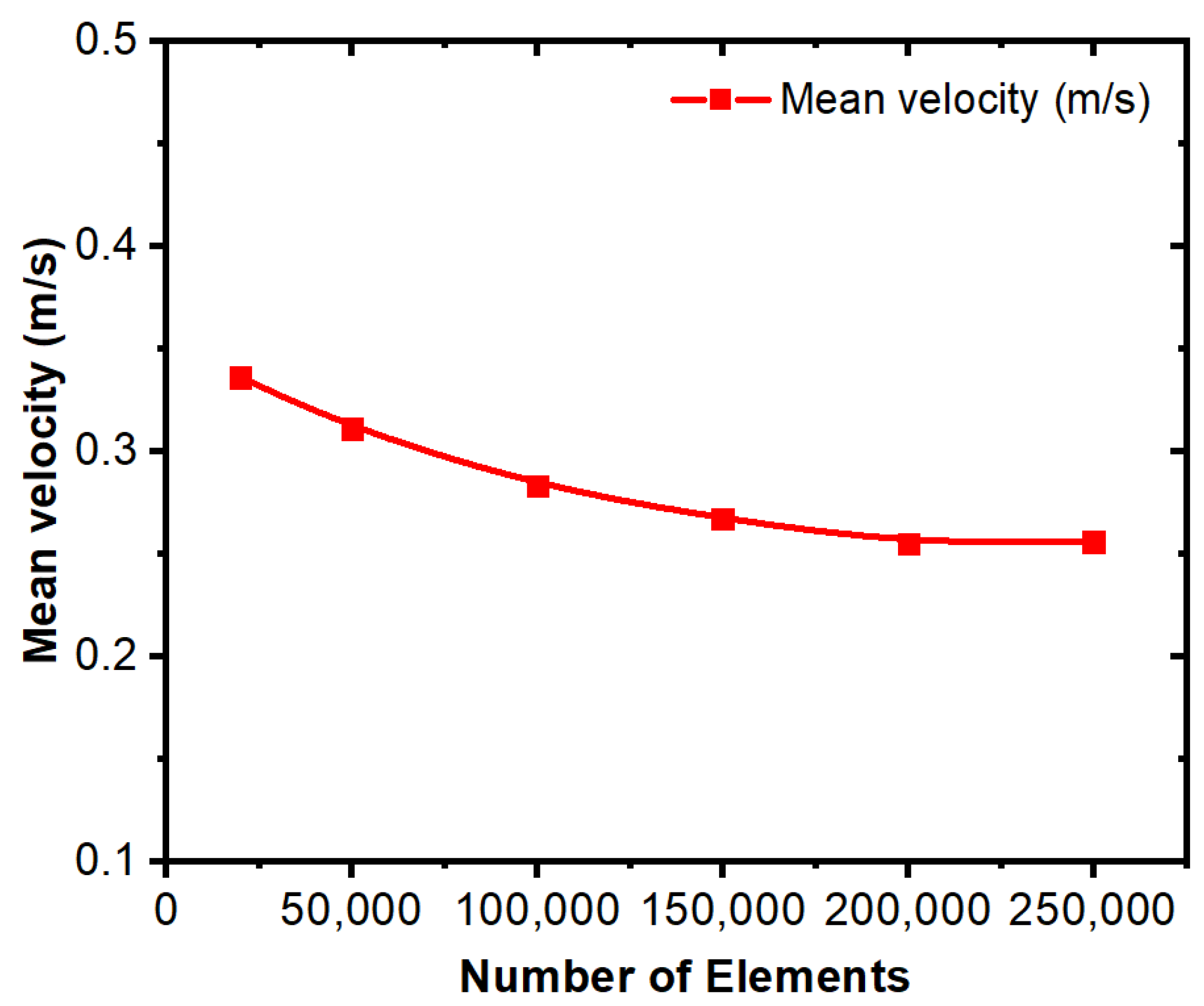
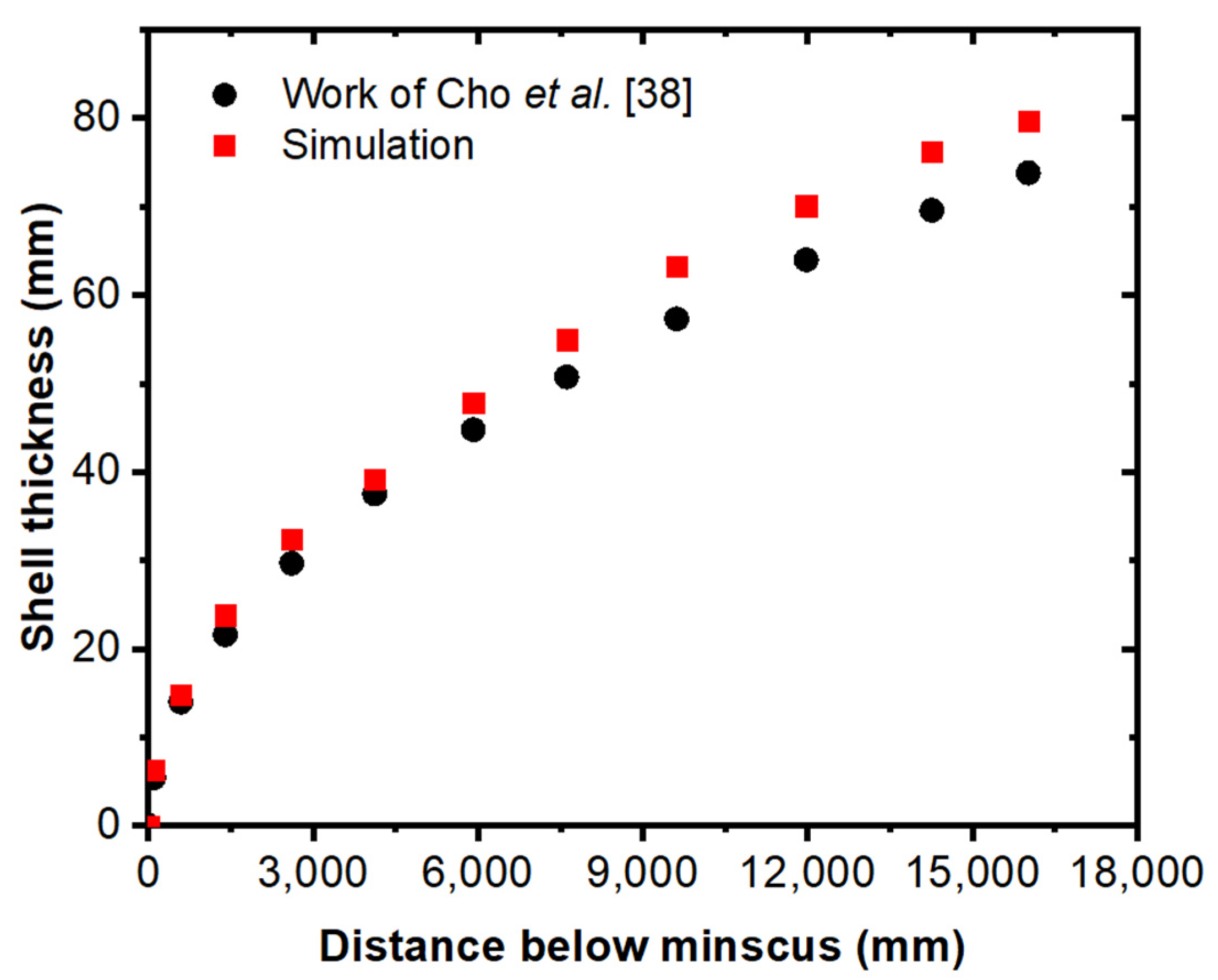
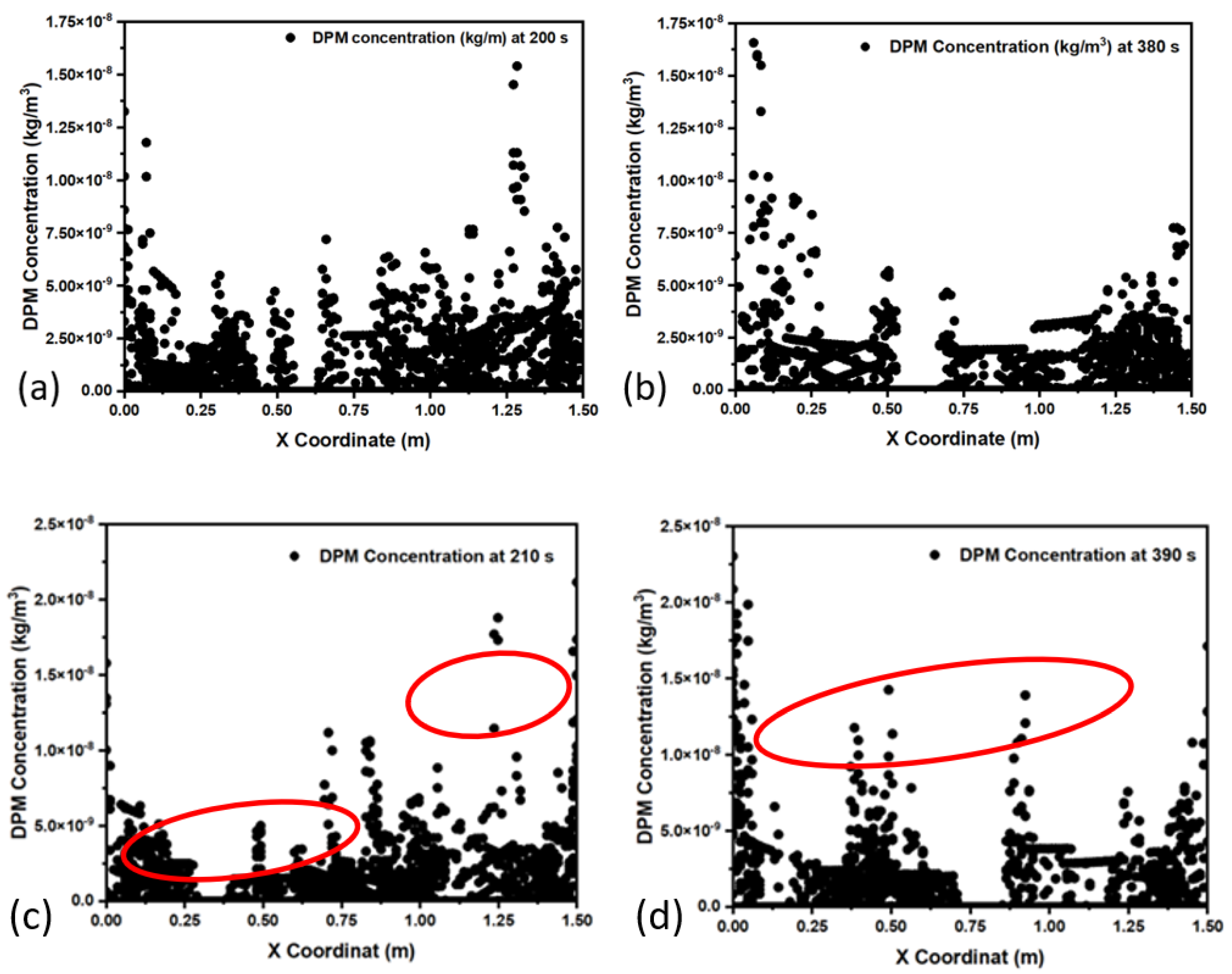
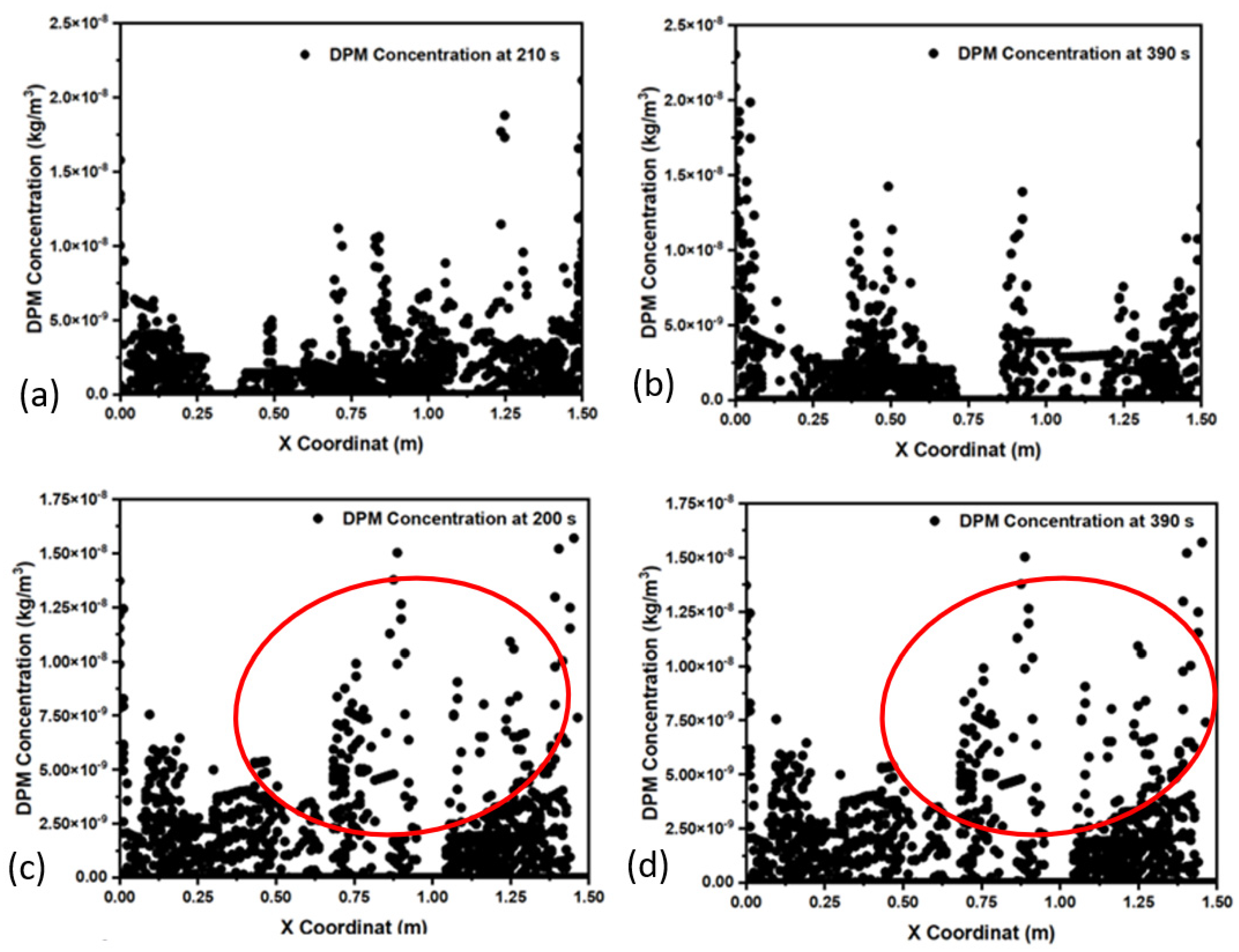
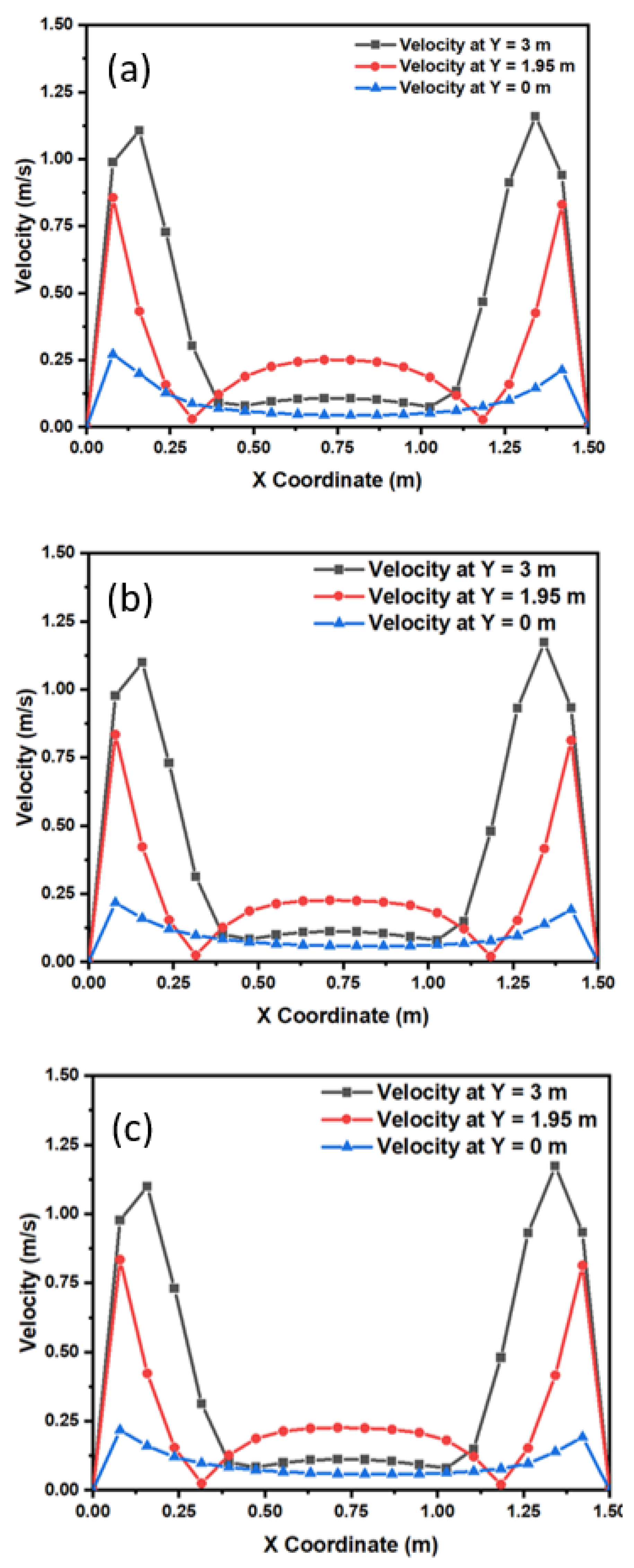

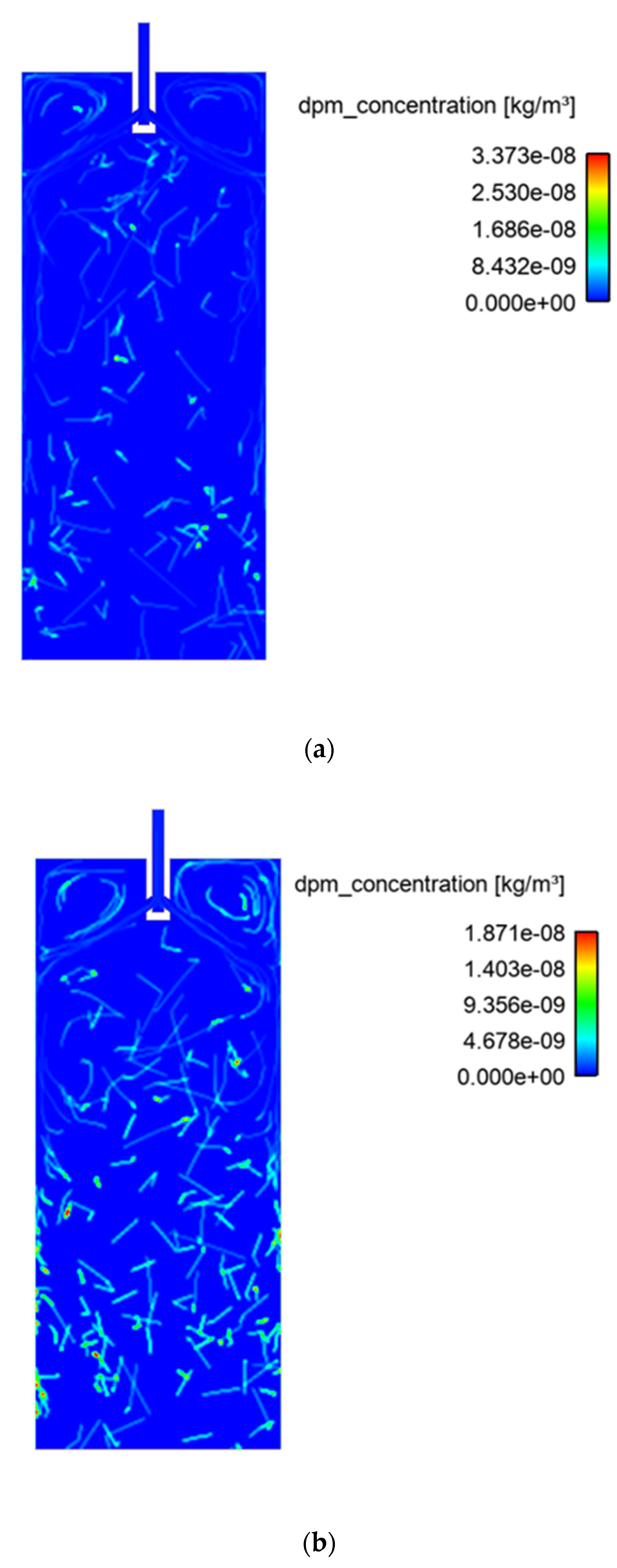
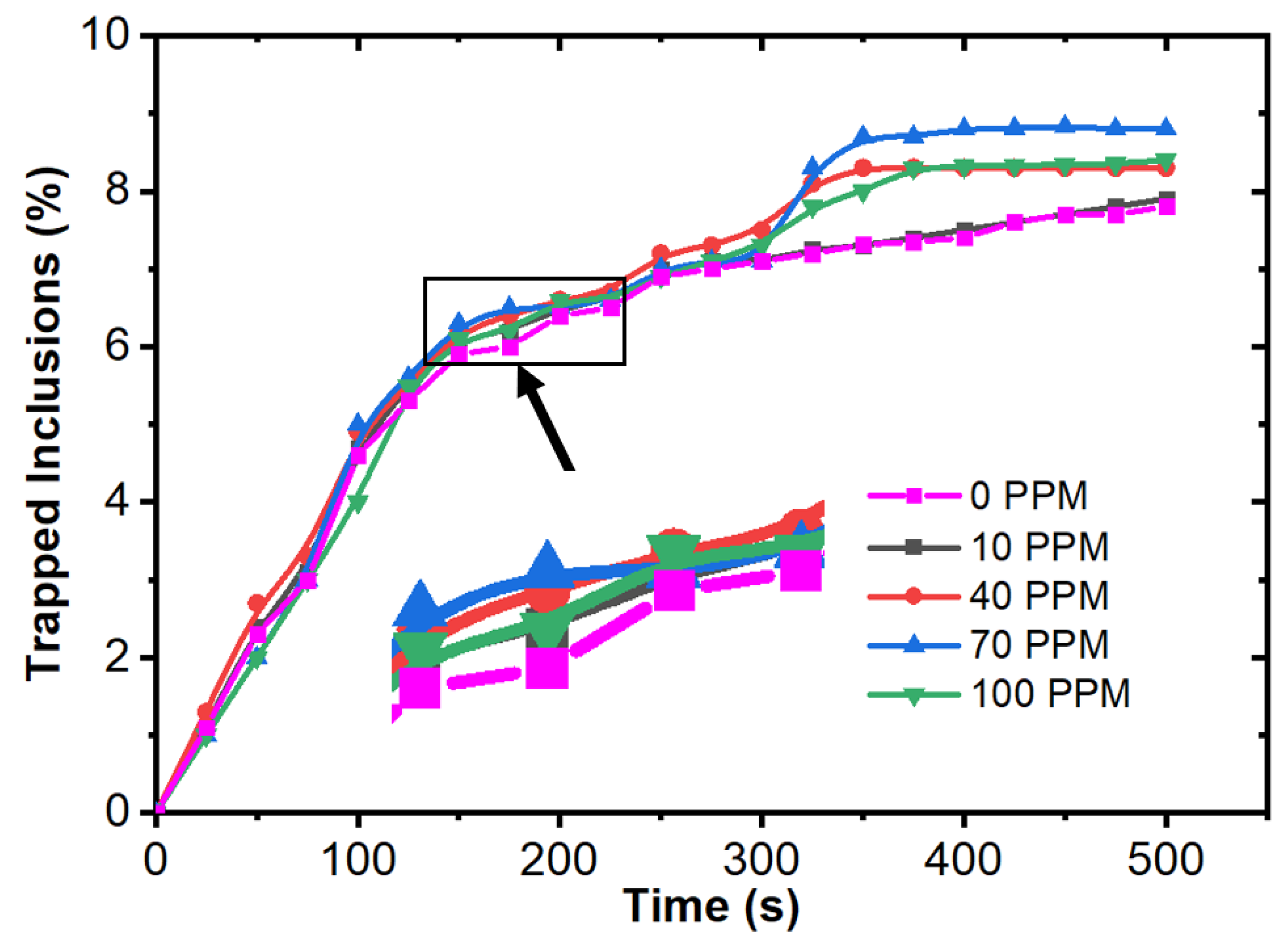
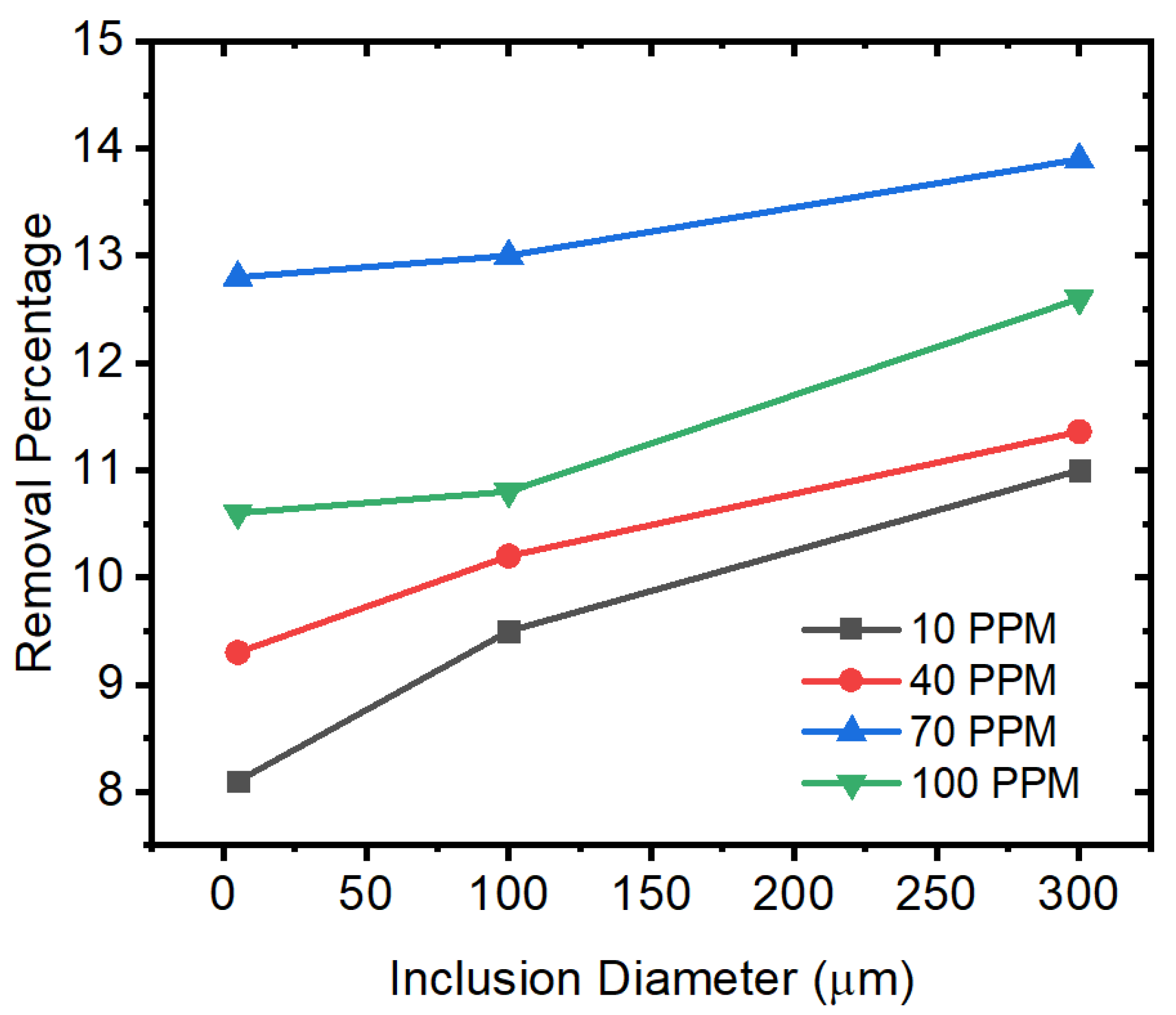
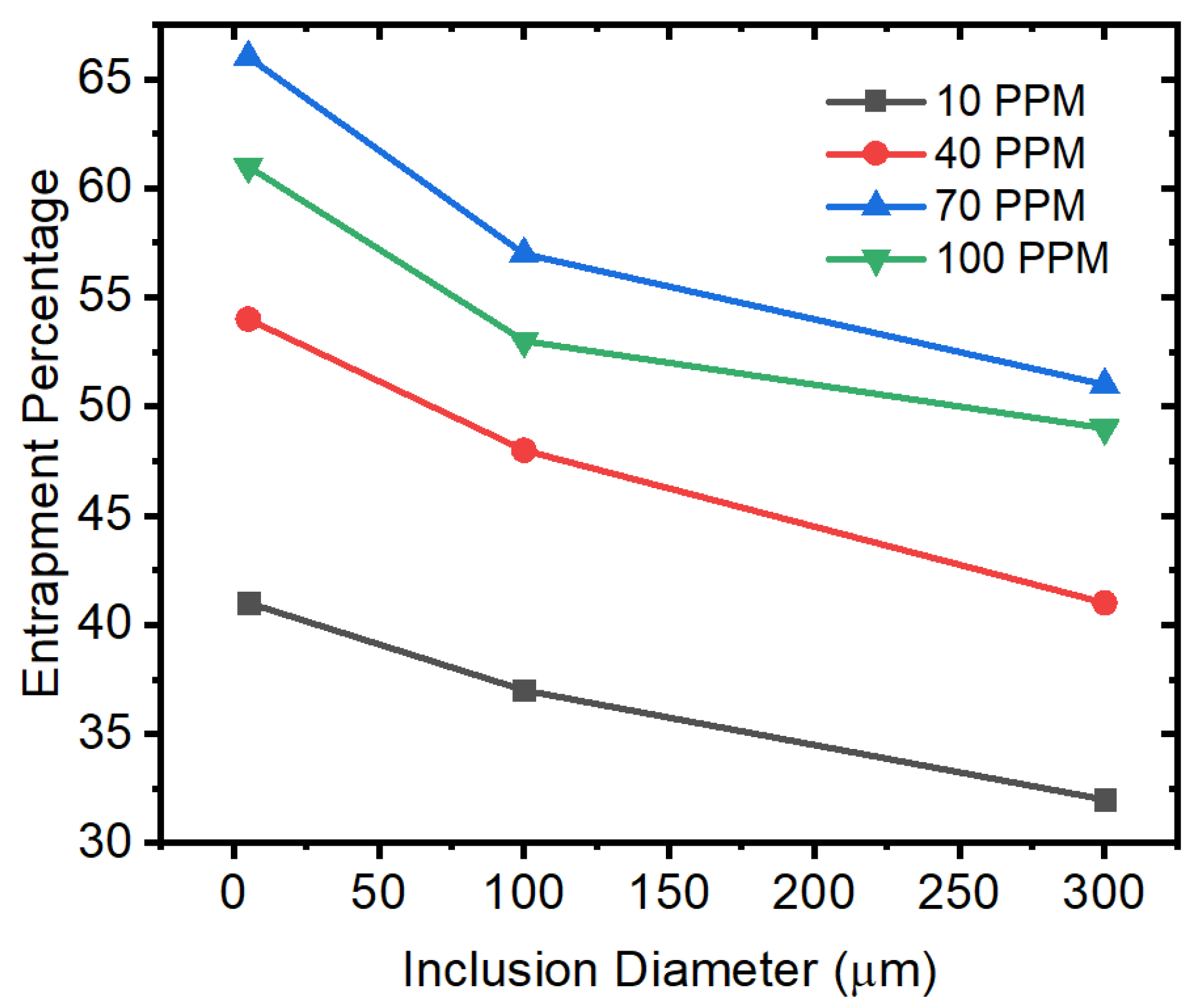
| Element | C | Mn | Si | P | Al | Nb |
|---|---|---|---|---|---|---|
| Concentration | ≤0.1 | ≤3.0 | ≤0.5 | ≤0.1 | ≤0.1 | ≤0.1 |
| Parameters | Values |
|---|---|
| Density of molten steel [36] | ρ (kg m−3) = 8621.17 − 0.88T |
| * Viscosity of molten steel [36] | μ (mPa s) = 0.2388 ∗ exp(47.44/(RT)) |
| Specific heat [37] | 750 J kg−1 K−1 |
| Thermal conductivity [37] | 41 W m−1 K−1 |
| Surface tension (σL) and interfacial tension (σPL) | Equations (9) and (10) {Ref: [10,11]} |
| Solidus temperature | 1781 K |
| Liquidus temperature | 1798 K |
| Alumina inclusion size | 5, 100, and 300 μm |
| Process Parameters | Values |
|---|---|
| Mold width | 1500 mm |
| Mold length | 3600 mm |
| SEN submergence depth | 160 mm |
| Nozzle port downward angle | 15 degree |
| Inlet velocity | 2 m/s |
| Outlet | Pressure outlet condition |
| Alumina inclusion density | 2500 kg/m3 |
| Shell surface temperature | 1273 K |
| Mold conductivity | 315 W/mk |
| Latent heat | 272,000 (J/kg) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddiqui, M.I.H.; Albaqami, A.; Arifudin, L.; Alluhydan, K.; Alnaser, I.A. Simulation of Inclusion Particle Motion Behavior under Interfacial Tension in Continuous Casting Mold. Materials 2022, 15, 7458. https://doi.org/10.3390/ma15217458
Siddiqui MIH, Albaqami A, Arifudin L, Alluhydan K, Alnaser IA. Simulation of Inclusion Particle Motion Behavior under Interfacial Tension in Continuous Casting Mold. Materials. 2022; 15(21):7458. https://doi.org/10.3390/ma15217458
Chicago/Turabian StyleSiddiqui, Md Irfanul Haque, Ayidh Albaqami, Latif Arifudin, Khalid Alluhydan, and Ibrahim Abdullah Alnaser. 2022. "Simulation of Inclusion Particle Motion Behavior under Interfacial Tension in Continuous Casting Mold" Materials 15, no. 21: 7458. https://doi.org/10.3390/ma15217458
APA StyleSiddiqui, M. I. H., Albaqami, A., Arifudin, L., Alluhydan, K., & Alnaser, I. A. (2022). Simulation of Inclusion Particle Motion Behavior under Interfacial Tension in Continuous Casting Mold. Materials, 15(21), 7458. https://doi.org/10.3390/ma15217458








