After numerical calculations, the following quantities and material behavior were assessed:
3.2. Assessment of the Level of Selected Components of the Stress Tensor and Selected Measures of Geometric Constraints
Along with the evaluation of the size and change of plastic zones, for the selected load moments presented in
Table 2, for each of the three tested specimens, the level of selected measures of geometric constraints, mentioned above, was assessed. Among them, the following can be distinguished:
Maximum stresses opening the crack surfaces, normalized by the yield point, .
Ratio of the mean stress and yield point, .
Stress triaxiality parameter, defined as the quotient of stresses in the thickness direction and the sum of the other two principal components of the stress tensor, .
Ratio of the effective stress calculated using the HMH hypothesis and yield point, .
Ratio of the mean stress and effective stress calculated using the HMH hypothesis, .
The changes of the above-mentioned quantities were plotted as a function of the normalized distance from the crack tip, calculated as
ψ =
r0·
σ0/
J, and as a function of the distance from the initial position of the crack tip, designated as
r0. The results of the analysis are presented in
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11.
Figure 7 shows the changes in the distribution of the maximum stresses opening the crack surfaces,
. For each of the analyzed thicknesses, it can be noticed that with the increase of the load, accompanied by the increase of the
J-integral and the increase of the crack length, the maximum stresses opening the crack surfaces slightly increase, reaching an almost steady value. Their value for moments with significant crack growth is
σzz = 5.0·
σ0. As the fracture length increases, accompanied by an increase in the
J-integral value, the position of the maximum stresses opening the crack surfaces increases relative to the initial point where the crack tip was located—the maximum stresses opening crack surfaces move away from the initial crack tip position. As can be seen, for each of the thicknesses, a different nature of the change in the distribution of the maximum stresses opening the crack surfaces,
, for the same material is observed, which is conditioned by completely different
J-
R curves that were used to simulate the crack propagation. Summarizing the graphs shown in
Figure 7, it can be stated that the thicker the specimen, the further from the crack tip the maximum stresses opening the crack surfaces are in the physical coordinates.
Almost identical conclusions can be drawn by analyzing the distribution of mean stresses normalized by the yield point,
(
Figure 8). With the approach to the crack’s tip, the mean stresses increase, reaching a maximum at a given distance, and then their value decreases—they show the character of changes identical to the maximum stresses opening the crack surfaces. As the external load increases, the value of the maximum mean stresses increases and tends to the value equal to
σm = 4.0·
σ0. The position of the maximum mean stresses depends on the thickness of the specimen—the thicker the specimen, the further from the initial position of the crack tip the maximum mean stress in the physical coordinates is. The locations of the maximum mean stresses and their values quite significantly depend on the external load.
Figure 9 shows the distributions of the stress triaxiality coefficient defined for the characteristic moments provided in
Table 2, defined as
. The graphs indicate that some of the curves are characteristic of the significant crack length increases observed in experimental tests [
5,
6]. In close proximity to the crack tip, the value of the triaxiality coefficient is equal to 0.5, then as you move away from the fracture tip, the triaxiality coefficient decreases to a value equal to the Poisson’s coefficient, i.e., 0.3. It should be noted that the graphs of changes in the value of the stress triaxiality coefficient have a different character, depending on whether they are plotted as a physical function or a normalized distance from the crack tip. It is left to the reader to interpret this conclusion.
Figure 10 shows the changes of effective stresses calculated according to the HMH hypothesis, with increasing external load and moving away from the crack tip. Near to the crack tip, values of effective stresses at the level of
σeff = 3.0·
σ0 are observed, and then as you move away from the crack tip, the value of effective stresses drops to the level equal to the yield point. The value of effective stresses equal to or greater than the yield point means that the material in front of the crack is fully plasticized. The decrease in the value of effective stresses below the yield point, visible in
Figure 10b,d,f, means that the material has not plasticized yet. The reader can confront these graphs with the appropriate distributions of plastic zones, which are shown in
Figure 4,
Figure 5 and
Figure 6, drawing conclusions individually.
Figure 11 shows the influence of the external load and the distance from the crack tip on the distribution of the quotient of average stresses and effective stresses. The quotient of
, with the approach to the crack tip, reaches a maximum, the value of which only slightly depends on the thickness of the specimen and the applied external load. There is a slight increase in the maximum value of the quotient
with increasing specimen thickness, as well as a quite significant increase with increasing external load. For a specimen with a thickness of
B = 5 mm, the quotient
does not exceed the value equal to 3, while for the thicknesses
B = 10 and
B = 15 mm, the quotient
for significant increases in the crack length reaches the value equal to 3.5. It can be noticed that the distributions of the quotient
in their graphic form resemble the diagrams of changes of average stresses, normalized by the yield point. As the crack crest is approached, the value of the quotient
increases, which reaches its maximum, and then the value of this quotient decreases. The position of the maximum of the ratio
is closely related to the external load—the higher its value, the further the maximum of the quotient
physically is from the initial position of the crack tip.
Figure 12, for one of the geometries considered in the study (specimen with a thickness of
B = 5 mm), shows how the levels of the principal components of the stress tensor, effective stresses and mean stresses change at different normalized points near the crack tip, depending on the external load expressed by the
J-integral value. It should be noted that the standardized position in front of the crack tip, marked with
ψ, was determined in relation to the initial physical location of the crack tip. Along with moving away from the crack tip, a decrease in the level of the main components of the stress tensor and the mean stresses,
σm/
σ0, is observed. In the very close vicinity of the crack tip for
ψ∈〈0.5, 1.0〉, an increase in the values of the main components of the stress tensor and mean stresses is observed. Moreover, for
ψ = 0.5, an almost constant value of effective stresses can be noticed, at the level of
σeff = 1.5·
σ0, which, at the moment of increasing the crack length by about 0.2 mm, significantly increases to the level of
σeff = 2.0·
σ0. Within the normalized distances from the initial position of the crack tip,
ψ∈〈1.0, 3.0〉, effective stresses until the crack length increases by 0.2 mm are practically constant and equal to the yield point. For further normalized distances from the crack tip, the level of effective stresses drops even below the yield point with increasing external load. The reader is left here to draw detailed conclusions from the analysis of
Figure 12d, as well as to evaluate the curves shown in
Figure 12f, which presents for a specimen with a thickness of
B = 5 mm changes in the quotient
for seven selected normalized distances from the crack tip, with increasing external load, expressed by the
J-integral value.
The effect of the normalized distance from the initial position of the crack tip and the external load expressed through the
J-integral on the value of the stress triaxiality coefficient, defined as
, for a specimen with a thickness of
B = 5 mm, is shown in
Figure 13. In close proximity to the crack tip, i.e.,
ψ = 0.5, it can be seen that the level of the stress triaxial coefficient,
, oscillates around the value of 0.5, as for the normalized distance of
ψ = 1.0, while in the latter case there is a slight decrease in the value of the stress triaxiality coefficient. As you move away from the crack tip, with increasing external load, you can notice a decrease in the level of the stress triaxiality coefficient (almost linear for the normalized distance
ψ = 2.0), to a value equal to 0.3, which corresponds to the value of the Poisson’s coefficient assumed in the calculations,
ν = 0.3. It should be noted that the farther it is from the crack tip, the faster the value of the stress triaxiality coefficient,
, reaches the value equal to
ν = 0.3 (i.e., it occurs at a lower level of the
J-integral, i.e., at a lower level of external load).
During the numerical calculations, the level of accumulated plastic strains near the crack tip was also assessed for the characteristic moments presented in
Table 2 (
Figure 14). The level of accumulated plastic strains and their distribution in front of the crack tip depends to a large extent on the specimen thickness and the external load, which for different geometries is accompanied by a different increase in the crack length. The analysis of the distributions presented in
Figure 14, combined with the assessment of the developing plastic zones, shows that in the area 1 mm from the crack tip, we are dealing with significant plastic deformations, regardless of the thickness of the specimen. To illustrate the proper level of accumulated plastic strains, in
Figure 14h,i, the ordinate has a logarithmic scale. The conclusions drawn from these three additional graphs, based on their analysis and an overview of the developing plastic zones (
Figure 4,
Figure 5 and
Figure 6), are left to the reader.
3.3. Analysis of Selected Quantities of Elastic–Plastic Fracture Mechanics
The above analysis of growing plastic zones because of increasing load, along with the assessment of the level of the stress tensor components, accumulated plastic strains or selected measures of geometric constraints, allows us to assess the behavior of 41Cr4 steel during the fracture process. For the three SEN(B) specimens, differing in thickness, the changes in the force,
P, loading the specimen, the increasing value of the
J-integral, the increase in the length of the crack,
da, the increasing crack tip opening displacement,
δT, and the changing value of the maximum stresses opening crack surfaces,
σ22_max/
σ0, are presented in
Figure 15. These graphs were prepared both as a function of the crack mouth displacement,
δM, which was measured at the edge of the specimen (at the free edge), and as a function of the load line displacement,
vLL, which was dictated by the fact that various normative documents [
1,
2,
3] assume an experimental analysis, based on other recommendations, as to the determination of the energy necessary to estimate the experimental value of the
J-integral.
In the case of a specimen with a thickness of
B = 5 mm (
Figure 15a,d), initially a stable increase in the crack length can be observed, and then, after reaching the opening of the joint surface at the level of
δM = 1.5 mm, there is a jump in the length of the crack, which is accompanied by a decreased force loading the specimen, a sharp increase in the
J-integral and a slight decrease in the value of the maximum stresses opening the crack surfaces. In the remaining analyzed range, the cracking process stabilizes, and the crack length increases quite steadily, which is accompanied by an almost linear increase in the value of the
J-integral and an increase in the crack tip opening displacement.
A slightly different nature of the changes can be noticed in the case of the analysis of the obtained results for the SEN(B) geometry with a thickness of
B = 10 mm. While in the case of geometry with a thickness of
B = 5 mm, a significant step increase in the crack length was observed, amounting to over 1 mm, for geometry with a thickness of
B = 10 mm, we speak of a step increase of 0.5 mm. This is reflected in
Figure 15b,e. During the presented load range, almost linear increases in the crack tip opening displacement,
δT, and the increase in the fracture length,
da, both as a function of the crack mouth displacement,
δM, and the load line displacement,
vLL, are observed. When the displacement of the load line displacement reaches the value
vLL = 1 mm, the crack length increases rapidly—the
J-integral value increases almost twice. It can be noted that the value of the maximum stresses opening the crack surfaces is almost constant and amounts to approximately (4.5–5.0)·
σ0. This means that in the case of the thickness
B = 10 mm, the increase in the length of the crack was not so significant as to affect the value of this measure of geometric constraints. It has been shown in [
13] that the increase in the crack length is usually accompanied by a decrease in the maximum values of stresses opening the crack surfaces. In the case of the analyzed geometry and the material used, the increase in the fracture length by over 2.5 mm (i.e., by 10% in relation to the width of the specimen,
W) significantly affects the level of maximum stresses opening the crack surfaces. This conclusion is also confirmed by the evaluation of the cracking process described in the previous paragraph for a specimen with a thickness of
B = 5 mm (
Figure 15a,d).
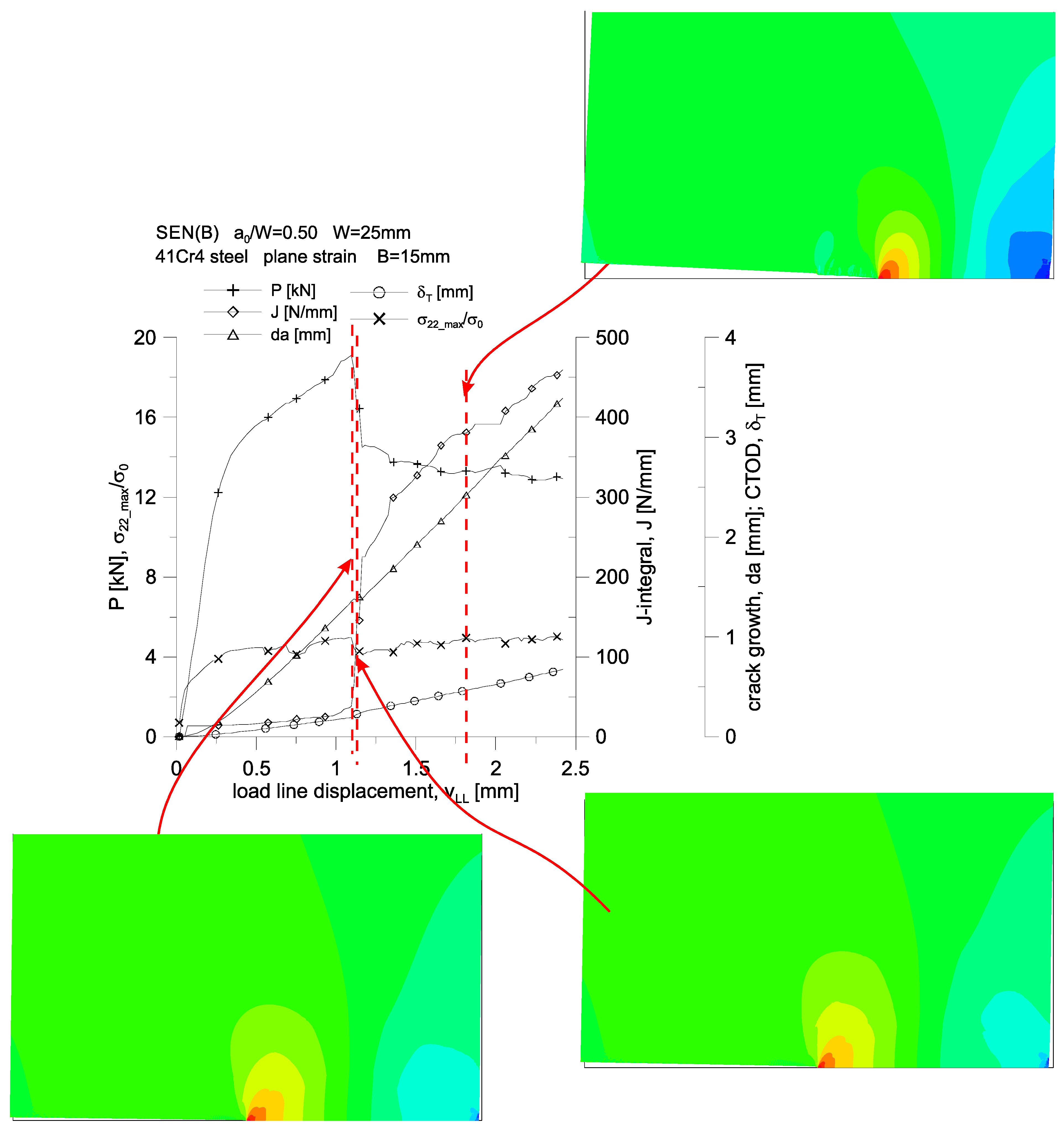
A stepwise, significant increase in the crack length is observed for a specimen with a thickness of
B = 15 mm (
Figure 15c,f)—it occurs when the load line displacement value,
vLL, is approximately equal to 1.1 mm. It can be noticed then that there is a sharp almost four-fold increase in the value of the
J-integral, while the value of the force loading the specimen decreases by about 25%. For the entire presented load spectrum, an almost linear increase in the crack length and an increase in the crack tip opening displacement are observed. This specimen is also characterized by an almost constant value of the maximum stresses opening the crack surfaces, amounting to about 4.0·
σ0 for the thickness
B = 15 mm.
Summarizing the briefly discussed course of the fracture process of 41Cr4 steel, it should be noted that the abrupt increases in the crack length are generally accompanied by a rapid increase in the value of the J-integral, as well as a decrease in the force loading the specimen. The remaining parameters show rather stable behavior against the rapidly growing crack.
When assessing changes in the basic fracture mechanics parameters, such as the
J-integral or the crack tip opening displacement,
δT, the relationship of both quantities with each other through the Shih relationship [
14] and the relationship of the
J-integral with the energy necessary to increase the fracture length cannot be ignored. Shih [
14] related the
J-integral with the crack tip opening displacement,
δT, with the form relation:
where
δT is the crack tip opening displacement,
J is the
J-integral,
σ0 is the yield point and
m is the proportionality coefficient, depending on the parameters of the Ramberg–Osgood curve, yield point, Young’s modulus and the stress distribution near the crack tip determined according to the HRR solution—usually it is the value equated with the d
n parameter, which is determined by knowing the parameters of the HRR field [
15,
16] and can also be determined using the computer program presented in [
17].
The crack tip opening displacement is determined based on numerical calculations, according to the scheme shown in
Figure 16 [
18]. The mutual relation of the
J-integral and the crack tip opening displacement is a linear relationship, where the coefficient of proportionality is the parameter
m. By dividing Equation (1) on both sides by the length of the non-cracked section of the specimen
b (where
b =
W −
a), we normalize both sides of Equation (1) [
18]:
Denoted by:
the proportionality coefficient, denoted by
m, linking the crack tip opening displacement,
δT, and the
J-integral, can be calculated as:
As can be seen, the value of the proportionality coefficient,
m, is equal to the tangent of the angle of inclination of the line
to the abscissa, which can be written as
m =
tg(
φ) [
18].
Figure 17c shows the influence of the specimen geometry on the value of the
m coefficient. As we can see, the value of this coefficient depends to a very small extent on the thickness of the structural element and varies from the value of 0.55 (
B = 5 mm) through 0.60 (
B = 10 mm) to the value of 0.70 (
B = 15 mm) (
Figure 18). Therefore, the conclusions presented in [
18] are confirmed, where it has been suggested that the proportionality coefficient,
dn, also denoted as
m, depends on the geometric constraints that the material opposes the plastic strains developing, both in-plane and out-of-plane constraints, however, a little less. It should be noted that assuming that the material used in the tests—41Cr4 steel—will be described with the appropriate constitutive compounds (Hook’s law and the Ramberg–Osgood relationship), assuming material constants: Young’s modulus
E = 209 GPa, Poisson’s coefficient
ν = 0.3, yield point
σ0 = 462 MPa, strain hardening constant
α = 1 and strain hardening exponent
n = 8.89—and then using the program mentioned in [
17], the following parameters of the HRR field are obtained [
15,
16] for the case of the dominance of the plane strain state, for the direction
θ = 0:
In = 4.61, d
n =
m = 0.477,
= 1.72,
= 2.46,
= 0.64. It turns out, therefore, that the determined value of the
dn parameter, based on the numerical model and some experimental data, is greater than the value estimated in accordance with the assumptions of the HRR field [
15,
16].
For many years, the basic formula used to estimate the value of the
J-integral was in the following form [
18,
19]:
where
b is the length of non-cracked section of the specimen (
b =
W −
a),
B is the specimen thickness,
A is the energy calculated as the area under the force,
P, curve as a function of the load line displacement,
vLL, or the crack mouth displacement,
δM, and
η is a proportionality coefficient, depending on the geometry—for SEN(B) specimens, it usually takes the value of 2. This formula still functions in the standard [
2], and many researchers decide to calculate the energy
A from the graph
P =
f(
vLL) or from plot
P =
f(
δM).
By normalizing Equation (6), dividing it on both sides by the product of the length of the non-cracked section of the specimen b and the yield stress σ
0, the following expression is obtained:
Denoted by:
it can be written that:
which, after transformation, allows to write the formula for the coefficient
η [
18]:
By plotting the changes of the normalized
J-integral, denoted by
, as a function of the normalized energy
A, denoted by
(
Figure 17a,b), and then analyzing them, we can confidently say that the value of the coefficient
η is equal to the tangent of the angel
φ (the slope of the curve
to the abscissae) [
18]. It can be concluded that the value of the coefficient
η depends on the thickness of the specimen; therefore, it is confirmed that the geometric constraints, both “in-plane” and “out-of-plane” constraints, affect its value.
Figure 18 shows how the value of the coefficient
η changes as a function of the increasing crack mouth displacement,
δM, and the increasing load line displacement,
vLL. The increase in load is accompanied by an attempt to obtain a fixed value, and for the thickness
B = 15 mm, a jump in the value of the parameter
η is observed, which is related to the step increase in the crack length. The analysis of
Figure 18 shows that, for the case where the energy
A is estimated based on the
P =
f(
δM) diagram (
Figure 18a), the value of the coefficient
η is equal to 3.44, 3.29 and 1.70, for thickness
B equal to 5, 10 and 15 mm, respectively. Thus, it is observed that the greater the thickness, the smaller the value of the
η coefficient. The same effect is shown in
Figure 18b. If the energy
A is determined based on the
P =
f(
vLL) diagram, the value of the coefficient
η is equal to 4.72, 4.42 and 2.23, respectively, for the thickness
B equal to 5, 10 and 15 mm.
Figure 19,
Figure 20 and
Figure 21, on the example of a specimen with a thickness of
B = 15 mm, show changes in the force loading the specimen, an increasing value of the
J-integral, an increase in the crack length,
da, an increasing crack tip opening displacement and a change in the maximum value of stresses opening the crack surfaces. The first two figures show the changes of the parameters as a function of the crack mouth displacement,
δM, while the third one presents these changes as a function of the load line displacement,
vLL. In these graphs, a dashed line marks three characteristic moments for which full plasticization of the non-cracked section of the specimen is observed.
The first characteristic moment from the left corresponds to the moment when the value of the
J-integral is equal to 75 N/mm (which corresponds to the critical value of the
J-integral determined on the basis of the standard [
2]) external load, then slightly, by about 8%, exceeds the permissible limit load for the considered geometry.
The second one corresponds to the hypothetical moment of the crack growth, at which, according to the
J-
R curve of the standard [
1,
2], crack growth begins—the value of the
J-integral is about 136 N/mm.
The third is the moment when a significant crack growth is observed, amounting to about 3.5 mm, for which the value of the J-integral is about 385 N/mm.