Inverse Identification of a Constitutive Model for High-Speed Forming Simulation: An Application to Electromagnetic Metal Forming
Abstract
1. Introduction
2. Formulations
2.1. Inverse Identification
2.1.1. Forward Model
2.1.2. Regularized Nonlinear Least Squares
2.2. Model Order Reduction
2.2.1. Low-Dimensional Approximation
2.2.2. Principal Component Analysis
2.2.3. Kriging Interpolation
3. Free Bulge Test with Electromagnetic Force
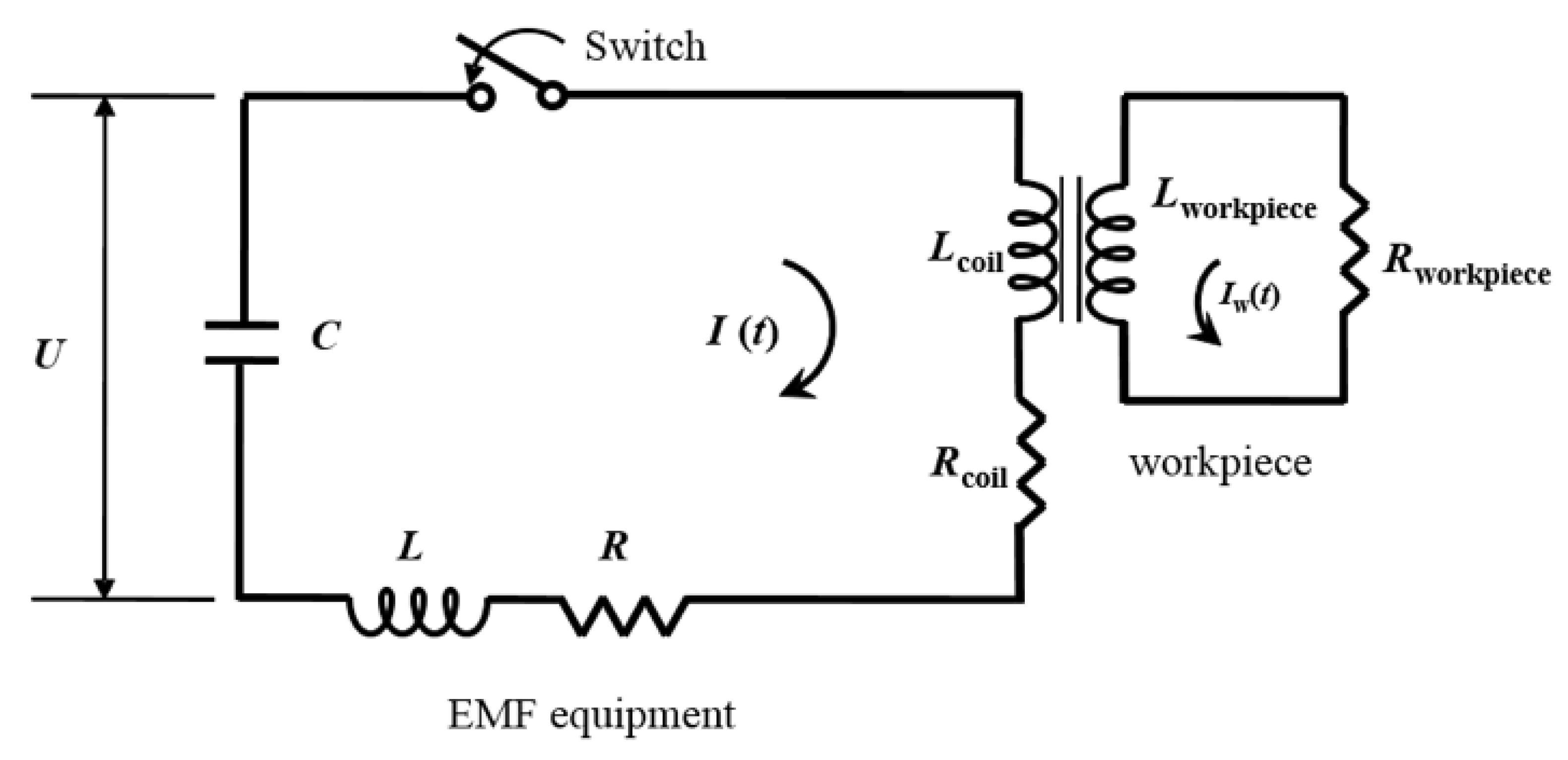
3.1. Electromagnetic Forming Experiment
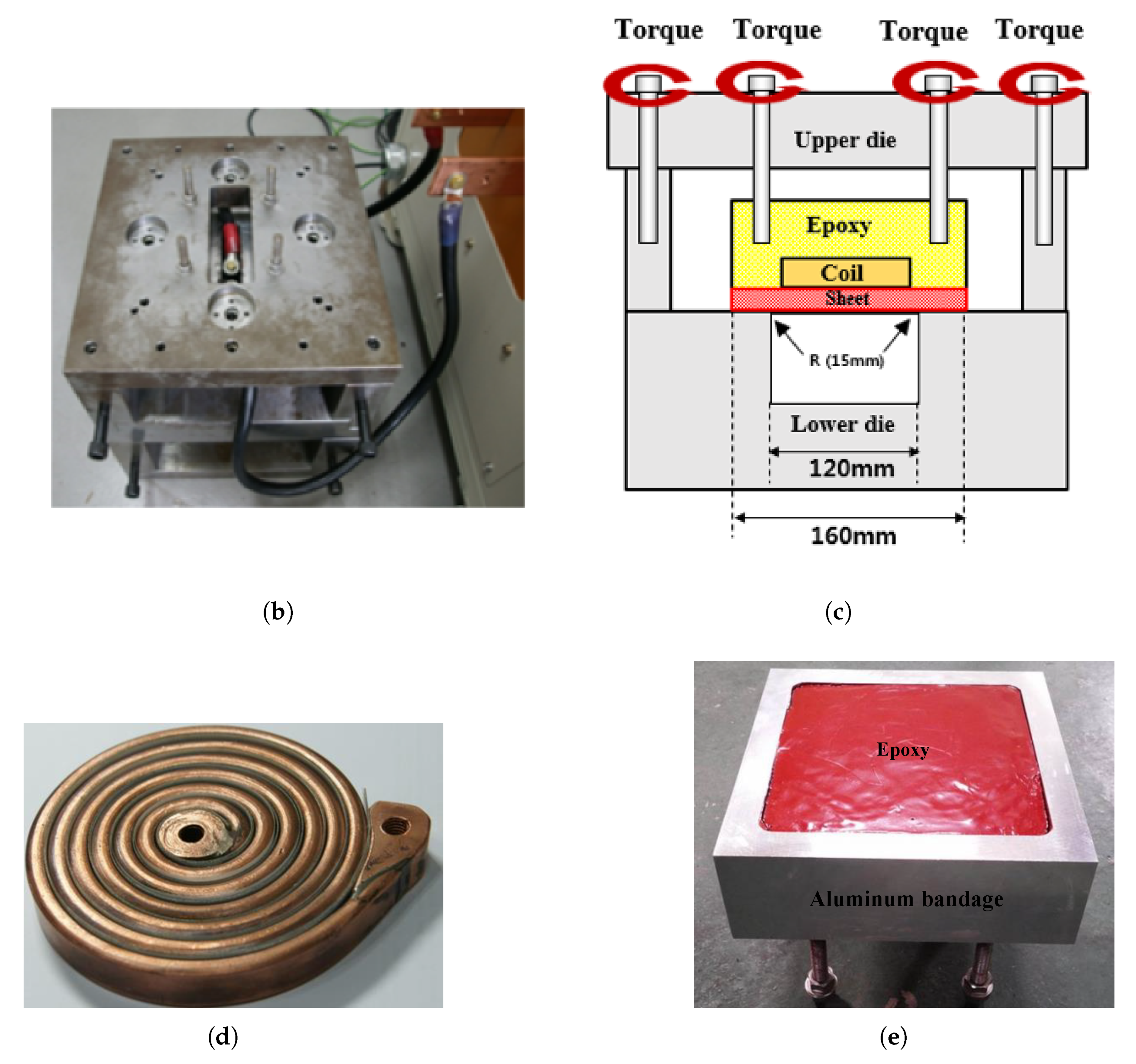
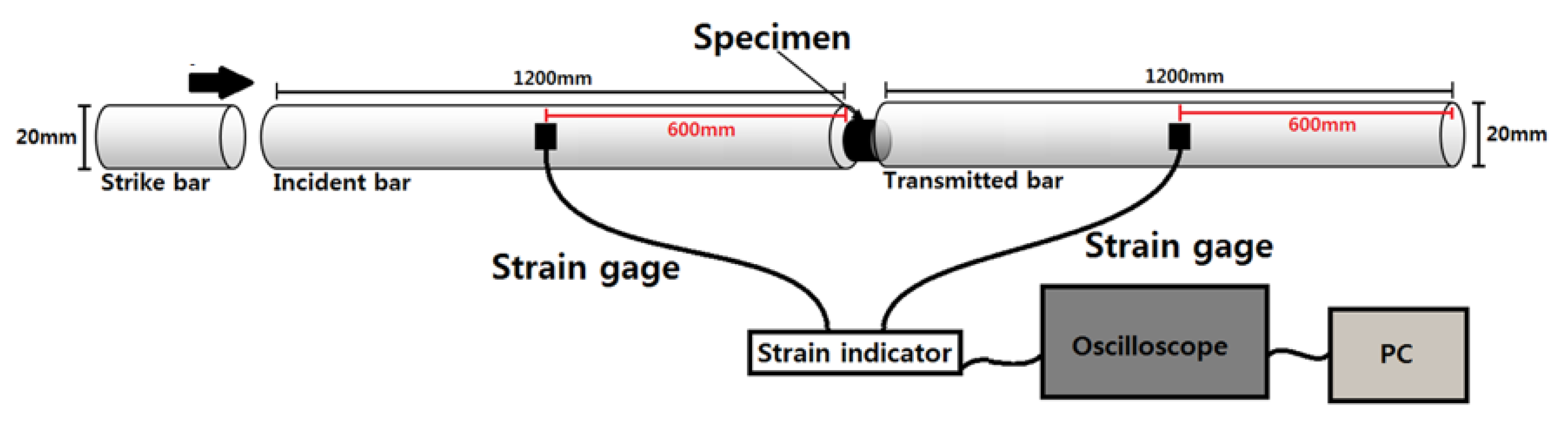
3.1.1. Experimental Procedure
3.1.2. Experimental Apparatus
3.2. Electromagnetic Forming Simulation
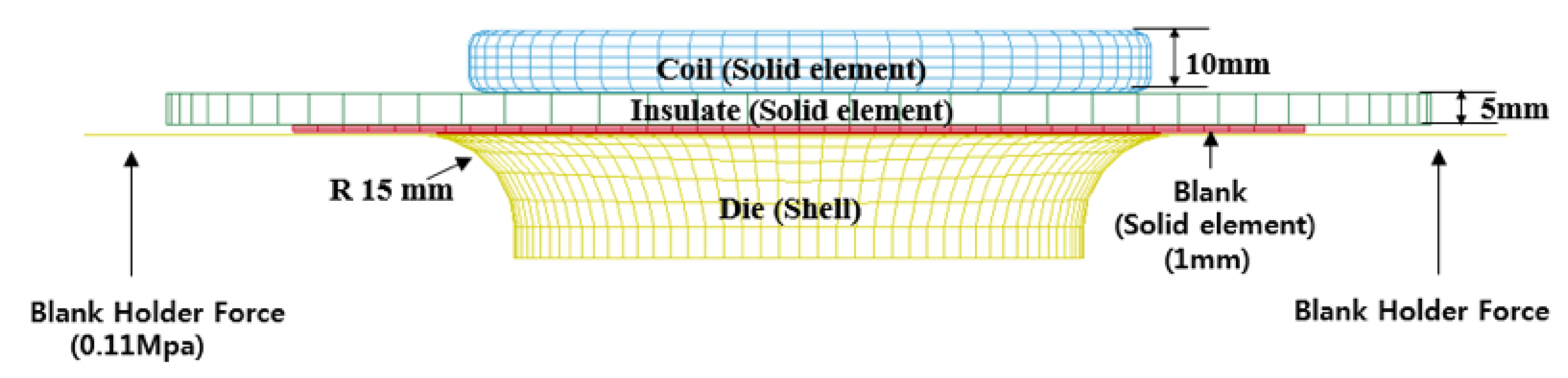
3.2.1. Coupled Finite/Boundary Element Model
3.2.2. Constitutive Model
4. Electromagnetic Forming Simulation Reduction
4.1. Reduced Model Construction
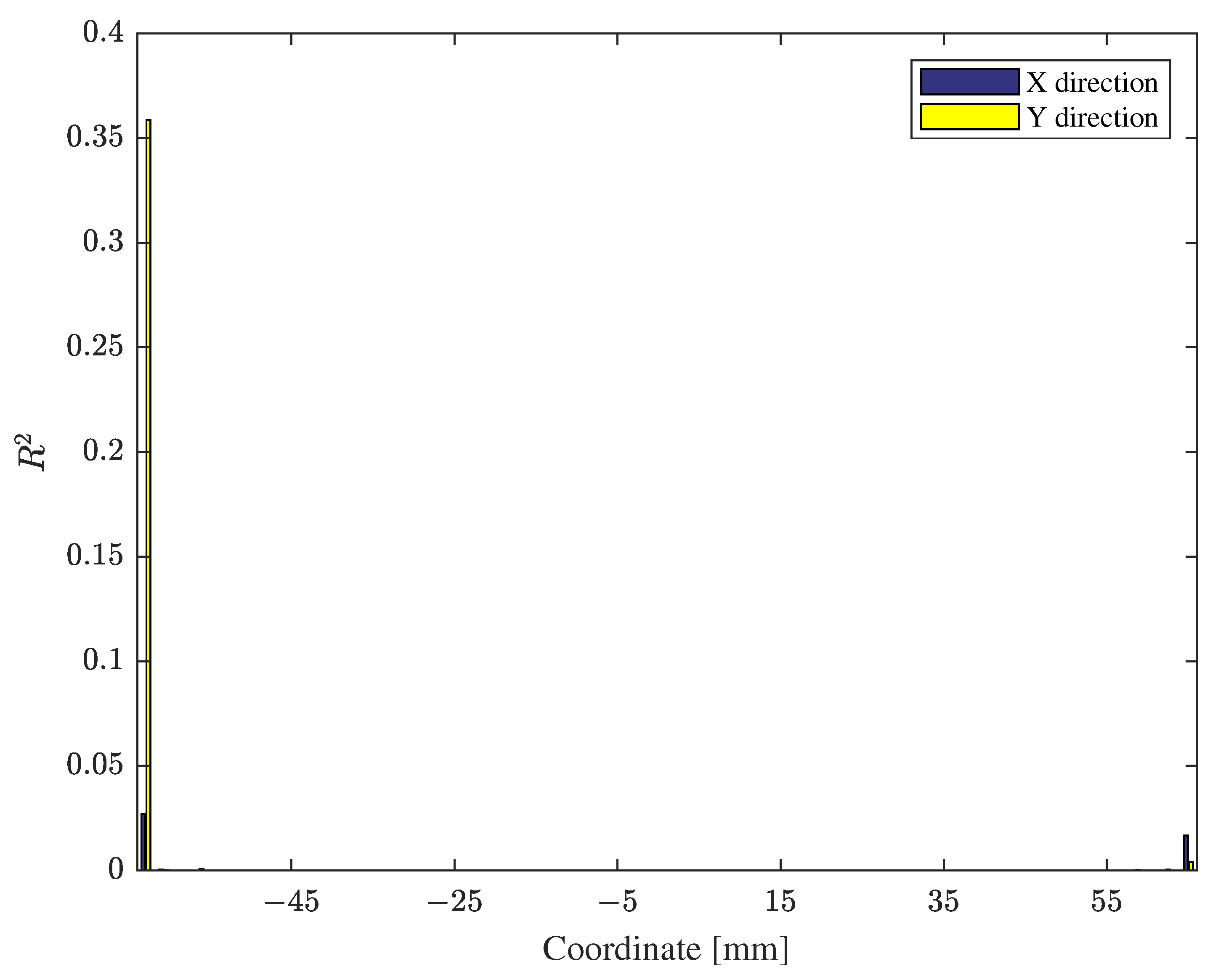
4.2. Reduced Model Verification
5. Inverse Identification Results
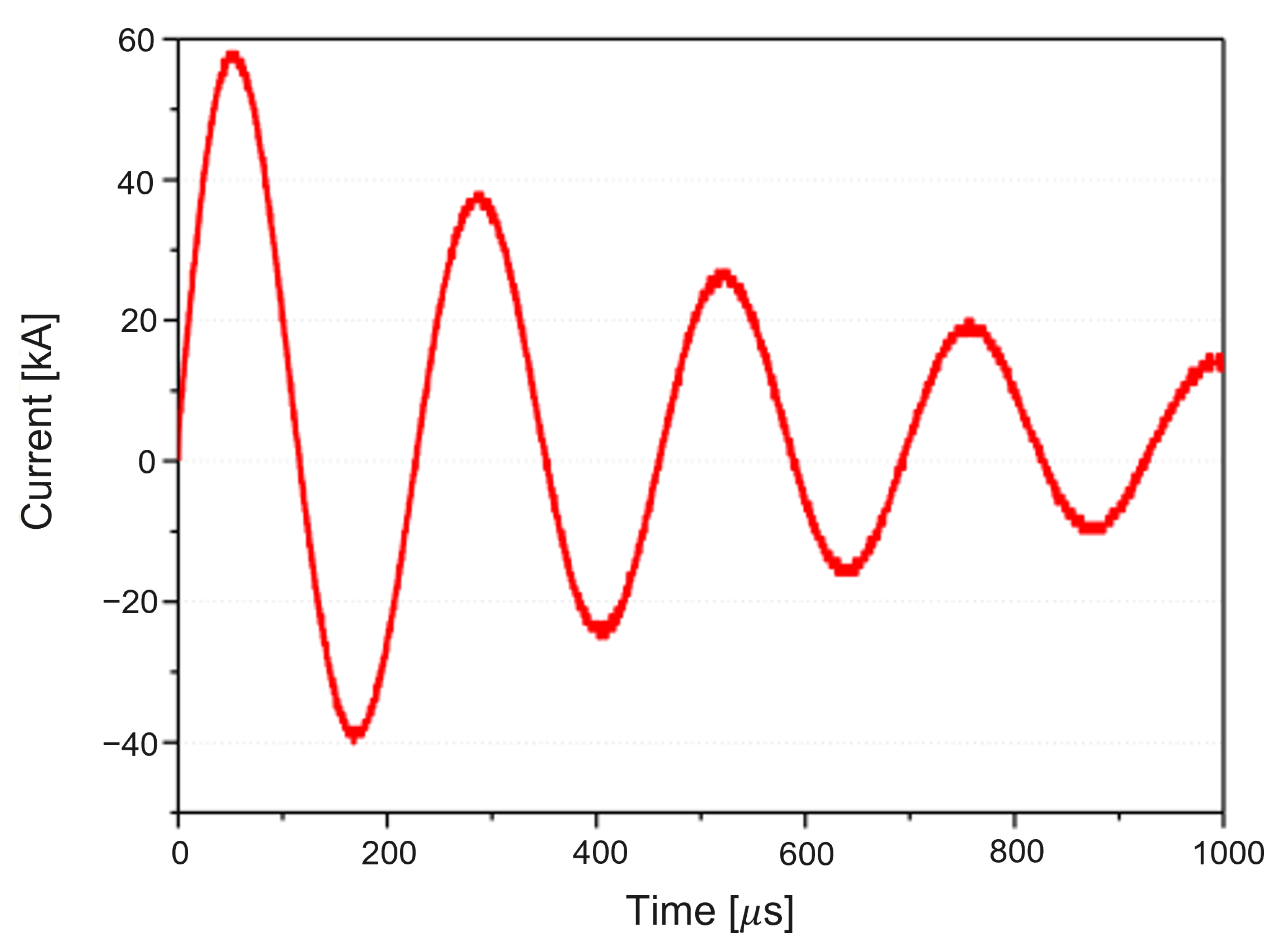
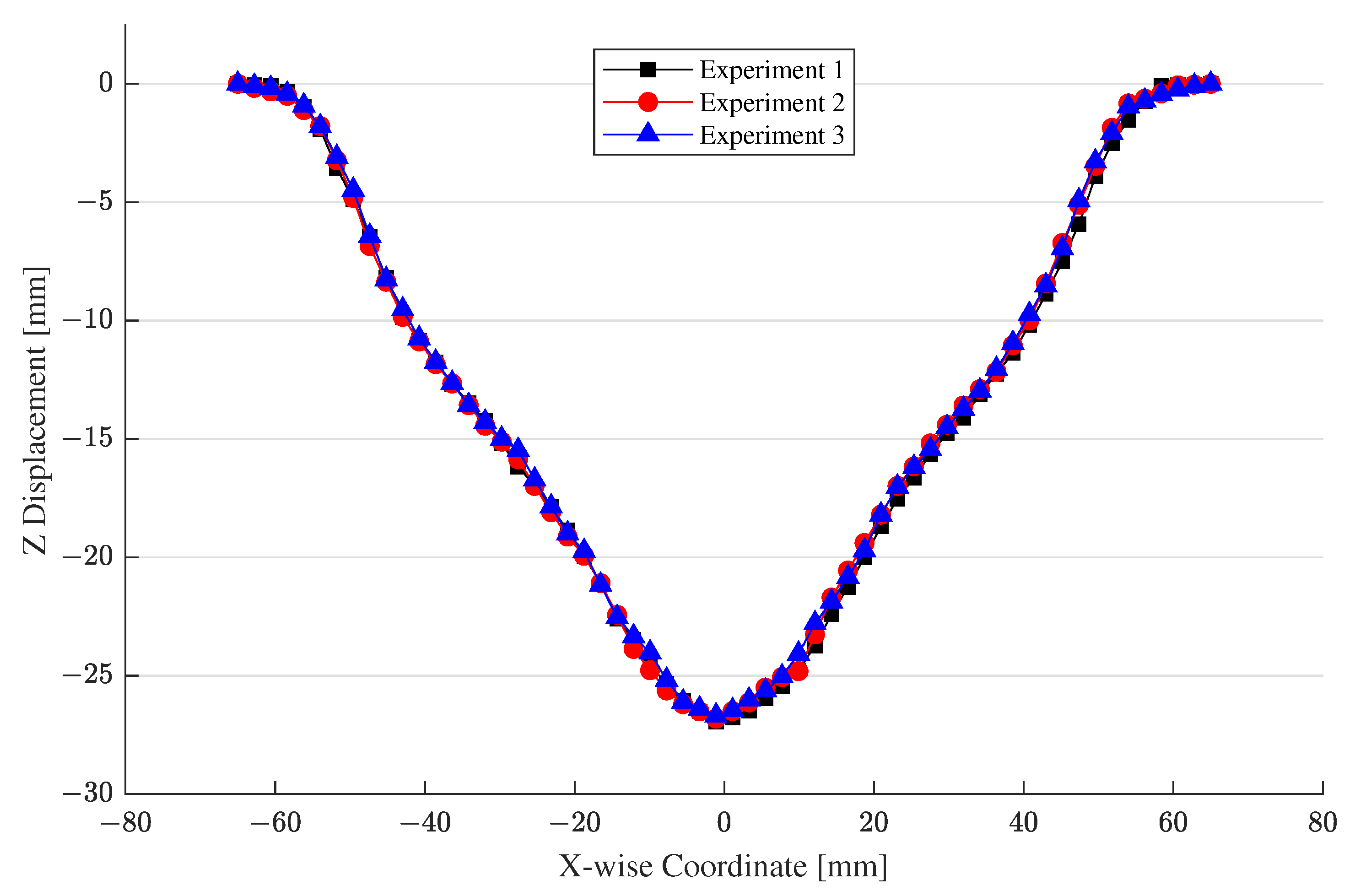
5.1. Experimental Measurements
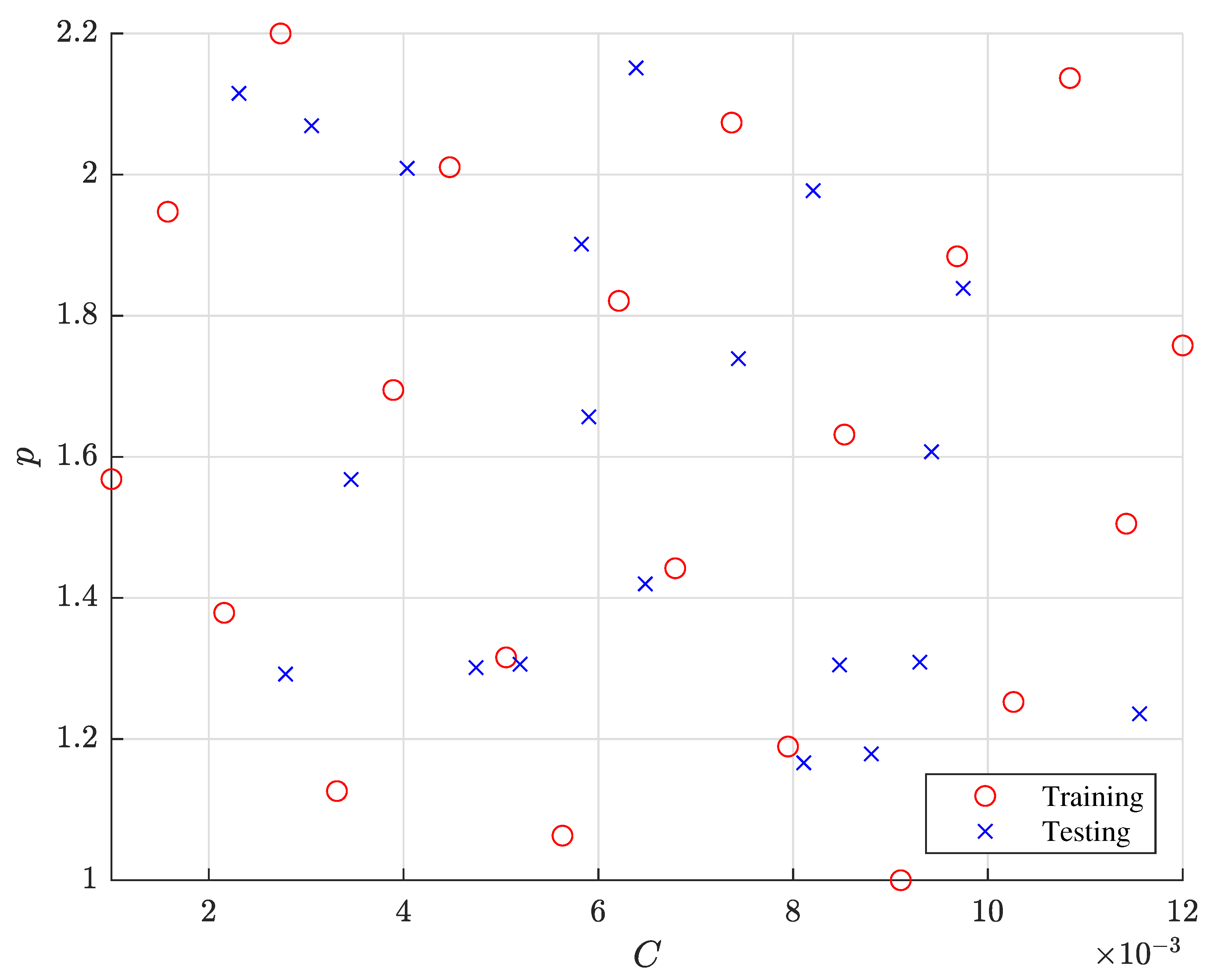
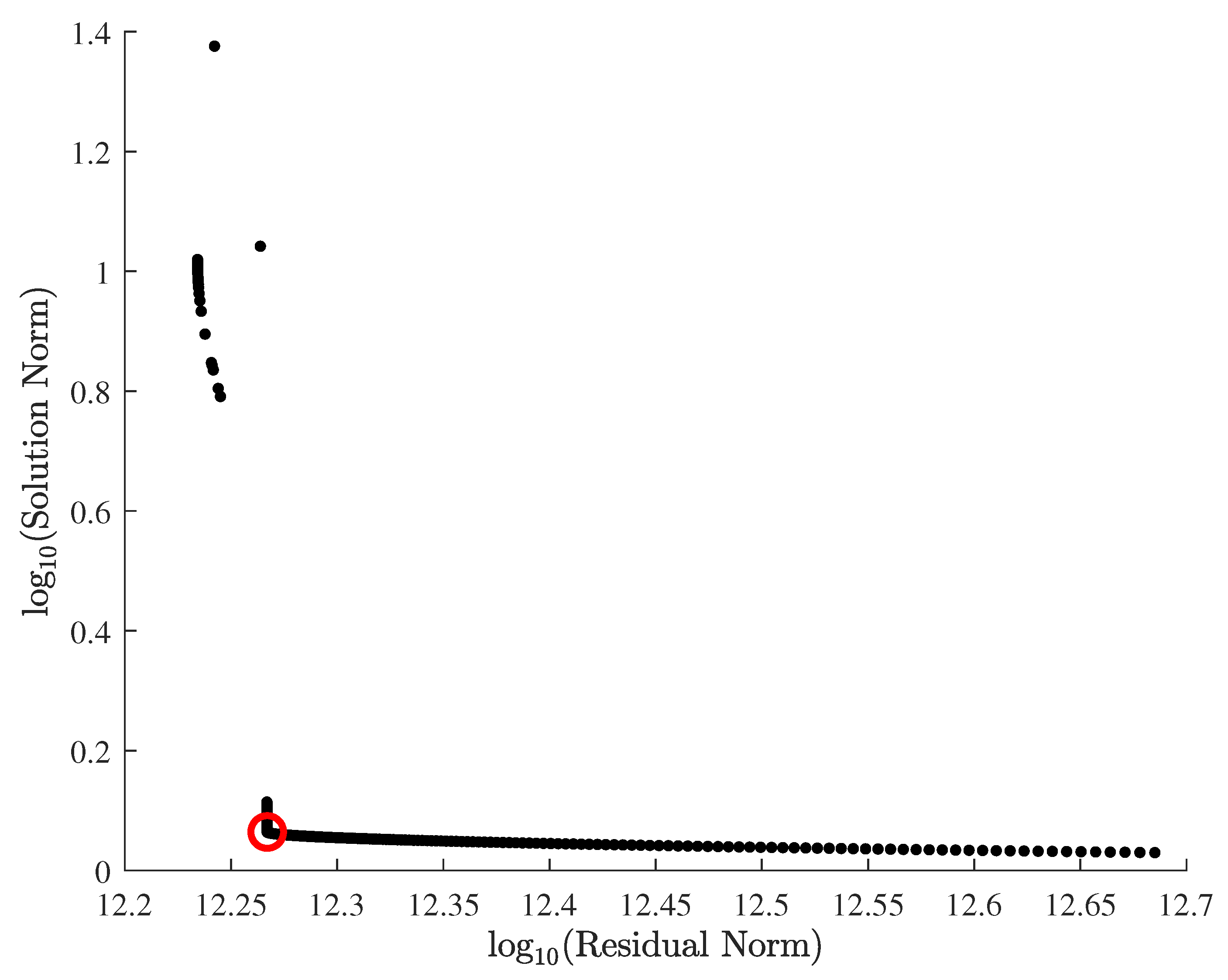
5.2. Parameter Estimation
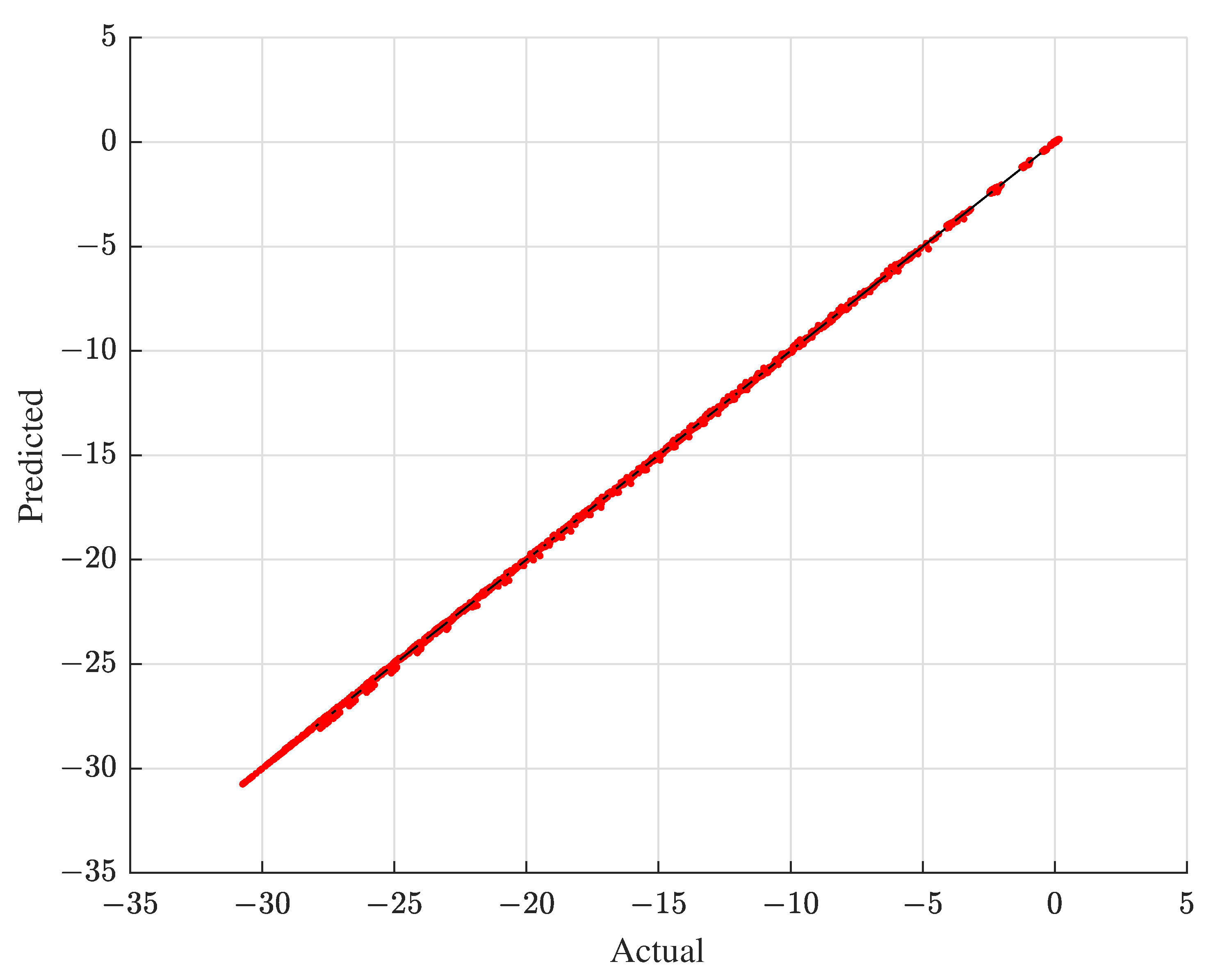
5.3. Simulation Model Verification and Validation
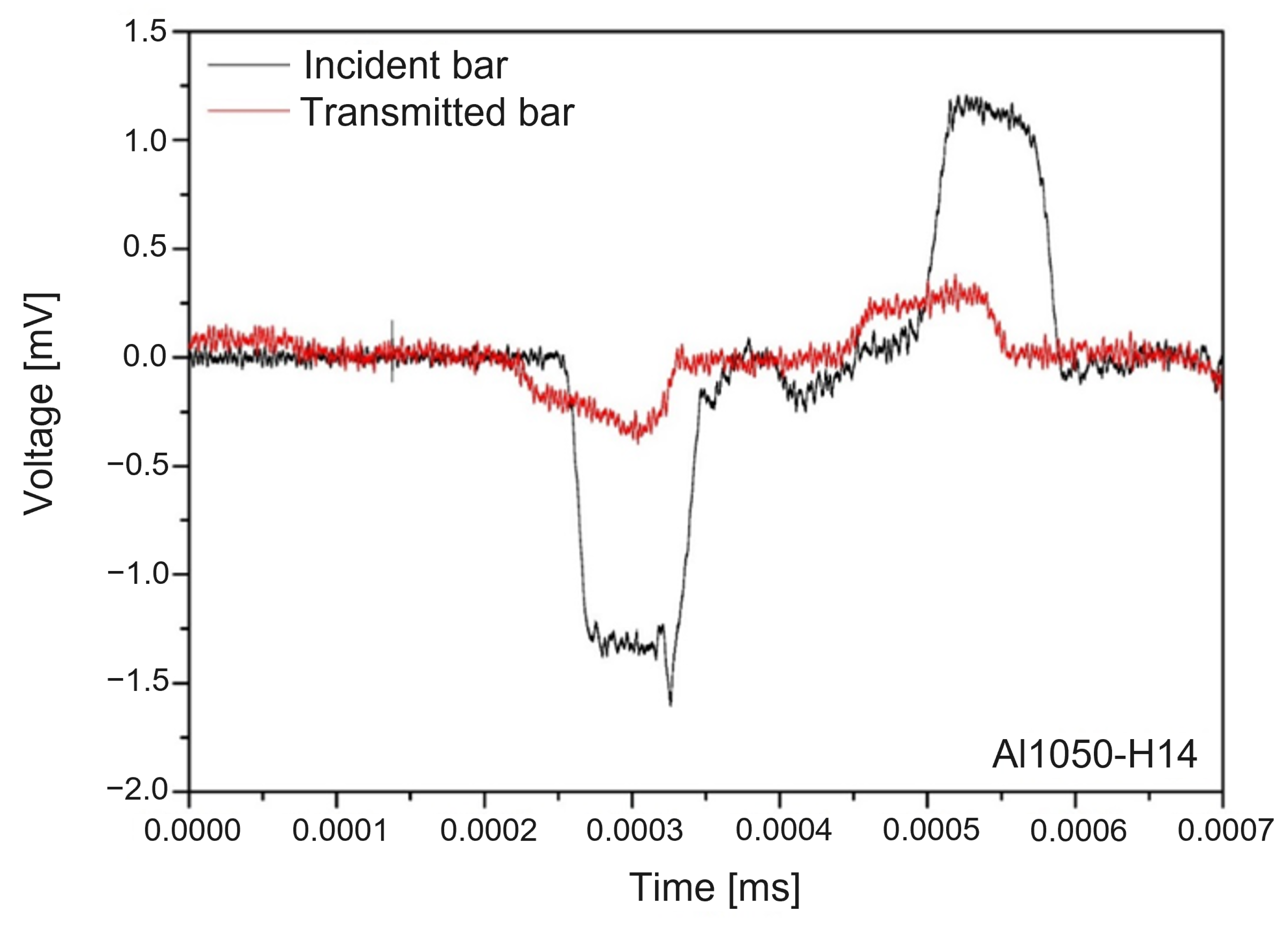
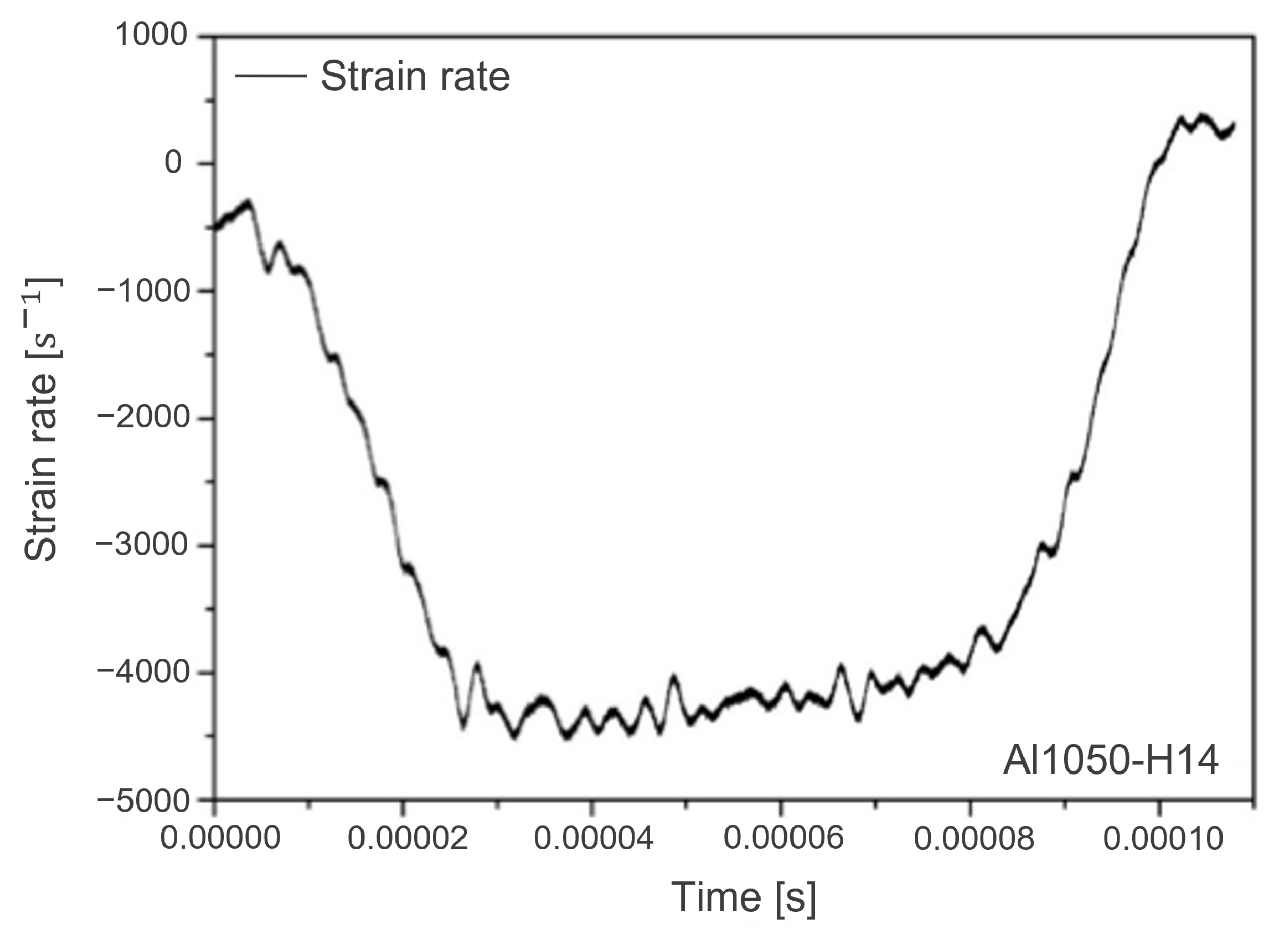
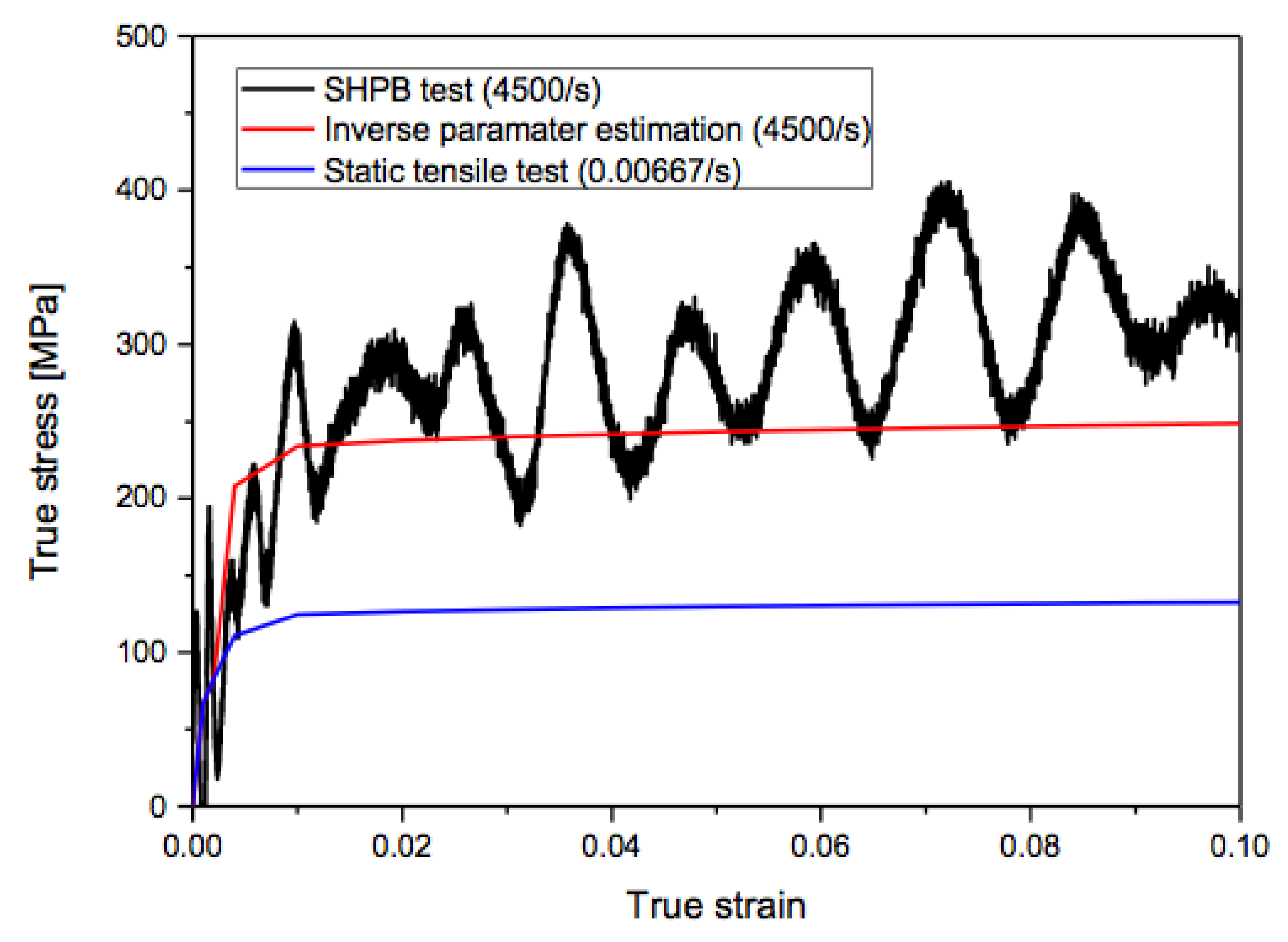
6. Validation with a Dynamic Material Test
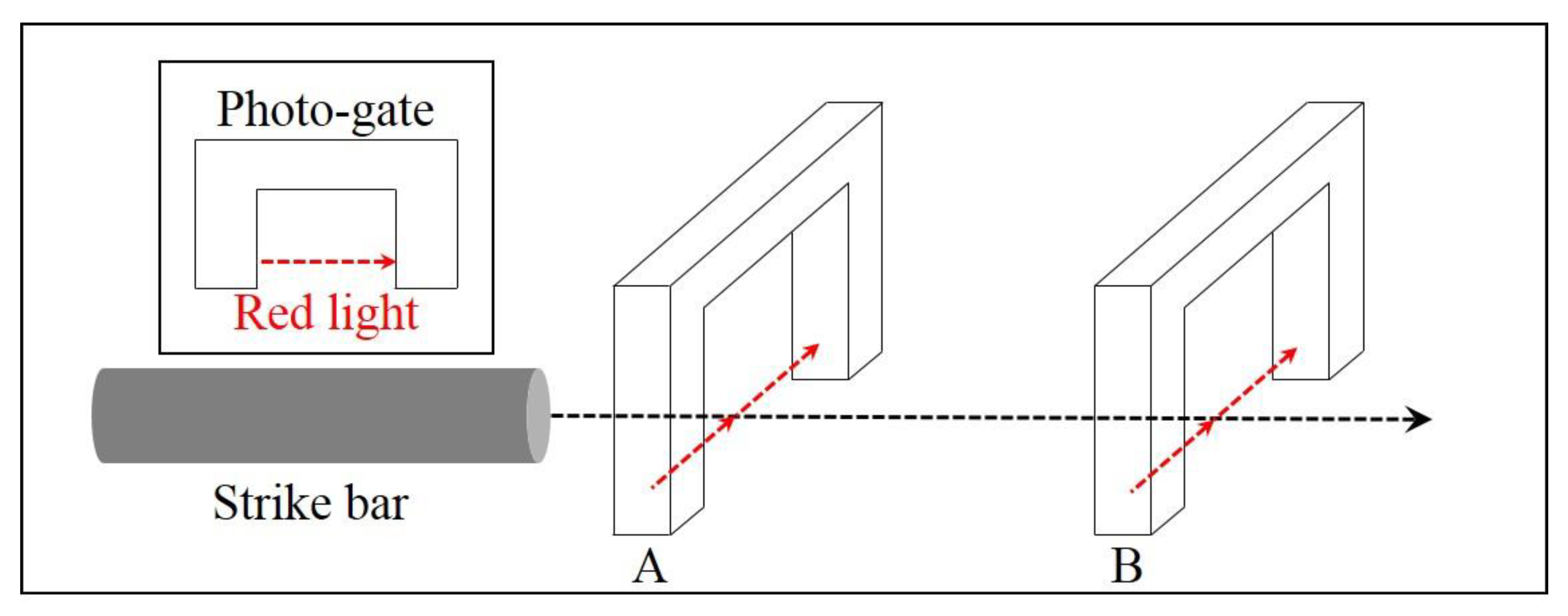
6.1. Experimental Apparatus
6.2. Validation Results
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lim, J.H. Study on Dynamic Tensile Test of Auto-Body Steel Sheet at the Intermediate Strain Rate for Material Constitutive Equations. Ph.D. Thesis, KAIST, Daejeon, Korea, 2005. [Google Scholar]
- Demir, O.K.; Höhling, O.; Risch, D.; Brosius, A.; Tekkaya, A.E. Determination of the Material Characteristics by Means of High Speed Tensile Test—Experiment and Simulation. Int. J. Mater. Form. 2008, 1, 1331–1334. [Google Scholar] [CrossRef][Green Version]
- Hhernandez, C.; Maranon, A.; Ashcroft, I.A.; Casa-Rodiruez, J.P. A Computational Determination of the Cowper-Symonds Parameters from a Single Taylor Test. Appl. Math. Model. 2013, 37, 4698–4708. [Google Scholar] [CrossRef]
- Gray, G., III. Classic split-Hopkinson pressure bar technique. ASM Int. 1999, 8, 1–36. [Google Scholar]
- Khan, A.S.; Huang, S. Experimental and theoretical study of mechanical behavior of 1100 aluminum in the strain rate range 10−5–104/s. Int. J. Plast. 1992, 8, 397–424. [Google Scholar] [CrossRef]
- Eakins, D.; Thadhani, N. Analysis of dynamic mechanical behavior in reverse Taylor anvil-on-rod impact tests. Int. J. Impact Eng. 2007, 34, 1821–1834. [Google Scholar] [CrossRef]
- Gerlach, R.; Kettenbeil, C.; Petrinic, N. A new split Hopkinson tensile bar design. Int. J. Impact Eng. 2012, 50, 63–67. [Google Scholar] [CrossRef]
- Malakizadi, A.; Cedergren, S.; Sadik, I.; Nyborg, L. Inverse identification of flow stress in metal cutting process using Response Surface Methodology. Simul. Model. Pract. Theory 2016, 60, 40–53. [Google Scholar] [CrossRef]
- Lan, J.; Dong, X.; Li, Z. Inverse Finite Element Approach and its Application in Sheet Metal Forming. J. Mater. Process. Technol. 2005, 170, 624–631. [Google Scholar] [CrossRef]
- Sasso, M.; Newaz, G.; Amodio, D. Material Characterization at High Strain Rate by Hopkinson Bar Test and Finite Element Optimization. Mater. Sci. Eng. A 2008, 487, 289–300. [Google Scholar] [CrossRef]
- Milani, A.S.; Dabboussi, W.; Nemes, J.A.; Abeyaratne, R.C. An Improved Multi-Objective Identification of Johnson-Cook Material Parameters. Int. J. Impact Eng. 2009, 36, 294–302. [Google Scholar] [CrossRef]
- Noh, H.G.; Lee, K.; Kang, B.S.; Kim, J. Inverse parameter estimation of the Cowper-Symonds material model for electromagnetic free bulge forming. Int. J. Precis. Eng. Manuf. 2016, 17, 1483–1492. [Google Scholar] [CrossRef]
- Woo, M.; Kim, J. Inverse parameter estimation to predict material parameters of the Cowper–Symonds constitutive equation in electrohydraulic forming process. J. Eng. Math. 2022, 132, 1–22. [Google Scholar] [CrossRef]
- Li, S.; Cui, X.; Feng, H.; Wang, G. An electromagnetic forming analysis modelling using nodal integration axisymmetric thin shell. J. Mater. Process. Technol. 2017, 244, 62–72. [Google Scholar] [CrossRef]
- Li, S.; Cui, X. Combined “mesh flow” and “re-meshing” technique for coupled magnetic-mechanical problem on electromagnetic forming process. Int. J. Adv. Manuf. Technol. 2020, 106, 5111–5127. [Google Scholar] [CrossRef]
- Mahmoud, M.; Bay, F.; Pino Muñoz, D. An Efficient Computational Model for Magnetic Pulse Forming of Thin Structures. Materials 2021, 14, 7645. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Nam, T.; Perullo, C.; Mavris, D.N. Reduced-Order Modeling of a High-Fidelity Propulsion System Simulation. AIAA J. 2011, 49, 1665–1682. [Google Scholar] [CrossRef]
- Woo, M.; Lee, K.; Song, W.; Kang, B.; Kim, J. Numerical Estimation of Material Properties in the Electrohydraulic Forming Process Based on a Kriging Surrogate Model. Math. Probl. Eng. 2020, 2020, 3219829. [Google Scholar] [CrossRef]
- Stein, M.L. Interpolation of Spatial Data: Some Theory for Kriging; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Psyk, V.; Risch, D.; Kinsey, B.; Tekkaya, A.; Kleiner, M. Electromagnetic forming-a review. J. Mater. Process. Technol. 2011, 211, 787–829. [Google Scholar] [CrossRef]
- Caldichoury, I.; L’Eplatternier, P. Validation Process of the Electromagnetism (EM) Solver in LS-DYNA V980: The team problems. In Proceedings of the 12th International LS-DYNA User Conference, Dearborn, MI, USA, 3–5 June 2012; pp. 1–14. [Google Scholar]
- Livermore Software Technology Corporation. EM Theory Manual: Electromagnetism and Linear Algebra in LS-DYNA; Livermore Software Technology Corporation: Livermore, CA, USA, 2012. [Google Scholar]
- Kim, J.; Noh, H.G.; Song, W.J.; Kang, B.S. Analysis of electromagnetic forming process using sequential electromagnetic-structural coupling simulation. Int. J. Appl. Electromagn. Mech. 2015, 49, 263–278. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Steinberg, D.; Cochran, S.; Guinan, M. A constitutive model for metals applicable at high-strain rate. J. Appl. Phys. 1980, 51, 1498–1504. [Google Scholar] [CrossRef]
- Unger, J.; Stiemer, M.; Schwarze, M.; Svendsen, B.; Blum, H.; Reese, S. Strategies for 3D simulation of electromagnetic forming processes. J. Mater. Process. Technol. 2008, 199, 341–362. [Google Scholar] [CrossRef]
- Couckuyt, I.; Dhaene, T.; Demeester, P. ooDACE Toolbox: A Flexible Object-Oriented Kriging Implementation. J. Mach. Learn. Res. 2014, 15, 3183–3186. [Google Scholar]
- The MathWorks, Inc. Optimization Toolbox User’s Guide (Release 2022b); The MathWorks, Inc.: Natick, MA, USA, 2022. [Google Scholar]
- Nocedal, J.; Wright, S.J. Sequential Quadratic Programming. In Numerical Optimization; Springer: New York, NY, USA, 1999; pp. 526–573. [Google Scholar] [CrossRef]













| Property | Value | Unit | |
|---|---|---|---|
| Coil (copper) | Resistivity | 1.72 × 10−8 | |
| Sheet (A11050-H14) | Resistivity | 2.82 × 10−8 | |
| Possion’s ratio | 0.35 | ||
| Density | 2980 | ||
| Elastic modulus | 69.0 |
| (C) | (p) | |||
|---|---|---|---|---|
| 1.680248 | 6.356147 | 5.429284 | 1.101648 | |
| 2.333454 | 8.448063 | 6.113093 | 9.340040 |
| MARE | ||
|---|---|---|
| 9.994027 | 3.449596 | |
| 9.687801 | 1.473284 |
| Training Data | Testing Data | |||
|---|---|---|---|---|
| MARE | MARE | |||
| Minimum | 9.998999 | 3.540579 | 9.995423 | 2.972685 |
| Maximum | 9.999990 | 2.277471 | 9.999966 | 1.641368 |
| Average | 9.999802 | 1.117795 | 9.999375 | 1.910738 |
| * | ||
|---|---|---|
| 6.6452 | 1.6318 | 3.8367 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, D.; Noh, H.-G.; Kim, J.; Lee, K. Inverse Identification of a Constitutive Model for High-Speed Forming Simulation: An Application to Electromagnetic Metal Forming. Materials 2022, 15, 7179. https://doi.org/10.3390/ma15207179
Kang D, Noh H-G, Kim J, Lee K. Inverse Identification of a Constitutive Model for High-Speed Forming Simulation: An Application to Electromagnetic Metal Forming. Materials. 2022; 15(20):7179. https://doi.org/10.3390/ma15207179
Chicago/Turabian StyleKang, Dayoung, Hak-Gon Noh, Jeong Kim, and Kyunghoon Lee. 2022. "Inverse Identification of a Constitutive Model for High-Speed Forming Simulation: An Application to Electromagnetic Metal Forming" Materials 15, no. 20: 7179. https://doi.org/10.3390/ma15207179
APA StyleKang, D., Noh, H.-G., Kim, J., & Lee, K. (2022). Inverse Identification of a Constitutive Model for High-Speed Forming Simulation: An Application to Electromagnetic Metal Forming. Materials, 15(20), 7179. https://doi.org/10.3390/ma15207179





