Electronic Band Structure and Surface States in Dirac Semimetal LaAgSb2
Abstract
1. Introduction
2. Techniques
2.1. Sample Preparation
2.2. Experimental Details
2.3. Calculation Details
3. Results and Discussion
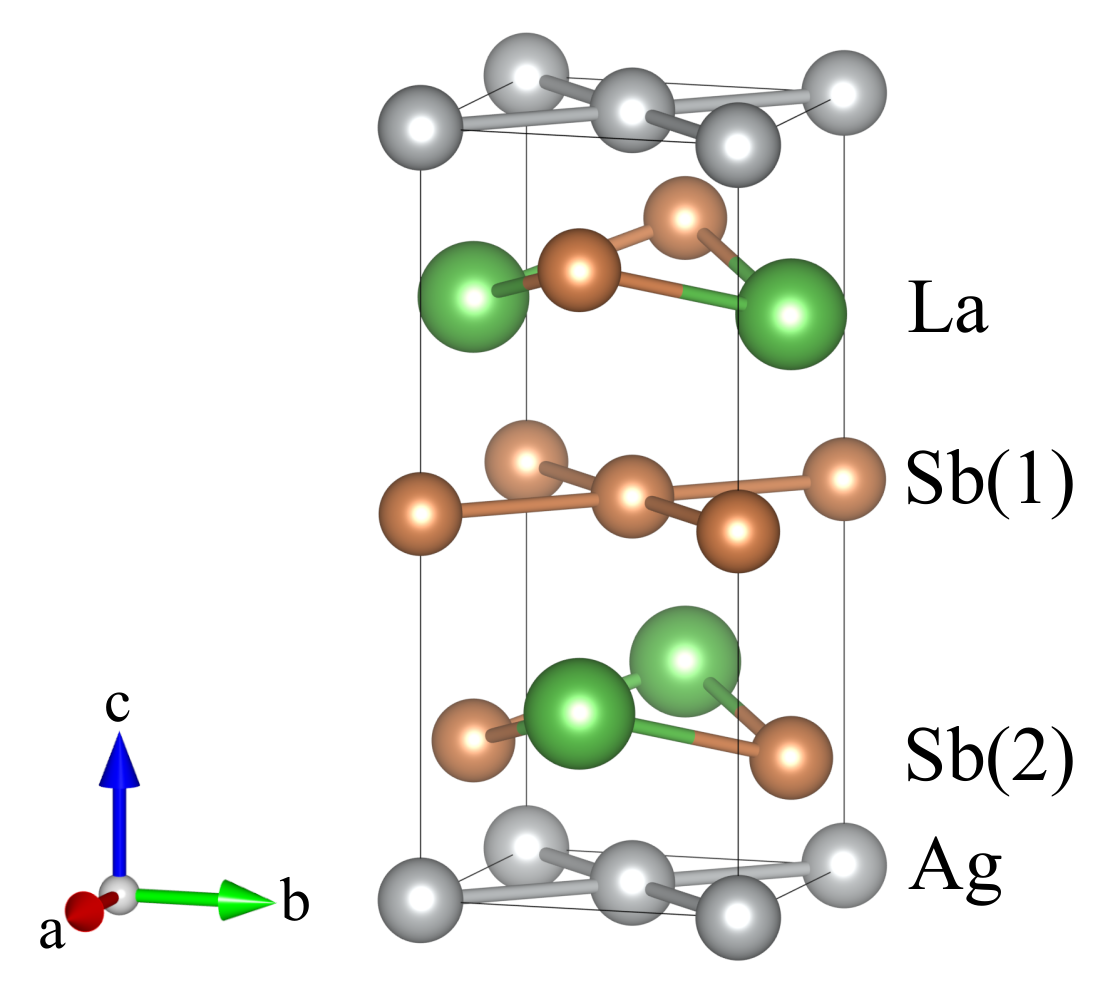
3.1. Crystal Structure
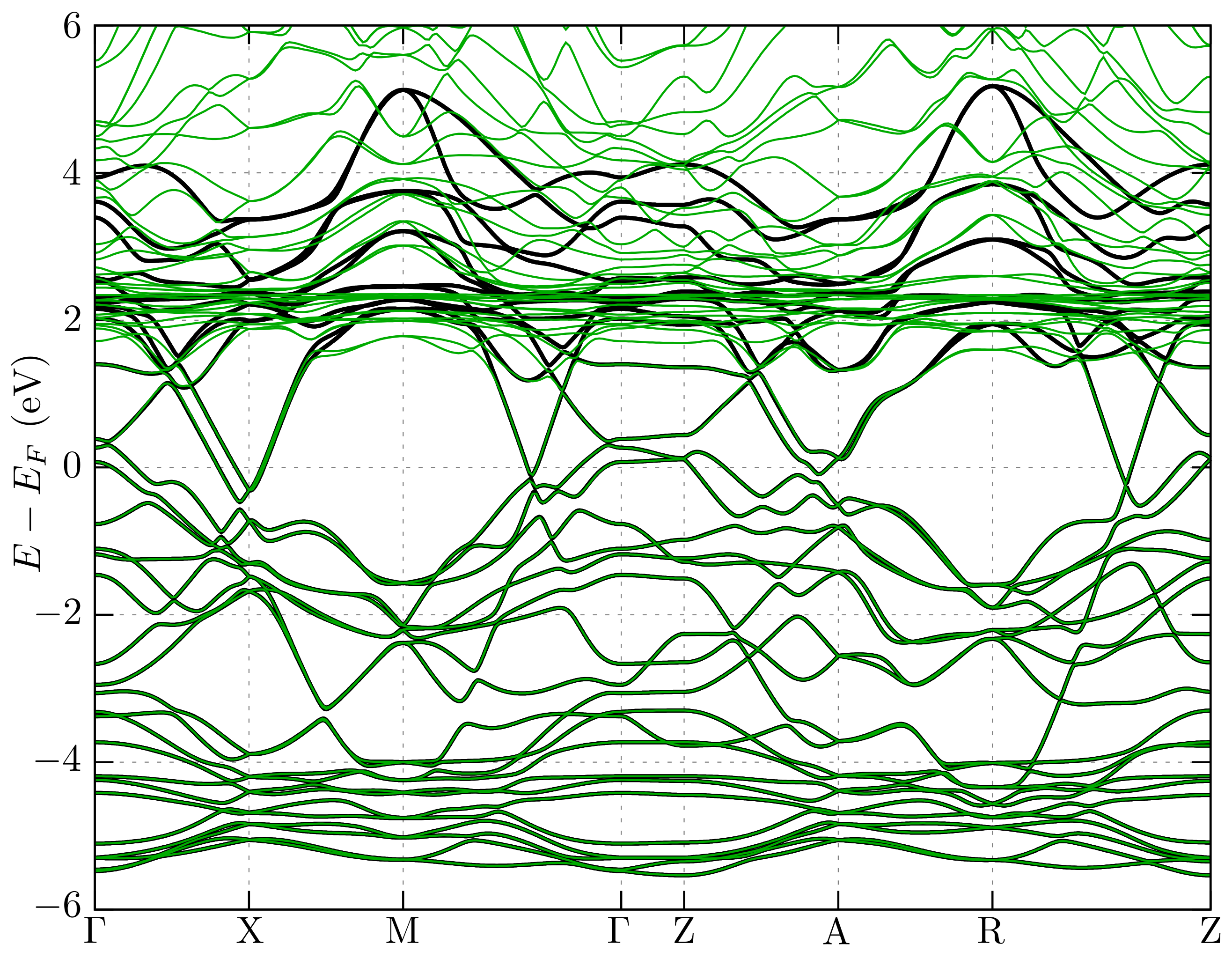
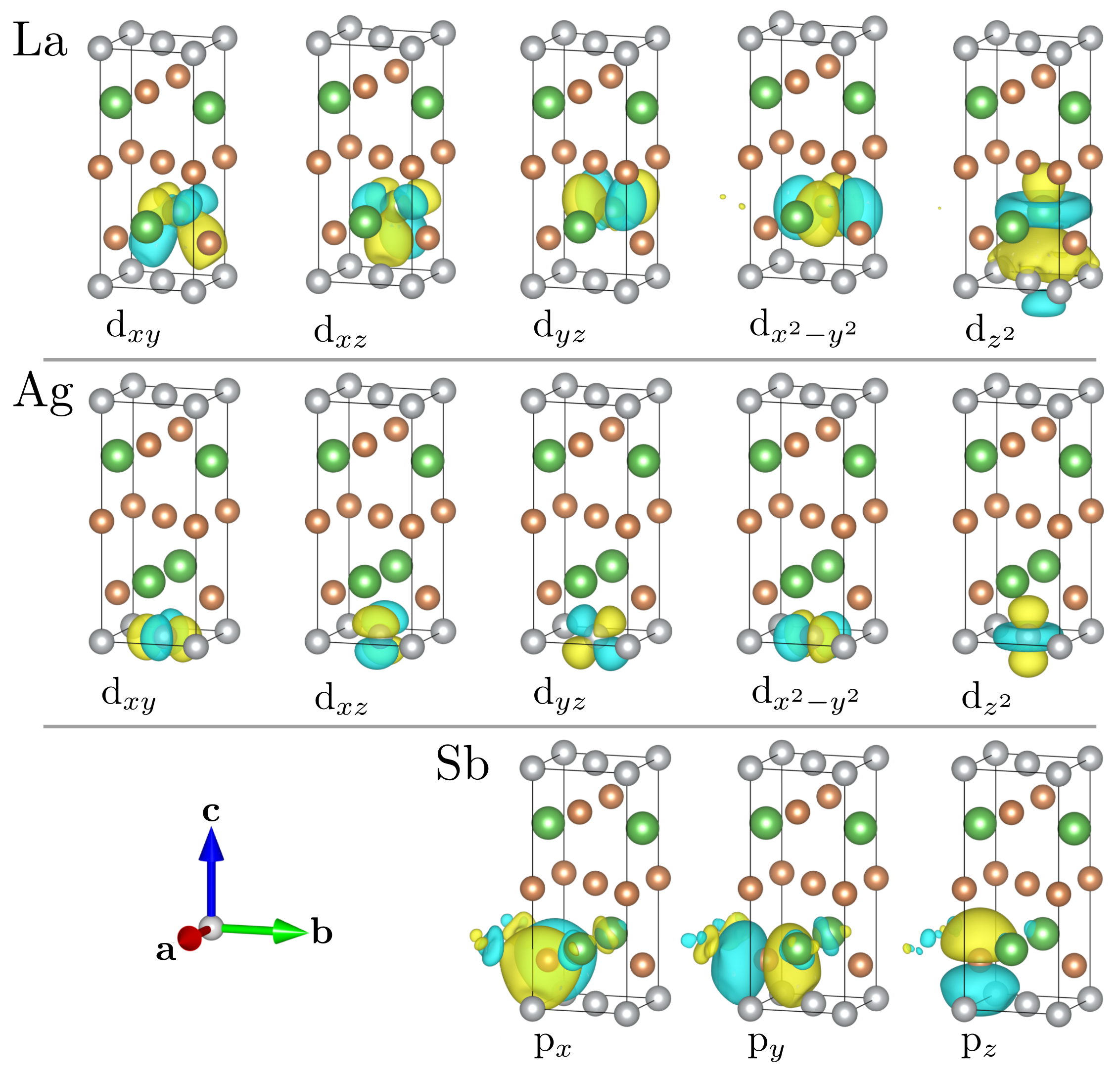
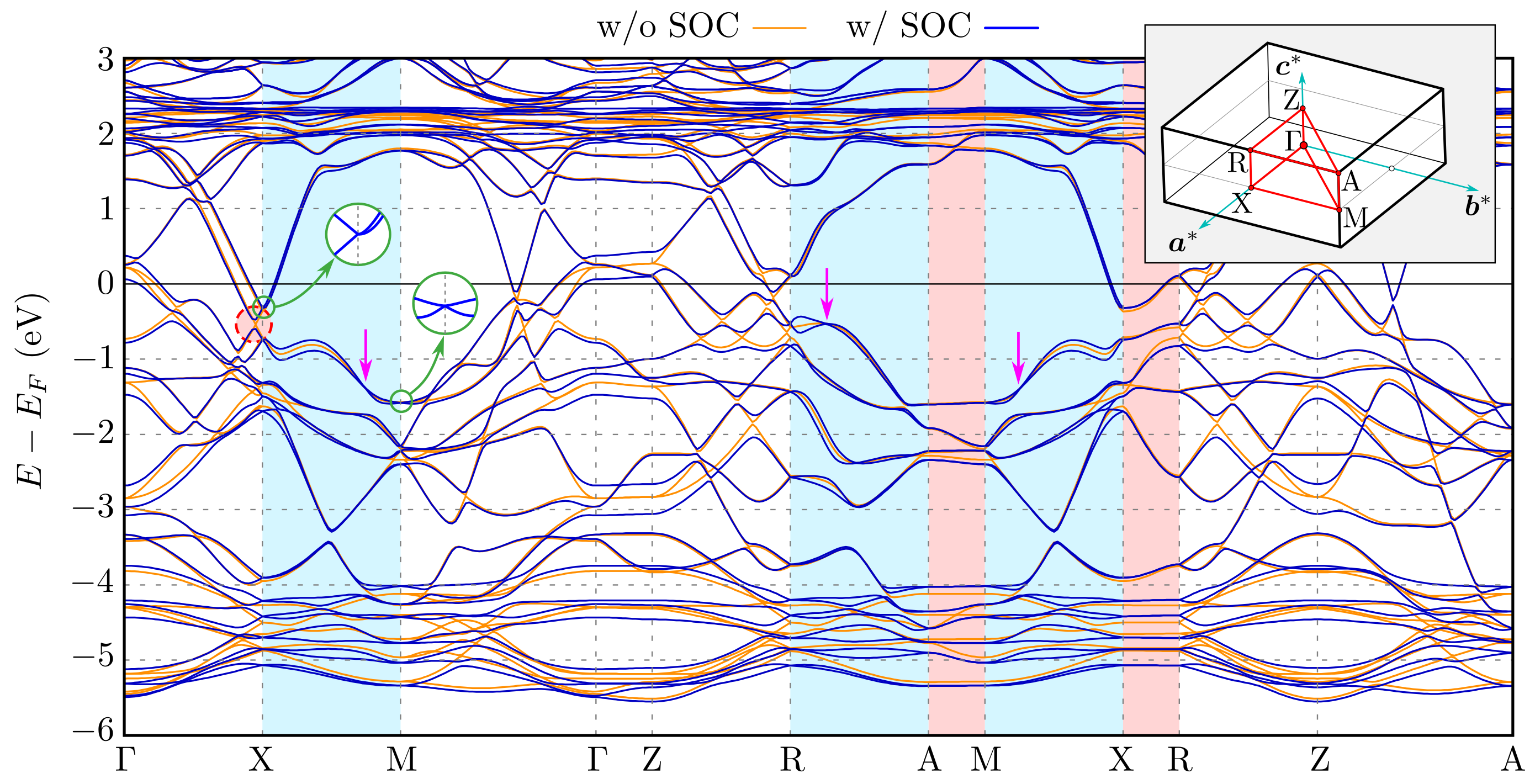
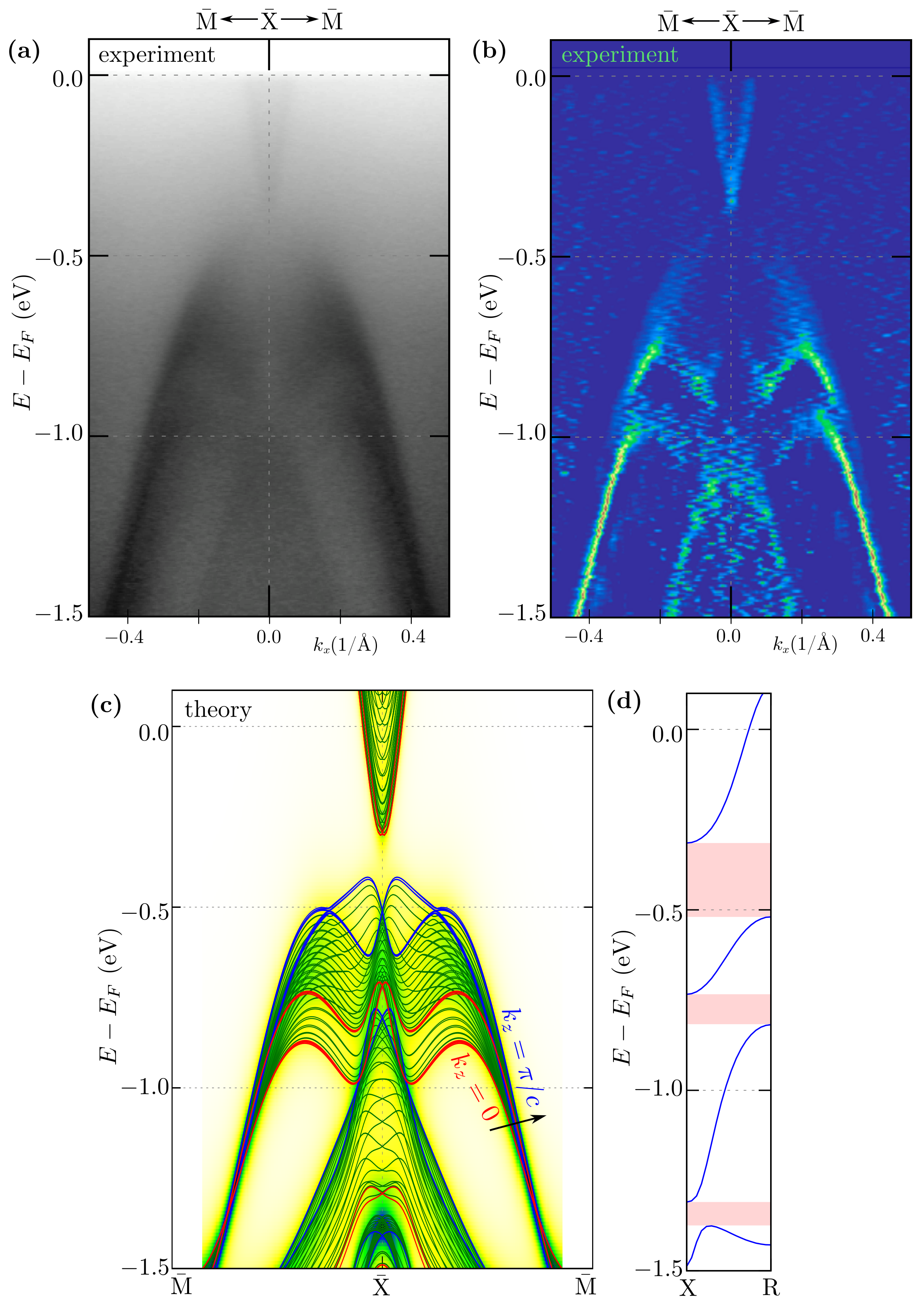
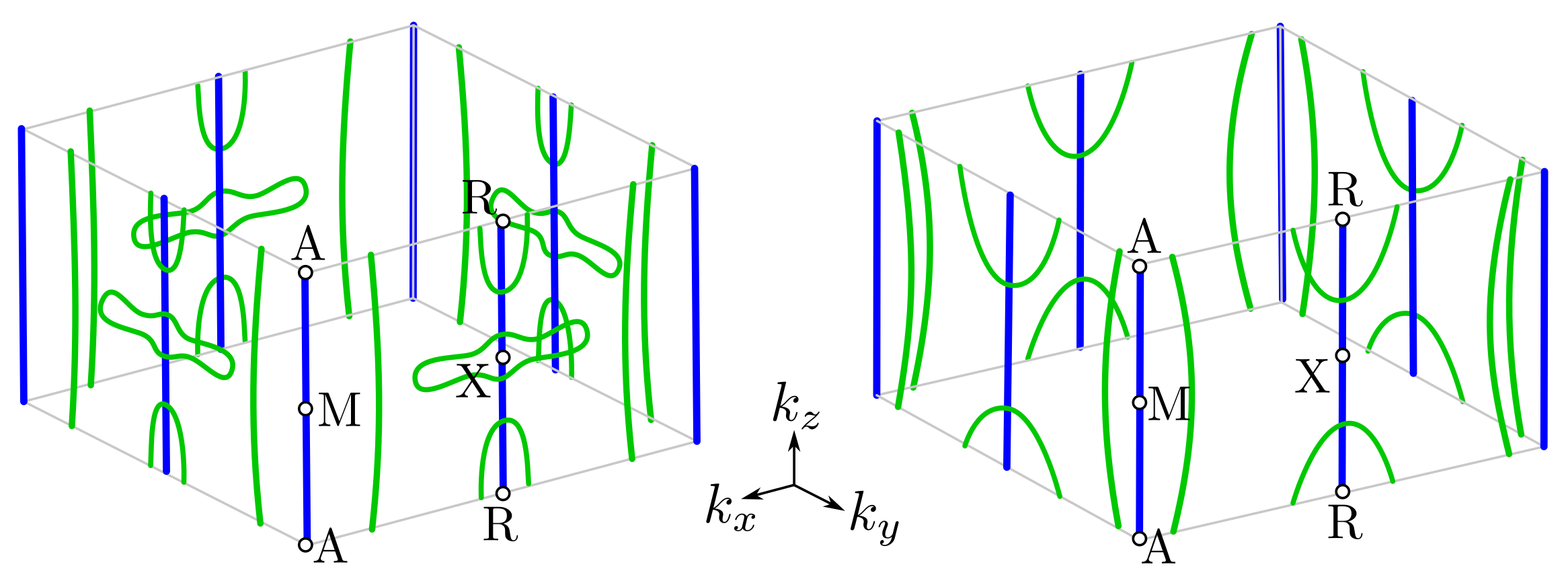
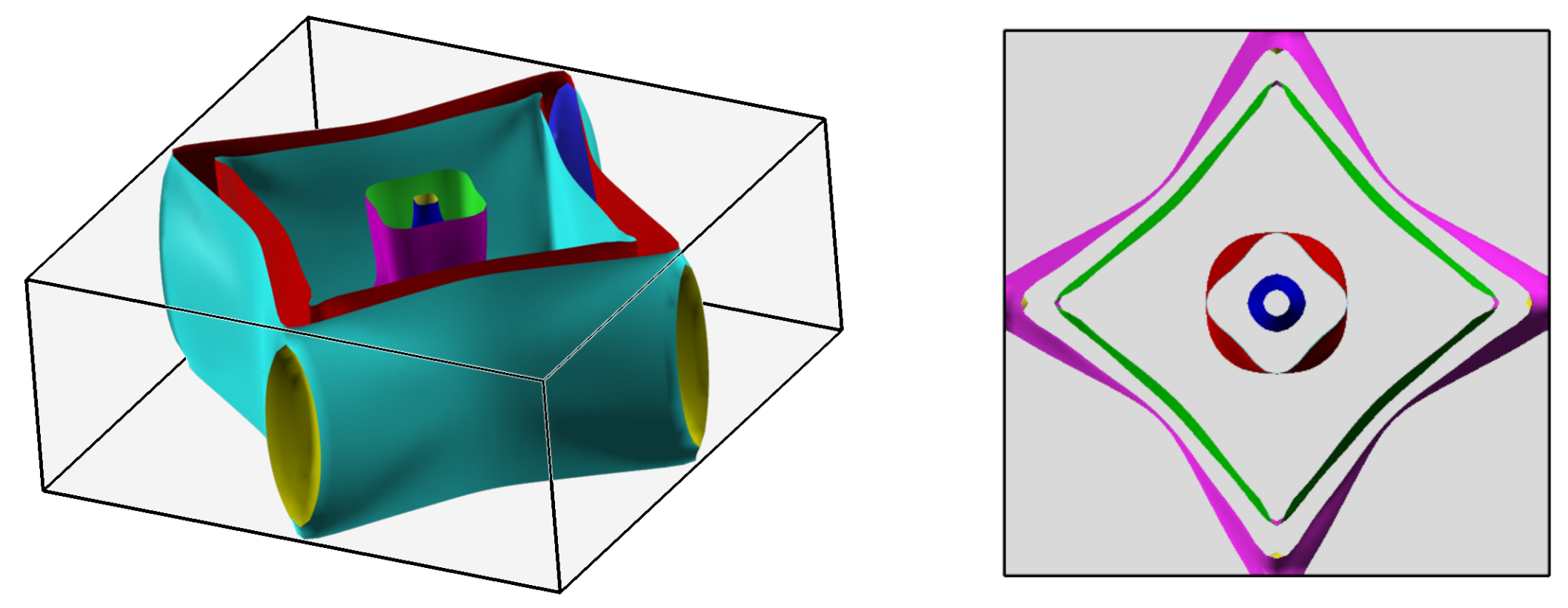
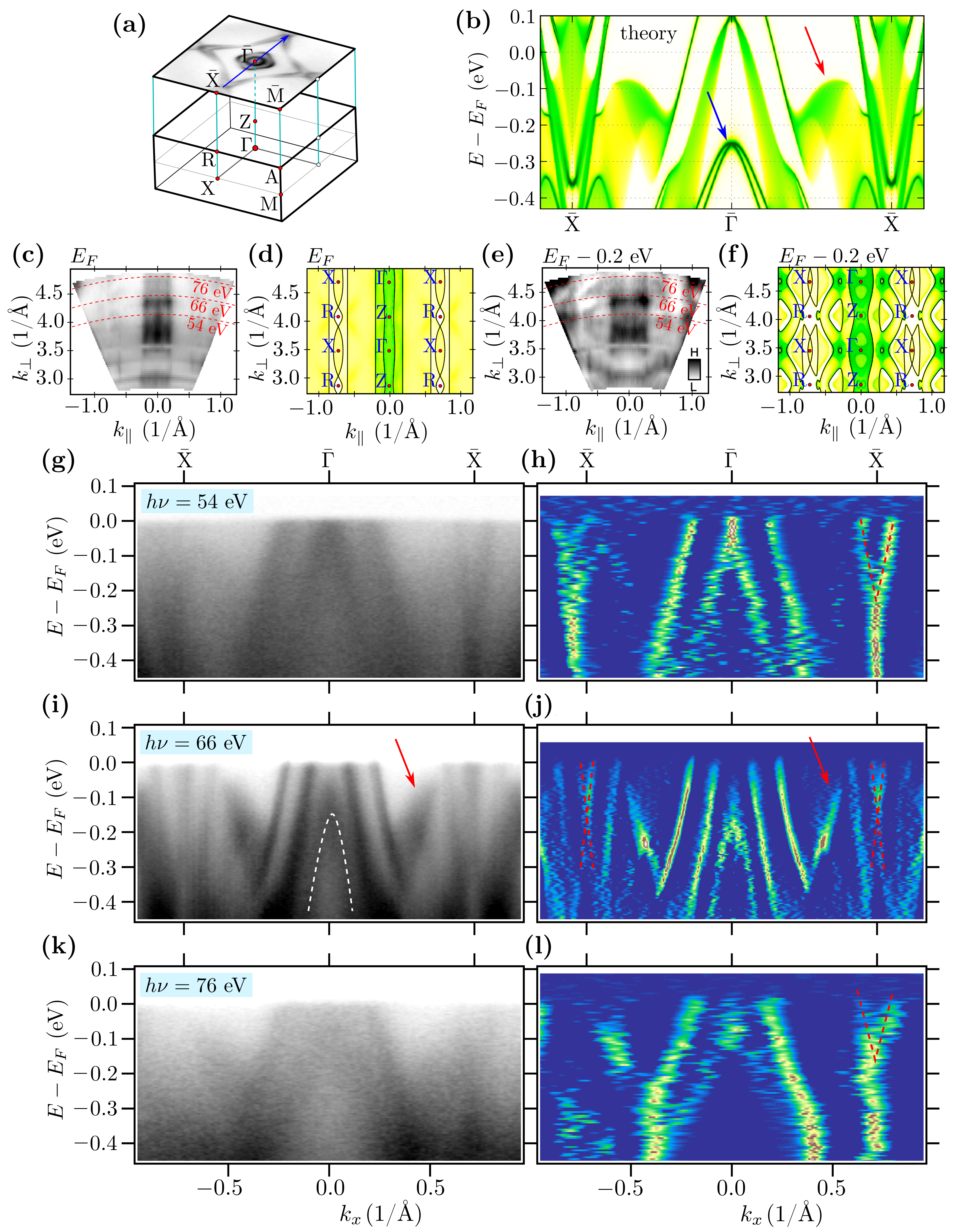
3.2. Band Structure and Fermi Surface
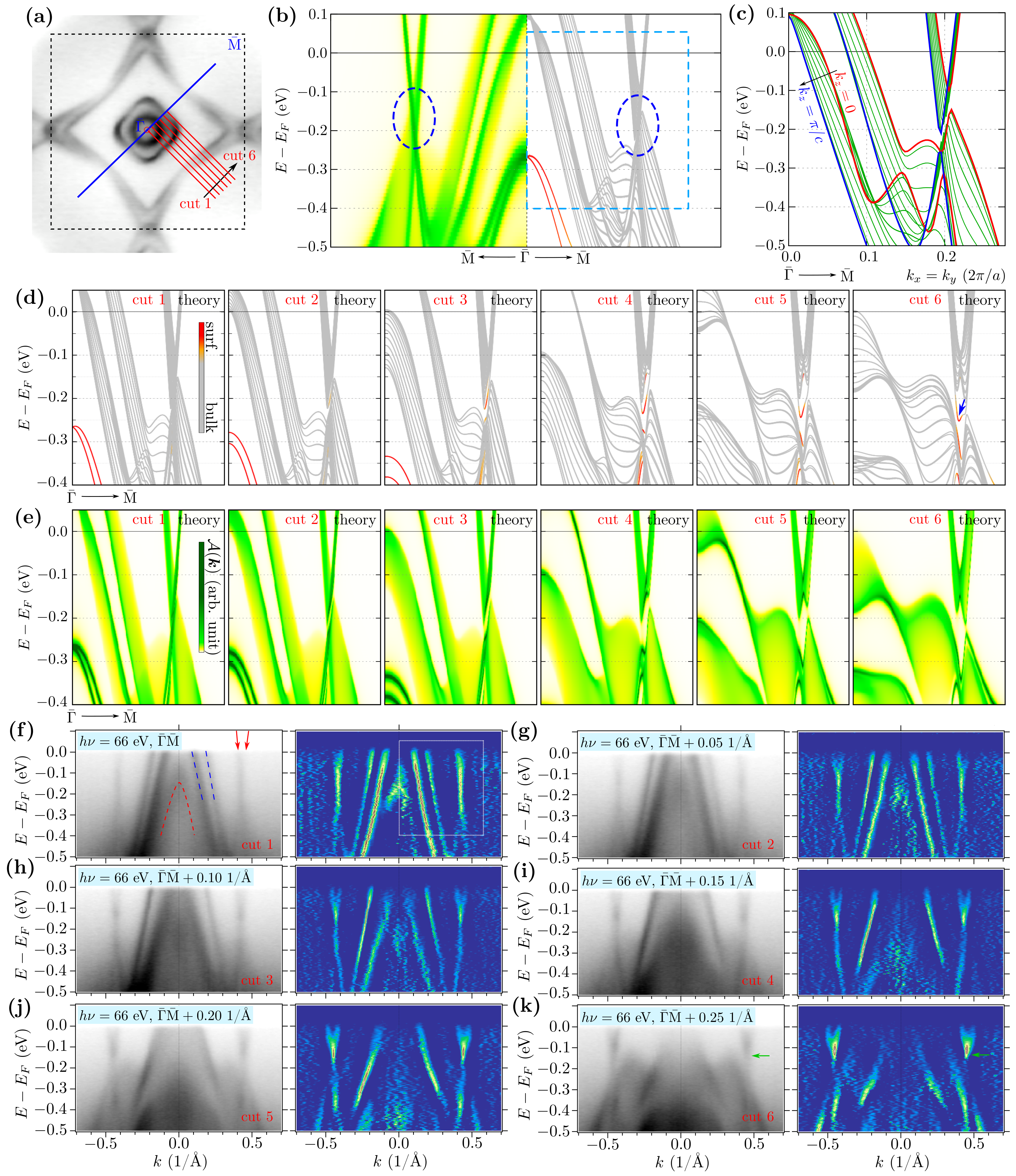
3.3. Surface States within Direct DFT Slab Calculations
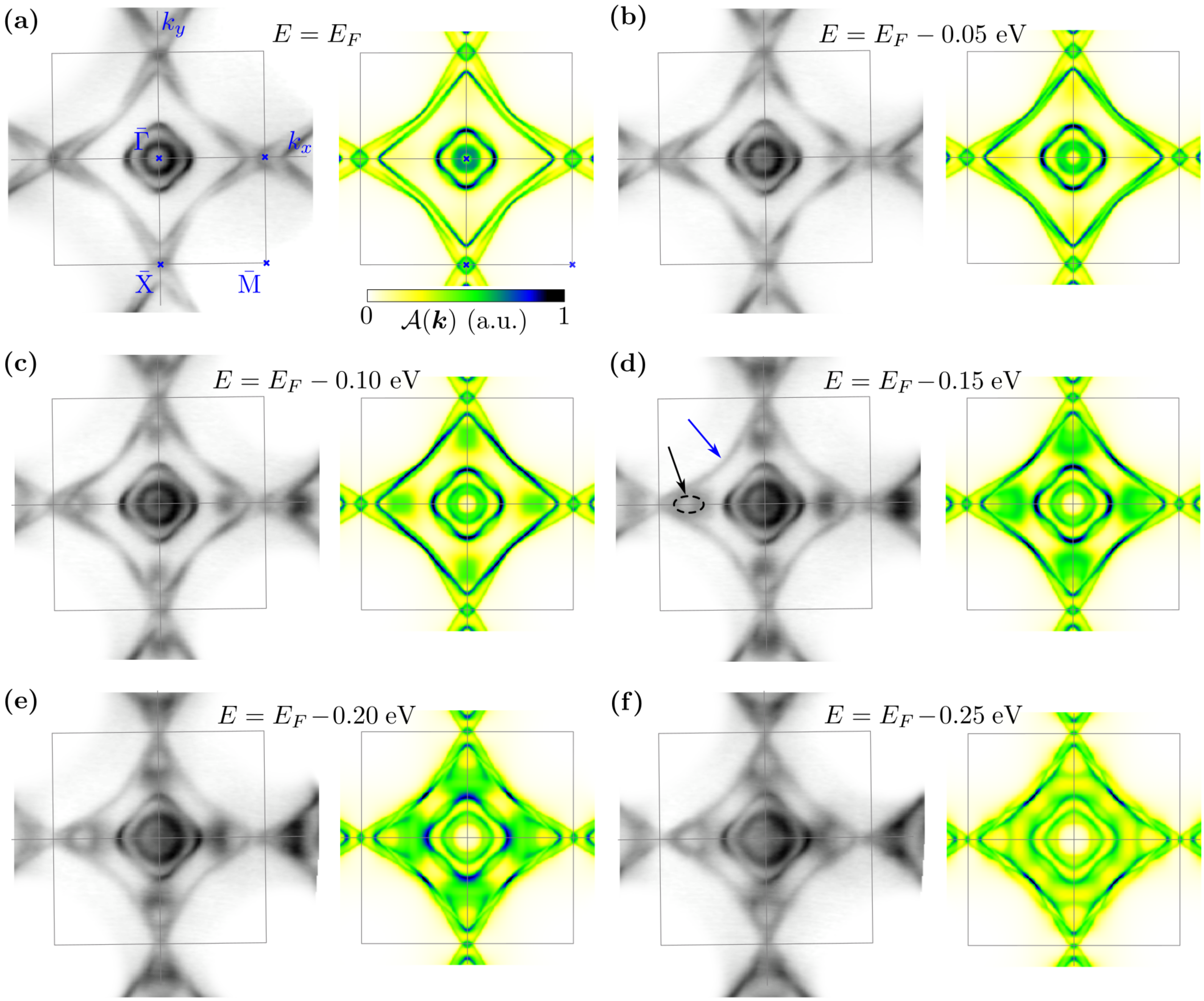
3.4. Surface States around and
3.5. Surface States along -
4. Summary
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Tight Binding Model in Maximally Localized Wannier Orbitals Basis
References
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Sato, M.; Ando, Y. Topological superconductors: A review. Rep. Prog. Phys. 2017, 80, 076501. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Xia, Y.; Qian, D.; Wray, L.; Meier, F.; Dil, J.H.; Osterwalder, J.; Patthey, L.; Fedorov, A.V.; Lin, H.; et al. Observation of Time-Reversal-Protected Single-Dirac-Cone Topological-Insulator States in Bi2Te3 and Sb2Te3. Phys. Rev. Lett. 2009, 103, 146401. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.X.; Qi, X.L.; Dai, X.; Fang, Z.; Zhang, S.C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438. [Google Scholar] [CrossRef]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 398. [Google Scholar] [CrossRef]
- Alpichshev, Z.; Analytis, J.G.; Chu, J.H.; Fisher, I.R.; Chen, Y.L.; Shen, Z.X.; Fang, A.; Kapitulnik, A. STM Imaging of Electronic Waves on the Surface of Bi2Te3: Topologically Protected Surface States and Hexagonal Warping Effects. Phys. Rev. Lett. 2010, 104, 016401. [Google Scholar] [CrossRef]
- Kuroda, K.; Arita, M.; Miyamoto, K.; Ye, M.; Jiang, J.; Kimura, A.; Krasovskii, E.E.; Chulkov, E.V.; Iwasawa, H.; Okuda, T.; et al. Hexagonally Deformed Fermi Surface of the 3D Topological Insulator Bi2Se3. Phys. Rev. Lett. 2010, 105, 076802. [Google Scholar] [CrossRef]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Schoop, L.M.; Pielnhofer, F.; Lotsch, B.V. Chemical Principles of Topological Semimetals. Chem. Mater. 2018, 30, 3155. [Google Scholar] [CrossRef]
- Klemenz, S.; Lei, S.; Schoop, L.M. Topological Semimetals in Square-Net Materials. Annu. Rev. Mater. Res. 2019, 49, 185. [Google Scholar] [CrossRef]
- Song, C.; Park, J.; Koo, J.; Lee, K.B.; Rhee, J.Y.; Bud’ko, S.L.; Canfield, P.C.; Harmon, B.N.; Goldman, A.I. Charge-density-wave orderings in LaAgSb2: An x-ray scattering study. Phys. Rev. B 2003, 68, 035113. [Google Scholar] [CrossRef]
- Chen, R.Y.; Zhang, S.J.; Zhang, M.Y.; Dong, T.; Wang, N.L. Revealing Extremely Low Energy Amplitude Modes in the Charge-Density-Wave Compound LaAgSb2. Phys. Rev. Lett. 2017, 118, 107402. [Google Scholar] [CrossRef]
- Lue, C.S.; Tao, Y.F.; Sivakumar, K.M.; Kuo, Y.K. Weak charge-density-wave transition in LaAgSb2 investigated by transport, thermal, and NMR studies. J. Phys. Condens. Matter 2007, 19, 406230. [Google Scholar] [CrossRef]
- Bosak, A.; Souliou, S.M.; Faugeras, C.; Heid, R.; Molas, M.R.; Chen, R.Y.; Wang, N.L.; Potemski, M.; Le Tacon, M. Evidence for nesting-driven charge density wave instabilities in the quasi-two-dimensional material LaAgSb2. Phys. Rev. Res. 2021, 3, 033020. [Google Scholar] [CrossRef]
- Akiba, K.; Nishimori, H.; Umeshita, N.; Kobayashi, T.C. Successive destruction of charge density wave states by pressure in LaAgSb2. Phys. Rev. B 2021, 103, 085134. [Google Scholar] [CrossRef]
- Bud’ko, S.L.; Wiener, T.A.; Ribeiro, R.A.; Canfield, P.C.; Lee, Y.; Vogt, T.; Lacerda, A.H. Effect of pressure and chemical substitutions on the charge-density-wave in LaAgSb2. Phys. Rev. B 2006, 73, 184111. [Google Scholar] [CrossRef]
- Torikachvili, M.S.; Bud’ko, S.L.; Law, S.A.; Tillman, M.E.; Mun, E.D.; Canfield, P.C. Hydrostatic pressure study of pure and doped La1-xRxAgSb2 (R = Ce, Nd) charge-density-wave compounds. Phys. Rev. B 2007, 76, 235110. [Google Scholar] [CrossRef]
- Myers, K.D.; Bud’ko, S.L.; Antropov, V.P.; Harmon, B.N.; Canfield, P.C.; Lacerda, A.H. de Haas–van Alphen and Shubnikov–de Haas oscillations in RAgSb2 (R = Y, La–Nd, Sm). Phys. Rev. B 1999, 60, 13371. [Google Scholar] [CrossRef]
- Myers, K.D.; Bud’ko, S.L.; Fisher, I.R.; Islam, Z.; Kleinke, H.; Lacerda, A.H.; Canfield, P.C. Systematic study of anisotropic transport and magnetic properties of RAgSb2 (R = Y, La–Nd, Sm, Gd–Tm). J. Magn. Magn. Mater. 1999, 205, 27. [Google Scholar] [CrossRef]
- Wang, K.; Petrovic, C. Multiband effects and possible Dirac states in LaAgSb2. Phys. Rev. B 2012, 86, 155213. [Google Scholar] [CrossRef]
- Park, J.; Lee, G.; Wolff-Fabris, F.; Koh, Y.Y.; Eom, M.J.; Kim, Y.K.; Farhan, M.A.; Jo, Y.J.; Kim, C.; Shim, J.H.; et al. Anisotropic Dirac Fermions in a Bi Square Net of SrMnBi2. Phys. Rev. Lett. 2011, 107, 126402. [Google Scholar] [CrossRef]
- Wang, K.; Graf, D.; Lei, H.; Tozer, S.W.; Petrovic, C. Quantum transport of two-dimensional Dirac fermions in SrMnBi2. Phys. Rev. B 2011, 84, 220401(R). [Google Scholar] [CrossRef]
- Wang, J.K.; Zhao, L.L.; Yin, Q.; Kotliar, G.; Kim, M.S.; Aronson, M.C.; Morosan, E. Layered transition-metal pnictide SrMnBi2 with metallic blocking layer. Phys. Rev. B 2011, 84, 064428. [Google Scholar] [CrossRef]
- Shi, X.; Richard, P.; Wang, K.; Liu, M.; Matt, C.E.; Xu, N.; Dhaka, R.S.; Ristic, Z.; Qian, T.; Yang, Y.F.; et al. Observation of Dirac-like band dispersion in LaAgSb2. Phys. Rev. B 2016, 93, 081105. [Google Scholar] [CrossRef]
- Bukowski, Z.; Tran, V.; Stepień-Damm, J.; Troć, R. Single crystal growth, crystal structure characterization and magnetic properties of UCo0.5Sb2. J. Solid State Chem. 2004, 177, 3934. [Google Scholar] [CrossRef]
- Zhang, P.; Richard, P.; Qian, T.; Xu, Y.M.; Dai, X.; Ding, H. A precise method for visualizing dispersive features in image plots. Rev. Sci. Instrum. 2011, 82, 043712. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Steiner, S.; Khmelevskyi, S.; Marsmann, M.; Kresse, G. Calculation of the magnetic anisotropy with projected-augmented-wave methodology and the case study of disordered Fe1-xCox alloys. Phys. Rev. B 2016, 93, 224425. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Sancho, M.P.L.; Sancho, J.M.L.; Sancho, J.M.L.; Rubio, J. Highly convergent schemes for the calculation of bulk and surface Green functions. J. Phys. F: Met. Phys. 1985, 15, 851. [Google Scholar] [CrossRef]
- Wu, Q.S.; Zhang, S.N.; Song, H.F.; Troyer, M.; Soluyanov, A.A. WannierTools: An open-source software package for novel topological materials. Comput. Phys. Commun. 2018, 224, 405. [Google Scholar] [CrossRef]
- Thirion, F.; Venturini, G.; Malaman, B.; Steinmetz, J.; Roques, B. Structures cristallines de Zr6Cu8Si12 et Hf2CuGe4 et caractérisation d’une famille de composés semimétalliques “pseudolamellaires” de formule ZrSi2Cux où x = 0,5, 1 et 1,33. J. Less Common Met. 1983, 95, 47. [Google Scholar] [CrossRef]
- Brylak, M.; Móller, M.H.; Jeitschko, W. Ternary Arsenides ACuAs2 and Ternary Antimonides AAgSb2 (A= Rare-Earth Elements and Uranium) with HfCuSi2-Type Structure. J. Solid State Chem. 1995, 115, 305. [Google Scholar] [CrossRef]
- Gondek, L.; Penc, B.; Szytuła, A.; Stusser, N. Thermal dependence of the lattice constants of LaAgSb2. J. Alloys Compd. 2002, 346, 80. [Google Scholar] [CrossRef]
- Hase, I.; Yanagisawa, T. Electronic Band Calculation of LaTSb2 (T = Cu, Ag, Au). Phys. Procedia 2014, 58, 42. [Google Scholar] [CrossRef][Green Version]
- Ruszała, P.; Winiarski, M.J.; Samsel-Czekała, M. Dirac-Like Electronic-Band Dispersion of LaSb2 Superconductor and Its Counterpart LaAgSb2. Acta Phys. Pol. A 2020, 138, 748. [Google Scholar] [CrossRef]
- Setyawan, W.; Curtarolo, S. High-throughput electronic band structure calculations: Challenges and tools. Comput. Mater. Sci. 2010, 49, 299. [Google Scholar] [CrossRef]
- Topp, A.; Lippmann, J.M.; Varykhalov, A.; Duppel, V.; Lotsch, B.V.; Ast, C.R.; Schoop, L.M. Non-symmorphic band degeneracy at the Fermi level in ZrSiTe. New J. Phys. 2016, 18, 125014. [Google Scholar] [CrossRef]
- Yang, S.Y.; Yang, H.; Derunova, E.; Parkin, S.S.P.; Yan, B.; Ali, M.N. Symmetry demanded topological nodal-line materials. Adv. Phys. X 2018, 3, 1414631. [Google Scholar] [CrossRef]
- Klemenz, S.; Schoop, L.; Cano, J. Systematic study of stacked square nets: From Dirac fermions to material realizations. Phys. Rev. B 2020, 101, 165121. [Google Scholar] [CrossRef]
- Wang, Y.; Qian, Y.; Yang, M.; Chen, H.; Li, C.; Tan, Z.; Cai, Y.; Zhao, W.; Gao, S.; Feng, Y.; et al. Spectroscopic evidence for the realization of a genuine topological nodal-line semimetal in LaSbTe. Phys. Rev. B 2021, 103, 125131. [Google Scholar] [CrossRef]
- Young, S.M.; Kane, C.L. Dirac Semimetals in Two Dimensions. Phys. Rev. Lett. 2015, 115, 126803. [Google Scholar] [CrossRef]
- Fu, B.B.; Yi, C.J.; Zhang, T.T.; Caputo, M.; Ma, J.Z.; Gao, X.; Lv, B.Q.; Kong, L.Y.; Huang, Y.B.; Richard, P.; et al. Dirac nodal surfaces and nodal lines in ZrSiS. Sci. Adv. 2019, 5, eaau6459. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Xu, X.; Jiang, J.; Wu, S.C.; Qi, Y.P.; Yang, L.X.; Wang, M.X.; Sun, Y.; Schröter, N.B.M.; Yang, H.F.; et al. Dirac line nodes and effect of spin-orbit coupling in the nonsymmorphic critical semimetals MSiS (M = Hf, Zr). Phys. Rev. B 2017, 95, 125126. [Google Scholar] [CrossRef]
- Takane, D.; Wang, Z.; Souma, S.; Nakayama, K.; Trang, C.X.; Sato, T.; Takahashi, T.; Ando, Y. Dirac-node arc in the topological line-node semimetal HfSiS. Phys. Rev. B 2016, 94, 121108(R). [Google Scholar] [CrossRef]
- Hosen, M.M.; Dimitri, K.; Belopolski, I.; Maldonado, P.; Sankar, R.; Dhakal, N.; Dhakal, G.; Cole, T.; Oppeneer, P.M.; Kaczorowski, D.; et al. Tunability of the topological nodal-line semimetal phase in ZrSiX-type materials (X = S, Se, Te). Phys. Rev. B 2017, 95, 161101(R). [Google Scholar] [CrossRef]
- Topp, A.; Queiroz, R.; Grüneis, A.; Müchler, L.; Rost, A.W.; Varykhalov, A.; Marchenko, D.; Krivenkov, M.; Rodolakis, F.; McChesney, J.L.; et al. Surface Floating 2D Bands in Layered Nonsymmorphic Semimetals: ZrSiS and Related Compounds. Phys. Rev. X 2017, 7, 041073. [Google Scholar] [CrossRef]
- Schoop, L.M.; Topp, A.; Lippmann, J.; Orlandi, F.; Müchler, L.; Vergniory, M.G.; Sun, Y.; Rost, A.W.; Duppel, V.; Krivenkov, M.; et al. Tunable Weyl and Dirac states in the nonsymmorphic compound CeSbTe. Sci. Adv. 2018, 4, eaar2317. [Google Scholar] [CrossRef]
- Regmi, S.; Dhakal, G.; Kabeer, F.C.; Harrison, N.; Kabir, F.; Sakhya, A.P.; Gofryk, K.; Kaczorowski, D.; Oppeneer, P.M.; Neupane, M. Observation of multiple nodal lines in SmSbTe. Phys. Rev. Mater. 2022, 6, L031201. [Google Scholar] [CrossRef]
- Schoop, L.M.; Ali, M.N.; Straßer, C.; Topp, A.; Varykhalov, A.; Marchenko, D.; Duppel, V.; Parkin, S.S.P.; Lotsch, B.V.; Ast, C.R. Dirac cone protected by non-symmorphic symmetry and three-dimensional Dirac line node in ZrSiS. Nat. Commun. 2016, 7, 11696. [Google Scholar] [CrossRef]
- Neupane, M.; Belopolski, I.; Hosen, M.M.; Sanchez, D.S.; Sankar, R.; Szlawska, M.; Xu, S.Y.; Dimitri, K.; Dhakal, N.; Maldonado, P.; et al. Observation of topological nodal fermion semimetal phase in ZrSiS. Phys. Rev. B 2016, 93, 201104(R). [Google Scholar] [CrossRef]
- Lou, R.; Ma, J.Z.; Xu, Q.N.; Fu, B.B.; Kong, L.Y.; Shi, Y.G.; Richard, P.; Weng, H.M.; Fang, Z.; Sun, S.S.; et al. Emergence of topological bands on the surface of ZrSnTe crystal. Phys. Rev. B 2016, 93, 241104(R). [Google Scholar] [CrossRef]
- Hosen, M.M.; Dimitri, K.; Aperis, A.; Maldonado, P.; Belopolski, I.; Dhakal, G.; Kabir, F.; Sims, C.; Hasan, M.Z.; Kaczorowski, D.; et al. Observation of gapless Dirac surface states in ZrGeTe. Phys. Rev. B 2018, 97, 121103(R). [Google Scholar] [CrossRef]
- Song, Y.K.; Wang, G.W.; Li, S.C.; Liu, W.L.; Lu, X.L.; Liu, Z.T.; Li, Z.J.; Wen, J.S.; Yin, Z.P.; Liu, Z.H.; et al. Photoemission Spectroscopic Evidence for the Dirac Nodal Line in the Monoclinic Semimetal SrAs3. Phys. Rev. Lett. 2020, 124, 056402. [Google Scholar] [CrossRef]
- Akiba, K.; Umeshita, N.; Kobayashi, T.C. Magnetotransport studies of the Sb square-net compound LaAgSb2 under high pressure and rotating magnetic fields. Phys. Rev. B 2022, 105, 035108. [Google Scholar] [CrossRef]
- Arakane, T.; Sato, T.; Souma, S.; Takahashi, T.; Watanabe, Y.; Inada, Y. Electronic structure of LaAgSb2 and CeAgSb2 studied by high-resolution angle-resolved photoemission spectroscopy. J. Magn. Magn. Mater. 2007, 310, 396. [Google Scholar] [CrossRef]
- Chamorro, J.R.; Topp, A.; Fang, Y.; Winiarski, M.J.; Ast, C.R.; Krivenkov, M.; Varykhalov, A.; Ramshaw, B.J.; Schoop, L.M.; McQueen, T.M. Dirac fermions and possible weak antilocalization in LaCuSb2. APL Mater. 2019, 7, 121108. [Google Scholar] [CrossRef]
- Borisenko, S.; Evtushinsky, D.; Gibson, Q.; Yaresko, A.; Koepernik, K.; Kim, T.; Ali, M.; van den Brink, J.; Hoesch, M.; Fedorov, A.; et al. Time-reversal symmetry breaking type-II Weyl state in YbMnBi2. Nat. Commun. 2019, 10, 3424. [Google Scholar] [CrossRef]
- Kealhofer, R.; Jang, S.; Griffin, S.M.; John, C.; Benavides, K.A.; Doyle, S.; Helm, T.; Moll, P.J.W.; Neaton, J.B.; Chan, J.Y.; et al. Observation of a two-dimensional Fermi surface and Dirac dispersion in YbMnSb2. Phys. Rev. B 2018, 97, 045109. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, Z.; Chen, C.; Shi, Y.; Xie, Z.; Yi, H.; Liang, A.; He, S.; He, J.; Peng, Y.; et al. Strong Anisotropy of Dirac Cones in SrMnBi2 and CaMnBi2 Revealed by Angle-Resolved Photoemission Spectroscopy. Sci. Rep. 2014, 4, 5385. [Google Scholar] [CrossRef]
- Marković, I.; Hooley, C.A.; Clark, O.J.; Mazzola, F.; Watson, M.D.; Riley, J.M.; Volckaert, K.; Underwood, K.; Dyer, M.S.; Murgatroyd, P.A.E.; et al. Weyl-like points from band inversions of spin-polarised surface states in NbGeSb. Nat. Commun. 2019, 10, 5485. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, S.C.; Yan, B. Topological surface states and Fermi arcs of the noncentrosymmetric Weyl semimetals TaAs, TaP, NbAs, and NbP. Phys. Rev. B 2015, 92, 115428. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. vesta3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272. [Google Scholar] [CrossRef]
- Kokalj, A. XCrySDen—A new program for displaying crystalline structures and electron densities. J. Mol. Graph. Model. 1999, 17, 176. [Google Scholar] [CrossRef]
- Marzari, N.; Mostofi, A.A.; Yates, J.R.; Souza, I.; Vanderbilt, D. Maximally localized Wannier functions: Theory and applications. Rev. Mod. Phys. 2012, 84, 1419. [Google Scholar] [CrossRef]
- Marzari, N.; Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 1997, 56, 12847. [Google Scholar] [CrossRef]
- Souza, I.; Marzari, N.; Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B 2001, 65, 035109. [Google Scholar] [CrossRef]
- Mostofi, A.A.; Yates, J.R.; Lee, Y.S.; Souza, I.; Vanderbilt, D.; Marzari, N. wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 2008, 178, 685. [Google Scholar] [CrossRef]
- Mostofi, A.A.; Yates, J.R.; Pizzi, G.; Lee, Y.S.; Souza, I.; Vanderbilt, D.; Marzari, N. An updated version of wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 2014, 185, 2309. [Google Scholar] [CrossRef]
- Pizzi, G.; Vitale, V.; Arita, R.; Blügel, S.; Freimuth, F.; Géranton, G.; Gibertini, M.; Gresch, D.; Johnson, C.; Koretsune, T.; et al. Wannier90 as a community code: New features and applications. J. Phys. Condens. Matter 2020, 32, 165902. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosmus, M.; Olszowska, N.; Bukowski, Z.; Starowicz, P.; Piekarz, P.; Ptok, A. Electronic Band Structure and Surface States in Dirac Semimetal LaAgSb2. Materials 2022, 15, 7168. https://doi.org/10.3390/ma15207168
Rosmus M, Olszowska N, Bukowski Z, Starowicz P, Piekarz P, Ptok A. Electronic Band Structure and Surface States in Dirac Semimetal LaAgSb2. Materials. 2022; 15(20):7168. https://doi.org/10.3390/ma15207168
Chicago/Turabian StyleRosmus, Marcin, Natalia Olszowska, Zbigniew Bukowski, Paweł Starowicz, Przemysław Piekarz, and Andrzej Ptok. 2022. "Electronic Band Structure and Surface States in Dirac Semimetal LaAgSb2" Materials 15, no. 20: 7168. https://doi.org/10.3390/ma15207168
APA StyleRosmus, M., Olszowska, N., Bukowski, Z., Starowicz, P., Piekarz, P., & Ptok, A. (2022). Electronic Band Structure and Surface States in Dirac Semimetal LaAgSb2. Materials, 15(20), 7168. https://doi.org/10.3390/ma15207168





