Next Article in Journal
Interfacial Phenomena at the Interface in the System «Carbon Primary Materials-Water Solutions of Surfactants» for Cement Materials
Next Article in Special Issue
Effects of Low-Temperature Construction Additives (LCAs) on the Performance of Asphalt Mixtures
Previous Article in Journal
Assessment of Boron Diffusivities in Nickel Borides by Two Mathematical Approaches
Previous Article in Special Issue
Artificial Weathering Resistance Test Methods for Building Performance Assessment of Profiles Made of Natural Fibre-Reinforced Polymer Composites
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 15
Issue 2
10.3390/ma15020552
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Research and TLS (LiDAR) Construction Diagnostics of Clay Brick Masonry Arched Stairs

by
Rafał Nowak
1,*,
Tomasz Kania
2,
Radosław Rutkowski
3 and
Ewa Ekiert
4
1
Department of General Civil Engineering, Faculty of Civil and Environmental Engineering, West Pomeranian University of Technology in Szczecin, Piastów Ave. 50a, 70-311 Szczecin, Poland
2
Department of General Civil Engineering, Faculty of Civil Engineering, Wrocław University of Science and Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland
3
Department of Technological Processes, Faculty of Economics and Transport Engineering, Maritime University of Szczecin, Wały Chrobrego 1-2, 70-500 Szczecin, Poland
4
Department of Chemical Inorganic Technology and Environment Engineering, Faculty of Chemical Technology and Engineering, West Pomeranian University of Technology in Szczecin, Piastów Ave. 42, 71-065 Szczecin, Poland
*
Author to whom correspondence should be addressed.
Materials 2022, 15(2), 552; https://doi.org/10.3390/ma15020552
Submission received: 28 November 2021 / Revised: 20 December 2021 / Accepted: 3 January 2022 / Published: 12 January 2022
(This article belongs to the Special Issue Testing of Materials and Elements in Civil Engineering (2nd Edition))
Browse Figures
Versions Notes

Abstract

:
The study presents the terrestrial laser scanning (TLS) diagnostic of the clay brick masonry arched staircase in a historic building. Based on the measurements of the existing arched stair flights, 1:1 scale experimental models with and without stair treads were made. Strength tests of the models were carried out for different concentrated force locations in relation to the supporting structure. Force, deflections and reaction in the upper support of the run were measured during the tests. The influence of the masonry steps on the curved vault on the load capacity and stiffness of the run structure was analyzed. The conducted experimental investigations showed that the key element responsible for the actual load-bearing capacity and stiffness of this type of stair flights were the treads above the masonry arch.

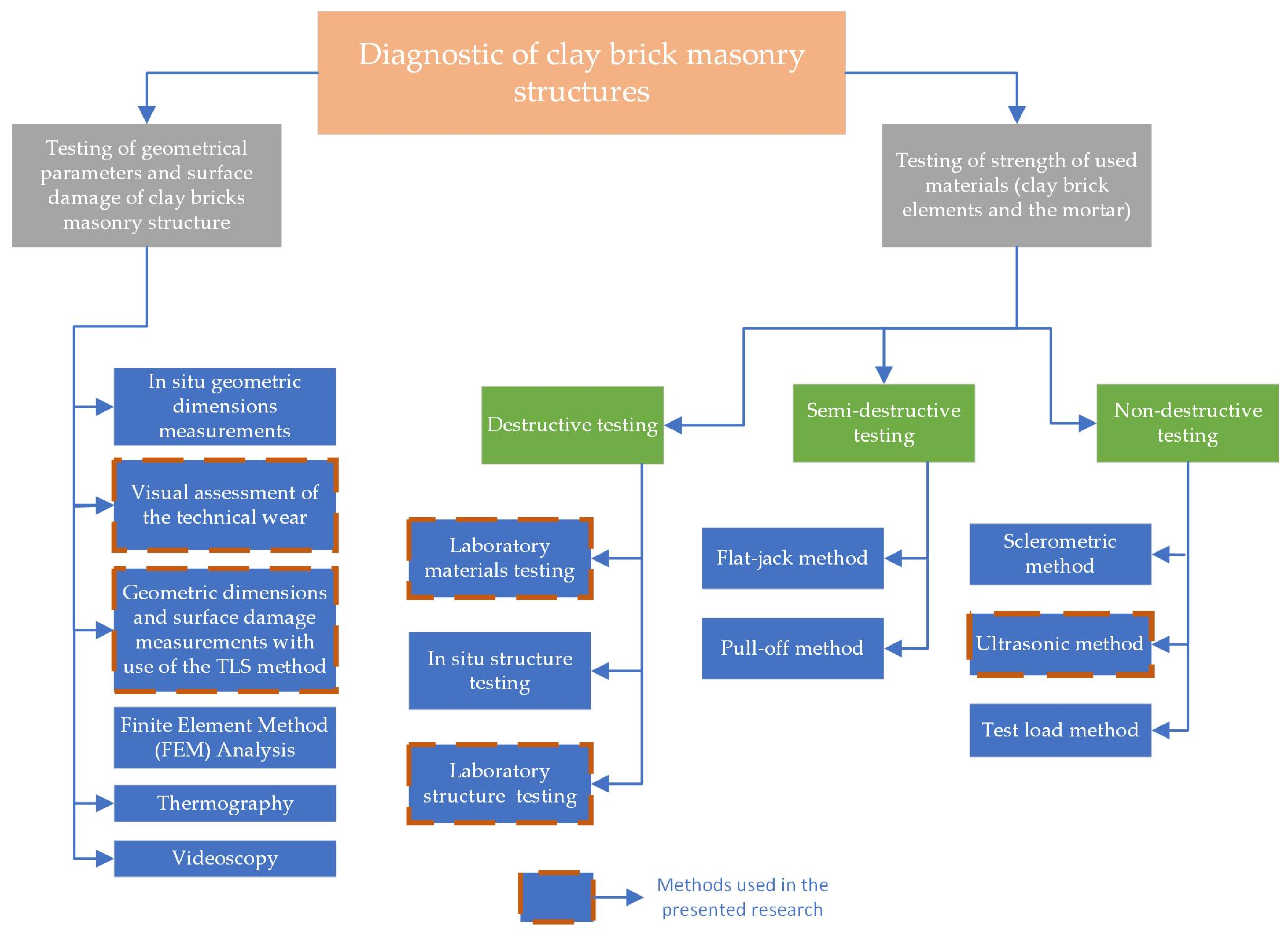
1. Introduction

In the authors’ countries, in historical buildings from the 19th century, masonry arch stairs were commonly used to connect floors [1]. The arches were shaped between steel beams as a load-bearing span for the staircase landings and flights. At that time, the technology of reinforced concrete was not yet known, so steel and masonry construction was the most popular, especially in residential buildings. The construction of staircases was mostly in the form of segmental or cross vaults. The structure of the flights was made as a stair arch with the thickness of half a brick (12 cm) and elevation f = 1/12–1/14 L [1] (Figure 1 and Figure 2).
A flight of arch stairs is characterized by a slender, long structure with a slope of approximately 35°–40°. One of the main permanent loads on the flight of stairs are the bricks along the entire flight. The steps have the least bricks in the middle of the stairs’ arch and the most at the ends. The steps are not connected with a typical masonry bond. The bricks must be cut to fit the actual geometry of the arches.
The flights and landings were supported by steel beams. The construction of flights had a good fire resistance (except for the steel beams), stiffness and durability. The constructions of brick stairs are still in use despite many years of service. Additionally, they are a testament of old times and often protected by the conservator as a part of cultural heritage. Their condition often raises concern because of the damages, mainly cracks or erosion of joints. The typical damages of brick staircase construction are: degradation of mortar and bricks, flattening of vaults and cracking. The damages arise as a result of overloading, wrongly executed repair works and dynamic loads. Sometimes, one can find constructional errors such as improper fixing of gear plates on I-beam flanges.
Information on calculation methods or principles of construction is often difficult to find. This type of construction was created mainly on the basis of experience with brick vaults. The steel beams supporting the vaults were calculated by the methods available at that time [1]. The operation of landing vaults is similar to balcony or roof vaults. On the other hand, staircase slabs are at an angle depending on their length and height. The distribution of stresses and internal forces is different from other staircase structures. A calculation scheme of an example of an arched masonry stairs with vaulted landings supported on steel beams is shown in Figure 3.
One of the most prevalent issues in this type of stairs is the necessity of diagnostics of their technical condition in order to confirm their durability and functional use. The chosen methods used in the diagnostics of masonry structures in the authors’ countries are shown in Figure 4.
The diagnosis of masonry structures primarily focuses on a visual assessment in order to detect cracks and damages [2,3,4,5]. The early diagnostics usually uses non-destructive measuring equipment, which allows the preliminary characteristics of existing materials or the degree of their degradation to be evaluated [6,7,8,9,10]. Those methods most often include sclerometric measurements (Schmidt hammer) or ultrasonic measurements. At that stage of diagnosis, infrared thermography is a novel and useful method for historic plaster and painted vaults. The management of the data derived from the application of infrared thermography, integrated with the information from visual inspections, the architectural survey and the historic analysis, allows a complete characterization of the historic plasters and painted masonry vaults to be obtained [11].
A more accurate determination of material properties in masonry structures involves sampling. In the case of brick alone, this process is feasible; however, sampling of mortar is significantly more difficult. Therefore, in many diagnostic operations, core samples are taken, also containing a fragment of mortar and masonry elements adjacent on both sides. The core samples, after certain correlations, are used to determine the load-bearing capacity of the whole masonry structure [12,13,14,15,16,17]. Even more accurate results may be obtained by test-loading a masonry section with actuators [18]. However, this method requires making cuts in the masonry in order to locate the beams to place the actuators. The method is mostly used as a validation is structural elements that are to undergo alteration, repair, or reconstruction.
A similar effect can be obtained if a section of the masonry is cut out and transported to the laboratory for experimental testing [14,18]. A less destructive solution is the flat-jack method [18,19]. It requires appropriate calibration procedures and precise preparation of the measurement base. Additionally, it may be imprecise in low buildings and lead to permanent damage when testing masonry with weak lime mortar [18]. The best measurement method is to perform a loading test with appropriate measurement [20,21,22,23,24], which does not lead to the destruction of the structure but allows the correlation between stresses and strains to be obtained, in order to assess the actual load-bearing capacity and stiffness. Final results on the load-bearing capacity of the structure can only be obtained from experimental destructive testing.
The finite element method (FEM) is a fundamental analysis for the assessment of masonry in seismic zones [25,26,27,28]. Nonlinear static calculation methods are commonly adopted for the evaluation of seismic performance [26,27,28,29,30,31,32]. Laurenco et al. [28] presented a research study on that subject with a yield criterion that included different strengths along each material axis. Baraldi et al. [31] presented the rigid beam model for studying the dynamic behavior of cantilever unreinforced masonry walls, considered along their thickness and subjected to out-of-plane loading. Celano et al. [32] presented research on the in-plane resistance of masonry walls with the use of two modeling approaches, a finite element model and a discrete macro-element model, with the use of non-linear analyses.
The TLS (terrestrial laser scanning) measurements using 3D scanners are starting to be used for structural diagnosis. Three-dimensional LiDAR (light detection and ranging) scanners have revolutionized the capability and accuracy of geometry measurements in construction, shipbuilding and other areas of science and technology [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. TLS can be used to measure damage to the surface layers of materials, including bricks and mortar, as well as to track moisture in structures [33,41,42,43,44,45,46,47,48,49]. TLS in structural analysis is primarily used to measure strain and deflections, as well as deformations, of structural elements [25,42,43,44,45,46,47,48,49,50]. This technique can also be used for control measurements at the stage of constructing [51]. Some researchers use TLS technology to monitor the condition of construction to prevent possible damage [52,53]. Additionally, detailed geometry studies using TLS are useful in post-disaster analyses of structures, including earthquakes [53].
The assessment of the technical condition of brick stairs is not an easy task. The first step usually consists of initial observations of the geometry and of looking for visible signs of damage. Usually, the construction is protected by plaster, so some defects may be hidden. Modern TLS measuring methods can also be helpful in preliminary surveys. Only by uncovering, it is possible to fully assess the quality of brick and mortar and their degree of degradation. The evaluation of the material properties of the structure is possible by taking representative samples and performing laboratory tests [2,10,54,55,56,57,58,59]. A deeper analysis of the performance of the structure and the causes of its damage is possible using FEM-based 3D models [57,58,59,60,61,62,63,64]. On this basis, it is possible to precisely select the reinforcement methods. The analysis in the elastic range is rather easy to perform, but the analysis in the plastic range, after cracking has occurred, requires time-consuming and expensive studies [60].
Studies of masonry arches and vaults can be found in the works [61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105]. In these studies, masonry vaults are characterized by significant arch rise and placement of the masonry stairs. A small number of researchers has taken up the problem of load-bearing capacity of masonry stairs. Research has mostly focused on establishing the principles and methods for structural calculations [92,93,94,95,96,97,98,99]. There is a visible lack of research on masonry staircases. The design of staircases is similar to masonry arch work; however, the arrangement of loads is different. In addition, the influence of the steps above the vault on the operation of the system is also significant.
The article presents a novel approach, in which experimental tests for staircases were made in a 1:1 scale resembling a real-life construction. Together with laboratory tests, the TLS diagnosis of an arched staircase in a real-life historic building is presented. The history of the TLS LiDAR measurement method dates back only 20 years [41,42,106]. The authors’ research study indicates that it can be used in the diagnosis of some types of building structures [41,42]. It is important to assess the applicability of the TLS method in the diagnosis of masonry stair structures, including arched staircases. The possibilities of its use in this area are presented in this article.

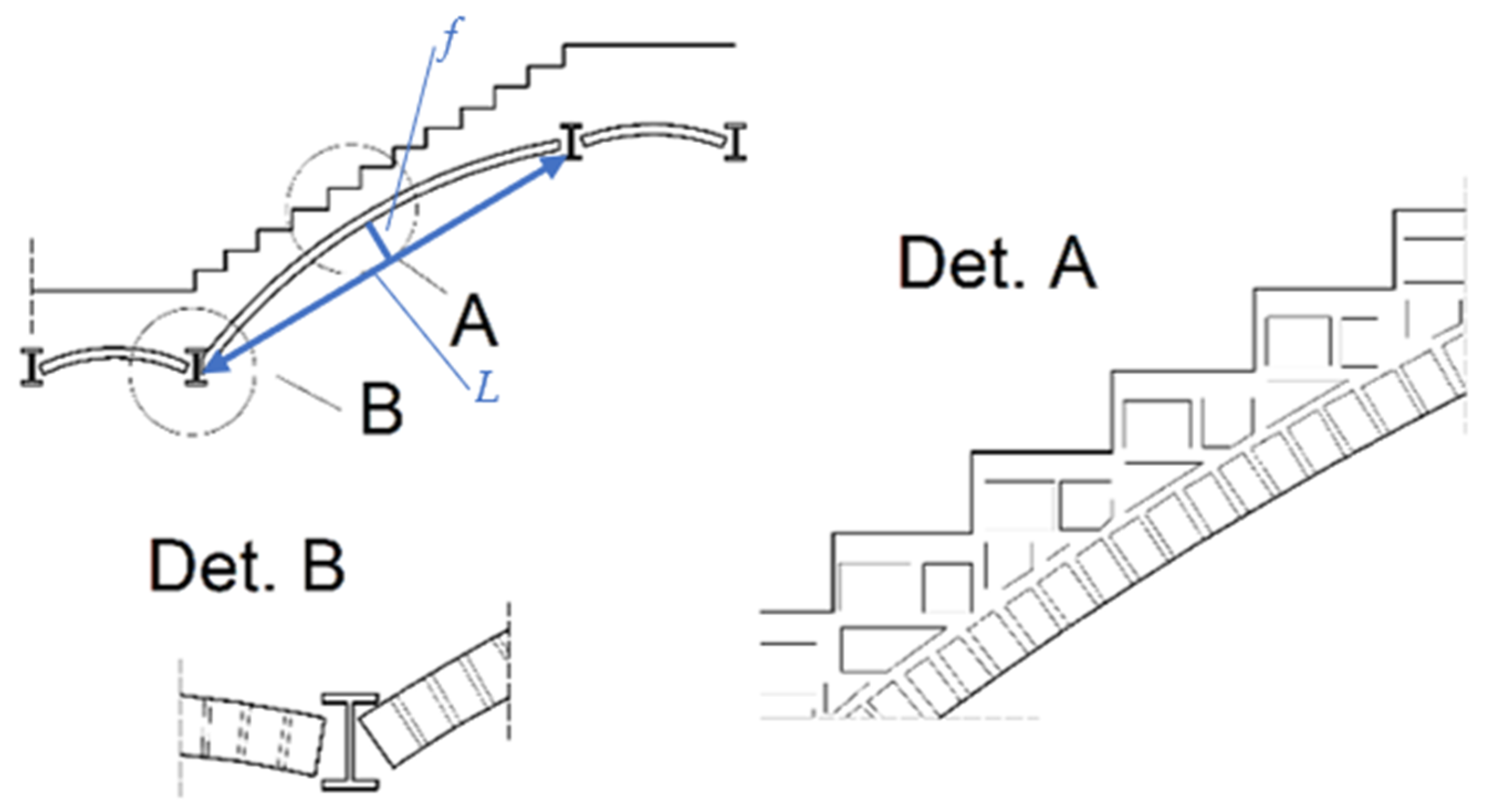
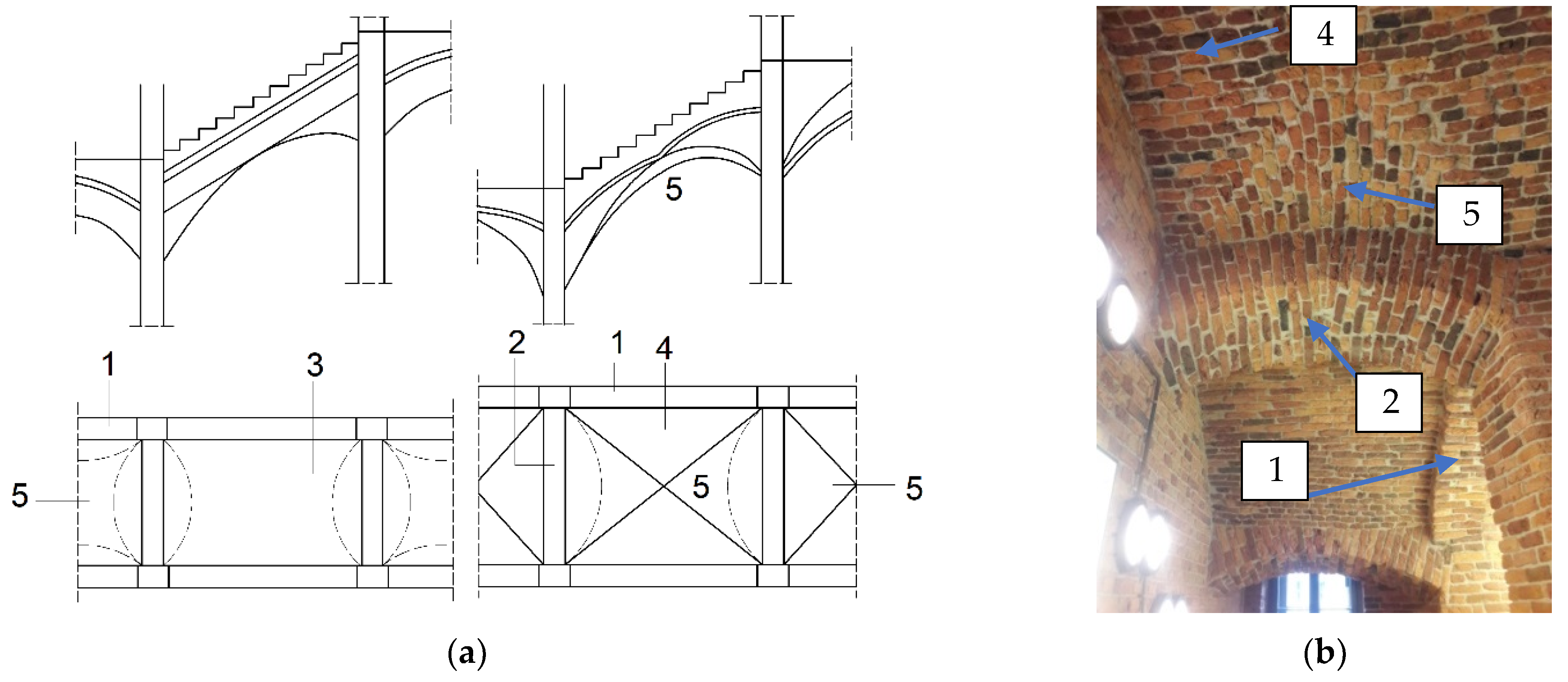
2. Real-Life Structure

2.1. Case Study Description

The building had four residential floors and an attic. The ceilings on the upper floors were made of wooden beams, while, on the first floor, they were made as arched segmental vaults on steel beams. The floors were 3.2 m high. The staircase was 2.5 m wide and 5.3 m long. The length of the landings was 1.6–1.7 m and the length of the flights was 2.6 m, with a width of 1.2 m. The analyzed stair flights were at an angle of 38°. The stairs were made of steel and masonry, with arched spans between the landings. The rise of the stair arch had a value of f = 1/19 L. Figure 5 shows the general view of the arched stair structure under consideration.
The measured dimensions of the bricks were 25 × 12 × 6.5 cm3. The brick and mortar compressive strength was estimated with use of the non-destructive, ultrasonic measurements according to the dependencies described in [107]. The dependency of bricks is shown in Equation (1).
f c , b r i c k = 1.4949 · e 0.002   · U P V     ( MPa ) ,
where fc,brick (MPa) is the compressive strength of the brick element and UPV (m/s) is the measured ultrasonic pulse velocity. The dependency of lime–cement mortar is presented in Equation (2).
f c , m o r t a r = − 5.5 + 0.007671 · U P V     ( MPa ) ,
where fc,mortar (MPa) is the compressive strength of lime–cement mortar. The results of the tests are presented in Table 1.
The compressive strength of the bricks varied in a wide range, from 10.4 to 28.4 MPa with a mean value of 17.6 MPa. The compressive strength of lime–cement mortar varied from 2.1 to 5.4 MPa with a mean value of 4.1 MPa. Due to the large discrepancy found between the strength values of the masonry units and mortar, it was decided to carry out laboratory tests using materials with standard properties. In this respect, a brick class of 25 MPa and a mortar class of 5 MPa were assumed.

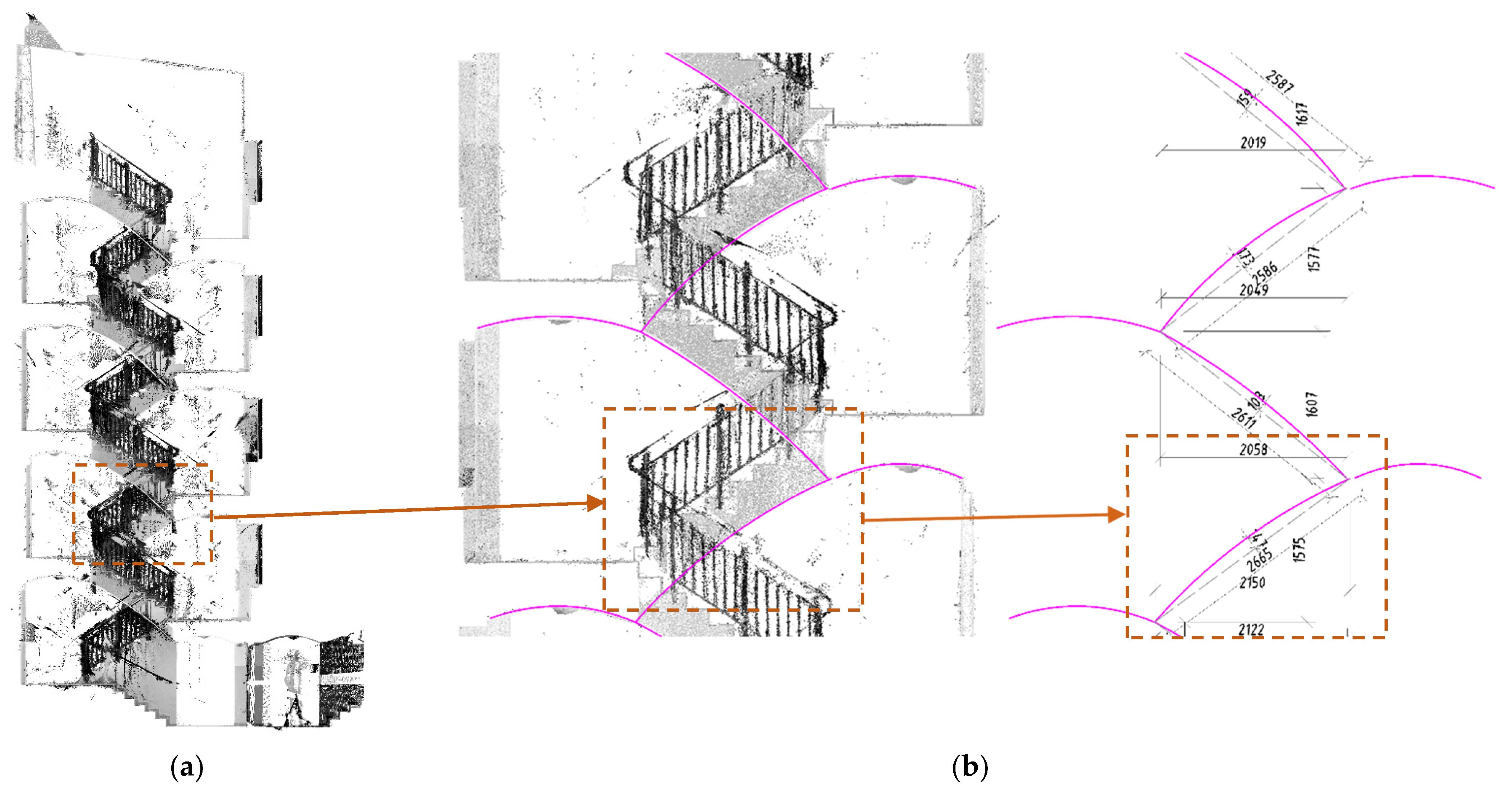
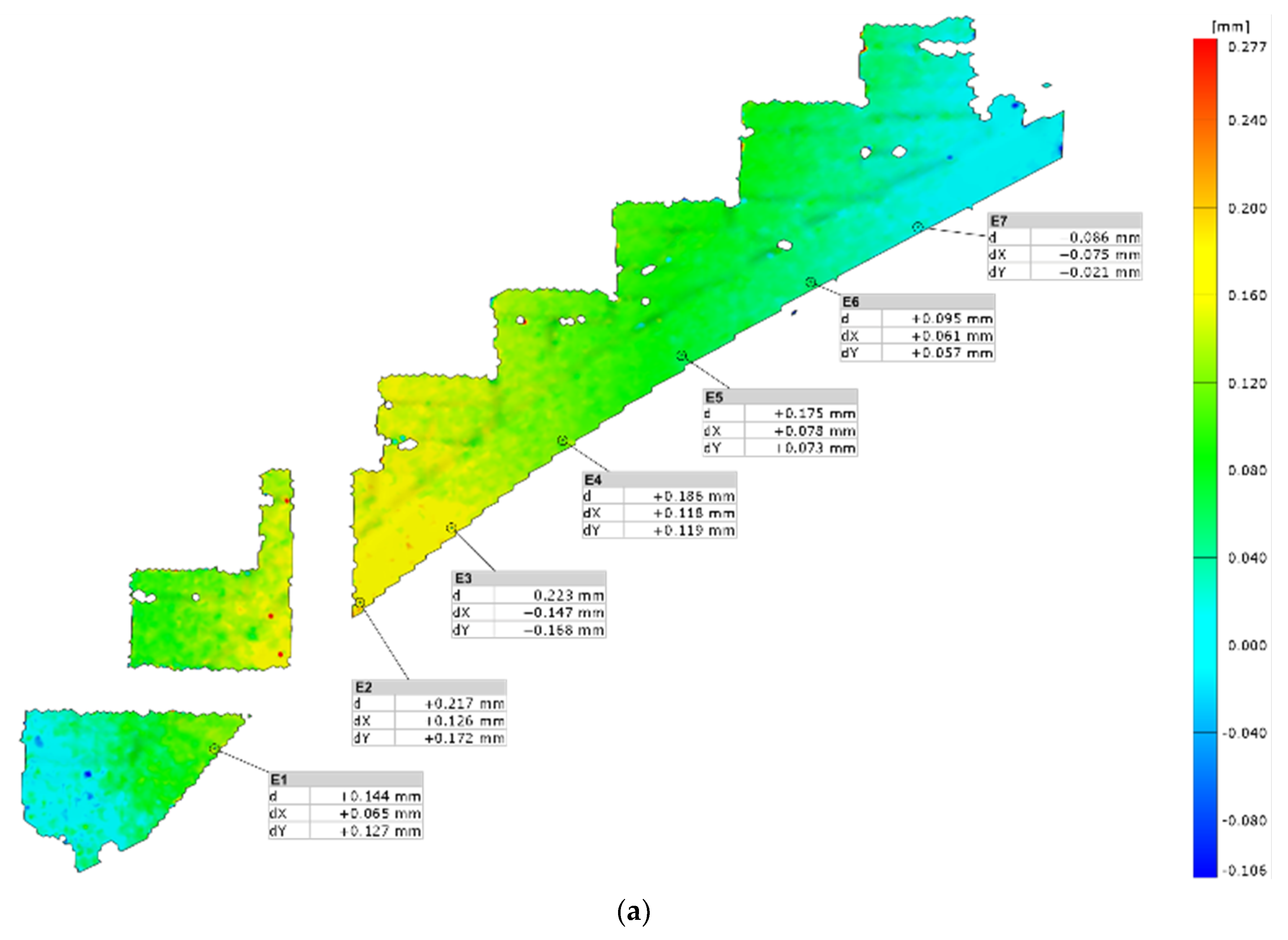
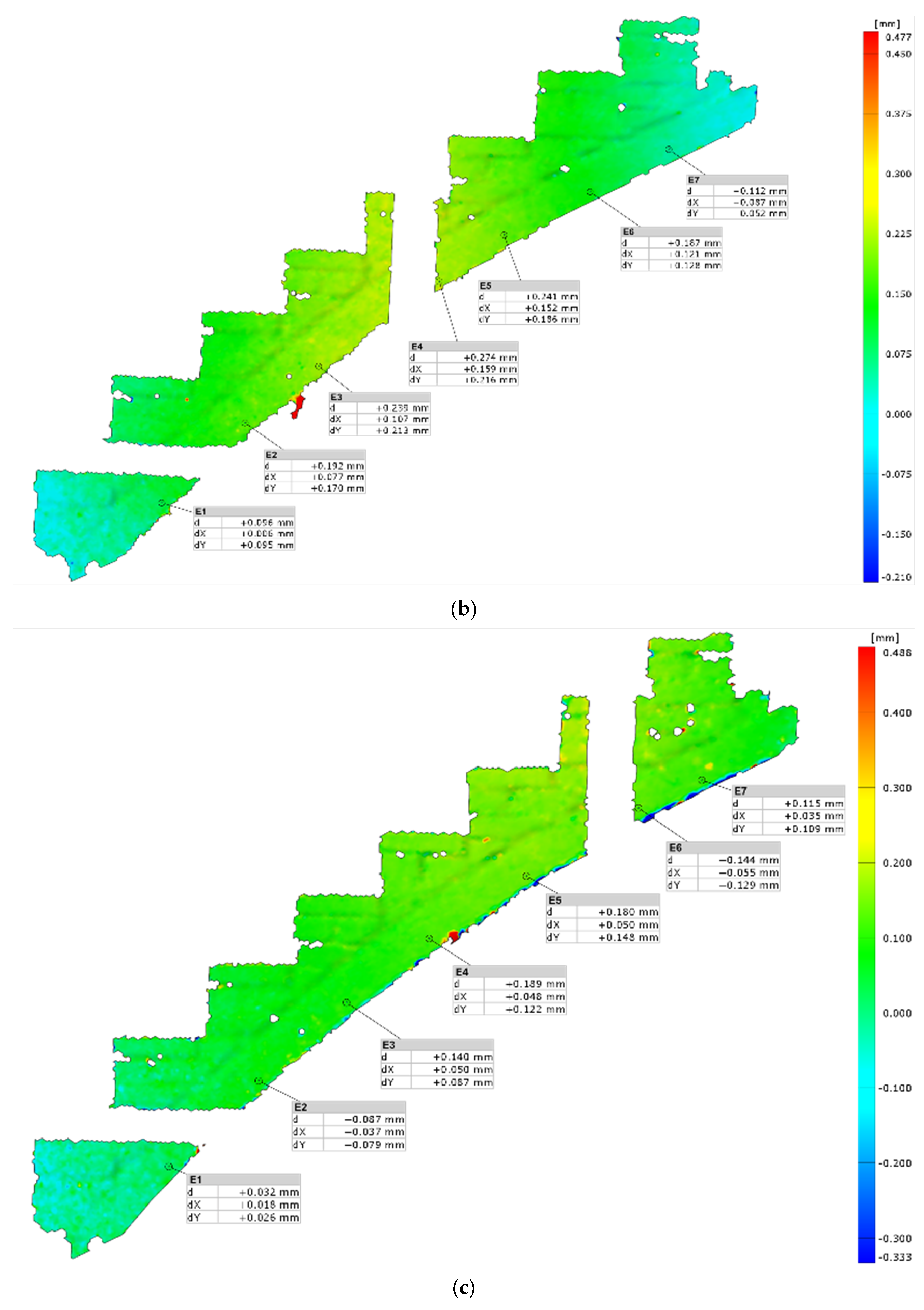
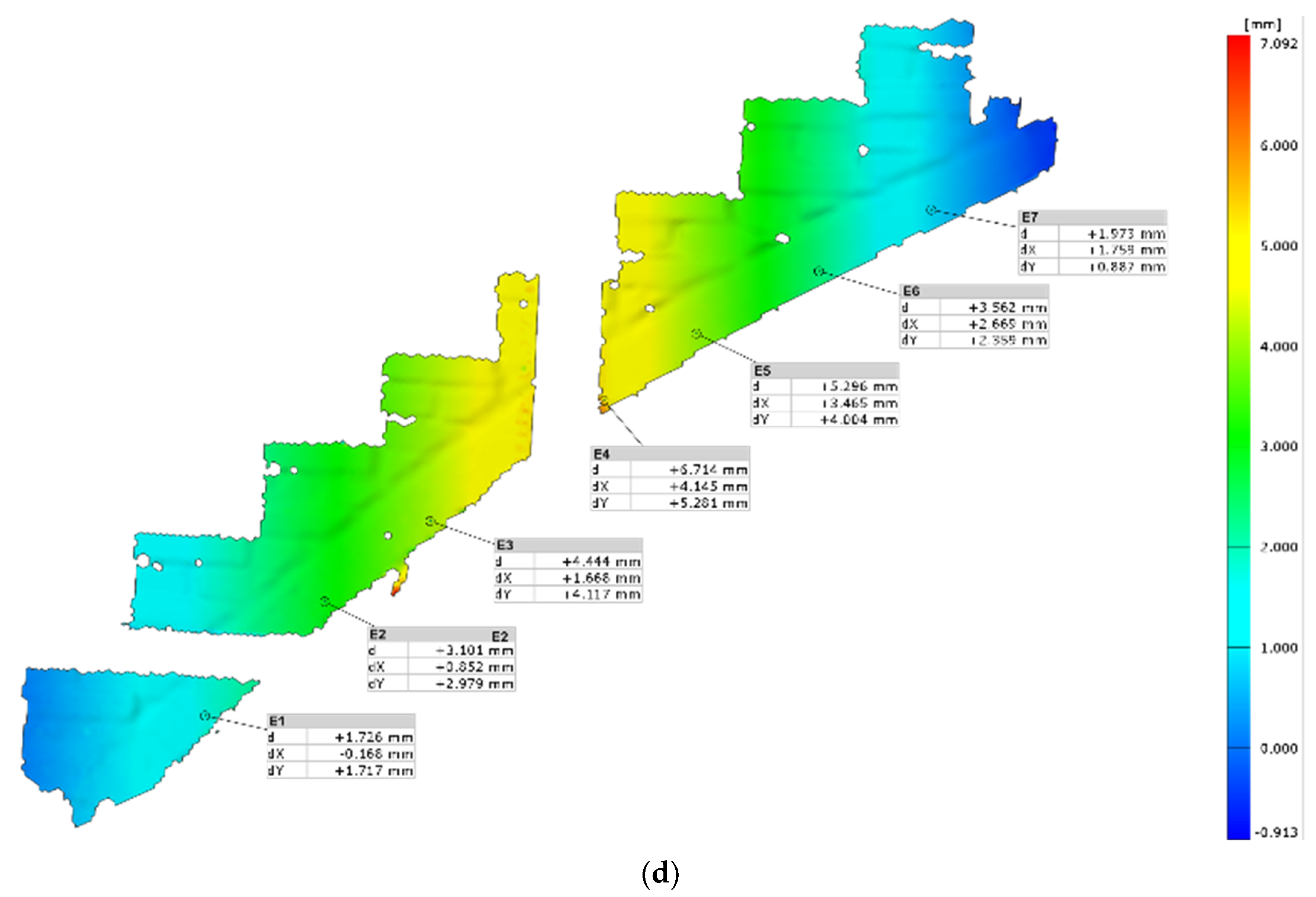
2.2. TLS Diagnostic on a Real-Life Structure

Stair geometry measurements and diagnostics were performed using TLS technology, using a stationary scanner Focus M70 (Faro, Lake Mary, FL, USA) with a single measurement accuracy of 0.2 mm. From the measurements, a point cloud in Autodesk Recap (RCP) format was obtained, which was then verified in CAD software (Version2021, San Rafael, Autodesk, CA, USA). RCP format files store spatially indexed point cloud data that can be processed in applications to view, edit and analyze object geometry. The purpose of the measurements was to analyze the geometry of the masonry arch. The aim of the study was to indicate the geometric irregularities, whose technical condition was visually inspected. After removing the plaster in the selected irregularity areas, the condition of masonry and mortar was evaluated.
The TLS measurements allowed us to determine the exact geometry of the stair flight. Figure 6 shows a general view of the obtained TLS measurement map along with a picture of the geometry of the curved staircase of the building.
Alongside TLS measurements, a visual evaluation of the mortar joints in the stair flights as well as of the treads was performed. Numerous damages and cracks were found. The most important was a crack in the joint on the masonry arch presented in Figure 7.
Incorrectly made support changed the distribution of internal forces in the masonry arch, which was the reason for the whole structural diagnosis. Support should have been put in place for the entire surface of the arch in the form of a centering with an appropriate shape to match the actual geometry of each stair flight arch. Figure 8 shows the output of TLS diagnostics for the run fault of the stair flight.
The weakest points of the analyzed masonry arch structure were the joints between bricks and mortar. On the basis of the research work carried out, it was decided to reinforce the whole structure of flights and landings with a steel structure fixed from the bottom.

3. Laboratory Tests

3.1. Materials

The tested samples and elements presented in this research study were built using clay brick, class 25. The dimensions of the bricks were 25 × 12 × 6.5 cm3 (the same as in the real-life stair flight construction). For the preparation of joints, lime–cement mortar, class M5, was used. For the preparation of masonry mortar, a factory-made, dry, lime–cement mortar class M5 mixture was used (Quick-mix TWM-M5; Sievert, Strzelin, Poland). The mixture consisted of a cement binder, slaked lime, quartz fillers and refining additives. The thickness of the joint was about 1 cm. To determine the properties of the materials used, initial tests in accordance with current standards [108,109,110,111] were conducted. The results of the tests are presented in Table 2.

3.2. Laboratory Models of Stair Flights

Laboratory tests were conducted on two models of the stair flights—without stair treads (M1) and with stair treads (M2). The models were made in a 1:1 scale based on the measurements of the analyzed construction, with a width of a single 25 cm brick (Figure 9).
The dimensions of the flight were taken from the real-life structure and were noted as follows:
  • Height 162 cm;
  • Length 210 cm;
  • Slope 38°;
  • Arch rise f = 14 cm.
The stair flight construction was supported on a self-made test bench frame. During the masonry works, a wooden structure with expanded polystyrene was used as a centering for the arch. The support was removed while the arch structure was drying, so that the structure could be pressed down naturally. Due to indoor conditions, the bricks were soaked in water before construction, then wetted with water daily during the mortar curing processes. In order to take measurements, a force gauge was placed in the upper corner of the flight to transfer the vertical force.
Measurements were conducted with inductive sensors (for vertical displacements) and two force gauges connected to an MGC Plus HBM Hottinger Bridge. In addition, the bridge was connected to the ARAMIS optical three-dimensional displacement and strain measurement system. The model was painted on the back side with a white–black pattern to enable image correlation. First, the model was tested in the elastic range with a concentrated force applied at three different locations, P1, P2 and P3. At the force application locations, horizontal surfaces were prepared with quick-setting mortar with a strength, after 24 h, of at least 25 MPa. The assumed limit loads at points P1 and P3 were up to 1.5 kN, while the limit for point P2 was noted when the first crack was registered, after which the test was stopped. The loads at P1, P2 and P3 were applied separately to the tested specimen. Then, on the basis of the M1 model, the M2 model was created by adding treads over the staircase (Figure 3). In order to create the geometry of the steps, it was necessary to precisely cut the bricks at the angles correlating with the arch.
The model with treads (M2) was tested similarly to the model without treads (M1). Points P1, P2 and P3 were determined at the same locations as in the case of the M1 model. Assumed force limits for points P1 and P3 were up to 6 kN. At the middle point, P2, the structure was loaded up to failure. The loads were applied separately to the specimen.

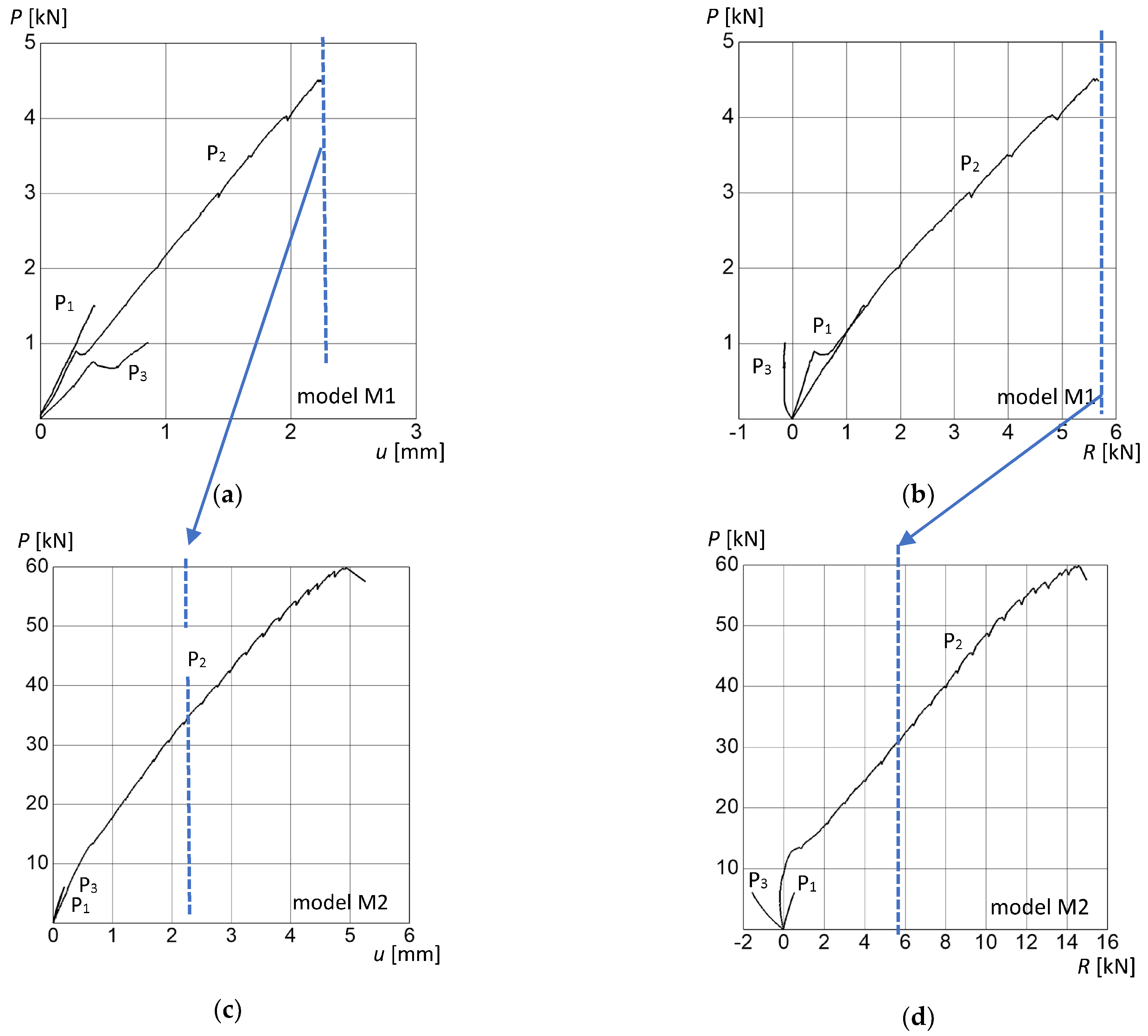
3.3. Results of Laboratory Tests

The model without treads (M1) was loaded with concentrated forces P1 = P3 = 1.5 kN. The value of the force at point P2 was increased until the first crack occurred at the load value of 4.5 kN. This moment was considered to be the end of elastic work of the structure. Failure was caused by the opening of the crack within the joint located under the concentrated force at point P2.
The model with masonry treads (M2) was loaded at the same locations as model M1 by applying concentrated forces on the masonry treads. At points P1 and P3, a structural load of P1 = P3 = 6 kN was applied. At the middle point, P2, the value of the load was increased until failure due to cracking, which occurred at a force of P = 59.8 kN. The results of the measurements of the displacement and support reactions of the researched models are presented in Figure 10.
By including the treads in the stair flight curve analysis, the load capacity was considerably higher than previously assumed. The load-bearing capacity for the model with treads was 13.3 times higher than in the model without treads. The deflection for the same load level P = 4 kN at point P2 for model M1 was u = 1.9 mm and, for model M2, u = 0.2 mm. The deflection value of model M2 was 9.5 times smaller than the deflection of model M1. The steps masoned above the staircase significantly increased the load-bearing capacity of the structure, as well as its stiffness. Figure 11 shows the failure mode of the tested models of stair arches and the results of the measurement of the deformations for M2 made with the ARAMIS system at the moment of destruction.
The model of structural failure changed, which, in the case of model M2, occurred as a result of cracking along the arch, at the interface of the arch with the brick treads. First of all, the masonry above the arch detached from the rest of the structure (masoned brick treads). This proved the significant importance of the stair treads above the arch in its load-bearing capacity. Once the crack formed between the arch and the treads, the rest of the structure exhibited rapid failure.
For model M1 (without treads), the deflection measured vertically in the load range up to 0.9 kN developed similarly for points P1 and P2. The deflection curve for P3 was significantly different from that for P1 and P2. Comparing the curves for a load level P = 1 kN, it was found that the smallest deflection of the structure was recorded for the load at point P1 (48.2 cm from the lower support), for which a vertical deflection of the structure u = 0.3 mm was measured. At point P2 (100.7 cm from the lower support), the vertical deflection u = 0.4 mm was obtained. At point P3 (153.2 cm from the lower support and 57.4 cm from the upper support), the highest vertical deflection of the structure u = 0.8 mm was achieved. At point P2, the deflection was 1.3 times higher in relation to point P1, while, at point P3, it was 2.7 times higher than at P1. That is, the lower the location of force along the staircase was, the lower the influence on the deformation of the structure.
Changing the location of the force had also a significant effect on the recorded reaction R in the upper part of the staircase. For model M1, in the case of force applied to the middle and lower parts of the staircase (P1 and P2), the reaction was positive, which means that it was directed vertically downwards and balanced the horizontal forces in the arch. However, for the force at point P3, the situation was completely different. Due to the different geometry of the arch compared to typical vaults, the reaction had the opposite direction. The arch in this place did not generate compressive force on the upper support, but, rather, a tension. Comparing the values of the reaction R between different force points at the force level P = 1 kN, it should be noted that the reaction for points P1 and P2 was similar and was about R = 0.8 kN. For point P3, the reaction was R = −0.1 kN, which was eight times lower. The reactions for points P1 and P2 had different values until the inflection point on the P2 curve, at force P = 0.9 kN.
Different results were obtained for model M2 (with treads). The differences in deflection u were less visible between P1 and P3. For the load level P = 5 kN at points P1 and P3, the deflection had a value of u = 0.2 mm. In the investigated load range, the addition of stair treads increased the stiffness of the structure regardless of force location.
For model M2, the reaction forces in the support differed from each other. Negative values for the support were registered again for point P3 but also partially for point P2. The reaction in the case of the force at the center (P2) operated in a tension range, up to P = 9 kN, after which it started to work in compression. At the force level P = 5 kN, the reaction at point P1 was R = 0.4 kN; at point P2, it was R = −0.2 kN; and, at point P3, it was R = −1.4 kN. The spreading force for the force P = 5 kN was recorded only for the force at point P1. In the case of force at points P2 and P3, tension was observed. The value of the reaction for P3 was seven times higher than for P2.
The results measured using the ARAMIS system allowed us to analyze the displacement with higher precision. For the reference load level P = 6 kN, there were visible differences in the operation of the structure depending on the load application point. Analyzing the displacement maps (Figure 12), it is visible that there were local deformations. Those were caused by the movement of the bricks toward each other due to the changes in the joints.
For model M2, regardless of the load application point, the values of arch displacement were of the same sign. This is different from a typical operation of a masonry arch. The biggest displacement of the staircase was achieved when the force was applied at point P2. The results for points P1 (value for E4, virtual point, in the middle, d = 0.186 mm) and P3 (also value for E4, virtual point, in the middle, d = 0.189 mm) were similar. The values of deflections at the points directly under the applied forces differed for P1 (virtual point E2, d = 0.217 mm) and P3 (virtual point E6, d = 0.144 mm), even though the total deflection at point E2 was similar. For the load level P = 6 kN, the highest resultant deflection for point P2 was d = 0.274 mm. This is a value that can be hardly seen with a naked eye. The failure of the structure was also at a small resultant displacement of d = 6.714 mm. These results confirm a significant influence of masonry treads on the rigidity of the whole structure. The treads are responsible for increased stiffness of a lean masonry arch. Due to the low values of the displacement of treads, the diagnostic of the structure should be performed with precise measurement equipment, such as 3D scanners (TLS).

4. Conclusions

Based on the research study presented, the following conclusions were drawn:
  • The TLS method allowed us to perform the geometric analysis and dimensioning of the existing arched stair structure.
  • The TLS measurements allowed us to detect geometric irregularities, which, complemented by visual diagnostic tests, allowed us to detect damage to their structure.
  • The damage to the flight was caused by improperly performed repair works—improper temporary support of the flight.
  • The conducted experimental investigations showed that the key element responsible for the actual load-bearing capacity and stiffness of the stair flight were the treads above the masonry arch.
  • The load-bearing capacity of the model with treads was 13.3 times higher than that of the model without treads.
  • The deflection value of model M2 was 9.5 times smaller than the deflection of model M1.
  • A different working mechanism was found for the stair arch model with brick threads (M2) compared to the arch without threads (M1).
  • The failure of model M1 was caused by the opening of the crack within the joint located under the concentrated force at point P2.
  • In the case of model M2, failure occurred as a result of cracking along the arch, at the interface of the arch with the brick treads.
  • In the case of arched stair renovation, it is crucial to properly connect the arches of the stair flights with the treads above. If there is no proper connection between the vaults and the treads, the increase in the load-bearing capacity shown in the research study should be excluded from the calculations.

Author Contributions

Conceptualization, R.N., T.K. and R.R.; methodology, R.N., T.K. and R.R.; validation, R.N. and T.K.; formal analysis, R.N., T.K., R.R. and E.E.; resources, R.N. and R.R.; writing—original draft preparation, R.N., T.K. and R.R.; writing—review and editing, R.N., T.K., R.R. and E.E. All authors have read and agreed to the published version of the manuscript.

Funding

This research study received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ahnert, R.; Krause, K.H. Typische Baukonstruktionen von 1860 bis 1960-Band 3; Beuth Verlag GmbH: Berlin, Germany, 2014. [Google Scholar]
  2. Małyszko, L.; Orłowicz, R. Konstrukcje Murowe. Zarysowania i Naprawy. (Structural Masonry. Cracks and Repairs); Wydawnictwo Uniwersytetu Warmińsko–Mazurskiego: Olsztyn, Poland, 2000. [Google Scholar]
  3. Nowak, R. Analiza Nośności i Mechanizmów Uszkodzeń Odcinkowych Ceglanych Nadproży Łukowych. Ph.D. Thesis, West Pomeranian University of Technology, Szczecin, Poland, 2014. (In Polish). [Google Scholar]
  4. Pawłowski, W.; Nowak, R. Architektura a statyka ceglanych nadproży łukowych. Przestrzeń Forma 2009, 12, 115–122. [Google Scholar]
  5. Stawiski, B.; Kania, T. Building diagnostics versus effectiveness of repairs. MATEC Web Conf. 2018, 174, 03005. [Google Scholar] [CrossRef]
  6. Drobiec, Ł.; Jasiński, R.; Mazur, W. Accuracy of Eddy-Current and Radar Methods Used in Reinforcement Detection. Materials 2019, 12, 1168. [Google Scholar] [CrossRef] [Green Version]
  7. Jasiński, R.; Drobiec, Ł.; Mazur, W. Validation of Selected Non-Destructive Methods for Determining the Compressive Strength of Masonry Units Made of Autoclaved Aerated Concrete. Materials 2019, 12, 389. [Google Scholar] [CrossRef] [Green Version]
  8. Hoła, A.; Matkowski, Z.; Hoła, J. Analysis of the Moisture Content of Masonry Walls in Historical Buildings Using the Basement of a Medieval Town Hall as an Example. Procedia Eng. 2017, 172, 363–368. [Google Scholar] [CrossRef]
  9. Lachowicz, J.; Rucka, M. Diagnostics of pillars in St. Mary’s Church (Gdańsk, Poland) using the GPR method. Int. J. Archit. Herit. 2018, 13, 1223–1233. [Google Scholar] [CrossRef]
  10. Schabowicz, K. Non-Destructive Testing of Materials in Civil Engineering. Materials 2019, 12, 3237. [Google Scholar] [CrossRef] [Green Version]
  11. Maione, A.; Argiento, L.U.; Cassapulla, C. Management of multi-source information to identify the typology of the horizontal structures in historical masonry buildings: The case study of the Museum of Capodimonte in Naples (Italy). Frattura Integrità Strutturale 2018, 46, 240–251. [Google Scholar] [CrossRef]
  12. Łątka, D.; Matysek, P. Badania konstrukcji murowych in-situ. Inżynieria Budownictwo 2017, 7, 360–363. [Google Scholar]
  13. Łątka, D.; Seręga, S.; Matysek, P. Estimation of Mortar Compressive Strength Based on Specimens Extracted from Masonry Bed Joints. In Proceedings of the Structural Analysis of Historical Constructions, Cusco, Peru, 11–13 September 2018; pp. 577–586. [Google Scholar]
  14. Tkacz, P. Ocena Wytrzymałości na Ściskanie Konstrukcji Murowych z Uwzględnieniem Badań In Situ. Ph.D. Thesis, West Pomeranian University of Technology, Szczecin, Poland, 2015. (In Polish). [Google Scholar]
  15. Matysek, P.; Witkowski, M. A Comparative Study on the Compressive Strength of Bricks from Different Historical Periods. Int. J. Archit. Herit. 2015, 10, 396–405. [Google Scholar] [CrossRef]
  16. Ramesh, M.; Azenha, M.; Lourenco, P. Mechanical properties of lime–cement masonry mortars in their early ages. Mater. Struct. 2019, 52, 13. [Google Scholar] [CrossRef]
  17. Ramesh, M.; Azenha, M.; Lourenco, P. Mechanical characterization of lime cement mortars: E-modulus and fracture energy. In Proceedings of the RILEM Spring Convention and Sustainable Materials, Systems and Structures Conference (SMSS 2019), Rovinj, Croatia, 18–22 March 2019. [Google Scholar]
  18. Matysek, P. Identyfikacja Wytrzymałości na Ściskanie i Odkształcalności Murów Ceglanych w Obiektach Istniejących; Cracow University o Technology: Cracow, Poland, 2014. (In Polish) [Google Scholar]
  19. Łątka, D.; Matysek, P. The Estimation of Compressive Stress Level in Brick Masonry Using the Flat-jack Method. Procedia Eng. 2017, 193, 266–272. [Google Scholar] [CrossRef]
  20. Runkiewicz, L.; Rodzik, W. Badania nieniszczące wytrzymałości murowanych obiektów zabytkowych. Inżynieria Budownictwo 1990, 2, 50–52. [Google Scholar]
  21. Runkiewicz, L.; Sieczkowski, J. Stosowanie obciążeń próbnych do oceny stanu technicznego budynków. Przegląd Budowlany 2015, 86, 7–8. [Google Scholar]
  22. Runkiewicz, L.; Biegus, A.; Brol, J.; Buczkowski, W.; Drobiec, Ł.; Gajownik, R.; Godlewski, T.; Hoła, J.; Hulimka, J.; Jakimowicz, M.; et al. Diagnostyka Obiektów Budowlanych. Zasady Wykonywania Ekspertyz; PWN: Warsaw, Poland, 2020. [Google Scholar]
  23. Kania, T.; Derkach, V.; Nowak, R. Testing Crack Resistance of Non-Load-Bearing Ceramic Walls with Door Openings. Materials 2021, 14, 1379. [Google Scholar] [CrossRef]
  24. Kregar, K.; Ambrožič, T.; Kogoj, D.; Vezočnik, R.; Marjetič, A. Determining the inclination of tall chimneys using the TPS and TLS approach. Measurement 2015, 75, 354–363. [Google Scholar] [CrossRef]
  25. Drygala, I.; Dulinska, J.; Bednarz, L.; Jasienko, J. Numerical evaluation of seismic-induced damages in masonry elements of historical arch viaduct. IOP Conf. Ser. Mater. Sci. Eng. 2018, 364, 012006. [Google Scholar] [CrossRef]
  26. Croce, P.; Beconcini, M.L.; Formichi, P.; Landi, F.; Puccini, B.; Zotti, V. Bayesian Methodology for Probabilistic Description of Mechanical Parameters of Masonry Walls. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 04021008. [Google Scholar] [CrossRef]
  27. Malomo, D.; DeJong, M.J. A Macro-Distinct Element Model (M-DEM) for out-of-plane analysis of unreinforced masonry structures. Eng. Struct. 2021, 244, 112754. [Google Scholar] [CrossRef]
  28. Lourenco, P.B. Computations on historic masonry structures. Prog. Struct. Eng. Mater. 2002, 4, 301–319. [Google Scholar] [CrossRef]
  29. Beconcini, M.L.; Croce, P.; Formichi, P.; Landi, F.; Puccini, B. Experimental Evaluation of Shear Behavior of Stone Masonry Wall. Materials 2021, 14, 2313. [Google Scholar] [CrossRef]
  30. Lourenço, P.B.; Rots, J.G.; Blaauwendraad, J. Continuum model for masonry: Parameter estimation and validation. J. Struct. Eng. 1998, 124, 642–652. [Google Scholar] [CrossRef]
  31. Baraldi., D.; Milani, G.; Sarhosis, V. A Rigid-Beam-Model for studying the dynamic behaviour of cantilever masonry walls. Structures 2021, 33, 2950–2963. [Google Scholar] [CrossRef]
  32. Celano, T.; Argiento, L.U.; Ceroni, F.; Casapulla, C. In-Plane Behaviour of Masonry Walls: Numerical Analysis and Design Formulations. Materials 2021, 14, 5780. [Google Scholar] [CrossRef]
  33. Suchocki, C.; Katzer, J.; Rapinski, J. Terrestrial Laser Scanner as a Tool for Assessment of Saturation and Moisture Movement in Building Materials. Period. Polytech. Civ. Eng. 2018, 62, 694–699. [Google Scholar] [CrossRef] [Green Version]
  34. Suchocki, C.; Jagoda, M.; Obuchovski, R.; Šlikas, D.; Sužiedelytė-Visockienė, J. The properties of terrestrial laser system intensity in measurements of technical conditions of architectural structures. Metrol. Meas. Syst. 2018, 25, 779–792. [Google Scholar] [CrossRef]
  35. Suchocki, C.; Katzer, J. TLS Technology in Brick Walls Inspection. In Proceedings of the Conference: 2018 Baltic Geodetic Congress (BGC Geomatics), Olsztyn, Poland, 21–23 June 2018; pp. 359–363. [Google Scholar]
  36. Suchocki, C.; Katzer, J.; Serrat, C.; Jagoda, M. Application of TLS Intensity Data for Detection of Brick Walls Defects. IOP Conf. Ser. Mater. Sci. Eng. 2019, 603, 022100. [Google Scholar] [CrossRef]
  37. Błaszczak-Bąk, W.; Suchocki, C.; Janicka, J.; Dumalski, A.; Duchnowski, R. Defect detection of historic structures in dark places based on the point cloud analysis by modified OptD Method. GeoInformation Disaster Manag. 2019, XLII-3/W8, 71–77. [Google Scholar] [CrossRef] [Green Version]
  38. Suchocki, C.; Błaszczak-Bąk, W.; Damięcka-Suchocka, M.; Jagoda, M.; Masiero, A. On the Use of the OptD Method for Building Diagnostics. Remote Sens. 2020, 12, 1806. [Google Scholar] [CrossRef]
  39. Suchocki, C.; Błaszczak-Bąk, W.; Janicka, J.; Dumalski, A. Detection of defects in building walls using modified OptD method for down-sampling of point clouds. Build. Res. Inf. 2020, 49, 197–215. [Google Scholar] [CrossRef]
  40. Błaszczak-Bąk, W.; Suchocki, C.; Janicka, J.; Dumalski, A.; Duchnowski, R.; Sobieraj-Żłobińska, A. Automatic Threat Detection for Historic Buildings in Dark Places Based on the Modified OptD Method. Int. J. Geo-Inf. 2020, 9, 123. [Google Scholar] [CrossRef] [Green Version]
  41. Suchocki, C. Comparison of Time-of-Flight and Phase-Shift TLS Intensity Data for the Diagnostics Measurements of Buildings. Materials 2020, 13, 353. [Google Scholar] [CrossRef] [Green Version]
  42. Nowak, R.; Orłowicz, R.; Rutkowski, R. Use of TLS (LiDAR) for Building Diagnostics with the Example of a Historic Building in Karlino. Buildings 2020, 10, 24. [Google Scholar] [CrossRef] [Green Version]
  43. Wierzbicki, K.; Szewczyk, P.; Paczkowski, W.; Wroblewski, T.; Skibicki, S. Torsional Stability Assessment of Columns Using Photometry and FEM. Buildings 2020, 10, 162. [Google Scholar] [CrossRef]
  44. Suchocki, C.; Błaszczak-Bąk, W.; Damięcka-Suchocka, M.; Jagoda, M.; Masiero, A. An example of using the OptD method to optimization of point clouds in the buildings diagnostics. In Proceedings of the 4th Joint International Symposium on Deformation Monitoring (JISDM), Athens, Greece, 15–17 May 2018. [Google Scholar]
  45. Suchocki, C.; Błaszczak-Bąk, W. Down-Sampling of Point Clouds for the Technical Diagnostics of Buildings and Structures. Geosciences 2019, 9, 70. [Google Scholar] [CrossRef] [Green Version]
  46. Dias, I.S.; Flores-Colen, I.; Silva, A. Critical Analysis about Emerging Technologies for Building’s Façade Inspection. Buildings 2021, 11, 53. [Google Scholar] [CrossRef]
  47. Mosalam, K.; Takhirov, S.; Park, S. Applications of laser scanning to structures in laboratory tests and field surveys. Struct. Control Health Monit. 2014, 21, 115–134. [Google Scholar] [CrossRef]
  48. Liu, J.; Zhang, Q.; Wu, J.; Zhao, Y. Dimensional accuracy and structural performance assessment of spatial structure components using 3D laser scanning. Autom. Constr. 2018, 96, 324–336. [Google Scholar] [CrossRef]
  49. Leonov, A.V.; Anikushkin, M.N.; Ivanov, A.V.; Ovcharov, S.V.; Bobkov, A.E.; Baturin, Y.M. Laser scanning and 3D modeling of the Shukhov hyperboloid tower in Moscow. J. Cult. Herit. 2015, 16, 551–559. [Google Scholar] [CrossRef]
  50. Feng, P.; Zou, Y.; Hu, L.; Liu, T. Use of 3D laser scanning on evaluating reduction of initial geometric imperfection of steel column with pre-stressed CFRP. Eng. Struct. 2019, 198, 109527. [Google Scholar] [CrossRef]
  51. Mora, R.; Martín-Jiménez, J.A.; Lagüela, S.; González-Aguilera, D. Automatic Point-Cloud Registration for Quality Control in Building Works. Appl. Sci. 2021, 11, 1465. [Google Scholar] [CrossRef]
  52. Erdélyi, J.; Kopáčik, A.; Kyrinovič, P. Spatial Data Analysis for Deformation Monitoring of Bridge Structures. Appl. Sci. 2020, 10, 8731. [Google Scholar] [CrossRef]
  53. Singhroy, V.; Fobert, M.-A.; Li, J.; Blais-Stevens, A.; Charbonneau, F.; Das, M. Advanced Radar Images for Monitoring Transportation, Energy, Mining and Coastal Infrastructure; Singhroy, V., Ed.; Springer: Cham, Switzerland, 2021; pp. 3–40. [Google Scholar] [CrossRef]
  54. Drobiec, Ł.; Piekarczyk, A.; Kubica, J. AAC bocks masonry compressed perpendicular and parallel to the bed joints. In Proceedings of the 12th International Brick/Block Masonry Conference, Madrid, Spain, 25–28 June 2000. [Google Scholar]
  55. Hulimka, J.; Kałuża, M.; Kubica, J. Failure and overhaul of a historic brick tower. Eng. Fail. Anal. 2019, 102, 46–59. [Google Scholar] [CrossRef]
  56. Hoła, J.; Schabowicz, K. Diagnostyka obiektów budownictwa ogólnego. In Proceedings of the XXX Jubileuszowe Ogólnopolskie Warsztaty Pracy Projektanta Konstrukcji, Szczyrk, Poland, 25–28 March 2015. [Google Scholar]
  57. Drobiec, Ł.; Grzyb, K.; Zając, J. Analysis of Reasons for the Structural Collapse of Historic Buildings. Sustainability 2021, 13, 10058. [Google Scholar] [CrossRef]
  58. Schabowicz, K. Testing of Materials and Elements in Civil Engineering. Materials 2021, 14, 3412. [Google Scholar] [CrossRef]
  59. Szabó, S.; Kövesdi, A.; Vasáros, Z.; Csicsely, Á.; Hegyi, D. The Cause of Damage and Failure of the Mud-brick Vault of the Khan in New-Gourna. Eng. Fail. Anal. 2021, 128, 105567. [Google Scholar] [CrossRef]
  60. Bednarz, Ł.; Drygała, I.; Dulińska, J.; Jasieńko, J. Study of Materials Behavior in a Monumental Vault Strengthened by a Carbon Net in a Mineral Matrix Subjected to Seismic Influence. Appl. Sci. 2021, 11, 1015. [Google Scholar] [CrossRef]
  61. Uranjek, M.; Lorenci, T.; Skrinar, M. Analysis of Cylindrical Masonry Shell in St. Jacob’s Church in Dolenja Trebuša, Slovenia—Case Study. Buildings 2019, 9, 127. [Google Scholar] [CrossRef] [Green Version]
  62. Bovo, M.; Mazzotti, C.; Savoia, M. Analysis of structural behaviuor of historical stone arches and vaults: Experimental tests and numerical analyses. In Proceedings of the International Conference on Structural Analysis of Historical Constructions (SAHC 2012), Wrocław, Poland, 15–17 October 2012; pp. 635–643. [Google Scholar]
  63. Jasieńko, J.; Bednarz, Ł.; Nowak, T. The effectiveness of strengthening historic brick vaults by contemporary methods. In Proceedings of the Protection of Historical Buildings, PROHITECH 09, Rome, Italy, 21–27 June 2009; Taylor & Francis Group: London, UK, 2009. [Google Scholar]
  64. Jasieńko, J.; Di Tommaso, A.; Bednarz, Ł. Experimental Investigations into Collapse of Masonry Arches Reinforced Using Different Compatible Technologies. In Proceedings of the Mechanics of Masonry Structures Strengthened with Composite Materials, MuRiCo., Venice, Italy, 22–24 April 2009. [Google Scholar]
  65. Boothby, T.E. Analysis of masonry arches and vaults. Prog. Struct. Eng. Mater. 2001, 3, 246–256. [Google Scholar] [CrossRef]
  66. Foraboschi, P. Strengthening of Masonry Arches with Fiber-Reinforced Polymer Strips. J. Compos. Constr. 2004, 8, 191–202. [Google Scholar] [CrossRef]
  67. Castori, G.; Borri, A.; Ebaugh, S.; Casadei, P. Strengthening masonry arches with composites. In Proceedings of the Third International Conference on FRP Composites in Civil Engineering (CICE 2006), Miami, FL, USA, 13–15 December 2006. [Google Scholar]
  68. Oliveira, D.; Basílio, I.; Lourenco, P. FRP strengthening of masonry arches towards an enhanced behaviour. In Proceedings of the Third International Conference on Bridge Maintenance, Safety and Management, Porto, Portugal, 16–19 July 2006. [Google Scholar]
  69. Borri, A.; Casadei, P.; Castori, G.; Ebaugh, S. Research on composite strengthening of masonry arches. In Proceedings of the 8th International Symposium on Fiber Reinforced Polymer Reinforcement for Concrete Structures (FRPRCS-8), Patras, Greece, 16 July 2007. [Google Scholar]
  70. Nowak, R.; Orłowicz, R. Mechanisms of brick arched lintels damage. Conserv. News 2009, 26, 253–259. [Google Scholar]
  71. Borri, A.; Casadei, P.; Castori, G.; Hammond, J. Strengthening of Brick Masonry Arches with Externally Bonded Steel Reinforced Composites. J. Compos. Constr. 2009, 13, 468–475. [Google Scholar] [CrossRef]
  72. Bati, S.B.; Rovero, S.; Tonietti, U. Experimental analysis on scale models of CFRP reinforced arches. In Proceedings of the Mechanics of Masonry Structures Strengthened with Composite Materials, MuRiCo., Venice, Italy, 22–24 April 2009. [Google Scholar]
  73. Bajno, D.; Bednarz, L.; Matkowski, Z.; Raszczuk, K. Monitoring of Thermal and Moisture Processes in Various Types of External Historical Walls. Materials 2020, 13, 505. [Google Scholar] [CrossRef] [Green Version]
  74. Bosnjak-Klecina, M.; Lozancic, S. Stability analysis for masonry-arch structures and vaulted structures. Gradevinar 2010, 62, 409–421. [Google Scholar]
  75. Gago, A.S.; Alfaiate, J.; Lamas, A. The effect of the infill in arched structures: Analytical and numerical modelling. Eng. Struct. 2011, 33, 1450–1458. [Google Scholar] [CrossRef]
  76. Cecchi, A. The curve of pressure in vertically loaded arches. Wiad. Konserw. 2013, 34, 18–22. [Google Scholar]
  77. Egidio, R.; Giada, C.; Annalisa, F.; Giuseppe, C. On the mixed collapse mechanism of semi-circular masonry arches. In Proceedings of the Structural Analysis of Historical Constructions–SAHC 2012, Wrocław, Poland, 15–17 October 2012; pp. 541–549. [Google Scholar]
  78. Albuerne, A.; Williams, M.; Lawson, V. Prediction of the Failure Mechanism of Arches under Base Motion Using DEM Based on the NSCD Method. In Proceedings of the Structural Analysis of Historical Constructions–SAHC 2012, Wrocław, Poland, 15–17 October 2012; pp. 41–47. [Google Scholar]
  79. Marfia, S.; Ricamato, M.; Sacco, E. Stress Analysis of Reinforced Masonry Arches. Int. J. Comput. Methods Eng. Sci. Mech. 2008, 9, 77–90. [Google Scholar] [CrossRef]
  80. Holzer, S.M. Numerical arch and vault analysis. J. Herit. Conserv. 2013, 34, 7–17. [Google Scholar]
  81. Hojdys, Ł.; Krajewski, P. Behavior of masonry arches strengthened with TRM. In Proceedings of the International Conference on Arch Bridges, Split, Croatia, 2–4 October 2013; pp. 739–746. [Google Scholar]
  82. Chen, J.F. Load-Bearing Capacity of Masonry Arch Bridges Strengthened with Fibre Reinforced Polymer Composites. Adv. Struct. Eng. 2016, 5, 37–44. [Google Scholar] [CrossRef]
  83. Reccia, E.; Cecchi, A.; Milani, G. FEM/DEM Approach for the Analysis of Masonry Arch Bridges. In Advances in Civil and Industrial Engineering; IGI Global: Hershey, PA, USA, 2016. [Google Scholar] [CrossRef] [Green Version]
  84. Ricci, E.; Sacco, E.; Piccioni, M. A method for the analysis of masonry arches. In Proceedings of the 10th International Conference on Structural Analysis of Historical Constructions, SAHC 2016, Leuven, Belgium, 13–15 September 2016; pp. 1067–1068. [Google Scholar]
  85. Pulatsu, B.; Erdogmus, E.; Lourenco, P. Discrete-continuum approach to assess 3D failure modes of masonry arch bridges. In Proceedings of the IABSE Symposium 2019 Guimarães: Towards a Resilient Built Environment-Risk and Asset Management, Guimarães, Portugal, 27–29 March 2019; pp. 570–577. [Google Scholar]
  86. Auciello, N.M. On the analysis of masonry arches. Int. J. Mason. Res. Innov. 2019, 4, 50. [Google Scholar] [CrossRef]
  87. Alecci, V.; De Stefano, M.; Focacci, F.; Luciano, R.; Rovero, L.; Stipo, G. Strengthening Masonry Arches with Lime-Based Mortar Composite. Buildings 2017, 7, 49. [Google Scholar] [CrossRef] [Green Version]
  88. Corradi, M.; Borri, A.; Castori, G.; Coventry, K. Experimental Analysis of Dynamic Effects of FRP Reinforced Masonry Vaults. Materials 2015, 8, 8059–8071. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  89. Ferretti, E.; Pascale, G. Some of the Latest Active Strengthening Techniques for Masonry Buildings: A Critical Analysis. Materials 2019, 12, 1151. [Google Scholar] [CrossRef] [Green Version]
  90. Yang, F.; Wen, X.; Wang, X.; Li, X.; Li, Z. A Model Study of Building Seismic Damage Information Extraction and Analysis on Ground-Based LiDAR Data. Adv. Civ. Eng. 2021, 2021, 5542012. [Google Scholar] [CrossRef]
  91. Filgueira, A.; González-Jorge, H.; Lagüela, S.; Díaz-Vilariño, L.; Arias, P. Quantifying the influence of rain in LiDAR performance. Measurement 2017, 95, 143–148. [Google Scholar] [CrossRef]
  92. Abdou, O.A.; Burdette, J.Q. Masonry stairs–design and material performance. Mason. Soc. Boulder 1993, 1, 739–754. [Google Scholar]
  93. Heyman, J. The Mechanics of Masonry Stairs; Computational Mechanics Publications Ltd.: Southampton, UK, 1995; pp. 259–265. [Google Scholar]
  94. Baratta, A.; Corbi, I. Statics and equilibrium paths of masonry stairs. Open Constr. Build. Technol. J. 2012, 6, 368–372. [Google Scholar] [CrossRef] [Green Version]
  95. Angelillo, M. Static analysis of a Guastavino helical stair as a layered masonry shell. Compos. Struct. 2015, 119, 298–304. [Google Scholar] [CrossRef]
  96. Gesualdo, A.; Cennamo, C.; Fortunato, A.; Frunzio, G.; Monaco, M.; Angelillo, M. Equilibrium formulation of masonry helical stairs. Meccanica 2017, 52, 1963–1974. [Google Scholar] [CrossRef]
  97. Rigo, B.; Bagi, K. Discrete element analysis of stone cantilever stairs. Meccanica 2018, 53, 1571–1589. [Google Scholar] [CrossRef]
  98. Briccola, D.; Bruggi, M.; Taliercio, A. Assessment of 3D Linear Elastic Masonry-Like Vaulted Structures. Key Eng. Mater. 2019, 817, 50–56. [Google Scholar] [CrossRef]
  99. Angelillo, M.; Olivieri, C.; DeJong, M. A new equilibrium solution for masonry spiral stairs. Eng. Struct. 2021, 238, 112176. [Google Scholar] [CrossRef]
  100. Nowak, R.; Kania, T.; Derkach, V.; Orłowicz, R.; Halaliuk, A.; Ekiert, E.; Jaworski, R. Strength Parameters of Clay Brick Walls with Various Directions of Force. Materials 2021, 14, 6461. [Google Scholar] [CrossRef] [PubMed]
  101. Nowak, R.; Orłowicz, R. Testing of Chosen Masonry Arched Lintels. Int. J. Archit. Herit. 2020, 15, 1895–1909. [Google Scholar] [CrossRef]
  102. Nowak, R.; Orłowicz, R. Selected problems of failures and repairs of historic masonry vaults. MATEC Web Conf. 2019, 284, 05008. [Google Scholar] [CrossRef]
  103. Nowak, R.; Orłowicz, R. Wpływ stanu technicznego muru na nośność zabytkowego łuku w Sankt Petersburgu. Mater. Bud. 2019, 5, 36–37. [Google Scholar] [CrossRef]
  104. De Santis, S.; Felice, G.; Roscini, F. Retrofitting of Masonry Vaults by Basalt Textile-Reinforced Mortar Overlays. Int. J. Archit. Herit. 2019, 13, 1061–1077. [Google Scholar] [CrossRef]
  105. Bespalov, V.; Orlovich, R.; Zimin, S. Stress-Strain State of Brick Masonry Vault with an Aperture. MATEC Web Conf. 2016, 53, 01009. [Google Scholar] [CrossRef] [Green Version]
  106. Pozo-Antonio, J.S.; Puente, I.; Pereira, M.F.C.; Rocha, C.S.A. Quantification and mapping of deterioration patterns on granite surfaces by means of mobile LiDAR data. Measurement 2019, 140, 227–236. [Google Scholar] [CrossRef]
  107. Stawiska, N.; Stawiski, B. Rewaloryzacja murów w obiektach zabytkowych. Wiadomości Konserwatorskie 2005, 18, 18–22. [Google Scholar]
  108. En 772-1+a1 Methods of Test for Masonry Units. In Determination of Compressive Strength; European Committee for Standardization: Brussels, Belgium, 2015.
  109. EN 1015-11 Methods of Test for Mortar for Masonry. In Determination of Flexural and Compressive Strength of Hardened Mortar; European Committee for Standardization: Brussels, Belgium, 2020.
  110. EN 1052-1 Methods of test for masonry. In Determination of Compressive Strength; European Committee for Standardization: Brussels, Belgium, 1998.
  111. ASTM E72 1989; Standard Tests for Conducting Strength Tests on Panels for Building Construction. American Society for Testing and Materials: West Conshohocken, PA, USA, 1989.
Materials 15 00552 g001 550
Figure 1. Masonry stairs with segmental vault and arched staircase slab, based on [1].
Figure 1. Masonry stairs with segmental vault and arched staircase slab, based on [1].
Materials 15 00552 g001
Materials 15 00552 g002 550
Figure 2. Brick stairs with column supports based on [1]. Scheme (a) and partial photo (b): 1—arched masonry stair sides; 2—arched masonry bolt; 3—barrel staircase with support on sides; 4—groin vault in stair flight; 5—groin or barrel vaults in stair landing.
Figure 2. Brick stairs with column supports based on [1]. Scheme (a) and partial photo (b): 1—arched masonry stair sides; 2—arched masonry bolt; 3—barrel staircase with support on sides; 4—groin vault in stair flight; 5—groin or barrel vaults in stair landing.
Materials 15 00552 g002
Materials 15 00552 g003 550
Figure 3. Calculation scheme of masonry stairs with segmental vault and arched staircase slab: 1—arched staircase slab; 2—landings.
Figure 3. Calculation scheme of masonry stairs with segmental vault and arched staircase slab: 1—arched staircase slab; 2—landings.
Materials 15 00552 g003
Materials 15 00552 g004 550
Figure 4. Flowchart for clay brick masonry structure diagnostics.
Figure 4. Flowchart for clay brick masonry structure diagnostics.
Materials 15 00552 g004
Materials 15 00552 g005 550
Figure 5. View of the researched masonry staircase.
Figure 5. View of the researched masonry staircase.
Materials 15 00552 g005
Materials 15 00552 g006 550
Figure 6. TLS data acquired from existing building: section view of building (a) and geometry measurements for analysis (b). The dashed line marks the stair flight which was subjected to further laboratory testing.
Figure 6. TLS data acquired from existing building: section view of building (a) and geometry measurements for analysis (b). The dashed line marks the stair flight which was subjected to further laboratory testing.
Materials 15 00552 g006
Materials 15 00552 g007 550
Figure 7. Section of the staircase with visible crack of the arch caused by improper renovation and deterioration of masonry joints.
Figure 7. Section of the staircase with visible crack of the arch caused by improper renovation and deterioration of masonry joints.
Materials 15 00552 g007
Materials 15 00552 g008 550
Figure 8. TLS data output for the point damage of the stair flight: section view of the stair flight (a) and point of damage (b).
Figure 8. TLS data output for the point damage of the stair flight: section view of the stair flight (a) and point of damage (b).
Materials 15 00552 g008
Materials 15 00552 g009 550
Figure 9. Laboratory models of stair flights (dimensions in mm): model M1—without treads (a); model M2—with treads (b). P1–P3—force application points; R—force from the arch registered with a force gauge; u—vertical displacement in the middle of the arch span.
Figure 9. Laboratory models of stair flights (dimensions in mm): model M1—without treads (a); model M2—with treads (b). P1–P3—force application points; R—force from the arch registered with a force gauge; u—vertical displacement in the middle of the arch span.
Materials 15 00552 g009
Materials 15 00552 g010 550
Figure 10. Experimental results of masonry staircases: relation P–u (vertical displacement in the middle of an arch in point P2) for model M1 (a); force P–reaction R for model M1 (b); force P–displacement u (vertical displacement in the middle of an arch in point P2) for model M2 (c); force P–reaction R for model M2 (d).
Figure 10. Experimental results of masonry staircases: relation P–u (vertical displacement in the middle of an arch in point P2) for model M1 (a); force P–reaction R for model M1 (b); force P–displacement u (vertical displacement in the middle of an arch in point P2) for model M2 (c); force P–reaction R for model M2 (d).
Materials 15 00552 g010
Materials 15 00552 g011a 550Materials 15 00552 g011b 550
Figure 11. Registered failure mode of tested models of stair arches: model M1 (a), model M2 (b) and measurements from ARAMIS of deformation during failure of model M2 (c).
Figure 11. Registered failure mode of tested models of stair arches: model M1 (a), model M2 (b) and measurements from ARAMIS of deformation during failure of model M2 (c).
Materials 15 00552 g011aMaterials 15 00552 g011b
Materials 15 00552 g012a 550Materials 15 00552 g012b 550Materials 15 00552 g012c 550
Figure 12. Results of experimental test of masonry staircases—displacement measured by ARAMIS: load P = 6 kN at point P1 (bottom) (a), load P = 6 kN at point P2 (middle) (b), load P = 6 kN at point P3 (top) (c) and load at failure P = 59.8 kN in point P2 (d). d—resultant displacement; dX—horizontal displacement; dY—vertical displacement.
Figure 12. Results of experimental test of masonry staircases—displacement measured by ARAMIS: load P = 6 kN at point P1 (bottom) (a), load P = 6 kN at point P2 (middle) (b), load P = 6 kN at point P3 (top) (c) and load at failure P = 59.8 kN in point P2 (d). d—resultant displacement; dX—horizontal displacement; dY—vertical displacement.
Materials 15 00552 g012aMaterials 15 00552 g012bMaterials 15 00552 g012c
Table
Table 1. Ultrasonic pulse velocity and calculated compressive strength of tested bricks and mortar.
Table 1. Ultrasonic pulse velocity and calculated compressive strength of tested bricks and mortar.
Ordinal NoBricksMortar
Ultrasonic Pulse Velocity
(m/s)		Compressive Strength (MPa)Ultrasonic Pulse Velocity
(m/s)		Compressive Strength (MPa)
1113014.311923.6
297110.412273.9
3147228.413174.6
4117215.614145.3
5107112.712764.3
6132721.29942.1
7119116.213214.6
8143226.214175.4
9110113.512764.3
Mean value1207.417.61270.44.2
Table
Table 2. Properties of used materials.
Table 2. Properties of used materials.
Load DiagramTestMaterialNo. of SamplesResultCoefficient of Variation
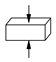Materials 15 00552 i001Compressive strength [108]Brick6fb = 26.6 MPa9%
Materials 15 00552 i002Tensile strengthBrick6ftb = 2.3 MPa18%
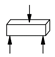Materials 15 00552 i003Flexural strength [109]Mortar9f = 2.7 MPa17%
Materials 15 00552 i004Compressive strength [109]Mortar12fm = 8.0 MPa23%
Materials 15 00552 i005Tensile strengthMortar6ftm = 1.0 MPa13%
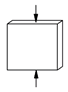Materials 15 00552 i006Compressive strength [110]
Young’s modulus [110]
Poisson’s coefficient [110]		Masonry6fm = 10.8 MPa
E = 6.6 GPa
ν = 0.14		7%
7%
17%
Materials 15 00552 i007Tensile splitting strength [111]Masonry6ft45 = 0.52 MPa11%
Materials 15 00552 i008Tensile strengthMasonry7ft90 = 0.11 MPa1%
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Nowak, R.; Kania, T.; Rutkowski, R.; Ekiert, E. Research and TLS (LiDAR) Construction Diagnostics of Clay Brick Masonry Arched Stairs. Materials 2022, 15, 552. https://doi.org/10.3390/ma15020552

AMA Style

Nowak R, Kania T, Rutkowski R, Ekiert E. Research and TLS (LiDAR) Construction Diagnostics of Clay Brick Masonry Arched Stairs. Materials. 2022; 15(2):552. https://doi.org/10.3390/ma15020552

Chicago/Turabian Style

Nowak, Rafał, Tomasz Kania, Radosław Rutkowski, and Ewa Ekiert. 2022. "Research and TLS (LiDAR) Construction Diagnostics of Clay Brick Masonry Arched Stairs" Materials 15, no. 2: 552. https://doi.org/10.3390/ma15020552

APA Style

Nowak, R., Kania, T., Rutkowski, R., & Ekiert, E. (2022). Research and TLS (LiDAR) Construction Diagnostics of Clay Brick Masonry Arched Stairs. Materials, 15(2), 552. https://doi.org/10.3390/ma15020552

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop