Accurate Characterization of the Adhesive Layer Thickness of Ceramic Bonding Structures Using Terahertz Time-Domain Spectroscopy
Abstract
1. Introduction
2. Theoretical Model
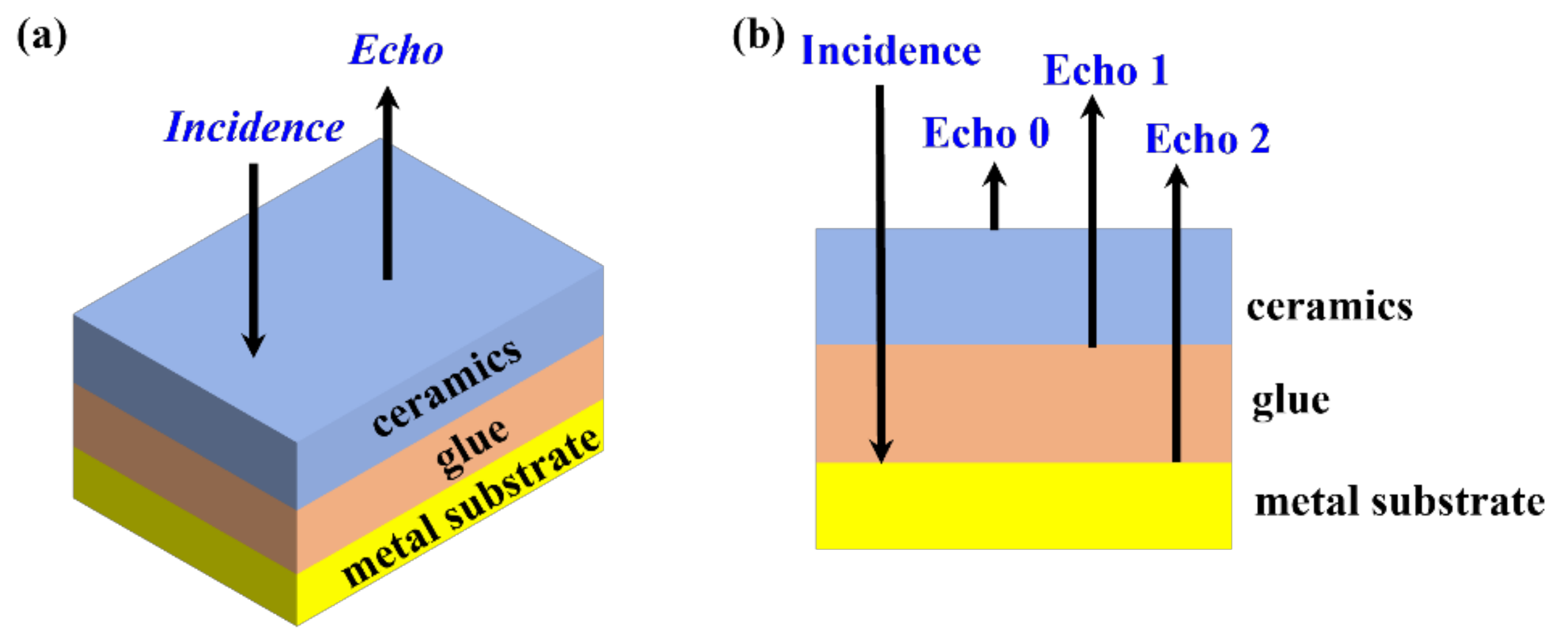
2.1. Transmission Mechanism of Terahertz Waves in Ceramic Glued Structures
2.2. Principle of Sparse Deconvolution
3. Experimental System and Samples
3.1. Experimental System
3.2. Sample
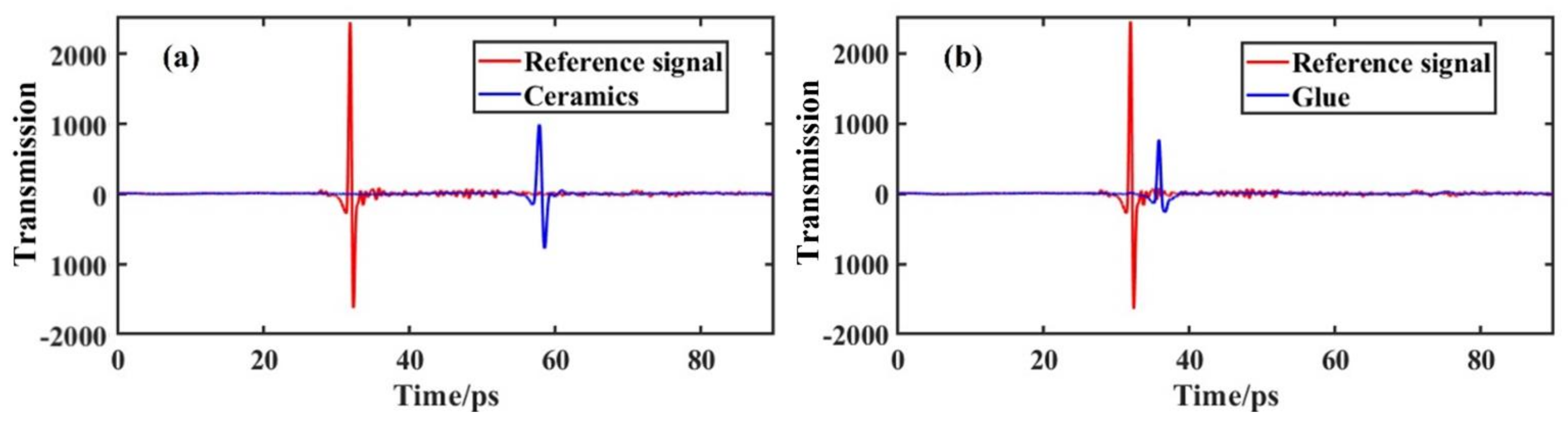
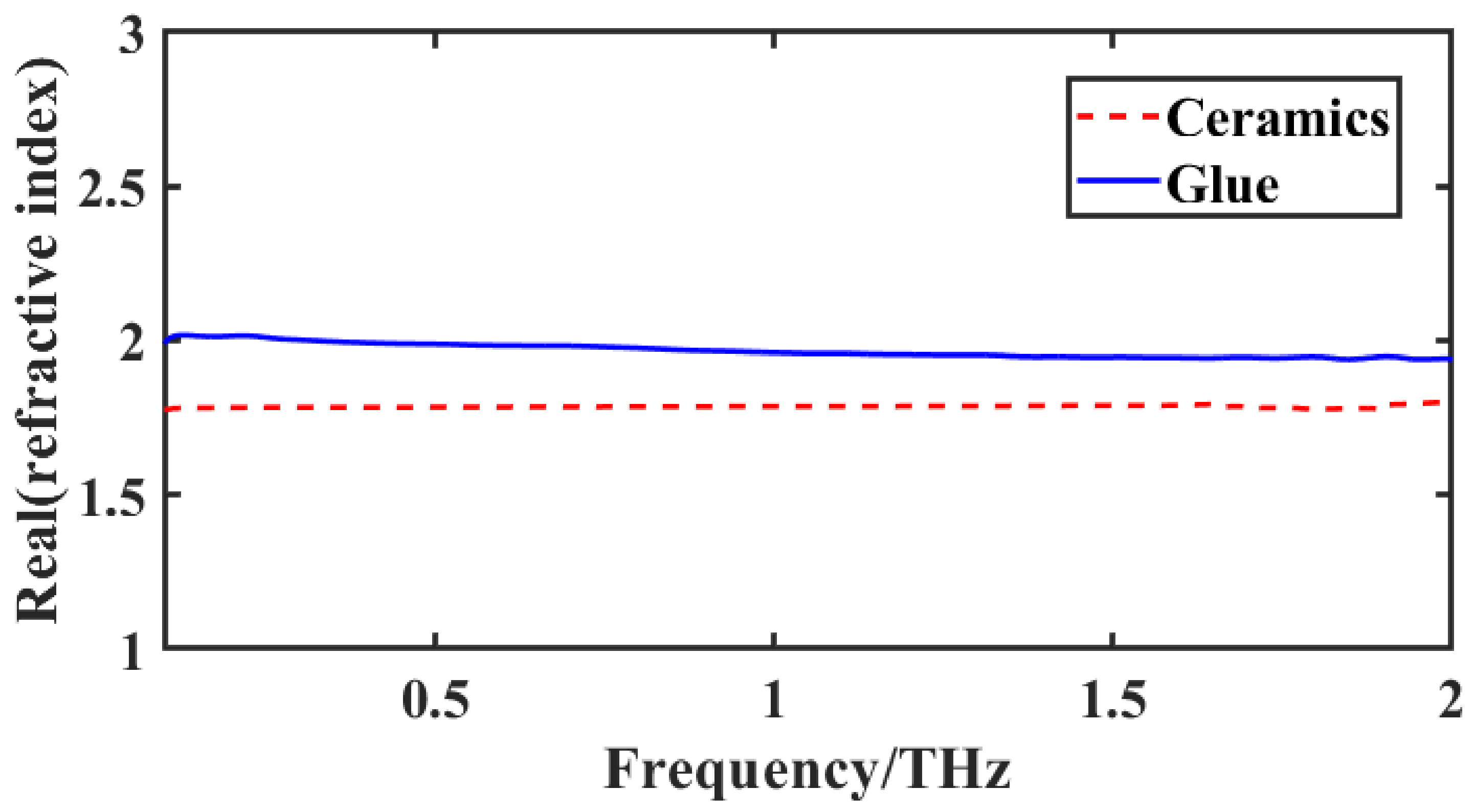
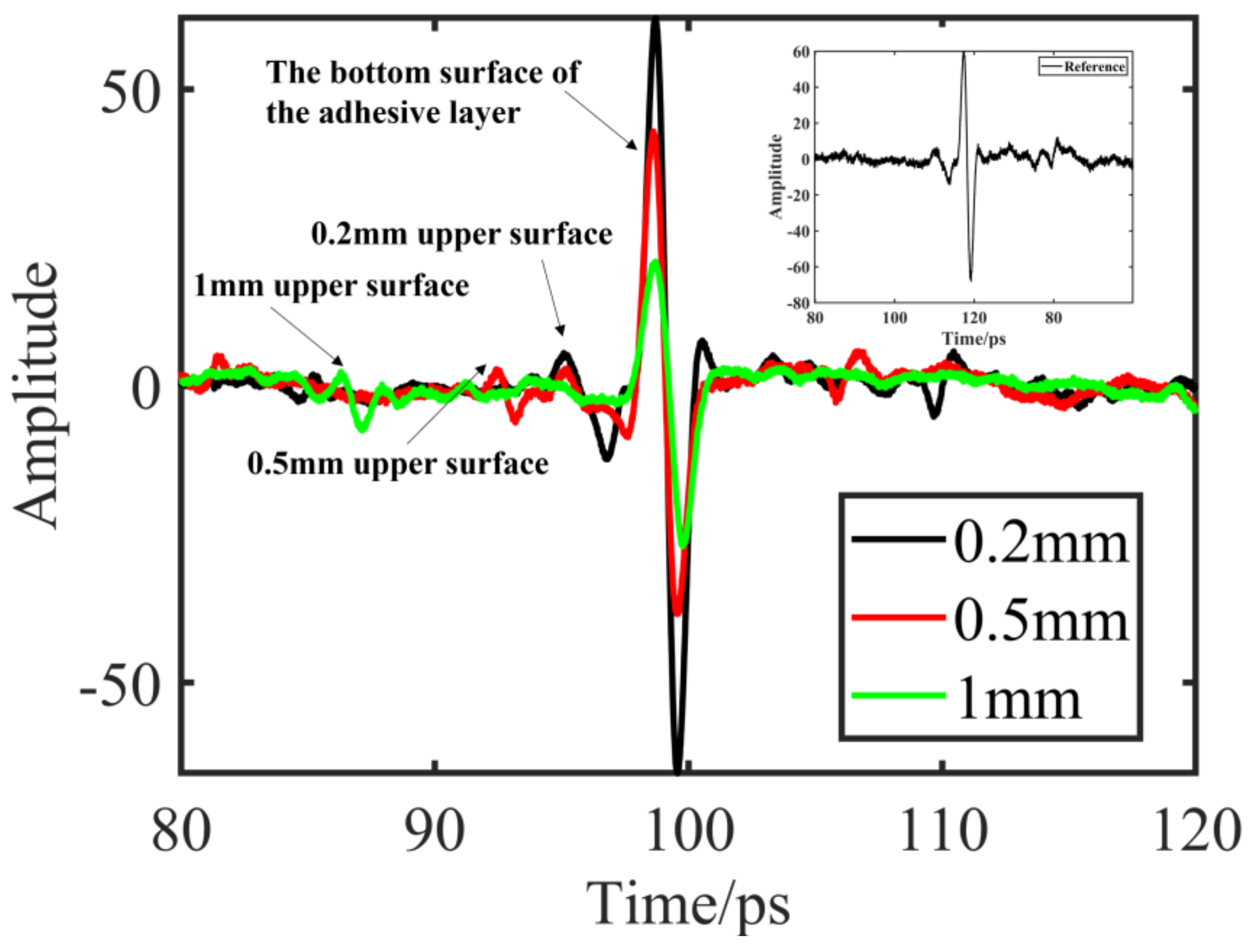
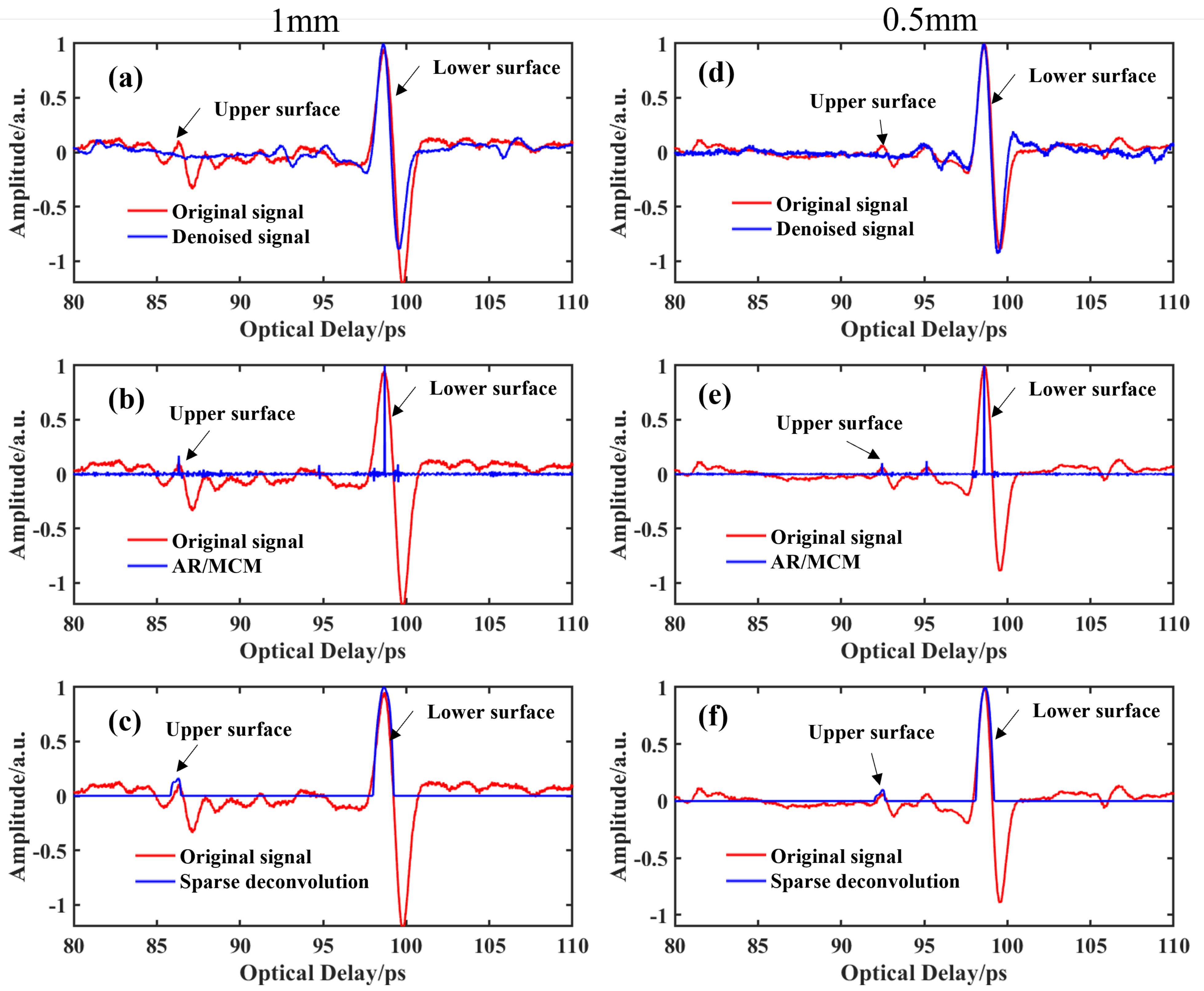
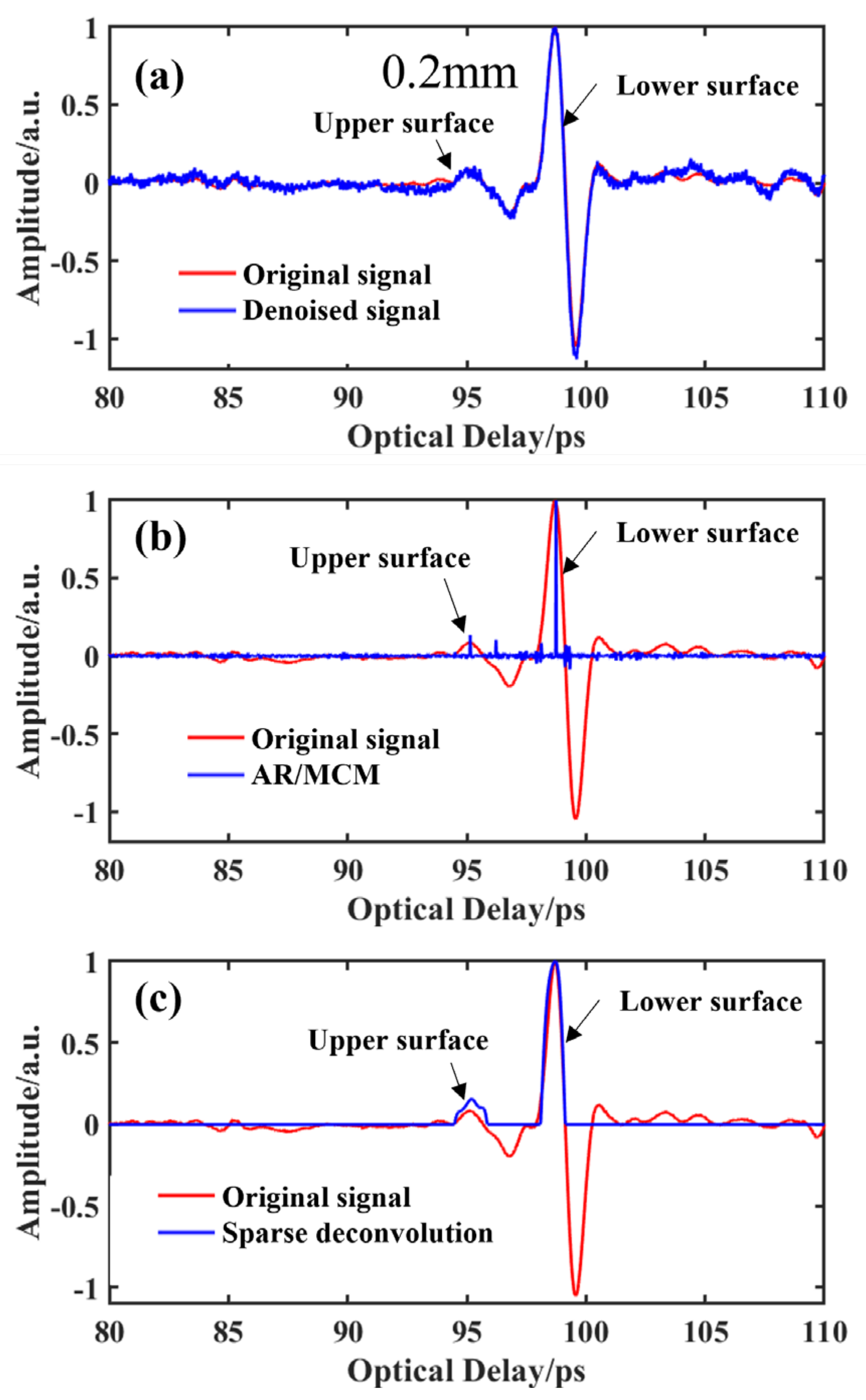
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tao, Y.H.; Fitzgerald, A.J.; Wallace, V.P. Non-Contact, non-destructive testing in various industrial sectors with terahertz technology. Sensors 2020, 20, 712. [Google Scholar] [CrossRef] [PubMed]
- Parrott, E.P.J.; Sy, S.M.Y.; Blu, T.; Wallace, V.P.; Pickwell-MacPherson, E. Terahertz pulsed imaging in vivo: Measurements and processing methods. J. Biomed. Opt. 2011, 16, 106010. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Wu, X.; Locquet, A.; Citrin, D.S. Terahertz Superresolution Stratigraphic Characterization of Multilayered Structures Using Sparse Deconvolution. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 260–267. [Google Scholar] [CrossRef]
- Hu, W.; Wang, W.; Ji, J.; Si, L. The spatial resolution enhancement deconvolution technique of the optimized wiener filter in Terahertz band. In Proceedings of the 9th UK-Europe-China Workshop on Millimetre Waves and Terahertz Technologies (UCMMT), Qingdao, China, 5–7 September 2016; pp. 120–123. [Google Scholar]
- Gupta, I.J.; Beak, M.J.; Moghaddar, A. Data extrapolation for high resolution radar imaging. IEEE Trans. Antennas Propag. 1994, 42, 1540–1545. [Google Scholar] [CrossRef]
- Zhai, M.; Locquet, A.; Roquelet, C.; Alexandre, P.; Daheron, L.; Citrin, D.S. Nondestructive measurement of mill-scale thickness on steel by terahertz time-of-flight tomography. Surf. Coat. Technol. 2020, 393, 125765. [Google Scholar] [CrossRef]
- Lines, L.R.; Clayton, R.W. A new approach to vibroseis deconvolution. Geophys. Prospect. 1977, 25, 417–433. [Google Scholar] [CrossRef]
- Walker, G.C.; Bowen, J.W.; Labaune, J.; Jackson, J.-B.; Hadjiloucas, S.; Roberts, J.; Mourou, G.; Menu, M. Terahertz deconvolution. Opt. Express 2012, 20, 27230–27242. [Google Scholar] [CrossRef]
- Kim, S.-J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An Interior-Point Method for Large-Scale-Regularized Least Squares. IEEE J. Sel. Top. Signal Process. 2007, 1, 606–617. [Google Scholar]
- Wang, X.; Cui, Y.; Sun, W.; Zhang, Y.; Zhang, C. Terahertz pulse reflective focal-plane tomography. Opt. Express 2007, 15, 14369–14375. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, D.; Wang, Z.; Zhang, Y.; Wu, J.; Wu, B.; Wu, X. Super-resolution reconstruction of terahertz images based on a deep-learning network with a residual channel attention mechanism. Appl. Opt. 2022, 61, 3363–3370. [Google Scholar] [CrossRef]
- Chen, Q.; Li, L.; Ren, J.; Zhang, D. Nondestructive testing of rubber materials based on terahertz time-domain spectroscopy technology. J. Terahertz Sci. Electron. Inf. Technol. 2019, 17, 379–384. [Google Scholar]
- Zhai, M.; Locquet, A.; Roquelet, C.; Ronqueti, L.A.; Citrin, D.S. Thickness characterization of multi-layer coated steel by terahertz time-of-flight tomography. NDT E Int. 2020, 116, 102358. [Google Scholar] [CrossRef]
- Qiao, X.; Zhang, X.; Ren, J.; Zhang, D.; Cao, G.; Li, L. Mean estimation empirical mode decomposition method for terahertz time-domain spectroscopy de-noising. Appl. Opt. 2017, 56, 7138–7145. [Google Scholar] [CrossRef] [PubMed]
- Selima, H.; Delgado-Prietob, M.; Trulla, J.; Picóc, R.; Romeralb, L.; Cojocaru, C. Defect reconstruction by non-destructive testing with laser induced ultrasonic detection. Ultrasonics 2020, 101, 106000. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Yan, K.; Lan, H.; Badal, J.; Qin, Z. Adaptive step-size fast iterative shrinkage-thresholding algorithm and sparse-spike deconvolution. Comput. Geosci. 2020, 134, 104343. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, X.; Zhang, L.; Yan, R.; Chen, X. Terahertz nondestructive quantitative characterization for layer thickness based on sparse representation method. NDT E Int. 2021, 124, 102536. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, C.; Harvey, D.M. Sparse signal representation and its applications in ultrasonic NDE. Ultrasonics 2012, 52, 351–363. [Google Scholar] [CrossRef]
- Looverbosch, T.V.D.; Bhuiyan, M.H.R.; Verboven, P.; Dierick, M.; Loo, D.V.; Beenbouwer, J.D.; Sijbers, J.; Nicolaï, B. Nondestructive internal quality inspection of pear fruit by X-ray CT using machine learning. Food Control 2020, 113, 107170. [Google Scholar] [CrossRef]
- Li, L.; Zhou, M.; Ren, J. Test of the adhesive thickness uniformity based on terahertz time-domain spectroscopy. Laser Infrared 2014, 44, 801–804. [Google Scholar]
- Jin, D.; Wang, B.; Dou, X.; Wang, S.; Zhi, M. The Effectiveness and Application of the Gradient Sparse Regularization-Based Deconvolution Method. IEEE Geosci. Remote Sens. Lett. 2021, 99, 8018605. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, Y.; Xiang, Y.; Rong, R. A Novel Iterative Shrinkage Algorithm for CS-MRI via Adaptive Regularization. IEEE Signal Process. Lett. 2017, 24, 1443–1447. [Google Scholar] [CrossRef]
- Wang, B.; Qin, X.; Meng, K.; Zhu, L.; Li, Z. Classification of Amino Acids Using Hybrid Terahertz Spectrum and an Efficient Channel Attention Convolutional Neural Network. Nanomaterials 2022, 12, 2114. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Qin, X.; Li, W.; Li, Z.; Zhu, L. Learned iterative shrinkage and thresholding algorithm for terahertz sparse deconvolution. Opt. Express 2022, 30, 18238–18249. [Google Scholar] [CrossRef]
- Zhong, S. Progress in terahertz nondestructive testing: A review. Front. Mech. Eng. 2019, 14, 273–281. [Google Scholar] [CrossRef]
- Wu, D.; Haude, C.; Burger, R.; Peters, O. Application of terahertz time domain spectroscopy for NDT of oxide-oxide ceramic matrix composites. Infrared Phys. Technol. 2019, 102, 102995. [Google Scholar] [CrossRef]
- Dong, J.; Locquet, A.; Declercq, N.F.; Citrin, D.S. Polarization-resolved terahertz imaging of intra- and inter-laminar damages in hybrid fiber-reinforced composite laminate subject to low-velocity impact. Compos. Part B Eng. 2016, 92, 167–174. [Google Scholar] [CrossRef]
- Krimi, S.; Torosyan, G.; Beigang, R. Advanced GPU-based terahertz approach for inline multilayer thickness measurements. IEEE J. Sel. Top. Quantum Electron. 2016, 23, 1–12. [Google Scholar] [CrossRef]
- Xu, C.; Yang, Z.; Qiao, B.; Chen, X. A parameter estimation based sparse representation approach for mode separation and dispersion compensation of Lamb waves in isotropic plate. Smart Mater. Struct. 2020, 29, 035020. [Google Scholar] [CrossRef]


| The Real Value (mm) | Wavelet Method | AR/MCM | Sparse Deconvolution |
|---|---|---|---|
| 1.0 | 0.95 | 0.96 | 0.98 |
| 0.50 | 0.47 | 0.48 | 0.49 |
| 0.20 | 0.24 | 0.23 | 0.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, D.; Wu, B.; Zhang, K.; Yang, B.; Wang, Z.; Wu, X. Accurate Characterization of the Adhesive Layer Thickness of Ceramic Bonding Structures Using Terahertz Time-Domain Spectroscopy. Materials 2022, 15, 6972. https://doi.org/10.3390/ma15196972
Yang X, Zhang D, Wu B, Zhang K, Yang B, Wang Z, Wu X. Accurate Characterization of the Adhesive Layer Thickness of Ceramic Bonding Structures Using Terahertz Time-Domain Spectroscopy. Materials. 2022; 15(19):6972. https://doi.org/10.3390/ma15196972
Chicago/Turabian StyleYang, Xiuwei, Dehai Zhang, Biyuan Wu, Kaihua Zhang, Bing Yang, Zhongmin Wang, and Xiaohu Wu. 2022. "Accurate Characterization of the Adhesive Layer Thickness of Ceramic Bonding Structures Using Terahertz Time-Domain Spectroscopy" Materials 15, no. 19: 6972. https://doi.org/10.3390/ma15196972
APA StyleYang, X., Zhang, D., Wu, B., Zhang, K., Yang, B., Wang, Z., & Wu, X. (2022). Accurate Characterization of the Adhesive Layer Thickness of Ceramic Bonding Structures Using Terahertz Time-Domain Spectroscopy. Materials, 15(19), 6972. https://doi.org/10.3390/ma15196972








