Characterization of Fatigue Crack Growth Based on Acoustic Emission Multi-Parameter Analysis
Abstract
1. Introduction
2. Material and Methods
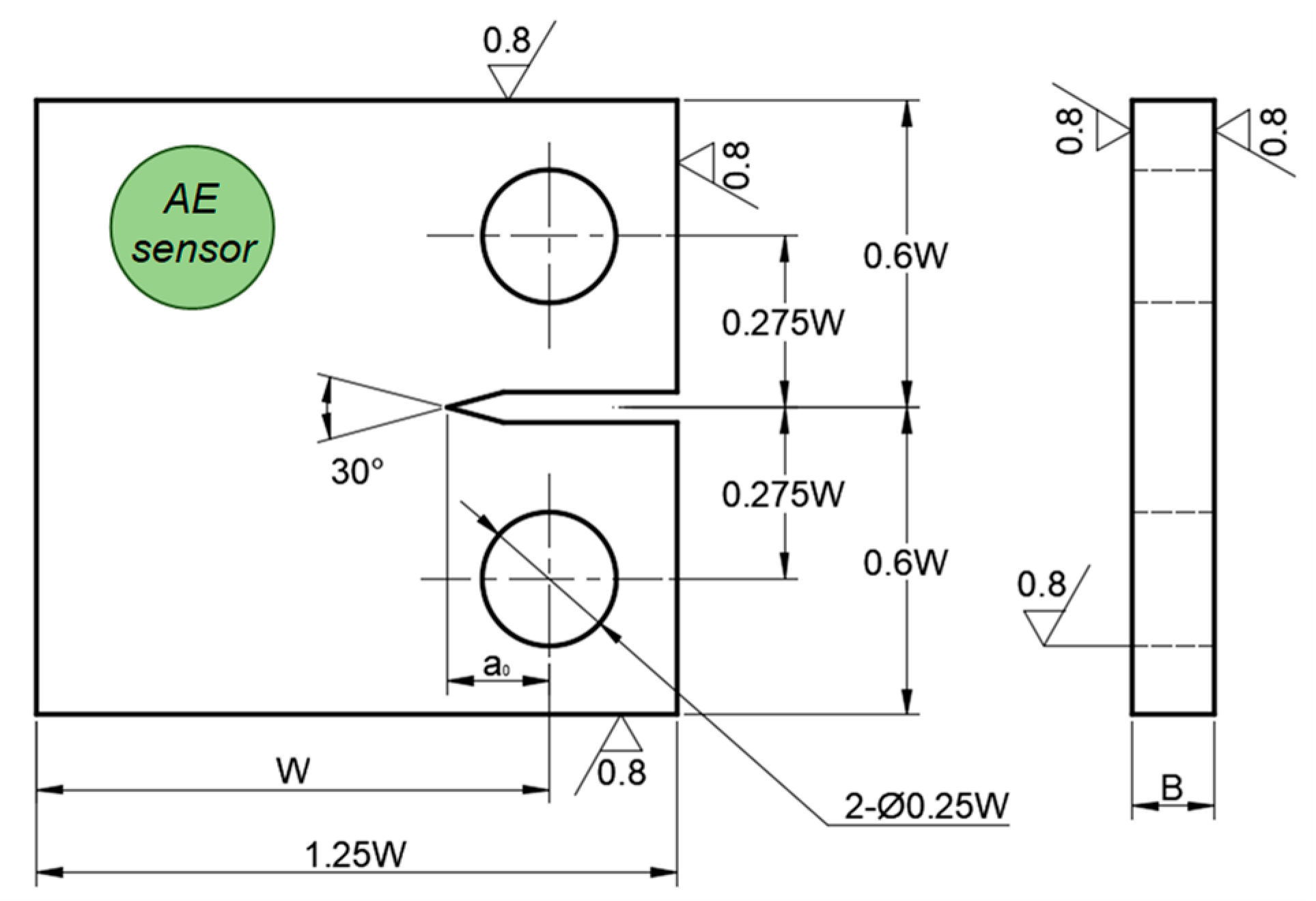
2.1. Fatigue Crack Growth Test
2.2. AE Monitoring Instrument
2.3. Extraction of Multiple AE Parameters
3. Results and Discussion
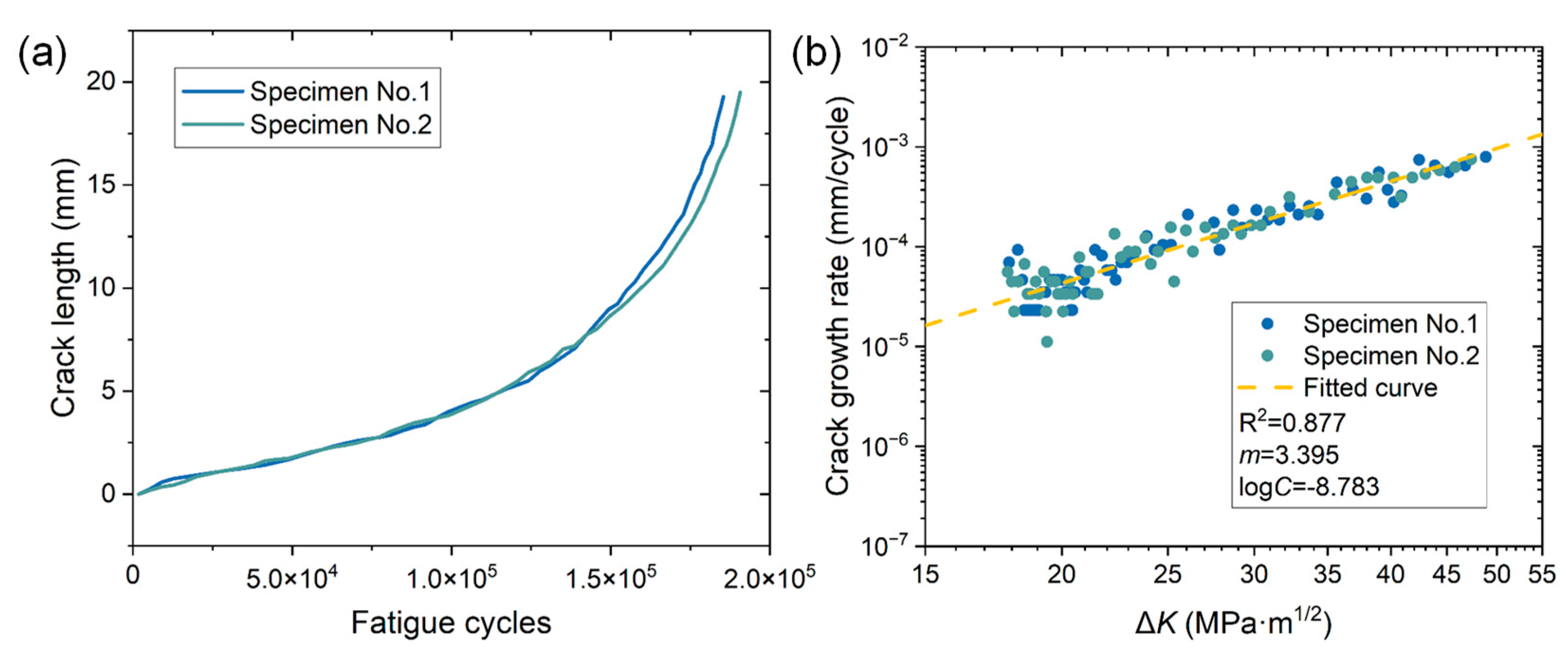
3.1. Fatigue Crack Growth Behavior
3.2. Characterization of FCG via AE Multi-Parameter Analysis
3.2.1. AE Time Domain Parameters
3.2.2. AE Frequency Domain Parameter
3.2.3. Coefficient of Variance of AE Data
3.3. Quantitative Correlations between Crack Growth Rate and AE Parameters
3.4. Fatigue Fracture Mechanism
4. Conclusions
- (1)
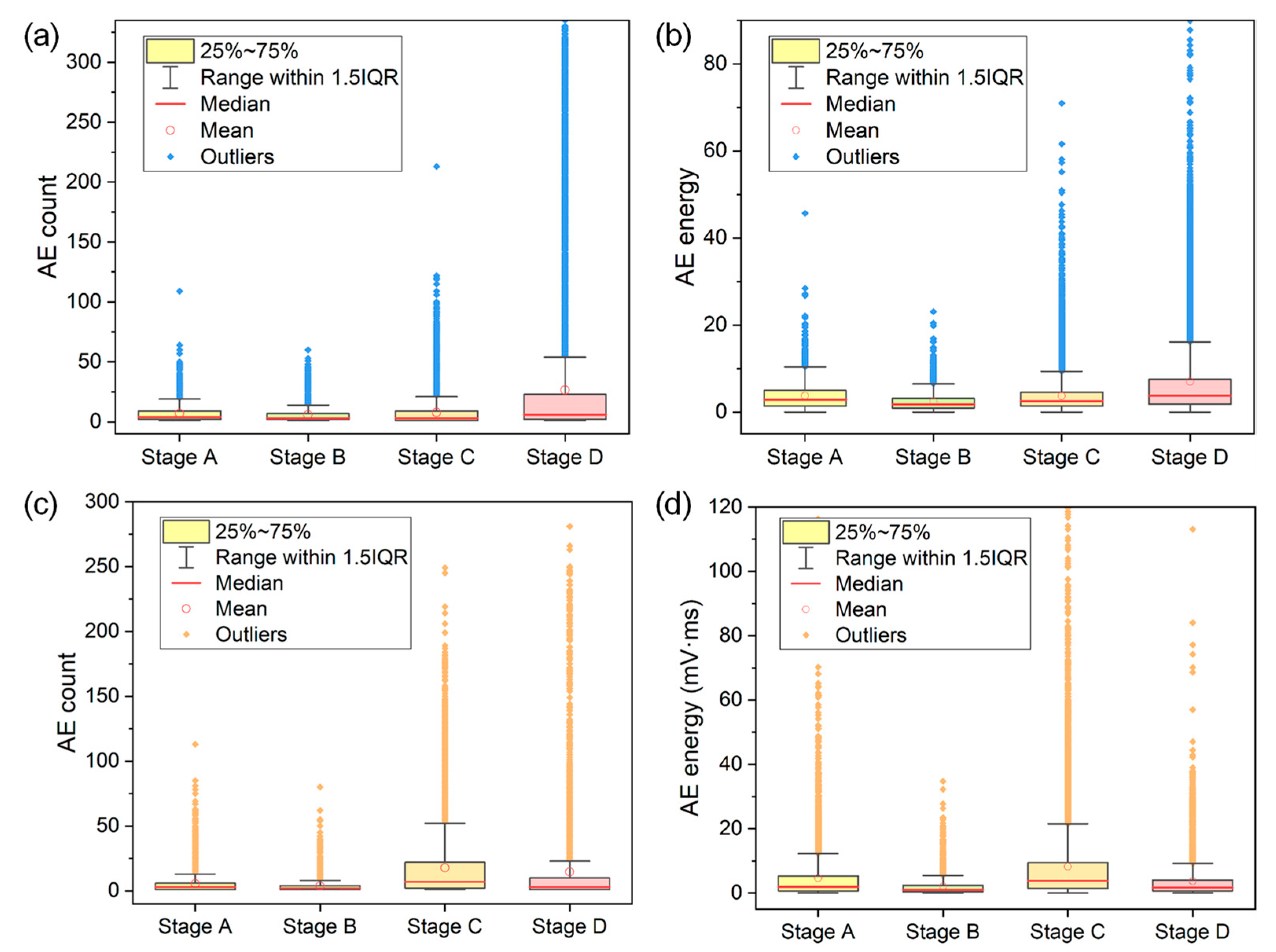
- Based on the combined analyses of AE time domain parameters and crack growth rate, four stages of FCG (i.e., stage A, B, C and D) of 2.25Cr1Mo0.25V steel can be distinguished. The four stages correspond to crack initiation, stable crack growth with low crack growth rate, stable crack growth with high crack growth rate, and unstable crack growth, respectively. The continuous emergence of a large number of AE signals with high count (>100) and high energy (>40 mV·ms) in stages C and D can help to provide early and effective warning signs for accelerated crack growth.
- (2)
- The centroid frequency of AE signals caused by FCG of 2.25Cr1Mo0.25V steel is distributed in a narrow range of 170–220 kHz. The centroid frequency may not be appropriate for assessing the crack growth condition due to low variability, however, the occurrence of such a frequency band can help to identify possible crack growth signals.
- (3)
- Linear correlations are found between crack growth rate and different AE parameters for quantifying crack growth. However, it should be noted that these quantitative correlations are only valid in current laboratory conditions. This is because AE signals are highly influenced by the sensor/source distance, specimen’s geometry and coupling quality [2], and consequently the quantitative relationships between AE and crack growth rate may not be obtained in the industrial environment. Before the practical application of this approach, the above-mentioned factors should be taken into account to reach a reliable quantification of fatigue crack of engineering structures.
- (4)
- The AE multi-parameter analysis is recommended for damage characterization due to its advantage of reducing errors in using individual AE parameters. In this study, based on the multi-parameter analysis, one can conclude the count, energy and kurtosis are superior parameters for both qualitatively and quantitatively characterizing the FCG of 2.25Cr1Mo0.25V steel.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Christian Grosse, M.O. Acoustic Emission Testing, Basics for Research-Applications in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Saeedifar, M.; Zarouchas, D. Damage characterization of laminated composites using acoustic emission: A review. Compos. Part B-Eng. 2020, 195, 108039. [Google Scholar] [CrossRef]
- Thatcher, J.E.; Crump, D.A.; Devivier, C.; Bailey, P.B.S.; Dulieu-Barton, J.M. Low cost infrared thermography for automated crack monitoring in fatigue testing. Opt. Lasers Eng. 2020, 126, 105914. [Google Scholar] [CrossRef]
- Morscher, G.N.; Maxwell, R. Monitoring tensile fatigue crack growth and fiber failure around a notch in laminate SIC/SIC composites utilizing acoustic emission, electrical resistance, and digital image correlation. J. Eur. Ceram. Soc. 2019, 39, 229–239. [Google Scholar] [CrossRef]
- Han, Z.; Luo, H.; Cao, J.; Wang, H. Acoustic emission during fatigue crack propagation in a micro-alloyed steel and welds. Mater. Sci. Eng. A 2011, 528, 7751–7756. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Z.; Shen, G. Influence of grain size on fatigue crack propagation and acoustic emission features in commercial-purity zirconium. Mater. Sci. Eng. A 2015, 636, 35–42. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Kordatos, E.Z.; Matikas, T.E. Acoustic emission for fatigue damage characterization in metal plates. Mech. Res. Commun. 2011, 38, 106–110. [Google Scholar] [CrossRef]
- Yu, J.; Ziehl, P.; Zárate, B.; Caicedo, J. Prediction of fatigue crack growth in steel bridge components using acoustic emission. J. Constr. Steel Res. 2011, 67, 1254–1260. [Google Scholar] [CrossRef]
- Chai, M.; Zhang, Z.; Duan, Q. A new qualitative acoustic emission parameter based on Shannon’s entropy for damage monitoring. Mech. Syst. Sign. Process. 2018, 100, 617–629. [Google Scholar] [CrossRef]
- Tanvir, F.; Sattar, T.; Mba, D.; Edwards, G. Identification of fatigue damage evaluation using entropy of acoustic emission waveform. SN Appl. Sci. 2020, 2, 1–15. [Google Scholar] [CrossRef]
- Karimian, S.F.; Modarres, M.; Bruck, H.A. A new method for detecting fatigue crack initiation in aluminum alloy using acoustic emission waveform information entropy. Eng. Fract. Mech. 2020, 223, 106771. [Google Scholar] [CrossRef]
- Roberts, T.M.; Talebzadeh, M. Acoustic emission monitoring of fatigue crack propagation. J. Constr. Steel Res. 2003, 59, 695–712. [Google Scholar] [CrossRef]
- Roberts, T.M.; Talebzadeh, M. Fatigue life prediction based on crack propagation and acoustic emission count rates. J. Constr. Steel Res. 2003, 59, 679–694. [Google Scholar] [CrossRef]
- Li, D.; Kuang, K.; Koh, C.G. Fatigue crack sizing in rail steel using crack closure-induced acoustic emission waves. Meas. Sci. Technol. 2017, 28, 065601. [Google Scholar] [CrossRef]
- Keshtgar, A.; Sauerbrunn, C.M.; Modarres, M. Structural reliability prediction using acoustic emission-based modeling of fatigue crack growth. Appl. Sci. 2018, 8, 1225. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, G.; Hu, K. Prediction of fatigue crack growth in gas turbine engine blades using acoustic emission. Sensors 2018, 18, 1321. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.; Han, Z.; Liu, Z.; Vallely, P.; Soua, S. Quantitative monitoring of brittle fatigue crack growth in railway steel using acoustic emission. P. I. Mech. Eng. F-J. Rail. 2018, 232, 1211–1224. [Google Scholar] [CrossRef]
- Chai, M.; Hou, X.; Zhang, Z.; Duan, Q. Identification and prediction of fatigue crack growth under different stress ratios using acoustic emission data. Int. J. Fatigue 2022, 160, 106860. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. ASME J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Kannan, V.P. Application of different acoustic emission descriptors in damage assessment of fiber reinforced plastics: A comprehensive review. Eng. Fract. Mech. 2020, 235, 107083. [Google Scholar] [CrossRef]
- Li, H.; Shen, R.; Li, D.; Jia, H.; Li, T.; Chen, T.; Hou, Z. Acoustic emission multi-parameter analysis of dry and saturated sandstone with cracks under uniaxial compression. Energies 2019, 12, 1959. [Google Scholar] [CrossRef]
- Gong, H.; Luo, Y.; Xu, K.; Huang, J.; Wang, G.; Li, X. Failure behaviors of fractured granite during loading and unloading under high confining pressure based on acoustic emission multi-parameter analysis. Theor. Appl. Fract. Mech. 2022, 121, 103442. [Google Scholar] [CrossRef]
- E647-15e1; A Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM International: West Conshohocken, PA, USA, 2016.
- Yang, L.; Kang, H.S.; Zhou, Y.C.; Zhu, W.; Cai, C.Y.; Lu, C. Frequency as a key parameter in discriminating the failure types of thermal barrier coatings: Cluster analysis of acoustic emission signals. Surf. Coat. Tech. 2015, 264, 97–104. [Google Scholar] [CrossRef]
- Ambrosio, D.; Dessein, G.; Wagner, V.; Yahiaoui, M.; Paris, J.Y.; Fazzini, M.; Cahuc, O. On the potential applications of acoustic emission in friction stir welding. J. Manuf. Process. 2022, 75, 461–475. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Kannan, V.P. Laplacian score and K-means data clustering for damage characterization of adhesively bonded CFRP composites by means of acoustic emission technique. Appl. Acoust. 2022, 185, 108425. [Google Scholar] [CrossRef]
- Xu, P.; Zhou, Z.; Liu, T.; Pan, S.; Tan, X. In-situ damage assessment of FML joints under uniaxial tension combining with acoustic emission and DIC: Geometric influence on damage formation. Thin Wall. Struct. 2022, 170, 108515. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, Y.; Fennis, S.A.A.M.; Hendriks, M.A.N. Developing a new acoustic emission source classification criterion for concrete structures based on signal parameters. Constr. Build. Mater. 2022, 318, 126163. [Google Scholar] [CrossRef]
- Herrmann, H.; Bucksch, H. Dictionary Geotechnical Engineering, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Ostash, O.P. New approaches in fatigue fracture mechanics. Mater. Sci. 2006, 42, 5. [Google Scholar] [CrossRef]
- Laird, C. The influence of metallurgical structure on the mechanisms of fatigue crack propagation. In Fatigue Crack Propagation; ASTM International: West Conshohocken, PA, USA, 1967. [Google Scholar]









| AE Parameter | Definition |
|---|---|
| Amplitude/peak amplitude | Largest voltage peak of the signal waveform. It is expressed in a decibel scale where 1 μV at the sensor is defined as 0 dB. |
| Count/ring-down count | Number of times where AE signal exceeds the employed threshold |
| Energy | Measured area under the rectified signal envelope above the threshold |
| Information entropy | Information or Shannon’s entropy of AE waveform. It denotes the disorder or uncertainty of the probability amplitude distribution. |
| Rise time | Time interval between the point where the AE signal exceeds the threshold and the point where the peak amplitude occurs |
| Duration | Time interval from the point where the AE signal exceeds the threshold to the last point where it crosses the threshold |
| Rise angle (RA) | Ratio of rise time to amplitude |
| Root mean square (RMS) | Square root of average of squared value of the signal |
| Kurtosis | Measure of the “tailedness” of the AE signal |
| Crest factor | Ratio of the peak value to the RMS value |
| Centroid frequency | Weighted average of the frequency content calculated by performing fast Fourier transform |
| AE Parameter | Amplitude | Count | Energy | Entropy | RA | RMS | Kurtosis | Crest Factor |
|---|---|---|---|---|---|---|---|---|
| Specimen 1 | 0.045 | 2.406 | 1.402 | 0.235 | 1.693 | 0.115 | 1.003 | 0.244 |
| Specimen 2 | 0.829 | 1.683 | 1.735 | 1.189 | 2.082 | 1.369 | 1.291 | 1.342 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, M.; Lai, C.; Xu, W.; Duan, Q.; Zhang, Z.; Song, Y. Characterization of Fatigue Crack Growth Based on Acoustic Emission Multi-Parameter Analysis. Materials 2022, 15, 6665. https://doi.org/10.3390/ma15196665
Chai M, Lai C, Xu W, Duan Q, Zhang Z, Song Y. Characterization of Fatigue Crack Growth Based on Acoustic Emission Multi-Parameter Analysis. Materials. 2022; 15(19):6665. https://doi.org/10.3390/ma15196665
Chicago/Turabian StyleChai, Mengyu, Chuanjing Lai, Wei Xu, Quan Duan, Zaoxiao Zhang, and Yan Song. 2022. "Characterization of Fatigue Crack Growth Based on Acoustic Emission Multi-Parameter Analysis" Materials 15, no. 19: 6665. https://doi.org/10.3390/ma15196665
APA StyleChai, M., Lai, C., Xu, W., Duan, Q., Zhang, Z., & Song, Y. (2022). Characterization of Fatigue Crack Growth Based on Acoustic Emission Multi-Parameter Analysis. Materials, 15(19), 6665. https://doi.org/10.3390/ma15196665






