Dynamic Mechanical Properties of Rolled Thin-Walled Steel Plates (TWSPs) Used for W-Beam Guardrails under Low and Medium Strain Rates
Abstract
:1. Introduction
2. Experimental Program
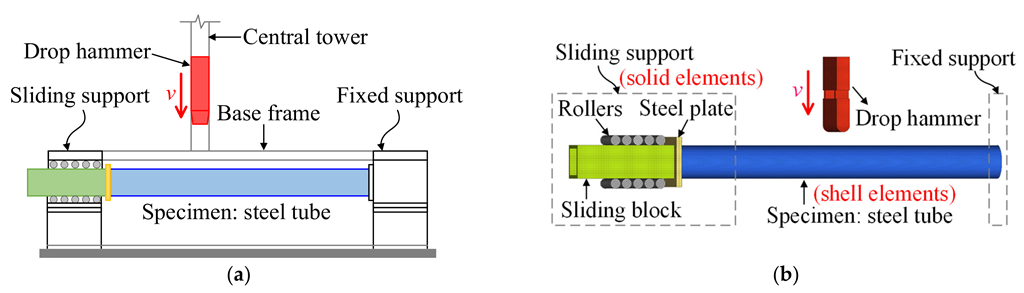
2.1. Test Setup and Measurement Devices
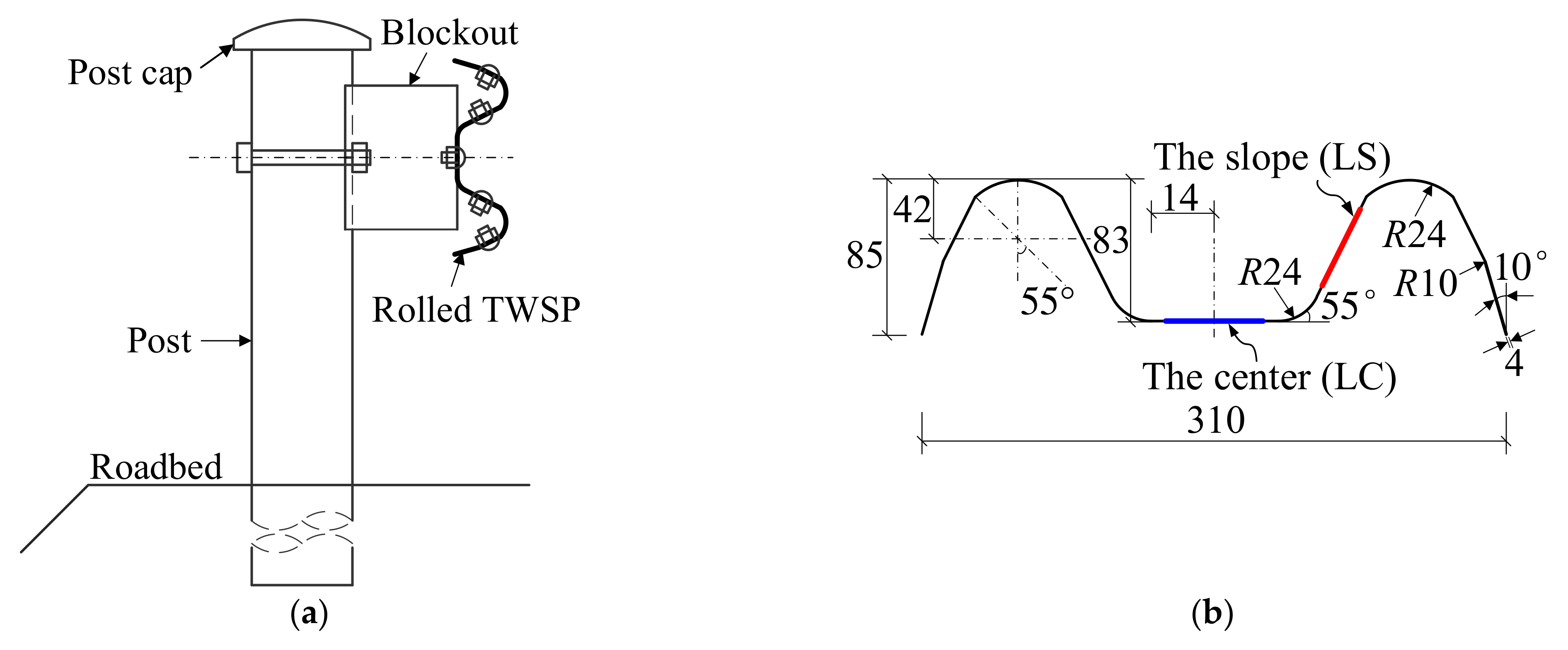
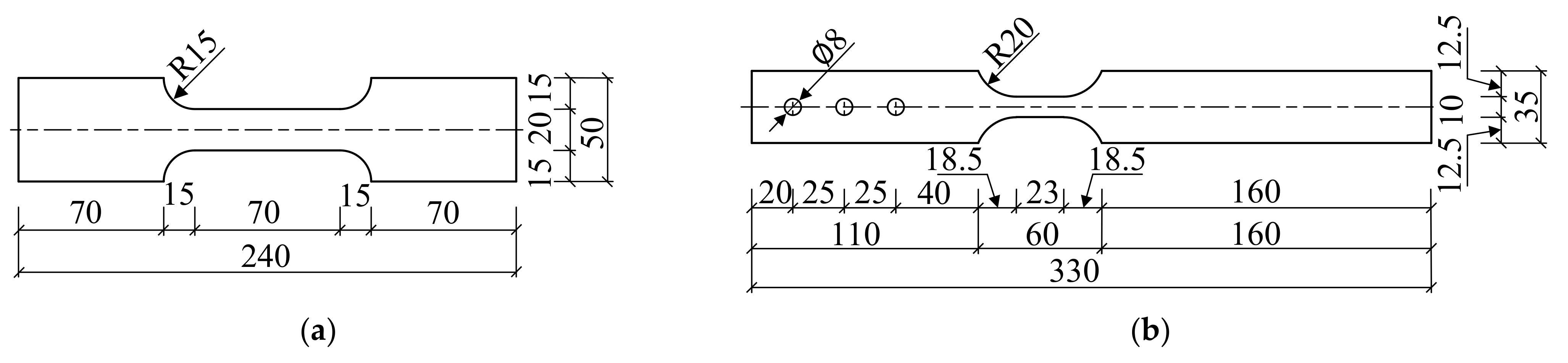
2.2. Specimen Design
3. Effects of Cold Rolling Treatment on Mechanical Properties of TWSPs
3.1. Test Specimens
3.2. Test Results and Analysis
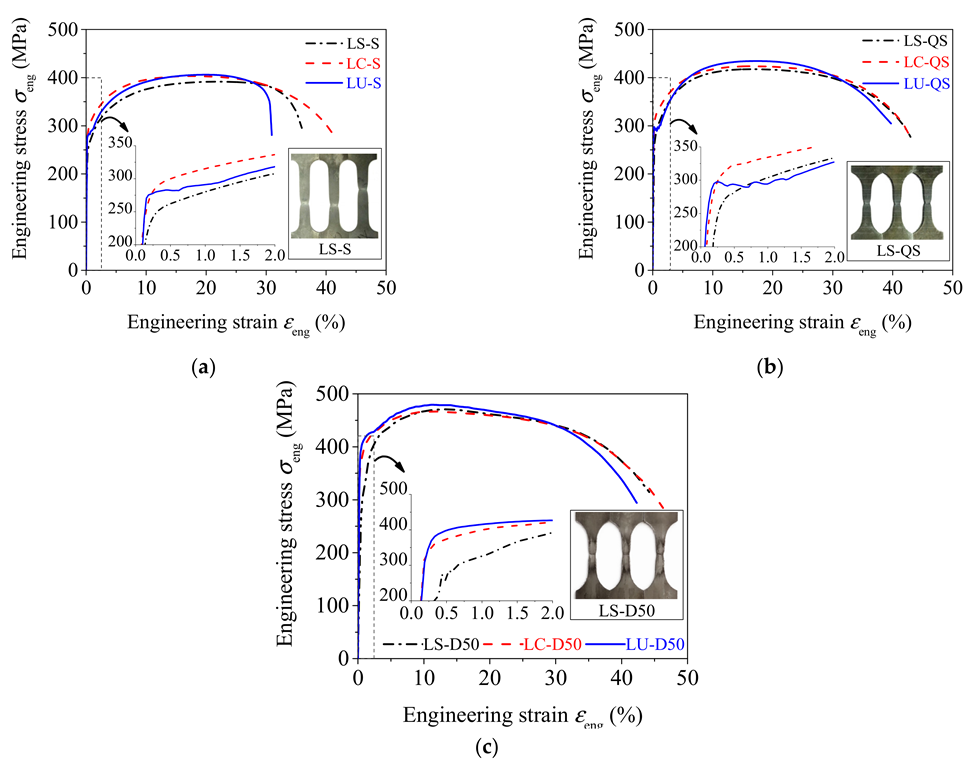
3.2.1. Tests Results
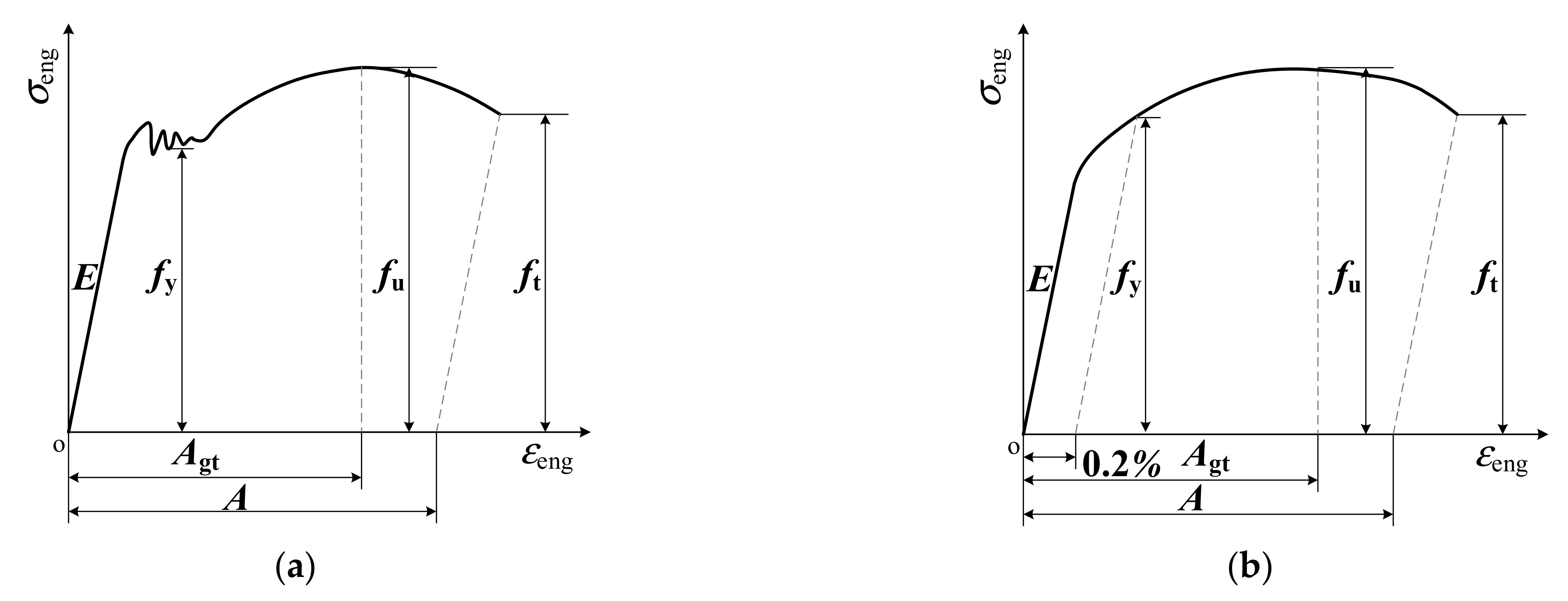
3.2.2. Analysis of Strength Parameters
3.2.3. Analysis of Deformation Parameters
4. Dynamic Responses of the Rolled TWSPs Using the Mechanical Models in Section 3
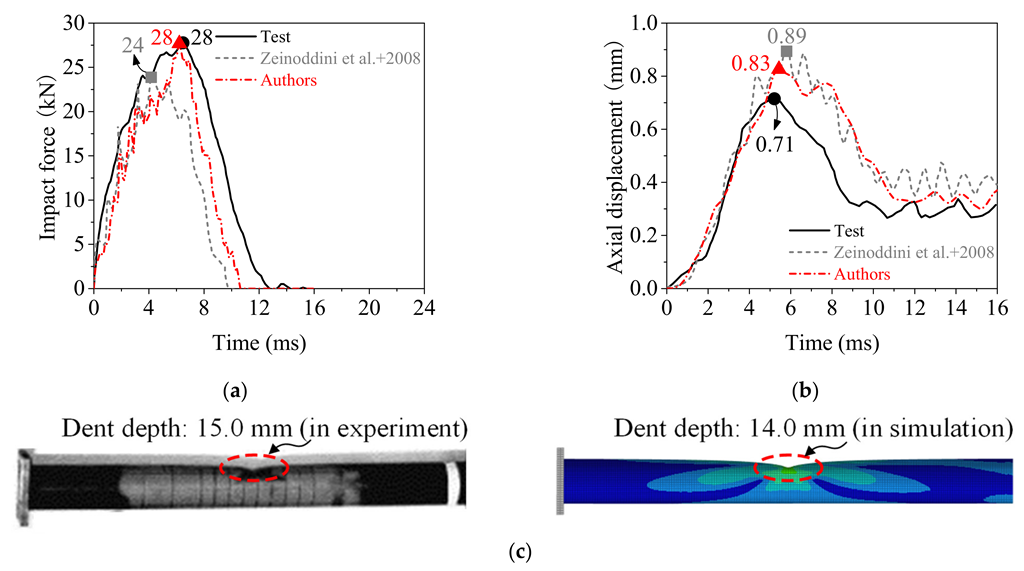
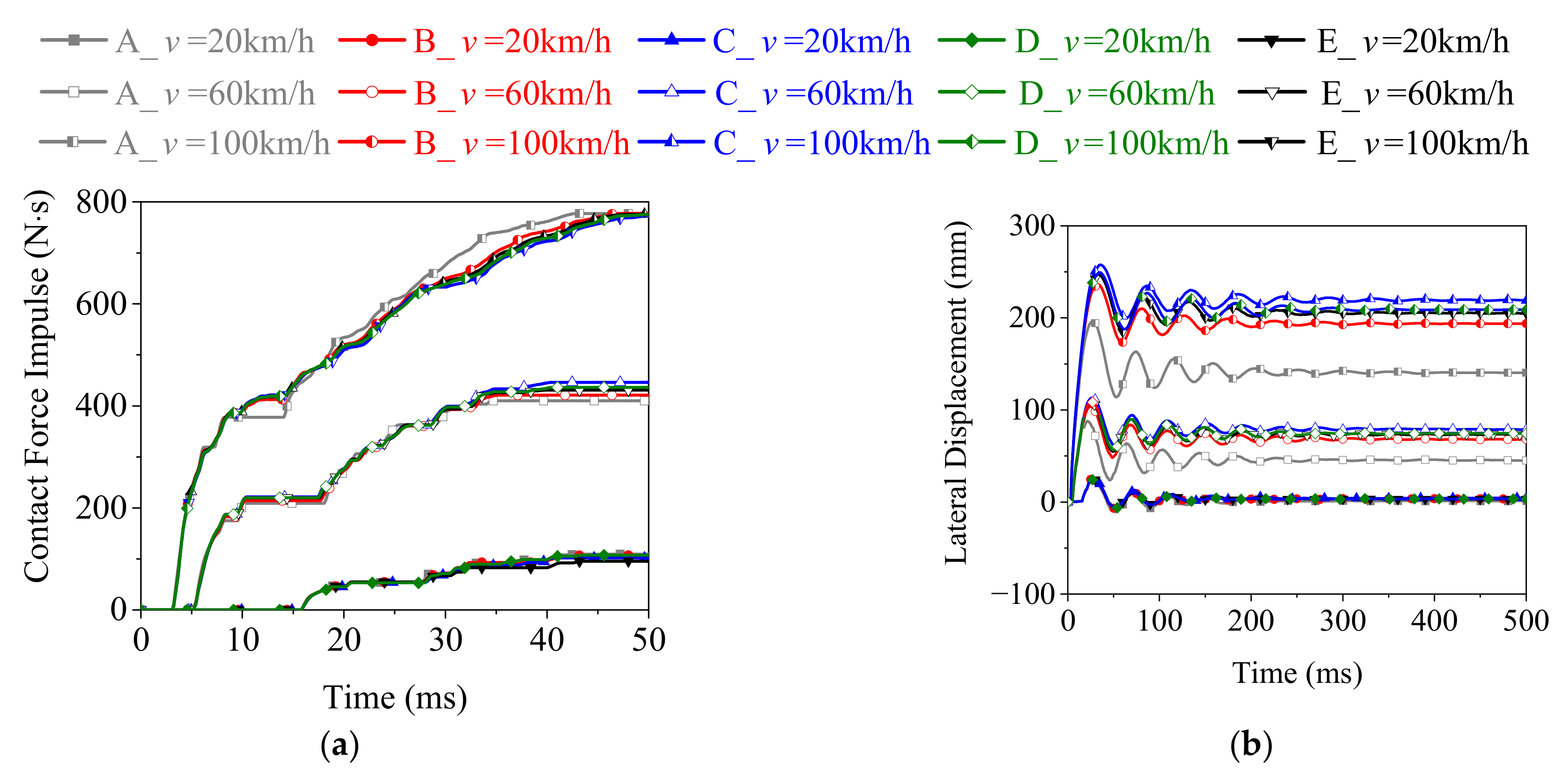
4.1. Validation of the Numerical Model
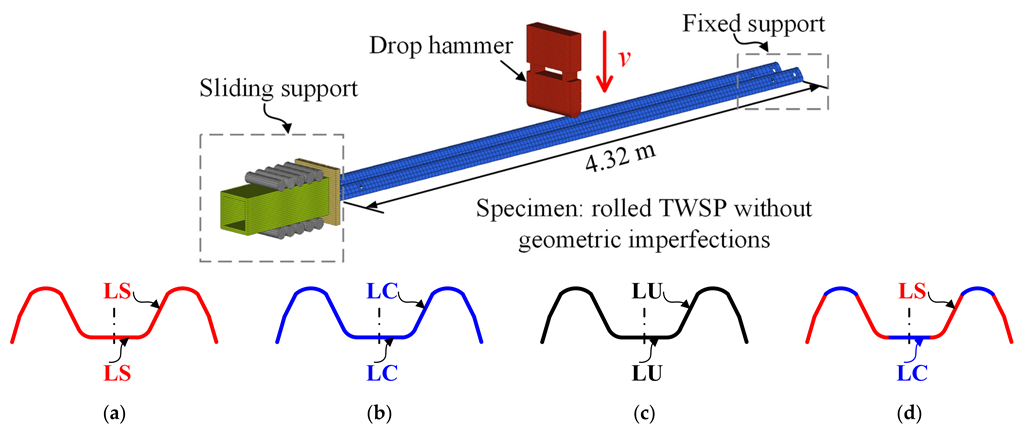
4.2. Numerical Model of the Drop Hammer Test on the Rolled TWSP
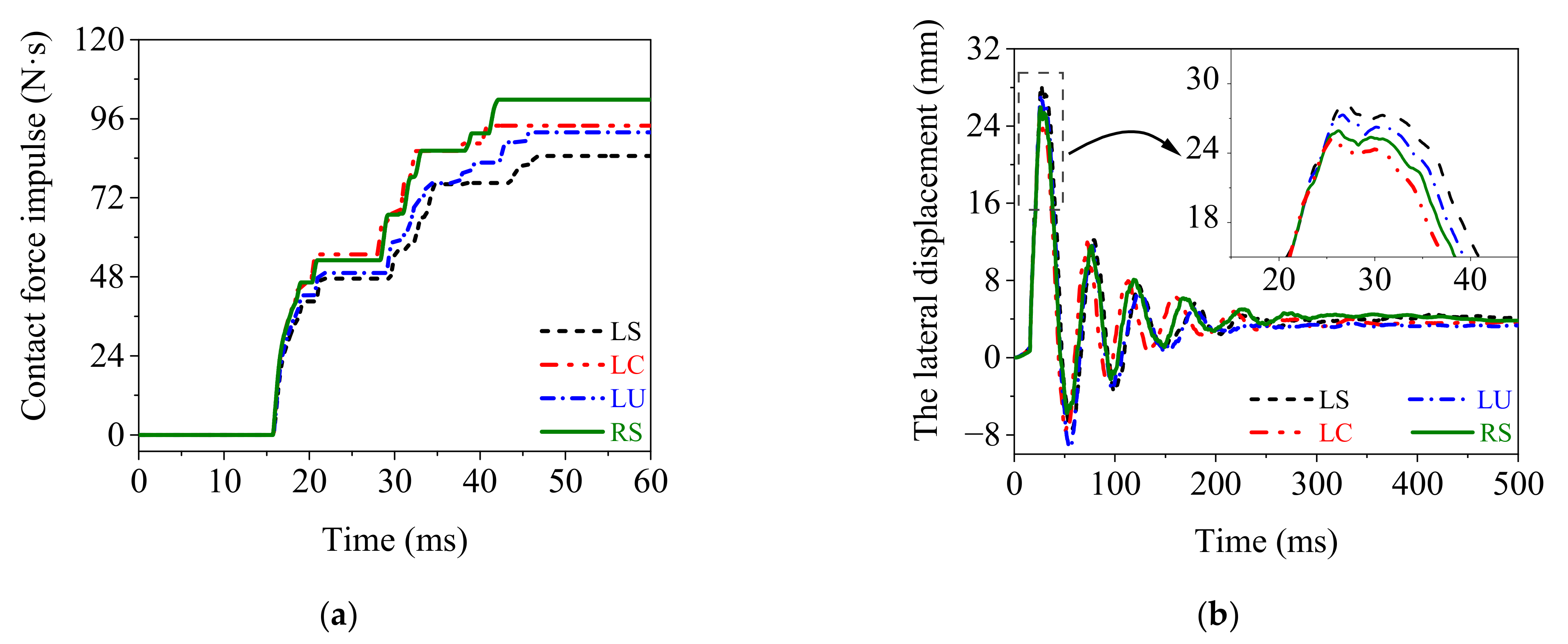
4.3. Dynamic Responses of the Rolled TWSP
5. Mechanical Model of the Rolled TWSP under Low and Medium Strain Rates
5.1. Test Specimens and Results
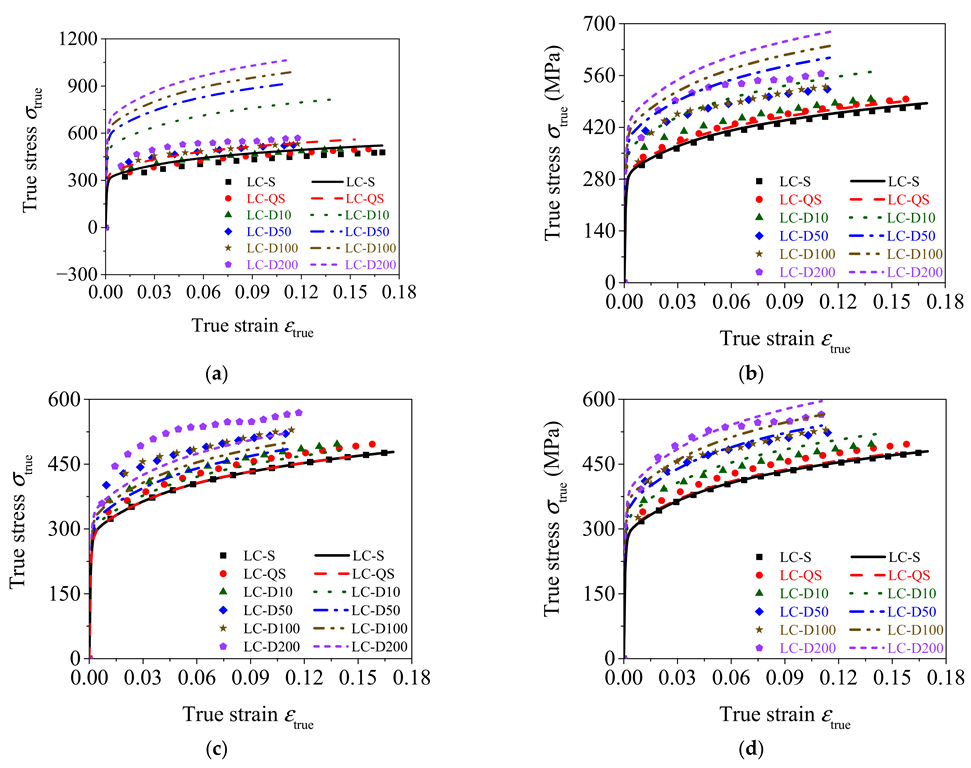
5.2. Calibration of Cowper–Symonds Model Parameters
5.3. Validation of the Calibrated Cowper–Symonds Models
6. Dynamic Responses of the Rolled TWSP Using Mechanical Models in Section 5
7. Conclusions
- (1)
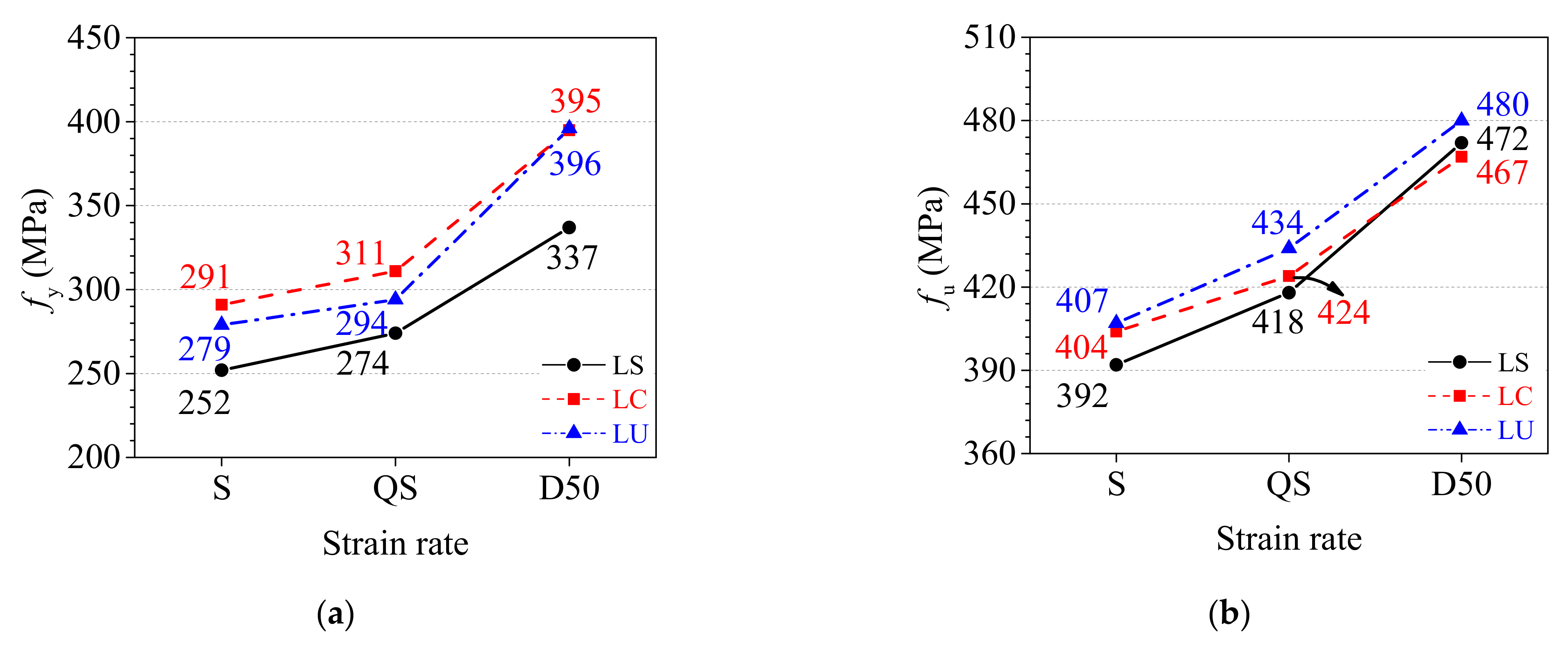
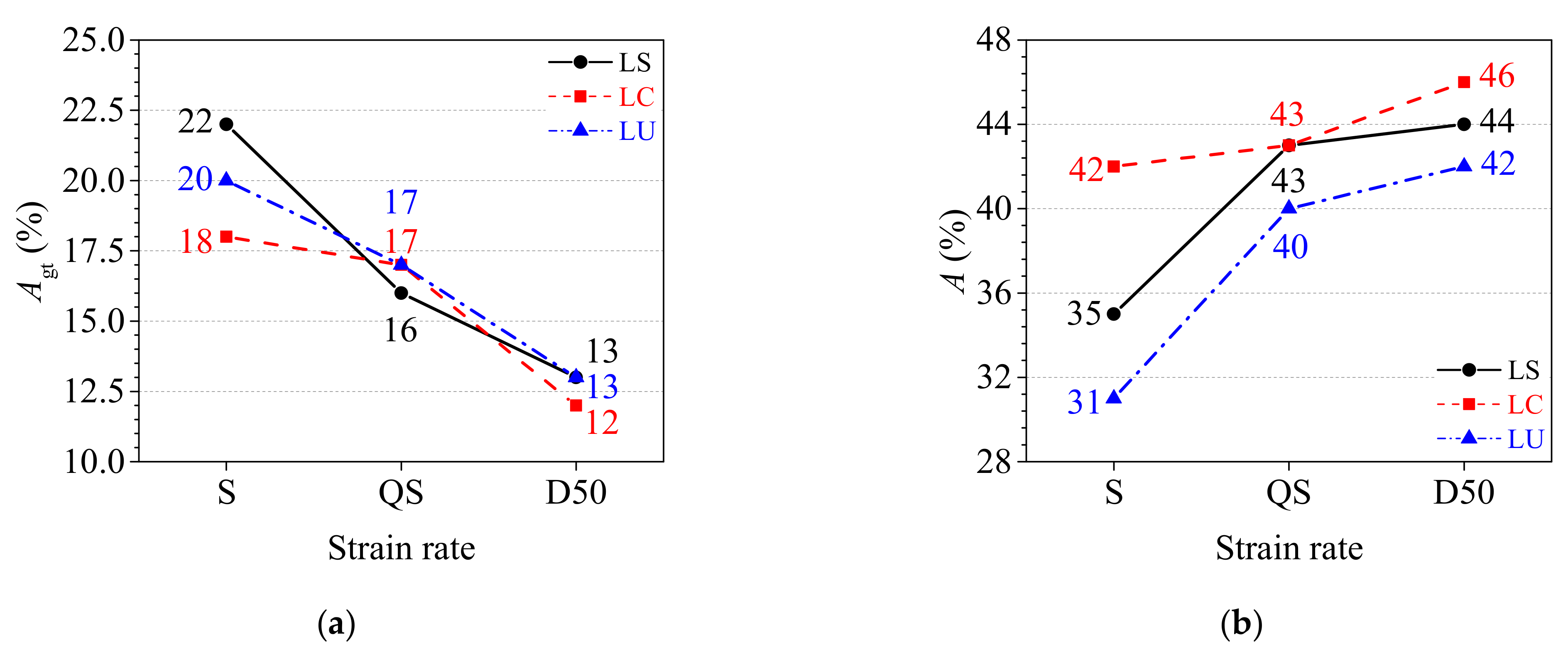
- The cold rolling treatment had little effect on the tensile strength of the TWSP material, compared with its effect on the yield strength. The static (= 0.00025 s−1), quasi-static ( = 0.01 s−1), and dynamic ( = 50 s−1) yield strengths of material at the cross-sectional slope of the rolled TSWP were 10%, 7%, and 15% lower than those of flat TWSP material, respectively. The static, quasi-static, and dynamic yield strengths of material at the cross-sectional center of the rolled TWSP were no more than 6% higher than those of the flat TWSP. The deviations in tensile strengths among material from different sampling locations of the TWSP were no greater than 5%. The cold rolling treatment also improved the deformability of the TWSP material.
- (2)
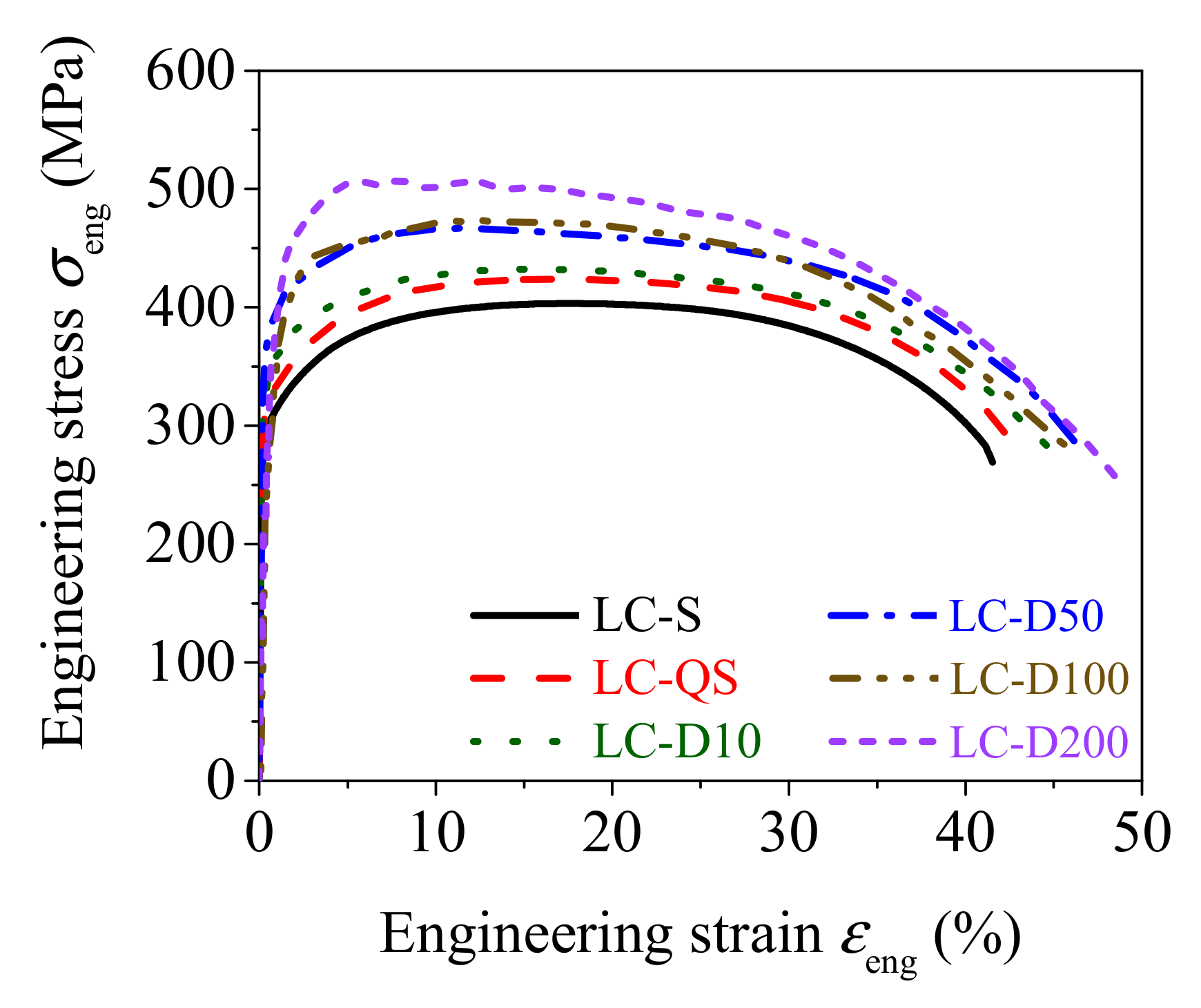
- The strain rate had a stronger effect on the yield strength than the tensile strength of the rolled TWSP material. The quasi-static and dynamic yield strength of the rolled TWSP material were no more than 10% and 36% higher than the static yield strength, respectively. The quasi-static and dynamic tensile strength were increased by no more than 7% and 20% compared with the static tensile strength, respectively. The total percentage extensions at maximum force and the percentage elongations after fracture of the rolled TWSP material decreased and increased as strain rates increased, respectively.
- (3)
- The cross-sectional center of rolled TWSPs is recommended as the representative sampling location for uniaxial tensile tests of rolled TWSP material because the dynamic responses of rolled TWSPs were reasonably captured when the stress–strain curves measured by the specimen extracted from cross-sectional center of rolled TWSP were used in simulation.
- (4)
- The strain rate effects of rolled TWSP material were significantly overestimated by the Cowper–Symonds model with parameters of C = 40 s−1 and p = 5 for strain rates ranging from 0.00025 to 200 s−1, but they were predicted well by the Cowper–Symonds model with parameters C = 4814 s−1 and p = 2.9 recommended in this study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Gabler, H.C.; Gabauer, D.J.; Hampton, C.E. Criteria for Restoration of Longitudinal Barriers; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 2010. [Google Scholar]
- Budzynski, M.; Jamroz, K.; Jelinski, L.; Bruski, D.; Pachocki, L.; Baginski, G. Assessing roadside hybrid energy absorbers using the example of SafeEnd. Materials 2022, 15, 1712. [Google Scholar] [CrossRef] [PubMed]
- Wolny, R.; Bruski, D.; Budzyński, M.; Pachocki, L.; Wilde, K. Influence of a lighting column in the working width of a W-beam barrier on TB51 crash test. Materials 2022, 15, 4926. [Google Scholar] [CrossRef] [PubMed]
- Calle, M.A.G.; Oshiro, R.E.; Alves, M. Ship collision and grounding: Scaled experiments and numerical analysis. Int. J. Impact Eng. 2017, 103, 195–210. [Google Scholar] [CrossRef]
- Heo, Y.; Kunnath, S.K. Sensitivity to constitutive modeling in fiber-based discretization of reinforced concrete members for performance-based seismic evaluation. Adv. Struct. Eng. 2009, 12, 37–51. [Google Scholar] [CrossRef]
- Chen, J.L.; Shu, W.Y.; Li, J.W. Experimental study on dynamic mechanical property of Q235 steel at different strain rates. J. Tongji Univ. Natur. Sci. 2016, 44, 1071–1075. (In Chinese) [Google Scholar] [CrossRef]
- Yin, H.; Xiao, Y.; Wen, G.; Fang, H. Design optimization of a new W-beam guardrail for enhanced highway safety performance. Adv. Eng. Softw. 2017, 112, 154–164. [Google Scholar] [CrossRef]
- Teng, T.L.; Liang, C.L.; Tran, T.T. Development and validation of a finite element model for road safety barrier impact tests. Simulation 2016, 92, 565–578. [Google Scholar] [CrossRef]
- GB/T 2975-2018; Steel and Steel Products—Location and Preparation of Samples and Test Pieces for Mechanical Testing. Standards Press of China: Beijing, China, 2018.
- E8/E8M-16a; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2015.
- GB/T 31439.1-2015; Corrugated Sheet Steel Beams for Road Guardrail—Part 1: W-Beam Guardrail. Standards Press of China: Beijing, China, 2015.
- GB/T 31439.2-2015; Corrugated Sheet STEEL beams for Road Guardrail—Part 2: Thrie-Beam Guardrail. Standards Press of China: Beijing, China, 2015.
- AASHTO M 180-18; Standard Specification for Corrugated Sheet Steel Beams for Highway Guardrail. American Association of State Highway and Transportation Officials: Washington, DC, USA, 2021.
- Oliver, S.; Jones, T.B.; Fourlaris, G. Dual phase versus TRIP strip steels: Comparison of dynamic properties for automotive crash performance. Mater. Sci. Technol. 2007, 23, 423–431. [Google Scholar] [CrossRef]
- Hou, S.; Tan, W.; Zheng, Y.; Han, X.; Li, Q. Optimization design of corrugated beam guardrail based on RBF-MQ surrogate model and collision safety consideration. Adv. Eng. Softw. 2014, 78, 28–40. [Google Scholar] [CrossRef]
- Cowper, G.R.; Symonds, P.S. Strain-Hardening and Strain-Rate Effects in the Impact Loading of Cantilever Beams; Division of Applied Mechanics Report No. 28; Brown University: Providence, RI, USA, 1957. [Google Scholar]
- Jones, N.; Jones, C. Inelastic failure of fully clamped beams and circular plates under impact loading. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2002, 216, 133–149. [Google Scholar] [CrossRef]
- Mortazavi, M.; Heo, Y. Dynamic constitutive model application and validation for offshore structures under dropped object impact loads. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, American Society of Mechanical Engineers, Madrid, Spain, 17–22 June 2018; p. 51227. [Google Scholar] [CrossRef]
- HSE (Health and Safety Executive). Elevated Temperature and High Strain Rate Properties of Offshore Steels; Offshore Technology Report No. OTO-2001-20; Steel Construction Institute: Chicago, IL, USA, 2001. [Google Scholar]
- GB/T 30069.1-2013; Metallic Materials—Tensile Testing at High Strain Rates—Part 1: ELASTIC-Bar-Type Systems. Standards Press of China: Beijing, China, 2013.
- GB/T 30069.2-2016; Metallic Materials—Tensile Testing at High Strain Rates—Part 2: Servo-Hydraulic and Other Test Systems. Standards Press of China: Beijing, China, 2016.
- Wang, W.; Zhang, X.; Chouw, N.; Li, Z.; Shi, Y. Strain rate effect on the dynamic tensile behaviour of flax fiber reinforced polymer. Compos. Struct. 2018, 200, 135–143. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H.; Shi, Y.; Cui, J. The mechanical properties of Polyvinyl Butyral (PVB) at high strain rates. Constr. Build. Mater. 2015, 93, 404–415. [Google Scholar] [CrossRef]
- GB/T 228.1-2010; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Standards Press of China: Beijing, China, 2010.
- Chen, J.L.; Li, J.W.; Li, Z.X. Experiment research on rate-dependent constitutive model of Q420 steel. Constr. Build. Mater. 2017, 153, 816–823. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, Z.; Huo, J.S. Tensile behavior of 400 MPa-grade anti-earthquake hot-rolled ribbed bar (HRB400E) over a wide strain rate range. Constr. Build. Mater. 2020, 249, 118729. [Google Scholar] [CrossRef]
- Guo, G.P.; Ding, C.F.; Ma, S.J.; Wang, H.; Wang, H.P.; Wang, X.; Wei, T.L.; Deng, L.W.; Ning, S.Y.; Du, Z.R.; et al. Mechanical Testing of Aeronautical Materials; China Machine Press: Beijing, China, 2017. [Google Scholar]
- DNV. Determination of Structural Capacity by Non- Linear FE Analysis Methods; Recommended Practice No. DNV-RP-C208; Det Norske Veritas (DNV): Oslo, Norway, 2013. [Google Scholar]
- Cadoni, E.; Fenu, L.; Forni, D. Strain rate behaviour in tension of austenitic stainless steel used for reinforcing bars. Constr. Build. Mater. 2012, 35, 399–407. [Google Scholar] [CrossRef]
- Zeinoddini, M.; Parke, G.A.R.; Harding, J.E. Axially pre-loaded steel tubes subjected to lateral impacts: An experimental study. Int. J. Impact Eng. 2002, 27, 669–690. [Google Scholar] [CrossRef]
- Belytschko, T.; Lin, J.I.; Tsay, C.S. Explicit algorithms for non-linear dynamics of shells. Comput. Meth. Appl. Mech. Eng. 1984, 42, 225–251. [Google Scholar] [CrossRef]
- Atahan, A.O. Finite element simulation of a strong-post W-beam guardrail system. Simulation 2002, 78, 587–599. [Google Scholar] [CrossRef]
- Plaxico, C.A.; Hackett, R.M.; Uddin, W. Simulation of a vehicle impacting a modified thrie-beam guardrail. Transp. Res. Record. 1997, 1599, 1–10. [Google Scholar] [CrossRef]
- Naser, M.Z.; Degtyareva, N.V. Temperature-induced instability in cold-formed steel beams with slotted webs subject to shear. Thin. Wall. Struct. 2019, 136, 333–352. [Google Scholar] [CrossRef]
- LS-DYNA. Keyword User’s Manual Volume 3 Multi-Physics Solvers; Livermore Software Technology Corporation: Livermore, CA, USA, 2018. [Google Scholar]
- Zeinoddini, M.; Harding, J.E.; Parke, G.A.R. Axially pre-loaded steel tubes subjected to lateral impacts (a numerical simulation). Int. J. Impact Eng. 2008, 35, 1267–1279. [Google Scholar] [CrossRef]
- Van Slycken, J.; Verleysen, P.; Degrieck, J.; Samek, L.; De Cooman, B.C. High-strain-rate behavior of low-alloy multiphase aluminium- and silicon-based transformation-induced plasticity steels. Metall. Mater. Trans. A 2006, 37, 1527–1539. [Google Scholar] [CrossRef]
- Staubhammer, K.P.; Murr, L.E. The effect of prior deformation on the residual microstructure of explosively deformed stainless steels. Mater. Sci. Eng. 1980, 44, 97–113. [Google Scholar] [CrossRef]
- Regazzoni, G.; Johnson, J.N.; Follansbee, P.S. Theoretical study of the dynamic tensile test. J. Appl. Mech. 1986, 53, 519–528. [Google Scholar] [CrossRef]
- Symonds, P.S. Survey of Methods of Analysis for Plastic Deformation of Structures under Dynamic Loading; Division of Engineering, Brown University: Providence, RI, USA, 1967. [Google Scholar]
- Hsu, S.S.; Jones, N. Quasi-static and dynamic axial crushing of thin-walled circular stainless steel, mild steel and aluminium alloy tubes. Int. J. Crashworthiness 2004, 9, 195–217. [Google Scholar] [CrossRef]
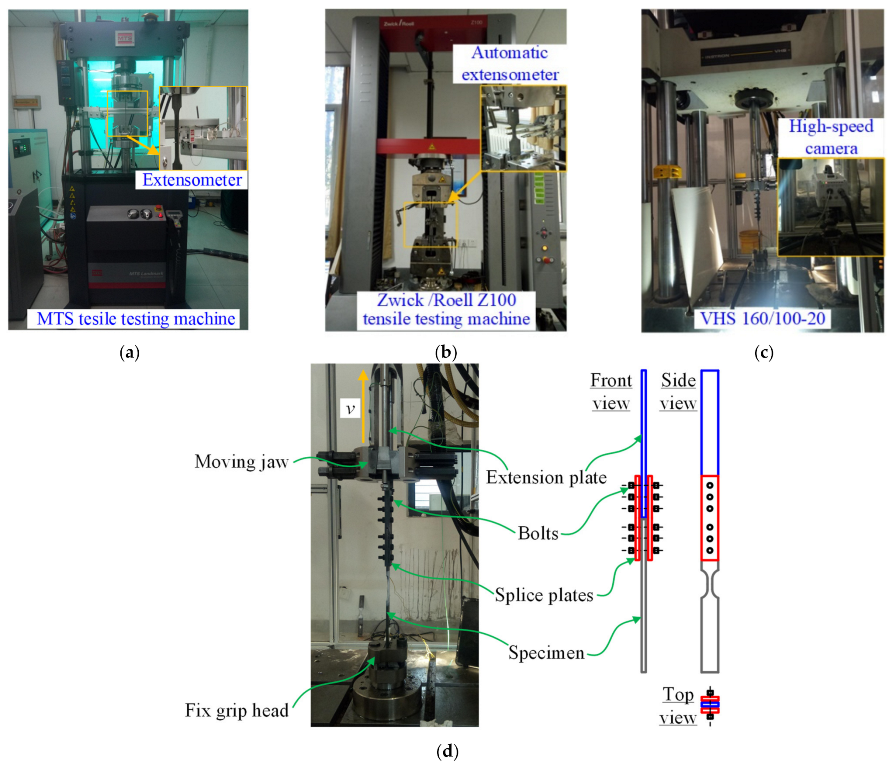


| Tensile Testing Machine | Test Pattern | Load Capacity (kN) | loading Velocity (mm/min) |
|---|---|---|---|
| MTS | static | 100 | 0.001–508 |
| Zwick/Roell Z100 | quasi-static | 100 | 0.0005–1500 |
| Instron VHS 160/100-20 | dynamic | 100 | ≤1,200,000 |
| Strain Rate (s−1) | Static = 0.00025 s−1) | Quasi-Static = 0.01 s−1) | Dynamic = 0.50 s−1) |
|---|---|---|---|
| Slope of rolled TWSP (LS) | LS-S | LS-QS | LS-D50 |
| Center of rolled TWSP (LC) | LC-S | LC-QS | LC-D50 |
| Unrolled flat TWSP (LU) | LU-S | LU-QS | LU-D50 |
| Strain Rates (s−1) | S ( = 0.00025) | QS ( = 0.01) | D50 ( = 0.50) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample Locations | LS | LC | LU | LS | LC | LU | LS | LC | LU | |
| Strength parameters | fy (MPa) | 252 | 291 | 279 | 274 | 311 | 294 | 337 | 395 | 396 |
| fu (Mpa) | 392 | 404 | 407 | 418 | 424 | 434 | 472 | 467 | 480 | |
| ft (Mpa) | 297 | 272 | 300 | 277 | 282 | 305 | 313 | 283 | 297 | |
| Deformation parameters | E (Gpa) | 188 | 243 | 204 | - | - | - | - | - | - |
| Agt (%) | 22 | 18 | 20 | 16 | 17 | 17 | 13 | 12 | 13 | |
| A (%) | 35 | 42 | 31 | 43 | 43 | 40 | 44 | 46 | 42 | |
| Labels of Specimens (s−1) | Tests in Section 3 | Additional Tests | |||||
|---|---|---|---|---|---|---|---|
| LC-S = 0.00025) | LC-QS = 0.01) | LC-D50 = 0.50) | LC-D10 = 10) | LC-D100 = 100) | LC-D200 = 200) | ||
| Strength parameters | fy (MPa) | 291 | 311 | 395 | 353 | 398 | 438 |
| fu (Mpa) | 404 | 424 | 467 | 433 | 475 | 509 | |
| ft (Mpa) | 272 | 282 | 283 | 266 | 248 | 258 | |
| Deformation parameters | Agt (%) | 18 | 17 | 12 | 15 | 12 | 12 |
| A (%) | 42 | 43 | 46 | 45 | 46 | 48 | |
| Labels of Specimens (s−1) | C = 40 s−1, p = 5 | C = 2635 s−1, p = 3.8 | C = 6993 s−1, p = 2.0 | C = 4814 s−1, p = 2.9 |
|---|---|---|---|---|
| LC-S = 0.00025) | 38.32 | 5.97 | 0.08 | 1.30 |
| LC-QS = 0.01) | 57.20 | 6.43 | 21.23 | 17.21 |
| LC-D10 = 10) | 275.24 | 59.68 | 21.38 | 15.54 |
| LC-D50 = 50) | 333.90 | 62.11 | 46.77 | 13.90 |
| LC-D100 = 100) | 402.76 | 100.60 | 45.90 | 48.12 |
| LC-D200 = 200) | 428.69 | 91.12 | 61.22 | 39.19 |
| Average value | 256.02 | 54.32 | 32.76 | 22.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Cheng, X.; Li, Y.; Yang, M.; Zhou, Y. Dynamic Mechanical Properties of Rolled Thin-Walled Steel Plates (TWSPs) Used for W-Beam Guardrails under Low and Medium Strain Rates. Materials 2022, 15, 6504. https://doi.org/10.3390/ma15196504
Liu F, Cheng X, Li Y, Yang M, Zhou Y. Dynamic Mechanical Properties of Rolled Thin-Walled Steel Plates (TWSPs) Used for W-Beam Guardrails under Low and Medium Strain Rates. Materials. 2022; 15(19):6504. https://doi.org/10.3390/ma15196504
Chicago/Turabian StyleLiu, Fangfang, Xiaowei Cheng, Yi Li, Manjuan Yang, and Yujing Zhou. 2022. "Dynamic Mechanical Properties of Rolled Thin-Walled Steel Plates (TWSPs) Used for W-Beam Guardrails under Low and Medium Strain Rates" Materials 15, no. 19: 6504. https://doi.org/10.3390/ma15196504
APA StyleLiu, F., Cheng, X., Li, Y., Yang, M., & Zhou, Y. (2022). Dynamic Mechanical Properties of Rolled Thin-Walled Steel Plates (TWSPs) Used for W-Beam Guardrails under Low and Medium Strain Rates. Materials, 15(19), 6504. https://doi.org/10.3390/ma15196504




