Isogeometric Analysis of Graphene-Reinforced Functionally Gradient Piezoelectric Plates Resting on Winkler Elastic Foundations
Abstract
:1. Introduction
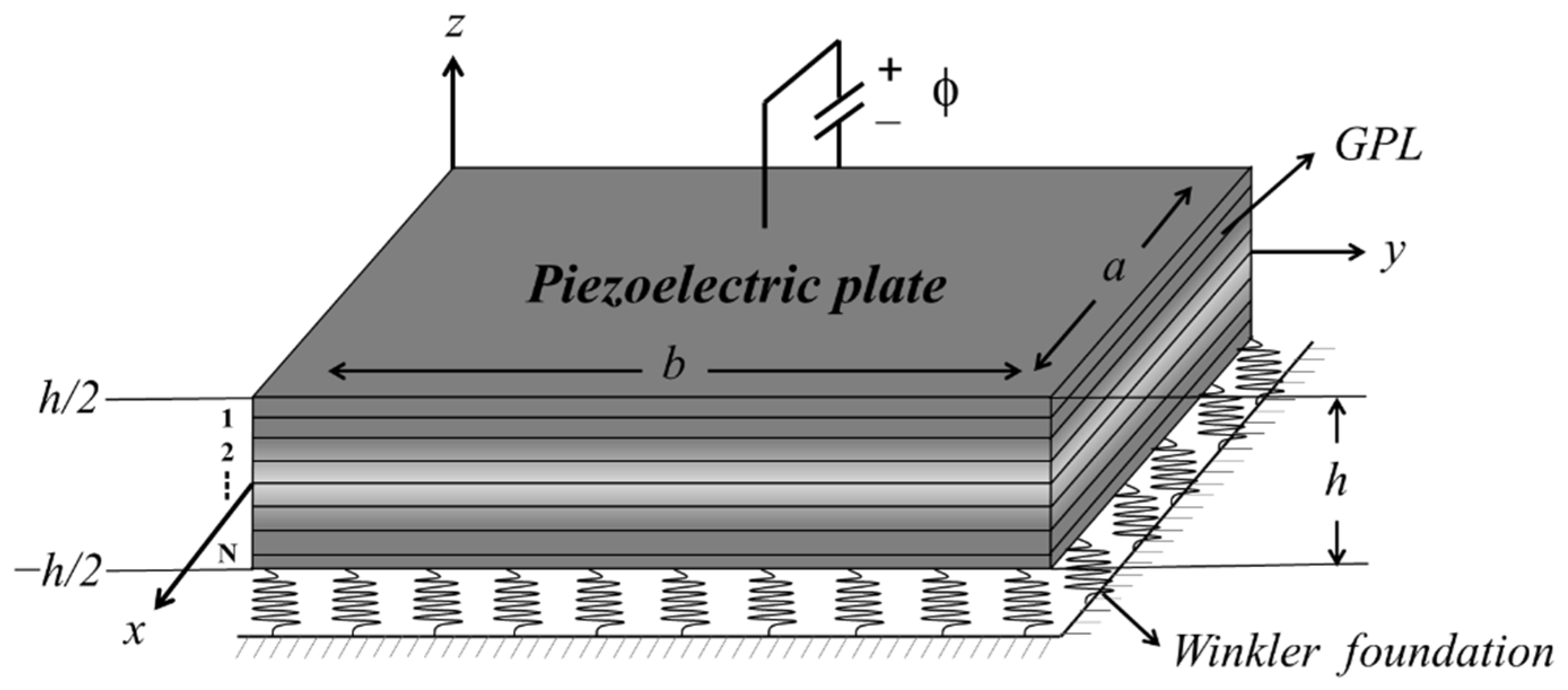
2. Theoretical Formulation
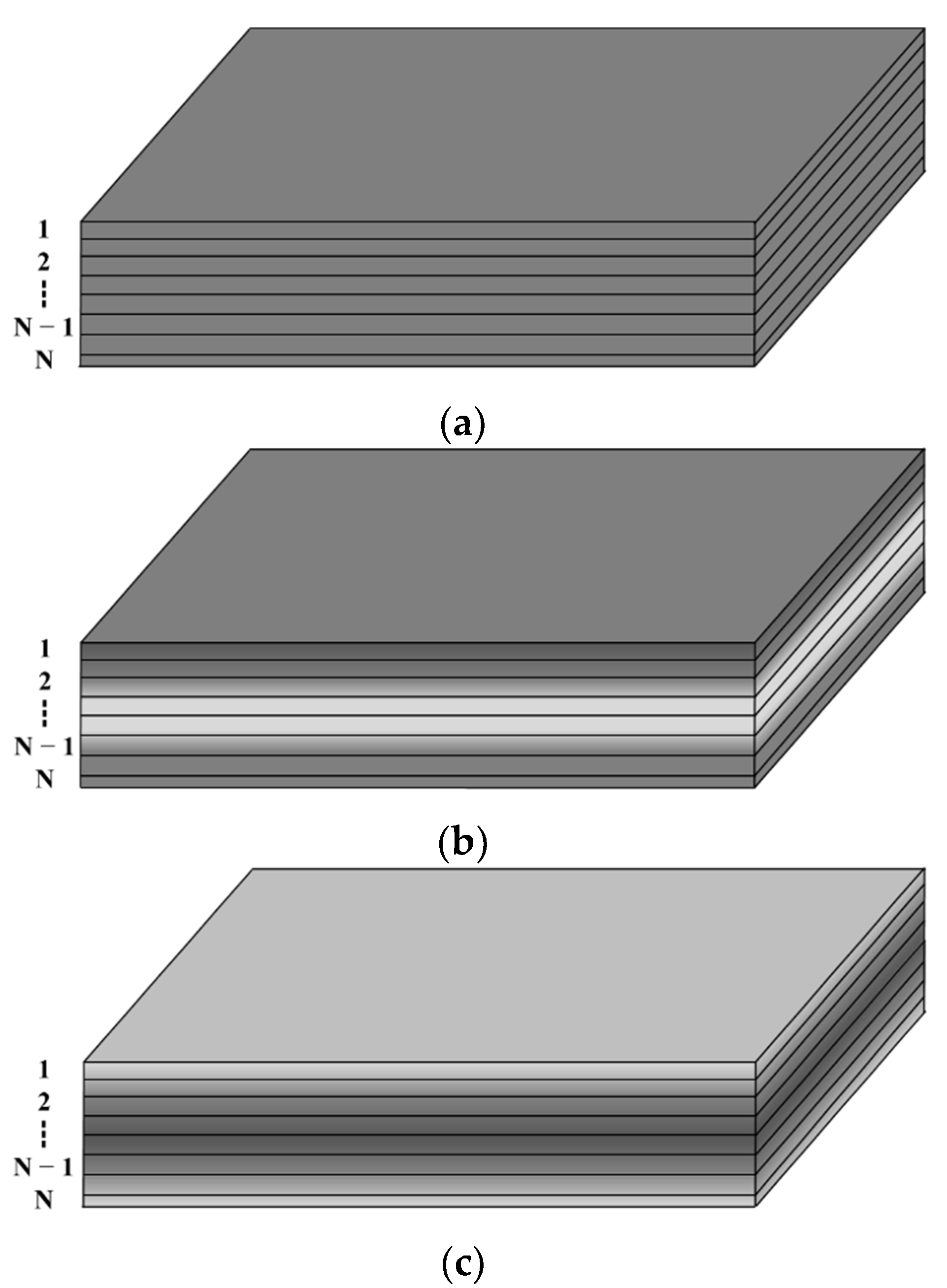
2.1. Material Properties
- The U type:
- The X type:
- The O type:
2.2. Governing Equations for the Refined Plate Theory
2.3. Weak Form
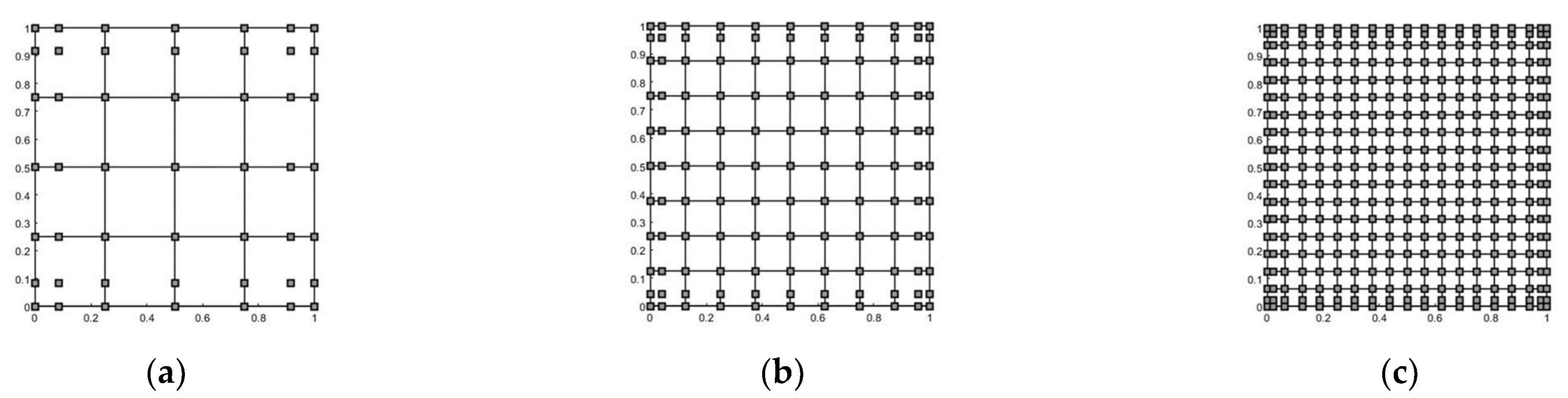
3. Isogeometric Plate Formulation
3.1. NURBS Basis Function
3.2. Approximations of the Displacement Field
3.3. Approximations of the Electric Potential
3.4. Isogeometric FG-GRP Plate Formulation
4. Numerical Investigation
4.1. Verification
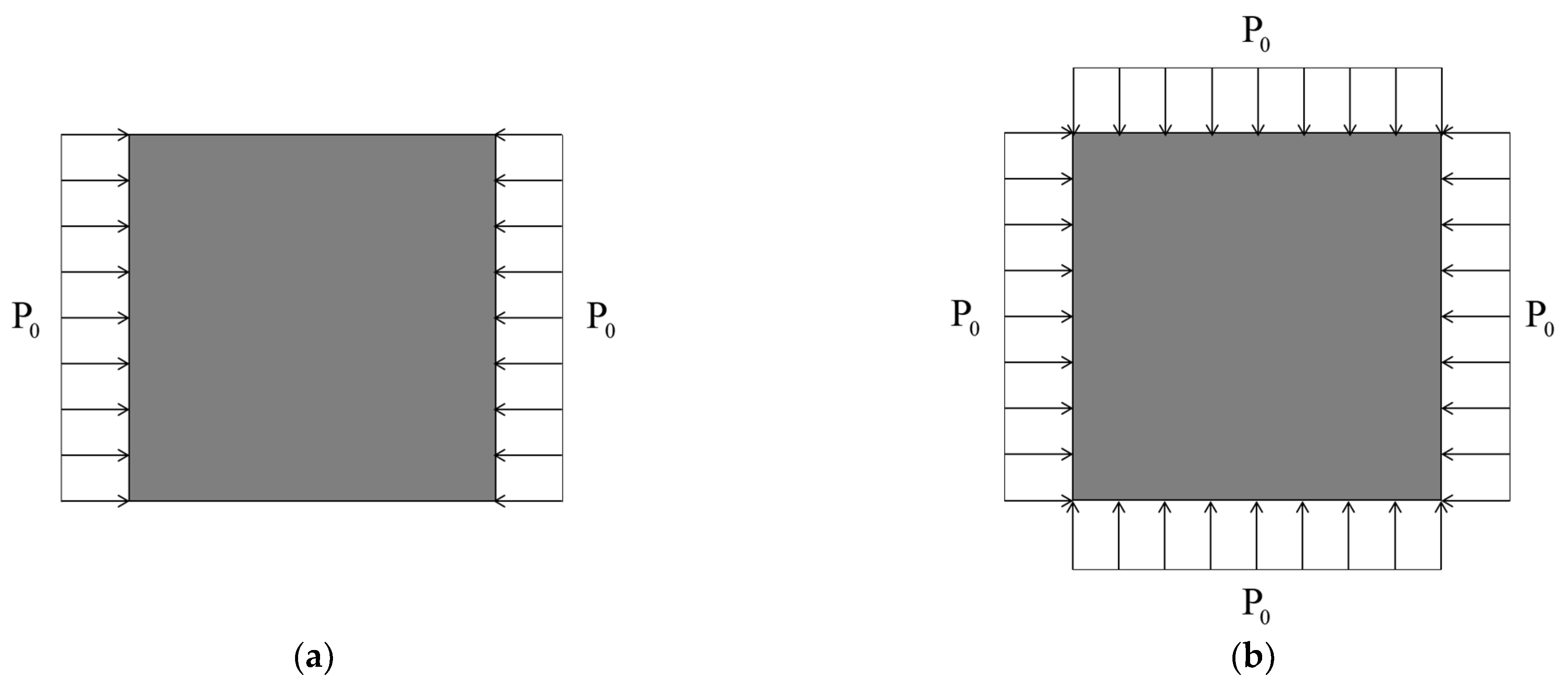
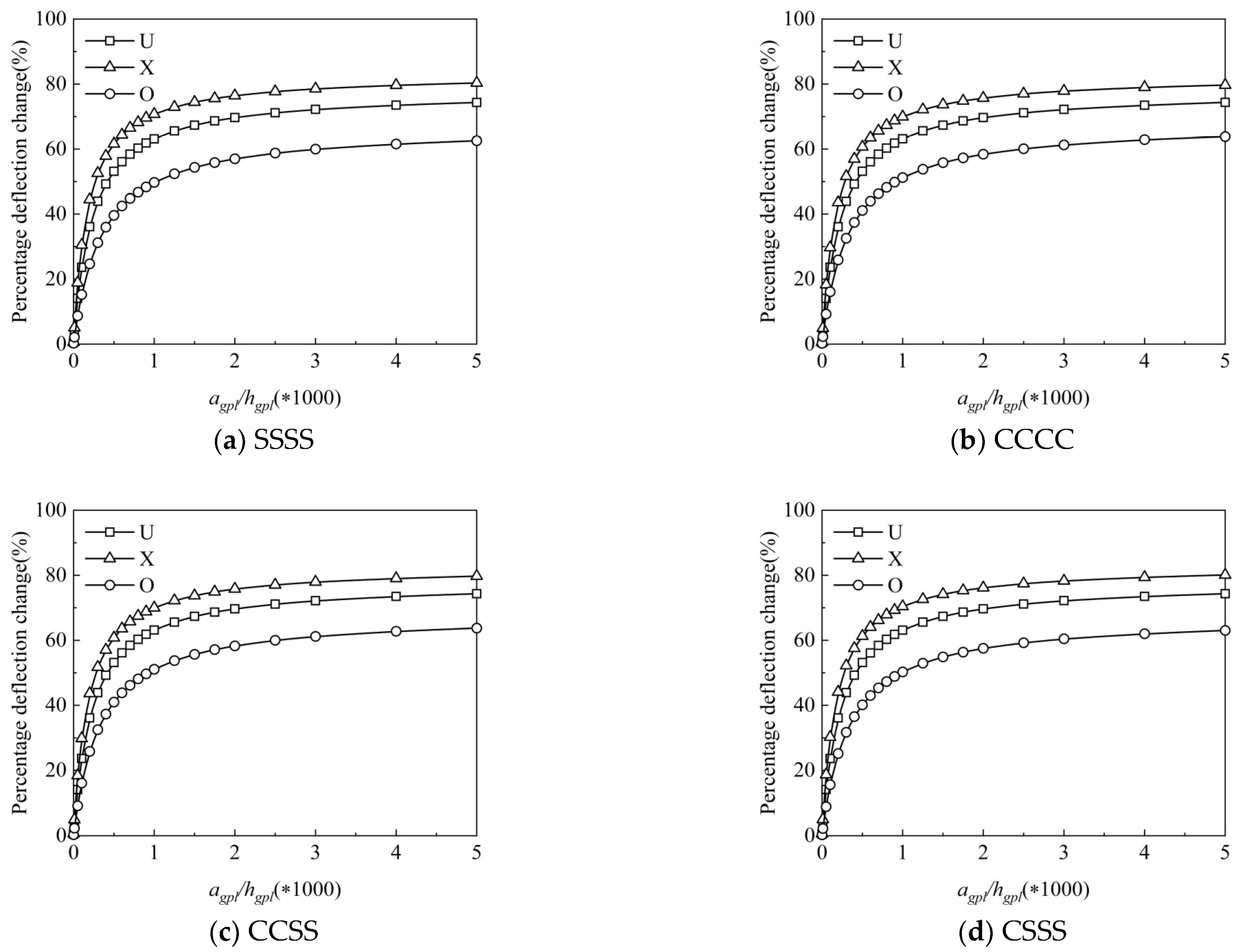
4.2. Static Analysis
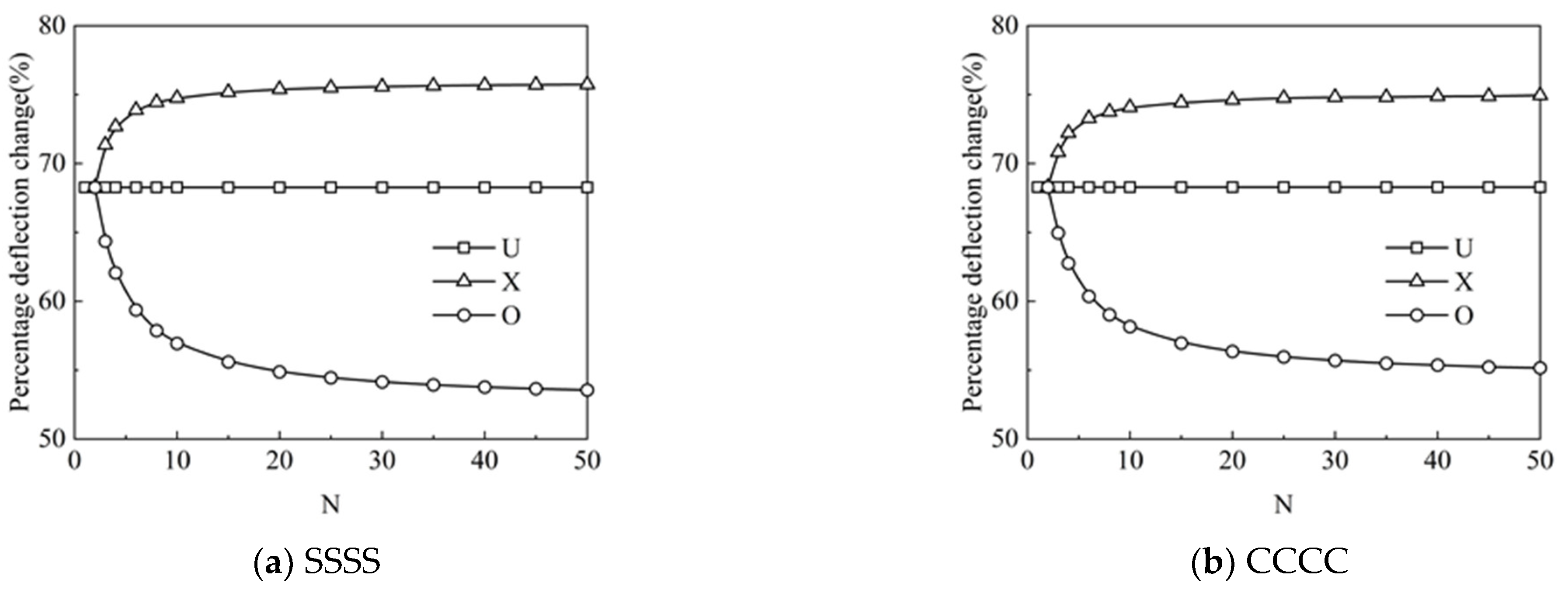
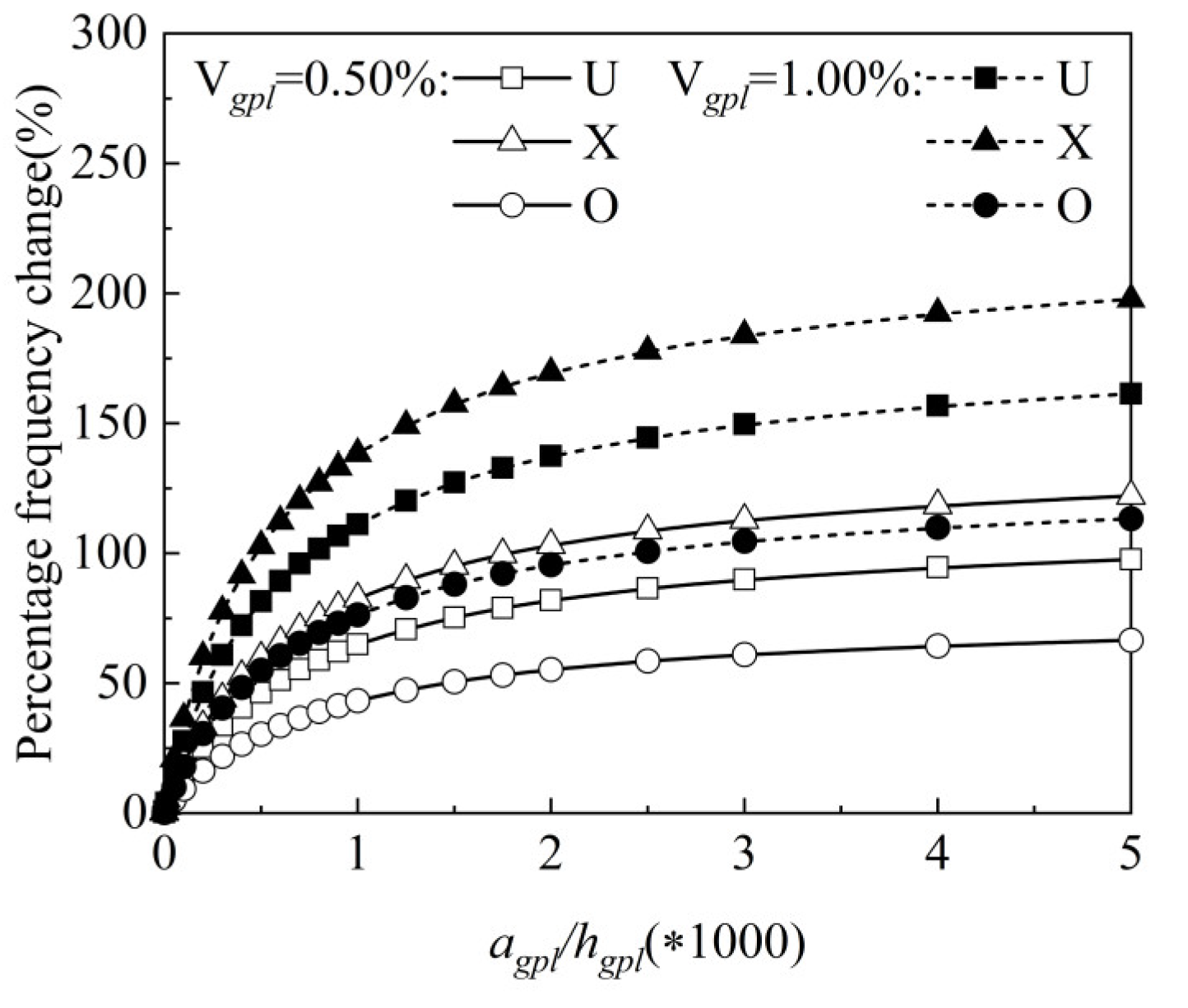
4.3. Vibration Analysis
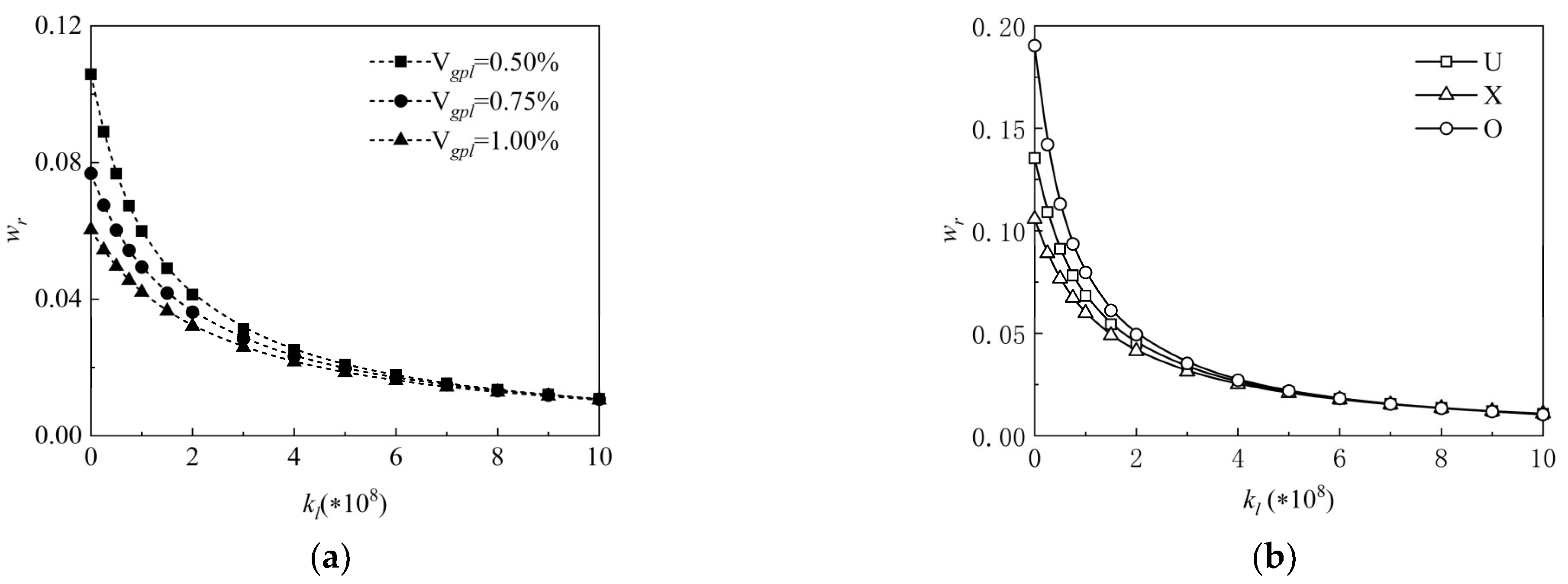
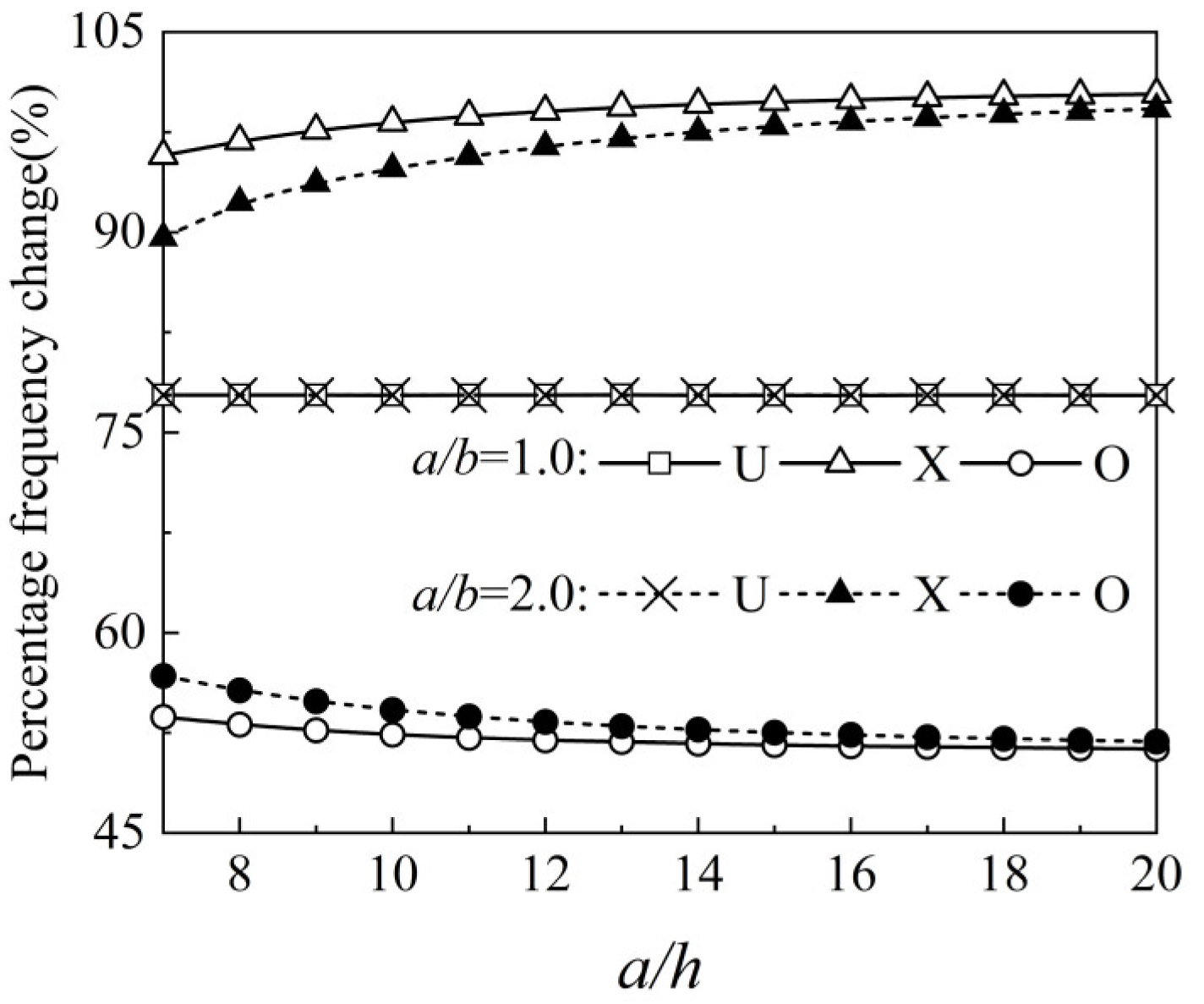
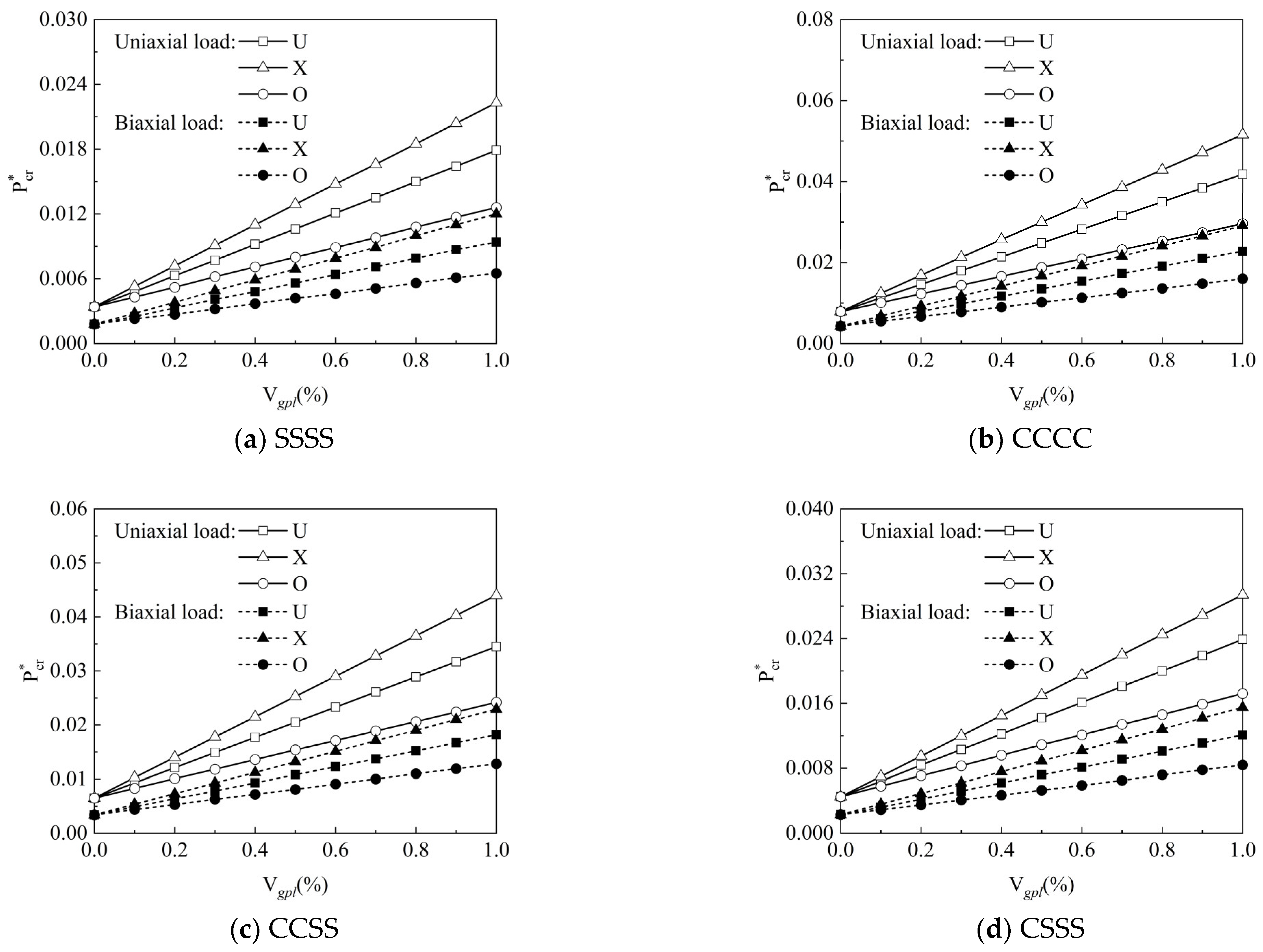
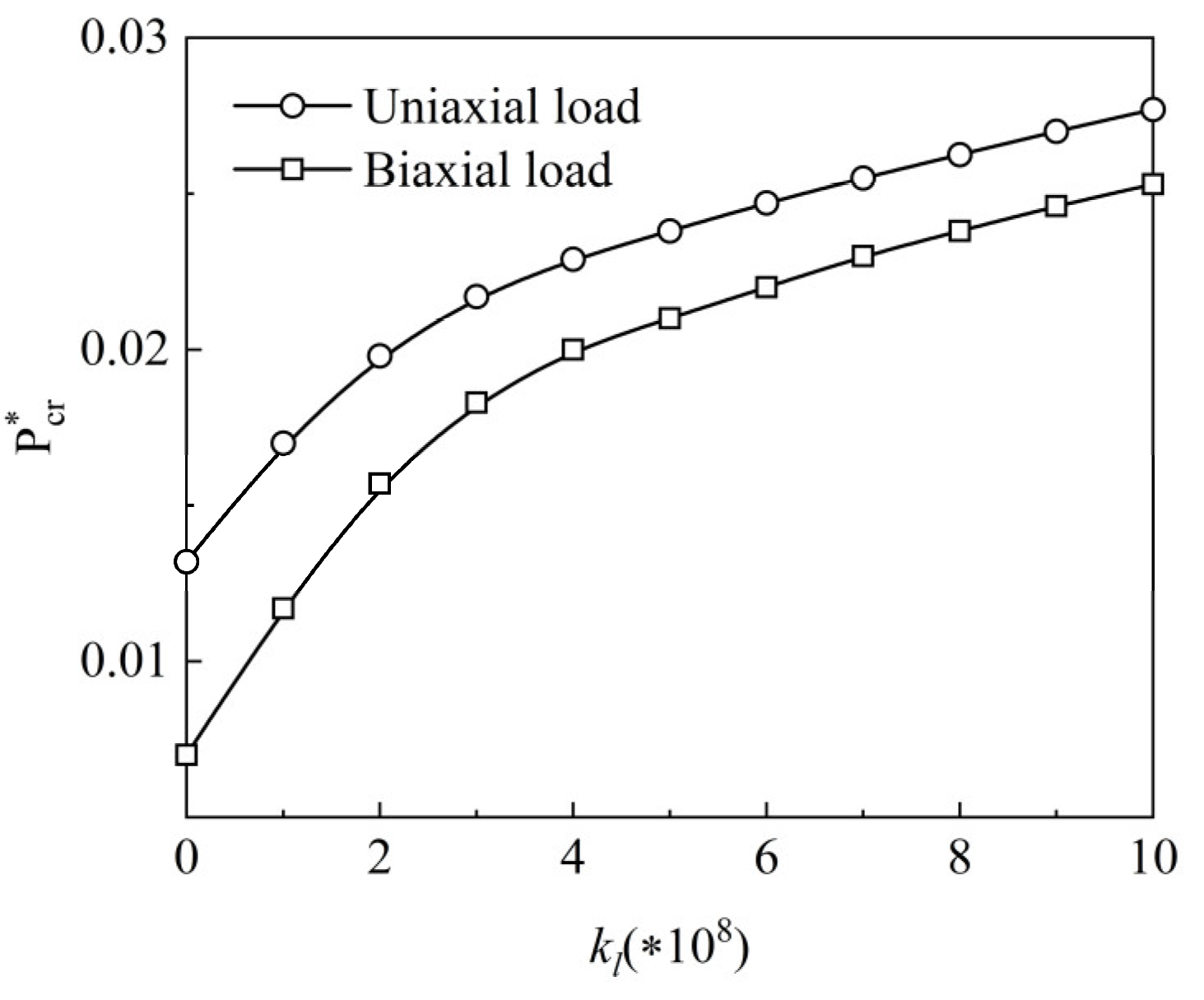
4.4. Buckling Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reddy, J.N. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Cherradi, N.; Kawasaki, A.; Gasik, M. Worldwide Trends in Functional Gradient Materials Research-and-development. Compos. Eng. 1994, 4, 883–894. [Google Scholar] [CrossRef]
- Naebe, M.; Shirvanimoghaddam, K. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 223–245. [Google Scholar] [CrossRef]
- Sobczak, J.J.; Drenchev, L. Metallic Functionally Graded Materials: A Specific Class of Advanced Composites. J. Mater. Sci. Technol. 2013, 29, 297–316. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Abbasipour, M.; Khajavi, R.; Yousefi, A.A.; Yazdanshenas, M.E.; Razaghian, F. The piezoelectric response of electrospun PVDF nanofibers with graphene oxide, graphene, and halloysite nanofillers: A comparative study. J. Mater. Sci. Mater. Electron. 2017, 28, 15942–15952. [Google Scholar] [CrossRef]
- Hu, Y.-C.; Hsu, W.-L.; Wang, Y.-T.; Ho, C.-T.; Chang, P.-Z. Enhance the pyroelectricity of polyvinylidene fluoride by graphene-oxide doping. Sensors 2014, 14, 6877–6890. [Google Scholar] [CrossRef]
- Maity, N.; Mandal, A.; Nandi, A.K. Hierarchical nanostructured polyaniline functionalized graphene/poly(vinylidene fluoride) composites for improved dielectric performances. Polymer 2016, 103, 83–97. [Google Scholar] [CrossRef]
- Lee, J.K.; Song, S.; Kim, B. Functionalized graphene sheets-epoxy based nanocomposite for cryotank composite application. Polym. Compos. 2012, 33, 1263–1273. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed graphene platelets (GPLs). Compos. Part B Eng. 2017, 110, 132–140. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, A.; Yang, J.; Lai, S.K.; Lv, J.; Fu, J.J.M.A. Analytical Prediction for Nonlinear Buckling of Elastically Supported FG-GPLRC Arches under a Central Point Load. Materials 2021, 14, 2026. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M.; Rabczuk, T. Nonlinear bending of functionally graded porous micro/nano-beams reinforced with graphene platelets based upon nonlocal strain gradient theory. Compos. Struct. 2018, 186, 68–78. [Google Scholar] [CrossRef]
- Li, X.; Song, M.; Yang, J.; Kitipornchai, S. Primary and secondary resonances of functionally graded graphene platelet-reinforced nanocomposite beams. Nonlinear Dyn. 2018, 95, 1807–1826. [Google Scholar] [CrossRef]
- Song, M.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2017, 159, 579–588. [Google Scholar] [CrossRef]
- Song, M.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Wang, X.; Zhao, Z.; Romero, C.S.; Yang, J. Nonlinear free vibration of graphene platelets (GPLs)/polymer dielectric beam. Smart Mater. Struct. 2019, 28, 55013. [Google Scholar] [CrossRef]
- Yang, B.; Mei, J.; Chen, D.; Yu, F.; Yang, J. 3D thermo-mechanical solution of transversely isotropic and functionally graded graphene reinforced elliptical plates. Compos. Struct. 2018, 184, 1040–1048. [Google Scholar] [CrossRef]
- Liu, D.Y.; Chen, D.; Yang, J.; Kitipornchai, S. Buckling and free vibration of axially functionally graded graphene reinforced nanocomposite beams. Eng. Struct. 2021, 249, 113327. [Google Scholar] [CrossRef]
- Li, C.; Zheng, S.; Chen, D. Size-dependent isogeometric analysis of bi-directional functionally graded microbeams reinforced by graphene nanoplatelets. Mech. Based Des. Struct. Mach. 2022, 1–19. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, R.; Lebrun, L.; Anderson, D.; Shrout, T.R. Piezoelectric materials for high power, high temperature applications. Mater. Lett. 2005, 59, 3471–3475. [Google Scholar] [CrossRef]
- Chen, X.L.; Zhao, Z.Y.; Liew, K.M. Stability of piezoelectric FGM rectangular plates subjected to non-uniformly distributed load, heat and voltage. Adv. Eng. Softw. 2008, 39, 121–131. [Google Scholar] [CrossRef]
- He, X.Q.; Ng, T.Y.; Sivashanker, S.; Liew, K.M. Active control of FGM plates with integrated piezoelectric sensors and actuators. Int. J. Solids Struct. 2001, 38, 1641–1655. [Google Scholar] [CrossRef]
- Liew, K.M.; He, X.Q.; Ng, T.Y.; Sivashanker, S. Active control of FGM plates subjected to a temperature gradient: Modelling via finite element method based on FSDT. Int. J. Numer. Methods Eng. 2001, 52, 1253–1271. [Google Scholar] [CrossRef]
- Layek, R.K.; Samanta, S.; Chatterjee, D.P.; Nandi, A.K. Physical and mechanical properties of poly (methyl methacrylate)-functionalized graphene/poly(vinylidine fluoride) nanocomposites: Piezoelectric β polymorph formation. Polymer 2010, 51, 5846–5856. [Google Scholar] [CrossRef]
- Abolhasani, M.M.; Shirvanimoghaddam, K.; Naebe, M. PVDF/graphene composite nanofibers with enhanced piezoelectric performance for development of robust nanogenerators. Compos. Sci. Technol. 2017, 138, 49–56. [Google Scholar] [CrossRef]
- Mao, J.-J.; Zhang, W. Linear and nonlinear free and forced vibrations of graphene reinforced piezoelectric composite plate under external voltage excitation. Compos. Struct. 2018, 203, 551–565. [Google Scholar] [CrossRef]
- Mao, J.-J.; Zhang, W. Buckling and post-buckling analyses of functionally graded graphene reinforced piezoelectric plate subjected to electric potential and axial forces. Compos. Struct. 2019, 216, 392–405. [Google Scholar] [CrossRef]
- Mao, J.J.; Lu, H.M.; Zhang, W.; Lai, S.K. Vibrations of graphene nanoplatelet reinforced functionally gradient piezoelectric composite microplate based on nonlocal theory. Compos. Struct. 2020, 236, 111813. [Google Scholar] [CrossRef]
- Ghabussi, A.; Ashrafi, N.; Shavalipour, A.; Hosseinpour, A.; Habibi, M.; Moayedi, H.; Babaei, B.; Safarpour, H. Free vibration analysis of an electro-elastic GPLRC cylindrical shell surrounded by viscoelastic foundation using modified length-couple stress parameter. Mech. Based Des. Struct. Mach. 2019, 49, 738–762. [Google Scholar] [CrossRef]
- Yang, Z.; Feng, C.; Yang, J.; Wang, Y.; Lv, J.; Liu, A.; Fu, J. Technology Geometrically nonlinear buckling of graphene platelets reinforced dielectric composite (GPLRDC) arches with rotational end restraints. Aerosp. Sci. Technol. 2020, 107, 106326. [Google Scholar] [CrossRef]
- Fu, Y.; Tang, X.; Jin, Q.; Wu, Z.J.M. An Alternative Electro-Mechanical Finite Formulation for Functionally Graded Graphene-Reinforced Composite Beams with Macro-Fiber Composite Actuator. Materials 2021, 14, 7802. [Google Scholar] [CrossRef]
- Hussein, O.S.; Mulani, S.B. Multi-dimensional optimization of functionally graded material composition using polynomial expansion of the volume fraction. Struct. Multidiscip. Optim. 2017, 56, 271–284. [Google Scholar] [CrossRef]
- Fakhari, V.; Ohadi, A. Nonlinear vibration control of functionally graded plate with piezoelectric layers in thermal environment. J. Vib. Control. 2011, 17, 449–469. [Google Scholar] [CrossRef]
- Fakhari, V.; Ohadi, A.; Yousefian, P. Nonlinear free and forced vibration behavior of functionally graded plate with piezoelectric layers in thermal environment. Compos. Struct. 2011, 93, 2310–2321. [Google Scholar] [CrossRef]
- Nourmohammadi, H.; Behjat, B. Geometrically nonlinear analysis of functionally graded piezoelectric plate using mesh-free RPIM. Eng. Anal. Bound. Elem. 2019, 99, 131–141. [Google Scholar] [CrossRef]
- Senthilnathan, N.R.; Lim, S.P.; Lee, K.H.; Chow, S.T. Buckling of Shear-Deformable Plates. AIAA J. 1987, 25, 1268–1271. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Nguyen, T.N.; Abdel-Wahab, M.; Bordas, S.P.A.; Nguyen-Xuan, H.; Vo, T.P. A refined quasi-3D isogeometric analysis for functionally graded microplates based on the modified couple stress theory. Comput. Methods Appl. Mech. Eng. 2017, 313, 904–940. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Sun, F.L.; Dong, C.Y.; Yang, H.S. Isogeometric boundary element method for crack propagation based on Bézier extraction of NURBS. Eng. Anal. Bound. Elem. 2019, 99, 76–88. [Google Scholar] [CrossRef]
- Uhm, T.-K.; Youn, S.-K. T-spline finite element method for the analysis of shell structures. Int. J. Numer. Methods Eng. 2009, 80, 507–536. [Google Scholar] [CrossRef]
- Kiani, Y. Isogeometric large amplitude free vibration of graphene reinforced laminated plates in thermal environment using NURBS formulation. Comput. Methods Appl. Mech. Eng. 2018, 332, 86–101. [Google Scholar] [CrossRef]
- Kiani, Y. NURBS-based isogeometric thermal postbuckling analysis of temperature dependent graphene reinforced composite laminated plates. Thin-Walled Struct. 2018, 125, 211–219. [Google Scholar] [CrossRef]
- Li, K.; Wu, D.; Chen, X.; Cheng, J.; Liu, Z.; Gao, W.; Liu, M. Isogeometric Analysis of functionally graded porous plates reinforced by graphene platelets. Compos. Struct. 2018, 204, 114–130. [Google Scholar] [CrossRef]
- Liu, T.; Li, C.; Wang, C.; Lai, J.W.; Cheong, K.H. A Simple-FSDT-Based Isogeometric Method for Piezoelectric Functionally Graded Plates. Mathematics 2020, 8, 2177. [Google Scholar] [CrossRef]
- Phung-Van, P.; De Lorenzis, L.; Thai, C.H.; Abdel-Wahab, M.; Nguyen-Xuan, H. Analysis of laminated composite plates integrated with piezoelectric sensors and actuators using higher-order shear deformation theory and isogeometric finite elements. Comput. Mater. Sci. 2015, 96, 495–505. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Wang, S.Y. A finite element model for the static and dynamic analysis of a piezoelectric bimorph. Int. J. Solids Struct. 2004, 41, 4075–4096. [Google Scholar] [CrossRef]
- Shojaee, S.; Valizadeh, N. NURBS-based isogeometric analysis for thin plate problems. Struct. Eng. Mech. 2012, 41, 617–632. [Google Scholar] [CrossRef]


| BC | Method | ω | |||
|---|---|---|---|---|---|
| Mode 1 | Mode 2 | Uniaxial | Biaxial | ||
| SSSS | IGA (7 × 7) | 0.9777 | 2.552 | 0.0097 | 0.0054 |
| IGA (11 × 11) | 0.9789 | 2.337 | 0.0106 | 0.0056 | |
| IGA (19 × 19) | 0.9789 | 2.337 | 0.0106 | 0.0056 | |
| Mao et al. [30,31] | 0.9789 | 2.337 | 0.0106 | 0.0056 | |
| CCCC | IGA (7 × 7) | 1.6728 | 3.2265 | 0.0246 | 0.0133 |
| IGA (11 × 11) | 1.6714 | 3.1905 | 0.0248 | 0.0135 | |
| IGA (19 × 19) | 1.6714 | 3.1905 | 0.0248 | 0.0135 | |
| Mao et al. [30,31] | 1.6716 | 3.1906 | 0.0248 | 0.0135 | |
| kl | BC | |||
|---|---|---|---|---|
| SSSS | SCSC | CSSS | ||
| 0 | Shojaee et al. [52] | 0.0040624 | 0.0019172 | 0.0028001 |
| FSDT | 0.0040665 | 0.0019205 | 0.0028000 | |
| RPT | 0.0040626 | 0.0019172 | 0.0027971 | |
| 5 | Shojaee et al. [52] | 0.0040097 | 0.0019053 | 0.0027602 |
| FSDT | 0.0040254 | 0.0019116 | 0.0027804 | |
| RPT | 0.0040215 | 0.0019083 | 0.0027775 | |
| 100 | Shojaee et al. [52] | 0.0032137 | 0.0017050 | 0.0023522 |
| FSDT | 0.0033740 | 0.0017565 | 0.0024524 | |
| RPT | 0.0033707 | 0.0017533 | 0.0024498 | |
| BC | GPL Patterns | Vgpl (%) | ||||
|---|---|---|---|---|---|---|
| 0 | 0.25 | 0.5 | 0.75 | |||
| SSSS | U | Mao et al. [30] | 0.551 | 0.794 | 0.9791 | 1.135 |
| FSDT | 0.551 | 0.7937 | 0.9789 | 1.1349 | ||
| RPT | 0.551 | 0.7937 | 0.9789 | 1.1349 | ||
| 44.2% | 77.8% | 106.1% | ||||
| X | Mao et al. [30] | 0.551 | 0.8678 | 1.0974 | 1.2875 | |
| FSDT | 0.5506 | 0.8648 | 1.0914 | 1.279 | ||
| RPT | 0.5506 | 0.8648 | 1.0914 | 1.279 | ||
| 57.1% | 98.2% | 132.3% | ||||
| O | Mao et al. [30] | 0.551 | 0.7108 | 0.8407 | 0.9534 | |
| FSDT | 0.5506 | 0.7099 | 0.8389 | 0.9508 | ||
| RPT | 0.5506 | 0.7099 | 0.8389 | 0.9508 | ||
| 28.9% | 52.4% | 72.7% | ||||
| CCCC | U | Mao et al. [30] | 0.9405 | 1.3554 | 1.6716 | 1.938 |
| FSDT | 0.94 | 1.3552 | 1.6714 | 1.9379 | ||
| RPT | 0.94 | 1.3552 | 1.6714 | 1.9379 | ||
| 44.2% | 77.8% | 106.2% | ||||
| X | Mao et al. [30] | 0.9405 | 1.4653 | 1.8468 | 2.1632 | |
| FSDT | 0.94 | 1.4669 | 1.8494 | 2.1666 | ||
| RPT | 0.94 | 1.4669 | 1.8494 | 2.1666 | ||
| 56.1% | 96.7% | 130.5% | ||||
| O | Mao et al. [30] | 0.9405 | 1.2257 | 1.4576 | 1.6562 | |
| FSDT | 0.94 | 1.2243 | 1.4523 | 1.6493 | ||
| RPT | 0.94 | 1.2243 | 1.4523 | 1.6493 | ||
| 30.2% | 54.5% | 75.5% | ||||
| Load Type | GPL Patterns | Vgpl (%) | ||||
|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.6 | 0.8 | |||
| Uniaxial | U | Mao et al. [31] | 0.0034 | 0.0063 | 0.0122 | 0.0151 |
| FSDT | 0.0034 | 0.0063 | 0.0122 | 0.0151 | ||
| RPT | 0.0034 | 0.0063 | 0.0121 | 0.0150 | ||
| 185.3% | 355.9% | 441.2% | ||||
| X | Mao et al. [31] | 0.0034 | 0.0073 | 0.0151 | 0.0190 | |
| FSDT | 0.0034 | 0.0073 | 0.0151 | 0.0190 | ||
| RPT | 0.0034 | 0.0072 | 0.0148 | 0.0185 | ||
| 211.8% | 435.3% | 544.1% | ||||
| O | Mao et al. [31] | 0.0034 | 0.0053 | 0.0089 | 0.0108 | |
| FSDT | 0.0034 | 0.0053 | 0.0089 | 0.0108 | ||
| RPT | 0.0034 | 0.0052 | 0.0089 | 0.0108 | ||
| 152.9% | 261.8% | 317.6% | ||||
| Biaxial | U | Mao et al. [31] | 0.0018 | 0.0033 | 0.0063 | 0.0079 |
| FSDT | 0.0018 | 0.0033 | 0.0063 | 0.0079 | ||
| RPT | 0.0018 | 0.0033 | 0.0064 | 0.0079 | ||
| 183.3% | 355.6% | 438.9% | ||||
| X | Mao et al. [31] | 0.0018 | 0.0039 | 0.0080 | 0.0101 | |
| FSDT | 0.0018 | 0.0039 | 0.0080 | 0.0101 | ||
| RPT | 0.0018 | 0.0038 | 0.0079 | 0.0100 | ||
| 211.1% | 438.9% | 555.6% | ||||
| O | Mao et al. [31] | 0.0018 | 0.0027 | 0.0046 | 0.0055 | |
| FSDT | 0.0018 | 0.0027 | 0.0046 | 0.0055 | ||
| RPT | 0.0018 | 0.0027 | 0.0046 | 0.0056 | ||
| 150.0% | 255.6% | 311.1% | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Zheng, S.; Chen, D. Isogeometric Analysis of Graphene-Reinforced Functionally Gradient Piezoelectric Plates Resting on Winkler Elastic Foundations. Materials 2022, 15, 5727. https://doi.org/10.3390/ma15165727
Liang Y, Zheng S, Chen D. Isogeometric Analysis of Graphene-Reinforced Functionally Gradient Piezoelectric Plates Resting on Winkler Elastic Foundations. Materials. 2022; 15(16):5727. https://doi.org/10.3390/ma15165727
Chicago/Turabian StyleLiang, Yanan, Shijie Zheng, and Dejin Chen. 2022. "Isogeometric Analysis of Graphene-Reinforced Functionally Gradient Piezoelectric Plates Resting on Winkler Elastic Foundations" Materials 15, no. 16: 5727. https://doi.org/10.3390/ma15165727
APA StyleLiang, Y., Zheng, S., & Chen, D. (2022). Isogeometric Analysis of Graphene-Reinforced Functionally Gradient Piezoelectric Plates Resting on Winkler Elastic Foundations. Materials, 15(16), 5727. https://doi.org/10.3390/ma15165727






