Symmetric Engineered High Polarization-Insensitive Double Negative Metamaterial Reflector for Gain and Directivity Enhancement of Sub-6 GHz 5G Antenna
Abstract
1. Introduction
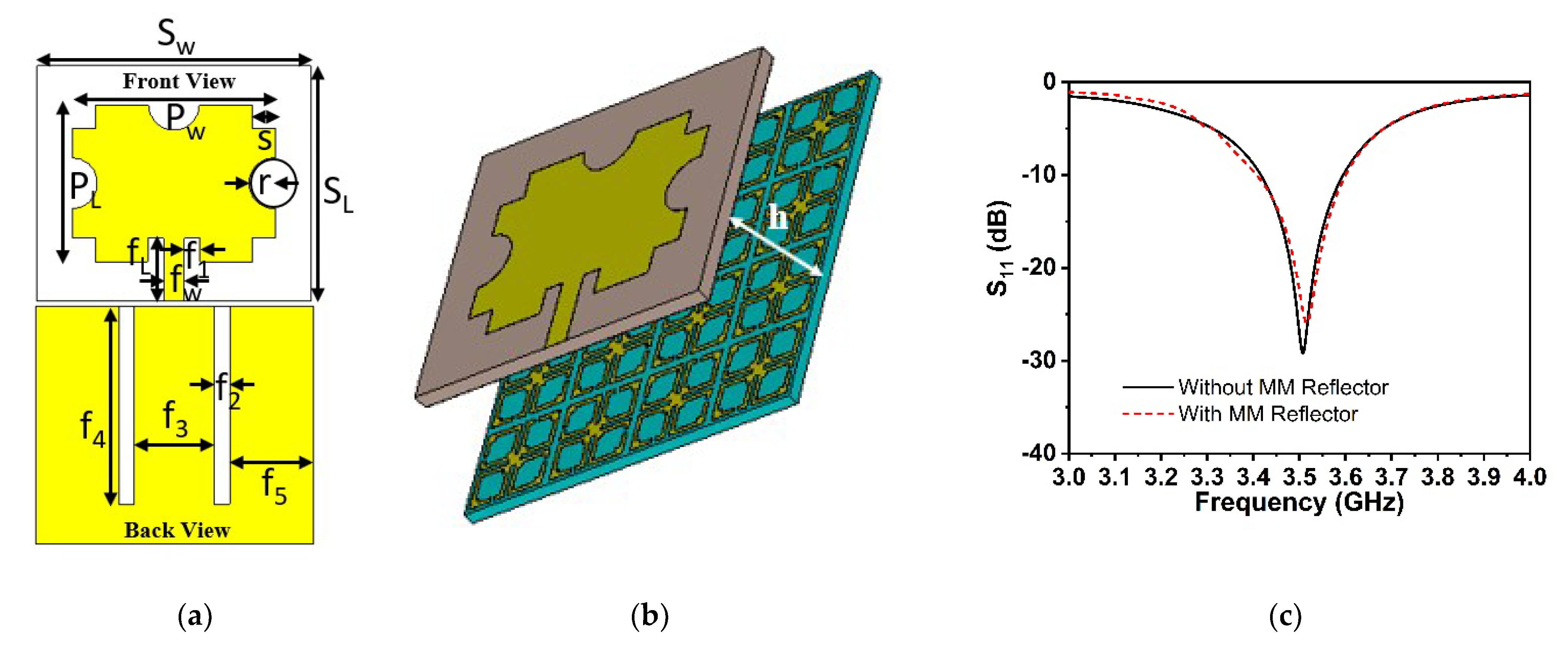
2. MM Design Methodology and Simulation Technique
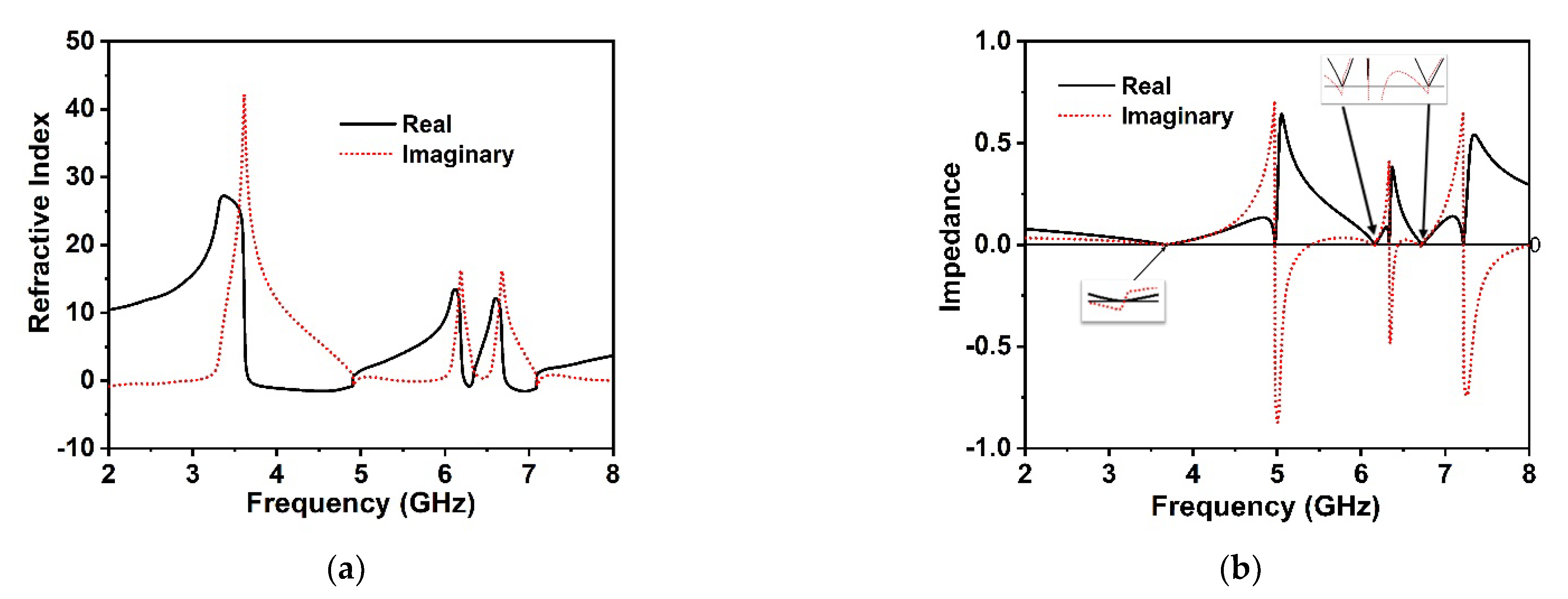
3. Unit Cell Performance
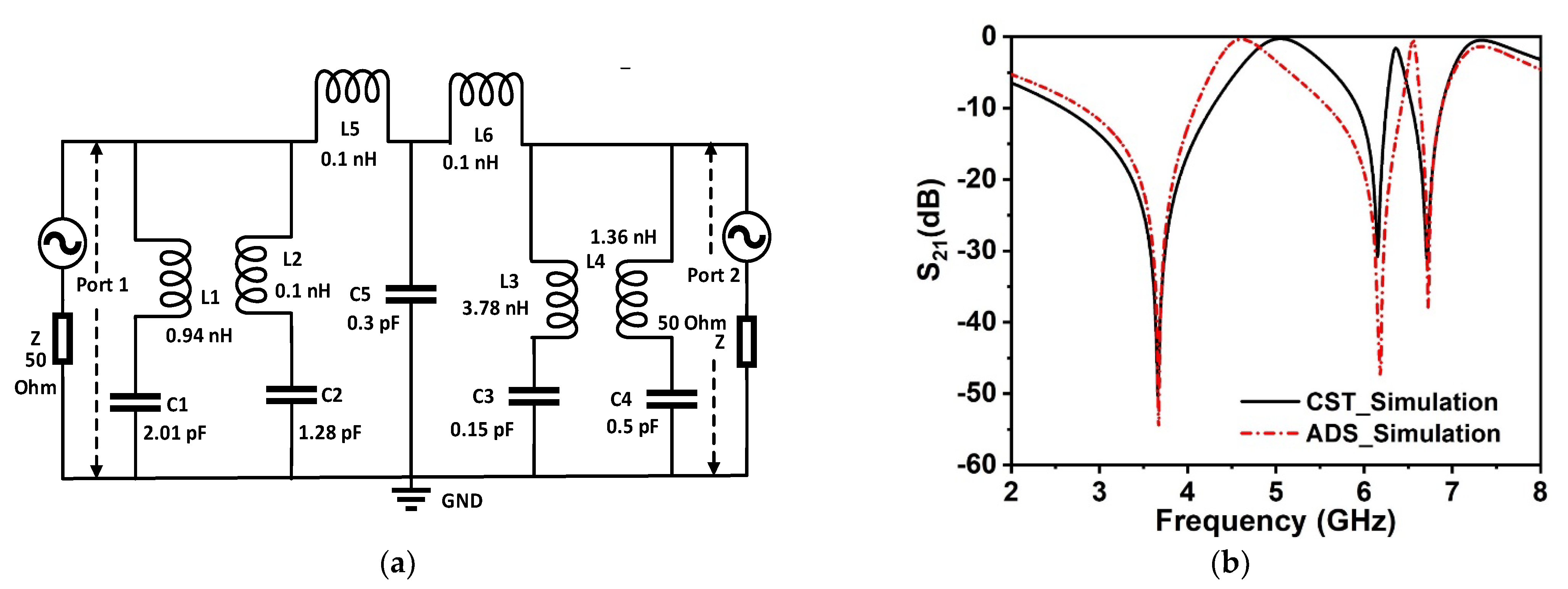
4. Equivalent Circuit Analysis of the Proposed Unit Cell
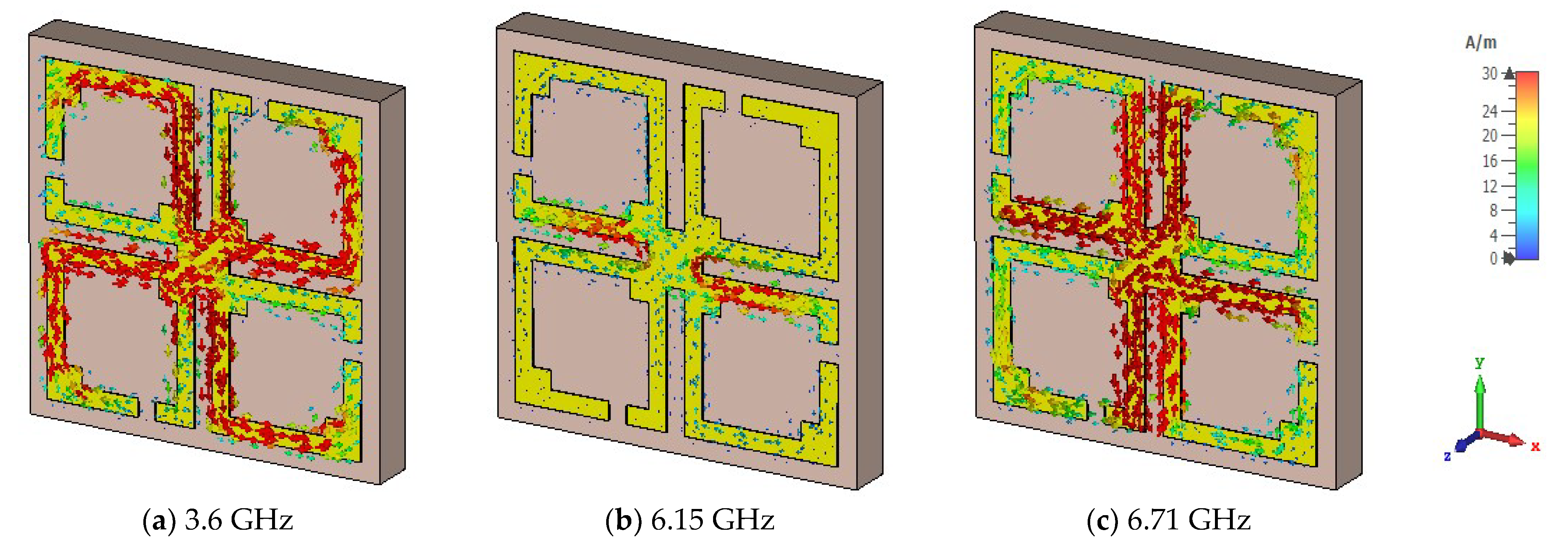
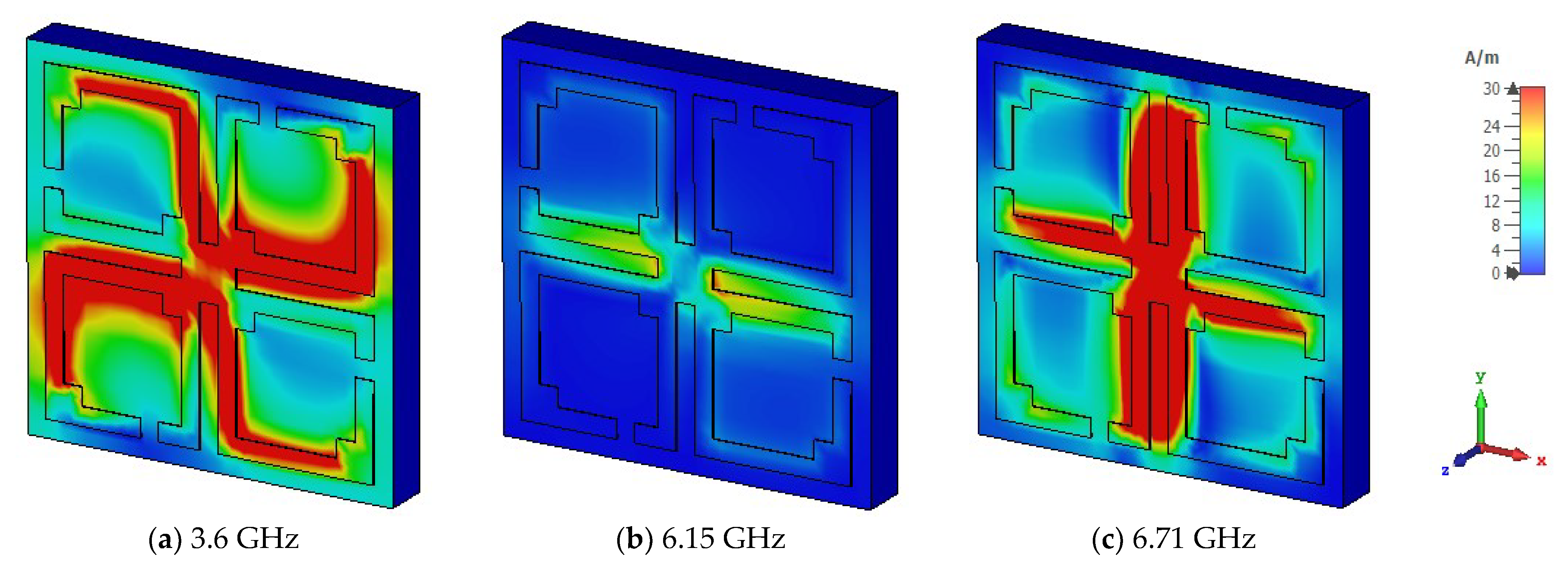
5. Surface Current Density, Magnetic Field, and Electric Field Studies
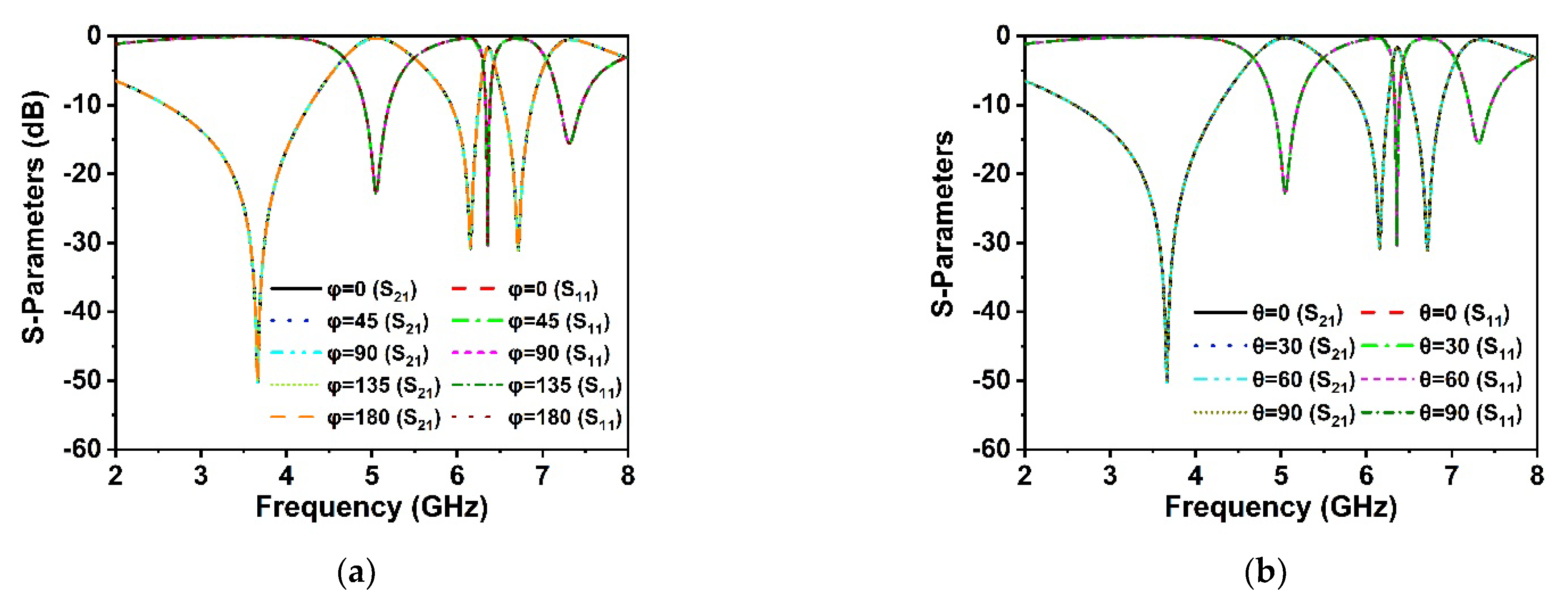
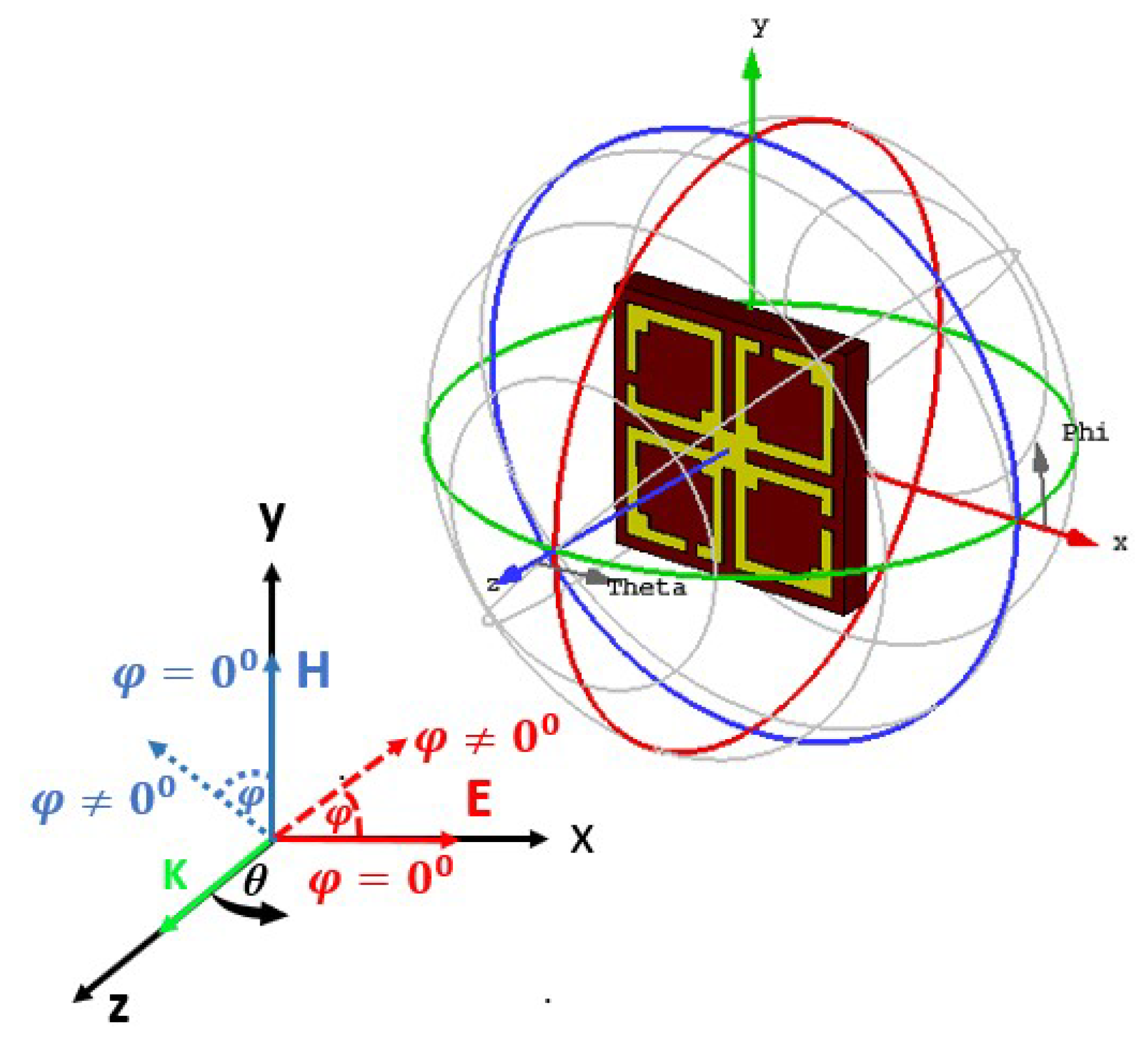
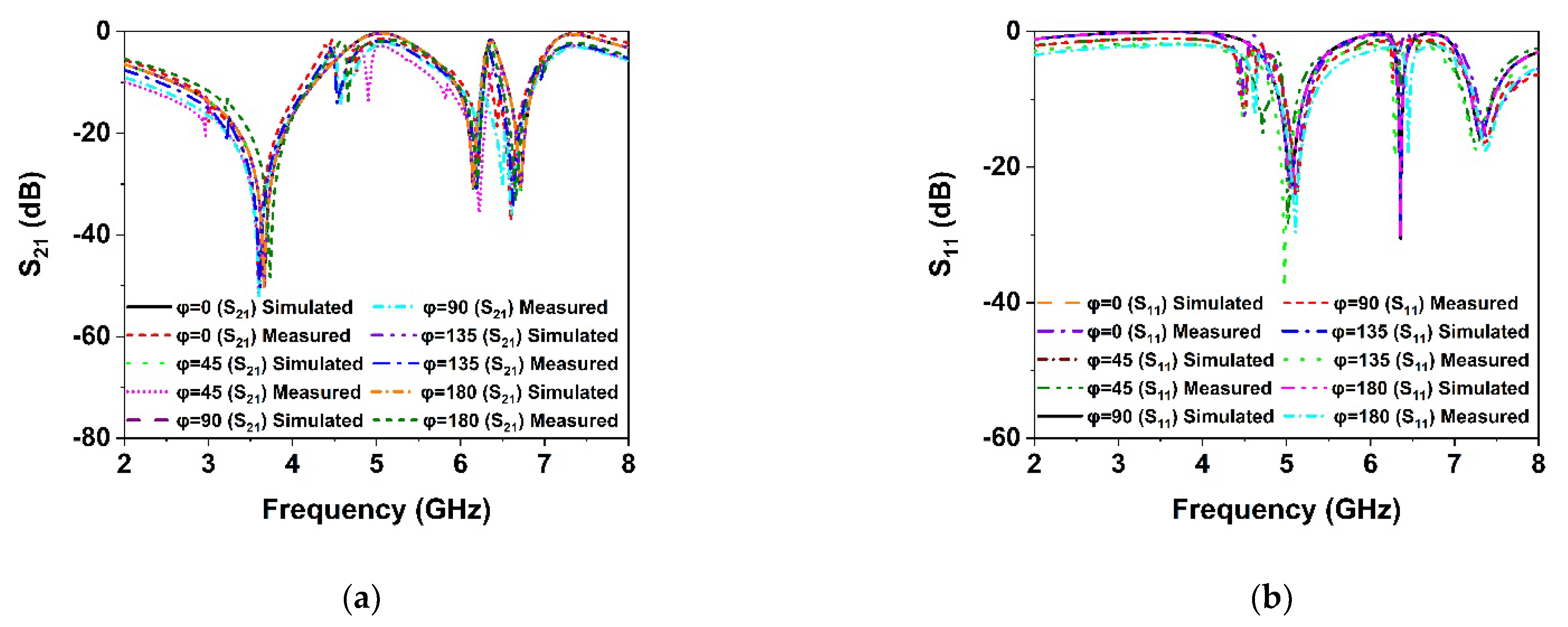
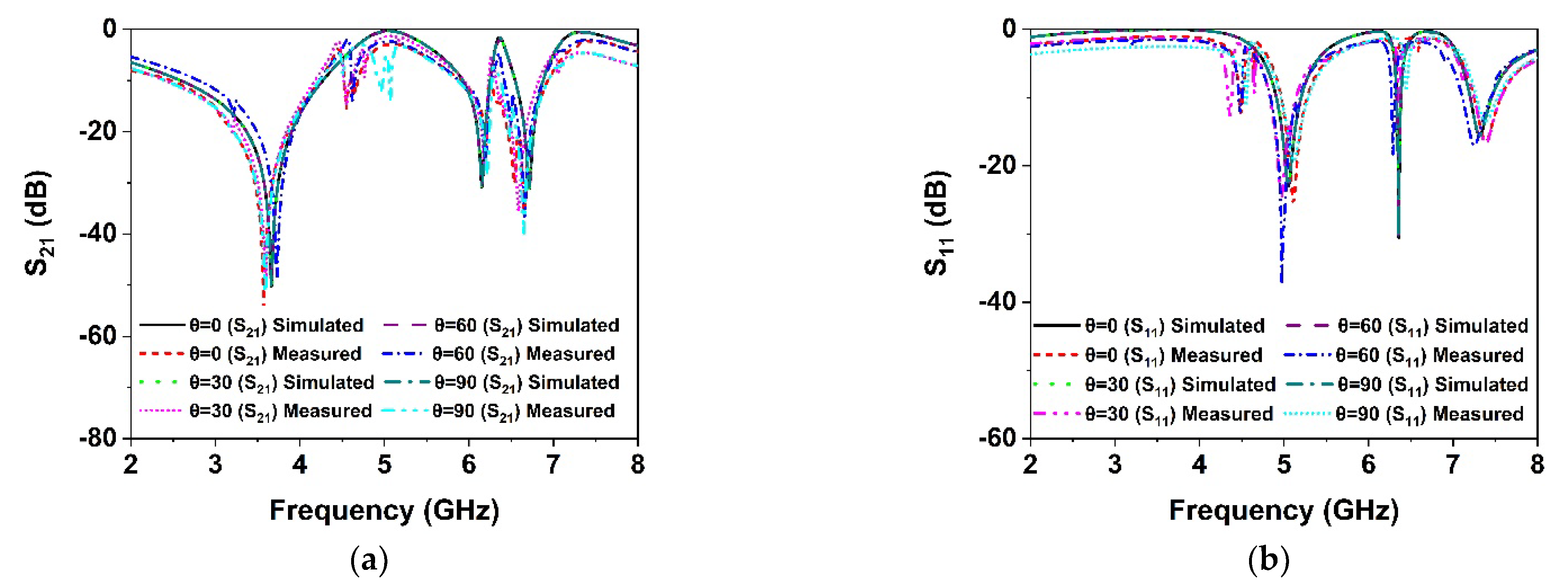
6. Polarization Insensitivity Analysis
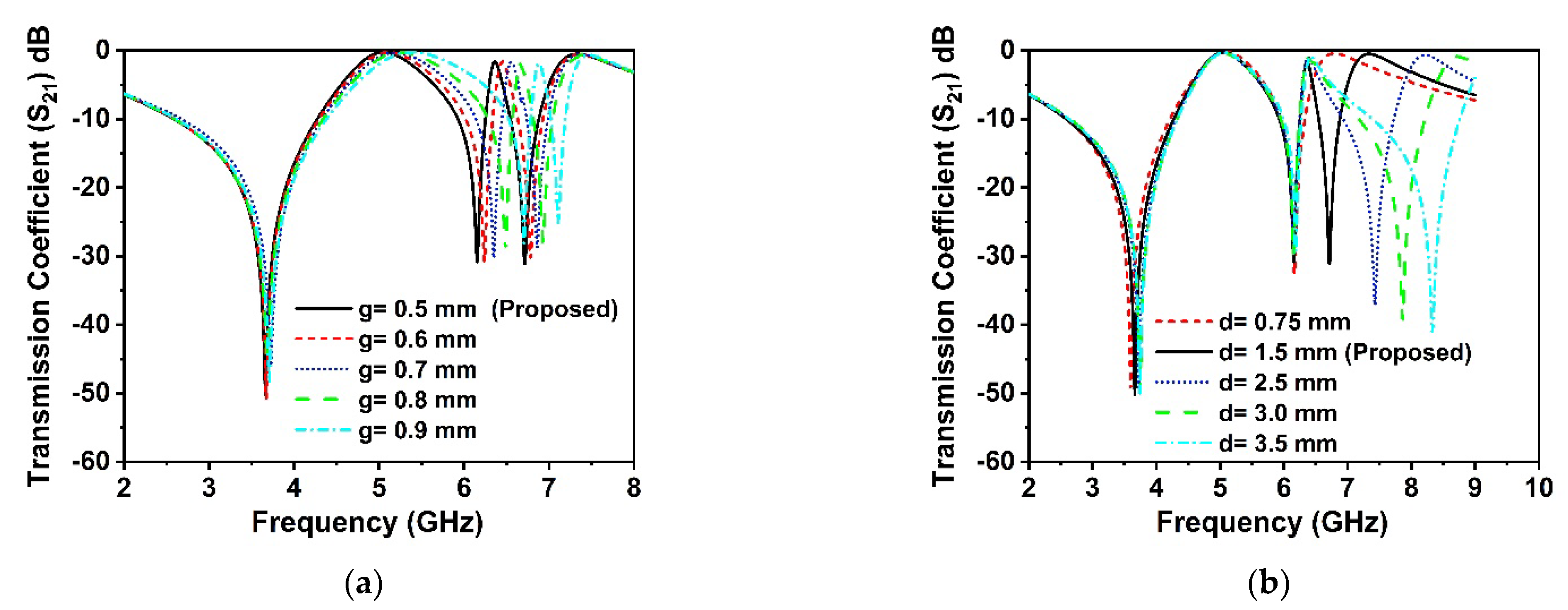
7. EMR and Parametric Study
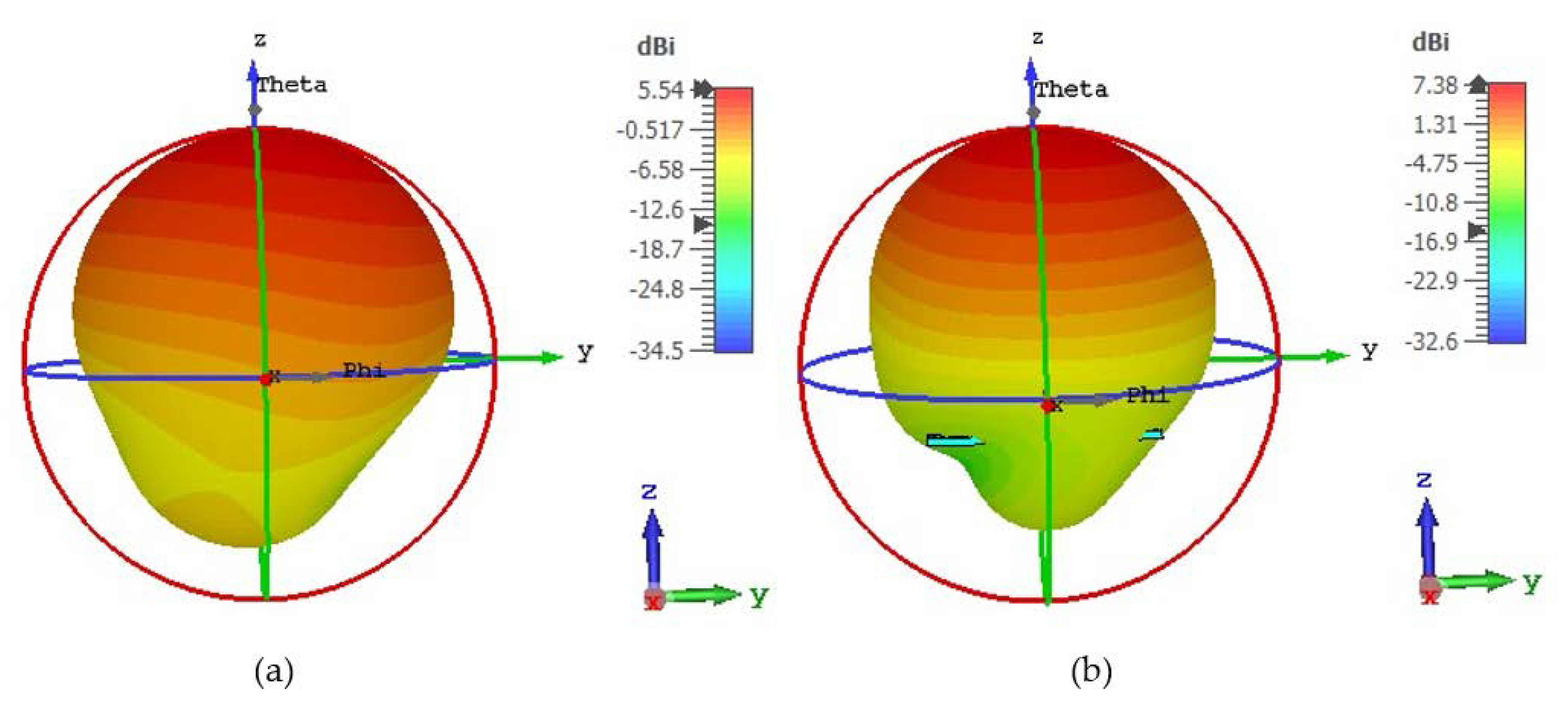
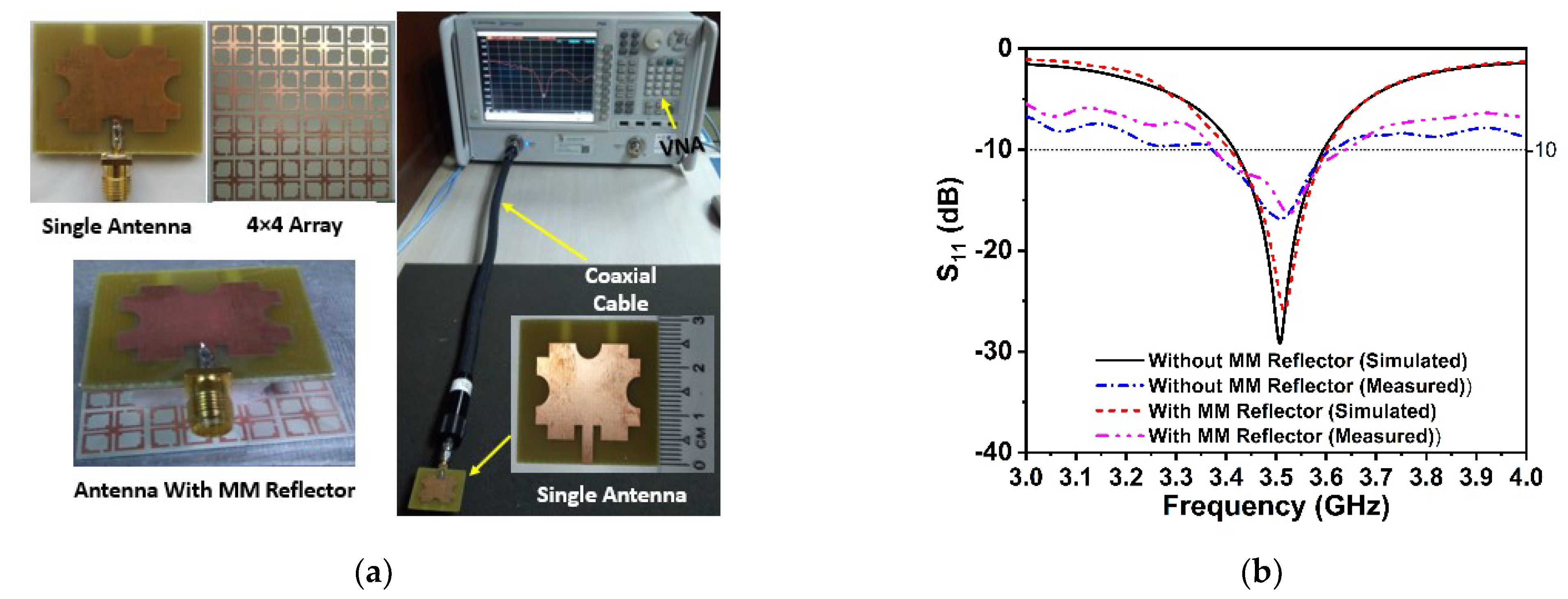
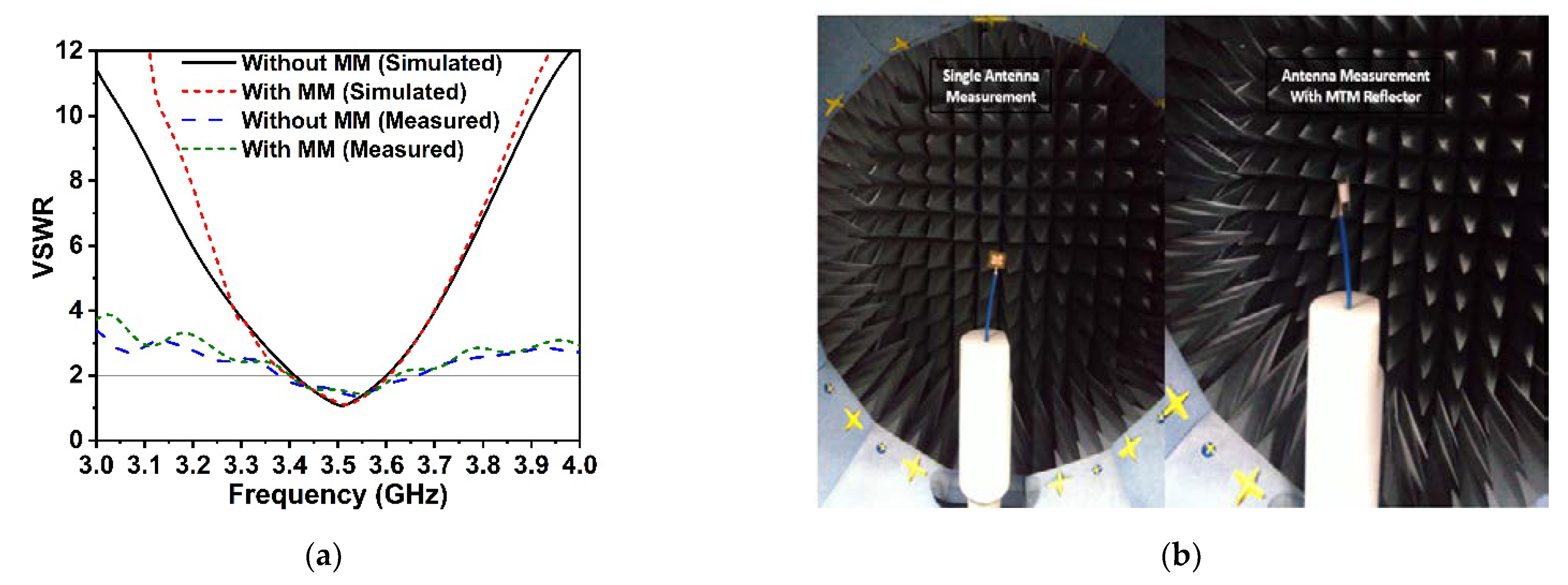
8. Experimental Results and Analysis
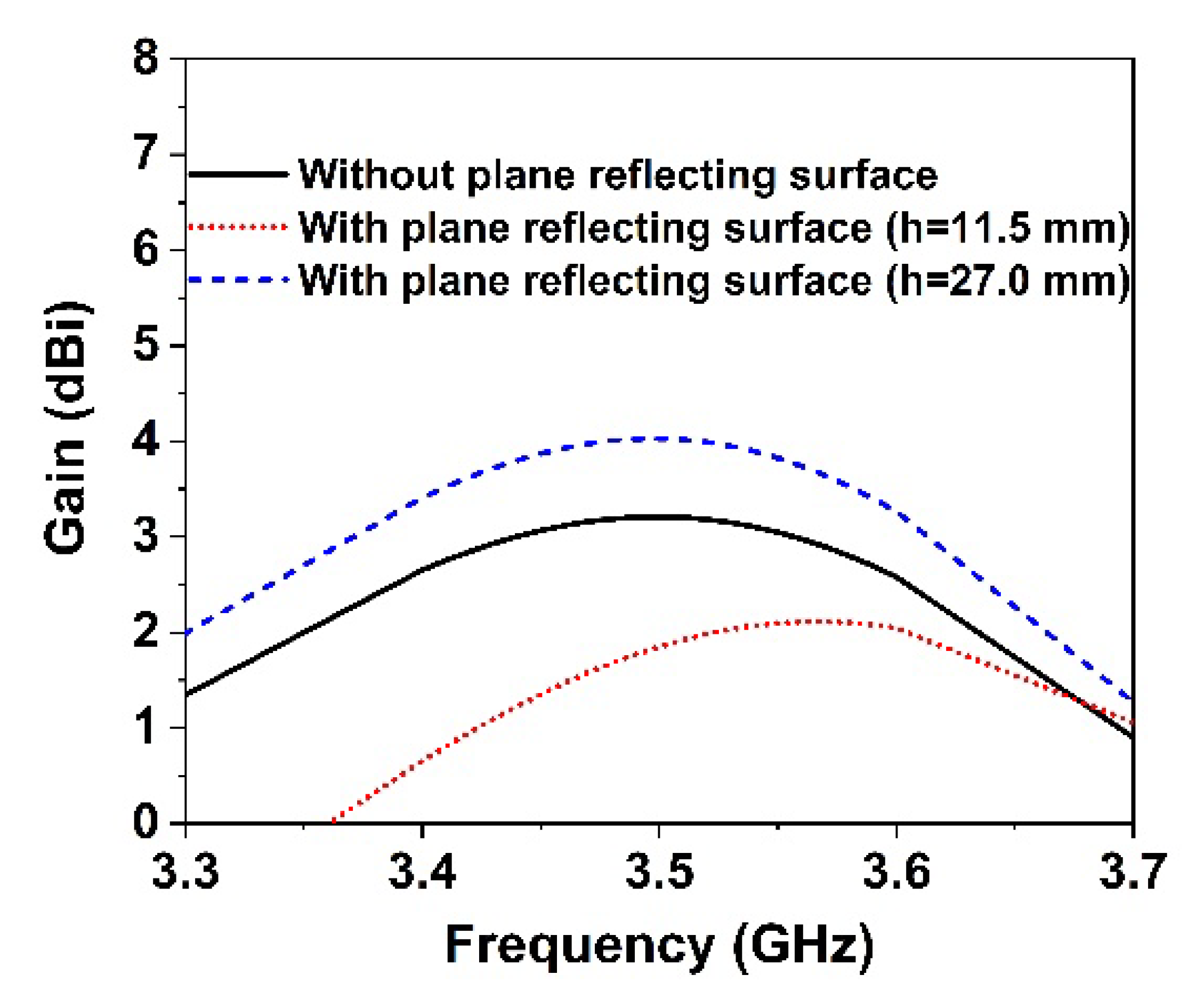
9. 5G Antenna with MM Reflector
10. Performance Comparison with the Existing Contributions
| Ref. and Year | Unit Cell Size (mm2) and Shape | ENG/DNG | Frequency Bands | EMR | Polarization Insensitivity (Maximum Angles) | Gain Enhancement (dBi) | Applications |
|---|---|---|---|---|---|---|---|
| [42] 2015 | 9 × 9 Asymmetric | Not shown | Ku | Not shown | Not shown | 1.0 | Radar cross-section (RCS) of reduction |
| [43] 2017 | 16 × 16 Axis Symmetric | DNG | X | 1.75 | 40° | Not shown | Microwave absorber (proposed) |
| [44] 2017 | 5 × 4.8 Symmetric | Not shown | Ku | Not shown | Not shown | 1.15 | Gain enhancement |
| [45] 2018 | 9.25 × 9.25 Symmetric | Not shown | Ku | Not shown | 90° | - | Antenna performance improvement |
| [25] 2018 | 7.7 × 7.7 Symmetric | DNG | C, X | 5.9 | Not shown | Not shown | Microwave (proposed) |
| [11] 2019 | 10 × 10 Asymmetric | DNG | Ku, K | 2 | 80° | Not shown | Microwave absorber (proposed) |
| [46] 2019 | 6 × 6 Asymmetric | Not shown | C | Not shown | Not shown | 1.3 | Gain enhancement |
| [28] 2020 | 11 × 11 Asymmetric | ENG | S | Not given | Not shown | 3.5 | Gain enhancement |
| [47] 2021 | 8 × 8 Symmetric | LHM | X, Ku | 4.327 | 45° | Not shown | Communication (Proposed) |
| [9] 2021 | 20 × 13 Asymmetric | MNG | X | 1.5 | Not shown | 0.3 | Gain enhancement |
| [12] 2021 | 15 × 15 Asymmetric | DNG | C | 3.5 | Not shown | Not shown | Microwave sensing |
| [48] 2022 | 10 × 10 Axis Symmetric | ENG | C | Not shown | Not shown | 0.6 | Gain enhancement |
| Proposed | 10 × 10 Symmetric | DNG | 5G Sub-6 GHz | 8.2 | 180° | 1.5 | Antenna gain enhancement |
11. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Veselago, V.G. The Electrodynamics of Substances with Simultaneously Negative Values of Img Align= Absmiddle Alt= ϵ Eps/Img and μ. Phys.-Uspekhi 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000, 84, 4184. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.A.; Smith, D.R.; Nemat-Nasser, S.C.; Schultz, S. Microwave transmission through a two-dimensional, isotropic, left-handed metamaterial. Appl. Phys. Lett. 2001, 78, 489–491. [Google Scholar] [CrossRef]
- Engheta, N.; Alù, A.; Ziolkowski, R.W.; Erentok, A. Fundamentals of waveguide and antenna applications involving DNG and SNG metamaterials. In Metamaterials: Physics and Engineering Explorations; Wiley-IEEE Press: Hoboken, NJ, USA, 2006; pp. 43–85. [Google Scholar] [CrossRef]
- Van Tuong, P.; Park, J.W.; Lam, V.D.; Jang, W.H.; Choi, E.H.; Nikitov, S.A.; Lee, Y.P. Negative refractive index at the third-order resonance of flower-shaped metamaterial. J. Lightwave Technol. 2012, 30, 3451–3455. [Google Scholar] [CrossRef]
- Tariq, S.; Naqvi, S.I.; Hussain, N.; Amin, Y. A Metasurface-Based MIMO Antenna for 5G Millimeter-Wave Applications. IEEE Access 2021, 9, 51805–51817. [Google Scholar] [CrossRef]
- Kumar, P.; Ali, T.; Pai, M.M. Electromagnetic Metamaterials: A New Paradigm of Antenna Design. IEEE Access 2021, 9, 18722–18751. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, Y. Low-profile omnidirectional WIFI antennas with pattern reconfigurability inspired by meta-resonators. IEEE Trans. Antennas Propag. 2020, 68, 6935–6942. [Google Scholar] [CrossRef]
- Rosaline, I. A Triple-Band Antenna with a Metamaterial Slab for Gain Enhancement and Specific Absorption Rate (SAR) Reduction. Prog. Electromagn. Res. C 2021, 109, 275–287. [Google Scholar] [CrossRef]
- Khan, J.; Sehrai, D.A.; Khan, M.A.; Khan, H.A.; Ahmad, S.; Ali, A.; Arif, A.; Memon, A.A.; Khan, S. Design and performance comparison of rotated Y-shaped antenna using different metamaterial surfaces for 5G mobile devices. Comput. Mater. Contin. 2019, 60, 409–420. [Google Scholar] [CrossRef]
- Hannan, S.; Islam, M.T.; Hoque, A.; Singh, M.J.; Almutairi, A.F. Design of a novel double negative metamaterial absorber atom for Ku and K band applications. Electronics 2019, 8, 853. [Google Scholar] [CrossRef]
- Hoque, A.; Islam, M.T.; Almutairi, A.F.; Chowdhury, M.E. DNG Metamaterial Reflector Using SOCT Shaped Resonator for Microwave Applications. IEEE Access 2021, 9, 59148–59159. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Chen, X.; Li, Q.; Zhang, Z. Analysis and Design of kHz-Metamaterial for Wireless Power Transfer. IEEE Trans. Magn. 2020, 56, 6703215. [Google Scholar] [CrossRef]
- Dou, K.; Xie, X.; Pu, M.; Li, X.; Ma, X.; Wang, C.; Luo, X. Off-axis multi-wavelength dispersion controlling metalens for multi-color imaging. Opto-Electron. Adv. 2020, 3, 190005. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Justice, B.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Luo, X. Principles of electromagnetic waves in metasurfaces. Sci. China Phys. Mech. Astron. 2015, 58, 594201. [Google Scholar] [CrossRef]
- Abed, A.T.; Singh, M.S.J.; Thiruchelvam, V.; Duraikannan, S.; Tawfeeq, O.A.; Tawfeeq, B.A.; Islam, M.T. Challenges and limits of fractal and slot antennas for WLAN, LTE, ISM, and 5G communication: A review paper. Ann. Telecommun. 2021, 76, 547–557. [Google Scholar] [CrossRef]
- Haraz, O.M.; Elboushi, A.; Alshebeili, S.A.; Sebak, A.-R. Dense dielectric patch array antenna with improved radiation characteristics using EBG ground structure and dielectric superstrate for future 5G cellular networks. IEEE Access 2014, 2, 909–913. [Google Scholar] [CrossRef]
- Khalid, M.; Iffat Naqvi, S.; Hussain, N.; Rahman, M.; Mirjavadi, S.S.; Khan, M.J.; Amin, Y. 4-Port MIMO antenna with defected ground structure for 5G millimeter wave applications. Electronics 2020, 9, 71. [Google Scholar] [CrossRef]
- Pepino, V.M.; da Mota, A.F.; Martins, A.; Borges, B.-H.V. 3-D-printed dielectric metasurfaces for antenna gain improvement in the Ka-band. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2133–2136. [Google Scholar] [CrossRef]
- Salleh, A.; Yang, C.; Alam, T.; Singh, M.; Samsuzzaman, M.; Islam, M. Development of microwave brain stroke imaging system using multiple antipodal vivaldi antennas based on raspberry Pi technology. J. Kejuruterran 2020, 32, 1–6. [Google Scholar]
- Singh, H.; Mittal, N.; Arora, O. Designing and analysis of frequency reconfigurable double negative flower leaf metamaterial resonator. Mater. Today Proc. 2020, 33, 1552–1557. [Google Scholar] [CrossRef]
- Guha, R.; Bandyopadhyay, A.K.; Varshney, A.K.; Datta, S.K.; Basu, B. Investigations into helix slow-wave structure assisted by double-negative metamaterial. IEEE Trans. Electron Devices 2018, 65, 5082–5088. [Google Scholar] [CrossRef]
- Almutairi, A.F.; Islam, M.S.; Samsuzzaman, M.; Islam, M.T.; Misran, N.; Islam, M.T. A complementary split ring resonator based metamaterial with effective medium ratio for C-band microwave applications. Results Phys. 2019, 15, 102675. [Google Scholar] [CrossRef]
- Khandelwal, M.K.; Arora, A.; Kumar, S.; Kim, K.W.; Choi, H.C. Dual band double negative (DNG) metamaterial with small frequency ratio. J. Electromagn. Waves Appl. 2018, 32, 2167–2181. [Google Scholar] [CrossRef]
- Ojo, R.; Jamlos, M.F.; Soh, P.J.; Jamlos, M.A.; Bahari, N.; Lee, Y.S.; Al-Bawri, S.S.; Abdul Karim, M.S.; Khairi, K.A. A triangular MIMO array antenna with a double negative metamaterial superstrate to enhance bandwidth and gain. Int. J. RF Microw. Comput.-Aided Eng. 2020, 30, e22320. [Google Scholar] [CrossRef]
- Hasan, M.-M.; Islam, M.-T.; Moniruzzaman, M.; Uddin, M.-H.; Sahar, N.-B.-M.; Samsuzzaman, M. Bilateral Coupled Epsilon Negative Metamaterial for Dual Band Wireless Communications. Comput. Mater. Contin. 2022, 71, 1263–1281. [Google Scholar]
- Sehrai, D.A.; Muhammad, F.; Kiani, S.H.; Abbas, Z.H.; Tufail, M.; Kim, S. Gain-enhanced metamaterial based antenna for 5G communication standards. CMC Comput. Mater. Contin. 2020, 64, 1587–1599. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; Islam, M.T.; Misran, N.; Samsuzzaman, M.; Alam, T.; Chowdhury, M.E. Inductively tuned modified split ring resonator based quad band epsilon negative (ENG) with near zero index (NZI) metamaterial for multiband antenna performance enhancement. Sci. Rep. 2021, 11, 11950. [Google Scholar] [CrossRef]
- Islam, M.R.; Islam, M.T.; Moniruzzaman, M.; Samsuzzaman, M.; Bais, B.; Arshad, H.; Muhammad, G. Square enclosed circle split ring resonator enabled epsilon negative (ENG) near zero index (NZI) metamaterial for gain enhancement of multiband satellite and radar antenna applications. Results Phys. 2020, 19, 103556. [Google Scholar] [CrossRef]
- Kakhki, M.B.; Dadgarpour, A.; Antoniades, M.A.; Sebak, A.-R.; Denidni, T.A. Dual complementary source magneto-electric dipole antenna loaded with split ring resonators. IEEE Access 2020, 8, 59351–59361. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, J.; Hou, Q.; Zhao, X. Broadband omnidirectional patch antenna with horizontal gain enhanced by near-zero-index metamaterial cover. IET Microw. Antennas Propag. 2020, 14, 671–676. [Google Scholar] [CrossRef]
- Ullah, S.; Ullah, S.; Khan, S. Design and analysis of a 60 GHz millimeter wave antenna. J. Teknol. 2016, 78, 63–68. [Google Scholar] [CrossRef][Green Version]
- Khan, J.; Sehrai, D.A.; Ahmad, S. Design and performance comparison of metamaterial based antenna for 4G/5G mobile devices. Int. J. Electron. Commun. Eng. 2018, 12, 382–387. [Google Scholar]
- Bait-Suwailam, M.M. Electromagnetic field interaction with metamaterials. In Electromagnetic Fields and Waves; IntechOpen: London, UK, 2019. [Google Scholar]
- Chen, X.; Grzegorczyk, T.M.; Wu, B.-I.; Pacheco, J., Jr.; Kong, J.A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 2004, 70, 016608. [Google Scholar] [CrossRef] [PubMed]
- Boylestad, R.L. Introductory Circuit Analysis; Pearson Education: London, UK, 2013. [Google Scholar]
- Bahl, I.; Bhartia, P. Microwave Solid State Circuit Design; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Saadat-Safa, M.; Nayyeri, V.; Khanjarian, M.; Soleimani, M.; Ramahi, O.M. A CSRR-based sensor for full characterization of magneto-dielectric materials. IEEE Trans. Microw. Theory Tech. 2019, 67, 806–814. [Google Scholar] [CrossRef]
- Bouzouad, M.; Chaker, S.; Bensafielddine, D.; Laamari, E. Gain enhancement with near-zero-index metamaterial superstrate. Appl. Phys. A 2015, 121, 1075–1080. [Google Scholar] [CrossRef]
- Enoch, S.; Tayeb, G.; Sabouroux, P.; Guérin, N.; Vincent, P. A metamaterial for directive emission. Phys. Rev. Lett. 2002, 89, 213902. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, J.; Cao, X.; Yuan, Z.; Yang, H. Wideband RCS reduction of a microstrip antenna using artificial magnetic conductor structures. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1582–1585. [Google Scholar] [CrossRef]
- Mahmood, A.; Ögücü Yetkin, G.; Sabah, C. Design and fabrication of a novel wideband DNG metamaterial with the absorber application in microwave X-band. Adv. Condens. Matter Phys. 2017, 2017, 1279849. [Google Scholar] [CrossRef]
- Zhang, L.; Dong, T. Low RCS and high-gain CP microstrip antenna using SA-MS. Electron. Lett. 2017, 53, 375–376. [Google Scholar] [CrossRef]
- Singh, D.; Srivastava, V.M. An analysis of RCS for dual-band slotted patch antenna with a thin dielectric using shorted stubs metamaterial absorber. AEU-Int. J. Electron. Commun. 2018, 90, 53–62. [Google Scholar] [CrossRef]
- Vani, H.; Goutham, M. Gain Enhancement of Microstrip Patch Antenna Using Metamaterial Superstrate. Appl. Comput. Electromagn. Soc. J. (ACES) 2019, 34, 1250–1253. [Google Scholar]
- Ramachandran, T.; Faruque, M.R.I.; Islam, M.T. A dual-band polarization-independent left-handed symmetrical metamaterial for communication system application. J. Mater. Res. Technol. 2021, 15, 731–744. [Google Scholar] [CrossRef]
- Bin Ashraf, F.; Alam, T.; Islam, M.T.; Singh, M.J.; Misran, N.B.; Islam, M.T. Inkjet Printed Metamaterial Loaded Antenna for WLAN/WiMAX Applications. CMC-Comput. Mater. Contin. 2022, 71, 2271–2284. [Google Scholar] [CrossRef]
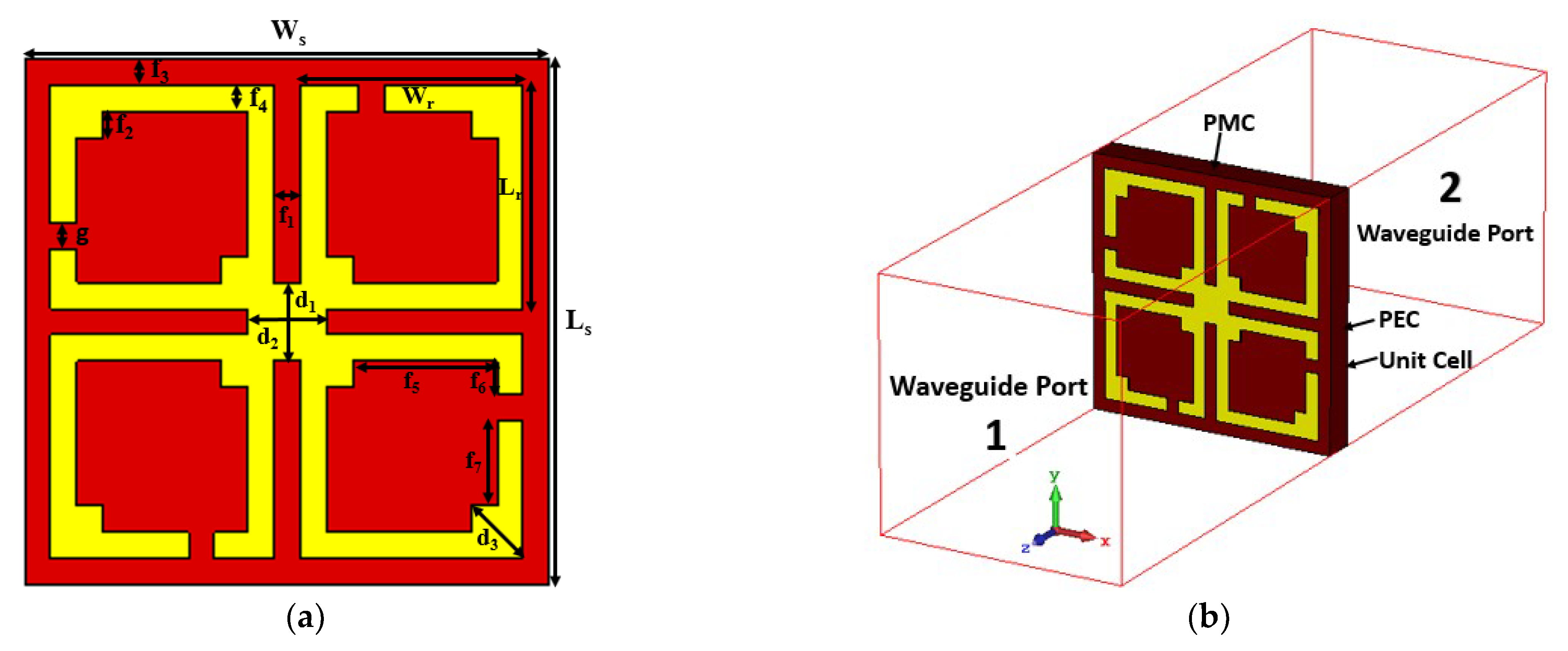








| Parameter | Size (mm) | Parameter | Size (mm) | Parameter | Size (mm) |
|---|---|---|---|---|---|
| Ls | 10 | Ws | 10 | f1, f2, f3, f4, g | 0.5 |
| Lr | 4.25 | Wr | 4.25 | f7, d1, d2 | 1.5 |
| f5 | 2.75 | f6 | 0.75 | d3 | 1.0 |
| Parameters | Frequency Range (GHz) | Bandwidth Threshold |
|---|---|---|
| S21 | 2.5–4.3, 5.9–6.3, 6.5–6.9 | |
| 3.6–5, 6.15–6.34, 6.7–7.24 | ||
| 3.74–4.39, 6.19–6.26, 6.75–6.96 | ||
| DNG region | 3.74–4.39, 6.19–6.26, 6.75–6.96 | |
| n | 3.6–4.9, 6.17–6.35, 6.7–7.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, M.M.; Islam, M.T.; Moniruzzaman, M.; Soliman, M.S.; Alshammari, A.S.; Sulayman, I.I.M.A.; Samsuzzaman, M.; Islam, M.S. Symmetric Engineered High Polarization-Insensitive Double Negative Metamaterial Reflector for Gain and Directivity Enhancement of Sub-6 GHz 5G Antenna. Materials 2022, 15, 5676. https://doi.org/10.3390/ma15165676
Hasan MM, Islam MT, Moniruzzaman M, Soliman MS, Alshammari AS, Sulayman IIMA, Samsuzzaman M, Islam MS. Symmetric Engineered High Polarization-Insensitive Double Negative Metamaterial Reflector for Gain and Directivity Enhancement of Sub-6 GHz 5G Antenna. Materials. 2022; 15(16):5676. https://doi.org/10.3390/ma15165676
Chicago/Turabian StyleHasan, Md. Mhedi, Mohammad Tariqul Islam, Md. Moniruzzaman, Mohamed S. Soliman, Ahmed S. Alshammari, Iman I. M. Abu Sulayman, Md. Samsuzzaman, and Md. Shabiul Islam. 2022. "Symmetric Engineered High Polarization-Insensitive Double Negative Metamaterial Reflector for Gain and Directivity Enhancement of Sub-6 GHz 5G Antenna" Materials 15, no. 16: 5676. https://doi.org/10.3390/ma15165676
APA StyleHasan, M. M., Islam, M. T., Moniruzzaman, M., Soliman, M. S., Alshammari, A. S., Sulayman, I. I. M. A., Samsuzzaman, M., & Islam, M. S. (2022). Symmetric Engineered High Polarization-Insensitive Double Negative Metamaterial Reflector for Gain and Directivity Enhancement of Sub-6 GHz 5G Antenna. Materials, 15(16), 5676. https://doi.org/10.3390/ma15165676






