Inversion Method of the Young’s Modulus Field and Poisson’s Ratio Field for Rock and Its Test Application
Abstract
:1. Introduction
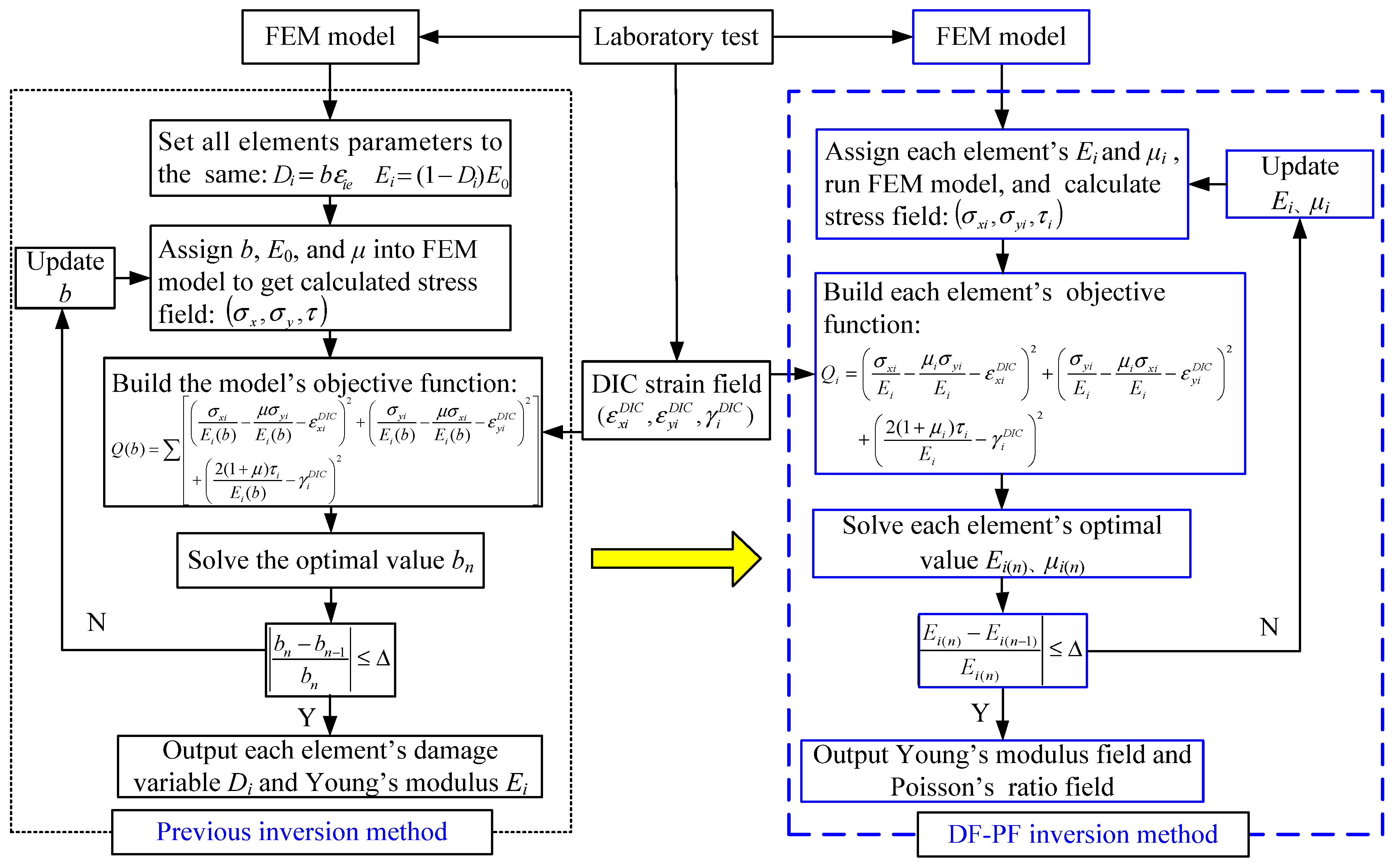
2. DF-PF Inversion Method
- (1)
- Carry out the laboratory test of rock specimen, and obtain the real strain field on the specimen surface by DIC method.
- (2)
- Then, FEM is used to establish the numerical model, and the geometric dimensions and boundary conditions of the numerical model are consistent with those in the laboratory test. Assign each element’s micro Young’s modulus Ei and micro Poisson’s ratio μi separately, and their initial value can be set as the results measured by ISRM suggested method.
- (3)
- Export the stress field obtained by FEM, and calculate the strain field by Hooke’s law. Then, an objective function Qi is established as the squared difference between the strains measured with the DIC and the strains calculated by FEM. Each element i establishes an independent objective function Qi, in which micro Young’s modulus Ei and micro Poisson’s ratio μi are taken as the inversion variables. The idea is to iteratively minimize the objective function with respect to Young’s modulus Ei and micro Poisson’s ratio μi. The objective function Qi is:where σxi, σyi, τi is the horizontal stress, vertical stress and shear stress of element i obtained by FEM, and , , is the horizontal strain, vertical strain and shear strain of element i obtained by the DIC test.
- (4)
- Solve the objective function Qi with the Nelder–Mead simplex method, and the optimal micro Young’s modulus Ei(n) and micro Poisson’s ratio μi(n) of each element in the current iterative step n can be obtained.
- (5)
- Input the new micro Young’s modulus and micro Poisson’s ratio of each element into the FEM model and repeat steps (2), (3) and (4). When the difference in the value of each element’s micro Young’s modulus between the two iteration steps is less than the allowable error Δ, stop the iteration. Then output the micro Young’s modulus and micro Poisson’s ratio of each element, and draw Young’s modulus field and Poisson’s ratio field.
3. Verification of the Method
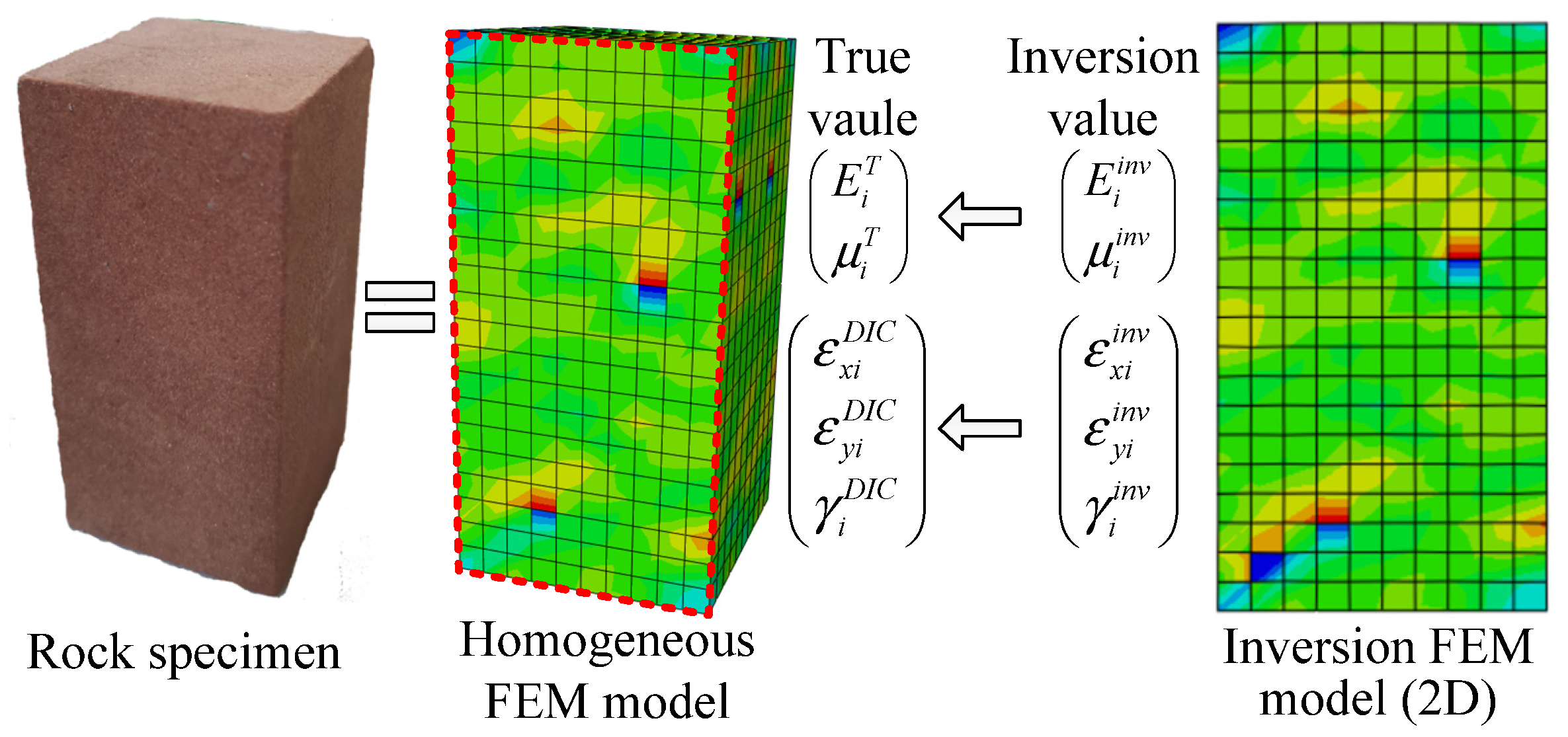
3.1. Verification Thought
3.2. Verification Schemes
- (1)
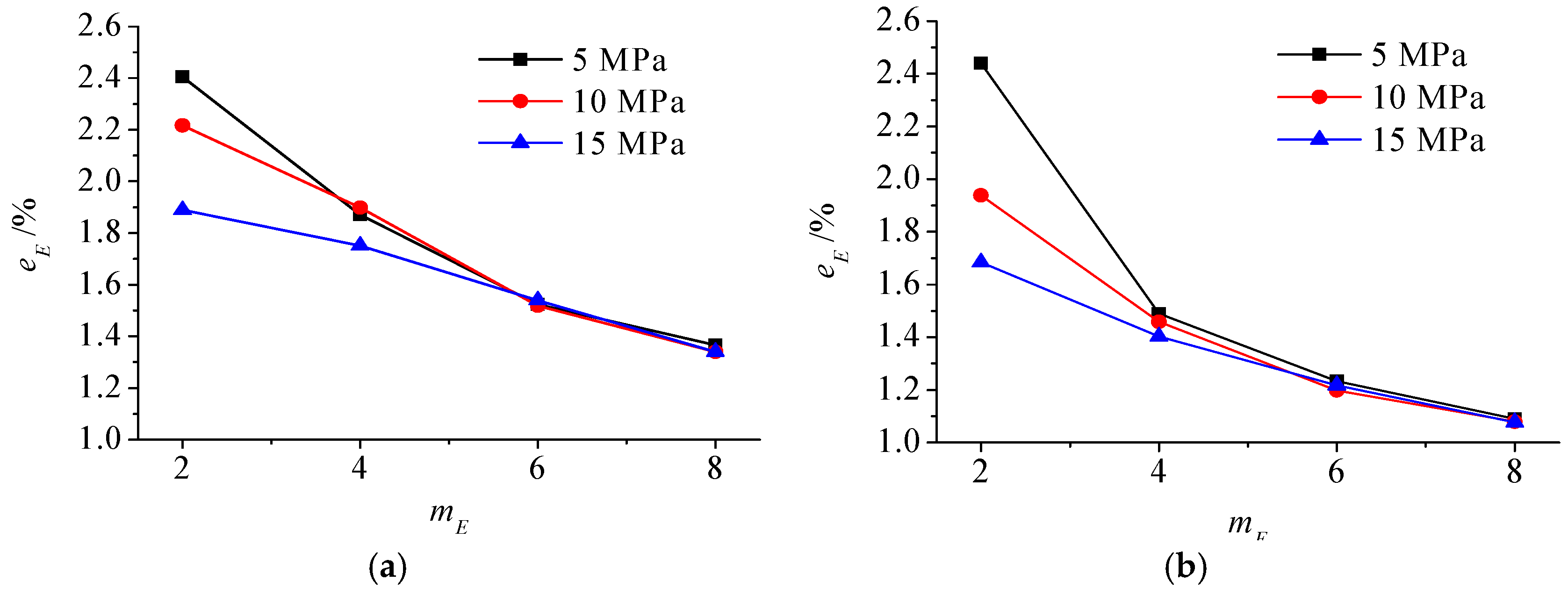
- In scheme I, a 2D uniaxial compression test was carried out to study the influences of micro Young’s modulus homogeneity and stress level. The size of the rock specimen model was 50 mm × 100 mm and was divided into 800 quadrilateral elements. The initial macro Young’s modulus and macro Poisson’s ratio were set to 10 GPa and 0.25. Micro Young’s modulus was set as heterogeneity, while micro Poisson’s ratio was homogeneous.
- (2)
- In scheme II, the 2D diametral compression test of the ring specimen was carried out to study the influence of the stress state. Compared with the uniaxial compression test, the element is in a complex stress state in the diametral compression test. The ring’s outer and inner diameters were 100 mm and 60 mm, respectively, divided into 608 quadrilateral elements.
- (3)
- Scheme III mainly studied the influence of the dimensional difference between the test and inversion models on the inversion results. The test model was a 3D uniaxial compression specimen, a cuboid of 50 mm × 50 mm × 100 mm and divided into 16,000 hexahedral elements. The inversion model was still the 2D uniaxial compression specimen, the same as in scheme I.
- (4)
- Scheme IV mainly studied the inversion accuracy when micro Poisson’s ratio and micro Young’s modulus were both heterogeneous, and it was researched by 2D uniaxial compression test and 3D uniaxial compression test.
- (1)
- eεx, eεy, and eγ: the mean value of the relative error of horizontal strain, vertical strain and shear strain between the DIC strain field and inversion strain field.
- (2)
- Rεx, Rεy, and Rγ: the correlation coefficient of horizontal, vertical, and shear strain between DIC strain field and inversion strain field. The more the correlation coefficient tends to 1, the better the correlation.
- (3)
- eE, and SE: the relative error and its standard deviation between the true value and the inversion value of Young’s modulus field.
- (4)
- eμ, and Sμ: the relative error and its standard deviation between the true value and the inversion value of Poisson’s ratio field.
- (5)
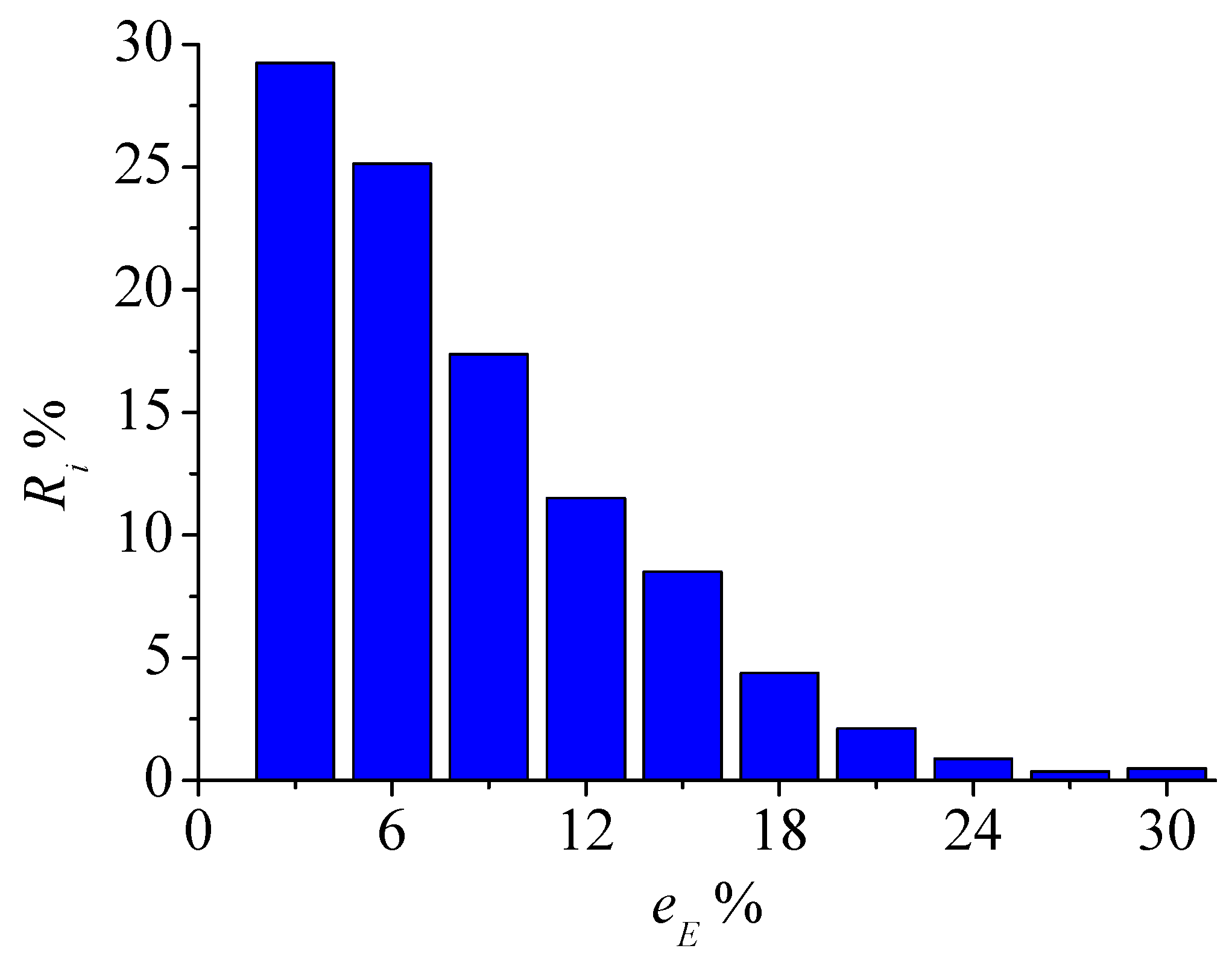
- Ri: the proportion of the elements in the whole specimen.
3.3. Results and Analysis
4. Application in Laboratory Test
4.1. Test Scheme
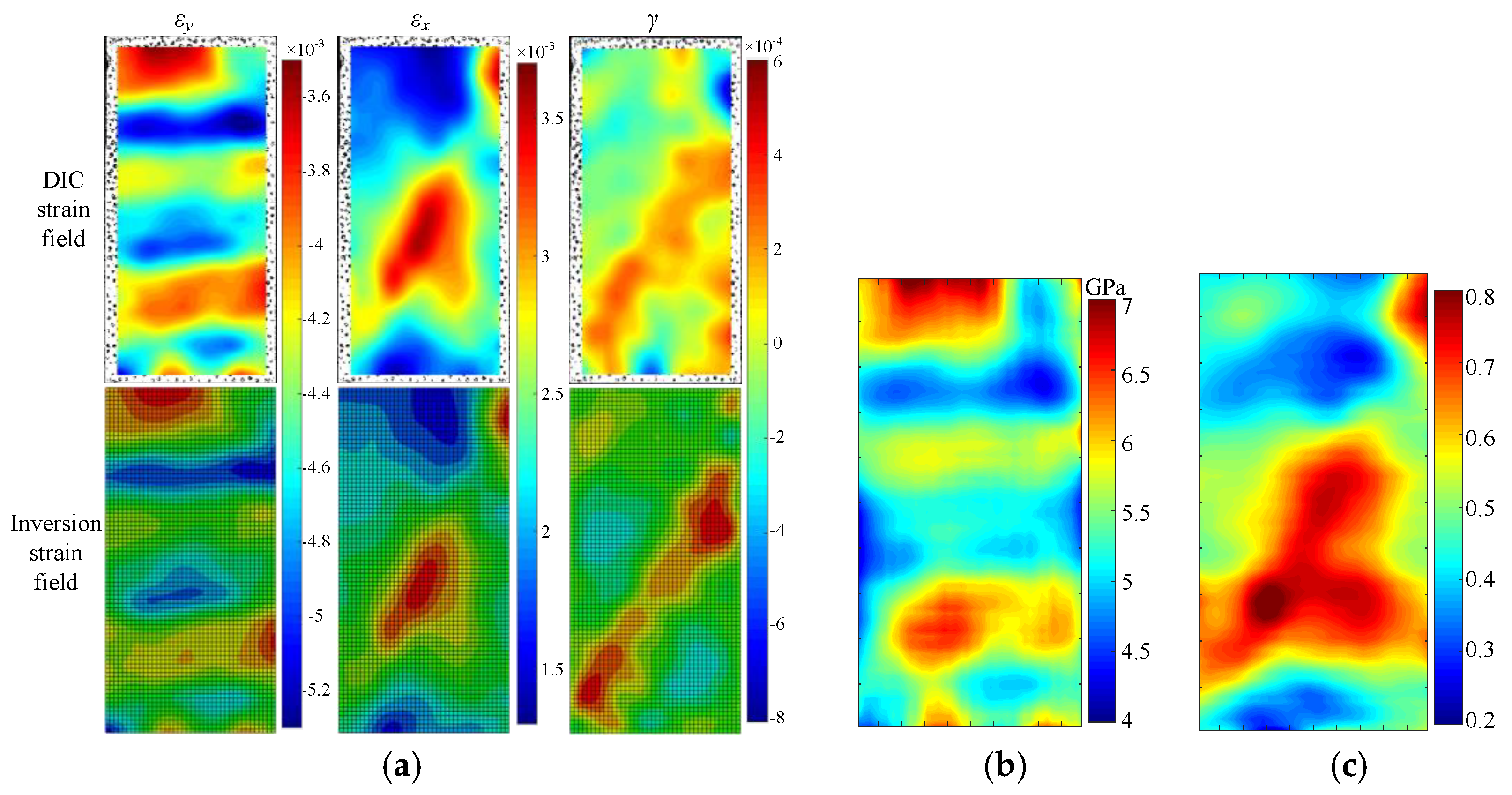
4.2. Inversion Results
4.3. Comparison with Conventional Test
4.4. Micro Parameter Evolution Analysis
5. Discussion
6. Conclusions
- (1)
- DF-PF inversion method provides a new effective method for the inversion of Young’s modulus field and Poisson’s ratio field for rocks in elastic and plastic deformation stages without obvious macro fractures. The average relative error is less than 10%.
- (2)
- The Young’s modulus field and Poisson’s ratio field are obtained in the laboratory test. The parameters field shows obvious localization characteristics, which provides abundant data for the research of the nonlinear damage evolution of rocks under different stress states.
- (3)
- Compared with the conventional measuring method, the error of macro Young’s modulus and macro Poisson’s ratio calculated by the DF-PF inversion method is less than 2.8% and 9.07%, respectively. The DF-PF inversion method can be used to measure rock macro mechanical parameters.
- (4)
- The relationship between micro Young’s modulus and maximum principal strain is an exponential function, and the relationship between micro Poisson’s ratio and principal strain ratio is linear. It provides a new method for the determination of damage equation in the rock heterogeneous damage constitutive model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.B.; Zhao, T.B.; Yin, Y.C.; Qiu, Y. Numerical Research on Energy Evolution in Granite under Different Confining Pressures Using Otsu’s Digital Image Processing and PFC2D. Symmetry 2019, 11, 131. [Google Scholar] [CrossRef] [Green Version]
- Carpinteri, A.; Corrado, M.; Lacidogna, G. Heterogeneous materials in compression: Correlations between absorbed, released and acoustic emission energies. Eng. Fail. Anal. 2013, 33, 236–250. [Google Scholar] [CrossRef]
- Birck, G.; Iturrioz, I.; Lacidogna, G.; Carpinteri, A. Damage process in heterogeneous materials analyzed by a lattice model simulation. Eng. Fail. Anal. 2016, 70, 157–176. [Google Scholar] [CrossRef]
- Tan, X.; Konietzky, H.; Chen, W. Numerical Simulation of Heterogeneous Rock Using Discrete Element Model Based on Digital Image Processing. Rock Mech. Rock Eng. 2016, 49, 4957–4964. [Google Scholar] [CrossRef]
- Lin, P.; Ma, T.H.; Liang, Z.Z.; Tang, C.A.; Wang, R. Failure and overall stability analysis on high arch dam based on DFPA code. Eng. Fail. Anal. 2014, 45, 164–184. [Google Scholar] [CrossRef]
- Sanchidrian, J.A.; Ouchterlony, F.; Segarra, P.; Moser, P. Size distribution functions for rock fragments. Int. J. Rock Mech. Min. Sci. 2014, 71, 381–394. [Google Scholar] [CrossRef]
- Chen, S.; Yue, Z.Q.; Kwan, A.K.H. Actual microstructure-based numerical method for mesomechanics of concrete. Comput. Concr. 2014, 12, 1–18. [Google Scholar] [CrossRef]
- Chen, S.; Yue, Z.Q.; Tham, L.G. Digital image-based numerical modeling method for prediction of inhomogeneous rock failure. Int. J. Rock Mech. Min. Sci. 2004, 41, 939–957. [Google Scholar] [CrossRef]
- Chen, S.; Qiao, C.S.; Ye, Q.; Khan, M.U. Comparative study on three-dimensional statistical damage constitutive modified model of rock based on power function and Weibull distribution. Environ. Earth Sci. 2018, 77, 108. [Google Scholar] [CrossRef]
- Pan, X.H.; Guo, W.; Wu, S.F.; Chu, J. An experimental approach for determination of the Weibull homogeneity index of rock or rock-like materials. Acta Geotech. 2020, 15, 375–391. [Google Scholar] [CrossRef]
- Shah, K.S.; Hashim, M.H.B.M.; Rehman, H.; Ariffin, K.S.B. Evaluating microscale failure response of various weathering grade sandstones based on micro-scale observation and micro-structural modelling subjected to wet and dry cycles. J. Min. Environ. 2022, 13, 341–355. [Google Scholar]
- Yin, D.H.; Xu, Q.J. Comparison of sandstone damage measurements based on non-destructive testing. Materials 2020, 13, 5154. [Google Scholar] [CrossRef]
- Tian, G.L.; Deng, H.W.; Xiao, Y.G.; Yu, S.T. Experimental study of multi-angle effects of micron-silica fume on micro-pore structure and macroscopic mechanical properties of rock-like material based on NMR and SEM. Materials 2022, 15, 3388. [Google Scholar] [CrossRef] [PubMed]
- Ma, Q.W.; Sandali, Y.; Zhang, R.N.; Ma, F.Y.; Wang, H.T.; Ma, S.P.; Shi, Q.F. Characterization of elastic modulus of granular materials in a new designed uniaxial oedometric system. Chin. Phys. Lett. 2016, 33, 038101. [Google Scholar] [CrossRef]
- Zhao, T.B.; Yin, Y.C.; Tan, Y.L.; Song, Y.M. Deformation tests and failure process analysis of anchorage structure. Int. J. Min. Sci. Technol. 2015, 25, 237–242. [Google Scholar] [CrossRef]
- Pan, B. Digital image correlation for surface deformation measurement: Historical developments, recent advances and future goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Munoz, H.; Taheri, A.; Chanda, E.K. Pre-peak and post-peak rock strain characteristics during uniaxial compression by 3D digital image correlation. Rock Mech. Rock Eng. 2016, 49, 2541–2554. [Google Scholar] [CrossRef]
- Pierron, F.; Sutton, M.A.; Tiwari, V. Ultra high speed DIC and virtual fields method analysis of a three point bending impact test on an aluminium bar. Exp. Mech. 2011, 51, 537–563. [Google Scholar] [CrossRef]
- Wan, H.P.; Ren, W.X. Parameter selection in finite-element-model updating by global sensitivity analysis using Gaussian process metamodel. J. Struct. Eng. 2015, 141, 04014164. [Google Scholar] [CrossRef]
- Mathieu, F.; Leclerc, H.; Hild, F.; Roux, S. Estimation of elastoplastic parameters via weighted FEMU and integrated-DIC. Exp. Mech. 2015, 55, 105–119. [Google Scholar] [CrossRef]
- Ogierman, W.; Kokot, G. Analysis of strain field heterogeneity at microstructure level and inverse identification of composite constituents by means of digital image correlation. Materials 2020, 13, 287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, Y.M.; Ling, X.K.; Zhang, J.Z.; Zhu, C.L.; Ren, H.; Yuan, D.S. Experimental study of DSCM-FEM inversion of mechanical parameters of rock and soil materials. Rock Soil Mech. 2021, 42, 2855–2864. (In Chinese) [Google Scholar] [CrossRef]
- Wu, J.N.; Xing, T.Z.; Song, Y.M. Rock mechanical parameter inversion based on DSCM-FEMU. Chin. J. Undergr. Space Eng. 2021, 17, 350–355, 364. (In Chinese) [Google Scholar]
- Liu, G.Y.; Wang, L.; Yi, Y.N.; Sun, L.B.; Shi, L.; Jiang, H.; Ma, S.P. Inverse identification of tensile and compressive damage properties of graphite material based on a single four-point bending test. J. Nucl. Mater. 2018, 509, 445–453. [Google Scholar] [CrossRef]
- Liu, G.Y.; Wang, L.; Yi, Y.N.; Sun, L.B.; Shi, L.; Ma, S.P. Inverse identification of graphite damage properties under complex stress states. Mater. Des. 2019, 183, 108135. [Google Scholar] [CrossRef]
- Xie, H.P.; Li, C.; He, Z.Q.; Li, C.B.; Lu, Y.Q.; Zhang, R.; Gao, M.Z.; Gao, F. Experimental study on rock mechanical behavior retaining the in situ geological conditions at different depths. Int. J. Rock Mech. Min. Sci. 2021, 138, 104548. [Google Scholar] [CrossRef]
- Zhou, X.P.; Cheng, H.; Feng, Y.F. An experimental study of crack coalescence behavior in rock-like materials containing multiple flaws under uniaxial compression. Rock Mech. Rock Eng. 2014, 47, 1961–1986. [Google Scholar] [CrossRef]
- Zhao, T.B.; Fang, K.; Wang, L.; Zou, J.; Wei, M. Estimation of elastic modulus of rock using modified point-load test. Geotech. Test. J. 2017, 40, 329–334. [Google Scholar] [CrossRef]
- Liu, X.S.; Ning, J.G.; Tan, Y.L.; Gu, Q.H. Damage constitutive model based on energy dissipation for intact rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 2016, 85, 27–32. [Google Scholar] [CrossRef]
- Ji, M.; Guo, H.J. Elastic-plastic threshold and rational unloading level of rocks. Appl. Sci. 2019, 9, 3164. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.Q.; Yang, J.; Xu, P. Analysis on pre-peak deformation and energy dissipation characteristics of sandstone under triaxial cyclic loading. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 24. [Google Scholar] [CrossRef]
- Wen, Z.J.; Tian, L.; Jiang, Y.J.; Zuo, Y.J.; Meng, F.B.; Dong, Y.; Lin, G.; Yang, T.; Lv, D.W. Research on damage constitutive model of inhomogeneous rocks based on strain energy density. Chin. J. Rock Mech. Eng. 2019, 38, 1332–1343. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, Q.; Zhong, S.; Cui, J.; Feng, X.T.; Song, L.B. Statistical characterization of the mechanical parameters of intact rock under triaxial compression: An experimental proof of the Jinping marble. Rock Mech. Rock Eng. 2016, 49, 4631–4646. [Google Scholar] [CrossRef]
- Pepe, G.; Cevasco, A.; Gaggero, L.; Berardi, R. Variability of intact rock mechanical properties for some metamorphic rock types and its implications on the number of test specimens. Bull. Eng. Geol. Environ. 2017, 76, 629–644. [Google Scholar] [CrossRef]

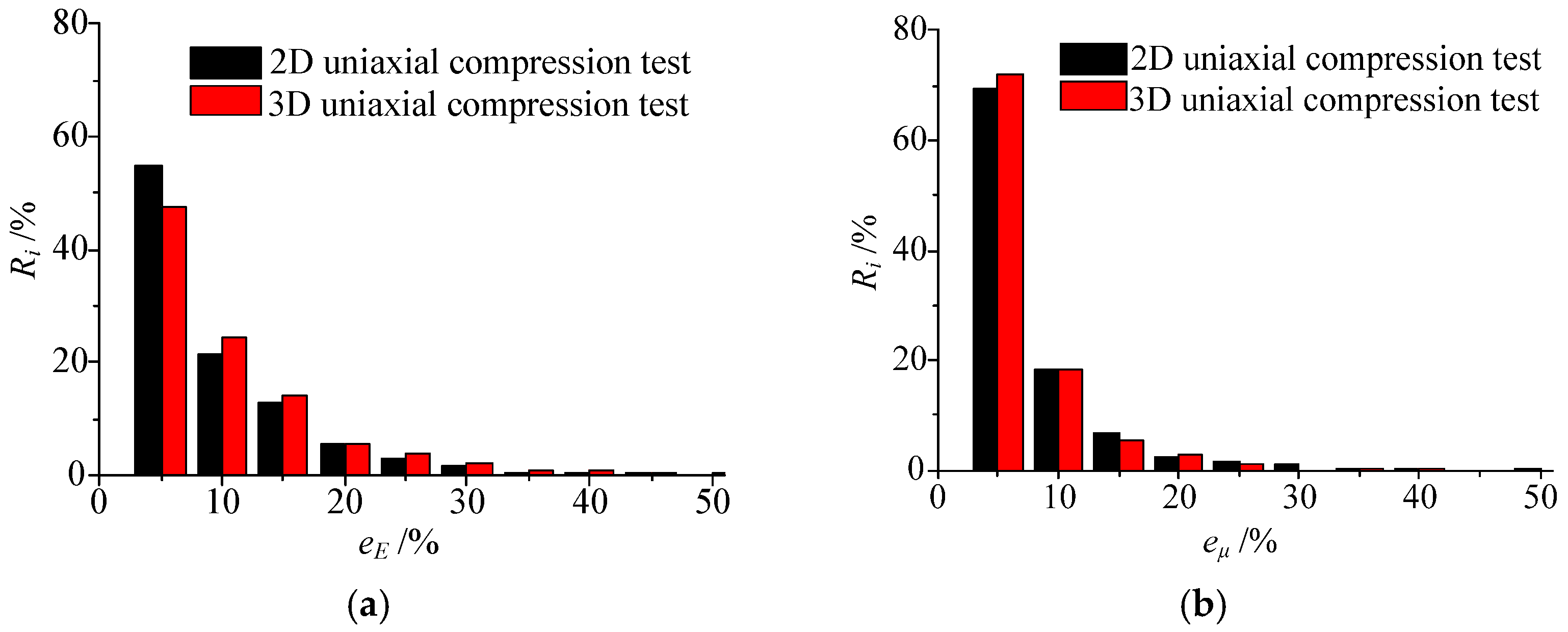



| Scheme | Influence Factor | Test Type | m | σ/MPa |
|---|---|---|---|---|
| I | mE and σ | 2D uniaxial compression test | 2, 4, 6, 8 | 5, 10, 15 |
| II | Stress state | 2D diametral compression test | 2, 4, 6 | 10 |
| III | Model dimensional difference | 3D uniaxial compression test | 2, 4, 6 | 10 |
| IV | mE, and mμ | 2D and 3D uniaxial compression test | 2 | 10 |
| Influence Factor | eE | SE | ||||
|---|---|---|---|---|---|---|
| mE | 2 | 4 | 6 | 2 | 4 | 6 |
| Scheme II | 1.87% | 0.88% | 0.82% | 1.80% | 1.23% | 0.92% |
| Scheme III | 6.61% | 3.47% | 2.60% | 5.25% | 2.97% | 2.21% |
| Test Model | eE | eμ |
|---|---|---|
| 2D uniaxial compression test | 8.67% | 6.18% |
| 3D uniaxial compression test | 9.89% | 5.83% |
| Specimen | Stress/MPa | Macro Young’s Modulus/GPa | Macro Poisson’s Ratio | |||
|---|---|---|---|---|---|---|
| DF-PF | LVDT (Error) | DIC (Error) | DF-PF | DIC (Error) | ||
| Sandstone | 18(69%σc) | 6.16 | 5.89 (4.58%) | 5.93 (3.88%) | 0.314 | 0.344 (8.72%) |
| 22(84%σc) | 5.85 | 6.09 (3.94%) | 5.88 (0.51%) | 0.436 | 0.463 (5.83%) | |
| 26(99%σc) | 5.52 | 6.00 (8.00%) | 5.45 (1.28%) | 0.604 | 0.681 (11.3%) | |
| Mean value | 5.84 | 5.99 (2.50%) | 5.75 (1.57%) | 0.451 | 0.496 (9.07%) | |
| Aluminum | 160 | 71.74 | 71.54 (0.28%) | 70.59 (1.63%) | 0.139 | 0.152 (8.55%) |
| 180 | 71.49 | 72.55 (1.46%) | 70.00 (2.12%) | 0.154 | 0.167 (7.78%) | |
| 200 | 74.60 | 73.53 (1.46%) | 72.73 (2.57%) | 0.193 | 0.210 (8.10%) | |
| Mean value | 72.61 | 72.54 (0.10%) | 71.11 (2.11%) | 0.162 | 0.176 (7.96%) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Liu, G.; Zhao, T.; Ma, Q.; Wang, L.; Zhang, Y. Inversion Method of the Young’s Modulus Field and Poisson’s Ratio Field for Rock and Its Test Application. Materials 2022, 15, 5463. https://doi.org/10.3390/ma15155463
Yin Y, Liu G, Zhao T, Ma Q, Wang L, Zhang Y. Inversion Method of the Young’s Modulus Field and Poisson’s Ratio Field for Rock and Its Test Application. Materials. 2022; 15(15):5463. https://doi.org/10.3390/ma15155463
Chicago/Turabian StyleYin, Yanchun, Guangyan Liu, Tongbin Zhao, Qinwei Ma, Lu Wang, and Yubao Zhang. 2022. "Inversion Method of the Young’s Modulus Field and Poisson’s Ratio Field for Rock and Its Test Application" Materials 15, no. 15: 5463. https://doi.org/10.3390/ma15155463
APA StyleYin, Y., Liu, G., Zhao, T., Ma, Q., Wang, L., & Zhang, Y. (2022). Inversion Method of the Young’s Modulus Field and Poisson’s Ratio Field for Rock and Its Test Application. Materials, 15(15), 5463. https://doi.org/10.3390/ma15155463






