Influence of Structural Porosity and Martensite Evolution on Mechanical Characteristics of Nitinol via In-Silico Finite Element Approach
Abstract
1. Introduction
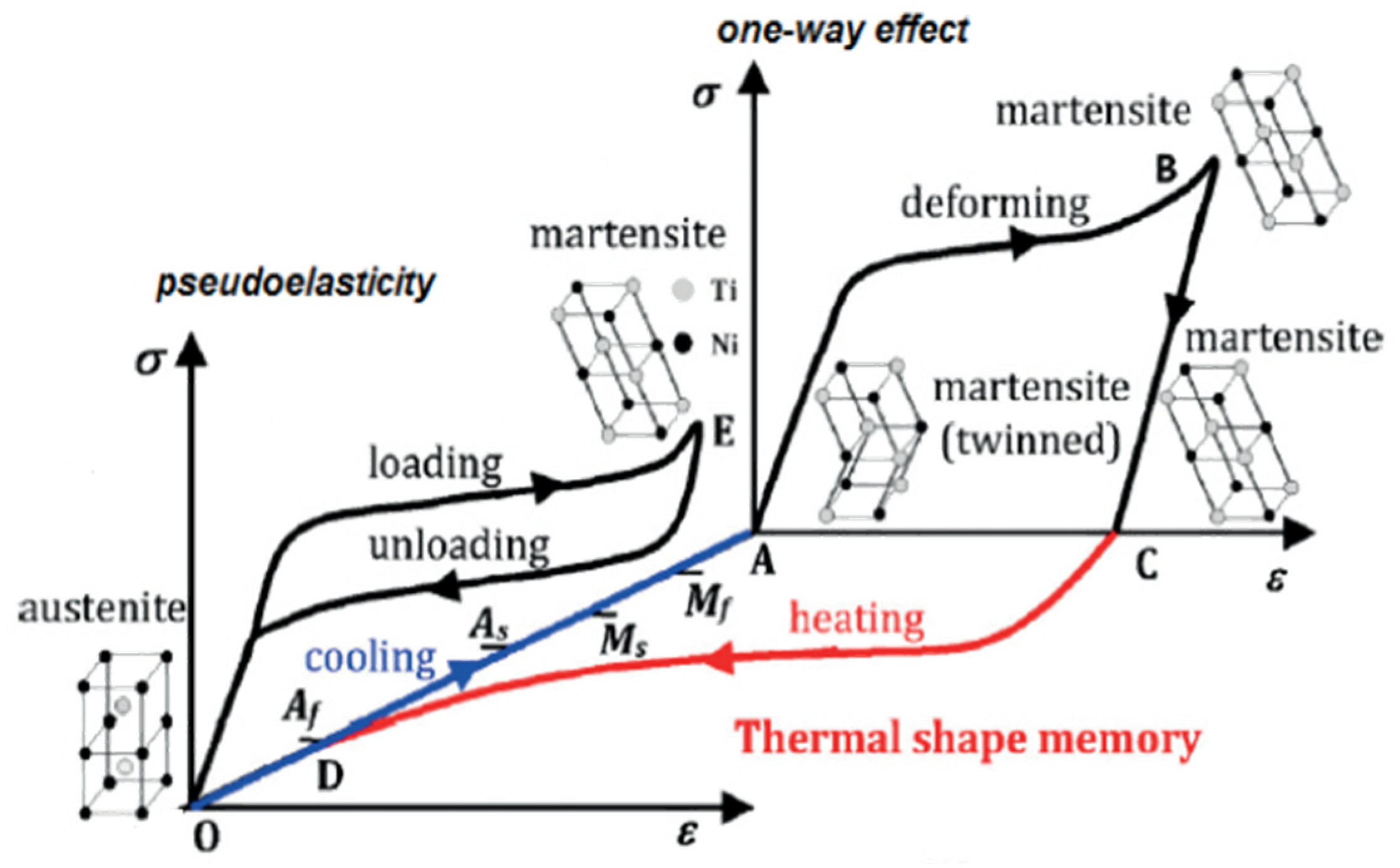
1.1. Kinematics of Phase Transformations
2. Materials and Methods
2.1. Constitutive Modelling of Nitinol SMAs
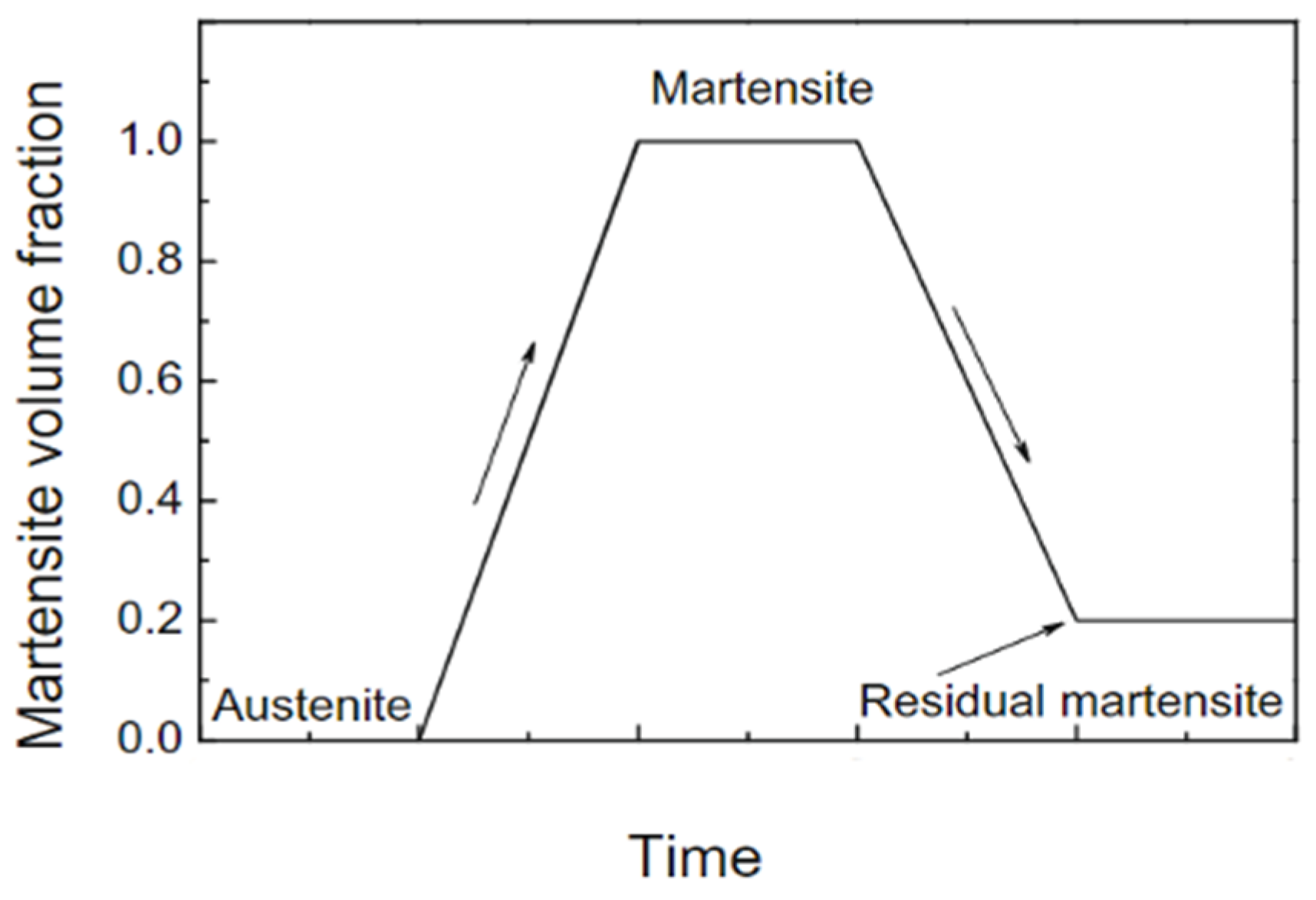
2.2. Microscale Models
2.3. Macroscale Models
- 1D and 3D constitutive model to reproduce superelasticity
- Time-discrete isothermal model
- Algorithmic implementation with a finite element (FE) framework.
- Conversion of austenite into single-variant martensite (A→S)
- Conversion of single-variant martensite into austenite (S→A)
- Reorientation of the single-variant martensite (S→S)
2.3.1. Conversion of Austenite into Single-Variant Martensite (A→S)
2.3.2. Conversion of Single-Variant Martensite into Austenite (S→A)
2.3.3. Reorientation of the Single-Variant Martensite (S→S)
2.4. Numerical Simulations
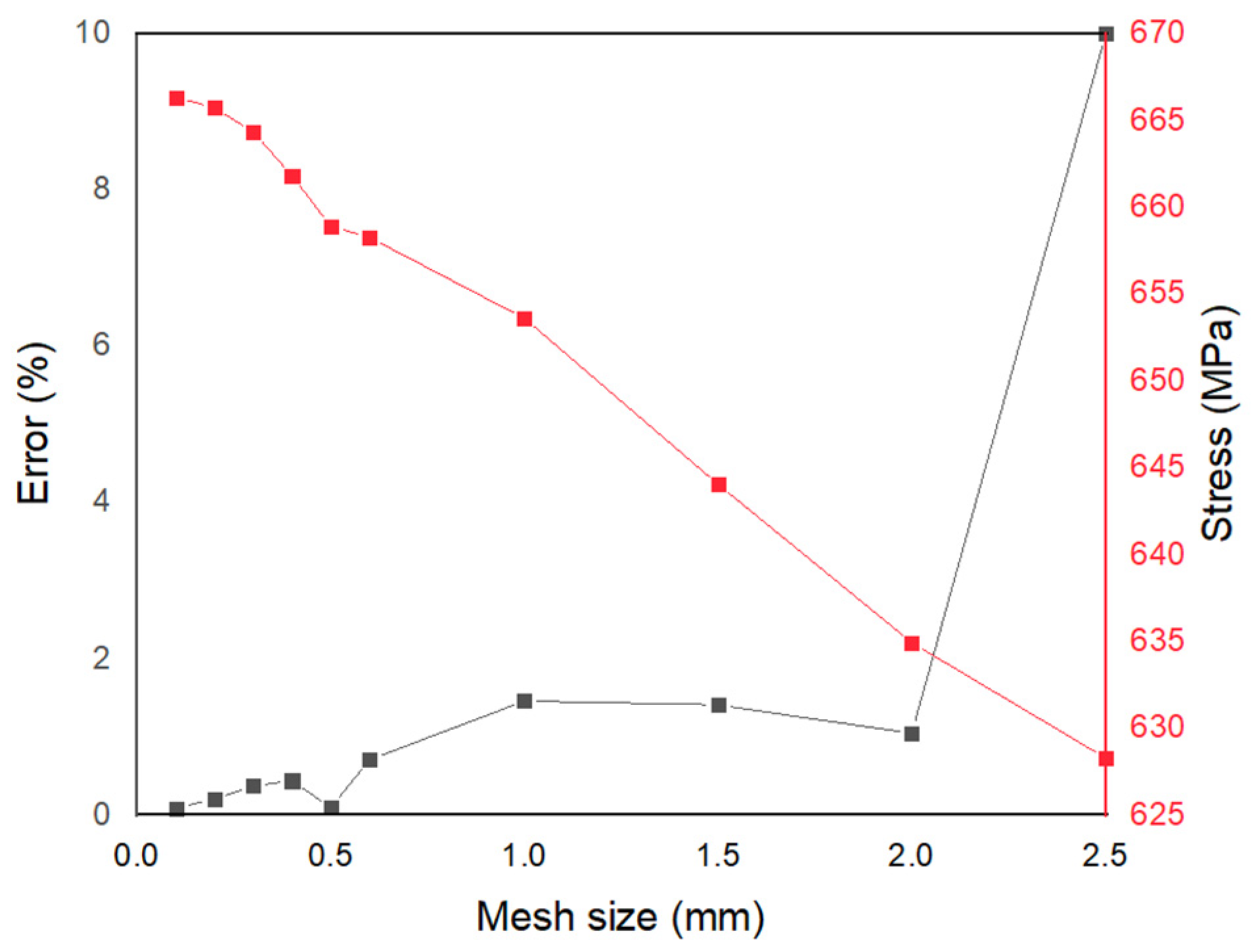
2.5. Mesh Convergence
3. Results
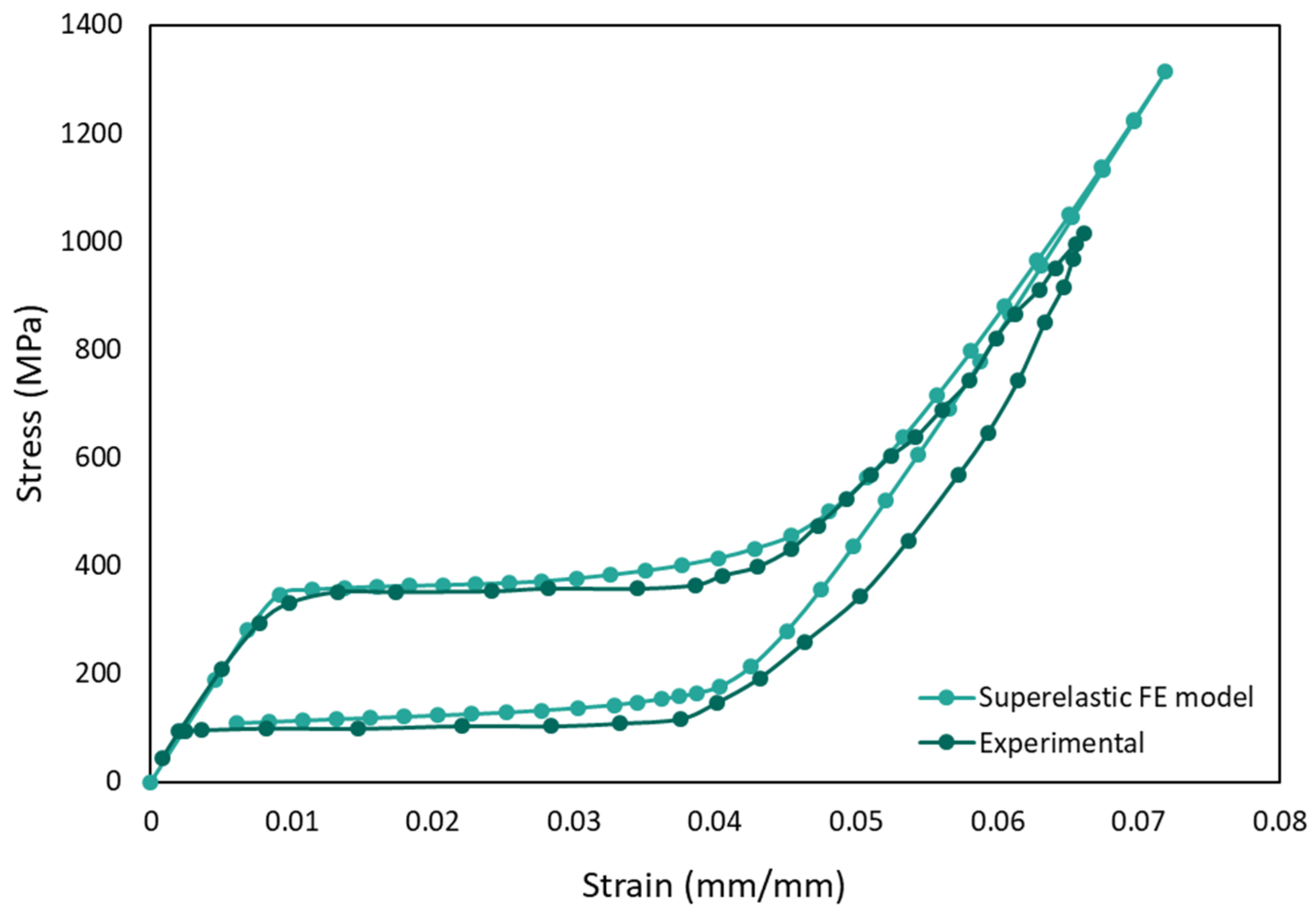
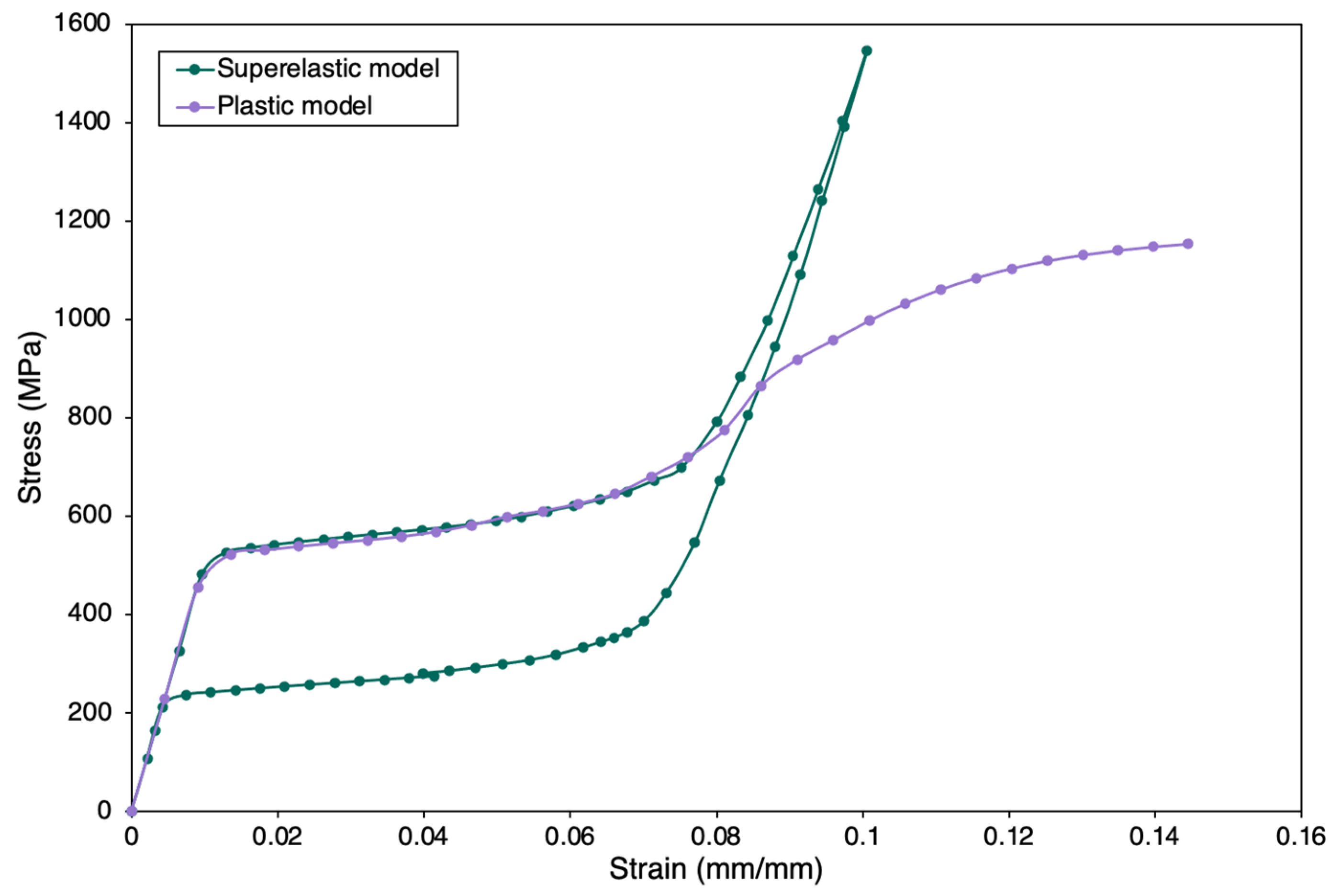
3.1. Model Validation
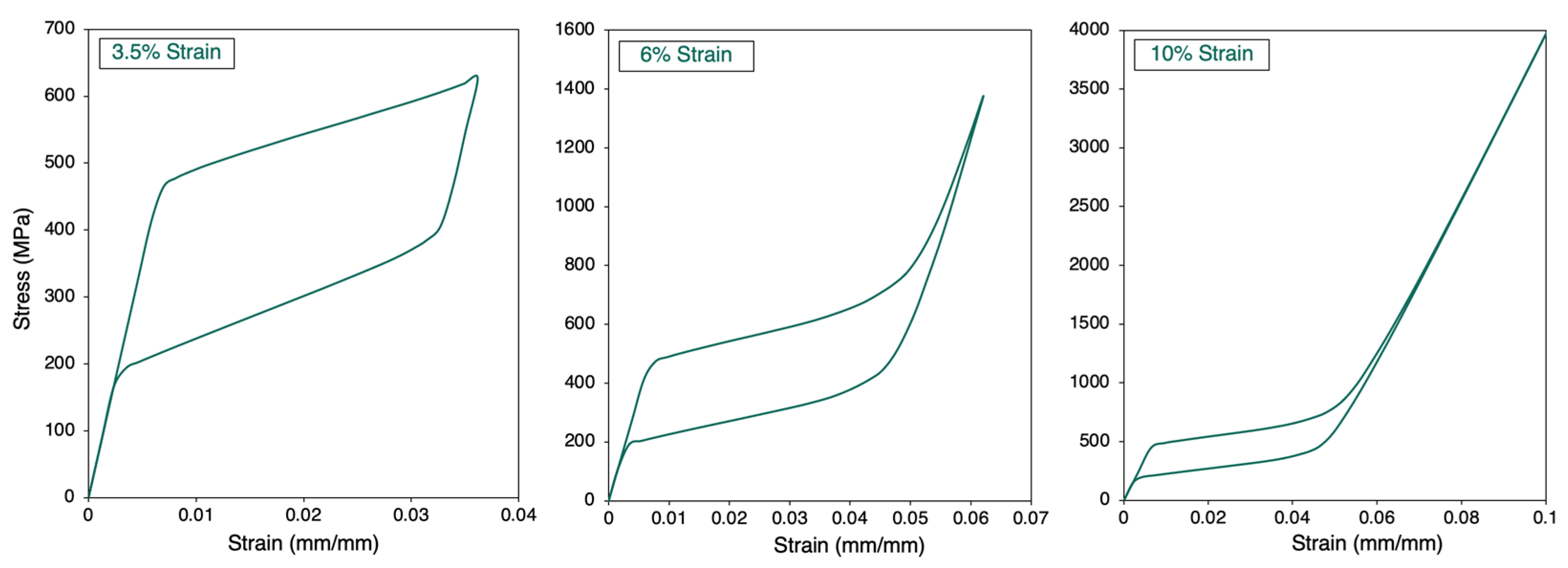
3.2. Response to Strain Levels
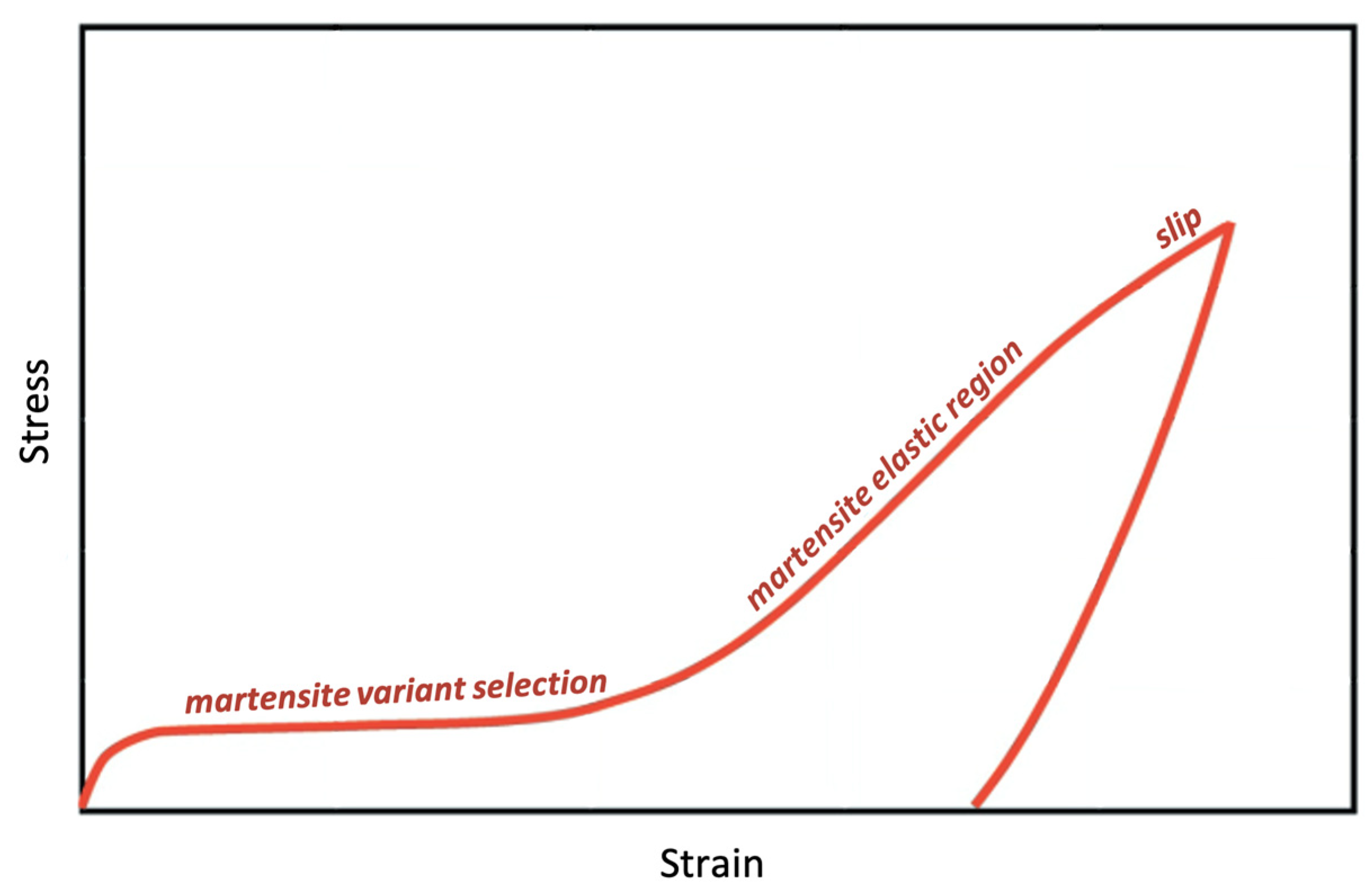
3.3. Asymmetry in Tension and Compression
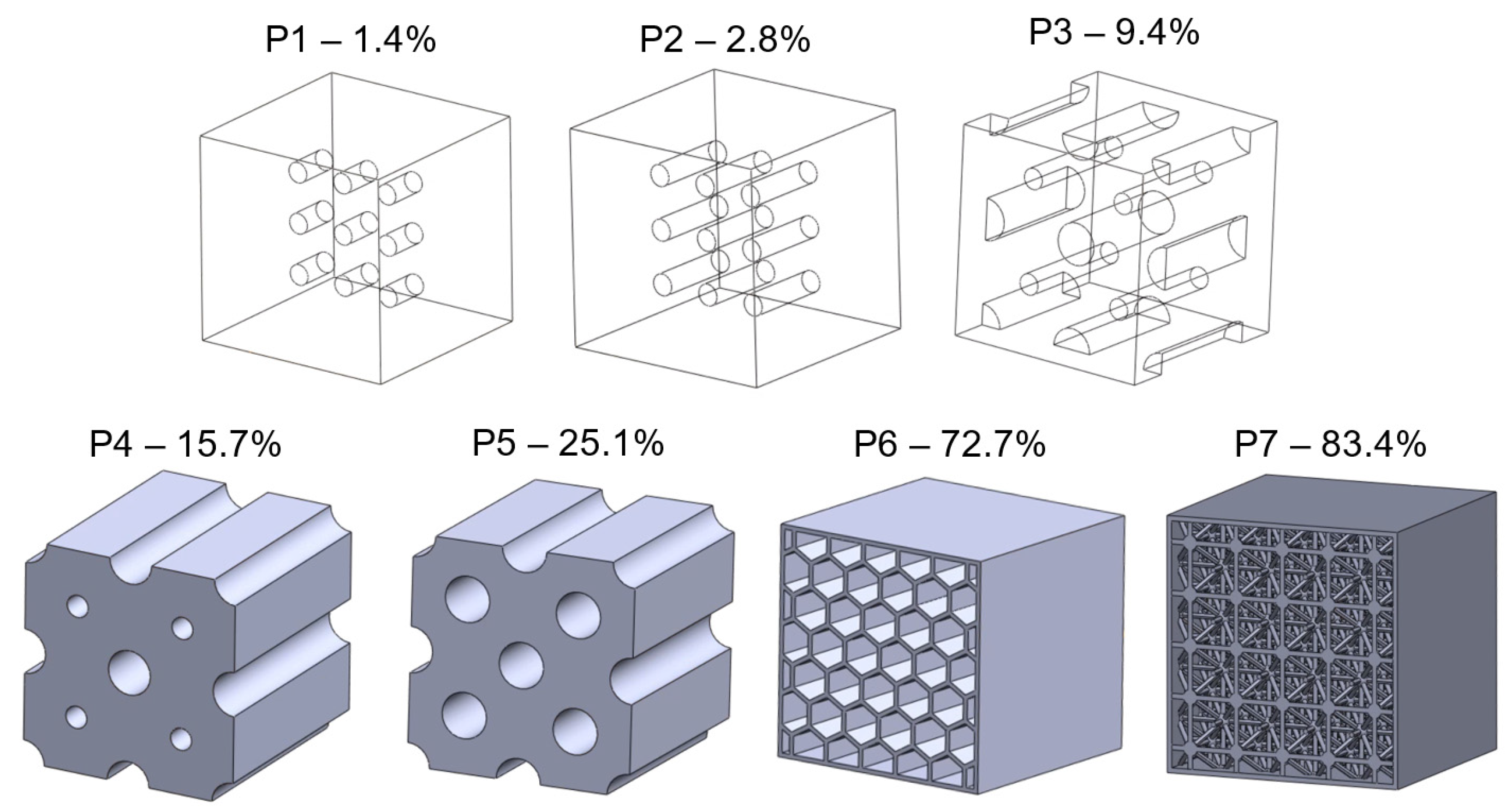
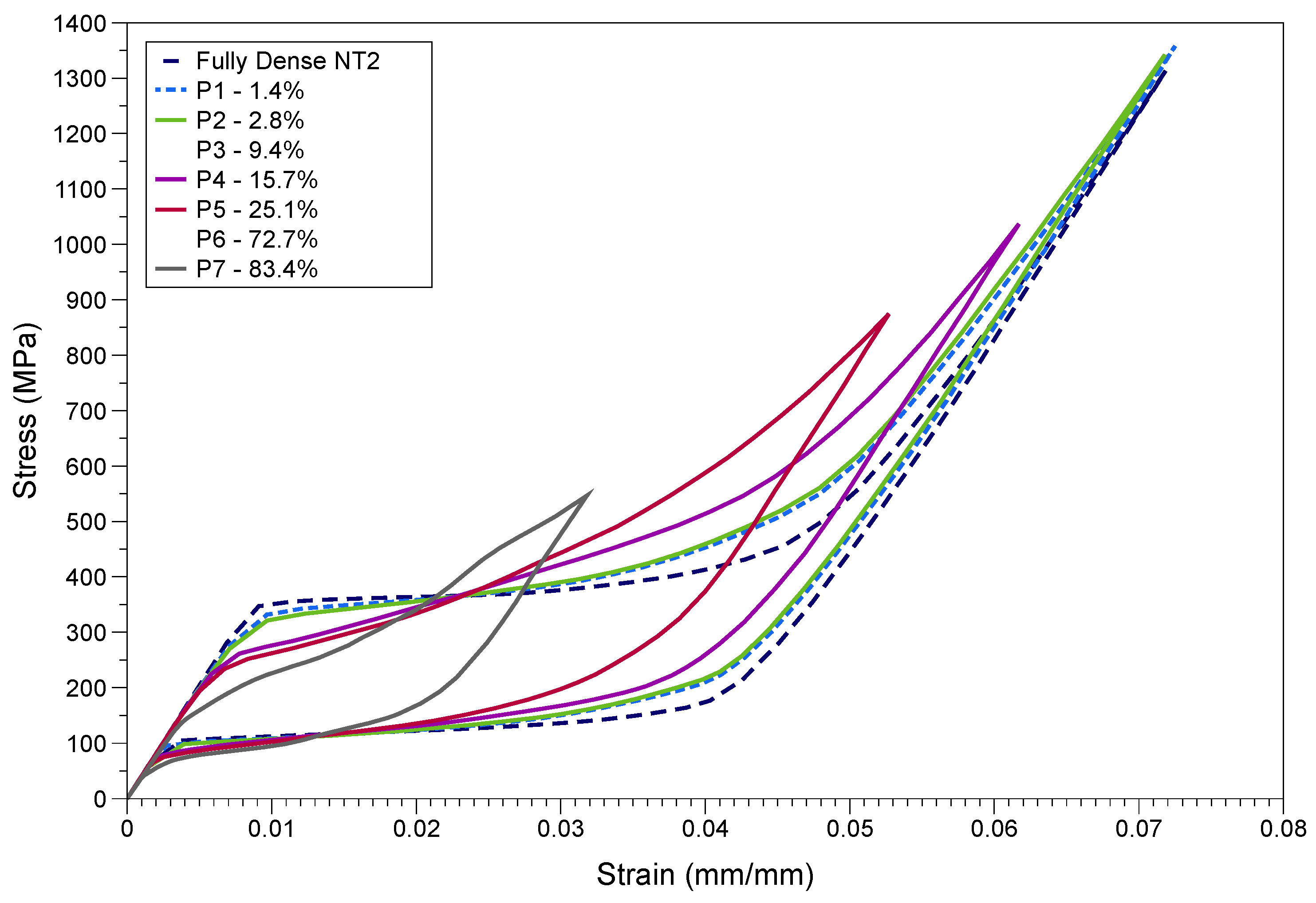
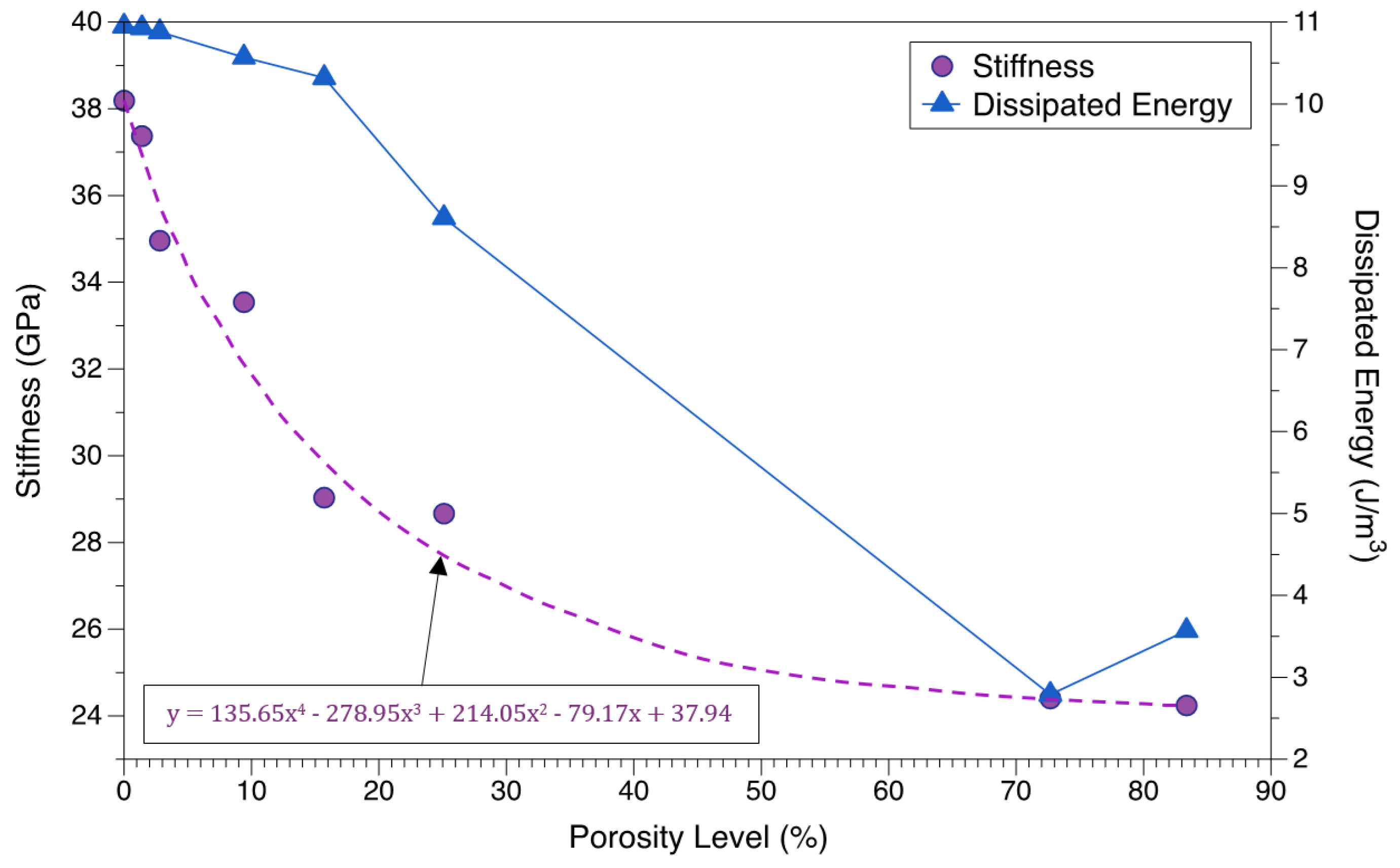
3.4. Compression of Porous Structures
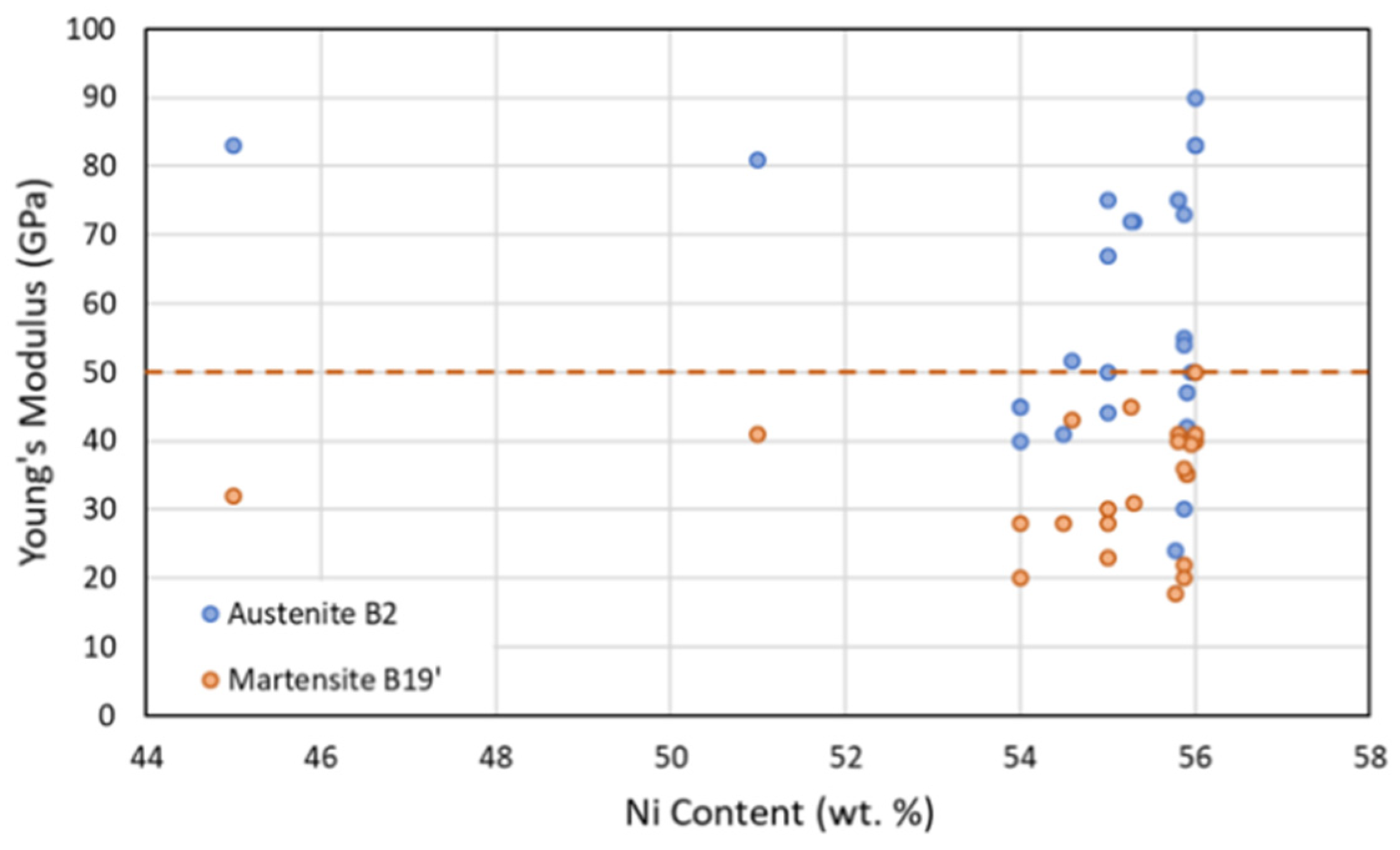
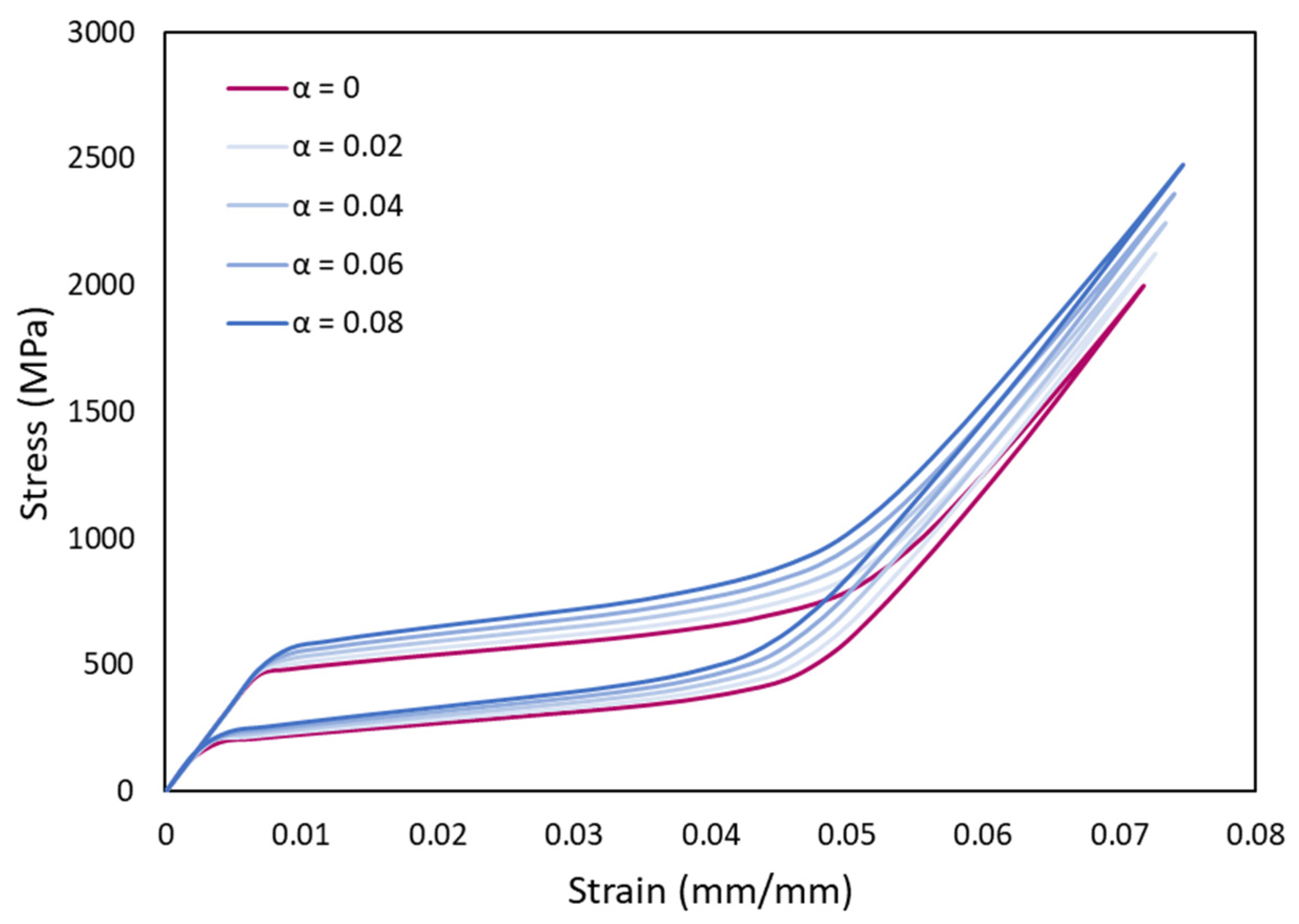
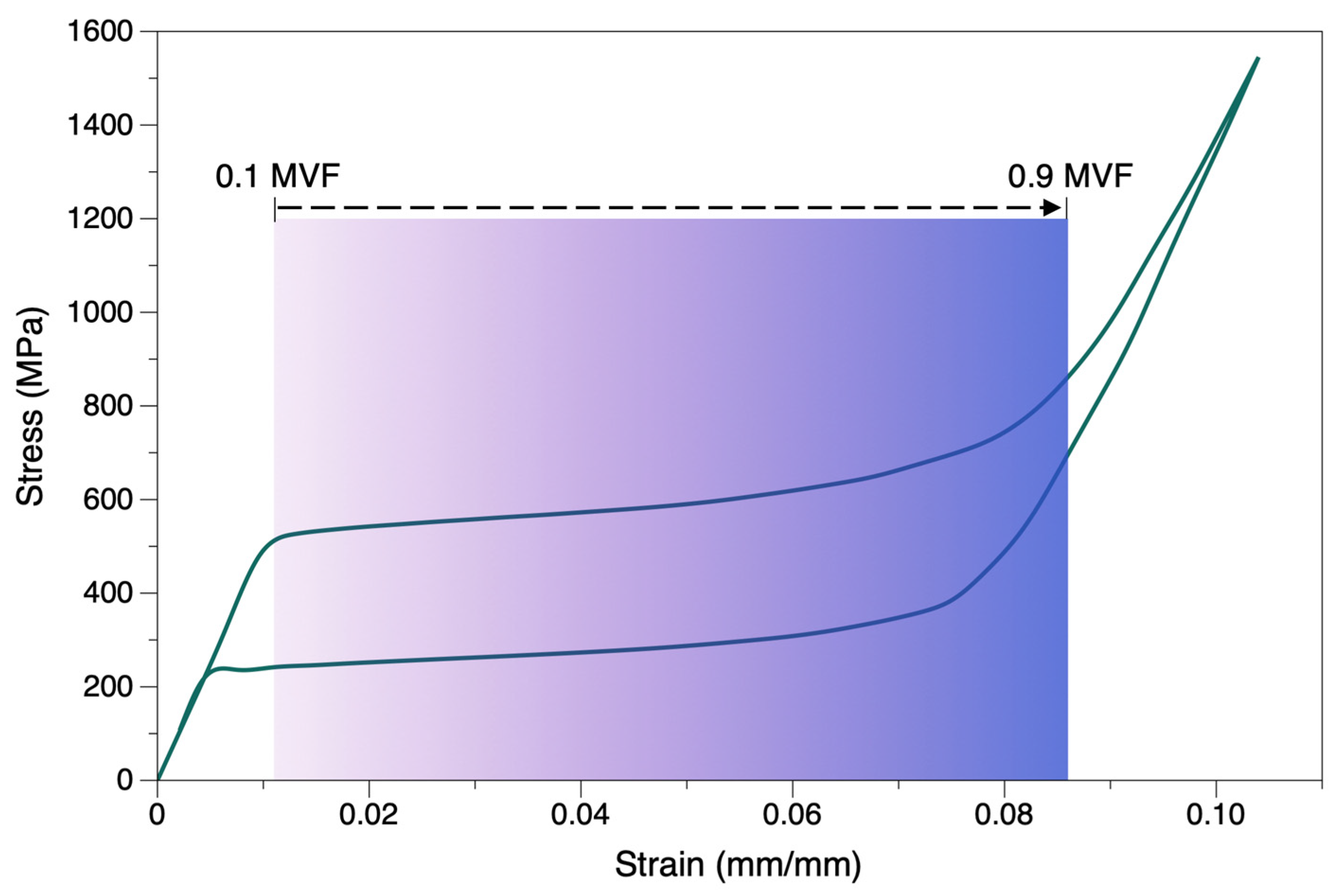
3.5. MVF vs. Elastic Modulus
4. Discussion
4.1. Mechanical Strain
4.2. Structural Porosity
4.3. Martensite Evolution vs. Stiffness
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Elastic Modulus Estimation from Martensite Volume Fraction
References
- Depriester, D.; Maynadier, A.; Lavernhe-Taillard, K.; Hubert, O. Thermomechanical modelling of a NiTi SMA sample submitted to displacement-controlled tensile test. Int. J. Solids Struct. 2014, 51, 1901–1922. [Google Scholar] [CrossRef]
- Aycock, K.I.; Weaver, J.D.; Paranjape, H.M.; Senthilnathan, K.; Bonsignore, C.; Craven, B.A. Full-field microscale strain measurements of a Nitinol medical device using digital image correlation. J. Mech. Behav. Biomed. Mater. 2021, 114, 104221. [Google Scholar] [CrossRef] [PubMed]
- Nematzadeh, F.; Sadrnezhaad, S.K. Finite element analysis of mechanical performance of Nitinol biliary stent: Effect of material properties. Mater. Res. Innov. 2013, 17, S53–S59. [Google Scholar] [CrossRef]
- Bram, M.; Ahmad-Khanlou, A.; Heckmann, A.; Fuchs, B.; Buchkremer, H.P.; Stöver, D. Powder metallurgical fabrication processes for NiTi shape memory alloy parts. Mater. Sci. Eng. 2002, 337, 254–263. [Google Scholar] [CrossRef]
- Saedi, S. Shape Memory Behavior of Dense and Porous NiTi Alloys Fabricated by Selective Laser Melting. Ph.D. Thesis, University of Kentucky, Lexington, KY, USA, 2017. [Google Scholar]
- Sridhar, S.K.; Stebner, A.P.; Rollett, A.D. Statistical variations in predicted martensite variant volume fractions in superelastically deformed NiTi modeled using habit plane variants versus correspondence variants. Int. J. Solids Struct. 2021, 221, 60–76. [Google Scholar] [CrossRef]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti–Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Contardo, L.; Guenin, G. Training and two-way memory effect in Cu-Zn-Al alloy. Acta Metall. Mater. 1990, 38, 1267–1272. [Google Scholar] [CrossRef]
- Weafer, F.M.; Guo, Y.; Bruzzi, M.S. The effect of crystallographic texture on stress-induced martensitic transformation in NiTi: A computational analysis. J. Mech. Behav. Biomed. Mater. 2016, 53, 210–217. [Google Scholar] [CrossRef]
- Guo, Y.; Klink, A.; Fu, C.; Snyder, J. Machinability and surface integrity of Nitinol shape memory alloy. CIRP Ann. 2013, 62, 83–86. [Google Scholar] [CrossRef]
- Costanza, G.; Tata, M.E. Shape memory alloys for aerospace, recent developments, and new applications: A short review. Materials 2020, 13, 1856. [Google Scholar] [CrossRef]
- Eaton-Evans, J.; Dulieu-Barton, J.M.; Little, E.G.; Brown, I.A. Observations during mechanical testing of Nitinol. J. Mech. Eng. Sci. 2008, 222, 97–105. [Google Scholar] [CrossRef]
- Liu, J. Compliant Mechanisms Using Superelastic Nitinol. Master’s Thesis, Pennsylvania State University, State College, PA, USA, 2012. [Google Scholar]
- Auricchio, F.; Taylor, R.L. Shape-memory alloys: Modelling and numerical simulations of the finite-strain superelastic behavior. Comput. Methods Appl. Mech. Eng. 1997, 143, 175–194. [Google Scholar] [CrossRef]
- Chekotu, J.C.; Groarke, R.; O’Toole, K.; Brabazon, D. Advances in selective laser melting of Nitinol shape memory alloy part production. Materials 2019, 12, 809. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.Y.; Dui, G.S. Temperature analysis of one-dimensional NiTi shape memory alloys under different loading rates and boundary conditions. Int. J. Solids Struct. 2013, 50, 3254–3265. [Google Scholar] [CrossRef]
- Laeng, J.; Xiu, Z.; Xu, X.; Sun, X.; Ru, H.; Liu, Y. Phase formation of Ni–Ti via solid state reaction. Phys. Scr. 2007, T129, 250–254. [Google Scholar] [CrossRef]
- Barbarino, S.; Saavedra-Flores, E.I.; Ajaj, R.M.; Dayyani, I.; Friswell, M.I. A review on shape memory alloys with applications to morphing aircraft. Smart Mater. Struct. 2014, 23, 063001. [Google Scholar] [CrossRef]
- Skalitzky, A.; Caleb, P.; Gurley, A.; Beale, D. Woven Nitinol Fabric Strips Characterized in Tension via Finite Element Analysis and Geometric Modelling. In Proceedings of the ASME 2019 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Louisville, KY, USA, 9–11 September 2019. [Google Scholar]
- Meier, H.; Haberland, C. Experimental studies on selective laser melting of metallic parts. Mater. Werks. 2008, 39, 665–670. [Google Scholar] [CrossRef]
- Haberland, C.; Elahinia, M.; Walker, J.M.; Meier, H.; Frenzel, J. On the development of high quality NiTi shape memory and pseudoelastic parts by additive manufacturing. Smart Mater. Struct. 2014, 23, 104002. [Google Scholar] [CrossRef]
- Walker, J.M.; Haberland, C.; Taheri Andani, M.; Karaca, H.E.; Dean, D.; Elahinia, M. Process development and characterization of additively manufactured nickel-titanium shape memory parts. J. Intel. Mater. Syst. Struct. 2016, 27, 2653–2660. [Google Scholar] [CrossRef]
- Ou, S.F.; Peng, B.Y.; Chen, Y.C.; Tsai, M.H. Manufacturing and characterization of NiTi alloy with functional properties by selective laser melting. Metals 2018, 8, 342. [Google Scholar] [CrossRef]
- Patterson, A.E.; Messimer, S.L.; Farrington, P.A. Overhanging features and the SLM/DMLS residual stresses problem: Review and future research need. Technologies 2017, 5, 15. [Google Scholar] [CrossRef]
- Song, B.; Zhao, X.; Li, S.; Han, C.; Wei, Q.; Wen, S.; Liu, J.; Shi, Y. Differences in microstructure and properties between selective laser melting and traditional manufacturing for fabrication of metal parts: A review. Front. Mech. Eng. 2015, 10, 111–125. [Google Scholar] [CrossRef]
- Andani, M.T.; Haberland, C.; Walker, J.M.; Karamooz, M.; Turabi, A.S.; Saedi, S.; Rahmanian, R.; Karaca, H.; Dean, D.; Kadkhodaei, M. Achieving biocompatible stiffness in NiTi through additive manufacturing. J. Intell. Mater. Syst. Struct. 2016, 27, 2661–2671. [Google Scholar] [CrossRef]
- Yusuf, S.M.; Gao, N. Influence of energy density on metallurgy and properties in metal additive manufacturing. Mater. Sci. Technol. 2017, 33, 1269–1289. [Google Scholar] [CrossRef]
- Jahadakbar, A.; Nematollahi, M.; Safaei, K.; Bayati, P.; Giri, G.; Dabbaghi, H.; Dean, D.; Elahinia, M. Design, modeling, additive manufacturing, and polishing of stiffness-modulated porous Nitinol bone fixation plates followed by thermomechanical and composition analysis. Metals 2020, 10, 151. [Google Scholar] [CrossRef]
- Safavi, M.S.; Bordbar-Khiabani, A.; Khalil-Allafi, J.; Mozafari, M.; Visai, L. Additive Manufacturing: An Opportunity for the Fabrication of Near-Net-Shape NiTi Implants. J. Manuf. Mater. Process. 2022, 6, 65. [Google Scholar] [CrossRef]
- Šittner, P.; Sedlák, P.; Seiner, H.; Sedmák, P.; Pilch, J.; Delville, R.; Heller, L.; Kadeřávek, L. On the coupling between martensitic transformation and plasticity in NiTi: Experiments and continuum based modelling. Prog. Mater. Sci. 2018, 98, 249–298. [Google Scholar] [CrossRef]
- Auricchio, F.; Taylor, R.L.; Lubliner, J. Shape-memory alloys: Macromodelling and numerical simulations of the superelastic behaviour. Comput. Methods Appl. Mech. Eng. 1997, 146, 281–312. [Google Scholar] [CrossRef]
- Paiva, A.; Savi, M.A. An overview of constitutive models for shape memory alloys. Math. Prob. Eng. 2006, 2006, 56876. [Google Scholar] [CrossRef]
- Duerig, T. The metallurgy of Nitinol as it pertains to medical devices. In Titanium in Medical and Dental Applications; Woodhead Publishing: Sawston, UK, 2018; pp. 555–570. [Google Scholar]
- Wang, X.; Xu, B.; Yue, Z. Phase transformation behavior of pseudoelastic NiTi shape memory alloys under large strain. J. Alloy. Compd. 2008, 463, 417–422. [Google Scholar] [CrossRef]
- Rebelo, N.; Perry, M. Finite element analysis for the design of Nitinol medical devices. Minim. Invasive Ther. Allied Technol. 2000, 9, 75–80. [Google Scholar] [CrossRef]
- Gara, D.K.; Potnuru, S. Quandaries during numerical analysis on shape memory product. Int. J. Mech. Prod. Eng. Res. Dev. 2020, 10, 271–282. [Google Scholar]
- Chiroiu, V.; Florinel Ionescu, M.; Sireteanu, T.; Ioan, R.; Munteanu, L. On intrinsic time measure in the modeling of cyclic behavior of a nitinol cubic block. Smart Mater. Struct. 2015, 24, 035022. [Google Scholar] [CrossRef][Green Version]
- Song, D.; Kang, G.; Kan, Q.; Yu, C.; Zhang, C. Non-proportional multiaxial transformation ratchetting of super-elastic NiTi shape memory alloy: Experimental observations. Mech. Mater. 2014, 70, 94–105. [Google Scholar] [CrossRef]
- Kan, Q.; Kang, G. Constitutive model for uniaxial transformation ratchetting of super-elastic NiTi shape memory alloy at room temperature. Int. J. Plast. 2010, 26, 441–465. [Google Scholar] [CrossRef]
- Šittner, P.; Heller, L.; Pilch, J.; Curfs, C.; Alonso, T.; Favier, D. Young’s modulus of austenite and martensite phases in superelastic NiTi wires. J. Mater. Eng. Perform. 2014, 23, 2303–2314. [Google Scholar] [CrossRef]
- Gugat, J.L.; Bechtold, C.; Chluba, C.; Quandt, E.; de Miranda, R.L. High-cycle mechanical fatigue performance of sputtered Nitinol. J. Mater. Eng. Perform. 2020, 29, 1892–1900. [Google Scholar] [CrossRef]
- Tucker, N.; Lindsey, K. An Introduction to Automotive Composites; Rapra Technology Limited: Shrewsbury, UK, 2002. [Google Scholar]
- Zaccaria, A.; Migliavacca, F.; Pennati, G.; Petrini, L. Modeling of braided stents: Comparison of geometry reconstruction and contact strategies. J. Biomech. 2020, 107, 109841. [Google Scholar] [CrossRef]
- Auricchio, F.; Conti, M.; De Beule, M.; De Santis, G.; Verhegghe, B. Carotid artery stenting simulation: From patient-specific images to finite element analysis. Med. Eng. Phys. 2011, 33, 281–289. [Google Scholar] [CrossRef]
- Derycke, L.; Perrin, D.; Cochennec, F.; Albertini, J.N.; Avril, S. Predictive numerical simulations of double branch stent-graft deployment in an aortic arch aneurysm. Ann. Biomed. Eng. 2019, 47, 1051–1062. [Google Scholar] [CrossRef]
- Sturla, F.; Ronzoni, M.; Vitali, M.; Dimasi, A.; Vismara, R.; Preston-Maher, G.; Burriesci, G.; Votta, E.; Redaelli, A. Impact of different aortic valve calcification patterns on the outcome of transcatheter aortic valve implantation: A finite element study. J. Biomech. 2016, 49, 2520–2530. [Google Scholar] [CrossRef] [PubMed]
- Gastaldi, D.; Sassi, V.; Petrini, L.; Vedani, M.; Trasatti, S.; Migliavacca, F. Continuum damage model for bioresorbable magnesium alloy devices—Application to coronary stents. J. Mech. Behav. Biomed. Mater. 2011, 4, 352–365. [Google Scholar] [CrossRef] [PubMed]
- Azaouzi, M.; Lebaal, N.; Makradi, A.; Belouettar, S. Optimization based simulation of self-expanding Nitinol stent. Mater. Des. 2013, 50, 917–928. [Google Scholar] [CrossRef]
- Petrini, L.; Trotta, A.; Dordoni, E.; Migliavacca, F.; Dubini, G.; Lawford, P.V.; Gosai, J.N.; Ryan, D.M.; Testi, D.; Pennati, G. A computational approach for the prediction of fatigue behavior in peripheral stents: Application to a clinical case. Ann. Biomed. Eng. 2016, 44, 536–547. [Google Scholar] [CrossRef] [PubMed]
- Confluent. Material Data Sheet: Superelastic Nitinol Alloys; Confluent Medical Technologies: Fremont, CA, USA, 2020. [Google Scholar]
- Filip, P.; Mazanec, K. Influence of work hardening on the reactive stress in a TiNi shape memory alloy. Mater. Sci. Eng. A 1994, A174, L41–L43. [Google Scholar] [CrossRef]
- Ulbrich. Nitinol Data Sheet; Ulbrich Stainless Steels and Special Metals Inc.: North Haven, CT, USA, 2020. [Google Scholar]
- Hodgson, D.E.; Biermann, R.J. Properties and Selection: Nonferrous Alloys and Special-Purpose Materials. In Shape Memory Alloys ASM Handbook; ASM International: Almere, The Netherlands, 1990; Volume 2. [Google Scholar]
- Liu, Y.; Xiang, H. Apparent modulus of elasticity of near-equiatomic NiTi. J. Alloys Comp. 1998, 270, 154–159. [Google Scholar] [CrossRef]
- Mahtabi, M.J.; Shamsaei, N.; Mitchell, M.R. Fatigue of Nitinol: The state-of-the-art and ongoing challenges. J. Mech. Behav. Biomed. Mater. 2015, 50, 228–254. [Google Scholar] [CrossRef]
- Nematzadeh, F.; Sadrnezhaad, S.K. Effects of material properties on mechanical performance of Nitinol stent designed for femoral artery: Finite element analysis. Sci. Iran. 2012, 19, 1564–1571. [Google Scholar] [CrossRef]
- Eshghinejad, A. Finite Element Study of a Shape Memory Alloy Bone Implant. Master’s Thesis, University of Toledo, Toledo, OH, USA, 2012. [Google Scholar]
- Lagoudas, D.C. Shape Memory Alloys: Modeling and Engineering Applications; Springer: New York, NY, USA, 2008. [Google Scholar]
- Qian, H.; Li, H.N.; Song, G. A Constitutive Model of Shape Memory Alloys with Consideration of Martensitic Hardening Effect. In Proceedings of the 11th Aerospace Division International Conference on Engineering, Science, Construction, and Operations in Challenging Environments, Long Beach, CA, USA, 3–5 March 2008. [Google Scholar]
- Sengupta, A.; Papadopoulos, P.; Taylor, R.L. Multiscale finite element modeling of superelasticity in Nitinol polycrystals. Comput. Mech. 2009, 43, 573–584. [Google Scholar] [CrossRef]
- Theriault, P.; Terriault, P.; Brailovski, V.; Gallo, R. Finite element modeling of a progressively expanding shape memory stent. J. Biomech. 2006, 39, 2837–2844. [Google Scholar] [CrossRef]
- Naceur, I.B.; Charfi, A.; Bouraoui, T.; Elleuch, K. Finite element modeling of superelastic nickel-titanium orthodontic wires. J. Biomech. 2014, 47, 3630–3638. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, A.; Papadopoulos, P. Constitutive modeling and finite element approximation of B2-R-B19′ phase transformations in Nitinol polycrystals. Comput. Methods Appl. Mech. Eng. 2009, 198, 3214–3227. [Google Scholar] [CrossRef]
- Mazzaccaro, D.; Berti, F.; Antonini, L.; Pennati, G.; Petrini, L.; Migliavacca, F.; Nano, G. Biomechanical interpretation of observed fatigue fractures of peripheral Nitinol stents in the superficial femoral arteries through in silico modelling. Med. Hypotheses 2020, 142, 109771. [Google Scholar] [CrossRef]
- Hazar, S.; Zaki, W.; Moumni, Z.; Anlas, G. Modeling of steady-state crack growth in shape memory alloys using a stationary method. Int. J. Plast. 2015, 67, 26–38. [Google Scholar] [CrossRef]
- Wang, X.M.; Wang, Y.F.; Lu, Z.Z.; Deng, C.H.; Yue, Z.F. An experimental study of the superelastic behavior in NiTi shape memory alloys under biaxial proportional and non-proportional cyclic loadings. Mech. Mater. 2010, 42, 365–373. [Google Scholar] [CrossRef]
- Auricchio, F.; Scalet, G.; Urbano, M. A numerical/experimental study of Nitinol actuator springs. J. Mater. Eng. Perform. 2014, 23, 2420–2428. [Google Scholar] [CrossRef]
- Kelly, N.; McGrath, D.J.; Sweeney, C.A.; Kurtenbach, K.; Grogan, J.A.; Jockenhoevel, S.; O’Brien, B.J.; Bruzzi, M.; McHugh, P.E. Comparison of computational modelling techniques for braided stent analysis. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 1334–1344. [Google Scholar] [CrossRef]
- Mahtabi, M.J.; Shamsaei, N. Fatigue modeling for superelastic NiTi considering cyclic deformation and load ratio effects. Shape Mem. Superelasticity 2017, 3, 250–263. [Google Scholar] [CrossRef]
- Ghriallais, R.N.; Bruzzi, M. Self-expanding stent modelling and radial force accuracy. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 318–333. [Google Scholar] [CrossRef]
- Huang, B.; Pu, W.; Zhang, H.; Wang, H.; Song, G. A phenomenological model for superelastic shape memory alloy helical springs. Adv. Struct. Eng. 2015, 18, 1345–1354. [Google Scholar] [CrossRef]
- Major, S.; Hubalovska, M. Using of finite element method and computational analysis of mechanical properties of stent-grafts. Int. J. Mech. 2015, 9, 319–322. [Google Scholar]
- Brinson, L.C. One dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Yang, S.Y.; Escobar, J.; Clifton, R.J. Computational modeling of stress-wave-induced martensitic phase transformations in NiTi. Math. Mech. Solids 2009, 14, 220–257. [Google Scholar] [CrossRef]
- Kumar, A. Comprehensive Modeling of Shape Memory Alloys for Actuation of Large-Scale Structures. Ph.D. Thesis, University of Akron, Akron, OH, USA, 2010. [Google Scholar]
- Huang, M.; Gao, X.; Brinson, L.C. Multivariant micromechanical model for SMAs. Part 2. Polycrystal model. Int. J. Plast. 2000, 16, 1371–1390. [Google Scholar] [CrossRef]
- Patoor, E.; Lagoudas, D.C.; Entchev, P.B.; Brinson, L.C.; Gao, X. Shape memory alloys. Part I: General properties and modeling of single crystals. Mech. Mater. 2006, 38, 391–429. [Google Scholar] [CrossRef]
- Levitas, V.I.; Ozsoy, I.B. Micromechanical modeling of stress-induced phase transformations. Part 1. Thermodynamics and kinetics of coupled interface propagation and reorientation. Int. J. Plast. 2009, 25, 239–280. [Google Scholar] [CrossRef]
- Dumoulin, C.; Cochelin, B. Mechanical behavior modeling of balloon-expandable stents. J. Biomech. 2000, 33, 1461–1470. [Google Scholar] [CrossRef]
- Etave, F.; Finet, G.; Boivin, M.; Boyer, J.C.; Rioufol, G.; Thollet, G. Mechanical properties of coronary stents determined by using finite element analysis. J. Biomech. 2001, 34, 1065–1075. [Google Scholar] [CrossRef]
- Gao, X.; Brinson, L. A simplified multivariant SMA model based on invariant plane nature of martensitic transformation. J. Intell. Mater. Syst. Struct. 2002, 13, 795–810. [Google Scholar] [CrossRef]
- Marketz, F.; Fischer, F.D. Modelling the mechanical behavior of shape memory alloys under variant coalescence. Comput. Mater. Sci. 1996, 5, 210–226. [Google Scholar] [CrossRef]
- Majo, D.G.; Paterson, R.J.; Curtis, R.V.; Saidb, R.; Wood, R.D.; Bonet, J. Optimisation of the superplastic forming of a dental implant for bone augmentation using finite element simulations. Dent. Mater. 2004, 20, 409–418. [Google Scholar] [CrossRef] [PubMed]
- Stebner, A.P.; Vogel, S.C.; Noebe, R.D.; Sisneros, T.A.; Clausen, B.; Brown, D.W. Micromechanical quantification of elastic, twinning, and slip strain partitioning exhibited by polycrystalline, monoclinic nickel–titanium during large uniaxial deformations measured via in-situ neutron diffraction. J. Mech. Phys. Solids 2013, 62, 2302–2330. [Google Scholar] [CrossRef]
- Young, M.L.; Wagner, M.F.X.; Frenzel, J.; Schmahl, W.W.; Eggeler, G. Phase volume fractions and strain measurements in an ultrafine-grained NiTi shape-memory alloy during tensile loading. Acta Mater. 2010, 58, 2344–2354. [Google Scholar] [CrossRef]
- Brinson, L.C.; Schmidt, I.; Lammering, R. Stress-induced transformation behavior of a polycrystalline NiTi shape memory alloy: Micro and micromechanical investigations via in situ optical microscopy. J. Mech. Phys. Solids 2004, 52, 1549–1571. [Google Scholar] [CrossRef]
- Sedmák, P.; Šittner, P.; Pilch, J.; Curfs, C. Instability of cyclic superelastic deformation of NiTi investigated by synchrotron x-ray diffraction. Acta Mater. 2015, 94, 257–270. [Google Scholar] [CrossRef]
- Cai, S.; Schaffer, J.E.; Yu, C.; Daymond Ren, Y. Evolution of intergranular stresses in a martensitic and an austenitic NiTi wire during loading-unloading tensile deformation metallurgical and material transactions. Metall. Mater. Trans. A 2015, 46, 2479–2490. [Google Scholar] [CrossRef]
- Sedmák, P.; Pilch, J.; Heller, L.; Kopeček, J.; Wright, J.; Sedlák, P. Grain-resolved analysis of localized deformation in nickel-titanium wire under tensile load. Science 2016, 353, 559–562. [Google Scholar] [CrossRef] [PubMed]
- Paranjape, H.M.; Paul, P.P.; Sharma, H.; Kenesei, P.; Park, J.S.; Duerig, T.W. Influences of granular constraints and surface effects on the heterogeneity of elastic, superelastic, and plastic responses of polycrystalline shape memory alloys. J. Mech. Phys. Solids 2017, 102, 46–66. [Google Scholar] [CrossRef]
- Boyd, J.G.; Lagoudas, D.C. A thermodynamical constitutive model for shape memory materials. Part I: The monolithic shape memory alloy. Int. J. Plast. 1996, 12, 805–842. [Google Scholar] [CrossRef]
- Huang, M.; Brinson, L. A multivariant model for single crystal SMA behavior. J. Mech. Phys. Solids 1998, 46, 1379–1409. [Google Scholar] [CrossRef]
- Boyd, J.G.; Lagoudas, D.C. Constitutive Model for Simultaneous Transformation and Reorientation in Shape Memory Materials. In Mechanics of Phase Transformation and Shape Memory Alloys; ASME Conference: Chicago, IL, USA, 1994. [Google Scholar]
- Liu, X.; Liu, G.; Ye, P.; Luo, Q.; Chang, Z. Investigation of mechanical behaviors and improved design of V-shaped braid stents. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2022, 236, 547–556. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Li, B. Finite element analysis of a superelastic shape memory alloy considering the effect of plasticity. J. Theor. Appl. Mech. 2017, 55, 1355–1368. [Google Scholar] [CrossRef]
- Duerig, T.W.; Pelton, A.R.; Bhattacharya, K. The measurement and interpretation of transformation temperatures in nitinol. Shape Mem. Superelasticity 2017, 3, 485–498. [Google Scholar] [CrossRef]
- Dora, T.R.K.; Goud, R.; Sahadevan, A.; Chand, A.H.; Jha, R.; De, P.S.; Kottada, R.S.; Nayan, N.; Gollapudi, S. Investigations into sample geometry effects on the superelastic and fatigue behavior of Nitinol: Modeling and experiments. Materialia 2021, 20, 101256. [Google Scholar] [CrossRef]
- Petrini, L.; Bertini, A. A three-dimensional phenomenological model describing cyclic behavior of shape memory alloys. Int. J. Plast. 2020, 125, 348–373. [Google Scholar] [CrossRef]
- Hartl, D.J.; Lagoudas, D.C. Analysis of Simultaneous Transformation and Plastic Deformation in Shape Memory Alloys. In Proceedings of the 19th International Conference on Adaptive Structures and Technologies, Ascona, Switzerland, 6–9 October 2008; pp. 431–439. [Google Scholar]
- Gibson, L.; Ashby, M. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Helbert, G.; Dieng, L.; Arnab Chirani, S.; Saint-Sulpice, L.; Lecompte, T.; Calloch, S.; Pilvin, P. Investigation of NiTi based damper effects in bridge cables vibration response: Damping capacity and stiffness changes. Eng. Struct. 2018, 165, 184–197. [Google Scholar] [CrossRef]
- Gullu, A.; Danquah, J.O.; Dilibal, S. Characterization of energy dissipative cushions made of Ni-Ti shape memory alloy. Smart Mater. Struct. 2022, 31, 015018. [Google Scholar] [CrossRef]
- Chekotu, J.C.; Goodall, R.; Kinahan, D.; Brabazon, D. Control of Ni-Ti phase structure, solid-state transformation temperatures and enthalpies via control of L-PBF process parameters. Mater. Des. 2022, 218, 110715. [Google Scholar] [CrossRef]
- Gupta, M.K.; Shankhdhar, A.; Kumar, A.; Vermon, A.; Singh, A.K.; Panwar, V. Temperature and strain rate dependent stress-strain behaviour of Nitinol. Mater. Today Proc. 2020, 43, 395–399. [Google Scholar] [CrossRef]
- Farber, E.; Orlov, A.; Popovich, A. Effect of Lattice Structures Topology on the Properties of the TiNi Alloy: Computer Simulation. In Proceedings of the Metal 2021, 30th Anniversary International Conference on Metallurgy and Materials, Brno, Czech Republic, 26–28 May 2021; pp. 964–969. [Google Scholar]
- Rajoriya, S.; Mishra, S. Size, length, temperature and loading range effects on deformation response of NiTi SMA wire: An analytical study. Innov. Infrastruct. Solut. 2022, 7, 217. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, L. Processing and damping capacity of NiTi foams with laminated pore architecture. J. Mech. Behav. Biomed. Mater. 2019, 96, 108–117. [Google Scholar] [CrossRef] [PubMed]






| Material | |||||||
|---|---|---|---|---|---|---|---|
| NT1 | 71.1 | 0.3 | 500 | 700 | 400 | 200 | 0.044 |
| NT2 | 41 | 0.33 | 380 | 390 | 145 | 110 | 0.040 |
| NT3 | 50.3 | 0.3 | 556 | 643 | 315 | 246 | 0.075 |
| Sample | Porosity (%) | Void Volume (mm3) |
|---|---|---|
| Fully Dense (FD) | 0 | 0 |
| P1 | 1.4 | 1.77 |
| P2 | 2.8 | 3.53 |
| P3 | 9.4 | 11.78 |
| P4 | 15.7 | 19.63 |
| P5 | 25.1 | 31.42 |
| P6 | 72.7 | 90.85 |
| P7 | 83.4 | 104.21 |
| Upper bound (56 wt.% Ni) | 83 | 41 | 0.3 |
| Lower bound (54 wt.% Ni) | 50.30 | 23.59 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chekotu, J.C.; Kinahan, D.; Goodall, R.; Brabazon, D. Influence of Structural Porosity and Martensite Evolution on Mechanical Characteristics of Nitinol via In-Silico Finite Element Approach. Materials 2022, 15, 5365. https://doi.org/10.3390/ma15155365
Chekotu JC, Kinahan D, Goodall R, Brabazon D. Influence of Structural Porosity and Martensite Evolution on Mechanical Characteristics of Nitinol via In-Silico Finite Element Approach. Materials. 2022; 15(15):5365. https://doi.org/10.3390/ma15155365
Chicago/Turabian StyleChekotu, Josiah Cherian, David Kinahan, Russell Goodall, and Dermot Brabazon. 2022. "Influence of Structural Porosity and Martensite Evolution on Mechanical Characteristics of Nitinol via In-Silico Finite Element Approach" Materials 15, no. 15: 5365. https://doi.org/10.3390/ma15155365
APA StyleChekotu, J. C., Kinahan, D., Goodall, R., & Brabazon, D. (2022). Influence of Structural Porosity and Martensite Evolution on Mechanical Characteristics of Nitinol via In-Silico Finite Element Approach. Materials, 15(15), 5365. https://doi.org/10.3390/ma15155365









