Process Parameter Modeling and Optimization of Abrasive Water Jet Dressing Fixed-Abrasive Pad Based on Box–Behnken Design
Abstract
:1. Introduction
2. Experiments
2.1. Experimental Materials
2.2. Experimental Setup
2.3. Experimental Design
2.4. Evaluation Indicators
3. Results and Discussion
3.1. Experimental Results and Regression Equations
3.2. Material Removal Rate Model and Its Analysis
3.2.1. ANOVA and Significance Testing of the Material Removal Rate Model
3.2.2. Composite Analysis of the Main Factors Affecting the Material Removal Rate of Quartz Glass
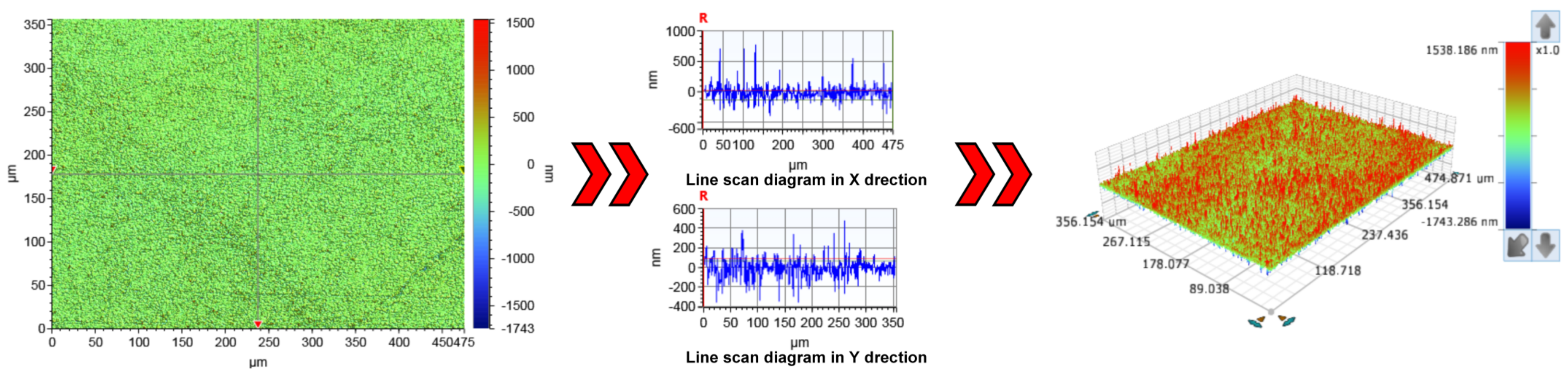
3.3. The Surface Morphology of FAP and Quartz Glass
3.4. Parameter Optimization and Validation
4. Conclusions
- The response surface and contour map can accurately analyze the jet system’s best range of process parameters, and when combined with the regression model, can optimize the process parameters of the jet system.
- After optimization, the best process parameters corresponding to quartz glass’s maximum material removal rate are jet pressure 3.8 MPa, abrasive concentration 3%, and nozzle angle 73°. That is, these process parameters are the best FAP dressing process parameters.
- By substituting the predicted optimal process parameters into the regression model, the predicted material removal rate of quartz glass is 464.574 nm/min. The experimental results show that the actual material removal rate of quartz glass is 469.136 nm/min. The predicted results are very close to the actual experimental results, except for a difference of 4.562 nm/min.
- The response surface model established in this paper has high accuracy and can be used to predict the results of an abrasive water jet dressing FAP.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Zhu, Y.; Li, X.; Zhu, N.; Li, J.; Su, J.; Zuo, D. Fixed abrasive laps magnesium aluminum spinel for average depth of cut and subsurface damage. J. Silic. 2017, 45, 402–409. [Google Scholar]
- Li, J.; Zhu, Y.; Zuo, D.; Lin, K.; Li, M. Fixed abrasive lapping and polishing of hard brittle materials. Key Eng. Mater. 2010, 426, 589–592. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Y.; Pang, M.; Li, Y.; Ma, L.; Yao, J.; Zhu, Y.; Su, J. Study on the response surface model of the lapping process parameters of quartz glass fixed abrasives. Surf. Technol. 2021, 50, 376–385. [Google Scholar]
- Wang, Z.; Pang, M.; Liang, M.; Wang, J.; Ma, L.; Liu, H.; Han, J.; Zhu, Y.; Su, J. Effect of material structure on spinel machinability in its fixed abrasive lapping. J. Manuf. Processes 2021, 68, 141–153. [Google Scholar]
- Hu, W.; Wang, Z.; Dong, Y.; Zhang, Z.; Zhu, Y. Surface Morphology Characterization of Fixed Abrasive Pads Based on Deep Learning. Diam. Abras. Eng. 2022, 42, 186–192. [Google Scholar] [CrossRef]
- Liang, H.; Martin, J.M.; Mogne, T.L. Interfacial transfer between copper and polyurethane in CMP. J. Elec. Matls. 2002, 31, 872–878. [Google Scholar] [CrossRef]
- Ju, Z.; Zhu, Y.; Zhang, F. Study on dressing technology and improving the self-dressing properties of FAP. Diam. Abras. Eng. 2017, 37, 11–15. [Google Scholar]
- Hua, Q.; Fang, H.; Yuan, J. Factors influencing the dressing effect of polishing pads for CMP. Light Ind. Mach. 2009, 5, 48–51. [Google Scholar]
- Zhao, W.; Zhou, Z.; Lv, B. Study of polishing pad trimming during CMP. New Technol. New Process 2007, 3, 24–27. [Google Scholar]
- Tang, X.; Zhu, Y.; Wang, C.; Gu, Y.; Ju, Z.; Li, J. Exploration of the self-dressing process of hydrophilic FAP. Nanotechnol. Precis. Eng. 2014, 12, 68–73. [Google Scholar]
- Young Choi, J.; Do Jeong, H. A study on polishing of molds using hydrophilic fixed abrasive pad. Int. J. Mach. Tools Manuf. 2004, 44, 1163–1169. [Google Scholar] [CrossRef]
- Pahuja, R.; Ramulu, M.; Hashish, M. Surface quality and kerf width prediction in abrasive water jet machining of metal-composite stacks. Composites 2019, 175, 107134. [Google Scholar] [CrossRef]
- Valicek, J.; Harnicarova, M.; Ochsner, A.; Hutyrova, Z.; Kusnerova, M.; Tozan, H.; Michenka, V.; Sepelak, V.; Mital, D.; Zajac, J. Quantifying the Mechanical Properties of Materials and the Process of Elastic-Plastic Deformation under External Stress on Material. Materials 2015, 8, 7401–7422. [Google Scholar] [CrossRef] [Green Version]
- Perec, A. Abrasive Suspension Water Jet Cutting Optimization Using Orthogonal Array Design. Procedia Eng. 2016, 149, 366–373. [Google Scholar] [CrossRef] [Green Version]
- Hashish, M. Trends and Cost Analysis of AWJ Operation at 600 MPa Pressure. J. Press. Vessel. Technol. 2009, 131, 21410. [Google Scholar] [CrossRef]
- Radvanská, A.; Hreha, P.; Knapcikova, L.; Petru, J.; Zlamal, T.; Monka, P. Influence of focusing tube wear on vibrations and surface roughness. Teh. Vjesn.-Tech. Gaz. 2015, 22, 271–278. [Google Scholar] [CrossRef] [Green Version]
- Miyachi, K.; Kurokawa, S.; Doi, T.; Seike, Y.; Izumikawa, S.; Akama, T.; Ohnishi, O. Unwoven Fabric Pads Non-Destructive conditioning by High Pressure Micro Jet in CMP Process. J. Jpn. Soc. Precis. Eng. 2010, 76, 1076–1081. [Google Scholar] [CrossRef] [Green Version]
- Holland, K.; Hurst, A.; Pinder, H. Improving cost of ownership and performance of CMP process and consumables. Micro -St. Monica- 2002, 20, 26–32. [Google Scholar]
- Tsai, M.-Y.; Yang, W.-Z. Water-jet-assisted diamond disk dressing characteristics of CMP polishing pad. Int. J. Adv. Manuf. Technol. 2012, 62, 645–654. [Google Scholar] [CrossRef]
- Wang, J. Study on the Material Removal Mechanism and Process of Fixed Abrasive Lapping Sapphire Workpieces. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2015. [Google Scholar]
- Reddy, P.; Reddy, G.; Seenayya, G. Production of thermostable pullulanase by Clostridium thermosulfurogenes SV2 in solid-state fermentation: Optimization of nutrients levels using response surface methodology. Bioprocess Eng. 1999, 21, 497–503. [Google Scholar] [CrossRef]
- Annadurai, G. Design of optimum response surface experiments for adsorption of direct dye on chitosan. Bioprocess Eng. 2000, 23, 451–455. [Google Scholar] [CrossRef]
- Ester, R.G.; Alvaro, B.N.; Alberto, C.B.J. Optimisation of medium composition for clavulanic acid production by Streptomyces clavuligerus. Biotechnol. Lett. 2001, 23, 157–161. [Google Scholar]
- Tang, X.; Zhu, Y.; Fu, J.; Wang, C.; Ju, Z. Study on the effect of copper powder content on the processing performance of FAP. Diam. Abras. Eng. 2012, 32, 10–13. [Google Scholar]
- Li, L.; Zhang, S.; He, Q.; Hu, X. Application of response surface method in experimental design and optimization. Res. Explor. Lab. 2015, 34, 41–45. [Google Scholar]




| Properties | Value |
|---|---|
| Density | 2.20–2.21 g/cm3 |
| Mohs hardness | 6.0–7.0 |
| Elasticity modulus | 77.8 GPa |
| Poisson ratio | 0.14–0.17 |
| Breaking tenacity | 0.75–0.80 MPa·m1/2 |
| Lapping Pressure | Types of Abrasive Fluids | Abrasive Fluid Flow Rate | Lapping Speed | Lapping Time |
|---|---|---|---|---|
| 27 KPa | Deionized water | 50 mL/min | 100 r/min | 30 min |
| Factor Encoded Value | Jet Pressure A/MPa | Abrasive Concentration B/% | Sprinkler Angle C/° |
|---|---|---|---|
| Up level (+1) | 5 | 7 | 80 |
| Lower level (−1) | 3 | 3 | 60 |
| Zero level (0) | 4 | 5 | 70 |
| Change radius ∆i | 1 | 2 | 10 |
| Abrasive Particle Size | Abrasive Flow Rate | FAP Rotate Speed | Traverse Velocity | Dressing Time | Abrasive Class |
|---|---|---|---|---|---|
| W3.5 | 102 g/min | 110 r/min | 2.5 mm/s | 5 min | Brown corundum |
| Factors | Jet Pressure A/MPa | Abrasive Concentration B/% | Sprinkler Angle C/° | MRR/Nm/Min | |
|---|---|---|---|---|---|
| Test Number | |||||
| 1 | −1 | −1 | 0 | 425.15 | |
| 2 | 1 | 1 | 0 | 220.68 | |
| 3 | 0 | 1 | −1 | 308.64 | |
| 4 | 1 | −1 | 0 | 253.09 | |
| 5 | −1 | 1 | 0 | 229.17 | |
| 6 | 1 | 0 | −1 | 203.70 | |
| 7 | 0 | 0 | 0 | 364.97 | |
| 8 | −1 | 0 | −1 | 198.30 | |
| 9 | 0 | −1 | −1 | 418.98 | |
| 10 | 0 | −1 | 1 | 401.23 | |
| 11 | 0 | 1 | 1 | 264.66 | |
| 12 | 0 | 0 | 0 | 393.52 | |
| 13 | −1 | 0 | 1 | 250.00 | |
| 14 | 1 | 0 | 1 | 204.48 | |
| 15 | 0 | 0 | 0 | 381.94 | |
| Source | Degrees of Freedom | Adj SS | Adj MS | F Value | p Value | Significance |
|---|---|---|---|---|---|---|
| Model | 9 | 101,251 | 11,250.1 | 12.36 | 0.006 | ** |
| X1 | 1 | 6087 | 6087.4 | 6.69 | 0.049 | * |
| X2 | 1 | 28,240 | 28,239.8 | 31.03 | 0.003 | ** |
| X3 | 1 | 11 | 10.7 | 0.01 | 0.918 | |
| Square | 3 | 59,403 | 19,800.9 | 21.76 | 0.003 | ** |
| X12 | 1 | 49,847 | 49,847.3 | 54.77 | 0.001 | ** |
| X22 | 1 | 1205 | 1205.4 | 1.32 | 0.302 | |
| X32 | 1 | 9169 | 9169.1 | 10.07 | 0.025 | * |
| Two-way interaction | 3 | 7510 | 2503.3 | 2.75 | 0.152 | |
| X1 ∗ X2 | 1 | 6690 | 6689.6 | 7.35 | 0.042 | * |
| X1 ∗ X3 | 1 | 648 | 648.4 | 0.71 | 0.437 | |
| X2 ∗ X3 | 1 | 172 | 172.1 | 0.19 | 0.682 | |
| Errors | 5 | 4551 | 910.1 | |||
| Missing fit | 3 | 4138 | 1379.4 | 6.69 | 0.133 | |
| Pure error | 2 | 412 | 206.2 | |||
| Total | 14 | 105,801 | ||||
| = 0.8796 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, S.; Ding, Y.; Yang, Y.; Ma, L.; Pang, M.; Han, J.; Su, J. Process Parameter Modeling and Optimization of Abrasive Water Jet Dressing Fixed-Abrasive Pad Based on Box–Behnken Design. Materials 2022, 15, 5251. https://doi.org/10.3390/ma15155251
Wang Z, Wang S, Ding Y, Yang Y, Ma L, Pang M, Han J, Su J. Process Parameter Modeling and Optimization of Abrasive Water Jet Dressing Fixed-Abrasive Pad Based on Box–Behnken Design. Materials. 2022; 15(15):5251. https://doi.org/10.3390/ma15155251
Chicago/Turabian StyleWang, Zhankui, Shiwei Wang, Yangyang Ding, Yakun Yang, Lijie Ma, Minghua Pang, Jianhai Han, and Jianxiu Su. 2022. "Process Parameter Modeling and Optimization of Abrasive Water Jet Dressing Fixed-Abrasive Pad Based on Box–Behnken Design" Materials 15, no. 15: 5251. https://doi.org/10.3390/ma15155251
APA StyleWang, Z., Wang, S., Ding, Y., Yang, Y., Ma, L., Pang, M., Han, J., & Su, J. (2022). Process Parameter Modeling and Optimization of Abrasive Water Jet Dressing Fixed-Abrasive Pad Based on Box–Behnken Design. Materials, 15(15), 5251. https://doi.org/10.3390/ma15155251






