Mechanical Properties, Constitutive Behaviors and Failure Criteria of Al-PTFE-W Reactive Materials with Broad Density
Abstract
:1. Introduction
2. Experimental
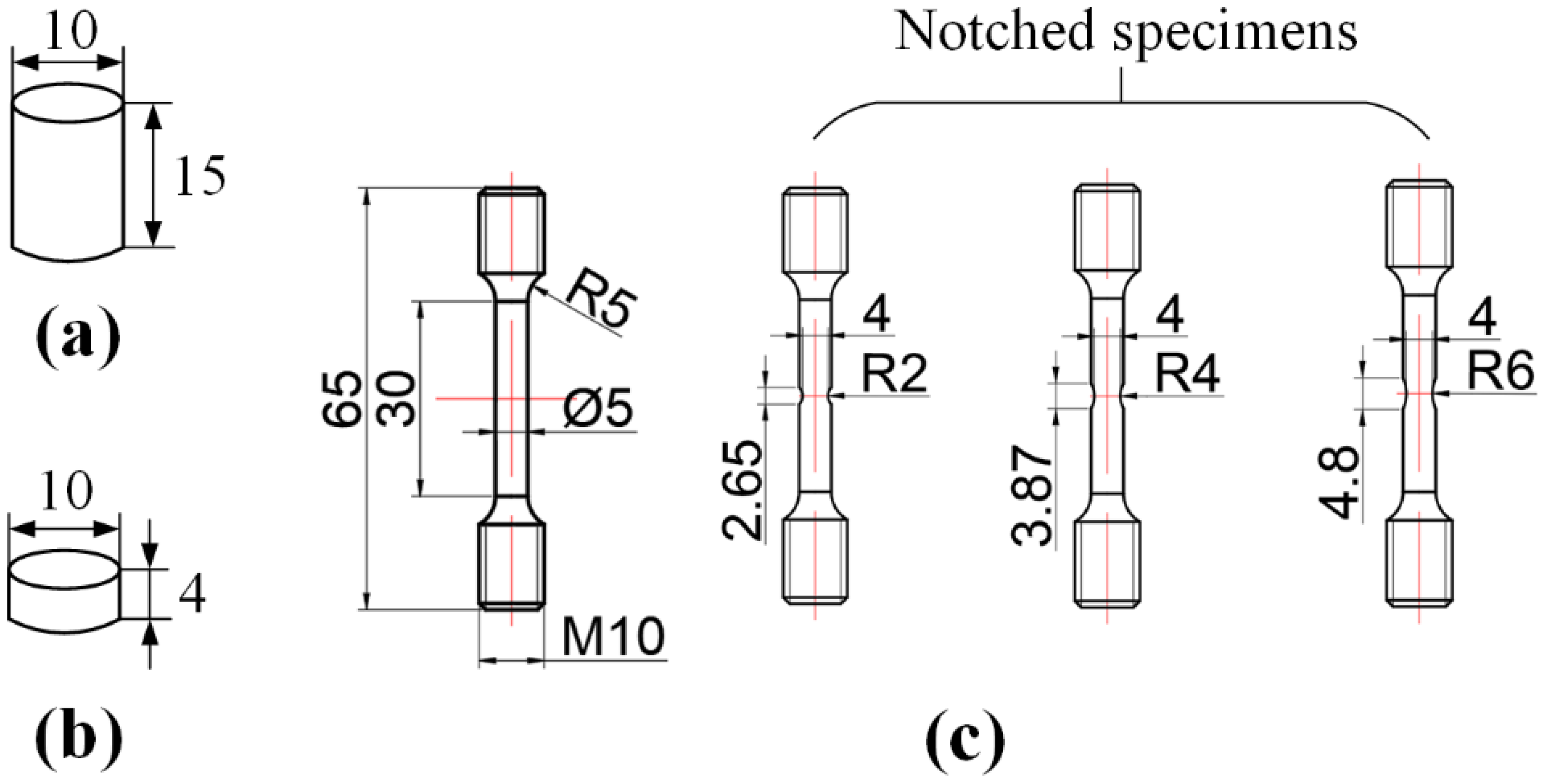
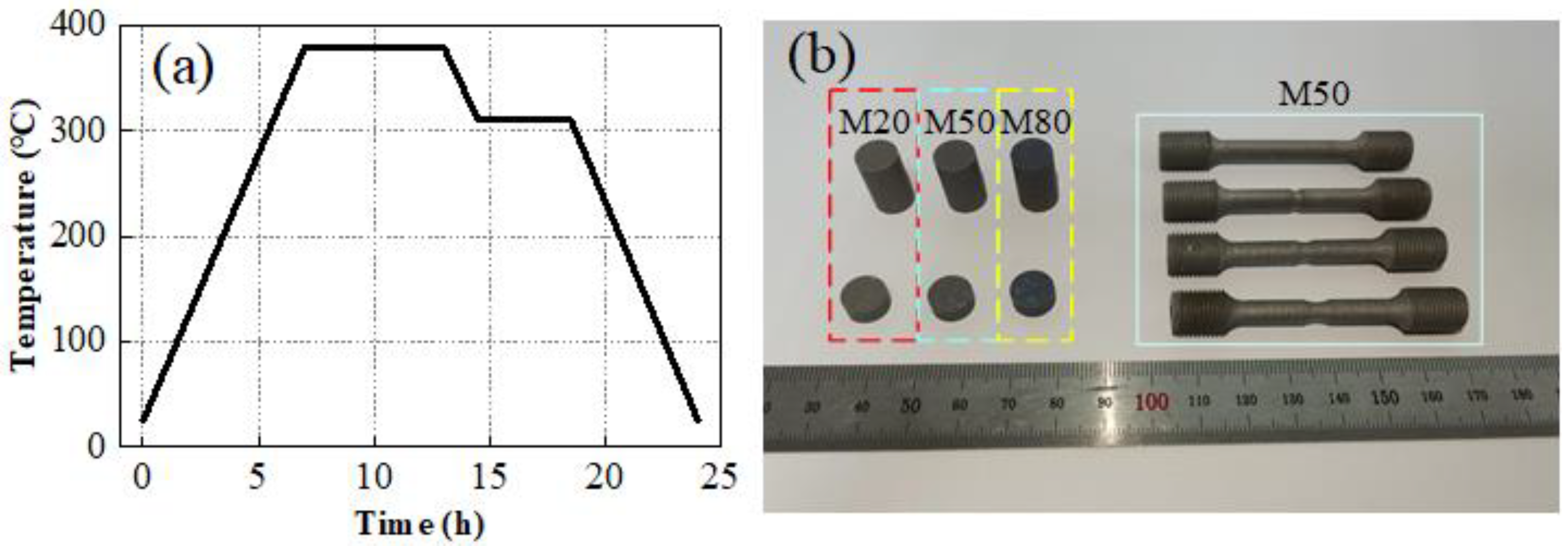
2.1. Specimen Fabrication
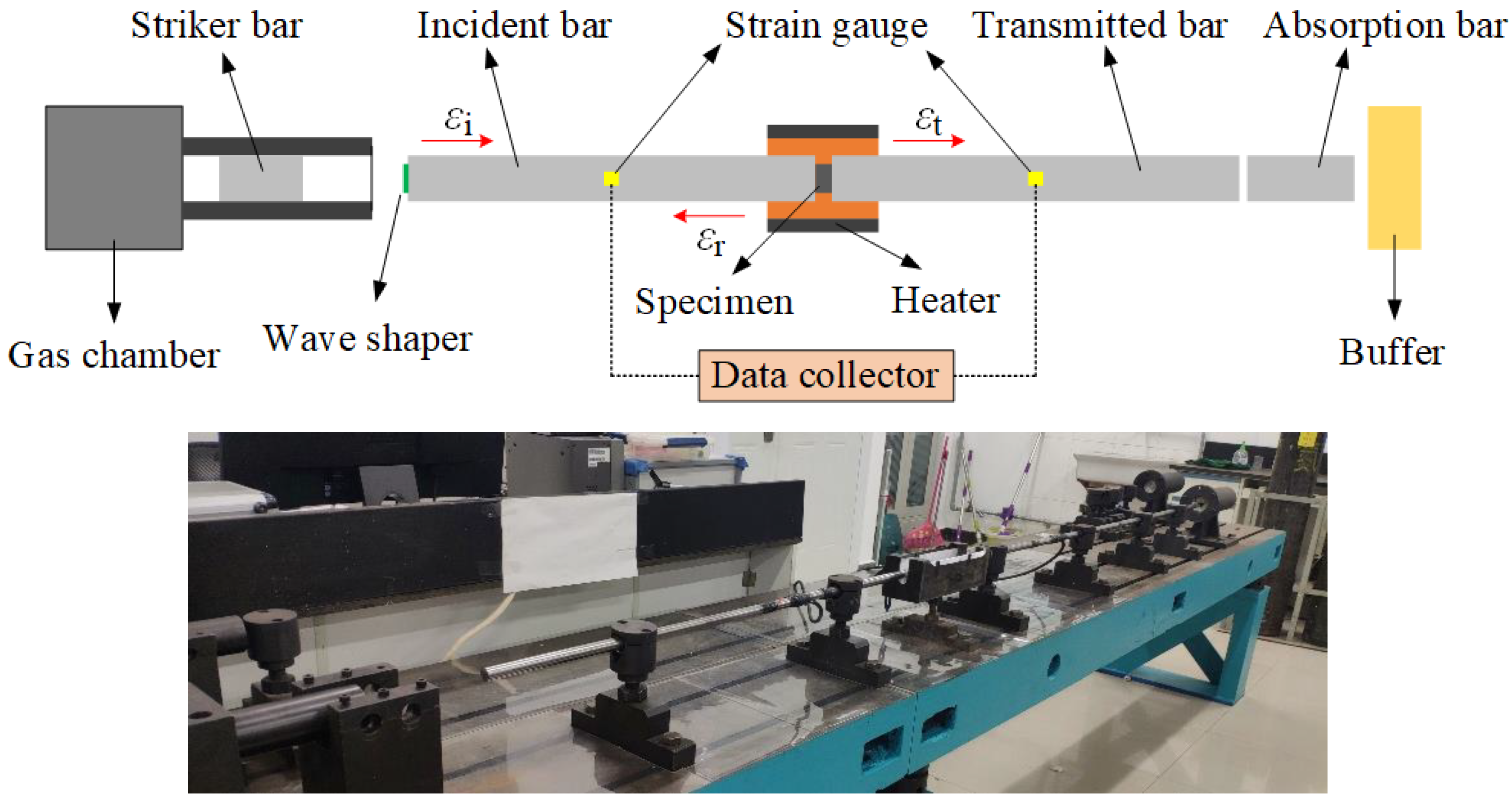
2.2. Quasi-Static and Dynamic Test Methods
- 1.
- Quasi-static compression and tension
- 2.
- Dynamic compression at elevated temperatures
3. Results and Discussion
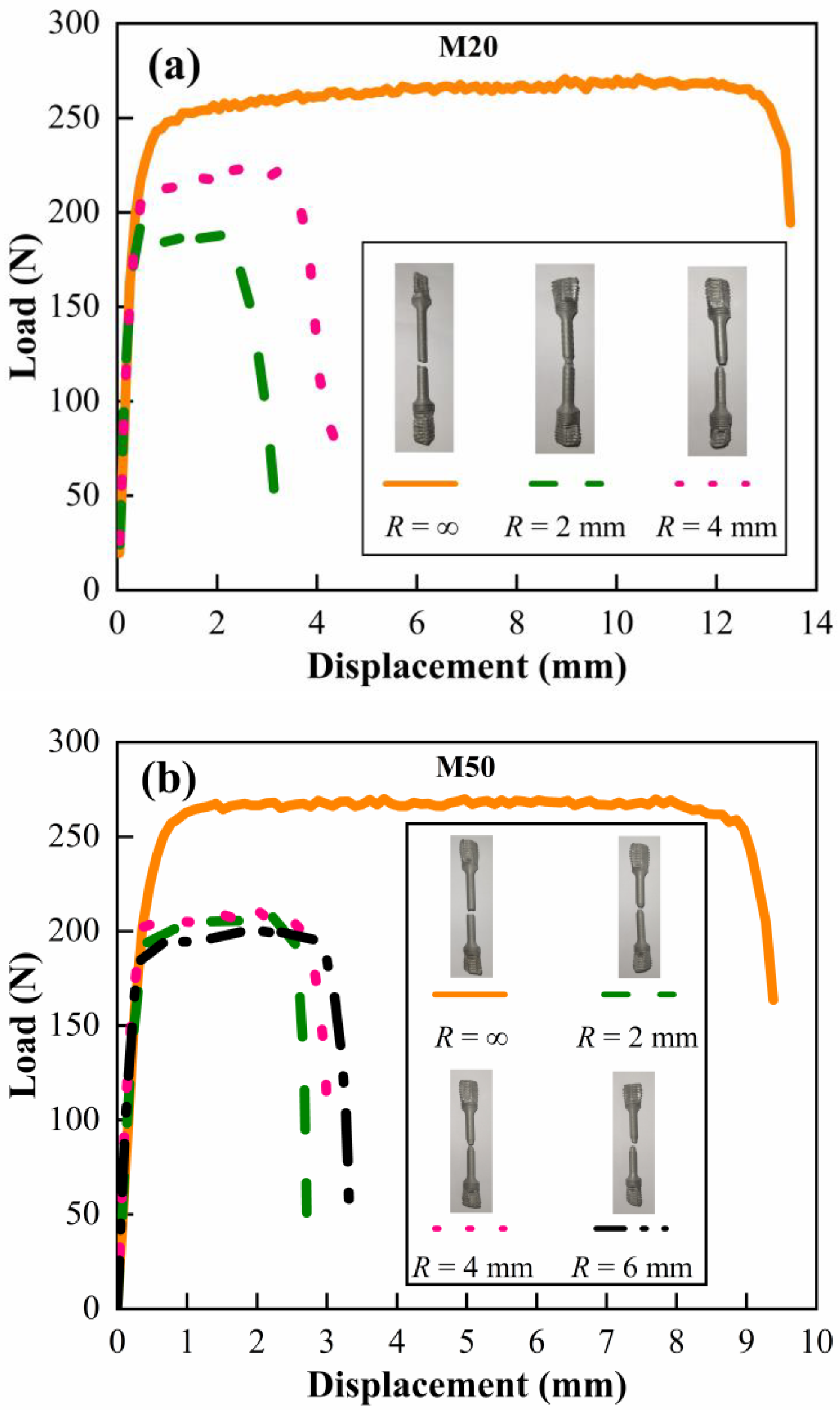
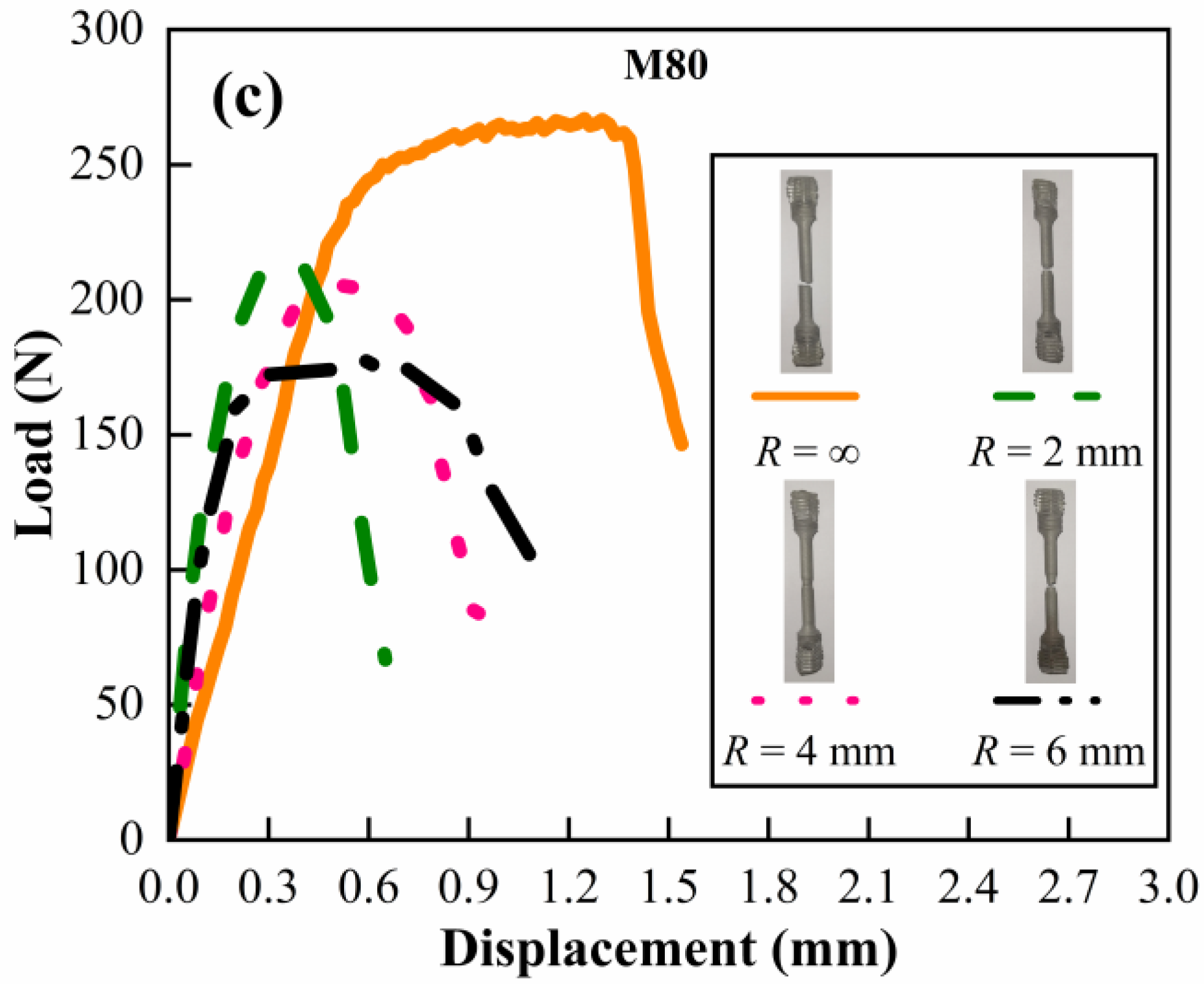
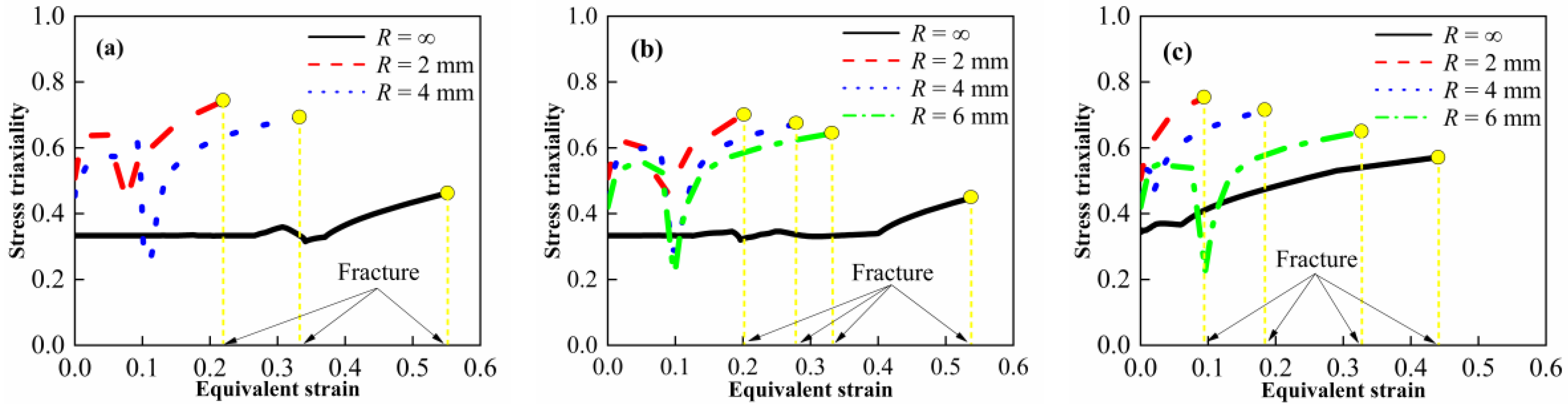
3.1. Stress State Analysis under Quasi-Static Condition
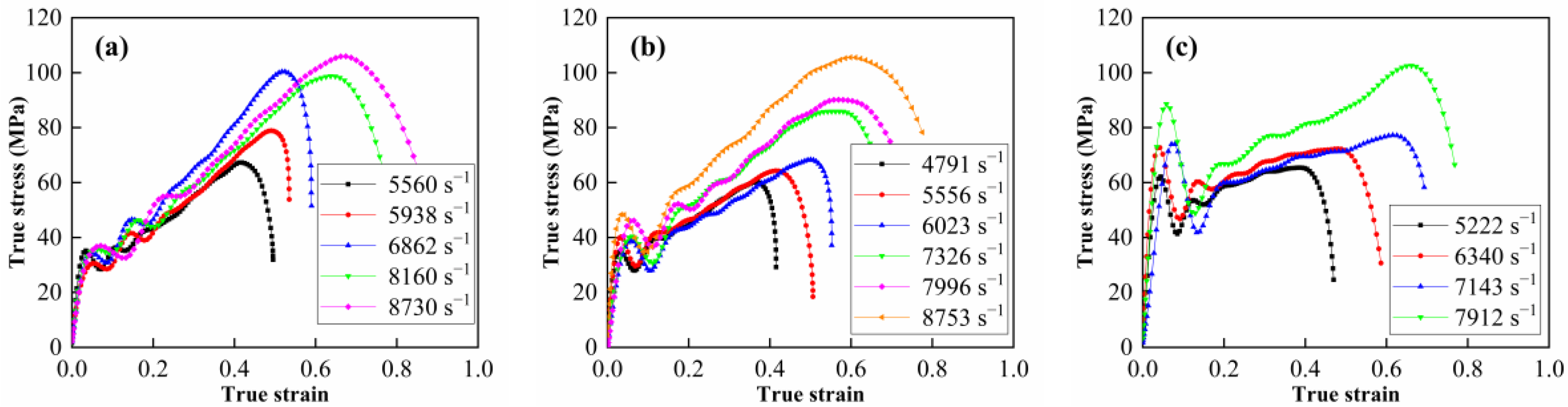
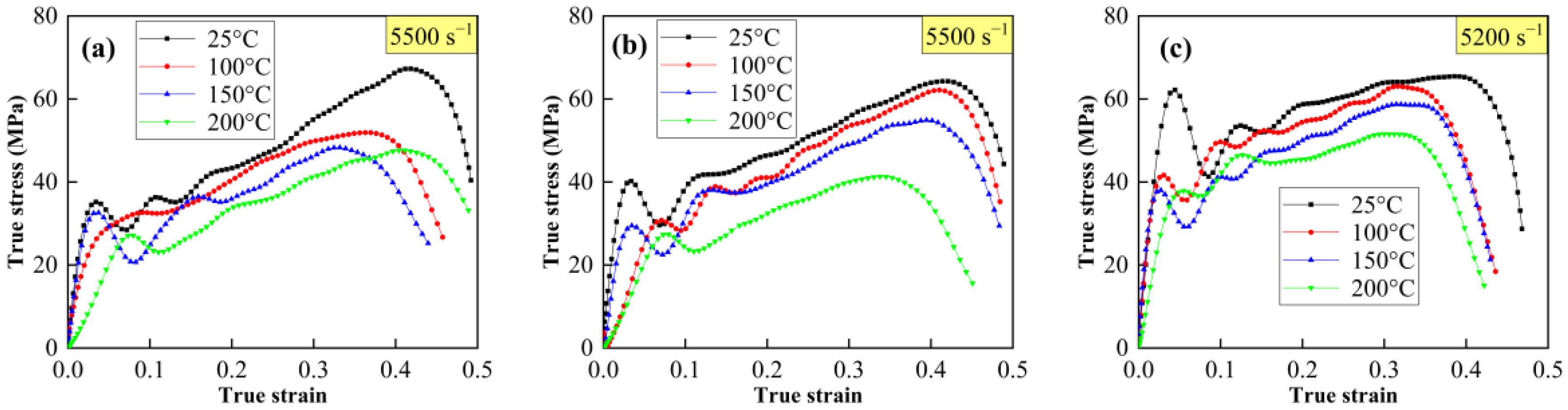
3.2. Strain Rate and Thermal Effect under Dynamic Compression
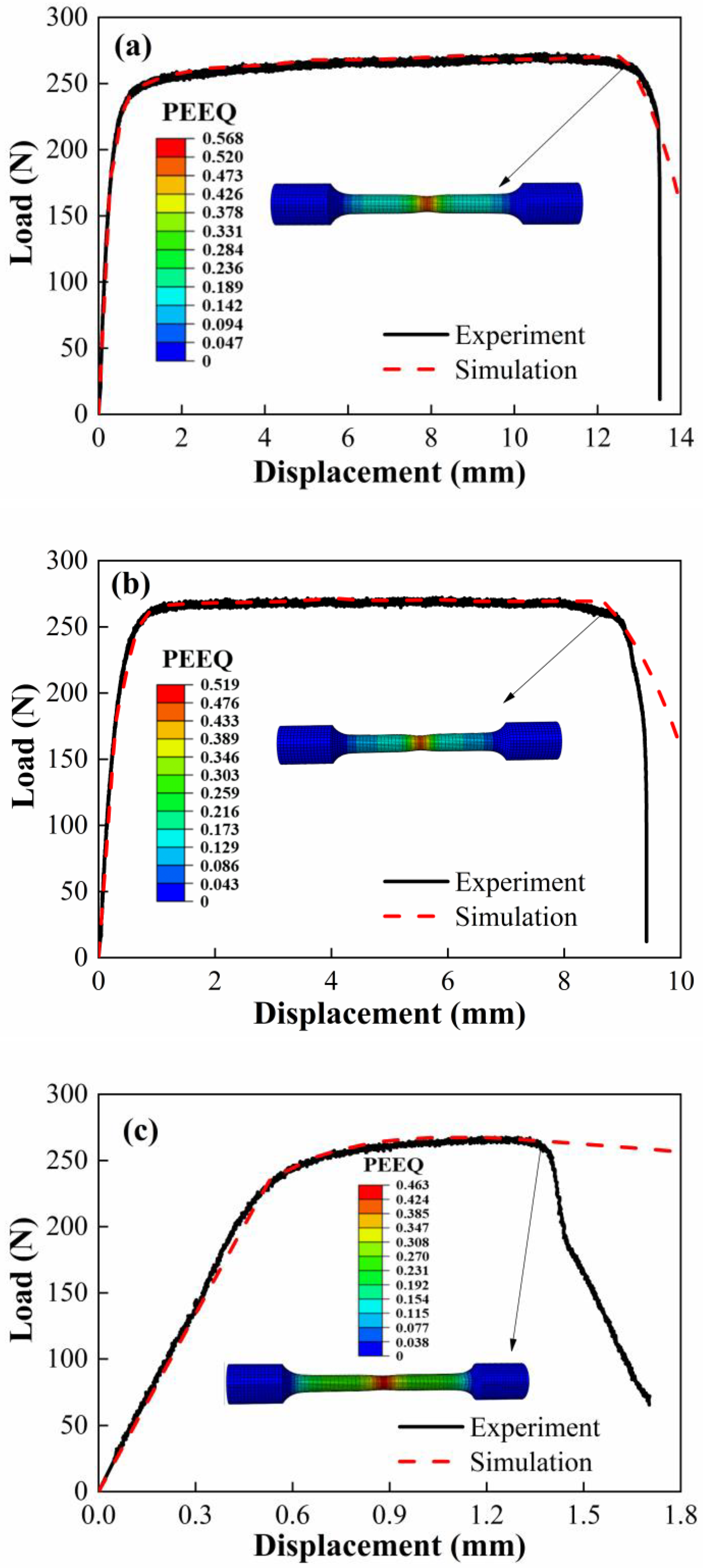
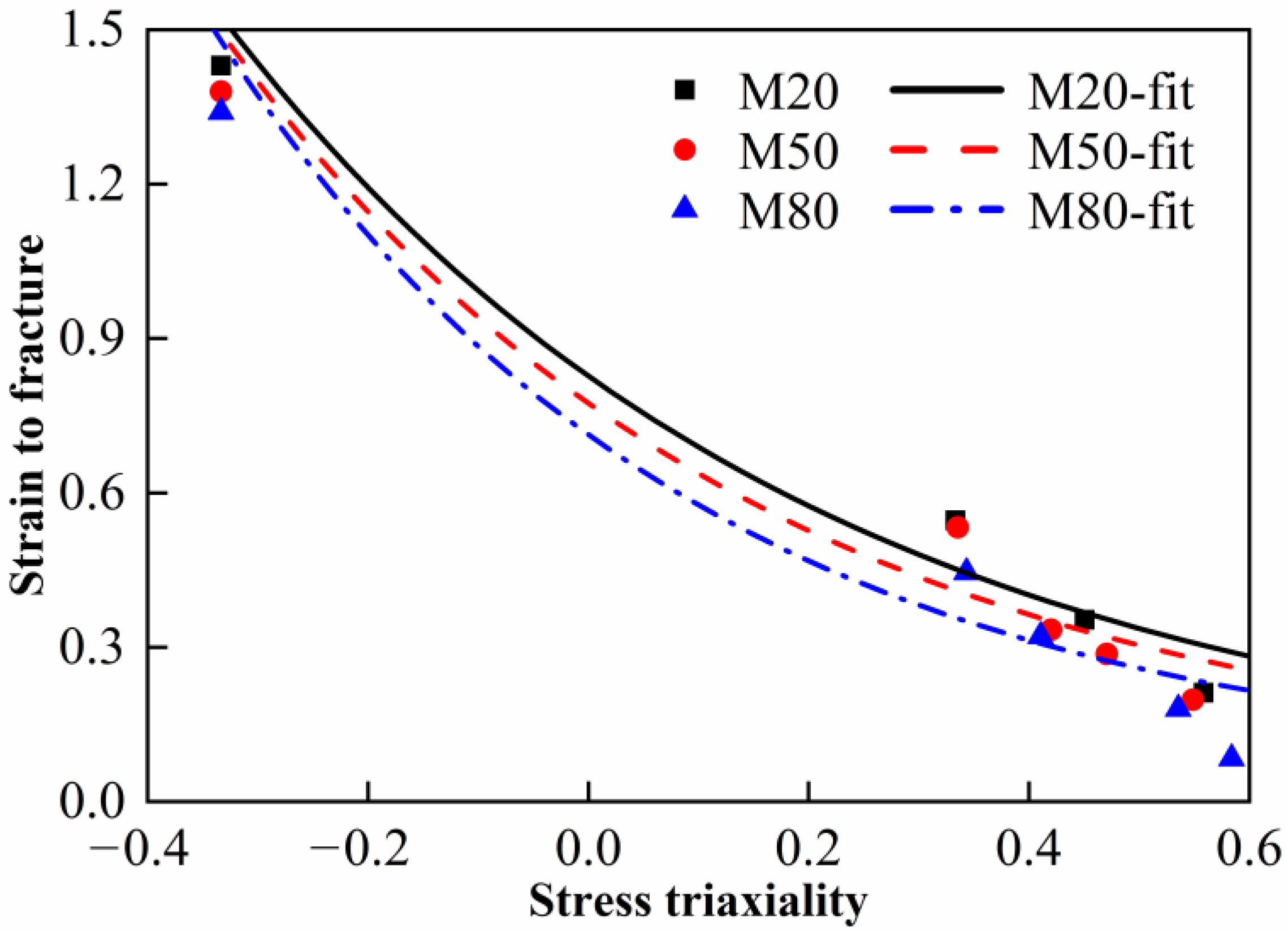
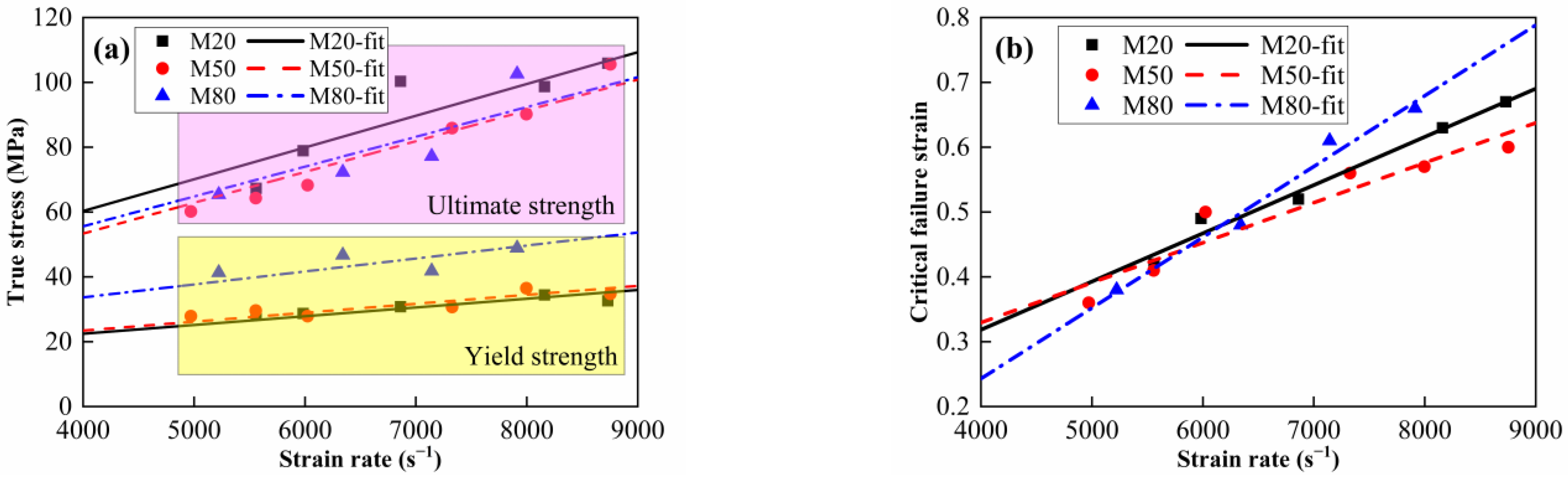
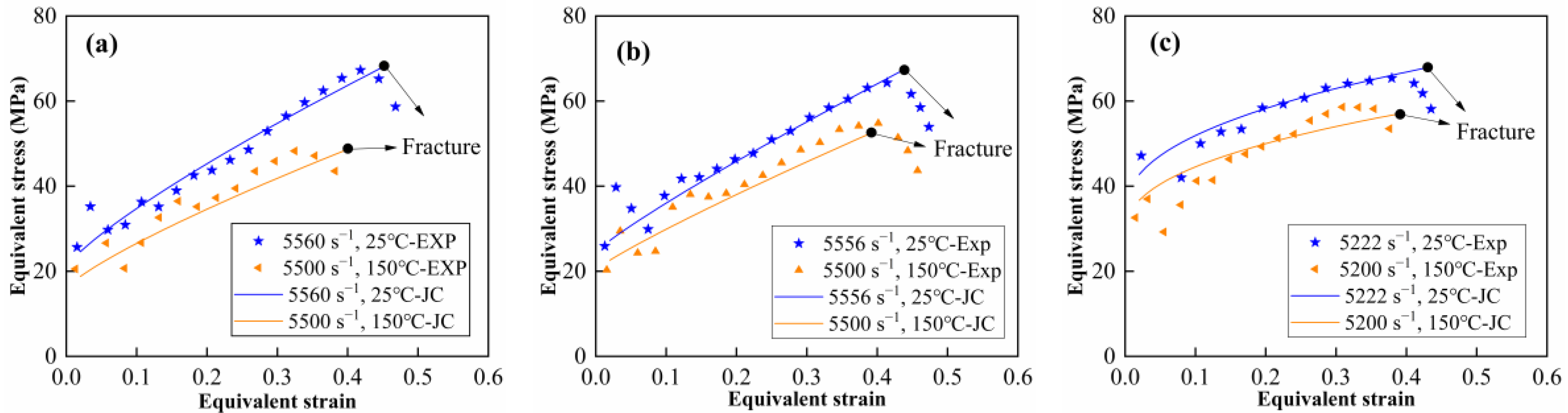
3.3. Constitutive and Failure Modeling
4. Conclusions
- (1)
- Under quasi-static (10−3 s−1) condition, the strength of the materials may be independent of stress state and W content. Regardless of compression or tension, the strength of the materials with W content from 20% to 80% ranges from 10 MPa to 20 MPa.
- (2)
- Under quasi-static condition, the compression plasticity of the materials is significantly superior to its tension plasticity. W content has no obvious influence on the compression plasticity, while tension plasticity is extremely sensitive to W content. As W content increases from 20% to 80%, the compression failure strain decreases from 1.43 to 1.34 with an amplitude of 6.2%, while the tension failure strain decreases from 0.3 to 0.036 with an amplitude of 88%.
- (3)
- The materials show an obvious strain rate strengthening effect and thermal softening effect under dynamic compression. However, the dynamic compression strengths and strain rate sensitivities of the materials with different W contents show no obvious difference. For the materials with a W content of 50%, the dynamic compression strength improves from 60.2 MPa to 105.6 MPa as the strain rate increases from 4971 s−1 to 8753 s−1 at ambient temperature; meanwhile, it decreases from 64.3 MPa to 41.3 MPa as the material temperature increases from 25 °C to 200 °C at the strain rate of 5500 s−1.
- (4)
- The Johnson–Cook constitutive (A, B, n, C and m) and failure parameters (D1~D5) were well-determined and predicted stress–strain curves are in good agreement with the experimental results. The results of this research would prove beneficial to the numerical studies, design and application of reactive materials.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Liu, J.; Li, S.; Zhang, X. Investigation on reaction energy, mechanical behavior and impact insensitivity of W-PTFE-Al composites with different W percentage. Mater. Des. 2016, 92, 397–404. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, Q.; Long, R.; Zhang, K.; Guo, J. Potential space debris shield structure using impact-initiated energetic materials composed of polytetrafluoroethylene and aluminum. Appl. Phys. Lett. 2016, 108, 135–183. [Google Scholar] [CrossRef]
- Liu, S.; Zheng, Y.; Yu, Q.; Ge, C.; Wang, H. Interval rupturing damage to multi-spaced aluminum plates impacted by reactive materials filled projectile. Int. J. Impact Eng. 2019, 130, 153–162. [Google Scholar] [CrossRef]
- Joshi, V. Process for Making Polytetrafluoroethylene-Aluminum Composite and Product Made. U.S. Patent 6,547,993 B1, 15 April 2003. [Google Scholar]
- Ge, C.; Yu, Q.; Zhang, H.; Qu, Z.; Wang, H.; Zheng, Y. On dynamic response and fracture-induced initiation characteristics of aluminum particle filled PTFE reactive material using hat-shaped specimens. Mater. Des. 2020, 188, 108472. [Google Scholar] [CrossRef]
- Raftenberg, M.N.; Mock, W., Jr.; Kirby, G.C. Modeling the impact deformation of rods of a pressed PTFE/Al composite mixture. Int. J. Impact Eng. 2008, 35, 1735–1744. [Google Scholar] [CrossRef]
- Wang, H.-F.; Geng, B.-Q.; Guo, H.-G.; Zheng, Y.-F.; Yu, Q.-B.; Ge, C. The effect of sintering and cooling process on geometry distortion and mechanical properties transition of PTFE/Al reactive materials. Def. Technol. 2020, 16, 720–730. [Google Scholar] [CrossRef]
- Tang, L.; Ge, C.; Guo, H.-G.; Yu, Q.-B.; Wang, H.-F. Force chains based mesoscale simulation on the dynamic response of Al-PTFE granular composites. Def. Technol. 2021, 17, 56–63. [Google Scholar] [CrossRef]
- Feng, B.; Fang, X.; Li, Y.-C.; Wang, H.-X.; Mao, Y.-M.; Wu, S.-Z. An initiation of Al-PTFE under quasi-static compression. Chem. Phys. Lett. 2015, 637, 38–41. [Google Scholar] [CrossRef]
- Feng, B.; Li, Y.C.; Wu, S.Z.; Wang, H.X.; Tao, Z.M.; Fang, X. A crack-induced initiation mechanism of Al-PTFE under quasi-static compression and the investigation of influencing factors. Mater. Des. 2016, 108, 411–417. [Google Scholar] [CrossRef]
- Osborne, D.T.; Pantoya, M.L. Effect of Al particle size on the thermal degradation of Al/Teflon mixtures. Combust. Sci. Technol. 2007, 179, 1467–1480. [Google Scholar] [CrossRef]
- Mock, W., Jr.; Holt, W.H. Impact initiation of rods of pressed polytetrafluoroethylene (PTFE) and aluminum powders. In Shock Compression of Condensed Matter-2005: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter; AIP Publishing: New York, NY, USA, 2006; pp. 1097–1100. [Google Scholar]
- Ames, R.G. Energy release characteristics of impact-initiated energetic materials. Mater. Res. Soc. Symp. Proc. 2005, 896, 321–333. [Google Scholar] [CrossRef]
- Xu, F.Y.; Liu, S.B.; Zheng, Y.F.; Yu, Q.B.; Wang, H.F. Quasi-static compression properties and failure of PTFE/Al/W reactive materials. Adv. Eng. Mater. 2017, 19, 1600350. [Google Scholar] [CrossRef] [Green Version]
- Herbold, E.; Nesterenko, V.F.; Benson, D.J.; Cai, J.; Vecchio, K.S.; Jiang, F.; Addiss, J.W.; Walley, S.M.; Proud, W.G. Particle size effect on strength, failure, and shock behavior in polytetrafluoroethylene-Al-W granular composite materials. J. Appl. Phys. 2008, 104, 103903. [Google Scholar] [CrossRef]
- Cai, J.; Walley, S.; Hunt, R.; Proud, W.; Nesterenko, V.; Meyers, M. High-strain, High-strain-rate flow and failure in PTFE/Al/W granular composites. Mater. Sci. Eng. A 2008, 472, 308–315. [Google Scholar] [CrossRef]
- Zhou, J.; He, Y.; He, Y.; Wang, C.T. investigation on impact initiation characteristics of fluropolymer-matrix reactive materials. Propellants Explos. Pyrotech. 2017, 42, 603–615. [Google Scholar] [CrossRef]
- Ren, H.L.; Li, W.; Liu, X.J.; Chen, Z. Reaction behaviors of Al/PTFE materials enhanced by W particles. Acta Armamentarii China 2016, 37, 872–878. [Google Scholar]
- Ge, C.; Maimaitituersun, W.; Dong, Y.; Tian, C. A study on the mechanical properties and impact-induced initiation characteristics of brittle PTFE/Al/W reactive materials. Materials 2017, 10, 452. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.Y.; Yu, Q.B.; Zheng, Y.F.; Lei, M.A.; Wang, H.F. Damage effects of aluminum plate by reactive material projectile impact. Int. J. Impact Eng. 2017, 104, 38–44. [Google Scholar] [CrossRef]
- Xu, F.Y.; Yu, Q.B.; Zheng, Y.F.; Lei, M.A.; Wang, H.F. Damage effects of double-spaced aluminum plates by reactive material projectile impact. Int. J. Impact Eng. 2017, 104, 13–20. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Ge, C. Characterization of the dynamic response and constitutive behavior of PTFE/Al/W reactive materials. Propellants Explos. Pyrotech. 2020, 45, 788–797. [Google Scholar] [CrossRef]
- Senthil, K.; Iqbal, M.; Chandel, P.; Gupta, N. Study of the constitutive behavior of 7075-T651 aluminum alloy. Int. J. Impact Eng. 2017, 108, 171–190. [Google Scholar] [CrossRef]
- Joun, M.; Eom, J.G.; Lee, M.C. A new method for acquiring true stress-strain curves over a large range of strains using a tensile test and finite element method. Mech. Mater. 2008, 40, 586–593. [Google Scholar] [CrossRef]
- Bridgeman, P.W. Studies in Large Plastic Flow and Fracture; McGraw-Hill: New York, NY, USA, 1952. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures, and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Hu, H.; Xu, Z.; Dou, W.; Huang, F. Effects of strain rate and stress state on mechanical properties of Ti-6Al-4V alloy. Int. J. Impact Eng. 2020, 145, 103689. [Google Scholar] [CrossRef]




| Material Types | Component Mass Ratios (wt. %) | TMD (g·cm−3) | Actual Density (g·cm−3) | ||
|---|---|---|---|---|---|
| Al | PTFE | W | |||
| M20 | 21.2 | 58.8 | 20 | 2.78 | 2.65 |
| M50 | 13.2 | 36.8 | 50 | 4.09 | 3.97 |
| M80 | 5.3 | 14.7 | 80 | 7.8 | 7.66 |
| Material Type | Elastic Modulus (MPa) | Yield Strength (MPa) | Ultimate Strength (MPa) | Critical Failure Strain | |
|---|---|---|---|---|---|
| Compression | M20 | 508.5 | 10.6 | 22.1 | 1.43 |
| M50 | 628.8 | 11.4 | 19.1 | 1.38 | |
| M80 | 734.6 | 16.5 | 20.9 | 1.34 | |
| Tension | M20 | 806 | 12.2 | 18.4 | 0.3 |
| M50 | 831 | 13.2 | 16.7 | 0.22 | |
| M80 | 874 | 13.4 | 14.1 | 0.036 |
| Material Type | Strain Rate (s−1) | Yield Strength (MPa) | Ultimate Strength (MPa) | Critical Failure Strain |
|---|---|---|---|---|
| M20 | 5560 | 28.5 | 67.3 | 0.42 |
| 5983 | 28.7 | 78.9 | 0.49 | |
| 6862 | 30.8 | 100.3 | 0.52 | |
| 8160 | 34.4 | 98.7 | 0.63 | |
| 8730 | 32.6 | 105.9 | 0.67 | |
| M50 | 4971 | 27.9 | 60.2 | 0.36 |
| 5556 | 29.6 | 64.3 | 0.41 | |
| 6023 | 27.9 | 68.3 | 0.5 | |
| 7326 | 30.7 | 85.9 | 0.56 | |
| 7996 | 36.5 | 90.2 | 0.57 | |
| 8753 | 34.8 | 105.6 | 0.6 | |
| M80 | 5222 | 41.3 | 65.4 | 0.38 |
| 6340 | 46.7 | 72.3 | 0.48 | |
| 7143 | 41.8 | 77.2 | 0.61 | |
| 7912 | 48.9 | 102.6 | 0.66 |
| Material Type | Temperature (°C) | Strain Rate (s−1) | Yield Strength (MPa) | Ultimate Strength (MPa) | Critical Failure Strain |
|---|---|---|---|---|---|
| M20 | 100 | 5500 | 27.3 | 51.9 | 0.37 |
| 150 | 20.8 | 48.3 | 0.33 | ||
| 200 | 23.1 | 47.6 | 0.4 | ||
| M50 | 100 | 5500 | 28.3 | 62.1 | 0.41 |
| 150 | 22.5 | 54.9 | 0.39 | ||
| 200 | 23.3 | 41.3 | 0.34 | ||
| M80 | 100 | 5200 | 35.7 | 62.9 | 0.32 |
| 150 | 29.2 | 58.7 | 0.31 | ||
| 200 | 36.6 | 51.5 | 0.31 |
| Material Type | A (MPa) | B (MPa) | n | C | m |
|---|---|---|---|---|---|
| M20 | 10.6 | 45.9 | 0.81 | 0.062 | 1.19 |
| M50 | 11.4 | 41.6 | 0.89 | 0.074 | 1.16 |
| M80 | 16.5 | 24.2 | 0.43 | 0.067 | 1.32 |
| Material Type | D1 | D2 | D3 | D4 | D5 |
|---|---|---|---|---|---|
| M20 | 0.02 | 0.807 | −1.873 | −0.0455 | −0.488 |
| M50 | 0.043 | 0.731 | −2.061 | −0.0461 | −0.399 |
| M80 | 0.049 | 0.664 | −2.3 | −0.0459 | −0.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Liu, A.; Ge, C.; Yuan, Y.; Wang, H. Mechanical Properties, Constitutive Behaviors and Failure Criteria of Al-PTFE-W Reactive Materials with Broad Density. Materials 2022, 15, 5167. https://doi.org/10.3390/ma15155167
Sun T, Liu A, Ge C, Yuan Y, Wang H. Mechanical Properties, Constitutive Behaviors and Failure Criteria of Al-PTFE-W Reactive Materials with Broad Density. Materials. 2022; 15(15):5167. https://doi.org/10.3390/ma15155167
Chicago/Turabian StyleSun, Tao, Aoxin Liu, Chao Ge, Ying Yuan, and Haifu Wang. 2022. "Mechanical Properties, Constitutive Behaviors and Failure Criteria of Al-PTFE-W Reactive Materials with Broad Density" Materials 15, no. 15: 5167. https://doi.org/10.3390/ma15155167
APA StyleSun, T., Liu, A., Ge, C., Yuan, Y., & Wang, H. (2022). Mechanical Properties, Constitutive Behaviors and Failure Criteria of Al-PTFE-W Reactive Materials with Broad Density. Materials, 15(15), 5167. https://doi.org/10.3390/ma15155167






