Theoretical Model for the Impact-Initiated Chemical Reaction of Al/PTFE Reactive Material
Abstract
:1. Introduction
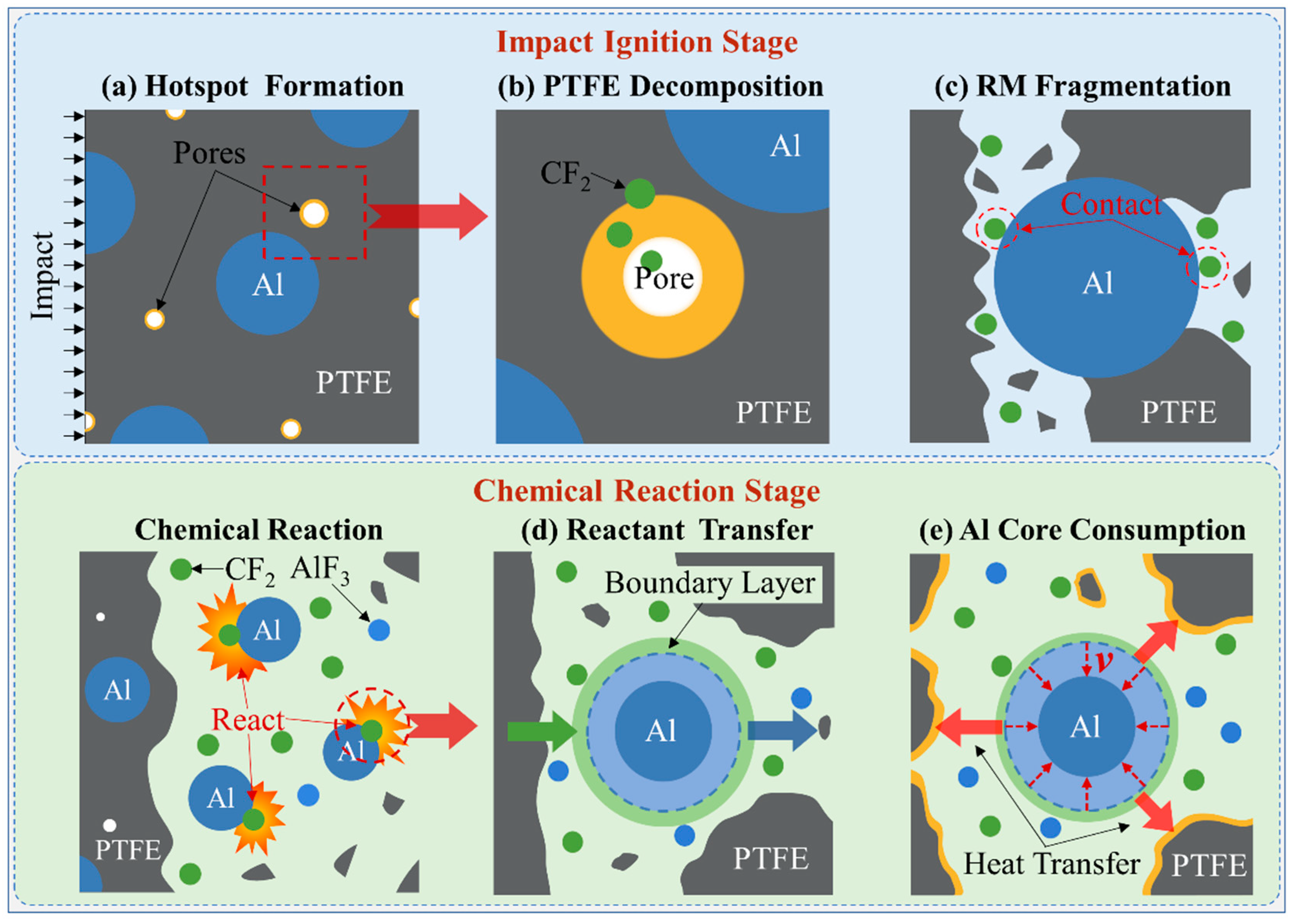
2. Evolution from Impact Ignition to Chemical Reaction
3. Impact Ignition Behavior of RM
3.1. Hotspot Formation Caused Temperature Rise
3.2. PTFE Decomposition Rate
3.3. Ignition Criteria
- PTFE depolymerizes to release gaseous reactant.
- The material is fragmented.
4. Impact-Initiated Chemical Reaction of RMs
4.1. Transfer Efficiency of Gaseous Reactants
4.2. Aluminum Core Consumption Rate
5. Validation of Impact-Initiated Chemical Reaction Model for RMs
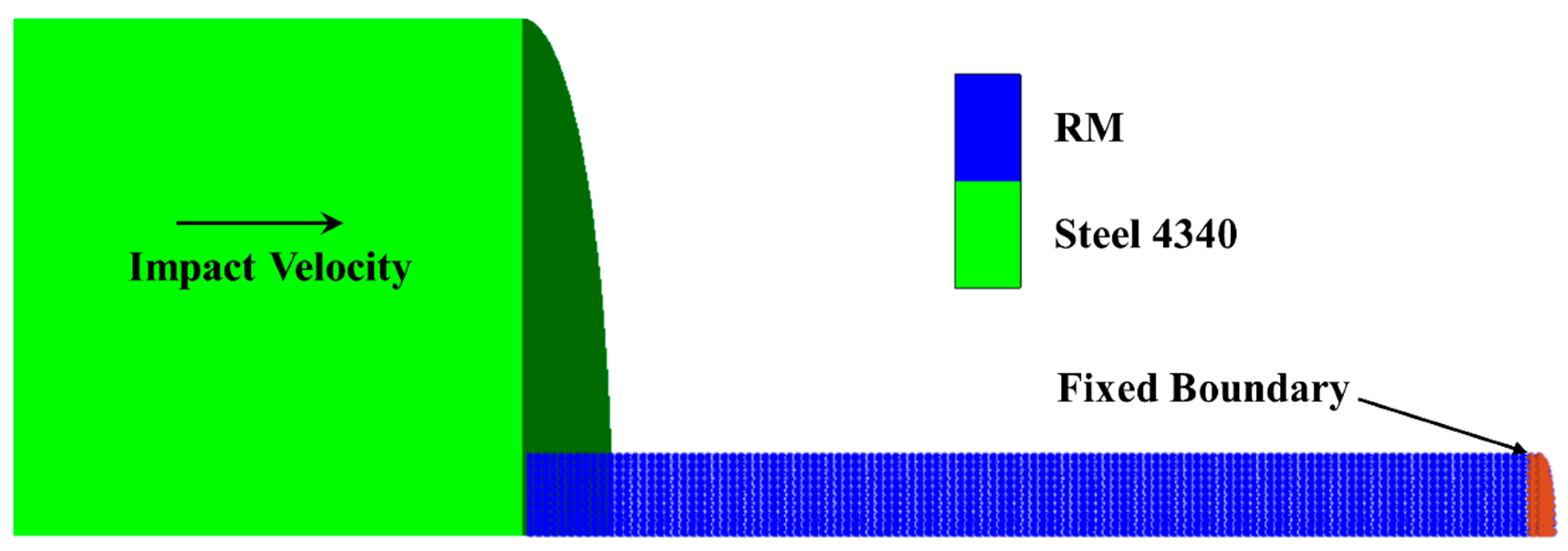
5.1. Calculation Process
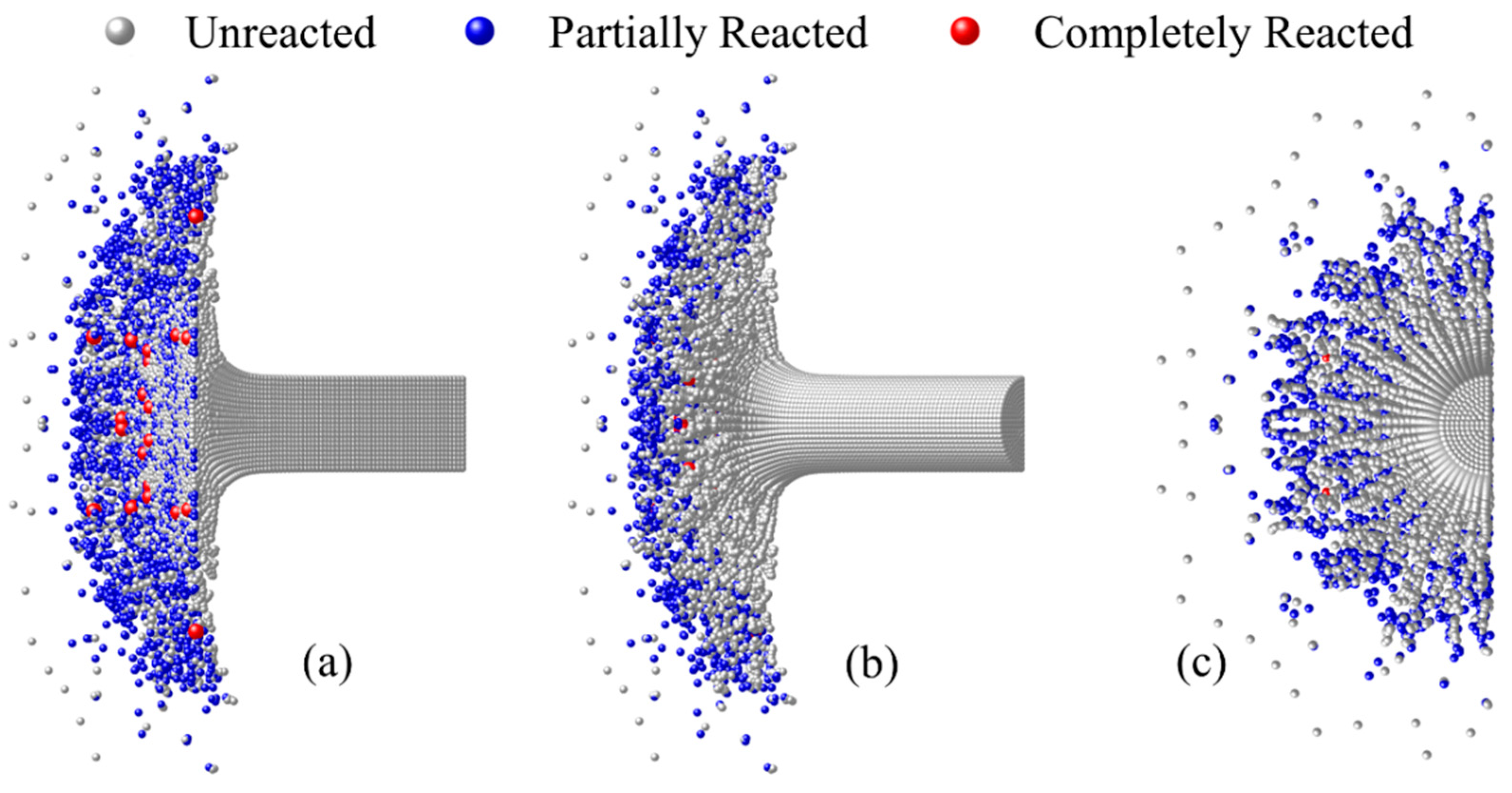
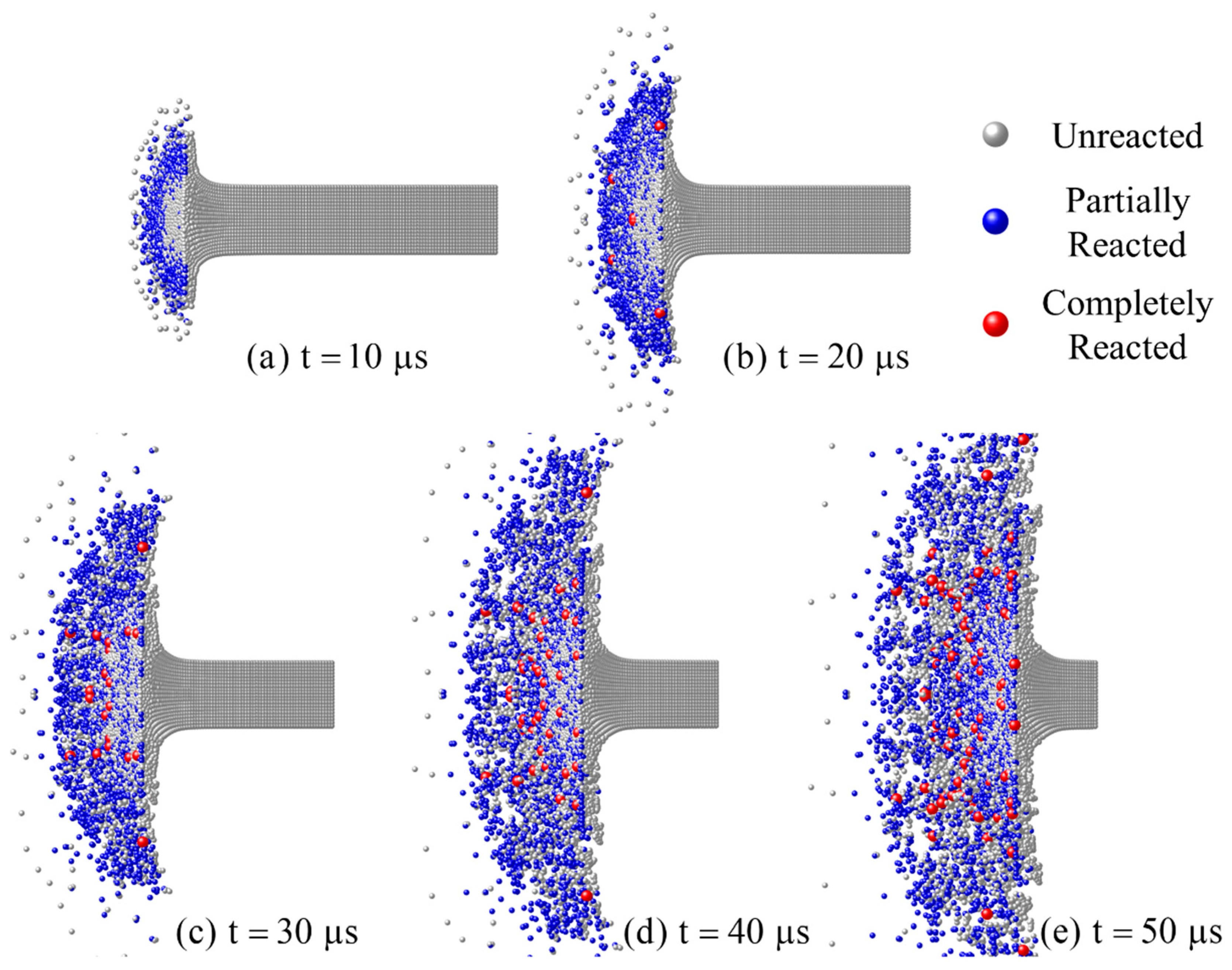
5.2. Calculation Results for Impact Ignition Behavior
5.3. Comparison with Experiment
6. Conclusions
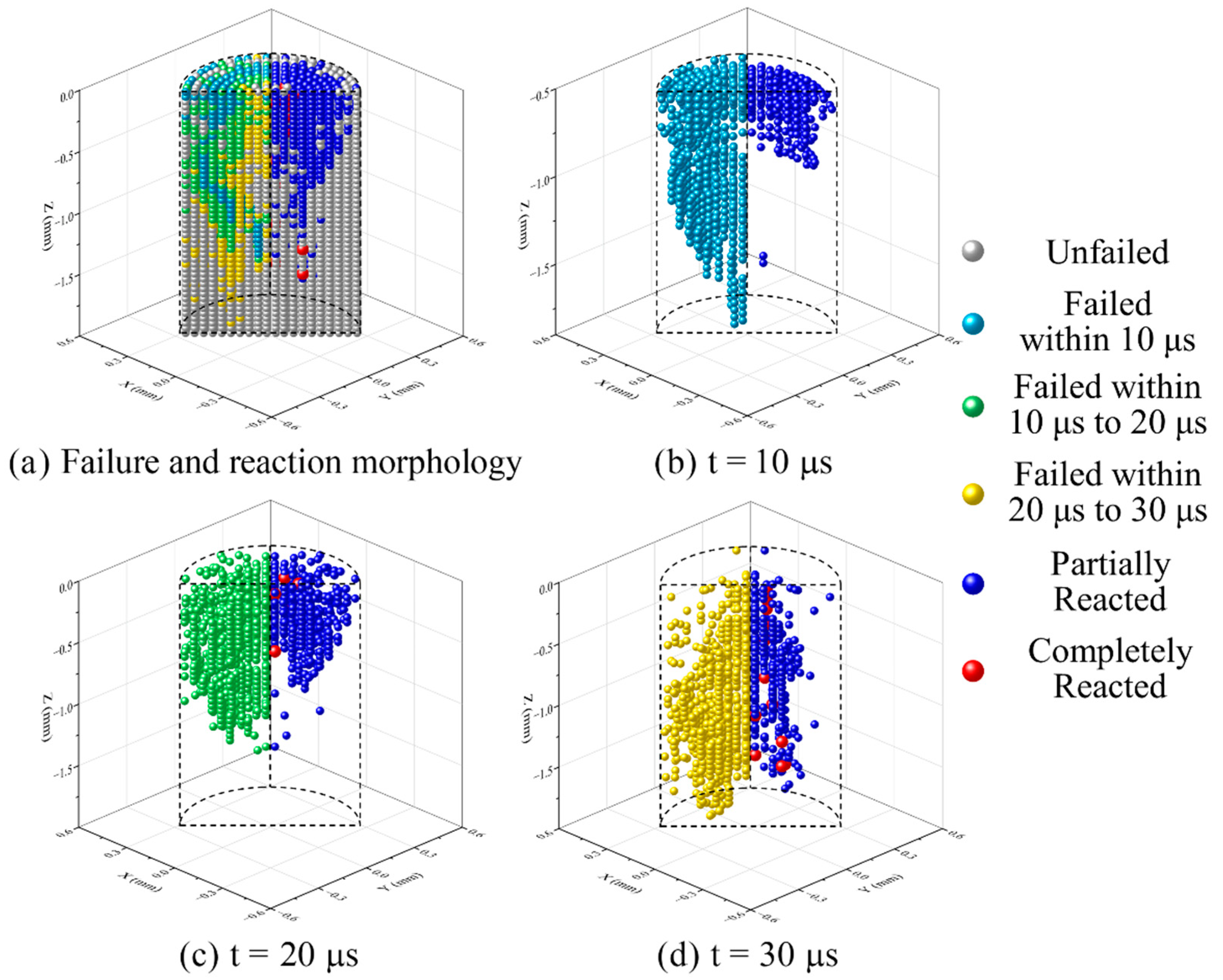
- (a)
- Based on the evolution from impact ignition to chemical reaction, the PTFE decomposition and material fragmentation were chosen as the impact ignition criteria. The hotspot formation mechanism of pore collapse was introduced to describe the temperature rise as well as the decomposition process of PTFE. The reaction rate equation was established based on the gas-solid chemical reaction model.
- (b)
- The decomposition products accumulated before the material fragmentation contact with Al particles and ignite the chemical reaction. The energy released by the initial chemical reaction pushes up the material temperature. When the material temperature exceeds the PTFE decomposition temperature, PTFE continues to decompose and react until the material is completely consumed. Otherwise, the chemical reaction stops, causing the RM to show unsustainable chemical reaction characteristics.
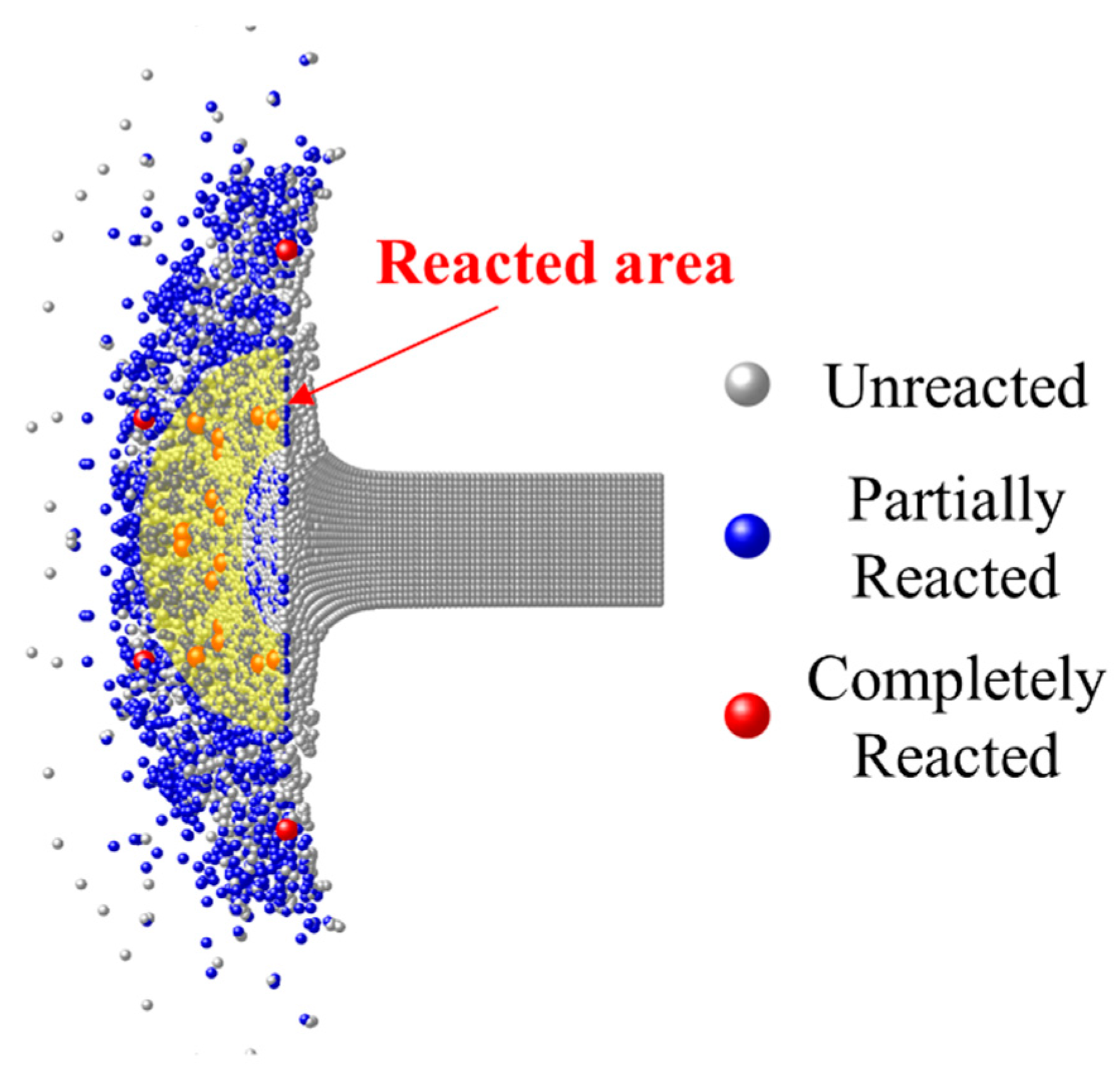
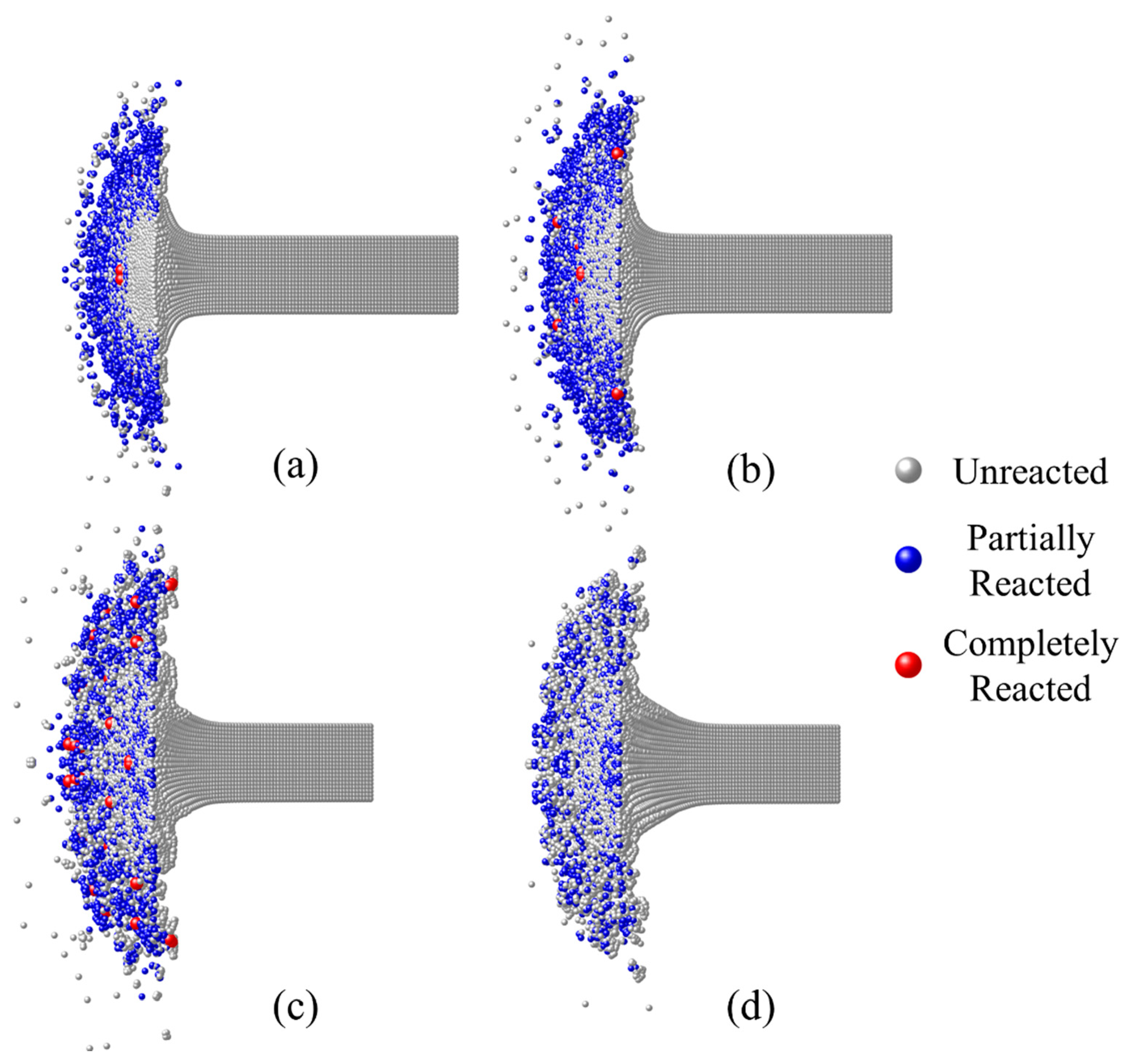
- (c)
- The material which can completely react needs to meet sufficient loading intensity and duration. The material in the shear band of the RM rod failed earliest, but the loading duration was short, hence only partially reacted particles occurred. The failed core material accumulated the most PTFE decomposition extent at the hotspot stage and produced the most completely reacted particles after the material fragmentation because of the long loading duration.
- (d)
- Based on the numerical simulation of the inert dynamic response of RM, the chemical reaction process of the Taylor rod is calculated using the model in this paper. The results are compared and qualitatively consistent with the experimental ones.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, F.Y.; Yu, Q.B.; Zheng, Y.F.; Lei, M.A.; Wang, H.F. Damage effects of double-spaced aluminum plates by reactive material projectile impact. Int. J. Impact Eng. 2017, 104, 13–20. [Google Scholar] [CrossRef]
- William, J.F. Reactive Fragrant Warhead for Enhanced Neutralization of Mortar, Rocket, and Missile Threats; ONR: Arlington, VA, USA, 2006. [Google Scholar]
- Baker, E.L.; Daniels, A.S.; Ng, K.W.; Martin, V.O.; Orosz, J.P. Barnie: A unitary demolition warhead. In Proceedings of the 19th International Symposium on Ballistics, Interlaken, Switzerland, 7–11 May 2001; pp. 7–11. [Google Scholar]
- Wang, H.; Zheng, Y.; Yu, Q.; Liu, Z.; Yu, W. Impact-induced initiation and energy release behavior of reactive materials. J. Appl. Phys. 2011, 110, 074904. [Google Scholar] [CrossRef]
- Dolgoborodov, A.; Makhov, M.N.; Kolbanev, I.V.; Streletskii, A.N.; Fortov, V.E. Detonation in an aluminum-Teflon mixture. J. Exp. Theor. Phys. Lett. 2005, 81, 311–314. [Google Scholar] [CrossRef]
- Ames, R. Energy Release Characteristics of Impact-Initiated Energetic Materials. MRS Online Proc. Libr. 2005, 896, 0896-H03-08. [Google Scholar] [CrossRef]
- Mock, W., Jr.; Holt, W.H. Impact Initiation of Rods of Pressed Polytetrafluoroethylene (PTFE) and Aluminum Powders. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2006; Volume 845, pp. 1097–1100. [Google Scholar] [CrossRef]
- Mock, W.; Drotar, J.T.; Elert, M.; Furnish, M.D.; Chau, R.; Holmes, N.; Nguyen, J. Effect of Aluminum Particle Size on the Impact Initiation of Pressed Ptfe/Al Composite Rods. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2008; pp. 971–974. [Google Scholar] [CrossRef]
- Ge, C.; Dong, Y.; Maimaitituersun, W.; Ren, Y.; Feng, S. Experimental Study on Impact-induced Initiation Thresholds of Polytetrafluoroethylene/Aluminum Composite. Propellants Explos. Pyrotech. 2017, 42, 514–522. [Google Scholar] [CrossRef]
- Ge, C.; Yu, Q.; Zhang, H.; Qu, Z.; Wang, H.; Zheng, Y. On dynamic response and fracture-induced initiation characteristics of aluminum particle filled PTFE reactive material using hat-shaped specimens. Mater. Des. 2020, 188, 108472. [Google Scholar] [CrossRef]
- Tang, L.; Wang, H.; Lu, G.; Zhang, H.; Ge, C. Mesoscale study on the shock response and initiation behavior of Al-PTFE granular composites. Mater. Des. 2021, 200, 109446. [Google Scholar] [CrossRef]
- Jiang, C.; Cai, S.; Mao, L.; Wang, Z. Effect of Porosity on Dynamic Mechanical Properties and Impact Response Characteristics of High Aluminum Content PTFE/Al Energetic Materials. Materials 2019, 13, 140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiao, L.; Zhang, X.F.; He, Y.; Zhao, X.N.; Guan, Z.W. Multiscale modelling on the shock-induced chemical reactions of multifunctional energetic structural materials. J. Appl. Phys. 2013, 113, 173513. [Google Scholar] [CrossRef]
- Zhou, J.; He, Y.; He, Y.; Wang, C.T. Investigation on Impact Initiation Characteristics of Fluoropolymer-matrix Reactive Materials. Propellants Explos. Pyrotech. 2017, 42, 603–615. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Mao, Y.; Gong, F. An effective way to enhance energy output and combustion characteristics of Al/PTFE. Combust. Flame 2020, 214, 419–425. [Google Scholar] [CrossRef]
- Guo, B.; Ren, K.; Li, Z.; Chen, R. Modelling on Shock-Induced Energy Release Behavior of Reactive Materials considering Mechanical-Thermal-Chemical Coupled Effect. Shock Vib. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Enling, T.; Hongwei, L.; Yafei, H.; Chuang, C.; Mengzhou, C.; Kai, G. Temperature evolution of Al/PTFE reactive materials irradiated by femtosecond pulse laser. Mater. Chem. Phys. 2020, 254, 123443. [Google Scholar] [CrossRef]
- McGregor, N.M.; Sutherland, G.T. Plate Impact Experiments on a Porous Teflon-Aluminum Mixture. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2004; pp. 1001–1004. [Google Scholar] [CrossRef]
- Ames, R. Vented Chamber Calorimetry for Impact-Initiated Energetic Materials. In Proceedings of the 43th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; American Institute of Aeronautics and Astronautics: Las Vegas, NV, USA, 2005; pp. 10–13. [Google Scholar] [CrossRef]
- Zhang, X.F.; Shi, A.S.; Qiao, L.; Zhang, J.; Zhang, Y.G.; Guan, Z.W. Experimental study on impact-initiated characters of multifunctional energetic structural materials. J. Appl. Phys. 2013, 113, 083508. [Google Scholar] [CrossRef]
- Xu, F.; Zheng, Y.; Yu, Q.; Wang, Y.; Wang, H. Experimental study on penetration behavior of reactive material projectile impacting aluminum plate. Int. J. Impact Eng. 2016, 95, 125–132. [Google Scholar] [CrossRef]
- Shangye, C.; Chunlan, J.; Liang, M.; Zaicheng, W.; Rong, H.; Sheng, Y. Impact Temperature Rise Law of Porous Aluminum-rich PTFE/Al Energetic Material. Acta Armamentarii 2021, 42, 225–233. [Google Scholar]
- Losada, M.; Chaudhuri, S. Theoretical Study of Elementary Steps in the Reactions between Aluminum and Teflon Fragments under Combustive Environments. J. Phys. Chem. A 2009, 113, 5933–5941. [Google Scholar] [CrossRef]
- Kim, K.; Sohn, C.H. Modeling of reaction buildup processes in shocked porous explosives. In Proceedings of the 8th Symposium (International) on Detonation, Albuquerque, NM, USA, 15–19 July 1985; Volume 926. [Google Scholar]
- Kim, K. Development of a model of reaction rates in shocked multicomponent explosives. In Proceedings of the 9th Symposium (International) on Detonation, Portland, OR, USA, 28 August–1 September 1989; pp. 593–603. [Google Scholar]
- Ge, C.; Dong, Y.; Maimaitituersun, W. Microscale Simulation on Mechanical Properties of Al/PTFE Composite Based on Real Microstructures. Materials 2016, 9, 590. [Google Scholar] [CrossRef] [Green Version]
- Liang, M.; Sheng, Y.; Wanxiang, H.; Chunlan, J.; Zaicheng, W. Thermochemical Reaction Characteristics of PTFE/Al Reactive Material. Acta Armamentarii 2020, 41, 1962–1969. [Google Scholar]
- Geng, B.; Wang, H.; Yu, Q.; Zheng, Y.; Ge, C. Bulk Density Homogenization and Impact Initiation Characteristics of Porous PTFE/Al/W Reactive Materials. Materials 2020, 13, 2271. [Google Scholar] [CrossRef]
- Yuzhong, H.; Bingcheng, F.; Jiping, C. Single Pulse Shock Tube Studies on the Decomposition of Fluoropolymers. Chin. J. Chem. Phys. 1993, 6, 199–205. [Google Scholar]
- Feng, B.; Li, Y.-C.; Hao, H.; Wang, H.-X.; Hao, Y.-F.; Fang, X. A Mechanism of Hot-spots Formation at the Crack Tip of Al-PTFE under Quasi-static Compression. Propellants Explos. Pyrotech. 2017, 42, 1366–1372. [Google Scholar] [CrossRef]
- Raftenberg, M.N.; Mock, W., Jr.; Kirby, G.C. Modeling the impact deformation of rods of a pressed PTFE/Al composite mixture. Int. J. Impact Eng. 2008, 35, 1735–1744. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Ge, C. Characterization of the Dynamic Response and Constitutive Behavior of PTFE/Al/W Reactive Materials. Propellants Explos. Pyrotech. 2020, 45, 788–797. [Google Scholar] [CrossRef]
- Ames, R.G.; Waggener, S.S. Reaction efficiencies for impact-initiated energetic materials. In Proceedings of the 32nd International Pyrotechnics Seminar, Karlsruhe, Germany, 28 June–1 July 2005; Volume 28. [Google Scholar]
- Szekely, J.; Evans, J.W.; Sohn, H.Y. Gas-Solid Reactions; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Lu, G.; Ge, C.; Liu, Z.; Tang, L.; Wang, H. Study on the Formation of Reactive Material Shaped Charge Jet by Trans-Scale Discretization Method. Crystals 2022, 12, 107. [Google Scholar] [CrossRef]






| Hotspot Stage | Chemical Reaction Stage | ||
|---|---|---|---|
| (Mbar) | 1.95 × 10−6 | (J/mol·K) | 8.314 |
| 13 | (Å) | 4.35 | |
| (g/cm3) | 2.23 | 0.417 | |
| (cm/μs·g) | 2.40 × 10−14 | (cm2/μs2·K) | 1.20 × 10−5 |
| A (Mbar) | B (Mbar) | N | C | m |
|---|---|---|---|---|
| 8.044 × 10−5 | 2.506 × 10−3 | 1.8 | 0.4 | 1 |
| D1 | D2 | D3 | D4 | D5 |
| 0.02 | 0.807 | −1.873 | −0.0392 | −0.488 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, G.; Li, P.; Liu, Z.; Xie, J.; Ge, C.; Wang, H. Theoretical Model for the Impact-Initiated Chemical Reaction of Al/PTFE Reactive Material. Materials 2022, 15, 5356. https://doi.org/10.3390/ma15155356
Lu G, Li P, Liu Z, Xie J, Ge C, Wang H. Theoretical Model for the Impact-Initiated Chemical Reaction of Al/PTFE Reactive Material. Materials. 2022; 15(15):5356. https://doi.org/10.3390/ma15155356
Chicago/Turabian StyleLu, Guancheng, Peiyu Li, Zhenyang Liu, Jianwen Xie, Chao Ge, and Haifu Wang. 2022. "Theoretical Model for the Impact-Initiated Chemical Reaction of Al/PTFE Reactive Material" Materials 15, no. 15: 5356. https://doi.org/10.3390/ma15155356
APA StyleLu, G., Li, P., Liu, Z., Xie, J., Ge, C., & Wang, H. (2022). Theoretical Model for the Impact-Initiated Chemical Reaction of Al/PTFE Reactive Material. Materials, 15(15), 5356. https://doi.org/10.3390/ma15155356






