A Damage Model of Concrete including Hysteretic Effect under Cyclic Loading
Abstract
:1. Introduction
2. Fundamental Governing Equations
2.1. Concrete Four-Parameter Damage Model
2.2. Stress Unloading Residual Strain Value
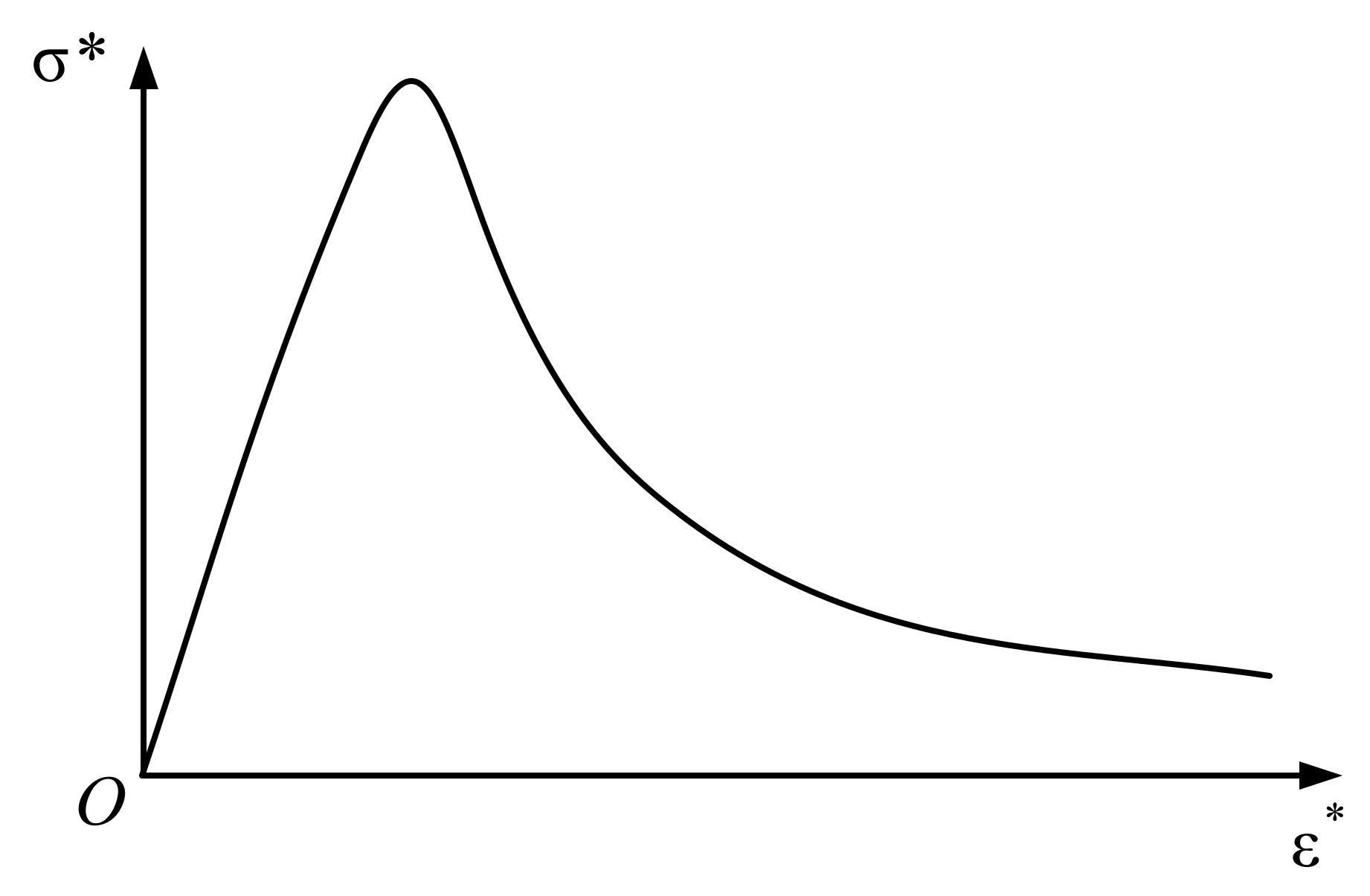
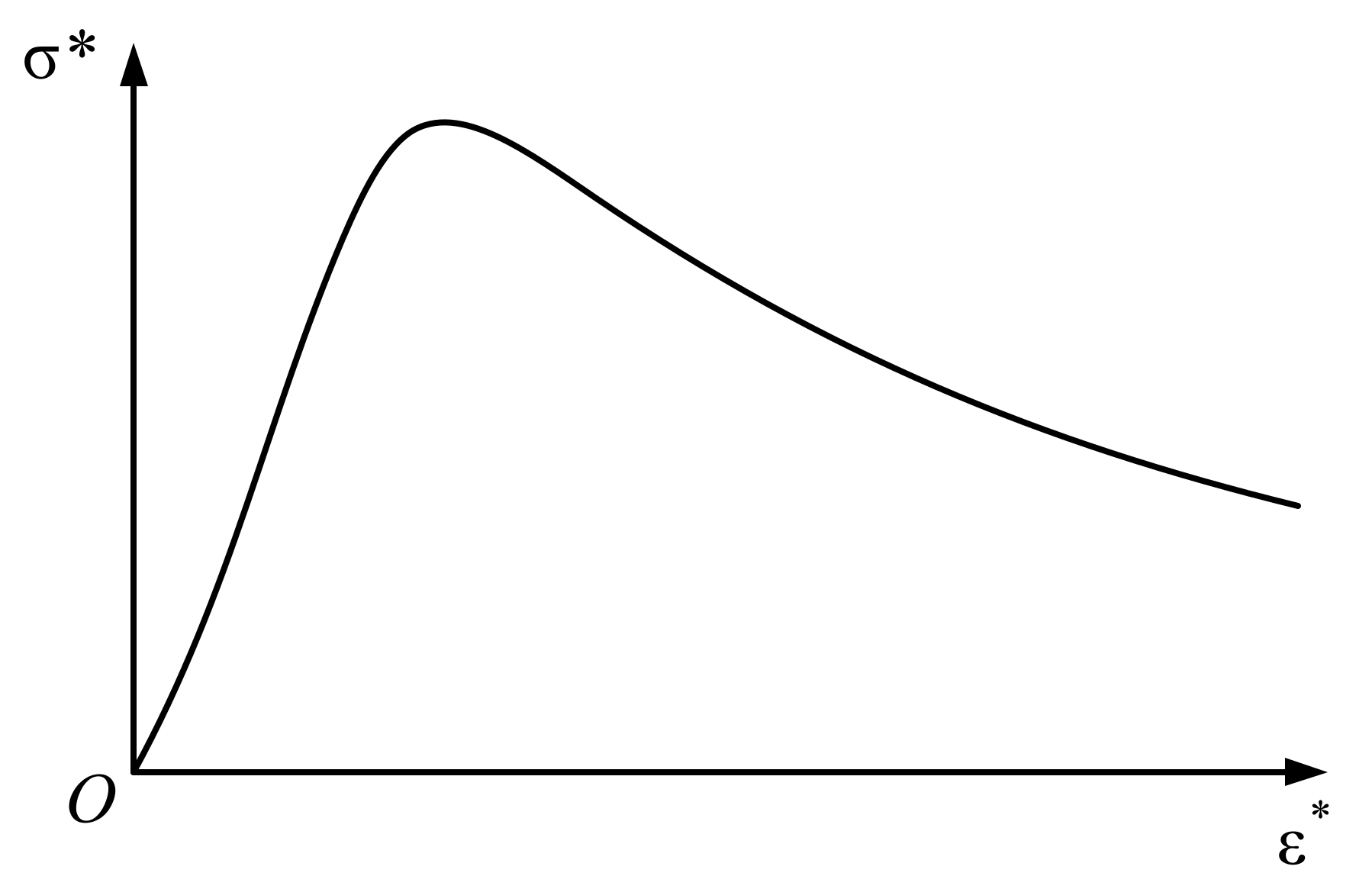
2.3. Uniaxial Stress–Strain Curve
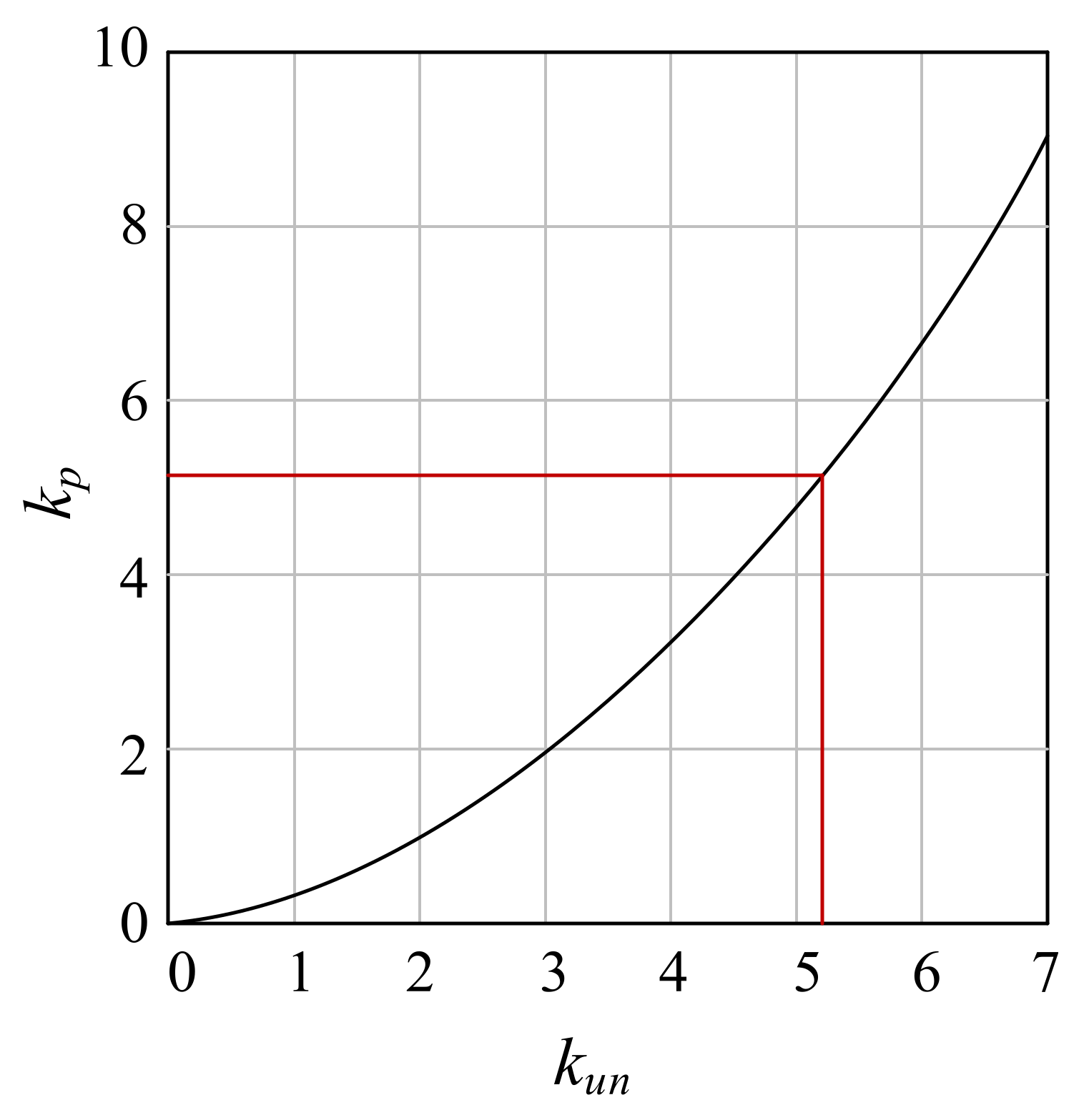
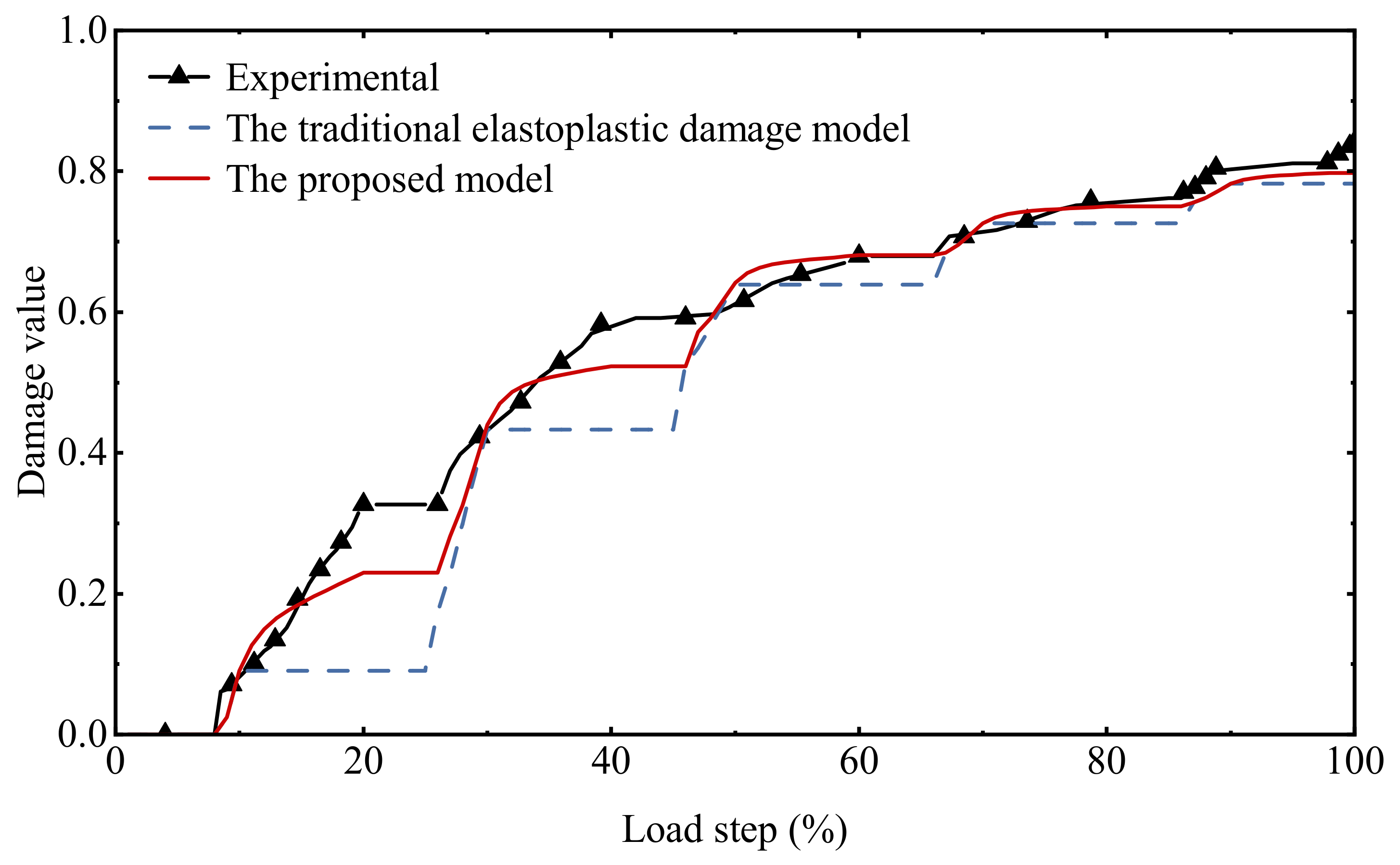
2.4. Damage Variable Values
3. Implementation Process
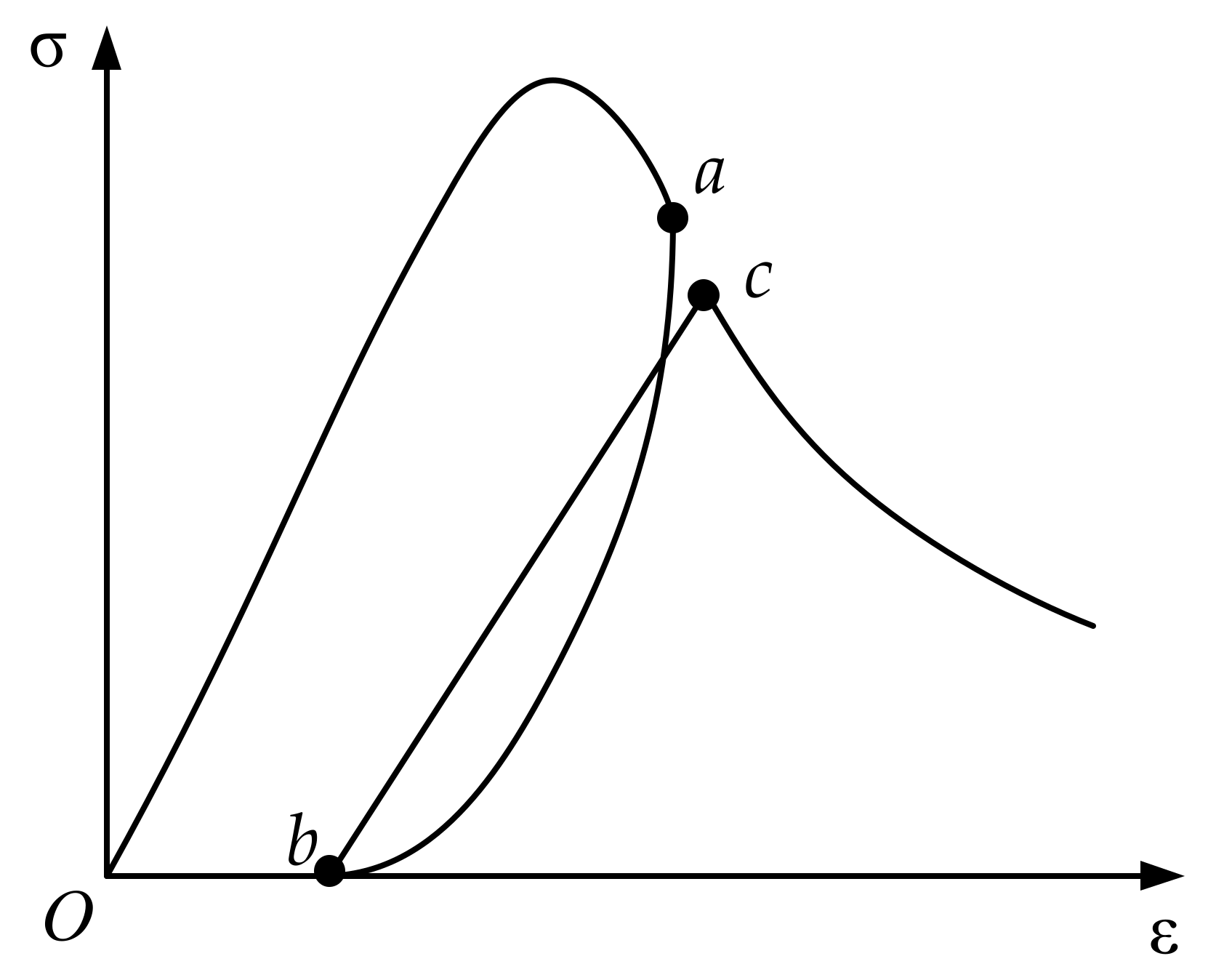
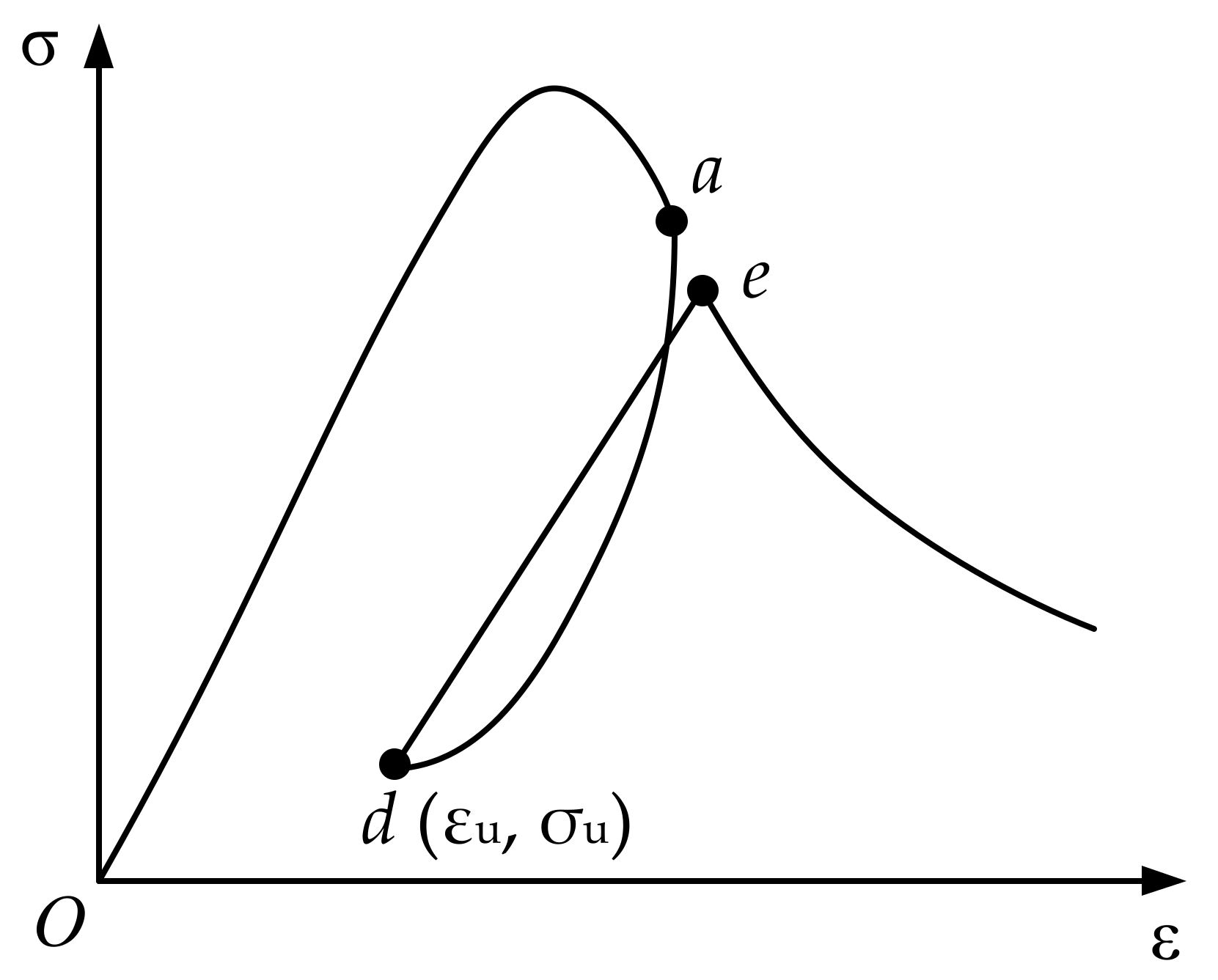
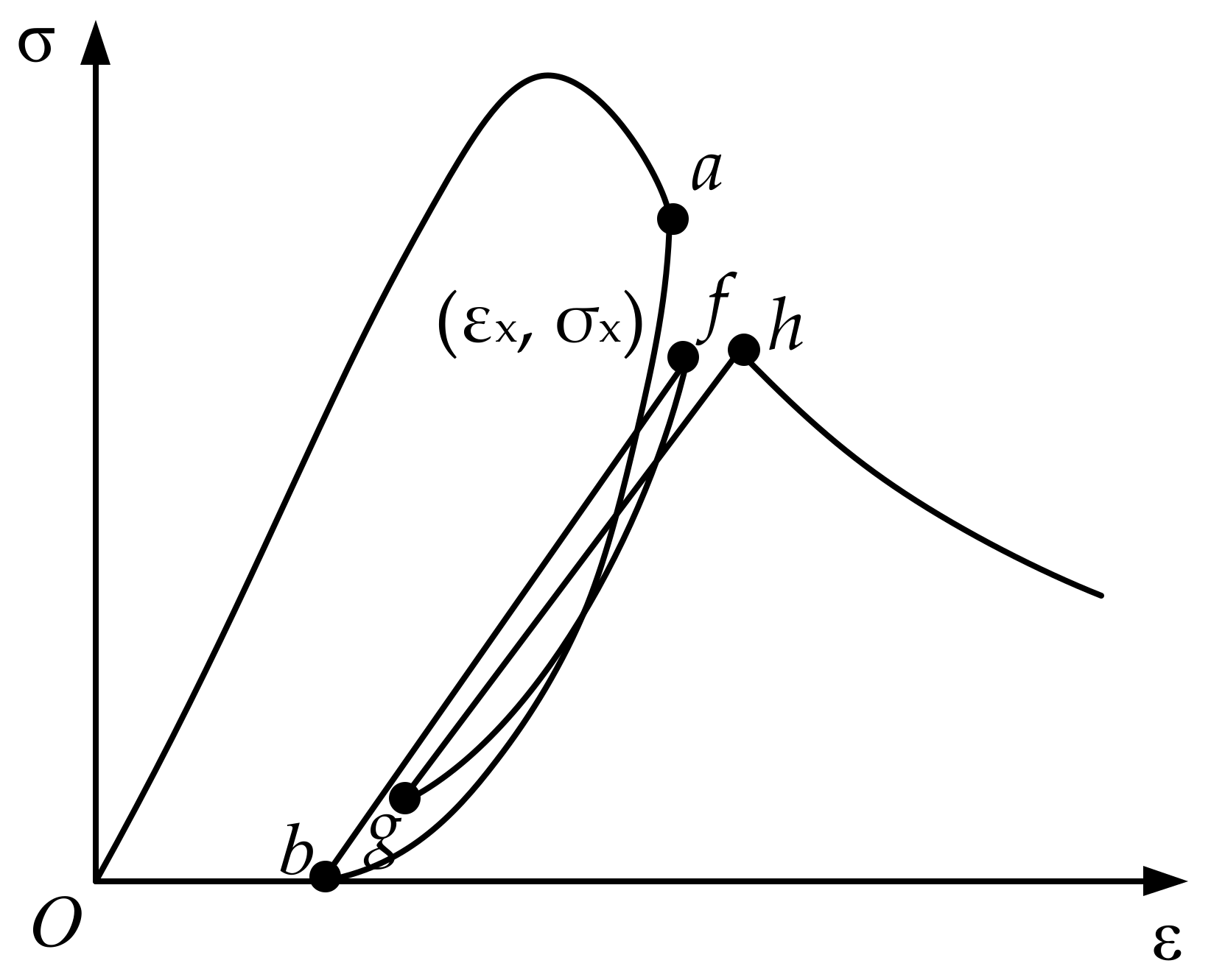
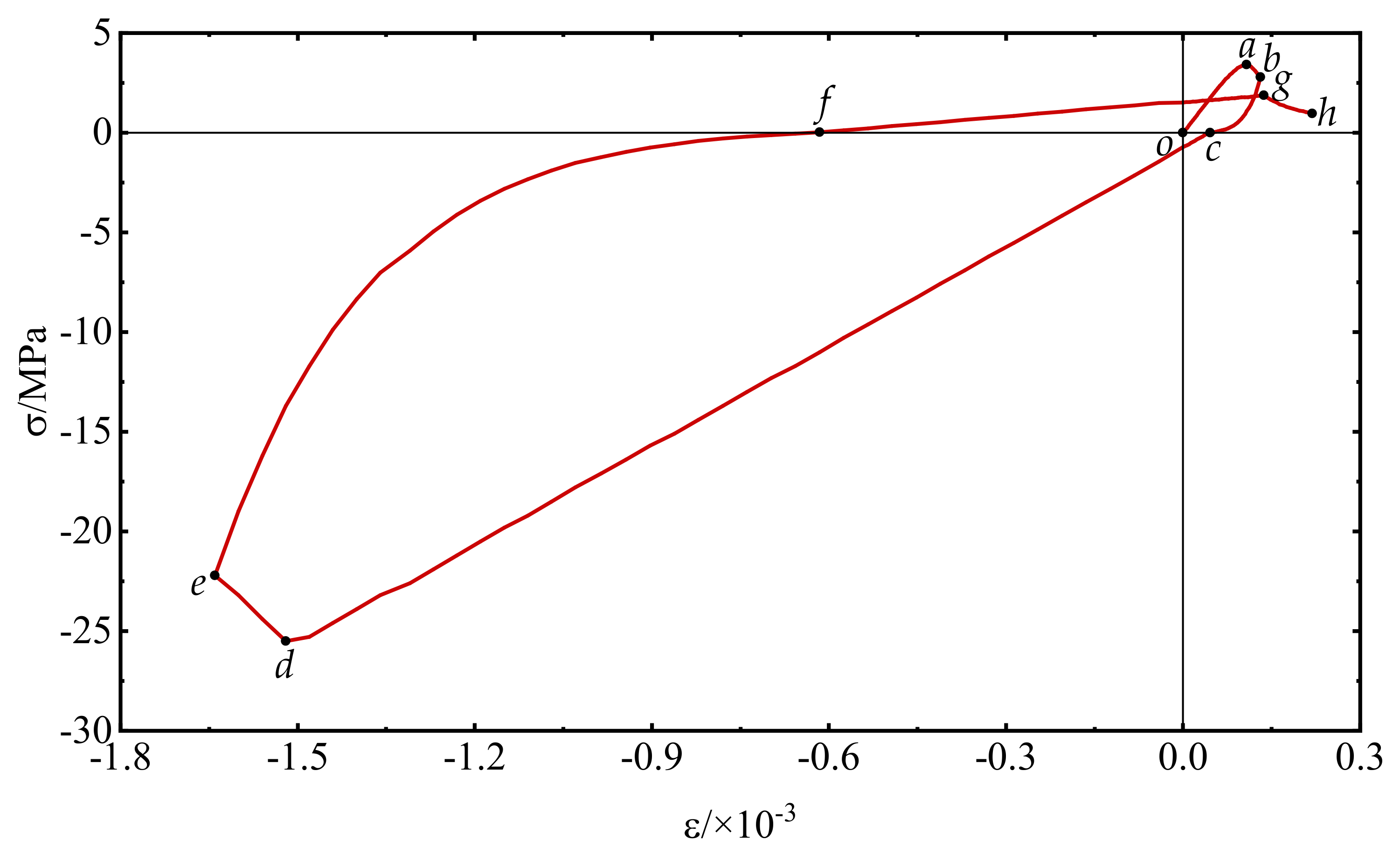
3.1. Complete Loading and Unloading Cycle
3.2. Partial Reload Cycle
3.3. Partial Unloading Cycle
3.4. Numerical Realization of the Model
- Calculating the equivalent strain by the Equation (3);
- Judging the tensile and compressive state by to adopt different stress–strain curves;
- Determining the state of the element at the current time step. In this paper, the states of the elements can be divided into five situations: (a) the loading state of the skeleton line, denoted as ; (b) the unloading state of the skeleton line, denoted as ; (c) the reload state, denoted as ; (d) the partial unloading state, denoted as ; (e) the pull-compression conversion state, denoted as
- When , , and computed ;
- When , and or , computed , ;
- When , and , computed ;
- When , and or , computed , ;
- When , and or , and , computed .
- Calculating the equivalent and the damage value , so that the true stress can be obtained.
4. Example Verification
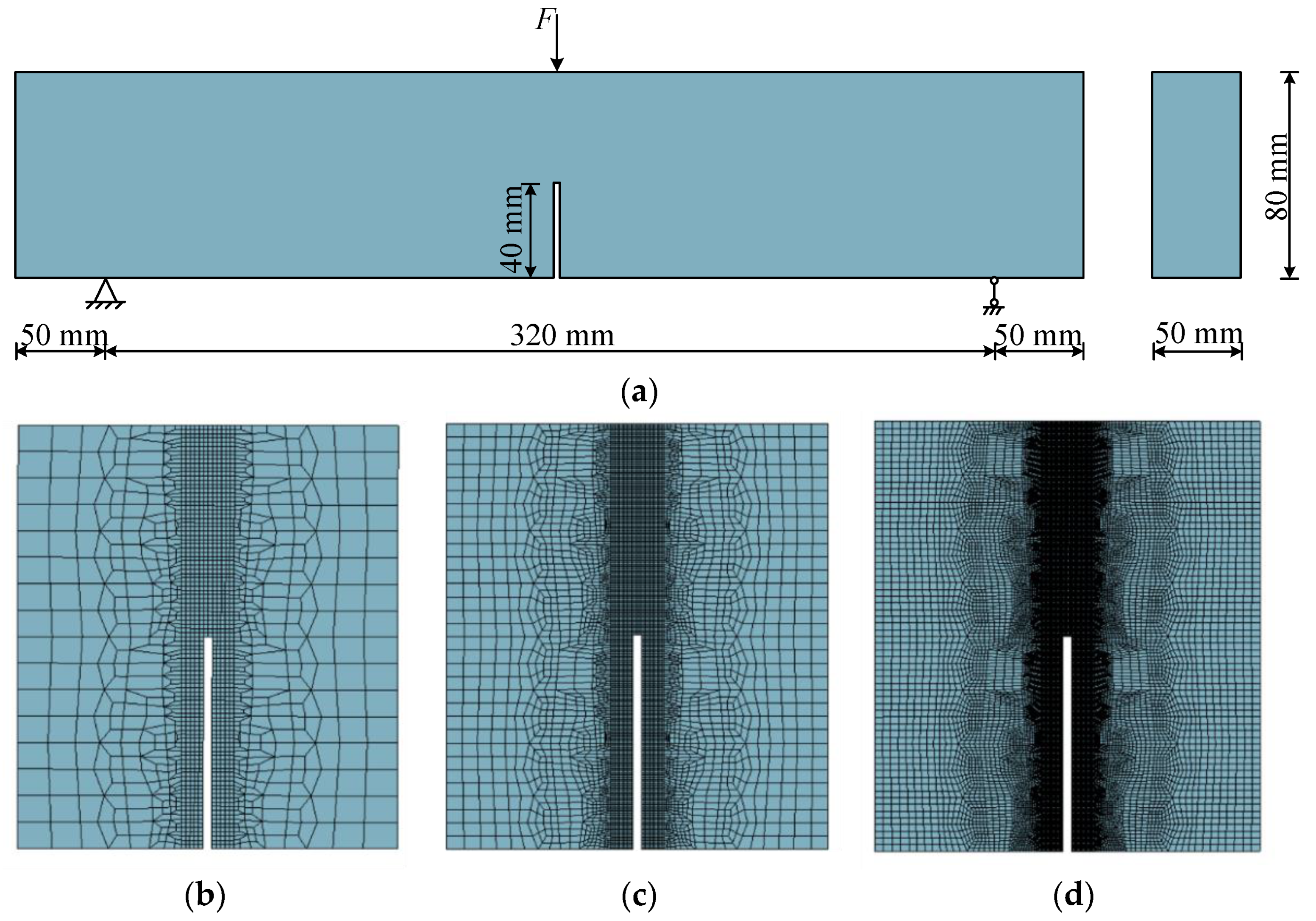
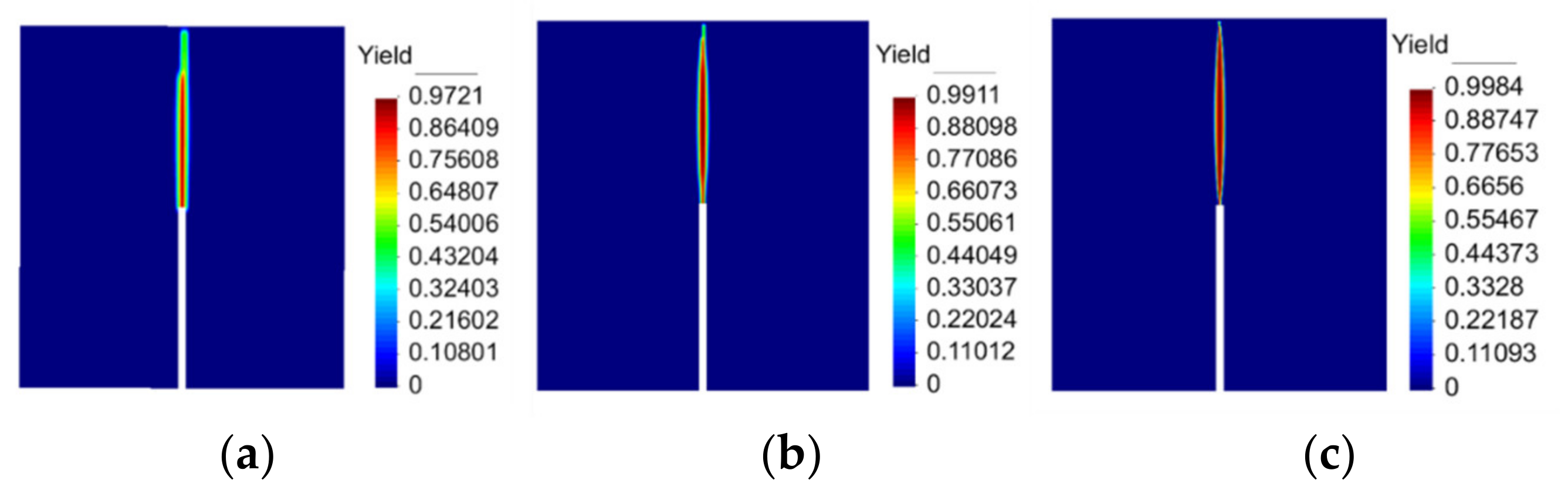
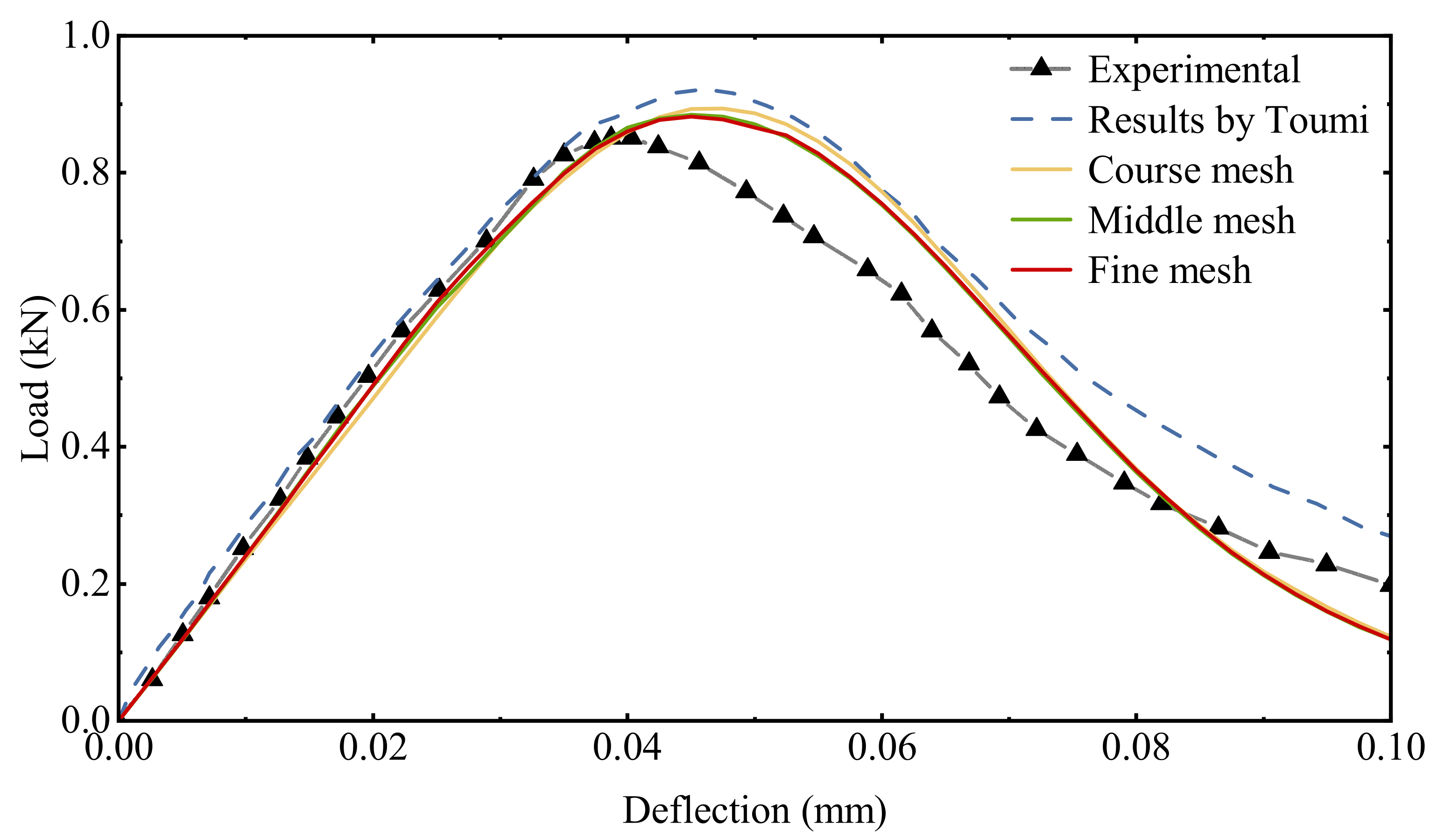
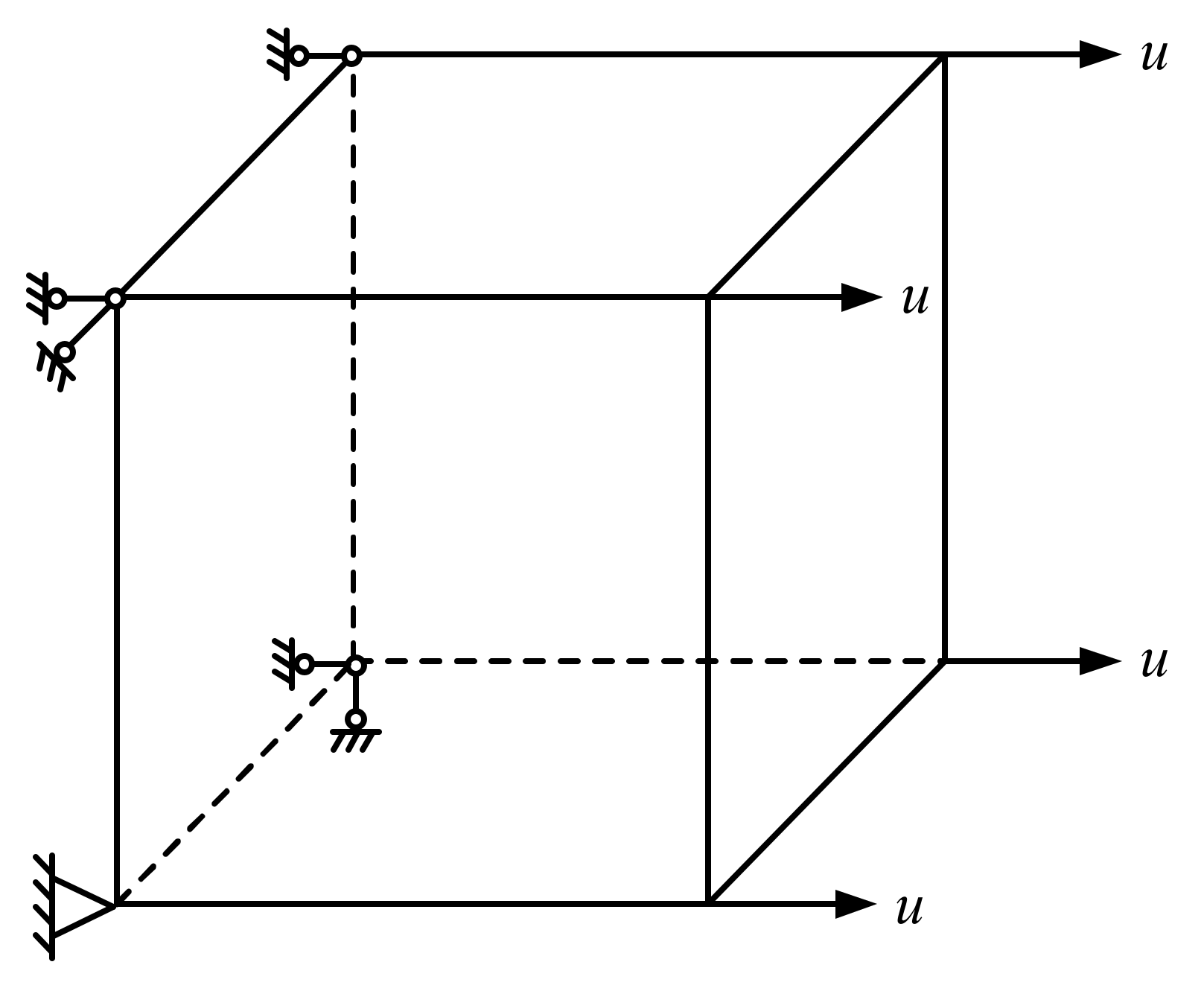
4.1. Three-Point Bending Beam
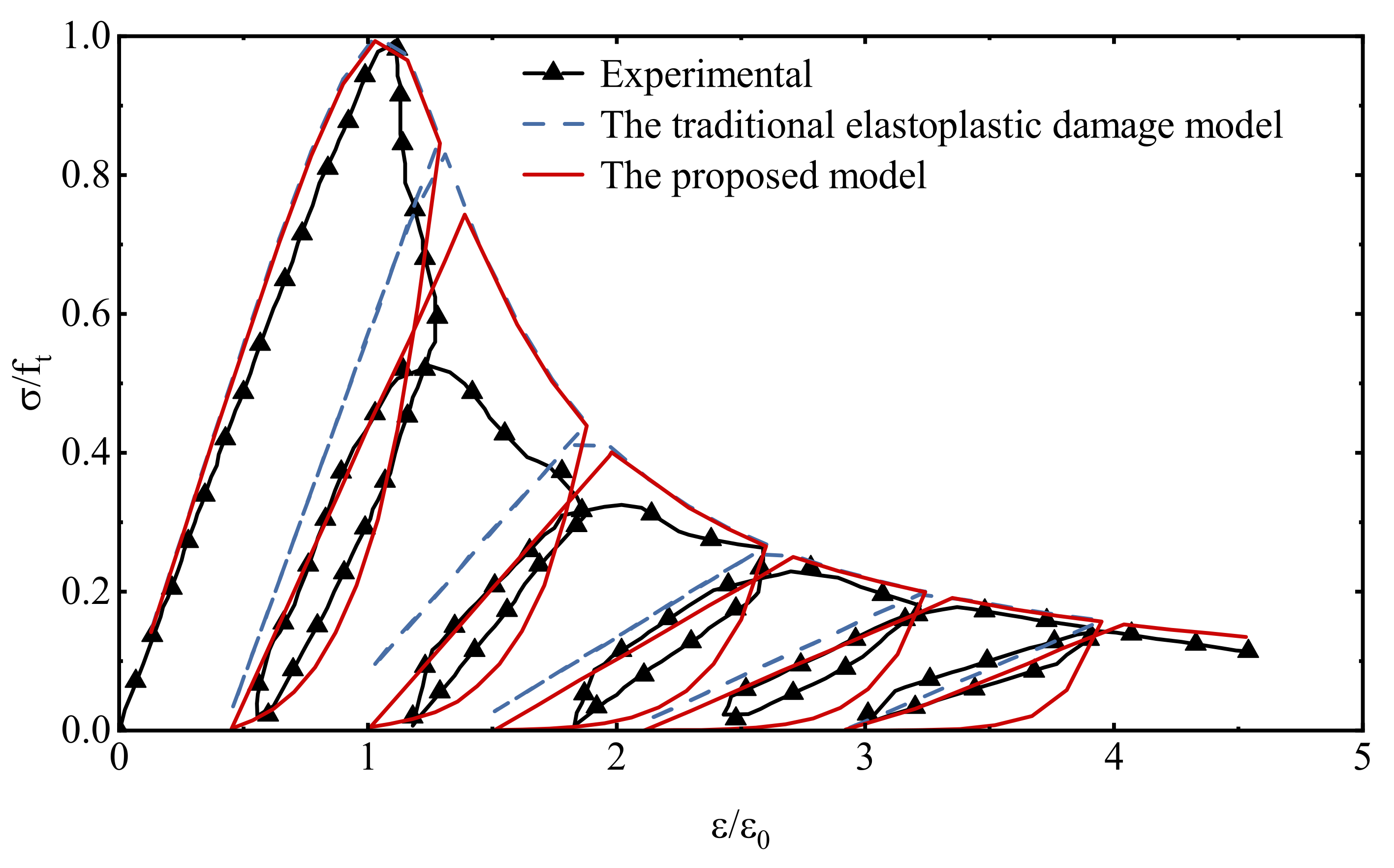
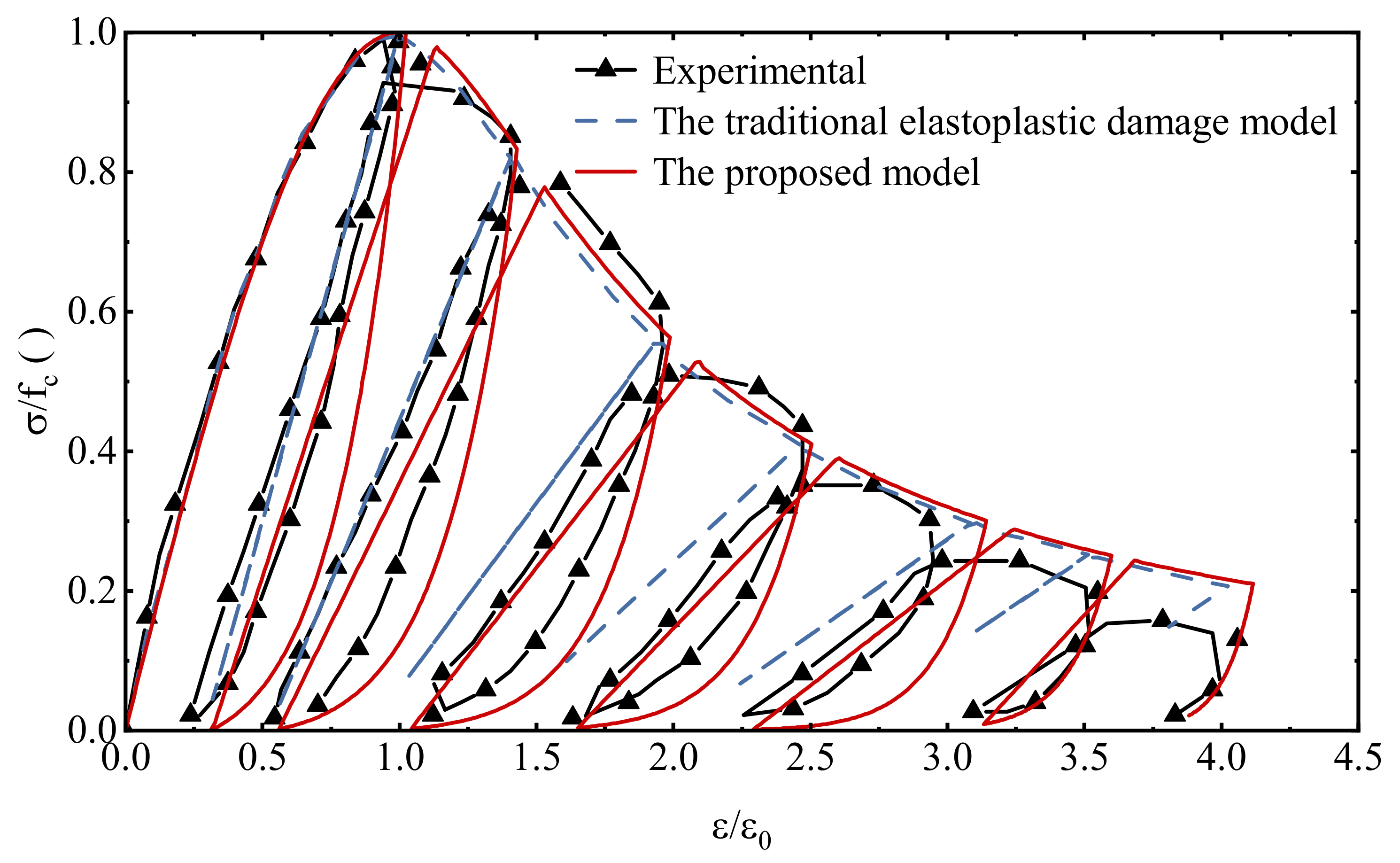
4.2. Uniaxial Cyclic Tensile Loading
4.3. Uniaxial Cyclic Compressive Loading
4.4. Uniaxial Reciprocating Loading
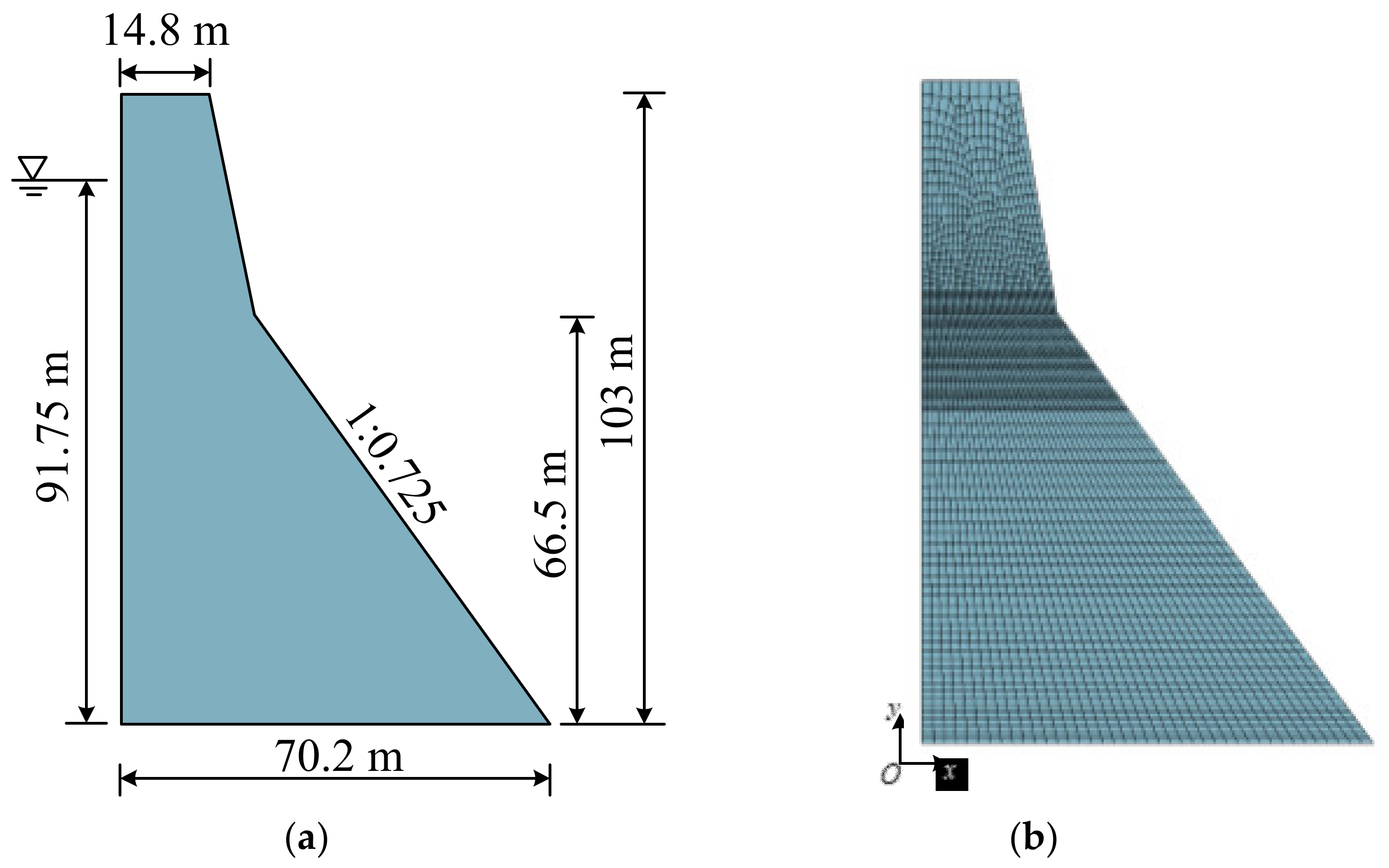
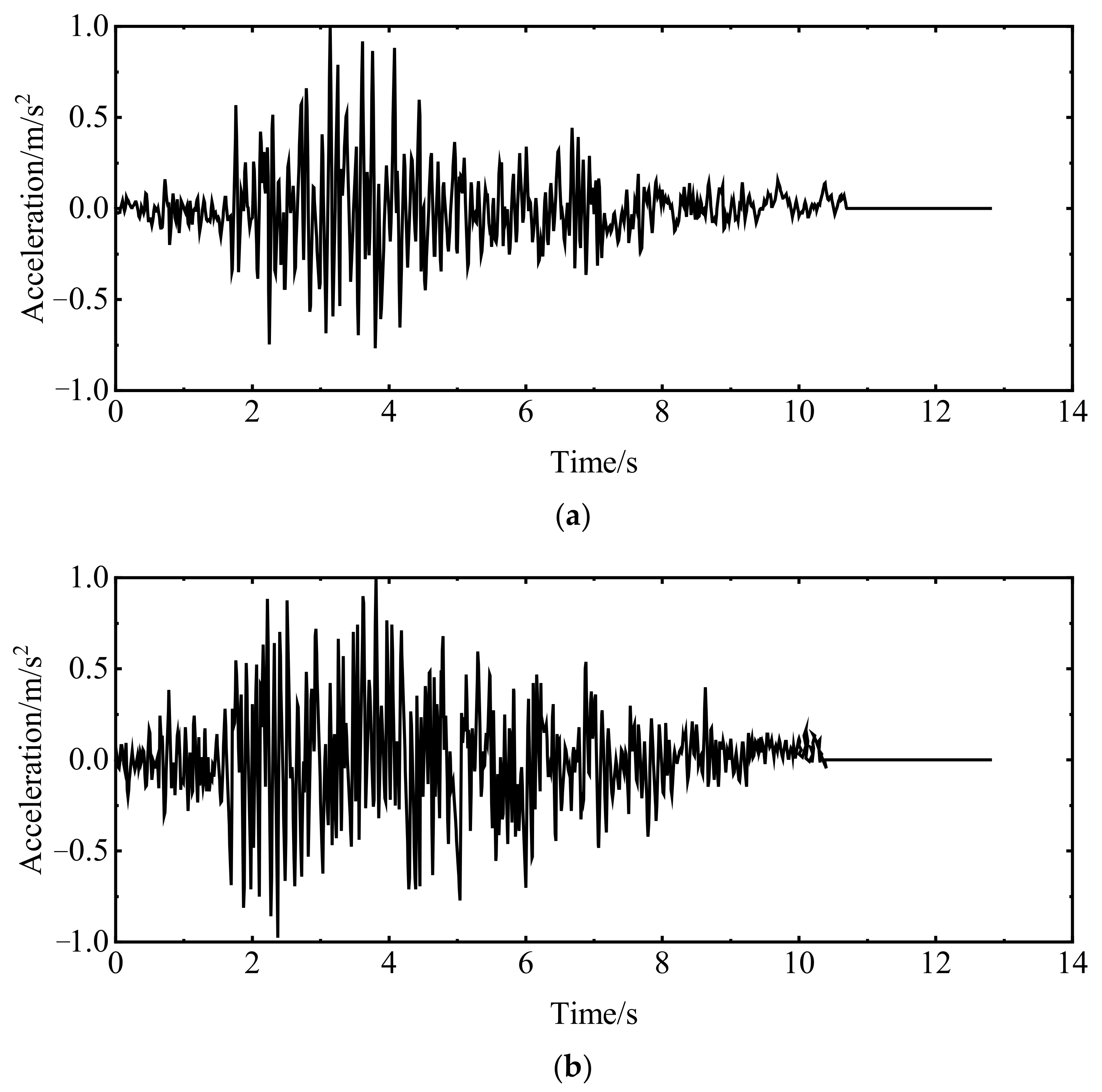
4.5. Koyna Gravity Dam Seismic Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hillerborg, A.; Modeer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–782. [Google Scholar] [CrossRef]
- Wang, G.H.; Wang, Y.X.; Lu, W.B.; Zhou, C.B.; Chen, M.; Yan, P. XFEM based seismic potential failure mode analysis of concrete gravity dam-water-foundation systems through incremental dynamic analysis. Eng. Struct. 2015, 98, 81–94. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Q.Q.; Guan, J.F.; Zhang, P.; Fang, H.Y.; Hu, S.W. Numerical simulation on size effect of fracture toughness of concrete based on mesomechanics. Materials 2020, 13, 1370. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hirmand, M.R.; Papoulia, K.D. A continuation method for rigid-cohesive fracture in a discontinuous Galerkin finite element setting. Int. J. Numer. Methods Eng. 2018, 115, 627–650. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Seyed-Kolbadi, S.M.; Mirzabozorg, H. A smeared crack model for seismic failure analysis of concrete gravity dams considering fracture energy effects. Struct. Eng. Mech. 2013, 48, 17–39. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Seyed-Kolbadi, S.M. Seismic cracking and instability of concrete dams: Smeared crack approach. Eng. Fail. Anal. 2015, 52, 45–60. [Google Scholar] [CrossRef]
- Chen, A.; Chen, W.-F. Constitutive relations for concrete. J. Eng. Mech. 1975, 101, 465–481. [Google Scholar] [CrossRef]
- Bažant, Z.P. Endochronic inelasticity and incremental plasticity. Int. J. Solids Struct. 1978, 14, 691–714. [Google Scholar] [CrossRef]
- Papanikolaou, V.K.; Kappos, A.J. Confinement-sensitive plasticity constitutive model for concrete in triaxial compression. Int. J. Solids Struct. 2007, 44, 7021–7048. [Google Scholar] [CrossRef] [Green Version]
- Rosati, L.; Valoroso, N. A return map algorithm for general isotropic elasto/visco-plastic materials in principal space. Int. J. Numer. Methods Eng. 2004, 60, 461–498. [Google Scholar] [CrossRef]
- Valliappan, S.; Yazdchi, M.; Khalili, N. Seismic analysis of arch dams—A continuum damage mechanics approach. Int. J. Numer. Methods Eng. 1999, 45, 1695–1724. [Google Scholar] [CrossRef]
- Yun, K.; Kim, T.J.; Jang, P.S.; Wang, Z.Q.; Ronald, S. An improved crack tracking algorithm with self-correction ability of the crack path and its application in a continuum damage model. Int. J. Numer. Methods Eng. 2019, 117, 249–269. [Google Scholar] [CrossRef]
- Mazars, J.; Hamon, F.; Grange, S. A new 3D damage model for concrete under monotonic, cyclic and dynamic loadings. Mater. Struct. 2015, 48, 3779–3793. [Google Scholar] [CrossRef] [Green Version]
- Cervera, M.; Oliver, J.; Faria, R. Seismic evaluation of concrete dams via continuum damage models. Earthq. Eng. Struct. Dyn. 1995, 24, 1225–1245. [Google Scholar] [CrossRef]
- Comi, C.; Perego, U. Fracture energy based bi-dissipative damage model for concrete. Int. J. Solids Struct. 2001, 38, 6427–6454. [Google Scholar] [CrossRef]
- Arruda, M.R.T.; Castro, L.M.S. A new hybrid-mixed stress model for the analysis of concrete structures using damage mechanics. Comput. Struct. 2013, 125, 23–44. [Google Scholar] [CrossRef]
- Badel, P.; Godard, V.; Leblond, J.B. Application of some anisotropic damage model to the prediction of the failure of some complex industrial concrete structure. Int. J. Solids Struct. 2007, 44, 5848–5874. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Wu, Y.F.; Xu, Y.; Fu, T.T. A thermodynamically consistent nonlocal damage model for concrete materials with unilateral effects. Comput. Meth. Appl. Mech. Eng. 2015, 297, 371–391. [Google Scholar] [CrossRef]
- Daneshyar, A.; Ghaemian, M. Coupling microplane-based damage and continuum plasticity models for analysis of damage-induced anisotropy in plain concrete. Int. J. Plasticity 2017, 95, 216–250. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Taqieddin, Z.N.; Kattan, P.I. Anisotropic damage-plasticity model for concrete. Int. J. Plasticity 2008, 24, 1946–1965. [Google Scholar] [CrossRef]
- Abu Al-Rub, R.K.; Kim, S.M. Computational applications of a coupled plasticity-damage constitutive model for simulating plain concrete fracture. Eng. Fract. Mech. 2010, 77, 1577–1603. [Google Scholar] [CrossRef]
- Sarikaya, A.; Erkmen, R.E. A plastic-damage model for concrete under compression. Int. J. Mech. Sci. 2019, 150, 584–593. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. A plastic-damage concrete model for earthquake analysis of dams. Earthq. Eng. Struct. Dyn. 1998, 27, 937–956. [Google Scholar] [CrossRef]
- Dabbagh, H.; Aslani, F. A comparative study on the cyclic constitutive models of concrete. In Proceedings of the 4th International Conference on Construction Materials—Performance, Innovations and Structural Implications (ConMat’09), Nagoya, Japan, 24–26 August 2009. [Google Scholar]
- Palermo, D.; Vecchio, F.J. Compression field modeling of reinforced concrete subjected to reversed loading: Verification. Aci. Struct. J. 2004, 101, 155–164. [Google Scholar]
- Mansour, M.; Hsu, T.T.C. Behavior of reinforced concrete elements under cyclic shear. II: Theoretical model. J. Struct. Eng. 2005, 131, 54–65. [Google Scholar] [CrossRef]
- Sakai, J.; Kawashima, K. Unloading and reloading stress-strain model for confined concrete. J. Struct. Eng. 2006, 132, 112–122. [Google Scholar] [CrossRef]
- Konstantinidis, D.; Kappos, A.J.; Izzuddin, B.A. Analytical model for unconfined and confined high strength concrete under cyclic loading. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Aslani, F.; Jowkarmeimandi, R. Stress-strain model for concrete under cyclic loading. Mag. Concr. Res. 2012, 64, 673–685. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z. Principles of Reinforced Concrete, 3rd ed.; Tsinghua University Press: Beijing, China, 2013; pp. 18–30. [Google Scholar]
- Zheng, L.; Zhu, B. Development of uniaxial cyclic constitutive model for concrete based on Chinese concrete code. Build. Struct. 2013, 43, 726–730. [Google Scholar]
- Yassin, M.M. Nonlinear Analysis of Prestressed Concrete Structures under Monotonic and Cyclic Loads; University of California, Berkeley: Berkeley, CA, USA, 1994. [Google Scholar]
- Hsieh, S.S.; Chen, W.F.; Ting, E.C. An Elastic-Fracture Model for Concrete. Eng. Mech. 1979, 18, 437–440. [Google Scholar]
- Li, T.C.; Wei, W. An isotropy damage model for concrete in strain space. In Proceedings of the 11th Biennial ASCE Aerospace Division International Conference on Engineering, Science, Construction, and Operations in Challenging Environments, Long Beach, CA, USA, 3–5 March 2008. [Google Scholar]
- Research Laboratory of Earthquake and Blast Resistant Engineering of Tsinghua University. The Experimental Investigation of Mechanical Behavior of Concrete; Tsinghua University Press: Beijing, China, 1996. [Google Scholar]
- Qi, H.J.; Li, T.C.; Liu, X.Q.; Zhao, L.H.; Lin, C.N.; Fan, S.J. A variable parameters damage model for concrete. Eng. Fract. Mech. 2020, 228, 106898. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, L.H.; Liu, Z.; Jia, M. An elastic-plastic damage constitutive model of concrete under cyclic loading and its numerical implementation. Eng. Mech. 2022, 39, 1–10. [Google Scholar]
- Karsan, I.D. Behavior of concrete under compressive loadings. J. Struct. Div. Asce 1969, 95, 2543–2564. [Google Scholar] [CrossRef]
- Yankelevsky, D.Z.; Reinhardt, H.W. Model for cyclic compressive behavior of concrete. J. Struct. Eng. 1987, 113, 228–240. [Google Scholar] [CrossRef]
- Bahn, B.Y.; Hsu, T.T.C. Stress-strain behavior of concrete under cyclic loading. Aci. Mater. J. 1998, 95, 178–193. [Google Scholar]
- Otter, D.E.; Naaman, A.E. Model for response of concrete to random compressive loads. J. Struct. Eng. 1989, 115, 2794–2809. [Google Scholar] [CrossRef]
- Sima, J.F.; Roca, P.; Molins, C. Cyclic constitutive model for concrete. Eng. Struct. 2008, 30, 695–706. [Google Scholar] [CrossRef] [Green Version]
- Toumi, A.; Bascoul, A. Mode I crack propagation in concrete under fatigue: Microscopic observations and modelling. Int. J. Numer. 2002, 26, 1299–1312. [Google Scholar] [CrossRef]
- Gopalaratnam, V.S.; Shah, S.P. Softening response of plain concrete in direct tension. Civ. Environ. Eng. 1985, 82, 310–323. [Google Scholar]
- Okamoto, S.; Shiomi, S.; Yamabe, K. Earthquake resistance of prestressed concrete structures. In Proceedings of the Annual Architectural Institute of Japan (AIJ) Convention, Japan, 1 January 1976. [Google Scholar]
- Council, N. Earthquake Engineering for Concrete Dams: Design, Performance, and Research Needs; The National Academies Press: Washington, DC, USA, 1990. [Google Scholar]
- Guo, S.S. Study on Seismic Damage Process Mechanism and Quantitative Evaluation Criteria of Concrete Damfoundation System Based on Parallel Computation; China Institute of Water Resources and Hydropower Research: Beijing, China, 2013. [Google Scholar]



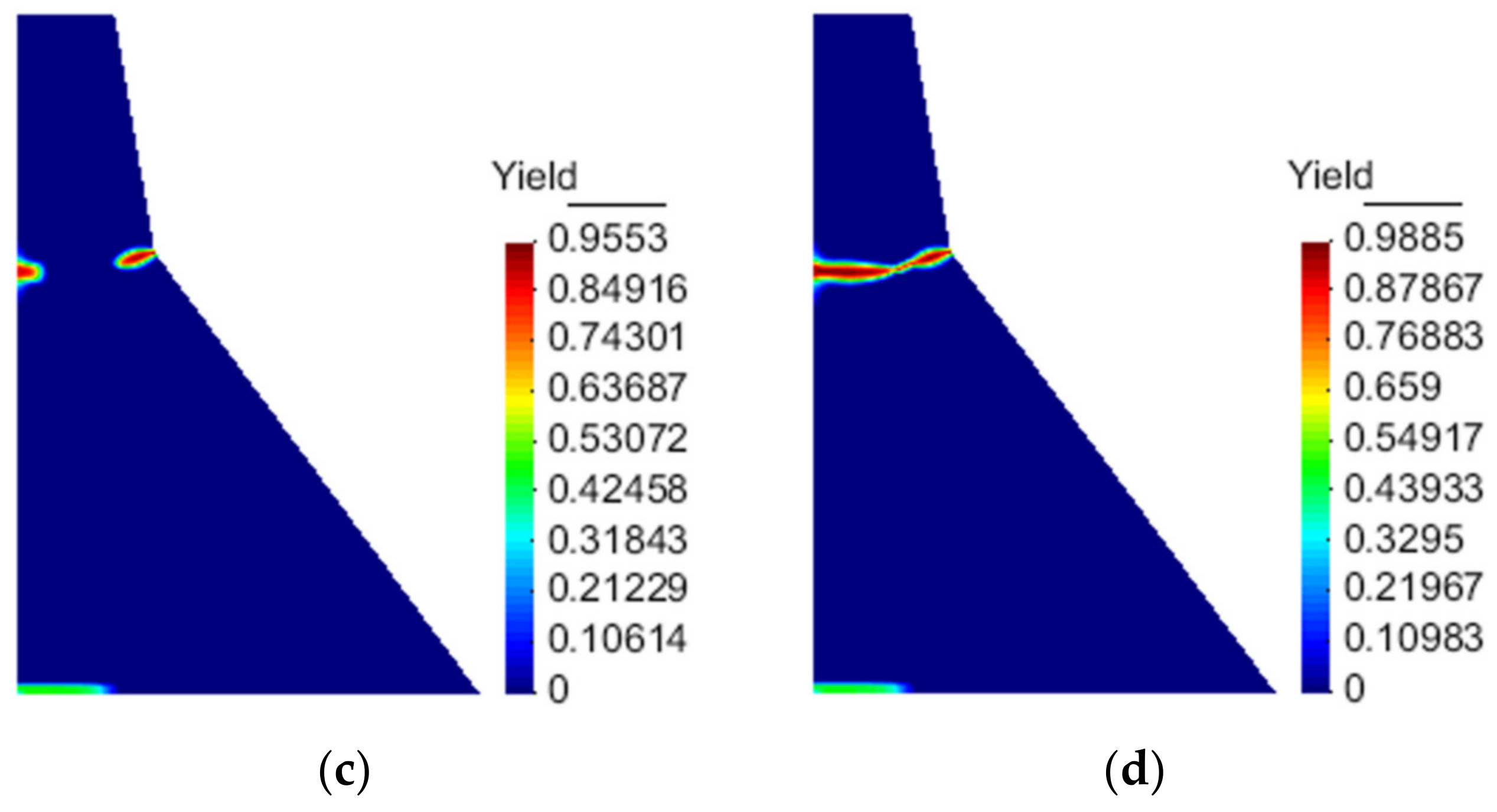
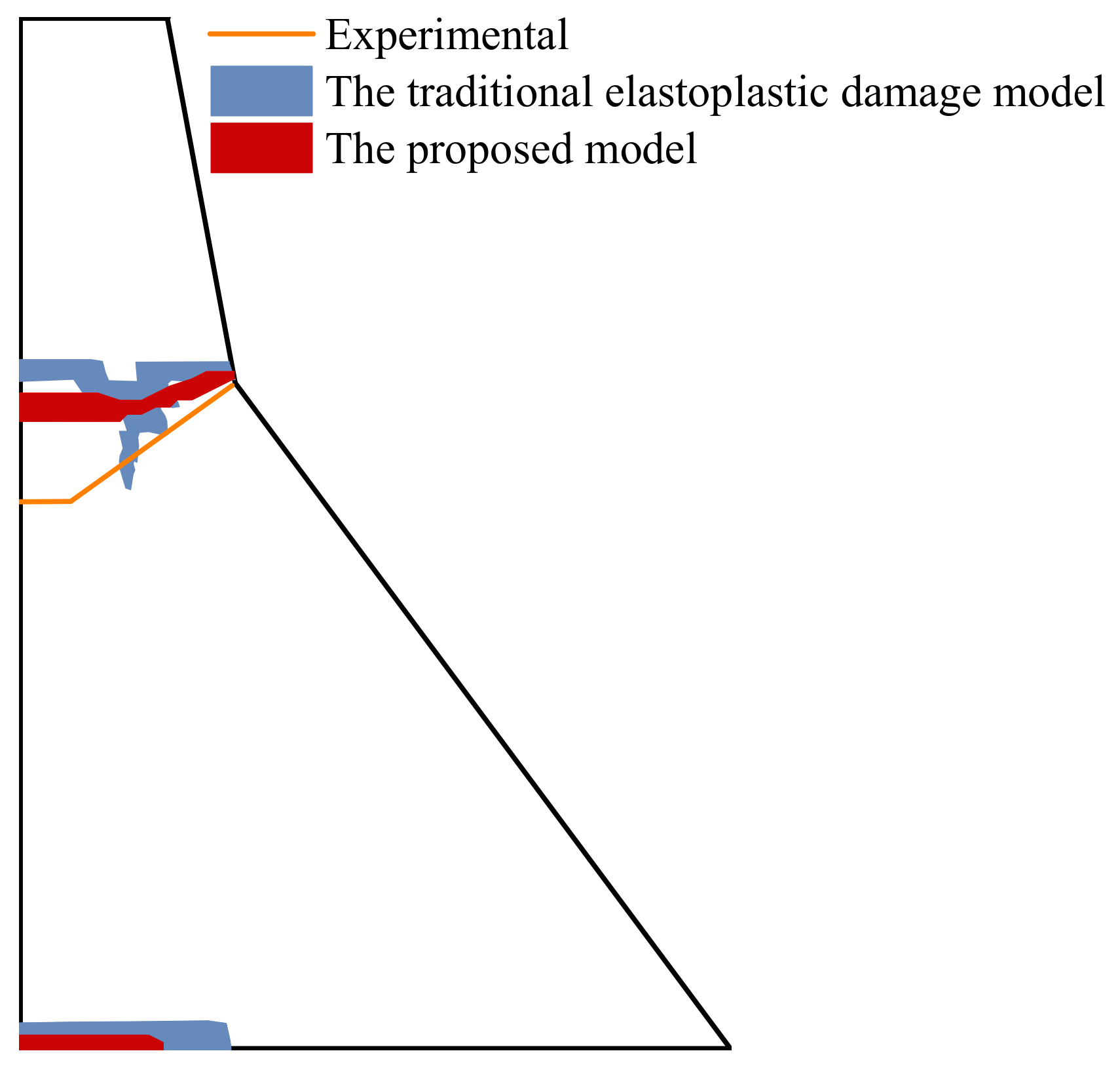
| Test | (kg/m3) | E (GPa) | (MPa) | |||||
|---|---|---|---|---|---|---|---|---|
| Three-point bending beam | 2400 | 31.6 | 5.2 | 0.2 | 0.10 | 8.44 | -- | |
| Uniaxial cyclic tensile load | 2400 | 31.7 | 3.4 | 0.17 | 0.10 | 3.76 | -- | |
| Uniaxial cyclic compressive load | 2400 | 22.4 | 4.0 | 0.2 | 0.10 | -- | 1.2 | |
| Koyna gravity dam | dam | 2643 | 31.0 | 2.9 | 0.2 | 0.12 | 2.62 | -- |
| foundation | 2700 | 20.0 | -- | 0.2 | -- | -- | -- | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, L.; Zhao, L.; Wu, Z.; Guo, B. A Damage Model of Concrete including Hysteretic Effect under Cyclic Loading. Materials 2022, 15, 5062. https://doi.org/10.3390/ma15145062
Liu Z, Zhang L, Zhao L, Wu Z, Guo B. A Damage Model of Concrete including Hysteretic Effect under Cyclic Loading. Materials. 2022; 15(14):5062. https://doi.org/10.3390/ma15145062
Chicago/Turabian StyleLiu, Zhi, Li Zhang, Lanhao Zhao, Zihan Wu, and Bowen Guo. 2022. "A Damage Model of Concrete including Hysteretic Effect under Cyclic Loading" Materials 15, no. 14: 5062. https://doi.org/10.3390/ma15145062
APA StyleLiu, Z., Zhang, L., Zhao, L., Wu, Z., & Guo, B. (2022). A Damage Model of Concrete including Hysteretic Effect under Cyclic Loading. Materials, 15(14), 5062. https://doi.org/10.3390/ma15145062





