Analytical and Numerical Investigation of the Behavior of Engineered Cementitious Composite Members under Shear Loads
Abstract
:1. Introduction
2. Research Significance
- To develop a reliable and robust three-dimensional FE procedure capable of predicting the shear behavior of ECC beams using existing models.
- To determine whether the existing AIJ A-method approach for determining the load-carrying capacity of ECC beams in shear is suitable.
3. Experimental Corroboration
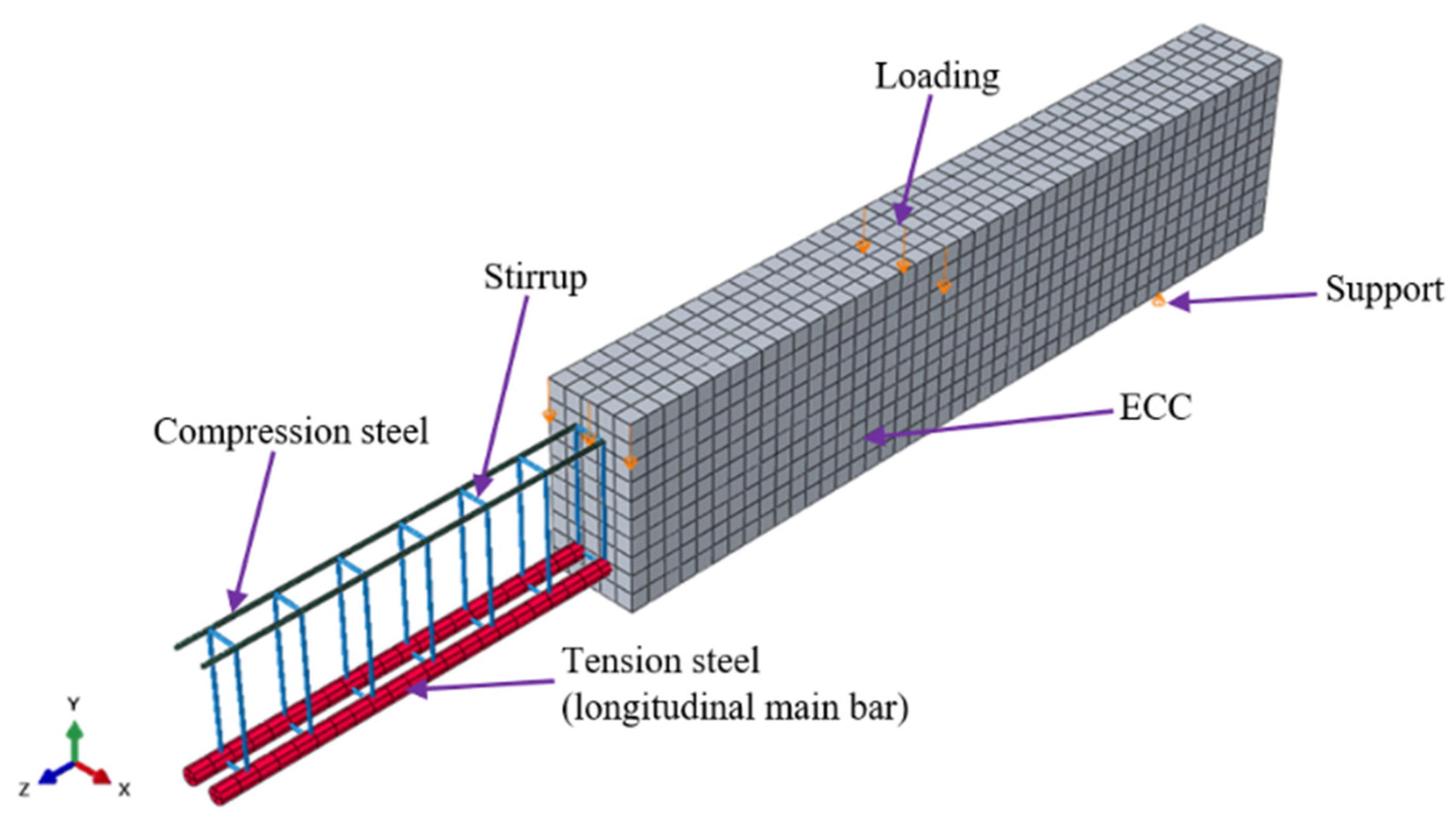
4. Modeling of Specimens
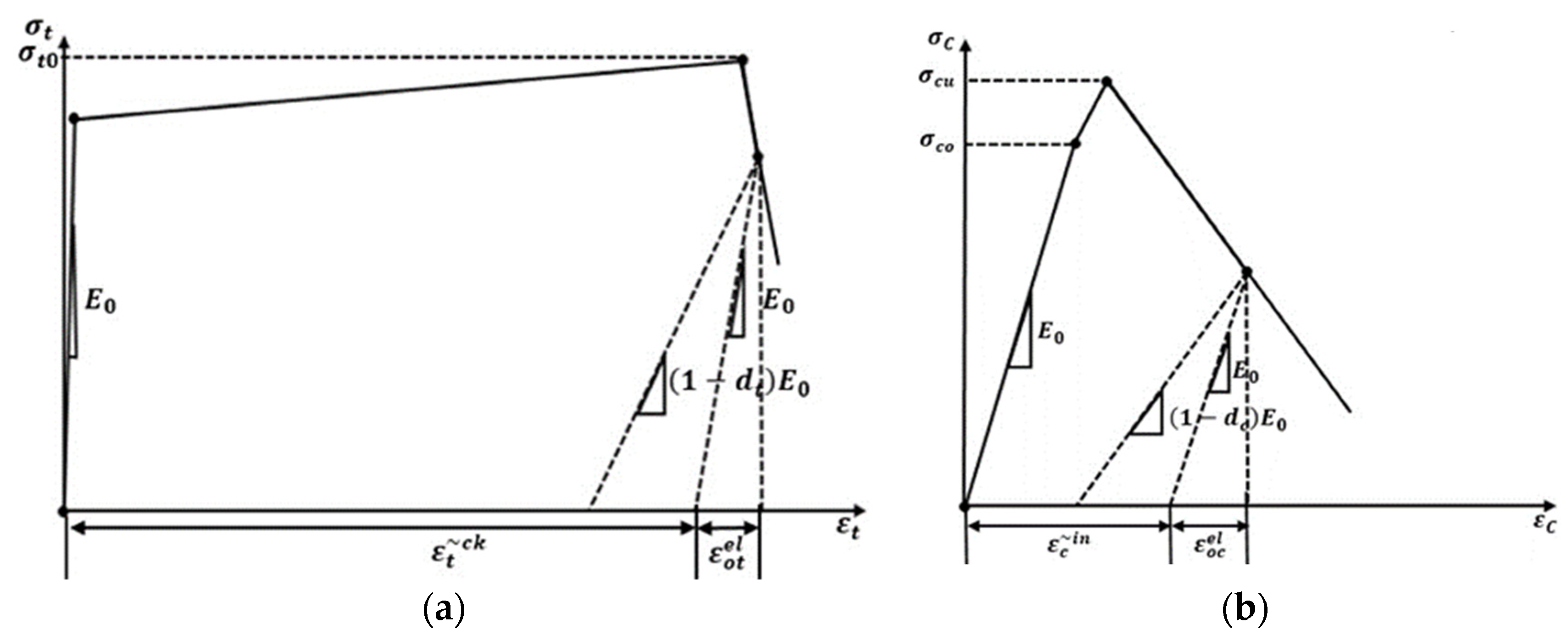
4.1. Characterization of the Material for Modeling
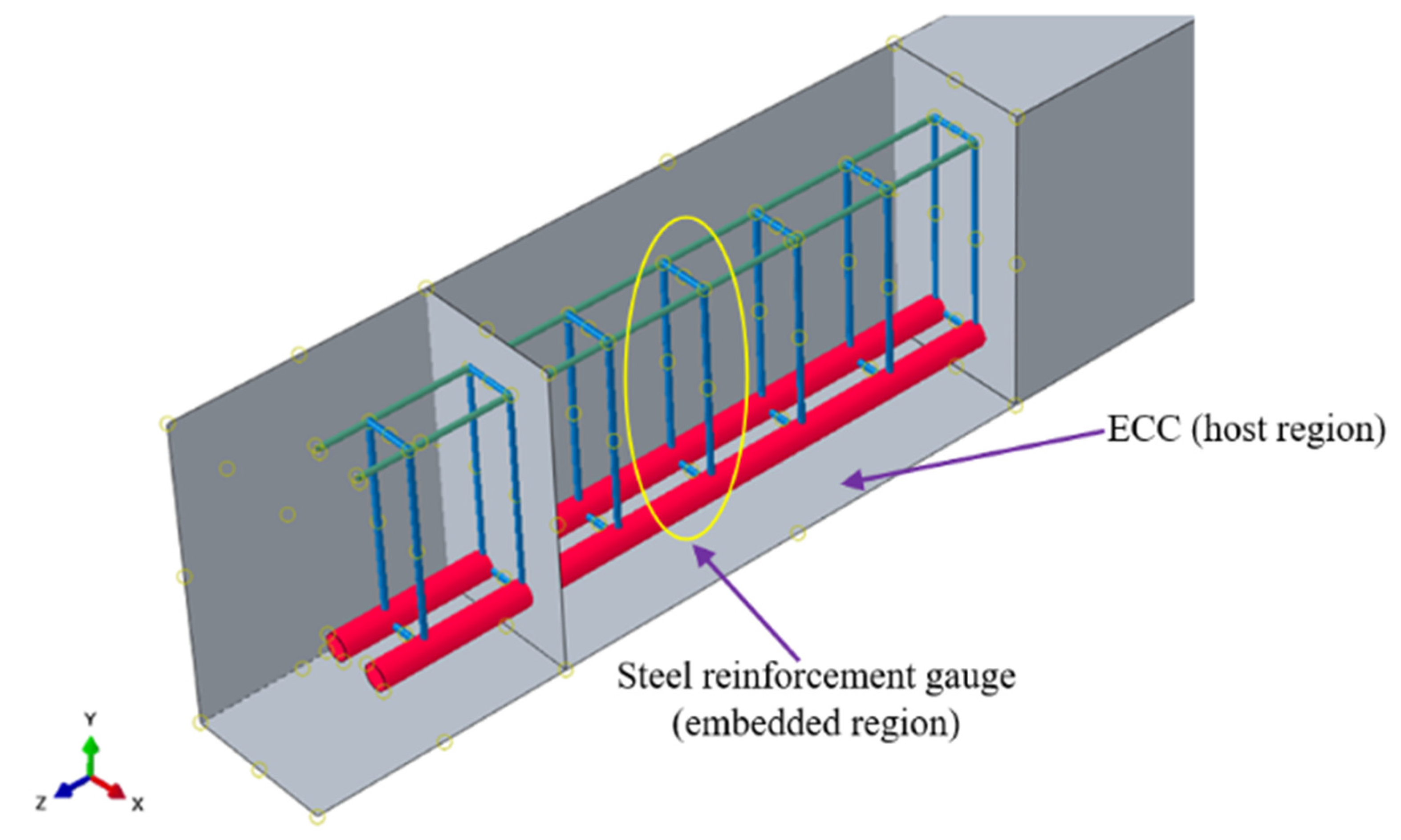
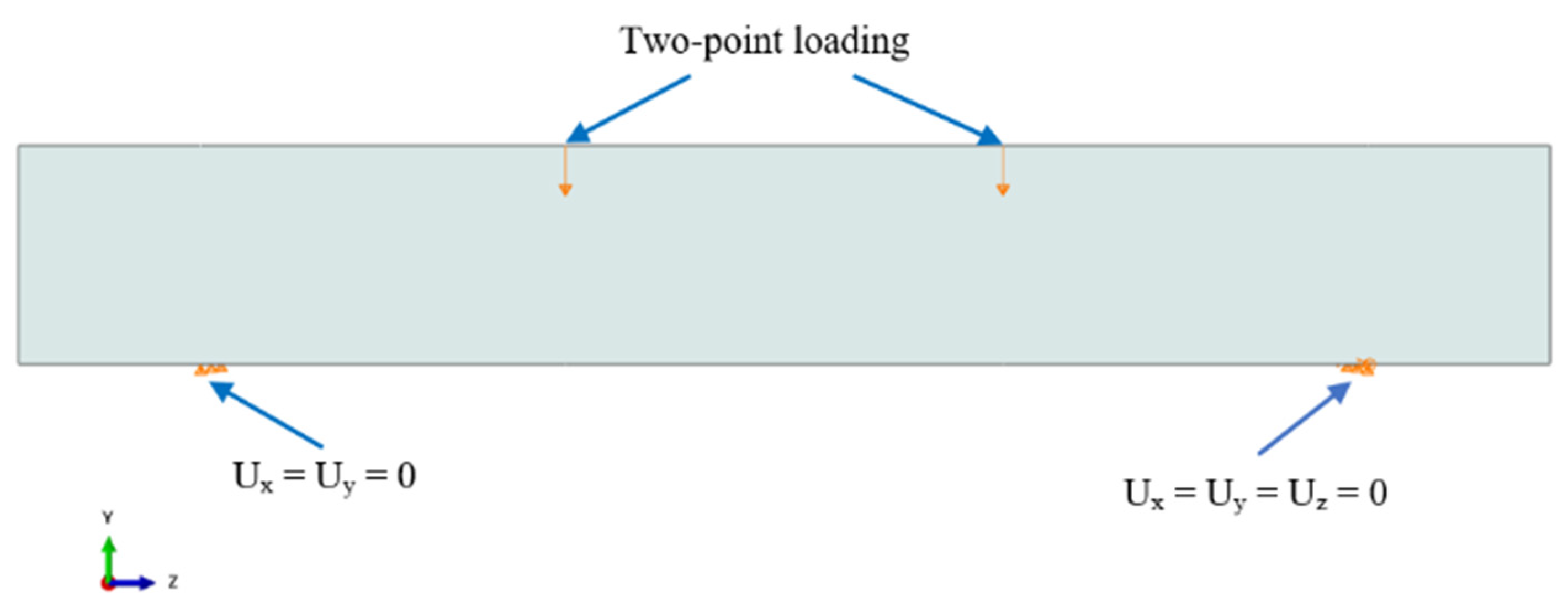
4.2. Geometrical Model
5. Results and Discussion
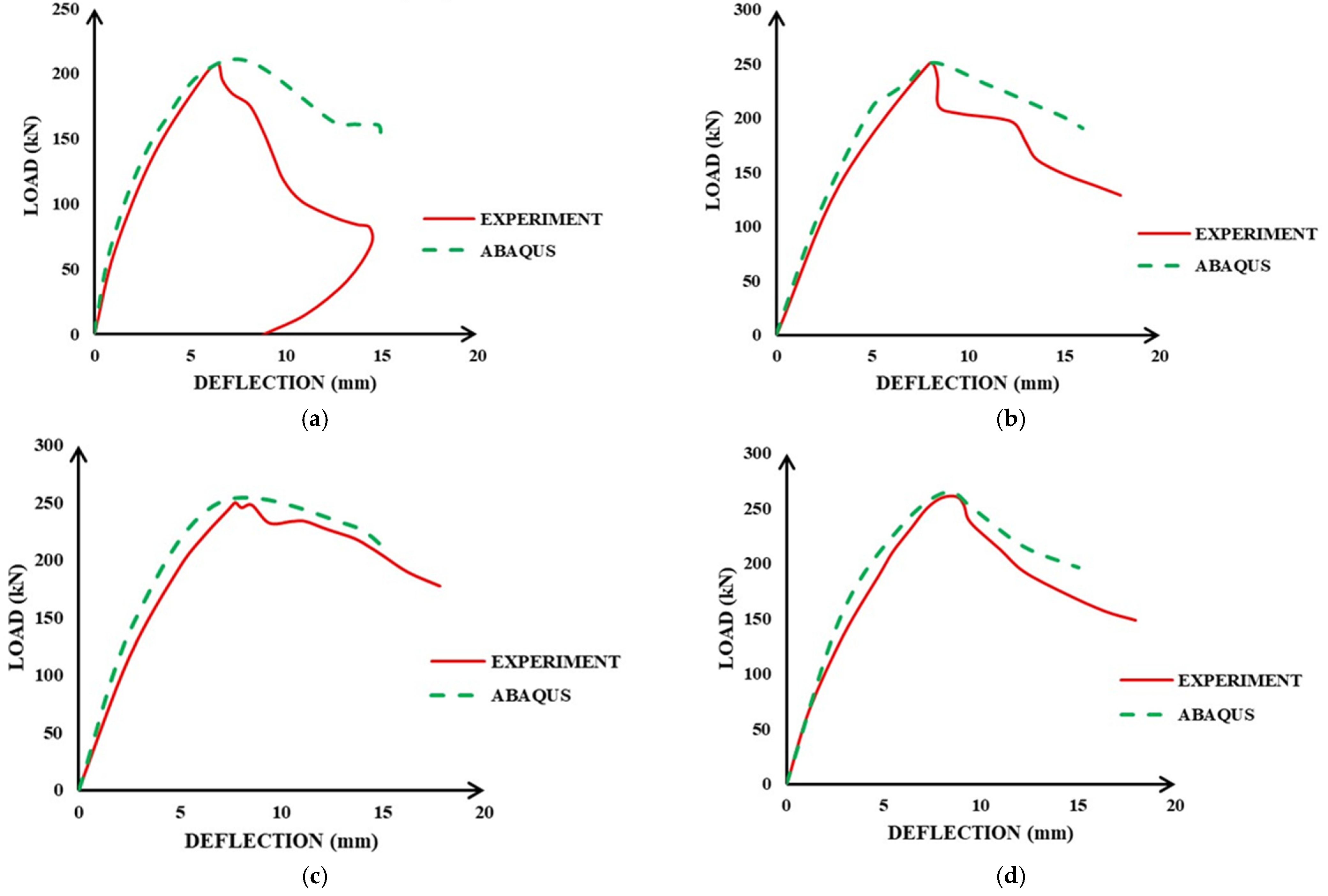
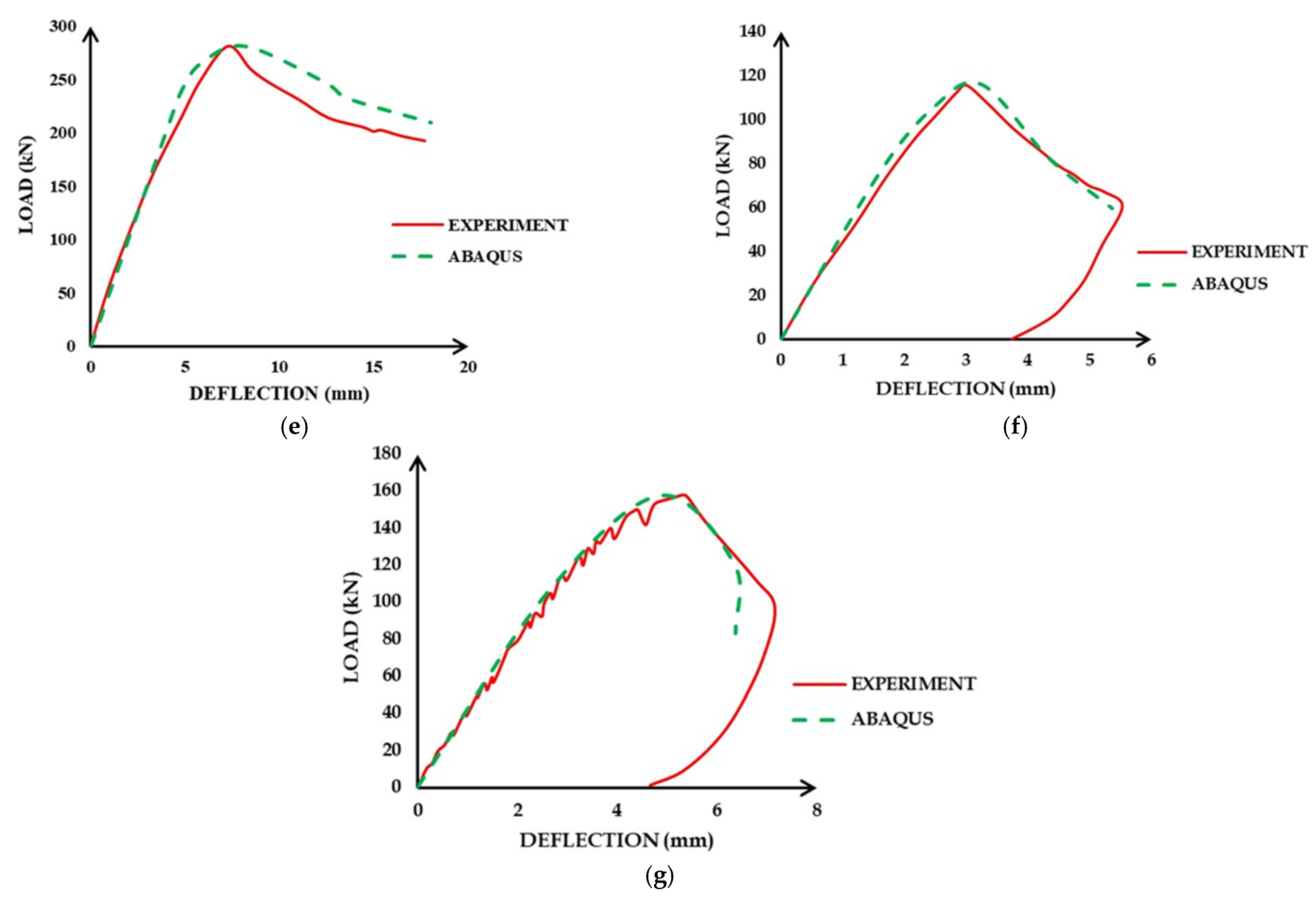
5.1. Results on Relation between Load and Displacement
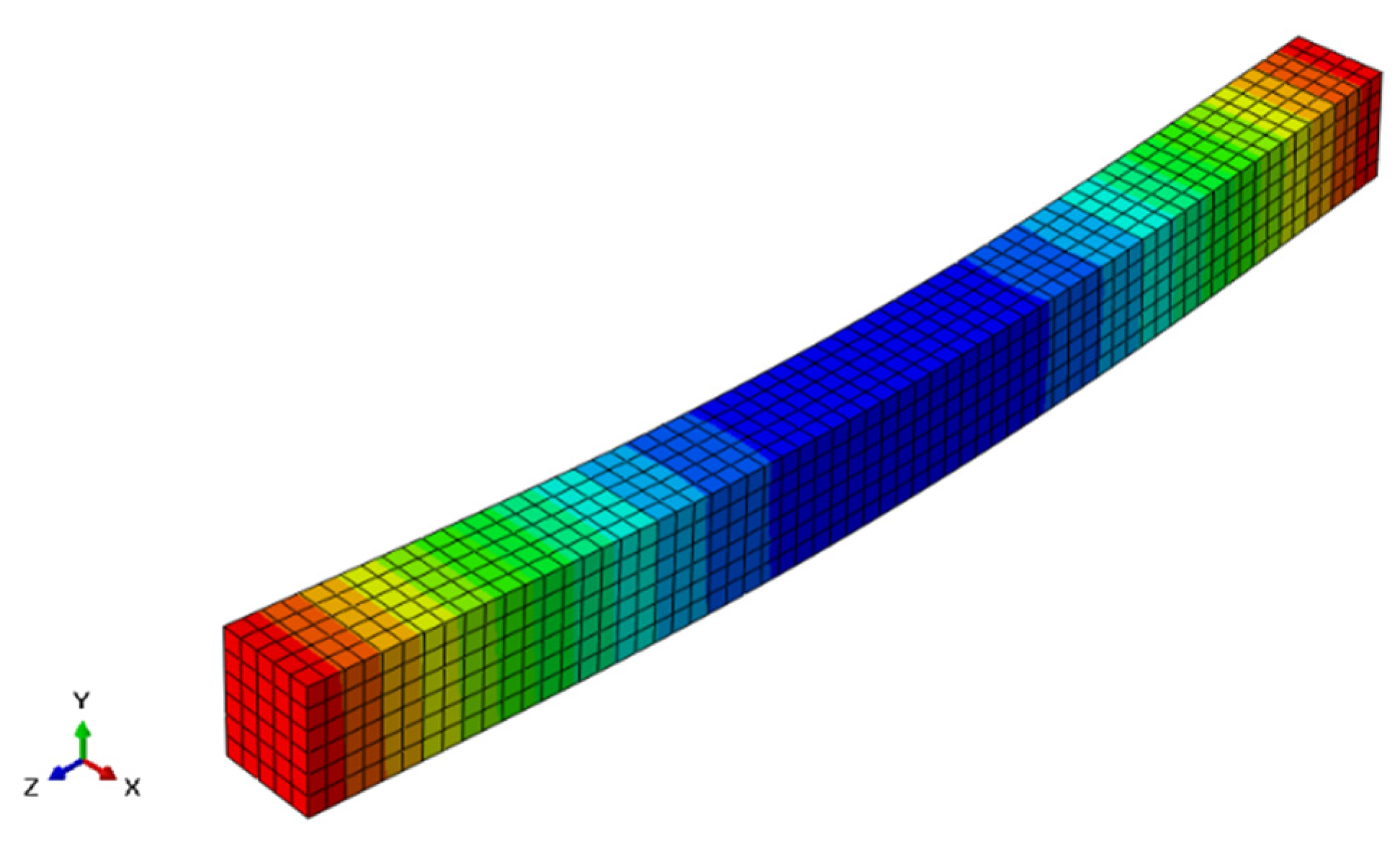
5.2. Ultimate Capacity and Failure Pattern
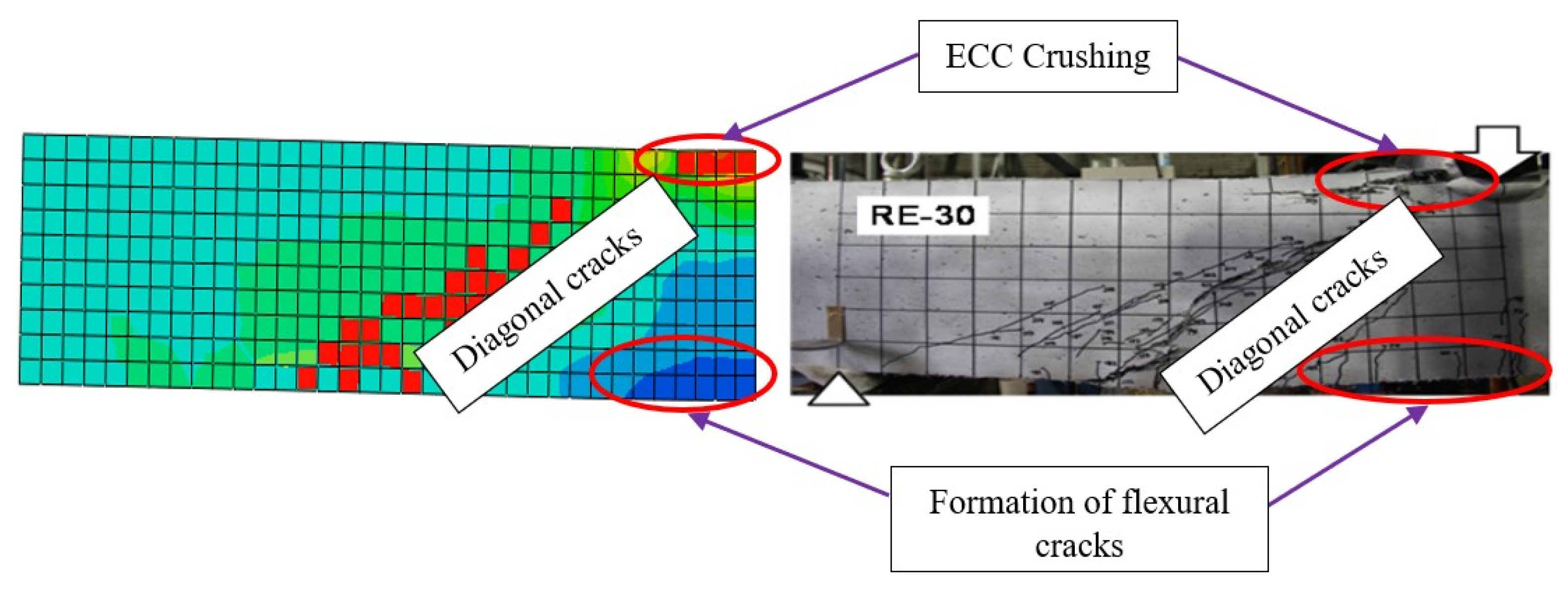
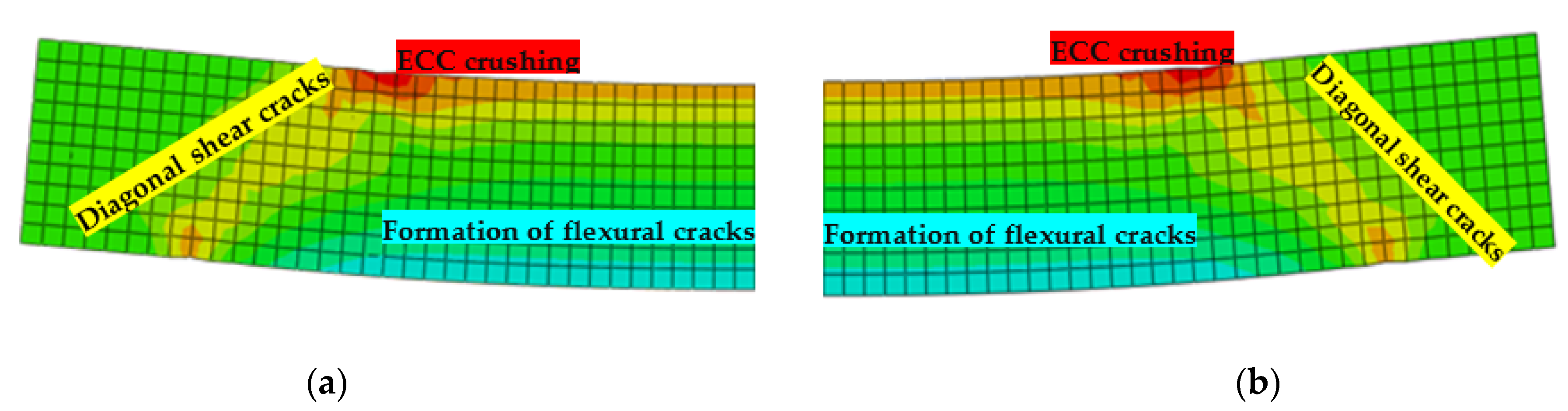
5.3. Crack Pattern
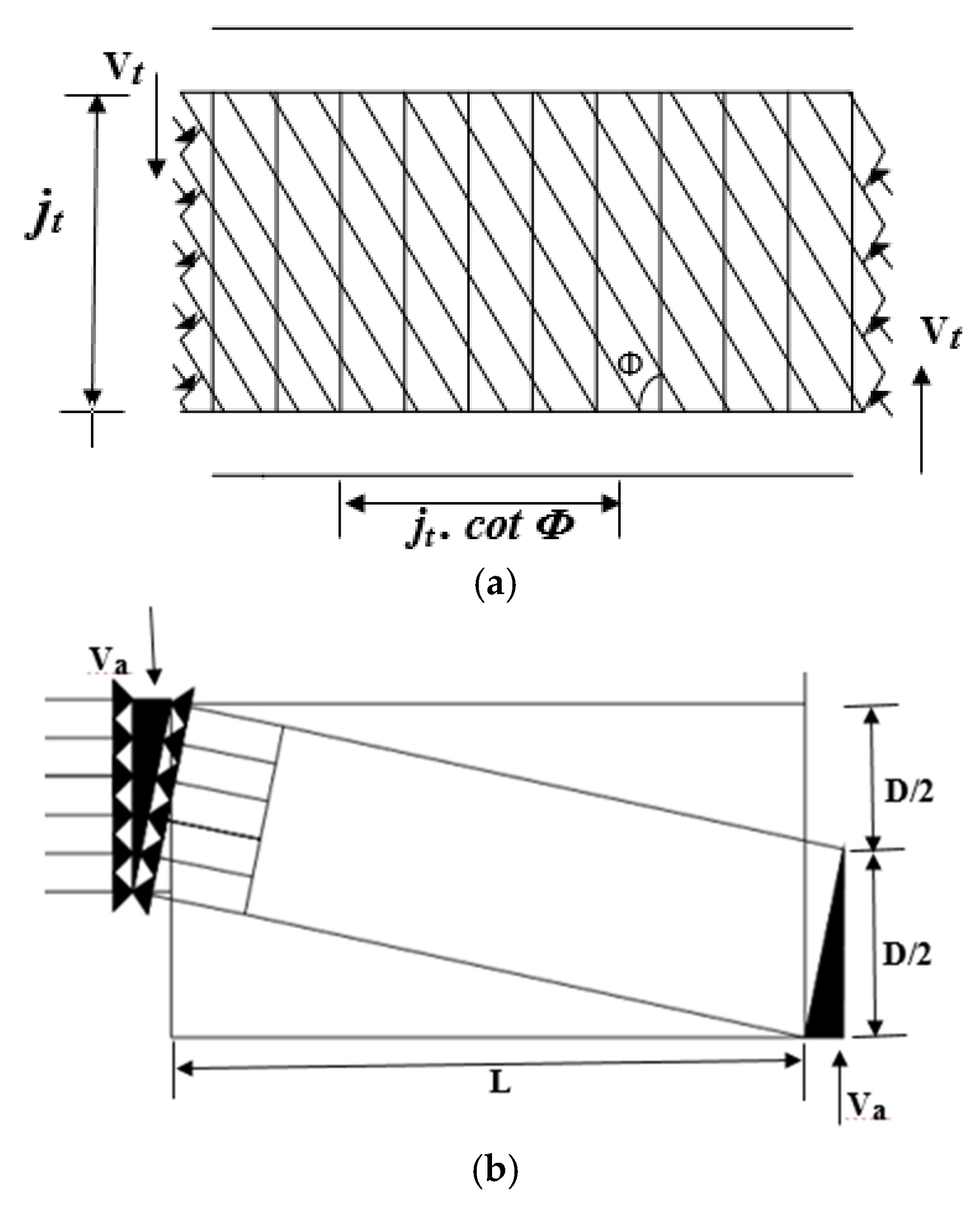
5.4. Ultimate Shear Capacity of ECC Beams
6. Parametric Study
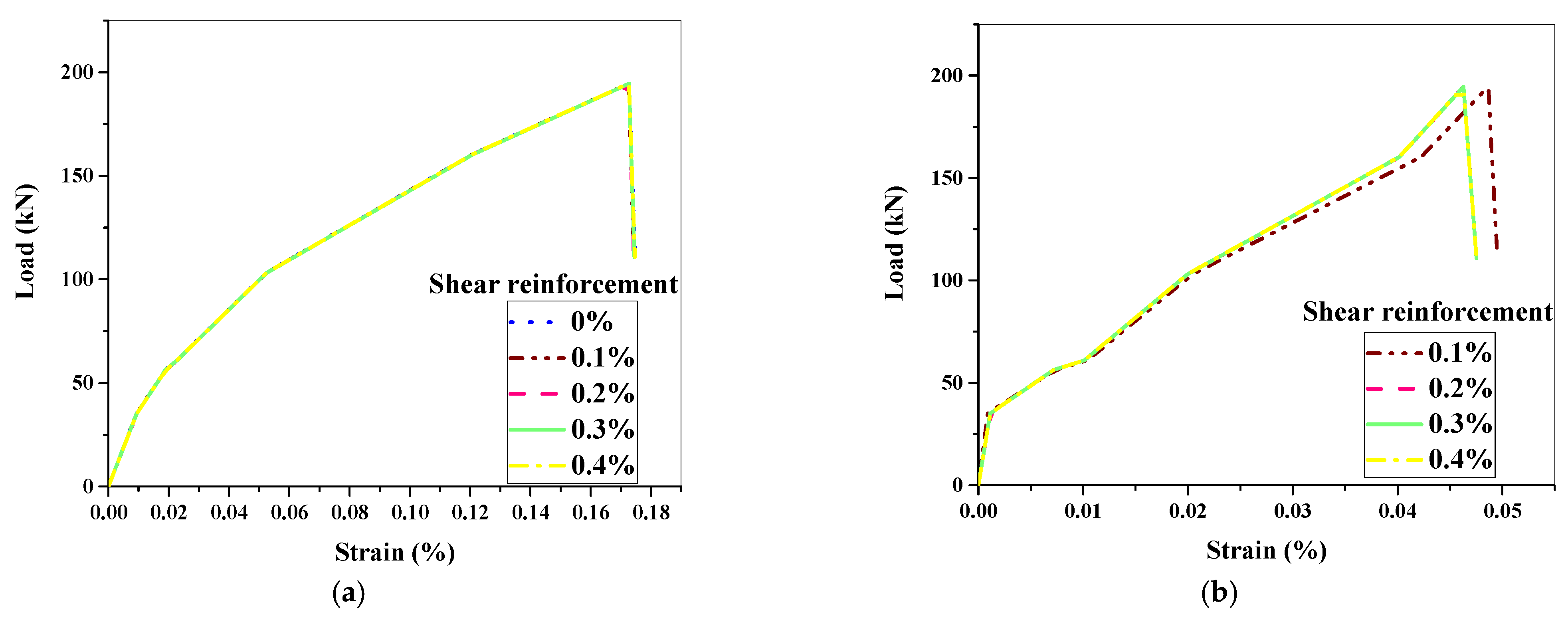
6.1. Analysis of Load–Strain Relationship
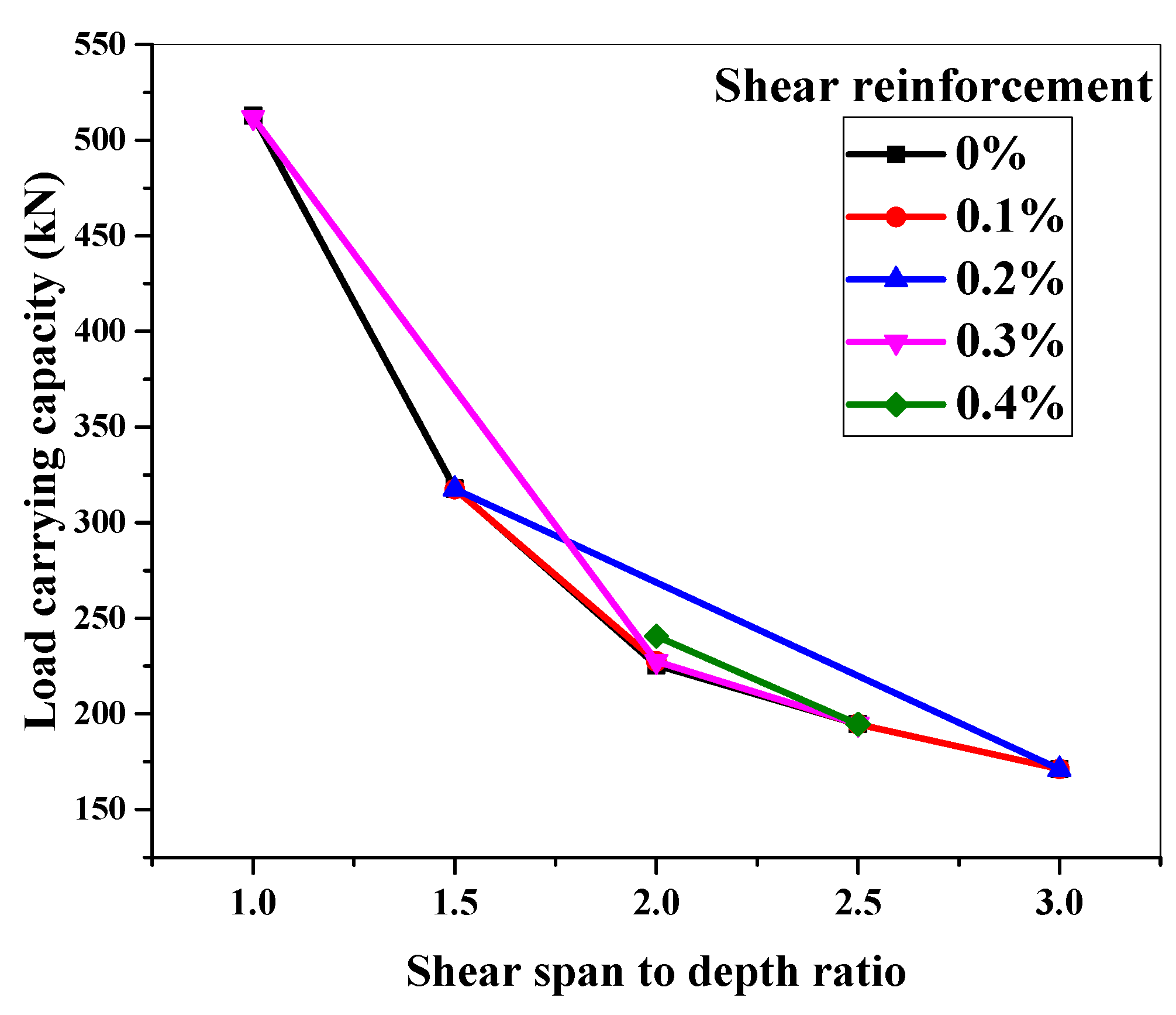
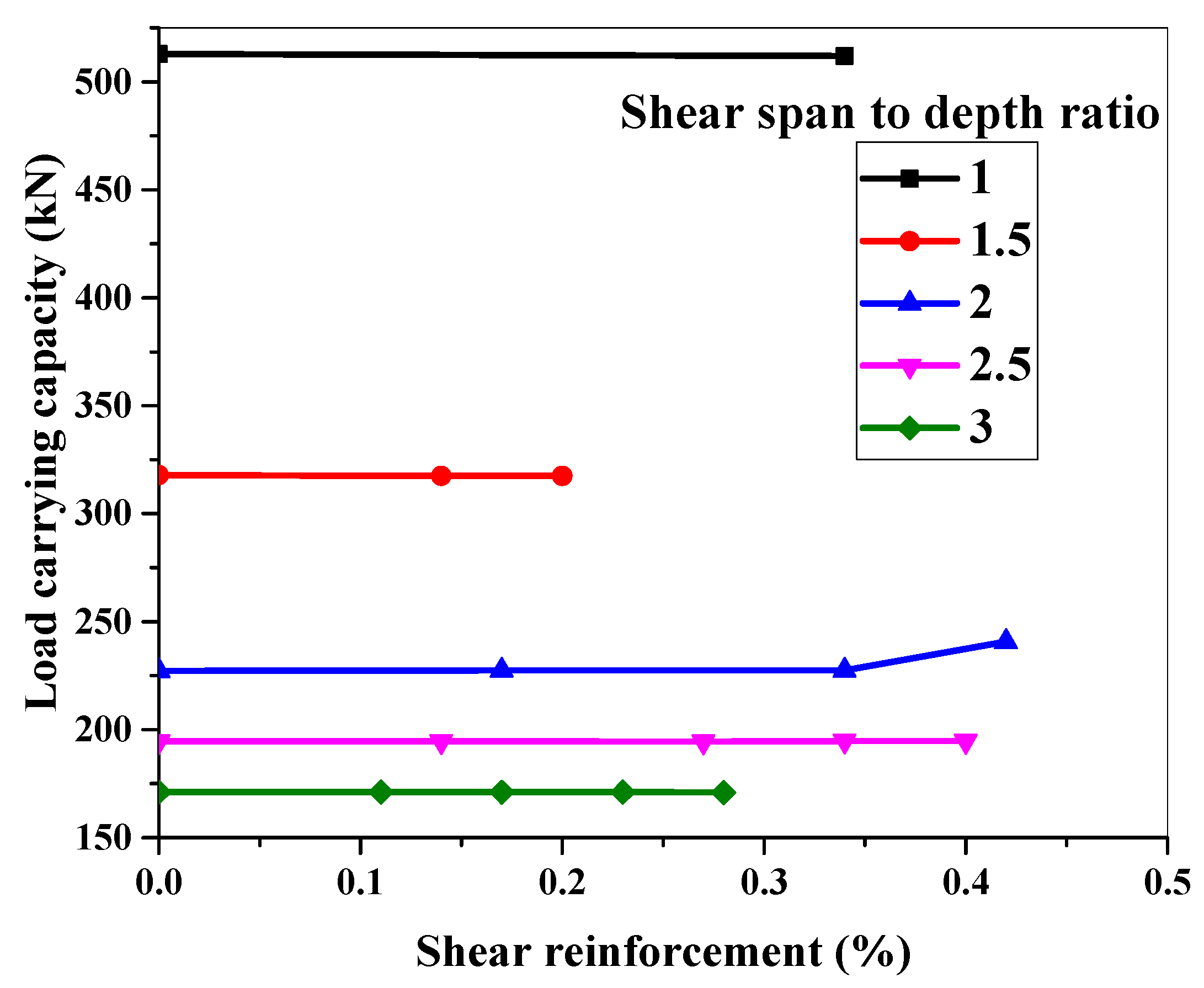
6.2. Shear Span-to-Depth Ratio against Particular Shear Reinforcement
6.3. Effect of Shear Reinforcement against Particular Shear Span-to-Depth Ratio
6.4. Crack Pattern and Failure Mode
6.5. Shear Capacity of Beams
7. Conclusions
- Damage parameters and a damage plasticity model from the nonlinear finite element platform can predict the overall behavior of ECC under shear-dominant loads.
- The numerical study validates the results of other researchers’ experimental investigations into load, deflection, and failure modes, which were very similar. The obtained numerical and experimental load–deflection responses exhibited close agreement with each other. Furthermore, the difference in the peak load of the numerical modeling and experimental responses of all the beams was within the range of 3%, irrespective of the amount of reinforcement and a/d ratios, which shows the robustness of the procedure adopted in the FE analysis.
- The existing AIJ A-method fairly estimated the shear capacity of ECC beams as the beams demonstrated flexure-dominated shear failure, i.e., cracking in flexure with high longitudinal stress.
- Because of the dominant shear failure, simulated reinforced ECC beams with lower a/d ratios had higher load-carrying capacities, regardless of the degree of shear reinforcement.
- Stirrups did not affect the load-carrying capabilities of ECC beams for varied a/d ratios, regardless of the transverse reinforcement ratio.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, V.C. On engineered cementitious composites (ECC)—A review of the material and its applications. J. Adv. Concr. Technol. 2003, 1, 215–230. [Google Scholar] [CrossRef] [Green Version]
- Al-Ameri, R.A.; Abid, S.R.; Murali, G.; Ali, S.H.; Özakça, M.; Vatin, N.I. Residual Impact Performance of ECC Subjected to Sub-High Temperatures. Materials 2022, 15, 454. [Google Scholar] [CrossRef] [PubMed]
- Li, V.C.; Wang, S. Flexural behaviors of glass fiber-reinforced polymer (GFRP) reinforced engineered cementitious composite beams. ACI Mater. J. 2002, 99, 11–21. [Google Scholar]
- Li, V.C.; Leung, C.K. Steady-state and multiple cracking of short random fiber composites. J. Eng. Mech. 1992, 118, 2246–2264. [Google Scholar] [CrossRef] [Green Version]
- Arulanandam, P.M.; Singh, S.B.; Kanakubo, T.; Sivasubramania, M.V.R. Behavior of engineered cementitious composite structural elements—A review. Indian Concr. J. 2020, 94, 5–28. [Google Scholar]
- Li, V.C. Engineered cementitious composites (ECC)—Tailored composites through micromechanical modeling. Can. Soc. Civ. Eng. 1997, 1–38. Available online: http://hdl.handle.net/2027.42/84667 (accessed on 28 June 2022).
- Li, V.C. Engineered Cementitious Composites (ECC)—Material, Structural, and Durability Performance. In Concrete Construction Engineering Handbook; Nawy, E., Ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Ge, W.-J.; Ashour, A.F.; Yu, J.; Gao, P.; Cao, D.-F.; Cai, C.; Ji, X. Flexural behavior of ECC–Concrete hybrid composite beams reinforced with FRP and steel bars. J. Compos. Constr. 2018, 23, 04018069. [Google Scholar] [CrossRef] [Green Version]
- Kanda, T.; Li, V.C. A new micromechanics design theory for pseudo strain hardening cementitious composites. ASCE J. Eng. Mech. 1999, 125, 373–381. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Yu, J.; Wu, H.; Jaworska, B.; Ellis, B.R.; Li, V.C. Discontinuous micro-fibers as intrinsic reinforcement for ductile engineered cementitious composites (ECC). Compos. Part B Eng. 2020, 184, 107741. [Google Scholar] [CrossRef]
- Sherir, M.A.A.; Hossain, K.M.A.; Lachemi, M. Structural performance of polymer fiber reinforced engineered cementitious composites subjected to static and fatigue flexural loading. Polymers 2015, 7, 1299–1330. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Li, V.C. Durability of HES-ECC Repair under Mechanical and Environmental Loading Conditions. In Proceedings of the High Performance Fiber Reinforced Cement Composites (HPFRCC5), Mainz, Germany, 10–13 July 2007; pp. 399–408. [Google Scholar]
- Bentz, E.C.; Vecchio, F.J.; Collins, M.P. Simplified modified compression field theory for calculating shear strength of reinforced concrete elements. ACI Struct. J. 2006, 103, 614–624. [Google Scholar] [CrossRef]
- Collins, M.P.; Bentz, E.C.; Sherwood, E.G.; Xie, L. An adequate theory for the shear strength of reinforced concrete structures. Mag. Concr. Res. 2008, 60, 635–650. [Google Scholar] [CrossRef] [Green Version]
- Kanda, T.; Watanabe, S. Application of pseudo strain hardening cementitious composites to shear resistant structural. Facture Mech. Concr. Struct. 1998, 1477–1490. Available online: http://hdl.handle.net/2027.42/84675 (accessed on 28 June 2022).
- Shimizu, K.; Toshiyuki, K.; Kanda, S.N.T. Shear Behaviour Of Steel Reinforced PVA-ECC Beams. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; Volume 78. [Google Scholar]
- Zhang, Y.X.; Ueda, N.; Umeda, Y.; Nakamura, H.; Kunieda, M. Evaluation of shear failure of strain hardening cementitious composite beams. Procedia Eng. 2011, 14, 2048–2057. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.B.; Madappa, V.R. Sivasubramanian. Response of Steel Reinforced Engineered Cementitious Composite Beams. In Proceedings of the International UKIERI Concrete Congress, New Delhi, India, 8–10 March 2011; pp. 231–244. [Google Scholar]
- Xu, S.; Hou, L.-J.; Zhang, X.-F. Shear behavior of reinforced ultrahigh toughness cementitious composite beams without transverse reinforcement. J. Mater. Civ. Eng. 2012, 24, 1283–1294. [Google Scholar] [CrossRef]
- Zhang, R.; Matsumoto, K.; Niwa, J.; Hirata, T.; Ishizeki, Y. Experimental Study on Shear Behavior of PP-ECC Beams with Different Stirrup Ratios. In Proceedings of the 13th East Asia-Pacific Conference on Structural Engineering and Construction, EASEC 2013, Sapporo, Japan, 11–13 September; pp. 1–9.
- Hou, L.; Xu, S.; Zhang, X.; Chen, D. Shear behaviors of reinforced ultrahigh toughness cementitious composite slender beams with stirrups. J. Mater. Civ. Eng. 2014, 26, 466–475. [Google Scholar] [CrossRef]
- Kanakubo, T.; Ozu, Y.; Namiki, K. Shear behavior of DFRCC coupling beams using PVA and steel fiber. The 2019 World Congress on Advances in Structural Engineering and Mechanics (ASEM19). Jeju Island, Korea, 17–21 September 2019. [Google Scholar]
- Said, M.; Montaser, W.; Elgammal, A.S.; Zahir, A.H.; Shaaban, I.G. Shear strength of reinforced mortar beams containing polyvinyl alcohol fibre (PVA). Int. J. Civ. Eng. 2021, 19, 1155–1178. [Google Scholar] [CrossRef]
- Hasib, M.S. Shear and Flexure Behavior of Hybrid Composite Beams with High Performance. Concretes. Thesis, Ryerson University, Toronto, ON, Canada, 2016. [Google Scholar]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic—Damage model for concrete. Int. J. solid Struct. 1987, 25, 299–326. [Google Scholar] [CrossRef]
- Hafezolghorani, M.; Hejazi, F.; Vaghei, R.; Bin Jaafar, M.S.; Karimzade, K. Simplified damage plasticity model for concrete. Struct. Eng. Int. 2017, 27, 68–78. [Google Scholar] [CrossRef]
- Dassault Systémes. ABAQUS User’s Manual; Version 6.12. 2012; Dassault Systémes: Providence, RI, USA, 2012. [Google Scholar]
- Demir, A.; Ozturk, H.; Bogdanovic, A.; Stojmanovska, M. Sensitivity of dilation angle in numerical simulation of reinforced concrete deep beams. Sci. J. Civ. Eng. 2017, 6, 33–37. [Google Scholar]
- Singh, S.B.; Munjal, P. Out-of-plane response of ECC strengthened masonry wallets with openings. KSCE J. Civ. Eng. 2020, 24, 2078–2087. [Google Scholar] [CrossRef]
- Kmiecik, P.; Kamiński, M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration. Arch. Civ. Mech. Eng. 2011, 11, 623–636. [Google Scholar] [CrossRef]
- Willam, K.J.; Warnke, E.P. Constitutive model for the triaxial behaviour of concrete. IABSE Proc. Section III 1975, 19, 1–30. [Google Scholar]
- Genikomsou, A.S.; Polak, M.A. Finite element analysis of punching shear of concrete slabs using damaged plasticity model in ABAQUS. Eng. Struct. 2015, 98, 38–48. [Google Scholar] [CrossRef]
- Naser, M.Z.; Hawileh, R.A.; Abdalla, J. Modeling strategies of finite element simulation of reinforced concrete beams strengthened with FRP: A review. J. Compos. Sci. 2021, 5, 19. [Google Scholar] [CrossRef]
- Bahraq, A.A.; Al-Osta, M.A.; Ahmad, S.; Al-Zahrani, M.M.; Al-Dulaijan, S.O.; Rahman, M.K. Experimental and numerical investigation of shear behavior of RC beams strengthened by ultra-high performance concrete. Int. J. Concr. Struct. Mater. 2019, 13, 6. [Google Scholar] [CrossRef]
- Khalil, A.E.H.; Etman, E.; Atta, A.; Essam, M. Nonl inear behavior of RC beams strengthened with strain hardening cementitious composites subjected to monotonic and cyclic loads. Alexandria Eng. J. 2016, 55, 1483–1496. [Google Scholar] [CrossRef]
- Khatib, M.; Abou Saleh, Z.; Baalbaki, O.; Temsah, Y. Numerical punching shear analysis of unbonded post-tensioned slabs with inverted-U shaped. KSCE J. Civ. Eng. 2018, 22, 4490–4499. [Google Scholar] [CrossRef]
- Lu, T.T.; Liang, X.W. Effect of HPFRCC on seismic performance of beam-column-slab subassembly. KSCE J. Civ. Eng. 2020, 24, 3785–3796. [Google Scholar] [CrossRef]
- Al-saawani, M.A.; Al-Negheimish, A.I.; El-Sayed, A.K.; Alhozaimy, A.M. Finite element modeling of debonding failures in FRP-strengthened concrete beams using cohesive zone model. Polymers 2022, 14, 1889. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Kytinou, V.K.; Voutetaki, M.E.; Karayannis, C.G. Flexural damage diagnosis in reinforced concrete beams using a wireless admittance monitoring system—Tests and finite element analysis. Sensors 2021, 21, 679. [Google Scholar] [CrossRef] [PubMed]
- Dudziak, S. Numerically efficient three-dimensional model for non-linear finite element analysis of reinforced concrete structures. Materials 2021, 14, 1578. [Google Scholar] [CrossRef] [PubMed]
- Kanakubo, T.; Shimizu, K.; Kanda, T.; Nagai, S. Evaluation of Bending and Shear Capacities of HPFRCC Members toward the Structural Application. In Proceedings of the Hokkaido University COE Workshop on High Performance Fiber Reinforced Composites for Sustainable Infrastructure System–Material Modeling, Structural Design and Application, Sapporo, Japan, 9 February 2007; pp. 1–10. [Google Scholar]
- Rokugo, K.; Kanda, T.; Kanakubo, T.; Fukuyama, H.; Uchida, Y.; Suwada, H.; Slowik, V. Strain Hardening Cement Composites: Structural Design and Performance: State -of-the-Art Report of the RILEM Technical Committee 208-HFC, SC3; Springer Science & Busniess Media: Belin, Germany, 2013; Volume 6, ISBN 9788578110796. [Google Scholar]
- Sunaga, D.; Namiki, K.; Kanakubo, T. Shear Behavior of DFRCC Coupling Beams Using PVA and Aramid Fibers. In Proceedings of the 17th World Conference on Earthquake Engineering, 17WCEE, Sendai, Japan, 13–18 September 2020; pp. 1–11. [Google Scholar]



| Sl. No. | Specimen ID | Dimension (B × D × L) * (mm) | Shear Span (a) (mm) | Shear Span-to-Depth Ratio | Longitudinal Reinforcement Ratio # (%) | Transverse Reinforcement Ratio (pw) $ (%) | Stirrup Spacing (mm) |
|---|---|---|---|---|---|---|---|
| 1. | P1 [20] | 150 × 300 ×2100 | 700 | 2.8 | 2.7 | 0 | 0 |
| 2. | P2 [20] | 150 × 300 ×2100 | 700 | 2.8 | 2.7 | 0.12 | 350 |
| 3. | P3 [20] | 150 × 300 ×2100 | 700 | 2.8 | 2.7 | 0.24 | 175 |
| 4. | P4 [20] | 150 × 300 ×2100 | 700 | 2.8 | 2.7 | 0.30 | 140 |
| 5. | P5 [20] | 150 × 300 ×2100 | 700 | 2.8 | 2.7 | 0.42 | 100 |
| 6. | P6 [24] | 100 × 200 ×1100 | 267 | 1.53 | 1.14 | 0 | 0 |
| 7. | P7 [24] | 100 × 200 ×1100 | 267 | 1.53 | 1.14 | 0.42 | 133.5 |
| Specimen ID | Tensile Strength (MPa) | Tensile Strain (%) | Compressive Strength (MPa) | Compressive Strain (%) | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| P1–P5 [20] | 4.0 | 1.2 | 32.7 | 0.8 | 18 | 0.19 |
| P6–P7 [24] | 5.1 | 1.7 | 73.0 | 1.1 | 20.4 | 0.20 |
| Notation | Value |
|---|---|
| Angle of dilation (Ψ) [28] | 20 |
| Eccentricity ratio (ε) [29] | 0.1 |
| Ratio of biaxial-to-axial compressive stress ) [30] | 1.16 |
| [31] | 0.67 |
| Viscosity Coefficient (µ) [32] | 0.01 |
| Sl. No. | Specimen ID | Experimental Results | FE Results | Pu, num/Pu, exp | % Difference in Ultimate Load | ||||
|---|---|---|---|---|---|---|---|---|---|
| Pu, exp (kN) | δu, exp (mm) | Mode of Failure | Pu, num (kN) | δu, num (mm) | Mode of Failure | ||||
| 1. | P1 [20] | 207.8 | 8.19 | ST | 208.6 | 6.4 | ST | 1.00 | 0.38 |
| 2. | P2 [20] | 250.2 | 10.02 | ST | 251.3 | 8.22 | ST | 1.00 | 0.44 |
| 3. | P3 [20] | 250.1 | 9.87 | ST | 252.4 | 6.93 | ST | 1.01 | 0.92 |
| 4. | P4 [20] | 260.4 | 10.55 | ST | 264.8 | 8.19 | ST | 1.02 | 1.69 |
| 5. | P5 [20] | 281.2 | 9.23 | ST | 284.1 | 8.18 | ST | 1.01 | 1.03 |
| 6. | P6 [24] | 115.7 | 3.00 | ST | 116.2 | 3.2 | ST | 1.00 | 0.43 |
| 7. | P7 [24] | 157.3 | 5.2 | ST | 158.2 | 4.9 | ST | 1.01 | 0.57 |
| Sl. No. | Specimen ID | Experimental Load (V, exp) (kN) | Vsu (V, theo) (kN) | Shear Strength Shared by | V, theo/V, exp | ||
|---|---|---|---|---|---|---|---|
| Truss Mechanism (Vt) (%) | Arch Mechanism (Va) (%) | Fiber Bridging Mechanism (Vf) (%) | |||||
| 1. | P1 [20] | 207.8 | 171.8 | 0 | 47 | 53 | 1.21 |
| 2. | P2 [20] | 250.2 | 188.5 | 12 | 40 | 48 | 1.32 |
| 3. | P3 [20] | 250.1 | 214.7 | 24 | 32 | 44 | 1.31 |
| 4. | P4 [20] | 260.4 | 231.9 | 28 | 29 | 43 | 1.27 |
| 5. | P5 [20] | 281.2 | 216.9 | 38 | 21 | 42 | 1.30 |
| 6. | P6 [24] | 115.7 | 170.1 | 0 | 58 | 42 | 0.68 |
| 7. | P7 [24] | 157.3 | 202.8 | 32 | 33 | 35 | 0.78 |
| Beam | Shear Span, a (mm) | Shear Span-to-Depth Ratio (a/d) | Transverse Reinforcement Ratio (%) |
|---|---|---|---|
| S-1 | 250 | 1 | 0 |
| S-2 | 250 | 1 | 0.3 |
| S-3 | 375 | 1.5 | 0 |
| S-4 | 375 | 1.5 | 0.1 |
| S-5 | 375 | 1.5 | 0.2 |
| S-6 | 250 | 2 | 0 |
| S-7 | 250 | 2 | 0.2 |
| S-8 | 250 | 2 | 0.3 |
| S-9 | 250 | 2 | 0.4 |
| S-10 | 625 | 2.5 | 0 |
| S-11 | 625 | 2.5 | 0.1 |
| S-12 | 625 | 2.5 | 0.2 |
| S-13 | 625 | 2.5 | 0.3 |
| S-14 | 625 | 2.5 | 0.4 |
| S-15 | 750 | 3 | 0 |
| S-16 | 750 | 3 | 0.1 |
| S-17 | 750 | 3 | 0.2 |
| S-18 | 750 | 3 | 0.3 |
| Beam | Total Shear Capacity (kN) | Shear Load Carried by | |
|---|---|---|---|
| ECC Matrix (%) | Stirrups (%) | ||
| S-1 | 256.5 | 100 | - |
| S-2 | 255.9 | 89.4 | 10.6 |
| S-3 | 158.9 | 100 | - |
| S-4 | 158.7 | 94.3 | 5.7 |
| S-5 | 158.7 | 91.5 | 8.5 |
| S-6 | 113.7 | 100 | - |
| S-7 | 113.7 | 88.1 | 11.9 |
| S-8 | 113.7 | 76.1 | 23.9 |
| S-9 | 113.7 | 70.2 | 29.8 |
| S-10 | 97.2 | 100 | - |
| S-11 | 97.2 | 90.7 | 9.3 |
| S-12 | 97.2 | 81.4 | 18.6 |
| S-13 | 97.3 | 76.8 | 23.2 |
| S-14 | 97.3 | 72.1 | 27.9 |
| S-15 | 85.5 | 100 | - |
| S-16 | 85.4 | 94.7 | 5.3 |
| S-17 | 85.5 | 89.4 | 10.6 |
| S-18 | 85.4 | 86.8 | 13.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arulanandam, P.M.; Sivasubramnaian, M.V.; Chellapandian, M.; Murali, G.; Vatin, N.I. Analytical and Numerical Investigation of the Behavior of Engineered Cementitious Composite Members under Shear Loads. Materials 2022, 15, 4640. https://doi.org/10.3390/ma15134640
Arulanandam PM, Sivasubramnaian MV, Chellapandian M, Murali G, Vatin NI. Analytical and Numerical Investigation of the Behavior of Engineered Cementitious Composite Members under Shear Loads. Materials. 2022; 15(13):4640. https://doi.org/10.3390/ma15134640
Chicago/Turabian StyleArulanandam, Preethy Mary, Madappa VR Sivasubramnaian, Maheswaran Chellapandian, Gunasekaran Murali, and Nikolai Ivanovich Vatin. 2022. "Analytical and Numerical Investigation of the Behavior of Engineered Cementitious Composite Members under Shear Loads" Materials 15, no. 13: 4640. https://doi.org/10.3390/ma15134640
APA StyleArulanandam, P. M., Sivasubramnaian, M. V., Chellapandian, M., Murali, G., & Vatin, N. I. (2022). Analytical and Numerical Investigation of the Behavior of Engineered Cementitious Composite Members under Shear Loads. Materials, 15(13), 4640. https://doi.org/10.3390/ma15134640









