Simulation of PLC Effect Using Regularized Large-Strain Elasto-Plasticity
Abstract
1. Introduction
2. Brief Description of Constitutive Models
2.1. Thermo-Visco-Plasticity
2.2. Estrin–McCormick Model with Optional Gradient Enhancement
3. Balance Equations
4. Implementation and Computational Tool
5. Simulation of PLC Effect
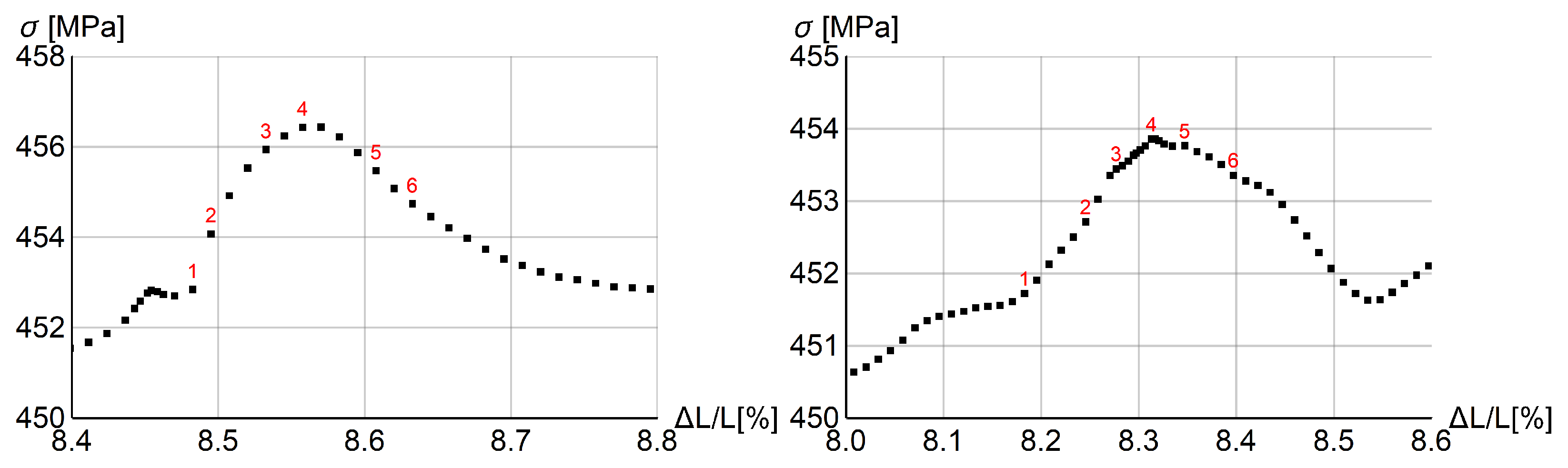
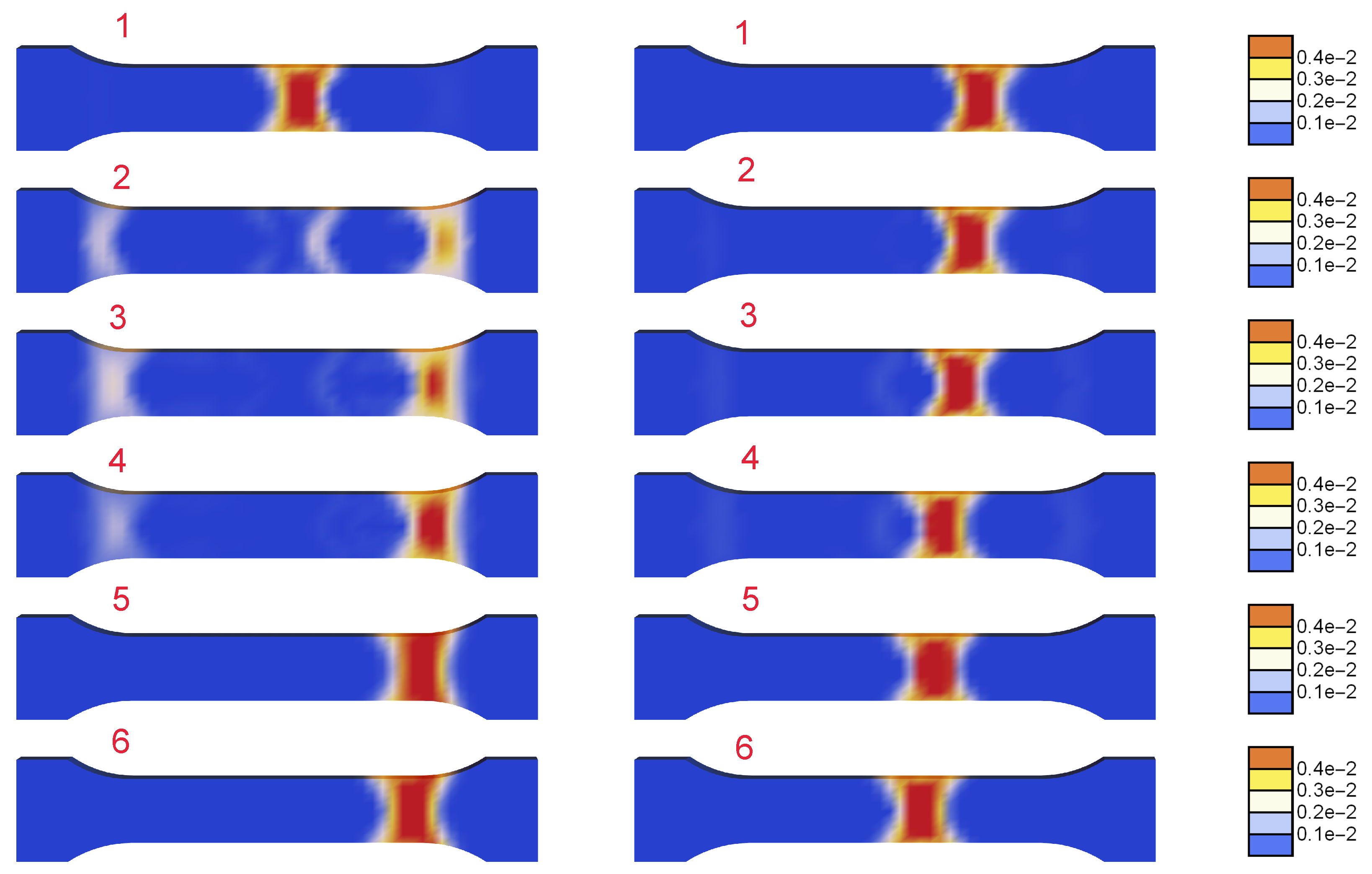
5.1. Test Description
5.2. Tensile Rod Benchmark Test
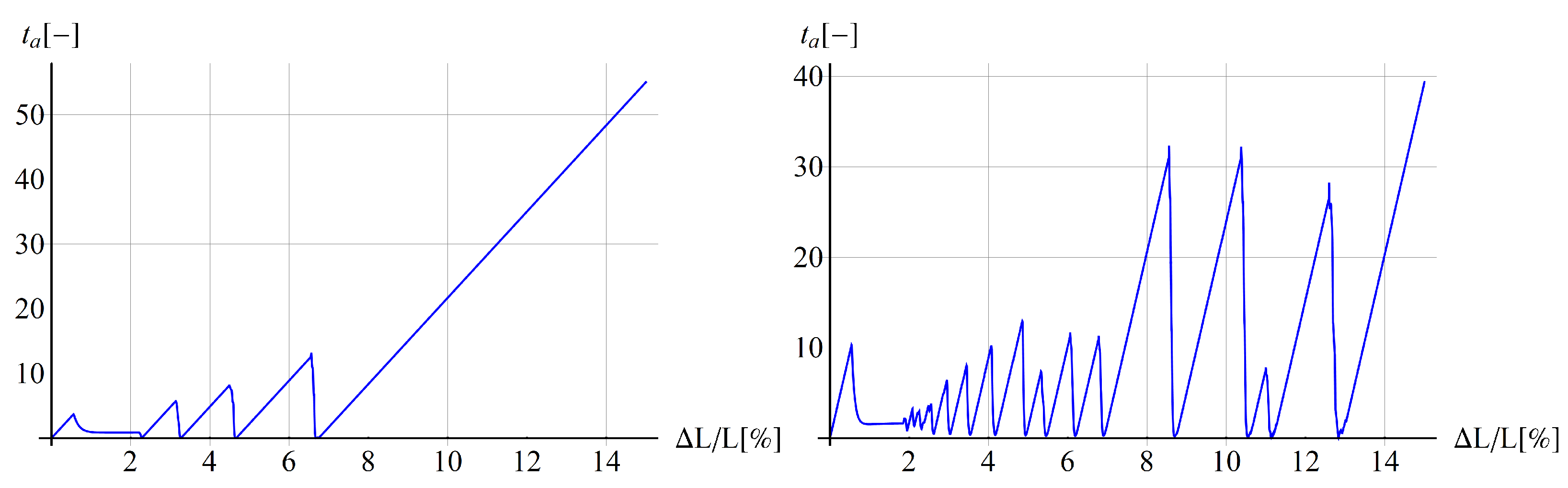
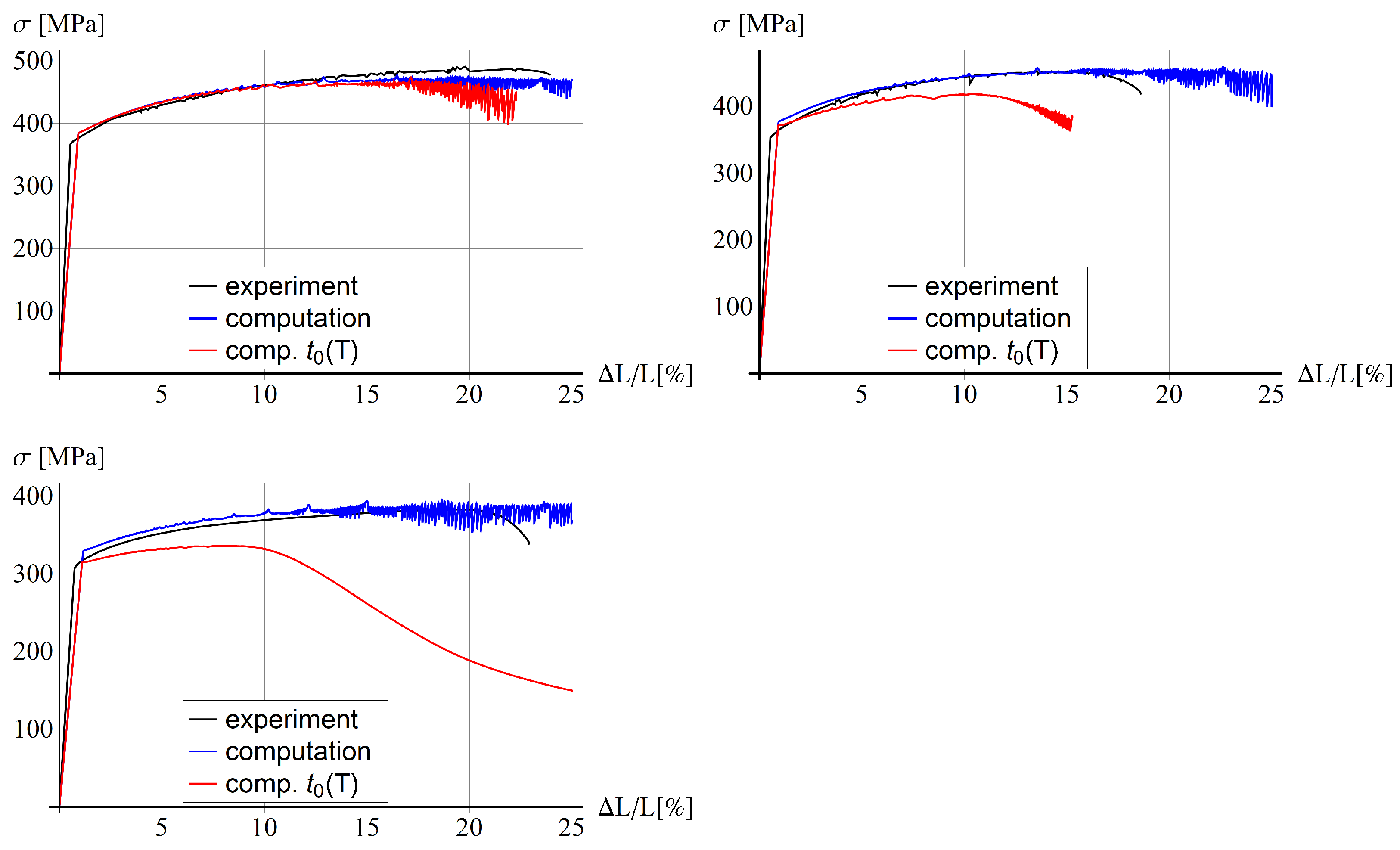
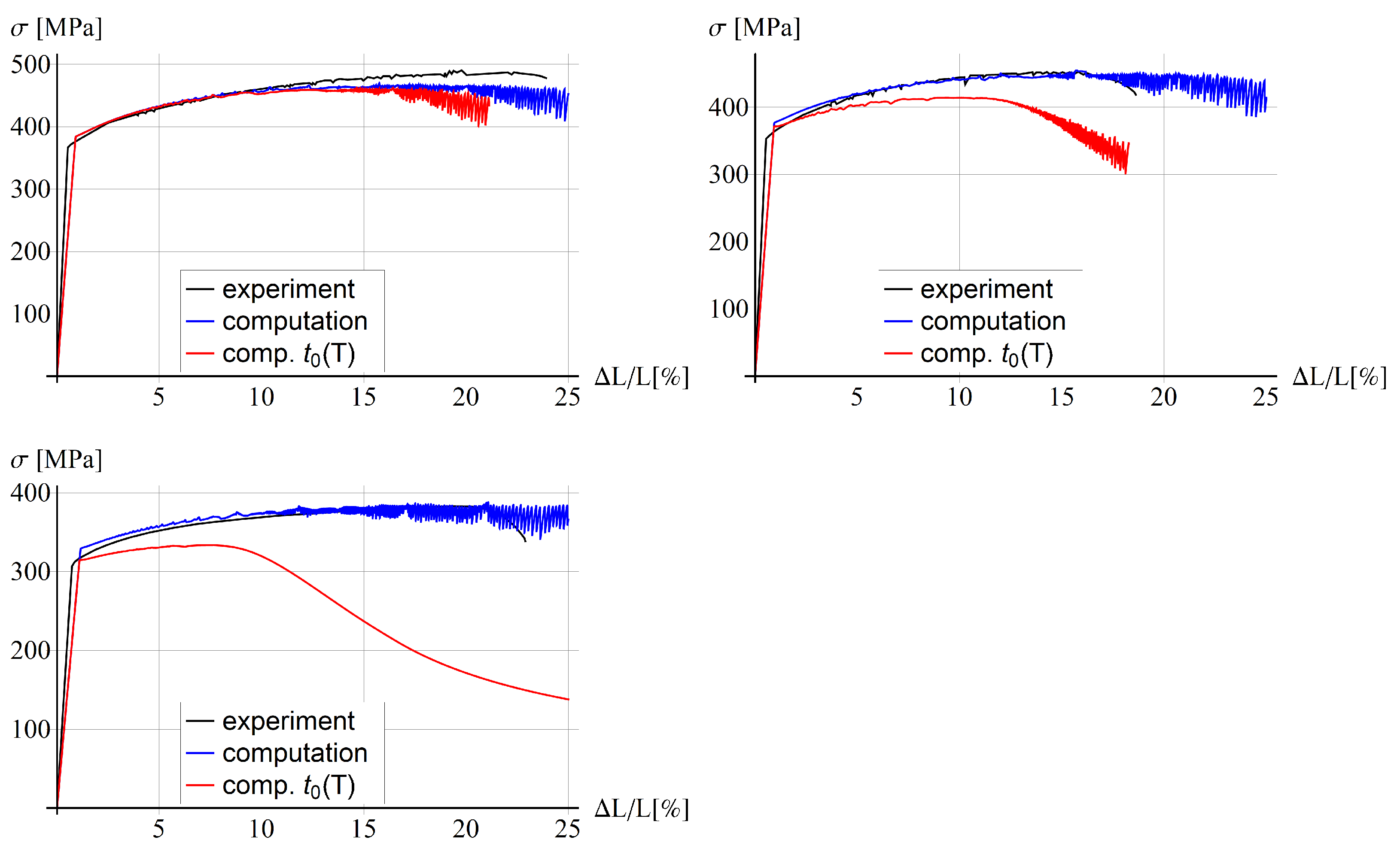
5.3. Comparison with Experiments for Bone-Shape Sample
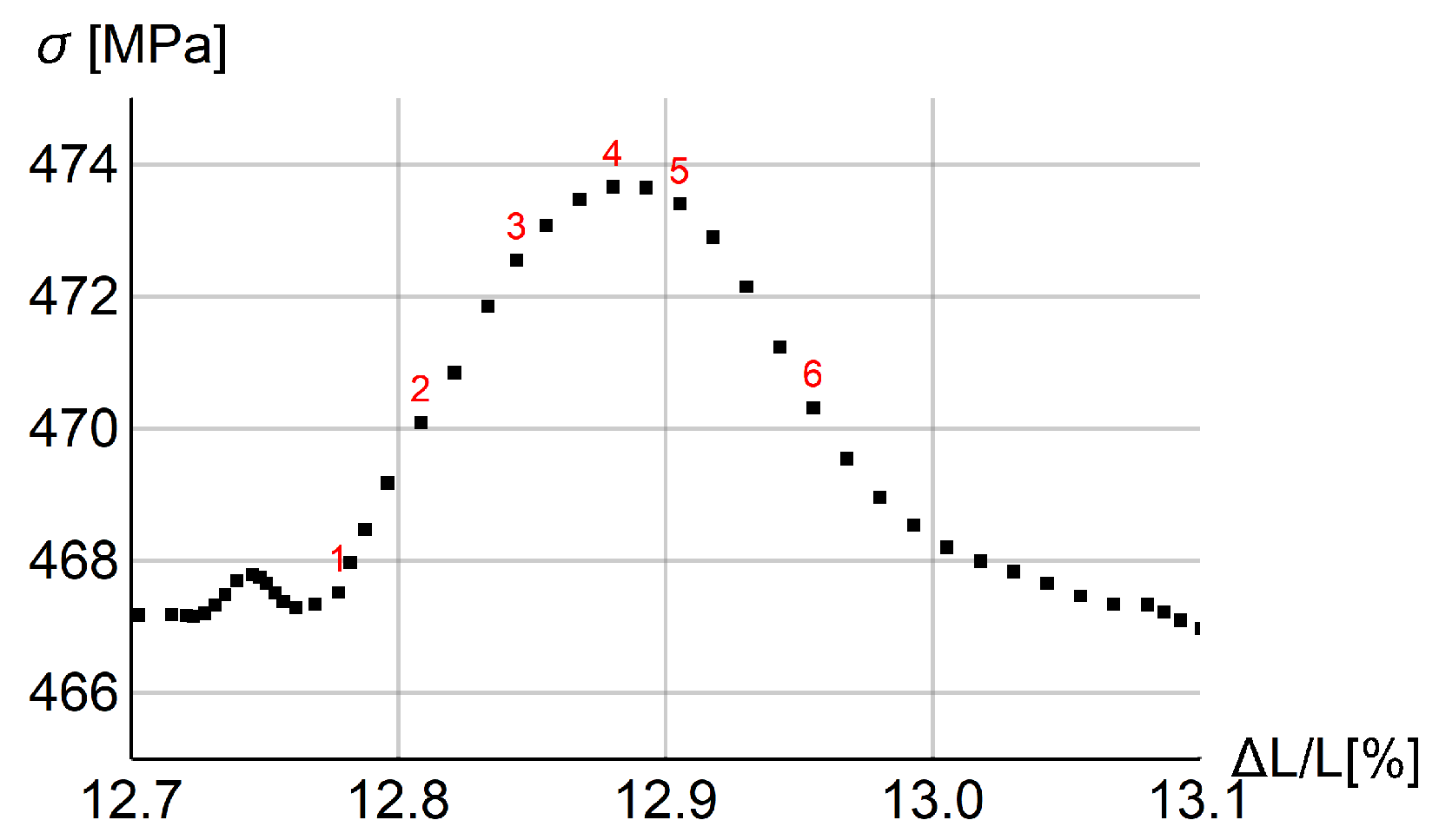
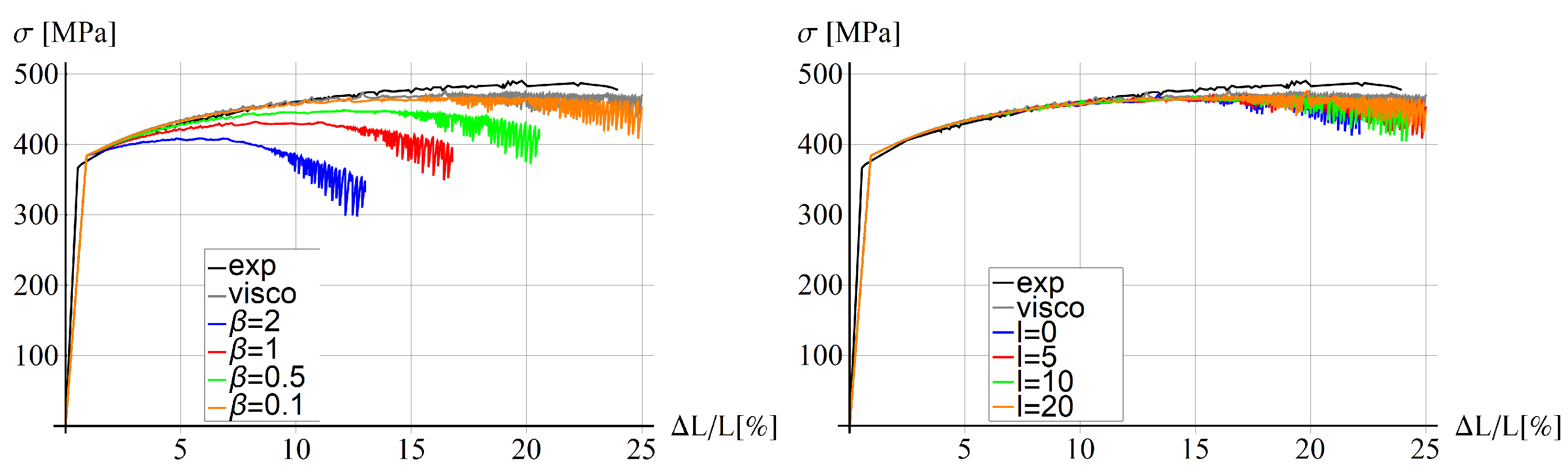
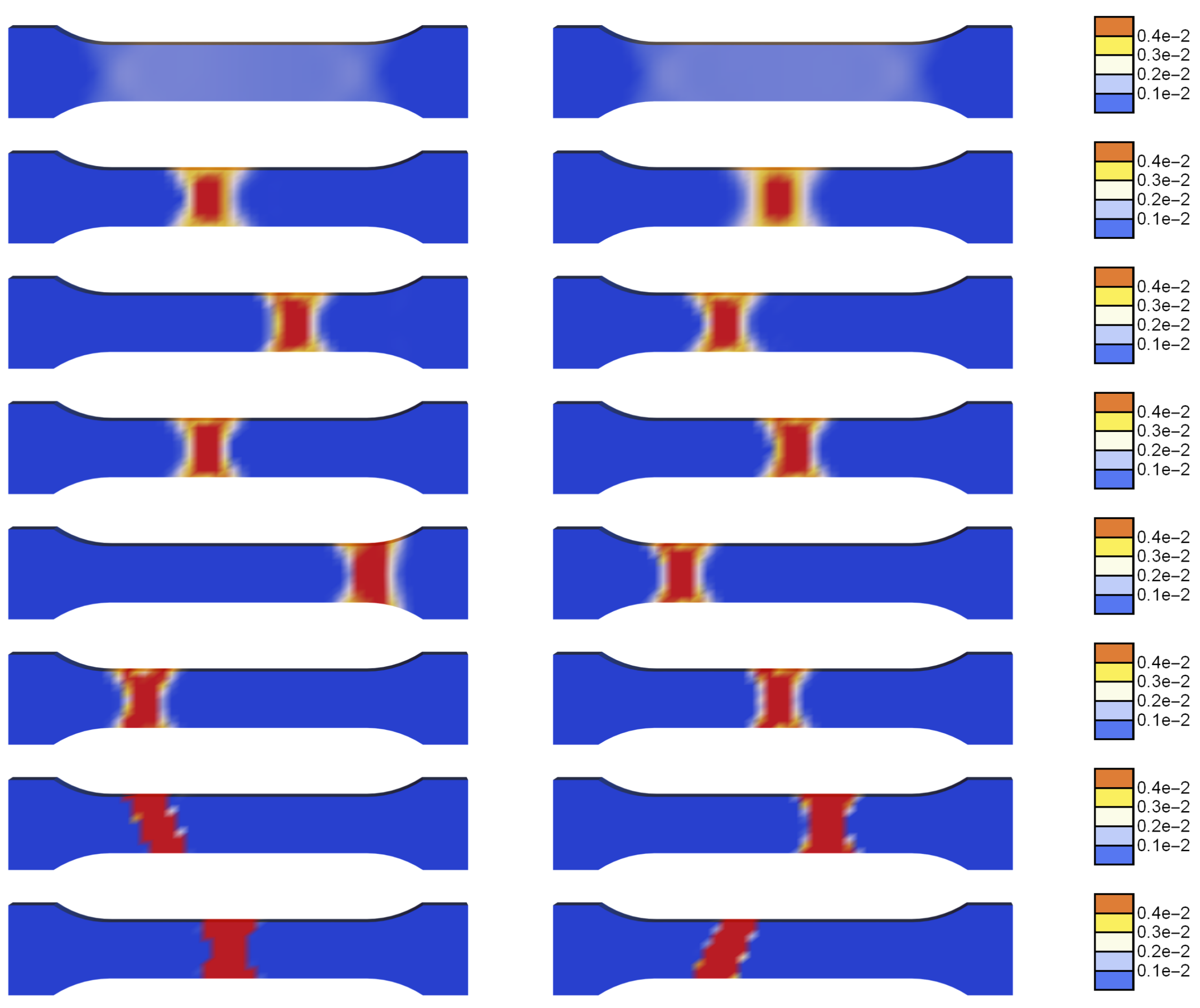
5.4. Parametric Study
5.4.1. Thermo-Visco-Plastic Model
5.4.2. Thermo-Visco-Plastic Model with Gradient Enhancement
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EMC | Estrin–McCormick model. |
| PLC | Portevin–Le Chatelier. |
| DSA | Dynamic Strain Aging. |
| HMH | Huber–Mises–Hencky. |
| BVP | Boundary Value Problem. |
| FE | Finite Elements. |
References
- Cottrell, A.; Bilby, B. Dislocation theory of yielding and strain ageing of iron. Proc. Phys. Soc. Sect. A 1949, 62, 49–62. [Google Scholar] [CrossRef]
- Bergstrom, Y.; Roberts, W. The application of dislocation model to dynamic strain ageing in α-iron containing interstitial atoms. Acta Metall. 1971, 19, 815–823. [Google Scholar] [CrossRef]
- Portevin, A.; Le Chatelier, F. Sur un phénomène observé lors de l’essai de traction d’alliages en cours de transformation. Comput. Rend. Acad. Sci. Paris 1923, 176, 507–510. [Google Scholar]
- Estrin, Y.; Kubin, L. Spatial coupling and propagative plastic instabilities. In Continuum Models for Materials with Microstructure; Mühlhaus, H.B., Ed.; John Wiley & Sons: Chichester, UK, 1995; pp. 395–450. [Google Scholar]
- Wang, W.M. Stationary and Propagative Instabilities in Metals—A Computational Point of View. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1997. [Google Scholar]
- Wang, W.M.; Sluys, L.J.; de Borst, R. Viscoplasticity for instabilities due to strain softening and strain-rate softening. Int. J. Numer. Meth. Eng. 1997, 40, 3839–3864. [Google Scholar] [CrossRef]
- Yilmaz, A. The Portevin–Le Chatelier effect: A review of experimental findings. Sci. Technol. Adv. Mater. 2011, 12, 063001. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Q.; Chen, X.; Chen., Z.; Jiang, Z.; Wu, X.; Fan, J. Three types of Portevin–Le Chatelier effects: Experiment and modelling. Acta Mater. 2007, 55, 2219–2228. [Google Scholar] [CrossRef]
- Tamimi, S.; Andrade-Campos, A.; Pinho-da Cruz, J. Modelling the Portevin-Le Chatelier effects in aluminium alloys: A review. J. Mech. Behav. Mater. 2015, 24, 67–78. [Google Scholar] [CrossRef][Green Version]
- McCormick, P.G. Theory of flow localization due to dynamic strain aging. Acta Metall. 1988, 36, 3061–3067. [Google Scholar] [CrossRef]
- McCormick, P.G.; Ling, C. Numerical modelling of the Portevin–Le Chatelier effect. Acta Metall. Mater. 1995, 43, 1969–1977. [Google Scholar] [CrossRef]
- Zhang, S.; McCormick, P.G.; Estrin, Y. The morphology of Portevin-Le Chatelier bands: Finite element simulation for Al-Mg-Si. Acta Mater. 2001, 49, 1087–1094. [Google Scholar] [CrossRef]
- Böhlke, T.; Bondár, G.; Estrin, Y.; Lebyodkin, M. Geometrically non-linear modeling of the Portevin–Le Chatelier effect. Computat. Mater. Sci. 2009, 44, 1076–1088. [Google Scholar] [CrossRef]
- Belotteau, J.; Berdin, C.; Forest, S.; Parrot, A.; Prioul, C. Mechanical behavior and crack tip plasticity of a strain aging sensitive steel. Mater. Sci. Eng. A 2009, 526, 156–165. [Google Scholar] [CrossRef]
- Berdin, C.; Wang, H. Local approach to ductile fracture and dynamic strain aging. Int. J. Fracture 2013, 182, 39–51. [Google Scholar] [CrossRef]
- Sarkar, A.; Maloy, S.A.; Murty, K.L. Investigation of Portevin-Le Chatelier effect in HT-9 steel. Mater. Sci. Eng. A 2015, 631, 120–125. [Google Scholar] [CrossRef]
- Ren, S.; Morgeneyer, T.; Mazière, M.; Forest, S.; Rousselier, G. Effect of Lüders and Portevin-Le Chatelier localization bands on plasticity and fracture of notched steel specimens studied by DIC and FE simulations. Int. J. Plasticity 2021, 136, 102880. [Google Scholar] [CrossRef]
- Kozłowska, A.; Grzegorczyk, B.; Morawiec, M.; Grajcar, A. Explanation of the PLC Effect in Advanced High-Strength Medium-Mn Steels—A Review. Materials 2019, 12, 1–14. [Google Scholar] [CrossRef]
- Benallal, A.; Berstad, T.; Børvik, T.; Hopperstad, O.; Koutiri, I.; de Codes, R.N. An experimental and numerical investigation of the behaviour of AA5083 aluminium alloy in presence of the Portevin–Le Chatelier effect. Int. J. Plasticity 2008, 24, 1916–1945. [Google Scholar] [CrossRef]
- Chen, J.; Zhen, L.; Fan, L.; Yang, S.; Dai, S.; Shao, W. Portevin-Le Chatelier effect in Al-Zn-Mg-Cu-Zr aluminum alloy. Trans. Nonferr. Metals Soc. China 2009, 19, 1071–1075. [Google Scholar] [CrossRef]
- Coër, J.; Manach, P.; Laurent, H.; Oliveira, M.; Menezes, L. Piobert–Lüders plateau and Portevin–Le Chatelier effect in an Al–Mg alloy in simple shear. Mech. Res. Commun. 2013, 48, 1–7. [Google Scholar] [CrossRef]
- Reyne, B.; Manach, P.Y.; Moës, N. Macroscopic consequences of Piobert–Lüders and Portevin–Le Chatelier bands during tensile deformation in Al-Mg alloys. Mater. Sci. Eng. A 2019, 746, 187–196. [Google Scholar] [CrossRef]
- Mazière, M.; Besson, J.; Forest, S.; Tanguy, B.; Chalons, H.; Vogel, F. Numerical aspects in the finite element simulation of the Portevin–Le Chatelier effect. Comput. Methods Appl. Mech. Engrg. 2010, 199, 734–754. [Google Scholar] [CrossRef]
- Manach, P.; Thuillier, S.; Yoon, J.; Coër, J.; Laurent, H. Kinematics of Portevin–Le Chatelier bands in simple shear. Int. J. Plasticity 2014, 58, 66–83. [Google Scholar] [CrossRef]
- Mansouri, L.Z.; Thuillier, S.; Manach, P.Y. Thermo-mechanical modeling of Portevin–Le Châtelier instabilities under various loading paths. Int. J. Mech. Sci. 2016, 115, 676–688. [Google Scholar] [CrossRef]
- Lebyodkin, M.; Dunin-Barakowskii, L.; Bréchet, Y.; Estrin, Y.; Kubin, L.P. Spatio-temporal dynamics of the Portevin–Le Chatelier effect: Experiment and modelling. Acta Mater. 2000, 48, 2529–2541. [Google Scholar] [CrossRef]
- Rizzi, E.; Hähner, P. On the Portevin–Le Chatelier effect: Theoretical modeling and numerical results. Int. J. Plasticity 2004, 20, 121–165. [Google Scholar] [CrossRef]
- Graff, S.; Forest, S.; Strudel, J.L.; Prioul, C.; Pilvin, P.; Béchade, J.L. Strain localization phenomena associated with static and dynamic strain ageing in notched specimens: Experiments and finite element simulations. Mater. Sci. Eng. A 2004, 387–389, 181–185. [Google Scholar] [CrossRef]
- Darowicki, K.; Orlikowski, J.; Zieliński, A. Investigation of changes in the type B PLC effect of Al–Mg–Cu type alloy for various strain rates. Mater. Sci. Eng. A 2008, 496, 478–482. [Google Scholar] [CrossRef]
- Mazière, M.; Forest, S. Strain gradient plasticity modeling and finite element simulation of Lüders band formation and propagation. Continuum Mech. Thermodyn. 2015, 27, 83–104. [Google Scholar] [CrossRef]
- Xu, J.; Chen, G.; Fu, S. Complexity analysis of the Portevin-Le Chatelier in an Al alloy at different temperatures. Theor. Appl. Mech. Lett. 2021, 11, 100233. [Google Scholar] [CrossRef]
- Skoczeń, B.; Bielski, J.; Tabin, J. Multiaxial constitutive model of discontinuous plastic flow at cryogenic temperatures. Int. J. Plasticity 2014, 55, 198–218. [Google Scholar] [CrossRef]
- Tabin, J. Kinematic and thermal characteristic of discontinuous plastic flow in metastable austenitic stainless steels. Mech. Mater. 2021, 163, 104090. [Google Scholar] [CrossRef]
- Bartels, A.; Bartel, T.; Canadija, M.; Mosler, J. On the thermomechanical coupling in dissipative materials: A variational approach for generalized standard materials. J. Mech. Phys. Solids 2015, 82, 218–234. [Google Scholar] [CrossRef]
- Li, Z.; Ma, Q.; Cui, J. Second-order two-scale finite element algorithm for dynamic thermo–mechanical coupling problem in symmetric structure. J. Comput. Phys. 2016, 314, 712–748. [Google Scholar] [CrossRef]
- Aldakheel, F.; Miehe, C. Coupled thermomechanical response of gradient plasticity. Int. J. Plasticity 2017, 91, 1–24. [Google Scholar] [CrossRef]
- Moleiro, F.; Madeira, J.; Carrera, E.; Reddy, J. Design optimization of functionally graded plates under thermo-mechanical loadings to minimize stress, deformation and mass. Compos. Struct. 2020, 245, 112360. [Google Scholar] [CrossRef]
- Ahmed, S.R.; Sarkar, P.R. Displacement-function modeling of thermo-mechanical behavior of fiber-reinforced composite structures. Int. J. Mech. Sci. 2021, 211, 106739. [Google Scholar] [CrossRef]
- Rose, L.; Menzel, A. Identification of thermal material parameters for thermo-mechanically coupled material models. Meccanica 2021, 56, 393–416. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Ma, Q.; Jiang, X. Thermo-mechanical coupling behavior of plate structure under re-entry aerodynamic environment. Int. J. Mech. Sci. 2022, 218, 107066. [Google Scholar] [CrossRef]
- Oppermann, P.; Denzer, R.; Menzel, A. A thermo-viscoplasticity model for metals over wide temperature ranges—Application to case hardening steel. Computat. Mech. 2022, 69, 541–563. [Google Scholar] [CrossRef]
- Wcisło, B.; Pamin, J. Local and non-local thermomechanical modeling of elastic-plastic materials undergoing large strains. Int. J. Numer. Meth. Eng. 2017, 109, 102–124. [Google Scholar] [CrossRef]
- Pamin, J.; Wcisło, B.; Kowalczyk-Gajewska, K. Gradient-enhanced large strain thermoplasticity with automatic linearization and localization simulations. J. Mech. Mater. Struct. 2017, 12, 123–146. [Google Scholar] [CrossRef]
- Holzapfel, G.A. Nonlinear Solid Mechanics. A Continuum Approach for Engineering; John Wiley & Sons: Chichester, UK, 2000. [Google Scholar]
- Wriggers, P.; Miehe, C.; Kleiber, M.; Simo, J. On the coupled thermomechnical treatment of necking problems via finite element methods. Int. J. Numer. Meth. Eng. 1992, 33, 869–883. [Google Scholar] [CrossRef]
- Simo, J.C.; Miehe, C. Associative coupled thermoplasticity at finite strains: Formulation, numerical analysis and implementation. Comput. Methods Appl. Mech. Eng. 1992, 98, 41–104. [Google Scholar] [CrossRef]
- Mucha, M.; Wcisło, B.; Pamin, J. Simulation of Lueders bands using regularized large strain elasto-plasticity. Arch. Mech. 2021, 73, 83–117. [Google Scholar] [CrossRef]
- Korelc, J. Automation of the Finite Element Method. In Nonlinear Finite Element Methods; Wriggers, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 483–508. [Google Scholar]
- Lipski, A.; Mroziński, S. The effects of temperature on the strength properties of aluminium alloy 2024-T3. Acta Mech. Autom. 2012, 6, 62–66. [Google Scholar]
- Simo, J.C. A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition: Part 1. Continuum formulation. Comput. Methods Appl. Mech. Eng. 1988, 66, 199–219. [Google Scholar] [CrossRef]
- Geers, M.G.D. Finite strain logarithmic hyperelasto-plasticity with softening: A strongly non-local implicit gradient framework. Comput. Methods Appl. Mech. Eng. 2004, 193, 3377–3401. [Google Scholar] [CrossRef]
- Ristinmaa, M.; Wallin, M.; Ottosen, N.S. Thermodynamic format and heat generation of isotropic hardening plasticity. Acta Mech. 2007, 194, 103–121. [Google Scholar] [CrossRef]
- Lee, E.H. Elastic plastic deformation at finite strain. ASME Trans. J. Appl. Mech. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- Lee, E.H.; Liu, D.T. Finite-strain elastic-plastic theory with application to plane-wave analysis. J. Appl. Phys. 1967, 38, 19–27. [Google Scholar] [CrossRef]
- Lu, S.C.H.; Pister, K.S. Decomposition of deformation and representation of the free energy function for isotropic thermoelastic solids. Int. J. Solids Struct. 1975, 11, 927–934. [Google Scholar] [CrossRef]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity. Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 1998; Volume 7. [Google Scholar]
- Wcisło, B. Simulations of thermal softening in large strain thermoplasticity with degradation. Eng. Trans. 2016, 4, 563–572. [Google Scholar]
- Okazawa, S. Structural bifurcation for ductile necking localization. Int. J. Non-Linear Mech. 2009, 45, 35–41. [Google Scholar] [CrossRef][Green Version]
- Peerlings, R.H.J.; de Borst, R.; Brekelmans, W.A.M.; de Vree, J.H.P. Gradient-enhanced damage for quasi-brittle materials. Int. J. Numer. Meth. Eng. 1996, 39, 3391–3403. [Google Scholar] [CrossRef]
- Wcisło, B.; Pamin, J.; Kowalczyk-Gajewska, K. Gradient-enhanced damage model for large deformations of elastic-plastic materials. Arch. Mech. 2013, 65, 407–428. [Google Scholar]
- Oka, F.; Mühlhaus, H.B.; Yashima, A.; Sawada, K. Quasi-Static and Dynamic Characteristics of Strain Gradient Dependent Non-Local Constitutive Models. In Material Instabilities in Solids; de Borst, R., van der Giessen, E., Eds.; Wiley: Chichester, UK, 1998; pp. 387–404. [Google Scholar]
- Sluys, L.J.; Wang, W.M. Macroscopic Modelling of Stationary and Propagative Instabilities. In Material Instabilities in Solids; de Borst, R., van der Giessen, E., Eds.; John Wiley & Sons: New York, NY, USA, 1998; pp. 489–505. [Google Scholar]
- Simo, J. Numerical Analysis and Simulation of Plasticity. In Handbook of Numerical Analysis. Numerical Methods for Solids (Part 3); Ciarlet, P., Lions, J., Eds.; Elsevier Science: Boca Raton, FL, USA, 1998; Volume VI, pp. 183–499. [Google Scholar]
- Miehe, C. Entropic thermoelasticity at finite strains. Aspects of the formulation and numerical implementation. Comput. Methods Appl. Mech. Eng. 1995, 120, 243–269. [Google Scholar] [CrossRef]
- Taylor, G.I.; Quinney, H. The latent energy remaining in a metal after cold working. Proc. R. Soc. Lond. Ser. A 1934, 143, 307–326. [Google Scholar] [CrossRef]
- Korelc, J. Automation of primal and sensitivity analysis of transient coupled problems. Computat. Mech. 2009, 44, 631–649. [Google Scholar] [CrossRef]
- Korelc, J.; Wriggers, P. Automation of Finite Element Methods; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- de Souza Neto, E.; Peric, D.; Owen, D. Computational Methods for Plasticity. Theory and Applications; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]




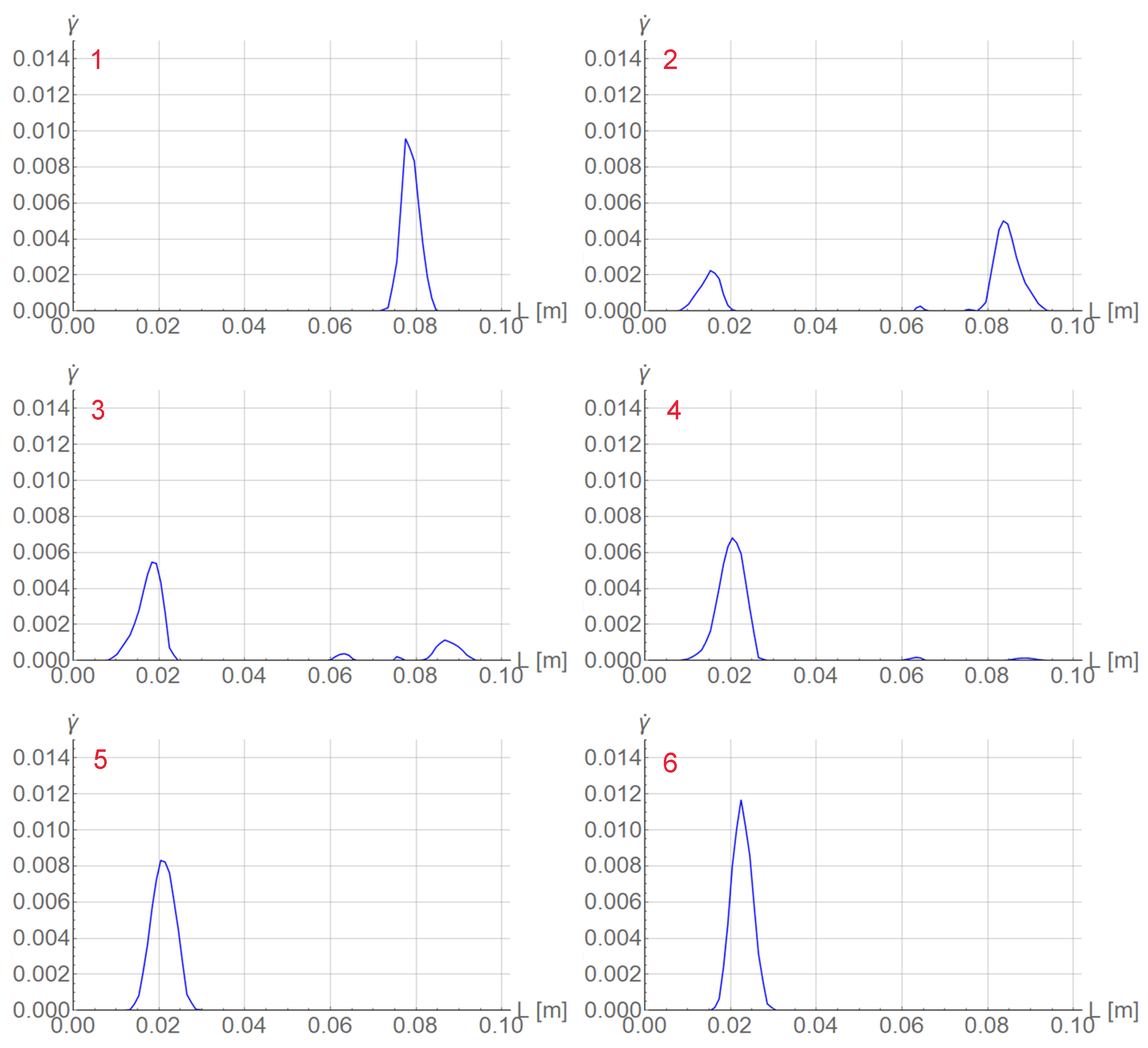
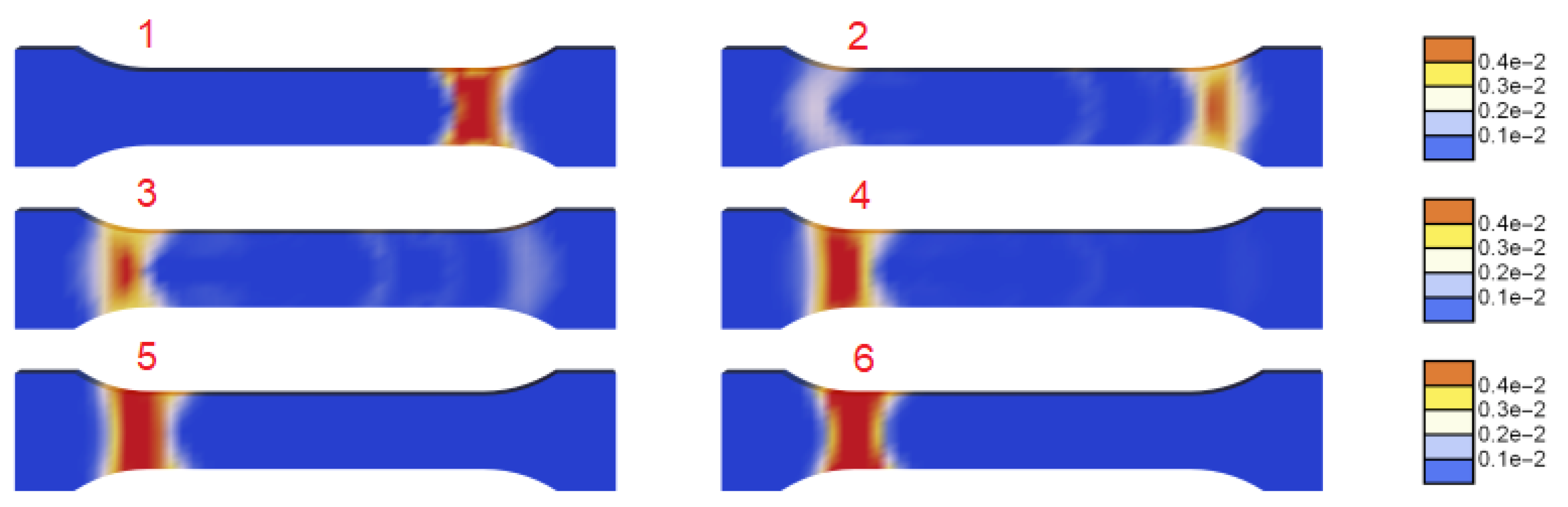
| Property | Symbol | Value | Unit |
|---|---|---|---|
| Young modulus | E | 68.56 | GPa |
| Poisson ratio | 0.3 | - | |
| Initial yield strength | 367.5 | MPa | |
| Final yield strength | 488.8 | MPa | |
| Saturation constant | 16 | MPa | |
| Viscosity | 40 | MPa · s | |
| Conductivity | k | 121 | J/(s·K·m) |
| Heat capacity | c | 2,423,750 | J/(C) |
| Thermal expansion coeff. | 23.2 | 1/C | |
| Thermal softening modulus | 0.0016 | 1/C | |
| Heat dissipation factor | 0.9 | - | |
| Solute diffusion time | 0.125 | s | |
| EMC model param. | 13.62 × 10 | - | |
| EMC model param. | 7.2 × 10 | - | |
| EMC model param. | 18.9 | MPa | |
| EMC model param. | 567.78 | MPa | |
| EMC model exponent | n | - | |
| EMC model param. | 0.051355 | 1/C | |
| EMC model param. | 0.03462 | s |
| Property | Symbol | 25 C | 100 C | 200 C | Unit |
|---|---|---|---|---|---|
| Young modulus | E | 68.56 | 65.56 | 46.62 | GPa |
| Initial yield strength | 367.5 | 360.3 | 312.9 | MPa | |
| Final yield strength | 488.8 | 466.2 | 383.2 | MPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mucha, M.; Wcisło, B.; Pamin, J. Simulation of PLC Effect Using Regularized Large-Strain Elasto-Plasticity. Materials 2022, 15, 4327. https://doi.org/10.3390/ma15124327
Mucha M, Wcisło B, Pamin J. Simulation of PLC Effect Using Regularized Large-Strain Elasto-Plasticity. Materials. 2022; 15(12):4327. https://doi.org/10.3390/ma15124327
Chicago/Turabian StyleMucha, Marzena, Balbina Wcisło, and Jerzy Pamin. 2022. "Simulation of PLC Effect Using Regularized Large-Strain Elasto-Plasticity" Materials 15, no. 12: 4327. https://doi.org/10.3390/ma15124327
APA StyleMucha, M., Wcisło, B., & Pamin, J. (2022). Simulation of PLC Effect Using Regularized Large-Strain Elasto-Plasticity. Materials, 15(12), 4327. https://doi.org/10.3390/ma15124327






