Stability Analysis of the Horseshoe Tunnel Face in Rock Masses
Abstract
:1. Introduction
2. Nonlinear Hoek–Brown Failure Criterion
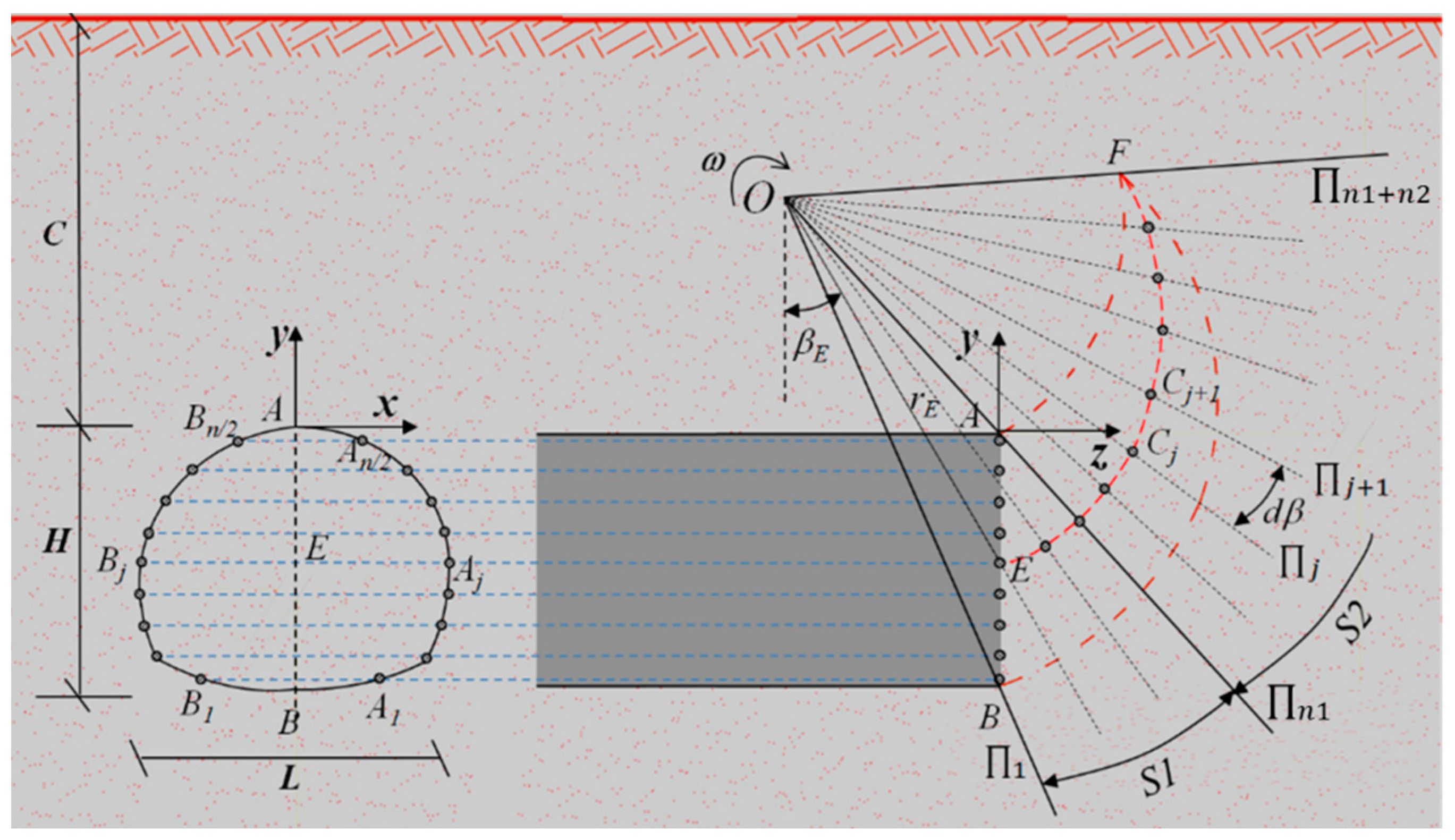
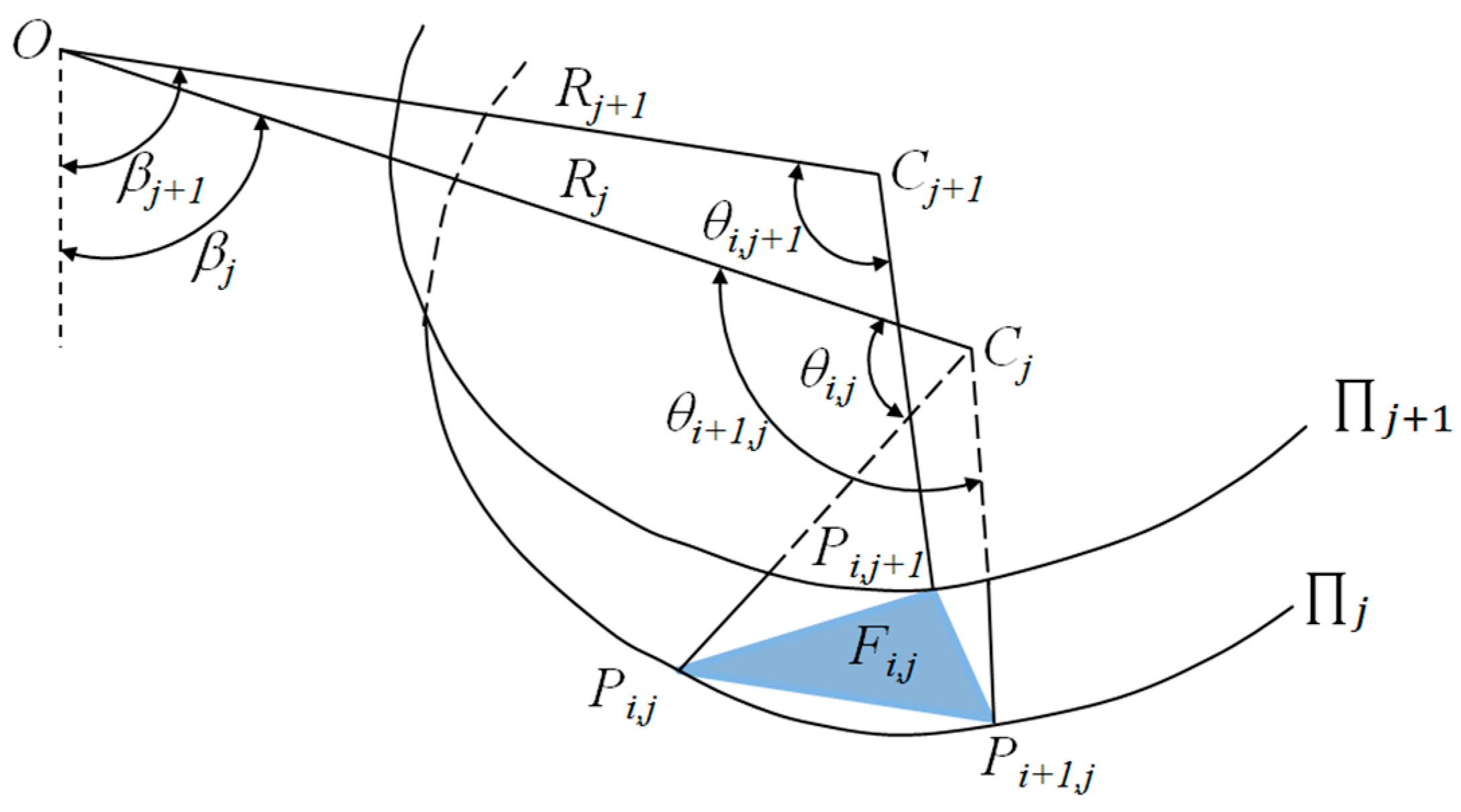
3. Rotational Failure Model for the Horseshoe Tunnel Face
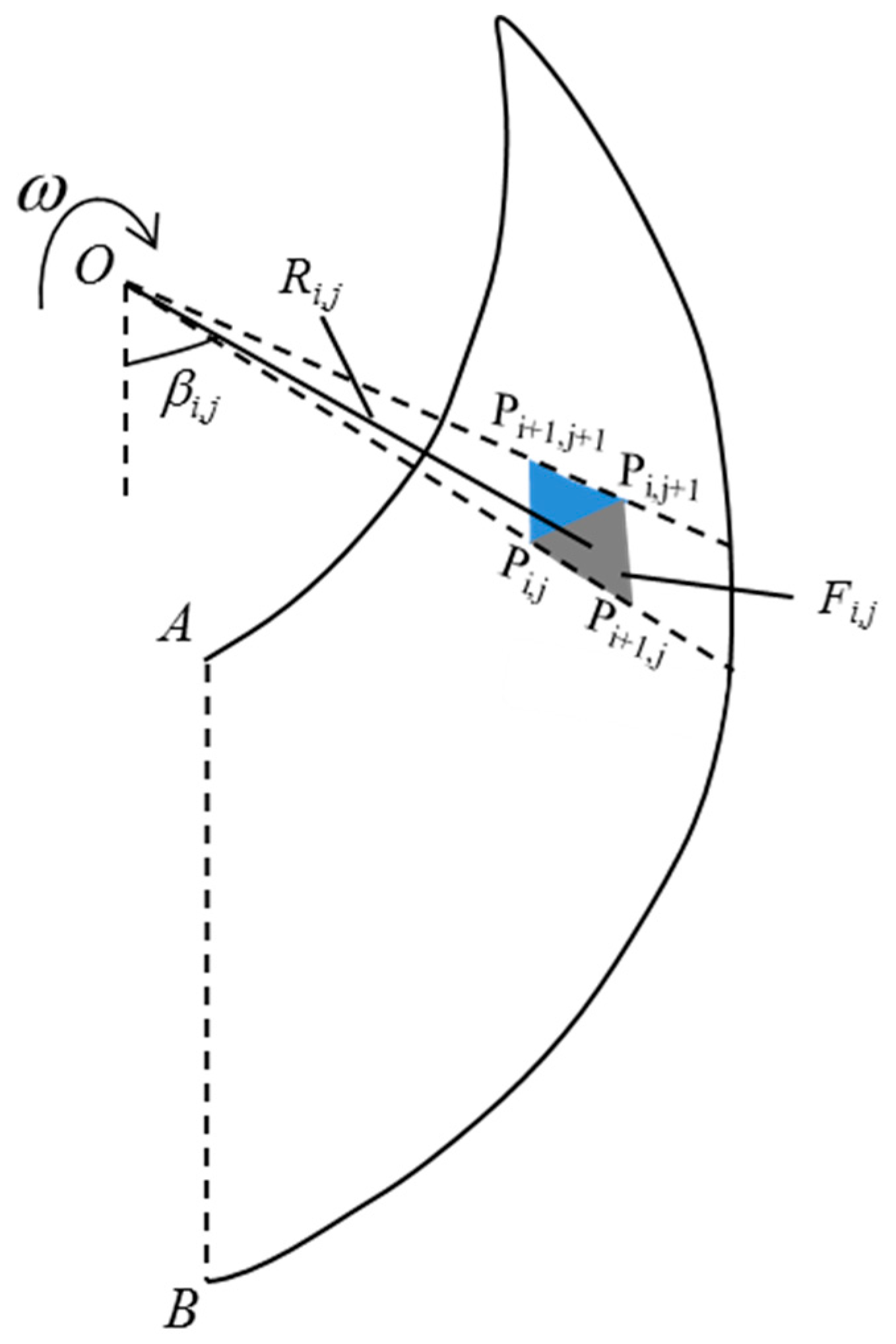
4. Work Rate Calculations
4.1. Internal Energy Dissipation Rate
4.2. Work Rate Exerted by the Rock Weight
4.3. Work Rate Exerted by the Supporting Pressure
4.4. Determination of the Limit Support Pressure
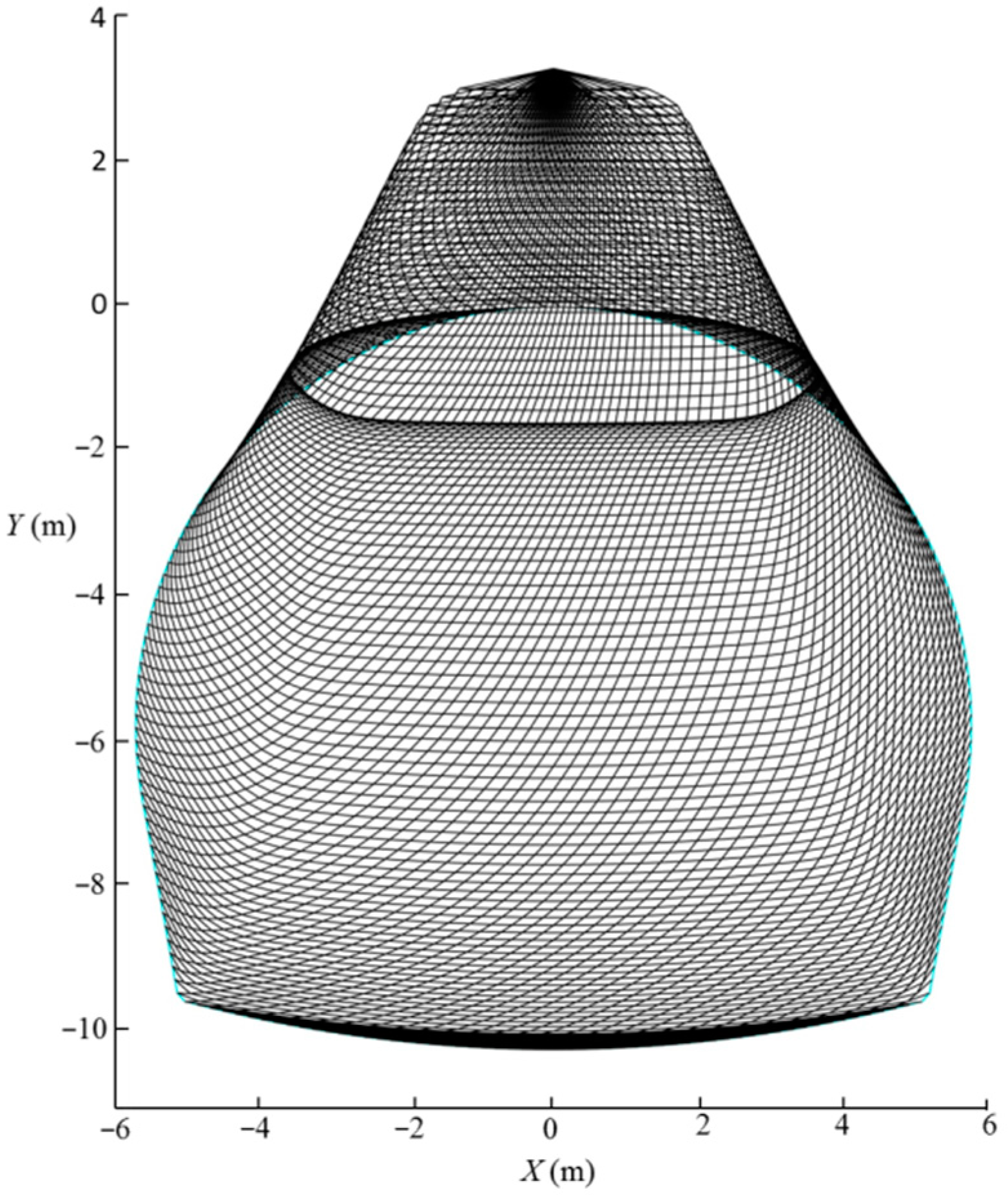
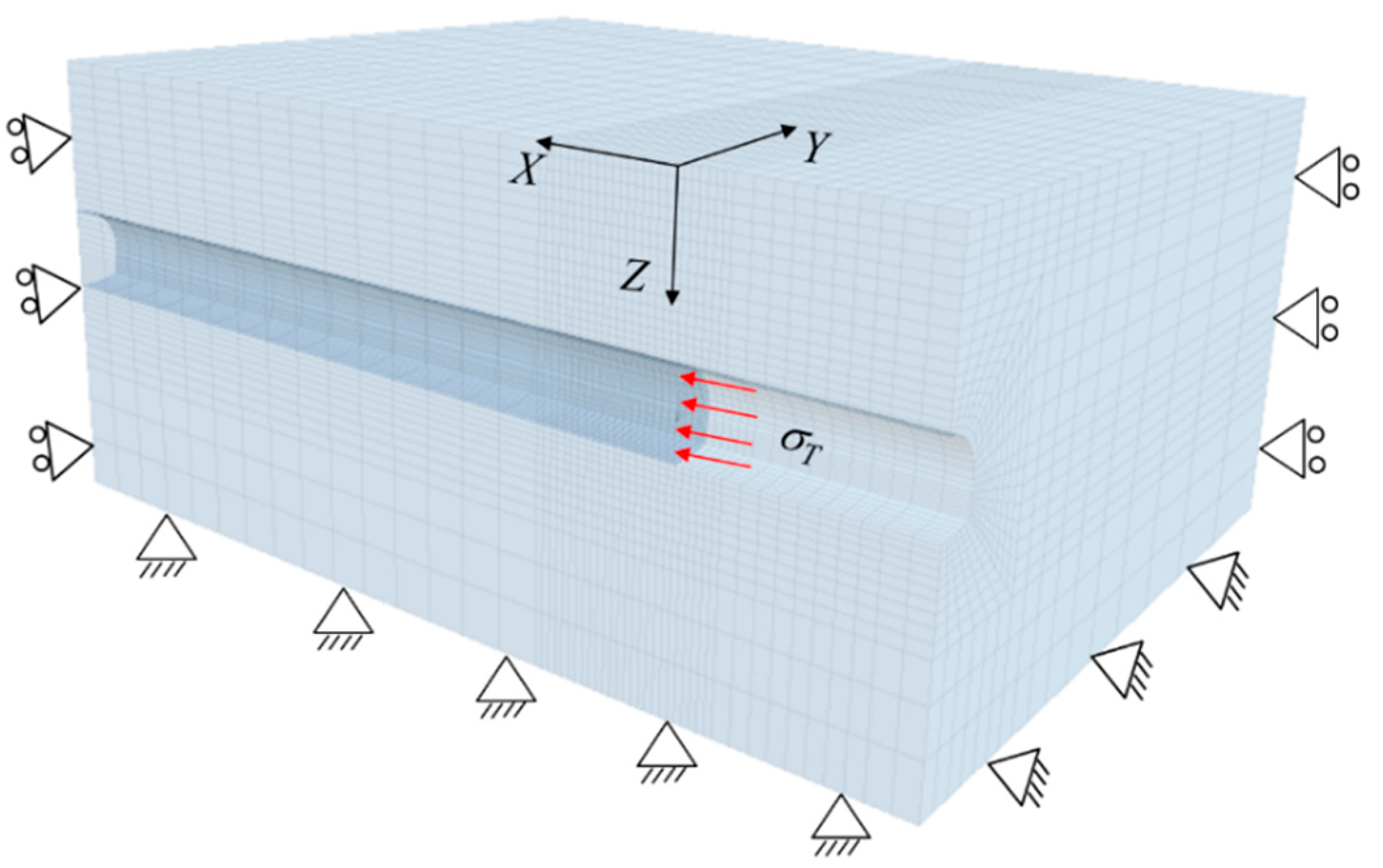
5. Validation
6. Parametric Analysis
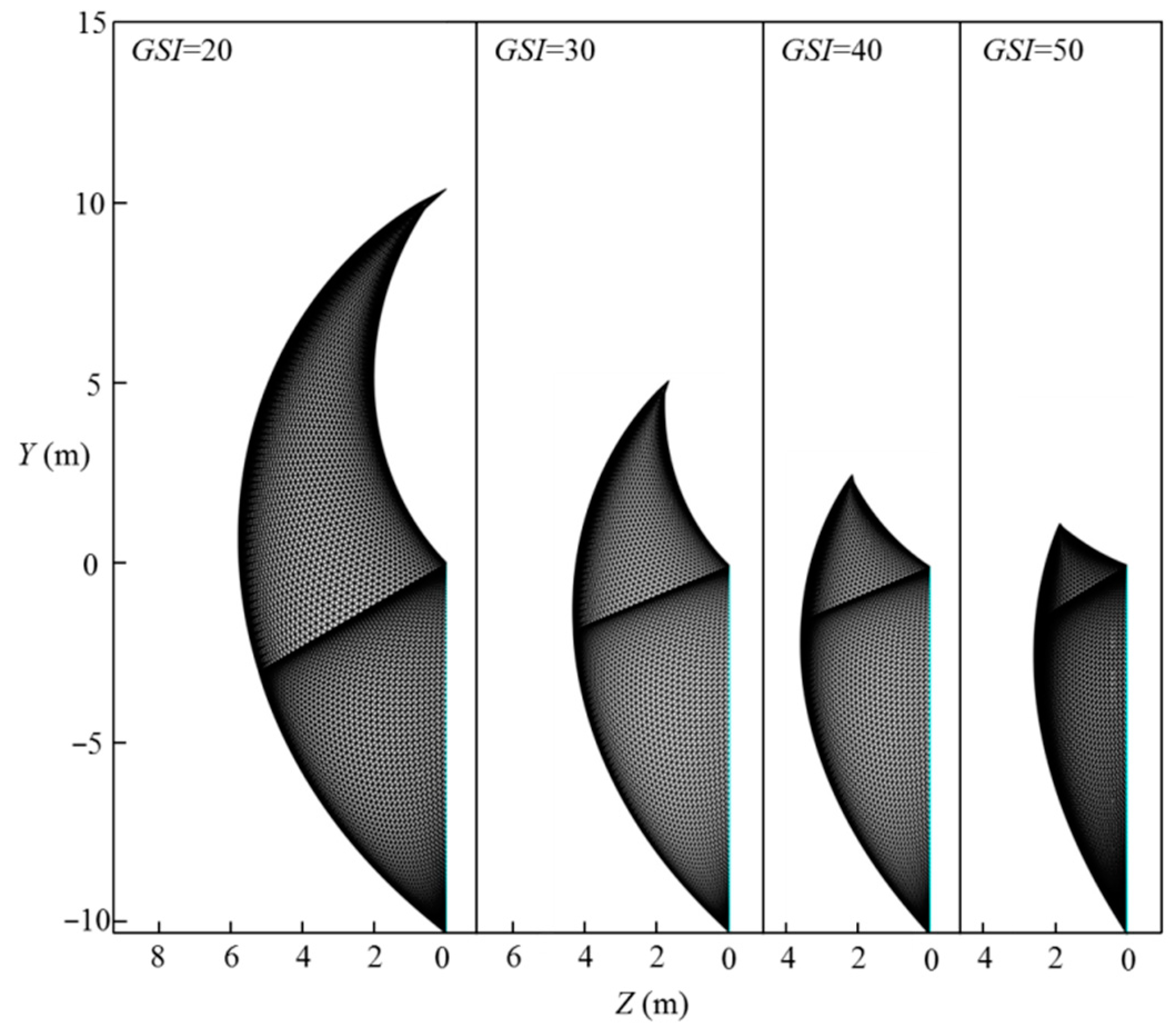
6.1. Effect of the Geological Strength Index, , on the Tunnel Face Stability
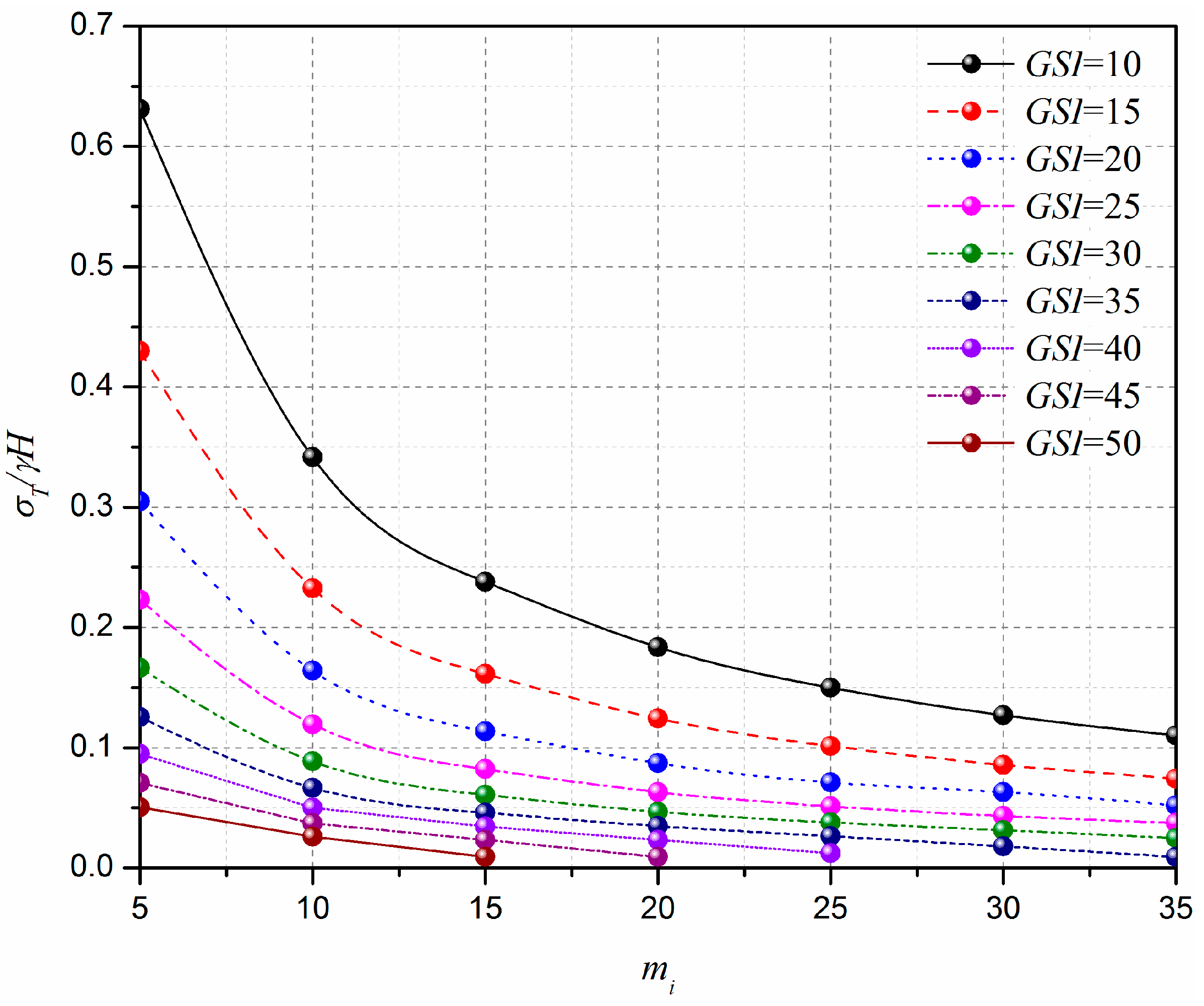
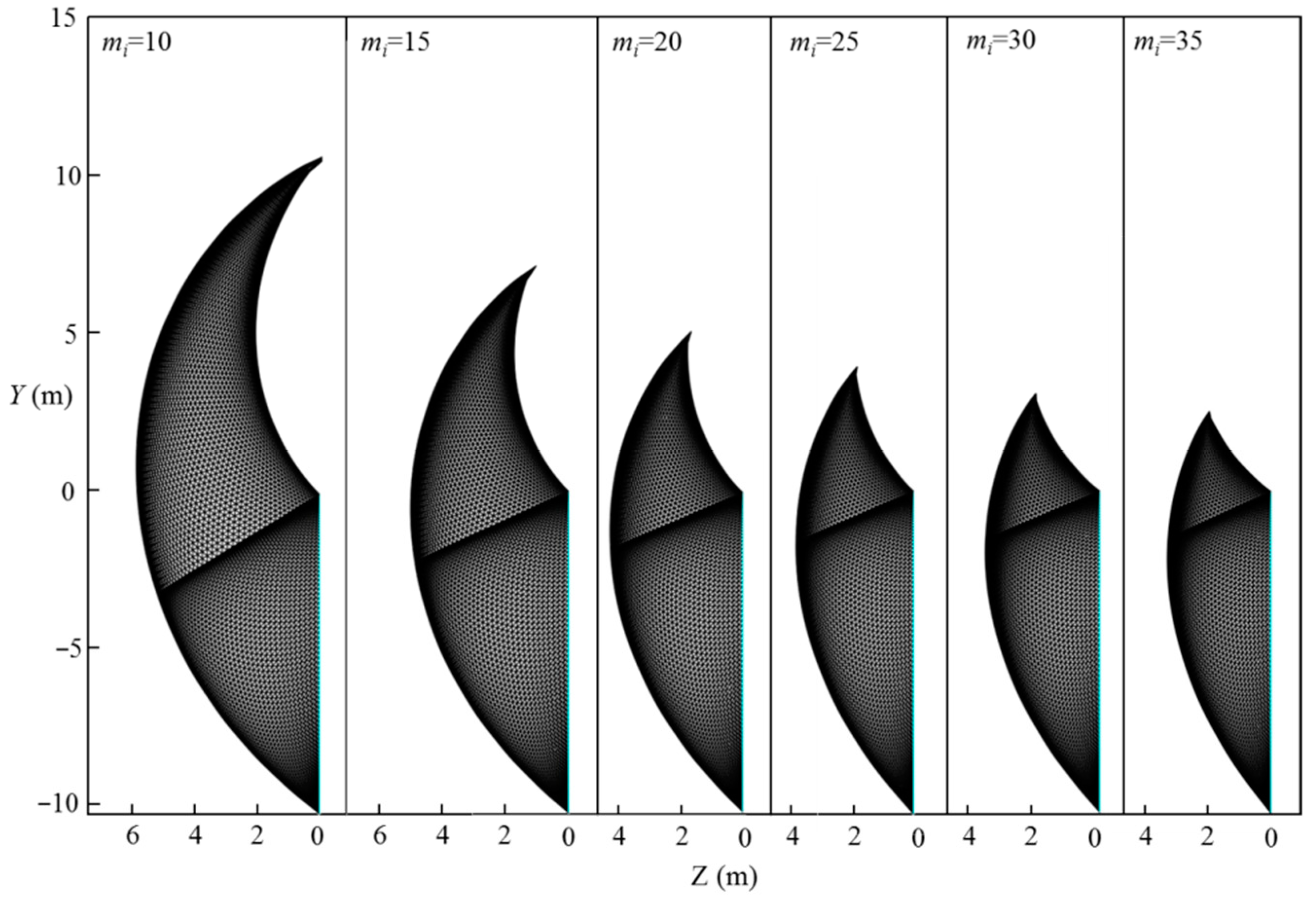
6.2. Effect of the Hoek–Brown Coefficient on the Tunnel Face Stability
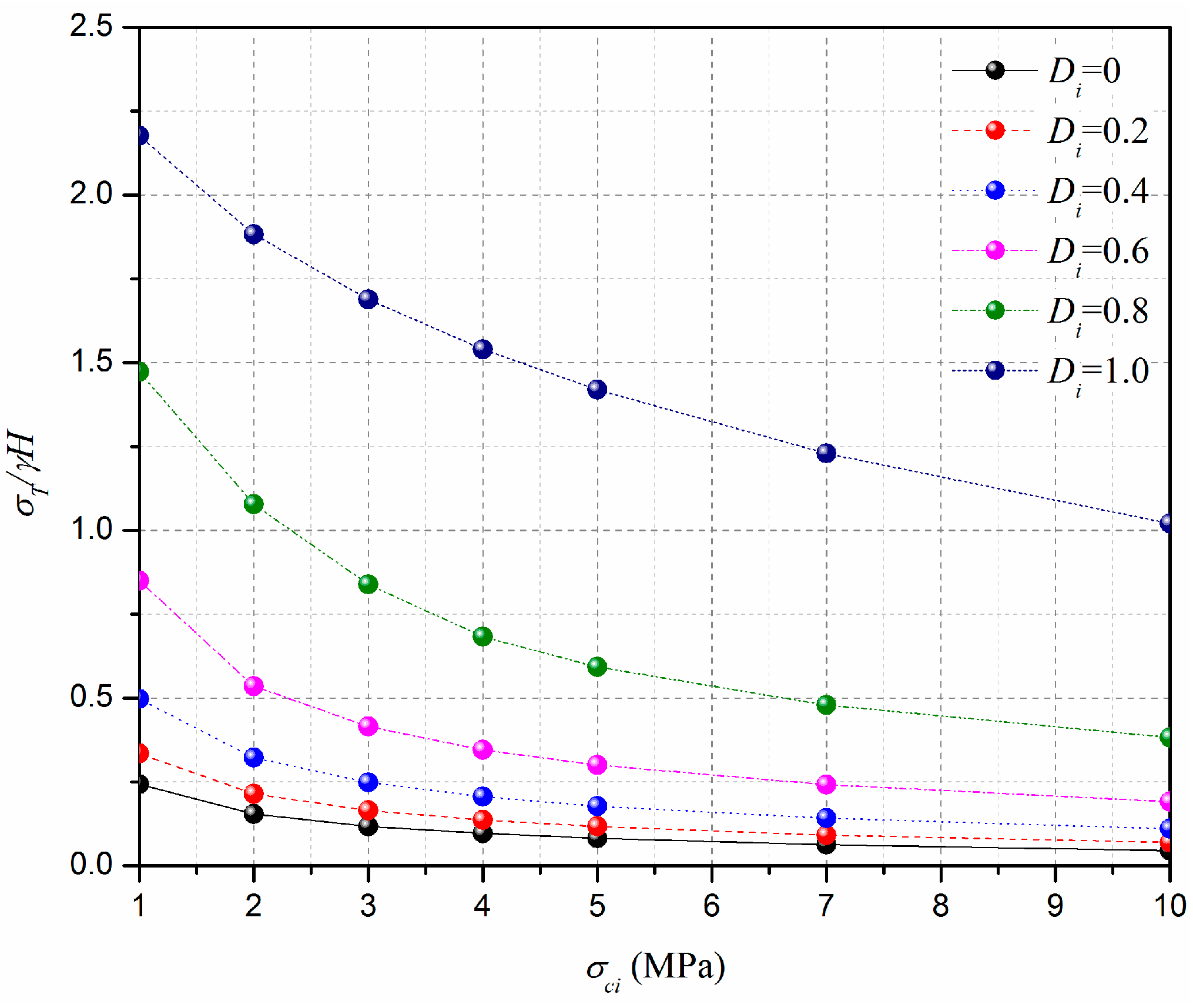
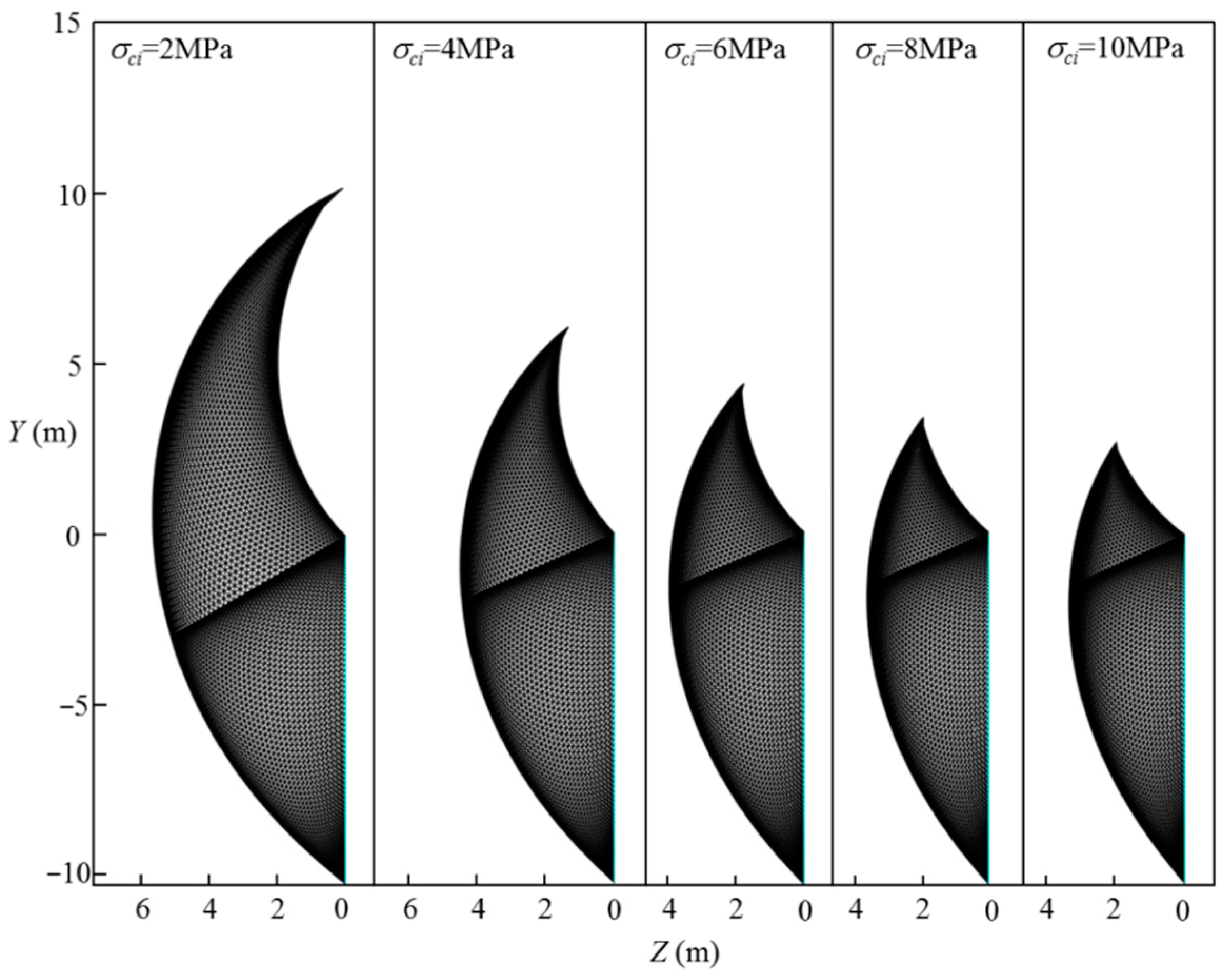
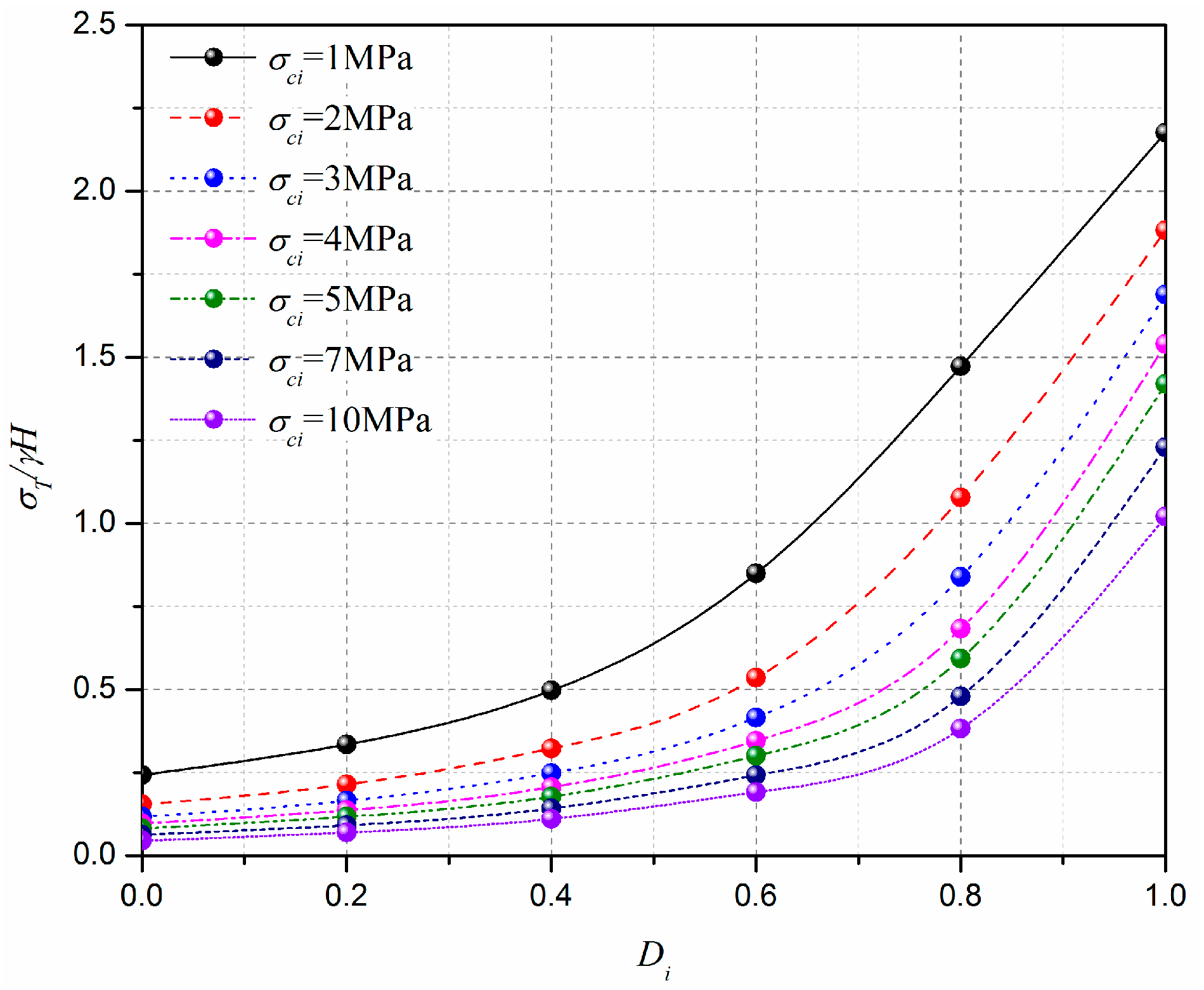
6.3. Effect of the Uniaxial Compressive Strength, , on the Tunnel Face Stability
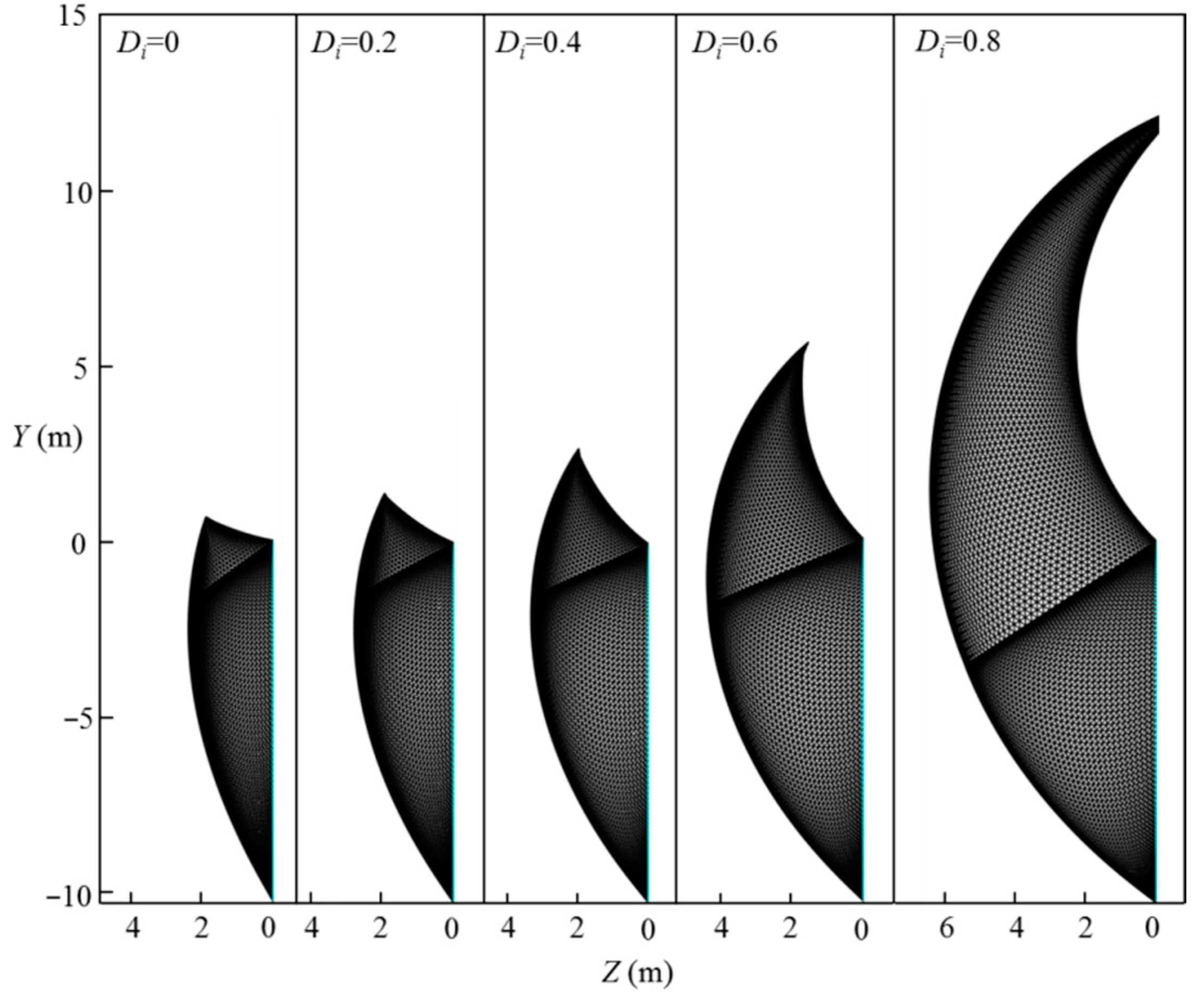
6.4. Effect of the Disturbance Coefficient of Rock, , on the Tunnel Face Stability
7. Conclusions
- (1)
- In this study, the nonlinear Hoek–Brown failure criterion is first incorporated into the stability analysis of horseshoe tunnel faces in rock masses. The comparisons between the results from the proposed method with the numerical results illustrate that the proposed method is an efficient and accurate approach to assessing the face stability of horseshoe tunnels.
- (2)
- Based on the proposed method, the effect of rock properties on the normalized limit support pressure and the 3D failure surface are presented. It is shown that, for selected cases, the normalized limit support pressure of the tunnel face greatly decreases with the increasing of GSI, mi, and σci, and decreasing of Di; the 3D failure surface become larger with the decreasing of GSI, mi, and σci, and increasing of Di; a larger 3D failure surface is associated with a high value of the normalized limit support pressure; and high GSI, mi, and σci are beneficial for the tunnel face stability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lü, X.; Zhou, Y.; Huang, M.; Zeng, S. Experimental study of the face stability of shield tunnel in sands under seepage condition. Tunn. Undergr. Space Technol. 2018, 74, 195–205. [Google Scholar] [CrossRef]
- Weng, X.; Sun, Y.; Yan, B.; Niu, H.; Lin, R.; Zhou, S. Centrifuge testing and numerical modeling of tunnel face stability considering longitudinal slope angle and steady state seepage in soft clay. Tunn. Undergr. Space Technol. 2020, 101, 103406. [Google Scholar] [CrossRef]
- Alagha, A.S.; Chapman, D.N. Numerical modelling of tunnel face stability in homogeneous and layered soft ground. Tunn. Undergr. Space Technol. 2019, 94, 103096. [Google Scholar] [CrossRef]
- Lü, X.; Su, Z.; Huang, M.; Zhou, Y. Strength reduction finite element analysis of a stability of large cross-river shield tunnel face with seepage. Eur. J. Environ. Civ. Eng. 2020, 24, 336–353. [Google Scholar] [CrossRef]
- Han, K.; Zhang, C.; Zhang, D. Upper-bound solutions for the face stability of a shield tunnel in multilayered cohesive-frictional soils. Comput. Geotech. 2016, 79, 1–9. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pres-surized shield. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 1363–1388. [Google Scholar] [CrossRef] [Green Version]
- Pan, Q.; Qu, X.; Liu, L.; Dias, D. A sequential sparse polynomial chaos expansion using Bayesian regression for geotechnical reliability estimations. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 874–889. [Google Scholar] [CrossRef]
- Zou, J.F.; Qian, Z.H.; Xiang, X.H.; Chen, G.H. Face stability of a tunnel excavated in saturated nonhomogeneous soils. Tunn. Undergr. Space Technol. 2019, 83, 1–17. [Google Scholar] [CrossRef]
- Zou, J.; Chen, G.; Qian, Z. Tunnel face stability in cohesion-frictional soils considering the soil arching effect by improved failure models. Comput. Geotech. 2019, 106, 1–17. [Google Scholar] [CrossRef]
- Chen, G.H.; Zou, J.F.; Qian, Z.H. An improved collapse analysis mechanism for the face stability of shield tunnel in layered soils. Geomech. Eng. 2019, 17, 97–107. [Google Scholar]
- Qian, Z.H.; Zou, J.F.; Pan, Q.J. 3D Discretized Rotational Failure Mechanism for Slope Stability Analysis. Int. J. Geomech. 2021, 21, 04021210. [Google Scholar] [CrossRef]
- Chen, G.H.; Zou, J.F.; Chen, J.Q. Shallow tunnel face stability considering pore water pressure in non-homogeneous and anisotropic soils. Comput. Geotech. 2019, 116, 103205. [Google Scholar] [CrossRef]
- Qian, Z.H.; Wei, X.X.; Huang, Q.; Zou, J.F. Earth Pressure Estimation of Undrained Soil–Wall Systems with Head Rotation. Int. J. Geomech. 2022, 22, 04022081. [Google Scholar] [CrossRef]
- Chen, R.P.; Tang, L.J.; Yin, X.S.; Chen, Y.M.; Bian, X.C. An improved 3D wedge-prism model for the face stability analysis of the shield tunnel in cohesionless soils. Acta Geotech. 2014, 10, 683–692. [Google Scholar] [CrossRef]
- Guang-hui, C.; Jin-feng, Z.; Qi, M.; Wu-jun, G.; Tai-zhong, Z. Face stability analysis of a shallow square tunnel in non-homogeneous soils. Comput. Geotech. 2019, 114, 103112. [Google Scholar] [CrossRef]
- Xie, X.; Zhao, M.; Shahrour, I. Face stability model for rectangular large excavations reinforced by pipe roofing. Tunn. Undergr Space Technol. 2019, 94, 103132. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. Upper-bound analysis on the face stability of a non-circular tunnel. Tunn. Undergr. Space Technol. 2017, 62, 96–102. [Google Scholar] [CrossRef]
- Hoek, E. Hoek-Brown Failure Criterion-2002 Edition. In Proceedings of the 5th North American Rock Mechanics Symposium, Toronto, ON, Canada, 7–10 July 2002; Volume 1, pp. 18–22. [Google Scholar]
- Priest, S.D. Determination of Shear Strength and Three-dimensional Yield Strength for the Hoek-Brown Criterion. Rock Mech. Rock Eng. 2005, 38, 299–327. [Google Scholar] [CrossRef]
- Yang, X.L.; Li, L.; Yin, J.H. Seismic and static stability analysis of rock slopes by a kinematical approach. Géotechnique 2004, 54, 542–549. [Google Scholar] [CrossRef]
- Li, P.; Chen, K.; Wang, F.; Li, Z. An upper-bound analytical model of blow-out for a shallow tunnel in sand considering the partial failure within the face. Undergr. Space Technol. 2019, 91, 102989. [Google Scholar] [CrossRef]
- Li, T.Z.; Yang, X.L. Three-dimensional face stability of shallow-buried tunnels with tensile strength cut-off. Comput. Geotech. 2019, 110, 82–93. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C. Face Stability Analysis for a Shield Tunnel in Anisotropic Sands. Int. J. Geomech. 2020, 20, 04020043. [Google Scholar] [CrossRef]
- Qian, Z.; Zou, J.; Tian, J.; Pan, Q. Estimations of active and passive earth thrusts of non-homogeneous frictional soils using a discretisation technique. Comput. Geotech. 2020, 119, 103366. [Google Scholar] [CrossRef]
- Qian, Z.; Zou, J.; Pan, Q.; Dias, D. Safety factor calculations of a tunnel face reinforced with umbrella pipes: A comparison analysis. Eng. Struct. 2019, 199, 109639. [Google Scholar] [CrossRef]
- Hoek, E.; Diederichs, M.S. Empirical estimation of rock mass modulus. Int. J. Rock Mech. Min. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Vásárhelyi, B. A possible method for estimating the Poisson’s rate values of the rock masses. Acta Geod. Geophys. 2009, 44, 313–322. [Google Scholar] [CrossRef]
- Chen, G.; Zou, J.; Liu, S. Stability Analysis of Pressurized 3D Tunnel Face with Tensile Strength Cutoff. Int. J. Geomech. 2021, 21, 04021226. [Google Scholar] [CrossRef]
- Senent, S.; Mollon, G.; Jimenez, R. Tunnel face stability in heavily fractured rock masses that follow the Hoek–Brown failure criterion. Int. J. Rock Mech. Min. 2013, 60, 440–451. [Google Scholar] [CrossRef]
- Zhang, G.H.; Zhang, B. Reliability analysis for seismic stability of tunnel faces in soft rock masses based on a 3D stochas-tic collapse model. J. Cent. South Univ. 2019, 26, 1706–1718. [Google Scholar] [CrossRef]
- Zhao, L.H.; Li, D.J.; Yang, F.; Li, L.; Cheng, X. Dimensionless Parameter Diagrams for the Active and Passive Stability of a Shallow 3D Tunnel Face. KSCE J. Civ. Eng. 2019, 23, 866–878. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Tan, Z.; Ma, M. Effect of the seepage flow on the face stability of a shield tunnel. Undergr. Space Technol. 2021, 112, 103900. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhang, Q.; Liu, A.; Chen, G. Stability Analysis of the Horseshoe Tunnel Face in Rock Masses. Materials 2022, 15, 4306. https://doi.org/10.3390/ma15124306
Liu J, Zhang Q, Liu A, Chen G. Stability Analysis of the Horseshoe Tunnel Face in Rock Masses. Materials. 2022; 15(12):4306. https://doi.org/10.3390/ma15124306
Chicago/Turabian StyleLiu, Jun, Qingsong Zhang, An Liu, and Guanghui Chen. 2022. "Stability Analysis of the Horseshoe Tunnel Face in Rock Masses" Materials 15, no. 12: 4306. https://doi.org/10.3390/ma15124306
APA StyleLiu, J., Zhang, Q., Liu, A., & Chen, G. (2022). Stability Analysis of the Horseshoe Tunnel Face in Rock Masses. Materials, 15(12), 4306. https://doi.org/10.3390/ma15124306




