Thermal Hazard Evaluation of Tert-Butyl Peroxy-3,5,5-trimethylhexanoate (TBPTMH) Mixed with Acid-Alkali
Abstract
:1. Introduction
2. Materials and Methods
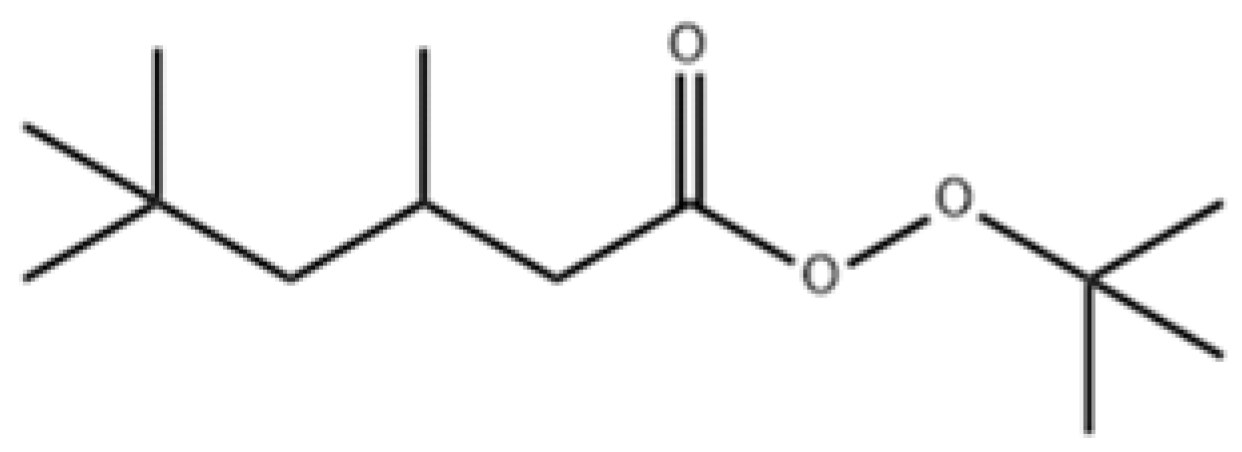
2.1. Sample Preparation
2.2. Differential Scanning Calorimetry
2.3. Adiabatic Calorimetry
2.4. Thermodynamic Analysis
2.4.1. Starink Method
2.4.2. Correction of Adiabatic Data
2.4.3. Adiabatic Dynamics Calculation
2.4.4. Thermal Decomposition Reaction Mechanism Function
2.5. Calculation of Thermal Decomposition Characteristic Parameters
2.5.1. Calculation of TMRad
2.5.2. Calculation of SADT
3. Results and Discussion
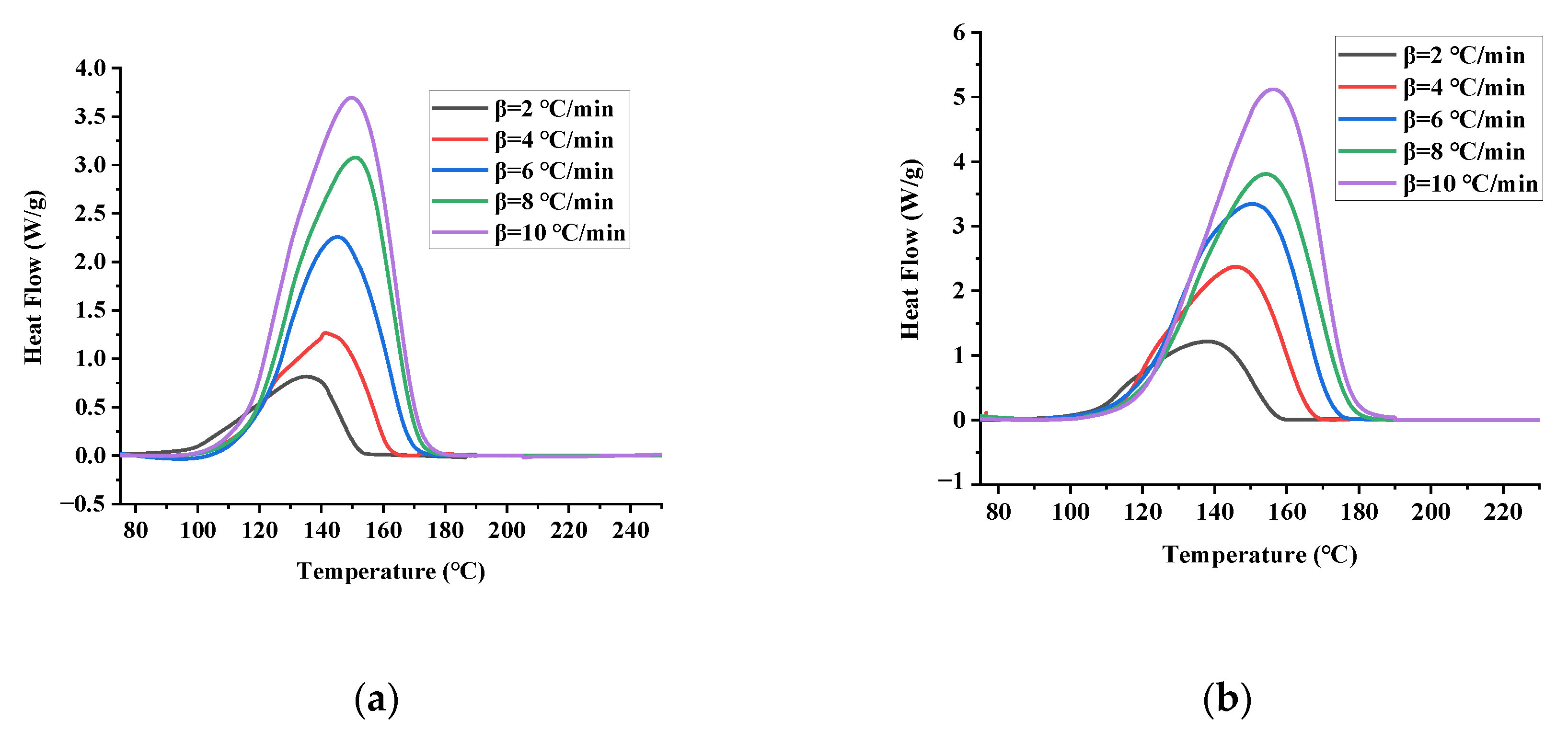
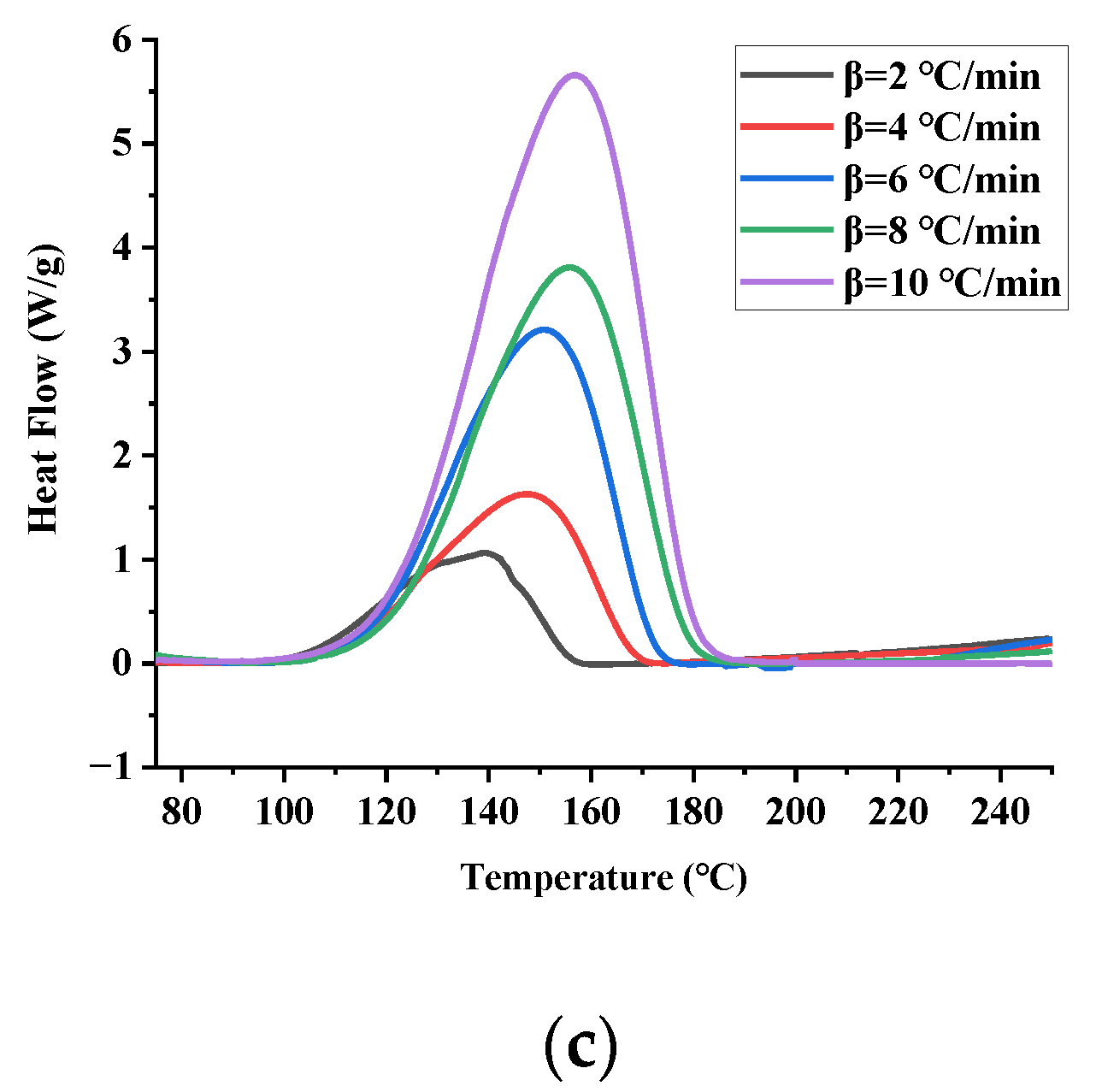
3.1. DSC Experiments
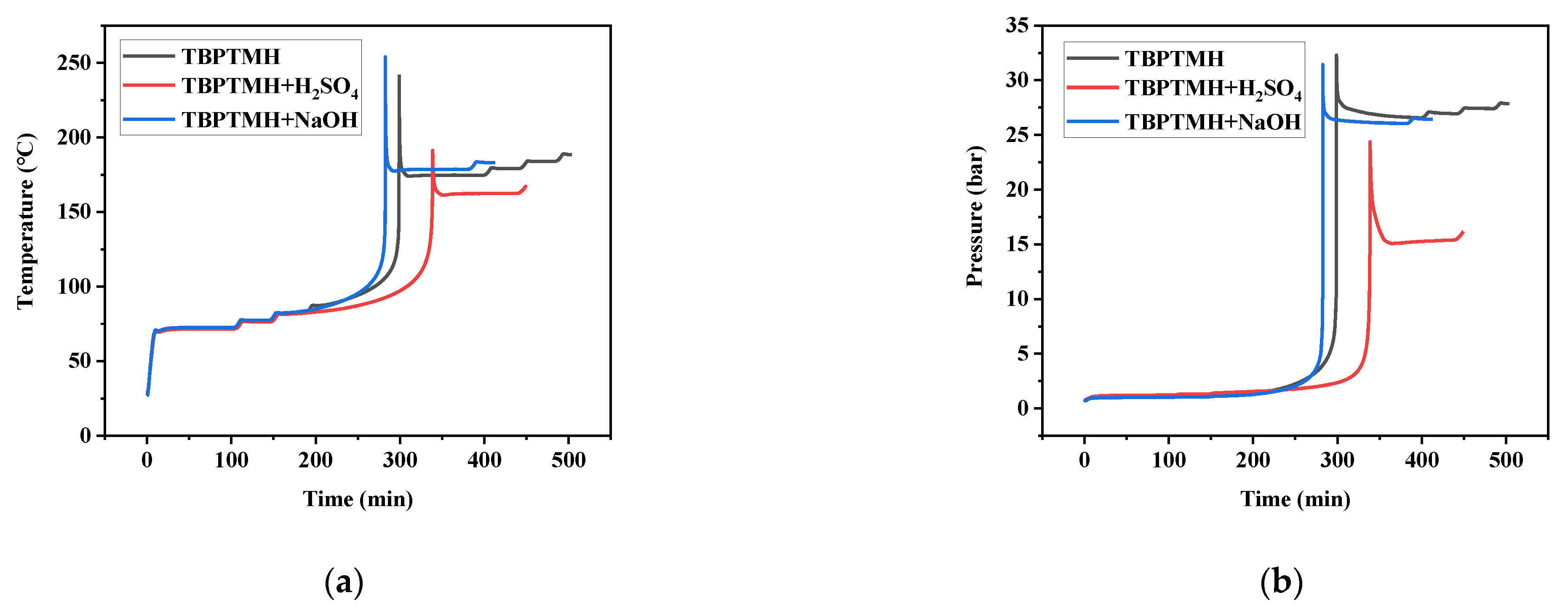
3.2. Phi-TEC II Experiments
3.3. Thermodynamic Analysis
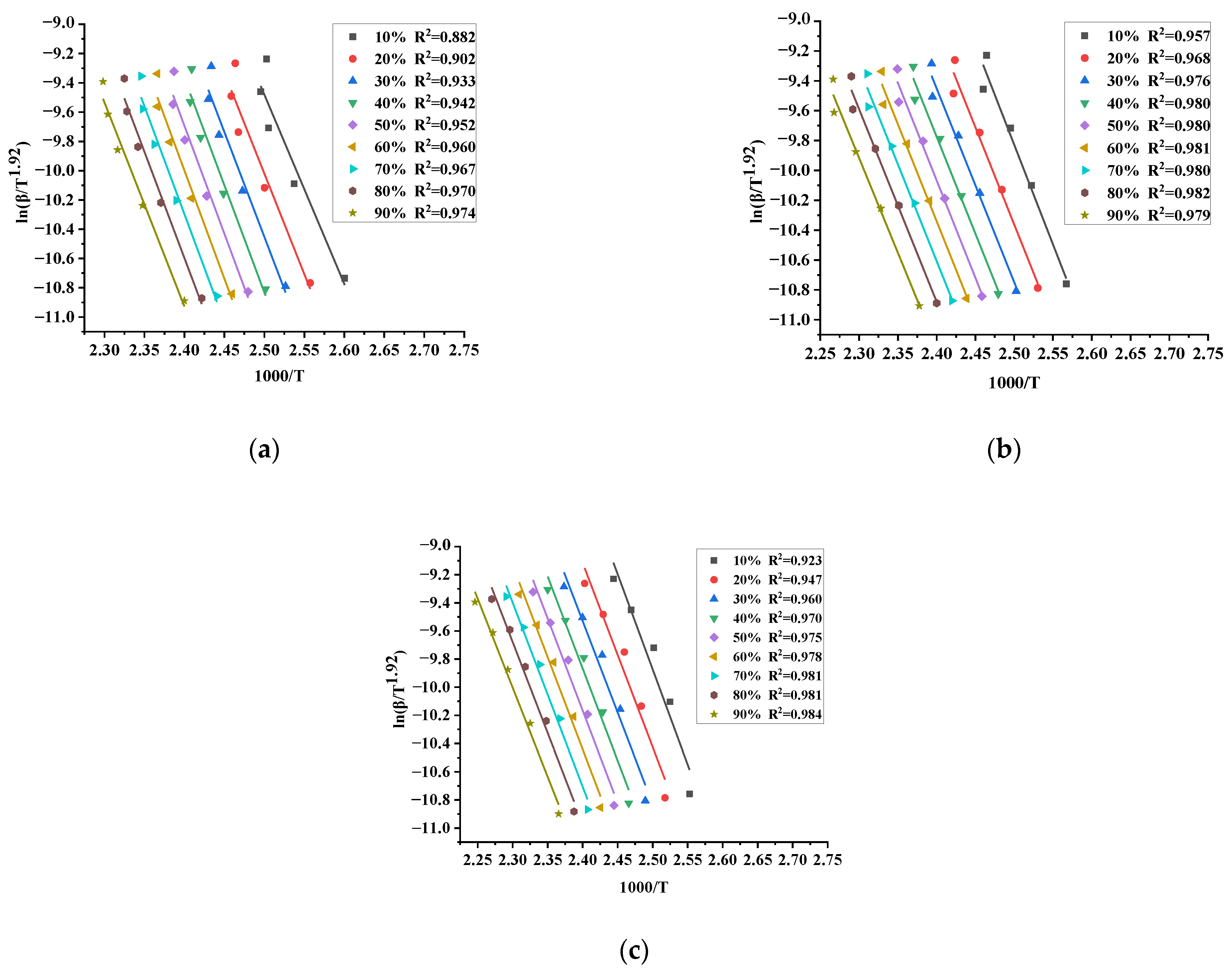
3.3.1. Starink Method
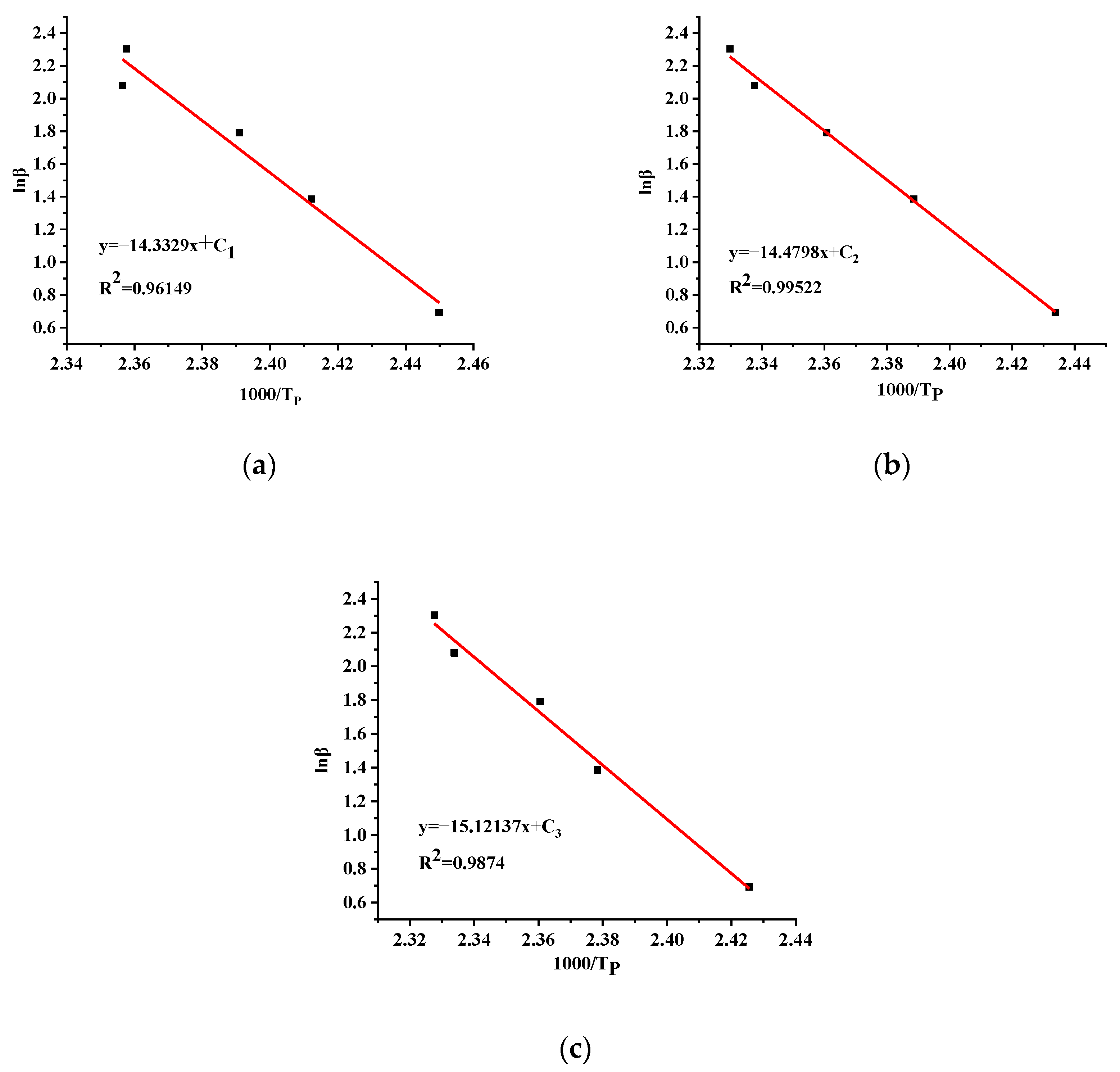
3.3.2. Correction of Adiabatic Data
3.3.3. Adiabatic Kinetic Calculation
3.3.4. Thermal Decomposition Reaction Mechanism Function
3.4. Thermal Decomposition Characteristic Parameters Calculation
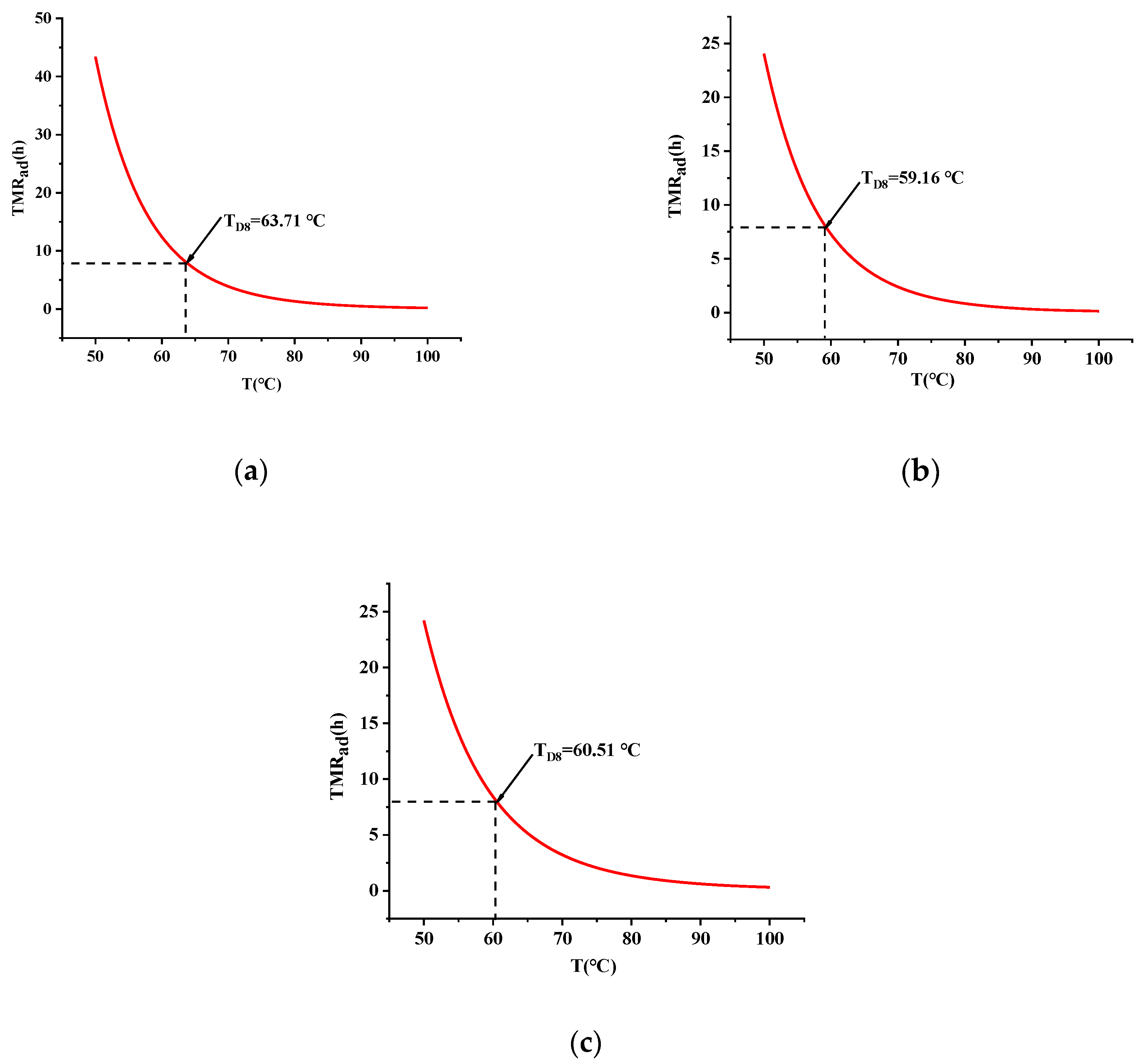
3.4.1. TMRad Calculation Results
3.4.2. SADT Calculation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Pre-exponential factor (s−1) |
| β | Heating rate (°C/min) |
| Cvb | Specific heat capacity of the sample ball (J g−1 K−1) |
| Cvs | Specific heat capacity of the sample (J g−1 K−1) |
| DSC | Differential scanning calorimetry |
| (dT/dt)max | Maximum temperature rise rate (°C min−1) |
| (dP/dt)max | Maximum pressure rise rate (bar min−1) |
| Ea | Activation energy (kJ mol−1) |
| G(α) | Denotes the mechanism |
| ΔH | Heat of decomposition |
| k | Rate constant |
| Mb | Mass of the sample ball (g) |
| Ms | Mass of the sample (g) |
| Phi-TEC II | Adiabatic calorimetry |
| Pmax | Maximum pressure (bar) |
| R | Gas constant (8.314 J mol−1 K−1) |
| S | Surface area of packaging (m2) |
| SADT | Self-accelerated decomposition temperature (°C) |
| T | Reaction temperature (°C) |
| ∆Tad | The adiabatic temperature rise (°C) |
| Tend | Ending temperature (°C) |
| Tf | The maximum decomposition temperature under adiabatic conditions (°C) |
| TMRad | Time to maximum rate under adiabatic conditions (h) |
| TNR | The critical non-return temperature (°C) |
| TP | Peak temperature (°C) |
| U | Surface heat transfer coefficient (J m−2 K−1) |
| ∅ | Thermal inertia factor |
References
- Chen, C.C.; Duh, Y.S.; Shu, C.M. Thermal polymerization of uninhibited styrene investigated by using microcalorimetry. J. Hazard. Mat. 2009, 163, 1385–1390. [Google Scholar] [CrossRef]
- Liu, S.H.; Hou, H.Y.; Chen, J.W.; Weng, S.Y.; Lin, Y.C.; Shu, C.M. Effects of thermal runaway hazard for three organic peroxides conducted by acids and alkalines with DSC, VSP2, and TAM III. Thermochim. Acta 2013, 566, 226–232. [Google Scholar] [CrossRef]
- Lee, M.H.; Chen, J.R.; Shiue, G.Y.; Lin, Y.F.; Shu, C.M. Simulation approach to benzoyl peroxide decomposition kinetics by thermal calorimetric technique. J. Taiwan Inst. Chem. E 2014, 45, 115–120. [Google Scholar] [CrossRef]
- Di Somma, I.; Marotta, R.; Andreozzi, R.; Caprio, V. Kinetic and chemical characterization of thermal decomposition of dicumylperoxide in cumene. J. Hazard. Mat. 2011, 187, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.C.; Shu, C.M. Prediction of thermal hazard for TBPTMH mixed with BPO through DSC and isoconversional kinetics analysis. J. Therm. Anal. Calorim. 2016, 126, 1937–1945. [Google Scholar] [CrossRef]
- Chen, W.C.; Yeh, C.T.; Shu, C.M. Incompatible effects of specific acids on the thermokinetics of 1,1-bis(tert-butylperoxy)-3,3,5-trimethylcyclohexane. J. Therm. Anal. Calorim. 2019, 135, 2747–2757. [Google Scholar] [CrossRef]
- Yang, Y.; Tsai, Y.T.; Cao, C.R.; Shu, C.M. Kinetic and thermal safety analysis for tert-butyl peroxy-3,5,5-trimethylhexanoate by advanced calorimetric technology. J. Therm. Anal. Calorim. 2017, 127, 2253–2262. [Google Scholar] [CrossRef]
- Tseng, J.M.; Chang, R.H.; Horng, J.J.; Chang, M.K.; Shu, C.M. Thermal hazard evaluation for methyl ethyl ketone peroxide mixed with inorganic acid. J. Therm. Anal. Calorim. 2006, 85, 189–194. [Google Scholar] [CrossRef]
- You, M.L.; Tseng, J.M.; Liu, M.Y.; Shu, C.M. Runaway reaction of lauroyl peroxide with nitric acid by DSC. J. Therm. Anal. Calorim. 2010, 102, 535–539. [Google Scholar] [CrossRef]
- Roduit, B.; Borgeat, C.; Berger, B.; Folly, P.; Andres, H.; Schadeli, U.; Vogelsanger, B. Up-scaling of DSC data of high energetic materials—Simulation of cook-off experiments. J. Therm. Anal. Calorim. 2006, 85, 195–202. [Google Scholar] [CrossRef]
- Liu, S.H.; Hou, H.Y.; Shu, C.M. Thermal hazard evaluation of the autocatalytic reaction of benzoyl peroxide using DSC and TAM III. Thermochim. Acta 2015, 605, 68–76. [Google Scholar] [CrossRef]
- Li, X.R.; Koseki, H. Study on the early stage of runaway reaction using Dewar vessels. J. Loss Prev. Process Ind. 2005, 18, 455–459. [Google Scholar] [CrossRef]
- Zhang, Y.; Ni, L.; Jiang, J.C.; Jiang, J.; Zhang, W.X.; Jiang, J.J.; Zhang, M.G. Thermal hazard analyses for the synthesis of benzoyl peroxide. J. Loss Prev. Process Ind. 2016, 43, 35–41. [Google Scholar] [CrossRef]
- Wu, S.H.; Shyu, M.L.; Yet-Pole, I.; Chi, J.H.; Shu, C.M. Evaluation of runaway reaction for dicumyl peroxide in a batch reactor by DSC and VSP2. J. Loss Prev. Process Ind. 2009, 22, 721–727. [Google Scholar] [CrossRef]
- Liu, X.H.; Zhu, S.B.; Zhu, X.Z.; Wu, X.L. Hazard Assessment of Hydrogen Peroxide with Polyphosphonic Acid by Vent Sizing Package 2. Procedia Eng. 2014, 84, 427–435. [Google Scholar]
- Wu, S.H.; Wu, J.Y.; Wu, Y.T.; Lee, J.C.; Huang, Y.H.; Shu, C.M. Explosion evaluation and safety storage analyses of cumene hydroperoxide using various calorimeters. J. Therm. Anal. Calorim. 2013, 111, 669–675. [Google Scholar] [CrossRef]
- Elder, J.P. The ‘E-ln(A)-f(alpha)’ triplet in non-isothermal reaction kinetics analysis. Thermochim. Acta 1998, 318, 229–238. [Google Scholar] [CrossRef]
- Wan, H.B.; Huang, Z. Kinetic Analysis of Pyrolysis and Thermo-Oxidative Decomposition of Tennis String Nylon Wastes. Materials 2021, 14, 7564. [Google Scholar] [CrossRef]
- Ab Rahim, A.H.; Abd Ghani, N.; Hasanudin, N.; Yunus, N.M.; Azman, N.S. Thermal Kinetics of Monocationic and Dicationic Pyrrolidinium-Based Ionic Liquids. Materials 2022, 15, 1247. [Google Scholar] [CrossRef] [PubMed]
- Arranz, J.I.; Miranda, M.T.; Montero, I.; Sepulveda, F.J. Thermal Study and Emission Characteristics of Rice Husk Using TG-MS. Materials 2021, 14, 6203. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Dang, J.; Hu, X.J.; Yan, H.Y. Reduction Kinetics of Hematite Powder in Hydrogen Atmosphere at Moderate Temperatures. Materials 2018, 8, 751. [Google Scholar] [CrossRef] [Green Version]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Ni, L.; Yao, H.; Yao, X.; Jiang, J.; Wang, Z.; Shu, C.M.; Pan, Y. Thermal hazard analysis and initial decomposition mechanism of 5-(4-pyridyl)tetrazolate-methylene tetrazole. Fuel 2020, 269, 117434. [Google Scholar] [CrossRef]
- Townsend, D.I.; Tou, J.C. Thermal hazard evaluation by an accelerating rate calorimeter. Thermochim. Acta 1980, 37, 1–30. [Google Scholar] [CrossRef]
- Fu, Z.M.; Li, X.R.; Koseki, H.; Mok, Y.S. Evaluation on thermal hazard of methylethyl ketone peroxide by using adiabatic method. J. Loss Prev. Process Ind. 2003, 16, 389–393. [Google Scholar] [CrossRef]
- Liu, S.H.; Zhan, X.B.; Lu, Y.M.; Xu, Z.L.; Wu, T. Thermal hazard evaluation of AIBME by micro-calorimetric technique coupled with kinetic investigation. J. Therm. Anal. Calorim. 2020, 141, 1443–1452. [Google Scholar] [CrossRef]
- Chi, J.H.; Wu, S.H.; Charpentier, J.C.; Yet-Pole, I.; Shu, C.M. Thermal hazard accident investigation of hydrogen peroxide mixing with propanone employing calorimetric approaches. J. Loss Prev. Process Ind. 2012, 25, 142–147. [Google Scholar] [CrossRef]
- Chen, J.P.; Isa, K. Thermal Decomposition of Urea and Urea Derivatives by Simultaneous TG/(DTA)/MS. J. Mass Spectrom. Soc. Jpn. 2007, 46, 299–303. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N. Determination of pre-exponential factors and of the mathematical functions f(alpha) or G(alpha) that describe the reaction mechanism in a model-free way. Thermochim. Acta 2013, 564, 59–69. [Google Scholar] [CrossRef]
- Guo, S.; Jia, M.; Qi, X.; Wan, W. Kinetic Mechanism and Effects of Molecular Structure on Thermal Hazards of Azo Compounds. J. Loss Prev. Process Ind. 2020, 66, 104207. [Google Scholar] [CrossRef]
- Trache, D.; Abdelaziz, A.; Siouani, B. A simple and linear isoconversional method to determine the pre-exponential factors and the mathematical reaction mechanism functions. J. Therm. Anal. Calorim. 2017, 128, 335–348. [Google Scholar] [CrossRef]
- Tou, J.C.; Whiting, L.F. The thermokinetic performance of an accelerating rate calorimeter. Thermochim. Acta 1981, 48, 21–42. [Google Scholar] [CrossRef]
- Kotoyori, T. Procedure to calculate the SADT for a powdery chemical of the quasi-AC type having an arbitrary shape an arbitrary size confined in an arbitrary closed container of the corresponding shapesize placed in the atmosphere under isothermal conditions. Ind. Saf. Ser. 2005, 7, 341–365. [Google Scholar]
- Yang, D.; Koseki, H.; Hasegawa, K. Predicting the self-accelerating decomposition temperature (SADT) of organic peroxides based on non-isothermal decomposition behavior. J. Loss Prev. Process Ind. 2002, 16, 411–416. [Google Scholar] [CrossRef]


| Author | Organic Peroxides | Experimental Equipment | Additives |
|---|---|---|---|
| Yang et al. [7] | TBPTMH | DSC | / |
| Chen et al. [5] | TBPTMH | DSC | BPO |
| Tseng et al. [8] | MEKPO | VSP2, DSC | HCl, HNO3, H3PO4, H2SO4 |
| Liu et al. [2] | CHP, BPO, DCPO | DSC, TAM III, VSP2 | H2SO4, NaOH, Na2SO3 |
| You et al. [9] | LPO | DSC | HNO3 |
| No. | No. | No. | |||
|---|---|---|---|---|---|
| 1 | 15 | 29 | |||
| 2 | 16 | 30 | |||
| 3 | 17 | 31 | |||
| 4 | 18 | 32 | |||
| 5 | 19 | 33 | |||
| 6 | 20 | 34 | |||
| 7 | 21 | 35 | |||
| 8 | 22 | 36 | |||
| 9 | 23 | 37 | |||
| 10 | 24 | 38 | |||
| 11 | 25 | 39 | |||
| 12 | 26 | 40 | |||
| 13 | 27 | / | / | ||
| 14 | 28 | / | / |
| Sample | Mass (mg) | T0 (°C) | Tp (°C) | Tend (°C) | ΔH (J/g) | |
|---|---|---|---|---|---|---|
| TBPTMH | 2 | 1.48 | 109.39 | 135.03 | 151.40 | 741.75 |
| 4 | 1.45 | 113.75 | 141.40 | 161.53 | 600.77 | |
| 6 | 1.45 | 118.32 | 145.10 | 168.00 | 743.98 | |
| 8 | 1.46 | 124.42 | 155.89 | 177.83 | 609.52 | |
| 10 | 1.52 | 125.67 | 155.78 | 178.07 | 741.08 | |
| TBPTMH + H2SO4 | 2 | 1.46 | 88.80 | 137.74 | 172.62 | 792.76 |
| 4 | 1.54 | 112.74 | 145.51 | 165.77 | 774.44 | |
| 6 | 1.50 | 119.02 | 150.44 | 172.12 | 804.83 | |
| 8 | 1.48 | 120.23 | 154.63 | 175.57 | 672.57 | |
| 10 | 1.52 | 121.89 | 156.07 | 176.98 | 712.87 | |
| TBPTMH + NaOH | 2 | 1.48 | 111.41 | 139.13 | 141.62 | 677.38 |
| 4 | 1.52 | 114.48 | 147.30 | 167.55 | 542.19 | |
| 6 | 1.52 | 118.16 | 150.48 | 171.48 | 715.07 | |
| 8 | 1.53 | 122.36 | 155.33 | 177.75 | 666.46 | |
| 10 | 1.49 | 122.91 | 156.47 | 179.56 | 831.12 |
| Sample | T0 (°C) | Tp (°C) | ΔTad (°C) | (dT/dt)max (°C/min) | (dP/dt)max (bar/min) | Pmax (bar) |
|---|---|---|---|---|---|---|
| TBPTMH | 87.68 | 242.1 | 154.42 | 167.9 | 137.93 | 32.3 |
| TBPTMH + H2SO4 | 81.58 | 191.24 | 109.66 | 61.77 | 49.21 | 24.37 |
| TBPTMH + NaOH | 83.20 | 253.98 | 170.78 | 192.85 | 168.36 | 31.43 |
| Ea (kJ/mol) | α | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | Average | |
| TBPTMH | 126.79 | 132.77 | 134.86 | 136.61 | 136.28 | 135.21 | 133.57 | 131.10 | 125.22 | 132.49 |
| TBPTMH + H2SO4 | 122.60 | 117.84 | 116.22 | 115.72 | 116.26 | 115.53 | 115.41 | 114.52 | 113.12 | 116.36 |
| TBPTMH + NaOH | 128.47 | 121.45 | 119.04 | 118.28 | 117.46 | 116.94 | 116.12 | 114.74 | 111.71 | 118.24 |
| Sample | T0 (°C) | Tp (°C) | ΔTad (°C) | dT/dtmax (°C/min) | dP/dtmax (bar/min) | |
|---|---|---|---|---|---|---|
| TBPTMH | 4.23 | 76.06 | 577.14 | 653.20 | 710.22 | 583.44 |
| TBPTMH + H2SO4 | 4.22 | 69.00 | 393.77 | 462.77 | 260.67 | 207.67 |
| TBPTMH + NaOH | 4.22 | 70.68 | 650.01 | 720.69 | 813.83 | 710.48 |
| Sample | Ea (kJ/mol) | A (1/s) | n |
|---|---|---|---|
| TBPTMH | 129.98 | 4.92 × 1016 | 2.6 |
| TBPTMH + H2SO4 | 115.47 | 8.73 × 1013 | 1 |
| TBPTMH + NaOH | 117.70 | 4.74 × 1014 | 2.3 |
| No. | Ea (kJ/mol) | R2 | No. | Ea (kJ/mol) | R2 |
|---|---|---|---|---|---|
| 1 | 164.22 | 0.9518 | 17 | 182.29 | 0.9952 |
| 2 | 186.10 | 0.9702 | 18 | 245.47 | 0.9953 |
| 13 | 56.21 | 0.9943 | 25 | 78.67 | 0.9479 |
| 15 | 87.75 | 0.9948 | 27 | 164.22 | 0.9518 |
| 16 | 119.30 | 0.9950 | 31 | 96.89 | 0.9784 |
| No. | Ea (kJ/mol) | R2 | No. | Ea (kJ/mol) | R2 |
|---|---|---|---|---|---|
| 2 | 185.17 | 0.9696 | 16 | 118.75 | 0.9951 |
| 3 | 44.70 | 0.9744 | 17 | 181.60 | 0.9953 |
| 13 | 55.90 | 0.9944 | 25 | 78.22 | 0.9469 |
| 14 | 76.85 | 0.9948 | 26 | 120.80 | 0.9497 |
| 15 | 87.33 | 0.9949 | 37 | 162.59 | 0.9854 |
| No. | Ea (kJ/mol) | R2 | No. | Ea (kJ/mol) | R2 |
|---|---|---|---|---|---|
| 2 | 186.79 | 0.9729 | 16 | 119.66 | 0.9963 |
| 3 | 45.13 | 0.9778 | 17 | 182.96 | 0.9965 |
| 13 | 56.35 | 0.9958 | 25 | 78.97 | 0.9514 |
| 14 | 77.46 | 0.9961 | 26 | 121.94 | 0.9539 |
| 15 | 88.01 | 0.9962 | 37 | 166.37 | 0.9866 |
| Sample | Packing Mass (kg) | TNR (°C) | SADT (°C) |
|---|---|---|---|
| TBPTMH | 10 | 64.89 | 57.58 |
| 25 | 62.45 | 55.25 | |
| 50 | 60.02 | 52.92 | |
| TBPTMH + H2SO4 | 10 | 60.00 | 52.01 |
| 25 | 57.84 | 49.95 | |
| 50 | 56.49 | 48.67 | |
| TBPTMH + NaOH | 10 | 59.81 | 51.98 |
| 25 | 57.45 | 49.73 | |
| 50 | 55.53 | 47.90 |
| SADT (°C) | Control Temperature (°C) | Alarm Temperature (°C) |
|---|---|---|
| SADT < 20 | <20 | SADT-10 |
| 20 ≤ SADT ≤ 35 | SADT-15 | SADT-10 |
| SADT > 35 | SADT-10 | SADT-5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, L.; Ni, L.; Pan, Y.; Zhang, X.; Ni, Y. Thermal Hazard Evaluation of Tert-Butyl Peroxy-3,5,5-trimethylhexanoate (TBPTMH) Mixed with Acid-Alkali. Materials 2022, 15, 4281. https://doi.org/10.3390/ma15124281
Xia L, Ni L, Pan Y, Zhang X, Ni Y. Thermal Hazard Evaluation of Tert-Butyl Peroxy-3,5,5-trimethylhexanoate (TBPTMH) Mixed with Acid-Alkali. Materials. 2022; 15(12):4281. https://doi.org/10.3390/ma15124281
Chicago/Turabian StyleXia, Li, Lei Ni, Yong Pan, Xin Zhang, and Yuqing Ni. 2022. "Thermal Hazard Evaluation of Tert-Butyl Peroxy-3,5,5-trimethylhexanoate (TBPTMH) Mixed with Acid-Alkali" Materials 15, no. 12: 4281. https://doi.org/10.3390/ma15124281
APA StyleXia, L., Ni, L., Pan, Y., Zhang, X., & Ni, Y. (2022). Thermal Hazard Evaluation of Tert-Butyl Peroxy-3,5,5-trimethylhexanoate (TBPTMH) Mixed with Acid-Alkali. Materials, 15(12), 4281. https://doi.org/10.3390/ma15124281








