Vibration Characteristics of a Laminated Composite Double-Cylindrical Shell System Coupled with a Variable Number of Annular Plates
Abstract
:1. Introduction
2. Analysis Model of the Laminated Composite Double Cylindrical Shell Structure
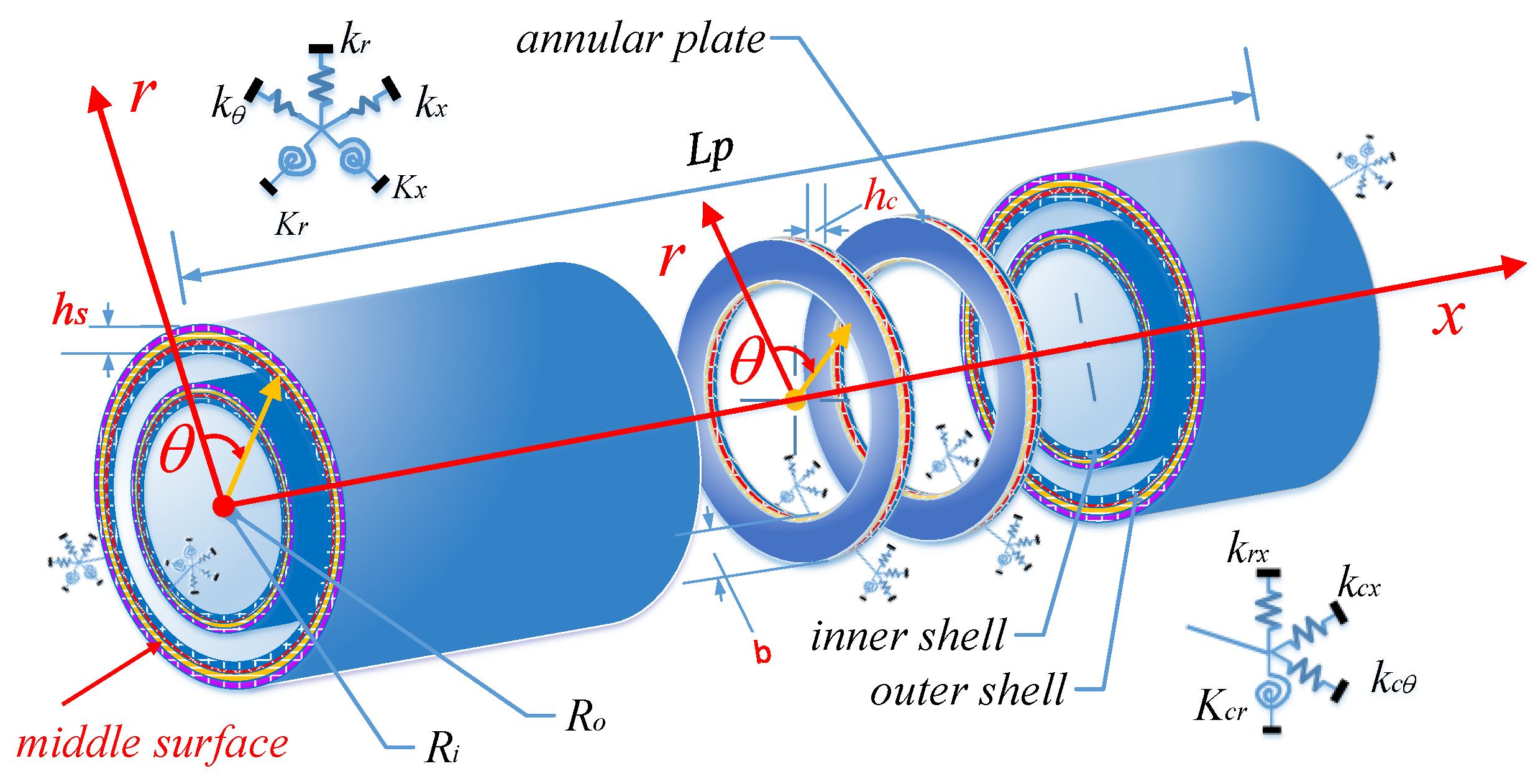
2.1. Description of the Model
2.2. Kinematic Relations and Stress Resultants
2.2.1. For Cylindrical Shell
2.2.2. For Annular Plate
2.3. Energy Expressions
2.4. Displacement Admissible Functions and Solution Process
3. Numerical Calculation and Analysis
3.1. Convergence and Validation Study of the LCDCSS
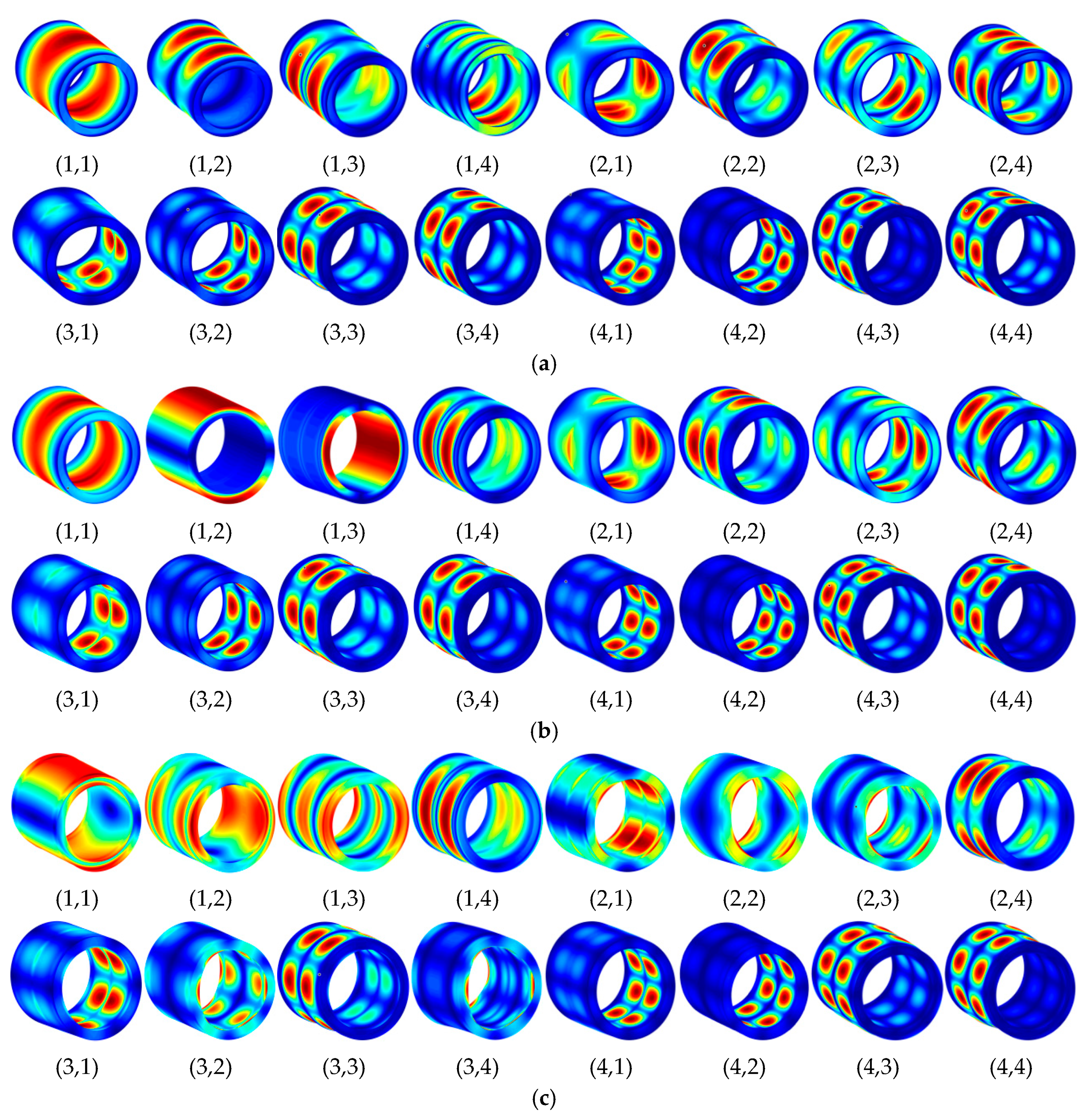
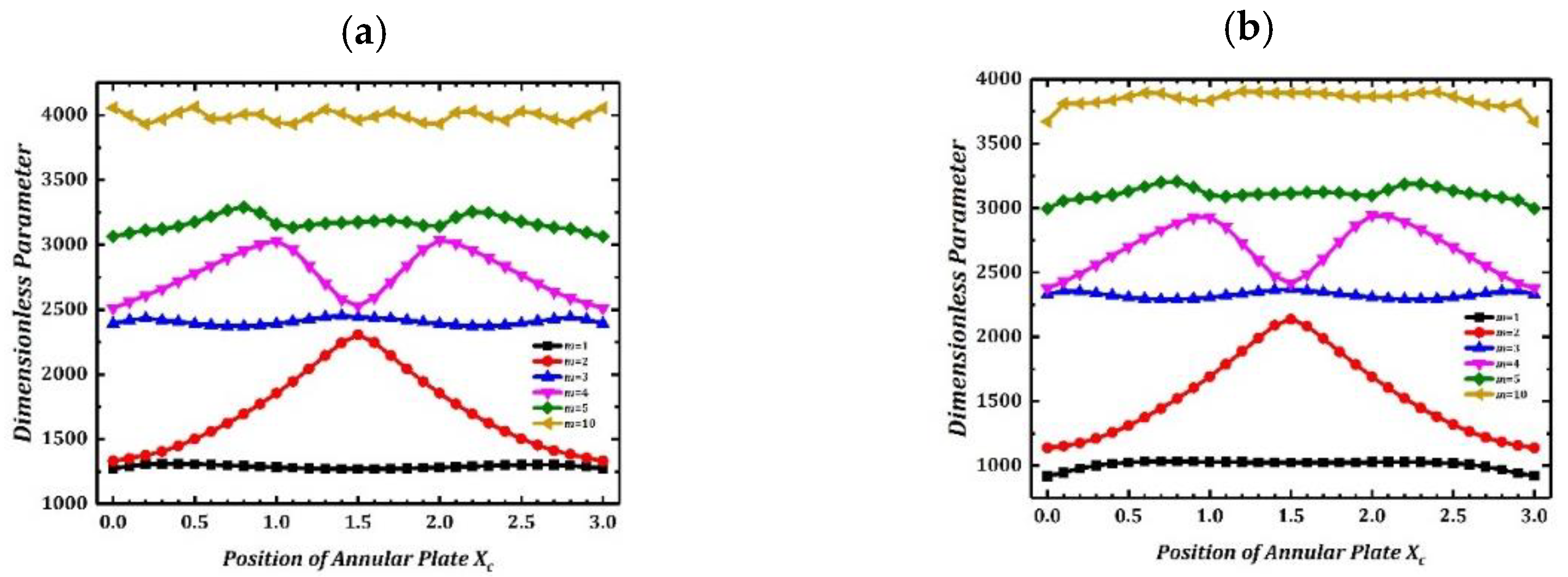
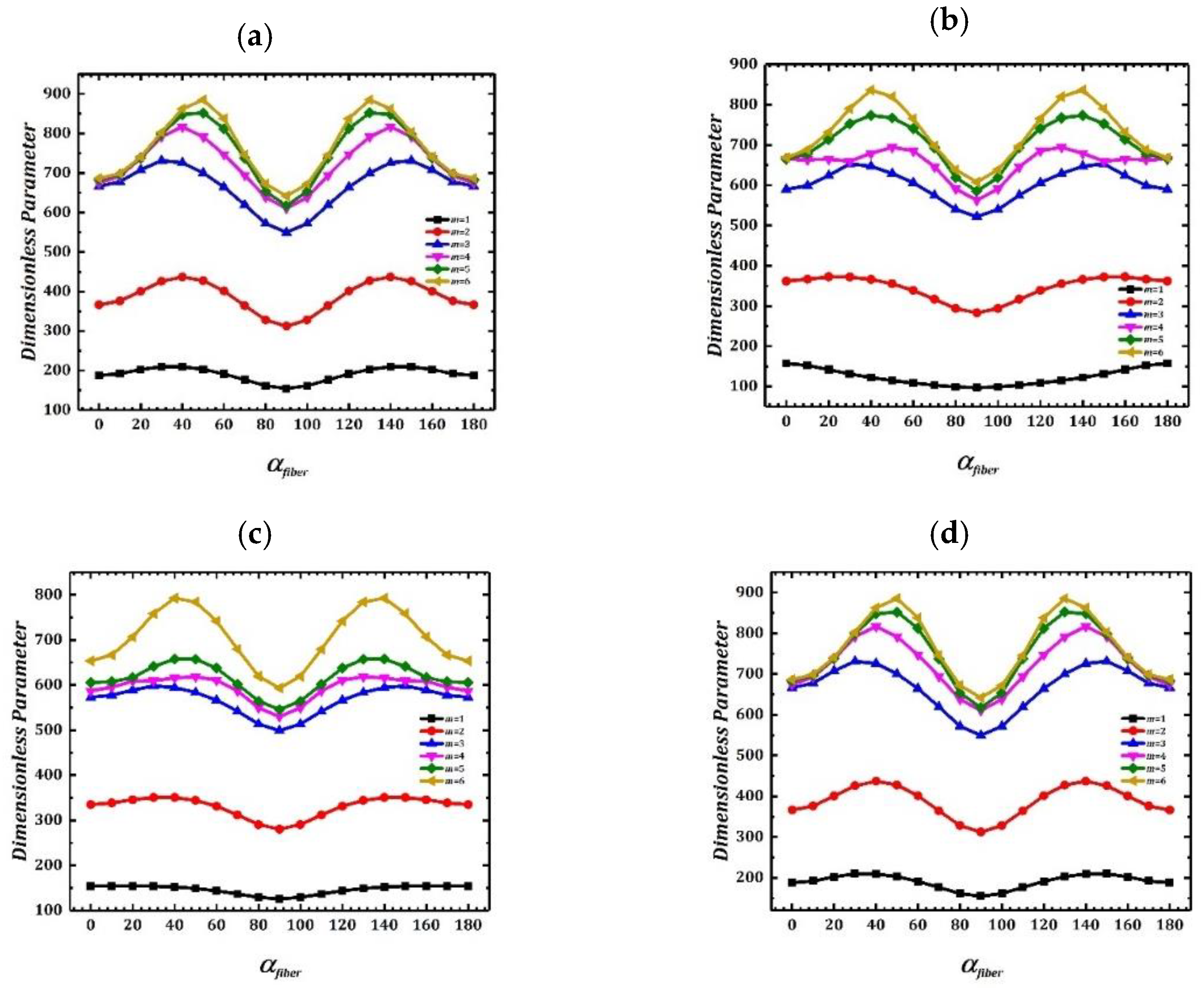
3.2. Free Vibration Analysis of the LCDSS
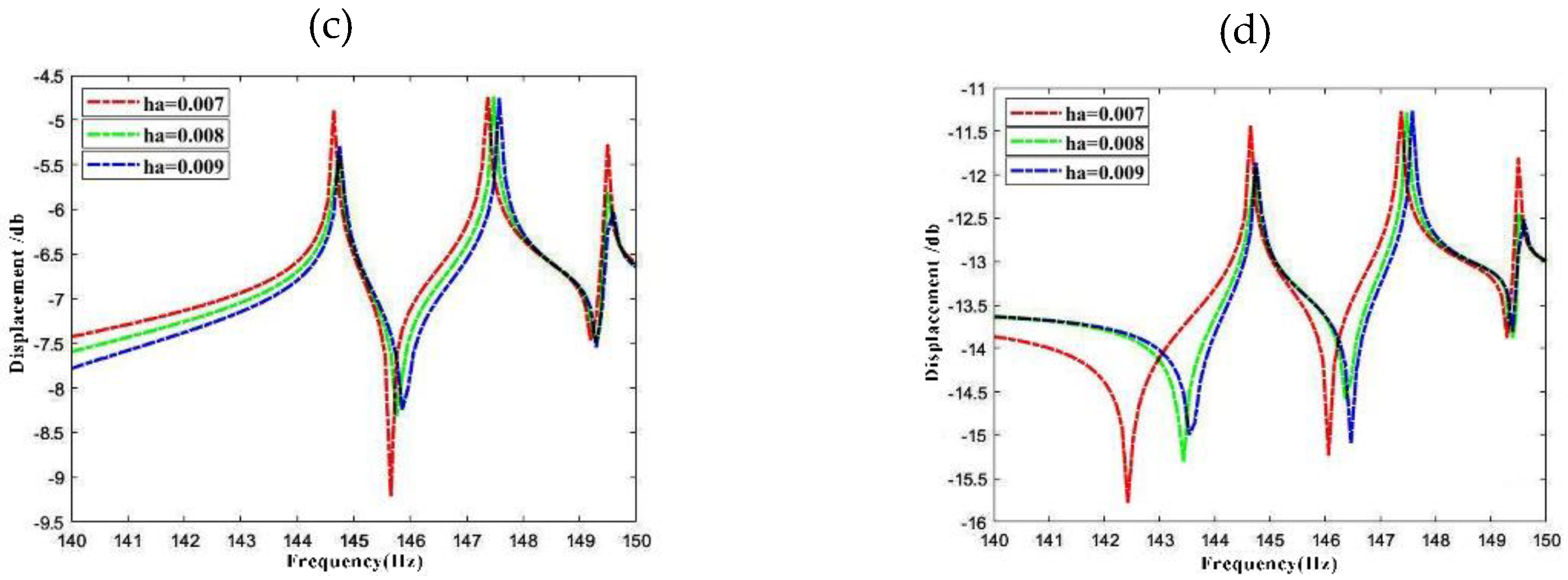
3.3. Steady State Response Analysis of the LCDCSS
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ming, P.; Norton, M. The measurement of structural mobilities of a circular cylindrical shell. J. Acoust. Soc. Am. 2000, 107, 1374–1382. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.J.; Reddy, J. Vibration suppression of laminated shell structures investigated using higher order shear deformation theory. Smart Mater. Struct. 2004, 13, 1176–1194. [Google Scholar] [CrossRef]
- Zhong, R.; Tang, J.; Wang, A.; Shuai, C.; Wang, Q. An exact solution for free vibration of cross-ply laminated composite cylindrical shells with elastic restraint ends. Comput. Math. Appl. 2019, 77, 641–661. [Google Scholar] [CrossRef]
- Hu, X.; Tsuiji, T. Vibration analysis of laminated cylindrical thin panels with twist and curvature. Int. J. Solids Struct. 2001, 38, 2713–2736. [Google Scholar] [CrossRef]
- Qu, Y.; Long, X.; Wu, S.; Meng, G. A unified formulation for vibration analysis of composite laminated shells of revolution including shear deformation and rotary inertia. Compos. Struct. 2013, 98, 169–191. [Google Scholar] [CrossRef]
- Maharjan, A.; Sang-Youl, L. Free Vibration Characteristics of Laminated Composite Cylindrical Shells Reinforced by SWCNT with a Central Cutout. J. Korean Soc. Adv. Compos. Struct. 2019, 10, 15–20. [Google Scholar] [CrossRef]
- Hafizah, A.K.N.; Viswanathan, K.K.; Aziz, Z.A.; Lee, J.H. Vibration of antisymmetric angle-ply composite annular plates of variable thickness. J. Mech. Sci. Technol. 2018, 32, 2155–2162. [Google Scholar] [CrossRef]
- Civalek, O. Vibration analysis of laminated composite conical shells by the method of discrete singular convolution based on the shear deformation theory. Compos. Part B Eng. 2013, 45, 1001–1009. [Google Scholar] [CrossRef]
- Zhao, J.; Choe, K.; Shuai, C.; Wang, A.; Wang, Q. Free vibration analysis of laminated composite elliptic cylinders with general boundary conditions. Compos. Part B Eng. 2019, 158, 55–66. [Google Scholar] [CrossRef]
- He, D.; Shi, D.; Wang, Q.; Shuai, C. Wave based method (WBM) for free vibration analysis of cross-ply composite laminated cylindrical shells with arbitrary boundaries. Compos. Struct. 2019, 213, 284–298. [Google Scholar] [CrossRef]
- Kumar, A.; Bhargava, P.; Chakrabarti, A. Vibration of laminated composite skew hypar shells using higher order theory. Thin-Walled Struct. 2012, 63, 82–90. [Google Scholar] [CrossRef]
- Jin, G.; Ye, T.; Chen, Y.; Su, Z.; Yan, Y. An exact solution for the free vibration analysis of laminated composite cylindrical shells with general elastic boundary conditions. Compos. Struct. 2013, 106, 114–127. [Google Scholar] [CrossRef]
- Jin, G.; Ye, T.; Jia, X.; Gao, S. A general Fourier solution for the vibration analysis of composite laminated structure elements of revolution with general elastic restraints. Compos. Struct. 2014, 109, 150–168. [Google Scholar] [CrossRef]
- Jin, G.; Ye, T.; Ma, X.; Chen, Y.; Su, Z.; Xie, X. A unified approach for the vibration analysis of moderately thick composite laminated cylindrical shells with arbitrary boundary conditions. Int. J. Mech. Sci. 2013, 75, 357–376. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, D.; Liang, Q.; Pang, F. Free vibrations of composite laminated doubly-curved shells and panels of revolution with general elastic restraints. Appl. Math. Model. 2017, 46, 227–262. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, D.; Pang, F.; Liang, Q. Vibrations of Composite Laminated Circular Panels and Shells of Revolution with General Elastic Boundary Conditions via Fourier-Ritz Method. Curved Layer. Struct. 2016, 3, 105–136. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, D.; Liang, Q.; Ahad, F. A unified solution for free in-plane vibration of orthotropic circular, annular and sector plates with general boundary conditions. Appl. Math. Model. 2016, 40, 9228–9253. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E.; Fantuzzi, N. General higher-order equivalent single layer theory for free vibrations of doubly-curved laminated composite shells and panels. Compos. Struct. 2013, 104, 94–117. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Xie, T. Vibration characteristics of a rotating composite laminated cylindrical shell in subsonic air flow and hygrothermal environment. Int. J. Mech. Sci. 2019, 150, 356–368. [Google Scholar] [CrossRef]
- Li, X. Parametric resonances of rotating composite laminated nonlinear cylindrical shells under periodic axial loads and hygrothermal environment. Compos. Struct. 2020, 255, 112887. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, R.; Shi, D.; Wang, Q. A simplified plate theory for vibration analysis of composite laminated sector, annular and circular plate. Thin-Walled Struct. 2019, 143, 106252. [Google Scholar] [CrossRef]
- Zuo, H.; Chen, Y.; Jia, F.; Yang, Z. Unified wavelet finite element formulation for static and vibration analysis of laminated composite shells. Compos. Struct. 2021, 272, 114207. [Google Scholar] [CrossRef]
- Liu, T.; Wang, A.; Wang, Q.; Qin, B. Wave based method for free vibration characteristics of functionally graded cylindrical shells with arbitrary boundary conditions. Thin-Walled Struct. 2019, 148, 19. [Google Scholar] [CrossRef]
- Bisheh, H.; Wu, N.; Rabczuk, T. Free vibration analysis of smart laminated carbon nanotube-reinforced composite cylindrical shells with various boundary conditions in hygrothermal environments. Thin-Walled Struct. 2020, 149, 106500. [Google Scholar] [CrossRef]
- Yamada, G.; Irie, T.; Tamiya, T. Free vibration of a circular cylindrical double-shell system closed by end plates. J. Sound 1986, 108, 297–304. [Google Scholar] [CrossRef]
- Yuan, J.; Dickinson, S.M. The Free Vibration of Circularly Cylindrical Shell and Plate Systems. J. Sound Vib. 1994, 175, 241–263. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, G.; Ma, X.; Ye, T. Vibration analysis of circular cylindrical double-shell structures under general coupling and end boundary conditions. Appl. Acoust. 2016, 110, 176–193. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.M.; Huang, Y.Y.; Chen, Y.B. Vibration and acoustic radiation from submerged spherical double-shell. China Ocean Eng. 2003, 17, 341–354. [Google Scholar]
- Dogan, V.; Vaicaitis, R. Nonlinear Response of Double-Wall Cylindrical Shells Subjected to Random Excitation. In Proceedings of the 9th Biennial International Conference on Engineering, Construction and Operations in Challenging Environment, League City, Houston, TX, USA, 7–10 March 2004; pp. 46–54. [Google Scholar]
- Qing, G.-H.; Liu, Y.-H.; Qiu, J.-J.; Meng, X.-J. A semi-analytical method for the free vibration analysis of thick double-shell systems. Finite Elements Anal. Des. 2006, 42, 837–845. [Google Scholar] [CrossRef]
- Wang, J.G.; Li, H.W. Analysis on Dynamic Failure Behaviors of Steel Double-Layer Latticed Cylindrical Shells with Three Circle Centers Used in a Gymnasium. Appl. Mech. Mater. 2013, 256–259, 706–709. [Google Scholar]
- Zhang, C.; Shang, D.J.; Li, Q. Effect of Drive Location on Vibro-Acoustic Characteristics of Submerged Double Cylindrical Shells with Damping Layers. Appl. Mech. Mater. 2013, 387, 59–63. [Google Scholar]
- Huang, Y.-Q.; Zhong, L.; Fu, J.-Y. Wind-induced vibration and equivalent wind load of double-layer cylindrical latticed shells. J. Vibroeng. 2014, 16, 1063–1078. [Google Scholar]
- Zhang, C.; Jin, G.; Ma, X.; Su, Z. Free Vibration of Rib Stiffened Double Cylindrical Shells with General Boundary Condition. In Proceedings of the 22nd International Congress on Sound and Vibration (ICSV), Florence, Italy, 12–16 July 2015. [Google Scholar]
- Xie, K.; Chen, M. Wave based method for vibration analysis of double-walled cylindrical shells. Appl. Acoust. 2018, 139, 293–306. [Google Scholar] [CrossRef]
- Wali, M.; Hentati, T.; Jarraya, A.; Dammak, F. Free vibration analysis of FGM shell structures with a discrete double directors shell element. Compos. Struct. 2015, 125, 295–303. [Google Scholar] [CrossRef]
- Choi, M.-S.; Yeo, D.-J. Free Vibration Analysis of Double Cylindrical Shells Using Transfer of Influence Coefficent. J. Power System Eng. 2017, 21, 48–54. [Google Scholar] [CrossRef] [Green Version]
- Mohammadimehr, M.; Zarei H., B.; Parakandeh, A.; Arani, A.G. Vibration analysis of double-bonded sandwich microplates with nanocomposite facesheets reinforced by symmetric and un-symmetric distributions of nanotubes under multi physical fields. Struct. Eng. Mech. 2017, 64, 361–379. [Google Scholar]
- Chen, M.; Wei, J.; Xie, K.; Deng, N.; Hou, G. Wave Based Method for Free Vibration Analysis of Ring Stiffened Cylindrical Shell with Intermediate Large Frame Ribs. Shock Vib. 2013, 20, 459–479. [Google Scholar] [CrossRef]
- Chen, Y.; Jin, G.; Liu, Z. Free vibration analysis of circular cylindrical shell with non-uniform elastic boundary constraints. Int. J. Mech. Sci. 2013, 74, 120–132. [Google Scholar] [CrossRef]



| n = 3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CC -CC | m | M = 6 | M = 10 | M = 14 | M = 18 | M = 22 | M = 26 | M = 30 | M = 34 | M = 38 | M = 42 | M = 46 | M = 50 |
| 1 | 206.2 | 201.8 | 198.8 | 196.2 | 195.9 | 195.0 | 194.5 | 194.2 | 193.9 | 193.8 | 193.6 | 193.4 | |
| 2 | 254.8 | 253.7 | 251.6 | 250.1 | 249.3 | 248.7 | 248.5 | 248.4 | 248.1 | 247.9 | 247.8 | 247.6 | |
| 3 | 285.1 | 272.4 | 267.4 | 266.4 | 266.1 | 265.8 | 265.7 | 265.6 | 265.5 | 265.4 | 265.4 | 265.3 | |
| 4 | 295.7 | 283.5 | 278.1 | 275.1 | 275.0 | 274.3 | 274.0 | 273.8 | 273.6 | 273.6 | 273.5 | 273.4 | |
| 5 | 408.2 | 401.2 | 397.1 | 394.4 | 393.4 | 392.2 | 391.7 | 391.4 | 390.8 | 390.5 | 390.3 | 390.1 | |
| FF -FF | 1 | 190.2 | 185.0 | 181.7 | 180.3 | 179.4 | 178.1 | 177.6 | 177.2 | 176.8 | 176.7 | 176.5 | 176.3 |
| 2 | 220.1 | 217.6 | 212.8 | 210.9 | 210.8 | 208.6 | 208.1 | 207.9 | 207.3 | 207.0 | 206.9 | 206.6 | |
| 3 | 270.1 | 268.4 | 266.0 | 265.4 | 265.4 | 264.8 | 264.7 | 264.7 | 264.6 | 264.5 | 264.5 | 264.4 | |
| 4 | 285.8 | 278.4 | 274.6 | 272.7 | 271.9 | 271.2 | 270.9 | 270.7 | 270.6 | 270.5 | 270.4 | 270.3 | |
| 5 | 333.6 | 328.6 | 322.8 | 320.2 | 320.1 | 316.9 | 316.5 | 316.1 | 315.3 | 315.0 | 314.7 | 314.3 | |
| SS -SS | 1 | 200.4 | 195.8 | 192.7 | 191.1 | 190.4 | 189.2 | 188.7 | 188.3 | 188.0 | 187.9 | 187.8 | 187.6 |
| 2 | 252.3 | 249.6 | 246.9 | 245.7 | 245.7 | 244.4 | 244.2 | 243.8 | 243.6 | 243.6 | 243.5 | 243.3 | |
| 3 | 272.3 | 270.0 | 266.9 | 266.1 | 266.0 | 265.4 | 265.3 | 265.1 | 265.1 | 265.1 | 265.0 | 264.9 | |
| 4 | 288.3 | 280.1 | 275.7 | 273.7 | 272.9 | 272.0 | 271.7 | 271.5 | 271.3 | 271.3 | 271.2 | 271.1 | |
| 5 | 400.2 | 392.7 | 388.3 | 386.2 | 386.0 | 384.0 | 383.5 | 382.7 | 382.4 | 382.3 | 382.1 | 381.8 | |
| FC -FC | 1 | 201.6 | 196.6 | 196.6 | 191.9 | 191.2 | 190.0 | 189.5 | 189.1 | 188.8 | 188.7 | 188.5 | 188.3 |
| 2 | 246.3 | 244.6 | 244.6 | 240.7 | 240.6 | 239.0 | 238.8 | 238.6 | 238.3 | 238.1 | 238.0 | 237.8 | |
| 3 | 273.2 | 269.5 | 269.5 | 265.7 | 265.6 | 265.1 | 265.0 | 264.9 | 264.8 | 264.8 | 264.7 | 264.7 | |
| 4 | 287.9 | 280.0 | 280.0 | 274.1 | 273.3 | 272.5 | 272.2 | 272.1 | 271.9 | 271.8 | 271.7 | 271.6 | |
| 5 | 390.4 | 381.2 | 381.2 | 373.3 | 373.0 | 370.5 | 370.1 | 369.7 | 369.1 | 368.8 | 368.5 | 368.2 | |
| BC | m | n = 1 | Error 1 | Error 2 | n = 2 | Error 1 | Error 2 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ref [27] | FEM | Present | (%) | (%) | Ref [27] | FEM | Present | (%) | (%) | ||
| CC –CC | 1 | 830.67 | 830.84 | 830.78 | −0.013 | 0.008 | 540.78 | 540.57 | 541.40 | −0.114 | −0.153 |
| 2 | 1382.7 | 1377.3 | 1382.6 | 0.005 | −0.387 | 979.84 | 975.19 | 980.62 | −0.080 | −0.557 | |
| 3 | 1385.5 | 1382.3 | 1383.8 | 0.125 | −0.106 | 995.01 | 996.17 | 995.89 | −0.089 | 0.028 | |
| 4 | 1536.2 | 1534.1 | 1534.5 | 0.109 | −0.028 | 1083.9 | 1083.3 | 1083.7 | 0.022 | -0.033 | |
| SS –SS | 1 | 773.99 | 774.31 | 774.33 | −0.044 | −0.003 | 428.31 | 427.85 | 429.25 | −0.220 | −0.328 |
| 2 | 974.97 | 973.03 | 974.92 | 0.005 | −0.194 | 950.53 | 944.75 | 951.24 | −0.075 | −0.687 | |
| 3 | 1218.2 | 1215.6 | 1217.6 | 0.046 | −0.168 | 972.67 | 974.36 | 974.13 | −0.150 | 0.024 | |
| 4 | 1380.1 | 1372.6 | 1379.6 | 0.036 | −0.510 | 1076.4 | 1075.4 | 1076.0 | 0.034 | −0.059 | |
| FF –FF | 1 | 956.58 | 950.88 | 957.90 | −0.138 | −0.738 | 210.99 | 208.23 | 211.88 | −0.424 | −1.755 |
| 2 | 1227.3 | 1221.2 | 1224.5 | 0.229 | −0.269 | 236.92 | 235.29 | 240.68 | −1.589 | −2.293 | |
| 3 | 1271.1 | 1271.1 | 1272.1 | −0.078 | −0.078 | 777.66 | 777.80 | 779.93 | −0.292 | −0.274 | |
| 4 | 1355.3 | 1346.4 | 1355.7 | −0.028 | −0.689 | 952.73 | 950.88 | 946.29 | 0.676 | 0.483 | |
| BC | m | n = 3 | Error 1 | Error 2 | n = 4 | Error 1 | Error 2 | ||||
| Ref [27] | FEM | Present | (%) | (%) | Ref [27] | FEM | Present | (%) | (%) | ||
| CC –CC | 1 | 523.93 | 517.91 | 521.89 | 0.389 | −0.769 | 545.06 | 543.67 | 546.61 | −0.284 | −0.540 |
| 2 | 740.85 | 742.00 | 742.18 | −0.179 | −0.024 | 588.35 | 587.24 | 590.35 | −0.339 | −0.529 | |
| 3 | 761.54 | 756.21 | 759.44 | 0.275 | −0.428 | 626.64 | 626.09 | 625.57 | 0.171 | 0.084 | |
| 4 | 805.56 | 804.71 | 804.63 | 0.115 | 0.010 | 627.56 | 626.57 | 627.94 | −0.060 | −0.218 | |
| SS –SS | 1 | 445.11 | 443.01 | 448.10 | −0.672 | −1.150 | 502.42 | 501.33 | 505.14 | −0.542 | −0.761 |
| 2 | 687.93 | 689.70 | 690.68 | −0.400 | −0.142 | 541.87 | 545.29 | 546.62 | −0.876 | −0.243 | |
| 3 | 722.33 | 718.60 | 722.60 | −0.038 | −0.557 | 596.94 | 594.84 | 596.85 | 0.015 | −0.338 | |
| 4 | 785.97 | 785.31 | 785.31 | 0.083 | 0.000 | 601.94 | 600.24 | 600.34 | 0.266 | −0.017 | |
| FF –FF | 1 | 429.45 | 425.74 | 431.62 | −0.506 | −1.382 | 500.47 | 503.97 | 503.74 | −0.653 | 0.046 |
| 2 | 515.85 | 510.74 | 520.01 | −0.807 | −1.816 | 541.04 | 542.63 | 544.53 | −0.644 | −0.349 | |
| 3 | 720.87 | 717.15 | 721.64 | −0.107 | −0.626 | 590.51 | 588.05 | 589.81 | 0.119 | −0.299 | |
| 4 | 729.39 | 723.6 | 733.88 | −0.615 | −1.420 | 599.67 | 597.89 | 597.77 | 0.317 | 0.020 |
| [0° 90° 90° 0°] | [45° −45° 45° −45°] | |||||||
|---|---|---|---|---|---|---|---|---|
| B.C. | CC–CC | CC–CC | ||||||
| m | kcu = 105 | kcv = 105 | kcw = 105 | kcx = 105 | kcu = 105 | kcv = 105 | kcw = 105 | kcx = 105 |
| 1 | 44.967 | 189.840 | 191.196 | 190.676 | 57.105 | 282.229 | 305.843 | 309.305 |
| 2 | 44.971 | 360.911 | 372.063 | 371.453 | 57.213 | 482.443 | 657.440 | 682.661 |
| 3 | 190.583 | 553.187 | 671.764 | 674.137 | 311.144 | 494.711 | 1029.792 | 999.627 |
| 4 | 371.525 | 629.980 | 679.502 | 678.936 | 689.441 | 677.832 | 1099.645 | 1053.731 |
| 5 | 674.644 | 687.826 | 688.259 | 684.037 | 745.276 | 832.207 | 1132.119 | 1144.327 |
| B.C. | SS–SS | SS–SS | ||||||
| m | kcu = 105 | kcv = 105 | kcw = 105 | kcx = 105 | kcu = 105 | kcv = 105 | kcw = 105 | kcx = 105 |
| 1 | 44.96 | 165.65 | 166.72 | 166.196 | 57.08 | 163.09 | 161.20 | 166.102 |
| 2 | 44.97 | 357.85 | 368.91 | 368.460 | 57.20 | 374.63 | 543.35 | 565.734 |
| 3 | 166.14 | 538.79 | 607.20 | 591.192 | 166.77 | 431.90 | 969.53 | 953.477 |
| 4 | 368.32 | 606.6 | 660.2 | 667.569 | 571.7 | 658.95 | 1093.0 | 1052.548 |
| 5 | 636.8 | 625.42 | 673.8 | 674.025 | 744.76 | 698.5 | 1125.9 | 1141.095 |
| B.C. | FF–FF | FF–FF | ||||||
| m | kcu = 105 | kcv = 105 | kcw = 105 | kcx = 105 | kcu = 105 | kcv = 105 | kcw = 105 | kcx = 105 |
| 1 | 44.968 | 202.37 | 222.30 | 200.59 | 57.079 | 178.34 | 245.07 | 246.23 |
| 2 | 45.515 | 282.73 | 297.49 | 294.36 | 57.888 | 238.50 | 282.33 | 289.75 |
| 3 | 195.49 | 378.91 | 385.95 | 384.23 | 242.777 | 331.24 | 355.58 | 367.23 |
| 4 | 294.88 | 452.46 | 472.03 | 470.0 | 287.619 | 424.28 | 685.21 | 718.05 |
| 5 | 384.34 | 573.59 | 659.19 | 646.0 | 373.156 | 516.01 | 1046.3 | 1015.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Shi, D.; He, D. Vibration Characteristics of a Laminated Composite Double-Cylindrical Shell System Coupled with a Variable Number of Annular Plates. Materials 2022, 15, 4246. https://doi.org/10.3390/ma15124246
Zhang Y, Shi D, He D. Vibration Characteristics of a Laminated Composite Double-Cylindrical Shell System Coupled with a Variable Number of Annular Plates. Materials. 2022; 15(12):4246. https://doi.org/10.3390/ma15124246
Chicago/Turabian StyleZhang, Ying, Dongyan Shi, and Dongze He. 2022. "Vibration Characteristics of a Laminated Composite Double-Cylindrical Shell System Coupled with a Variable Number of Annular Plates" Materials 15, no. 12: 4246. https://doi.org/10.3390/ma15124246
APA StyleZhang, Y., Shi, D., & He, D. (2022). Vibration Characteristics of a Laminated Composite Double-Cylindrical Shell System Coupled with a Variable Number of Annular Plates. Materials, 15(12), 4246. https://doi.org/10.3390/ma15124246






