Evolution of Shear Surface Morphology of Jointed Rock Masses Based on Gaussian Filtering Method under Freeze-Thaw Cycles
Abstract
:1. Introduction
2. Experiment Overviews
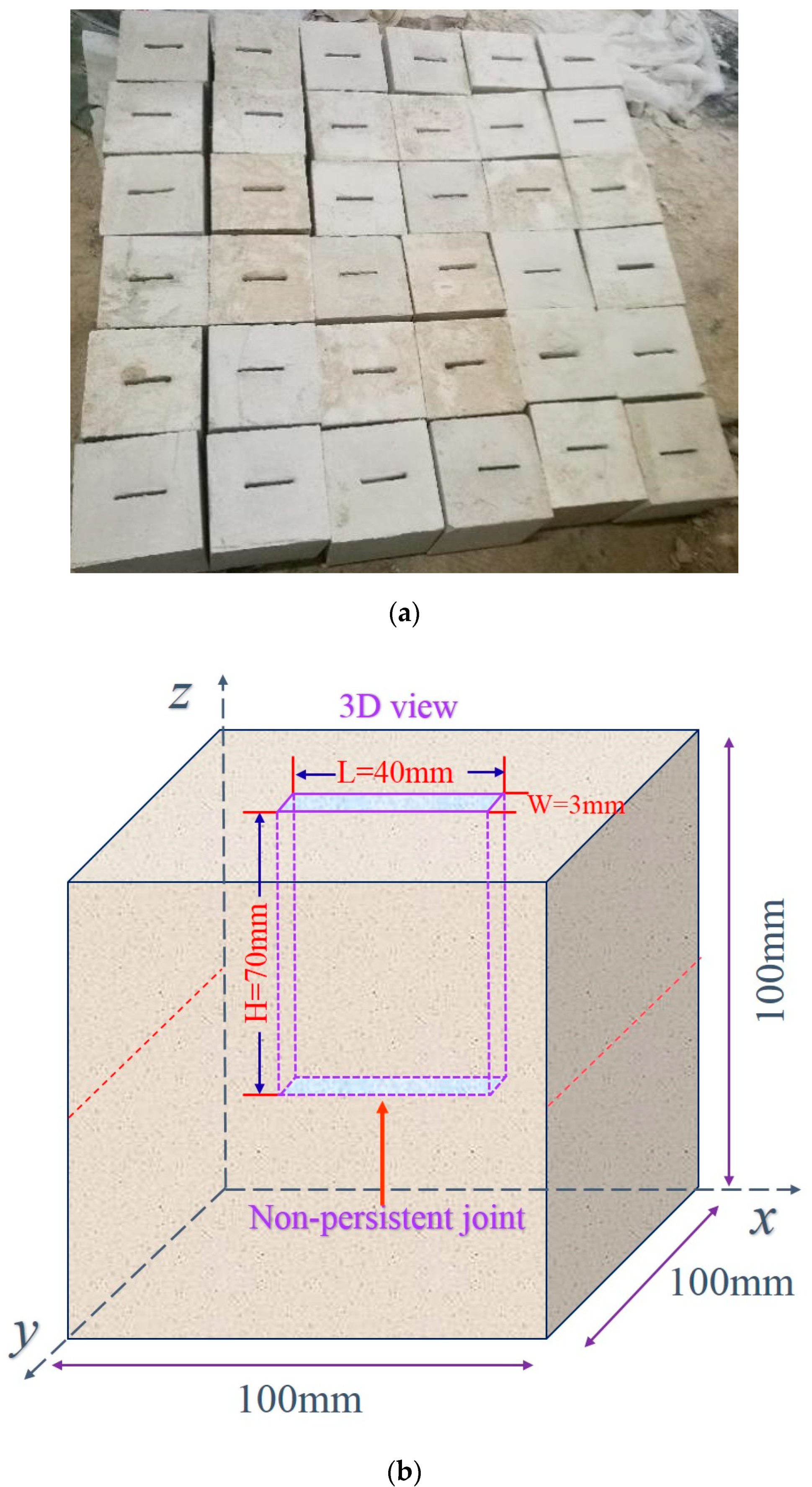
2.1. Preparation of Jointed Rock Specimens
2.2. Experimental Equipment and Scheme
- (1)
- In the conventional direct shear test, some joint samples were subjected to three cyclic shear tests and were grouped according to the number of freeze-thaw cycles. In the test process, the joint shear surface was scanned after each shear test. Then, after the scanning was completed, the upper and lower parts of the sample were placed in coincidence. Before the second shear, the joint sample was closed to ensure that the upper and lower sides of the joint were in a state of joint bonding.
- (2)
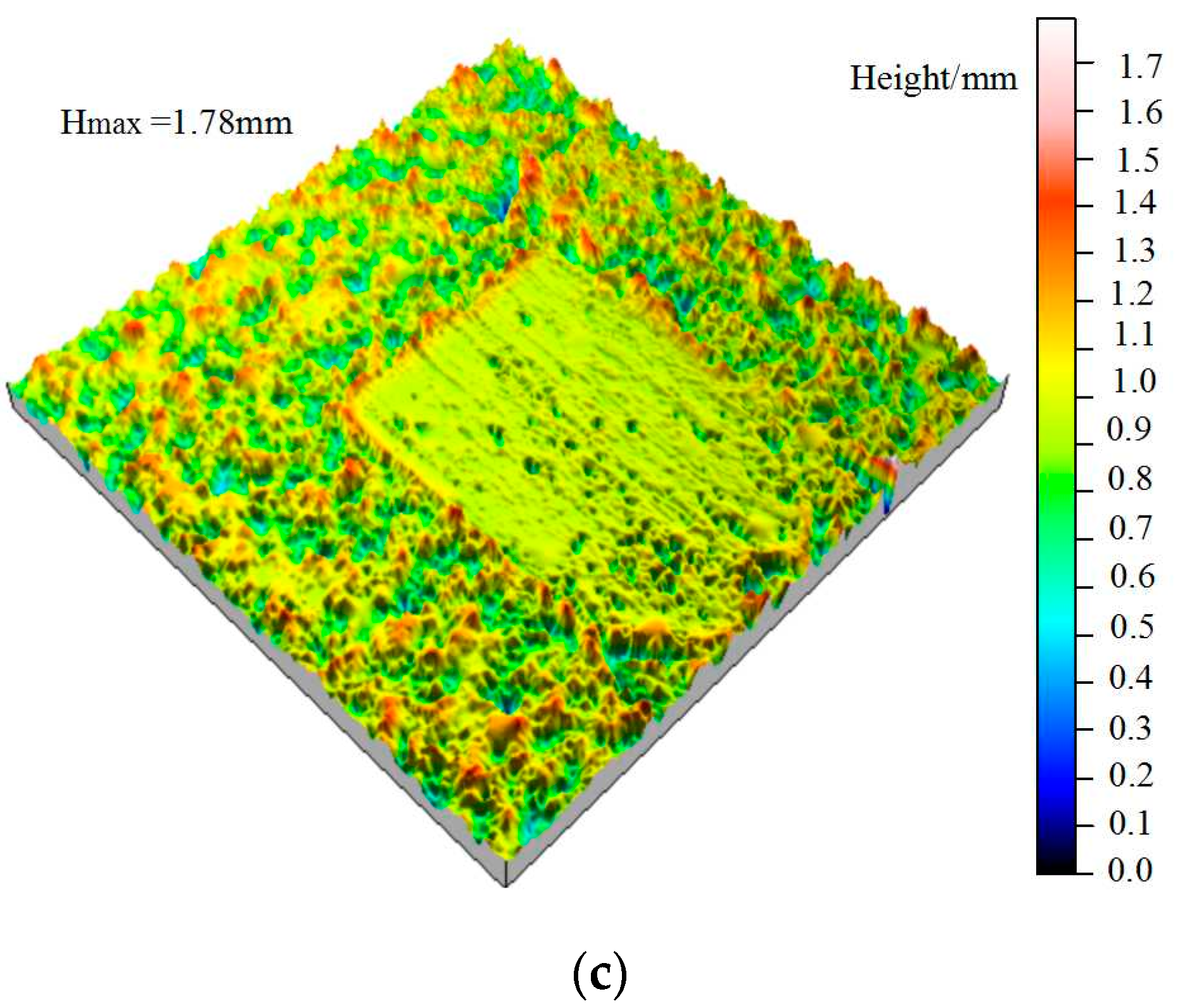
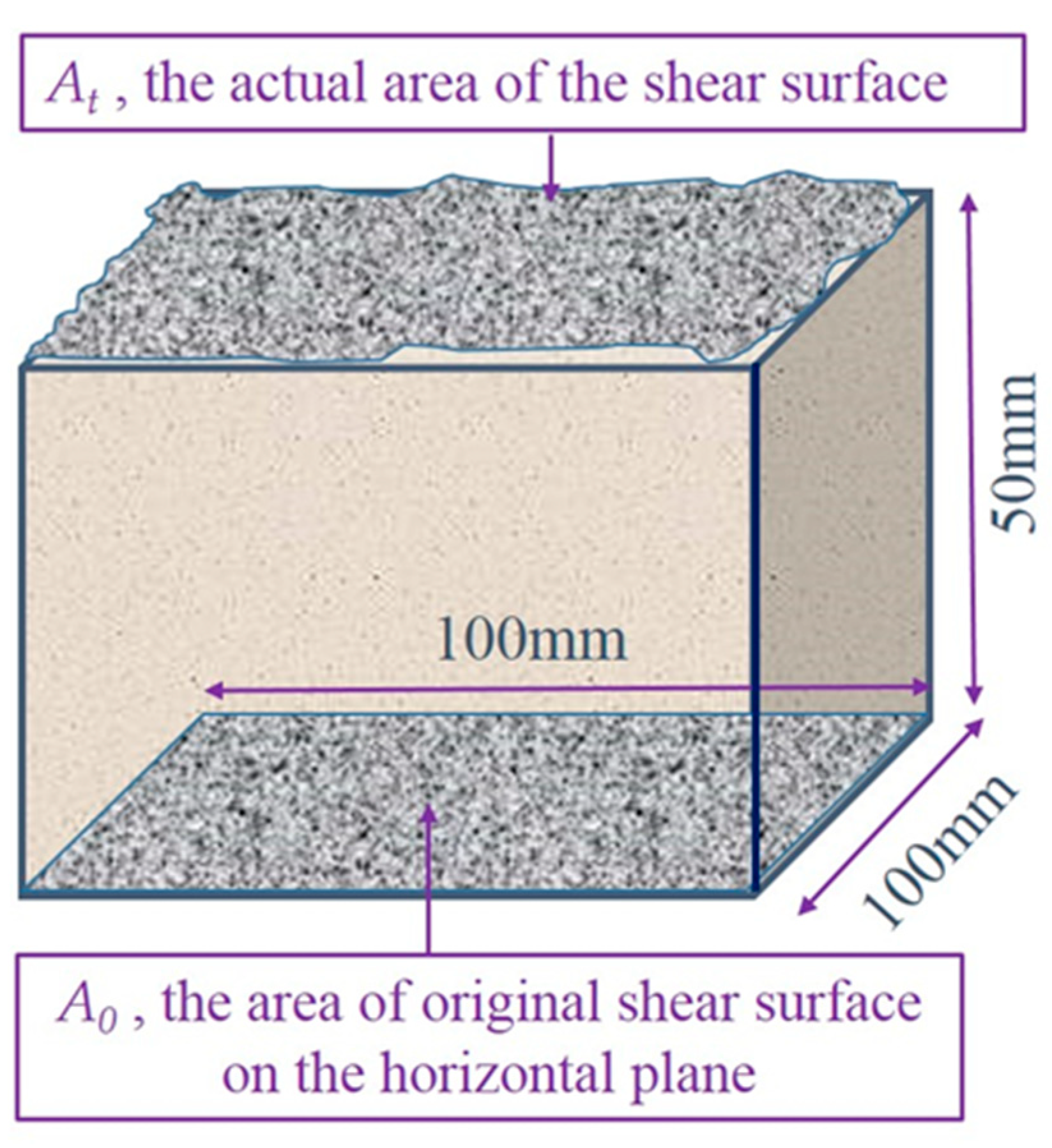
- After each shearing experiment, the shear surface was scanned at the point spacing of 0.01 mm to obtain the morphology of the jointed rock mass shear surface. Owing to the non-contact laser scanning technique, the acquisition process of elevation data will not damage the shear surface. Then, combined with the supporting data analysis software TalyMap, the morphology data can be processed and analyzed. The scanning measurement follows the principle of triangular optics; the whole process is to convert the asperities data of the shear surface topography into a current signal through the photoelectric conversion system. Then, the current signal after magnification and analogue-to-digital conversion, the reading, storage, processing, and three-dimensional visualization of the shear surface topography can be realized. In doing so, the obtained surface morphology parameters can accurately represent the roughness of the shear surface.
3. Gaussian Filtering Principle
3.1. Gaussian Filtering on the Shear Surface
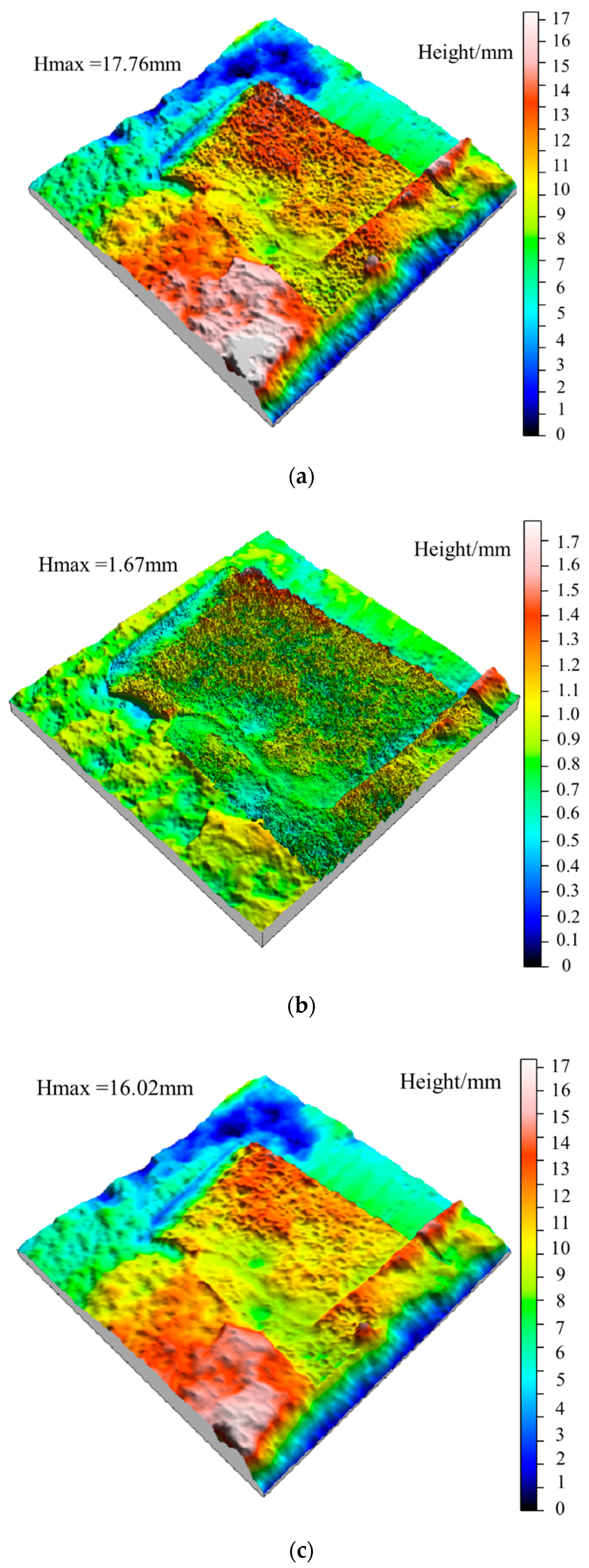
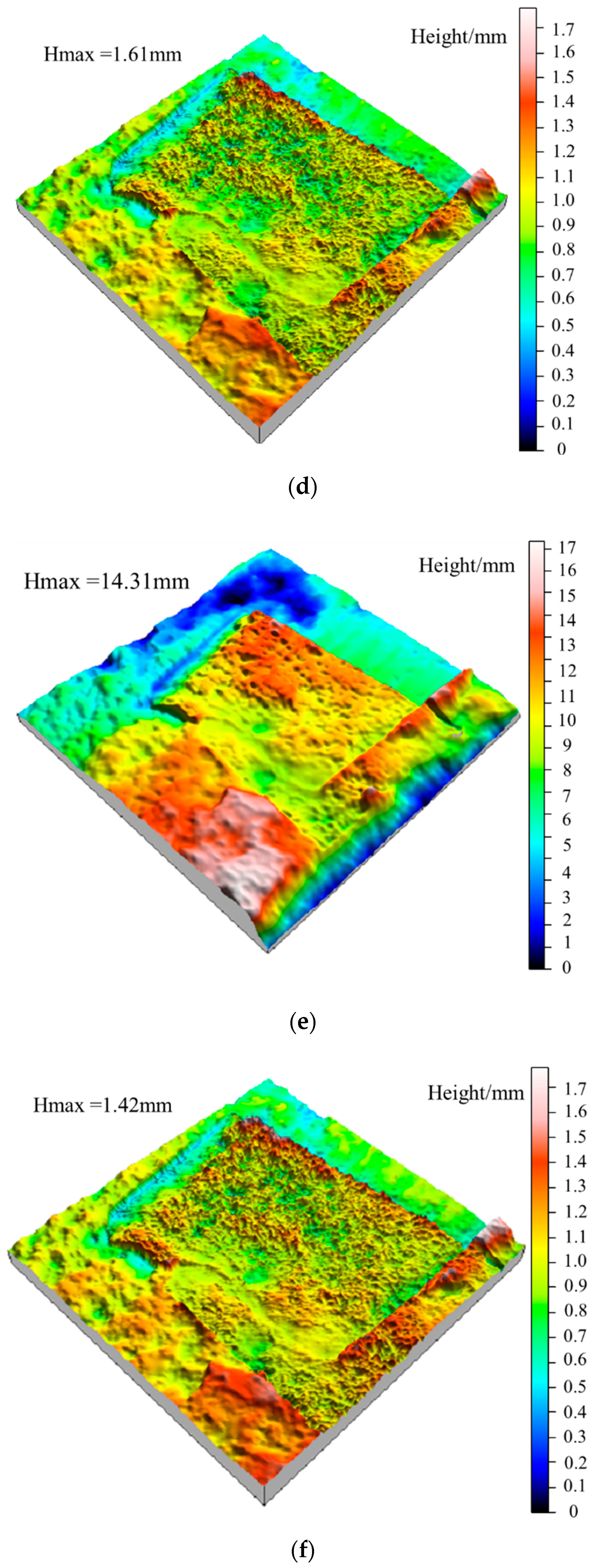
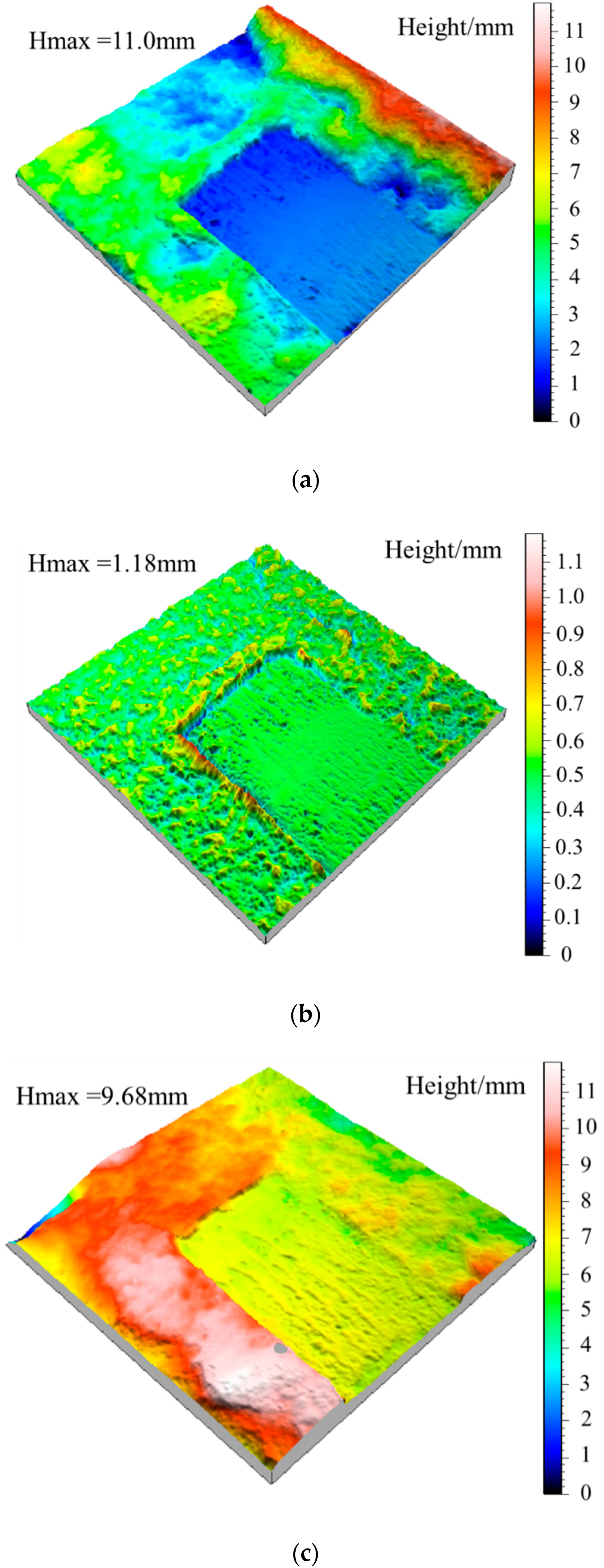
3.2. Surface Morphology Analysis after Gaussian Filtering
4. Three-Dimensional Roughness Parameters of the Shear Surface
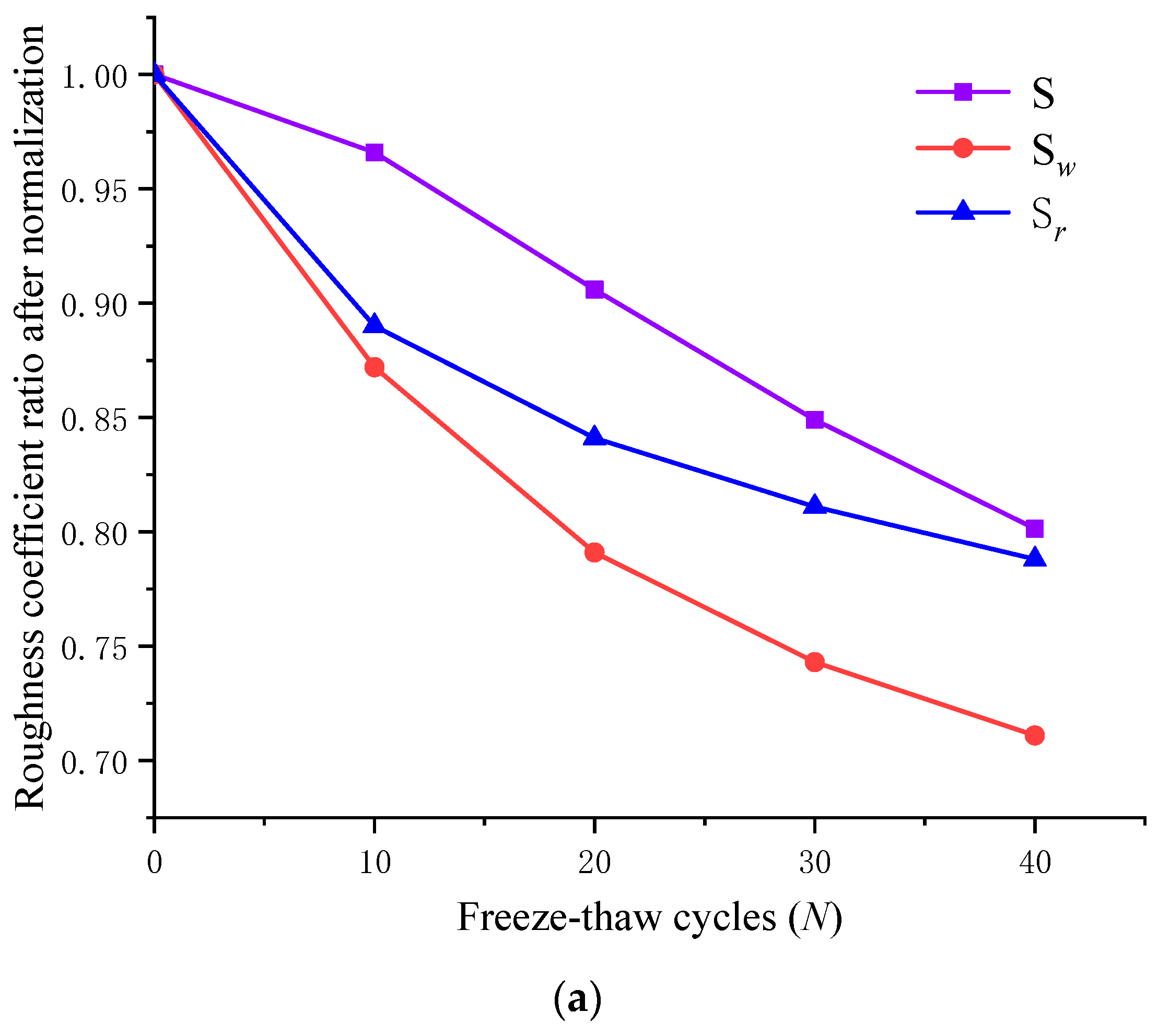
4.1. Roughness Coefficient Ratio S
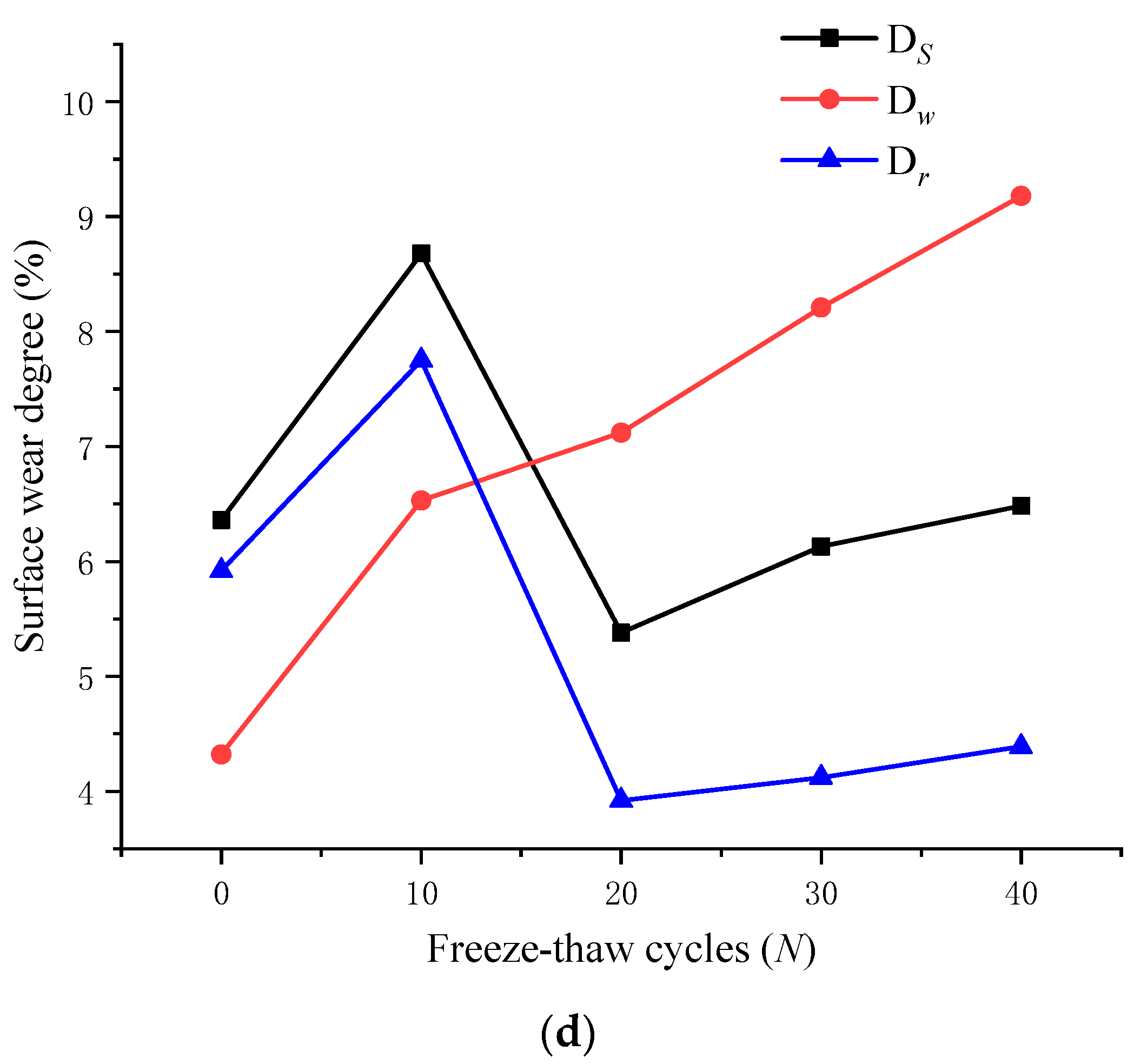
4.2. Shear Surface Degree of Wear Ds
5. Analysis of Experimental Results
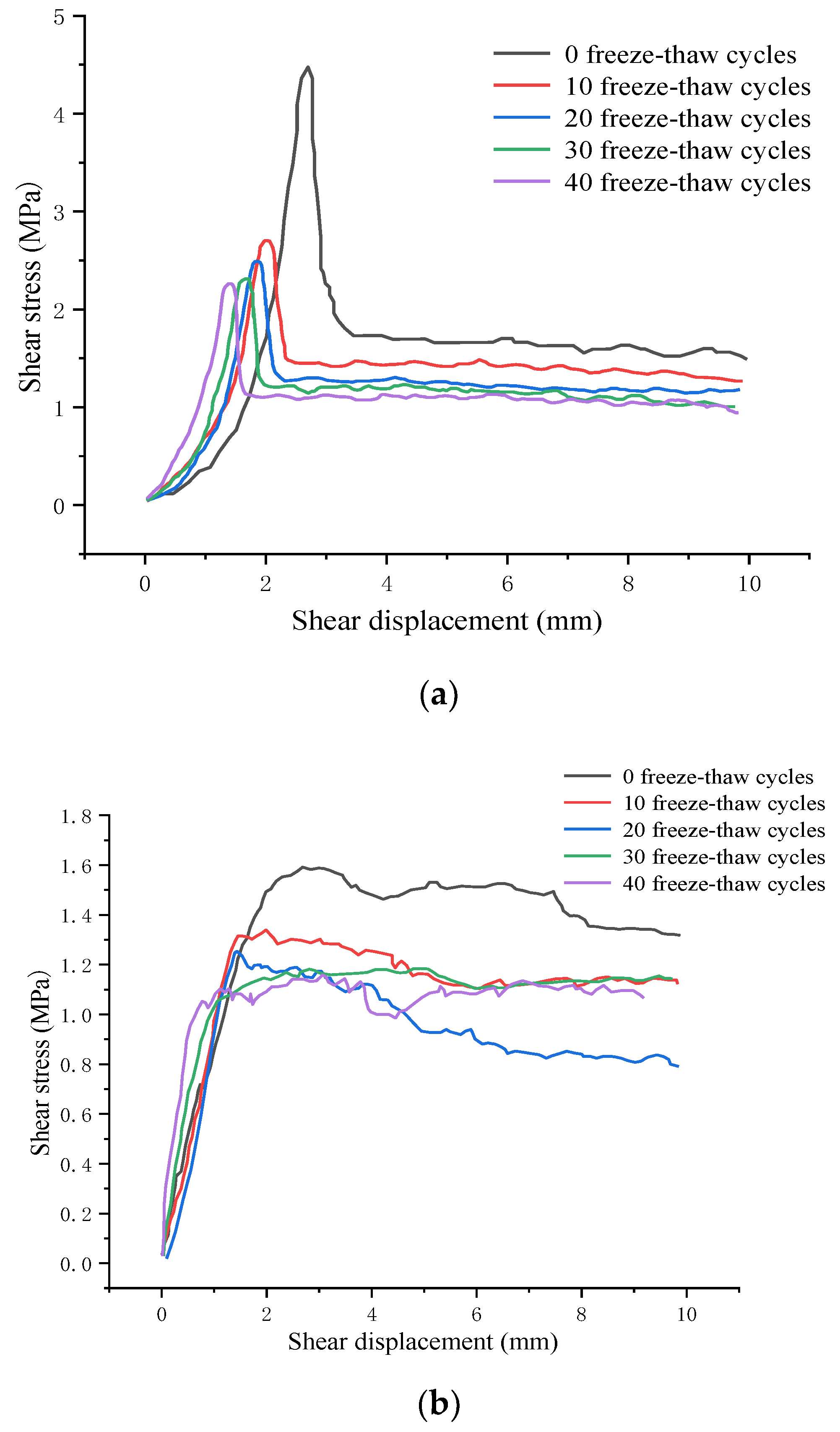
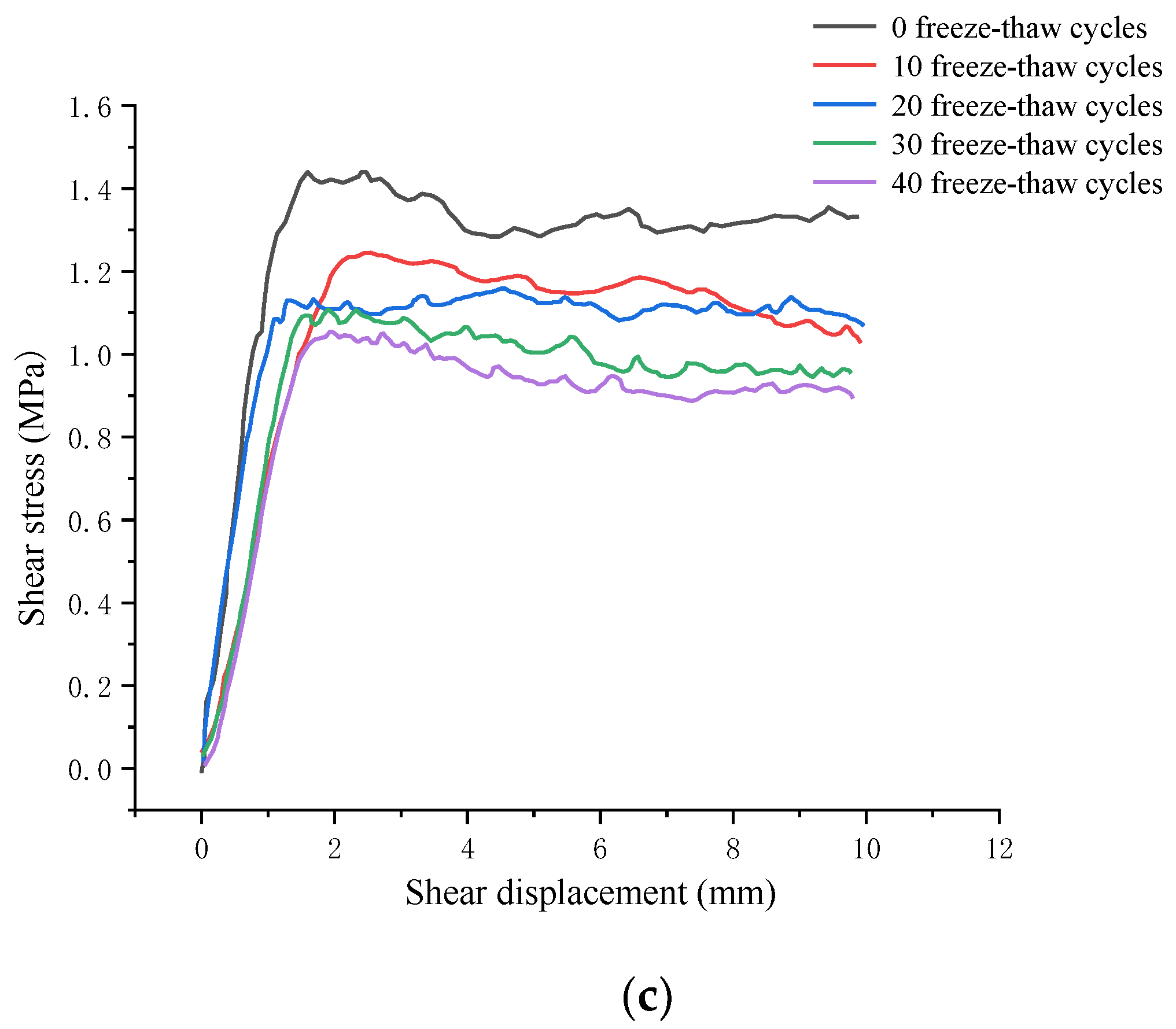
5.1. Analysis of Shear Stress—Displacement Curves
5.2. Variation of Waviness and Unevenness Surface Morphologies
5.3. Variation of Three-Dimensional Roughness Parameters
6. Conclusions
- (1)
- After the freeze-thaw cycle, the actual shear surface area decreases more significantly than fresh jointed rocks during the shear test, and the roughness coefficient ratio S also decreases significantly. Meanwhile, the roughness of the waviness and roughness surfaces decreases significantly with the increase of freeze-thaw cycles.
- (2)
- Surface wear degree D can be used to characterize the degree of shear surface damage. With the increase of freeze-thaw cycles, the of the waviness surface and the of the unevenness surface change differently, which is related closely to the failure mode of the asperity caused by freeze-thaw damage. The failure of the first-order asperity increases with freeze-thaw cycles, leading to the gradual increase of surface wear degree Dw of waviness. At the early stage of the freeze-thaw cycles, most second-order asperities are flattened during shearing, causing the uneven surface wear degree to be high first and then low. As the freeze-thaw cycles increase, the damage of the surface asperities intensifies, leading to the constant increase of the waviness surface wear degree.
- (3)
- At the early stage of freeze-thaw cycles, the morphology variation of the shear surface and its unevenness surface after the shear test are similar. During this period, the damage of the shear surface is mainly dominated by the roughness surface, so the wear of the second-order asperities is the main factor of the shear surface wear. However, with the increase of freeze-thaw cycles, the damage degree of the first-order asperity becomes the critical factor determining the surface wear characteristics, so the waviness surface would mainly control the evolution of the shear surface morphology.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Y.L.; Zhang, C.S.; Wang, Y.X.; Lin, H. Shear-related roughness classification and strength model of natural rock joint based on fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. Sci. 2021, 137, 104550. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Liu, Q.; Zhang, C.; Liao, J.; Lin, H.; Wang, Y. Coupled seepage-damage effect in fractured rock masses: Model development and a case study. Int. J. Rock Mech. Min. Sci. 2021, 144, 104822. [Google Scholar] [CrossRef]
- Lin, H.; Lei, D.; Zhang, C.; Wang, Y. Deterioration of non-persistent rock joints: A focus on impact of freeze-thaw cycles. Int. J. Rock Mech. Min. Sci. 2020, 135, 104515. [Google Scholar] [CrossRef]
- Xie, S.J.; Lin, H.; Chen, Y.F.; Wang, Y.X. A new nonlinear empirical strength criterion for rocks under conventional triaxial compression. J. Cent. South Univ. 2021, 28, 1448–1458. [Google Scholar] [CrossRef]
- Tang, W.; Lin, H.; Chen, Y.; Feng, J.; Hu, H. Mechanical Characteristics and Acoustic Emission Characteristics of Mortar-Rock Binary Medium. Buildings 2022, 12, 665. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Y.; Yang, Y.; Sun, Q.; Luo, T.; Zhang, H. Influence of surface roughness and hydrophilicity on bonding strength of concrete-rock interface. Constr. Build. Mater. 2019, 213, 156–166. [Google Scholar] [CrossRef]
- Fan, X.; Yang, Z.; Li, K. Effects of the lining structure on mechanical and fracturing behaviors of four-arc shaped tunnels in a jointed rock mass under uniaxial compression. Theor. Appl. Fract. Mech. 2021, 112, 102887. [Google Scholar] [CrossRef]
- Zhang, C.; Zou, P.; Wang, Y.; Jiang, T.; Lin, H.; Cao, P. An elasto-visco-plastic model based on stress functions for deformation and damage of water-saturated rocks during the freeze-thaw process. Constr. Build. Mater. 2020, 250, 118862. [Google Scholar] [CrossRef]
- Wen, S.; Zhang, C.; Zhang, Y. Favorable driving direction of double shield TBM in deep mixed rock strata: Numerical investigations to reduce shield entrapment. Geomech. Eng. 2019, 17, 237–245. [Google Scholar]
- Han, D.; Li, K.; Meng, J. Evolution of nonlinear elasticity and crack damage of rock joint under cyclic tension. Int. J. Rock Mech. Min. Sci. 2020, 128, 104286. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F. A damage constitutive model for intermittent jointed rocks under cyclic uniaxial compression. Int. J. Rock Mech. Min. Sci. 2018, 103, 289–301. [Google Scholar] [CrossRef]
- Xu, Y.; Dai, F.; Zhao, T.; Xu, N.W.; Liu, Y. Fracture Toughness Determination of Cracked Chevron Notched Brazilian Disc Rock Specimen via Griffith Energy Criterion Incorporating Realistic Fracture Profiles. Rock Mech. Rock Eng. 2016, 49, 3083–3093. [Google Scholar] [CrossRef]
- Wei, Y.; Huiya, Z.; Zhu, Y.; Tang, J.; Tang, J.; Wang, W.; Lin, H.; Wan, N.; Wang, A. Determination method of the slope critical failure state based on the monitoring data fusion. Rock Soil Mech. 2022, 4, 1–13. [Google Scholar] [CrossRef]
- Patton, F.D. Multiple modes of shear failure in rock. In Proceedings of the 1st ISRM Congress, Lisbon, Portugal, 25 September–1 October 1966. [Google Scholar]
- Barton, N.R.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Rock Eng. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Belem, T.; Souley, M.; Homand, F. Modeling surface roughness degradation of rock joint wall during monotonic and cyclic shearing. Acta Geotech. 2007, 2, 227–248. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, Q.; Chen, N.; Wei, W.; Feng, X. Laboratory Investigation on Shear Behavior of Rock Joints and a New Peak Shear Strength Criterion. Rock Mech. Rock Eng. 2016, 49, 3495–3512. [Google Scholar] [CrossRef]
- Homand, F.; Belem, T.; Souley, M. Friction and degradation of rock joint surfaces under shear loads. Int. J. Numer. Anal. Methods Geomech. 2010, 25, 973–999. [Google Scholar] [CrossRef]
- Belem, T.; Homand-Etienne, F.; Souley, M. Quantitative Parameters for Rock Joint Surface Roughness. Rock Mech. Rock Eng. 2000, 33, 217–242. [Google Scholar] [CrossRef]
- Ghobadi, M.H.; Babazadeh, R. Experimental Studies on the Effects of Cyclic Freezing-Thawing, Salt Crystallization, and Thermal Shock on the Physical and Mechanical Characteristics of Selected Sandstones. Rock Mech. Rock Eng. 2015, 48, 1001–1016. [Google Scholar] [CrossRef]
- Wang, L.; Li, N.; Qi, J.; Tian, Y.; Xu, S. A study on the physical index change and triaxial compression test of intact hard rock subjected to freeze-thaw cycles. Cold Reg. Sci. Technol. 2019, 160, 39–47. [Google Scholar]
- Krautblatter, M.; Funk, D.; Günzel, F.K. Why permafrost rocks become unstable: A rock–ice-mechanical model in time and space. Earth Surf. Processes Landf. 2013, 38, 876–887. [Google Scholar] [CrossRef] [Green Version]
- Mu, J.Q.; Pei, X.J.; Huang, R.Q.; Rengers, N.; Zou, X.Q. Degradation characteristics of shear strength of joints in three rock types due to cyclic freezing and thawing. Cold Reg. Ence Technol. 2017, 138, 91–97. [Google Scholar] [CrossRef]
- Davies, M.C.R.; Hamza, O.; Harris, C. The effect of rise in mean annual temperature on the stability of rock slopes containing ice-filled discontinuities. Permafr. Periglac. Processes 2001, 12, 137–144. [Google Scholar] [CrossRef]
- Lei, D.; Lin, H.; Chen, Y.; Cao, R.; Wen, Z. Effect of Cyclic Freezing-Thawing on the Shear Mechanical Characteristics of Nonpersistent Joints. Adv. Mater. Ence Eng. 2019, 2019, 9867681. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Yang, X.; Huang, S.; Yin, D.; Liu, G. Experimental Study on the Shear Behavior of the Bonding Interface Between Sandstone and Cement Mortar Under Freeze–Thaw. Rock Mech. Rock Eng. 2020, 53, 881–907. [Google Scholar] [CrossRef]
- Huang, S.; Liu, Q.; Cheng, A.; Liu, Y. Preliminary experimental study of frost heaving pressure in crack and frost heaving propagation in rock mass under low temperature. Yantu Lixue Rock Soil Mech. 2018, 39, 78–84. [Google Scholar]
- XIA Caichu, S.Z. Engineering Rock Joint Mechanical; Tongji University Press: Shanghai, China, 2002. [Google Scholar]
- Theiler, J. Estimating fractal dimension. Joptsocama 1990, 7, 1055–1073. [Google Scholar] [CrossRef] [Green Version]







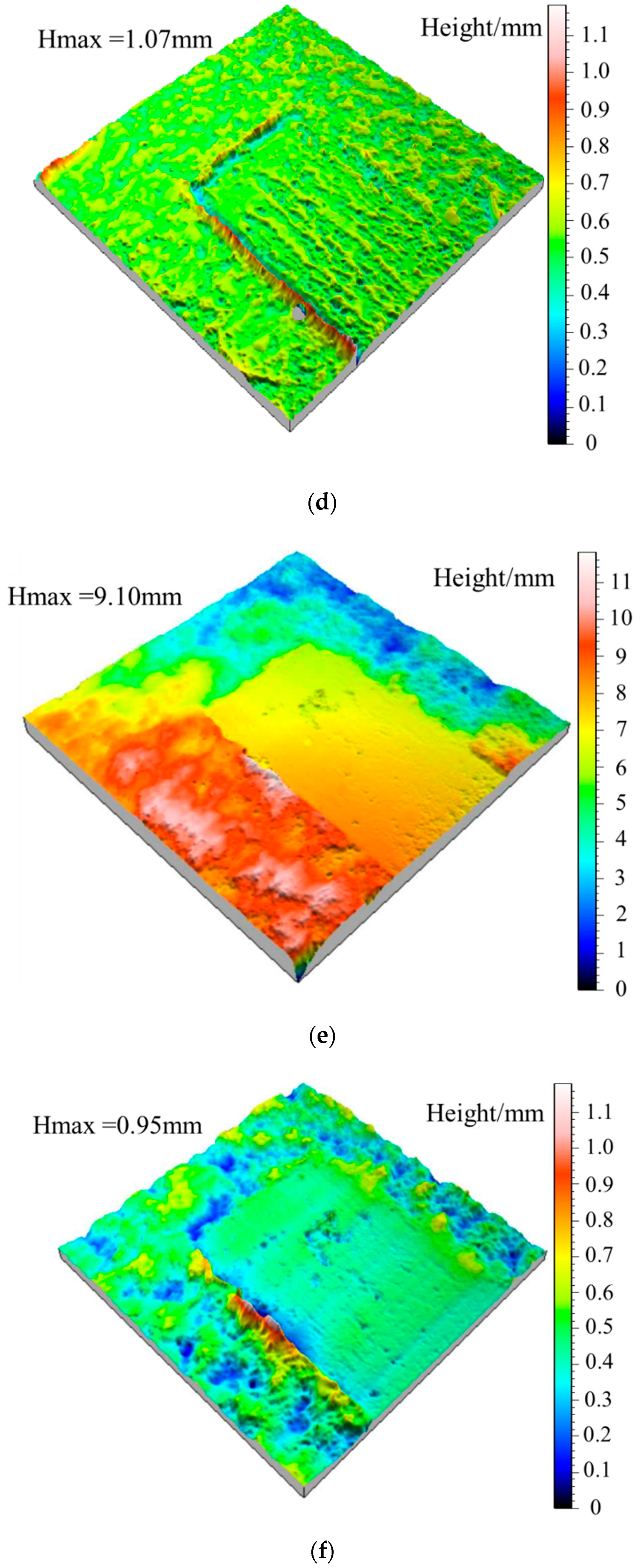
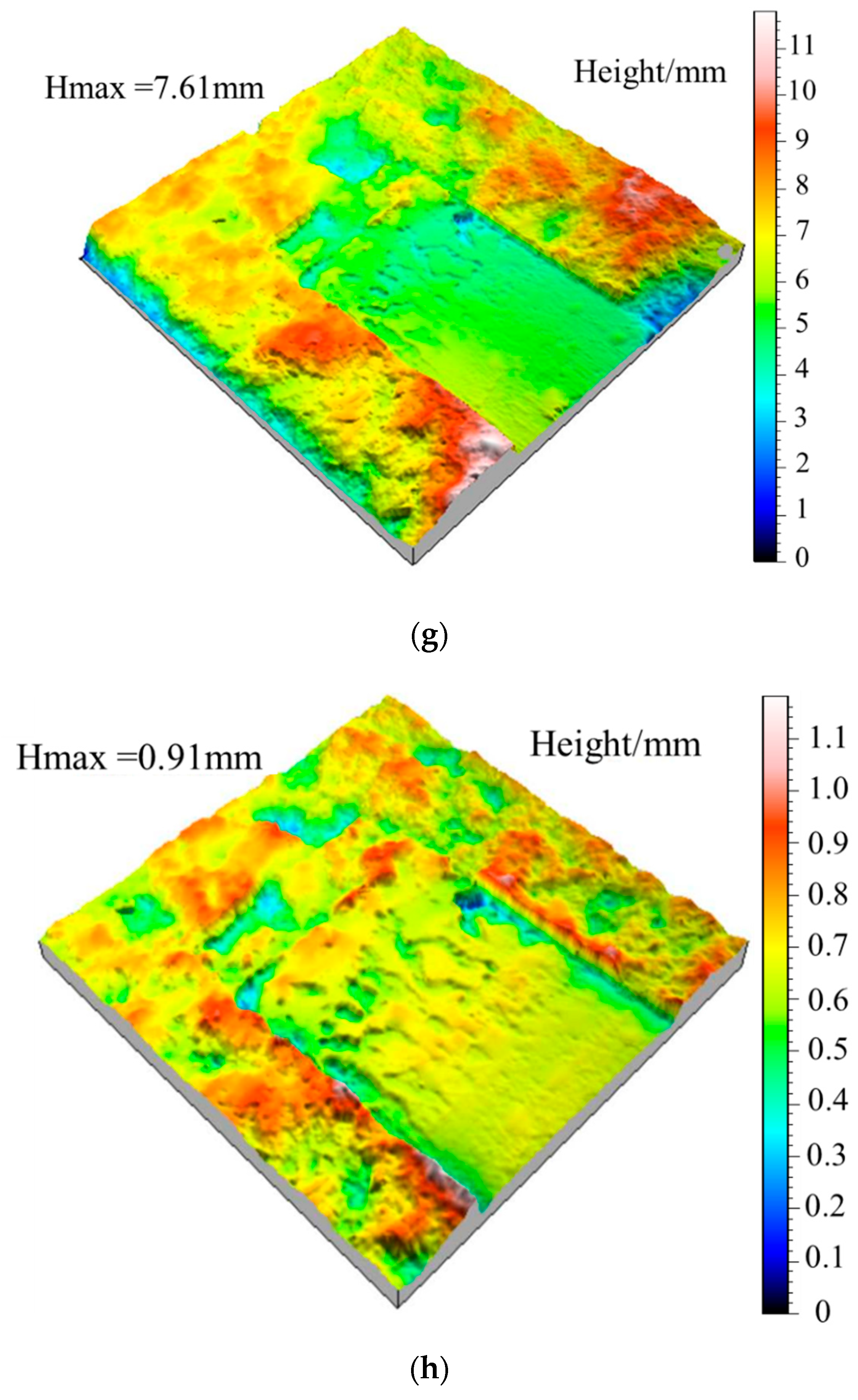

| Freeze-Thaw Cycles (N) | Original Shear Surface | Waviness Surface | Unevenness Surface |
|---|---|---|---|
| 0 | 2.12 | 2.10 | 2.34 |
| 10 | 2.16 | 2.13 | 2.36 |
| 20 | 2.19 | 2.16 | 2.39 |
| 30 | 2.20 | 2.17 | 2.43 |
| 40 | 2.26 | 2.21 | 2.45 |
| Shear Test Times | Freeze-Thaw Cycles (N) | S/% | |||||
|---|---|---|---|---|---|---|---|
| 2 | 0 | 10,000 | 14,039.5 | 11,880.1 | 10,633.9 | 40.39 | 7.62 |
| 10 | 13,570.4 | 11,681.3 | 10,611.2 | 35.70 | 12.32 | ||
| 20 | 13,299.2 | 11,570.6 | 10,577.3 | 32.99 | 9.43 | ||
| 30 | 13,010.6 | 11,520.4 | 10,530.6 | 30.10 | 6.77 | ||
| 40 | 12,717.9 | 11,249.3 | 10,321.4 | 27.17 | 5.13 | ||
| 3 | 0 | 10,000 | 12,650.3 | 11,200.4 | 10,298.7 | 26.50 | 6.46 |
| 10 | 12,421.7 | 11,110.6 | 10,281.3 | 24.21 | 8.68 | ||
| 20 | 12,292.3 | 11,071.5 | 10,263.4 | 22.92 | 5.38 | ||
| 30 | 12,142.6 | 11,029.8 | 10,222.6 | 21.43 | 6.13 | ||
| 40 | 11,932.7 | 10,824.5 | 10,018.8 | 19.33 | 4.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, D.; Chen, Y.; Lin, H.; Zhang, C.; Lu, Z.; Wang, G.; Zhang, Y. Evolution of Shear Surface Morphology of Jointed Rock Masses Based on Gaussian Filtering Method under Freeze-Thaw Cycles. Materials 2022, 15, 4228. https://doi.org/10.3390/ma15124228
Lei D, Chen Y, Lin H, Zhang C, Lu Z, Wang G, Zhang Y. Evolution of Shear Surface Morphology of Jointed Rock Masses Based on Gaussian Filtering Method under Freeze-Thaw Cycles. Materials. 2022; 15(12):4228. https://doi.org/10.3390/ma15124228
Chicago/Turabian StyleLei, Daxing, Yifan Chen, Hang Lin, Chunshun Zhang, Zhigang Lu, Guangli Wang, and Yaoping Zhang. 2022. "Evolution of Shear Surface Morphology of Jointed Rock Masses Based on Gaussian Filtering Method under Freeze-Thaw Cycles" Materials 15, no. 12: 4228. https://doi.org/10.3390/ma15124228
APA StyleLei, D., Chen, Y., Lin, H., Zhang, C., Lu, Z., Wang, G., & Zhang, Y. (2022). Evolution of Shear Surface Morphology of Jointed Rock Masses Based on Gaussian Filtering Method under Freeze-Thaw Cycles. Materials, 15(12), 4228. https://doi.org/10.3390/ma15124228







