The Kinetics of Pyrite Dissolution in Nitric Acid Solution
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Procedure
2.3. Analysis
3. Results and Discussion
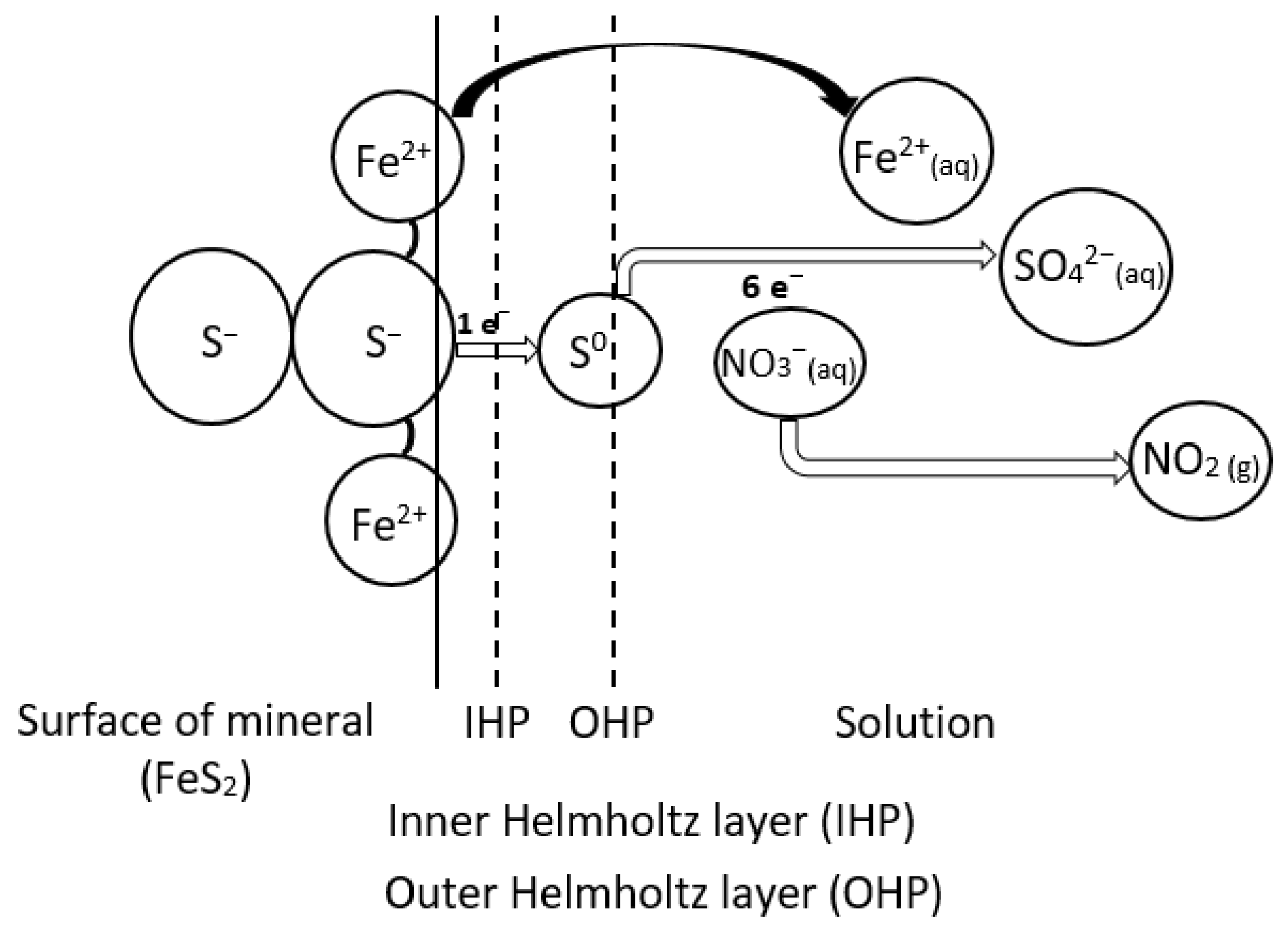
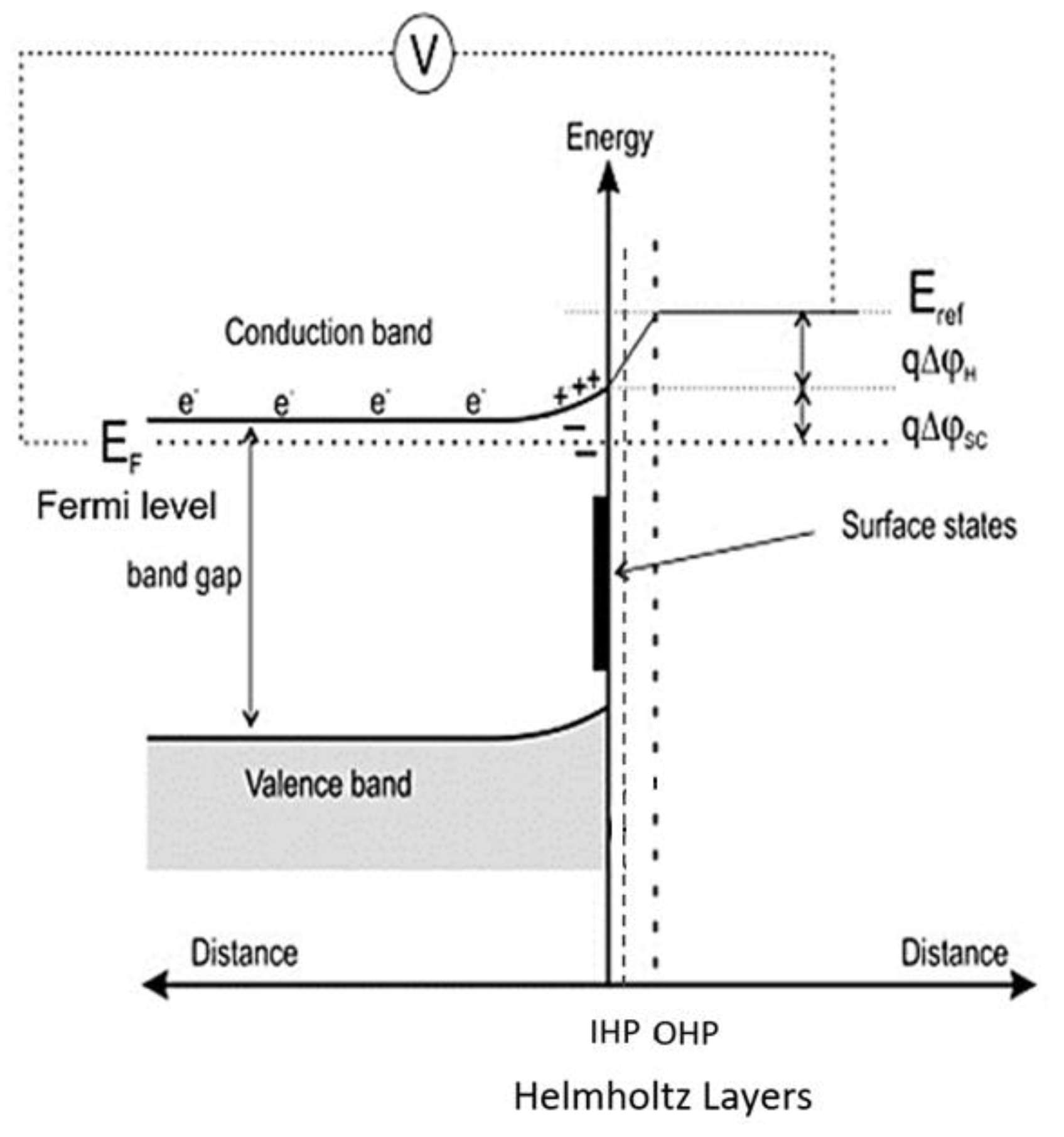
3.1. Mechanism of the Pyrite–Nitric Acid Dissolution
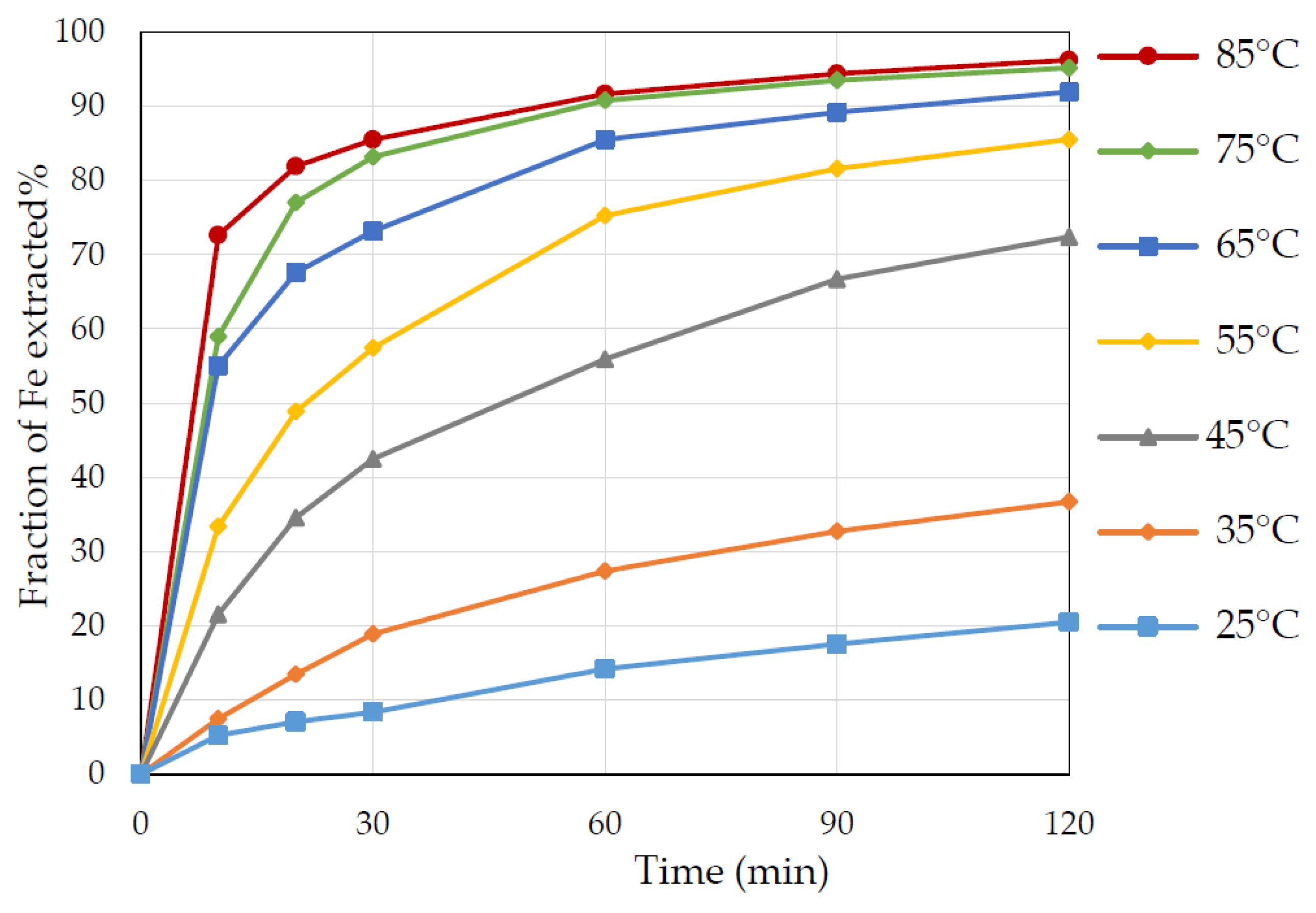
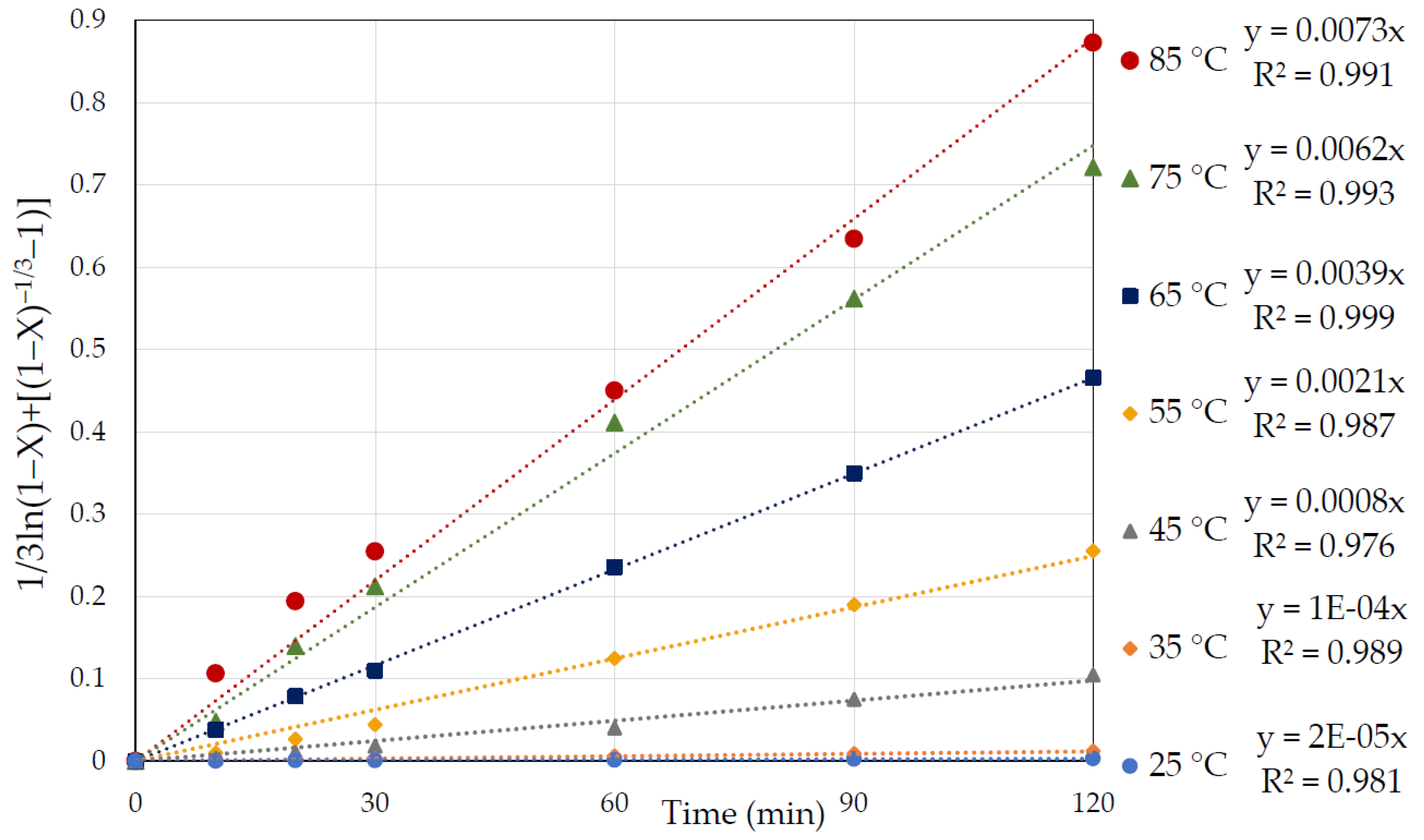
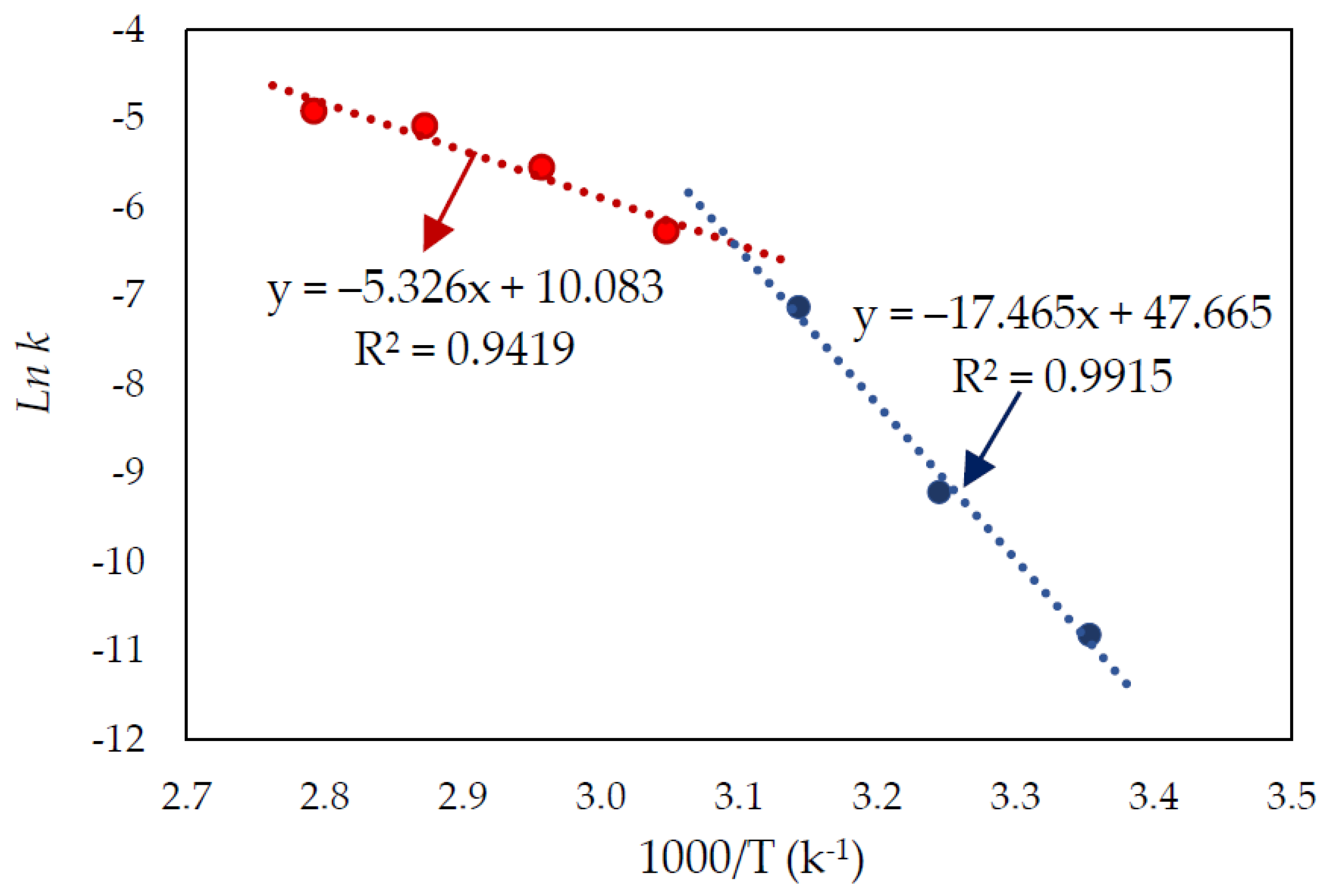
3.2. Effect of Temperature
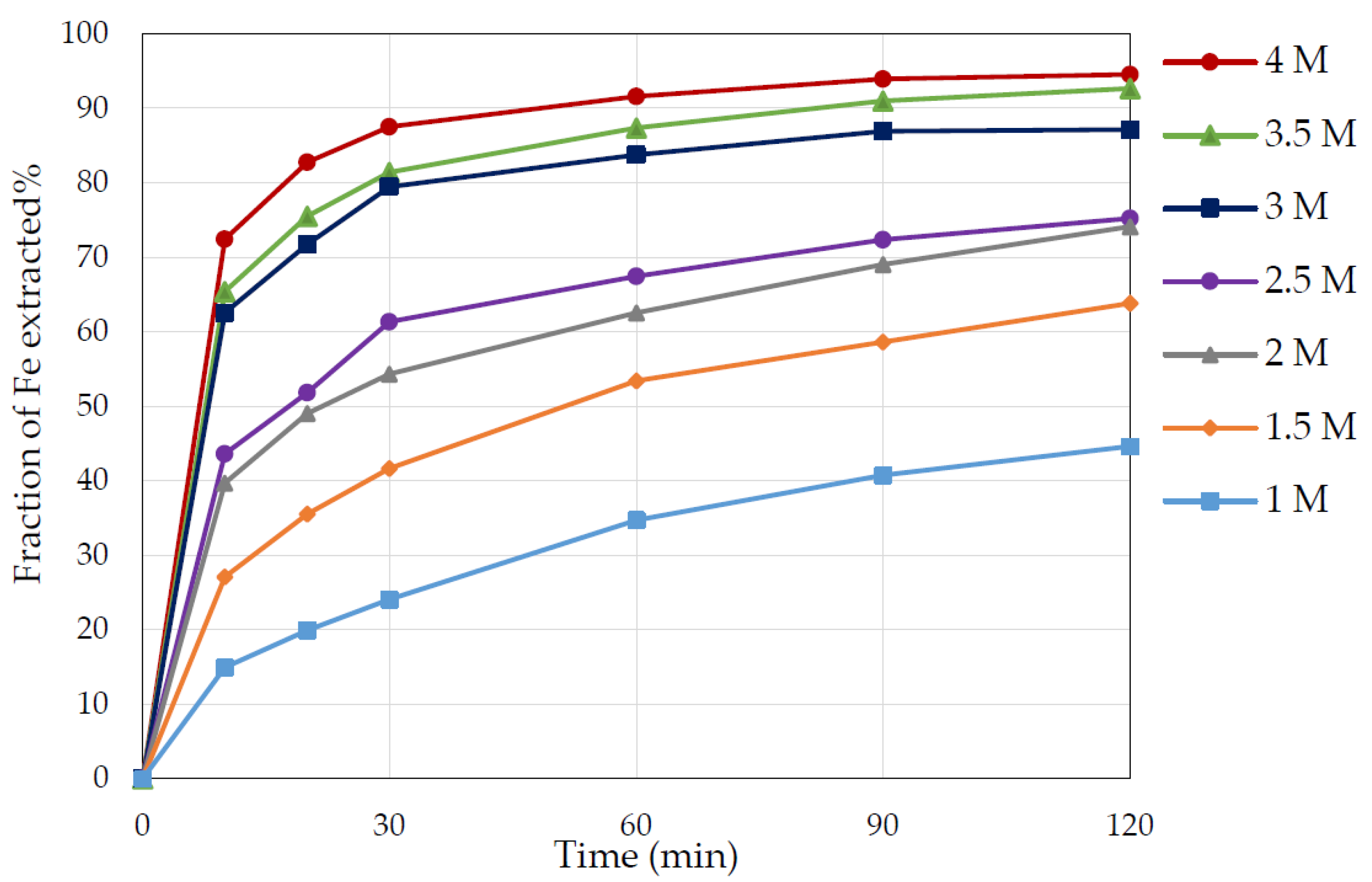
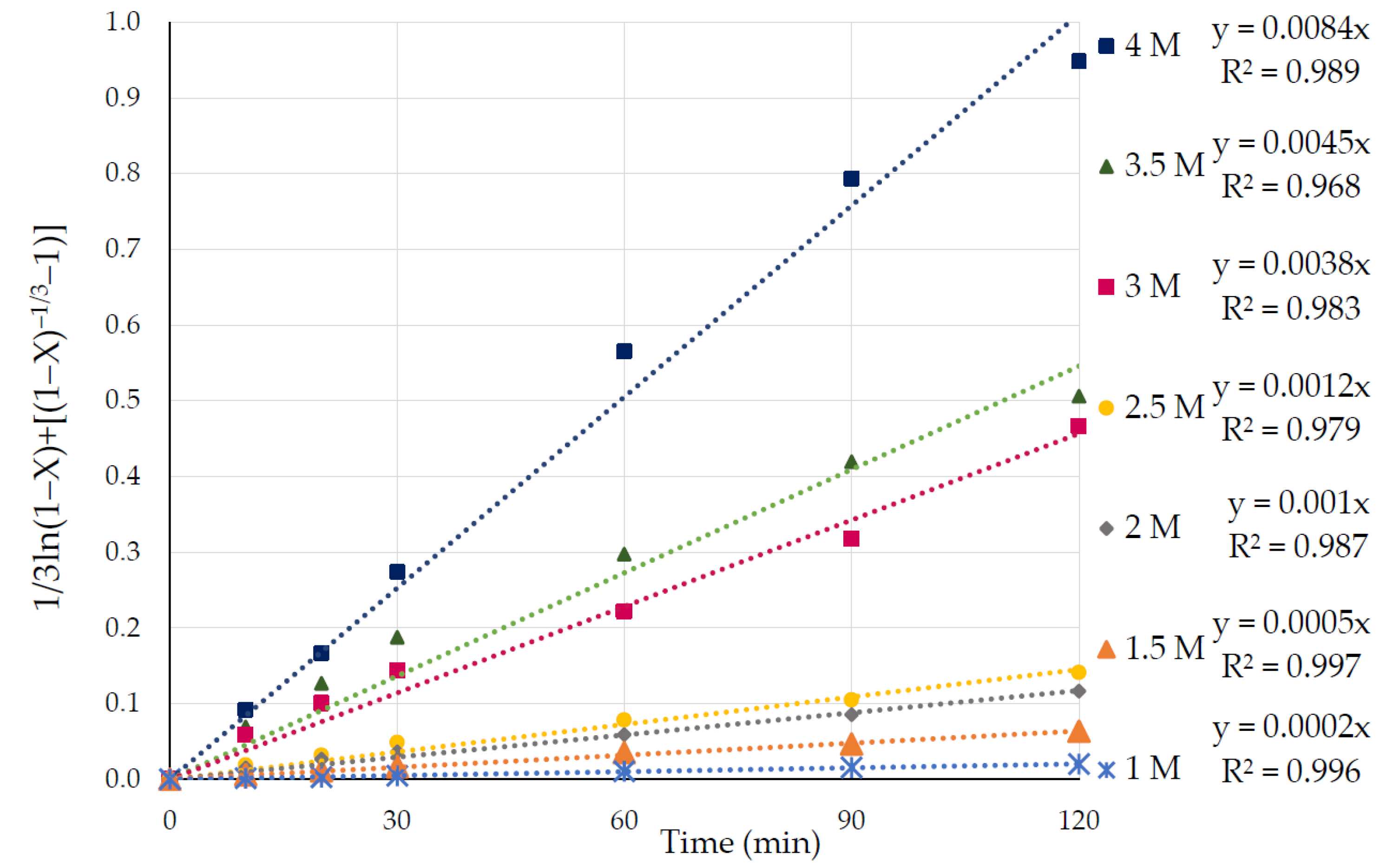
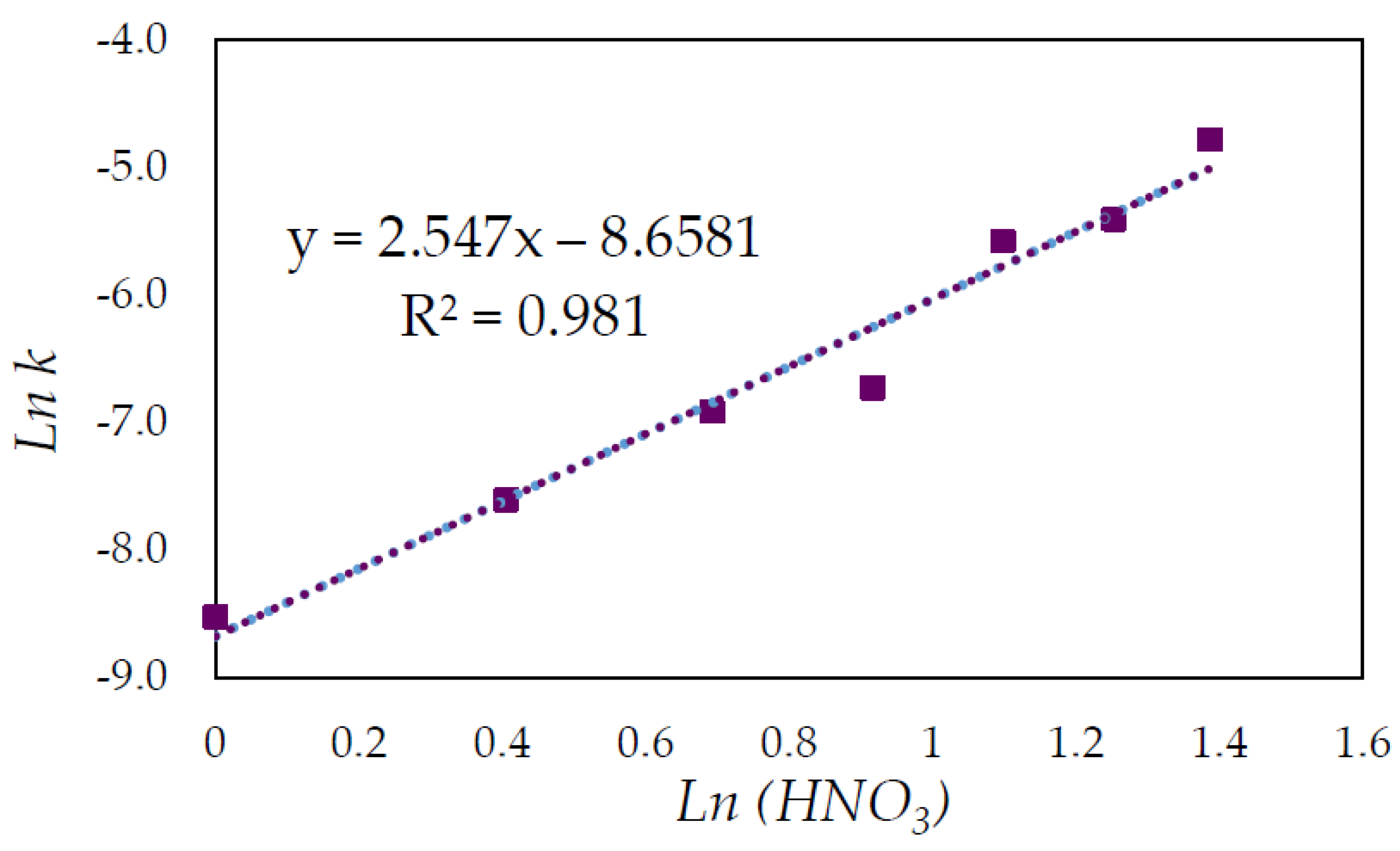
3.3. Effect of Nitric Acid Concentration
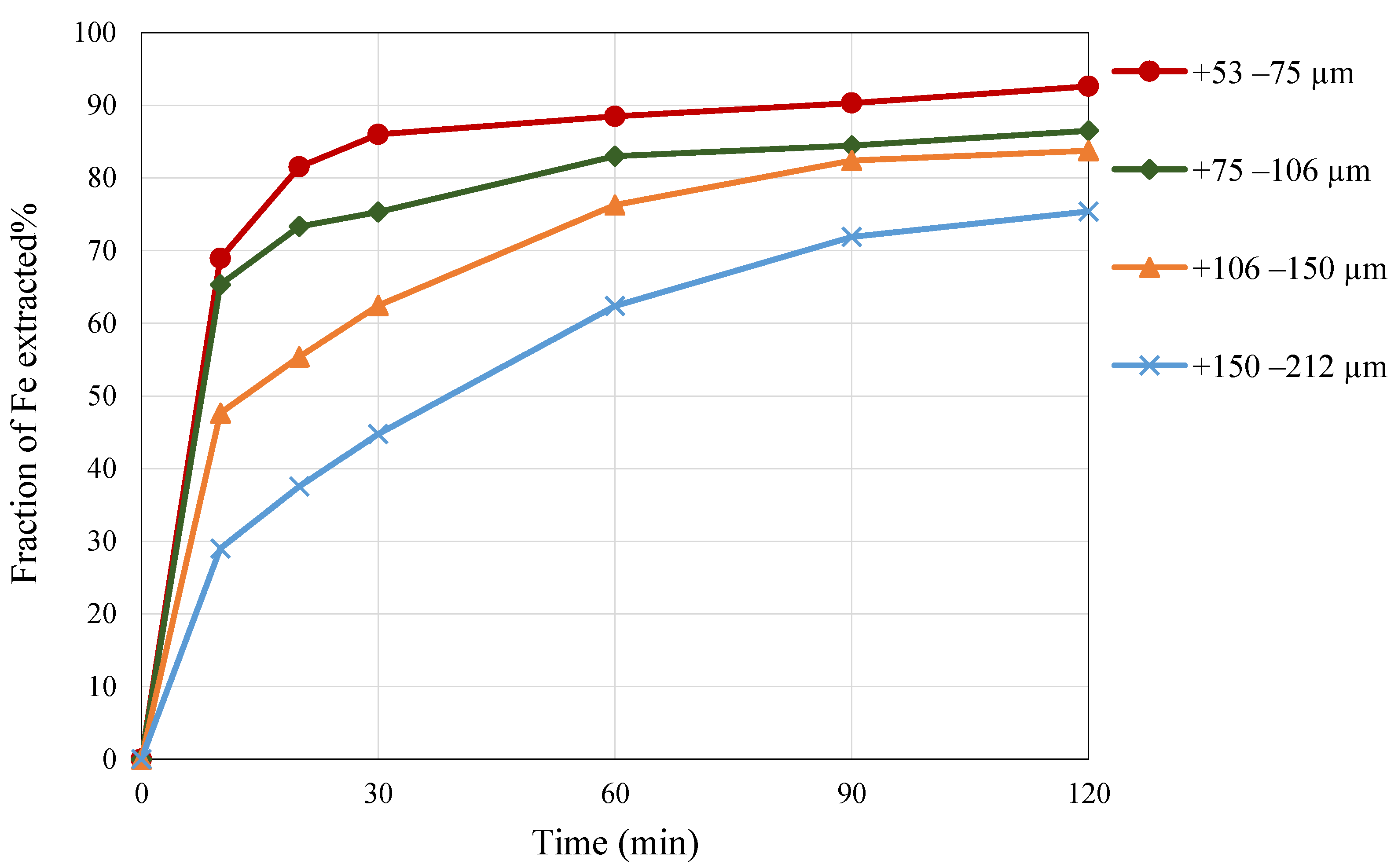
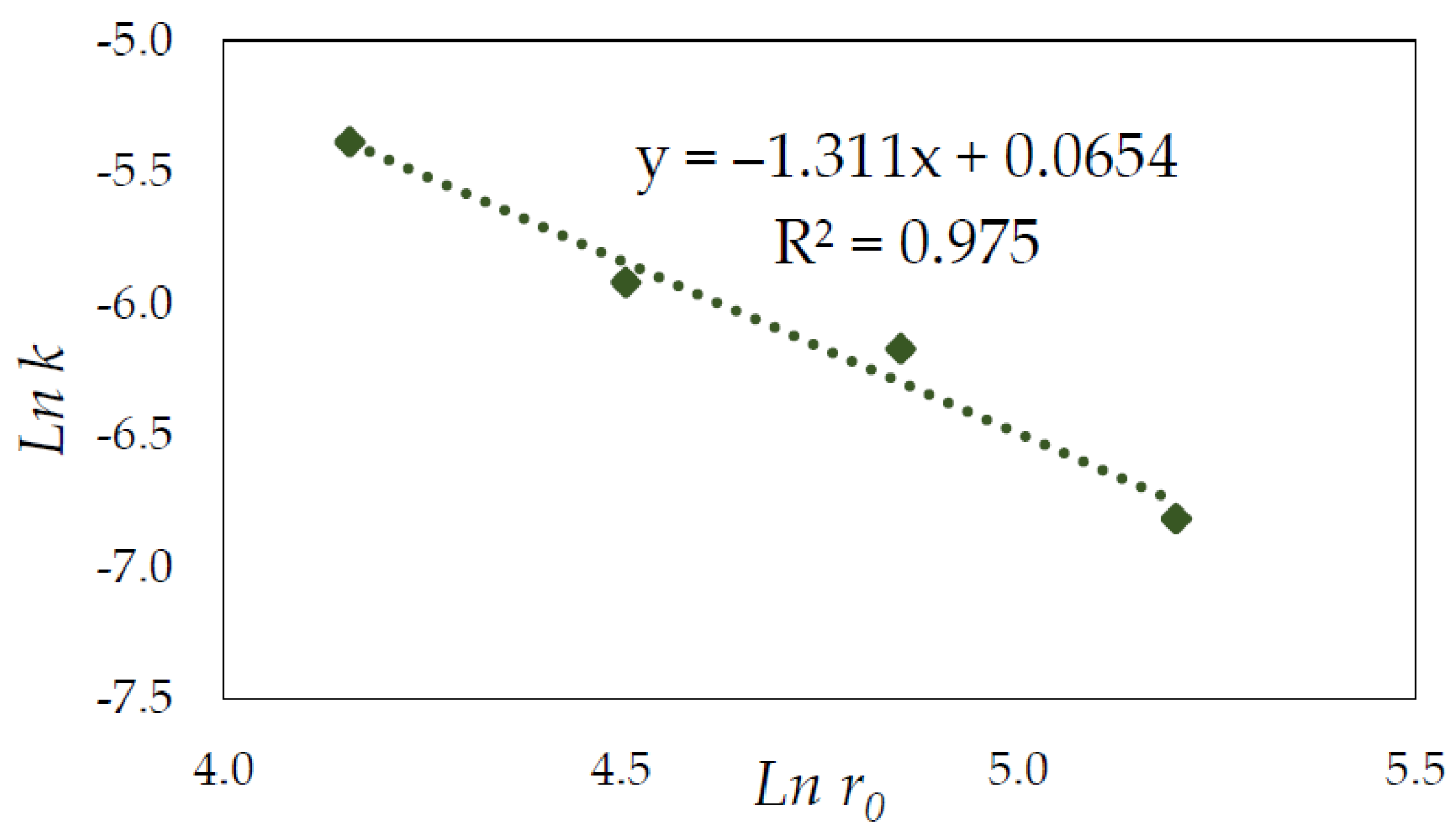
3.4. Effect of Particle Size
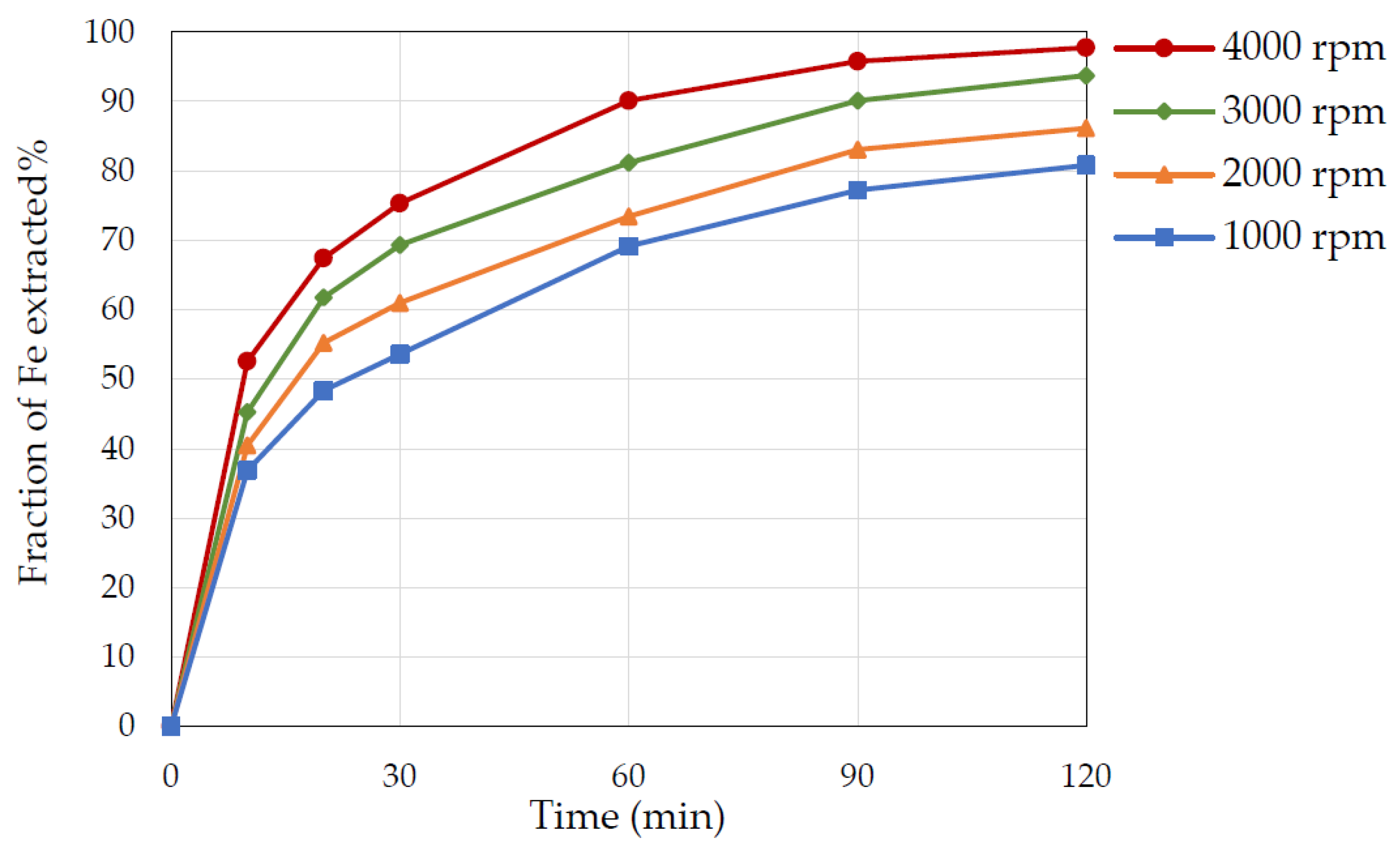
3.5. Effect of Stirring Speed
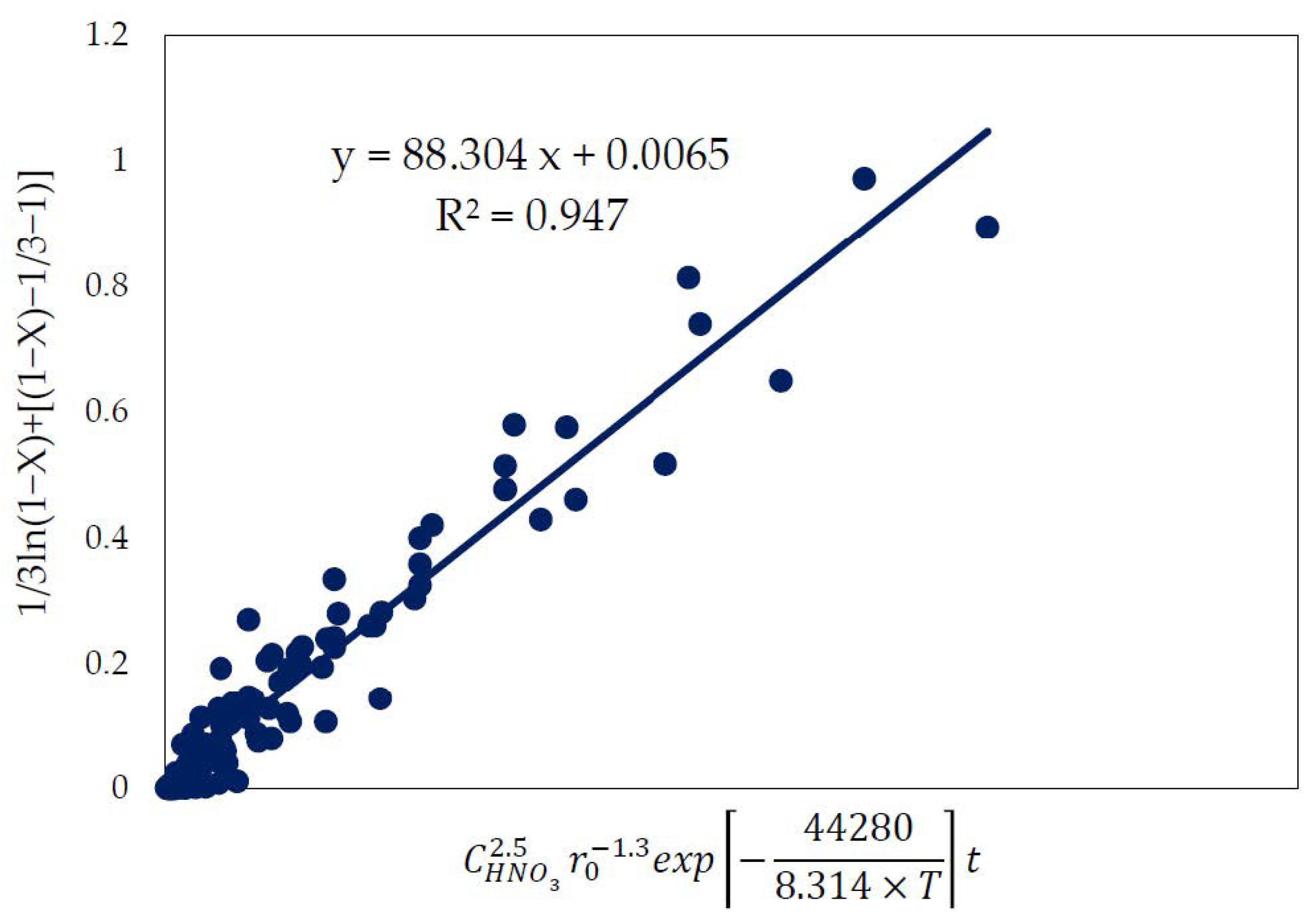
3.6. Kinetic Model
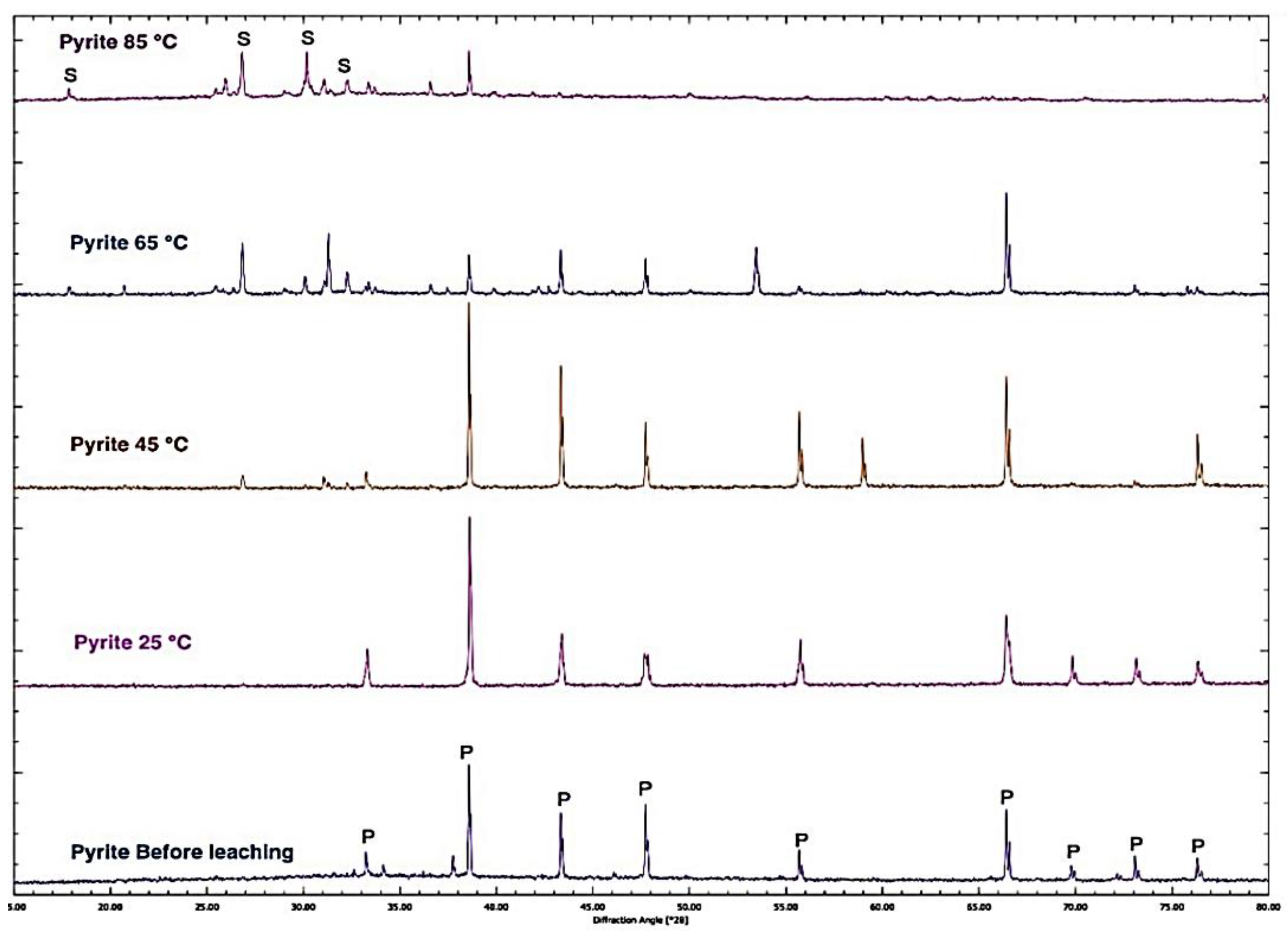
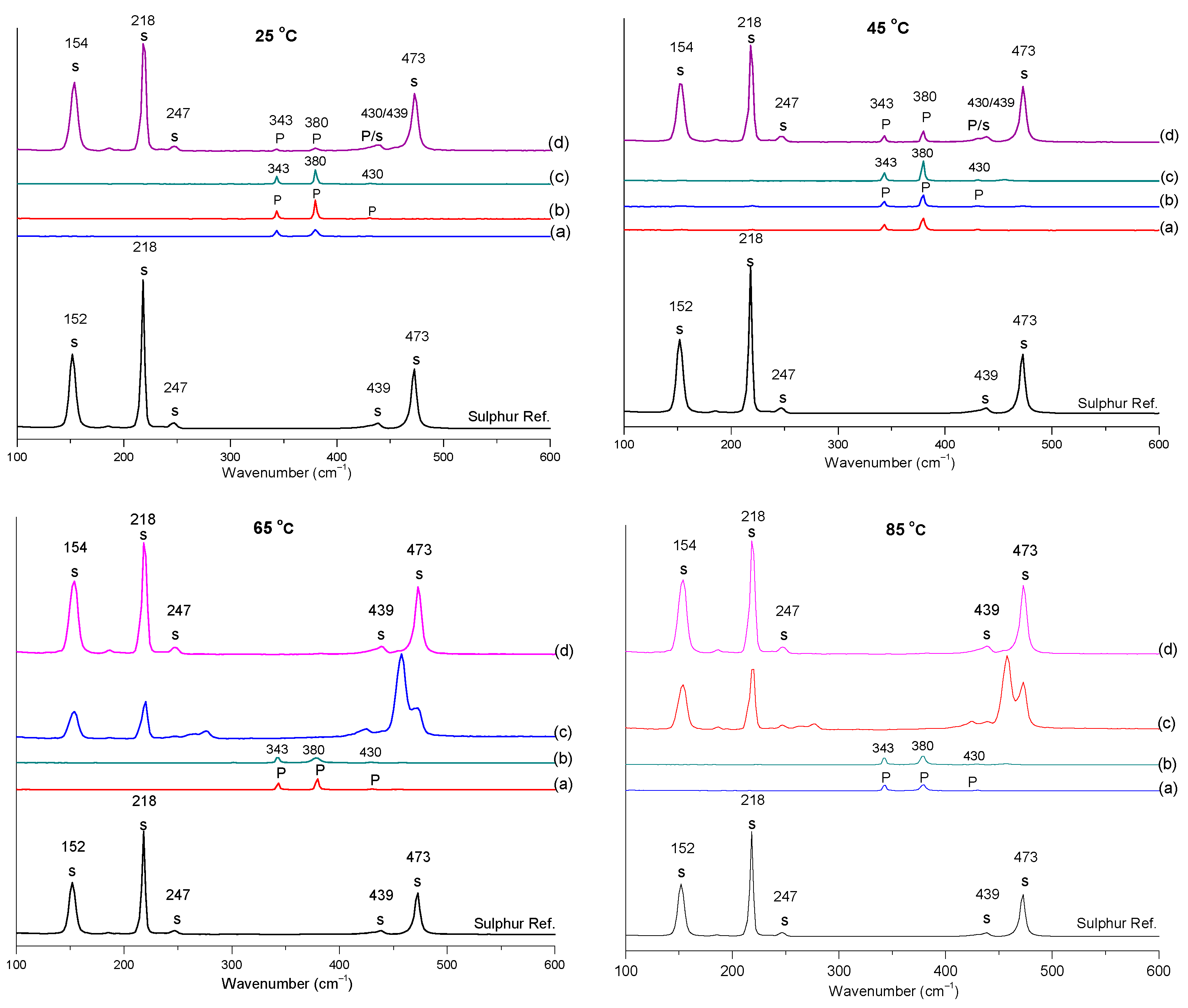
3.7. Characteristics of Solid Residue
4. Conclusions
- ▪
- Pyrite dissolution at temperatures higher than 45 °C and up to 85 °C was between 72% and 95% after 120 min leaching in 3 M HNO3.
- ▪
- At nitric acid concentrations between 2.5 M and 4 M, HNO3 had a powerful oxidising ability, resulting in an ample pyrite dissolution of between 74% and 95%.
- ▪
- Reducing the fraction size of pyrite from +150–212 µm to +53–75 µm led to an increase in iron extraction from 75% to approximately 92%.
- ▪
- Increasing the stirring speed from 1000 rpm to 4000 rpm resulted in Fe extraction of 80% to 98%.
- ▪
- The SEM images of the residue at different temperatures showed the surface of the pyrite grain became rough and pitted with cavities, and the oxidative dissolution in the nitric acid led to the formation of sulphur as the product.
- ▪
- The XRD pattern of pyrite before leaching and the residue of leached pyrite in 3 M nitric acid at varied temperatures revealed that the intensity of the pyrite peaks decreased with an increasing temperature due to the pyrite dissolution and a new sulphur phase appeared.
- ▪
- The XRD Rietveld refinement identified two sulphur species, i.e., S8 and S6, which formed during the dissolution process.
- ▪
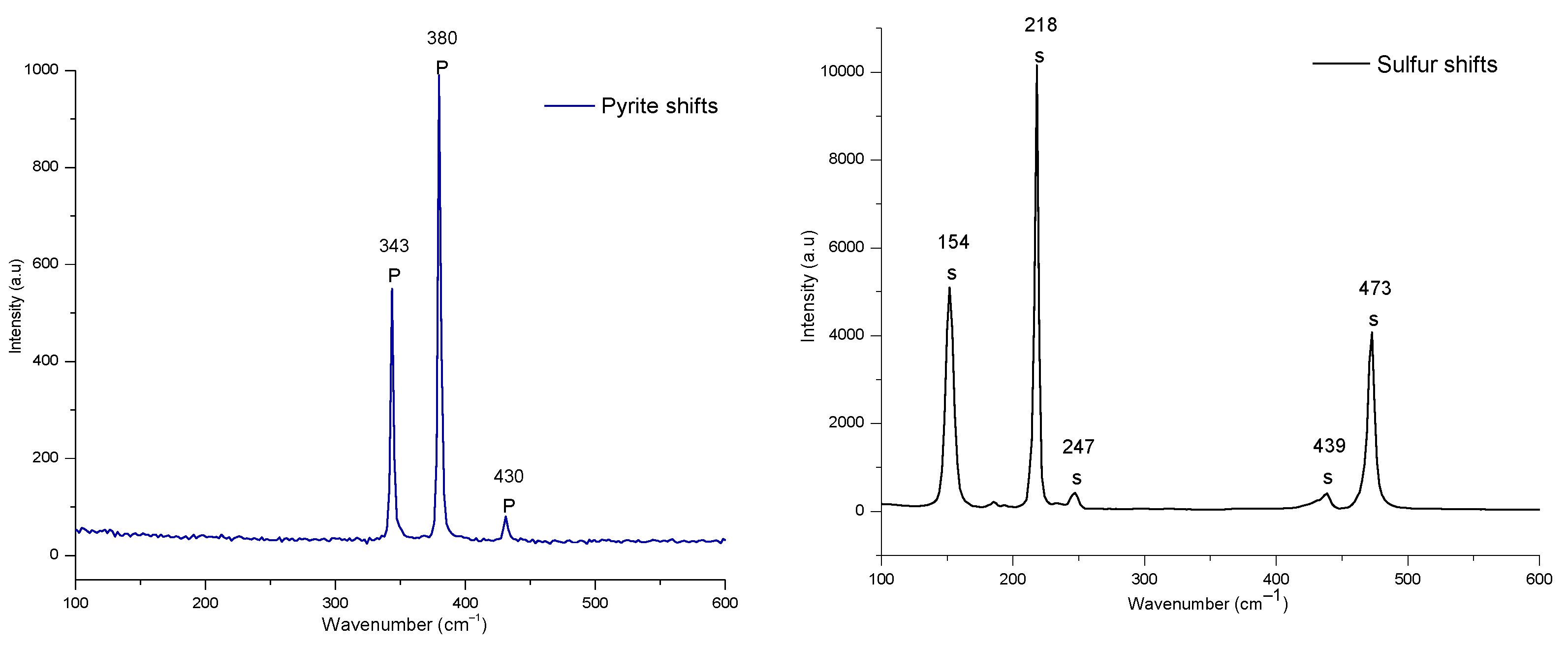
- The Raman analysis also confirmed the formation of sulphur at all the studied temperatures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Rogozhnikov, D.; Karimov, K.; Shoppert, A.; Dizer, O.; Naboichenko, S. Kinetics and mechanism of arsenopyrite leaching in nitric acid solutions in the presence of pyrite and Fe(III) ions. Hydrometallurgy 2021, 199, 105525. [Google Scholar] [CrossRef]
- Teimouri, S.; Potgieter, J.H.; Simate, G.S.; van Dyk, L.; Dworzanowski, M. Oxidative leaching of refractory sulphidic gold tailings with an ionic liquid. Miner. Eng. 2020, 156, 106484. [Google Scholar] [CrossRef]
- Medina, D.; Anderson, C.G. A review of the cyanidation treatment of copper-gold ores and concentrates. Metals 2020, 10, 897. [Google Scholar] [CrossRef]
- Vaughan, J.P. The process mineralogy of gold: The classification of ore types. J. Miner. Met. Mater. Soc. 2004, 56, 46–48. [Google Scholar] [CrossRef]
- Rogozhnikov, D.A.; Shoppert, A.A.; Dizer, O.A.; Karimov, K.A.; Rusalev, R.E. Leaching kinetics of sulfides from refractory gold concentrates by nitric acid. Metals 2019, 9, 465. [Google Scholar] [CrossRef] [Green Version]
- Cho, K.; Kim, H.; Myung, E.; Purev, O.; Choi, N.; Park, C. Recovery of Gold from the Refractory Gold Concentrate Using Microwave Assisted Leaching. Metals 2020, 10, 571. [Google Scholar] [CrossRef]
- Zhang, S. Oxidation of Refractory Gold Concentrates and Simultaneous Dissolution of Gold in aerated Alkaline Solutions. Ph.D. Thesis, Murdock University, Murdoch, WA, Australia, 2004; pp. 1–358. [Google Scholar]
- Fleming, C.A. Basic iron sulphate—A potential killer for pressure oxidation processing of refractory gold concentrates if not handled appropriately. SGS Miner. Serv. Tech. Bull. 2009, 6, 10. [Google Scholar]
- Runkel, M.; Sturm, P. Pyrite roasting, an alternative to sulphur burning. J. S. Afr. Inst. Min. Metall. 2009, 109, 491–496. [Google Scholar]
- Rusanen, L.; Aromaa, J.; Forsen, O. Pressure oxidation of pyrite-arsenopyrite refractory gold concentrate. Physicochem. Probl. Miner. Process. 2013, 49, 101–109. [Google Scholar]
- Deng, T.; Liao, M. Gold recovery enhancement from a refractory flotation concentrate by sequential bioleaching and thiourea leach. Hydrometallurgy 2002, 63, 249–255. [Google Scholar] [CrossRef]
- Romero, R.; Mazuelos, A.; Palencia, I.; Carranza, F. Copper recovery from chalcopyrite concentrates by the BRISA process. Hydrometallurgy 2003, 70, 205–215. [Google Scholar] [CrossRef]
- Gao, G.; Li, D.; Zhou, Y.; Sun, X.; Sun, W. Kinetics of high-sulphur and high-arsenic refractory gold concentrate oxidation by dilute nitric acid under mild conditions. Miner. Eng. 2009, 22, 111–115. [Google Scholar] [CrossRef]
- Wang, G.H.; Xie, J.P.; Li, S.P.; Guo, Y.J.; Pan, Y.; Wu, H.; Liu, X.X. Two-step oxidation of refractory gold concentrates with different microbial communities. J. Microbiol. Biotechnol. 2016, 26, 1871–1880. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Darvanjooghi, M.H.K.; Magdouli, S.; Brar, S.K.; Abdollahi, H.; Zolfaghari, M. Bio-oxidation of Gold from Refractory Sulfide Ores: A Journey Ahead. Geomicrobiol. J. 2022, 39, 399–415. [Google Scholar] [CrossRef]
- Xu, R.; Li, Q.; Meng, F.; Yang, Y.; Xu, B.; Yin, H.; Jiang, T. Bio-oxidation of a double refractory gold ore and investigation of preg-robbing of gold from thiourea solution. Metals 2020, 10, 1216. [Google Scholar] [CrossRef]
- Dizer, O.; Rogozhnikov, D.; Karimov, K.; Kuzas, E.; Suntsov, A. Nitric Acid Dissolution of Tennantite, Chalcopyrite and Sphalerite in the Presence of Fe (III) Ions and FeS2. Materials 2022, 15, 1545. [Google Scholar] [CrossRef]
- Almeida, T.D.C.; Garcia, E.M.; da Silva, H.W.A.; Matencio, T.; Lins, V.D.F.C. Electrochemical study of chalcopyrite dissolution in sulfuric, nitric and hydrochloric acid solutions. Int. J. Miner. Process. 2016, 149, 25–33. [Google Scholar] [CrossRef]
- Celep, O.; Yazici, E.Y.; Deveci, H. A preliminary study on nitric acid pre-treatment of refractory gold/silver ores. In Proceedings of the IMCET 2017 New Trends Mining—25th International Mining Congress and Exhibition of Antalya, Antalya, Turkey, 11–14 April 2017; pp. 463–468. [Google Scholar]
- Li, D. Developments in the pretreatment of refractory gold minerals by nitric acid. In Proceedings of the World Gold Conference Southern African Institute of Mining and Metallurgy, Johannesburg, South Africa, 26–30 October 2009; Volume 2, pp. 145–150. [Google Scholar]
- Bryson, L.J.; Crundwell, F.K. The anodic dissolution of pyrite (FeS2) in hydrochloric acid solutions. Hydrometallurgy 2014, 143, 42–53. [Google Scholar] [CrossRef]
- Holmes, P.R.; Crundwell, F.K. The kinetics of the oxidation of pyrite by ferric ions and dissolved oxygen: An electrochemical study. Geochim. Cosmochim. Acta 2000, 64, 263–274. [Google Scholar] [CrossRef]
- Descostes, M.; Vitorge, P.; Beaucaire, C. Pyrite dissolution in acidic media. Geochim. Cosmochim. Acta 2004, 68, 4559–4569. [Google Scholar] [CrossRef]
- Long, H.; Dixon, D.G. Pressure oxidation of pyrite in sulfuric acid media: A kinetic study. Hydrometallurgy 2004, 73, 335–349. [Google Scholar] [CrossRef]
- Salas-Martell, D.; Pareja-Guzman, G.; Tello-Hijar, J.; Rodriguez-Reyes, J.C.F. Leaching of a pyrite-based ore containing copper using sulfuric acid and hydrogen peroxide. Int. J. Ind. Chem. 2020, 11, 195–201. [Google Scholar] [CrossRef]
- Cho, E.H.; Chang, K.H.; Rollins, R.R. A Kinetic study of leaching of coal pyrite with nitric acid. Metall. Trans. B 1983, 14, 317–324. [Google Scholar] [CrossRef]
- Pilawa, B.; Wiȩckowski, A.B.; Pietrzak, R.; Wachowska, H. Oxidation of demineralized coal and coal free of pyrite examined by EPR spectroscopy. Fuel 2002, 81, 1925–1931. [Google Scholar] [CrossRef]
- Crundwe, F.K. The influence of the electronic structure of solids on the anodic dissolution and leaching of Semiconducting Sulphide Minerals. Hydrometallurgy 1988, 21, 155–190. [Google Scholar] [CrossRef]
- Crundwell, F.K. The dissolution and leaching of minerals: Mechanisms, myths and misunderstandings. Hydrometallurgy 2013, 139, 132–148. [Google Scholar] [CrossRef]
- Faraji, F.; Alizadeh, A.; Rashchi, F.; Mostoufi, N. Kinetics of leaching: A review. Rev. Chem. Eng. 2020, 1, 1–36. [Google Scholar] [CrossRef]
- Dickinson, C.F.; Heal, G.R. Solid-liquid diffusion controlled rate equations. Thermochim. Acta 1999, 340–341, 89–103. [Google Scholar] [CrossRef]
- Li, K.; Chen, J.; Zou, D.; Liu, T.; Li, D. Kinetics of nitric acid leaching of cerium from oxidation roasted Baotou mixed rare earth concentrate. J. Rare Earths 2019, 37, 198–204. [Google Scholar] [CrossRef]
- Xia, J.l.; Yang, Y.; He, H.; Zhao, X.J.; Liang, C.L.; Zheng, L.; Ma, C.Y.; Zhao, Y.D.; Nie, Z.Y.; Qiu, G.Z. Surface analysis of sulfur speciation on pyrite bioleached by extreme thermophile Acidianus manzaensis using Raman and XANES spectroscopy. Hydrometallurgy 2010, 100, 129–135. [Google Scholar] [CrossRef]
- Toniazzo, V.; Mustin, C.; Portal, J.M.; Humbert, B.; Benoit, R.; Erre, R. Elemental sulfur at the pyrite surfaces: Speciation and quantification. Appl. Surf. Sci. 1999, 143, 229–237. [Google Scholar] [CrossRef]
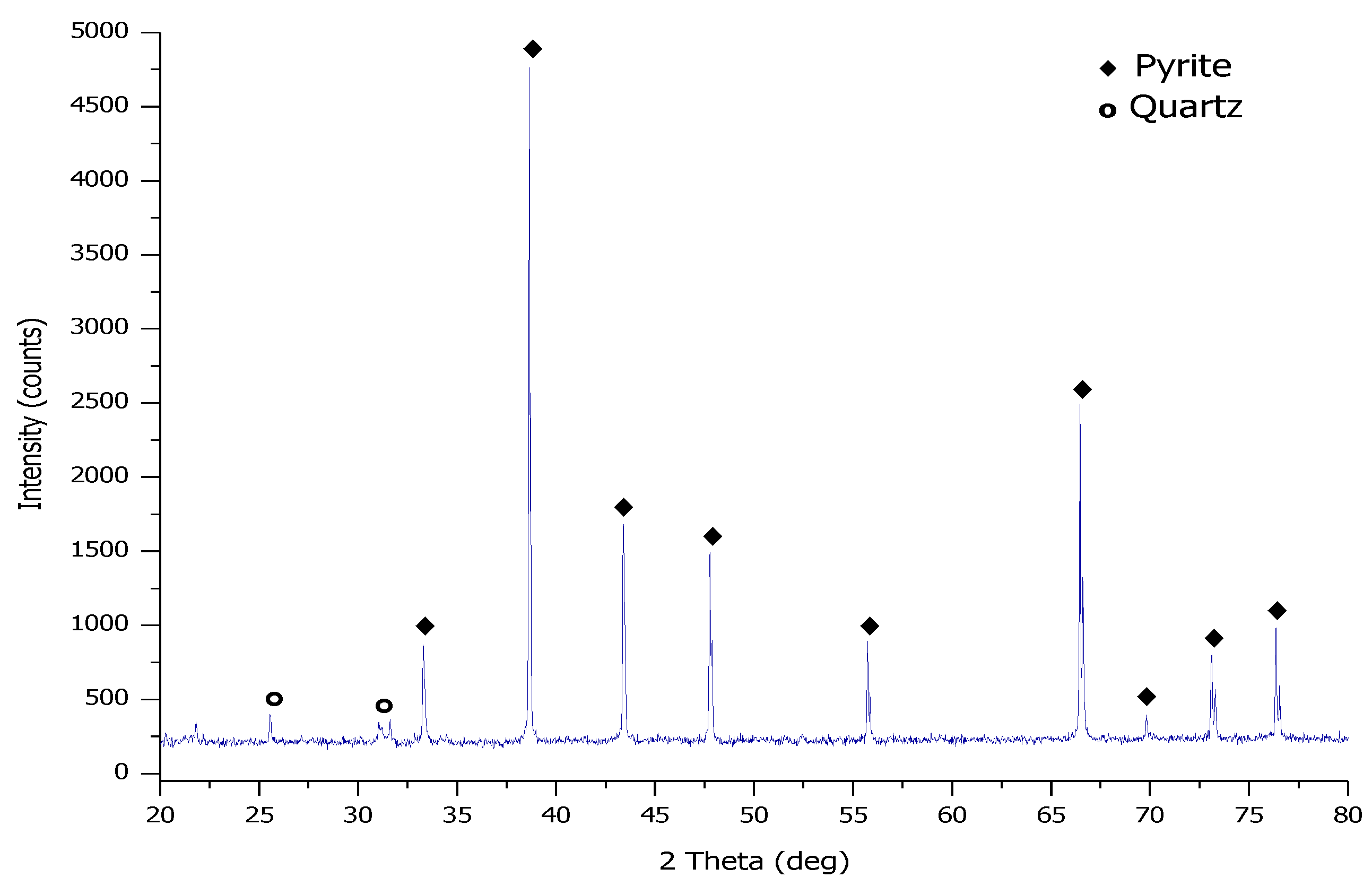
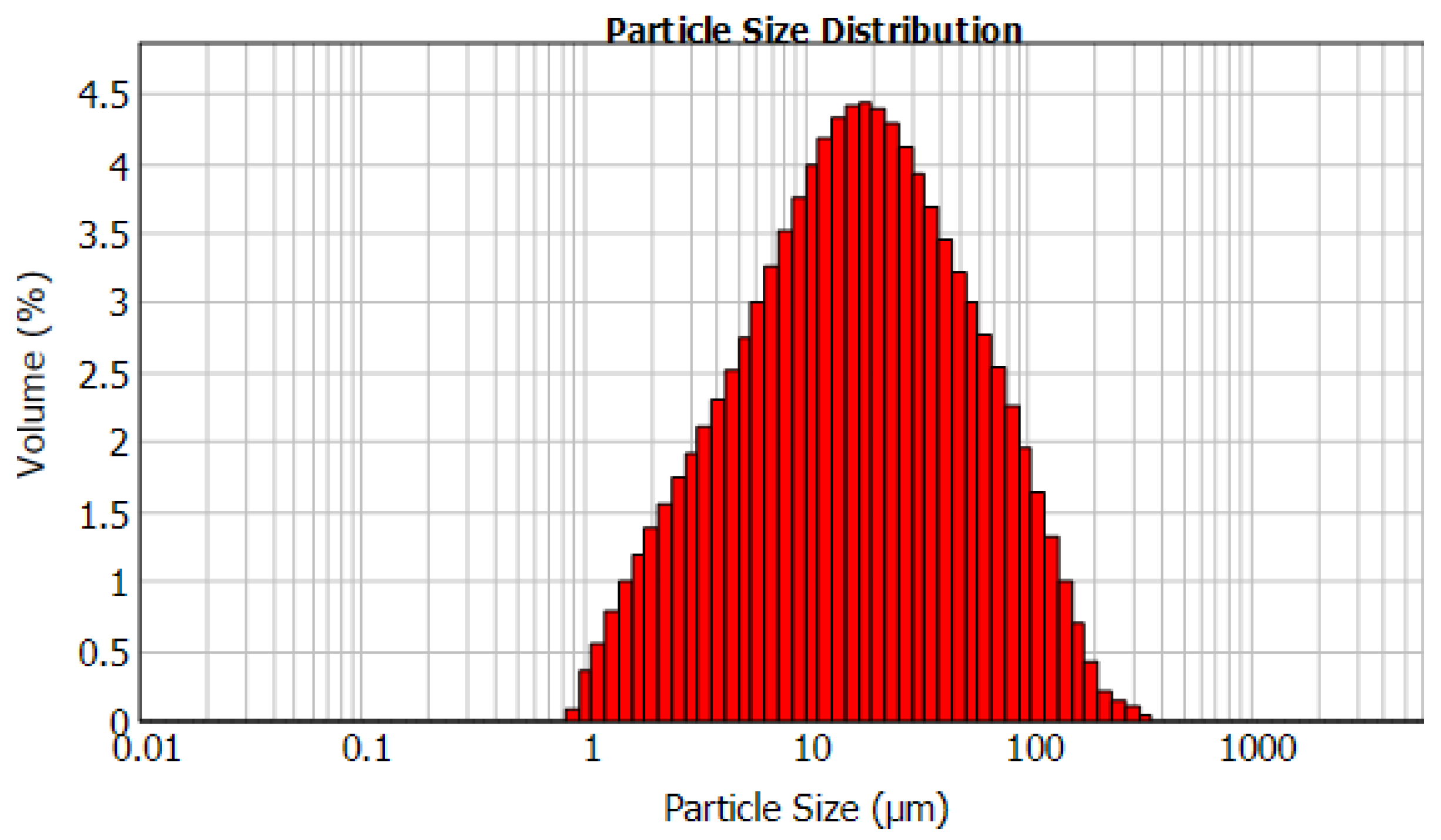



| Chemical Composition | Al2O3 | SiO2 | TiO2 | CaO | S * | FeS2 | LOI |
|---|---|---|---|---|---|---|---|
| Wt% | 2.25 | 4.19 | 0.45 | 1.38 | 13.41 | 69.12 | 9.16 |
| Temp./Phases | Pyrite (FeS2) (Mole Fraction) | Quartz (SiO2) | Sulphur (S8) | Sulphur Epsilon (S6) |
|---|---|---|---|---|
| Leaching at 25 °C | 96.5% (0.8) | 0.5% | 3.1% | – |
| Leaching at 45 °C | 85.1% (0.7) | 3.8% | 11.1 | – |
| Leaching at 65 °C | 11.3% (0.09) | 3.3% | 74.7% | 10.7% |
| Leaching at 85 °C | 5% (0.04) | – | 84.0% | 11.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teimouri, S.; Potgieter, J.H.; van Dyk, L.; Billing, C. The Kinetics of Pyrite Dissolution in Nitric Acid Solution. Materials 2022, 15, 4181. https://doi.org/10.3390/ma15124181
Teimouri S, Potgieter JH, van Dyk L, Billing C. The Kinetics of Pyrite Dissolution in Nitric Acid Solution. Materials. 2022; 15(12):4181. https://doi.org/10.3390/ma15124181
Chicago/Turabian StyleTeimouri, Samaneh, Johannes Herman Potgieter, Lizelle van Dyk, and Caren Billing. 2022. "The Kinetics of Pyrite Dissolution in Nitric Acid Solution" Materials 15, no. 12: 4181. https://doi.org/10.3390/ma15124181
APA StyleTeimouri, S., Potgieter, J. H., van Dyk, L., & Billing, C. (2022). The Kinetics of Pyrite Dissolution in Nitric Acid Solution. Materials, 15(12), 4181. https://doi.org/10.3390/ma15124181








