Applying the FMR Technique to Analyzing the Influence of Nitriding on the Magnetic Properties of Steel
Abstract
:1. Introduction
2. Research Methodology
3. Results and Discussion
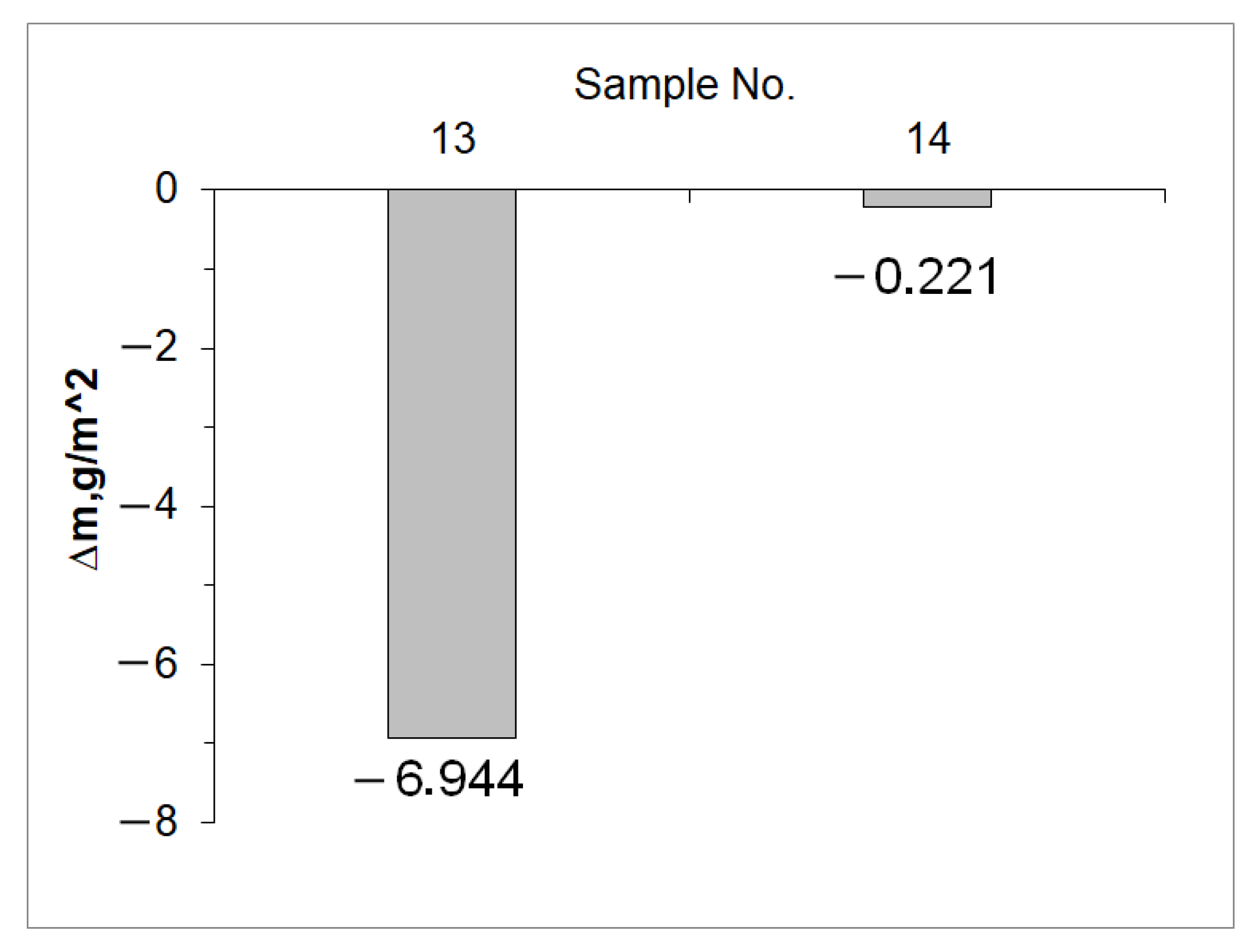
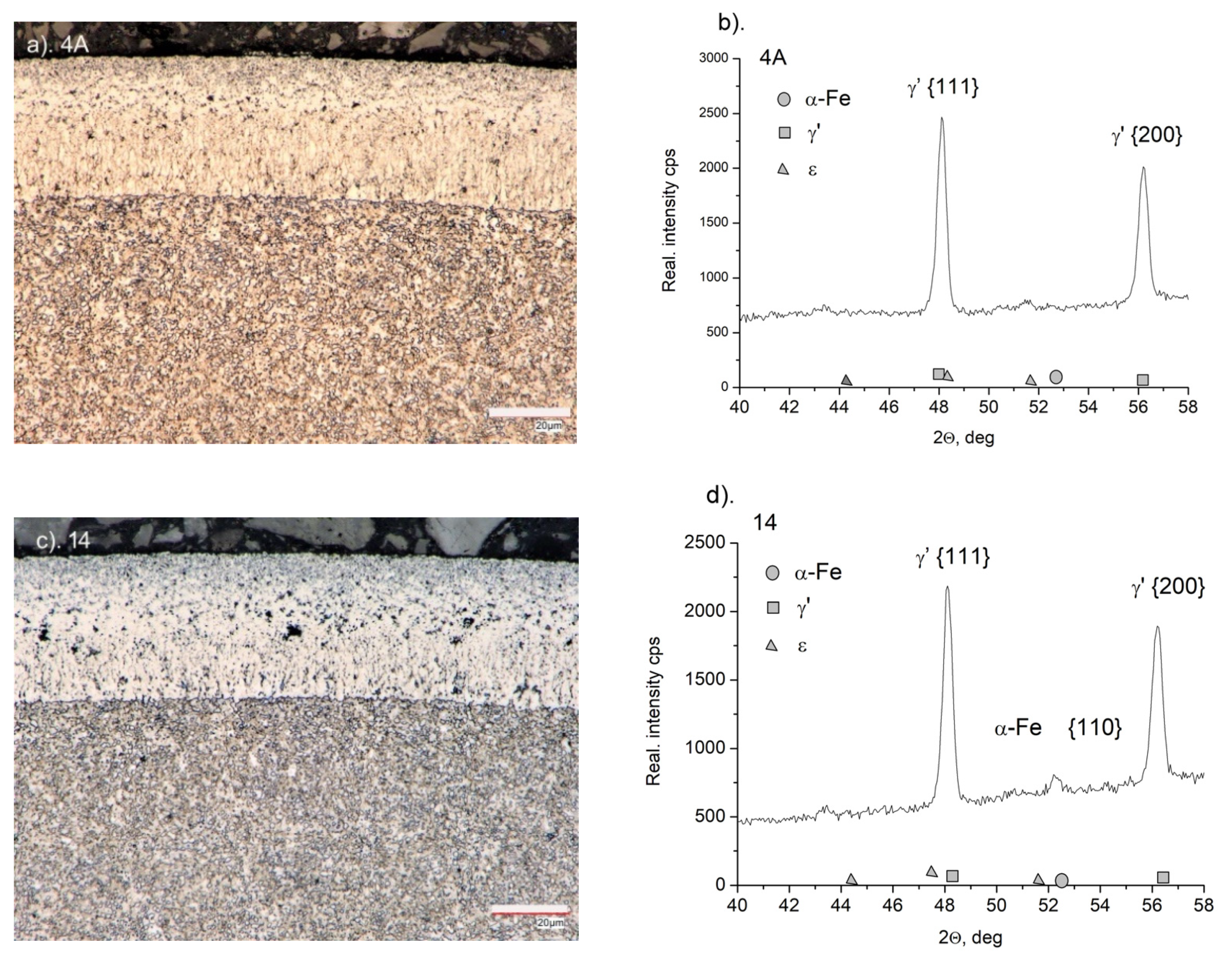
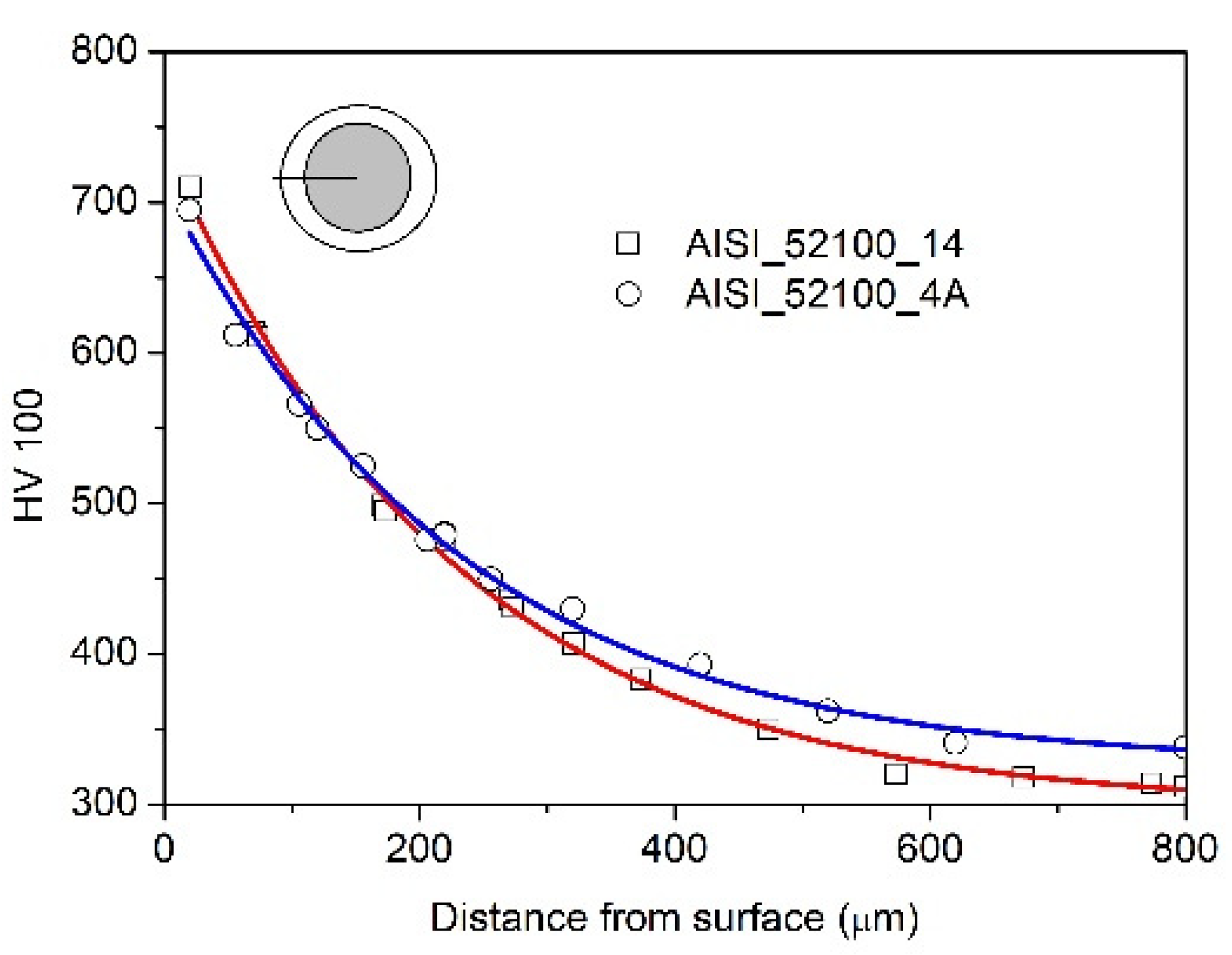
3.1. Mechanical Properties
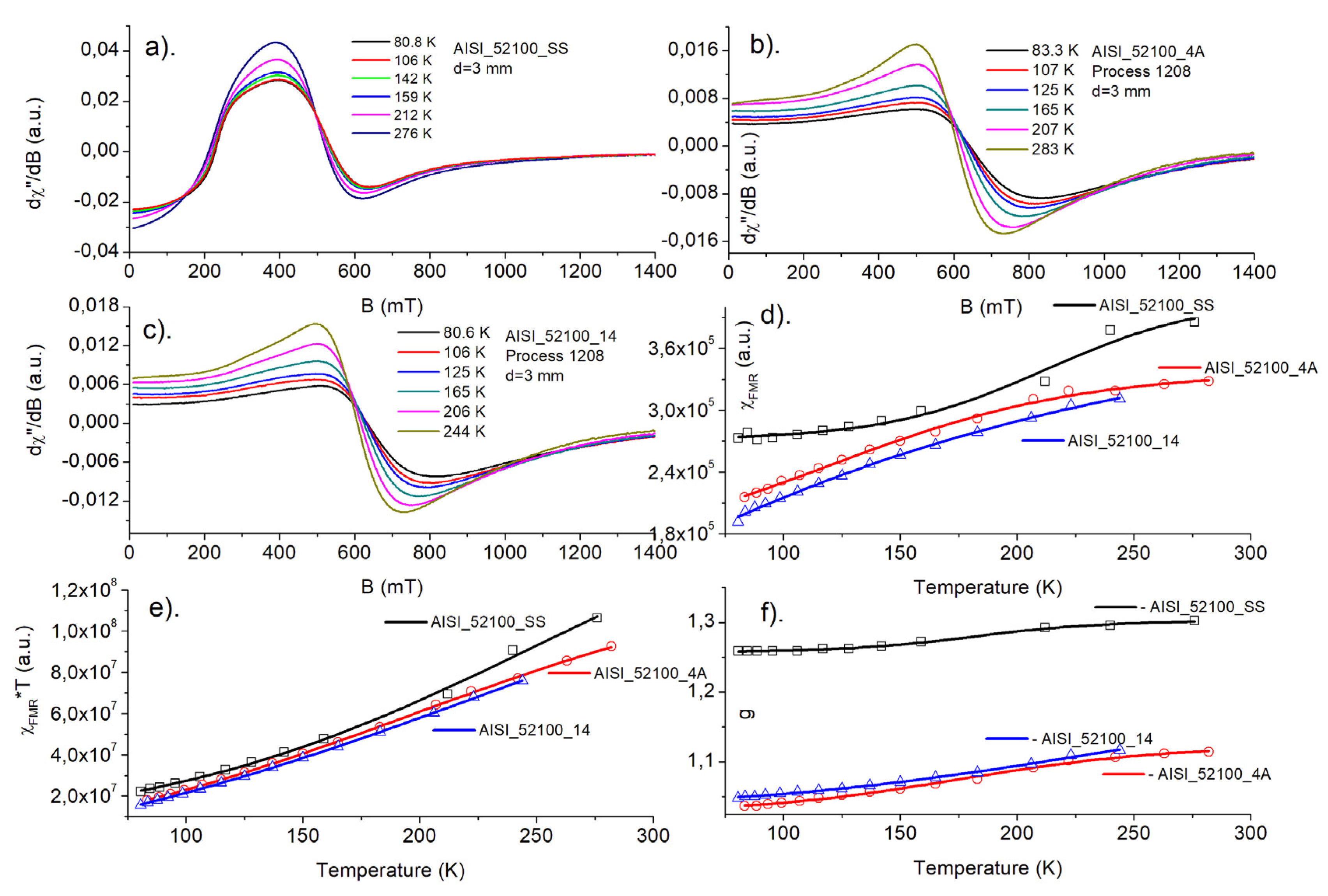
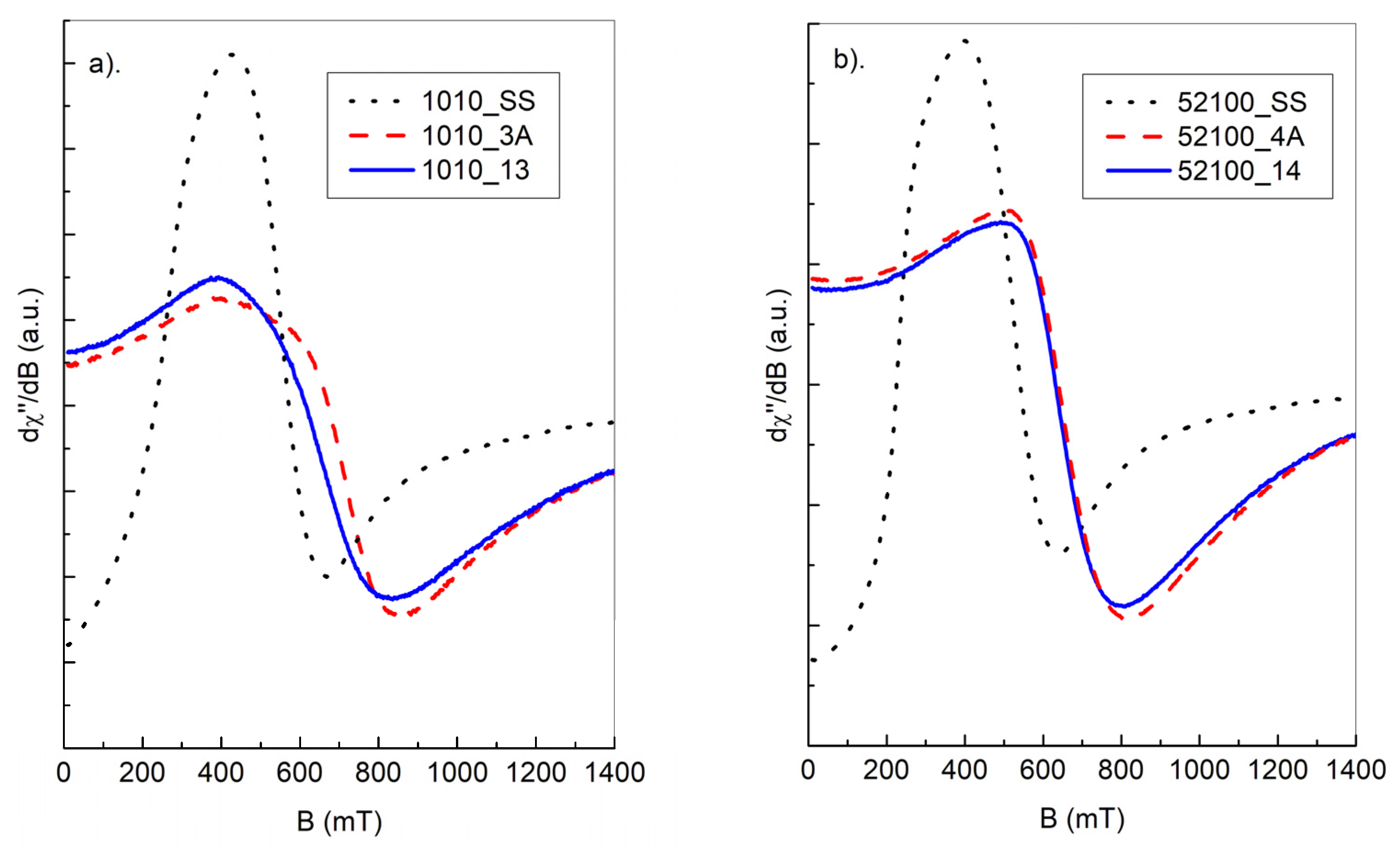
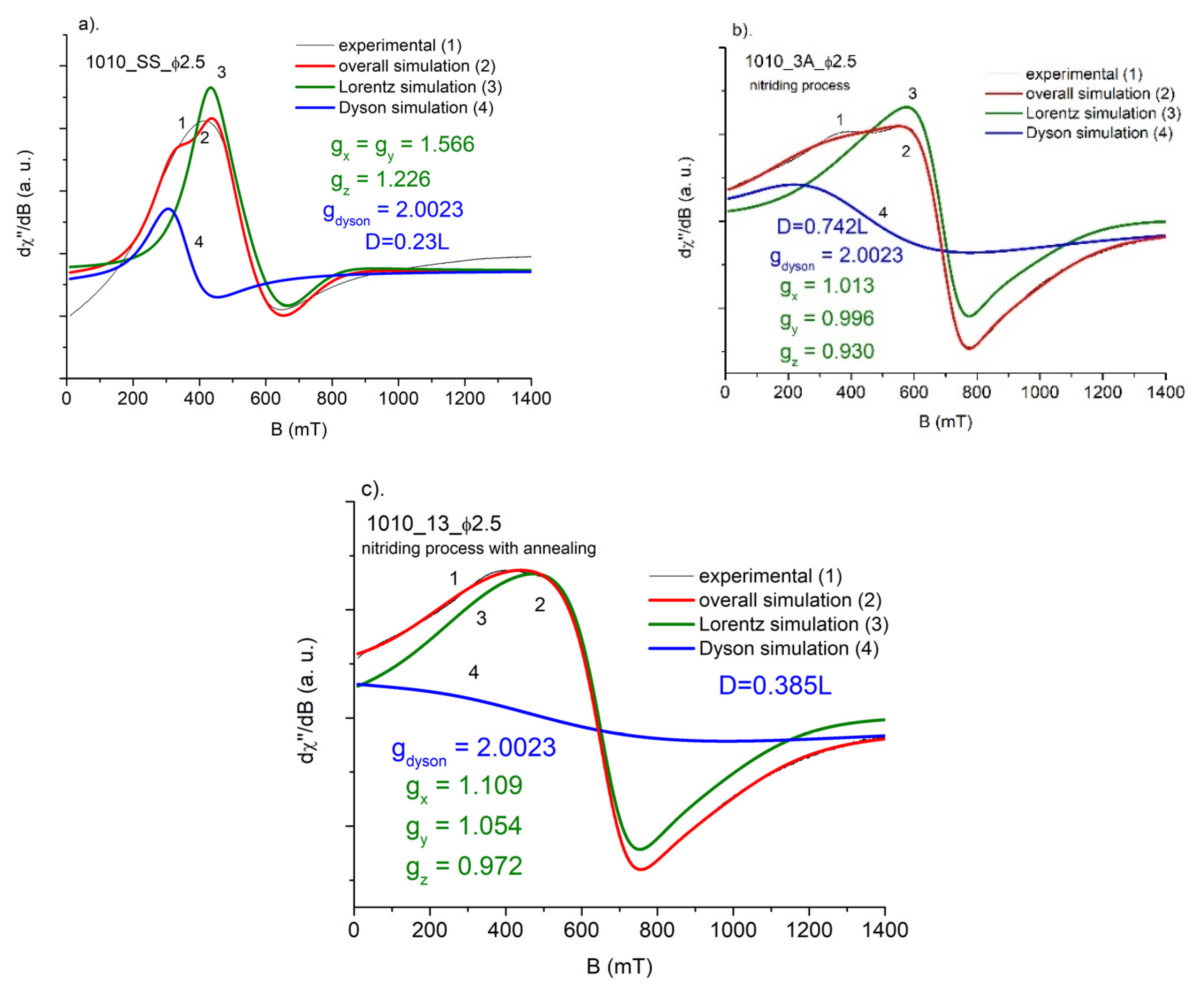
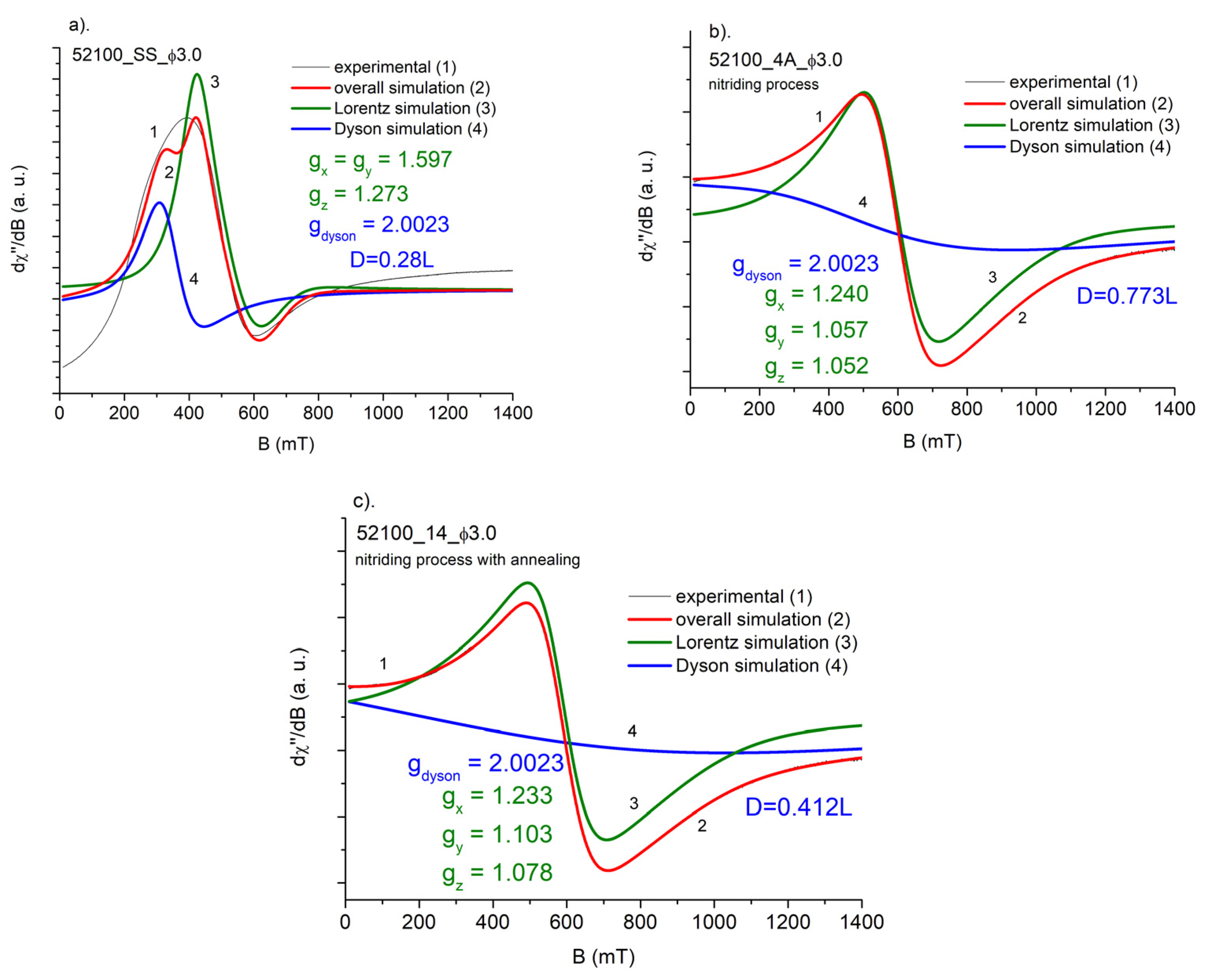
3.2. FMR Spectra
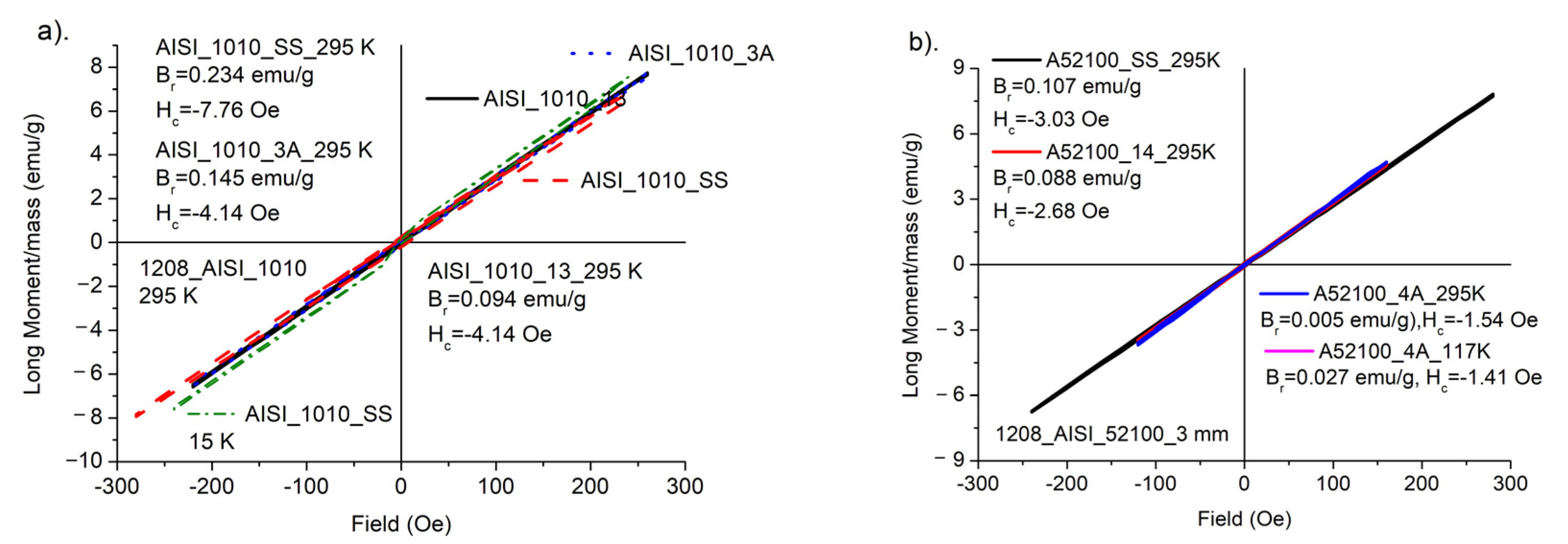
3.3. Magnetic Susceptibility Measurements
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lehrer, E. Über das Eisen—Wasserstoff—Ammoniak Gleichgewicht. Z. Für. Elektrochem. 1930, 36, 383–393. [Google Scholar] [CrossRef]
- Somers, M.A.J. IFHTSE Global 21: Heat treatment and surface engineering in the twenty-first century. In: Part 14—Development of compound layer during nitriding and nitrocarburizing; current understanding and future challenges. Int. Heat Treat. Surf. Eng. 2011, 5, 7–16. [Google Scholar] [CrossRef]
- Michalski, J.; Tacikowski, J.; Wach, P.; Lunarska, E.; Baum, H. Formation of single-phase layer of γ’-nitride in controlled gas nitriding. Met. Sci. Heat Treat. 2005, 47, 516–519. [Google Scholar] [CrossRef]
- Massalski, T.B. Binary Alloy Phase Diagrams; ASM Metals Park: Cleveland, OH, USA, 1990; ISBN 978-1-62708-163-4. [Google Scholar]
- Kardonina, N.I.; Yurovskikh, A.S.; Kolpakov, A.S. Transformations in the Fe-N System. Met. Sci. Heat Treat. 2010, 52, 457–467. [Google Scholar] [CrossRef]
- Du Marchie van Voorthuysen, E.H.; Boerma, D.O.; Chechenin, N.C. Low-temperature extension of the Lehrer diagram and the iron-nitrogen phase diagram. Metall. Mater. Trans. A 2002, 33, 2593–2598. [Google Scholar] [CrossRef]
- Liapina, T.; Leineweber, A.; Mittemeijer, E.J. Nitrogen redistribution in ε/γ’-iron nitride compound layers upon annealing. Scr. Mater. 2003, 48, 1643–1648. [Google Scholar] [CrossRef]
- Yurovskikh, A.S.; Kardonina, N.I.; Kolpakov, A.S. Phase transformations in nitrided iron powders. Met. Sci. Heat Treat. 2015, 57, 507–514. [Google Scholar] [CrossRef]
- Ratajski, J. Wybrane Aspekty Współczesnego Azotowania Gazowego Pod Kątem Sterowania Procesem; Wydawnictwo Uczelniane Politechniki Koszalińskiej: Koszalin, Poland, 2003. [Google Scholar]
- Michalski, J.; Tacikowski, J. Termodynamiczne i kinetyczne aspekty regulowanego azotowania gazowego (Thermodynamic and kinetic aspects of regulated gas nitriding). Inż. Powierz. 2019, 26, 3–10. [Google Scholar] [CrossRef]
- Michalski, J.; Fuks, H.; Kaczmarek, S.M.; Leniec, G.; Kucharska, B.; Wach, P. The magnetic properties of steel after the gas nitriding process. Mater. Eng. 2017, 4, 170–176. [Google Scholar] [CrossRef]
- Mombourquette, M.J.; Weil, J.A.; McGavi, D.G. EPR-NMR User’s Manual; Department of Chemistry, University of Saskatchewan: Saskatoon, SK, Canada, 1996. [Google Scholar]
- Dyson, F.J. Electron spin resonance absorption in metals. II. Theory of electron diffusion and the skin effect. Phys. Rev. 1955, 98, 349. [Google Scholar] [CrossRef]
- Bojanowski, B.; Kaczmarek, S.M. Electron spin resonance of FeVO4. Mater. Sci.-Pol. 2014, 32, 188–192. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarek, S.M.; Fuks, H.; Berkowski, M.; Głowacki, M.; Bojanowski, B. EPR properties of concentrated NdVO4 single crystal system. Appl. Magn. Res. 2015, 46, 1023–1033. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaczmarek, S.M.; Leniec, G.; Michalski, J. Influence of Nitriding on Magnetic Properties of Steel Ball Samples; Lambert Academic Publishing: Saarbrücken, Germany, 2019; ISBN 978-620-0-23000-3. [Google Scholar]
- Crangle, J.; Fogarty, A.; Taylor, M.J. Weak ferromagnetism in ‘non-magnetic’ austenitic stainless steel. J. Magn. Magn. Mater. 1992, 111, 255–259. [Google Scholar] [CrossRef]
- Jian, Z.; Kumar, N.P.; Zhong, M.; Yemin, H.; Reddy, P.V. Structural, Magnetic and Dielectric Properties of Bi0.9Re0.1FeO3(Re = La, Sm, Gd and Y). J. Supercond. Nov. Magn. 2015, 28, 2627–2635. [Google Scholar] [CrossRef]



| Grade Steel | Sample No. | Φ (mm) | Element Content in wt.% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C | Mn | Si | P | S | Ni | Cr | |||
| AISI 1010 | 3A; 13 | 2.50 | 0.10 | 0.5 | 01 | 0.04 | 0.05 | - | - |
| AISI 52100 | 4A; 14 | 3.00 | 1.0 | 0.4 | 0.3 | 0.02 | 0.02 | - | 1.5 |
| Parameters of the Nitriding Processes (1208) | Parameters of the Annealing Processes | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample No. | Stage I | Stage II | Inlet Atmosphere | T [°C] | t [h] | Inlet Atmosphere | ||||
| T [°C] | t [h] | Np [atm−05] | T [°C] | t [h] | Np [atm−05] | |||||
| 3A; 4A | 580 | 5 | 3.20 | 600 | 11 | 0.50 | NH3/NH3zd | - | - | - |
| 13; 14 | 580 | 5 | 3.20 | 600 | 11 | 0.50 | NH3/NH3zd | 520 | 4 | N2/Ar/P = 150 Pa |
| Grade Steel | Sample No. | Φ (mm) | |||
|---|---|---|---|---|---|
| gmp (µm) | gpor (µm) | PC WL | |||
| AISI 1010 | 3A | 3.0 | 50 ± 1 | 20 ± 1 | Fe4N-γ’ |
| AISI 1010 | 13 | 3.0 | 56 ± 1 | 25 ± 1 | Fe4N-γ’; Fe-α |
| AISI 52100 | 4A | 2.5 | 37 ± 1 | 11 ± 1 | Fe4N-γ’ |
| AISI 52100 | 14 | 2.5 | 38 ± 1 | 10 ± 1 | Fe4N-γ’; Fe-α |
| Sample | Starting (SS) | Nitrided | Nitrided and Annealed |
|---|---|---|---|
| AISI 1010 | 0.23 L | 0.74 L | 0.38 L |
| AISI 52100 | 0.28 L | 0.78 L | 0.48 L |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaczmarek, S.M.; Michalski, J.; Leniec, G.; Fuks, H.; Frączek, T.; Dudek, A. Applying the FMR Technique to Analyzing the Influence of Nitriding on the Magnetic Properties of Steel. Materials 2022, 15, 4080. https://doi.org/10.3390/ma15124080
Kaczmarek SM, Michalski J, Leniec G, Fuks H, Frączek T, Dudek A. Applying the FMR Technique to Analyzing the Influence of Nitriding on the Magnetic Properties of Steel. Materials. 2022; 15(12):4080. https://doi.org/10.3390/ma15124080
Chicago/Turabian StyleKaczmarek, Slawomir Maksymilian, Jerzy Michalski, Grzegorz Leniec, Hubert Fuks, Tadeusz Frączek, and Agata Dudek. 2022. "Applying the FMR Technique to Analyzing the Influence of Nitriding on the Magnetic Properties of Steel" Materials 15, no. 12: 4080. https://doi.org/10.3390/ma15124080
APA StyleKaczmarek, S. M., Michalski, J., Leniec, G., Fuks, H., Frączek, T., & Dudek, A. (2022). Applying the FMR Technique to Analyzing the Influence of Nitriding on the Magnetic Properties of Steel. Materials, 15(12), 4080. https://doi.org/10.3390/ma15124080







