Tool Wear Prediction When Machining with Self-Propelled Rotary Tools
Abstract
1. Introduction
2. Literature Survey
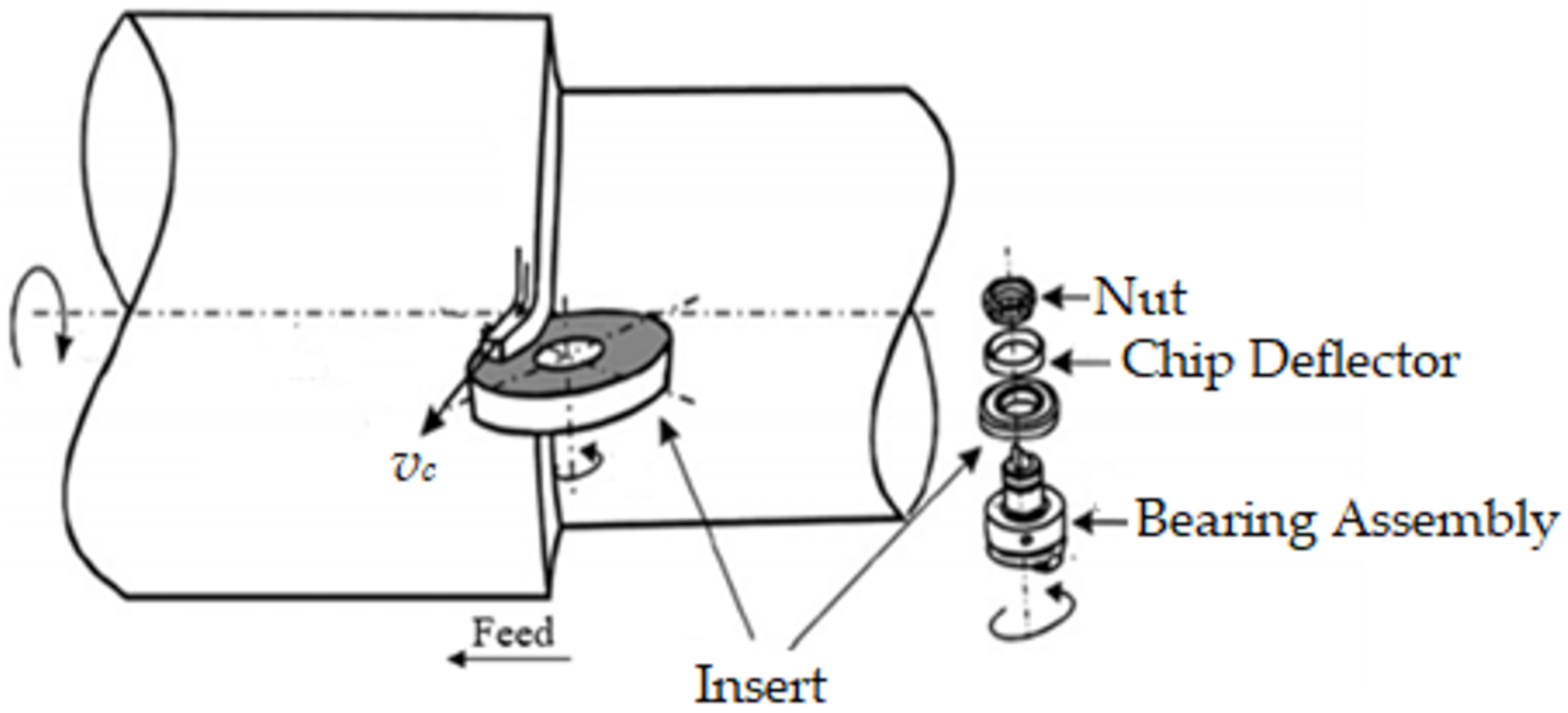
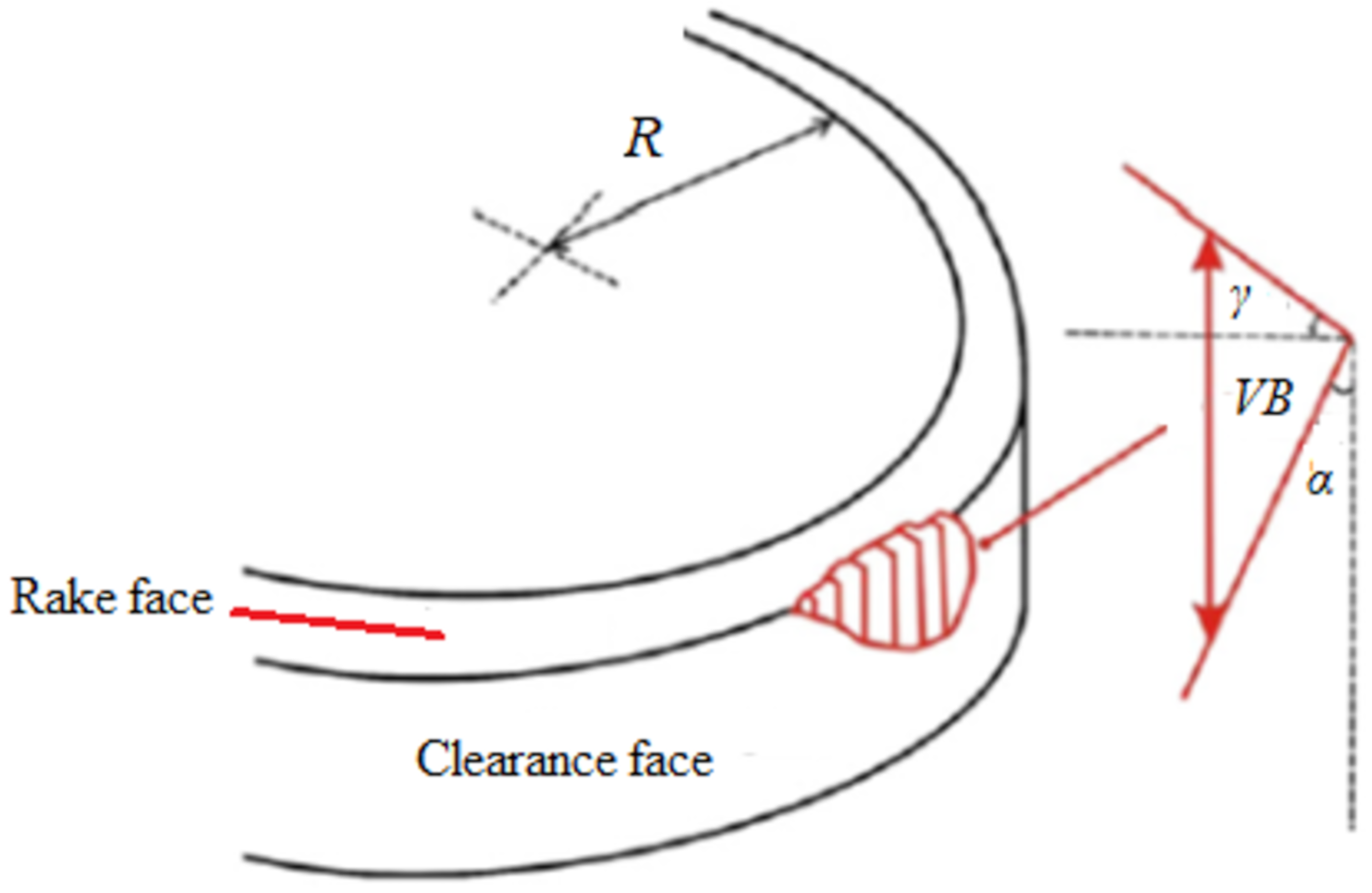
3. Tool Wear Model Development
4. Experimental Procedure
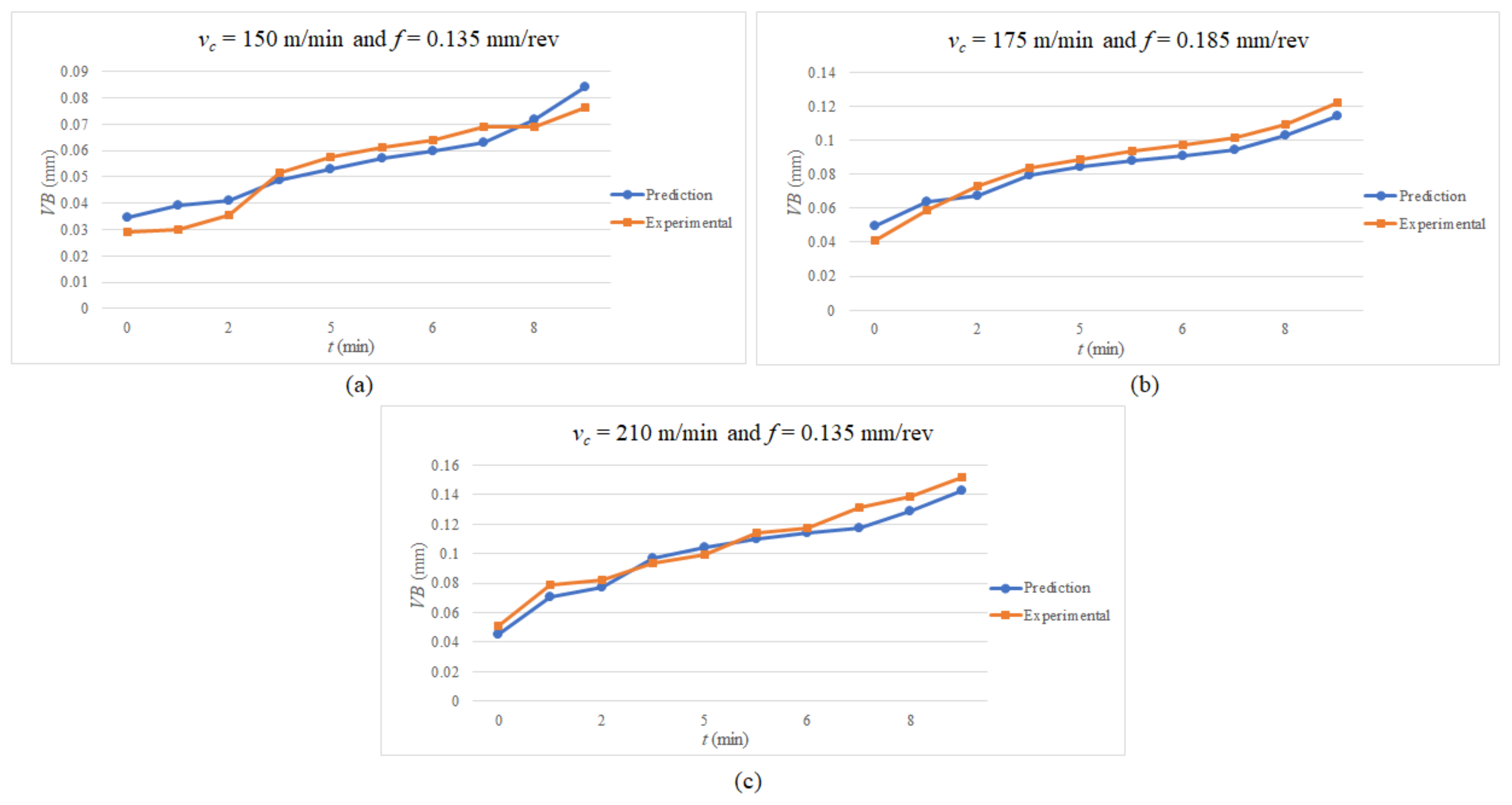
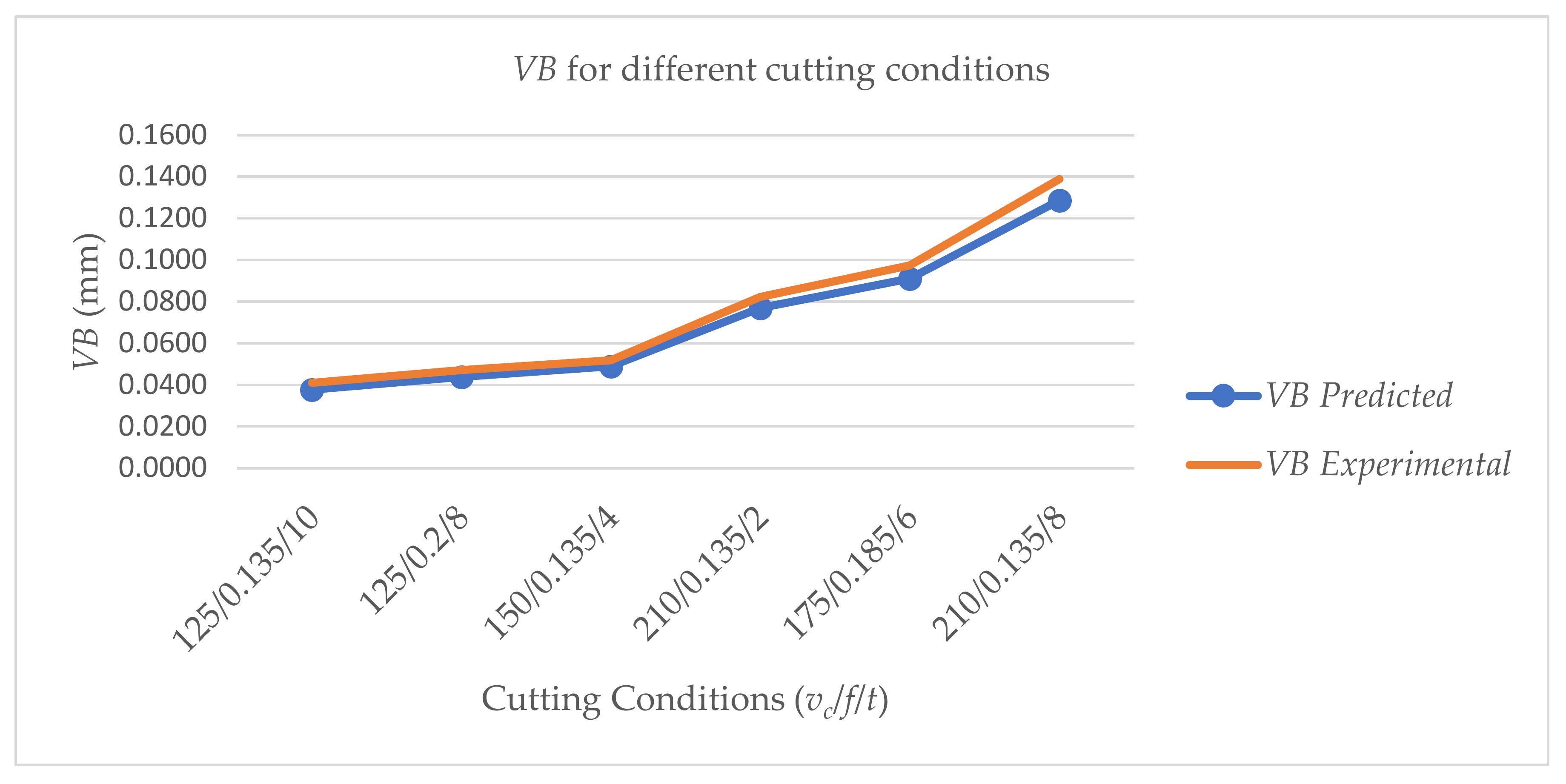
5. Results and Model Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A | Flank wear area |
| C | Constant |
| cBN | Cubic Boron Nitride |
| D | Insert diameter |
| d | Depth of cut |
| f | Feed |
| GP | Genetic programming |
| k | Empirical constant |
| Lc | Contact length |
| LSR | Least squares regression |
| MRR | Material removal rate |
| n | Factor added to estimate the flank wear of the rotary tool |
| PcBN | Polycrystalline Cubic Boron Nitride |
| R | Radius of the rotary tool/insert |
| r | Cutting edge radius |
| SPRT | Self-propelled rotary tools |
| t | Cutting time |
| VB | Flank wear |
| vc | Cutting speed |
| α | Clearance angle |
| γ | Rake angle |
| λ | Inclination angle |
References
- Ahmed, W.; Hegab, H.; Mohany, A.; Kishawy, H. Sustainability assessment of difficult-to-cut materials using rotary tools: A step towards sustainable machining environment. Procedia Manuf. 2021, 53, 92–98. [Google Scholar] [CrossRef]
- Ahmed, W.; Hegab, H.; Kishawy, H.A.; Mohany, A. Estimation of temperature in machining with self-propelled rotary tools using finite element method. J. Manuf. Process. 2021, 61, 100–110. [Google Scholar] [CrossRef]
- Jianxin, D.; Jiantou, Z.; Hui, Z.; Pei, Y. Wear mechanisms of cemented carbide tools in dry cutting of precipitation hardening semi-austenitic stainless steels. Wear 2011, 270, 520–527. [Google Scholar] [CrossRef]
- Courbon, C.; Sajn, V.; Kramar, D.; Rech, J.; Kosel, F.; Kopac, J. Investigation of machining performance in high pressure jet assisted turning of Inconel 718: A numerical model. J. Mater. Process. Technol. 2011, 211, 1834–1851. [Google Scholar] [CrossRef]
- Mia, M.; Dhar, N.R. Effect of high pressure coolant jet on cutting temperature, tool wear and surface finish in turning hardened (Hrc 48) steel. J. Mech. Eng. 2015, 45, 1–6. [Google Scholar] [CrossRef][Green Version]
- Al Bashir, M.; Mia, M.; Dhar, N.R. Investigations on Surface Milling of Hardened AISI 4140 Steel with Pulse Jet MQL Applicator. J. Inst. Eng. Ser. C 2018, 99, 301–314. [Google Scholar] [CrossRef]
- dos Santos, F.A.; de Pinto, M.A.C.; dos Santos, R.O.B.; Bimestre, T.A.; Gama, R.P. Comparative analysis of the application of lubricant coolant by the MQF technique in the face milling machining process of hardened D2 steel alloy. Braz. J. Dev. 2021, 7, 10349–10370. [Google Scholar] [CrossRef]
- Krolczyk, G.M.; Maruda, R.W.; Krolczyk, J.B.; Wojciechowski, S.; Mia, M.; Nieslony, P.; Budzik, G. Ecological trends in machining as a key factor in sustainable production—A review. J. Clean. Prod. 2019, 218, 601–615. [Google Scholar] [CrossRef]
- Mia, M.; Dhar, N.R. Effects of duplex jets high-pressure coolant on machining temperature and machinability of Ti-6Al-4V superalloy. J. Mater. Process. Technol. 2018, 252, 688–696. [Google Scholar] [CrossRef]
- Goindi, G.S.; Sarkar, P. Dry machining: A step towards sustainable machining—Challenges and future directions. J. Clean. Prod. 2017, 165, 1557–1571. [Google Scholar] [CrossRef]
- Abbas, A.T.; El Rayes, M.M.; Luqman, M.; Naeim, N.; Hegab, H.; Elkaseer, A. On the Assessment of Surface Quality and Productivity Aspects in Precision Hard Turning of AISI 4340 Steel Alloy: Relative Performance of Wiper vs. Conventional Inserts. Materials 2020, 13, 2036. [Google Scholar] [CrossRef] [PubMed]
- Astakhov, V.P. Machining of Hard Materials–Definitions and Industrial Applications. In Machining of Hard Materials; Davim, J.P., Ed.; Springer: London, UK, 2011; pp. 1–32. ISBN 978-1-84996-450-0. [Google Scholar]
- Afteni, M.; Terecoasa, I.; Afteni, C.; Paunoiu, V. Study on Hard Turning Process Versus Grinding in Manufacturing Some Bearing Inner Rings. In Proceedings of the 5th International Conference on Advanced Manufacturing Engineering and Technologies, Online, 23 April 2017; Majstorovic, V., Jakovljevic, Z., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 95–111. [Google Scholar]
- Kishawy, H.A.; Pang, L.; Balazinski, M. Modeling of tool wear during hard turning with self-propelled rotary tools. Int. J. Mech. Sci. 2011, 53, 1015–1021. [Google Scholar] [CrossRef]
- Samantaraya, D.; Lakade, S. Hard Turning Cutting Tool Materials used in Automotive and Bearing Manufacturing Applications–A review. IOP Conf. Ser. Mater. Sci. Eng. 2020, 814, 012005. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Z. Influences of coating thickness on cutting temperature for dry hard turning Inconel 718 with PVD TiAlN coated carbide tools in initial tool wear stage. J. Manuf. Process. 2020, 56, 1155–1165. [Google Scholar] [CrossRef]
- Şap, E.; Usca, U.A.; Gupta, M.K.; Kuntoğlu, M. Tool wear and machinability investigations in dry turning of Cu/Mo-SiCp hybrid composites. Int. J. Adv. Manuf. Technol. 2021, 114, 379–396. [Google Scholar] [CrossRef]
- Nakayama, K.; Arai, M.; Kanda, T. Machining Characteristics of Hard Materials. CIRP Ann. 1988, 37, 89–92. [Google Scholar] [CrossRef]
- Karthik, M.S.; Raju, V.R.; Reddy, K.N.; Balashanmugam, N.; Sankar, M.R. Cutting parameters optimization for surface roughness during dry hard turning of EN 31 bearing steel using CBN insert. Mater. Today Proc. 2020, 26, 1119–1125. [Google Scholar] [CrossRef]
- Seleznev, A.; Pinargote, N.W.S.; Smirnov, A. Machinability of Nickel-Based Superalloys Using Ceramic Tools. Automot. Eng. 2021. [Google Scholar] [CrossRef]
- Bag, R.; Panda, A.; Sahoo, A.K.; Kumar, R. Cutting tools characteristics and coating depositions for hard part turning of AISI 4340 martensitic steel: A review study. Mater. Today Proc. 2020, 26, 2073–2078. [Google Scholar] [CrossRef]
- Sobiyi, K.; Sigalas, I.; Akdogan, G.; Turan, Y. Performance of mixed ceramics and CBN tools during hard turning of martensitic stainless steel. Int. J. Adv. Manuf. Technol. 2015, 77, 861–871. [Google Scholar] [CrossRef]
- Boing, D.; Schroeter, R.B.; de Oliveira, A.J. Three-dimensional wear parameters and wear mechanisms in turning hardened steels with PCBN tools. Wear 2018, 398–399, 69–78. [Google Scholar] [CrossRef]
- Heydari, B.; Mahdi, M.A.; Reza, K.Z.H. The Effect of Workpiece Hardness and Cutting Parameters on Surface Roughness in Dry Hard Turning of X210Cr12 Cold Tool Steel. Modares Mech. Eng. 2017, 17, 241–247. [Google Scholar]
- Tang, L.; Gao, C.; Huang, J.; Shen, H.; Lin, X. Experimental investigation of surface integrity in finish dry hard turning of hardened tool steel at different hardness levels. Int. J. Adv. Manuf. Technol. 2015, 77, 1655–1669. [Google Scholar] [CrossRef]
- Tang, L.; Cheng, Z.; Huang, J.; Gao, C.; Chang, W. Empirical models for cutting forces in finish dry hard turning of hardened tool steel at different hardness levels. Int. J. Adv. Manuf. Technol. 2015, 76, 691–703. [Google Scholar] [CrossRef]
- Tang, L.; Sun, Y.; Li, B.; Shen, J.; Meng, G. Wear performance and mechanisms of PCBN tool in dry hard turning of AISI D2 hardened steel. Tribol. Int. 2019, 132, 228–236. [Google Scholar] [CrossRef]
- Shihab, S.K.; Khan, Z.A.; Mohammad, A.; Siddiquee, A.N. A review of turning of hard steels used in bearing and automotive applications. Prod. Manuf. Res. 2014, 2, 24–49. [Google Scholar] [CrossRef]
- Olgun, U.; Budak, E. Machining of Difficult-to-Cut-Alloys Using Rotary Turning Tools. Procedia CIRP 2013, 8, 81–87. [Google Scholar] [CrossRef]
- Dessoly, V.; Melkote, S.; Lescalier, C. Modeling and verification of cutting tool temperatures in rotary tool turning of hardened steel. Int. J. Mach. Tools Manuf. 2004, 44, 1463–1470. [Google Scholar] [CrossRef]
- Kishawy, H.A.; Becze, C.E.; McIntosh, D.G. Tool performance and attainable surface quality during the machining of aerospace alloys using self-propelled rotary tools. J. Mater. Process. Technol. 2004, 152, 266–271. [Google Scholar] [CrossRef]
- Ezugwu, E.O. Improvements in the machining of aero-engine alloys using self-propelled rotary tooling technique. J. Mater. Process. Technol. 2007, 185, 60–71. [Google Scholar] [CrossRef]
- Ahmed, W.; Hegab, H.; Mohany, A.; Kishawy, H. On machining hardened steel AISI 4140 with self-propelled rotary tools: Experimental investigation and analysis. Int. J. Adv. Manuf. Technol. 2021, 133, 3163–3176. [Google Scholar] [CrossRef]
- Da Silva, R.H.L.; Hassui, A. Cutting force and surface roughness depend on the tool path used in side milling: An experimental investigation. Int. J. Adv. Manuf. Technol. 2018, 96, 1445–1455. [Google Scholar] [CrossRef]
- Chen, P.; Hoshi, T. High-Performance Machining of SiC Whisker-Reinforced Aluminium Composite by Self-Propelled Rotary Tools. CIRP Ann. 1992, 41, 59–62. [Google Scholar] [CrossRef]
- Umer, U.; Kishawy, H.; Abidi, M.H.; Mian, S.H.; Moiduddin, K. Evaluation of Self-Propelled Rotary Tool in the Machining of Hardened Steel Using Finite Element Models. Materials 2020, 13, 5092. [Google Scholar] [CrossRef] [PubMed]
- Kishawy, H.A.; Wilcox, J. Tool wear and chip formation during hard turning with self-propelled rotary tools. Int. J. Mach. Tools Manuf. 2003, 43, 433–439. [Google Scholar] [CrossRef]
- Li, G.; Li, N.; Wen, C.; Ding, S. Investigation and modeling of flank wear process of different PCD tools in cutting titanium alloy Ti6Al4V. Int. J. Adv. Manuf. Technol. 2018, 95, 719–733. [Google Scholar] [CrossRef]
- Choudhury, S.K.; Srinivas, P. Tool wear prediction in turning. J. Mater. Process. Technol. 2004, 153–154, 276–280. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Z.; Wang, B.; Hou, X. Modeling of plastic deformation induced by thermo-mechanical stresses considering tool flank wear in high-speed machining Ti-6Al-4V. Int. J. Mech. Sci. 2018, 140, 1–12. [Google Scholar] [CrossRef]
- Bombiński, S.; Kossakowska, J.; Jemielniak, K. Detection of accelerated tool wear in turning. Mech. Syst. Signal Process. 2022, 162, 108021. [Google Scholar] [CrossRef]
- Sikdar, S.K.; Chen, M. Relationship between Tool Flank Wear Area and Component Forces in Single Point Turning. J. Mater. Process. Technol. 2002, 128, 210–215. [Google Scholar] [CrossRef]
- Choudhury, S.; Kishore, K. Tool wear measurement in turning using force ratio. Int. J. Mach. Tools Manuf. 2000, 40, 899–909. [Google Scholar] [CrossRef]
- Tooptong, S.; Park, K.-H.; Kwon, P. A comparative investigation on flank wear when turning three cast irons. Tribol. Int. 2018, 120, 127–139. [Google Scholar] [CrossRef]
- Nooraie, R.Y.; Safari, M.; Pak, A. Tool wear estimation in machining based on the flank wear inclination angle changes using the FE method. Mach. Sci. Technol. 2020, 24, 425–445. [Google Scholar] [CrossRef]
- Equeter, L.; Ducobu, F.; Rivière-Lorphèvre, E.; Abouridouane, M.; Klocke, F.; Dehombreux, P. Estimation of the influence of tool wear on force signals: A finite element approach in AISI 1045 orthogonal cutting. AIP Conf. Proc. 2018, 1960, 070012. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, D. Finite-element-analysis of the effect of different wiper tool edge geometries during the hard turning of AISI 4340 steel. Simul. Model. Pract. Theory 2019, 94, 250–263. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Z.; Yang, G.; Zhou, A.; Wang, G.; Qin, S.; Wang, A.; Wang, W.; Zhang, X. Finite element analysis and wear mechanism of B4C–TiB2 ceramic tools in turning AISI 4340 workpieces. Ceram. Int. 2021, 48, 5459–5467. [Google Scholar] [CrossRef]
- Dawson, T.G.; Kurfess, T.R. Modeling the Progression of Flank Wear on Uncoated and Ceramic-Coated Polycrystalline Cubic Boron Nitride Tools in Hard Turning. J. Manuf. Sci. Eng. 2004, 128, 104–109. [Google Scholar] [CrossRef]
- He, J. 4340 Steel|36CrNiMo4|1.6511|EN24|SNCM439. Otai Special Steel. Available online: https://www.astmsteel.com/product/4340-steel-aisi/ (accessed on 21 August 2021).
- Babu, B.V.; Karthik, S. Genetic Programming for Symbolic Regression of Chemical Process Systems. Eng. Lett. 2007, 14, 42–55. [Google Scholar]
- McCormick, E.; Lang, H.; de Silva, C.W. Automated Multi-Domain Engineering Design through Linear Graph and Genetic Programming. arXiv 2021, arXiv:2109.12388. [Google Scholar] [CrossRef]
- Mehr, A.D.; Nourani, V.; Kahya, E.; Hrnjica, B.; Sattar, A.M.A.; Yaseen, Z.M. Genetic programming in water resources engineering: A state-of-the-art review. J. Hydrol. 2018, 566, 643–667. [Google Scholar] [CrossRef]
- Hadi, S.J.; Tombul, M. Monthly streamflow forecasting using continuous wavelet and multi-gene genetic programming combination. J. Hydrol. 2018, 561, 674–687. [Google Scholar] [CrossRef]
- Zhong, J.; Feng, L.; Cai, W.; Ong, Y.-S. Multifactorial Genetic Programming for Symbolic Regression Problems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4492–4505. [Google Scholar] [CrossRef]
- Qi, C.; Tang, X.; Dong, X.; Chen, Q.; Fourie, A.; Liu, E. Towards Intelligent Mining for Backfill: A genetic programming-based method for strength forecasting of cemented paste backfill. Miner. Eng. 2019, 133, 69–79. [Google Scholar] [CrossRef]
- Salgotra, R.; Gandomi, M.; Gandomi, A.H. Time Series Analysis and Forecast of the COVID-19 Pandemic in India using Genetic Programming. Chaos Solitons Fractals 2020, 138, 109945. [Google Scholar] [CrossRef] [PubMed]



| Element | C | Mn | P | S | Si | Ni | Cr | Mo |
|---|---|---|---|---|---|---|---|---|
| Composition (%) | 0.38–0.43 | 0.60–0.80 | 0.035 | 0.040 | 0.15–0.35 | 1.65–2.00 | 0.70–0.90 | 0.20–0.30 |
| Rake angle (γ) | −5° |
| Clearance angle (α) | 7° |
| Inclination angle (λ) | 17° |
| Insert diameter (D) | 16 mm |
| Cutting edge radius (r) | 0.05 mm |
| Cutting Trials | Cutting Speed, vc (m/min) | Feed, f (mm/rev) | Time, t (min) | Flank Wear, VBexp (mm) |
|---|---|---|---|---|
| 1 | 100 | 0.15 | 12 | 0.014 |
| 2 | 100 | 0.25 | 3.5 | 0.096 |
| 3 | 150 | 0.2 | 2 | 0.047 |
| 4 | 225 | 0.175 | 5.5 | 0.108 |
| 5 | 250 | 0.125 | 2.5 | 0.112 |
| 6 | 250 | 0.25 | 0.25 | 0.126 |
| Run | Experimental | ||||
|---|---|---|---|---|---|
| vc (m/min) | f (mm/rev) | t (min) | VBexp (mm) | kexp | |
| 1 | 100 | 0.15 | 12 | 0.014 | 2.773 × 10−5 |
| 2 | 100 | 0.25 | 3.5 | 0.096 | 0.0115473 |
| 3 | 150 | 0.2 | 2 | 0.047 | 0.0020464 |
| 4 | 225 | 0.175 | 5.5 | 0.108 | 0.0045042 |
| 5 | 250 | 0.125 | 2.5 | 0.112 | 0.0098543 |
| 6 | 250 | 0.25 | 0.25 | 0.126 | 0.1363748 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umer, U.; Mian, S.H.; Mohammed, M.K.; Abidi, M.H.; Moiduddin, K.; Kishawy, H. Tool Wear Prediction When Machining with Self-Propelled Rotary Tools. Materials 2022, 15, 4059. https://doi.org/10.3390/ma15124059
Umer U, Mian SH, Mohammed MK, Abidi MH, Moiduddin K, Kishawy H. Tool Wear Prediction When Machining with Self-Propelled Rotary Tools. Materials. 2022; 15(12):4059. https://doi.org/10.3390/ma15124059
Chicago/Turabian StyleUmer, Usama, Syed Hammad Mian, Muneer Khan Mohammed, Mustufa Haider Abidi, Khaja Moiduddin, and Hossam Kishawy. 2022. "Tool Wear Prediction When Machining with Self-Propelled Rotary Tools" Materials 15, no. 12: 4059. https://doi.org/10.3390/ma15124059
APA StyleUmer, U., Mian, S. H., Mohammed, M. K., Abidi, M. H., Moiduddin, K., & Kishawy, H. (2022). Tool Wear Prediction When Machining with Self-Propelled Rotary Tools. Materials, 15(12), 4059. https://doi.org/10.3390/ma15124059







