Designing and Calculating the Nonlinear Elastic Characteristic of Longitudinal–Transverse Transducers of an Ultrasonic Medical Instrument Based on the Method of Successive Loadings
Abstract
:1. Introduction
2. The Method of Successive Loadings (MSL)
3. Applying MSL in the Numerical Method (Matlab) and FEM (Ansys Workbench)
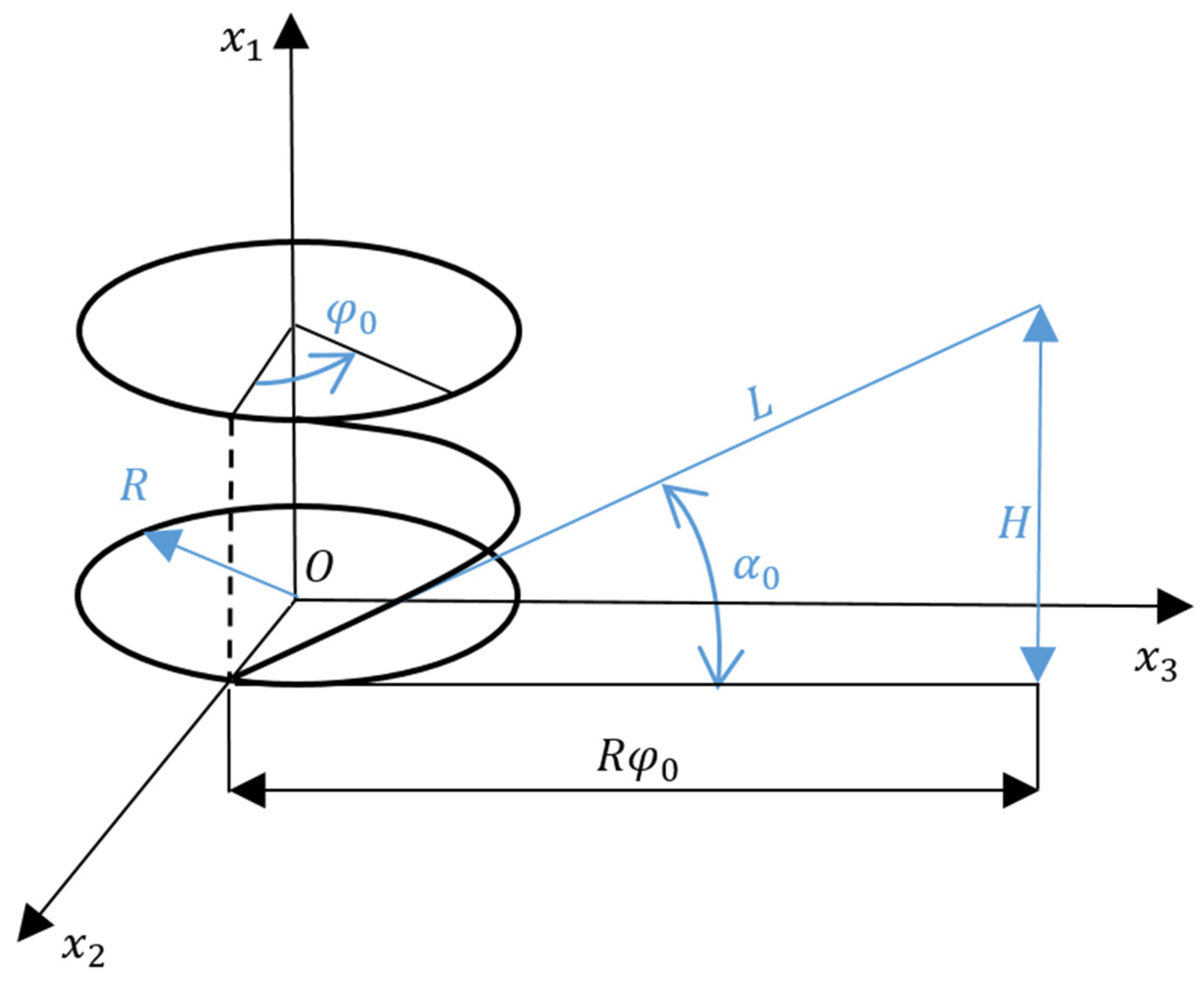
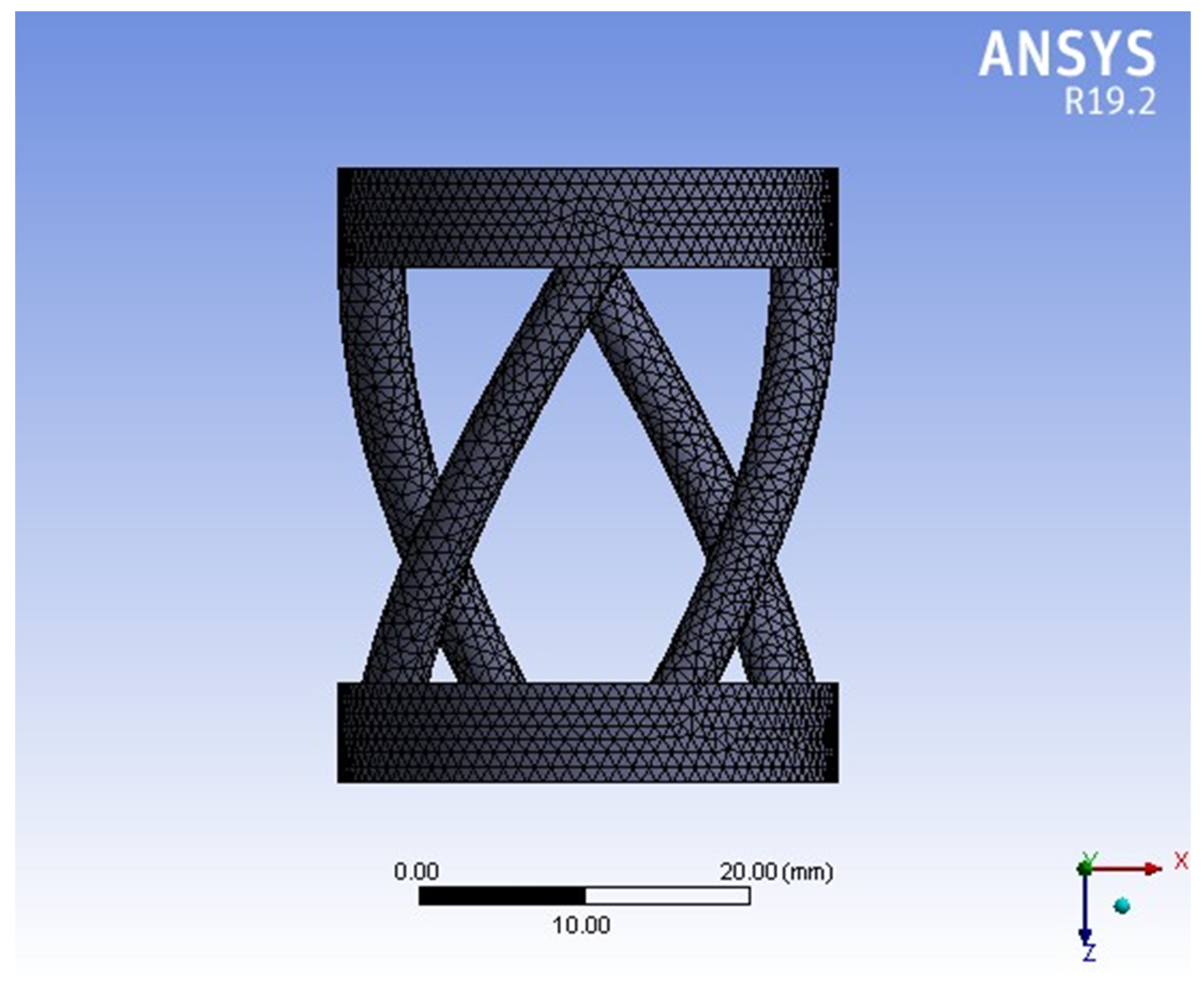
3.1. Designing the Model of Longitudinal–Transverse Transducers
3.2. Calculating the Nonlinear Elastic Characteristic of Longitudinal–Transverse Transducers
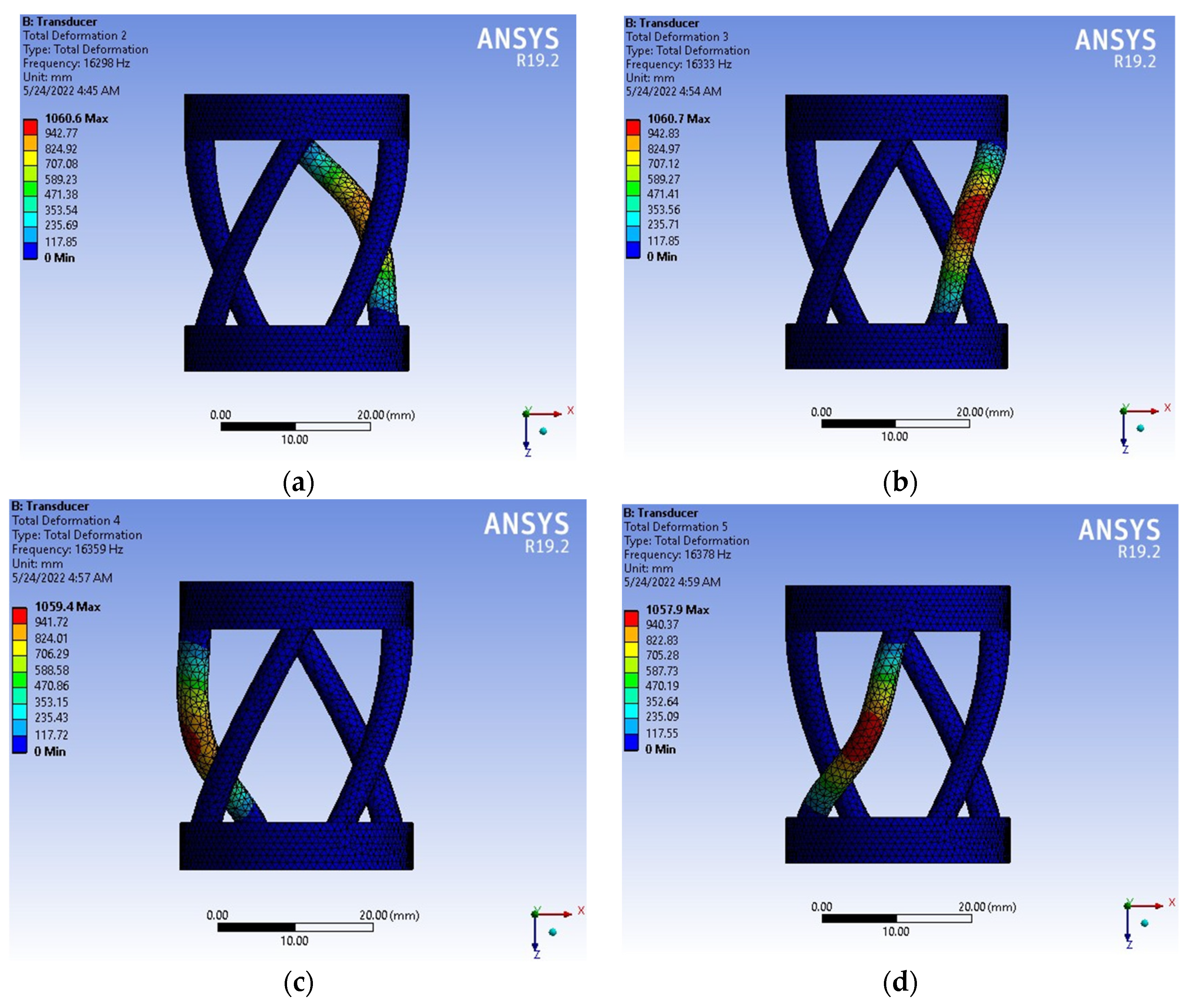
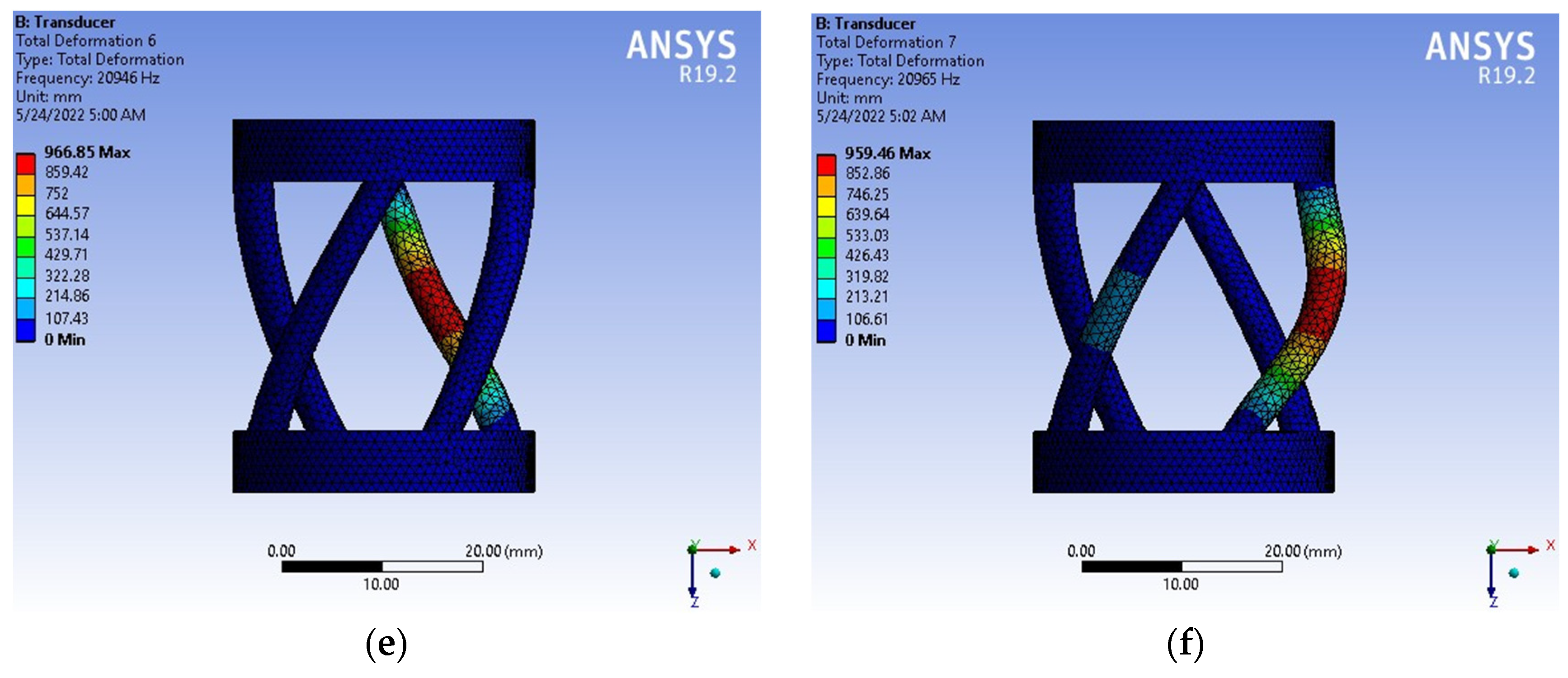
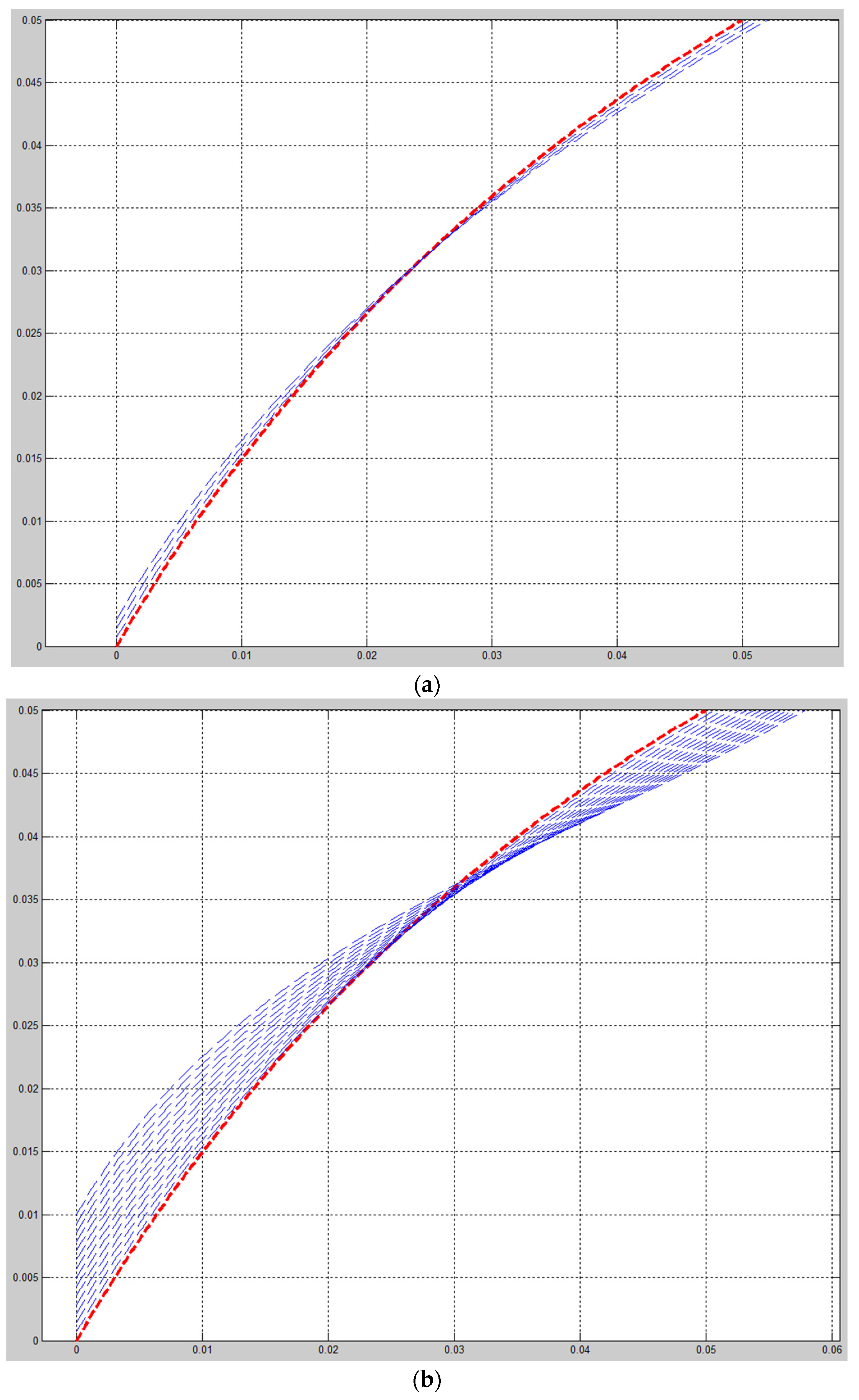
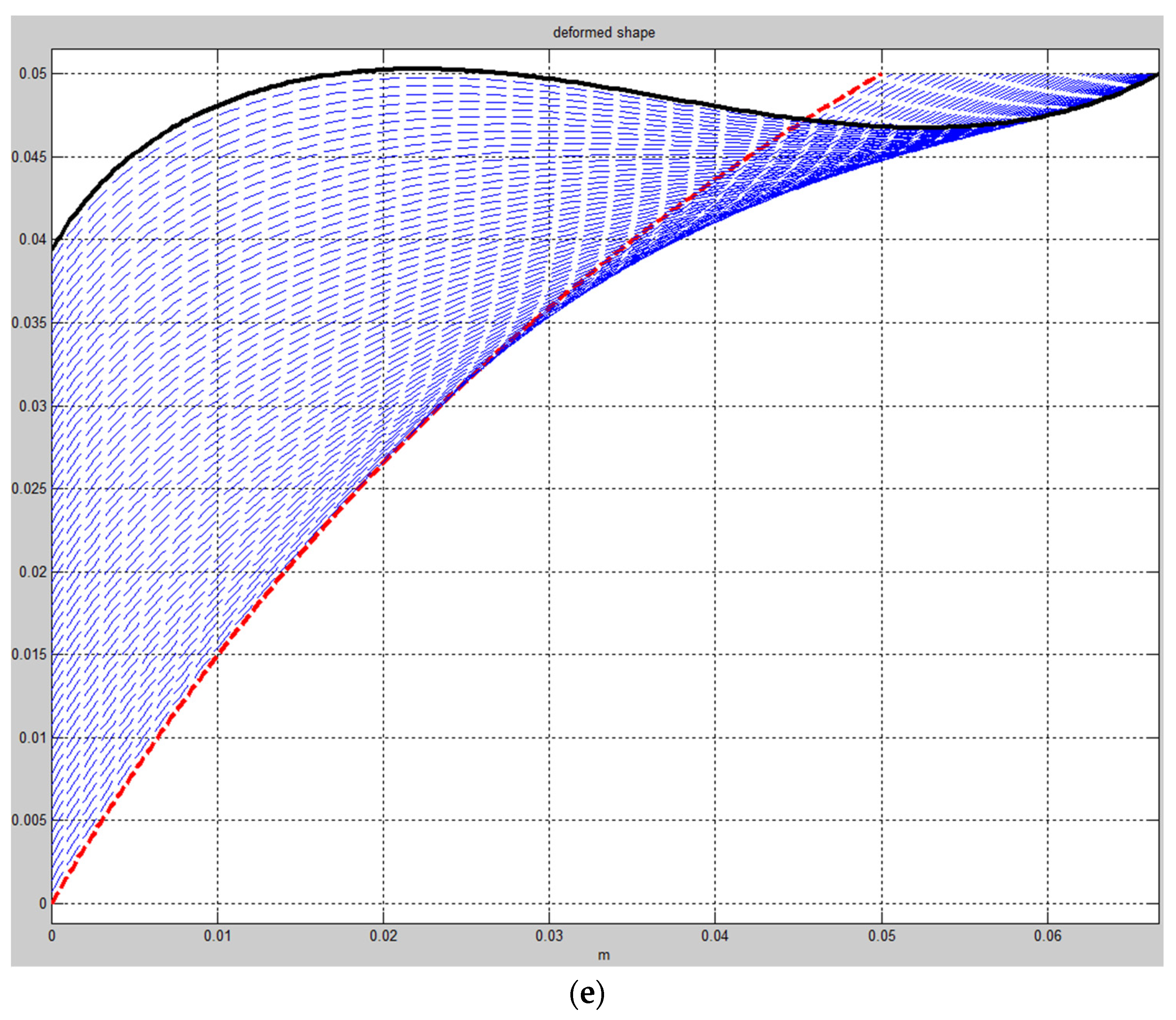
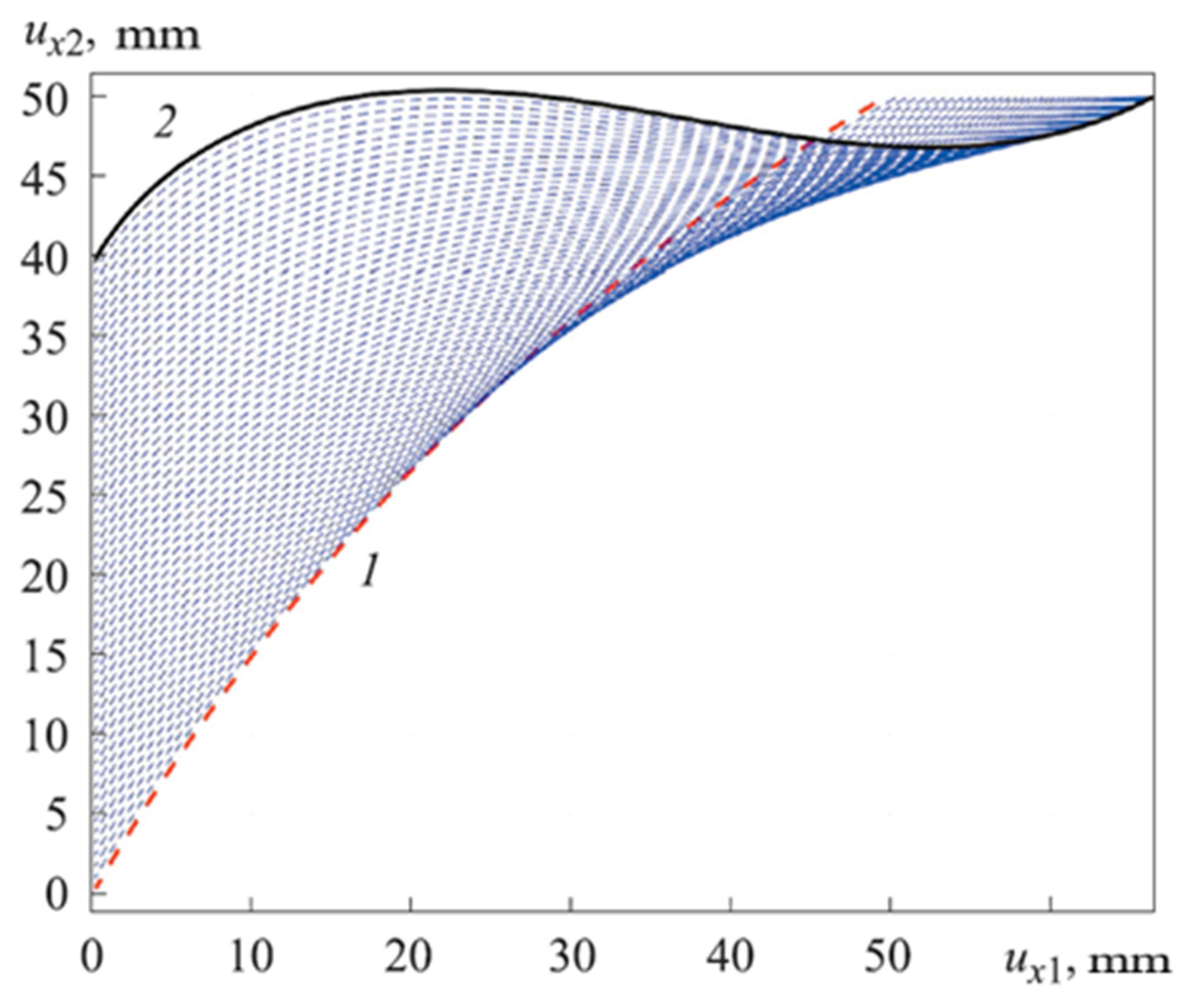
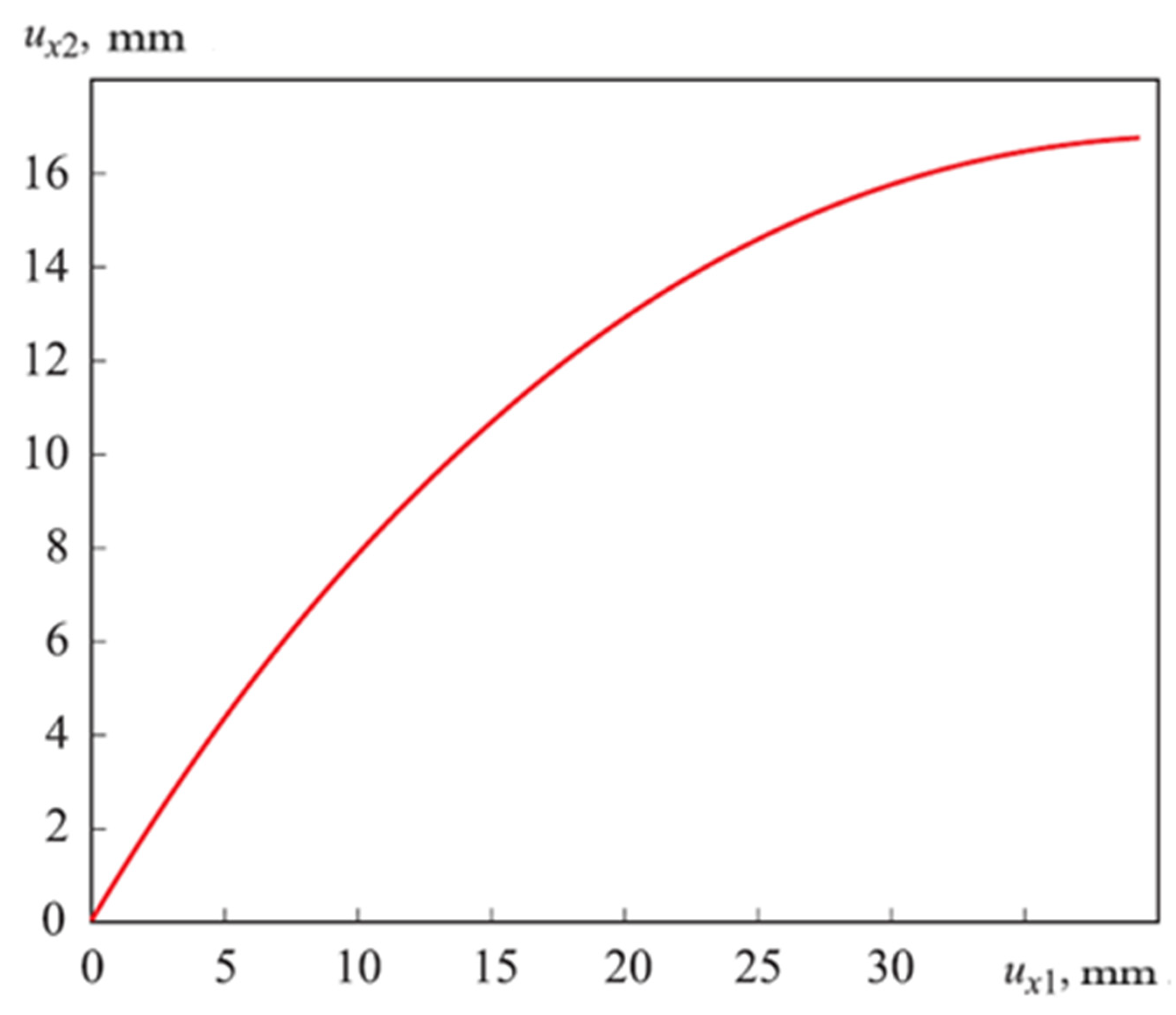
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simo, J.C.; Tarnow, N.; Doblare, M. Non-linear dynamics of three-dimensional rods: Exact energy and momentum conservation algorithms. Int. J. Numer. Methods Eng. 1995, 38, 1431–1473. [Google Scholar] [CrossRef]
- Gerstmayr, J.; Shabana, A.A. Analysis of thin beams and cables using the absolute nodal coordinate formulation. Nonlinear Dyn. 2006, 45, 109–130. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, Y.; Zhang, B. The complex-mode vibration of ultrasonic vibration systems. Ultrasonics 2002, 40, 907–911. [Google Scholar] [CrossRef]
- Alnefaie, K. Lateral and longitudinal vibration of a rotating flexible beam coupled with torsional vibration of a flexible shaft. Int. J. Mech. Mechatron. Eng. 2018, 7, 884–891. [Google Scholar]
- Cardoni, A.; Harkness, P.; Lucas, M. Ultrasonic rock sampling using longitudinal-torsional vibrations. Phys. Procedia 2010, 3, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Pani, S.; Senapati, S.; Patra, K.; Nath, P. Review of an Effective Dynamic Vibration Absorber for a Simply Supported Beam and Parametric Optimization to Reduce Vibration Amplitude. Int. J. Eng. Res. Appl. 2017, 7 Pt 3, 49–77. [Google Scholar] [CrossRef]
- He, B.; Rui, X.; Zhang, H. Transfer Matrix Method for Natural Vibration Analysis of Tree System. Math. Probl. Eng. 2012, 2012, 393204. [Google Scholar] [CrossRef] [Green Version]
- Allen, M.S.; Sracic, M.W.; Chauhan, S.; Hansen, M.H. Output-Only Modal Analysis of Linear Time Periodic Systems with Application to Wind Turbine Simulation Data. In Structural Dynamics and Renewable Energy; Proulx, T., Ed.; Springer: New York, NY, USA, 2011; Volume 1, pp. 361–374. [Google Scholar] [CrossRef] [Green Version]
- Allen, M.S.; Kuether, R.J.; Deaner, B.; Sracic, M.W. A numerical continuation method to compute nonlinear normal modes using modal reduction. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012; AIAA: Reston, VA, USA, 2012; pp. 9548–9567. [Google Scholar] [CrossRef] [Green Version]
- Structural Dynamics of Linear Elastic Single-Degree-of-Freedom (SDOF) Systems. Instructional Material Complementing FEMA 451, Design Examples. Available online: http://www.ce.memphis.edu/7119/PDFs/FEAM_Notes/Topic03StructuralDynamicsofSDOFSystemsNotes.pdf (accessed on 1 January 2020).
- Wen-Xi, H.; Xiao, X.Y.; Yun-Ling, J.; Dong-Fang, Y. Automatic segmentation method for voltage sag detection and characterization. In Proceedings of the 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; IEEE: New York, NY, USA, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Zilletti, M.; Elliott, S.J.; Rustighi, E. Optimisation of dynamic vibration absorbers to minimise kinetic energy and maximise internal power dissipation. J. Sound Vib. 2012, 331, 4093–4100. [Google Scholar] [CrossRef] [Green Version]
- Kulterbaev, K.P.; Baragunova, L.A.; Shogenova, M.M.; Shardanova, M.A. The Solution of a Spectral Task on Variable Section Compressed Beams Oscillations by Numerical Methods Materials. Sci. Forum 2019, 974, 704–710. [Google Scholar] [CrossRef]
- Kulterbaev, K.P.; Alokova, M.H.; Baragunova, L.A. Mathematical modeling of flexural oscillations of a vertical rod of variable section. News High. Educ. Inst. N.-Caucasion Region. Techn. Sci. 2015, 4, 100–106. [Google Scholar]
- Gavryushin, S.S.; Baryshnikova, O.O.; Boriskin, O.F. Numerical Analysis of Structural Elements of Machines and Devices; BMSTU Publishing: Moscow, Russia, 2014; p. 479. [Google Scholar]
- Kikvidze, O.G.; Kikvidze, L.G. Large Displacements of Thermoelastic Rods during Plane Bending. In Problems of Applied Mechanics; Publishing House “Committee of IFToMM of Georgia”: Tbilisi, Georgia, 2001; Chapter 4; pp. 73–77. [Google Scholar]
- Kikvidze, O.G.; Kikvidze, L.G. The geometrically nonlinear problem of bending thermoelastic rods. In Collection of International Symposium “Problems of Thin-Walled Spatial Structures”; Georgian Technical University: Tbilisi, Georgia, 2007; pp. 28–31. [Google Scholar]
- Kikvidze, O.G. Large displacements of thermoelastic rods during bending. In Problems of Mechanical Engineering and Machine reliability; RAS: Moscow, Russia, 2003; Chapter 1; pp. 49–53. [Google Scholar]
- Bîrsan, M.; Altenbach, H. Theory of thin thermoelastic rods made of porous materials. Arch. Appl. Mech. 2011, 81, 1365–1391. [Google Scholar] [CrossRef]
- Starovoitov, E.I.; Leonenko, D.V.; Tarlakovskii, D.V. Thermal-force deformation of a physically nonlinear three-layer stepped rod. J. Eng. Phys. Thermophys. 2016, 89, 1582–1590. [Google Scholar] [CrossRef]
- Baisarova, G.; Brzhanov, R.; Kikvidze, O.G.; Lahno, V. Computer simulation of large displacements of thermoelastic rods. J. Theor. Appl. Inf. Technol. 2019, 97, 4188–4201. [Google Scholar]
- Svetlitskii, V.A. Construction Machinery Mechanic. In Mechanics Rods; Fizmatlit Publ.: Moscow, Russia, 2009; Volume 1, p. 408. [Google Scholar]
- Bednarcyk, B.A.; Aboudi, J.; Arnold, S.M.; Pineda, E.J. A multiscale two-way thermomechanically coupled micromechanics analysis of the impact response of thermo-elastic-viscoplastic composites. Int. J. Solids Struct. 2019, 161, 228–242. [Google Scholar] [CrossRef]
- Qiu, B.; Kan, Q.; Kang, G.; Yu, C.; Xie, X. Rate-dependent transformation ratcheting-fatigue interaction of super-elastic NiTi alloy under uniaxial and torsional loadings: Experimental observation. Int. J. Fatigue 2019, 127, 470–478. [Google Scholar] [CrossRef]
- Rossmann, L.; Sarley, B.; Hernandez, J.; Kenesei, P.; Köster, A.; Wischek, J.; Almer, J.; Maurel, V.; Bartsch, M.; Raghavan, S. Method for conducting in situ high-temperature digital image correlation with simultaneous synchrotron measurements under thermomechanical conditions. Rev. Sci. Instruments 2020, 91, 033705. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.-J.; Zhou, H.; Zhu, W.; Zhu, J. A thermally-coupled elastic large-deformation model of a multilayered functionally graded material curved beam. Compos. Struct. 2020, 244, 112241. [Google Scholar] [CrossRef]
- Frantık, P. Simulation of the stability loss of the von Mises truss in an unsymmetrical stress state. Eng. Mech. 2007, 14, 155–161. Available online: http://www.engineeringmechanics.cz/pdf/14_3_155.pdf (accessed on 1 January 2020).
- Greco, M.; Vicente, C.E.R. Analytical solutions for geometrically nonlinear trusses. Rev. Esc. Minas 2009, 62, 205–214. [Google Scholar] [CrossRef] [Green Version]
- Cвeтлицкий, B.A.; Hapaйкин, O.C. Уnpyгиe элeмeнты мaшин; Maшинocтpoeниe: Moscow, Russia, 1989; p. 29. (In Russian) [Google Scholar]
- Kala, Z. Stability of von-Misses Truss with Initial Random Imperfections. Procedia Eng. 2017, 172, 473–480. [Google Scholar] [CrossRef]
- Gacesa, M.; Jelenic, G. Modified fixed-pole approach in geometrically exact spatial beam finite elements. Finite Elem. Anal. Des. 2015, 99, 39–48. [Google Scholar] [CrossRef]
- Kalina, M. Stability Problems of Pyramidal von Mises Planar Trusses with Geometrical Imperfection. Int. J. Theor. Appl. Mech. 2016, 1, 118–123. Available online: https://www.iaras.org/iaras/filedownloads/ijtam/2016/009-0018.pdf (accessed on 25 April 2022).
- Ligarò, S.S.; Valvo, P.S. Large Displacement Analysis of Elastic Pyramidal Trusses. Int. J. Solids Struct. 2006, 43, 4867–4887. Available online: https://www.researchgate.net/profile/Paolo_Valvo/publication/229292690 (accessed on 1 January 2020). [CrossRef]
- Mikhlin, Y.V. Nonlinear normal vibration modes and their applications. In Proceedings of the 9th Brazilian Conference on Dynamics Control and their Applications, Serra Negra, Brazil, 7–11 June 2010; pp. 151–171. Available online: https://www.sbmac.org.br/dincon/trabalhos/PDF/invited/68092.pdf (accessed on 25 April 2022).
- Jelenic, G.; Crisfield, M.A. Geometrically exact 3D beam theory: Implementation of a strain-invariant finite element for static and dynamics. Comput. Methods Appl. Mech. Eng. 1999, 171, 141–171. [Google Scholar] [CrossRef]
- Shabana, A.A.; Yakoub, R.Y. Three dimensional absolute nodal coordinate formulation for beam elements: Theory. ASME J. Mech. Des. 2001, 123, 606–613. [Google Scholar] [CrossRef]
- Simo, J.C.; Vu-Quoc, L. A three-dimensional finite-strain rod model. Part II: Geometric and computational aspects. Comput. Methods Appl. Mech. Eng. 1986, 58, 79–116. [Google Scholar] [CrossRef]
- Papa, E.; Jelenic, G.; Gacesa, M. Configuration-dependent interpolation in higher-order 2D beam finite elements. Finite Elem. Anal. Des. 2014, 78, 47–61. [Google Scholar] [CrossRef]
- Cвeтлицкий, B.A. мexaникa cтepжнeй. Динaмикa; Maшинocтpoeниe: Moscow, Russia, 1987; p. 55. (In Russian) [Google Scholar]
- Xiao, N.; Zhong, H. Non-linear quadrature element analysis of planar frames based on geometrically exact beam theory. Int. J. Non-Lin. Mech. 2012, 47, 481–488. [Google Scholar] [CrossRef]
- Makinen, J. Total Lagrangian Reissner’s geometrically exact beam element without singularities. Int. J. Numer. Methods Eng. 2007, 70, 1009–1048. [Google Scholar] [CrossRef]
- Zacny, K.; Bar-Cohen, Y.; Brennan, M.; Briggs, G.; Cooper, G.; Davis, K.; Dolgin, B.; Glaser, D.; Glass, B.; Gorevan, S.; et al. Drilling Systems for Extraterrestrial Subsurface Exploration. Astrobiology 2008, 8, 665–706. [Google Scholar] [CrossRef] [Green Version]
- Bar-Cohen, Y.; Sherrit, S.; Dolgin, B.; Bridges, N.; Bao, X.; Chang, Z.; Yen, A.; Saunders, R.; Pal, D.; Kroh, J.; et al. Ultrasonic/sonic driller/corer (USDC) as a sampler for planetary exploration. In Proceedings of the 2001 IEEE Aerospace Conference, Big Sky, MT, USA, 10–17 March 2001. [Google Scholar] [CrossRef] [Green Version]
- Bar-Cohen, Y.; Bao, X.; Chang, Z.; Sherrit, S. An ultrasonic sampler and sensor platform for in situ astrobiological exploration. In Proceedings of the SPIE Smart Structures Conference, San Diego, CA, USA, 2–6 March 2003; Volume 5056, pp. 457–465. [Google Scholar] [CrossRef] [Green Version]
- Badescu, M.; Stroescu, S.; Sherrit, S.; Aldrich, J.; Bao, X.; Bar-Cohen, Y.; Chang, Z.; Hernandez, W.; Ibrahim, A. Rotary hammer ultrasonic/sonic drill system. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 602–607. [Google Scholar] [CrossRef]
- Tsujino, J. Ultrasonic motor using a one-dimensional longitudinal-torsional vibration converter with diagonal slits. Smart Mater. Struct. 1997, 7, 345–351. [Google Scholar] [CrossRef]
- Ohnishi, O.; Myohga, O.; Uchikawa, T.; Tamegai, M.; Inoue, T.; Takahashi, S. Piezoelectric ultrasonic motor using longitudinal-torsional composite resonance vibration. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1993, 40, 687. [Google Scholar] [CrossRef] [PubMed]
- Harkness, P.; Cardoni, A.; Lucas, M. Vibration considerations in design of an ultrasonic driller/corer for planetary rock sampling. In Proceedings of the ISMA 2008: International Conference on Noise and Vibration Engineering, Leuven, Belgium, 15–17 September 2008. [Google Scholar]
- Harkness, P.; Cardoni, A.; Lucas, M. An ultrasonic corer for planetary rock sample retrieval. In Proceedings of the 7th International Conference on Modern Practice in Stress and Vibration Analysis, Cambridge, UK, 8–10 September 2009. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J.S.; Garcia, E.; Goldfarb, M. Design of symmetric conic-section flexure hinges based on closed-form compliance equations. Mech. Mach. Theory 2002, 37, 477–498. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X.; Wang, R.; Liu, Q. A simple compliance modeling method for flexure hinges. Sci. China Technol. Sci. 2015, 58, 56–63. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X.; Liu, Q.; Zhao, S. Multi-objective optimum design of fast tool servo based on improved differential evolution algorithm. J. Mech. Sci. Technol. 2011, 25, 3141–3149. [Google Scholar] [CrossRef]
- Gao, W.; Araki, T.; Kiyono, S.; Okazaki, Y.; Yamanaka, M. Precision nano-fabrication and evaluation of a large area sinusoidal grid surface for a surface encoder. Precis. Eng. 2003, 27, 289–298. [Google Scholar] [CrossRef]
- Liu, C.; Ta, D.; Hu, B.; Le, L.H.; Wang, W. The analysis and compensation of cortical thickness effect on ultrasonic backscatter signals in cancellous bone. J. Appl. Phys. 2014, 116, 124903. [Google Scholar] [CrossRef]
- Fontes-Pereira, A.J.; Matusin, D.; Rosa, P.; Schanaider, A.; von Krüger, M.; Pereira, W. Ultrasound method applied to characterize healthy femoral diaphysis of Wistar rats in vivo. Braz. J. Med. Biol. Res. 2021, 47, 403–410. [Google Scholar] [CrossRef] [Green Version]




| Density | 7.85 × 106 kg/mm3 |
| Young’s Modulus (MPa) | Poisson’s Ratio | Tensile Yield Strength (MPa) | Tensile Ultimate Strength (MPa) |
|---|---|---|---|
| 2 × 105 | 0.3 | 250 | 460 |
| Reality in Medicine (kHz) [48] | 20 | |
|---|---|---|
| (kHz) | ||
| (kHz) | ||
| (kHz) |
| FEM (Ansys) (mm) | Numerical Method (Matlab) (mm) | (%) ErrorMax.def |
|---|---|---|
| 1060.6 | ||
| 1060.7 | ||
| 1059.4 | 983.54 | |
| 1057.9 | ||
| 966.85 | ||
| 959.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.-D.; Huang, S.-C. Designing and Calculating the Nonlinear Elastic Characteristic of Longitudinal–Transverse Transducers of an Ultrasonic Medical Instrument Based on the Method of Successive Loadings. Materials 2022, 15, 4002. https://doi.org/10.3390/ma15114002
Nguyen H-D, Huang S-C. Designing and Calculating the Nonlinear Elastic Characteristic of Longitudinal–Transverse Transducers of an Ultrasonic Medical Instrument Based on the Method of Successive Loadings. Materials. 2022; 15(11):4002. https://doi.org/10.3390/ma15114002
Chicago/Turabian StyleNguyen, Huu-Dien, and Shyh-Chour Huang. 2022. "Designing and Calculating the Nonlinear Elastic Characteristic of Longitudinal–Transverse Transducers of an Ultrasonic Medical Instrument Based on the Method of Successive Loadings" Materials 15, no. 11: 4002. https://doi.org/10.3390/ma15114002
APA StyleNguyen, H.-D., & Huang, S.-C. (2022). Designing and Calculating the Nonlinear Elastic Characteristic of Longitudinal–Transverse Transducers of an Ultrasonic Medical Instrument Based on the Method of Successive Loadings. Materials, 15(11), 4002. https://doi.org/10.3390/ma15114002






