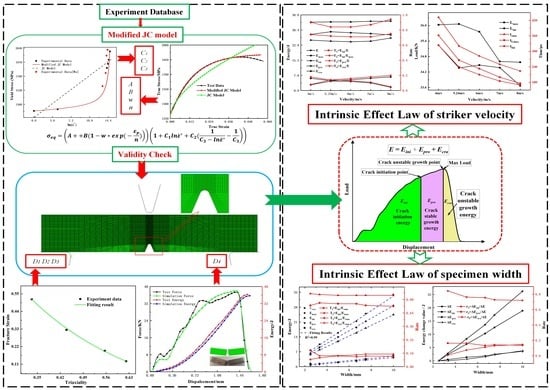
Study on Intrinsic Influence Law of Specimen Size and Loading Speed on Charpy Impact Test
Abstract
:1. Introduction
2. Experimental and Methods
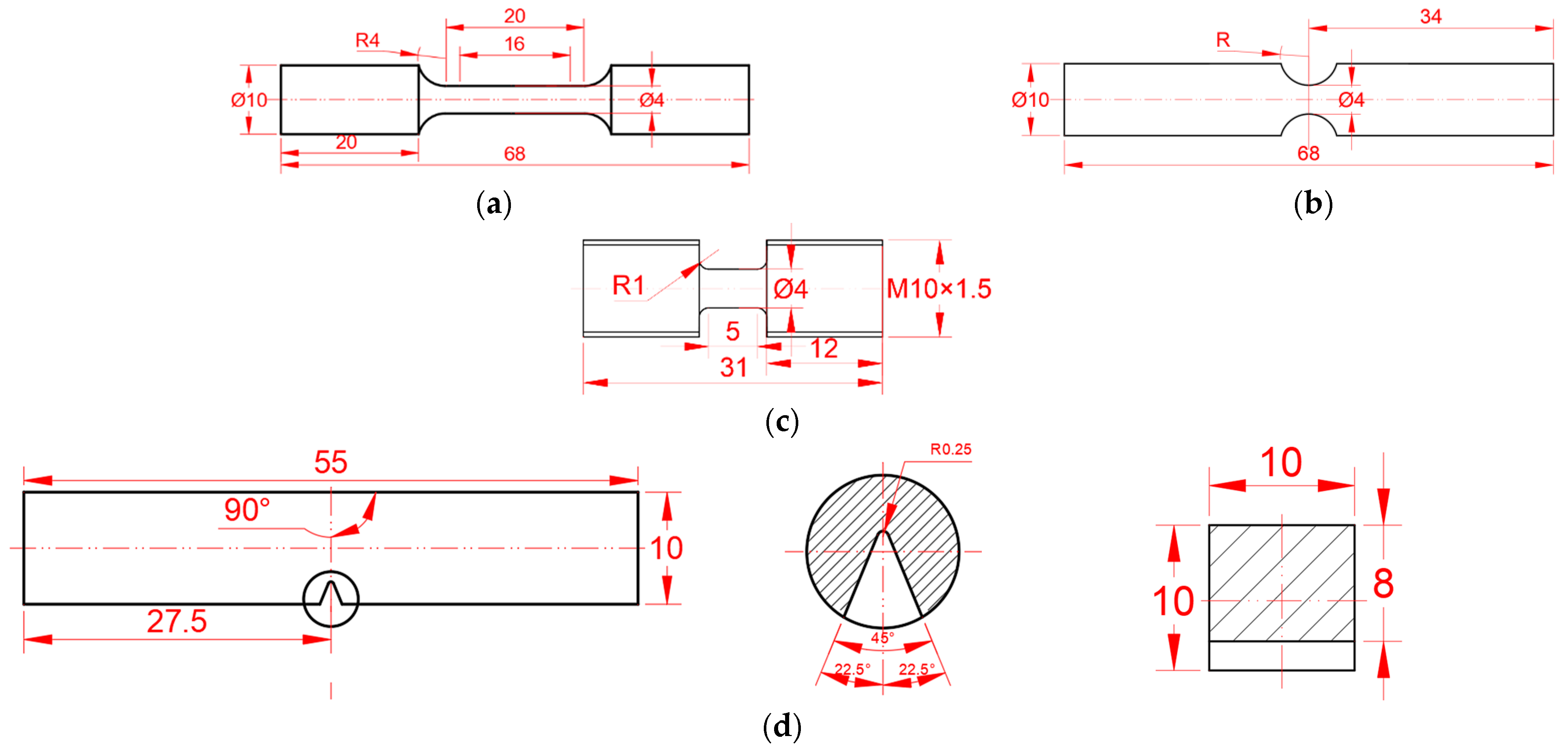
2.1. Experimental Design
2.2. Experimental Methods and Results
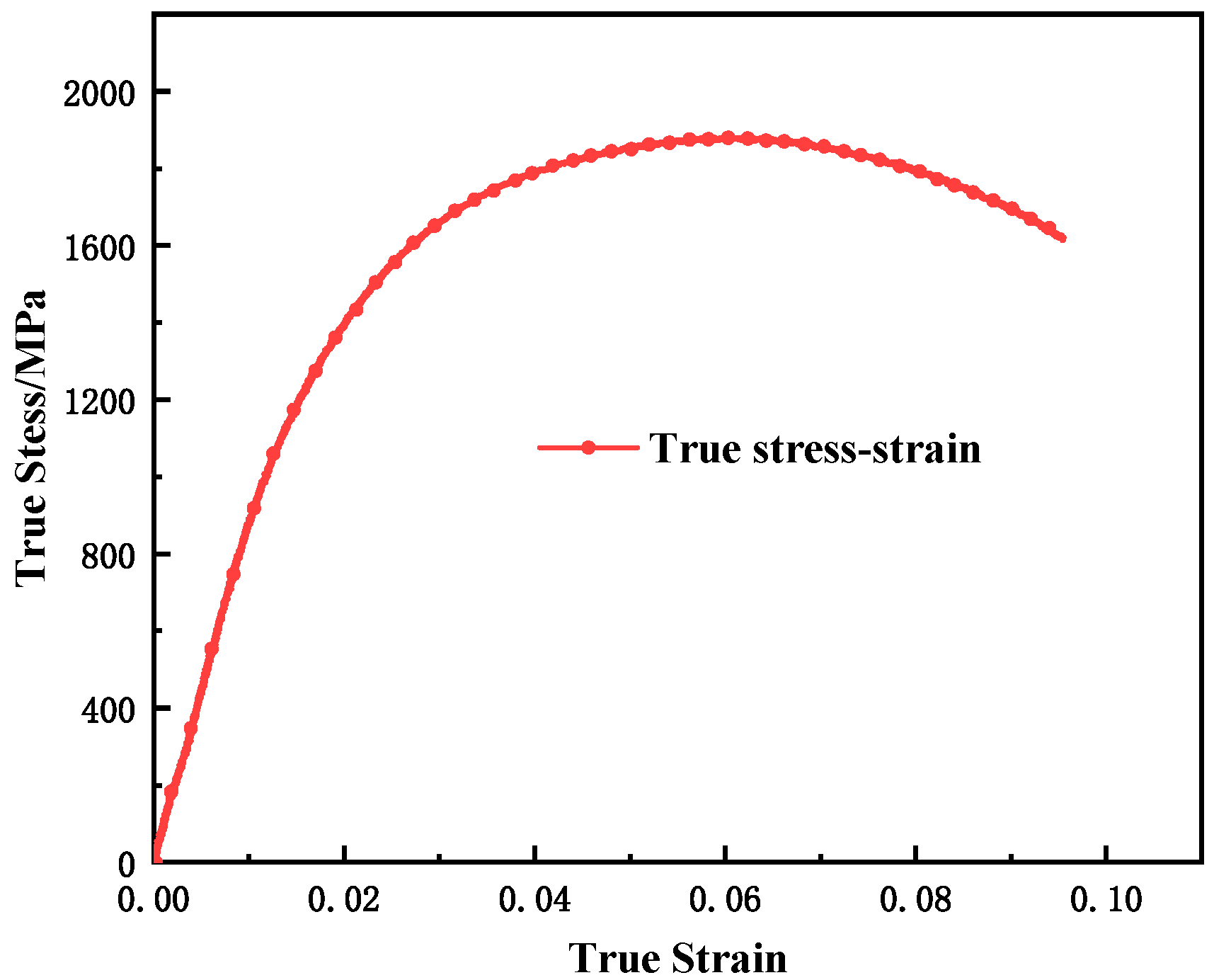
2.2.1. Static Smooth and Notched Test
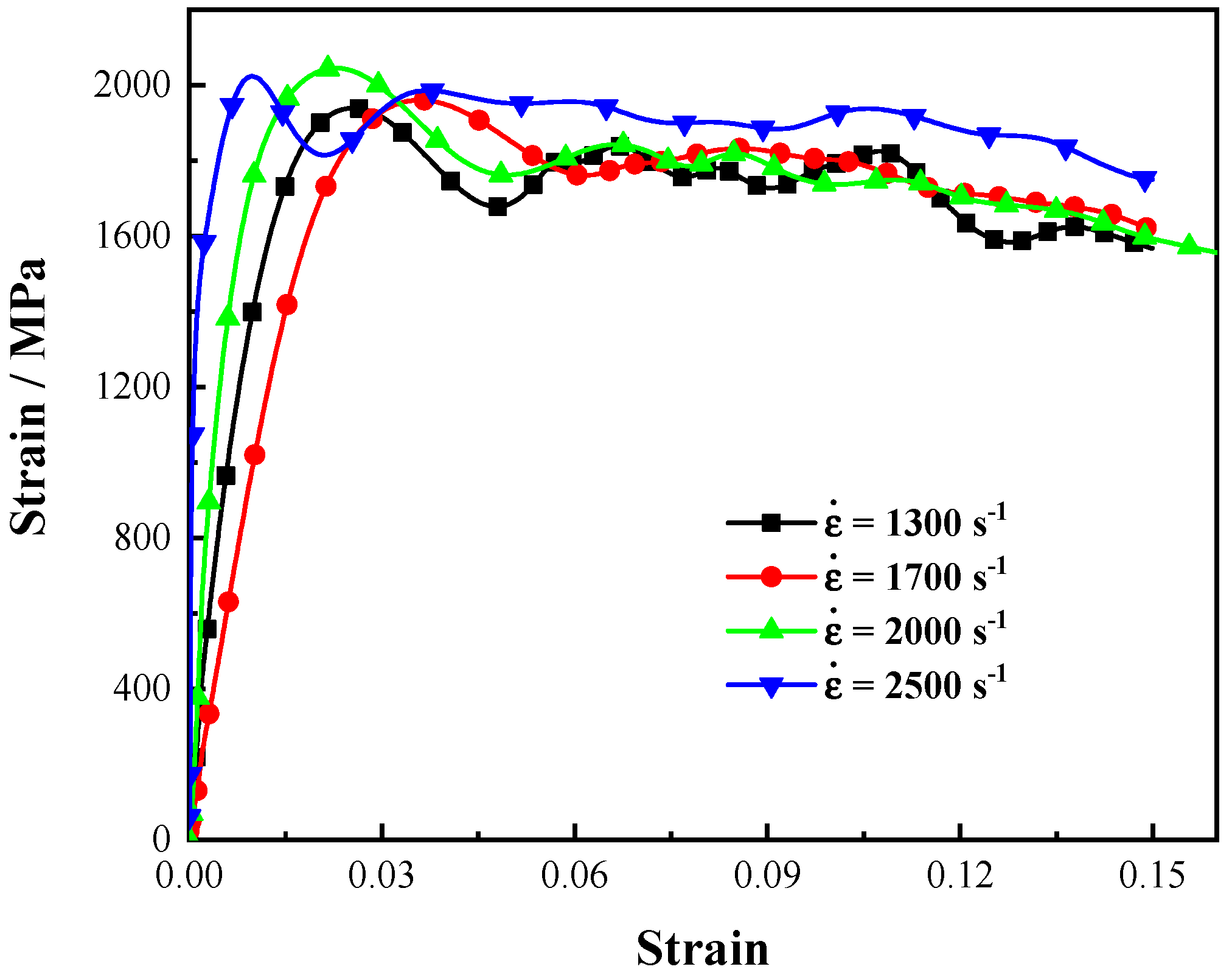
2.2.2. Dynamic Tensile Test
2.2.3. Charpy Impact Test
3. Material Model and Parameter Determination
3.1. JC Model
3.2. MJC Model
3.2.1. Modification of Strength Part
3.2.2. Modification of Strain Rate
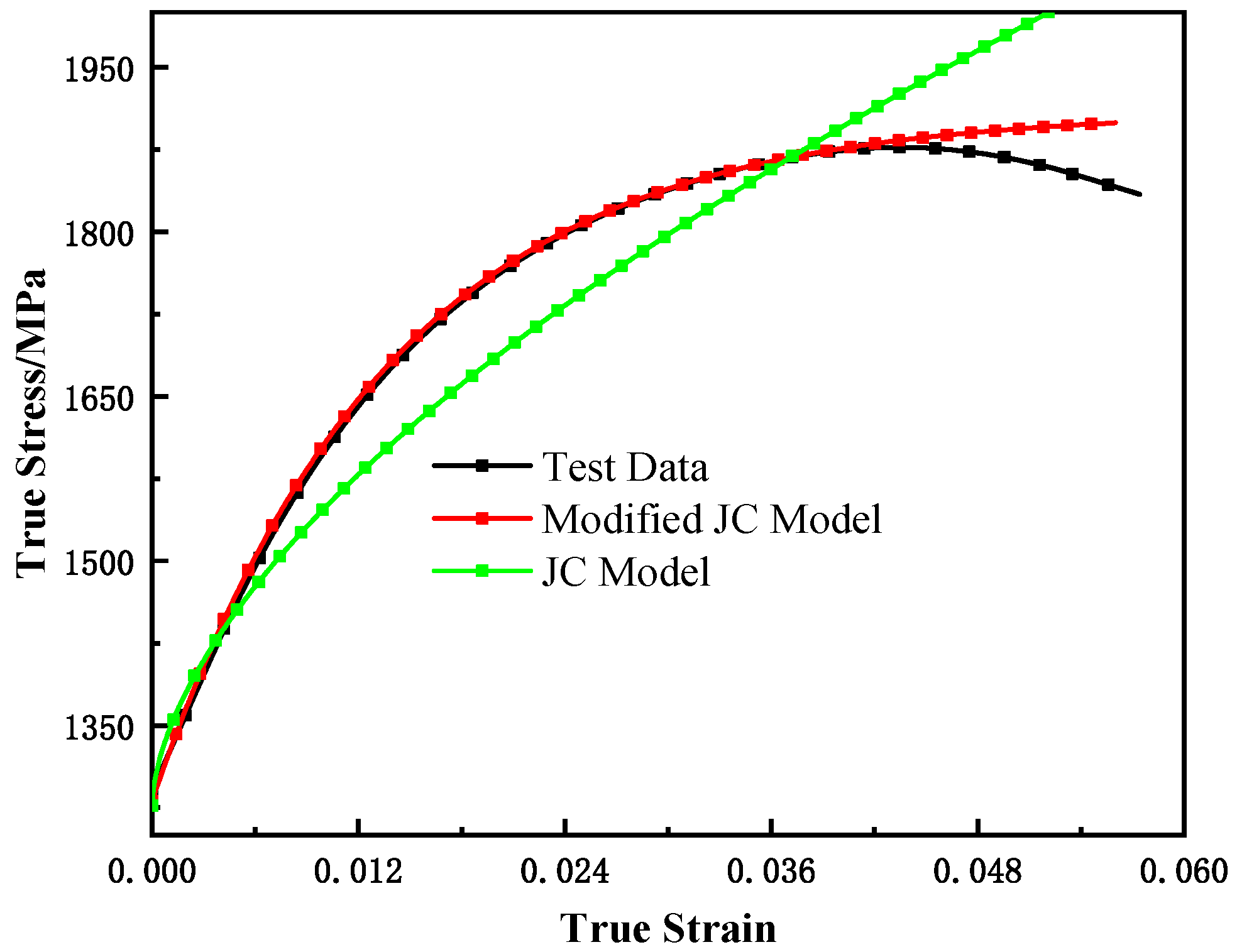
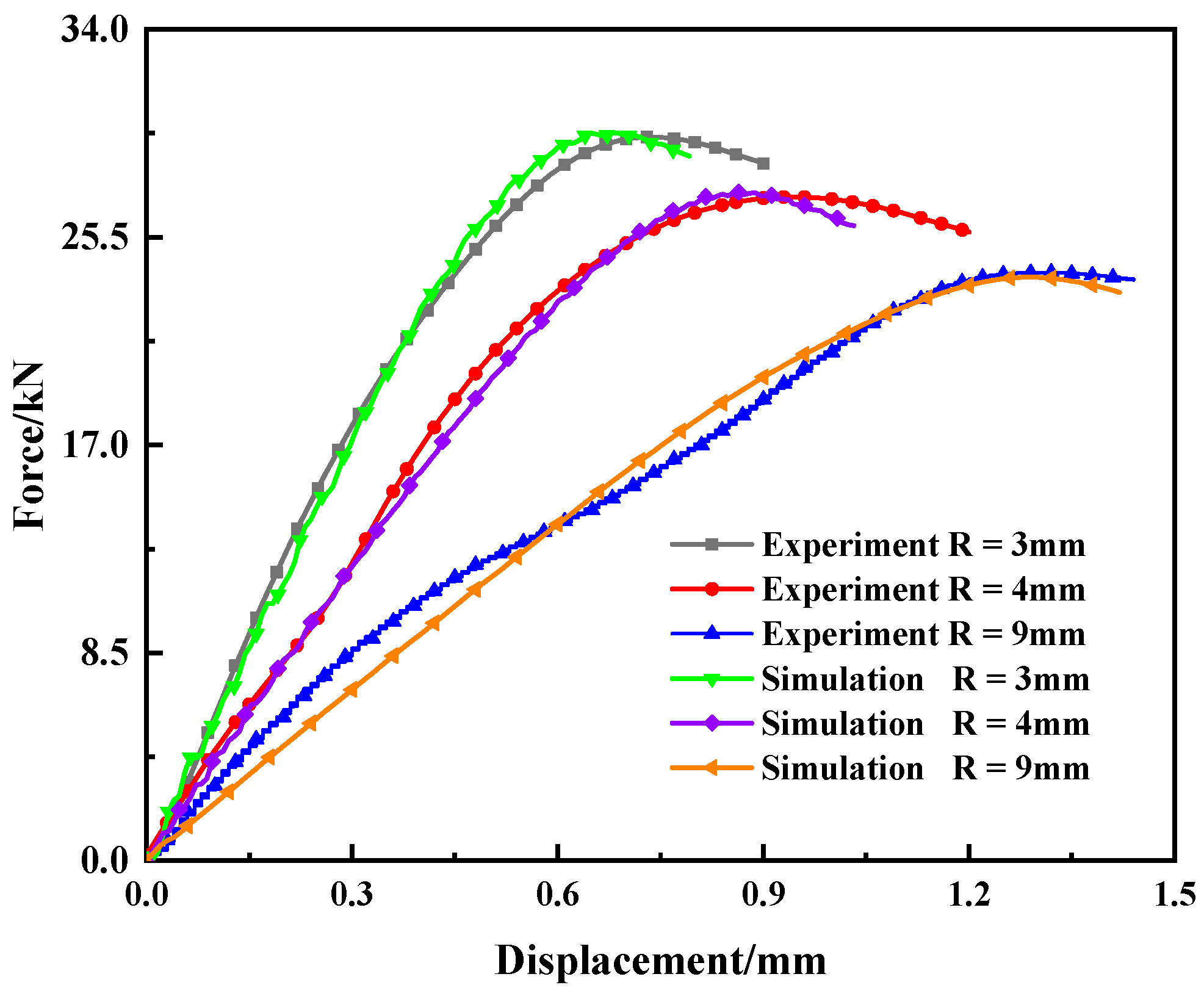
3.2.3. Model Validation
3.3. Johnson–Cook Failure Model
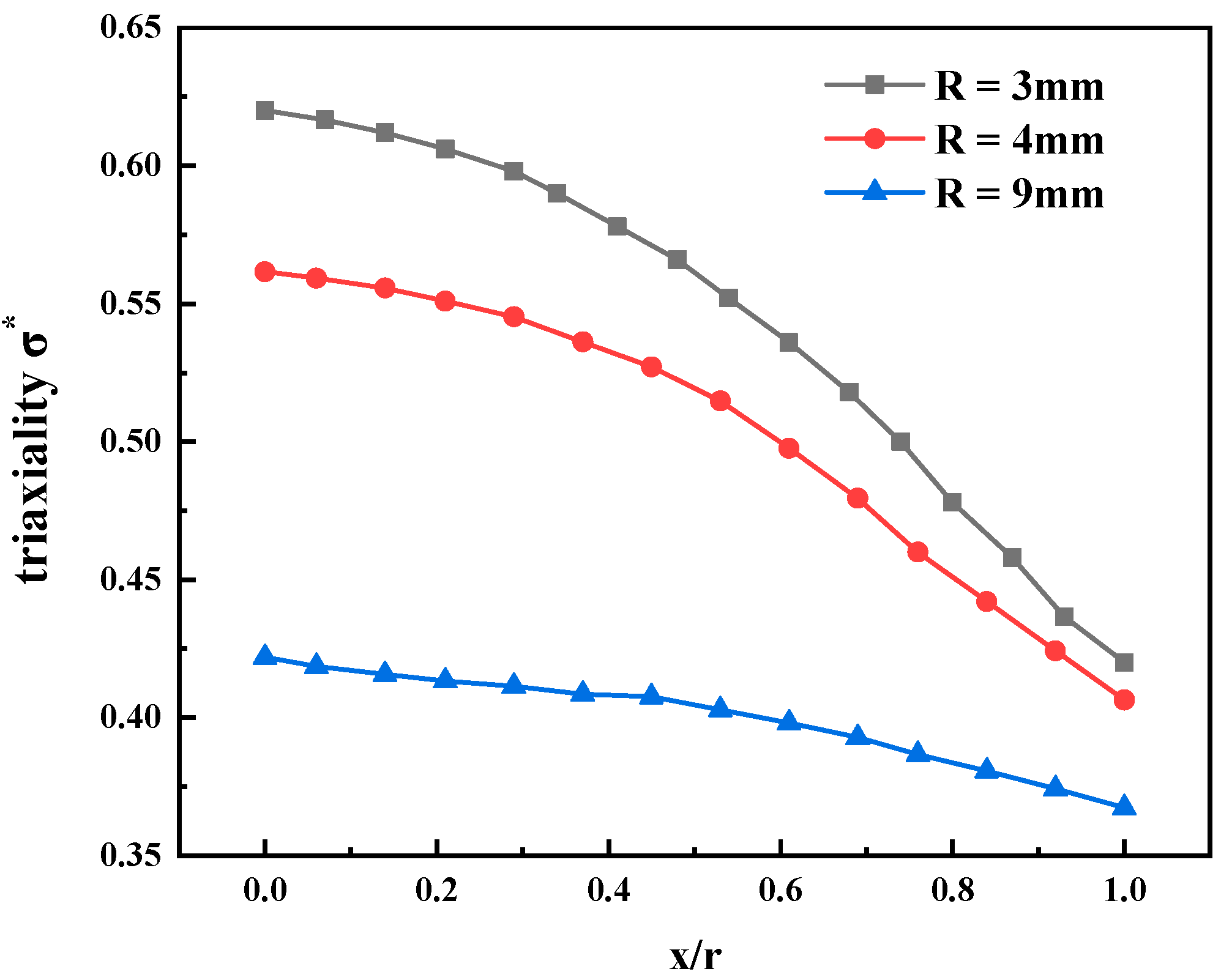
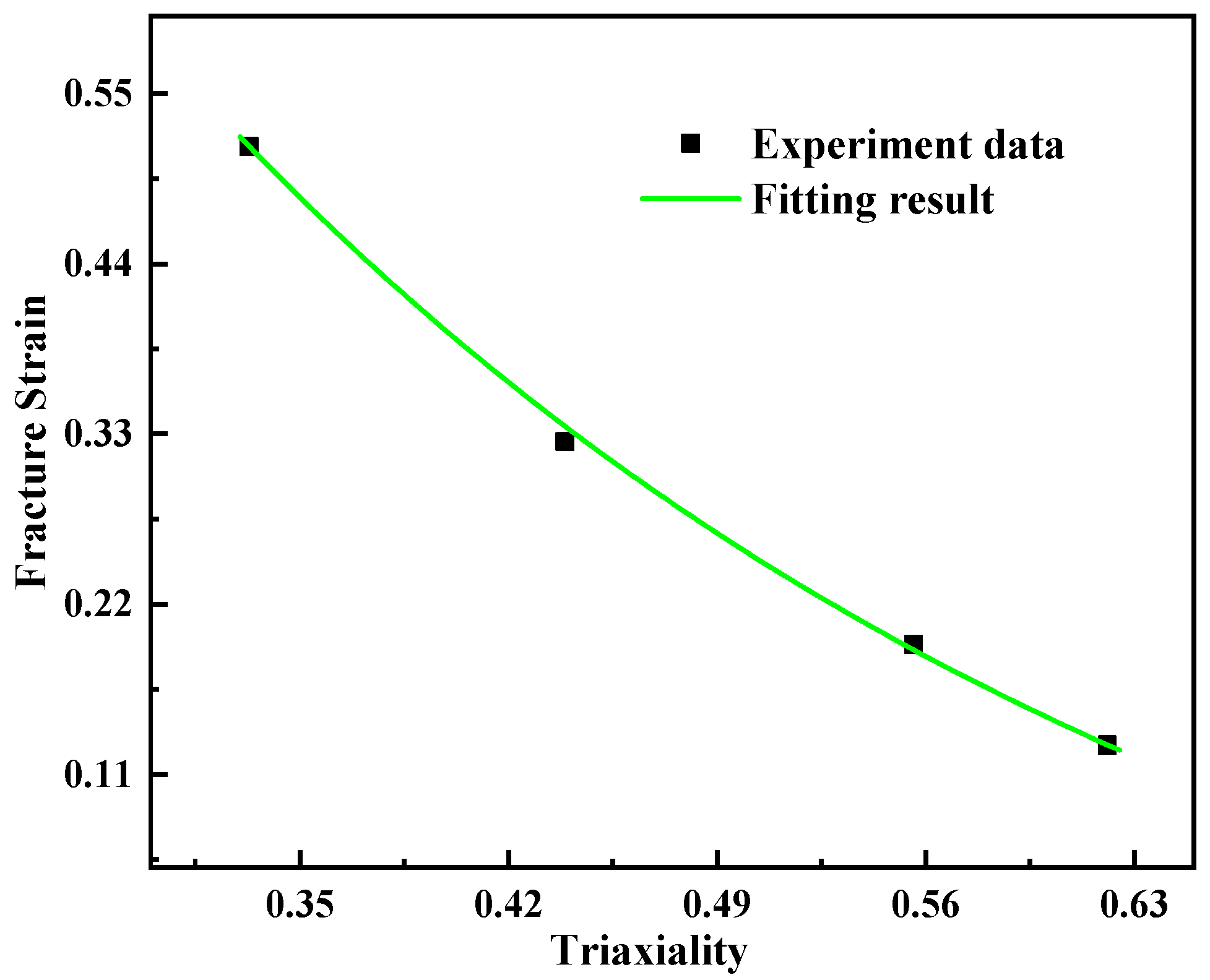
3.3.1. Determination of Damage Parameters D1, D2, and D3
3.3.2. Determination of Damage Parameter D4
4. Results and Discussion
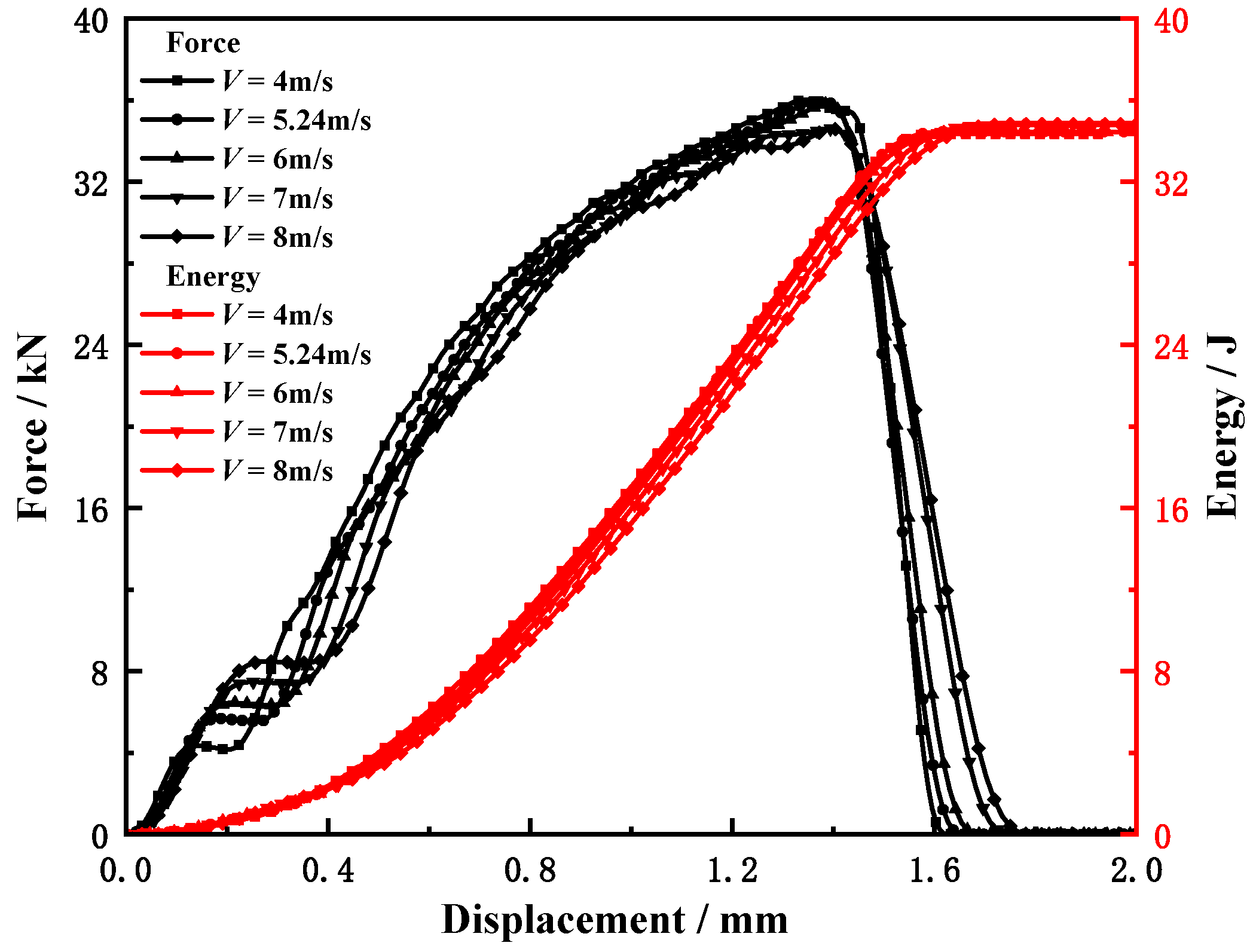
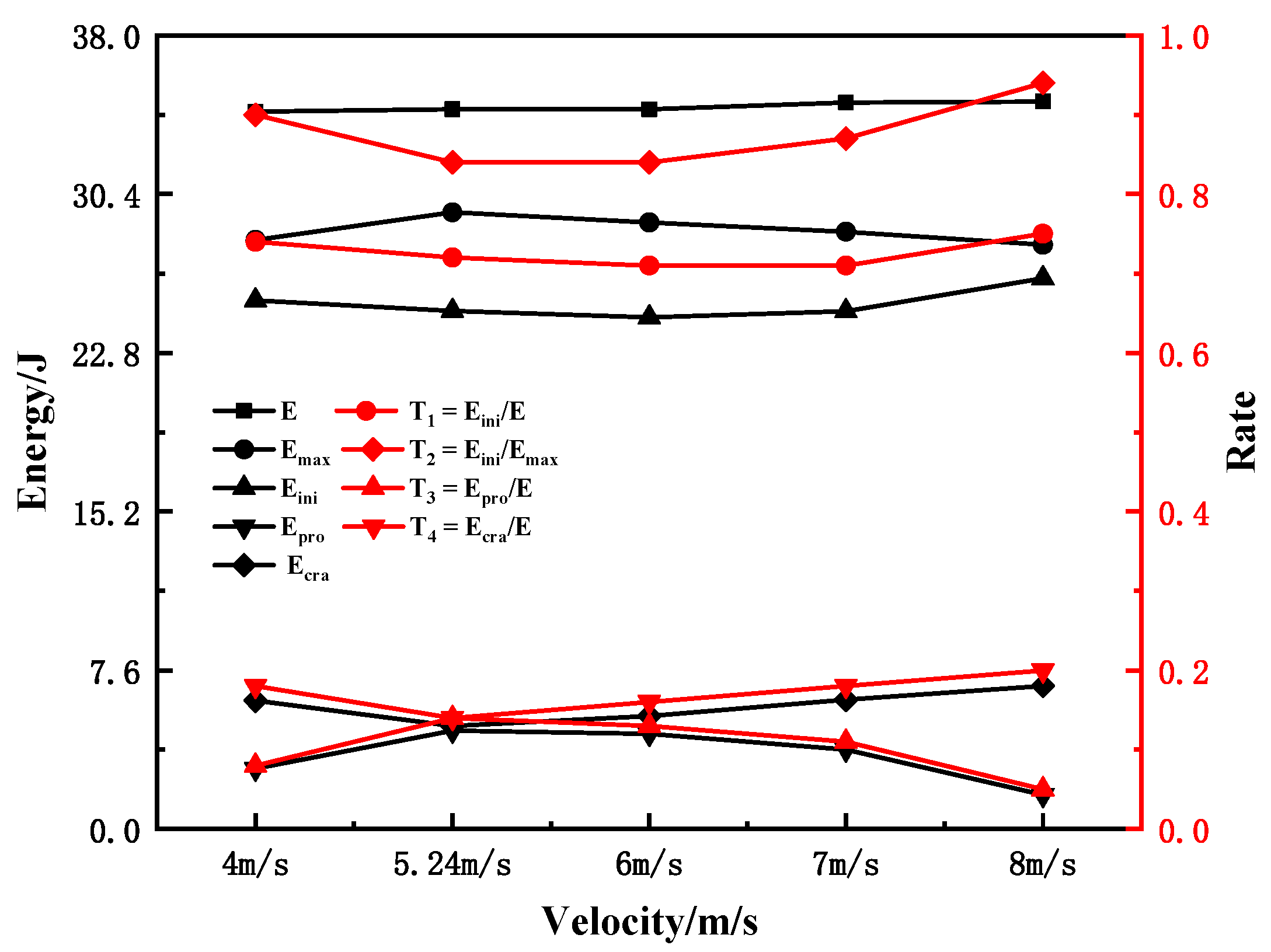
4.1. Effect of Striker Velocity
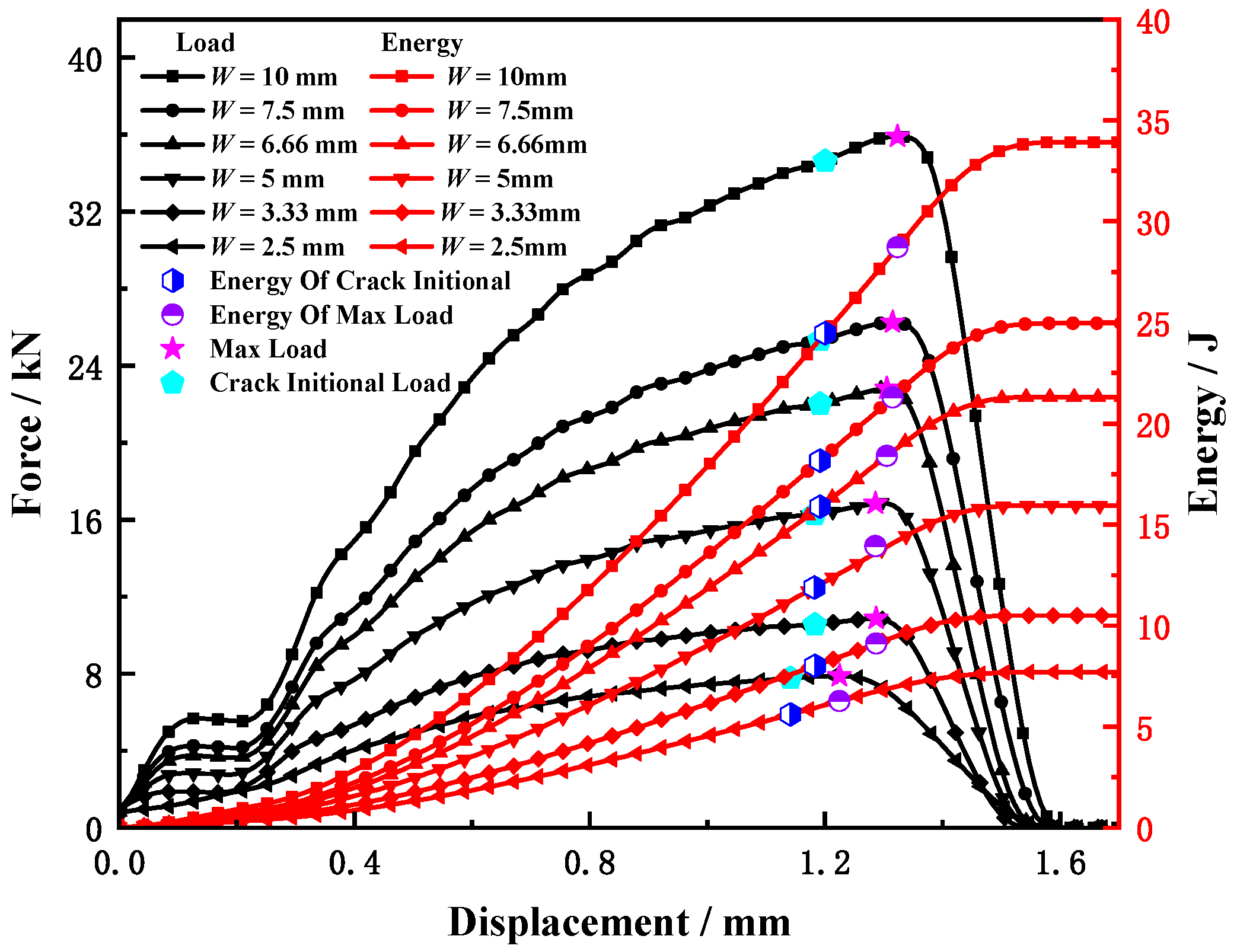
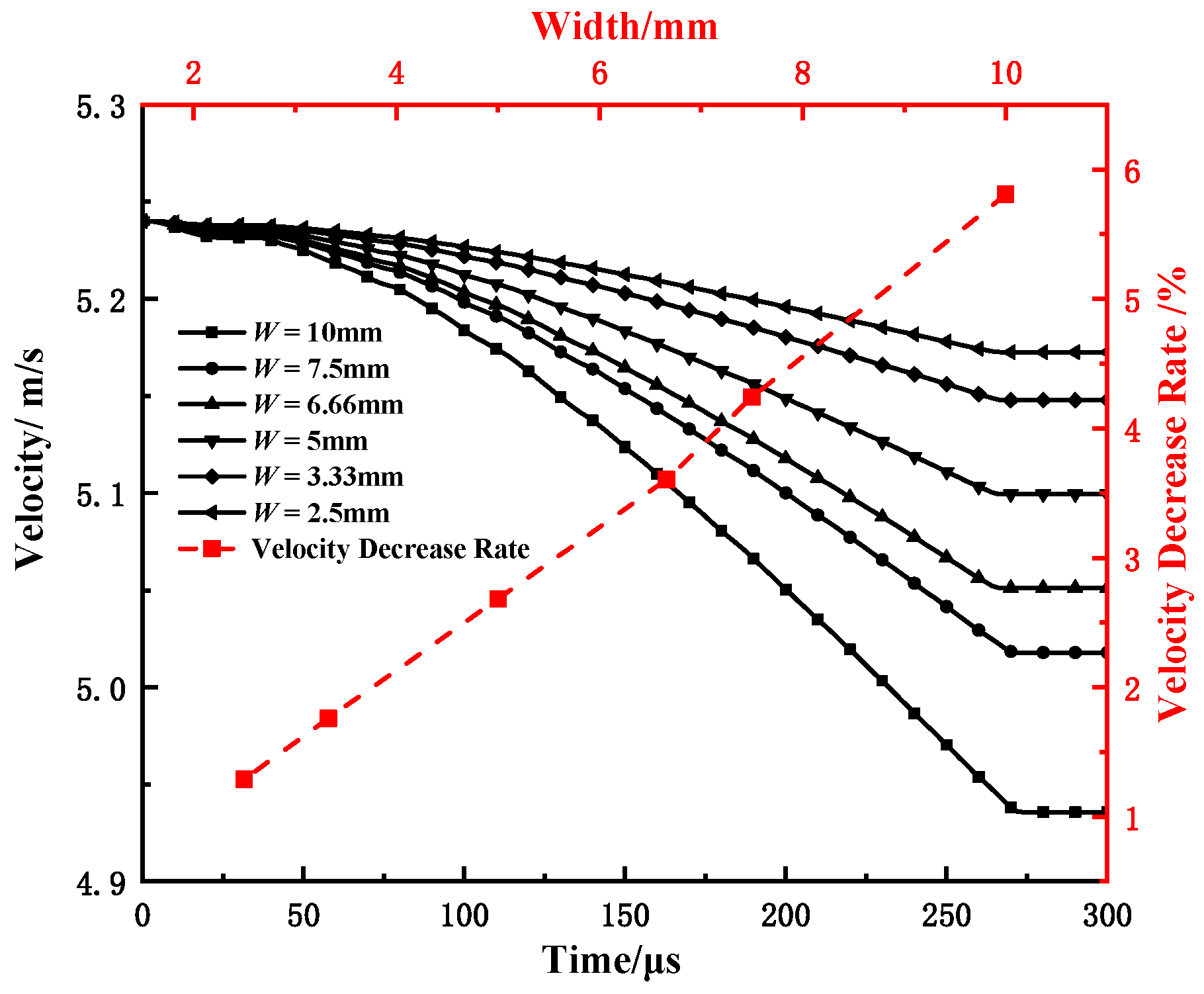
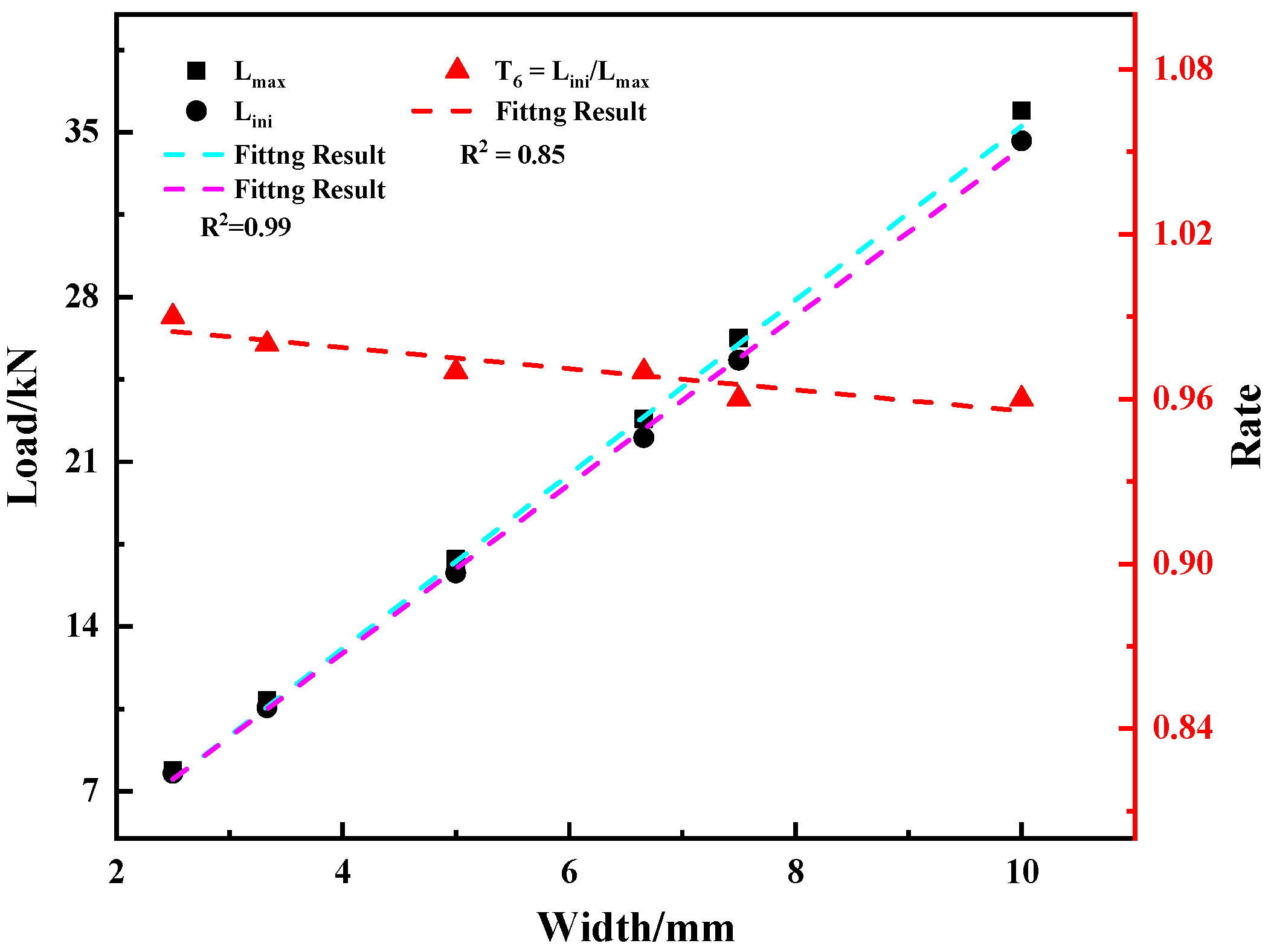
4.2. Effect of Specimen Width
5. Conclusions
- The MJC model was established, and the MJC model parameters (A = 1290 MPa, B = 595 MPa, w = 1.084, n = 0.01435, C1 = 0.0025, C2 = 0.029, C3 = 15.25) and JC fracture model parameters (D1 = −0.1663, D2 = 1.7969, D3 = −2.9078, D4 = 0.07) were determined. The instrumented Charpy test was simulated, and the simulation and test results were in good agreement. It is proven that the MJC model and JC fracture models can simulate the deformation behavior and failure characteristics of the material under dynamic conditions.
- The influence of the pendulum speed on the energy and characteristic load of each part is small and can be ignored. However, it had a significant influence on the response of the Charpy specimen. The faster the pendulum speed, the shorter the time between the crack initiation load and the maximum load is, and the closer it is.
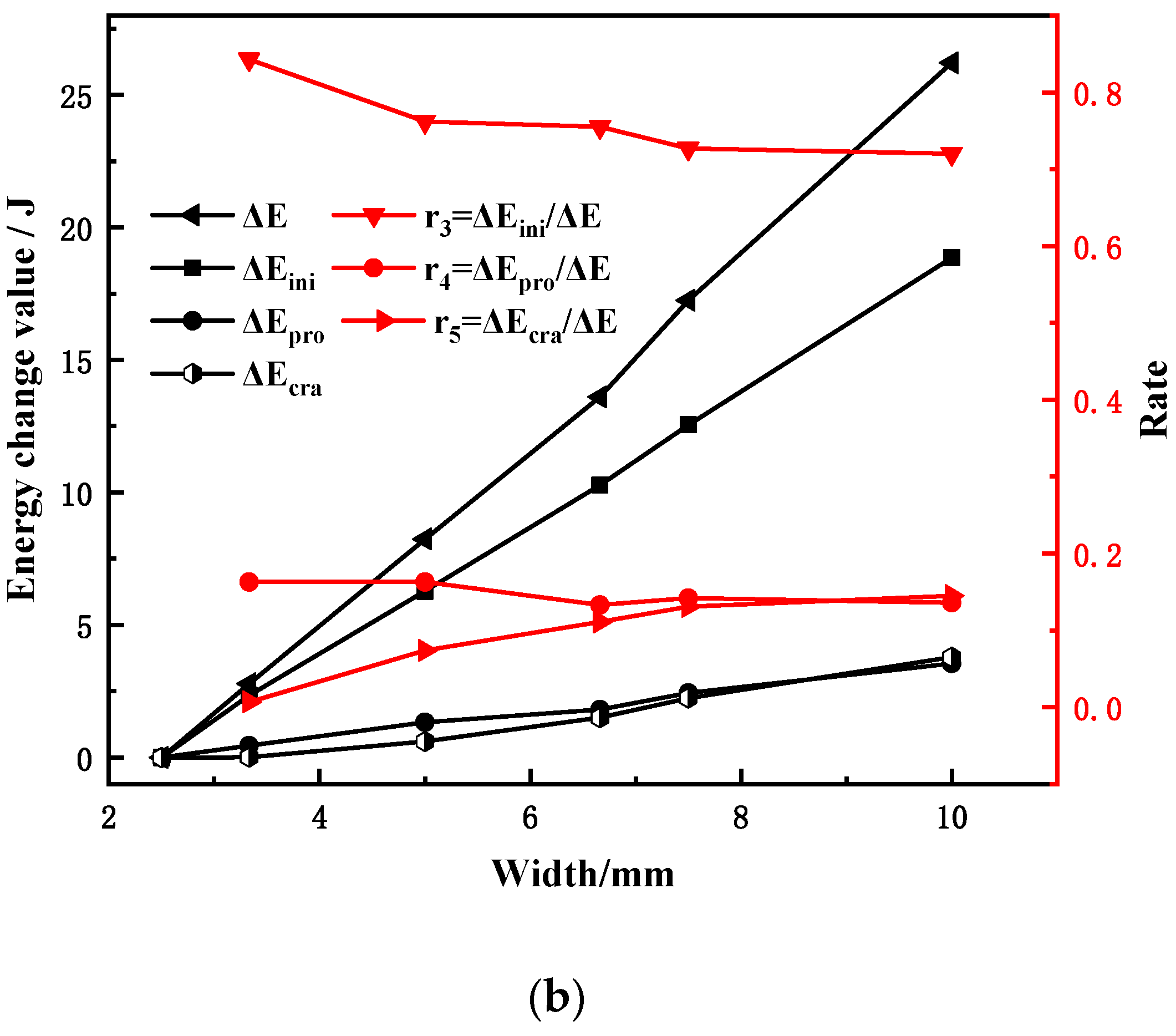
- The width of the sample has a significant influence on the energy and characteristic load of each part, but the law of influence on the energy of each part is quite different; the linear correlation between the crack initiation energy and the sample width is very strong, whereas the linear correlations between the stable crack propagation energy and crack unstable propagation energy and the sample width are weak. With the increases in the width of the specimen, the difference between the stable crack propagation energy, the unstable crack propagation energy, and the crack initiation energy is larger.
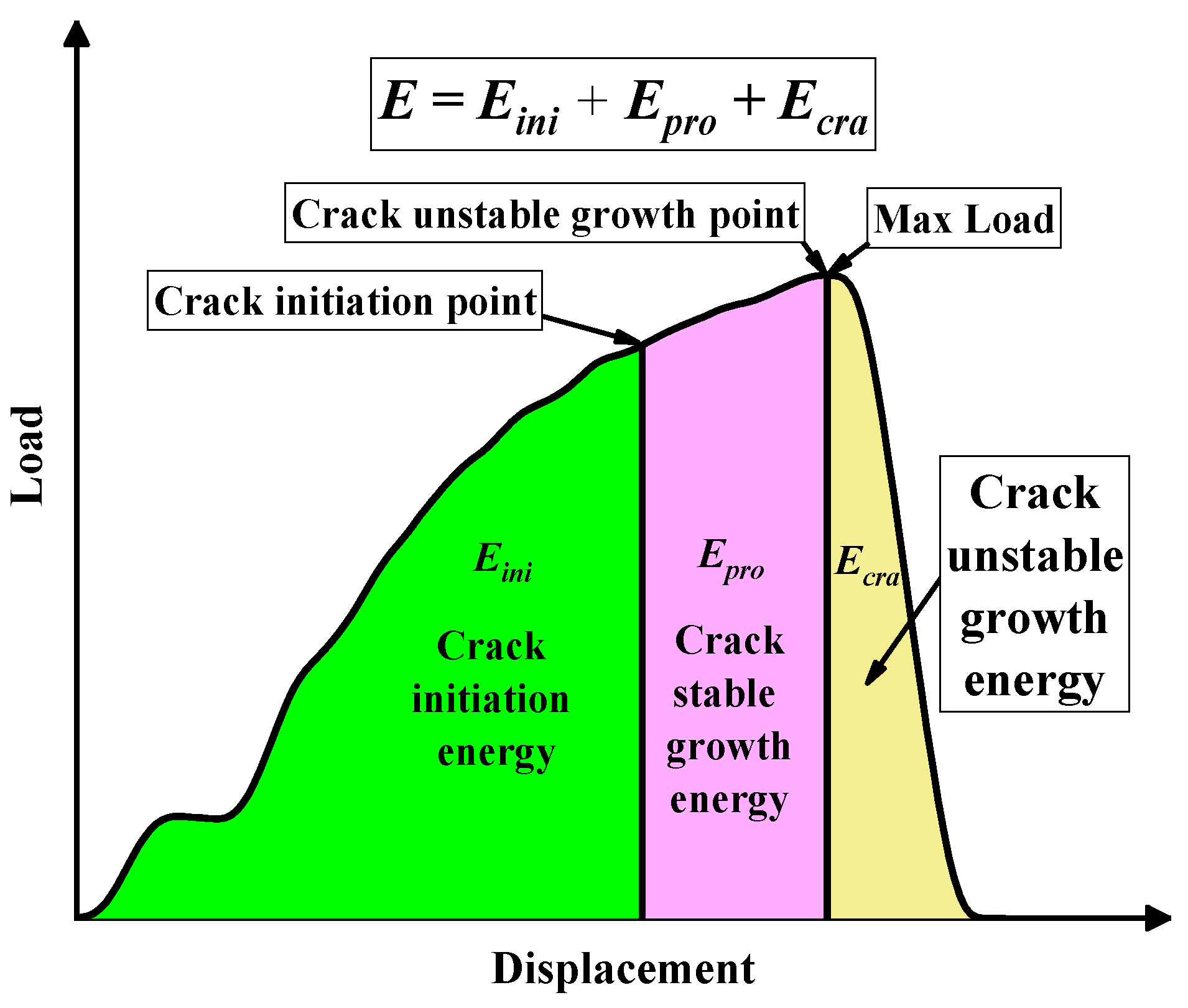
- Under the condition of different sample widths, more than 70% of the impact energy was consumed in the crack initiation stage. The ability of a material to resist crack initiation and resist stable crack propagation is the key to its resistance to fracture [11]. Therefore, in the selection of materials, comparison and analysis of the crack initiation energy and stable crack propagation energy can better ensure the accuracy of material selection.
- With the increase in sample width, the increment of crack initiation energy and the increment of the crack stable growth energy decreased gradually. This discovery reveals that the internal mechanism of the Charpy impact toughness decreases with the increase in sample size. This finding also reveals the internal reason why the linear transformation relationship between the Charpy impact energy of SCVN specimens and CVN specimens is not tenable when the specimens are small. Because of the 30CrMnSiNi2A steel material selected in this study, the linear correlation between the SCVN specimens and CVN specimens was good. This finding needs to be confirmed through in-depth studies on various materials.
- The energy of each part of the correlation model for the SCVN and CVN specimens in the impact test was established. Equations (19)–(21) can be used to convert the Charpy impact test results of any width to standard test results more accurately.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | initial yield stress of materials at reference strain rate and reference temperature |
| B | strain hardening modulus |
| C1, C2 | the strain rate-hardening parameter |
| C3 | the natural logarithm of the critical strain rate level |
| CVN | full-size Charpy V-notch specimens |
| D1, D2, D3, D4, | the material damage parameters |
| E | impact energy |
| Emax | maximum load energy |
| Eini | crack initiation energy |
| Epro | crack stable propagation energy |
| Ecra | crack instability propagation energy |
| ΔE | increase in impact energy |
| ΔEini | increase in crack initiation energy |
| ΔEpro | increase in crack stable propagation energy |
| ΔEcra | increase in crack instability propagation energy |
| Lmax | maximum load |
| Lini | crack initiation load |
| r1 | the change rate of maximum load displacement |
| r2 | the change rate of crack initiation displacement |
| r3 | the rate of ΔEini/ΔE |
| r4 | the rate of ΔEpro/ΔE |
| r5 | the rate of ΔEcra/ΔE |
| ε | engineering strain |
| εf | fracture strain |
| εp | plastic strain |
| εt | true stain |
| dimensionless strain rate | |
| reference strain rate | |
| σ | engineering stress |
| σeq | equivalent flow stress |
| σm | mean stress or hydrostatic stress |
| σt | true stress |
| σ∗ | stress triaxiality |
| SCVN | sub-size Charpy V-notch specimens |
| SLini | crack initiation displacement |
| SLmax | maximum load displacement |
| T | working temperature |
| T0 | room temperature |
| Tr | melting temperature |
| tIni | crack initiation time |
| tsum | total time |
| tLmax | maximum load time |
| T1 | the ratio of crack initiation energy to total energy |
| T2 | the ratio of crack initiation energy to maximum load energy |
| T3 | the ratio of the crack stable propagation energy to the total energy |
| T4 | the ratio of crack instability propagation energy to total energy |
| t1 | the ratio of crack initiation load to max load |
| w, n | strain hardening index parameters |
| W | width |
References
- Liu, J.; Guo, Q.; Yu, M.; Songmei, L. SCC investigation of low alloy ultra-high strength steel 30CrMnSiNi2A in 3.5 wt% NaCl solution by slow strain rate technique. Chin. J. Aeronaut. 2014, 27, 1327–1333. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Yao, W.; Huang, F.L.; Zhang, L.; LI, Y. Experimental study on dynamic mechanical properties of ultrahigh strength 30CrMnSiNi2A steel. J. Trans. Beijing Inst. Technol. 2010, 30, 258–262. [Google Scholar]
- Siewert, T.A.; Manahan, M.P.; McCowan, C.N.; Holt, J.M.; Marsh, F.J.; Ruth, E.A. The history and importance of impact testing. In Pendulum Impact Testing: A Century of Progress; ASTM International: West Conshohocken, PA, USA, 2000. [Google Scholar]
- Kobayashi, H.; Onoue, H. Brittle fracture of liberty ships. Fail. Knowl. Database 1943, 100, 67. [Google Scholar]
- Hertzberg, R.W. Deformation and fracture mechanics of engineering materials. J. Mater. Educ. 1997, 19, 227–232. [Google Scholar] [CrossRef] [Green Version]
- Benzerga, A.A.; Tvergaard, V.; Needleman, A. Size effects in the Charpy V-notch test. Int. J. Fract. 2002, 116, 275–296. [Google Scholar] [CrossRef]
- Corwin, W.R.; Klueh, R.L.; Vitek, J.M. Effect of specimen size and nickel content on the impact properties of 12 Cr-1 MoVW ferritic steel. J. Nucl. Mater. 1984, 122, 343–348. [Google Scholar] [CrossRef] [Green Version]
- Corwin, W.R.; Lucas, G.E. The Use of Small-Scale Specimens for Testing Irradiated Material: A Symposium Sponsored by ASTM Committee E-10 on Nuclear Technology and Applications, Albuquerque, NM, 23 September 1983; ASTM International: West Conshohocken, PA, USA, 1986; ISBN 0803104405. [Google Scholar]
- Schubert, L.E.; Kumar, A.S.; Rosinki, S.T.; Hamilton, M.L. Effect of specimen size on the impact properties of neutron irradiated A533B steel. J. Nucl. Mater. 1995, 225, 231–237. [Google Scholar]
- Pineau, A.; Benzerga, A.A.; Pardoen, T. Failure of metals I: Brittle and ductile fracture. Acta Mater. 2016, 107, 424–483. [Google Scholar] [CrossRef] [Green Version]
- Duan, Q.Q.; Qu, R.T.; Zhang, P.; Zhang, Z.J.; Zhang, Z.F. Intrinsic impact toughness of relatively high strength alloys. Acta Mater. 2018, 142, 226–235. [Google Scholar] [CrossRef]
- Cao, Y.; Zhen, Y.; Song, M.; Yi, H.; Li, F.; Li, X. Determination of Johnson-Cook parameters and evaluation of Charpy impact test performance for X80 pipeline steel. Int. J. Mech. Sci. 2020, 179, 105627. [Google Scholar] [CrossRef]
- Louden, B.S.; Kumar, A.S.; Garner, F.A.; Hamilton, M.L.; Hu, W.L. The influence of specimen size on Charpy impact testing of unirradiated HT-9. J. Nucl. Mater. 1988, 155, 662–667. [Google Scholar] [CrossRef]
- Lin, Y.; Yu, Q.; Pan, J.; Duan, F.; Ritchie, R.O.; Li, Y. On the impact toughness of gradient-structured metals. Acta Mater. 2020, 193, 125–137. [Google Scholar] [CrossRef]
- Server, W.L. Static and dynamic fibrous initiation toughness results for nine pressure vessel materials. In Elastic-Plastic Fracture; ASTM International: West Conshohocken, PA, USA, 1979. [Google Scholar]
- Wullaert, R.A. Applications of the instrumented Charpy impact test. In Impact Testing of Metals; ASTM International: West Conshohocken, PA, USA, 1970. [Google Scholar]
- Sheckherd, J.W.; Kangilaski, M.; Bauer, A.A. Impact properties of shock-strengthened type 316 stainless steel. In Instrumented Impact Testing; ASTM International: West Conshohocken, PA, USA, 1974. [Google Scholar]
- Samuel, K.G.; Sreenivasan, P.R.; Ray, S.K.; Rodriguez, P. Evaluation of ageing-induced embrittlement in an austenitic stainless steel by instrumented impact testing. J. Nucl. Mater. 1987, 150, 78–84. [Google Scholar] [CrossRef]
- Iyer, K.R.; Miclot, R.B. Instrumented Charpy testing for determination of the J-integral. In Instrumented Impact Testing; ASTM International: West Conshohocken, PA, USA, 1974. [Google Scholar]
- Ghoneim, M.M.; Hammad, F.H. Instrumented impact testing of an irradiated 20MnMoNi55 PVS weld material. J. Nucl. Mater. 1992, 186, 196–202. [Google Scholar] [CrossRef]
- Toshiro, K.; Isamu, Y.; Mitsuo, N. Evaluation of dynamic fracture toughness parameters by instrumented Charpy impact test. Eng. Fract. Mech. 1986, 24, 773–782. [Google Scholar] [CrossRef]
- Ray, S.K.; Sreenivasan, P.R.; Samuel, K.G.; Rodriguez, P. Quality control for nuclear grade austenitic stainless steels using charpy impact testing. In Fracture 84; Elsevier: Amsterdam, The Netherlands, 1984; pp. 3221–3228. [Google Scholar]
- Kobayashi, T. Analysis of impact properties of A533 steel for nuclear reactor pressure vessel by instrumented Charpy test. Eng. Fract. Mech. 1984, 19, 49–65. [Google Scholar] [CrossRef]
- Chen, X.; Peng, Y.; Peng, S.; Yao, S.; Chen, C.; Xu, P. Flow and fracture behavior of aluminum alloy 6082-T6 at different tensile strain rates and triaxialities. PLoS ONE 2017, 12, e0181983. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanguy, B.; Besson, J.; Piques, R.; Pineau, A. Ductile to brittle transition of an A508 steel characterized by Charpy impact test: Part II: Modeling of the Charpy transition curve. Eng. Fract. Mech. 2005, 72, 413–434. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.L.; Jeong, D.Y. Application of a stress triaxiality dependent fracture criterion in the finite element analysis of unnotched Charpy specimens. Theor. Appl. Fract. Mech. 2010, 54, 54–62. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Bao, Y.; Lee, Y.-W.; Bai, Y. Calibration and evaluation of seven fracture models. Int. J. Mech. Sci. 2005, 47, 719–743. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Banerjee, A.; Dhar, S.; Acharyya, S.; Datta, D.; Nayak, N. Determination of Johnson cook material and failure model constants and numerical modelling of Charpy impact test of armour steel. Mater. Sci. Eng. A 2015, 640, 200–209. [Google Scholar] [CrossRef]
- Madhusudhan, D.; Chand, S.; Ganesh, S.; Saibhargavi, U. (Eds.) Modeling and Simulation of Charpy Impact Test of Maraging Steel 300 Using Abaqus; IOP Conference Series; Materials Science and Engineering; IOP Publishing: Hyderabad, India, 2018. [Google Scholar]
- ASTM A370-19; Standard Test Methods and Definitions for Mechanical Testing of Steel Products. ASTM International: West Conshohocken, PA, USA, 2019.
- Hu, H.; Xu, Z.; Dou, W.; Huang, F. Effects of strain rate and stress state on mechanical properties of Ti-6Al-4V alloy. Int. J. Impact Eng. 2020, 145, 103689. [Google Scholar] [CrossRef]
- Ludwik, P. Elemente der Technologischen Mechanik; Springer: Berlin/Heidelberg, Germany, 1909; ISBN 3662392658. [Google Scholar]
- Voce, E. The relationship between stress and strain for homogeneous deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Sung, J.H.; Kim, J.H.; Wagoner, R.H. A plastic constitutive equation incorporating strain, strain-rate, and temperature. Int. J. Plast. 2010, 26, 1746–1771. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Effect of strain rate on ductile fracture initiation in advanced high strength steel sheets: Experiments and modeling. Int. J. Plast. 2014, 56, 19–44. [Google Scholar] [CrossRef]
- Fras, T.; Roth, C.C.; Mohr, D. Fracture of high-strength armor steel under impact loading. Int. J. Impact Eng. 2018, 111, 147–164. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Ductile fracture experiments with locally proportional loading histories. Int. J. Plast. 2016, 79, 328–354. [Google Scholar] [CrossRef]
- Follansbee, P.S.; Kocks, U.F. A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable. Acta Metall. 1988, 36, 81–93. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Hu, X.; Yuan, K.; Meng, W.; Li, P. Impact resistance prediction of superalloy honeycomb using modified Johnson–Cook constitutive model and fracture criterion. Int. J. Impact Eng. 2019, 131, 66–77. [Google Scholar] [CrossRef]
- Wang, J.; Guo, W.-G.; Li, P.; Zhou, P. Modified Johnson-Cook description of wide temperature and strain rate measurements made on a nickel-base superalloy. Mater. High Temp. 2017, 34, 157–165. [Google Scholar] [CrossRef]
- Wu, H.J.; Sun, K.; Guo, C.; Huang, F.L.; Ma, X.F. Experimental Studies on Fracture Properties of 30CrMnSiNi2A Steel. AMR 2014, 875–877, 478–484. [Google Scholar] [CrossRef]
- Bridgman, P.W. Studies in Large Plastic Flow and Fracture; Harvard University Press: Cambridge, MA, USA, 2013; ISBN 0674731336. [Google Scholar]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Hancock, J.W.; Mackenzie, A.C. On the mechanisms of ductile failure in high-strength steels subjected to multi-axial stress-states. J. Mech. Phys. Solids 1976, 24, 147–160. [Google Scholar] [CrossRef]
- Dou, W.; Xu, Z.; Hu, H.; Huang, F. A generalized plasticity model incorporating stress state, strain rate and temperature effects. Int. J. Impact Eng. 2021, 155, 103897. [Google Scholar] [CrossRef]
- ASTM E23-07; Standard Test Methods for Notched Bar Impact Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2007.



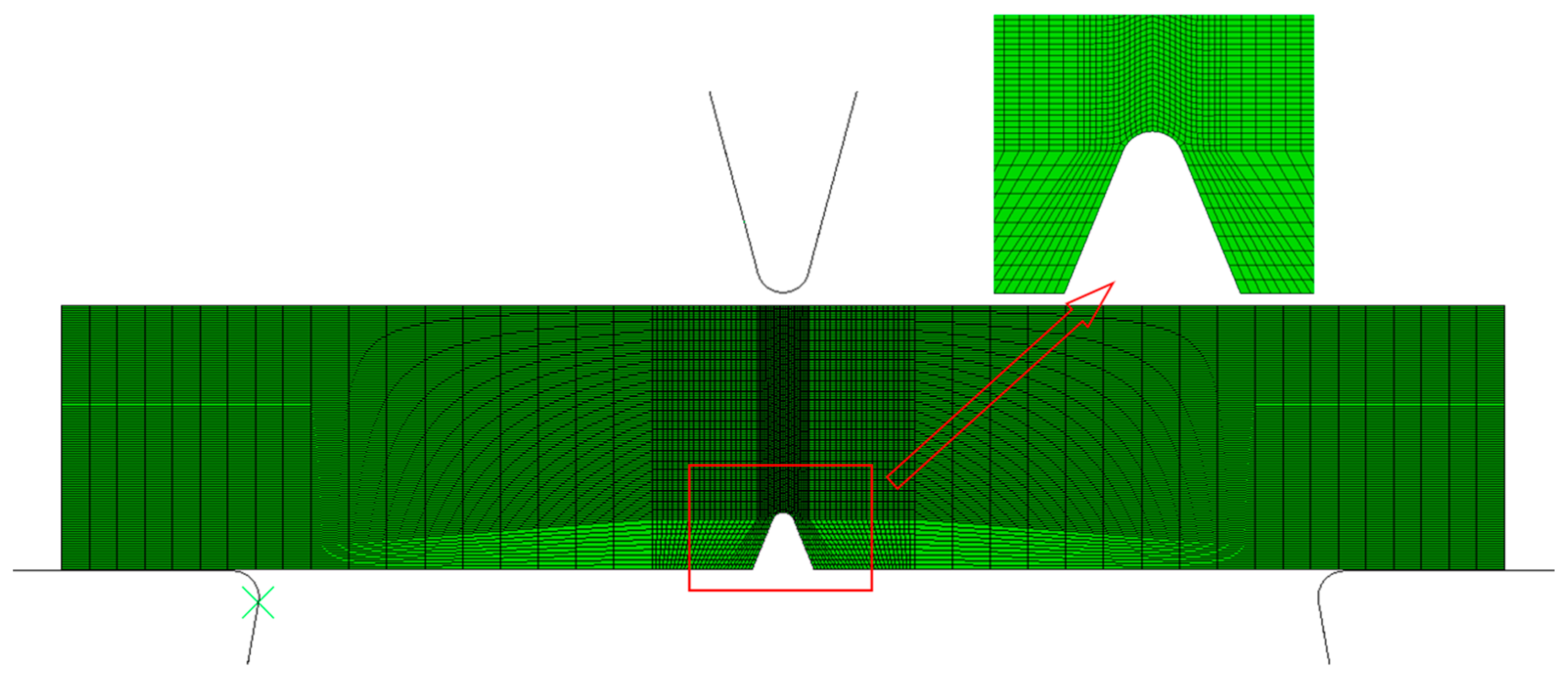
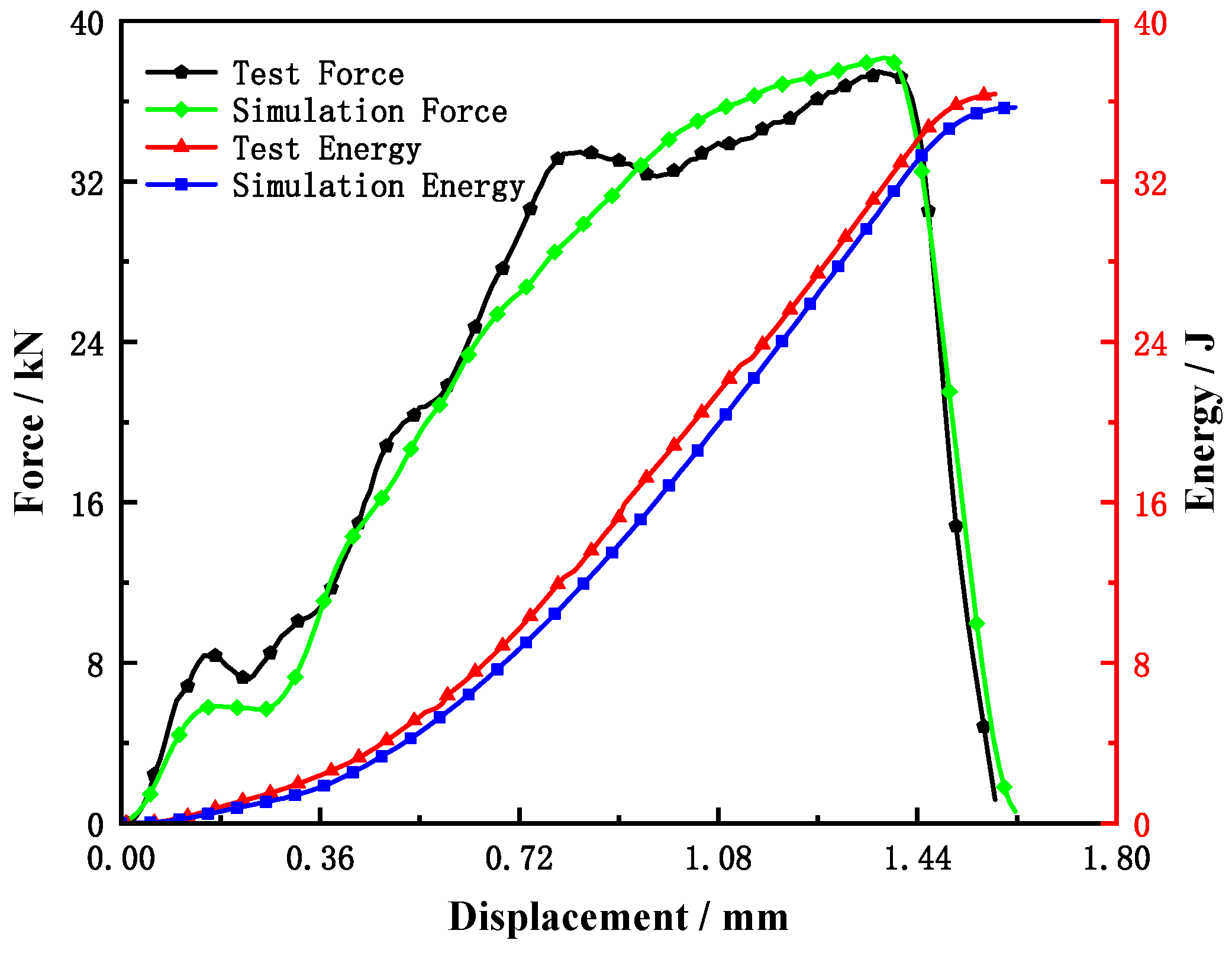
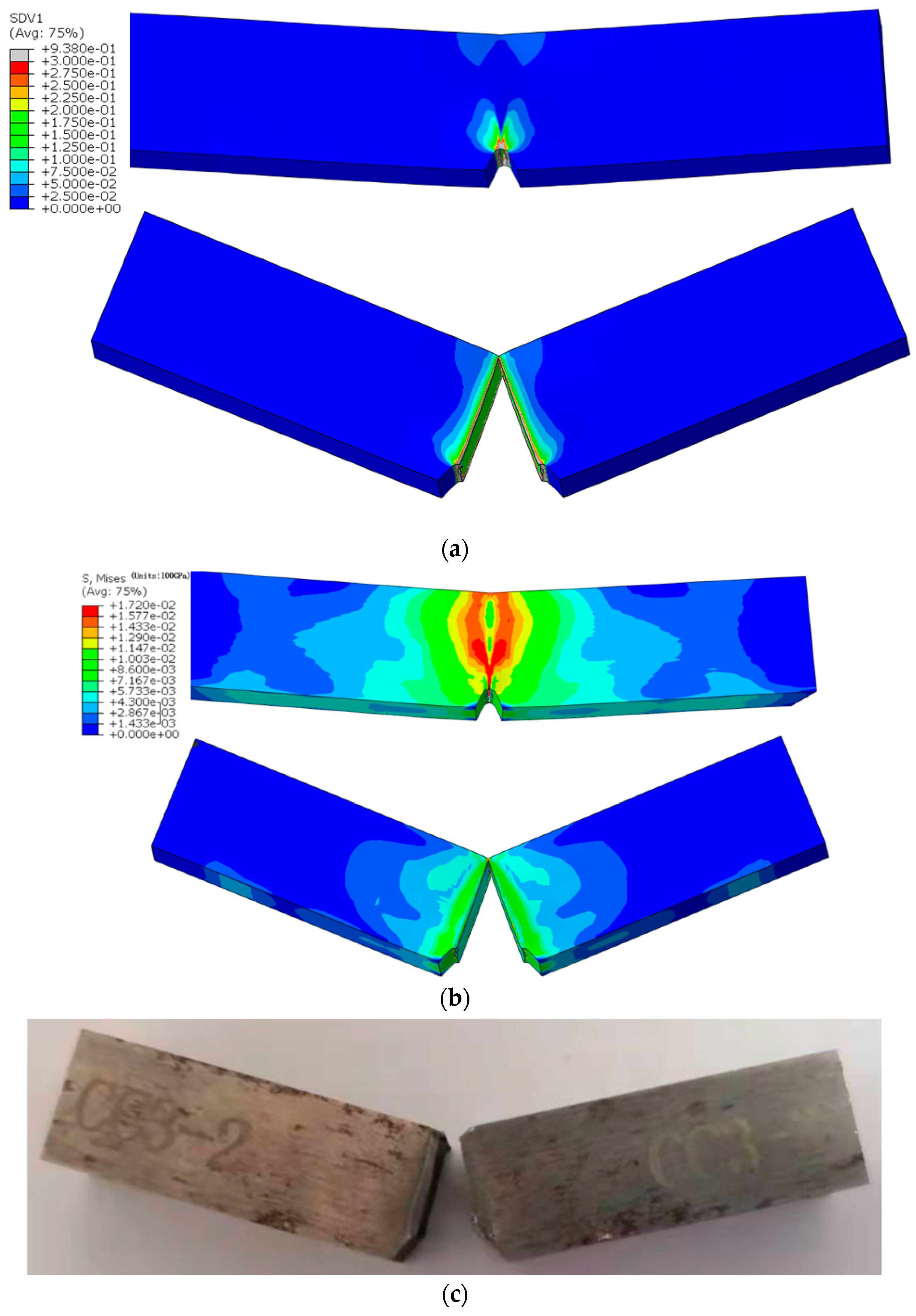




| C | Si | Mn | S | P | Ni | Cr | Mo | V | Cu | Ti | W |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.28 | 1.06 | 1.11 | 0.005 | 0.011 | 1.51 | 1.05 | 0.1 | 0.01 | 0.17 | 0.03 | 0.03 |
| Static State | Dynamic State | |||||
|---|---|---|---|---|---|---|
| strain rates | 10−3 s−1 | 10−1 s−1 | 1300 s−1 | 1700 s−1 | 2000 s−1 | 2500 s−1 |
| yield strength/MPa | 1290 | 1300 | 1790 | 1850 | 1900 | 2000 |
| ultimate strength/MPa | 1916 | 1905 | ||||
| R/mm | r/mm | ||||
|---|---|---|---|---|---|
| Model | Simulation | ||||
| 3 | 2 | 1.875 | 0.129 | 0.62 | 0.62 |
| 4 | 2 | 1.815 | 0.194 | 0.56 | 0.56 |
| 9 | 2 | 1.700 | 0.325 | 0.44 | 0.42 |
| Experiment Data | Simulation Data | Error | |
|---|---|---|---|
| Maximum load/kN | 37.39 | 38.13 | 1.98% |
| Impact energy/J | 36.33 | 35.68 | −1.79% |
| V/m/s | tsum/μs | tLsmax/μs | tIni/μs | Lmax/kN | Lini/kN |
|---|---|---|---|---|---|
| 4 | 432 | 362 | 324 | 36.03 | 35.24 |
| 5.24 | 321 | 266 | 240 | 36.06 | 34.36 |
| 6 | 282 | 233 | 210 | 35.76 | 34.47 |
| 7 | 250 | 200 | 185 | 34.61 | 34.37 |
| 8 | 224 | 176 | 170 | 34.58 | 33.67 |
| V/m/s | E/J | Emax/J | Eini/J | Epro/J | Ecra/J | T1 | T2 | T3 | T4 |
|---|---|---|---|---|---|---|---|---|---|
| 4 | 34.35 | 28.20 | 25.31 | 9.04 | 6.15 | 0.74 | 0.90 | 0.08 | 0.18 |
| 5.24 | 34.46 | 29.52 | 24.81 | 9.65 | 4.94 | 0.72 | 0.84 | 0.14 | 0.14 |
| 6 | 34.45 | 29.04 | 24.49 | 9.96 | 5.41 | 0.71 | 0.84 | 0.13 | 0.16 |
| 7 | 34.79 | 28.60 | 24.80 | 9.99 | 6.19 | 0.71 | 0.87 | 0.11 | 0.18 |
| 8 | 34.83 | 27.98 | 26.36 | 8.48 | 6.85 | 0.75 | 0.94 | 0.05 | 0.20 |
| W /mm | tmax /μs | tini /μs | Lmax /kN | Lini /kN | SLmax /mm | SLini /mm | t1 | r1 /% | r2 /% |
|---|---|---|---|---|---|---|---|---|---|
| 10 | 258 | 234 | 35.90 | 34.53 | 1.32 | 1.20 | 0.96 | 5.17 | 8.05 |
| 7.5 | 258 | 234 | 26.26 | 25.32 | 1.32 | 1.19 | 0.96 | 4.37 | 7.36 |
| 6.66 | 256 | 234 | 22.78 | 22.02 | 1.31 | 1.19 | 0.97 | 4.47 | 6.58 |
| 5 | 256 | 234 | 16.85 | 16.28 | 1.29 | 1.18 | 0.97 | 3.56 | 4.97 |
| 3.33 | 256 | 234 | 10.73 | 10.55 | 1.29 | 1.18 | 0.97 | 3.62 | 5.07 |
| 2.5 | 250 | 234 | 7.85 | 7.77 | 1.23 | 1.14 | 0.98 | 0.00 | 0.00 |
| W/mm | E/J | Emax/J | Eini/J | Epro/J | Ecra/J | ΔE/J | ΔEini/J | ΔEpro/J | ΔEcra/J |
|---|---|---|---|---|---|---|---|---|---|
| 10 | 33.92 | 29.08 | 24.13 | 4.25 | 5.19 | 26.21 | 18.86 | 3.55 | 3.79 |
| 7.5 | 24.96 | 21.30 | 18.16 | 3.14 | 3.65 | 17.25 | 12.55 | 2.44 | 2.25 |
| 6.66 | 21.31 | 18.63 | 15.89 | 2.51 | 2.91 | 13.60 | 10.28 | 1.81 | 1.51 |
| 5 | 15.94 | 13.93 | 11.89 | 2.04 | 2.01 | 8.24 | 6.28 | 1.34 | 0.61 |
| 3.33 | 10.49 | 9.34 | 7.96 | 1.11 | 1.42 | 2.79 | 2.35 | 0.45 | 0.02 |
| 2.5 | 7.71 | 6.42 | 5.66 | 0.70 | 1.40 | 0.00 | 0.00 | 0.00 | 0.00 |
| W/mm | T1 | T2 | T3 | T4 | r3 | r4 | r5 | ||
| 10 | 0.72 | 0.83 | 0.13 | 0.15 | 0.720 | 0.136 | 0.145 | ||
| 7.5 | 0.73 | 0.85 | 0.12 | 0.15 | 0.727 | 0.142 | 0.131 | ||
| 6.66 | 0.75 | 0.85 | 0.11 | 0.14 | 0.755 | 0.133 | 0.111 | ||
| 5 | 0.75 | 0.85 | 0.12 | 0.13 | 0.762 | 0.163 | 0.074 | ||
| 3.33 | 0.76 | 0.86 | 0.11 | 0.13 | 0.843 | 0.163 | 0.007 | ||
| 2.5 | 0.74 | 0.87 | 0.08 | 0.18 | 0.00 | 0.00 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, W.; Pi, A.; Zhao, Z.; Wang, S.; Wei, C.; Jie, Z.; Huang, F. Study on Intrinsic Influence Law of Specimen Size and Loading Speed on Charpy Impact Test. Materials 2022, 15, 3855. https://doi.org/10.3390/ma15113855
Jia W, Pi A, Zhao Z, Wang S, Wei C, Jie Z, Huang F. Study on Intrinsic Influence Law of Specimen Size and Loading Speed on Charpy Impact Test. Materials. 2022; 15(11):3855. https://doi.org/10.3390/ma15113855
Chicago/Turabian StyleJia, Wang, Aiguo Pi, Zhang Zhao, Shaohong Wang, Chen Wei, Zhou Jie, and Fenglei Huang. 2022. "Study on Intrinsic Influence Law of Specimen Size and Loading Speed on Charpy Impact Test" Materials 15, no. 11: 3855. https://doi.org/10.3390/ma15113855
APA StyleJia, W., Pi, A., Zhao, Z., Wang, S., Wei, C., Jie, Z., & Huang, F. (2022). Study on Intrinsic Influence Law of Specimen Size and Loading Speed on Charpy Impact Test. Materials, 15(11), 3855. https://doi.org/10.3390/ma15113855