Influence of Foam Morphology on Flow and Heat Transport in a Random Packed Bed with Metallic Foam Pellets—An Investigation Using CFD
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Configuration
2.2. Particle-Resolved CFD
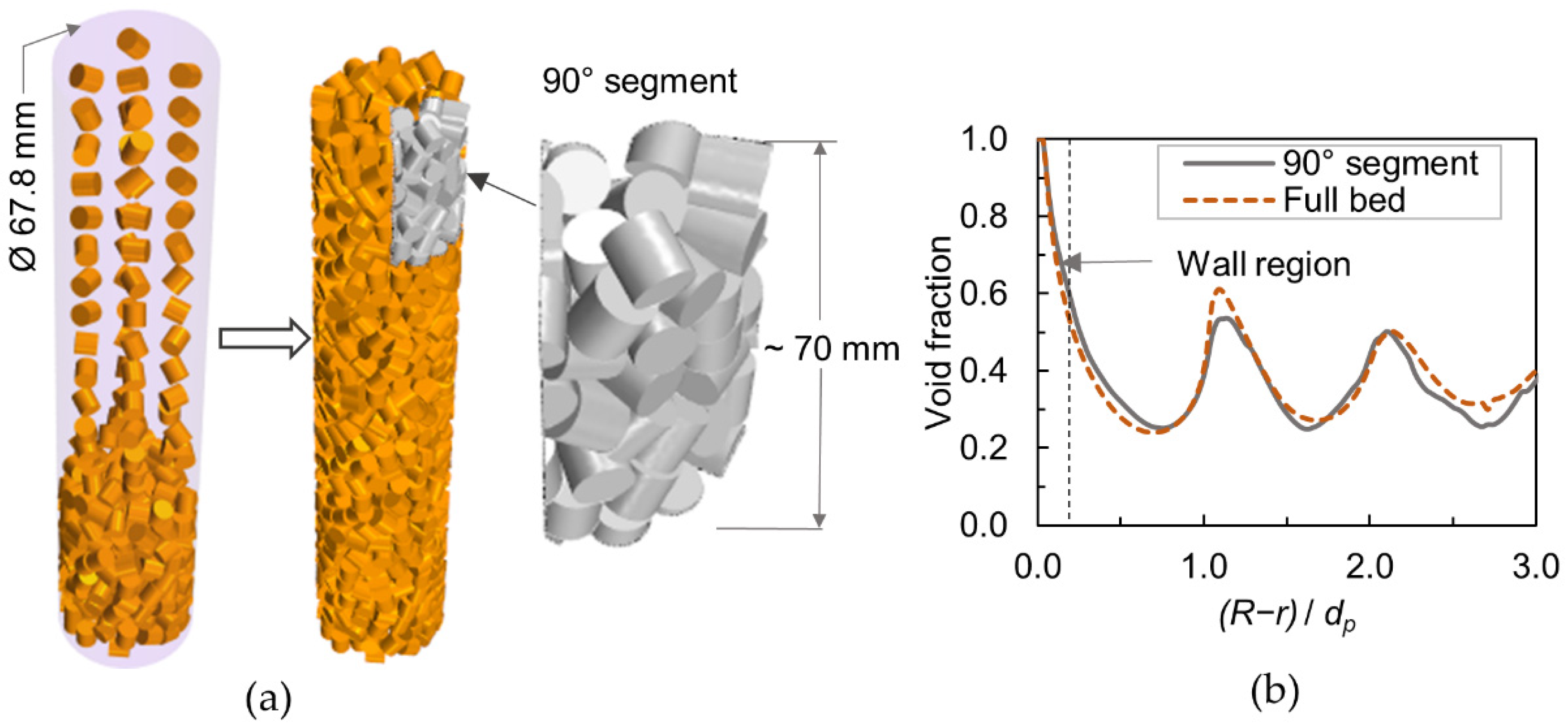
2.2.1. Packed Bed Geometry
2.2.2. Model Equations
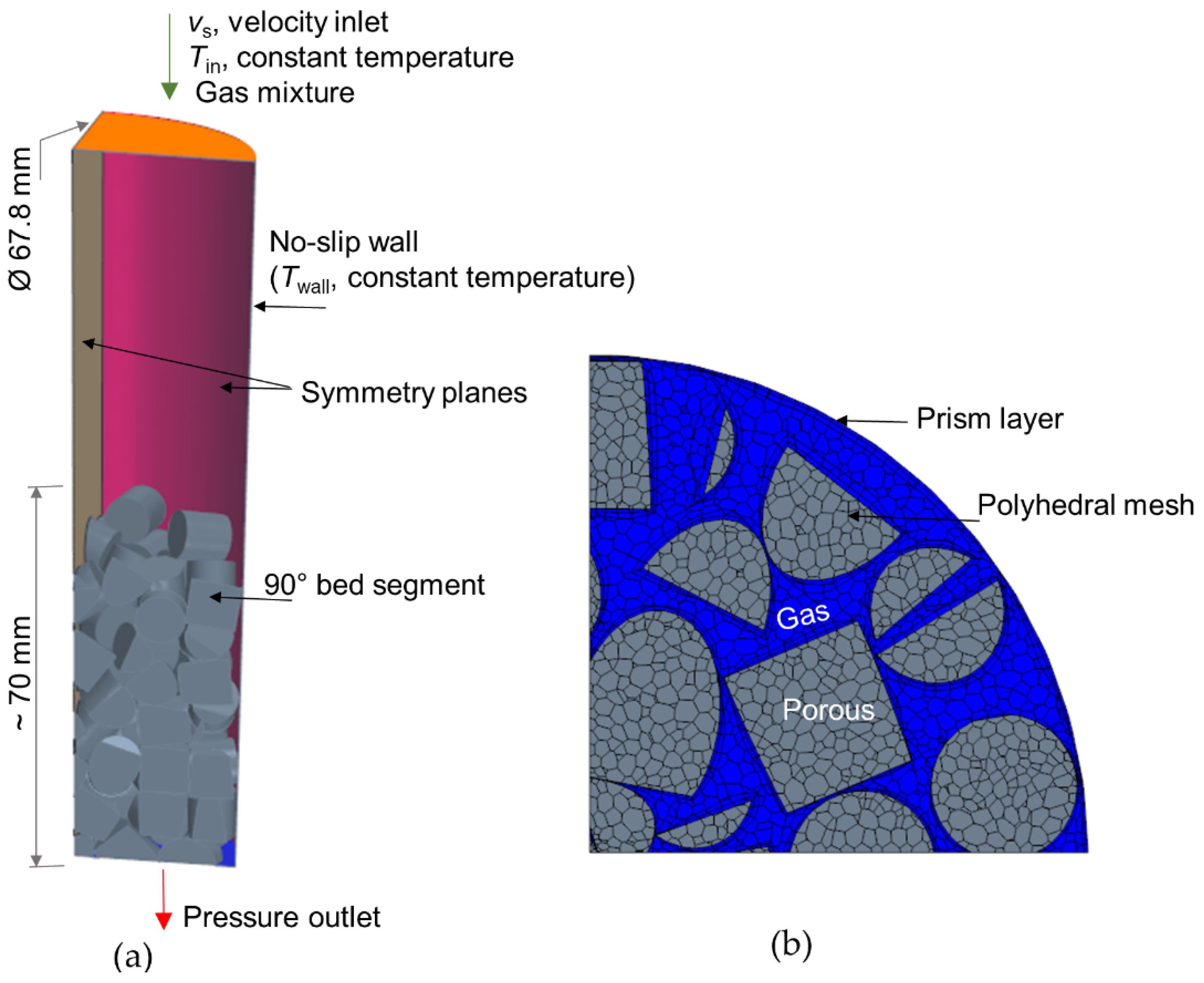
2.2.3. Computational Domain, Boundary Conditions, and Solving
3. Results and Discussion
3.1. Validation with Experimental Data
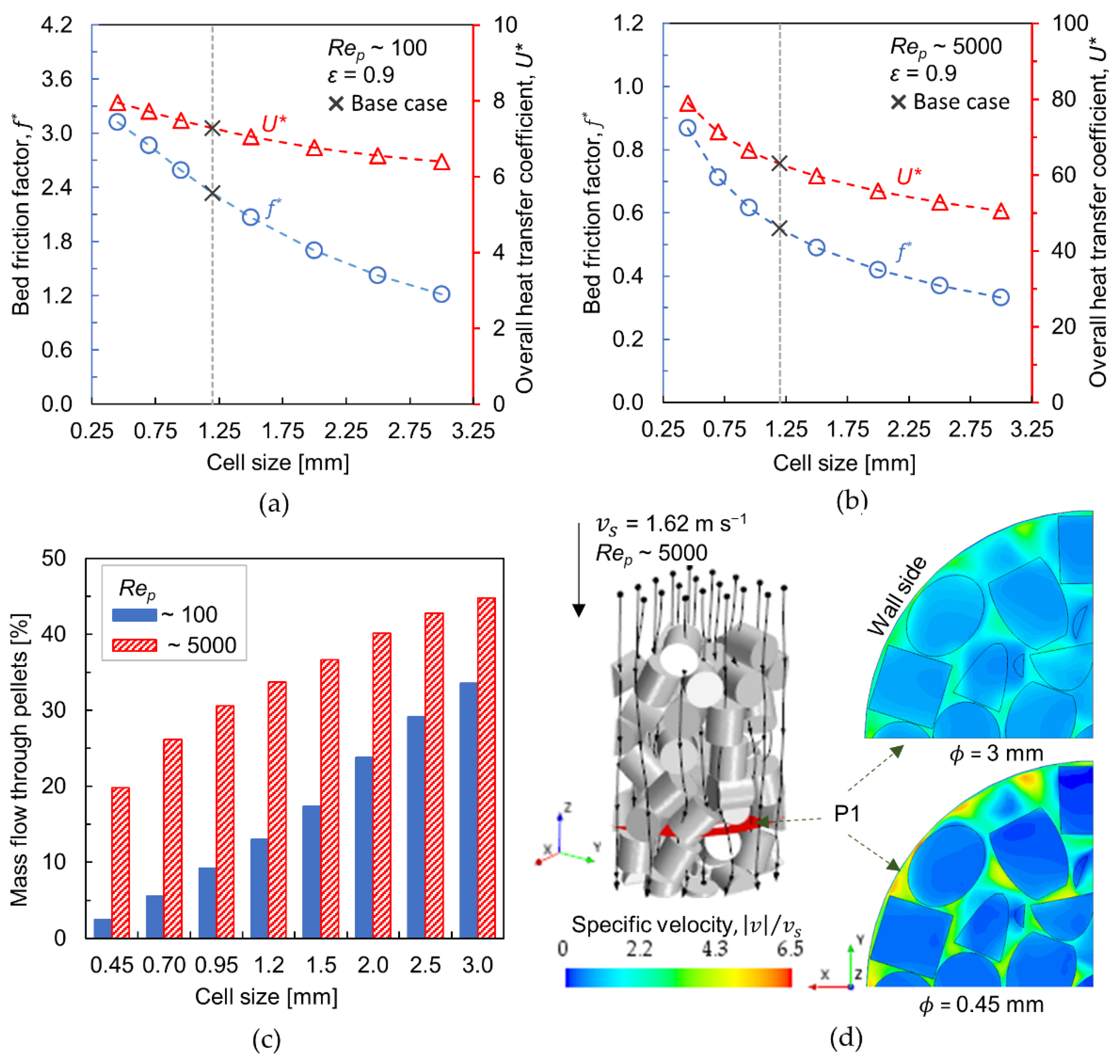
3.2. Effect of Cell Size
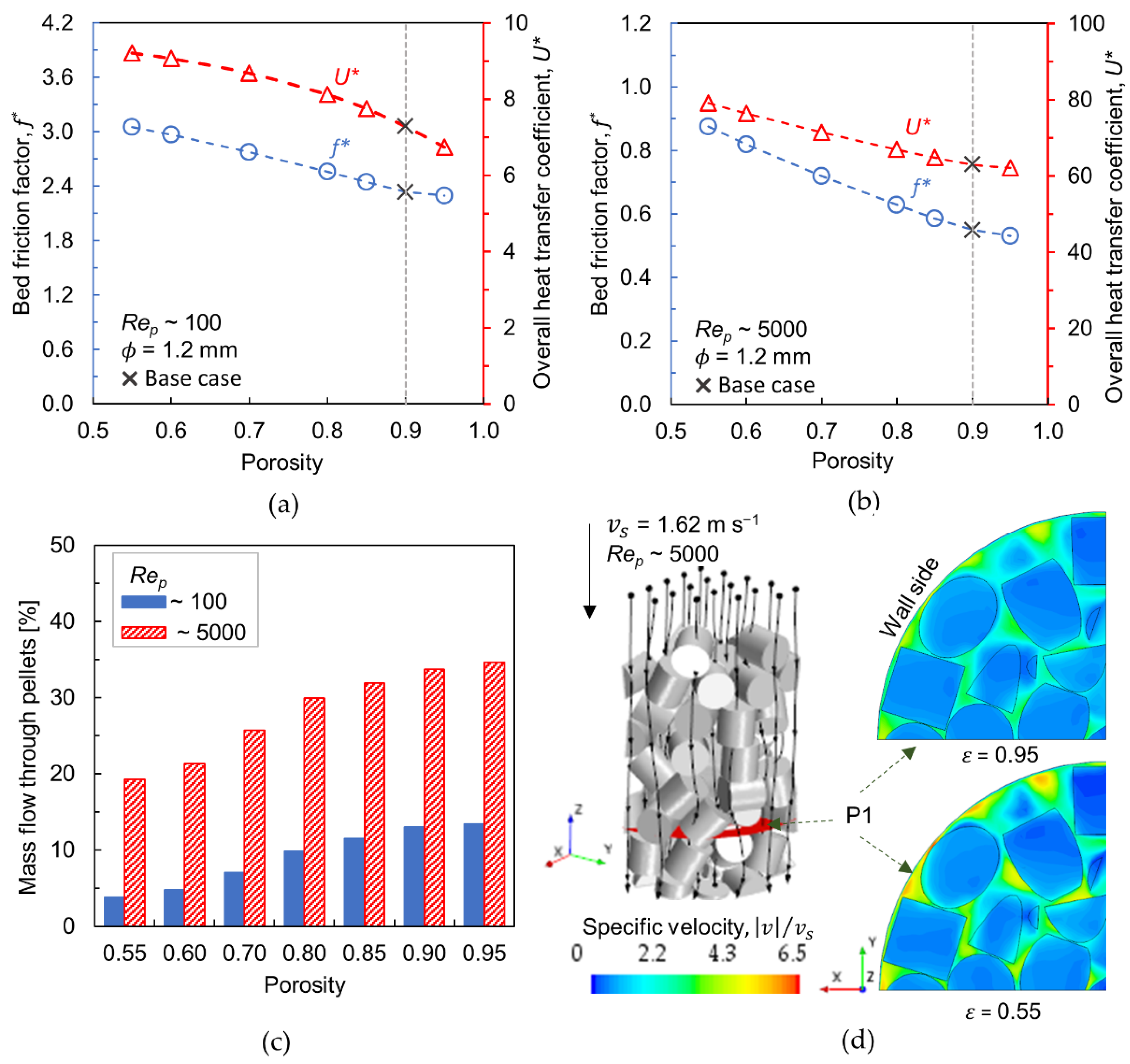
3.3. Effect of Porosity
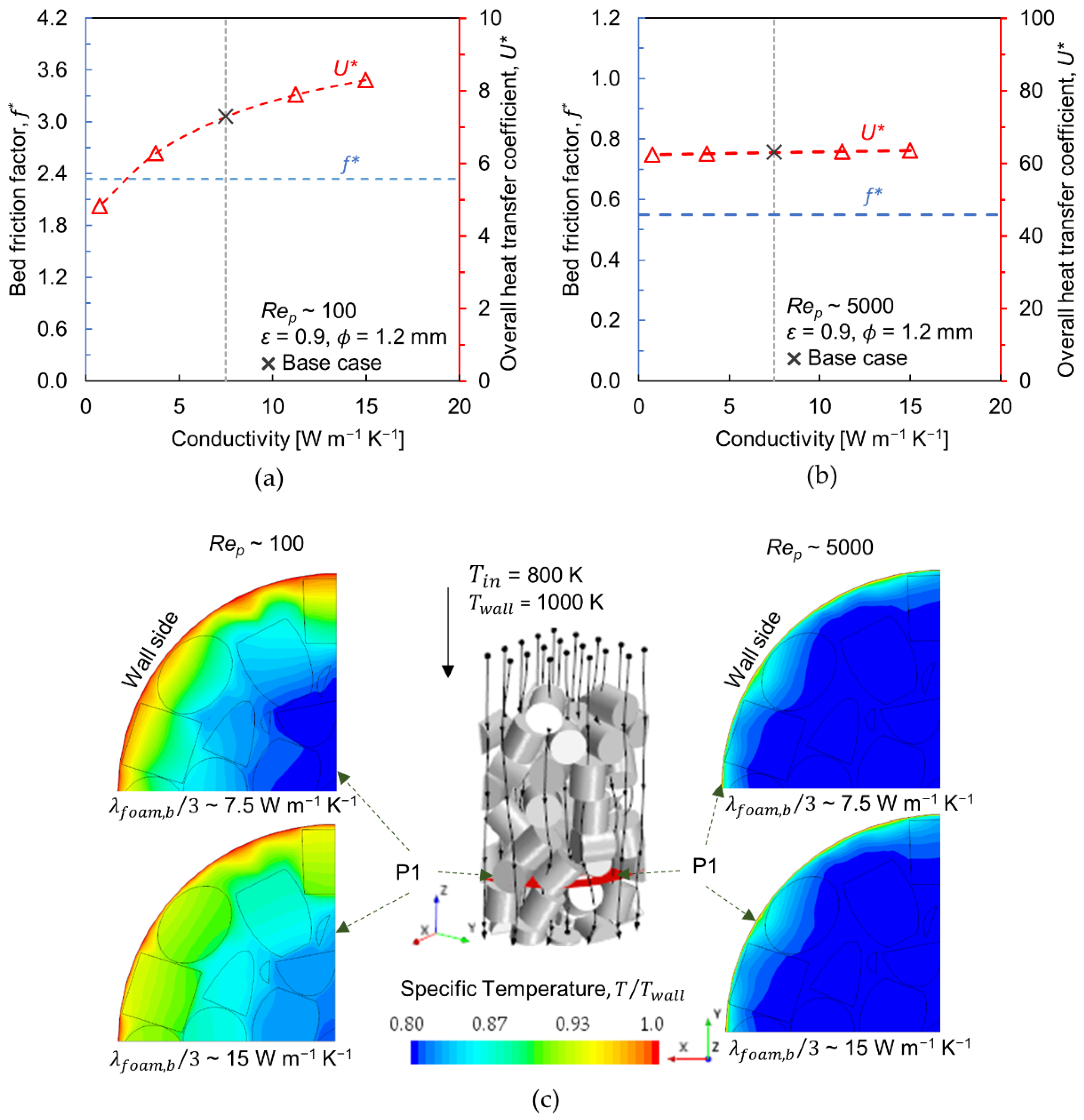
3.4. Effect of Conductivity
3.5. Design Study
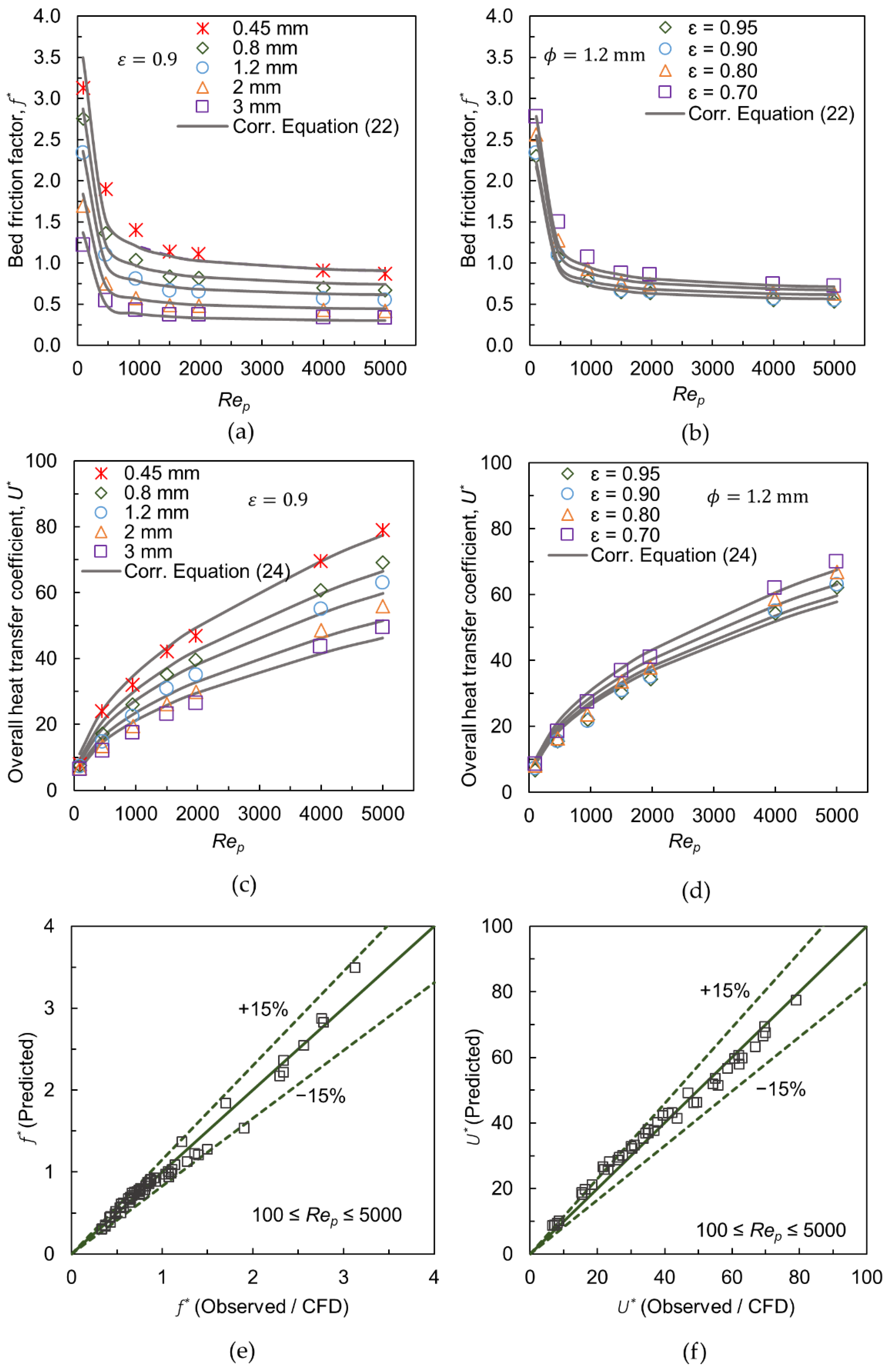
3.6. Correlations for Friction Factor and Heat Transfer Coefficient
4. Conclusions
- The friction factor and the overall heat transfer coefficient decrease with an increase in cell size and porosity.
- The observed behavior contradicts the desired requirements in a packed bed, i.e., lower pressure drop and higher heat transfer.
- The transport behavior in a foam-packed bed is dependent on the amount of flow stream through the pellets, which is regulated by the flow velocity in addition to foam morphologies.
- The intra-particle flow increases by increasing the cell size and porosity added with higher flow velocity.
- The influence of the conductivity of foam pellets on the overall heat transfer of a packed bed is found to be negligible at higher flow rates; the convective heat transfer mechanism is dominant in such conditions, which can be influenced most significantly by the pellet shape and dimensions.
- Foam morphologies, as well as shape, should be optimized to achieve a trade-off between pressure drop and heat transfer efficiency.
- A design study has shown that a cell size of 0.45 mm and a porosity of 0.80 is the optimal foam morphology of a cylindrical foam pellet for Rep~5000.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Design | Cell Size [mm] | Porosity | f* | U* | PR |
|---|---|---|---|---|---|
| 1 | 1.20 | 0.90 | 0.550 | 62.980 | 125.411 |
| 2 | 2.75 | 0.95 | 0.334 | 50.916 | 101.499 |
| 3 | 0.71 | 0.90 | 0.710 | 71.261 | 141.812 |
| 4 | 1.73 | 0.65 | 0.662 | 68.289 | 135.916 |
| 5 | 1.98 | 0.85 | 0.455 | 57.640 | 114.825 |
| 6 | 1.47 | 0.95 | 0.478 | 59.212 | 117.946 |
| 7 | 3.00 | 0.80 | 0.395 | 53.934 | 107.473 |
| 8 | 1.22 | 0.75 | 0.668 | 68.943 | 137.217 |
| 9 | 0.96 | 0.55 | 0.952 | 82.523 | 164.093 |
| 10 | 2.49 | 0.75 | 0.476 | 58.451 | 116.427 |
| 11 | 2.49 | 0.90 | 0.370 | 52.923 | 105.476 |
| 12 | 0.45 | 0.85 | 0.910 | 81.035 | 161.161 |
| 13 | 0.96 | 0.95 | 0.596 | 65.472 | 130.349 |
| 14 | 2.24 | 0.65 | 0.592 | 64.430 | 128.268 |
| 15 | 0.96 | 0.90 | 0.614 | 66.352 | 132.09 |
| 16 | 2.75 | 0.75 | 0.453 | 57.101 | 113.749 |
| 17 | 0.96 | 0.60 | 0.892 | 79.938 | 158.984 |
| 18 | 2.49 | 0.85 | 0.401 | 54.551 | 108.701 |
| 19 | 0.96 | 0.65 | 0.837 | 77.374 | 153.911 |
| 20 | 0.96 | 0.85 | 0.652 | 68.222 | 135.793 |
| 21 | 2.24 | 0.75 | 0.503 | 59.950 | 119.398 |
| 22 | 1.22 | 0.60 | 0.815 | 76.196 | 151.577 |
| 23 | 0.71 | 0.75 | 0.841 | 77.659 | 154.478 |
| 24 | 1.73 | 0.75 | 0.570 | 63.648 | 126.725 |
| 25 | 0.45 | 0.95 | 0.851 | 78.207 | 155.563 |
| 26 | 1.73 | 0.95 | 0.438 | 56.997 | 113.557 |
| 27 | 0.96 | 0.75 | 0.739 | 72.650 | 144.56 |
| 28 | 1.47 | 0.60 | 0.759 | 73.239 | 145.719 |
| 29 | 1.22 | 0.95 | 0.528 | 61.940 | 123.352 |
| 30 | 1.22 | 0.90 | 0.546 | 62.796 | 125.046 |
| 31 | 2.24 | 0.85 | 0.426 | 55.992 | 111.559 |
| 32 | 1.47 | 0.65 | 0.708 | 70.734 | 140.761 |
| 33 | 2.75 | 0.85 | 0.379 | 53.270 | 106.161 |
| 34 | 2.75 | 0.90 | 0.349 | 51.672 | 102.994 |
| 35 | 0.45 | 0.80 | 0.961 | 83.312 | 165.664 |
| 36 | 1.47 | 0.85 | 0.530 | 61.826 | 123.121 |
| 37 | 1.47 | 0.75 | 0.614 | 66.031 | 131.448 |
| 38 | 1.22 | 0.65 | 0.763 | 73.667 | 146.571 |
| 39 | 0.45 | 0.90 | 0.868 | 79.022 | 157.176 |
| 40 | 2.24 | 0.95 | 0.378 | 53.545 | 106.712 |
| 41 | 1.98 | 0.75 | 0.534 | 61.660 | 122.786 |
| 42 | 1.73 | 0.90 | 0.455 | 57.822 | 115.19 |
| 43 | 0.71 | 0.85 | 0.749 | 73.210 | 145.672 |
| 44 | 0.71 | 0.95 | 0.693 | 70.384 | 140.076 |
| 45 | 2.24 | 0.90 | 0.394 | 54.334 | 108.274 |
| 46 | 1.73 | 0.80 | 0.528 | 61.527 | 122.526 |
| 47 | 1.98 | 0.80 | 0.493 | 59.584 | 118.675 |
| 48 | 0.71 | 0.65 | 0.946 | 82.473 | 163.999 |
| 49 | 2.49 | 0.70 | 0.518 | 60.585 | 120.651 |
| 50 | 2.24 | 0.80 | 0.463 | 57.904 | 115.345 |
| 51 | 0.71 | 0.80 | 0.793 | 75.370 | 149.946 |
| 52 | 0.96 | 0.80 | 0.694 | 70.389 | 140.083 |
| 53 | 2.24 | 0.70 | 0.546 | 62.118 | 123.691 |
| 54 | 1.47 | 0.70 | 0.659 | 68.321 | 135.983 |
| 55 | 1.98 | 0.90 | 0.422 | 55.944 | 111.466 |
| 56 | 3.00 | 0.85 | 0.360 | 52.118 | 103.876 |
| 57 | 1.47 | 0.90 | 0.495 | 60.061 | 119.626 |
| 58 | 0.96 | 0.70 | 0.787 | 74.970 | 149.154 |
| 59 | 3.00 | 0.75 | 0.432 | 55.895 | 111.358 |
| 60 | 1.22 | 0.55 | 0.872 | 78.927 | 156.982 |
| 61 | 1.98 | 0.70 | 0.577 | 63.907 | 127.237 |
| 62 | 3.00 | 0.95 | 0.316 | 49.803 | 99.2887 |
| 63 | 1.22 | 0.70 | 0.715 | 71.210 | 141.706 |
| 64 | 1.73 | 0.70 | 0.615 | 65.915 | 131.214 |
| 65 | 0.71 | 0.70 | 0.891 | 80.017 | 159.143 |
| 66 | 3.00 | 0.90 | 0.331 | 50.547 | 100.763 |
| 67 | 1.22 | 0.80 | 0.624 | 66.723 | 132.822 |
| 68 | 1.73 | 0.85 | 0.489 | 59.553 | 118.616 |
| 69 | 2.75 | 0.65 | 0.540 | 61.407 | 122.275 |
| 70 | 1.98 | 0.95 | 0.405 | 55.136 | 109.867 |
| 71 | 2.75 | 0.70 | 0.494 | 59.219 | 117.944 |
| 72 | 2.75 | 0.80 | 0.415 | 55.110 | 109.806 |
| 73 | 3.00 | 0.70 | 0.473 | 57.987 | 115.501 |
Nomenclature
| Latin symbols | ||
| area | m2 | |
| pore diameter | m | |
| particle diameter | m | |
| diameter of sphere of equivalent particle volume | m | |
| strut diameter | m | |
| tube diameter | m | |
| friction factor | ||
| bed length | m | |
| pressure drop | Pa | |
| Peclet number | ||
| particle Reynolds number | ||
| temperature | K | |
| overall heat transfer coefficient | W m−2 K−1 | |
| normalized heat transfer coefficient | ||
| superficial velocity | m s−1 | |
| Greek symbols | ||
| foam porosity | ||
| thermal conductivity | W m−1 K−1 | |
| effective radial conductivity | W m−1 K−1 | |
| dynamic viscosity | Pa s | |
| mean bed voidage | ||
| density | kg m−3 | |
| foam cell size | m | |
| limiting value | ||
References
- Han, X.-H.; Wang, Q.; Park, Y.-G.; T’Joen, C.; Sommers, A.; Jacobi, A. A Review of Metal Foam and Metal Matrix Composites for Heat Exchangers and Heat Sinks. Heat Transf. Eng. 2012, 33, 991–1009. [Google Scholar] [CrossRef] [Green Version]
- Azzi, W.; Roberts, W.L.; Rabiei, A. A study on pressure drop and heat transfer in open cell metal foams for jet engine applications. Mater. Des. 2007, 28, 569–574. [Google Scholar] [CrossRef]
- Lakshmi-Narayana, A.; Dhananjaya, M.; Guru-Prakash, N.; Mauger, A.; Julien, C.M.; Hussain, O.M. Li2TiO3/Ni foam composite as high-performance electrode for energy storage and conversion. Heliyon 2019, 5, e02060. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ismagilov, Z.R.; Pushkarev, V.V.; Podyacheva, O.Y.; Koryabkina, N.A.; Veringa, H.A. A Catalytic Heat-Exchanging Tubular Reactor for Combining of High Temperature Exothermic and Endothermic Reactions. Chem. Eng. J. 2001, 82, 355–360. [Google Scholar] [CrossRef]
- Lu, T.J.; Stone, H.A.; Ashby, M.F. Heat transfer in open-cell metal foams. Acta Mater. 1998, 46, 3619–3635. [Google Scholar] [CrossRef]
- Balzarotti, R.; Ambrosetti, M.; Beretta, A.; Groppi, G.; Tronconi, E. Investigation of packed conductive foams as a novel reactor configuration for methane steam reforming. Chem. Eng. J. 2020, 391, 123494. [Google Scholar] [CrossRef]
- Choi, B.; Kim, J.; Tillman, A.; Torkuhl, L.; Beton, D.; Kolvenbach, R. Method for Producing a Metal Foam Pellet, Pellet, Catalyst Filling and Static Mixer. EP3354337A1, 1 August 2018. [Google Scholar]
- Walther, G.; Klöden, B.; Büttner, T.; Weißgärber, T.; Kieback, B.; Böhm, A.; Naumann, D.; Saberi, S.; Timberg, L. A New Class of High Temperature and Corrosion Resistant Nickel-Based Open-Cell Foams. Adv. Eng. Mater. 2008, 10, 803–811. [Google Scholar] [CrossRef]
- Kim, S.; Lee, C.-W. A review on manufacturing and application of open-cell metal foam. Procedia Mater. Sci. 2014, 4, 305–309. [Google Scholar] [CrossRef]
- Flaischlen, S.; Kutscherauer, M.; Wehinger, G.D. Local Structure Effects on Pressure Drop in Slender Fixed Beds of Spheres. Chem. Ing. Tech. 2020, 93, 273–281. [Google Scholar] [CrossRef]
- Dixon, A.G. Fixed bed catalytic reactor modelling-the radial heat transfer problem. Can. J. Chem. Eng. 2012, 90, 507–527. [Google Scholar] [CrossRef]
- Incera Garrido, G.; Patcas, F.C.; Lang, S.; Kraushaar-Czarnetzki, B. Mass transfer and pressure drop in ceramic foams: A description for different pore sizes and porosities. Chem. Eng. Sci. 2008, 63, 5202–5217. [Google Scholar] [CrossRef]
- Giani, L.; Groppi, G.; Tronconi, E. Mass-Transfer Characterization of Metallic Foams as Supports for Structured Catalysts. Ind. Eng. Chem. Res. 2005, 44, 4993–5002. [Google Scholar] [CrossRef]
- Dong, Y.; Korup, O.; Gerdts, J.; Roldán Cuenya, B.; Horn, R. Microtomography-based CFD modeling of a fixed-bed reactor with an open-cell foam monolith and experimental verification by reactor profile measurements. Chem. Eng. J. 2018, 353, 176–188. [Google Scholar] [CrossRef]
- Bracconi, M.; Ambrosetti, M.; Maestri, M.; Groppi, G.; Tronconi, E. A fundamental investigation of gas/solid mass transfer in open-cell foams using a combined experimental and CFD approach. Chem. Eng. J. 2018, 352, 558–571. [Google Scholar] [CrossRef]
- Aguirre, A.; Chandra, V.; Peters, E.A.J.F.; Kuipers, J.A.M.; Neira D’Angelo, M.F. Open-cell foams as catalysts support: A systematic analysis of the mass transfer limitations. Chem. Eng. J. 2020, 393, 124656. [Google Scholar] [CrossRef]
- Kolaczkowski, S.T.; Awdry, S.; Smith, T.; Thomas, D.; Torkuhl, L.; Kolvenbach, R. Potential for metal foams to act as structured catalyst supports in fixed-bed reactors. Catal. Today 2016, 273, 221–233. [Google Scholar] [CrossRef]
- Jurtz, N.; Kraume, M.; Wehinger, G.D. Advances in fixed-bed reactor modeling using particle-resolved computational fluid dynamics (CFD). Rev. Chem. Eng. 2019, 35, 139–190. [Google Scholar] [CrossRef] [Green Version]
- Dixon, A.G.; Partopour, B. Computational Fluid Dynamics for Fixed Bed Reactor Design. Annu. Rev. Chem. Biomol. Eng. 2020, 11, 109–130. [Google Scholar] [CrossRef] [Green Version]
- George, G.R.; Bockelmann, M.; Schmalhorst, L.; Beton, D.; Gerstle, A.; Torkuhl, L.; Lindermeir, A.; Wehinger, G.D. Workflow for computational fluid dynamics modeling of fixed-bed reactors packed with metal foam pellets: Hydrodynamics. AIChE J. 2021, 46, 559. [Google Scholar] [CrossRef]
- George, G.R.; Bockelmann, M.; Schmalhorst, L.; Beton, D.; Gerstle, A.; Lindermeir, A.; Wehinger, G.D. Radial heat transport in a fixed-bed reactor made of metallic foam pellets: Experiment and Particle-resolved Computational Fluid Dynamics. Int. J. Heat Mass Transfer 2022. submitted. [Google Scholar]
- Dixon, A.G.; Boudreau, J.; Rocheleau, A.; Troupel, A.; Taskin, M.E.; Nijemeisland, M.; Stitt, E.H. Flow, Transport, and Reaction Interactions in Shaped Cylindrical Particles for Steam Methane Reforming. Ind. Eng. Chem. Res. 2012, 51, 15839–15854. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Kraume, M.; Berg, V.; Korup, O.; Mette, K.; Schlögl, R.; Behrens, M.; Horn, R. Investigating dry reforming of methane with spatial reactor profiles and particle-resolved CFD simulations. AIChE J. 2016, 62, 4436–4452. [Google Scholar] [CrossRef]
- Jurtz, N.; Srivastava, U.; Moghaddam, A.A.; Kraume, M. Particle-Resolved Computational Fluid Dynamics as the Basis for Thermal Process Intensification of Fixed-Bed Reactors on Multiple Scales. Energies 2021, 14, 2913. [Google Scholar] [CrossRef]
- Coumans, E. Bullet Physics Library. Available online: http://www.bulletphysics.org (accessed on 10 October 2020).
- Flaischlen, S.; Wehinger, G.D. Synthetic Packed-Bed Generation for CFD Simulations: Blender vs. STAR-CCM+. ChemEngineering 2019, 3, 52. [Google Scholar] [CrossRef] [Green Version]
- Boccardo, G.; Augier, F.; Haroun, Y.; Ferré, D.; Marchisio, D.L. Validation of a novel open-source work-flow for the simulation of packed-bed reactors. Chem. Eng. J. 2015, 279, 809–820. [Google Scholar] [CrossRef] [Green Version]
- Partopour, B.; Dixon, A.G. An integrated workflow for resolved-particle packed bed models with complex particle shapes. Powder Technol. 2017, 322, 258–272. [Google Scholar] [CrossRef]
- Siemens Digital Industries Software, Simcenter STAR-CCM+User Guide, Version 2020.1; Siemens: Plano, TX, USA, 2020.
- Dixon, A.G.; Nijemeisland, M.; Stitt, E.H. Packed Tubular Reactor Modeling and Catalyst Design using Computational Fluid Dynamics. Adv. Chem. Eng. 2006, 31, 307–389. [Google Scholar] [CrossRef]
- John, B.; Senthilkumar, P.; Sadasivan, S. Applied and Theoretical Aspects of Conjugate Heat Transfer Analysis: A Review. Arch. Comput. Methods Eng. 2019, 26, 475–489. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer International Publishing: Cham, Switzerland, 2020; ISBN 9783319996912. [Google Scholar]
- Lacroix, M.; Nguyen, P.; Schweich, D.; Pham Huu, C.; Savin-Poncet, S.; Edouard, D. Pressure drop measurements and modeling on SiC foams. Chem. Eng. Sci. 2007, 62, 3259–3267. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Ranut, P. On the effective thermal conductivity of aluminum metal foams: Review and improvement of the available empirical and analytical models. Appl. Therm. Eng. 2016, 101, 496–524. [Google Scholar] [CrossRef]
- Schuetz, M.A.; Glicksman, L.R. A basic study of heat transfer through foam insulation. J. Cell. Plast. 1984, 20, 114–121. [Google Scholar] [CrossRef]
- Flynn, D.R. Thermal Conductivity of Semiconductive Solids; Method for Steady-State Measurements on Small Disk Reference Samples: Technical Progress Report. 1961. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/RPT/nbsreport7466.pdf (accessed on 15 May 2021).
- Kutscherauer, M.; Böcklein, S.; Mestl, G.; Turek, T.; Wehinger, G.D. An improved contact modification routine for a computationally efficient CFD simulation of packed beds. Chem. Eng. J. Adv. 2022, 9, 100197. [Google Scholar] [CrossRef]
- Eppinger, T.; Wehinger, G.D. A Generalized Contact Modification for Fixed-Bed Reactor CFD Simulations. Chem. Ing. Tech. 2021, 93, 143–153. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Flaischlen, S. Computational Fluid Dynamics Modeling of Radiation in a Steam Methane Reforming Fixed-Bed Reactor. Ind. Eng. Chem. Res. 2019, 58, 14410–14423. [Google Scholar] [CrossRef]
- Xu, J.; Froment, G.F. Methane steam reforming: II. Diffusional limitations and reactor simulation. AIChE J. 1989, 35, 97–103. [Google Scholar] [CrossRef]
- Das, S.; Deen, N.G.; Kuipers, J.A.M. Multiscale modeling of fixed-bed reactors with porous (open-cell foam) non-spherical particles: Hydrodynamics. Chem. Eng. J. 2018, 334, 741–759. [Google Scholar] [CrossRef]
- Tsotsas, E.; Schlünder, E.U. Heat transfer in packed beds with fluid flow: Remarks on the meaning and the calculation of a heattransfer coefficient at the wall. Chem. Eng. Sci. 1990, 45, 819. [Google Scholar] [CrossRef]
- Tsotsas, E. M7 Heat and Mass Transfer in Packed Beds with Fluid Flow. In VDI Heat Atlas; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1327–1340. ISBN 978-3-540-77876-9. [Google Scholar]



| Pellet | 1 | [mm] | 2 | Cp [J kg−1 K−1] | 3 | ||
|---|---|---|---|---|---|---|---|
 | 11.45 | 6.78 | 1.2 ± 0.12 | 0.90 ± 0.02 | 0.19 ± 0.003 | 580 | 650 |
| Inlet Velocity, vs [m s−1] | 0.032 and 1.62 |
| Particle Reynolds number, Rep | ~100 and ~5000 |
| Feed compositions (in mole fraction): | |
| Steam | 0.7485 |
| CH4 | 0.2143 |
| CO2 | 0.0025 |
| N2 | 0.0347 |
| Inlet temperature, Tin [K] | 800 |
| Wall temperature, Twall [K] | 1000 |
| Total pressure [bar] | 29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
George, G.R.; Bockelmann, M.; Schmalhorst, L.; Beton, D.; Gerstle, A.; Lindermeir, A.; Wehinger, G.D. Influence of Foam Morphology on Flow and Heat Transport in a Random Packed Bed with Metallic Foam Pellets—An Investigation Using CFD. Materials 2022, 15, 3754. https://doi.org/10.3390/ma15113754
George GR, Bockelmann M, Schmalhorst L, Beton D, Gerstle A, Lindermeir A, Wehinger GD. Influence of Foam Morphology on Flow and Heat Transport in a Random Packed Bed with Metallic Foam Pellets—An Investigation Using CFD. Materials. 2022; 15(11):3754. https://doi.org/10.3390/ma15113754
Chicago/Turabian StyleGeorge, Ginu R., Marina Bockelmann, Leonhard Schmalhorst, Didier Beton, Alexandra Gerstle, Andreas Lindermeir, and Gregor D. Wehinger. 2022. "Influence of Foam Morphology on Flow and Heat Transport in a Random Packed Bed with Metallic Foam Pellets—An Investigation Using CFD" Materials 15, no. 11: 3754. https://doi.org/10.3390/ma15113754
APA StyleGeorge, G. R., Bockelmann, M., Schmalhorst, L., Beton, D., Gerstle, A., Lindermeir, A., & Wehinger, G. D. (2022). Influence of Foam Morphology on Flow and Heat Transport in a Random Packed Bed with Metallic Foam Pellets—An Investigation Using CFD. Materials, 15(11), 3754. https://doi.org/10.3390/ma15113754






