1. Introduction
The basic concept of the additive manufacturing (AM) process is to produce the desired shape directly from 3D digital modeling data [
1]. Unlike traditional machining processes, such as casting or cutting, the materials are stacked layer by layer to create products [
1,
2]. Because of this basic process difference, special measures (such as design for AM) in the design stage of additive products can resolve the disadvantages of the existing traditional manufacturing processes [
2] and can easily control the AM process. Therefore, AM is attracting attention as a desirable manufacturing method for the design and production of high-performance components [
1].
Metal AM has a high degree of freedom in molding, such as custom designs; however, problems in the mechanical properties of the product may occur because of the anisotropy of the structure due to the nature of the manufacturing process [
3]. The DED process is additively manufactured by depositing in a local area [
2,
4], and the PBF process is a molding technique in which a flat powder area is melted and stacked with the selective thermal energy of a laser [
2]. In particular, in the manufacture of products, the PBF process is widely used in the AM process as a representative example of metal AM [
1]. The material has a thermal history during melting and solidification, and the solidified microstructure has directionality according to the movement path of the heat source. This affects the microstructure and mechanical properties of the alloys. As a major phenomenon, deformation by residual stress is induced, leading to distortion of or damage to the product. The directionality of the microstructure appears as an anisotropic property of the product. This problem causes dimensional inaccuracy of the product or affects the dynamic or static behavior of the structure, becoming another variable to be considered in the design stage. This acts as a constraint on the design and lowers the usefulness of metal AM with high formability.
To solve these problems, a periodic layer rotation strategy has been used to suppress the directionality of the material. Arısoy et al. stated that when the appropriate energy density and hatching angle were set to 67°, a fine grain size was obtained, and an isotropic structure was exhibited [
5]. According to a study by Guan et al., fabricating a product with the PBF process using an appropriate hatch angle results in part exhibiting excellent tensile properties because it realizes microstructural isotropy and avoids stress concentration [
6]. However, these studies were confirmed only through tensile tests at the specimen level.
In order to evaluate from a product level point of view, a study on mechanical properties evaluation considering macrostructure has also been conducted. Macrostructure characteristics were evaluated using the lamination process parameters similar to those of the AlSi10Mg material applied in this study. Thijs et al. The macrostructure of additive manufacturing materials revealed that morphological and crystallographic textures are realized from scanning strategies, which are expressed as anisotropy or isotropy [
7]. Xiong et al. also confirmed the anisotropy of the macroscopic structure in the variable state of the additive manufacturing process similar to the application of AlSi10Mg material. In this study, it was shown that the crystal orientation of the melt pool boundary was dominant in determining the anisotropy of the material [
8]. It is also explained that the scan direction has a significant influence on the anisotropy. It was proved that when the hatch angle is 90 degrees, the texture of the microstructure is further lowered, and the product is made isotropic. Furthermore, it was explained that if the product is laminated with a hatch angle other than 90 degrees, the texture of the product can be further lowered and made more isotropic. These studies commonly explain that the microscopic anisotropy of a material, which is expressed microscopically according to the heat flow characteristics in the additive manufacturing process, is only a small part, and the influence of the macroscopic structural characteristics obtained from the scan direction is more dominant.
The present study determined whether the anisotropic feature of the product generated along the laser scanning vector was removed using the periodic layer rotation strategy and expressed as isotropy. In
Section 2, classical lamination theory was used to determine whether the AM part using the raster pattern strategy exhibited anisotropic properties when the mechanical properties of the product were inferred to be isotropic from the periodic layer rotation strategy. The verification of the basis of isotropy inferred from the evaluation of these numerical viewpoints was verified by a comparison with experiments and finite element (FE) analysis.
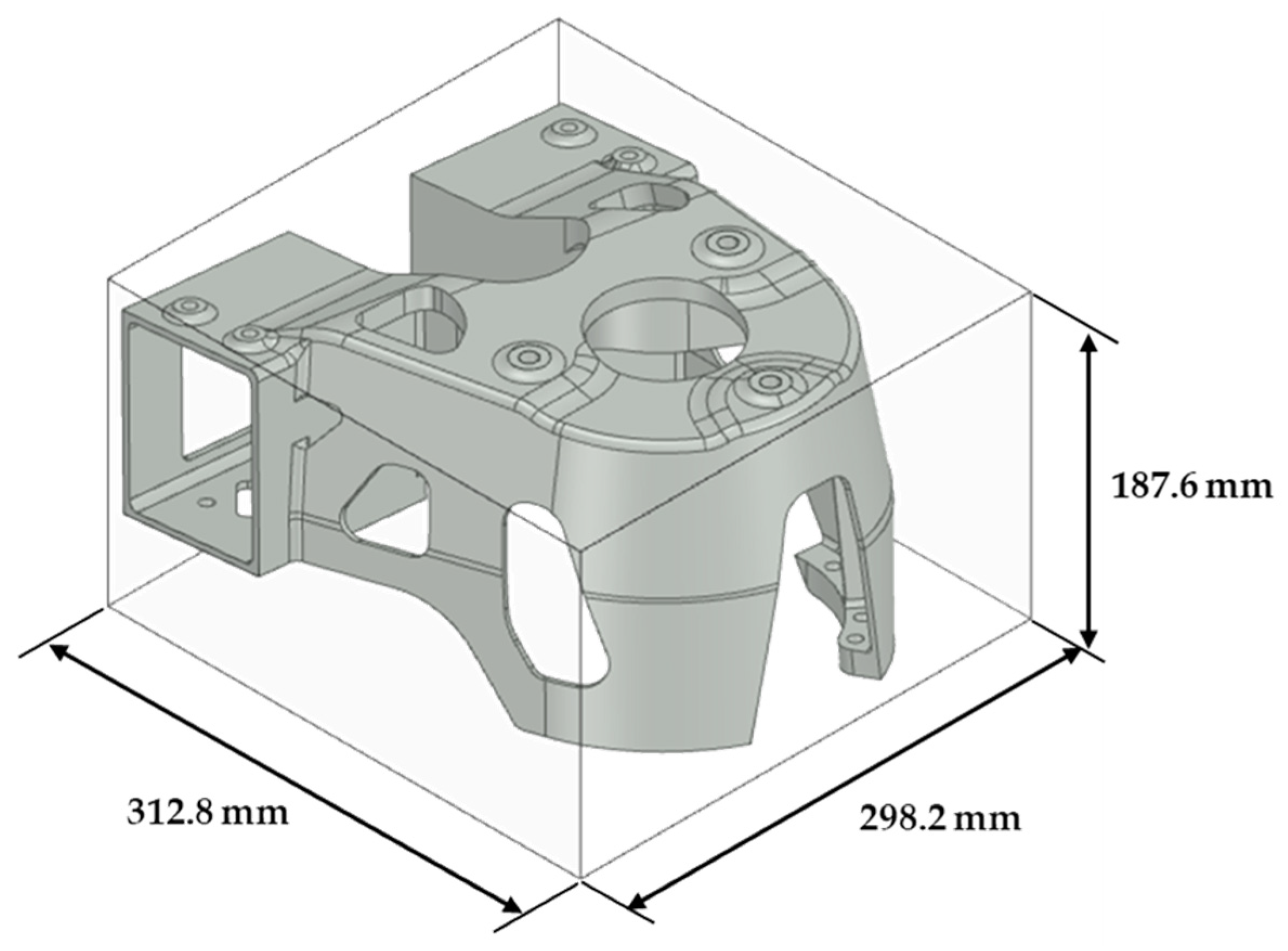
Section 3 describes the design process of the vehicle shock absorber mount and shows the AM process of applying periodic layer rotation. In
Section 4, tensile and modal tests performed on additive-manufactured products are described, and each product is verified through a comparison of the FE analysis to which isotropic properties are applied. Finally,
Section 5 presents a discussion of the study results, and
Section 6 presents the conclusion.
2. Evaluation of Mechanical Properties Using Classical Lamination Theory
This section evaluates the material properties of the products from a numerical perspective using the AM method of periodically rotating layers. The intrinsic strain method is widely used to perform additive process simulations [
9]. This methodology is highly similar to the approach used in the classical lamination theory applied to characterize the behavior of composites [
10,
11]. The PBF process is also a layer-by-layer manufacturing process and has many similarities to the techniques used to produce composite laminates. In both cases, the final structure is layered, and anisotropy is induced. Here, the hatching sequence of the AM process produces the same effect as the fiber orientation of the composite [
12]. Therefore, using the classical lamination theory, it is possible to infer the material properties at the product level. The strain tensor of the layer unit has a property that is orthogonal because of the hatching property, such as the fiber direction of the composite material. Additionally, the deformation component in the build direction (
) becomes negligible as it is compensated by the re-coating step of the PBF process. Therefore, the strain at the layer level can be viewed as a plane stress state in the hatch direction (
) and its perpendicular direction (
) in the layer plane. Here,
is expressed in lowercase letters, as they represent the local coordinate system.
The hatching sequence of the metal AM process requires the following three assumptions in the classical lamination theory to simply analyze the problem of the composite laminate from the perspective of material mechanics [
10,
13,
14]:
When the composite laminate was not subjected to bending, the strain in the thickness direction of the laminate was constant;
The strain on each ply in the plane was equal to the strain on the laminate;
The modulus of elasticity of each ply in the plane was different; thus, the stress had a different value for each ply.
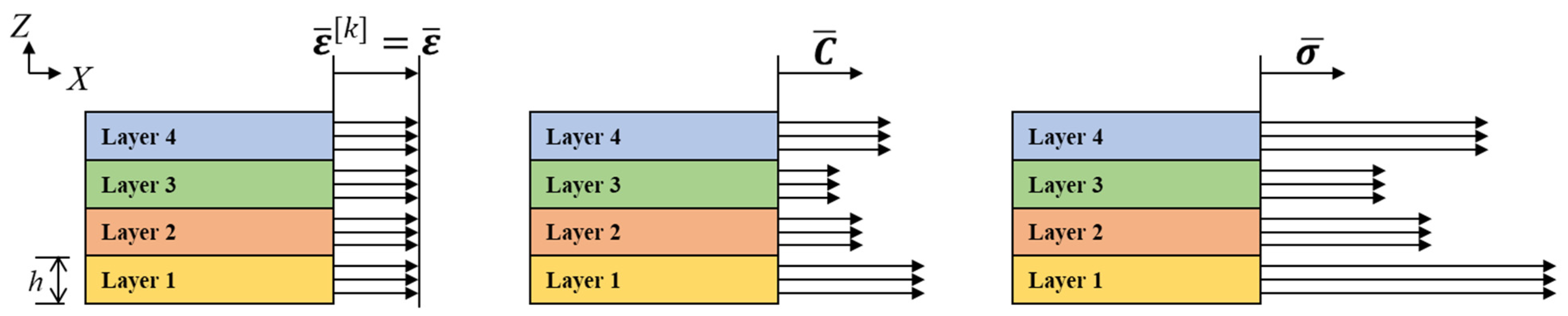
The three assumptions are expressed as Equation (1) by writing the stress of the
layer (ply), which is a plane stress state, in the global coordinate system (
coordinates) with the build direction as the axis.
where
is the stress component of the
layer (ply) displayed with respect to the plane,
represents the elastic constitutive matrix of the material in the global coordinates, and
represents the strain component of the
layer (ply) displayed with respect to the layer plane. Additionally, the bar above the vector or matrix indicates that it is displayed in the global coordinate system. A schematic representation of Equation (1) is shown in
Figure 1.
In the case of stacking with rotation for each layer and according to the classical lamination theory, the strain appears to be the same throughout the entire layer. That is, it is expressed as
. However, because the hatching directions of each layer are different, each stiffness matrix is expressed differently based on the global coordinates. Therefore, the stress is also different for each layer in the global coordinate system. Here, the sum of the stresses acting on a unit volume can be calculated by integrating the stress components of each layer. Furthermore, because the heights
of the layers in the unit volume are the same, the force per unit length
can be expressed as Equation (2):
where
is the number of layers per unit volume. Substituting Equation (1) into Equation (2) yields
Here,
is the amount integrated in the thickness direction; therefore, it becomes the force per unit length in the thickness direction of the layer. Therefore, stiffness
is expressed as
Therefore, the force per unit length
is
By considering the stress in the plane state, Equation (5) can be rewritten in matrix form as follows:
Then, Equation (1) on the
layer unit can be rewritten in matrix form as
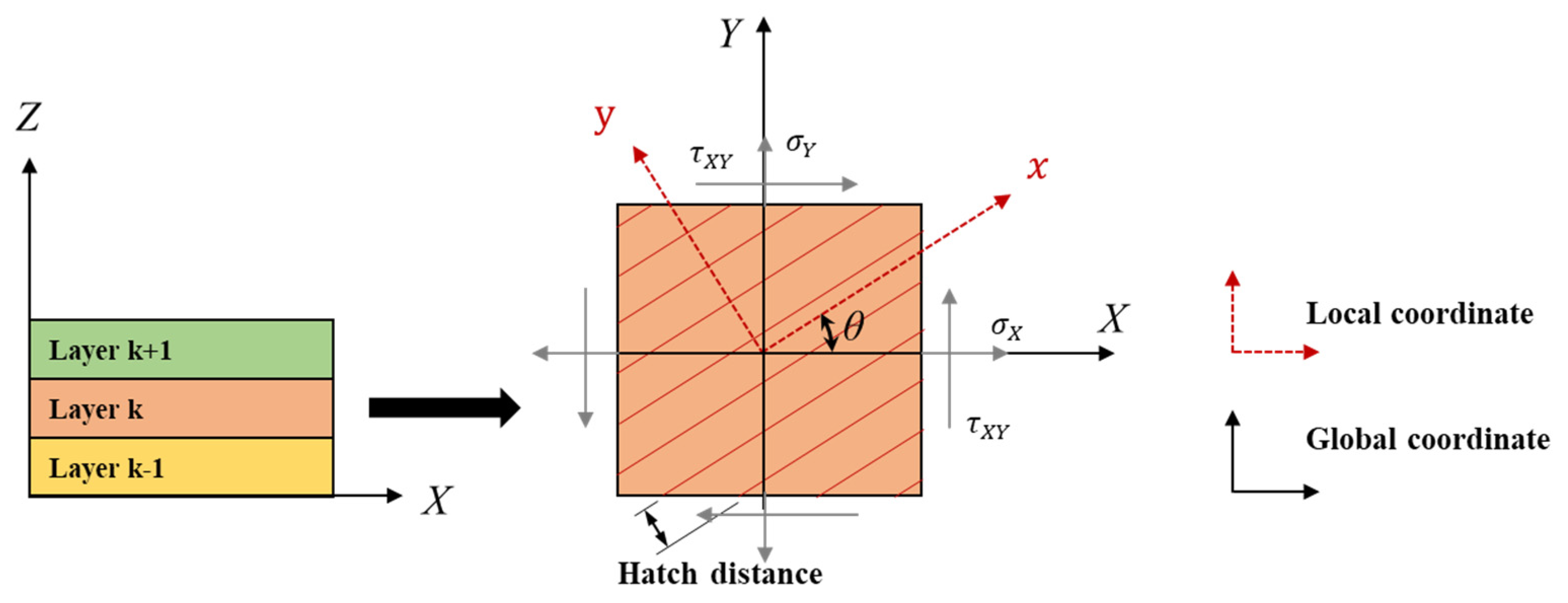
As shown in
Figure 2, if the transformation and stiffness matrices of the local coordinate system are written before the coordinate transformation for each layer, the transformation can be expressed as follows:
Here,
is
and
is
, and
and
are the coordinate transformation matrices, respectively. Therefore, if the stress-strain relationship in the plane stress state is written as a local coordinate system, it can be expressed as
Using the transformation matrix of Equation (8), the elastic constitutive matrix
, of the
layer can be expressed as:
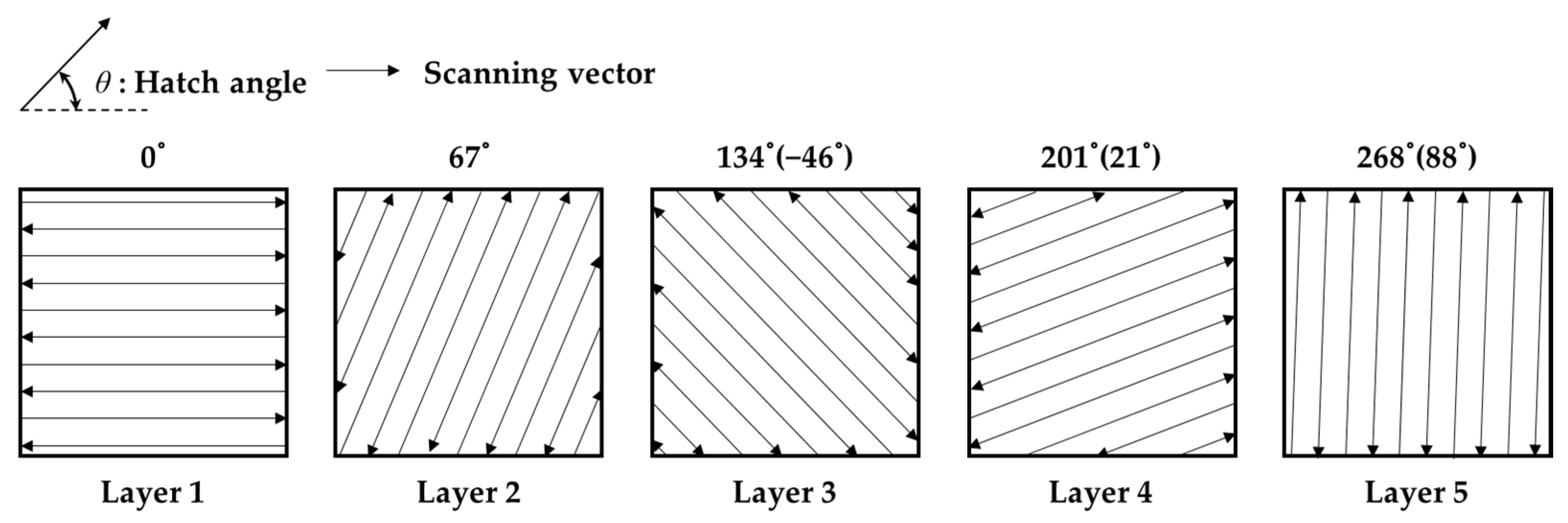
Figure 3 shows the scanning vector up to the fifth layer when the hatch angle is 67°. The scanning vectors follow a raster pattern. It can be observed that the subsequent vector is rotated by 180° to change the direction. Here, the maximum hatch angle is expressed as 90° and above 180°, which is the same as the
value. If only integers are considered for the hatch angles, in the case of the hatch angles of prime numbers that do not have a common divisor with 180, and if 180 layers are stacked, all angles from 0° to 179° can be expressed. Therefore, considering the case of a unit volume expressed by all hatch angles from 0° to 179°, the equivalent stiffness matrix can be considered isotropic. When the axis transformation of some layers in the unit volume is 0° and 90°, some components of the stiffness matrix are calculated as zero, as shown in Equation (11).
where the subscript following the vertical bar represents the corresponding hatch angle. Similarly, if
and
exist simultaneously, this can be written as:
Therefore, some components of the equivalent stiffness matrix
are as follows:
Equation (6) can be expressed by simply using the following invariant definition [
10]:
Using the invariant result, an example in which 180 layers are included in a unit volume and the layer rotation is 67° can be written as the following transformed stiffness matrix:
Here, subscript
denotes the sum of all layers in a unit volume, which is additively manufactured with a hatch angle incremented by 67°. The relationship between each component can be rewritten as follows:
That is, Equation (16) shows that is expressed as a stiffness matrix of quasi-isotropic conditions from the rotation of the periodic layer.
5. Discussion
As a characteristic of the AM process, anisotropy of macrostructure occurs because of various causes such as the scan direction, melting, fusion, and cooling of the powdered material, and the anisotropy of the material manifests depending on the scanning direction of the laser. A periodic layer rotation strategy was used to suppress the anisotropic properties of the material, which affects the mechanical properties of the product. In this study, the authors aimed to determine whether the periodic layer rotation strategy resulted in isotropic properties, even at the product level. Using the classical lamination theory, it was confirmed that the product fabricated with the periodic layer rotation strategy was isotropically inferred, and the mechanical properties of the additive-manufactured products were evaluated by comparing the stiffness, strength, vibration analysis of the FE model, and experimental results.
The layer-by-layer manufacturing and hatching sequence of the PBF process exhibited the same effect as the layer structure and fiber direction of the composites, and induced anisotropy was present. Therefore, by applying the classical lamination theory to characterize the behavior of the composite, the mechanical properties of the product built using the periodic layer rotation strategy were inferred. As one of the periodic layer rotation strategies, in the case of a hatch angle expressed by a prime number such as 67°, all integer hatch angles were expressed when 180 layers were stacked, which was calculated isotropically according to the equivalent stiffness matrix calculation of the classical lamination theory.
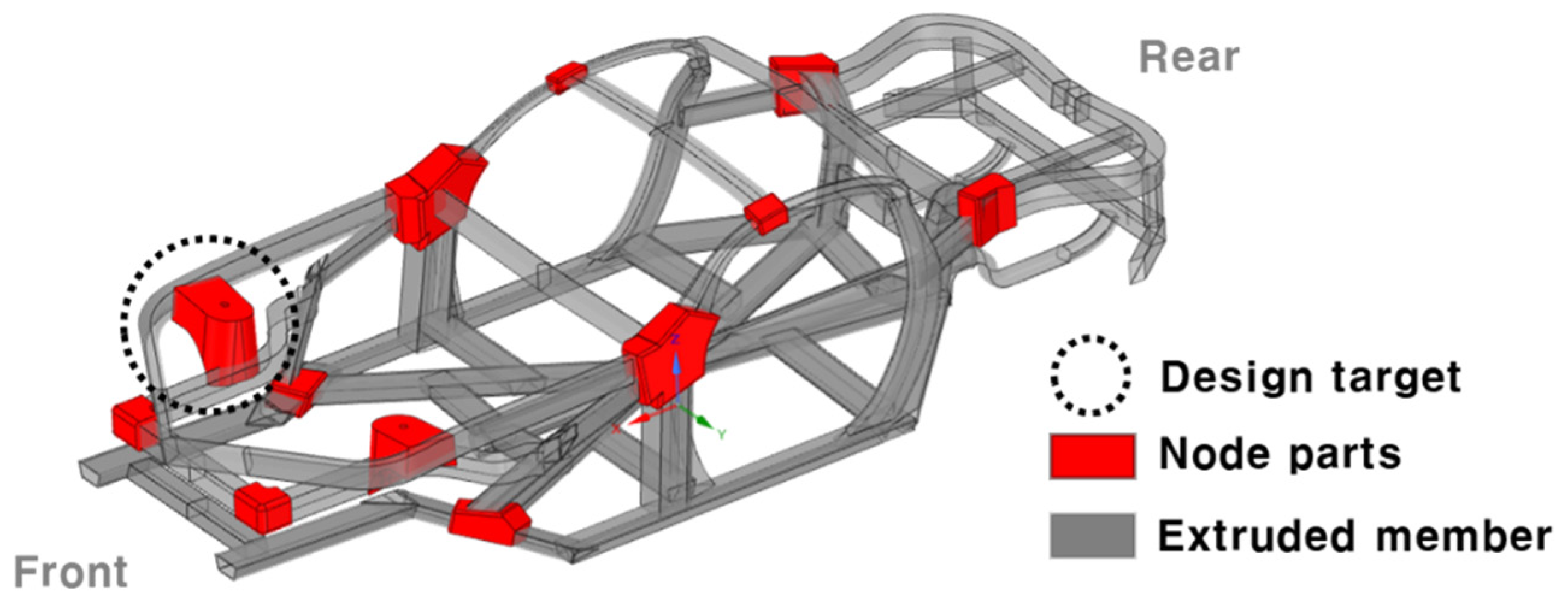
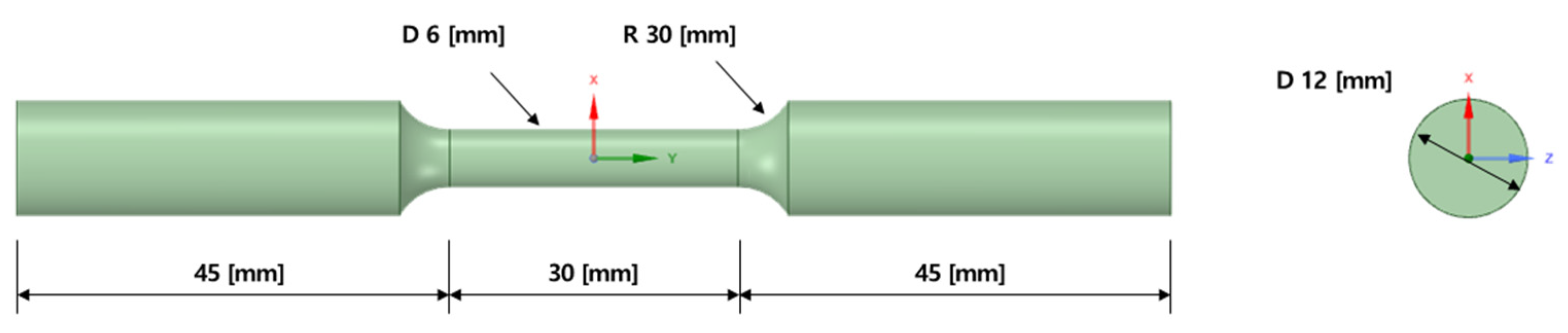
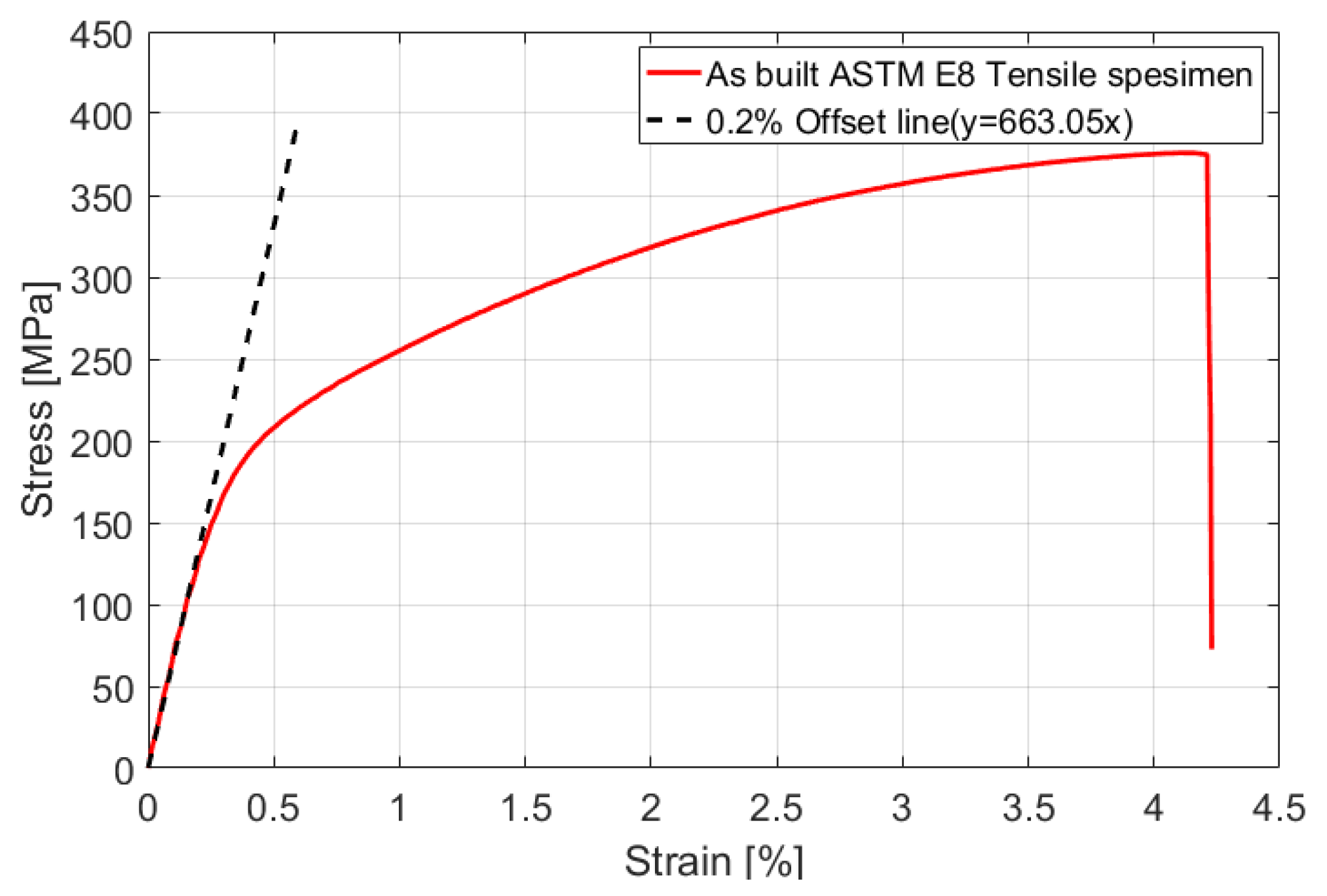
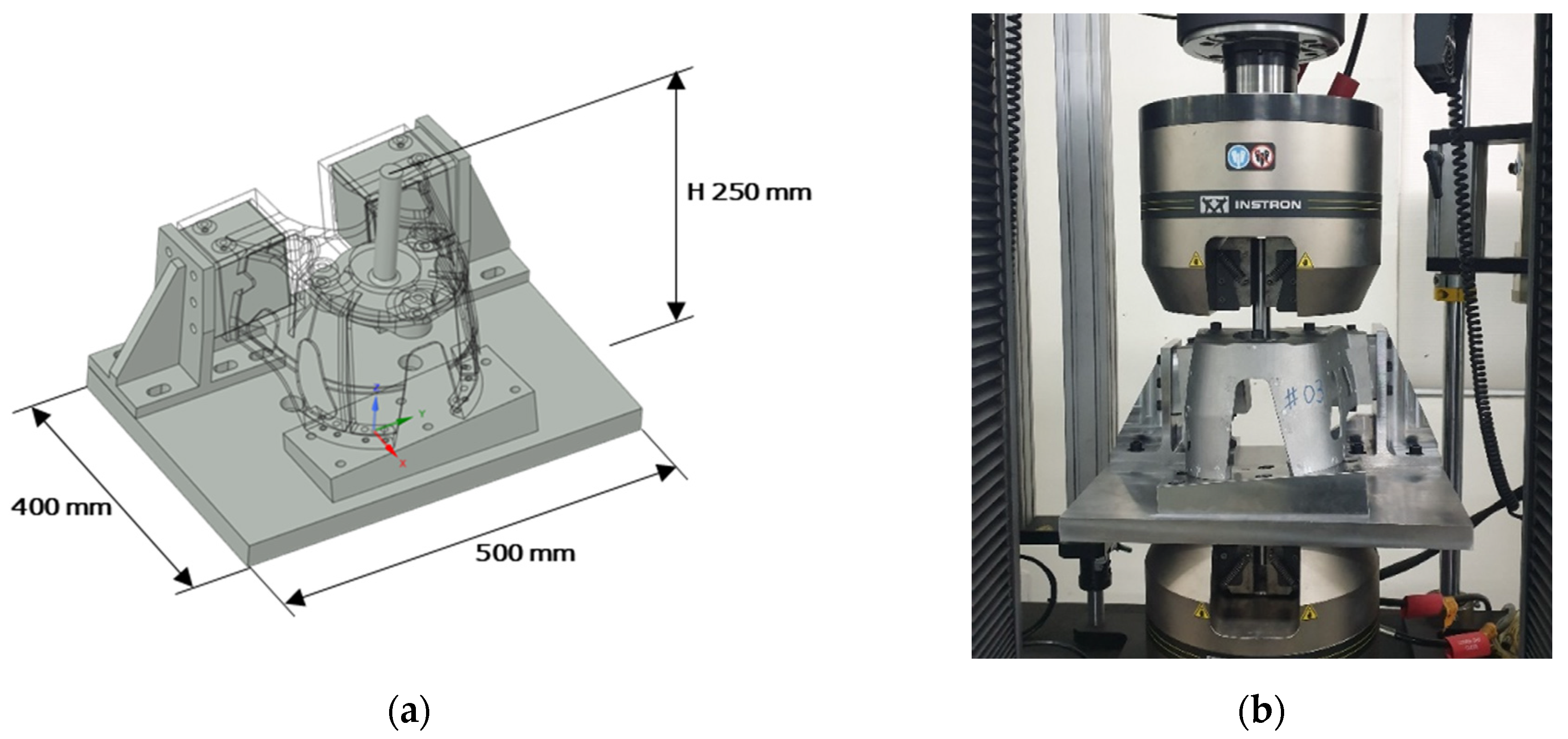
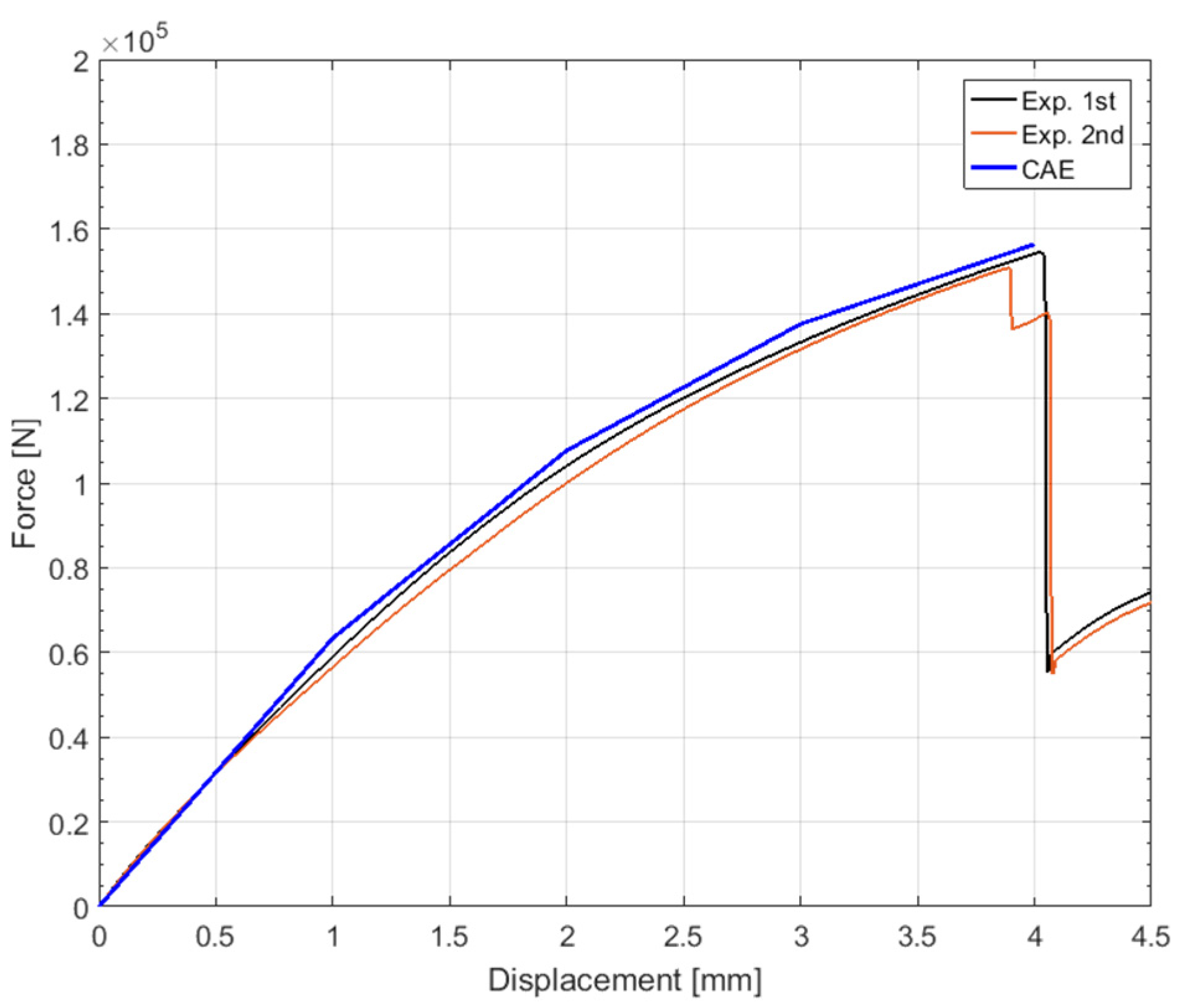
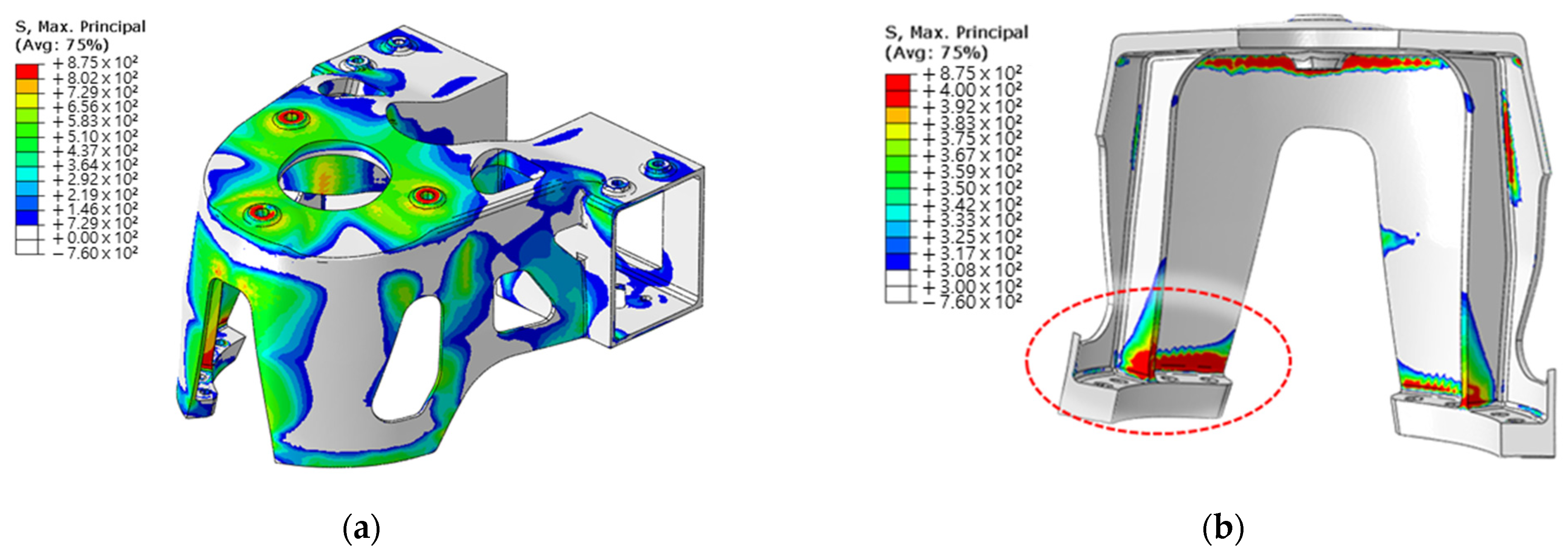
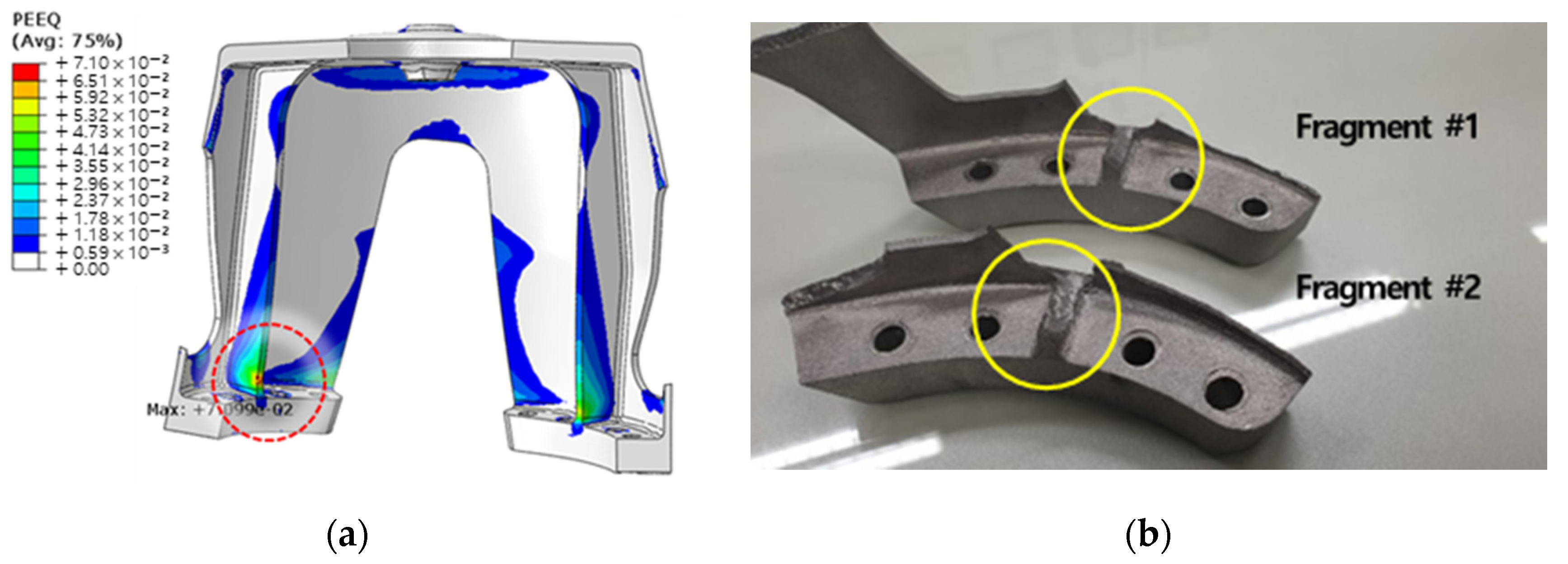
To verify the numerical prediction of isotropic properties through the classical lamination theory at the product level, a shock absorber node, which is part of a vehicle space frame, was manufactured, and tensile and modal tests were performed. The analysis results, which considered the material properties of the FE model to be isotropic, were compared with the results of each experiment. From the tensile tests, the error of the maximum load between the analysis and the test was 2.35%, and it was possible to predict the initial failure location from the results of the FE analysis. The coincidence of the load-displacement curves was confirmed, indicating that the additively manufactured product can be considered isotropic. Importantly, this does not necessarily evaluate to isotropic. With a combination of complex anisotropy, stiffness can be expressed equally. This is because only a single system stiffness was compared for specific directional loads and boundary conditions. Therefore, only the possibility that the material for the product can be considered isotropic is confirmed. Additionally, due to the shape of the part, parts considered anisotropic may also break at the same location.
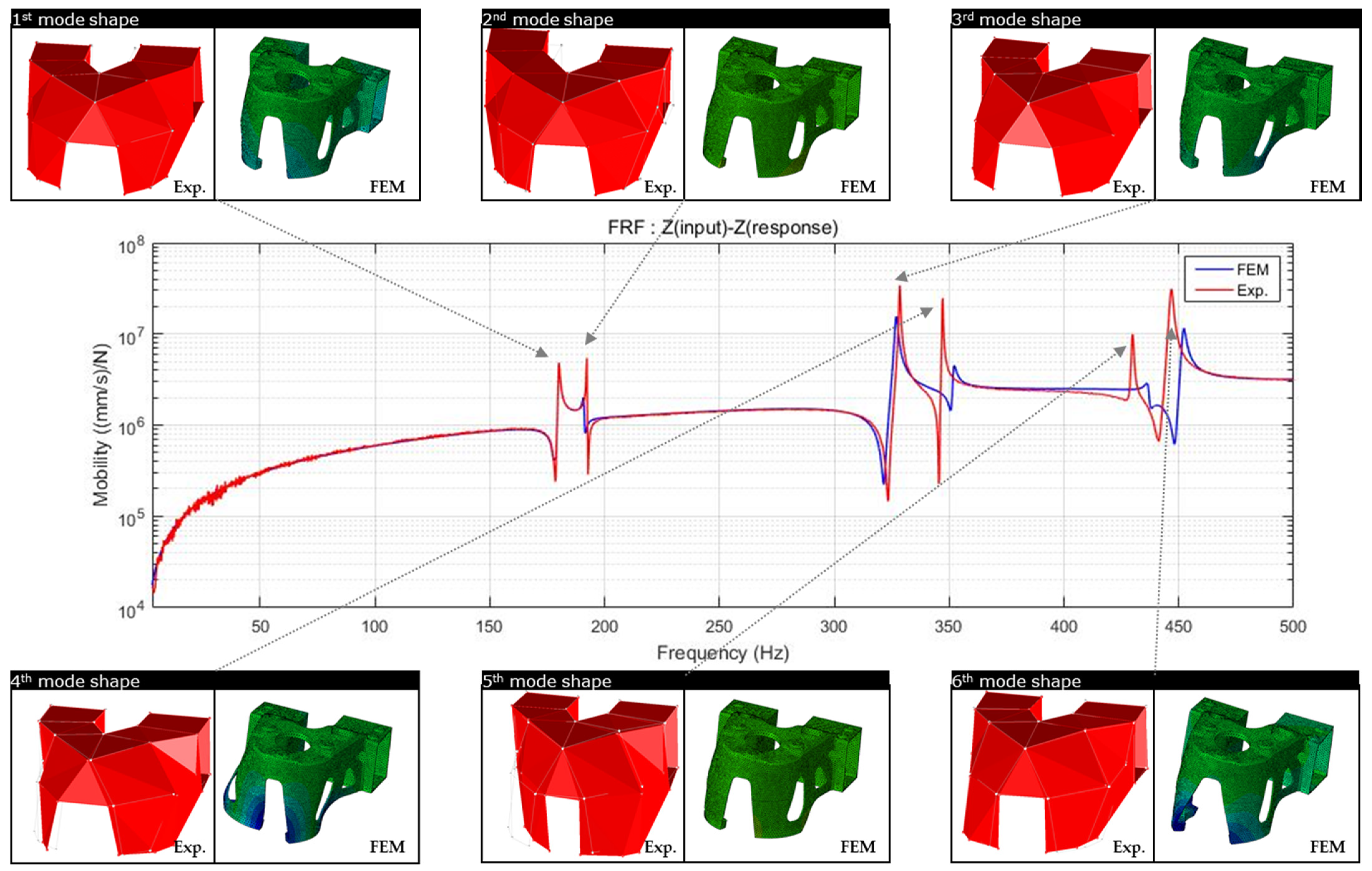
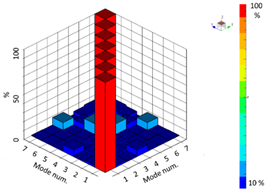
Additionally, in order to clearly explain the mechanical properties, natural frequency and mode shape analyses were performed to clearly explain this. Products with different anisotropy characteristics, that is, when the scan patterns are different, the natural frequencies are different. From the study of West et al., it was confirmed that the natural frequency was different from the microstructure difference caused by the difference in the scanning strategy [
19]. Therefore, it is confirmed that the scan pattern has a sufficient effect on the mechanical properties of the macroscopic structure. In the comparison between the modal test and the FE analysis, the independent first to sixth natural frequency results were compared, and the maximum error (at the fifth natural frequency) was confirmed to be 1.62%. The mode shape analysis shows the shape by considering the mass of the product and the overall and local stiffness values. From the experimental and modal shape analysis of the finite element model, it was confirmed that the expressions of torsion and bending were the same in the deformation behavior of the global and local domains. That is, it was confirmed that the FE analysis, which considered the material properties to be isotropic, was in suitable agreement with the experimental results. Modal analysis is a free vibration analysis for the condition in which there is no damping and external force in the structure, and the eigenvalue problem expressed as a simple harmonic motion has a unique solution, which appears as a result of the natural frequency. Therefore, if the natural frequency of the finite element model considered isotropic and the natural frequency result of the experiment are the same, it means that the product is isotropically built.
In this study, the macrostructure is considered from the product level point of view. Here, depending on the characteristics of the heat flow, the crystal direction of the microstructure may appear, and the anisotropy may appear different from the scan pattern. However, in terms of thermal management and product deformation suppression, the effect is insignificant to consider the thermal characteristics such as the design of the support and the position of the product in the chamber. In addition, the support attached to the large shape of the product level is applied locally, and the thermal properties are reflected only in a very small part of the overall structure. Therefore, microstructure analysis of microstructures according to geometry and support structure that determines heat flow characteristics was excluded. That is, it was judged that the effect would not be significant from the macrostructure point of view. From the previous work of Guan et al. [
6] and this study, Experimentation and FE analysis verified that the mechanical properties of the products fabricated by periodic layer rotation AM using the raster scanning method were isotropic. The macrostructural properties of additively manufactured products are anisotropic along the scan direction. When a raster pattern or unidirectional scanning strategy is used in a single layer cross-section, it is expressed as an orthotropic of the macroscopic structure. To simplify and numerically calculate this, the classical lamination theory can be used, and when several layers are overlapped with a hatch angle, it is confirmed that if all directions are expressed with periodicity, it is expressed as isotropy. In addition, as the hatch angle that can express the scan vector in all directions is implemented more isotropic [
6], it is necessary to apply the hatch angle with an appropriate period in consideration of all layers. This simple application of the classical lamination theory and the finite element analysis method at the macro level has the advantage of being simpler and faster to apply. Moreover, because the microscopic anisotropy of complex materials was not considered, the FE analysis time was greatly reduced, and applicable results were expected to be obtained.