Finite Element Simulation of a Crack Growth in the Presence of a Hole in the Vicinity of the Crack Trajectory
Abstract
:1. Introduction
2. ANSYS SMART Crack Growth
3. Results and Discussion
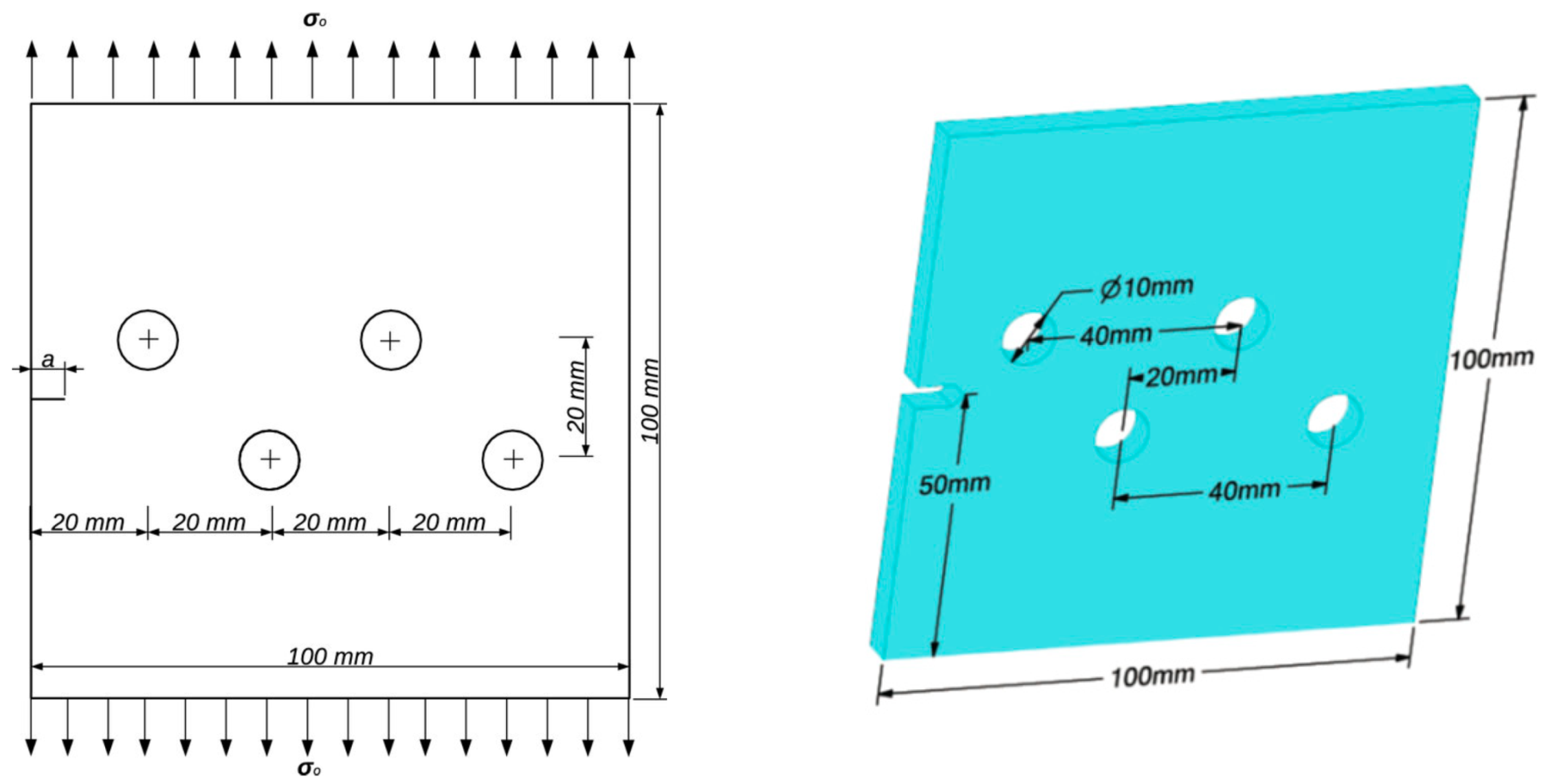
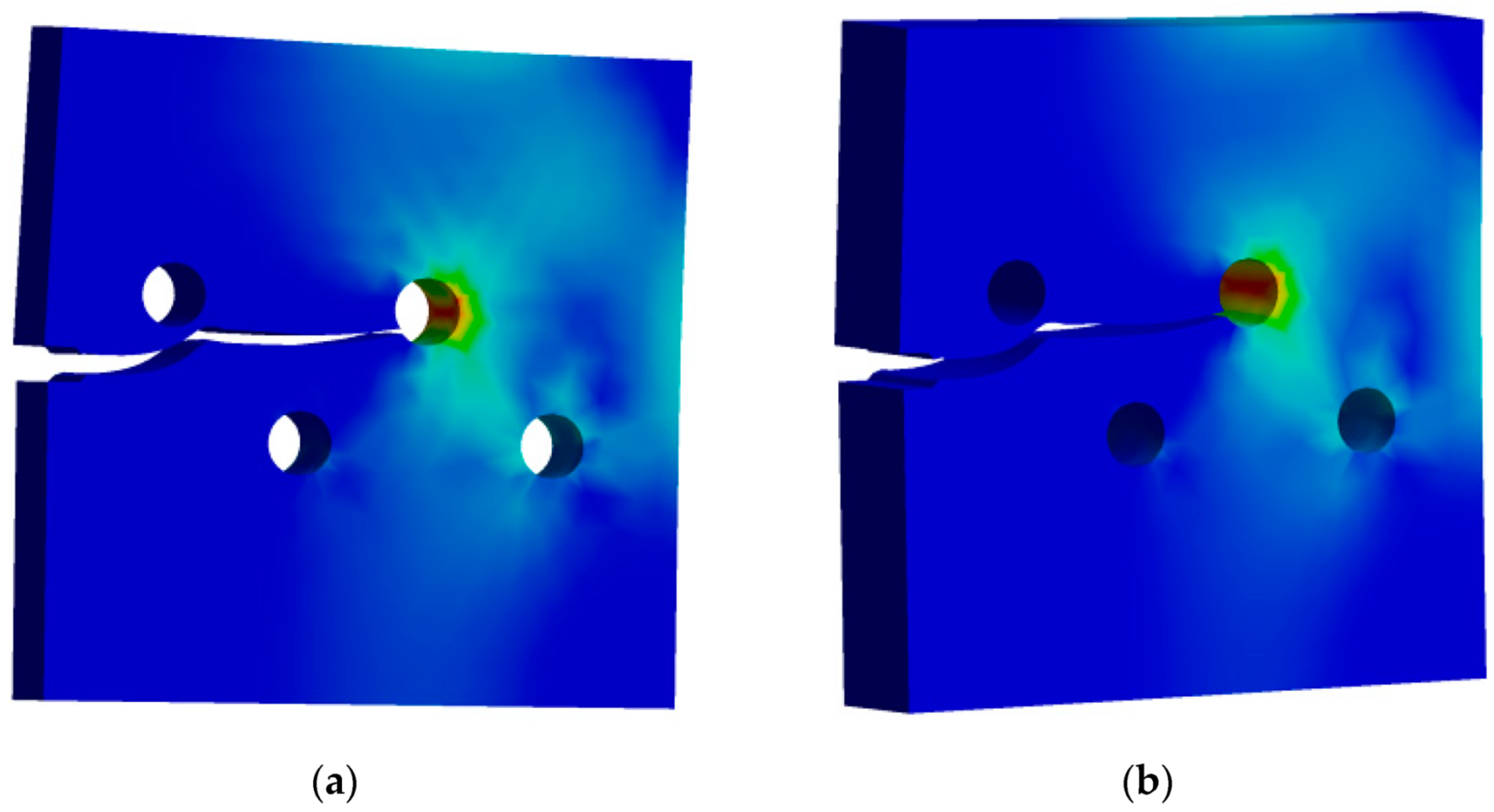
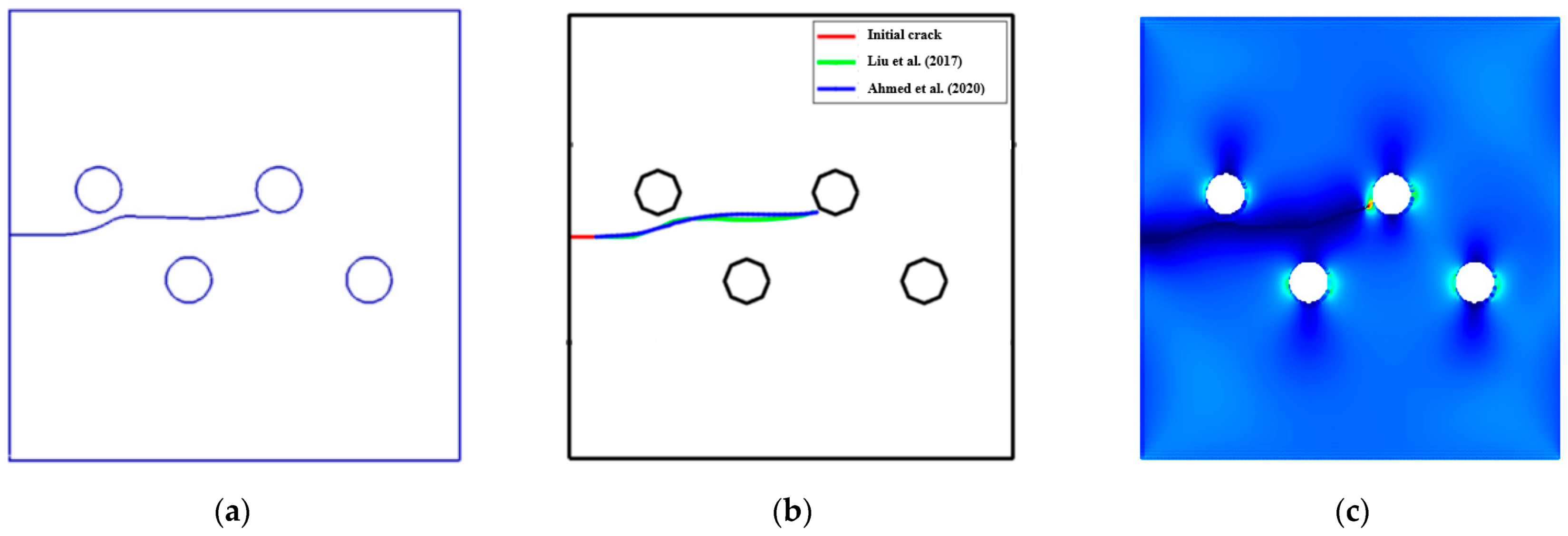
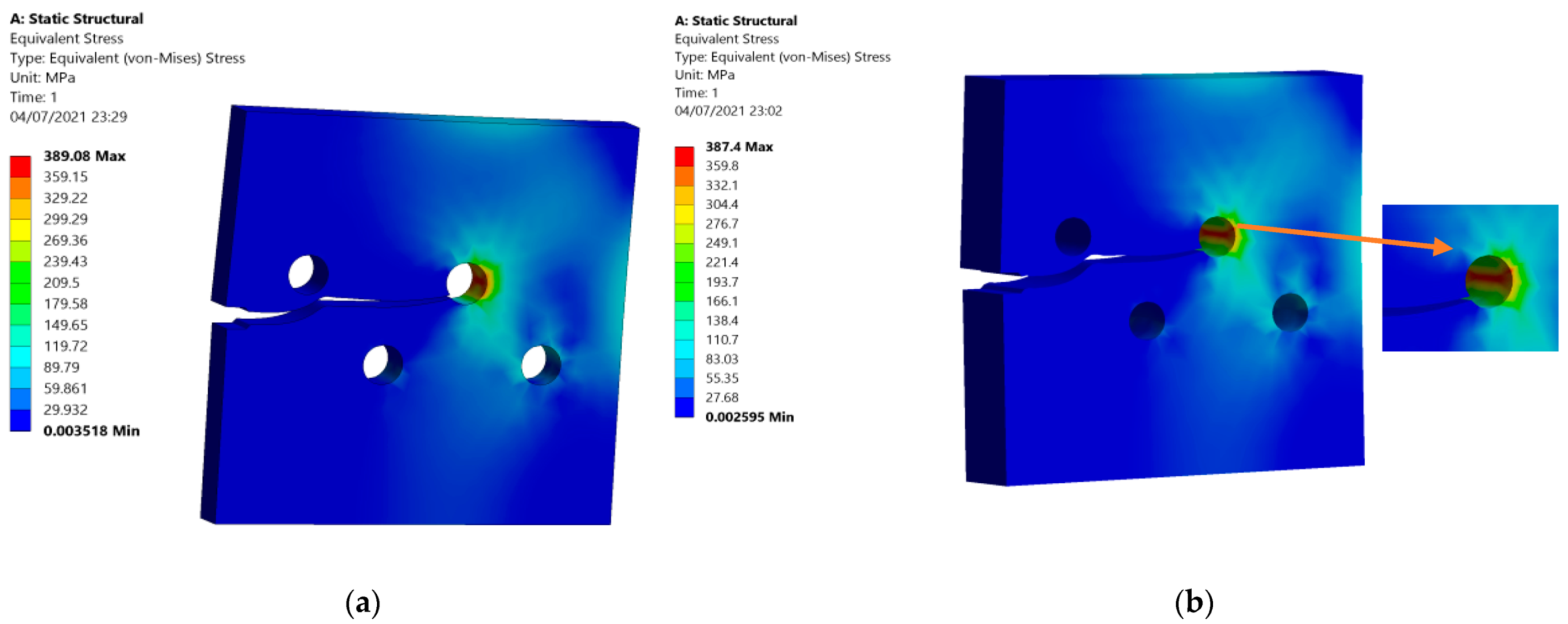
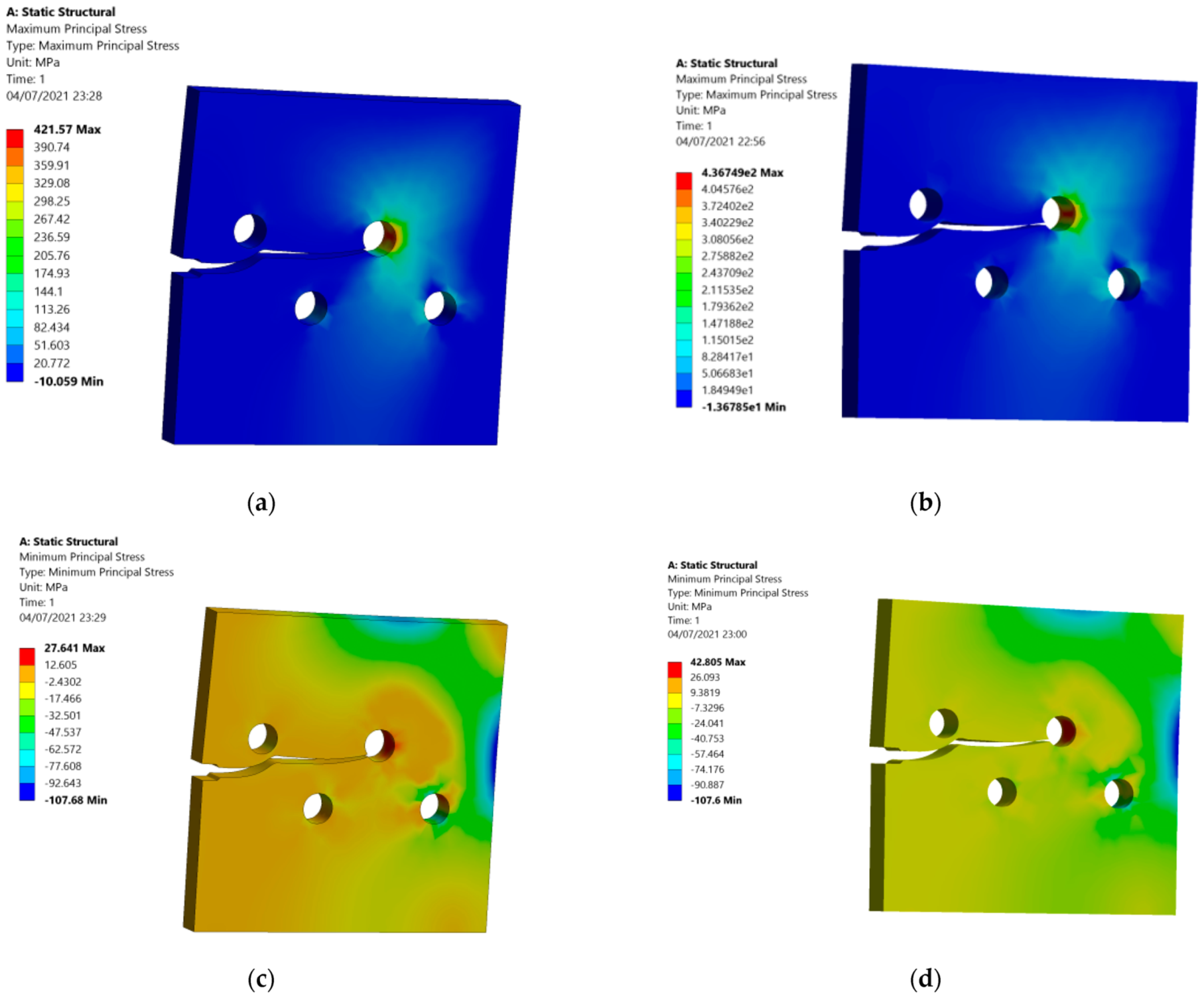
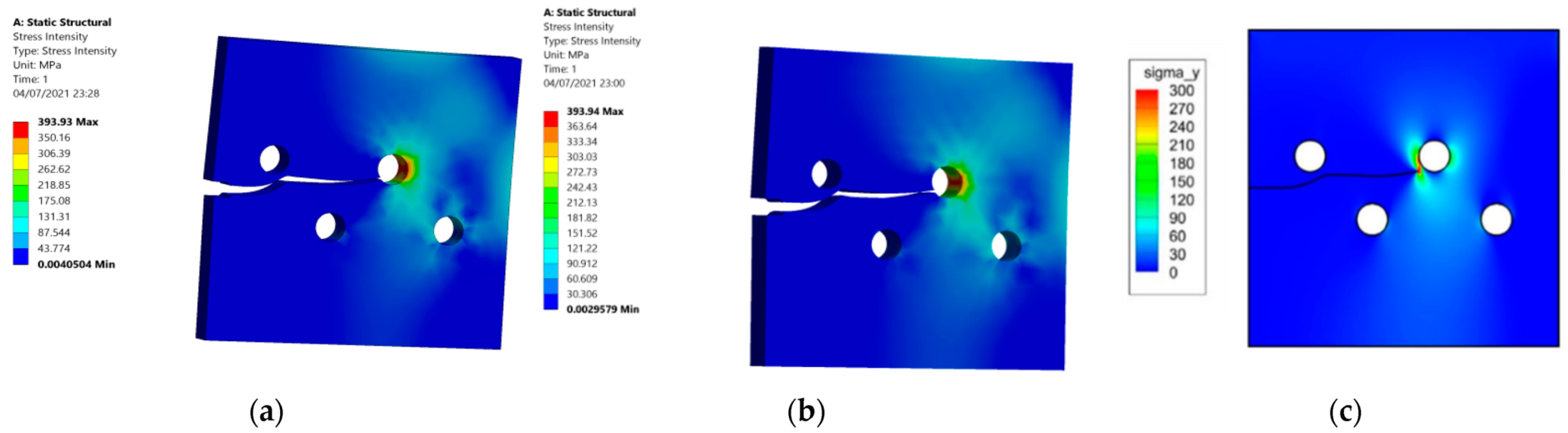
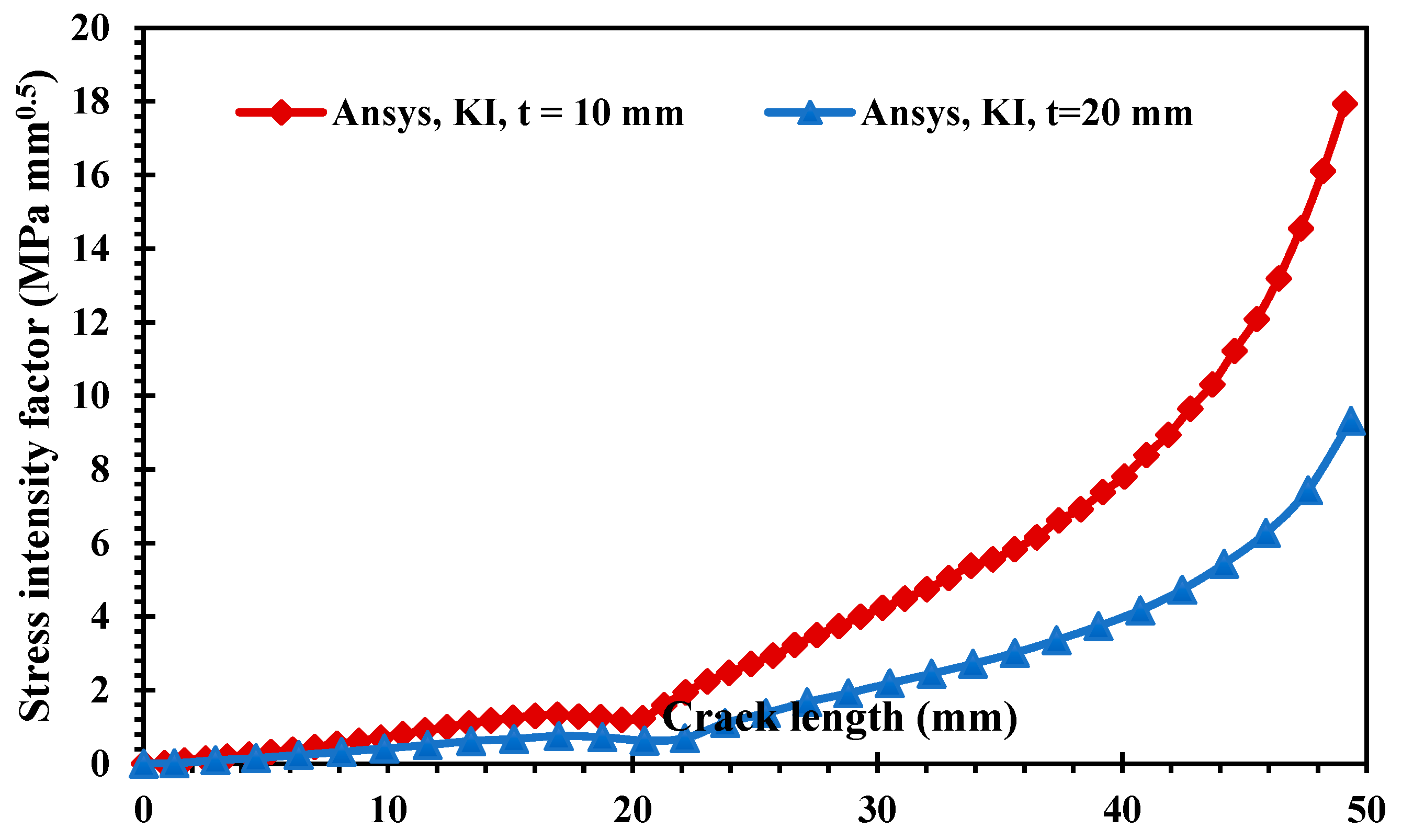
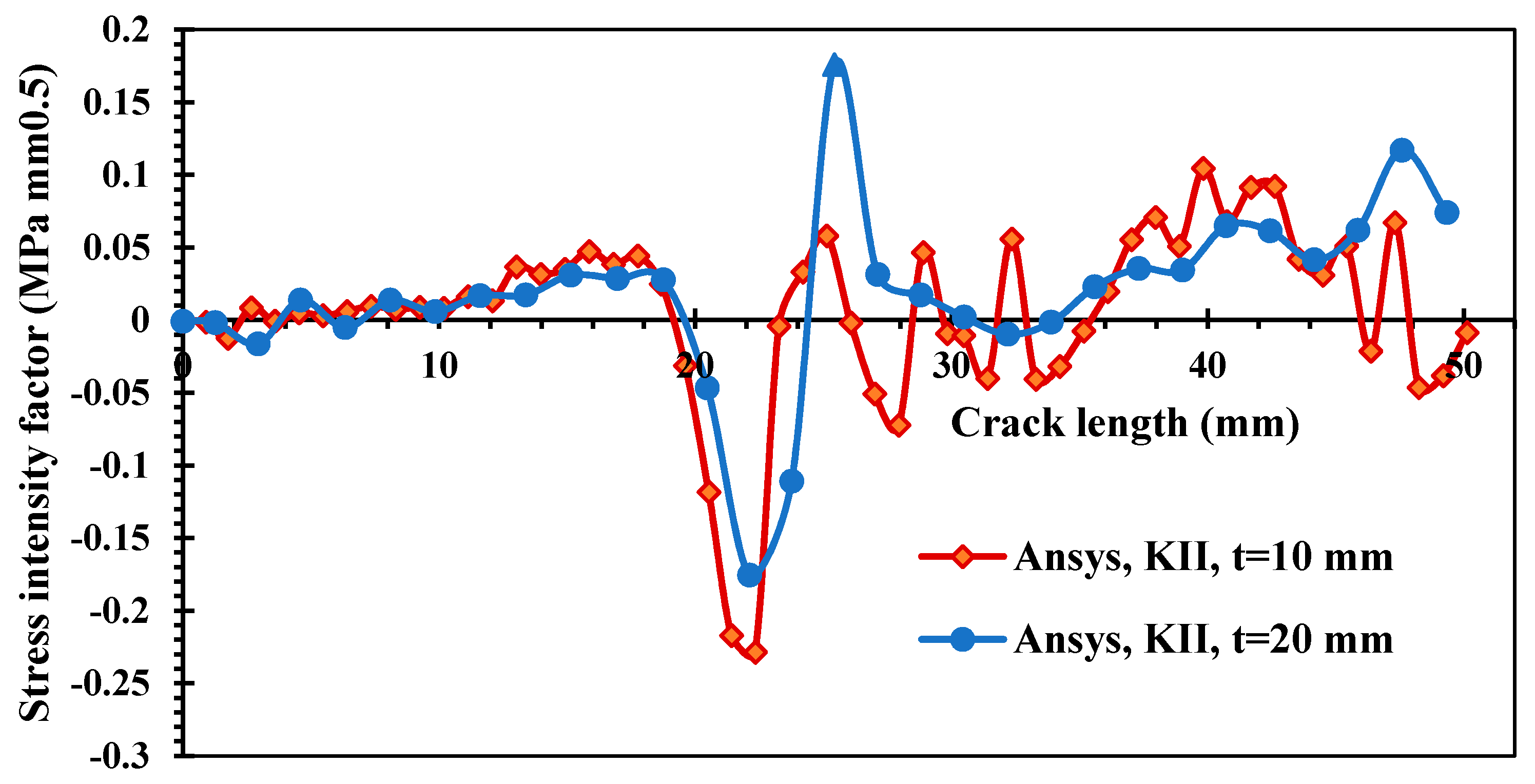
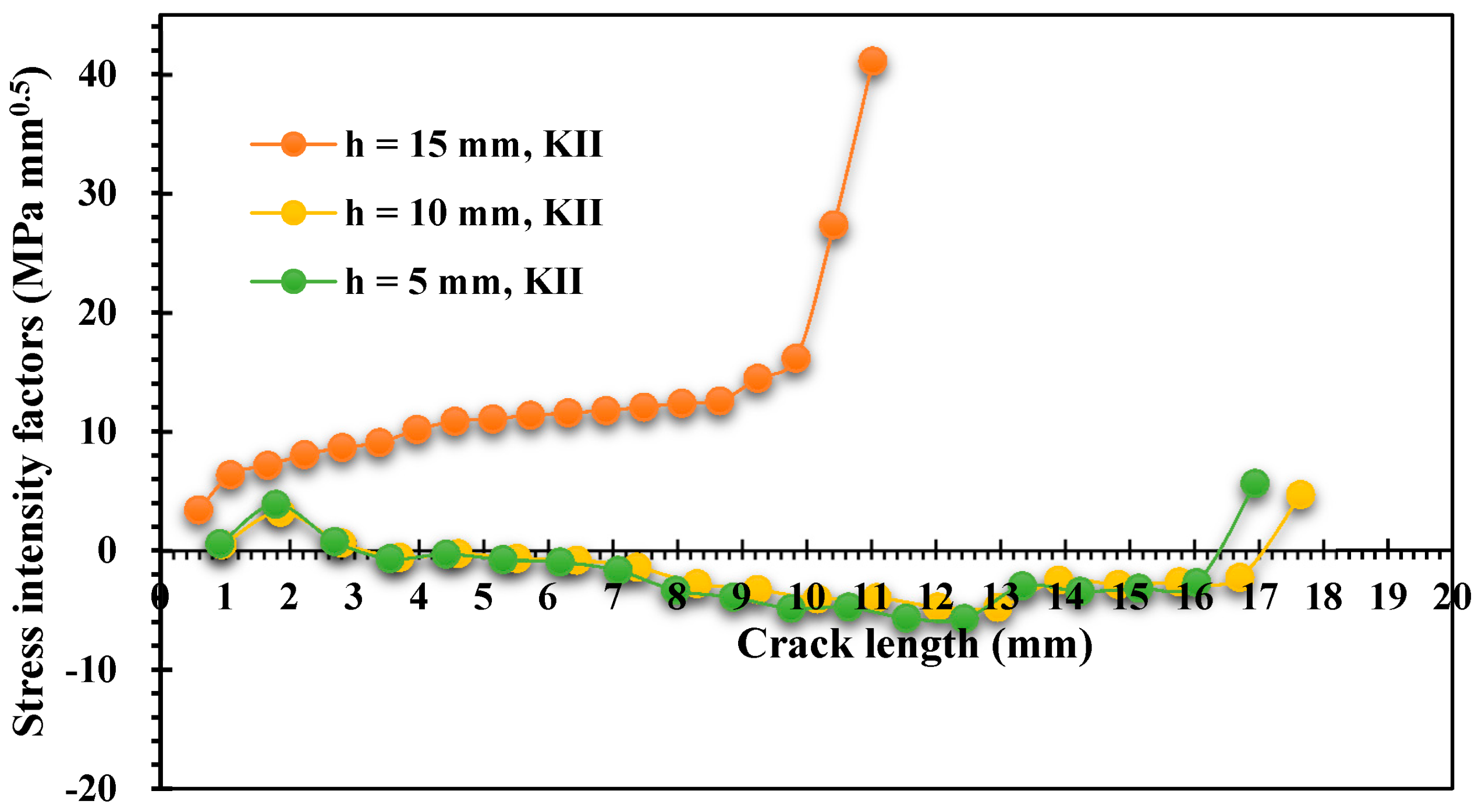
3.1. A Cracked Plate with Four Holes
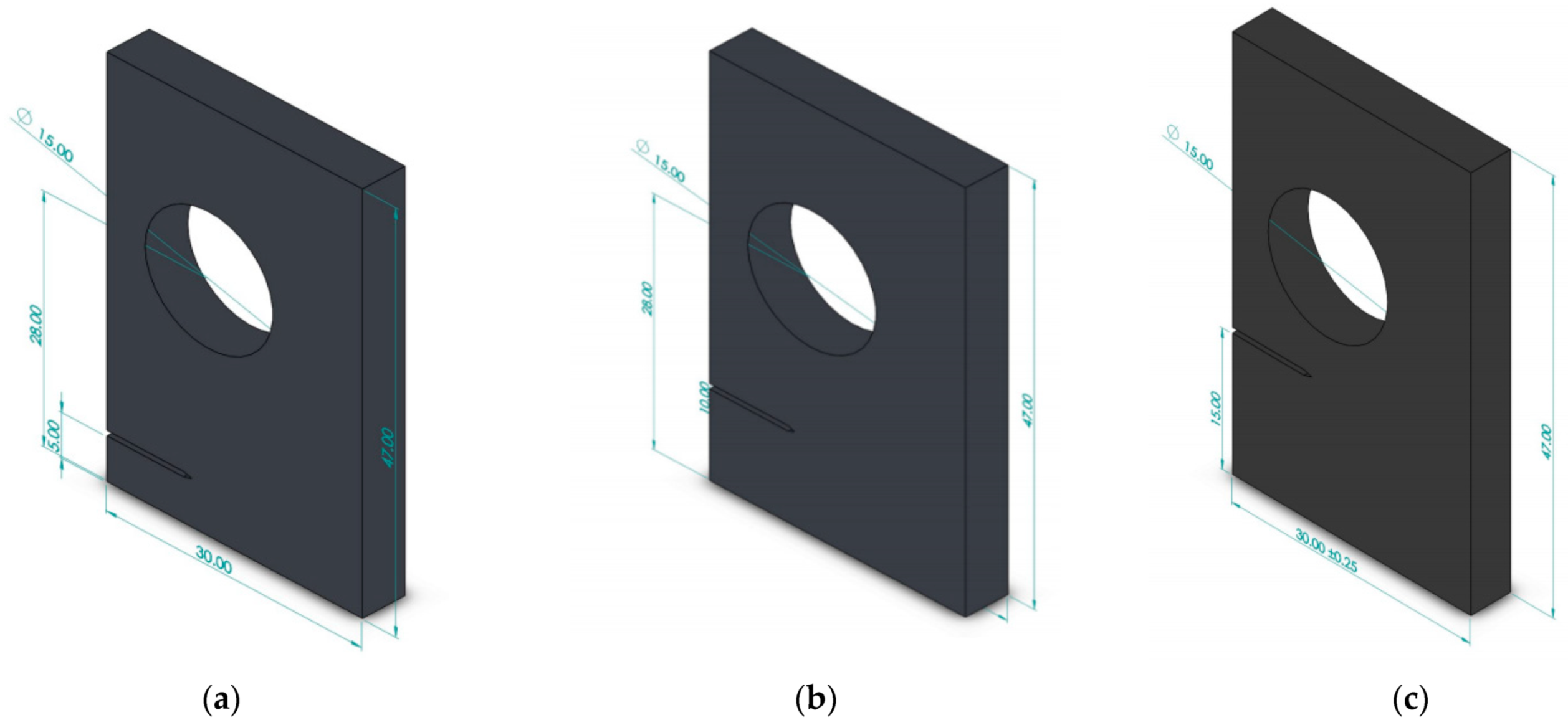
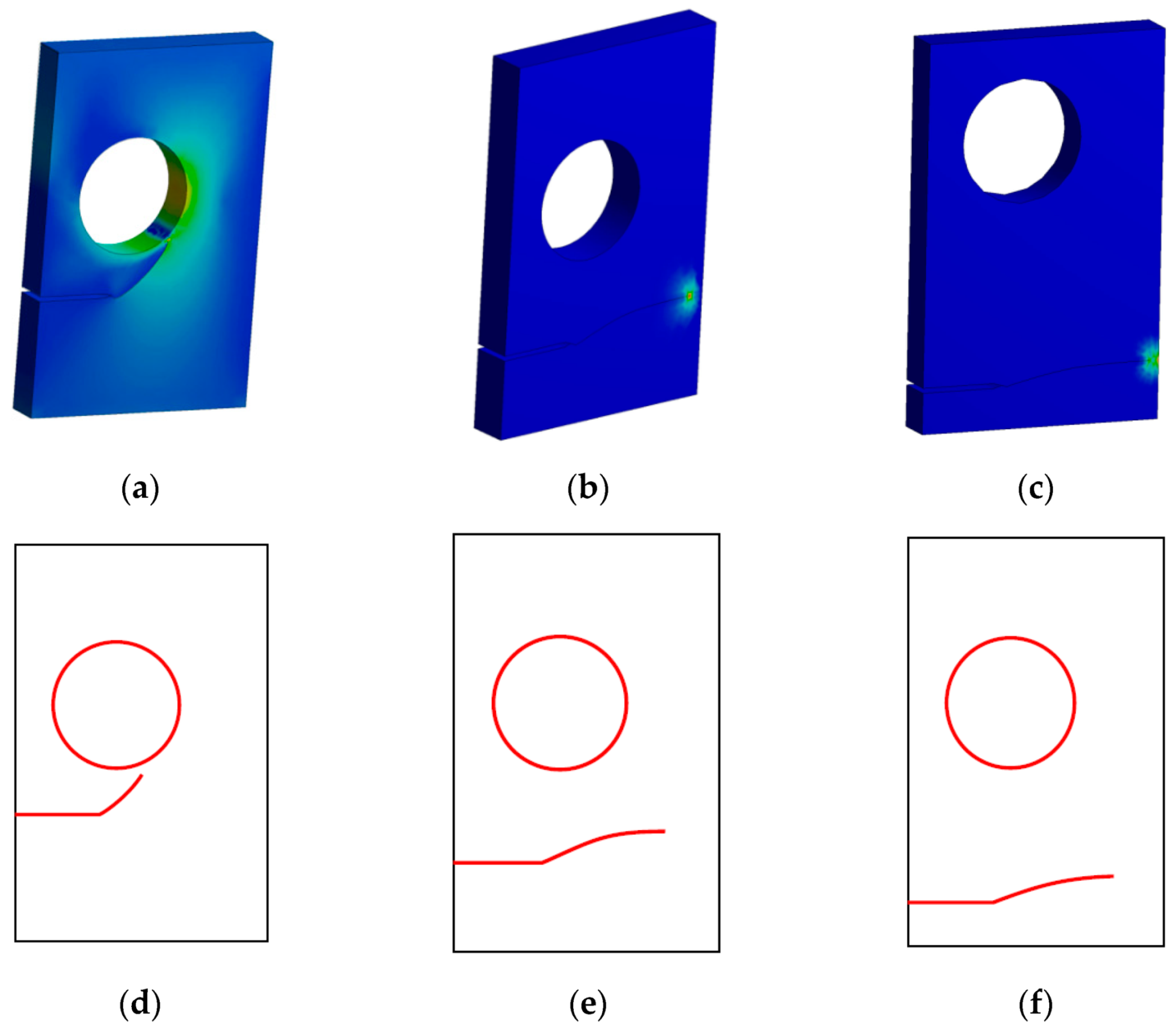
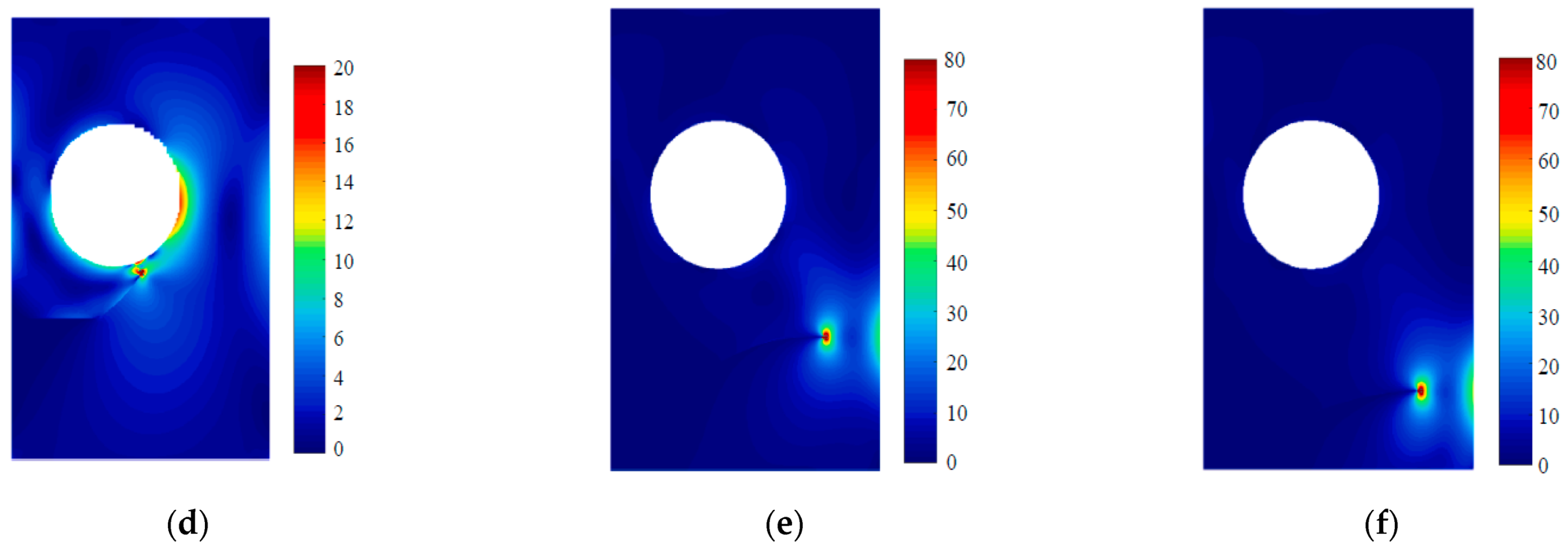
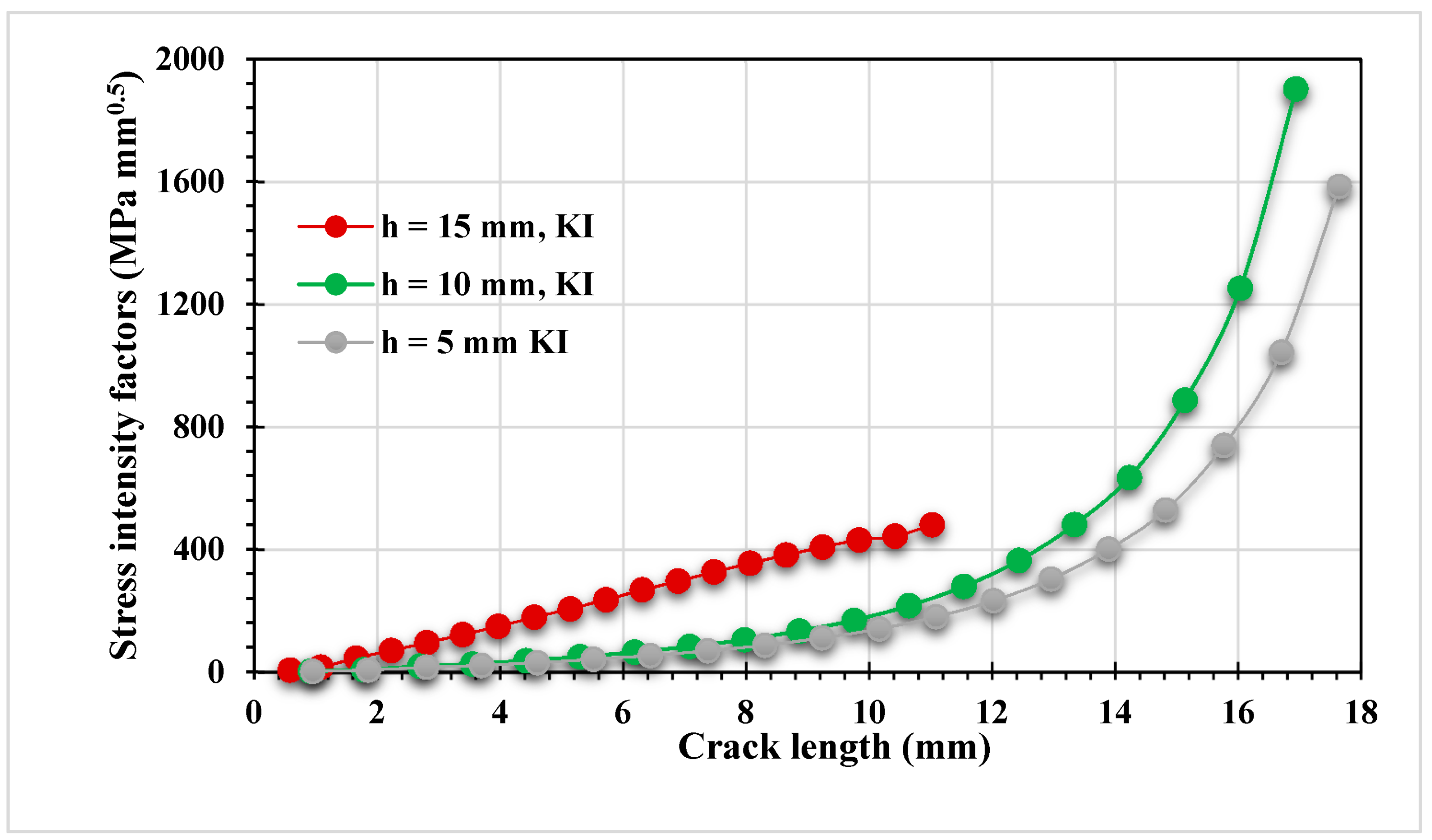
3.2. A Plate with a Circular Hole and an Edge Crack with Different Pre-Crack Locations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Branco, R.; Antunes, F.; Costa, J. A review on 3D-FE adaptive remeshing techniques for crack growth modelling. Eng. Fract. Mech. 2015, 141, 170–195. [Google Scholar] [CrossRef]
- Li, X.; Li, H.; Liu, L.; Liu, Y.; Ju, M.; Zhao, J. Investigating the crack initiation and propagation mechanism in brittle rocks using grain-based finite-discrete element method. Int. J. Rock Mech. Min. Sci. 2020, 127, 104219. [Google Scholar] [CrossRef]
- Leclerc, W.; Haddad, H.; Guessasma, M. On the suitability of a Discrete Element Method to simulate cracks initiation and propagation in heterogeneous media. Int. J. Solids Struct. 2017, 108, 98–114. [Google Scholar] [CrossRef]
- Shao, Y.; Duan, Q.; Qiu, S. Adaptive consistent element-free Galerkin method for phase-field model of brittle fracture. Comput. Mech. 2019, 64, 741–767. [Google Scholar] [CrossRef]
- Kanth, S.A.; Harmain, G.; Jameel, A. Modeling of Nonlinear Crack Growth in Steel and Aluminum Alloys by the Element Free Galerkin Method. Mater. Today Proc. 2018, 5, 18805–18814. [Google Scholar] [CrossRef]
- Huynh, H.D.; Nguyen, M.N.; Cusatis, G.; Tanaka, S.; Bui, T.Q. A polygonal XFEM with new numerical integration for linear elastic fracture mechanics. Eng. Fract. Mech. 2019, 213, 241–263. [Google Scholar] [CrossRef]
- Surendran, M.; Natarajan, S.; Palani, G.; Bordas, S.P. Linear smoothed extended finite element method for fatigue crack growth simulations. Eng. Fract. Mech. 2019, 206, 551–564. [Google Scholar] [CrossRef]
- Dekker, R.; van der Meer, F.; Maljaars, J.; Sluys, L. A cohesive XFEM model for simulating fatigue crack growth under mixed-mode loading and overloading. Int. J. Numer. Methods Eng. 2019, 118, 561–577. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, S.; Wulfinghoff, S.; Reese, S. Prediction of fracture and damage in micro/nano coating systems using cohesive zone elements. Int. J. Solids Struct. 2017, 121, 62–74. [Google Scholar] [CrossRef]
- Santana, E.; Portela, A. Dual boundary element analysis of fatigue crack growth, interaction and linkup. Eng. Anal. Bound. Elem. 2016, 64, 176–195. [Google Scholar] [CrossRef]
- Tanaka, S.; Suzuki, H.; Sadamoto, S.; Imachi, M.; Bui, T.Q. Analysis of cracked shear deformable plates by an effective meshfree plate formulation. Eng. Fract. Mech. 2015, 144, 142–157. [Google Scholar] [CrossRef]
- Khosravifard, A.; Hematiyan, M.; Bui, T.; Do, T. Accurate and efficient analysis of stationary and propagating crack problems by meshless methods. Theor. Appl. Fract. Mech. 2017, 87, 21–34. [Google Scholar] [CrossRef]
- Zhang, W.; Tabiei, A. An Efficient Implementation of Phase Field Method with Explicit Time Integration. J. Appl. Comput. Mech. 2020, 6, 373–382. [Google Scholar]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Sukumar, N.; Prévost, J.-H. Modeling quasi-static crack growth with the extended finite element method Part I: Computer implementation. Int. J. Solids Struct. 2003, 40, 7513–7537. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. Simulation of Quasi-Static Crack Propagation by Adaptive Finite Element Method. Metals 2021, 11, 98. [Google Scholar] [CrossRef]
- Lin, X.; Smith, R. Finite element modelling of fatigue crack growth of surface cracked plates: Part I: The numerical technique. Eng. Fract. Mech. 1999, 63, 503–522. [Google Scholar] [CrossRef]
- Muixí, A.; Marco, O.; Rodríguez-Ferran, A.; Fernández-Méndez, S. A combined XFEM phase-field computational model for crack growth without remeshing. Comput. Mech. 2021, 67, 231–249. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. 2D finite element simulation of mixed mode fatigue crack propagation for CTS specimen. J. Mater. Res. Technol. 2020, 9, 7850–7861. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. Numerical Analysis of Fatigue Crack Growth Path and Life Predictions for Linear Elastic Material. Materials 2020, 13, 3380. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Computational Simulation of 3D Fatigue Crack Growth under Mixed-Mode Loading. Appl. Sci. 2021, 11, 5953. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Numerical Modeling of Crack Growth under Mixed-Mode Loading. Appl. Sci. 2021, 11, 2975. [Google Scholar] [CrossRef]
- Carter, B.; Wawrzynek, P.; Ingraffea, A. Automated 3-D crack growth simulation. Int. J. Numer. Methods Eng. 2000, 47, 229–253. [Google Scholar] [CrossRef]
- Hou, J.; Goldstraw, M.; Maan, S.; Knop, M.; Defence Science and Technology Organization Victoria (Australia) Aeronautical and Maritime Research Laboratory. An Evaluation of 3D Crack Growth Using ZENCRACK; Department of Defence, DSTO: Victoria, Australia, 2001.
- Shahani, A.; Farrahi, A. Experimental investigation and numerical modeling of the fatigue crack growth in friction stir spot welding of lap-shear specimen. Int. J. Fatigue 2019, 125, 520–529. [Google Scholar] [CrossRef]
- Malekan, M.; Khosravi, A.; St-Pierre, L. An Abaqus plug-in to simulate fatigue crack growth. Eng. Comput. 2021, 1–15. [Google Scholar] [CrossRef]
- Rocha, A.; Akhavan-Safar, A.; Carbas, R.; Marques, E.; Goyal, R.; El-zein, M.; da Silva, L. Numerical analysis of mixed-mode fatigue crack growth of adhesive joints using CZM. Theor. Appl. Fract. Mech. 2020, 106, 102493. [Google Scholar] [CrossRef]
- Teh, S.; Andriyana, A.; Ramesh, S.; Putra, I.; Kadarno, P.; Purbolaksono, J. Tetrahedral meshing for a slanted semi-elliptical surface crack at a solid cylinder. Eng. Fract. Mech. 2021, 241, 107400. [Google Scholar] [CrossRef]
- Paris, P.C. A Brief History of the Crack Tip Stress Intensity Factor and Its Application; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Zhao, T.; Zhang, J.; Jiang, Y. A study of fatigue crack growth of 7075-T651 aluminum alloy. Int. J. Fatigue 2008, 30, 1169–1180. [Google Scholar] [CrossRef]
- Singh, V.K.; Gope, P.C. Experimental evaluation of mixed mode stress intensity factor for prediction of crack growth by phoelastic method. J. Fail. Anal. Prev. 2013, 13, 217–226. [Google Scholar] [CrossRef]
- Forth, S.C.; Newman, J.C., Jr.; Forman, R.G. On generating fatigue crack growth thresholds. Int. J. Fatigue 2003, 25, 9–15. [Google Scholar] [CrossRef]
- Bjørheim, F. Practical Comparison of Crack Meshing in ANSYS Mechanical APDL 19.2. Master’s Thesis, University of Stavanger, Vistavanger, Norway, 2019. [Google Scholar]
- Wawrzynek, P.; Carter, B.; Banks-Sills, L. The M-Integral for Computing Stress Intensity Factors in Generally Anisotropic Materials; National Aeronautics and Space Administration, Marshall Space Flight Center: Hanover, NH, USA, 2005.
- Citarella, R.; Giannella, V.; Lepore, M.; Dhondt, G. Dual boundary element method and finite element method for mixed-mode crack propagation simulations in a cracked hollow shaft. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 84–98. [Google Scholar] [CrossRef]
- Dhondt, G.; Hackenberg, H.-P. Use of a rotation-invariant linear strain measure for linear elastic crack propagation calculations. Eng. Fract. Mech. 2021, 247, 107634. [Google Scholar] [CrossRef]
- ANSYS. Academic Research Mechanical, Release 19.2, Help System. In Coupled Field Analysis Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Liu, Y.; Li, Y.; Xie, W. Modeling of multiple crack propagation in 2-D elastic solids by the fast multipole boundary element method. Eng. Fract. Mech. 2017, 172, 1–16. [Google Scholar] [CrossRef]
- Ahmed, T.; Yavuz, A.; Turkmen, H.S. Fatigue crack growth simulation of interacting multiple cracks in perforated plates with multiple holes using boundary cracklet method. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 333–348. [Google Scholar] [CrossRef]
- Wiragunarsa, I.M.; Zuhal, L.R.; Dirgantara, T.; Putra, I.S. A particle interaction-based crack model using an improved smoothed particle hydrodynamics for fatigue crack growth simulations. Int. J. Fract. 2021, 229, 229–244. [Google Scholar] [CrossRef]
- Fang, W.; Chen, X.; Yu, T.; Bui, T.Q. Effects of arbitrary holes/voids on crack growth using local mesh refinement adaptive XIGA. Theor. Appl. Fract. Mech. 2020, 109, 102724. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshoaibi, A.M.; Fageehi, Y.A. Finite Element Simulation of a Crack Growth in the Presence of a Hole in the Vicinity of the Crack Trajectory. Materials 2022, 15, 363. https://doi.org/10.3390/ma15010363
Alshoaibi AM, Fageehi YA. Finite Element Simulation of a Crack Growth in the Presence of a Hole in the Vicinity of the Crack Trajectory. Materials. 2022; 15(1):363. https://doi.org/10.3390/ma15010363
Chicago/Turabian StyleAlshoaibi, Abdulnaser M., and Yahya Ali Fageehi. 2022. "Finite Element Simulation of a Crack Growth in the Presence of a Hole in the Vicinity of the Crack Trajectory" Materials 15, no. 1: 363. https://doi.org/10.3390/ma15010363
APA StyleAlshoaibi, A. M., & Fageehi, Y. A. (2022). Finite Element Simulation of a Crack Growth in the Presence of a Hole in the Vicinity of the Crack Trajectory. Materials, 15(1), 363. https://doi.org/10.3390/ma15010363






