Machine Learning Enhanced Dynamic Response Modelling of Superelastic Shape Memory Alloy Wires
Abstract
1. Introduction
2. Methodology
2.1. Superelastic SMA Response
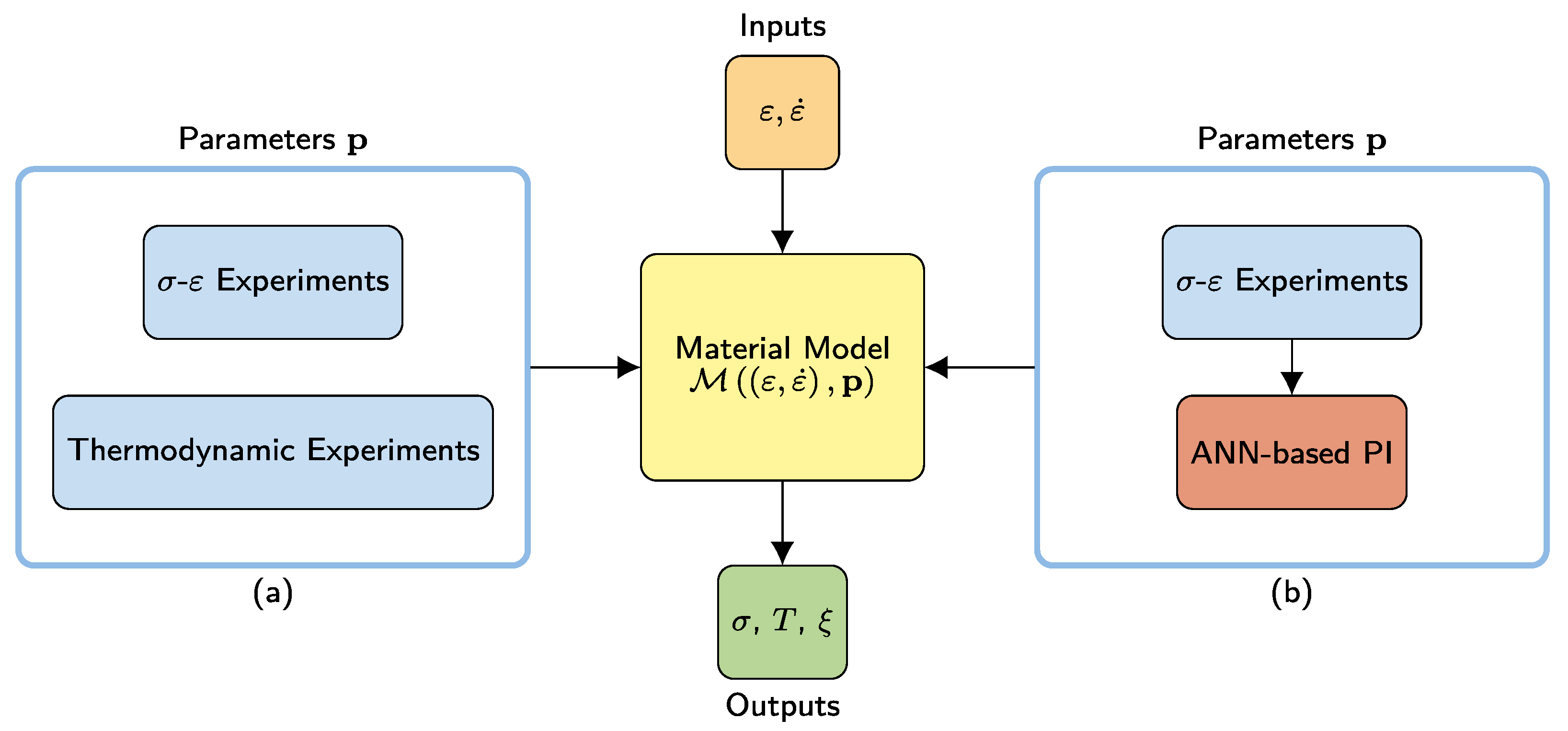
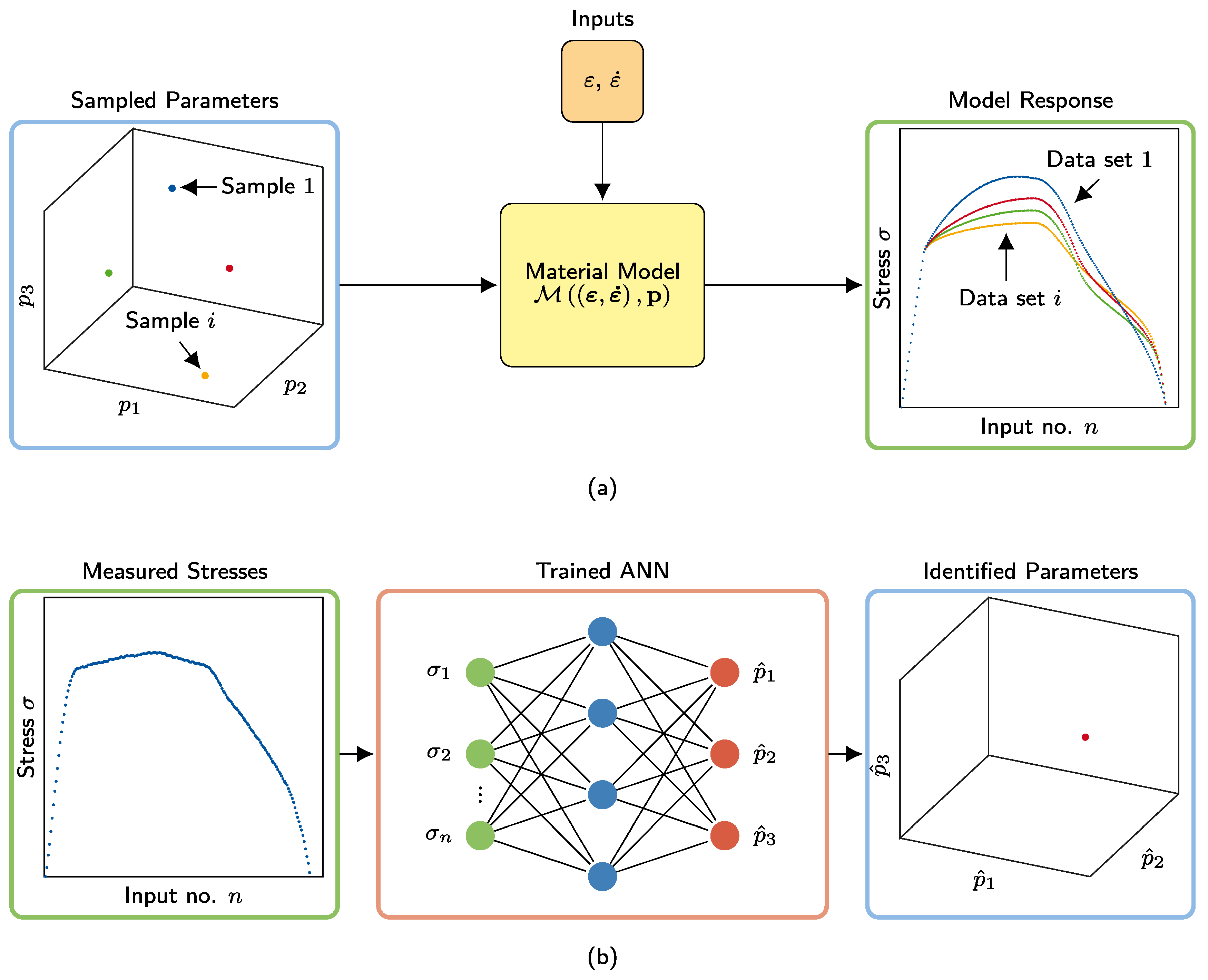
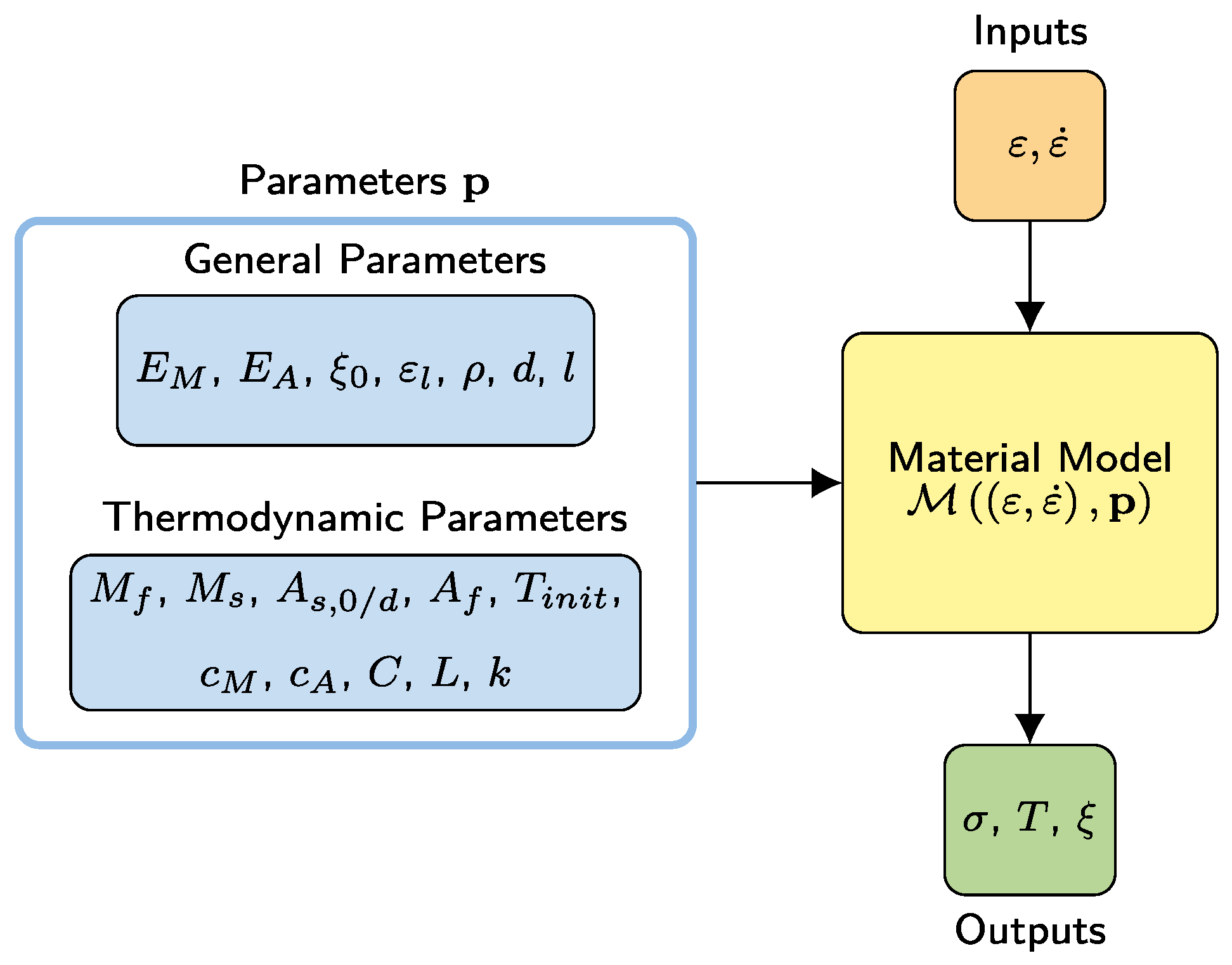
2.2. Machine-Learning-Based Parameter Identification
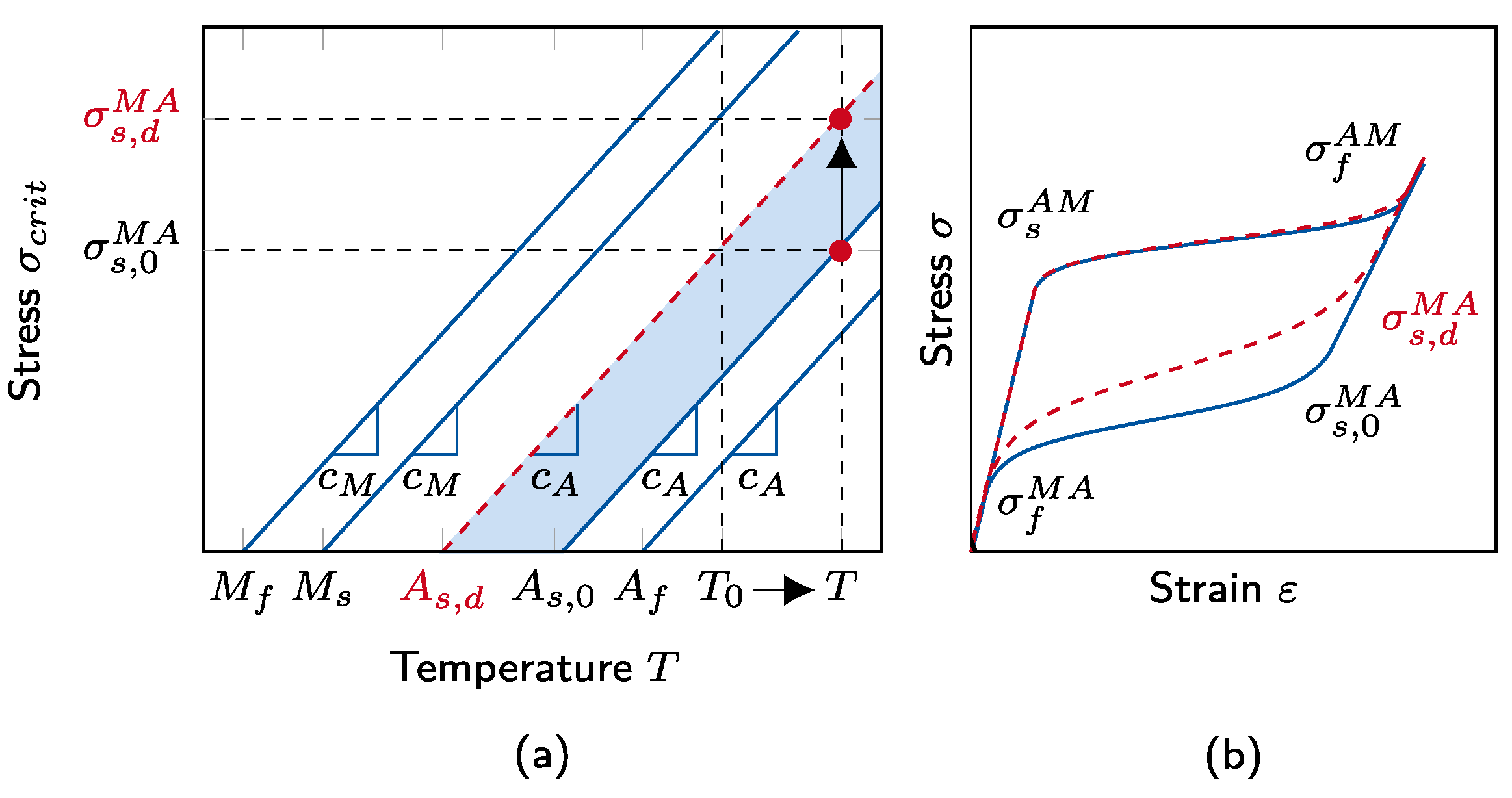
2.3. Constitutive Modelling of Superelastic SMA Wire Response
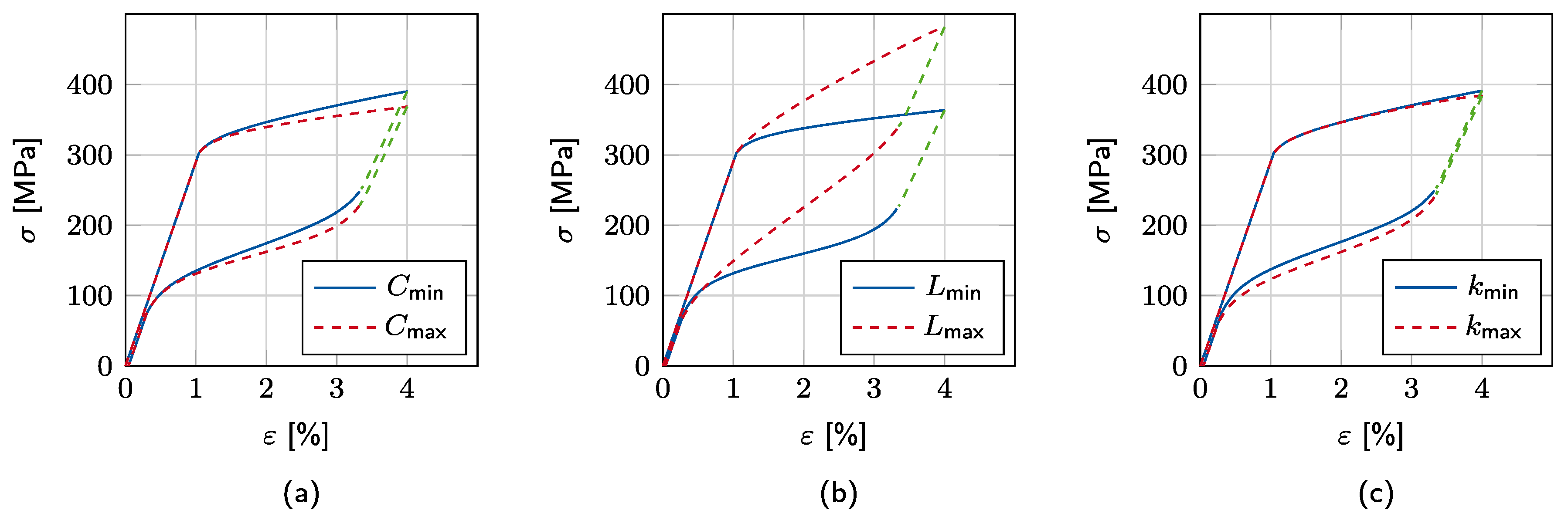
Parameter Influence on Stress–Strain Response
3. Results and Discussion
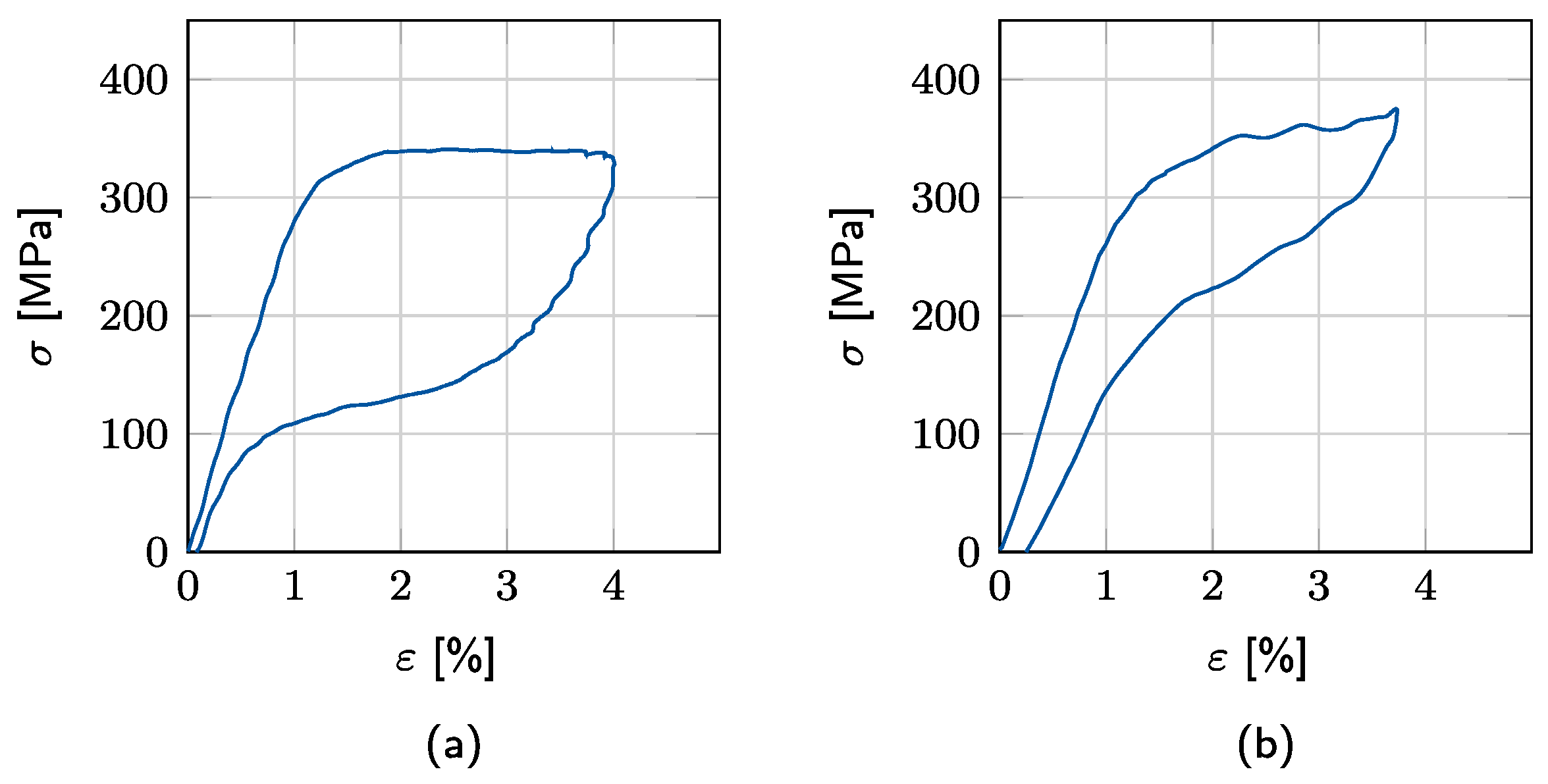
3.1. Stress–Strain Experiments
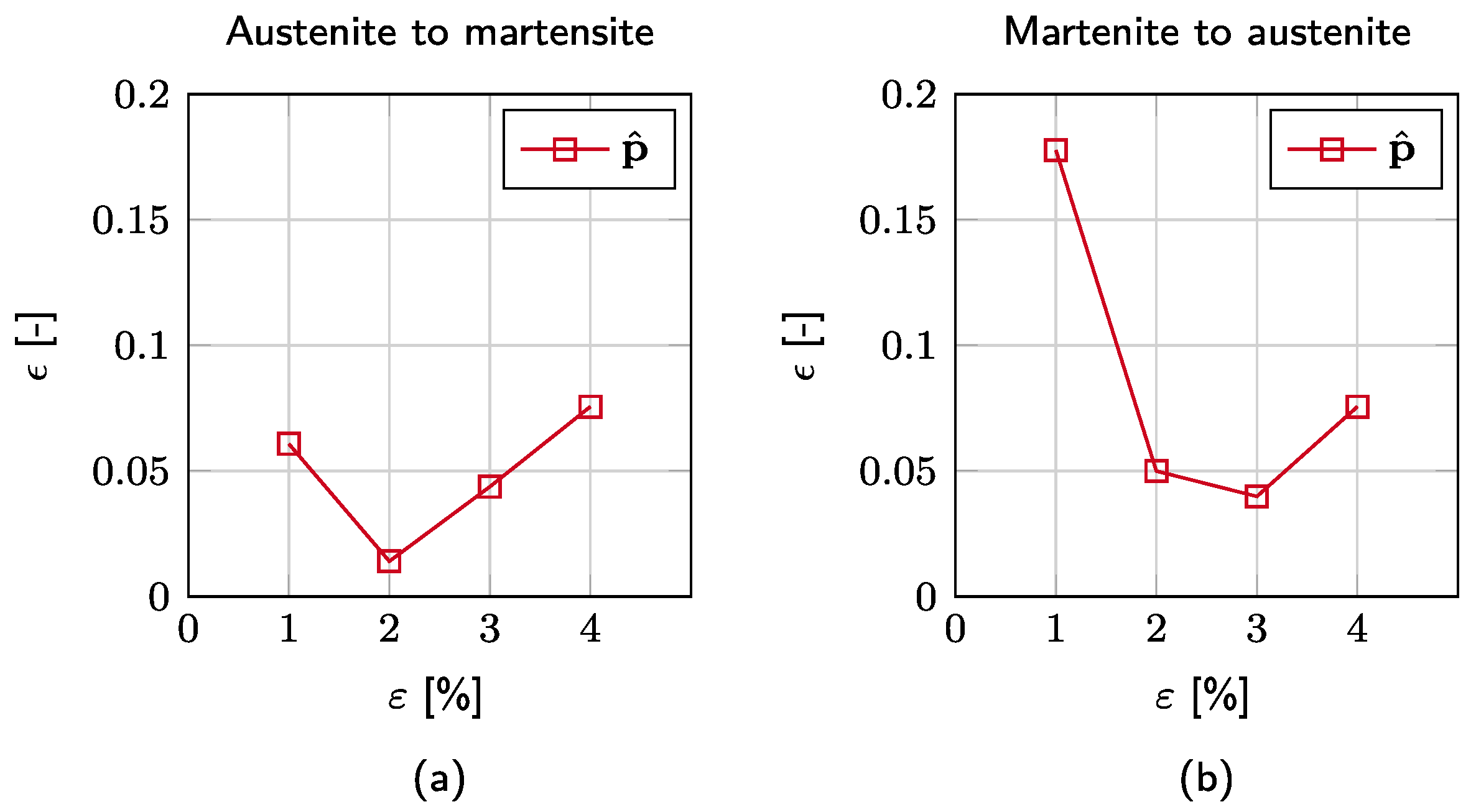
3.2. Identification of Thermodynamic Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| LHS | Latin Hypercube Sampling |
| SMA | Shape Memory Alloy |
| AM | Austenite to Martensite |
| MA | Martensite to Austenite |
| ML | Machine Learning |
| PI | Parameter Identification |
References
- Qiu, C.; Zhu, S. Shake table test and numerical study of self-centering steel frame with SMA braces. Earthq. Eng. Struct. Dyn. 2017, 46, 117–137. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Qiu, C.; Zhao, X. Seismic Behavior of Superelastic Shape Memory Alloy Spring in Base Isolation System of Multi-Story Steel Frame. Materials 2019, 12, 997. [Google Scholar] [CrossRef]
- Liang, D.; Zheng, Y.; Fang, C.; Yam, M.; Zhang, C. Shape memory alloy (SMA)-cable-controlled sliding bearings: Development, testing, and system behavior. Smart Mater. Struct. 2020, 29, 085006. [Google Scholar] [CrossRef]
- Ozbulut, O.E.; Hurlebaus, S.; DesRoches, R. Seismic response control using shape memory alloys: A review. J. Intell. Mater. Syst. Struct. 2011, 22, 1531–1549. [Google Scholar] [CrossRef]
- Fang, C.; Wang, W. Shape Memory Alloys for Seismic Resilience; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Tabrizikahou, A.; Kuczma, M.; Nowotarski, P.; Kwiatek, M.; Javanmardi, A. Sustainability of Civil Structures through the Application of Smart Materials: A Review. Materials 2021, 14, 4824. [Google Scholar] [CrossRef]
- Costanza, G.; Tata, M.E. Shape Memory Alloys for Aerospace, Recent Developments, and New Applications: A Short Review. Materials 2020, 13, 1856. [Google Scholar] [CrossRef] [PubMed]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Brinson, L.C. One-dimensional constitutive behaviour of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable. J. Intell. Mater. Syst. Struc. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Auricchio, F.; Sacco, E. A One-Dimensional Model for Superelastic Shape-Memory Alloys with Different Elastic Properties Between Austenite and Martensite. Int. J. Non-Linear Mech. 1997, 32, 1101–1114. [Google Scholar] [CrossRef]
- Auricchio, F.; Sacco, E. Thermo-Mechanical Modelling of a Superelastic Shape-Memory Wire Under Cyclic Stretching–Bending Loadings. Int. J. Solids Struct. 2001, 38, 6123–6145. [Google Scholar] [CrossRef]
- Zhu, S.; Zhang, Y. A Thermomechanical Constitutive Model for Superelastic SMA Wire with Strain-Rate Dependence. J. Smart Mater. Struct. 2007, 16, 1696–1707. [Google Scholar] [CrossRef]
- Kaup, A.; Altay, O.; Klinkel, S. Macroscopic modeling of strain-rate dependent energy dissipation of superelastic SMA dampers considering destabilization of martensitic lattice. Smart Mater. Struct. 2019, 29, 025005. [Google Scholar] [CrossRef]
- Kaup, A.; Ding, H.; Wang, J.; Altay, O. Strain rate dependent formulation of the latent heat evolution of superelastic shape memory alloy wires incorporated in multistory frame structures. J. Intell. Mater. Syst. Struct. 2020, 32, 1198–1214. [Google Scholar] [CrossRef]
- Cisse, C.; Zaki, W.; Ben Zineb, T. A Review of Constitutive Models and Modeling Techniques for Shape Memory Alloys. Int. J. Plast. 2016, 76, 244–284. [Google Scholar] [CrossRef]
- Depriester, D.; Maynadier, A.; Lavernhe-Taillard, K.; Hubert, O. Thermomechanical modelling of a NiTi SMA sample submitted to displacement-controlled tensile test. Int. J. Solids Struct. 2014, 51, 1901–1922. [Google Scholar] [CrossRef]
- Xiao, Y.; Zeng, P.; Lei, L.; Du, H. Experimental investigation on rate dependence of thermomechanical response in superelastic NiTi shape memory alloy. J. Mater. Eng. Perform. 2015, 24, 3755–3760. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Garrett, J.H., Jr.; Wu, X. Knowledge-based modeling of material behavior with neural networks. J. Eng. Mech. 1991, 117, 132–153. [Google Scholar] [CrossRef]
- Furukawa, T.; Yagawa, G. Implicit constitutive modelling for viscoplasticity using neural networks. Int. J. Numer. Methods Eng. 1998, 43, 195–219. [Google Scholar] [CrossRef]
- Ozbulut, O.; Hurlebaus, S. Neuro-fuzzy Modeling of Temperature- and Strain-rate-dependent Behavior of NiTi Shape Memory Alloys for Seismic Applications. J. Intell. Mater. Syst. Struct. 2010, 21, 837–849. [Google Scholar] [CrossRef]
- Huber, N.; Tsakmakis, C. A neural network tool for identifying the material parameters of a finite deformation viscoplasticity model with static recovery. Comput. Methods Appl. Mech. Eng. 2001, 191, 353–384. [Google Scholar] [CrossRef]
- Helm, D. Pseudoelasticity: Experimental observations, thermomechanical modeling, and identification of the material parameters. In Proceedings of the SPIE 5387, Smart Structures and Materials 2004: Active Materials: Behavior and Mechanics, San Diego, CA, USA, 21 July 2004; pp. 198–209. [Google Scholar] [CrossRef]
- Henrickson, J.; Kirkpatrick, K.; Valasek, J. Characterization of Shape Memory Alloys Using Artificial Neural Networks. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013; p. 129. [Google Scholar] [CrossRef][Green Version]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Tanaka, K. A thermomechanical sketch of shape memory effect: One-dimensional tensile behavior. Res. Mech. Int. J. Struct. Mech. Mater. Sci. 1986, 18, 251–263. [Google Scholar]
- Sadjadpour, A.; Bhattacharya, K. A micromechanics inspired constitutive model for shape-memory alloys: The one-dimensional case. Smart Mater. Struct. 2007, 16, 51–62. [Google Scholar] [CrossRef]
- Liang, C. The Constitutive Modeling of Shape Memory Alloys. PhD Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1990. [Google Scholar]
- Sato, Y.; Tanaka, K. Estimation of energy dissipation in alloys due to stress-induced martensitic transformation. Res. Mech. 1988, 23, 381–393. [Google Scholar]
- Liang, C.; Rogers, C.A. One-dimensional thermomechanical constitutive relations for shape memory materials. J. Intell. Mater. Syst. Struct. 1997, 8, 285–302. [Google Scholar] [CrossRef]
- Kaup, A.; Altay, O.; Klinkel, S. Strain amplitude effects on the seismic performance of dampers utilizing shape memory alloy wires. Eng. Struct. 2021, 244, 112708. [Google Scholar] [CrossRef]
- Kato, H. Latent heat storage capacity of NiTi shape memory alloy. J. Mater. Sci. 2021, 56, 8243–8250. [Google Scholar] [CrossRef]
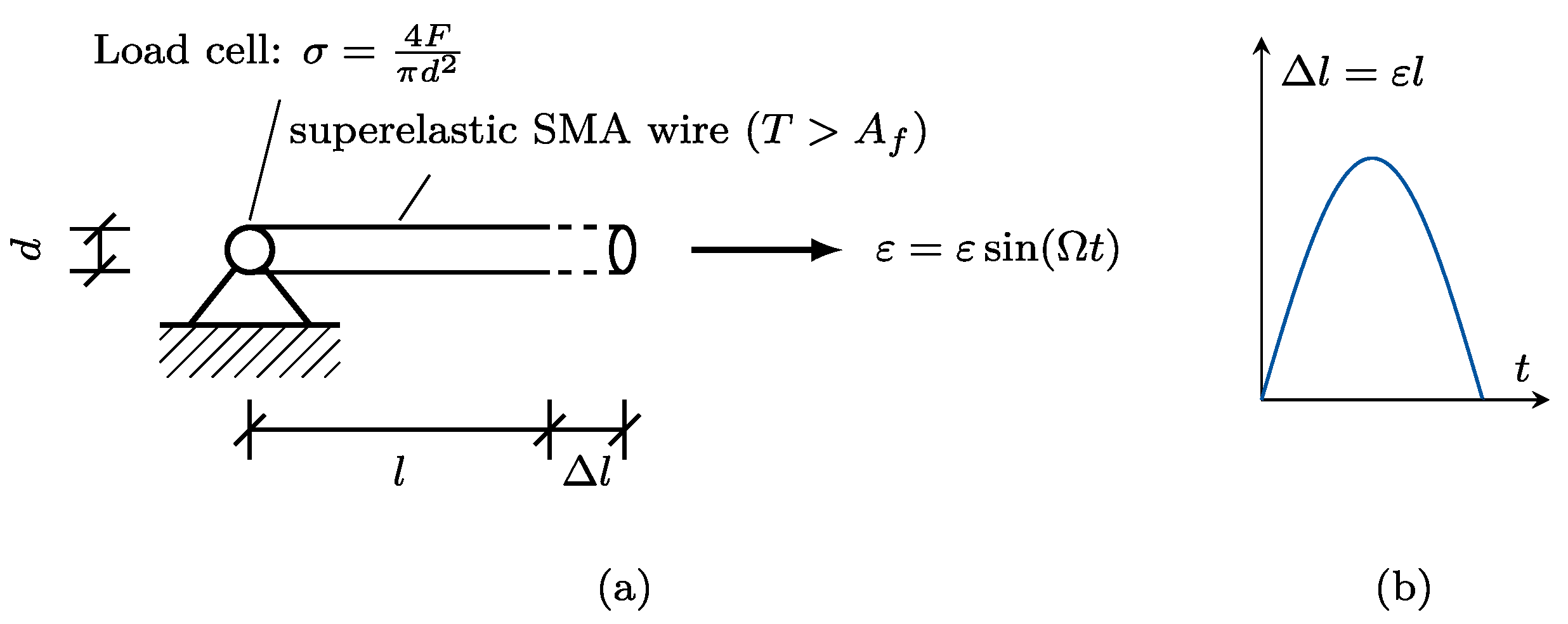
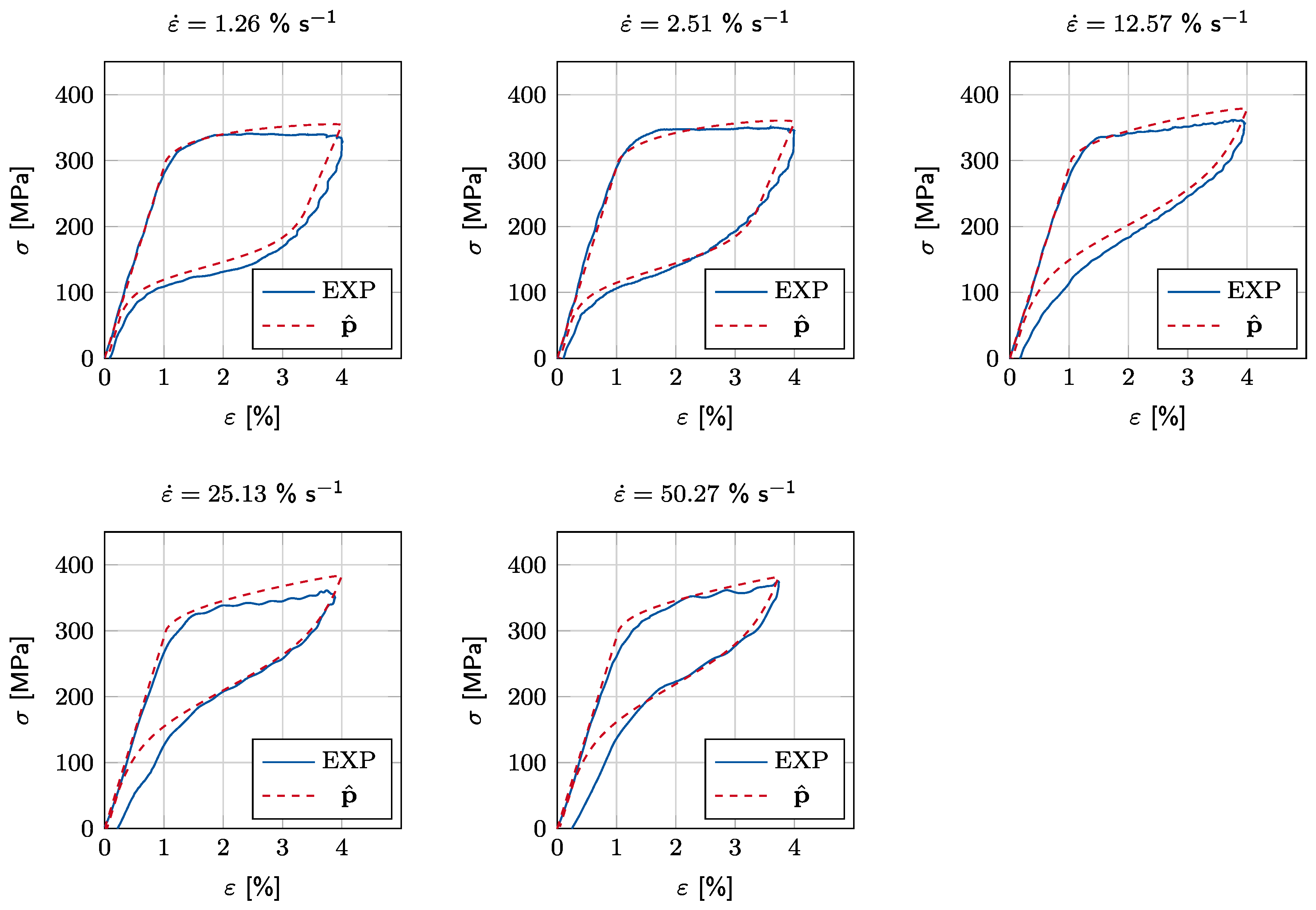
| Parameter | Value | Unit | |
|---|---|---|---|
| Young’s modulus of martensite | 14,100 | MPa | |
| Young’s modulus of austenite | 29,000 | MPa | |
| Critical stress–temperature slope of martensite | MPa K−1 | ||
| Critical stress–temperature slope of austenite | MPa K−1 | ||
| Maximum strain at | - | ||
| Martensite transformation finish temperature | K | ||
| Martensite transformation start temperature | K | ||
| Austenite transformation start temperature | K | ||
| Austenite transformation finish temperature | K | ||
| Ambient temperature | K | ||
| Density | 6500 | kg m−3 | |
| Diameter | d | m | |
| Wire length | l | m |
| Parameter | min | max | Unit | |
|---|---|---|---|---|
| Specific heat | C | 800 | 2000 | J(kgK)−1 |
| Latent heat | L | 400 | 40,000 | J kg−1 |
| Heat-transfer coefficient | k | W K−1 | ||
| Austenite transformation start temperature | K |
| [% s−1] | [%] | [J(kgK) −1] | [J kg−1] | [W K−1] | [K] |
|---|---|---|---|---|---|
| 4 | 1146 | 5404 | |||
| 4 | 1824 | 18,773 | |||
| 4 | 1827 | 18,583 | |||
| 4 | 1888 | 23,278 | |||
| 4 | 1896 | 25,108 | |||
| Final result : | 1716 | 18,229 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenzen, N.; Altay, O. Machine Learning Enhanced Dynamic Response Modelling of Superelastic Shape Memory Alloy Wires. Materials 2022, 15, 304. https://doi.org/10.3390/ma15010304
Lenzen N, Altay O. Machine Learning Enhanced Dynamic Response Modelling of Superelastic Shape Memory Alloy Wires. Materials. 2022; 15(1):304. https://doi.org/10.3390/ma15010304
Chicago/Turabian StyleLenzen, Niklas, and Okyay Altay. 2022. "Machine Learning Enhanced Dynamic Response Modelling of Superelastic Shape Memory Alloy Wires" Materials 15, no. 1: 304. https://doi.org/10.3390/ma15010304
APA StyleLenzen, N., & Altay, O. (2022). Machine Learning Enhanced Dynamic Response Modelling of Superelastic Shape Memory Alloy Wires. Materials, 15(1), 304. https://doi.org/10.3390/ma15010304






