Validation of an Image Analysis Method for Evaluating the Chemical Resistance of Glass Fibers to Alkaline Environments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fibers and Pretreatment Process
2.2. Fiber Resistance and Static Tensile Strength Test
2.3. Fiber Weight and Maximum Breaking Force
2.4. Calculation of the Theoretical Chemical Resistance
2.5. Fiber Surface Observation Using SEM and Image Analysis
2.6. Statistical Analysis
3. Results and Discussion
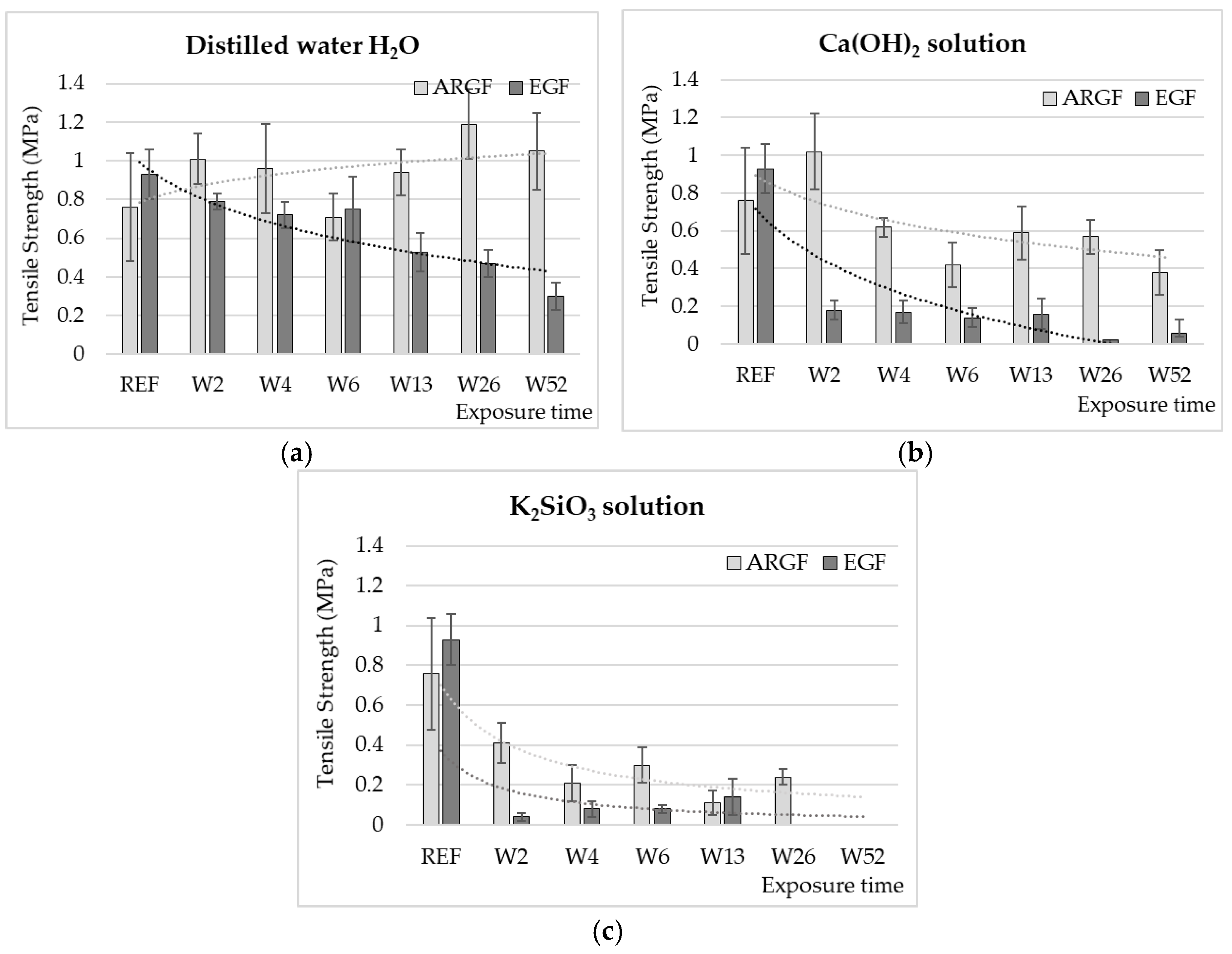
3.1. Tensile Strength
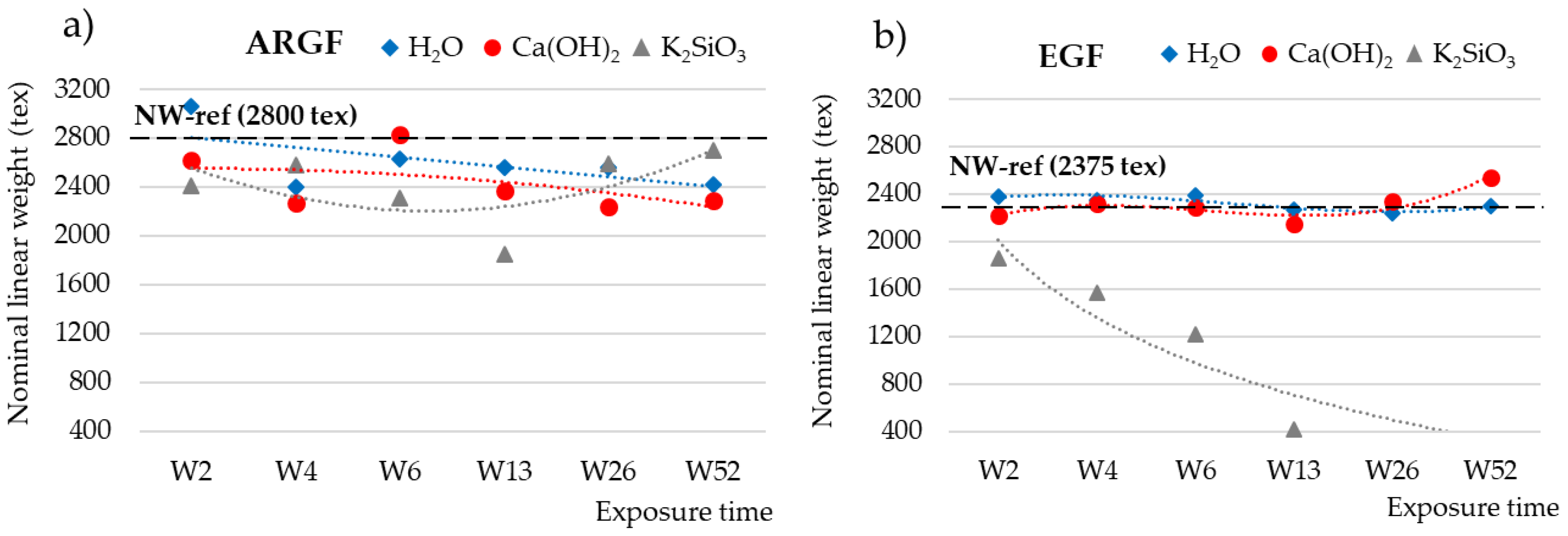
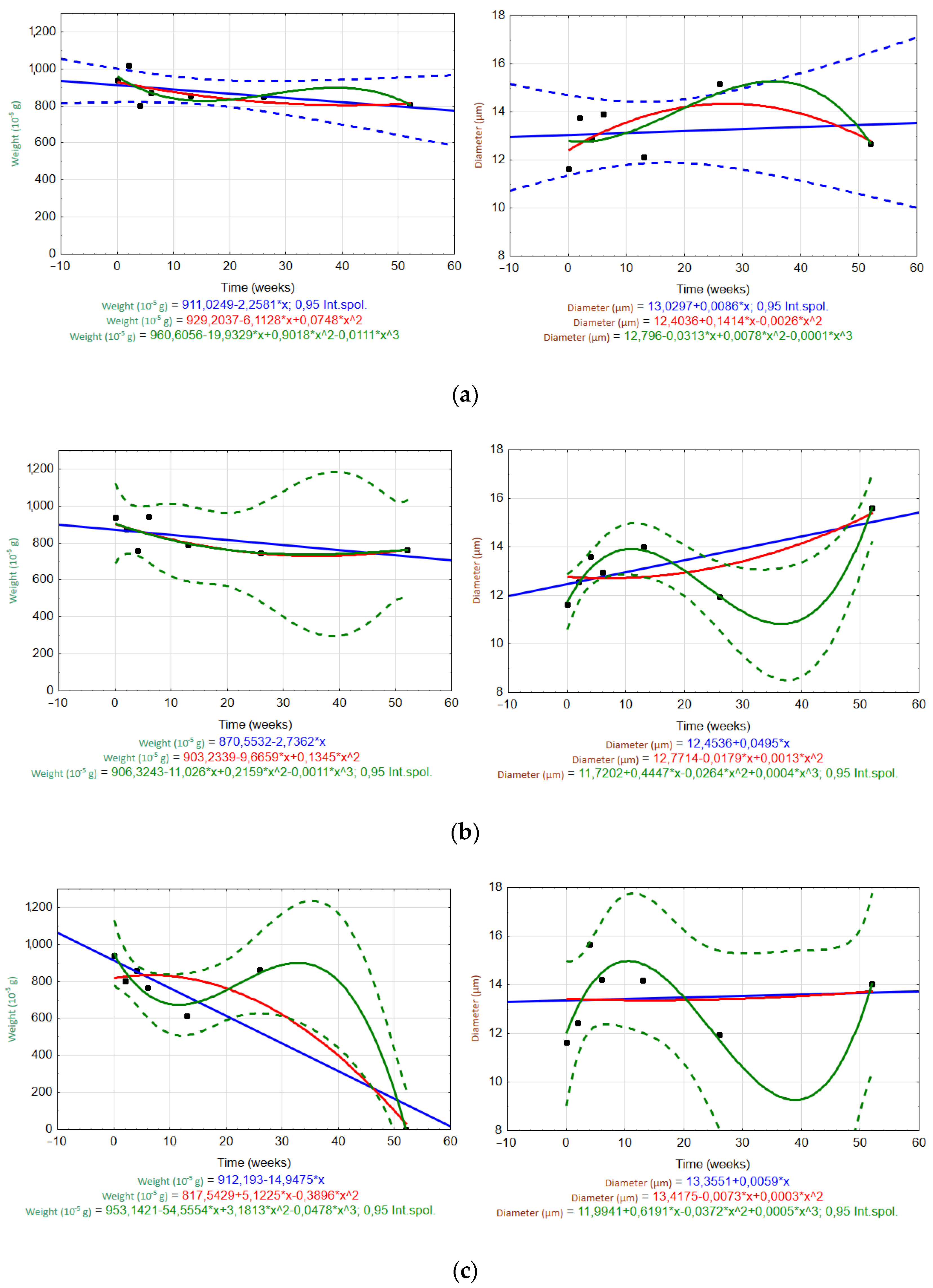
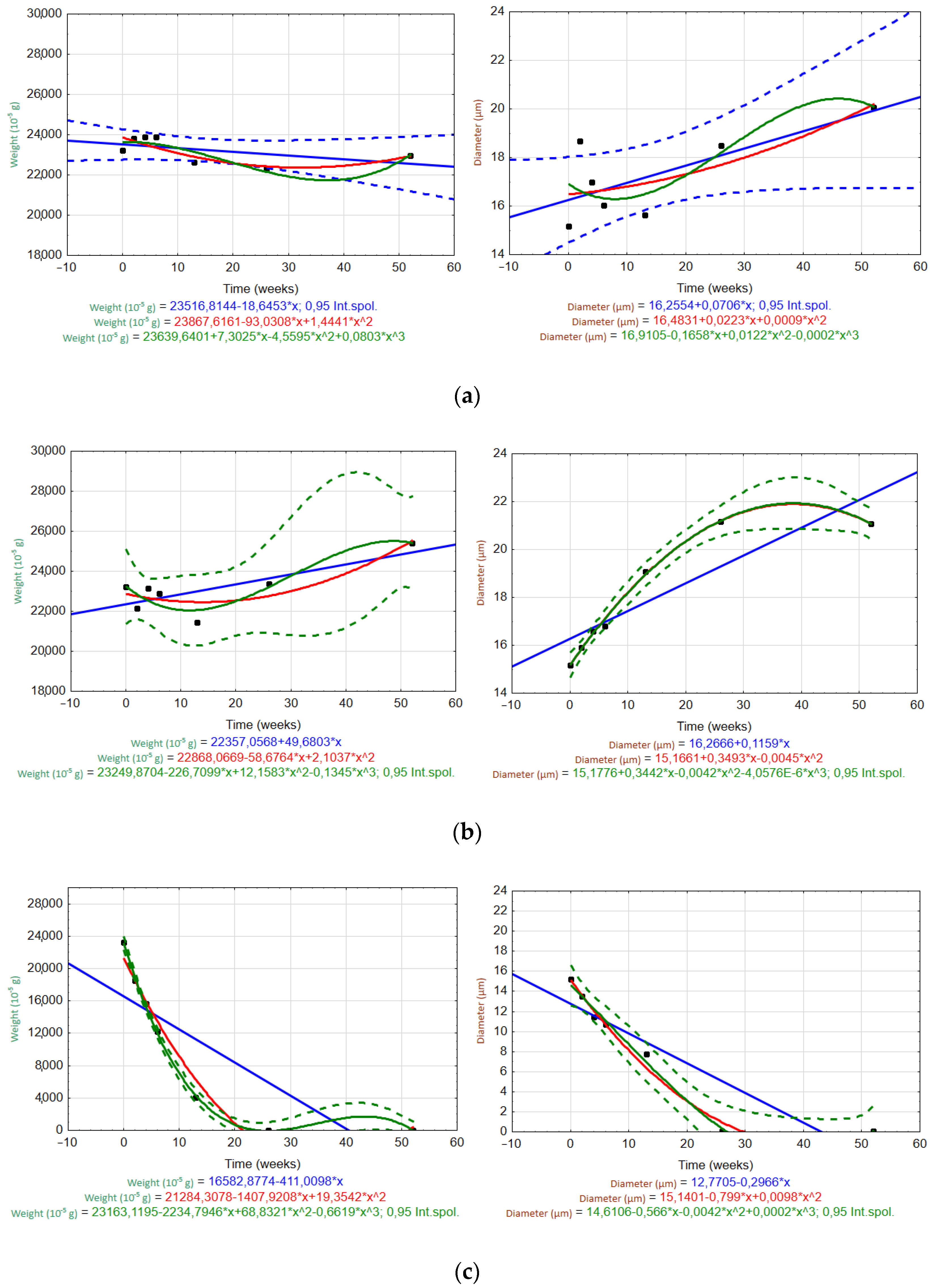
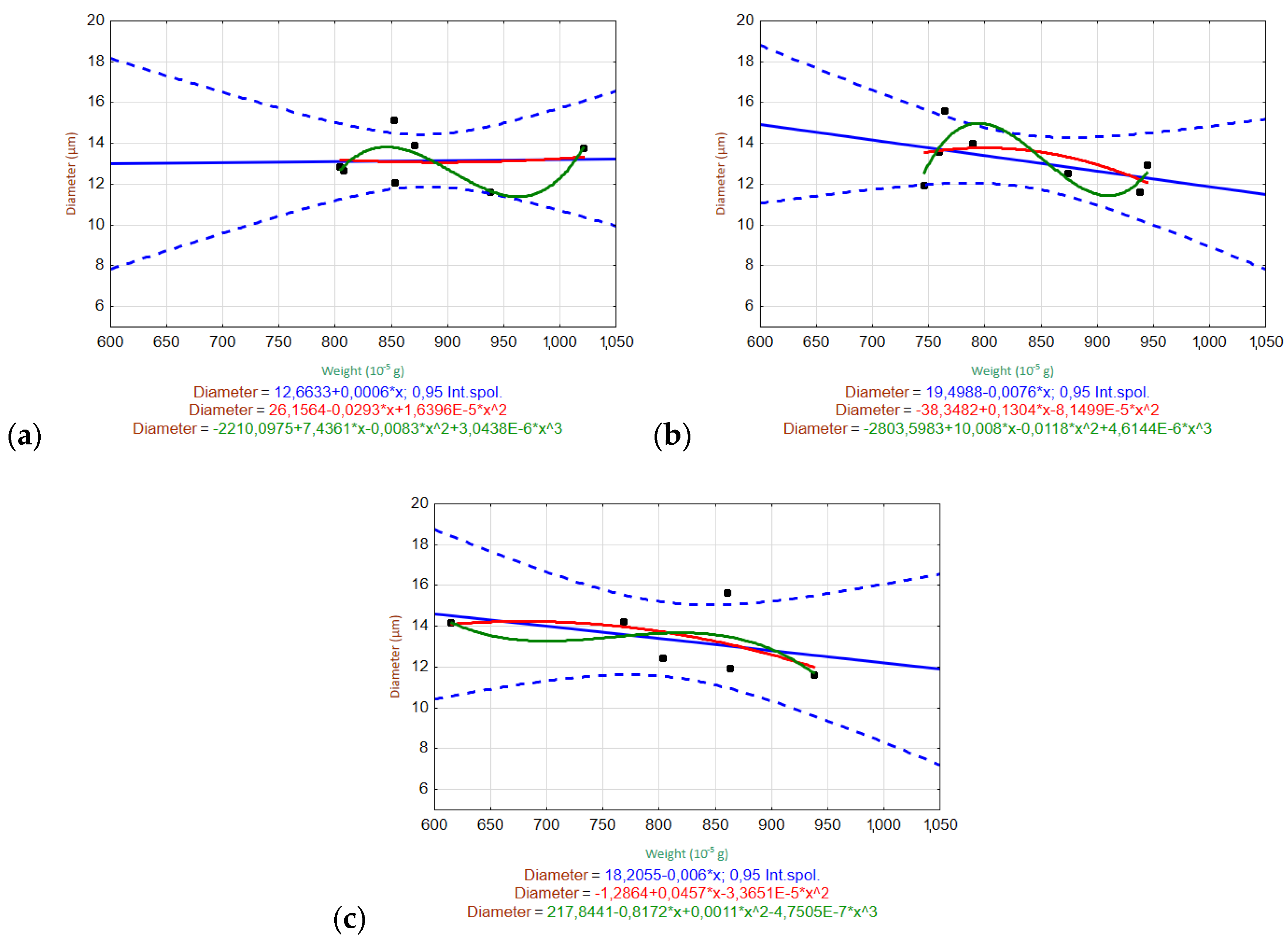
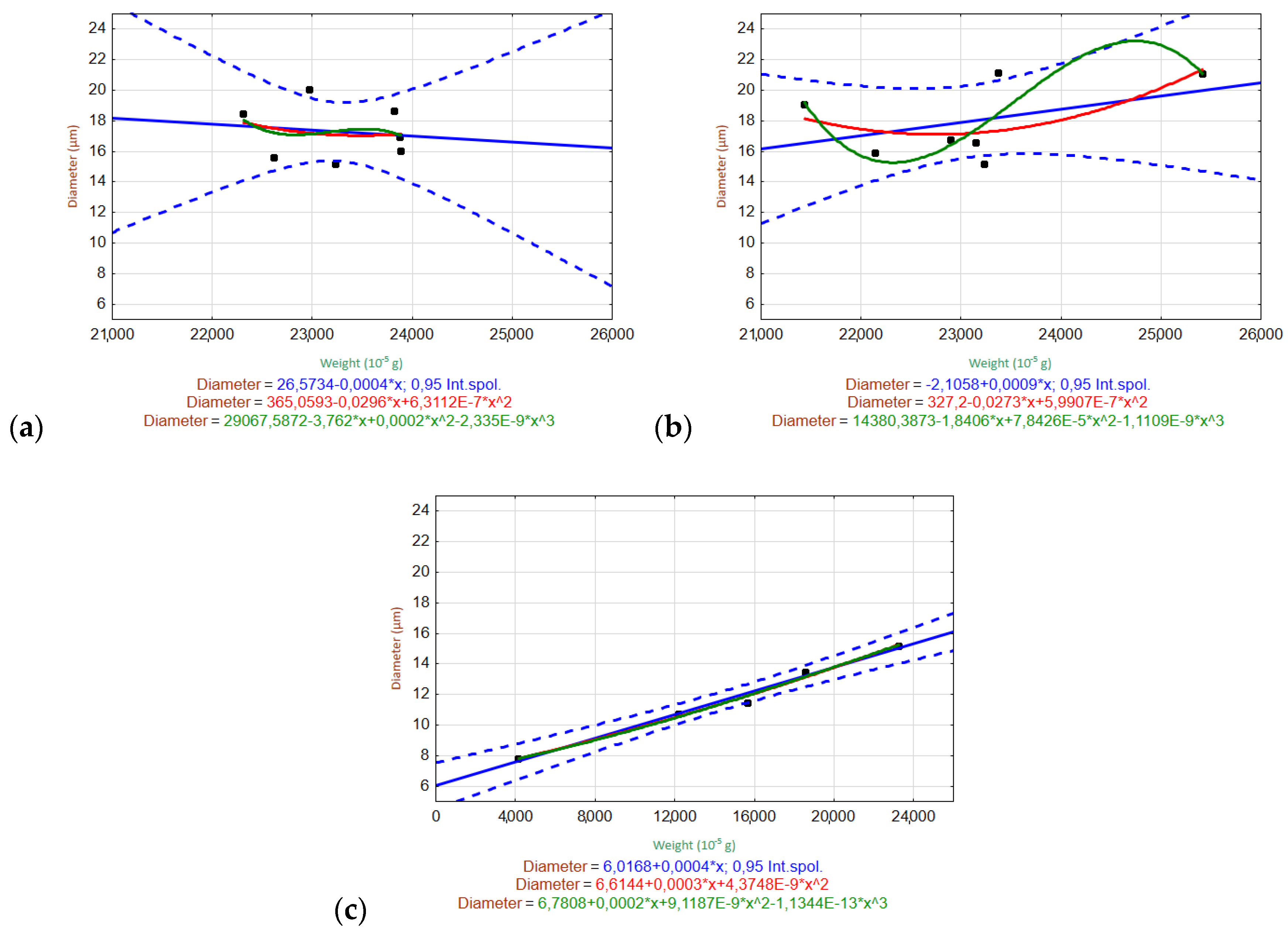
3.2. Weight Loss and Nominal Weight
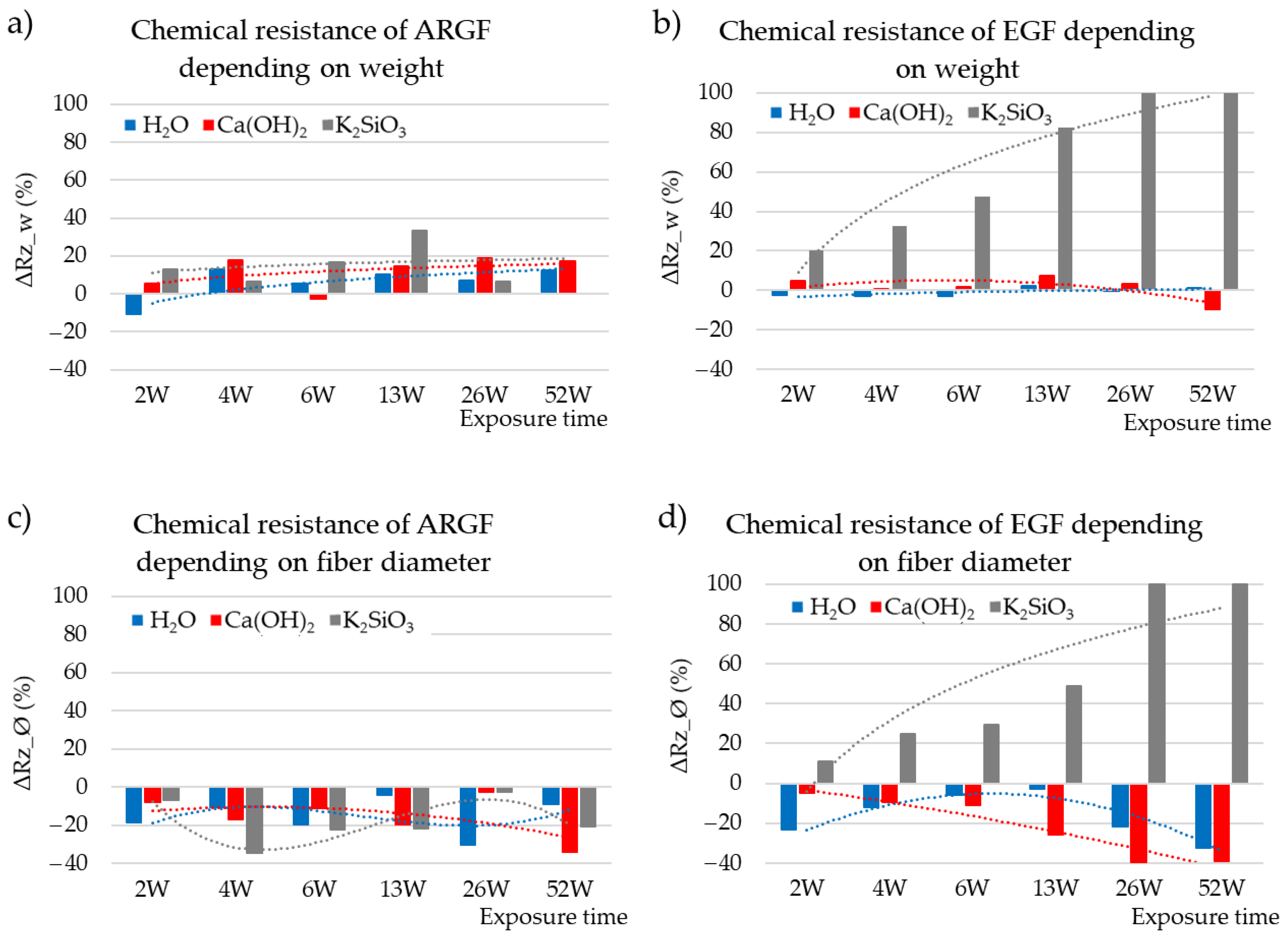
3.3. Chemical Resistance
3.4. SEM Analysis
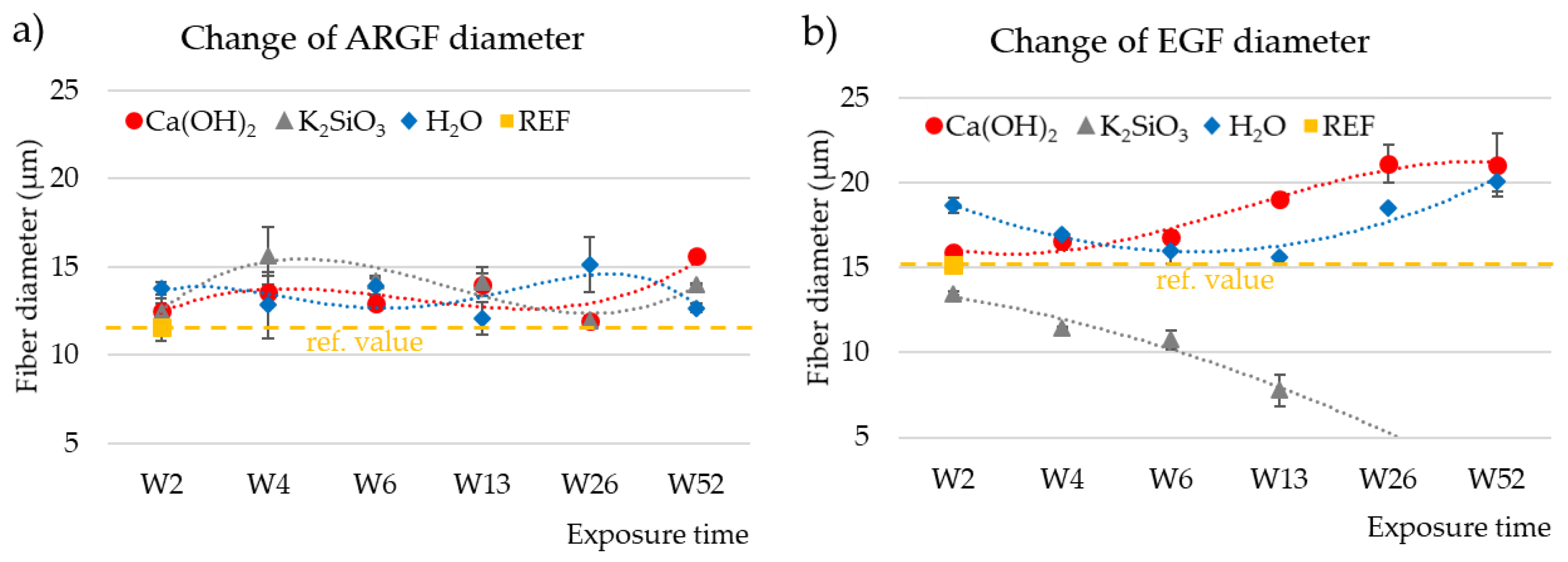
3.5. Determination of Fiber Diameter by Image Analysis
3.6. Statistical Analysis
3.6.1. Trends or Patterns over Time
3.6.2. Relationships of Variables
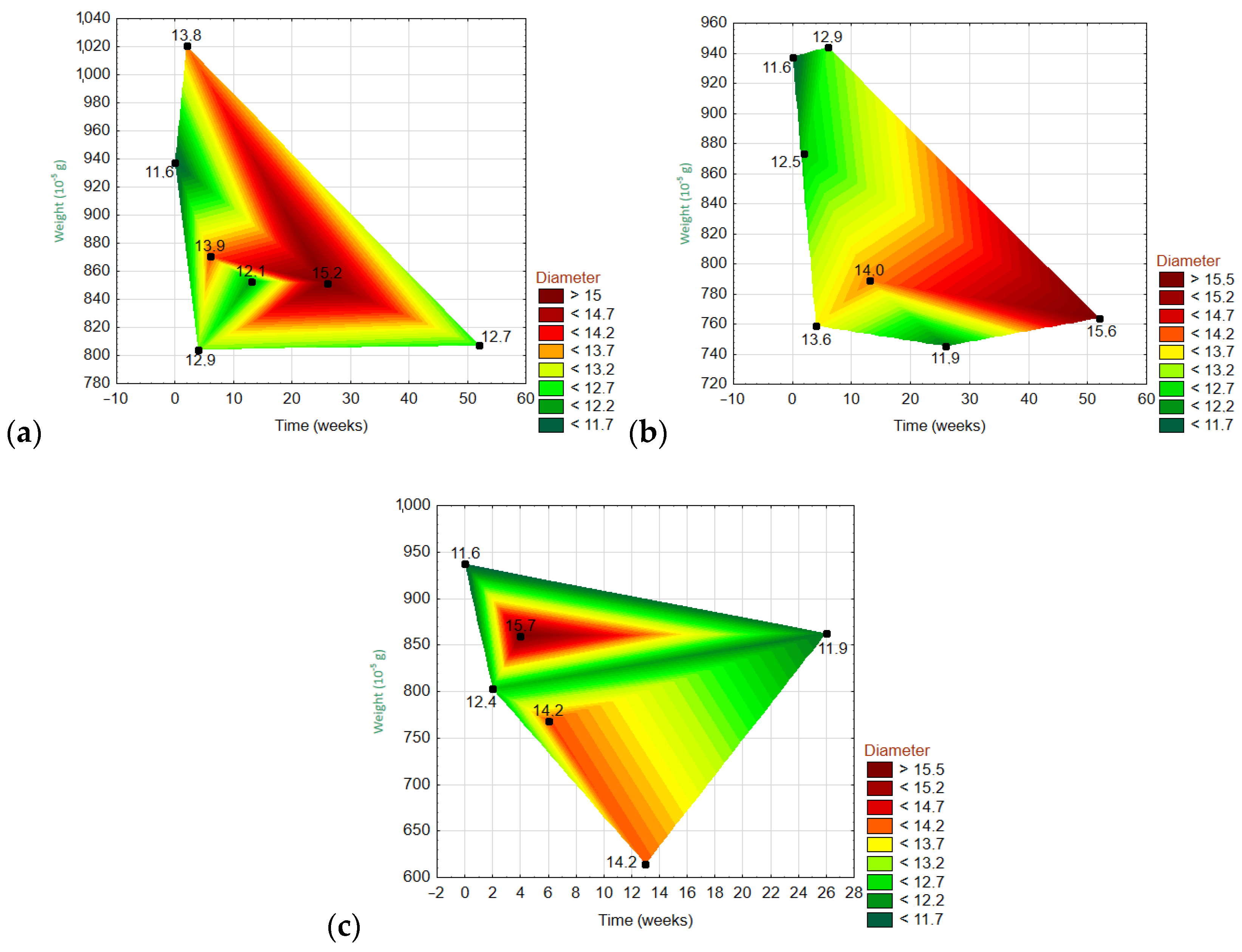
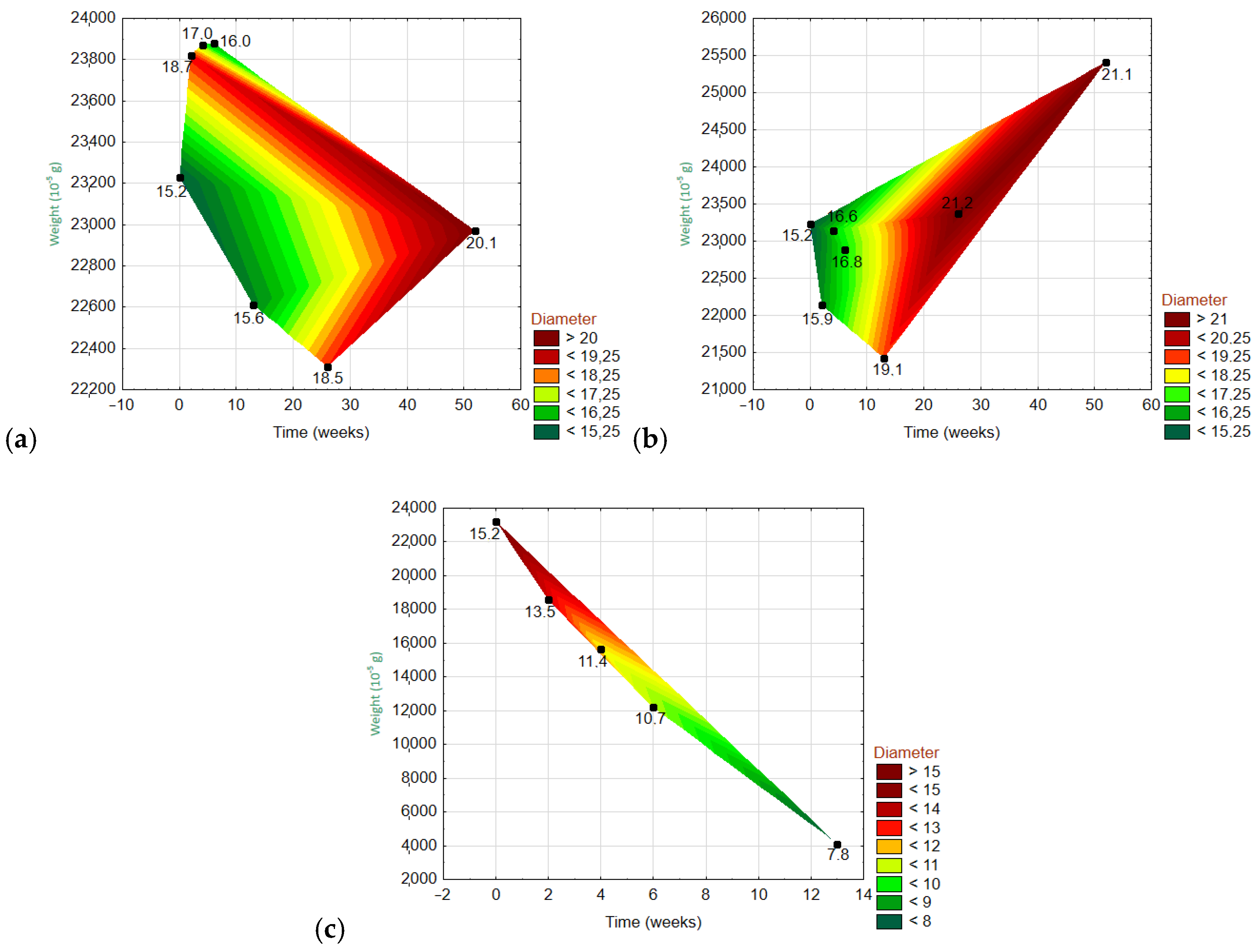
3.6.3. Dependencies of Three Variables
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arabi, N.; Molez, L.; Rangeard, D. Durability of Alkali-Resistant Glass Fibers Reinforced Cement Composite. Microstructural Observations of Degradation. Period. Polytech. Civ. Eng. 2018, 63, 10631. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, V.T. Chemical attack on alkali-resistant glass fibres in a hydrating cement matrix. J. Non-Cryst. Solids 1992, 151, 236–244. [Google Scholar] [CrossRef]
- Ehrenstein, G.W.; Theriault, R.P. Polymeric Materials Structure, Properties, Applications; Scientia: Munich, Germany, 2001. [Google Scholar]
- Scheffler, C.; Gao, S.I.; Plonka, R.; Mäder, E.; Hempel, S.; Butler, M.; Mechtcherine, V. Interphase modification of alkali-resistant glass fibres and carbon fibres for textile reinforced concrete II. Water adsorption and composite interphases. Compos. Sci. Technol. 2009, 69, 905–912. [Google Scholar] [CrossRef]
- Dwight, D.W. Glass Fiber Reinforcements. In Comprehensive Composite Materials; Pergamon: Oxford, UK, 2000; pp. 231–261. [Google Scholar]
- Kimura, I.; Yoshimura, T. Alkali Resistant Glass Fibers. U.S. Patent US3861927A, 31 January 1975. [Google Scholar]
- Scheffler, C.; Förster, T.; Mäder, E.; Heinrich, G.; Hempel, S.; Mechtcherine, V. Aging of alkali-resistant glass and basalt fibers in alkaline solutions: Evaluation of the failure stress by Weibull distribution function. J. Non-Cryst. Solids 2009, 355, 2588–2595. [Google Scholar] [CrossRef]
- Bin, W.; Hailin, C.; Shenhua, S. Tensile behavior contrast of basalt and glass fibers after chemical treatment. Mater. Des. 2010, 31, 4244–4250. [Google Scholar] [CrossRef]
- Cousin, P.; Hassan, M.; Vijay, P.V.; Robert, M.; Benmokrane, B. Chemical resistance of carbon, basalt, and glass fibers used in FRP reinforcing bars. J. Compos. Mater. 2019, 53, 3651–3670. [Google Scholar] [CrossRef]
- Gang, W.; Xin, W.; Zhishen, W.; Zhiqiang, D.; Guangchao, Z. Durability of basalt fibers and composites in corrosive environments. J. Compos. Mater. 2014, 49, 873–887. [Google Scholar] [CrossRef]
- Chunhong, T.; Hao, J.; Xu, Z.; Guangyao, L.; Junjia, C. Corrosion Behavior and Mechanism of Basalt Fibers in Sodium Hydroxide Solution. Materials 2018, 11, 1381. [Google Scholar] [CrossRef] [Green Version]
- Ying, S.; Zhou, X. Chemical and Thermal Resistance of Basalt Fiber in Inclement Environments. J. Wuhan Univ. Technol. Sci. Ed. 2013, 28, 560–565. [Google Scholar] [CrossRef]
- Zinck, P.; Mäder, E.; Gerard, J.F. Role of silane coupling agent and polymeric film former for tailoring glass fiber sizings. J. Mater. Sci. 2001, 36, 5245–5252. [Google Scholar] [CrossRef]
- Gao, S.L.; Mäder, E. Environmental resistance and mechanical performance of alkali-resistant glass fibers with surface sizings. J. Non-Cryst. Solids 2003, 325, 230–241. [Google Scholar] [CrossRef]
- Ghugal, Y.; Deshmukh, B. Performance of Alkali-resistant Glass Fiber Reinforced Concrete. J. Reinf. Plast. Compos. 2005, 25, 617–630. [Google Scholar] [CrossRef]
- David, R. Alkali-Resistant Glass Fibres. U.S. Patent US4330628A, 18 May 1982. [Google Scholar]
- Scheffler, C.; Gao, S.I.; Plonka, R.; Mäder, E.; Hempel, S.; Butler, M.; Mechtcherine, V. Interphase modification of alkali-resistant glass fibres and carbon fibres for textile reinforced concrete I. Fibre properties and durability. Compos. Sci. Technol. 2009, 69, 531–538. [Google Scholar] [CrossRef]
- Kopecskó, K. Durability of Glass Fibres. In Proceedings of the 6th International RILEM Symposium on Fibre-Reinforced Concrete (FRC), Varenna, Italy, 20–22 September 2004. [Google Scholar]
- Bentur, A.; Diamond, S. Aging and microstructure of glass fiber cement composites. Durab. Build. Mater. 1987, 4, 201–226. [Google Scholar]
- Shah, S.P.; Ludirdja, D.; Daniel, J.I.; Mobasher, B. Toughness durability of glass fiber reinforcement concrete system. ACI Mater. J. 1988, 85, 352–360. [Google Scholar]
- Förster, T.; Scheffler, C.; Mäder, E.; Heinrich, G.; Jesson, D.A.; Watts, J.F. Dissolution behaviour of model basalt fibres studied by surface analysis methods. Appl. Surf. Sci. 2014, 322, 78–84. [Google Scholar] [CrossRef]
- ISO 695 ISO 695:1991; Glass—Resistance to Attack by a Boiling Aqueous Solution of Mixed Alkali—Method of Test and Classification. Publication date: 1991-05 (Previously: ISO 695:1984); ISO Standards Catalogue: Geneva, Switzerland, 1991.
- ISO 11566:1996; Carbon Fibre—Determination of the Tensile Properties of Single-Filament Specimens. Publication Date: 1996-08; ISO Standards Catalogue: Geneva, Switzerland, 1996.
- EN ISO 13934-1:2013; Textiles—Tensile Properties of Fabrics—Part 1: Determination of Maximum Force and Elongation at Maximum Force Using the Strip Method. Publication date: 2013-04 (Previously: ISO 13934-1:1999); ISO Standards Catalogue: Geneva, Switzerland, 2013.
- Militký, J.; Kovačič, L. Chemical Degradation of Basalt Fibers. Textile Indus. Technol. 2009, 3C, 55–59. [Google Scholar]
- Ryvolová, M.; Svobodová, L.; Bakalova, T.; Voleský, L. Influence of Basic Environment of Geopolymer Composites on Degradation Rates of E and AR Type Glass Fibers. Manuf. Technol. 2021, 21, 247–254. [Google Scholar] [CrossRef]
- Havlíček, K.; Svobodová, L.; Bakalova, T.; Lederer, T. Influence of electrospinning methods on characteristics of polyvinyl butyral and polyurethane nanofibres essential for biological applications. Mater. Des. 2020, 194, 108898. [Google Scholar] [CrossRef]
- Mäder, E.; Plonka, R.; Schiekel, M.; Hempel, R. Concrete Coatings on Alkali-Resistant Glass Fibres for the Improvement of Concrete. J. Ind. Text. 2004, 33, 191–207. [Google Scholar] [CrossRef]
- Oka, Y.; Ricker, S.; Tomozawa, M. Calcium deposition on glass surface as an inhibitor to alkaline attack. J. Am. Ceram. Soc. 1979, 62, 631–632. [Google Scholar] [CrossRef]
- Li, Z.; Xiao, T.; Pan, Q.; Cheng, J.; Zhao, S. Corrosion behaviour and mechanism of basalt fibres in acidic and alkaline environments. Corros. Sci. 2016, 110, 15–22. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryvolová, M.; Svobodová, L.; Bakalova, T. Validation of an Image Analysis Method for Evaluating the Chemical Resistance of Glass Fibers to Alkaline Environments. Materials 2022, 15, 161. https://doi.org/10.3390/ma15010161
Ryvolová M, Svobodová L, Bakalova T. Validation of an Image Analysis Method for Evaluating the Chemical Resistance of Glass Fibers to Alkaline Environments. Materials. 2022; 15(1):161. https://doi.org/10.3390/ma15010161
Chicago/Turabian StyleRyvolová, Martina, Lucie Svobodová, and Totka Bakalova. 2022. "Validation of an Image Analysis Method for Evaluating the Chemical Resistance of Glass Fibers to Alkaline Environments" Materials 15, no. 1: 161. https://doi.org/10.3390/ma15010161
APA StyleRyvolová, M., Svobodová, L., & Bakalova, T. (2022). Validation of an Image Analysis Method for Evaluating the Chemical Resistance of Glass Fibers to Alkaline Environments. Materials, 15(1), 161. https://doi.org/10.3390/ma15010161






