Simulations of the Behaviour of Steel Ferromagnetic Fibres Commonly Used in Concrete in a Magnetic Field
Abstract
:1. Introduction
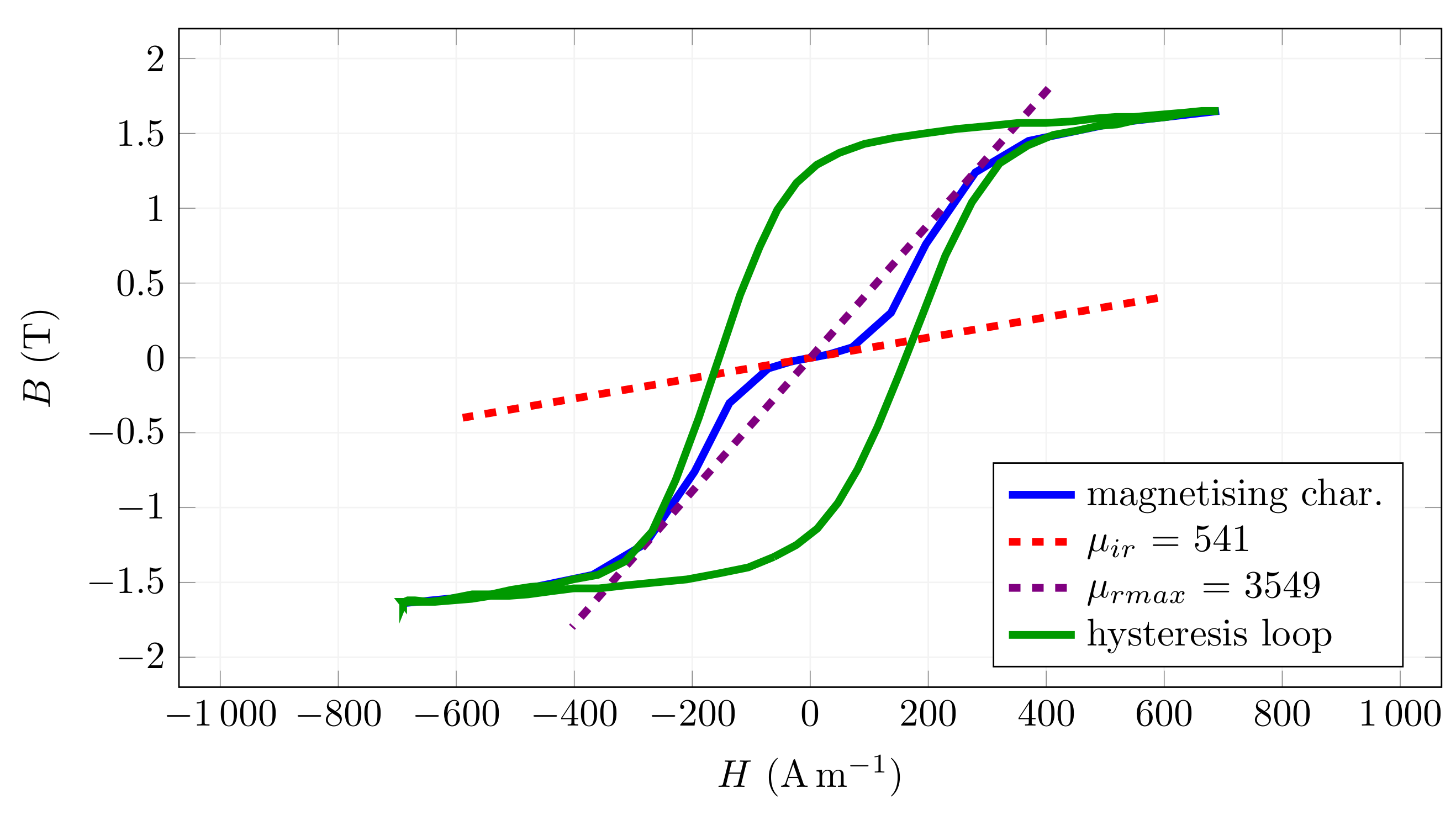
2. Materials and Methods
3. Results and Discussion
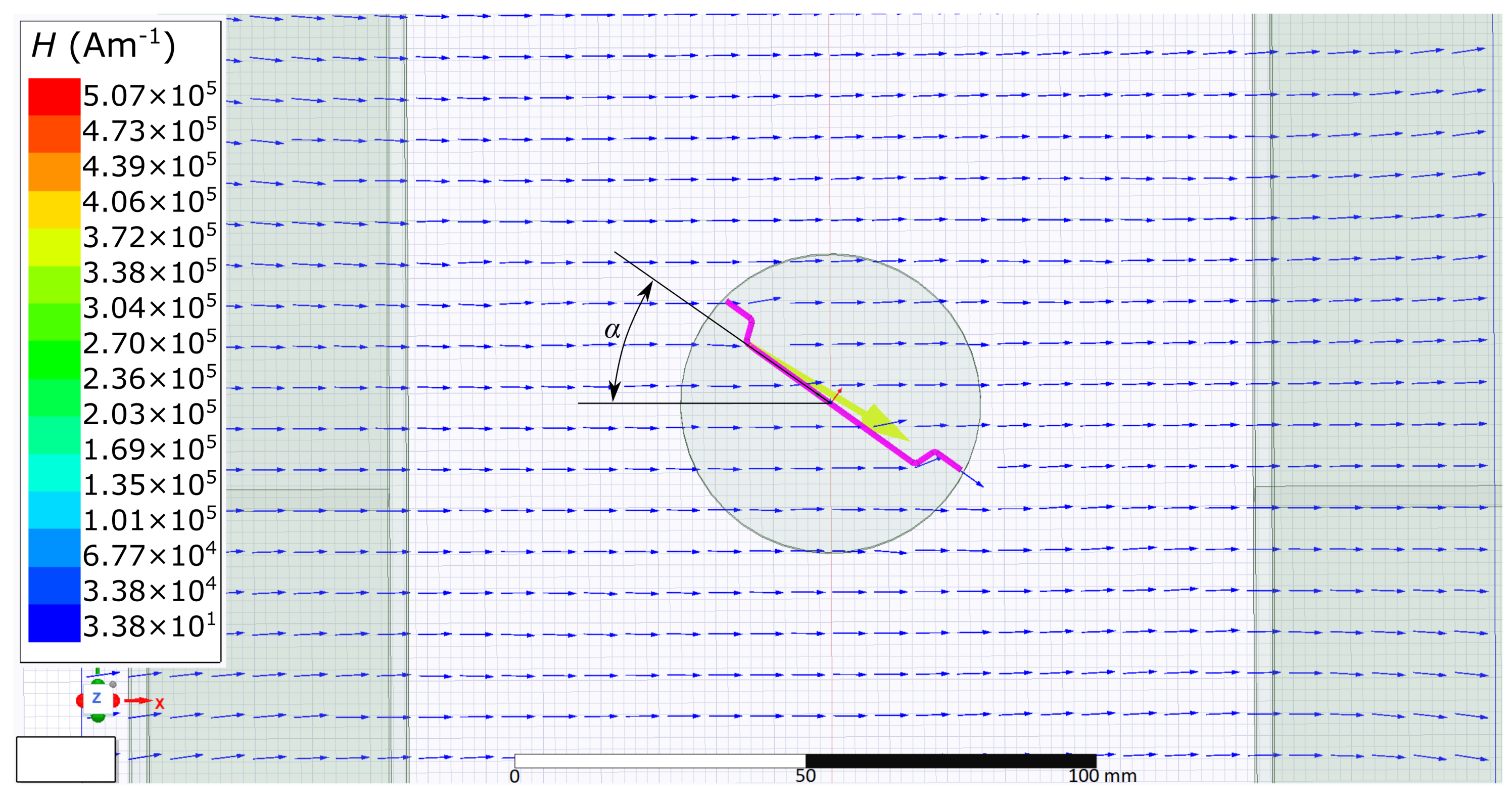
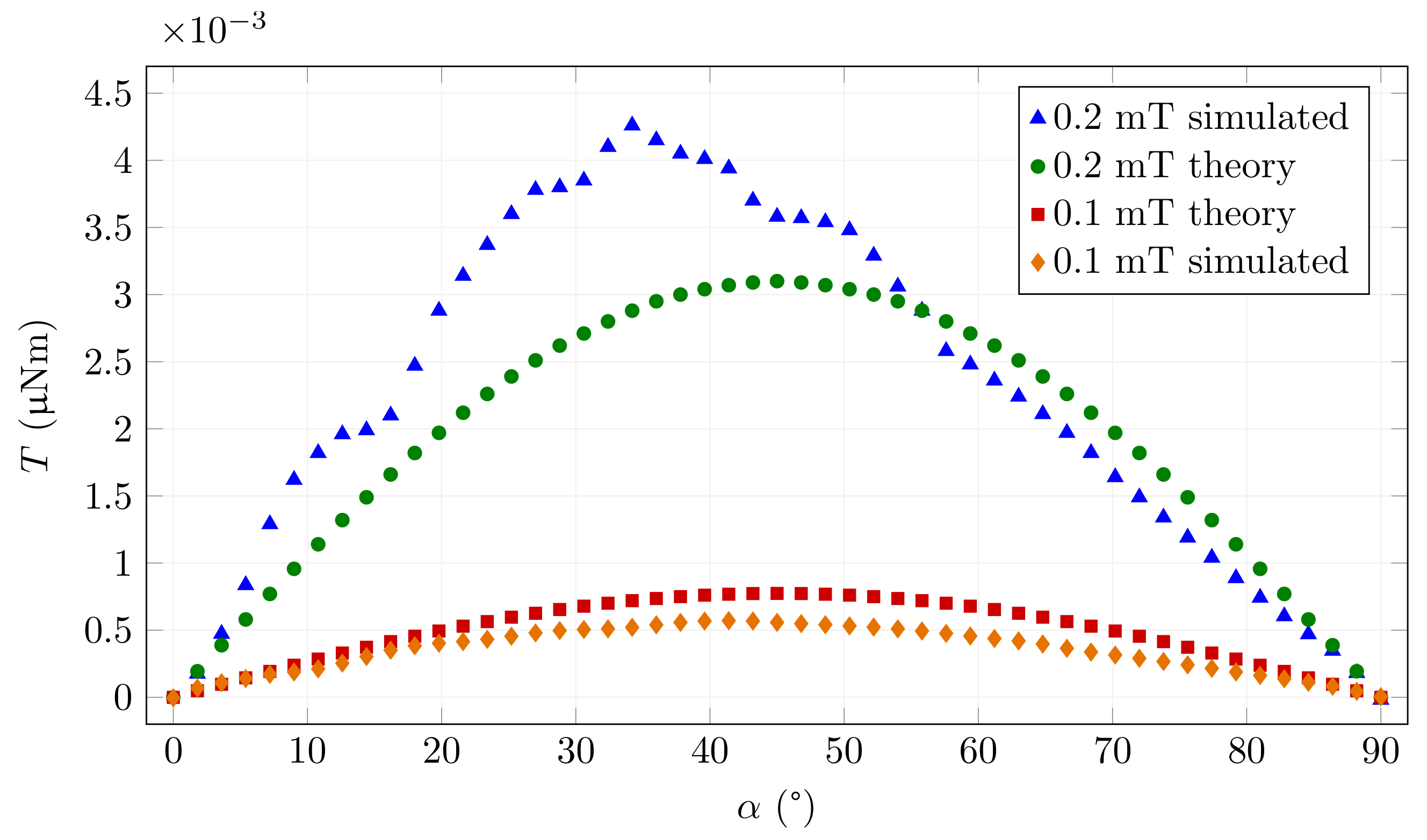
3.1. Simulation of Weak Magnetic Field
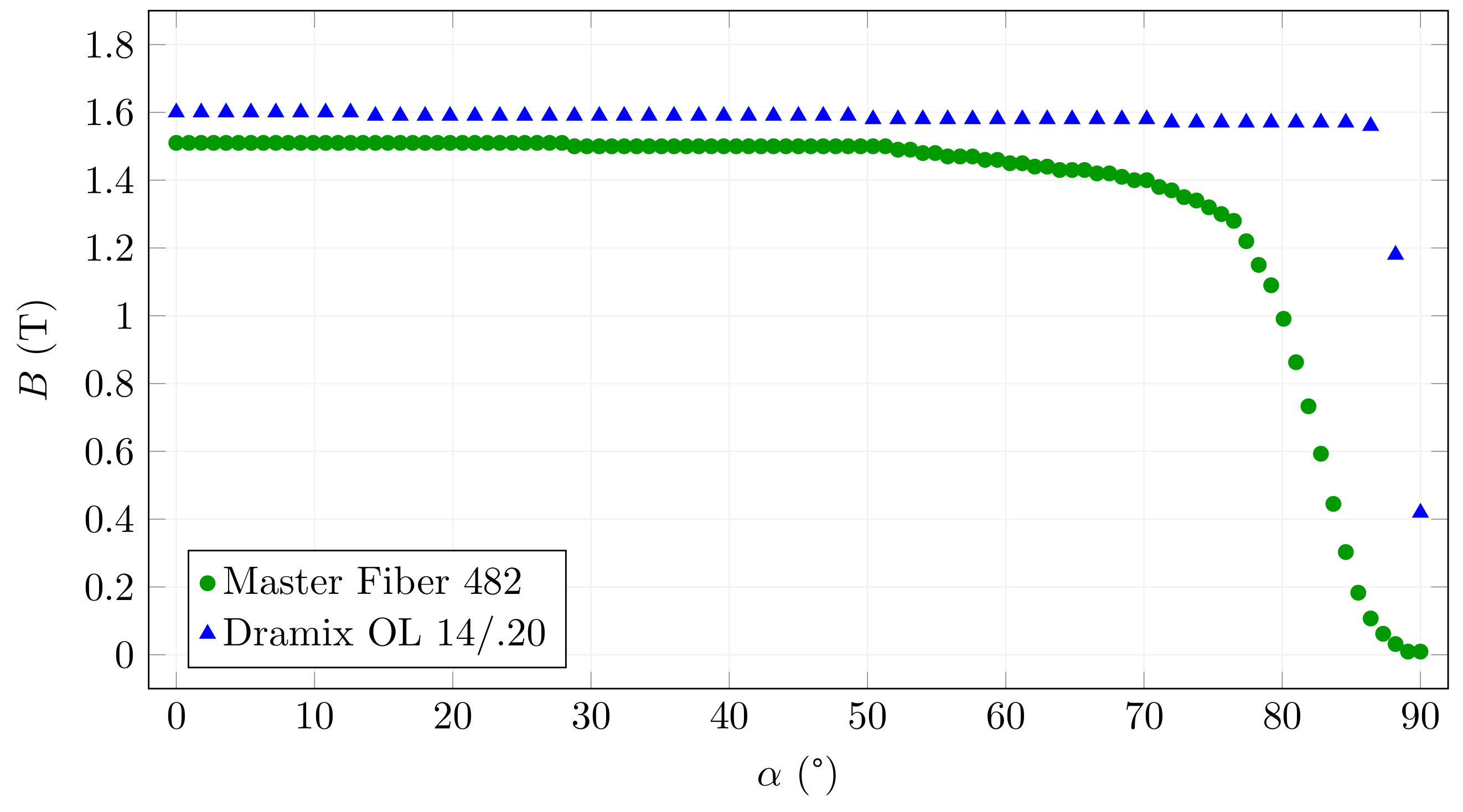
3.2. Simulation of Magnetically Saturated Fibres
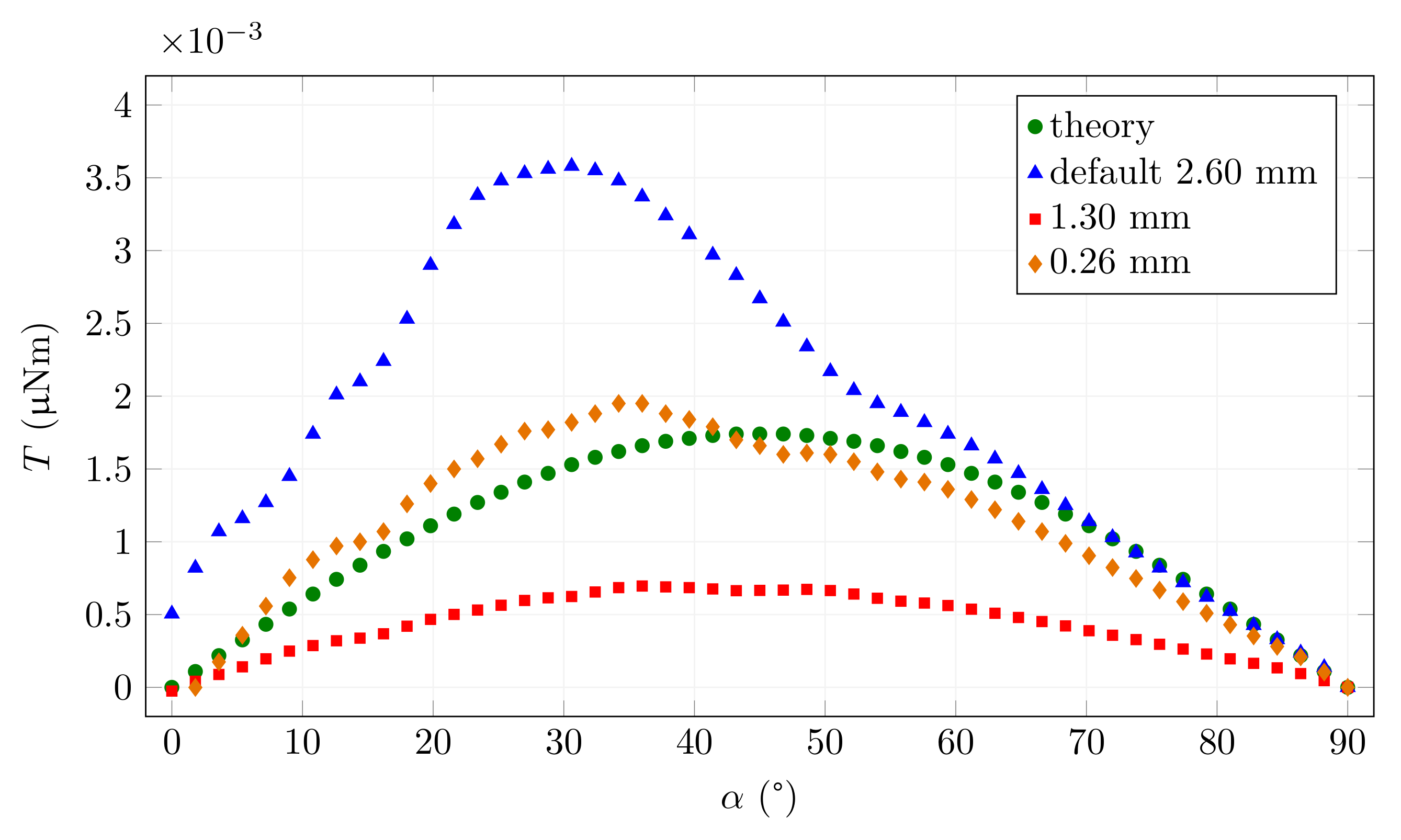
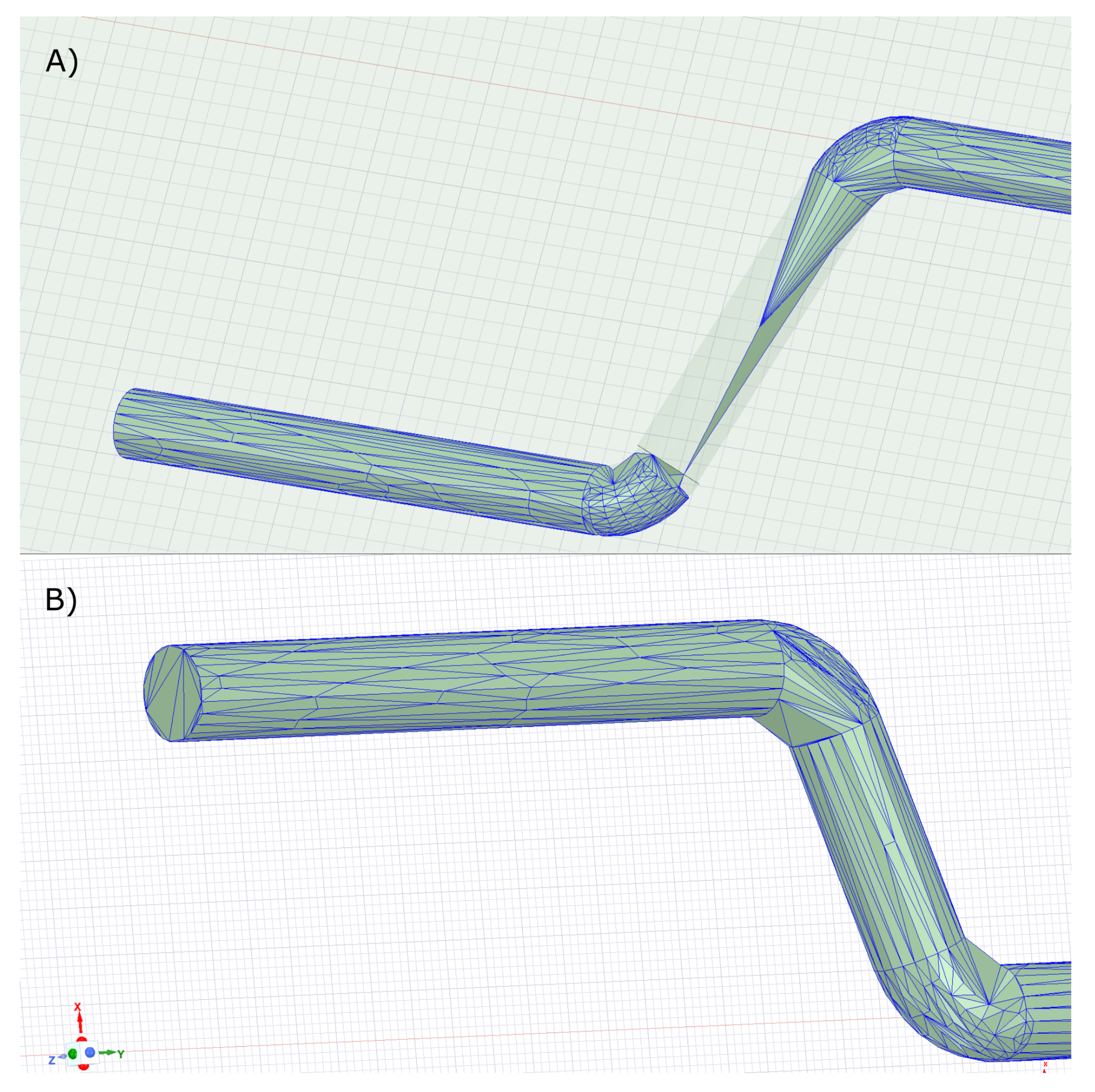
3.3. The Effect of Computational Mesh Size
3.4. The Results of Commonly Used Fibres
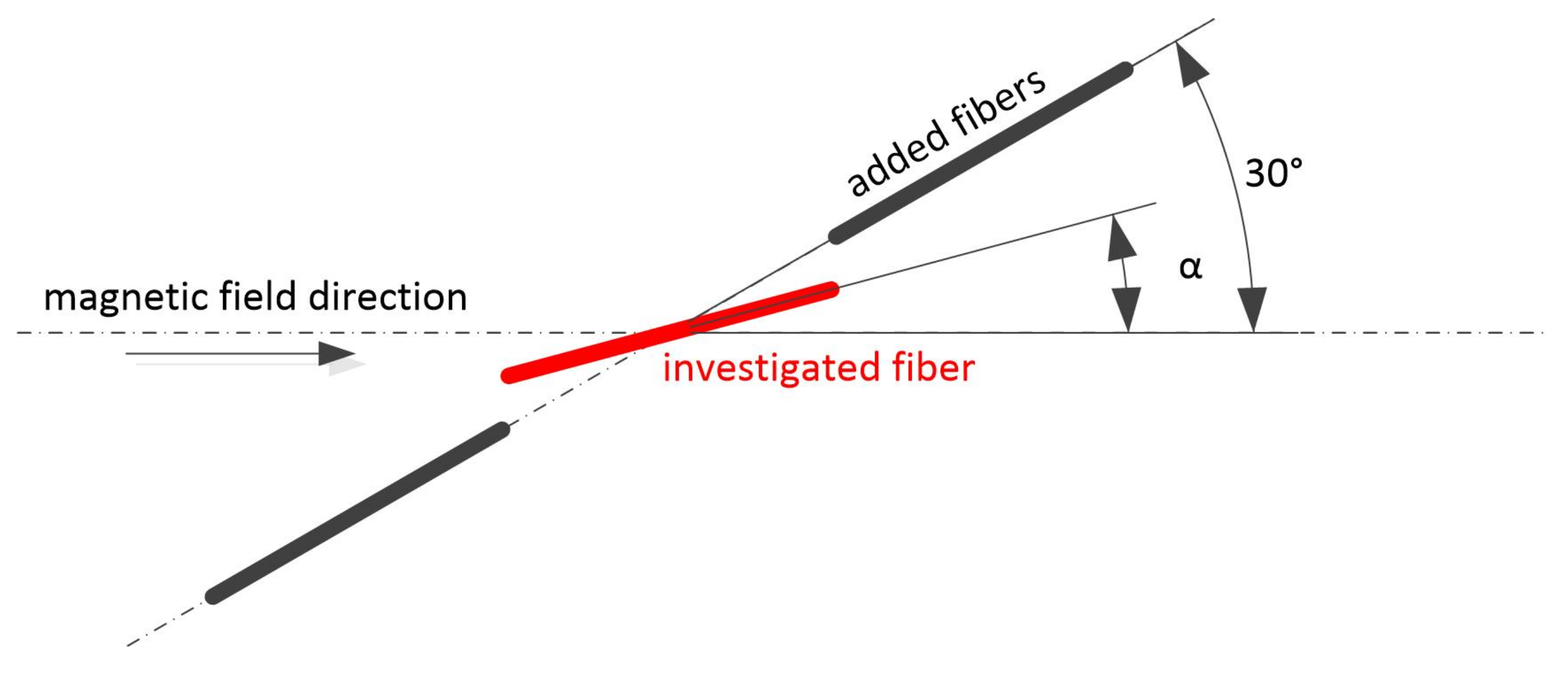
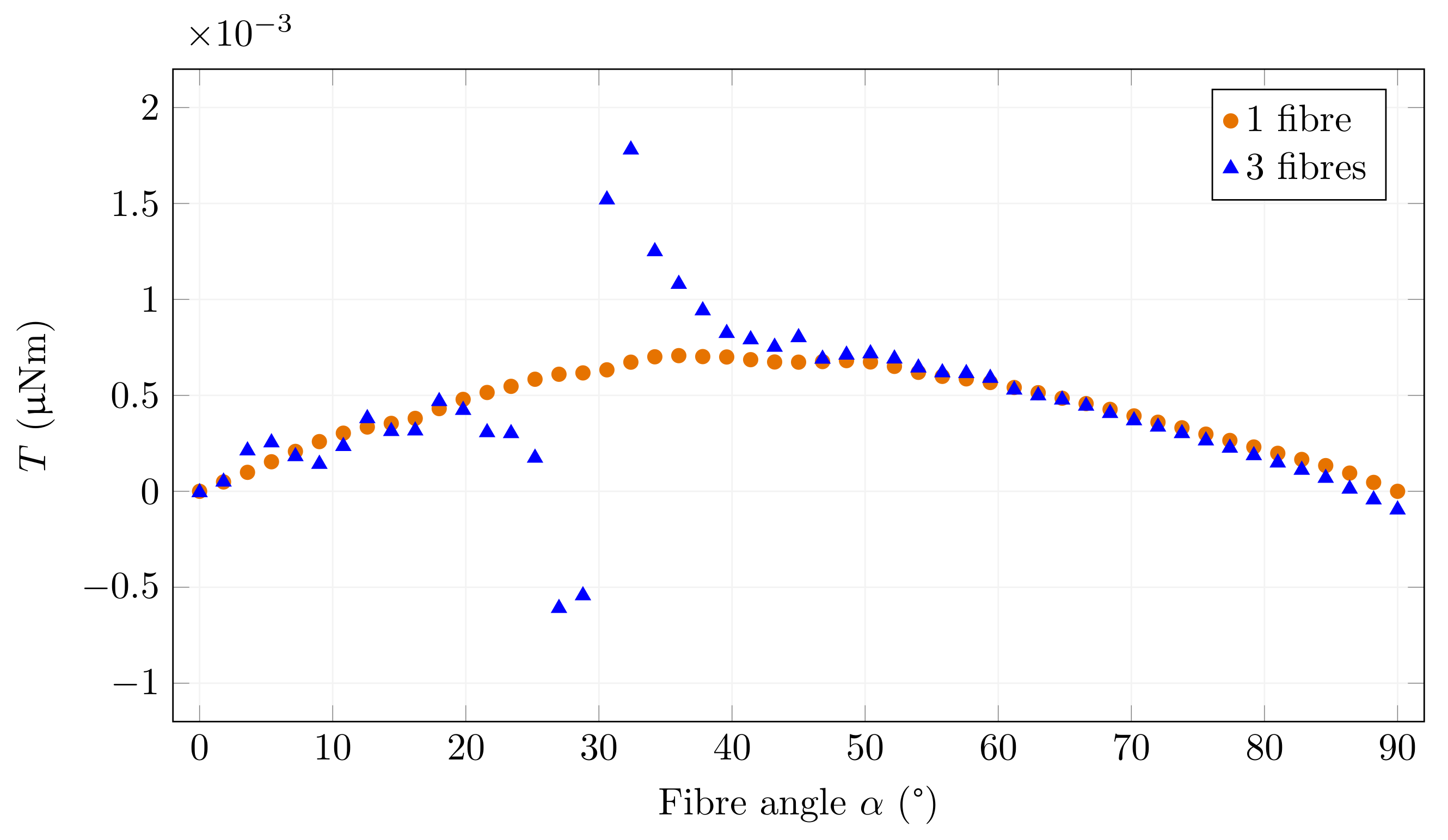
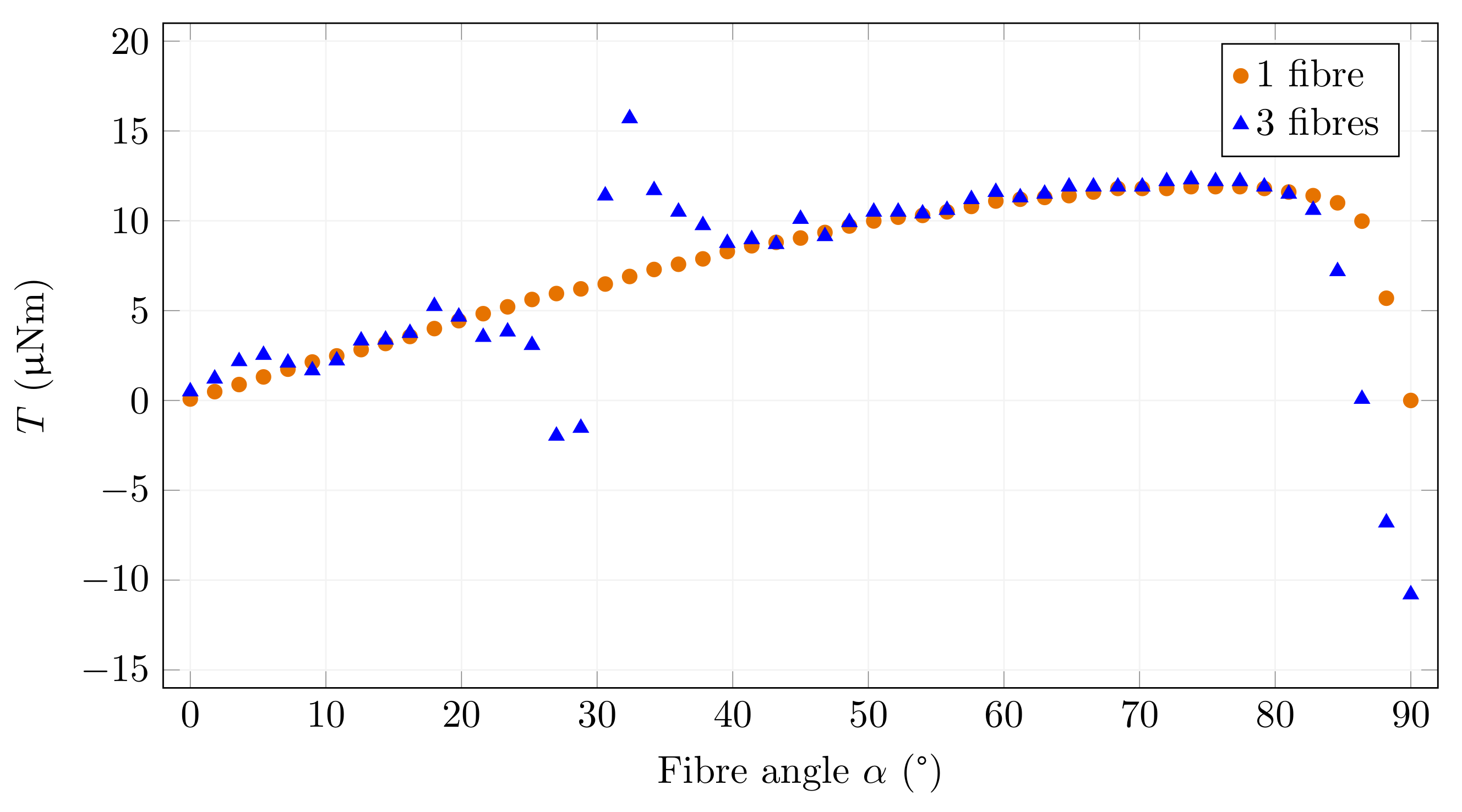
3.5. Examples of Fibre Interaction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bentur, A.; Mindess, S. Fibre Reinforced Cementitious Composites; CRC Press: Boca Raton, FL, USA, 2019; p. 624. [Google Scholar]
- Serna, P.; Llano-Torre, A.; Martí-Vargas, J.R.; Navarro-Gregori, J. Fibre Reinforced Concrete: Improvements and Innovations, 1st ed.; Springer: Cham, Switzerland, 2021; p. 2021. [Google Scholar]
- Yoo, D.Y.; Banthia, N. Mechanical and structural behaviors of ultra-high-performance fiber-reinforced concrete subjected to impact and blast. Constr. Build. Mater. 2017, 149, 416–431. [Google Scholar] [CrossRef]
- Wei, J.; Li, J.; Wu, C.; Liu, Z.-X.; Li, J. Hybrid fibre reinforced ultra-high performance concrete beams under static and impact loads. Eng. Struct. 2021, 245, 112921. [Google Scholar] [CrossRef]
- Vivas, J.; Zerbino, R.; Torrijos, M.; Giaccio, G. Effect of the fibre type on concrete impact resistance. Constr. Build. Mater. 2020, 264, 120200. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.; Fang, J.; Su, Y.; Wu, C. Ultra-high performance concrete targets against high velocity projectile impact—A-state-of-the-art review. Int. J. Impact Eng. 2022, 160, 104080. [Google Scholar] [CrossRef]
- Eik, M.; Puttonen, J.; Herrmann, H. An orthotropic material model for steel fibre reinforced concrete based on the orientation distribution of fibres. Compos. Struct. 2015, 121, 324–336. [Google Scholar] [CrossRef]
- Zhou, B.; Uchida, Y. Relationship between fiber orientation/distribution and post-cracking behaviour in ultra-high-performance fiber-reinforced concrete (UHPFRC). Cem. Concr. Compos. 2017, 83, 66–75. [Google Scholar] [CrossRef]
- Švec, O.; Žirgulis, G.; Bolander, J.E.; Stang, H. Influence of formwork surface on the orientation of steel fibres within self-compacting concrete and on the mechanical properties of cast structural elements. Cem. Concr. Compos. 2014, 50, 60–72. [Google Scholar] [CrossRef]
- Ďubek, M.; Makýš, P.; Petro, M.; Ellingerová, H.; Antošová, N. The Development of Controlled Orientation of Fibres in SFRC. Materials 2021, 14, 4432. [Google Scholar] [CrossRef]
- Kobaka, J. A Statistical Model of Fibre Distribution in a Steel Fibre Reinforced Concrete. Materials 2021, 14, 7297. [Google Scholar] [CrossRef]
- Ding, T.; Xiao, J.; Zou, S.; Zhou, X. Anisotropic behavior in bending of 3D printed concrete reinforced with fibers. Compos. Struct. 2020, 254, 112808. [Google Scholar] [CrossRef]
- Sun, J.; Aslani, F.; Lu, J.; Wang, L.; Huang, Y.; Ma, G. Fibre-reinforced lightweight engineered cementitious composites for 3D concrete printing. Ceram. Int. 2021, 47, 27107–27121. [Google Scholar] [CrossRef]
- Arunothayan, A.R.; Nematollahi, B.; Ranade, R.; Bong, S.H.; Sanjayan, J.G.; Khayat, K.H. Fiber orientation effects on ultra-high performance concrete formed by 3D printing. Cem. Concr. Res. 2021, 143, 106384. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, C.; Liu, Z.; Wang, H.; Ren, Q. Mechanical anisotropy of ultra-high performance fibre-reinforced concrete for 3D printing. Cem. Concr. Compos. 2022, 125, 104310. [Google Scholar] [CrossRef]
- Raju, R.A.; Lim, S.; Akiyama, M.; Kageyama, T. Effects of concrete flow on the distribution and orientation of fibers and flexural behavior of steel fiber-reinforced self-compacting concrete beams. Constr. Build. Mater. 2020, 262, 119963. [Google Scholar] [CrossRef]
- Alberti, M.; Enfedaque, A.; Gálvez, J. A review on the assessment and prediction of the orientation and distribution of fibres for concrete. Compos. Part B Eng. 2018, 151, 274–290. [Google Scholar] [CrossRef]
- Zhao, Y.; Bi, J.; Wang, Z.; Huo, L.; Guan, J.; Zhao, Y.; Sun, Y. Numerical simulation of the casting process of steel fiber reinforced self-compacting concrete: Influence of material and casting parameters on fiber orientation and distribution. Constr. Build. Mater. 2021, 312, 125337. [Google Scholar] [CrossRef]
- Miller, A.I.; Björklund, F.R. Method of Reinforcing Concrete with Fibres. U.S. Patent US4062913A, 13 December 1977. [Google Scholar]
- Wijffels, M.; Wolfs, R.; Suiker, A.; Salet, T. Magnetic orientation of steel fibres in self-compacting concrete beams: Effect on failure behaviour. Cem. Concr. Compos. 2017, 80, 342–355. [Google Scholar] [CrossRef]
- Villar, V.P.; Medina, N.F. Alignment of hooked-end fibres in matrices with similar rheological behaviour to cementitious composites through homogeneous magnetic fields. Constr. Build. Mater. 2018, 163, 256–266. [Google Scholar] [CrossRef]
- Hajforoush, M.; Kheyroddin, A.; Rezaifar, O. Investigation of engineering properties of steel fiber reinforced concrete exposed to homogeneous magnetic field. Constr. Build. Mater. 2020, 252, 119064. [Google Scholar] [CrossRef]
- Xue, W.; Chen, J.; Xie, F.; Feng, B. Orientation of Steel Fibers in Magnetically Driven Concrete and Mortar. Materials 2018, 11, 170. [Google Scholar] [CrossRef] [Green Version]
- Künzel, K.; Papež, V.; Carrera, K.; Konrád, P.; Mára, M.; Kheml, P.; Sovják, R. Electromagnetic Properties of Steel Fibres for Use in Cementitious Composites, Fibre Detection and Non-Destructive Testing. Materials 2021, 14, 2131. [Google Scholar] [CrossRef] [PubMed]
- ANSYS Inc. ANSYS 2021 R1. 2021. 275 Technology Drive, Canonsburg, PA 15317, USA. Available online: https://www.ansys.com/ (accessed on 23 February 2021).
- Jin, J.M. The Finite Element Method in Electromagnetics, 3rd ed.; Wiley-IEEE Press: Piscataway, NJ, USA, 2014; p. 876. [Google Scholar]
- Ghani, S.A.; Ahmad Khiar, M.S.; Chairul, I.S.; Lada, M.Y.; Rahim, N.H. Study of magnetic fields produced by transmission line tower using finite element method (FEM). In Proceedings of the 2014 2nd International Conference on Technology, Informatics, Management, Engineering Environment, Bandung, Indonesia, 19–21 August 2014; pp. 64–68. [Google Scholar] [CrossRef]
- Giorla, D.; Roccella, R.; Lo Frano, R.; Sannazzaro, G. EM zooming procedure in ANSYS Maxwell 3D. Fusion Eng. Des. 2018, 132, 67–72. [Google Scholar] [CrossRef]
- Bronaugh, E.L. Helmholtz coils for calibration of probes and sensors: Limits of magnetic field accuracy and uniformity. In Proceedings of the International Symposium on Electromagnetic Compatibility, Atlanta, GA, USA, 14–18 August 1995; pp. 72–76. [Google Scholar]
- Parry, J. Helmholtz Coils and Coil Design. In Methods in Palaeomagnetism; Developments in Solid Earth Geophysics; Collinson, D., Creer, K., Runcorn, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3, pp. 551–567. [Google Scholar] [CrossRef]
- Romana, L.; Jindřich, F.; Soukupová, L.; Valentin, J. Ultrasound gel as suitable tool for simulation of the fibre orientation in the fibre reinforced concrete. In Experimental Stresss Analysis; Czech Society for Mechanics: Prague, Czech Republic, 2016; pp. 1–4. [Google Scholar]
- Ida, N. Engineering Electromagnetics, 4th ed.; Springer: Cham, Switzerland, 2021; p. 1028. [Google Scholar] [CrossRef]



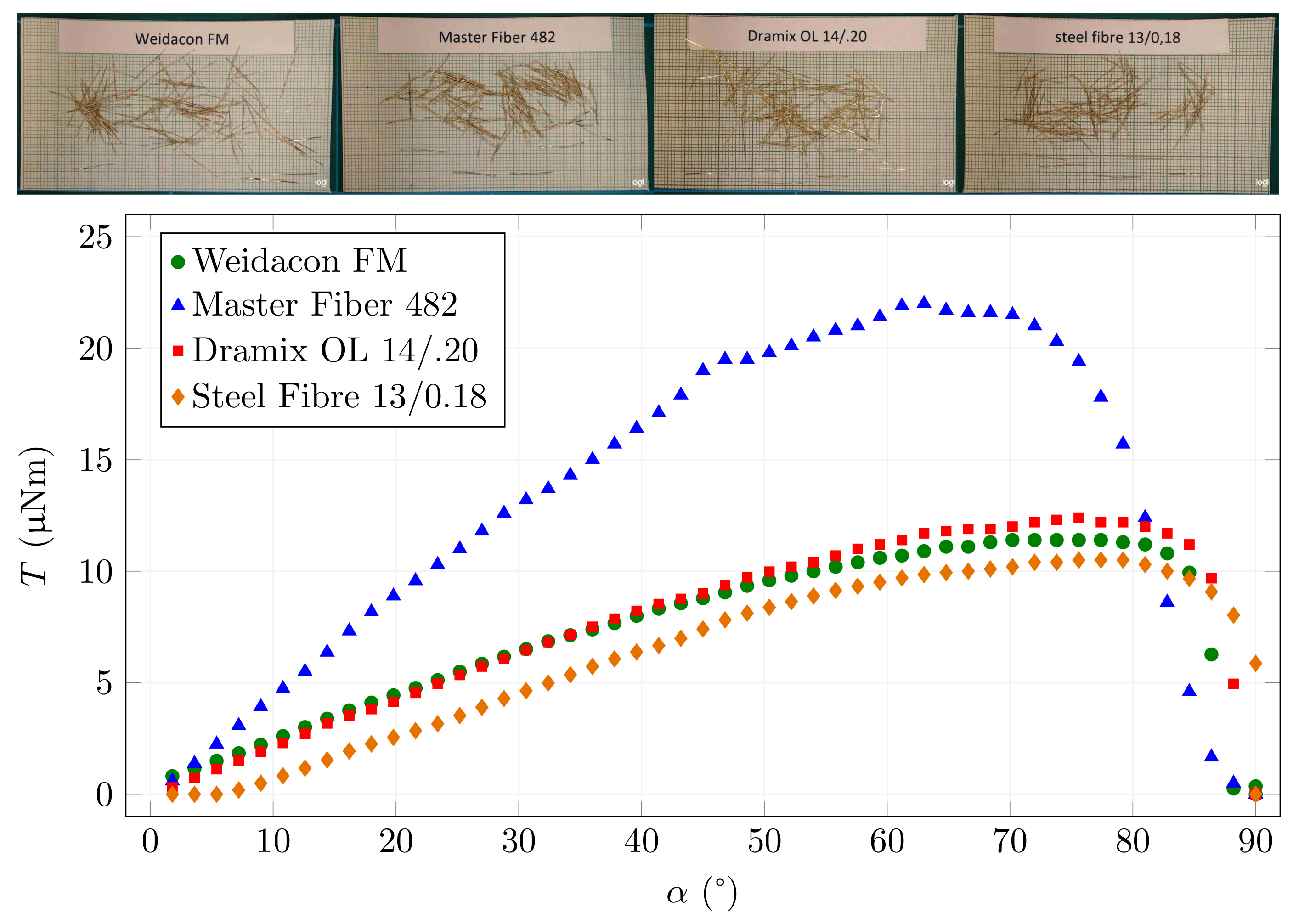
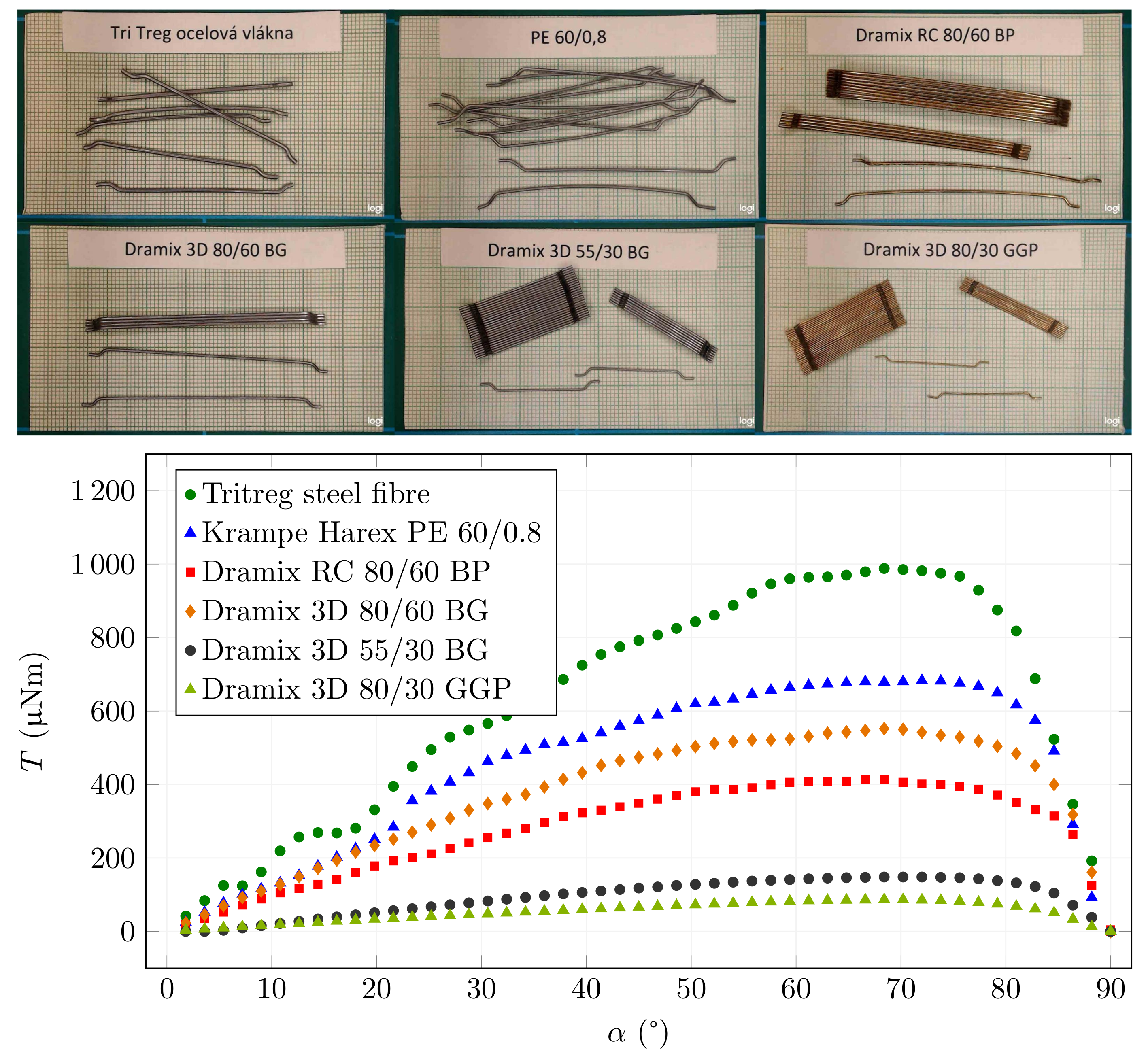
| Fibre Type | Length | Diameter | Volume | |||
|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | - | (Am) | (T) | |
| Master Fiber 482 1 | 13 | 0.32 | 1.05 | 388 | 150 | 1.60 |
| Dramix OL 14/0.20 2 | 13 | 0.22 | 0.49 | 512 | 164 | 1.59 |
| Dramix 3D 55/30 BG 2 | 30 | 0.56 | 7.39 | 541 | 161 | 1.70 |
| Dramix 3D 80/30 GGP 2 | 30 | 0.38 | 3.40 | 488 | 154 | 1.79 |
| Dramix 3D 80/60 BG 2 | 60 | 0.75 | 26.51 | 547 | 192 | 1.77 |
| Dramix RC 80/60 BP 2 | 60 | 0.72 | 24.43 | 428 | 182 | 1.70 |
| Steel Fibre 13/0.18 3 | 13 | 0.185 | 0.35 | 469 | 146 | 1.79 |
| Tritreg Steel Fibers 4 | 50 | 1.05 | 43.30 | 605 | 203 | 1.83 |
| Krampe Harex PE 60/0.8 5 | 60 | 0.784 | 28.96 | 555 | 199 | 1.75 |
| Weidacon FM 3 | 13 | 0.19 | 0.37 | 528 | 188 | 1.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nováková, K.; Carrera, K.; Konrád, P.; Künzel, K.; Papež, V.; Sovják, R. Simulations of the Behaviour of Steel Ferromagnetic Fibres Commonly Used in Concrete in a Magnetic Field. Materials 2022, 15, 128. https://doi.org/10.3390/ma15010128
Nováková K, Carrera K, Konrád P, Künzel K, Papež V, Sovják R. Simulations of the Behaviour of Steel Ferromagnetic Fibres Commonly Used in Concrete in a Magnetic Field. Materials. 2022; 15(1):128. https://doi.org/10.3390/ma15010128
Chicago/Turabian StyleNováková, Kateřina, Kristýna Carrera, Petr Konrád, Karel Künzel, Václav Papež, and Radoslav Sovják. 2022. "Simulations of the Behaviour of Steel Ferromagnetic Fibres Commonly Used in Concrete in a Magnetic Field" Materials 15, no. 1: 128. https://doi.org/10.3390/ma15010128
APA StyleNováková, K., Carrera, K., Konrád, P., Künzel, K., Papež, V., & Sovják, R. (2022). Simulations of the Behaviour of Steel Ferromagnetic Fibres Commonly Used in Concrete in a Magnetic Field. Materials, 15(1), 128. https://doi.org/10.3390/ma15010128








