Discrete Element Method Modeling for the Failure Analysis of Dry Mono-Size Coke Aggregates
Abstract
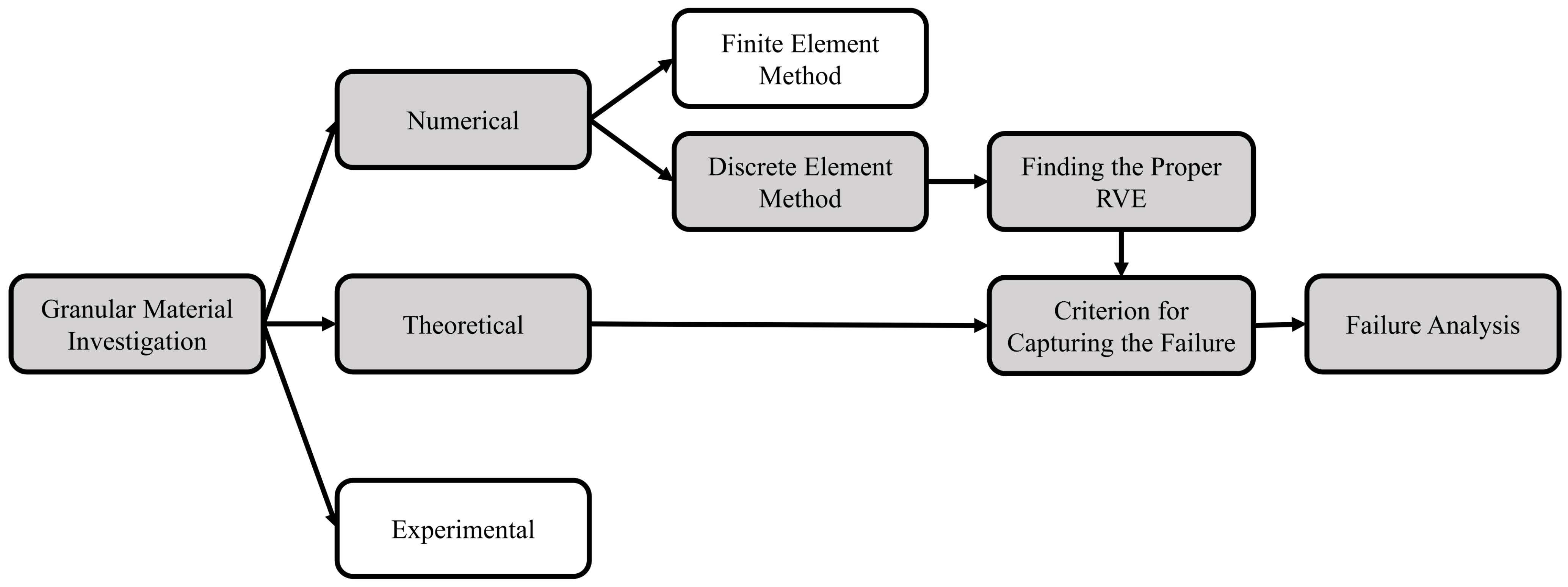
1. Introduction
2. Second-Order Work Criterion
Kinetic Energy of the Granular System and External and Internal Second-Order Work
3. Discrete Element Method (DEM) Simulation
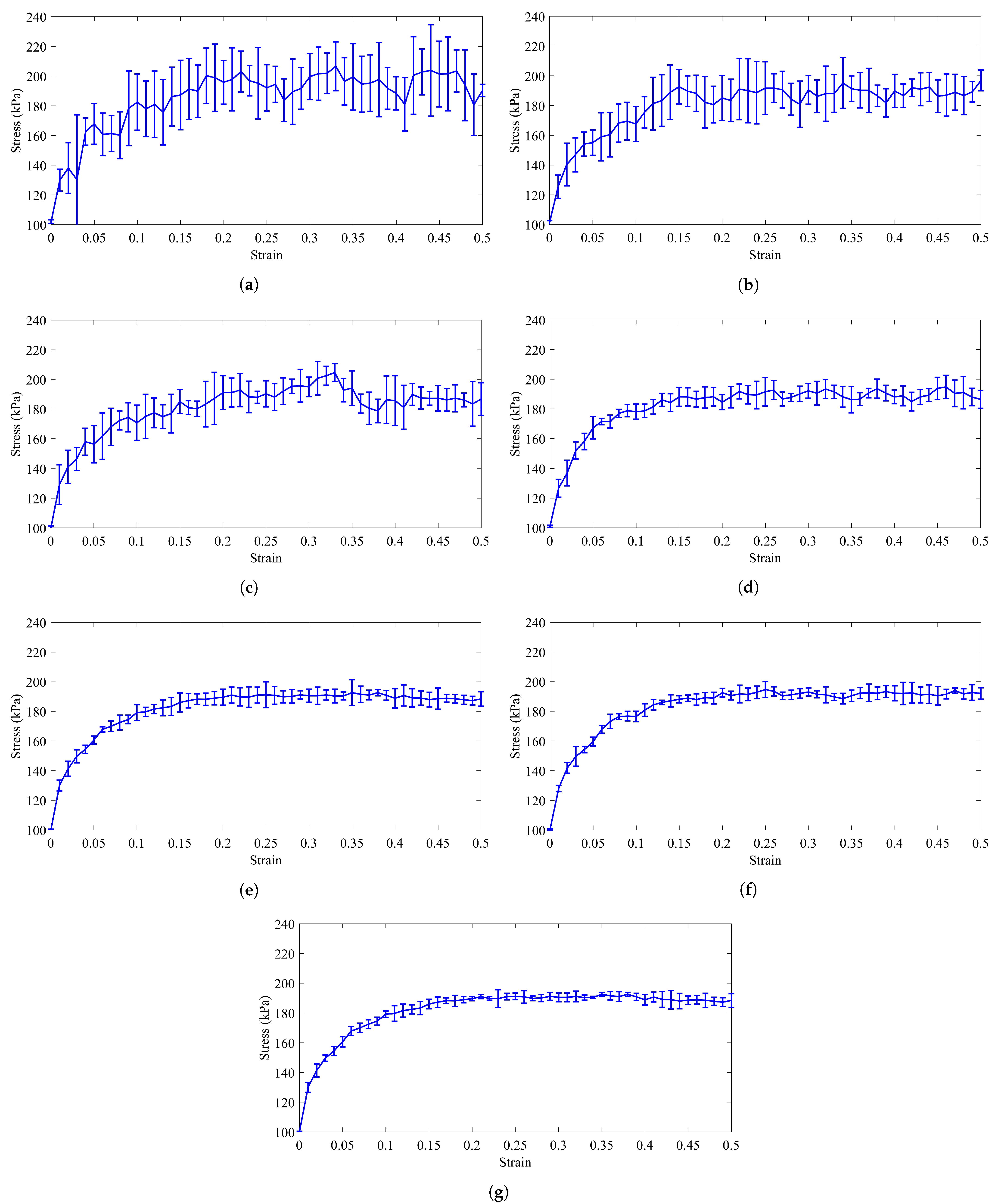
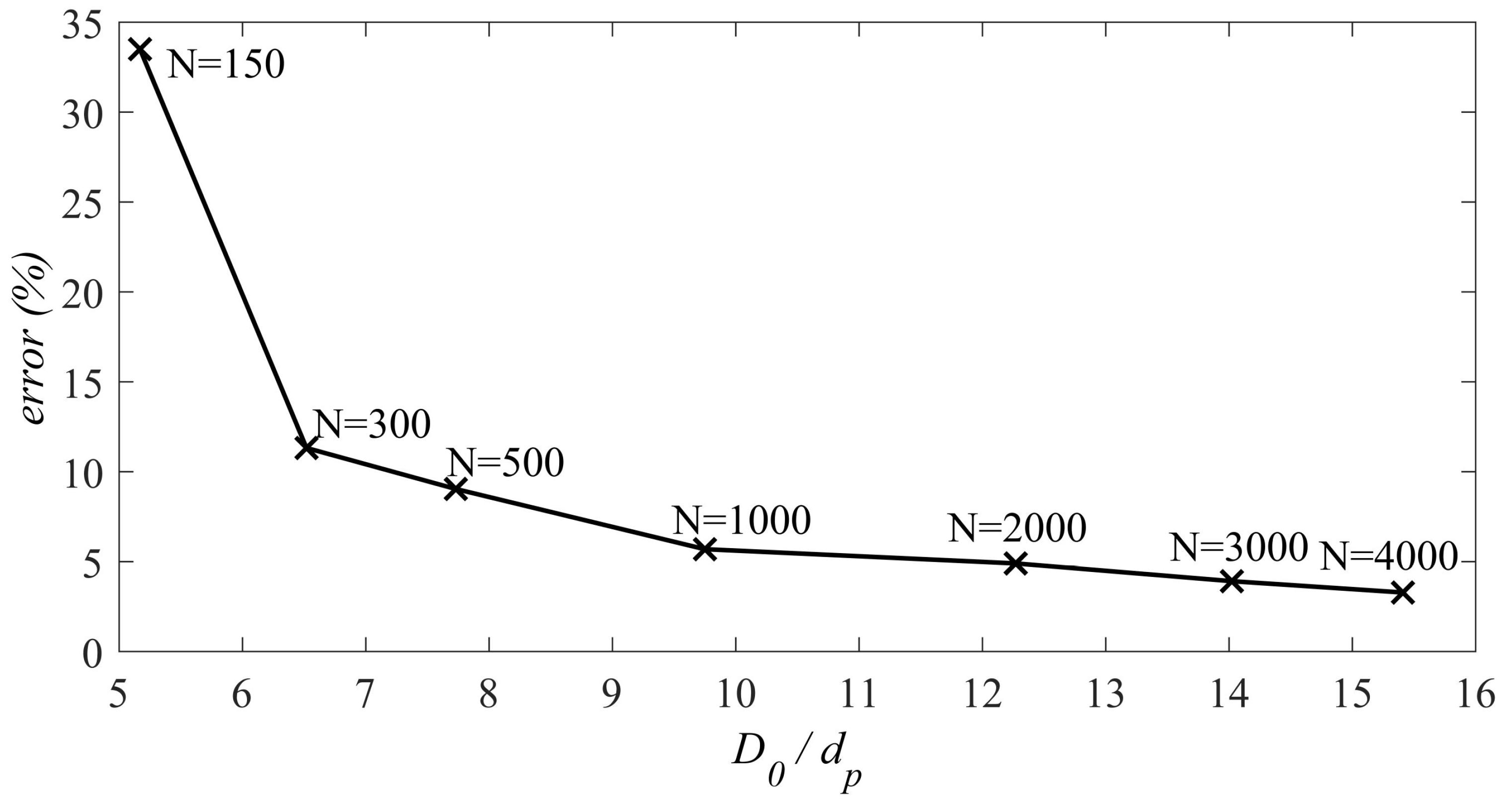
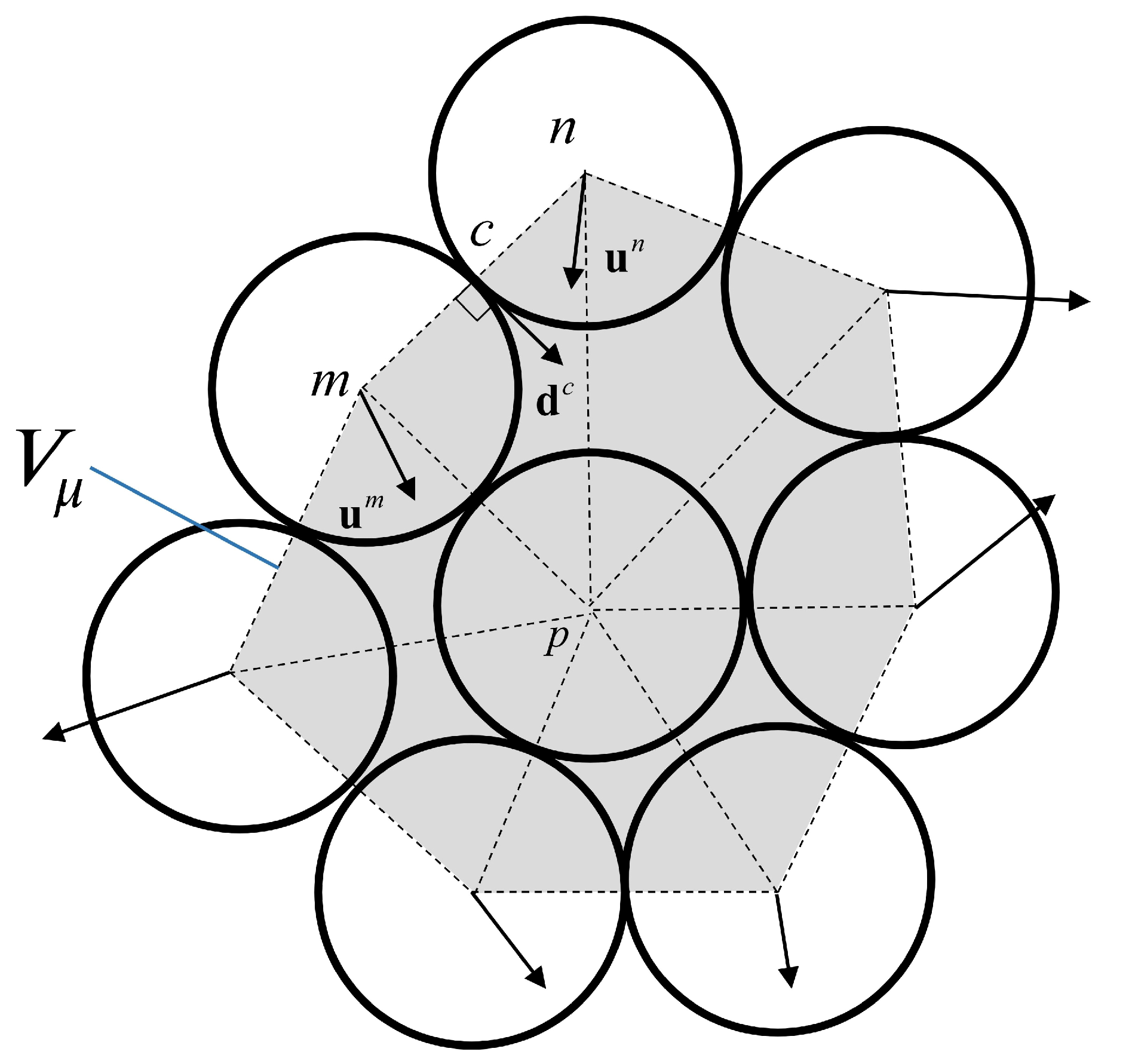
3.1. Determination of a Proper Representative Volume Element (RVE)
3.1.1. First Criterion: Having a More Homogeneous Force Chain Network
3.1.2. Second and Third Criteria: Smooth the Stress-Strain Curve and Repetitive Behavior
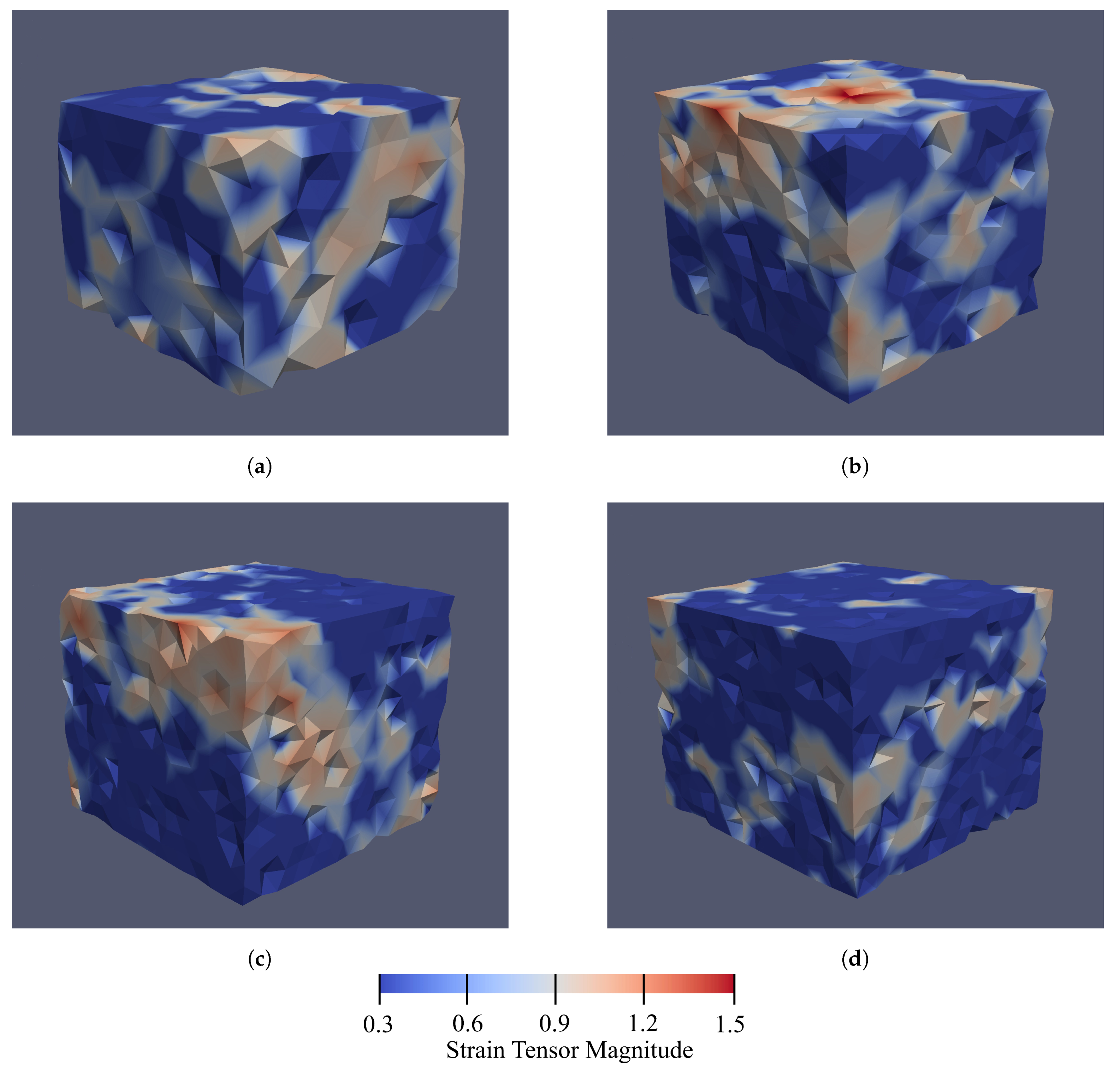
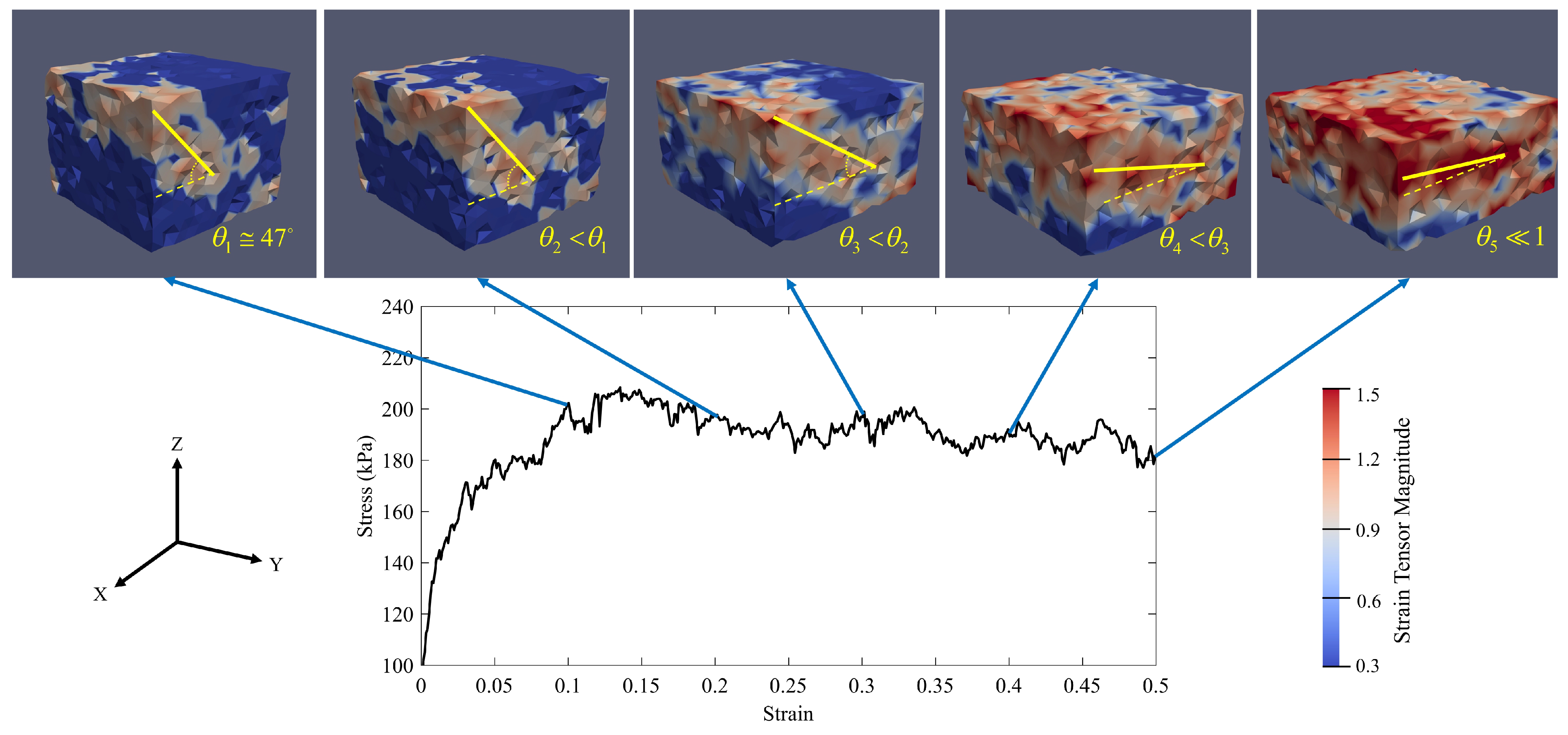
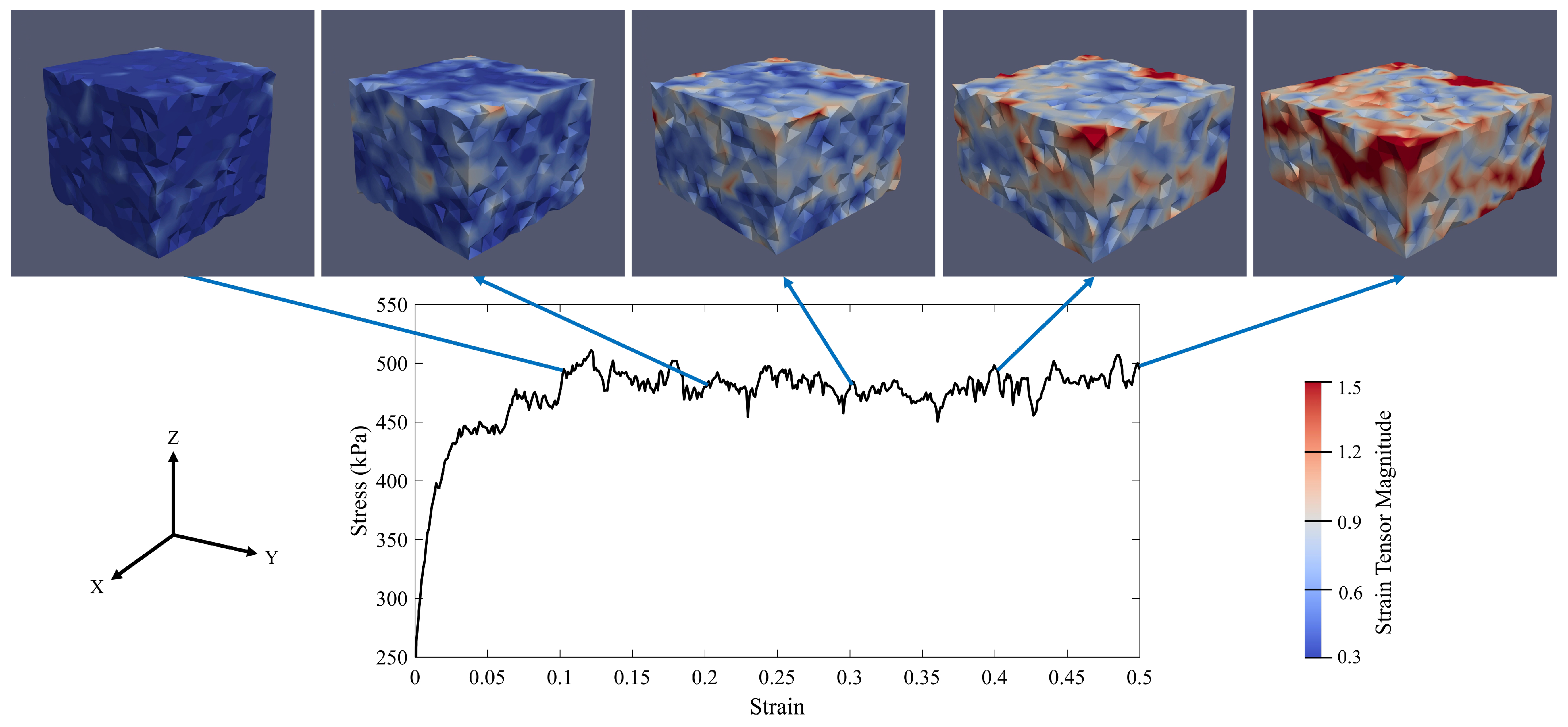
3.1.3. Fourth Criterion: Higher Chance of Capturing the Strain Localization
4. Failure Analysis
4.1. Second-Order Work from Macroscopic Variables
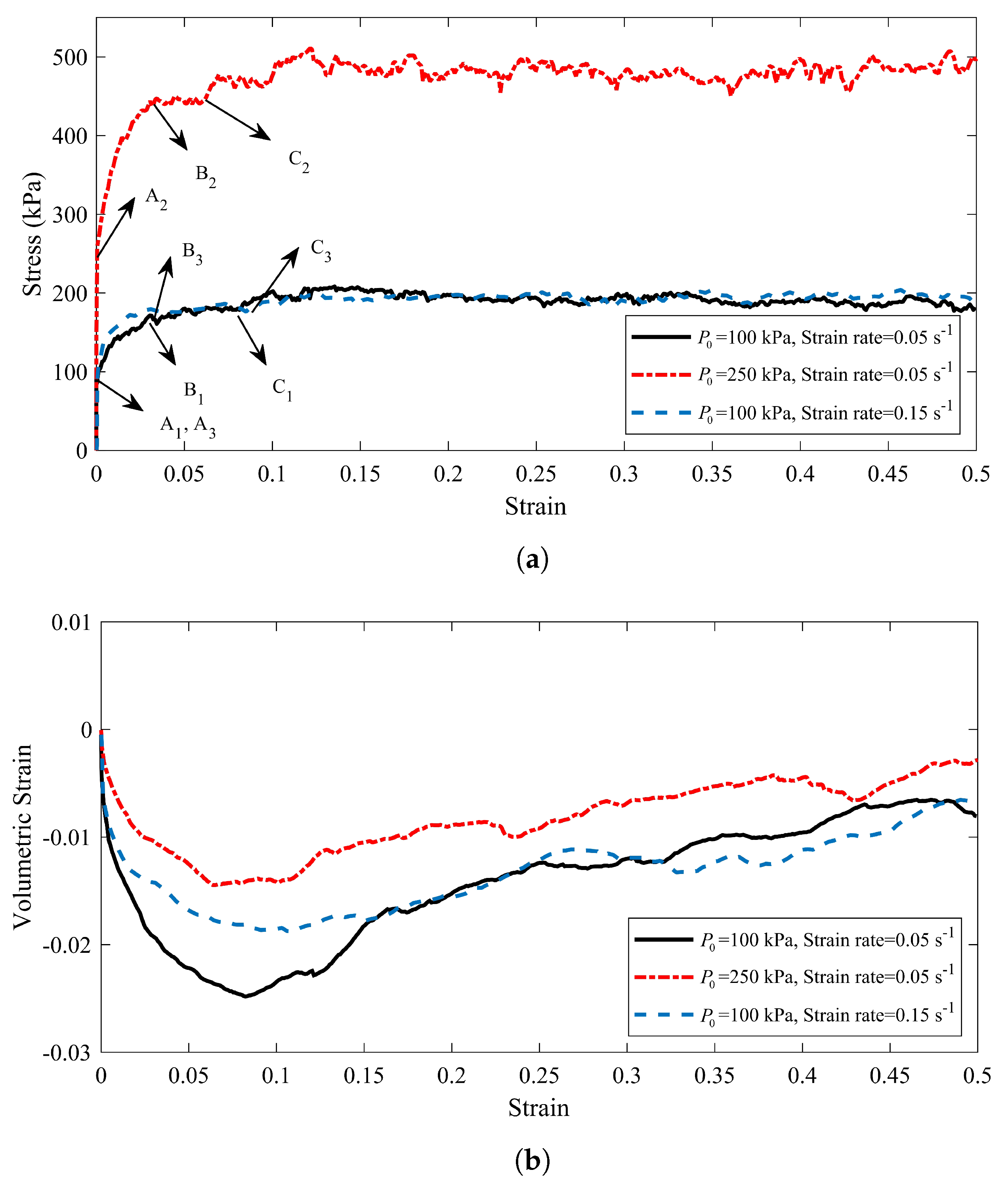
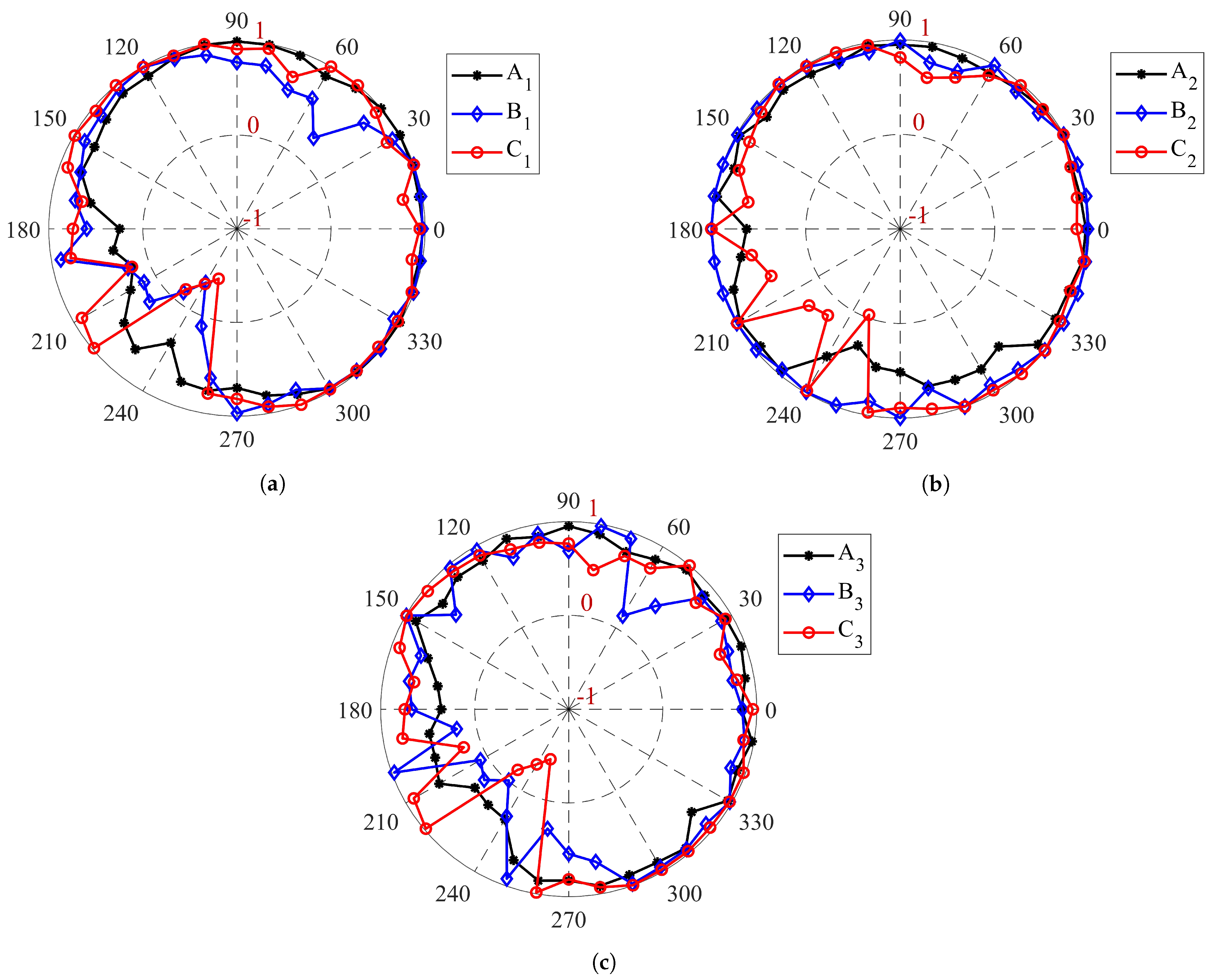
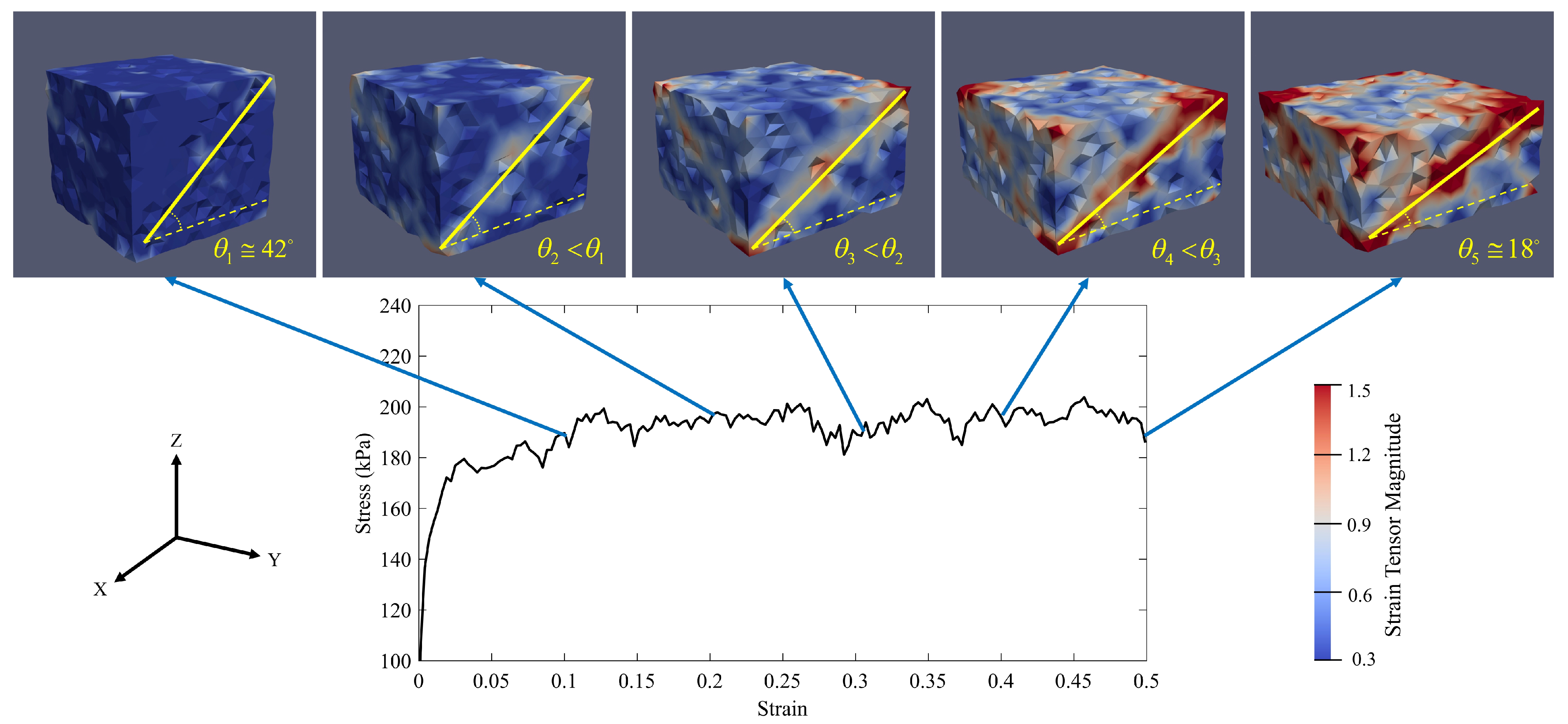
4.2. Failure Mode along the Drained Compression Path
5. Conclusions
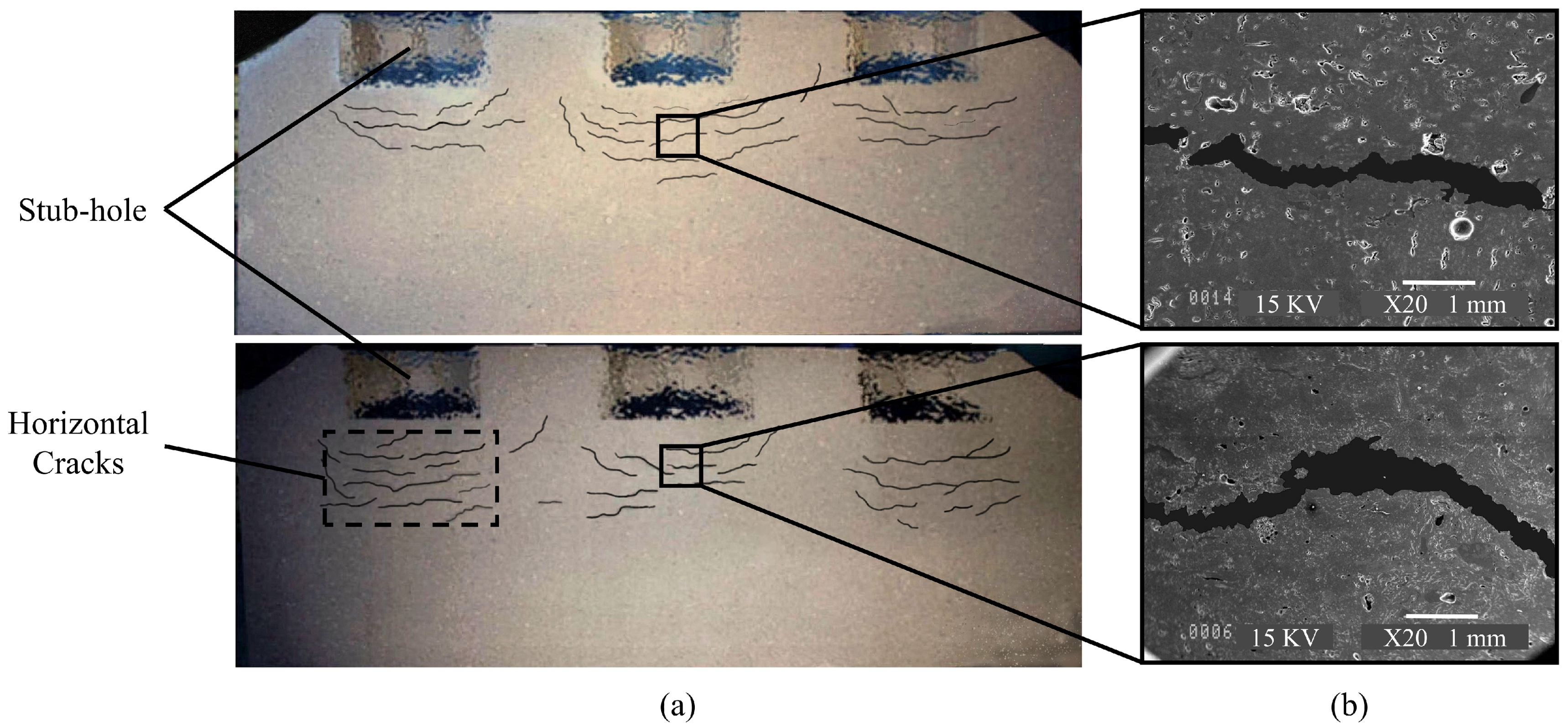
- It has been shown that the strain localization could happen in the carbon anodes during the compaction process and if this localized zone is a type of the compaction band, it could be responsible for the crack generation under the stub-holes in the carbon anodes. Because the carbon anode paste behavior during the compaction process is too complex for consideration, the dry mono-sized spherical coke aggregates have been examined.
- When considering failure as a bifurcation from a quasi-static regime to a dynamical one, a failure criterion was inferred, and the notion of the bifurcation domain was specified. The relationship between the kinetic energy of the granular materials and the internal and external second-order work has been evolved. It has been shown that when the failure occurred, the stresses that sense at the boundaries cannot reflect the real stress inside the material.
- Using the DEM simulation, the optimum number of particles which could represent the bulk material for the failure analysis is justified. Four criteria, including having a more uniform force path network, having a smother stress-strain diagram, repetitive behavior of the RVE, and a higher chance of the capturing the strain localization, have been exploited. It has been proved that the RVE with 3000 particles could represent the bulk material behavior in failure analysis.
- The second-order criterion was used for finding the failure threshold in the specimens. The evolution of the shear band to the compaction band was investigated. Moreover, the effect of the confining pressure and the strain rate on the failure of the specimens have been studied. It revealed that, by enhancing the confining pressure, the failure mode of the specimen would be of the diffusing type. However, by increasing the strain rate, the mode of the failure would be the localized type. In addition, the strain rate could postpone the formation of the compaction band, which can generate a susceptible area for the crack generation. The results highlighted that increasing the confining pressure and the axial strain rate could be suggested solutions for preventing the localization or postponing of the formation of the compaction bands in the carbon anode.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| the strain tensor | |
| the Cauchy stress tensor | |
| micro-strain tensor | |
| complementary area vector belonging to the c the pair of grains () | |
| the deformation gradient tensor | |
| the first Piola-Kirchhoff stress tensor | |
| displacement vector (m) | |
| velocity vector (m/s) | |
| position vector in material configuration | |
| position vector in spacial configuration | |
| kinetic energy (J) | |
| angular velocity of particle (rad/s) | |
| porosity | |
| confining pressure (Pa) | |
| the angle between the localized band and the maximum principal stress plane () | |
| friction angle (rad) | |
| the area of the surface perpendicular to the direction of () | |
| C | current configuration |
| initial configuration | |
| the normalized second-order work | |
| the second-order work (J) | |
| initial size of RVE (m) | |
| diameter of particle (m) | |
| external force in the direction of (N) | |
| overlap at the contact point (m) | |
| incremental tangential displacement at the contact point (m) | |
| inertia tensor transformed to the global frame(kg) | |
| tangential spring stiffness (N/m) | |
| normal spring stiffness (N/m) | |
| mass of particle (kg) | |
| S | surface boundary in current configuration () |
| surface boundary in initial configuration () | |
| t | time (s) |
| N | number of particle |
| external stress in the direction of (Pa) | |
| V | volume in current configuration () |
| linear velocity of particle (m/s) | |
| volume in initial configuration () | |
| volume of polyhedral domain () |
Appendix A
Appendix B
References
- Welch, B.J. Aluminum production paths in the new millennium. JoM 1999, 51, 24–28. [Google Scholar] [CrossRef]
- Rhedey, P. A Review of factors affecting carbon anode consumption in the electrolytic production of aluminum. Essent. Read. Light Met. 2016, 611–622. [Google Scholar] [CrossRef]
- Hulse, K.L. Anode Manufacture: Raw Materials, Formulation and Processing Parameters; R& D Carbon Limited: Sierre, Switzerland, 2000. [Google Scholar]
- Dorcheh, K.A. Investigation of the Materials and Paste Relationships to Improve Forming Process and Anode Quality. Ph.D. Thesis, Université Laval, Québec City, QC, Canada, 2013. [Google Scholar]
- Majidi, B. Discrete Element Method Simulation of Packing and Rheological Properties of Coke and Coke/Pitch Mixtures. Ph.D. Thesis, Université Laval, Québec City, QC, Canada, 2018. [Google Scholar]
- Azari, K.; Alamdari, H.; Ammar, H.; Fafard, M.; Adams, A.; Ziegler, D. Influence of mixing parameters on the density and compaction behavior of carbon anodes used in aluminum production. In Advanced Materials Research; Trans Tech Publications Ltd.: Bäch, Schwyz, Switzerland, 2012; Volume 409, pp. 17–22. [Google Scholar] [CrossRef]
- Amrani, S.; Kocaefe, D.; Kocaefe, Y.; Morais, B.; Blaney, G. Effect of heating rate on the crack formation during baking in carbon anodes used in aluminum industry. In Light Metals; Springer: Cham, Switzerland, 2014; pp. 1175–1180. [Google Scholar] [CrossRef]
- Meier, M.W. Cracking Behaviour of Anodes; R & D Carbon Ltd.: Sierre, Switzerland, 1996. [Google Scholar]
- Schneider, J.; Coste, B. Thermomechanical modelling of thermal shock in anodes. In Light Metals; TMS Annual Meeting, Minerals, Metals & Materials Society: Denver, CO, USA, 1993; pp. 621–628. [Google Scholar]
- Boubaker, M.B.; Picard, D.; Duchesne, C.; Tessier, J.; Alamdari, H.; Fafard, M. Non-destructive testing of baked anodes based on modal analysis and principal component analysis. In Light Metals; Springer: Cham, Switzerland, 2017; pp. 1289–1298. [Google Scholar] [CrossRef]
- Chaouki, H.; Picard, D.; Ziegler, D.; Azari, K.; Alamdari, H.; Fafard, M. Viscoplastic modeling of the green anode paste compaction process. J. Appl. Mech. 2016, 83. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Chaouki, H.; Thibodeau, S.; Fafard, M.; Ziegler, D.; Alamdari, H. Characterization of the Hot Anode Paste Compaction Process: A Computational and Experimental Study. Materials 2019, 12, 800. [Google Scholar] [CrossRef]
- Andrade, J.E.; Avila, C.; Hall, S.; Lenoir, N.; Viggiani, G. Multiscale modeling and characterization of granular matter: From grain kinematics to continuum mechanics. J. Mech. Phys. Solids 2011, 59, 237–250. [Google Scholar] [CrossRef]
- Majidi, B.; Melo, J.; Fafard, M.; Ziegler, D.; Alamdari, H. Packing density of irregular shape particles: DEM simulations applied to anode-grade coke aggregates. Adv. Powder Technol. 2015, 26, 1256–1262. [Google Scholar] [CrossRef]
- Majidi, B.; Rouget, G.; Fafard, M.; Ziegler, D.; Alamdari, H. Discrete element method investigation of bulk density and electrical resistivity of calcined coke mixes. Metals 2017, 7, 154. [Google Scholar] [CrossRef]
- Rouget, G.; Majidi, B.; Picard, D.; Gauvin, G.; Ziegler, D.; Mashreghi, J.; Alamdari, H. Electrical resistivity measurement of petroleum coke powder by means of four-probe method. Metall. Mater. Trans. B 2017, 48, 2543–2550. [Google Scholar] [CrossRef]
- Daouadji, A.; Darve, F.; Al Gali, H.; Hicher, P.; Laouafa, F.; Lignon, S.; Nicot, F.; Nova, R.; Pinheiro, M.; Prunier, F.; et al. Diffuse failure in geomaterials: Experiments, theory and modelling. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 1731–1773. [Google Scholar] [CrossRef]
- Nicot, F.; Sibille, L.; Darve, F. Failure in Granular Materials: Macro and Micro Views. In Bifurcations, Instabilities and Degradations in Geomaterials; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–12. [Google Scholar] [CrossRef]
- Nicot, F.; Darve, F. Diffuse and localized failure modes: Two competing mechanisms. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 586–601. [Google Scholar] [CrossRef]
- Sibille, L.; Hadda, N.; Nicot, F.; Tordesillas, A.; Darve, F. Granular plasticity, a contribution from discrete mechanics. J. Mech. Phys. Solids 2015, 75, 119–139. [Google Scholar] [CrossRef]
- Hadda, N.; Sibille, L.; Nicot, F.; Wan, R.; Darve, F. Failure in granular media from an energy viewpoint. Granul. Matter 2016, 18, 50. [Google Scholar] [CrossRef]
- Chu, J.; Leong, W.; Loke, W.; Wanatowski, D. Instability of loose sand under drained conditions. J. Geotech. Geoenviron. Eng. 2012, 138, 207–216. [Google Scholar] [CrossRef]
- Simitses, G.; Hodges, D.H. Fundamentals of Structural Stability; Butterworth-Heinemann: Burlington, MA, USA, 2006. [Google Scholar]
- Tordesillas, A.; Muthuswamy, M. On the modeling of confined buckling of force chains. J. Mech. Phys. Solids 2009, 57, 706–727. [Google Scholar] [CrossRef]
- Ziegler, H. Principles of Structural Stability; Birkhäuser: Basel, Switzerland, 1977. [Google Scholar] [CrossRef]
- Wan, R.; Pinheiro, M.; Daouadji, A.; Jrad, M.; Darve, F. Diffuse instabilities with transition to localization in loose granular materials. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1292–1311. [Google Scholar] [CrossRef]
- Oda, M.; Kazama, H. Microstructure of shear bands and its relation to the mechanisms of dilatancy and failure of dense granular soils. Geotechnique 1998, 48, 465–481. [Google Scholar] [CrossRef]
- Darve, F.; Flavigny, E.; Meghachou, M. Constitutive modelling and instabilities of soil behaviour. Comput. Geotech. 1995, 17, 203–224. [Google Scholar] [CrossRef]
- Liapounoff, A. Problème général de la stabilité du mouvement. In Annales de la Faculté des Sciences de Toulouse: Mathématiques; Éd. Privat, Imprimeur-Libraire: Toulouse, France, 1907; Volume 9, pp. 203–474. [Google Scholar] [CrossRef]
- Nova, R. Controllability of the incremental response of soil specimens subjected to arbitrary loading programmes. J. Mech. Behav. Mater. 1994, 5, 193–202. [Google Scholar] [CrossRef]
- Nicot, F.; Darve, F.; Dat Vu Khoa, H. Bifurcation and second-order work in geomaterials. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 1007–1032. [Google Scholar] [CrossRef]
- Chambon, R. Some theoretical results about second-order work, uniqueness, existence and controllability independent of the constitutive equation. In Mathematics and Mechanics of Granular Materials; Hill, J.M., Selvadurai, A., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 53–61. [Google Scholar] [CrossRef]
- Darve, F.; Laouafa, F. Instabilities in granular materials and application to landslides. Mech. Cohesive-Frict. Mater. 2000, 5, 627–652. [Google Scholar] [CrossRef]
- Nicot, F.; Darve, F. A micro-mechanical investigation of bifurcation in granular materials. Int. J. Solids Struct. 2007, 44, 6630–6652. [Google Scholar] [CrossRef]
- Hill, R. A general theory of uniqueness and stability in elastic-plastic solids. J. Mech. Phys. Solids 1958, 6, 236–249. [Google Scholar] [CrossRef]
- Darve, F.; Servant, G.; Laouafa, F.; Khoa, H. Failure in geomaterials: Continuous and discrete analyses. Comput. Methods Appl. Mech. Eng. 2004, 193, 3057–3085. [Google Scholar] [CrossRef]
- Darve, F.; Sibille, L.; Daouadji, A.; Nicot, F. Bifurcations in granular media: Macro-and micro-mechanics approaches. Comptes Rendus Mécanique 2007, 335, 496–515. [Google Scholar] [CrossRef]
- Lade, P.V. Instability, shear banding, and failure in granular materials. Int. J.Solids Struct. 2002, 39, 3337–3357. [Google Scholar] [CrossRef]
- Rice, J.R.; Rudnicki, J. A note on some features of the theory of localization of deformation. Int. J. Solids Struct. 1980, 16, 597–605. [Google Scholar] [CrossRef]
- Aydin, A.; Borja, R.I.; Eichhubl, P. Geological and mathematical framework for failure modes in granular rock. J. Struct. Geol. 2006, 28, 83–98. [Google Scholar] [CrossRef]
- Rudnicki, J.W.; Rice, J. Conditions for the localization of deformation in pressure-sensitive dilatant materials. J. Mech. Phys. Solids 1975, 23, 371–394. [Google Scholar] [CrossRef]
- Calvetti, F.; Combe, G.; Lanier, J. Experimental micromechanical analysis of a 2D granular material: Relation between structure evolution and loading path. Mech. Cohes. Frict. Mater. 1997, 2, 121–163. [Google Scholar] [CrossRef]
- Bésuelle, P.; Desrues, J.; Raynaud, S. Experimental characterisation of the localisation phenomenon inside a Vosges sandstone in a triaxial cell. Int. J. Rock Mech. Min. Sci. 2000, 37, 1223–1237. [Google Scholar] [CrossRef]
- Desrues, J.; Viggiani, G. Strain localization in sand: An overview of the experimental results obtained in Grenoble using stereophotogrammetry. Int. J. Numer. Anal. Methods Geomech. 2004, 28, 279–321. [Google Scholar] [CrossRef]
- Zhuang, L.; Nakata, Y.; Kim, U.G.; Kim, D. Influence of relative density, particle shape, and stress path on the plane strain compression behavior of granular materials. Acta Geotech. 2014, 9, 241–255. [Google Scholar] [CrossRef]
- Wu, K.; Pizette, P.; Becquart, F.; Remond, S.; Abriak, N.; Xu, W.; Liu, S. Experimental and numerical study of cylindrical triaxial test on mono-sized glass beads under quasi-static loading condition. Adv. Powder Technol. 2017, 28, 155–166. [Google Scholar] [CrossRef]
- Alikarami, R.; Andò, E.; Gkiousas-Kapnisis, M.; Torabi, A.; Viggiani, G. Strain localisation and grain breakage in sand under shearing at high mean stress: Insights from in situ X-ray tomography. Acta Geotech. 2015, 10, 15–30. [Google Scholar] [CrossRef]
- Borja, R.I. Computational modeling of deformation bands in granular media. II. Numerical simulations. Comput. Methods Appl. Mech. Eng. 2004, 193, 2699–2718. [Google Scholar] [CrossRef]
- Andrade, J.E.; Borja, R.I. Capturing strain localization in dense sands with random density. Int. J. Numer. Methods Eng. 2006, 67, 1531–1564. [Google Scholar] [CrossRef]
- Wang, B.; Chen, Y.; Wong, T.F. A discrete element model for the development of compaction localization in granular rock. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Guo, N.; Zhao, J. 3D multiscale modeling of strain localization in granular media. Comput. Geotech. 2016, 80, 360–372. [Google Scholar] [CrossRef]
- Liang, W.; Zhao, J. Multiscale modeling of large deformation in geomechanics. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1080–1114. [Google Scholar] [CrossRef]
- Alshibli, K.A.; Alsaleh, M.I.; Voyiadjis, G.Z. Modelling strain localization in granular materials using micropolar theory: Numerical implementation and verification. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1525–1544. [Google Scholar] [CrossRef]
- De Borst, R. Simulation of strain localization: A reappraisal of the Cosserat continuum. Eng. Comput. 1991. [Google Scholar] [CrossRef]
- Tang, H.; Dong, Y.; Wang, T.; Dong, Y. Simulation of strain localization with discrete element-Cosserat continuum finite element two scale method for granular materials. J. Mech. Phys. Solids 2019, 122, 450–471. [Google Scholar] [CrossRef]
- Scholtès, L.; Donzé, F.V. A DEM model for soft and hard rocks: Role of grain interlocking on strength. J. Mech. Phys. Solids 2013, 61, 352–369. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, W.; Yuan, Z.; Fish, J. A nonlocal multiscale discrete-continuum model for predicting mechanical behavior of granular materials. Int. J. Numer. Methods Eng. 2016, 106, 129–160. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, J.; Liang, W. Pattern transitions of localized deformation in high-porosity sandstones: Insights from multiscale analysis. Comput. Geotech. 2020, 126, 103733. [Google Scholar] [CrossRef]
- Khoa, H.D.V.; Georgopoulos, I.O.; Darve, F.; Laouafa, F. Diffuse failure in geomaterials: Experiments and modelling. Comput. Geotech. 2006, 33, 1–14. [Google Scholar] [CrossRef]
- Lade, P.V. Static instability and liquefaction of loose fine sandy slopes. J. Geotech. Eng. 1992, 118, 51–71. [Google Scholar] [CrossRef]
- Chu, J.; Leroueil, S.; Leong, W. Unstable behaviour of sand and its implication for slope instability. Can. Geotech. J. 2003, 40, 873–885. [Google Scholar] [CrossRef]
- Borja, R.I. Conditions for instabilities in collapsible solids including volume implosion and compaction banding. Acta Geotech. 2006, 1, 107–122. [Google Scholar] [CrossRef][Green Version]
- Sun, W. A unified method to predict diffuse and localized instabilities in sands. Geomech. Geoeng. 2013, 8, 65–75. [Google Scholar] [CrossRef]
- Borja, R.I. Localized and diffuse bifurcations in porous rocks undergoing shear localization and cataclastic flow. In Computational Plasticity; Oñate, E., Owen, R., Eds.; Springer: Dordrecht, The Netherlands, 2007; Volume 7, pp. 37–53. [Google Scholar] [CrossRef]
- Borja, R.I. Condition for liquefaction instability in fluid-saturated granular soils. Acta Geotech. 2006, 1, 211. [Google Scholar] [CrossRef]
- Andrade, J.E. A predictive framework for liquefaction instability. Géotechnique 2009, 59, 673–682. [Google Scholar] [CrossRef]
- Sibille, L.; Donzé, F.V.; Nicot, F.; Chareyre, B.; Darve, F. From bifurcation to failure in a granular material: A DEM analysis. Acta Geotech. 2008, 3, 15. [Google Scholar] [CrossRef]
- Aydin, A.; Johnson, A.M. Analysis of faulting in porous sandstones. J. Struct. Geol. 1983, 5, 19–31. [Google Scholar] [CrossRef]
- Aydin, A. Small faults formed as deformation bands in sandstone. In Rock Friction and Earthquake Prediction; Springer: Berlin/Heidelberg, Germany, 1978; pp. 913–930. [Google Scholar] [CrossRef]
- Davatzes, N.C.; Aydin, A.; Eichhubl, P. Overprinting faulting mechanisms during the development of multiple fault sets in sandstone, Chimney Rock fault array, Utah, USA. Tectonophysics 2003, 363, 1–18. [Google Scholar] [CrossRef]
- Antonellini, M.A.; Aydin, A.; Pollard, D.D. Microstructure of deformation bands in porous sandstones at Arches National Park, Utah. J. Struct. Geol. 1994, 16, 941–959. [Google Scholar] [CrossRef]
- Sternlof, K.R.; Karimi-Fard, M.; Pollard, D.; Durlofsky, L. Flow and transport effects of compaction bands in sandstone at scales relevant to aquifer and reservoir management. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Mollema, P.; Antonellini, M. Compaction bands: A structural analog for anti-mode I cracks in aeolian sandstone. Tectonophysics 1996, 267, 209–228. [Google Scholar] [CrossRef]
- Sternlof, K.R.; Rudnicki, J.W.; Pollard, D.D. Anticrack inclusion model for compaction bands in sandstone. J. Geophys. Res. B 2005, 110. [Google Scholar] [CrossRef]
- Holcomb, D.; Rudnicki, J.W.; Issen, K.A.; Sternlof, K. Compaction localization in the Earth and the laboratory: State of the research and research directions. Acta Geotech. 2007, 2, 1–15. [Google Scholar] [CrossRef]
- Issen, K.; Casey, T.; Dixon, D.; Richards, M.; Ingraham, J. Characterization and modeling of localized compaction in aluminum foam. Scr. Mater. 2005, 52, 911–915. [Google Scholar] [CrossRef]
- Bastawros, A.; Bart-Smith, H.; Evans, A. Experimental analysis of deformation mechanisms in a closed-cell aluminum alloy foam. J. Mech. Phys. Solids 2000, 48, 301–322. [Google Scholar] [CrossRef]
- Park, C.; Nutt, S. Anisotropy and strain localization in steel foam. Mat. Sci. Eng. A 2001, 299, 68–74. [Google Scholar] [CrossRef]
- Papka, S.D.; Kyriakides, S. In-plane crushing of a polycarbonate honeycomb. Int. J. Solids Struct. 1998, 35, 239–267. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Katsman, R.; Aharonov, E.; Scher, H. Localized compaction in rocks: Eshelby’s inclusion and the spring network model. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Katsman, R.; Aharonov, E.; Scher, H. A numerical study on localized volume reduction in elastic media: Some insights on the mechanics of anticracks. J. Geophys. Res. B 2006, 111. [Google Scholar] [CrossRef]
- Katsman, R.; Aharonov, E. A study of compaction bands originating from cracks, notches, and compacted defects. J. Struct. Geol. 2006, 28, 508–518. [Google Scholar] [CrossRef]
- Thibodeau, S.; Alamdari, H.; Ziegler, D.P.; Fafard, M. New insight on the restructuring and breakage of particles during uniaxial confined compression tests on aggregates of petroleum coke. Powder Technol. 2014, 253, 757–768. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Prunier, F.; Djeran-Maigre, I.; Nicot, F. Kinetic energy and collapse of granular materials. Granul. Matter 2016, 18, 5. [Google Scholar] [CrossRef]
- Nicot, F.; Sibille, L.; Darve, F. Failure in rate-independent granular materials as a bifurcation toward a dynamic regime. Int. J. Plast. 2012, 29, 136–154. [Google Scholar] [CrossRef]
- Hadda, N.; Nicot, F.; Bourrier, F.; Sibille, L.; Radjai, F.; Darve, F. Micromechanical analysis of second order work in granular media. Granul. Matter 2013, 15, 221–235. [Google Scholar] [CrossRef]
- Sibille, L.; Nicot, F.; Donze, F.; Darve, F. Material instability in granular assemblies from fundamentally different models. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 457–481. [Google Scholar] [CrossRef]
- Holzapfel, A.G. Nonlinear Solid Mechanics: A Continuum Approach for Engineering; John Wiley & Sons, Chichen.: Chichester, NY, USA, 2000. [Google Scholar] [CrossRef]
- Nicot, F.; Hadda, N.; Bourrier, F.; Sibille, L.; Wan, R.; Darve, F. Inertia effects as a possible missing link between micro and macro second-order work in granular media. Int. J. Solids Struct. 2012, 49, 1252–1258. [Google Scholar] [CrossRef]
- Basar, Y.; Weichert, D. Nonlinear Continuum Mechanics of Solids: Fundamental Mathematical and Physical Concepts; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Šmilauer, V.; Catalano, E.; Chareyre, B.; Dorofeenko, S.; Duriez, J.; Gladky, A.; Kozicki, J.; Modenese, C.; Scholtès, L.; Sibille, L.; et al. Yade documentation. The Yade Project. 2015. Available online: http://yade-dem.org/doc/ (accessed on 22 April 2021).
- He, X.; Wu, W.; Cai, G.; Qi, J.; Kim, J.R.; Zhang, D.; Jiang, M. Work–energy analysis of granular assemblies validates and calibrates a constitutive model. Granul. Matter 2020, 22, 28. [Google Scholar] [CrossRef]
- Nicot, F.; Lerbet, J.; Darve, F. Second-order work criterion: From material point to boundary value problems. Acta Mech. 2017, 228, 2483–2498. [Google Scholar] [CrossRef]
- Stroeven, M.; Askes, H.; Sluys, L. Numerical determination of representative volumes for granular materials. Comput. Methods Appl. Mech. Eng. 2004, 193, 3221–3238. [Google Scholar] [CrossRef]
- Evesque, P.; Adjemian, F. Stress fluctuations and macroscopic stick-slip in granular materials. Eur. Phys. J. E 2002, 9, 253–259. [Google Scholar] [CrossRef]
- Catalano, E.; Chareyre, B.; Barthélemy, E. Pore-scale modeling of fluid-particles interaction and emerging poromechanical effects. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 51–71. [Google Scholar] [CrossRef]
- Bagi, K. Stress and strain in granular assemblies. Mech. Mater. 1996, 22, 165–178. [Google Scholar] [CrossRef]
- Bagi, K. Analysis of microstructural strain tensors for granular assemblies. Int. J. Solids Struct. 2006, 43, 3166–3184. [Google Scholar] [CrossRef]
- Zhu, H.; Nguyen, H.N.; Nicot, F.; Darve, F. On a common critical state in localized and diffuse failure modes. J. Mech. Phys. Solids 2016, 95, 112–131. [Google Scholar] [CrossRef]
- Bardet, J.P. Numerical simulations of the incremental responses of idealized granular materials. Int. J. Plast. 1994, 10, 879–908. [Google Scholar] [CrossRef]
- Tordesillas, A.; Pucilowski, S.; Sibille, L.; Nicot, F.; Darve, F. Multiscale characterisation of diffuse granular failure. Philos. Mag. 2012, 92, 4547–4587. [Google Scholar] [CrossRef]
- Das, A.; Tengattini, A.; Nguyen, G.D.; Viggiani, G.; Hall, S.A.; Einav, I. A thermomechanical constitutive model for cemented granular materials with quantifiable internal variables. Part II—Validation and localization analysis. J. Mech. Phys. Solids 2014, 70, 382–405. [Google Scholar] [CrossRef]


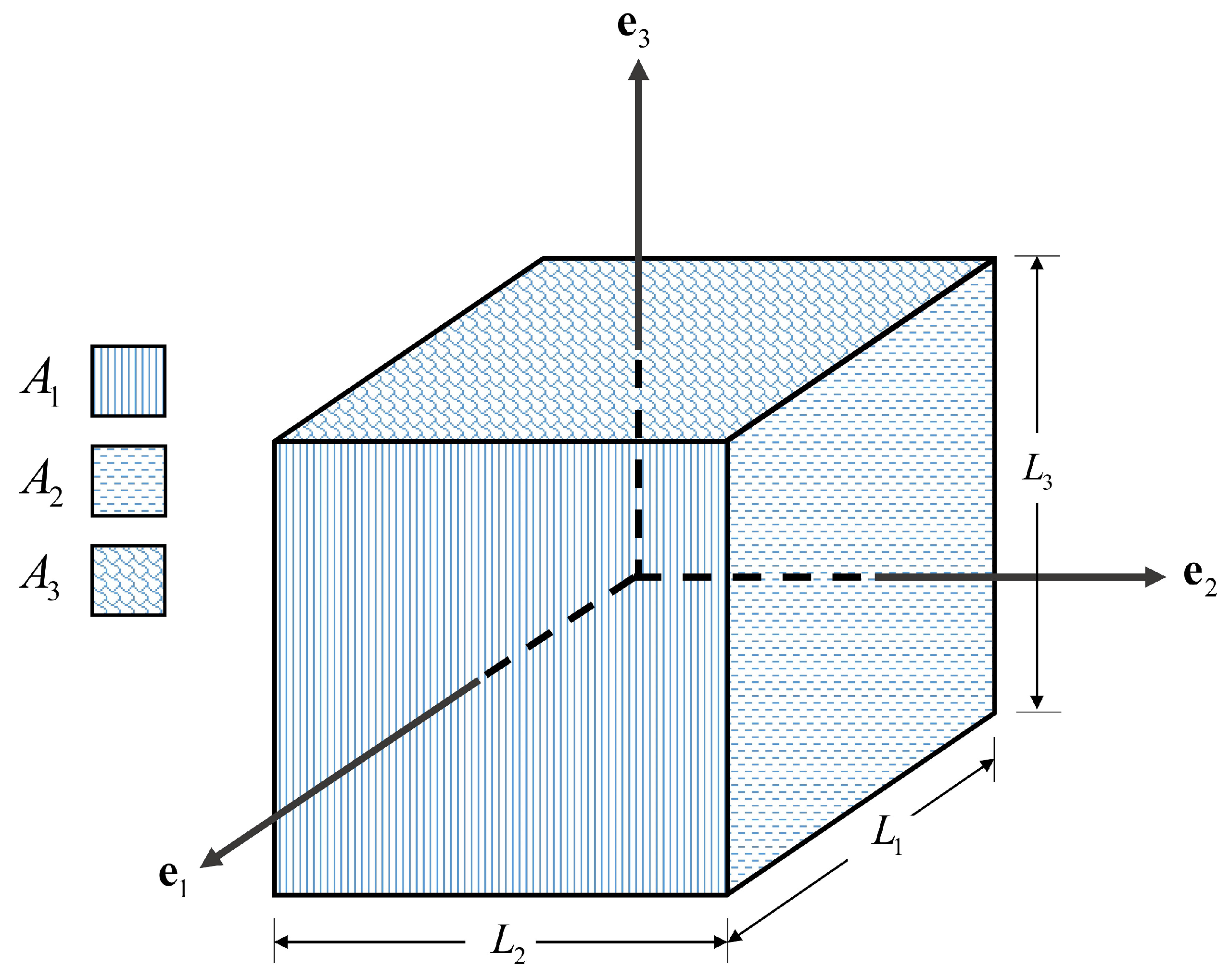



| Radii (mm) | Density (kg/m) | Elastic Modulus (MPa) | Poisson Ratio | Friction Angle (rad) | Damping Ratio |
|---|---|---|---|---|---|
| 1.87 | 1377 | 681 | 0.3 | 0.31 | 0.4 |
| Number of the Particles in the RVE | Average Force (N) | Standard Deviation (N) |
|---|---|---|
| 150 | 13.72 | 10.68 |
| 300 | 12.65 | 9.94 |
| 500 | 12.84 | 10.55 |
| 1000 | 12.76 | 9.69 |
| 2000 | 12.71 | 10.13 |
| 3000 | 12.49 | 9.39 |
| 4000 | 14.53 | 9.87 |
| Specimen | Specimen | Specimen | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0413 | 0.0833 | 0 | 0.0365 | 0.067 | 0 | 0.04 | 0.092 | |
| 0 | 0.69 | 0.74 | 0 | 0.62 | 0.76 | 0 | 0.65 | 0.75 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghi-Chahardeh, A.; Mollaabbasi, R.; Picard, D.; Taghavi, S.M.; Alamdari, H. Discrete Element Method Modeling for the Failure Analysis of Dry Mono-Size Coke Aggregates. Materials 2021, 14, 2174. https://doi.org/10.3390/ma14092174
Sadeghi-Chahardeh A, Mollaabbasi R, Picard D, Taghavi SM, Alamdari H. Discrete Element Method Modeling for the Failure Analysis of Dry Mono-Size Coke Aggregates. Materials. 2021; 14(9):2174. https://doi.org/10.3390/ma14092174
Chicago/Turabian StyleSadeghi-Chahardeh, Alireza, Roozbeh Mollaabbasi, Donald Picard, Seyed Mohammad Taghavi, and Houshang Alamdari. 2021. "Discrete Element Method Modeling for the Failure Analysis of Dry Mono-Size Coke Aggregates" Materials 14, no. 9: 2174. https://doi.org/10.3390/ma14092174
APA StyleSadeghi-Chahardeh, A., Mollaabbasi, R., Picard, D., Taghavi, S. M., & Alamdari, H. (2021). Discrete Element Method Modeling for the Failure Analysis of Dry Mono-Size Coke Aggregates. Materials, 14(9), 2174. https://doi.org/10.3390/ma14092174







