Influence of Quenching and Subsequent Annealing on the Conductivity and Electromechanical Properties of Na1/2Bi1/2TiO3-BaTiO3
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
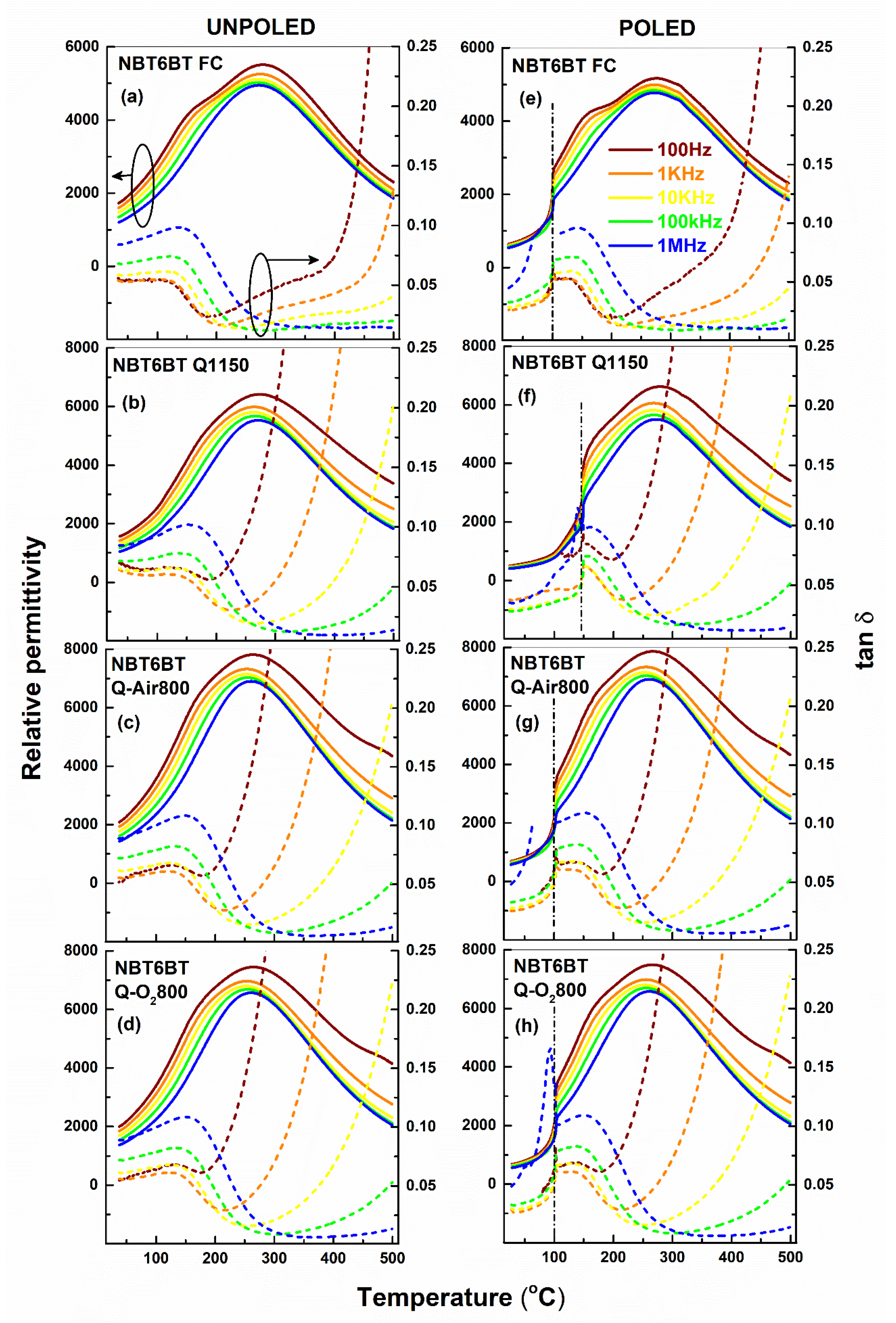
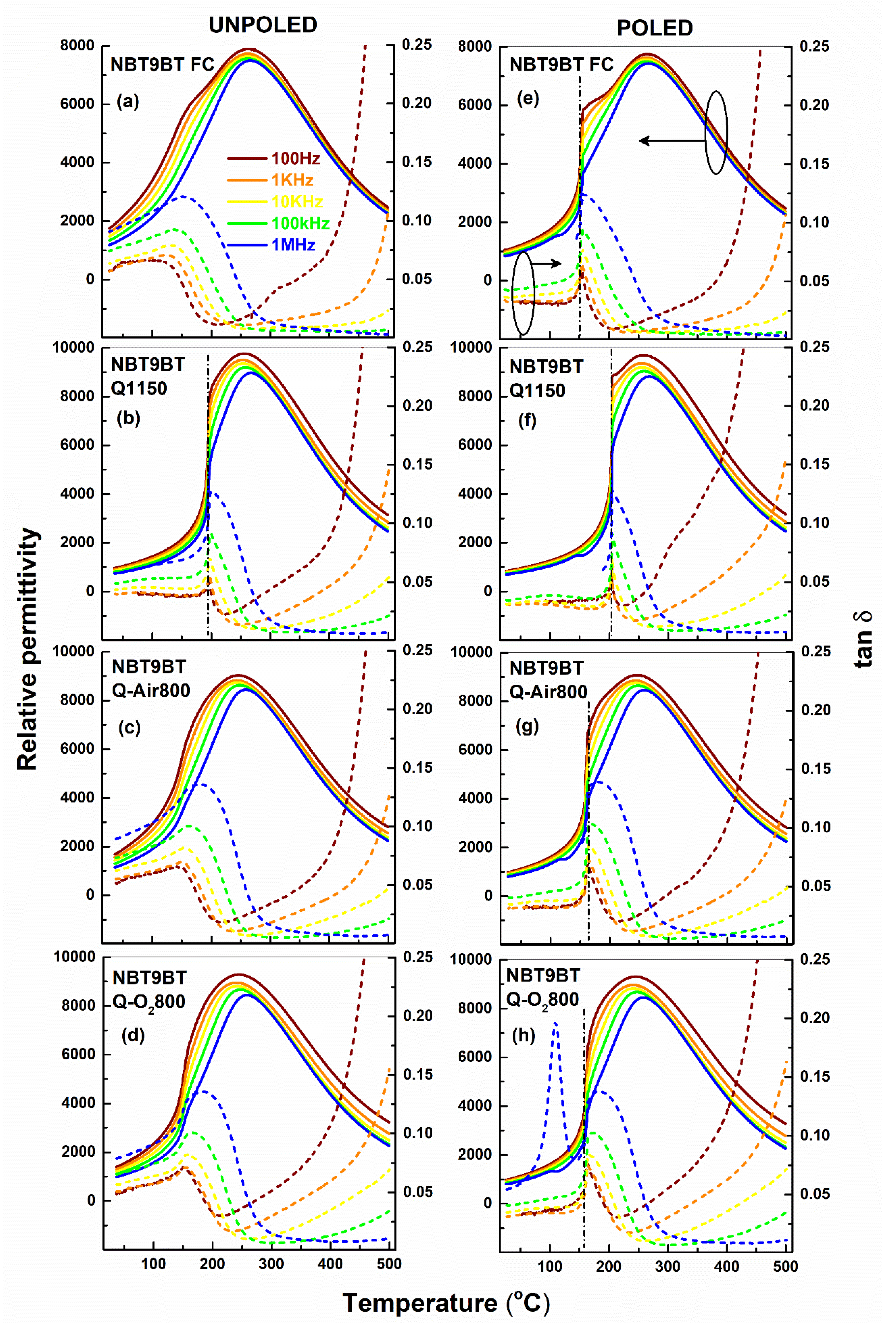
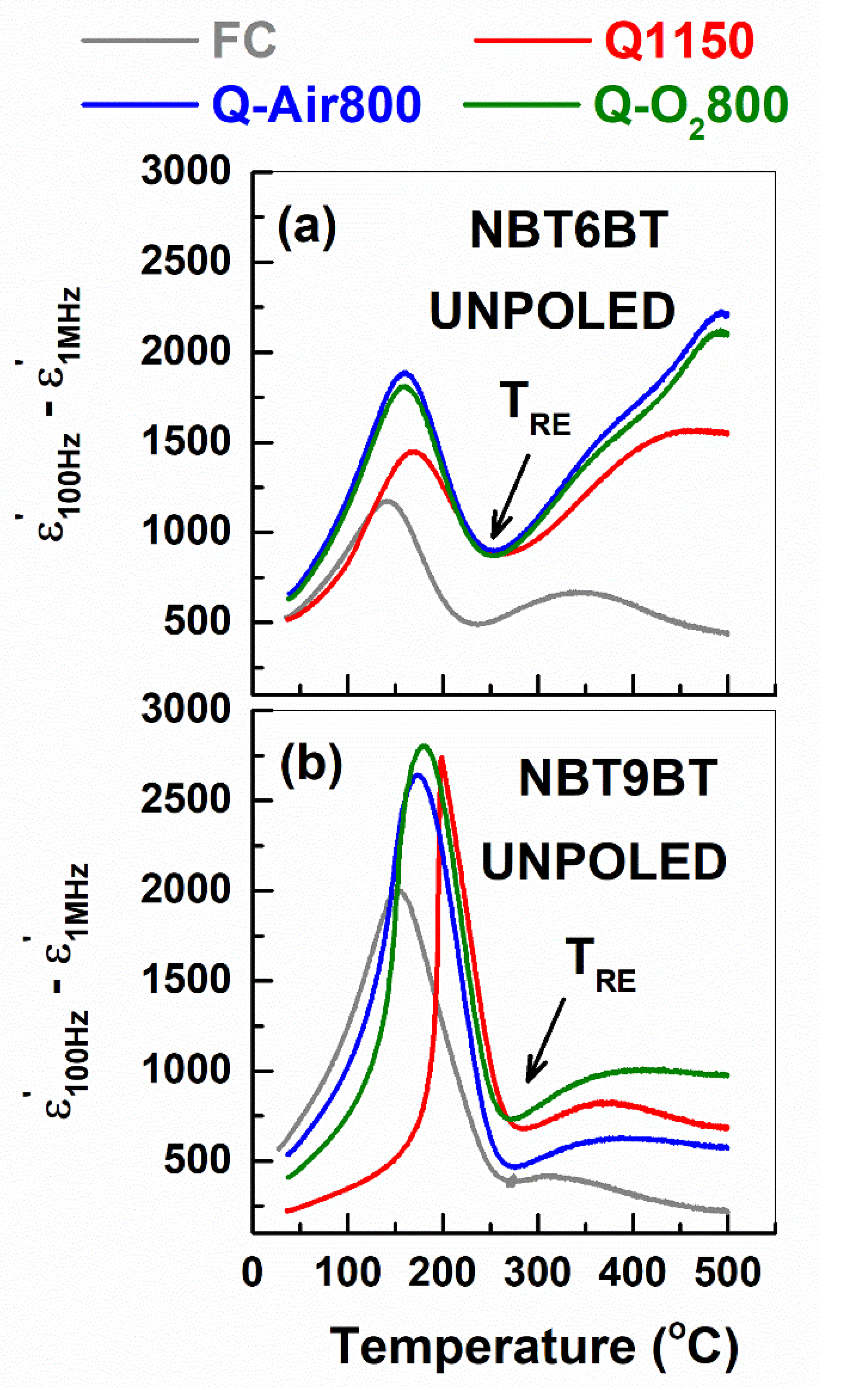
3.1. Influence of Annealing on the Dielectric Properties of Quenched Samples
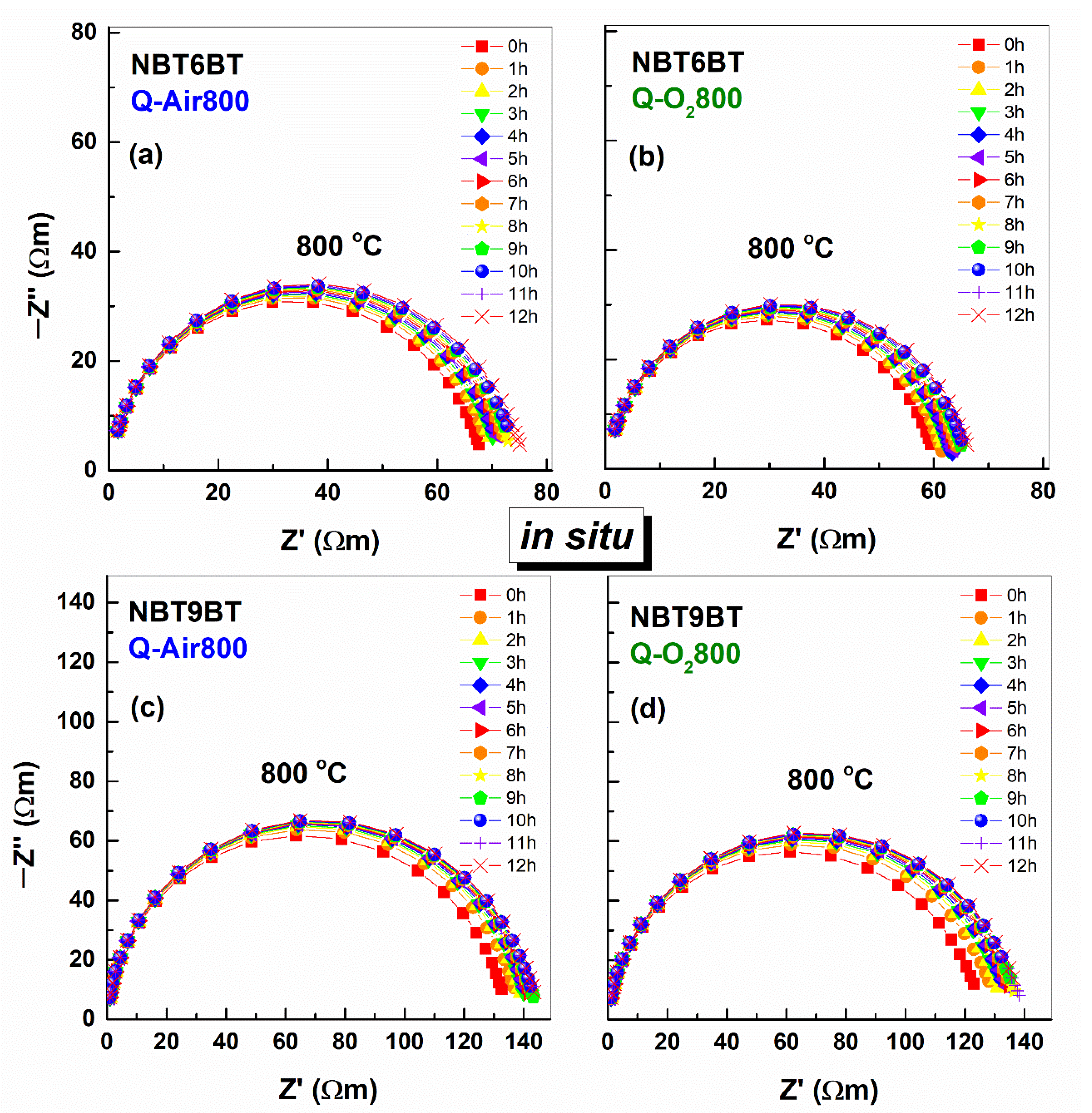
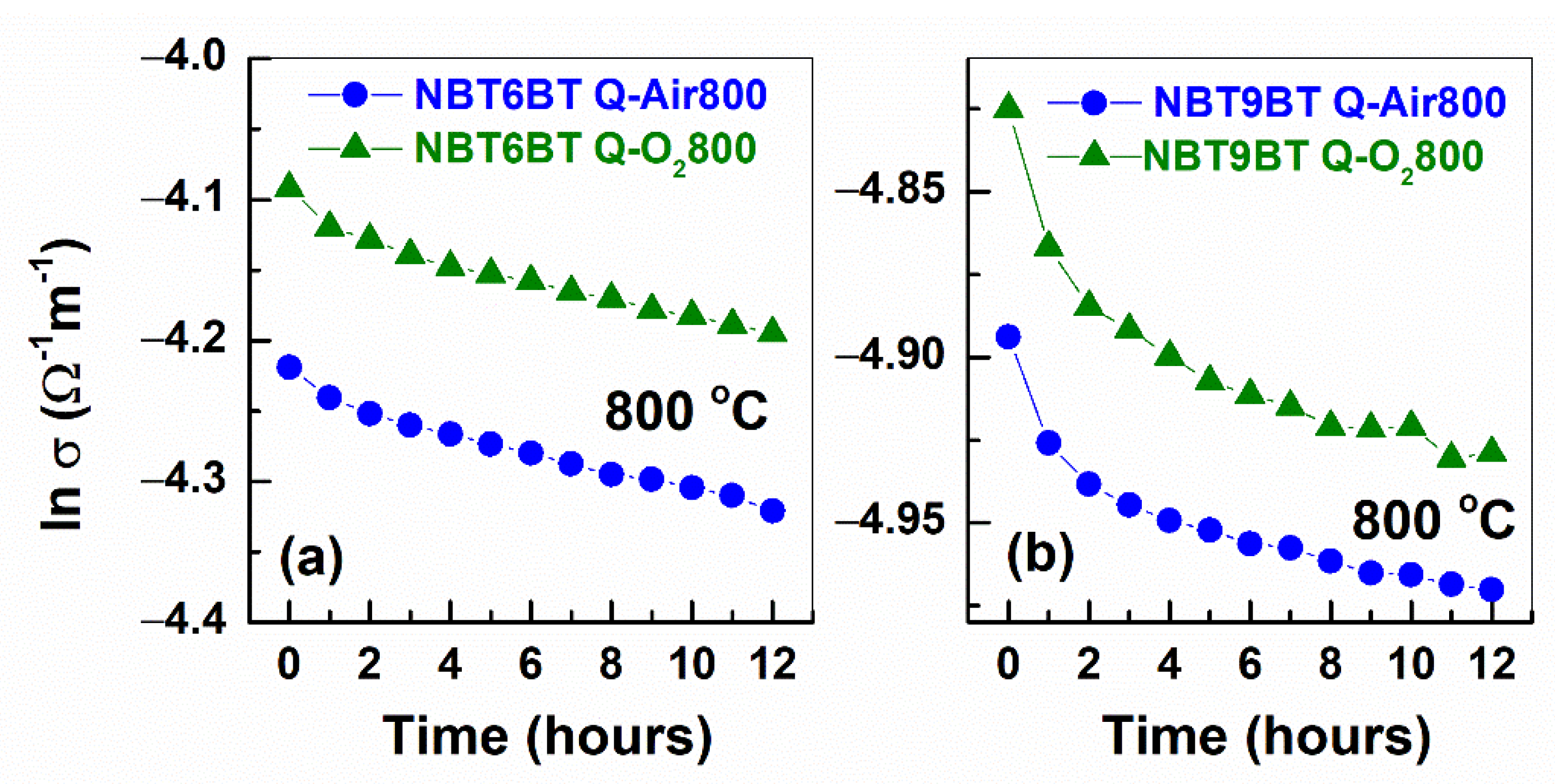
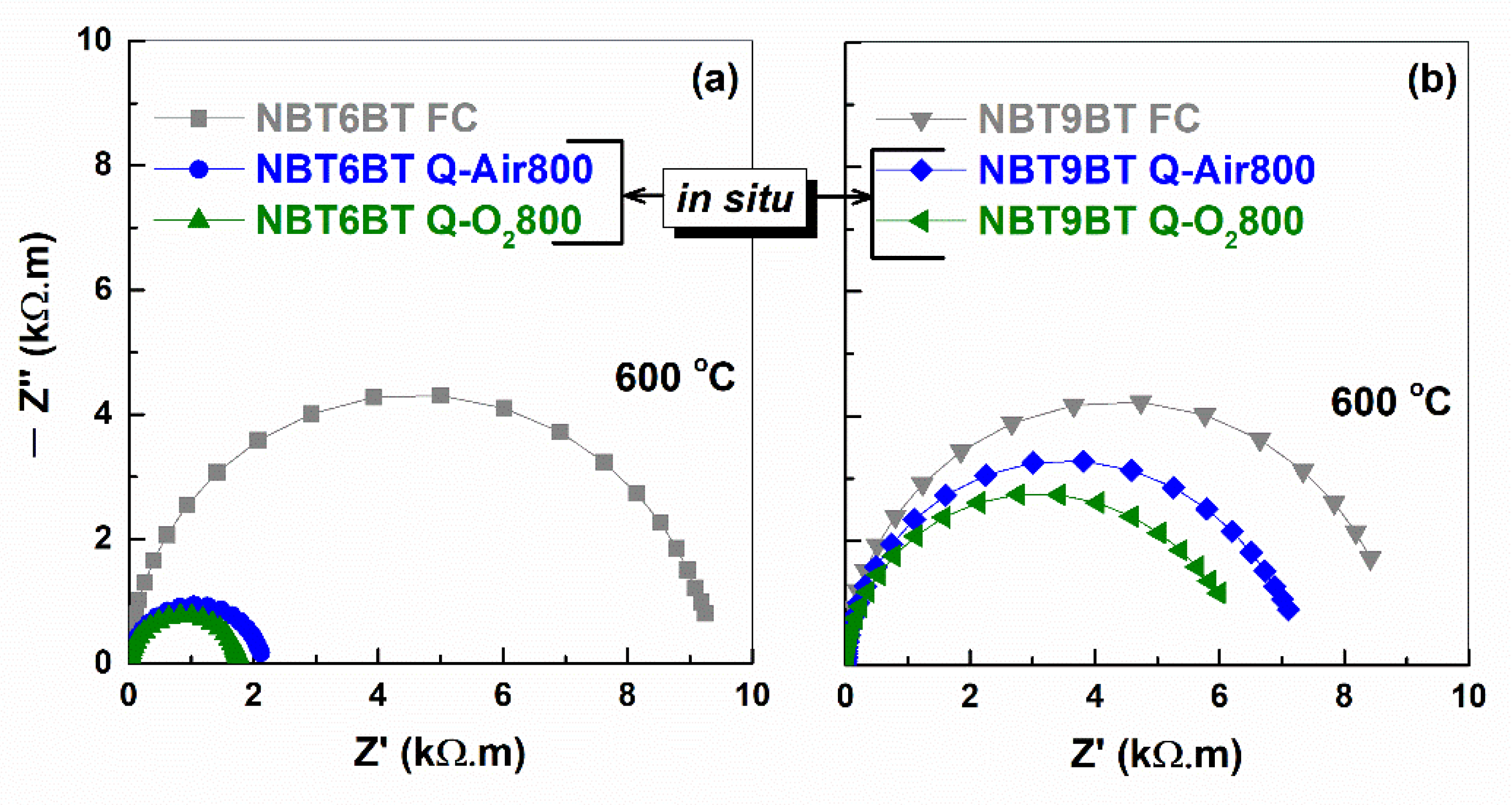
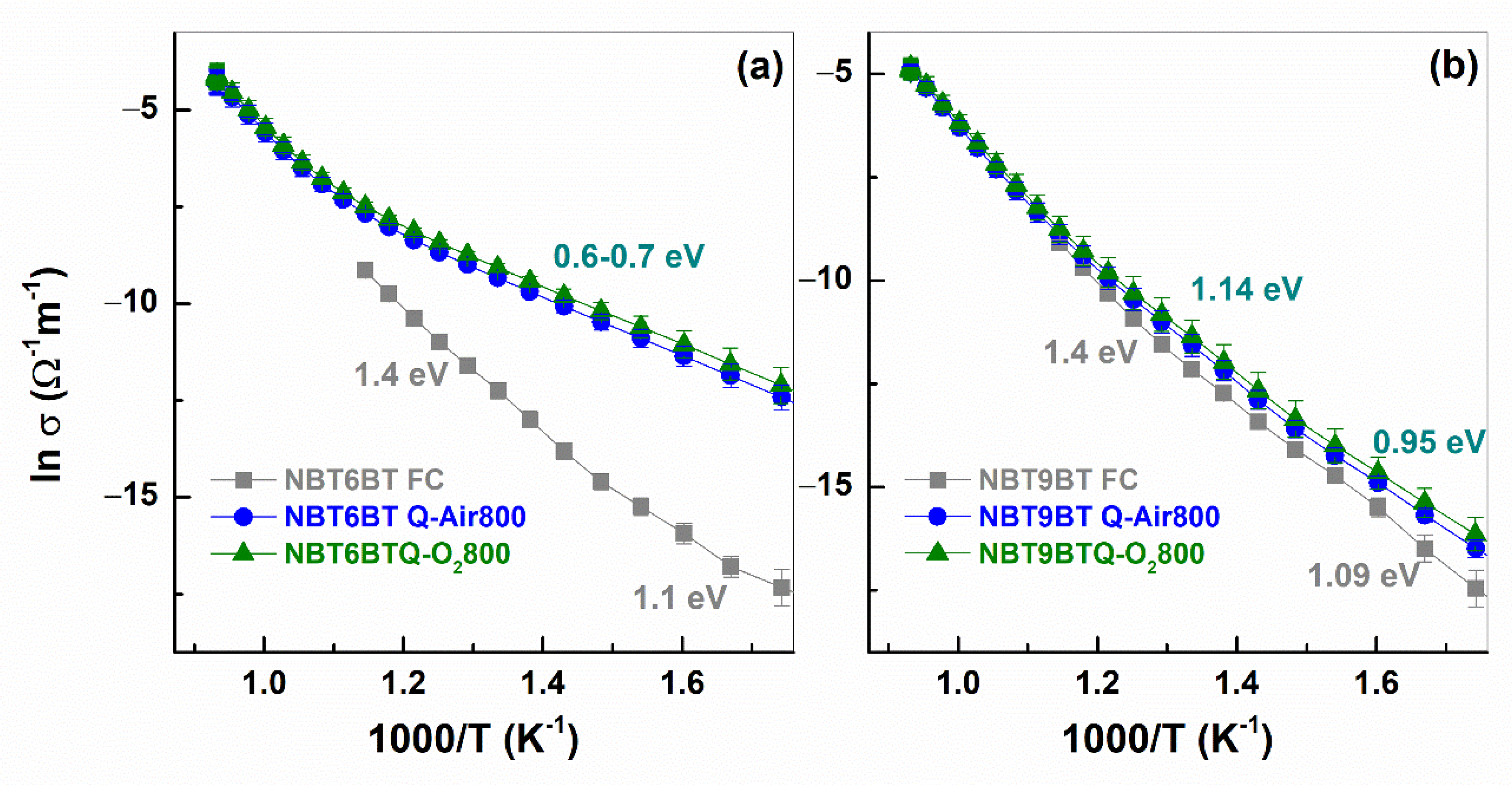
3.2. Annealing Effects on the Conductivity of Quenched Samples
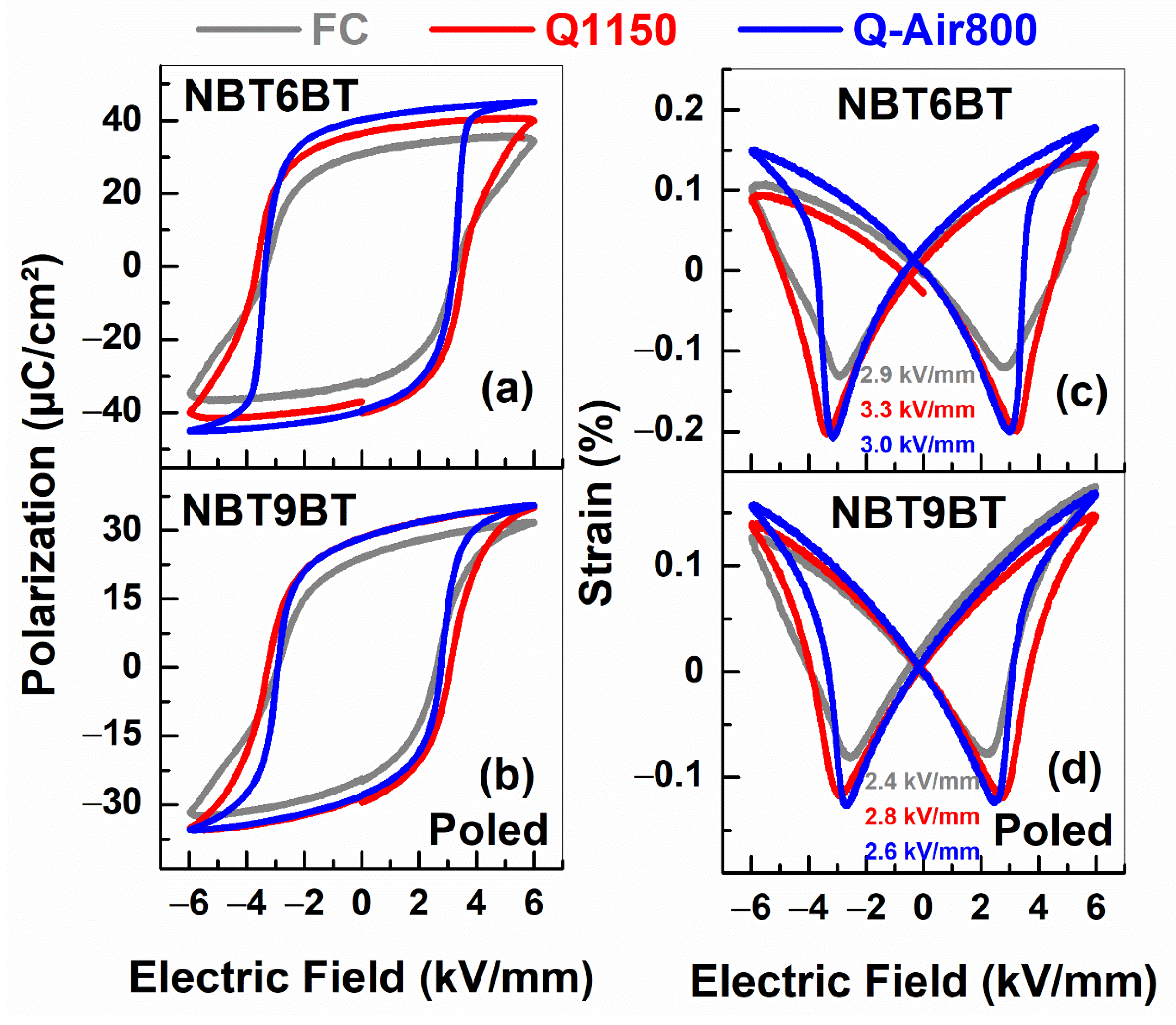
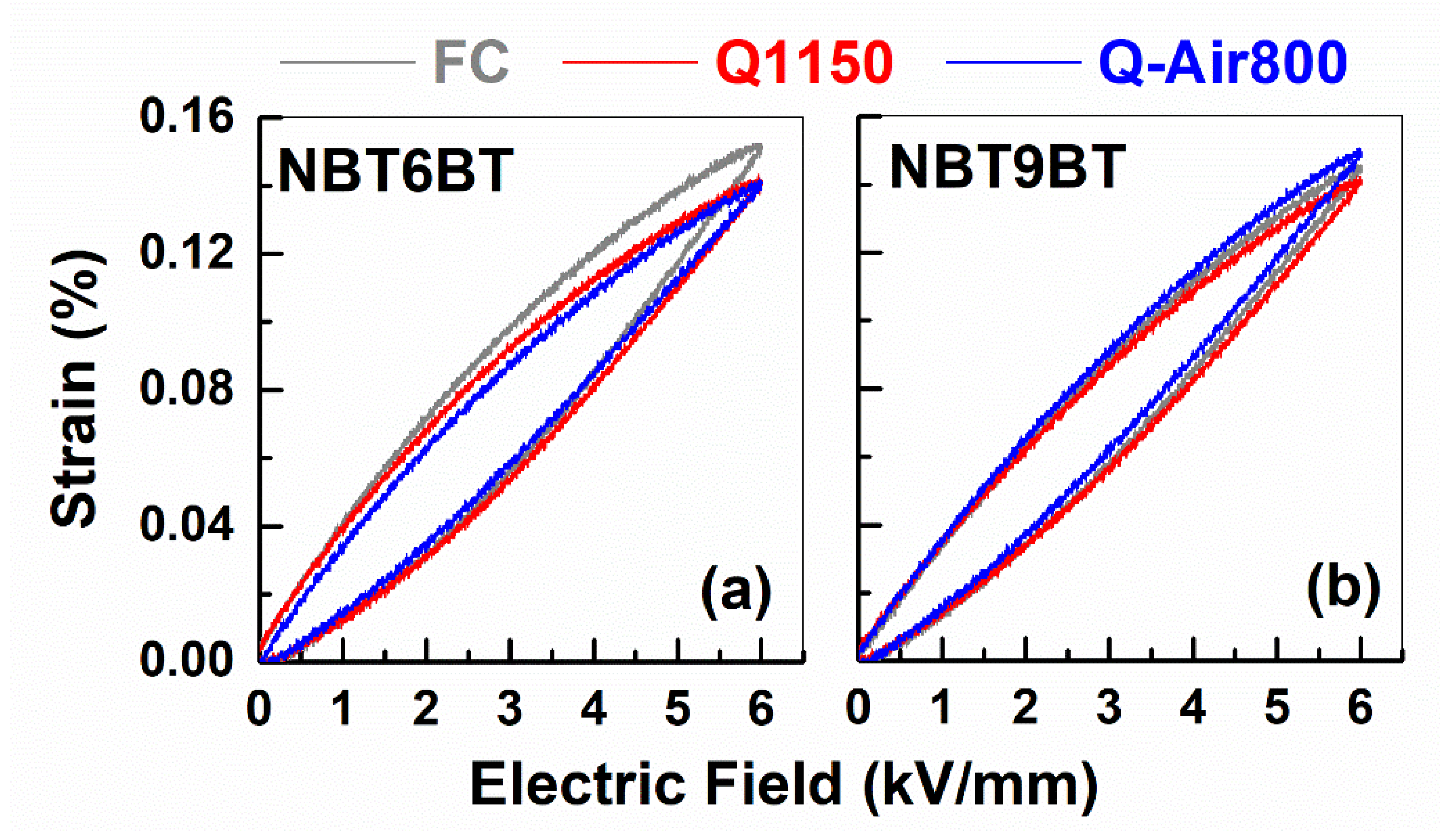
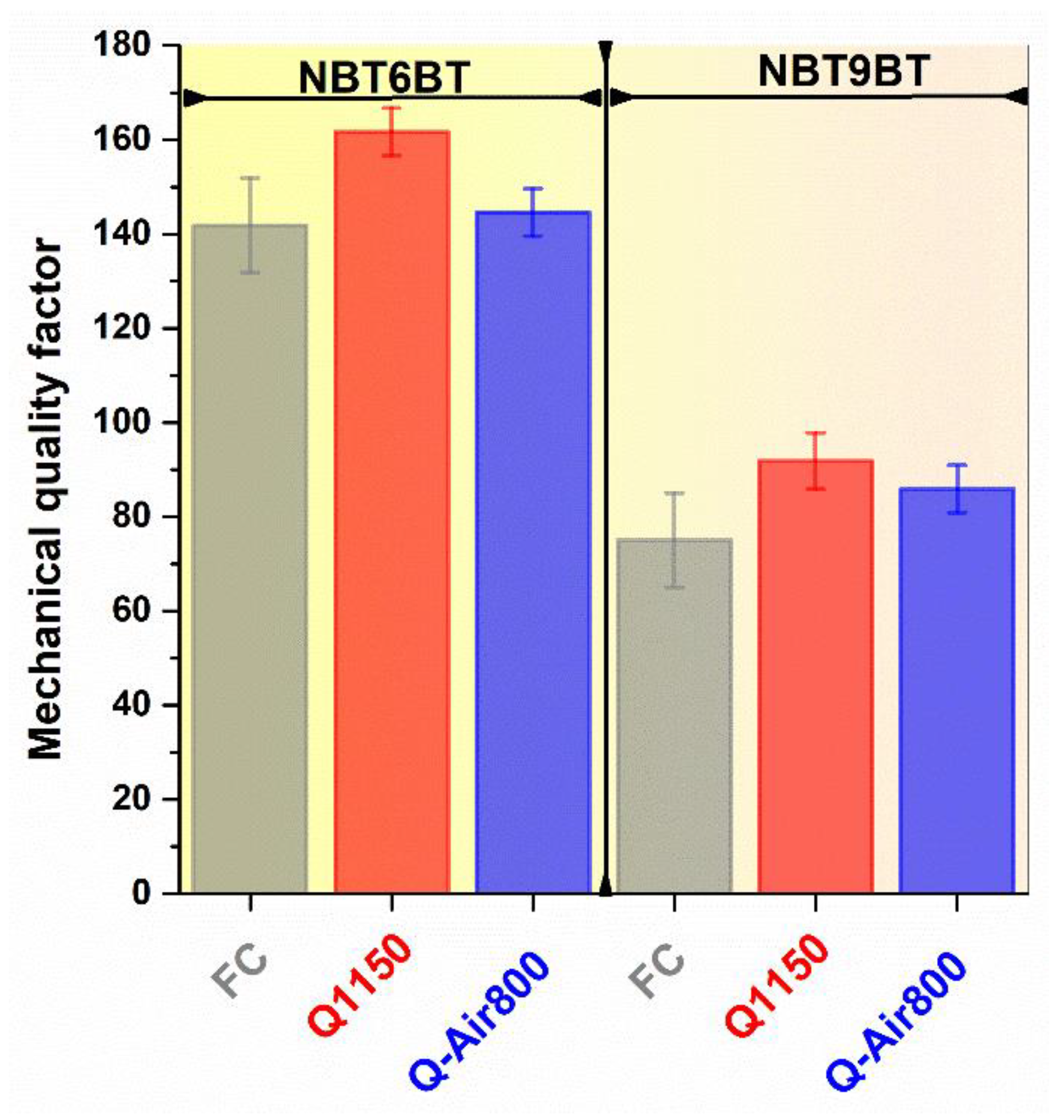
3.3. Electromechanical Hardening
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
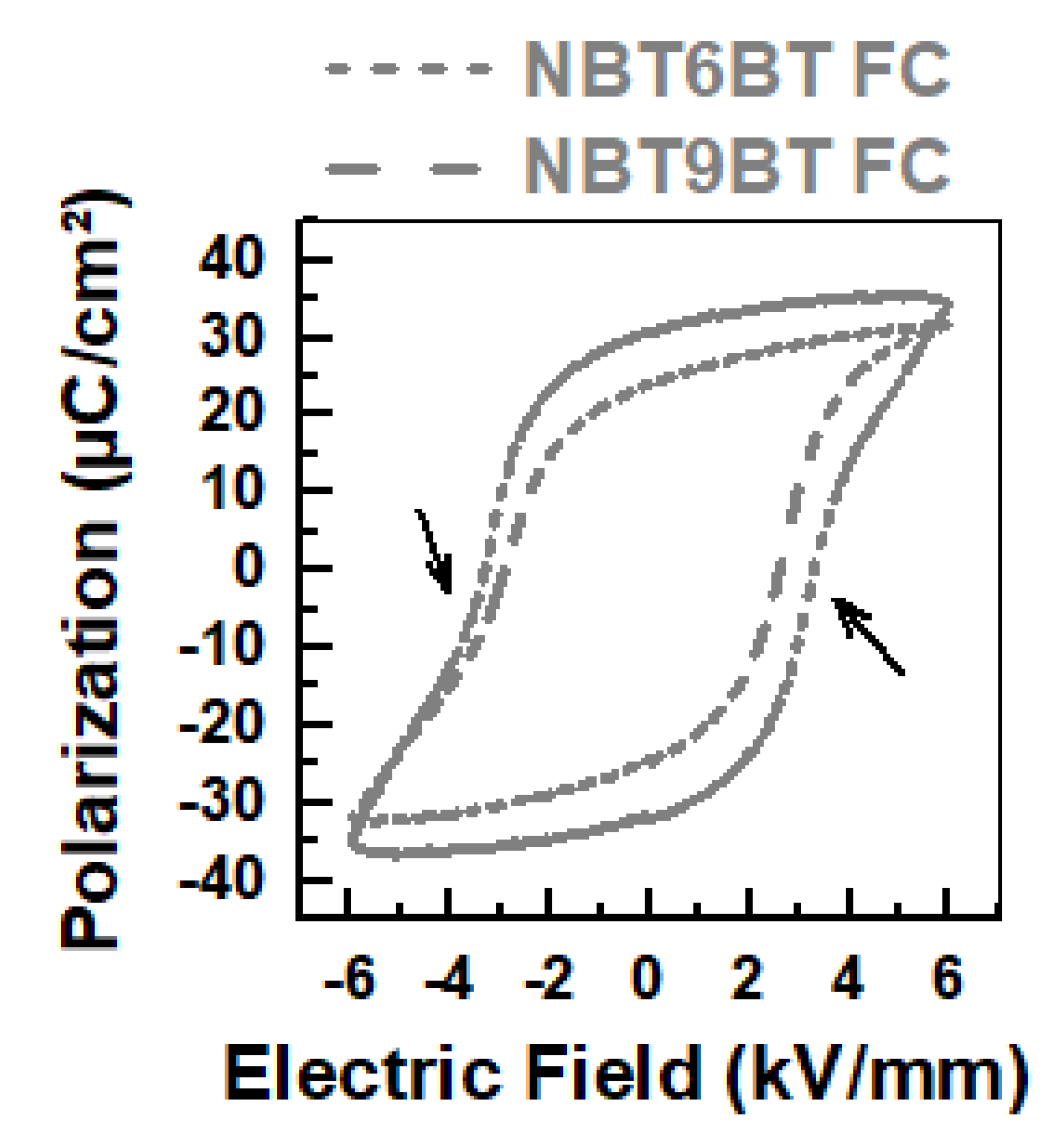
References
- Bell, A.J.; Deubzer, O. Lead-free piezoelectrics—The environmental and regulatory issues. MRS Bull. 2018, 43, 581–587. [Google Scholar] [CrossRef]
- Acosta, M.; Novak, N.; Rojas, V.; Patel, S.; Vaish, R.; Koruza, J.; Rossetti, G.A.; Rödel, J. BaTiO3-based piezoelectrics: Fundamentals, current status, and perspectives. Appl. Phys. Rev. 2017, 4, 041305. [Google Scholar] [CrossRef]
- Koruza, J.; Venkataraman, L.K.; Malič, B. Lead-free perovskite ferroelectrics. Magn. Ferroelectr. Multiferroic Met. Oxides 2018, 2018, 51–69. [Google Scholar] [CrossRef]
- Koruza, J.; Liu, H.; Höfling, M.; Zhang, M.-H.; Veber, P. (K,Na)NbO3-based piezoelectric single crystals: Growth methods, properties, and applications. J. Mater. Res. 2020, 35, 990–1016. [Google Scholar] [CrossRef]
- Rojac, T.; Bencan, A.; Malic, B.; Tutuncu, G.; Jones, J.L.; Daniels, J.E.; Damjanovic, D. BiFeO3 Ceramics: Processing, Electrical, and Electromechanical Properties. J. Am. Ceram. Soc. 2014, 97, 1993–2011. [Google Scholar] [CrossRef]
- Wang, D.; Wang, G.; Murakami, S.; Fan, Z.; Feteira, A.; Zhou, D.; Sun, S.; Zhao, Q.; Reaney, I.M. BiFeO3-BaTiO3: A new generation of lead-free electroceramics. J. Adv. Dielectr. 2018, 8. [Google Scholar] [CrossRef]
- Li, M.; Pietrowski, M.J.; De Souza, R.A.; Zhang, H.; Reaney, I.M.; Cook, S.N.; Kilner, J.A.; Sinclair, D.C. A family of oxide ion conductors based on the ferroelectric perovskite Na0.5Bi0.5TiO3. Nat. Mater. 2014, 13, 31–35. [Google Scholar] [CrossRef]
- Höfling, M.; Steiner, S.; Hoang, A.-P.; Seo, I.-T.; Frömling, T. Optimizing the defect chemistry of Na1/2Bi1/2TiO3-based materials: Paving the way for excellent high temperature capacitors. J. Mater. Chem. C 2018, 6, 4769–4776. [Google Scholar] [CrossRef]
- Tou, T.; Hamaguti, Y.; Maida, Y.; Yamamori, H.; Takahashi, K.; Terashima, Y. Properties of (Bi0.5Na0.5)TiO3–BaTiO3–(Bi0.5Na0.5)(Mn1/3Nb2/3)O3 Lead-Free Piezoelectric Ceramics and Its Application to Ultrasonic Cleaner. Jpn. J. Appl. Phys. 2009, 48, 07GM03. [Google Scholar] [CrossRef]
- Doshida, Y.; Shimizu, H.; Mizuno, Y.; Tamura, H. Investigation of High-Power Properties of (Bi,Na,Ba)TiO3 and (Sr,Ca)2NaNb5O15 Piezoelectric Ceramics. Jpn. J. Appl. Phys. 2013, 52, 7. [Google Scholar] [CrossRef]
- Wang, X.; Venkataraman, L.K.; Tan, C.; Li, Y. Fracture behavior in electrically poled alkaline bismuth- and potassium- based lead-free piezoceramics using Vickers indentation. Scr. Mater. 2021, 194, 113647. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, M.; Chen, W.; Liu, H.-X.; Kim, B.-H.; Ahn, B.-K. Effect of CoO additive on structure and electrical properties of (Na0.5Bi0.5)0.93Ba0.07TiO3 ceramics prepared by the citrate method. Acta Mater. 2008, 56, 642–650. [Google Scholar] [CrossRef]
- Li, L.; Zhu, M.; Zhou, K.; Wei, Q.; Zheng, M.; Hou, Y. Delayed thermal depolarization of Bi0.5Na0.5TiO3-BaTiO3 by doping acceptor Zn2+ with large ionic polarizability. J. Appl. Phys. 2017, 122, 204104. [Google Scholar] [CrossRef]
- Venkataraman, L.K.; Zhu, T.; Salazar, M.P.; Hofmann, K.; Iqbal Waidha, A.; Jaud, J.C.; Groszewicz, P.B.; Rödel, J. Thermal depolarization and electromechanical hardening in Zn2+-doped Na1/2Bi1/2TiO3-BaTiO3. J. Am. Ceram. Soc. 2021. [Google Scholar] [CrossRef]
- Groh, C.; Franzbach, D.J.; Jo, W.; Webber, K.G.; Kling, J.; Schmitt, L.A.; Kleebe, H.-J.; Jeong, S.-J.; Lee, J.-S.; Roedel, J. Relaxor/Ferroelectric Composites: A Solution in the Quest for Practically Viable Lead-Free Incipient Piezoceramics. Adv. Funct. Mater. 2013, 24, 356–362. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, Z.; Guo, F.-F.; Liu, W.-C.; Ning, H.; Chen, Y.-F.; Lu, M.-H.; Yang, B.; Chen, J.; Zhang, S.-T.; et al. Semiconductor/relaxor 0–3 type composites without thermal depolarization in Bi0.5Na0.5TiO3-based lead-free piezoceramics. Nat. Commun. 2015, 6, 6615. [Google Scholar] [CrossRef]
- Yin, J.; Wang, Y.; Zhang, Y.; Wu, B.; Wu, J. Thermal depolarization regulation by oxides selection in lead-free BNT/oxides piezoelectric composites. Acta Mater. 2018, 158, 269–277. [Google Scholar] [CrossRef]
- Muramatsu, H.; Nagata, H.; Takenaka, T. Quenching effects for piezoelectric properties on lead-free (Bi1/2Na1/2)TiO3 ceramics. Jpn. J. Appl. Phys. 2016, 55, 10TB07. [Google Scholar] [CrossRef]
- Koch, L.; Steiner, S.; Meyer, K.-C.; Seo, I.-T.; Albe, K.; Frömling, T. Ionic conductivity of acceptor doped sodium bismuth titanate: Influence of dopants, phase transitions and defect associates. J. Mater. Chem. C 2017, 5, 8958–8965. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, Y.; Withers, R.L.; Brink, F.; Chen, H. Large Electric Field-Induced Strain and Antiferroelectric Behavior in (1-x)(Na0.5Bi0.5)TiO3-xBaTiO3 Ceramics. Chem. Mater. 2011, 23, 219–228. [Google Scholar] [CrossRef]
- Hu, H.; Zhu, M.; Xie, F.; Lei, N.; Chen, J.; Hou, Y.; Yan, H. Effect of Co2O3 Additive on Structure and Electrical Properties of 85(Bi1/2Na1/2)TiO3-12(Bi1/2K1/2)TiO3-3BaTiO3 Lead-Free Piezoceramics. J. Am. Ceram. Soc. 2009, 92, 2039–2045. [Google Scholar] [CrossRef]
- Lalitha, K.V.; Riemer, L.M.; Koruza, J.; Rödel, J. Hardening of electromechanical properties in piezoceramics using a composite approach. Appl. Phys. Lett. 2017, 111, 022905. [Google Scholar] [CrossRef]
- Lalitha, K.V.; Koruza, J.; Rödel, J. Propensity for spontaneous relaxor-ferroelectric transition in quenched (Na1/2Bi1/2)TiO3-BaTiO3 compositions. Appl. Phys. Lett. 2018, 113, 252902. [Google Scholar] [CrossRef]
- Wei, Q.; Riaz, A.; Zhukov, S.; Hofmann, K.; Zhu, M.; Hou, Y.; Rödel, J.; Kodumudi Venkataraman, L. Quenching-circumvented ergodicity in relaxor Na1/2Bi1/2TiO3-BaTiO3-K0.5Na0.5NbO3. J. Am. Ceram. Soc. 2021. [Google Scholar] [CrossRef]
- Ma, C.; Guo, H.; Beckman, S.P.; Tan, X. Creation and Destruction of Morphotropic Phase Boundaries through Electrical Poling: A Case Study of Lead-Free(Bi1/2Na1/2)TiO3−BaTiO3 Piezoelectrics. Phys. Rev. Lett. 2012, 109, 107602. [Google Scholar] [CrossRef]
- Jo, W.; Daniels, J.E.; Jones, J.L.; Tan, X.; Thomas, P.A.; Damjanovic, D.; Roedel, J. Evolving morphotropic phase boundary in lead-free (Bi1/2Na1/2)TiO3–BaTiO3 piezoceramics. J. Appl. Phys. 2011, 109, 014110. [Google Scholar] [CrossRef]
- Seifert, D.; Li, L.; Lee, K.-Y.; Hoffmann, M.; Sinclair, D.; Hinterstein, M. Processing and properties of translucent bismuth sodium titanate ceramics. J. Eur. Ceram. Soc. 2021, 41, 1221–1229. [Google Scholar] [CrossRef]
- Seo, I.-T.; Steiner, S.; Frömling, T. The effect of A site non-stoichiometry on 0.94(NayBix)TiO3-0.06BaTiO3. J. Eur. Ceram. Soc. 2017, 37, 1429–1436. [Google Scholar] [CrossRef]
- Schader, F.H.; Wang, Z.; Hinterstein, M.; Daniels, J.E.; Webber, K.G. Stress-modulated relaxor-to-ferroelectric transition in lead-free(Na1/2Bi1/2)TiO3−BaTiO3 ferroelectrics. Phys. Rev. B 2016, 93, 134111. [Google Scholar] [CrossRef]
- Anton, E.-M.; Jo, W.; Damjanovic, D.; Rödel, J. Determination of depolarization temperature of (Bi1/2Na1/2)TiO3-based lead-free piezoceramics. J. Appl. Phys. 2011, 110, 094108. [Google Scholar] [CrossRef]
- Härdtl, K. Electrical and mechanical losses in ferroelectric ceramics. Ceram. Int. 1982, 8, 121–127. [Google Scholar] [CrossRef]
- Genenko, Y.A.; Glaum, J.; Hoffmann, M.J.; Albe, K. Mechanisms of aging and fatigue in ferroelectrics. Mater. Sci. Eng. B 2015, 192, 52–82. [Google Scholar] [CrossRef]
- European Standard EN 50324-2. Piezoelectric Properties of Ceramic Materials and Components Part 2: Methods of Measurement—Low Power. European Committee for Standards: Brussels, Belgium, 2002. [Google Scholar]
- Craciun, F.; Galassi, C.; Birjega, R. Electric-field-induced and spontaneous relaxor-ferroelectric phase transitions in (Na1/2Bi1/2)1 − xBaxTiO3. J. Appl. Phys. 2012, 112, 124106. [Google Scholar] [CrossRef]
- Kumar, N.; Shi, X.; Hoffman, M. Spontaneous relaxor to ferroelectric transition in lead-free relaxor piezoceramics and the role of point defects. J. Eur. Ceram. Soc. 2020, 40, 2323–2330. [Google Scholar] [CrossRef]
- Ma, C.; Tan, X.; Dul’kin, E.; Roth, M. Domain structure-dielectric property relationship in lead-free (1−x)(Bi1/2Na1/2)TiO3-xBaTiO3 ceramics. J. Appl. Phys. 2010. [Google Scholar] [CrossRef]
- Fetzer, A.-K.; Wohninsland, A.; Hofmann, K.; Clemens, O.; Venkataraman, L.K.; Kleebe, H.-J. Domain structure and phase evolution in quenched and furnace cooled lead-free Na1/2Bi1/2TiO3–BaTiO3 ceramics. Open Ceram. 2021, 5, 100077. [Google Scholar] [CrossRef]
- Li, Z.T.; Liu, H.; Thong, H.C.; Xu, Z.; Zhang, M.H.; Yin, J.; Li, J.F.; Wang, K.; Chen, J. Enhanced Temperature Stability and Defect Mechanism of BNT-Based Lead-Free Piezoceramics Investigated by a Quenching Process. Adv. Electron. Mater. 2018, 1800756. [Google Scholar] [CrossRef]
- Ren, P.; Wang, J.; Wang, Y.; Lalitha, K.V.; Zhao, G. Origin of enhanced depolarization temperature in quenched Na0.5Bi0.5TiO3-BaTiO3 ceramics. J. Eur. Ceram. Soc. 2020, 40, 2964–2969. [Google Scholar] [CrossRef]
- Zhang, M.-H.; Breckner, P.; Frömling, T.; Rödel, J.; Lalitha, K.V. Role of thermal gradients on the depolarization and conductivity in quenched Na1/2Bi1/2TiO3-BaTiO3. Appl. Phys. Lett. 2020, 116, 262902. [Google Scholar] [CrossRef]
- Li, X.; Nie, S.; Wang, F.; Zhao, X.; Zhang, H.; Luo, H.; Li, G.; Ko, J.-H.; Guo, Z.; Jiang, Z.; et al. Local-structure evidence for a phase transition in a lead-free single crystal of (Na1/2Bi1/2)TiO3−0.06BaTiO3 by absorption fine-structure spectroscopy with synchrotron x-ray radiation. Phys. Rev. B 2020, 101, 104105. [Google Scholar] [CrossRef]
- Moriyoshi, C.; Takeda, S.; Kuroiwa, Y.; Goto, M. Off-centering of a Bi ion in cubic phase of (Bi1/2Na1/2)TiO3. Jpn. J. Appl. Phys. 2014, 53, 09PD02. [Google Scholar] [CrossRef]
- Nagata, H.; Takagi, Y.; Yoneda, Y.; Takenaka, T. Correlation between depolarization temperature and lattice distortion in quenched (Bi1/2Na1/2)TiO3-based ceramics. Appl. Phys. Express 2020, 13, 061002. [Google Scholar] [CrossRef]
- Wohninsland, A.; Fetzer, A.-K.; Riaz, A.; Kleebe, H.-J.; Rödel, J.; Venkataraman, L.K. Correlation between enhanced lattice distortion and volume fraction of polar nanoregions in quenched Na1/2Bi1/2TiO3–BaTiO3 ceramics. Appl. Phys. Lett. 2021, 118, 072903. [Google Scholar] [CrossRef]
- Harada, S.; Takagi, Y.; Nagata, H.; Takenaka, T. Quenching effects on electrical properties of Cu-doped (Bi1/2Na1/2)TiO3-based solid solution ceramics. J. Mater. Res. 2021, 1–8. [Google Scholar] [CrossRef]
| Sample | at 40 °C and 10kHz | TF-R, °C (Poled) | Tm, °C at 1MHz (Unpoled) | TRE, °C (Unpoled) | |
|---|---|---|---|---|---|
| NBT6BT | |||||
| FC | 533 | 656 | 100 | 272 | 231 |
| Q1150 | 523 | 486 | 143 | 272 | 259 |
| Q-Air800 | 664 | 702 | 100 | 261 | 255 |
| Q-O2800 | 638 | 680 | 100 | 261 | 250 |
| NBT9BT | |||||
| FC | 657 | 1041 | 151 | 267 | 268 |
| Q1150 | 227 | 825 | 203 | 267 | 283 |
| Q-Air800 | 549 | 963 | 163 | 259 | 276 |
| Q-O2800 | 416 | 966 | 159 | 258 | 272 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kodumudi Venkataraman, L. Influence of Quenching and Subsequent Annealing on the Conductivity and Electromechanical Properties of Na1/2Bi1/2TiO3-BaTiO3. Materials 2021, 14, 2149. https://doi.org/10.3390/ma14092149
Kodumudi Venkataraman L. Influence of Quenching and Subsequent Annealing on the Conductivity and Electromechanical Properties of Na1/2Bi1/2TiO3-BaTiO3. Materials. 2021; 14(9):2149. https://doi.org/10.3390/ma14092149
Chicago/Turabian StyleKodumudi Venkataraman, Lalitha. 2021. "Influence of Quenching and Subsequent Annealing on the Conductivity and Electromechanical Properties of Na1/2Bi1/2TiO3-BaTiO3" Materials 14, no. 9: 2149. https://doi.org/10.3390/ma14092149
APA StyleKodumudi Venkataraman, L. (2021). Influence of Quenching and Subsequent Annealing on the Conductivity and Electromechanical Properties of Na1/2Bi1/2TiO3-BaTiO3. Materials, 14(9), 2149. https://doi.org/10.3390/ma14092149





