Strategies to Improve the Energy Storage Properties of Perovskite Lead-Free Relaxor Ferroelectrics: A Review
Abstract
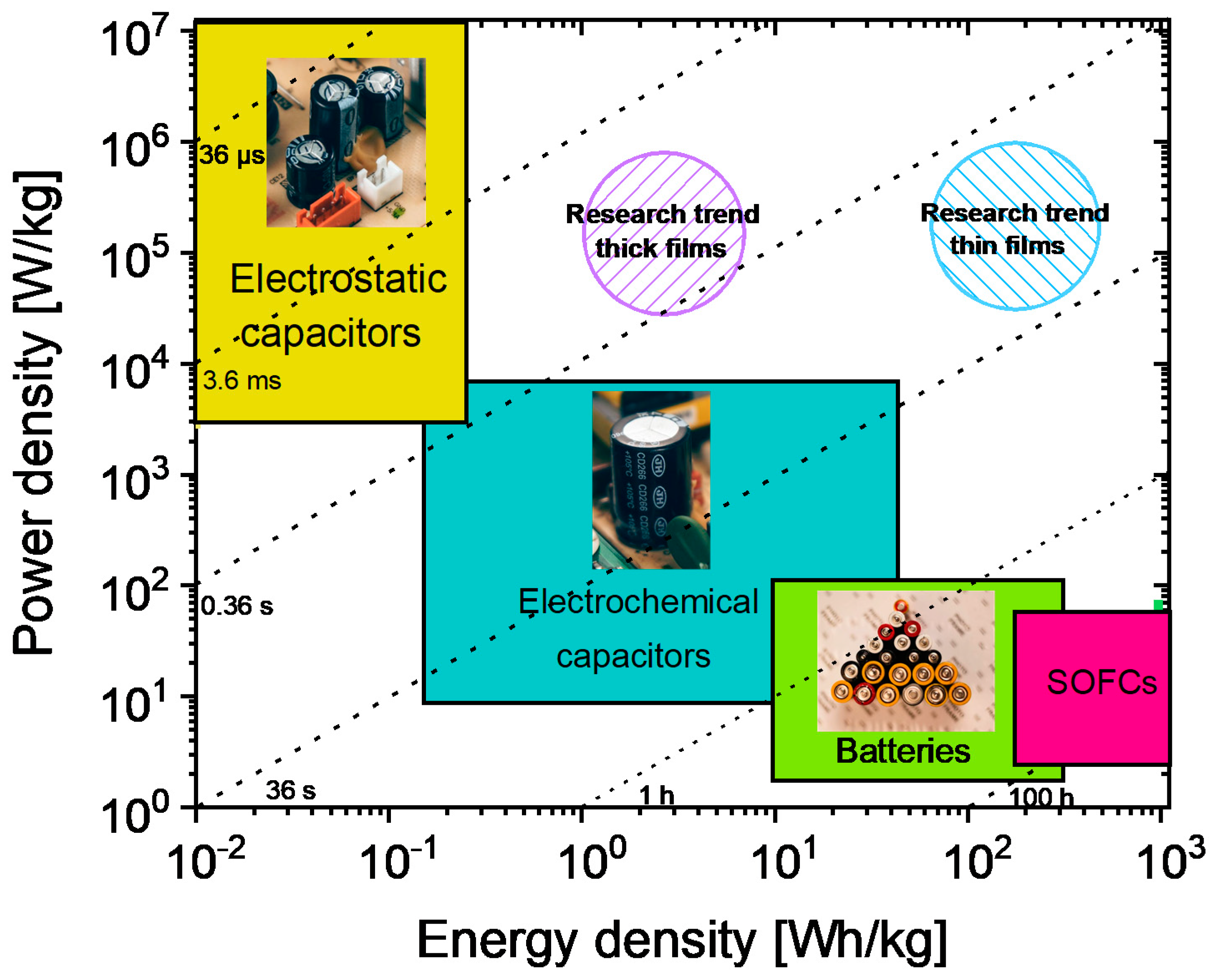
1. Introduction
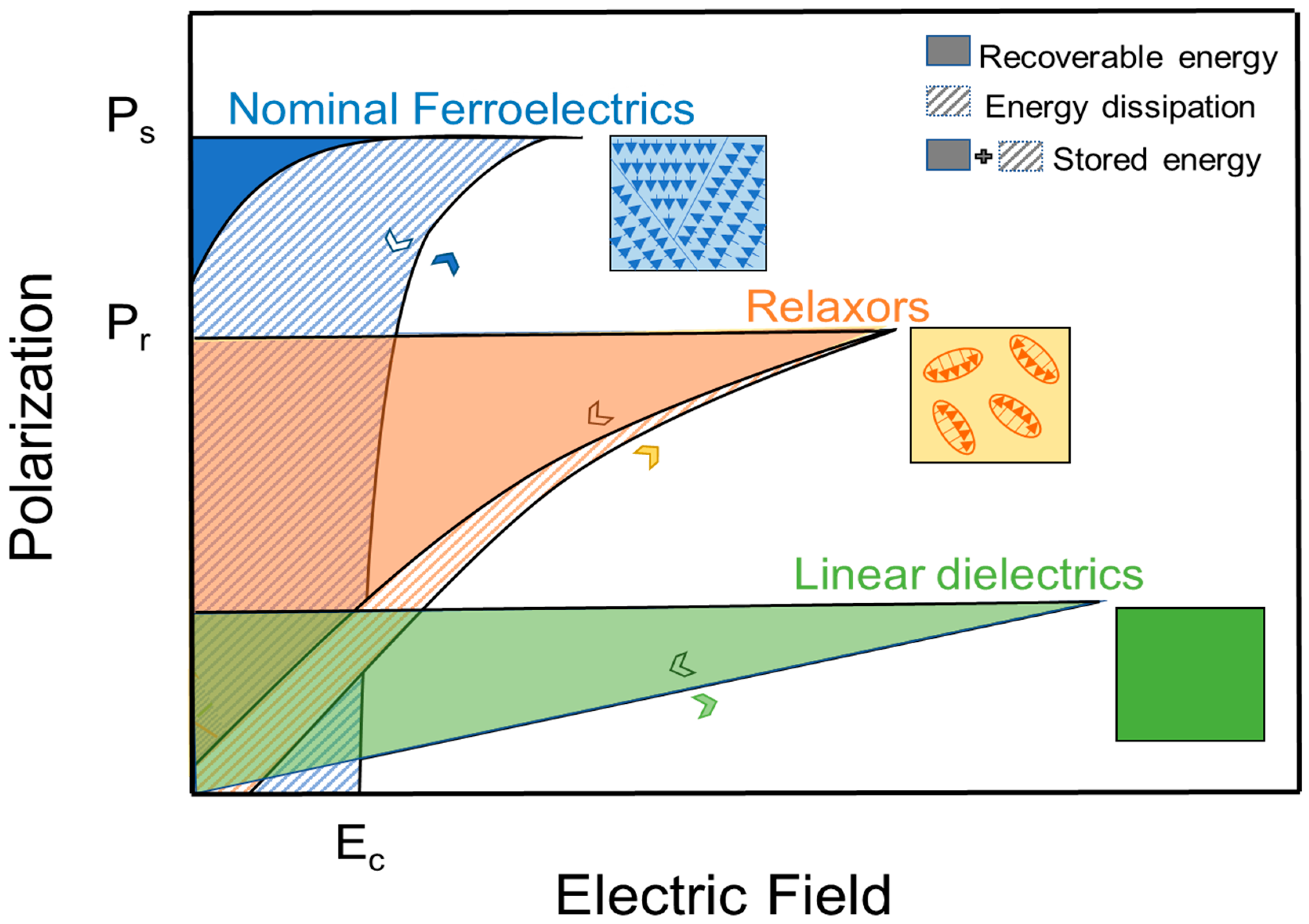
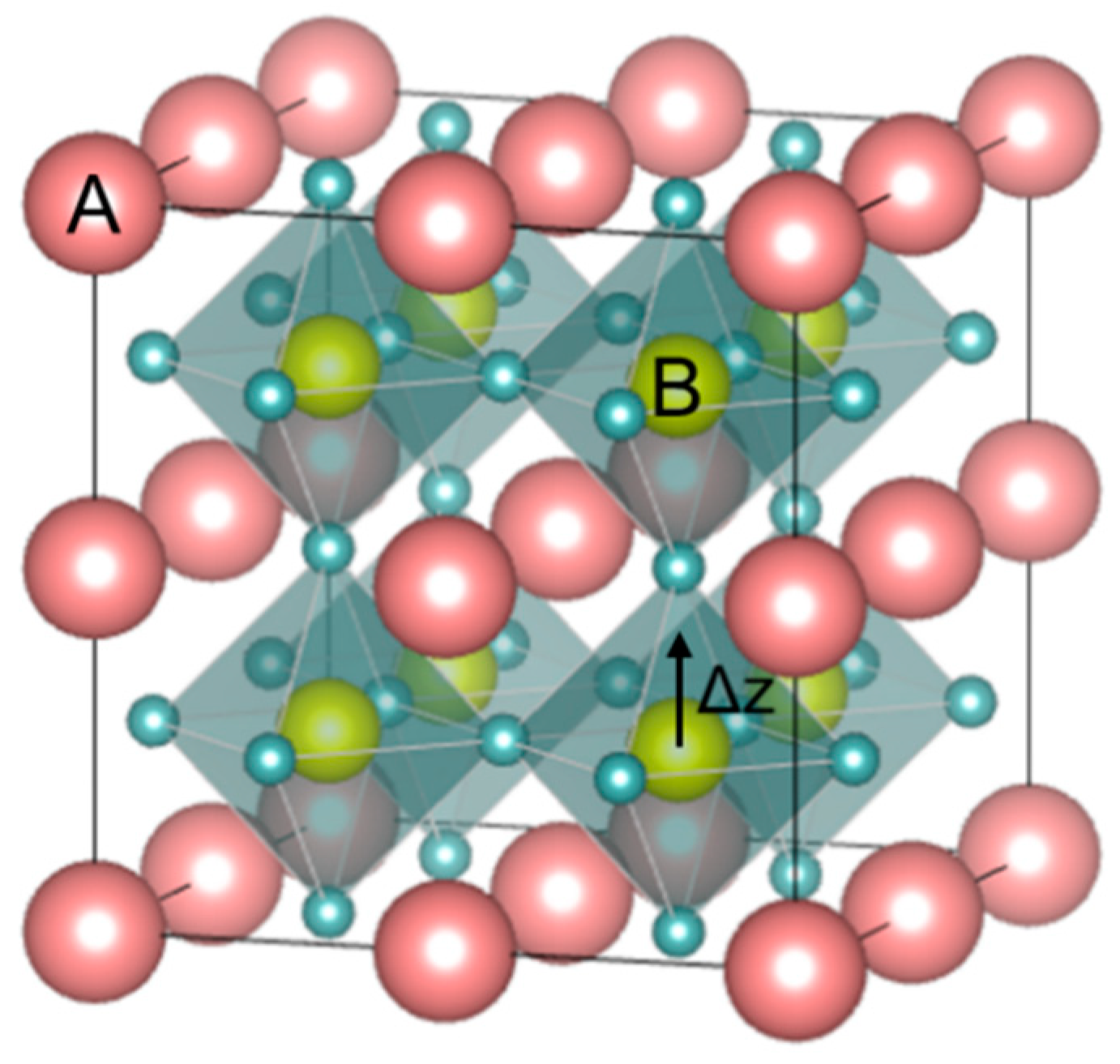
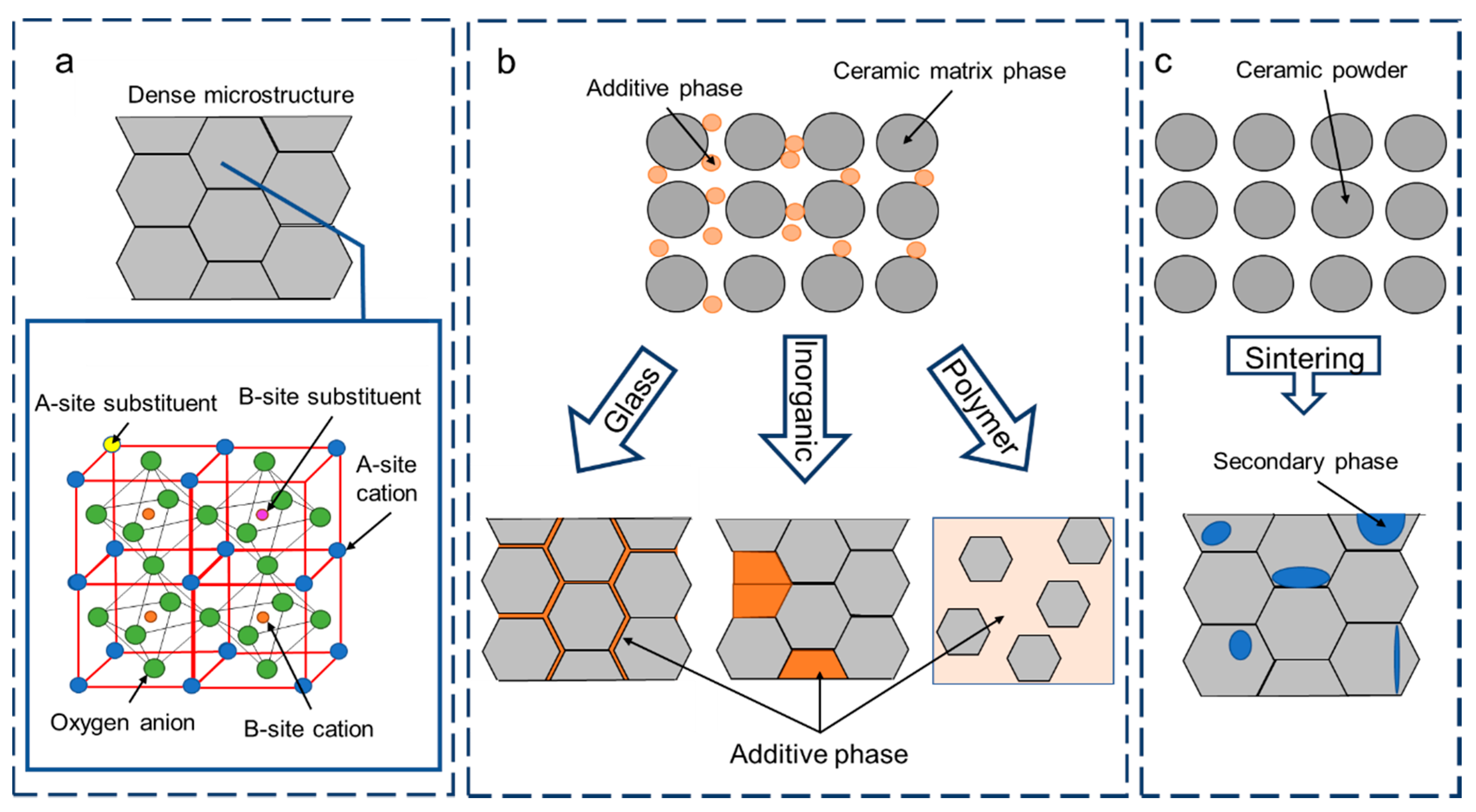
2. Perovskite-Based Relaxor Ferroelectrics
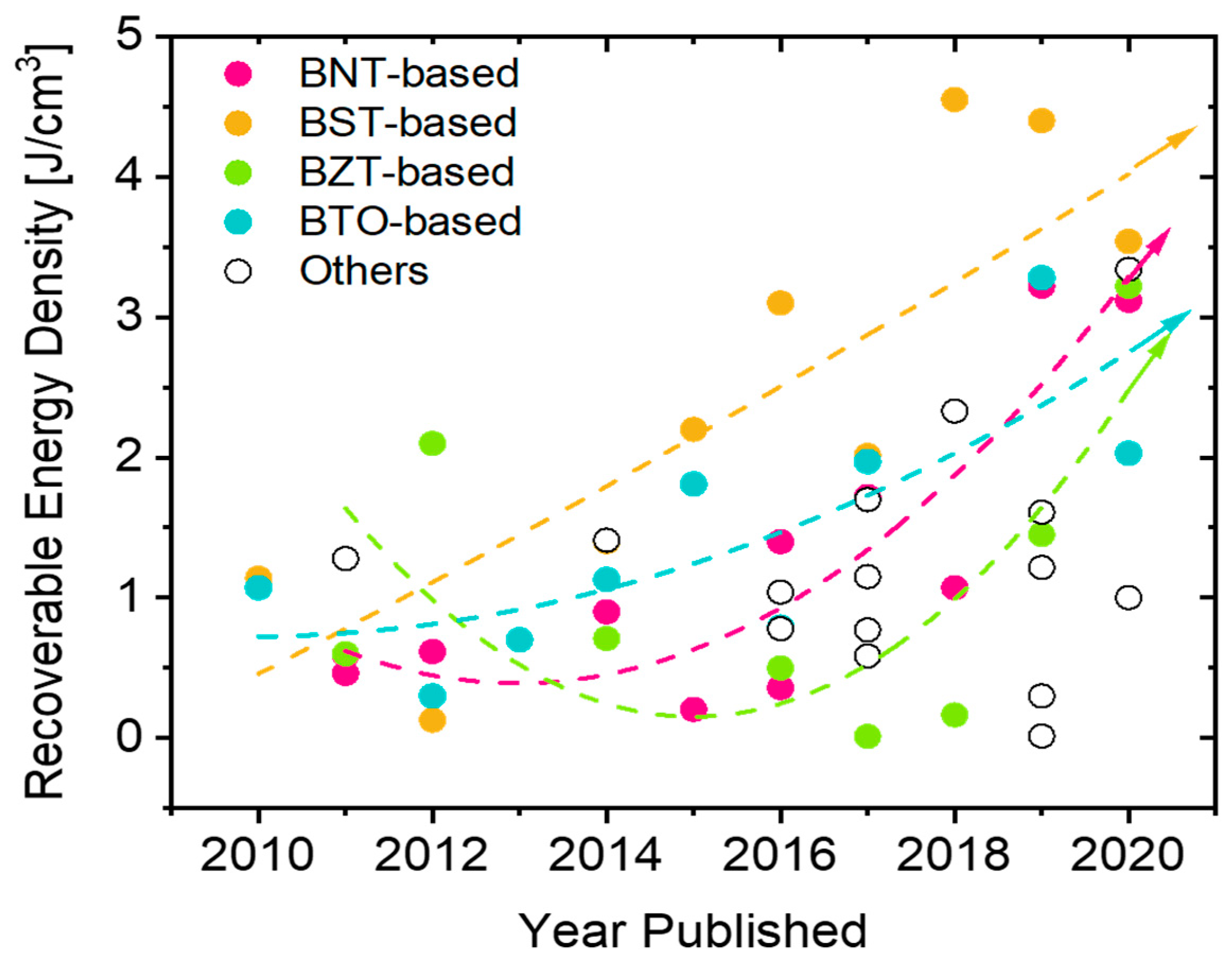
3. Tuning Energy Density by Chemical Substitution
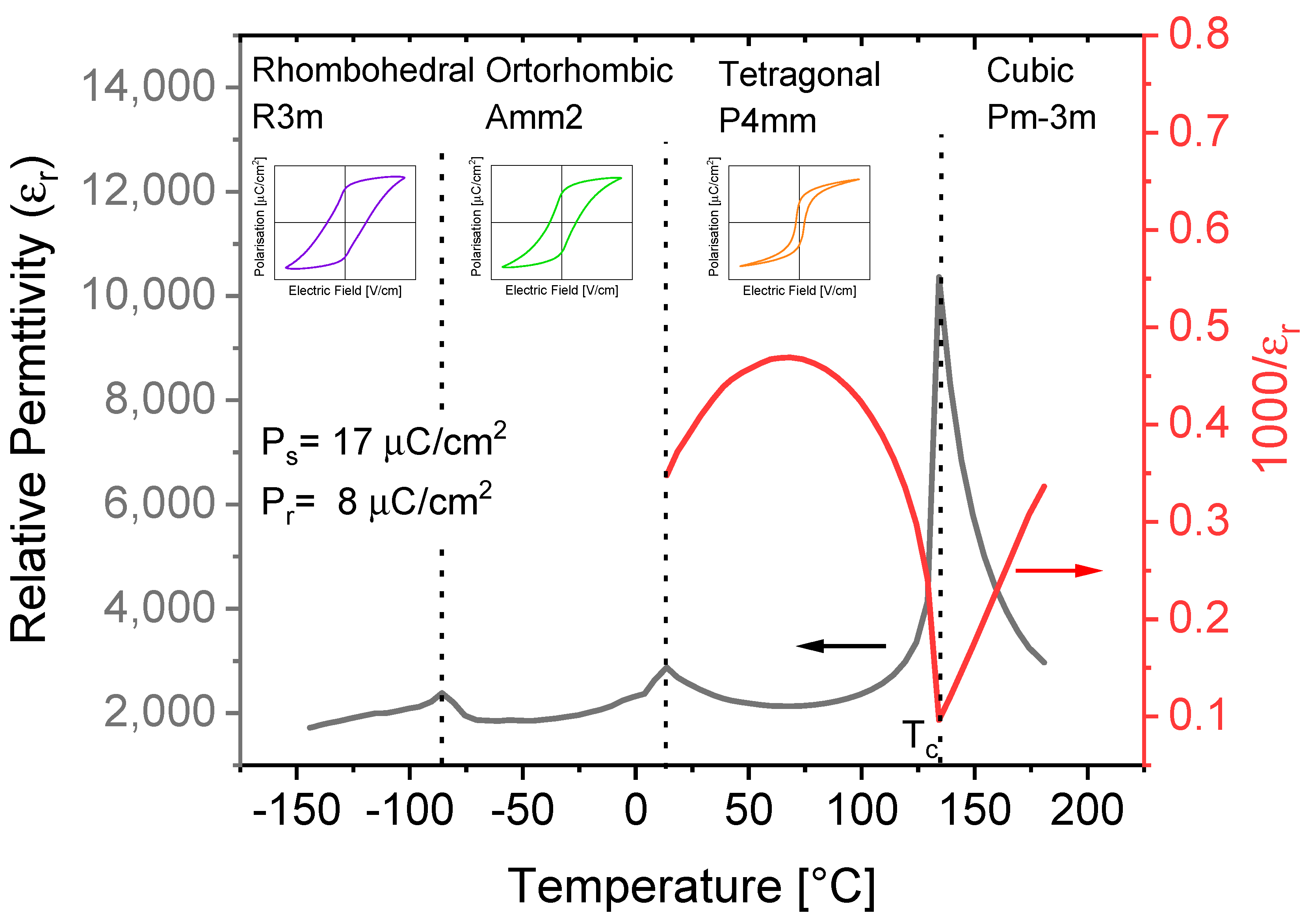
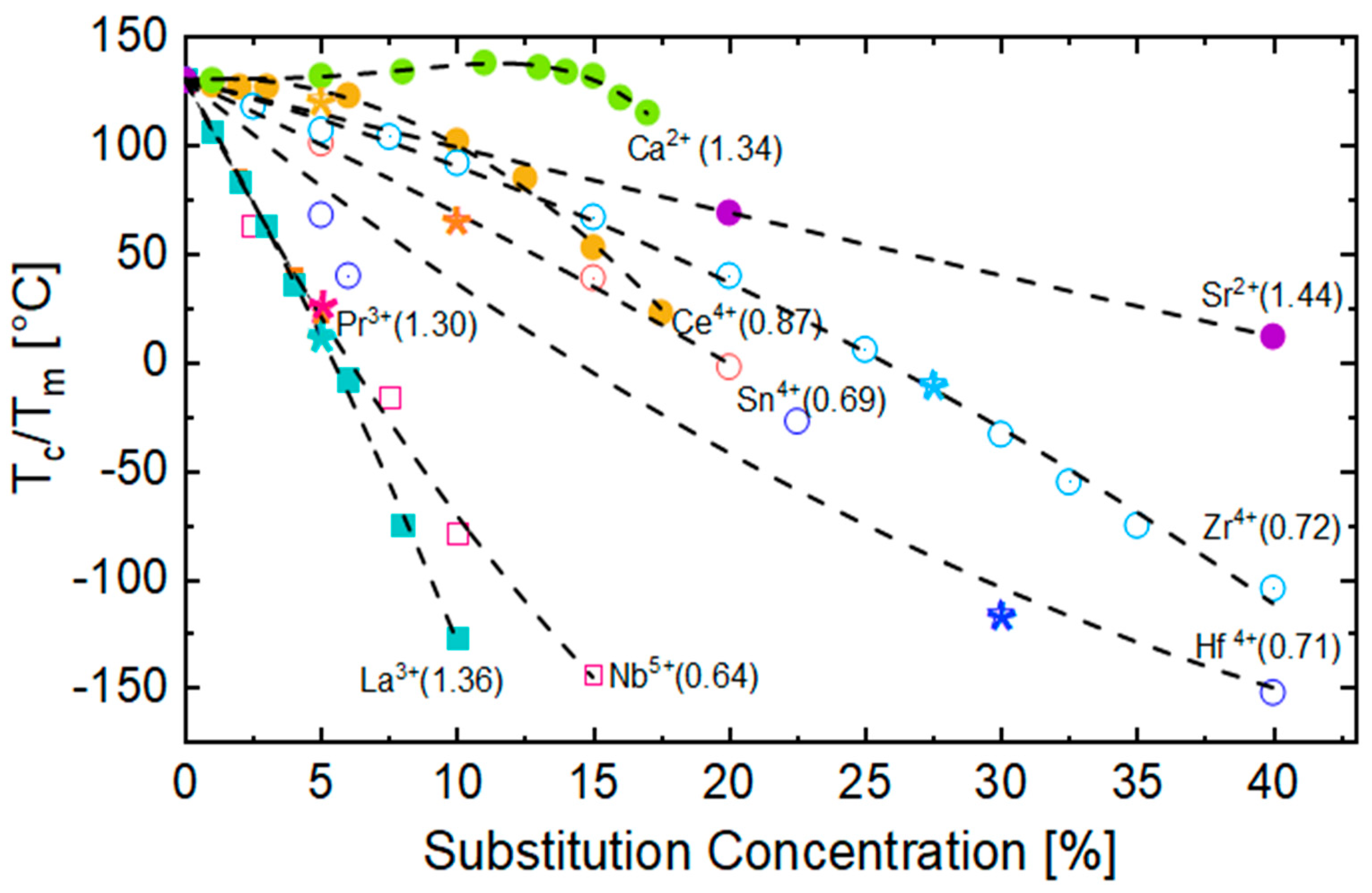
3.1. Effect on Curie Temperature
3.2. Effect on Relative Permittivity
3.3. Effect on Polarization
3.4. Effect on Breakdown Strength
4. Tuning Energy Density by Chemical Additives
4.1. Glass Additives
- During sintering, excessive liquid phase formation with higher glass content could promote grain growth, and increase microstructural defects such as porosity, causing the so-called “de-sintering” phenomenon, ultimately degrading the electrical properties of the system [90].
4.2. Inorganic Additives
4.3. Polymer Additives
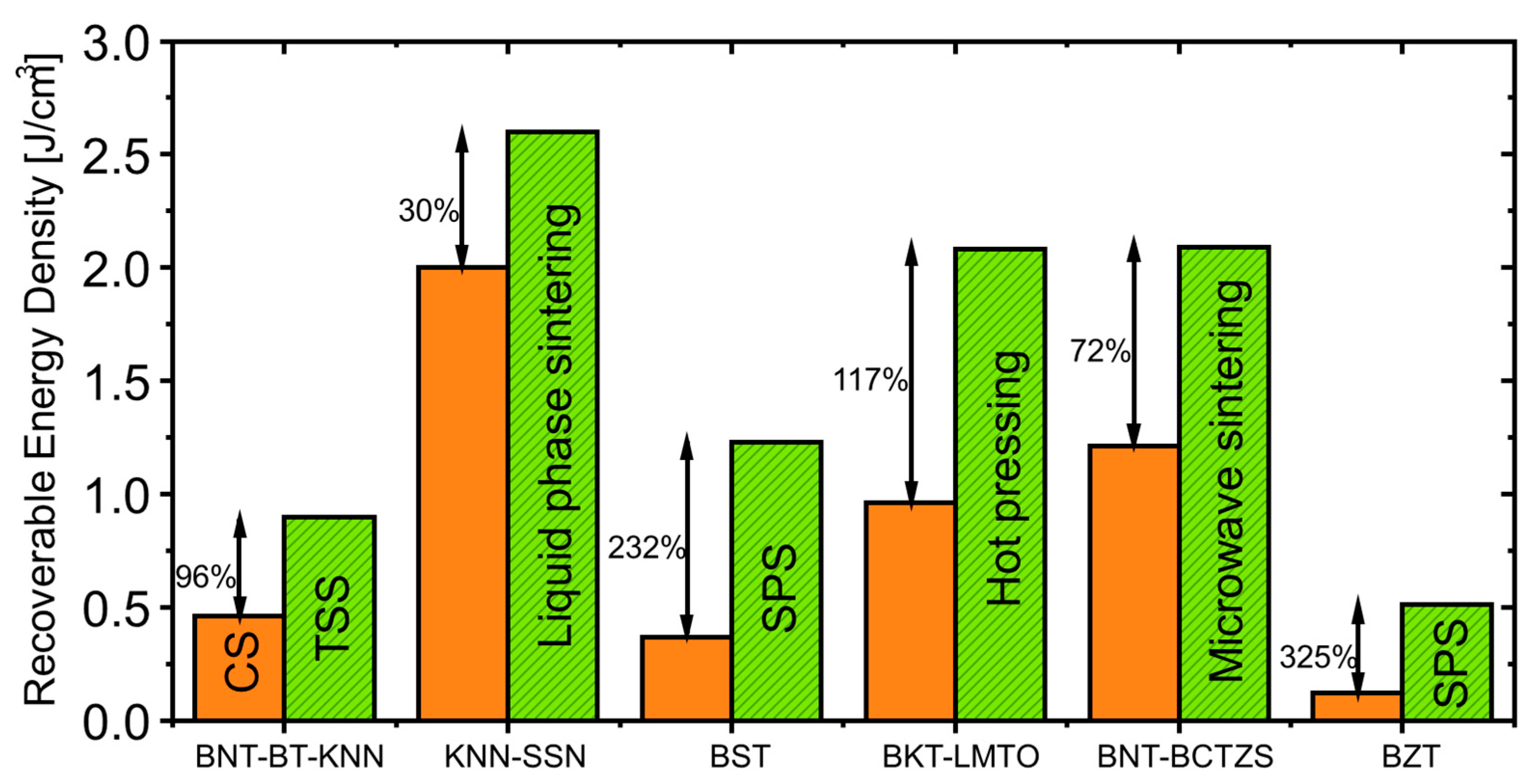
5. Tuning Energy Density by Processing Methods
5.1. Bulk Ceramics
- (a)
- Role of temperature
- (b)
- Role of Pressure
- (c)
- Role of the electric field
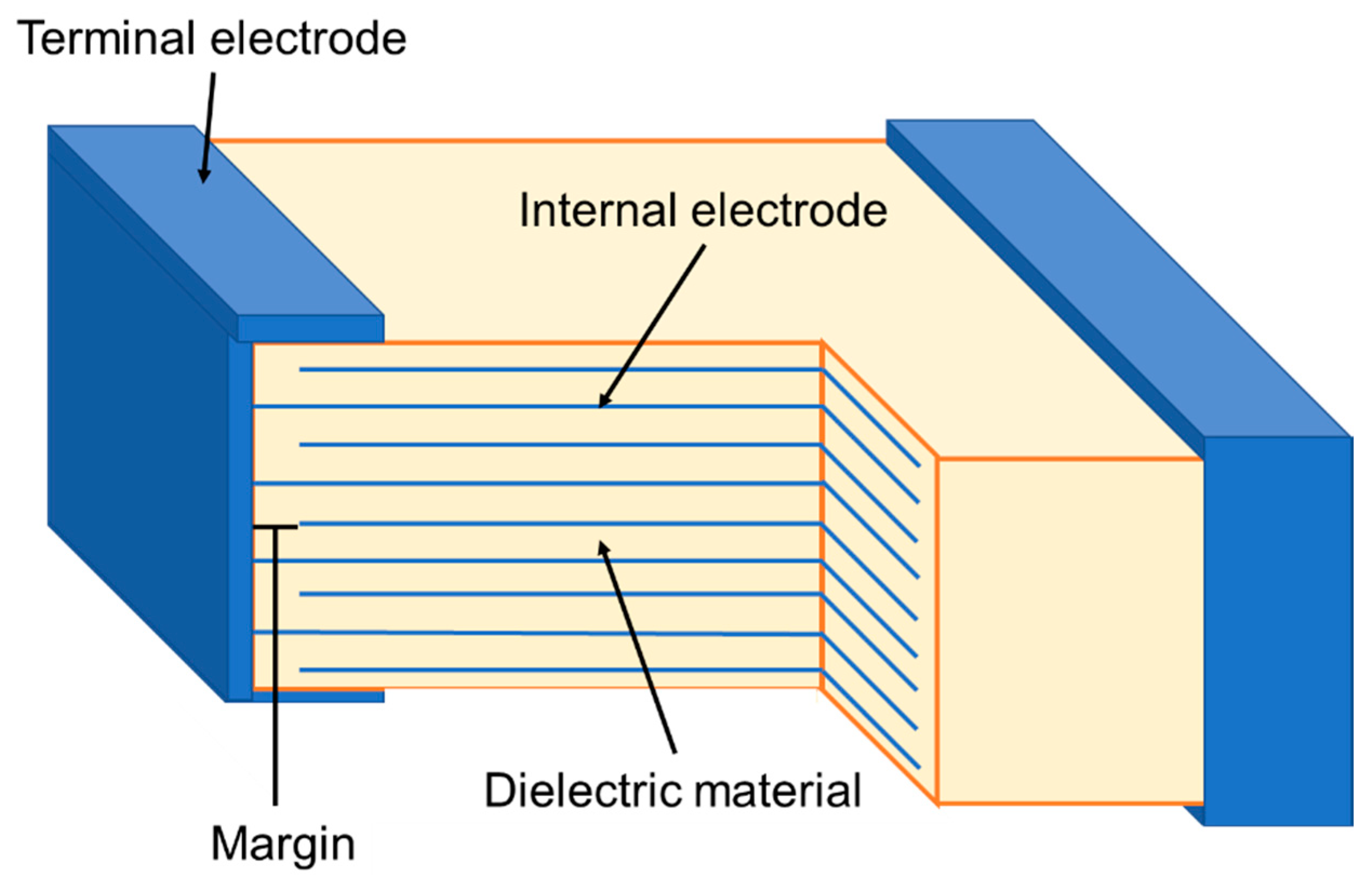
5.2. Multilayer Thick Films
- Capacitance and available area (A) of the dielectric material
- Reduction in voltage requirements
- BDS and sample thickness
- (a)
- Bulk ceramics to MLCCs:
- The sintering temperature in TSS can be substantially lower than the conventional sintering, which makes it beneficial to co-fire electrodes that are cheap and have lower melting temperatures.
- The G is low in TSS, making it feasible to reduce d of dielectric layers that can significantly reduce the defect concentration and increase BDS.
- (b)
- Composite multilayer architectures
- (c)
- Strategies related to multilayer design
- (d)
- Strategies related to tape casting parameters
5.3. Thin Films
- (a)
- Choice of substrate
- (b)
- Choice of deposition techniques
- Sputtering and PLD allow having tight control over the stoichiometry and microstructure of the deposited film. This is especially advantageous to deposit films of complex chemistry (like relaxors) with desired microstructure and orientation [170]. The biggest drawback of physical methods like PLD is the high infrastructure cost [158], together with a non-trivial control on the microstructural properties of the films (unless in-situ characterization methods are used).
- The sol-gel technique has high versatility, suitability to deposit almost all the perovskite compounds, simplicity, low infrastructure cost, and the possibility of large-scale deposition. Also, control on microstructural properties of the films, including grain size and orientation, and film thickness, is possible by tuning the concentration of the precursor solutions and the thermal cycles. However, films produced by sol-gel usually contain more microstructural defects than by PLD, and this can strongly influence the ED of the deposited material [160,161,172].
- (c)
- Choice of processing parameters
- (d)
- Review on high ED thin-film systems
- (e)
- Thin-film-based multilayer ceramic capacitors:
- MLCCs comprise numerous dielectric layers alternated with metallic electrodes, where the interface in-between plays a major role in final Jr values, both due to effects on BDS and on leakage currents. This becomes especially critical for thin-film MLCCs since the material to electrode ratio can be substantially large compared to conventional thick film MLCCs. Therefore, interfacial reactions such as interdiffusion and oxidation, the appearance of defects at the interface, and adhesion issues are all not trivial [187].
- It is difficult to guarantee the integrity of the multilayer structure upon several deposition cycles involving the dielectric layer and electrode. The electrodes must survive several annealing cycles without any substantial changes [185]. Pt electrode is generally a good choice to improve the electrical properties, but the high cost could be a limiting factor for industrialization. For this reason, base metal electrodes such as nickel [188] or copper [187] have been investigated. Deposition in an oxidizing atmosphere is not suitable for such metals, imposing constraints on the deposition and annealing conditions.
- Increasing the number of layers and electrodes, even if the processing is well-tuned to avoid interfacial defects, increases the probability of finding a critical defect in the dielectric layers, with consequently increased probability of electrical failure.
- Using photolithography routes to prepare a thin-film MLCC increases the risk of a non-perfect adhesion between layers, of uneven deposition of the top layers, difficulties in alignment for each layer, use of unrealistically wide margins (leading to poor area efficiency), and the extended times for stack buildup, leading to high costs [189].
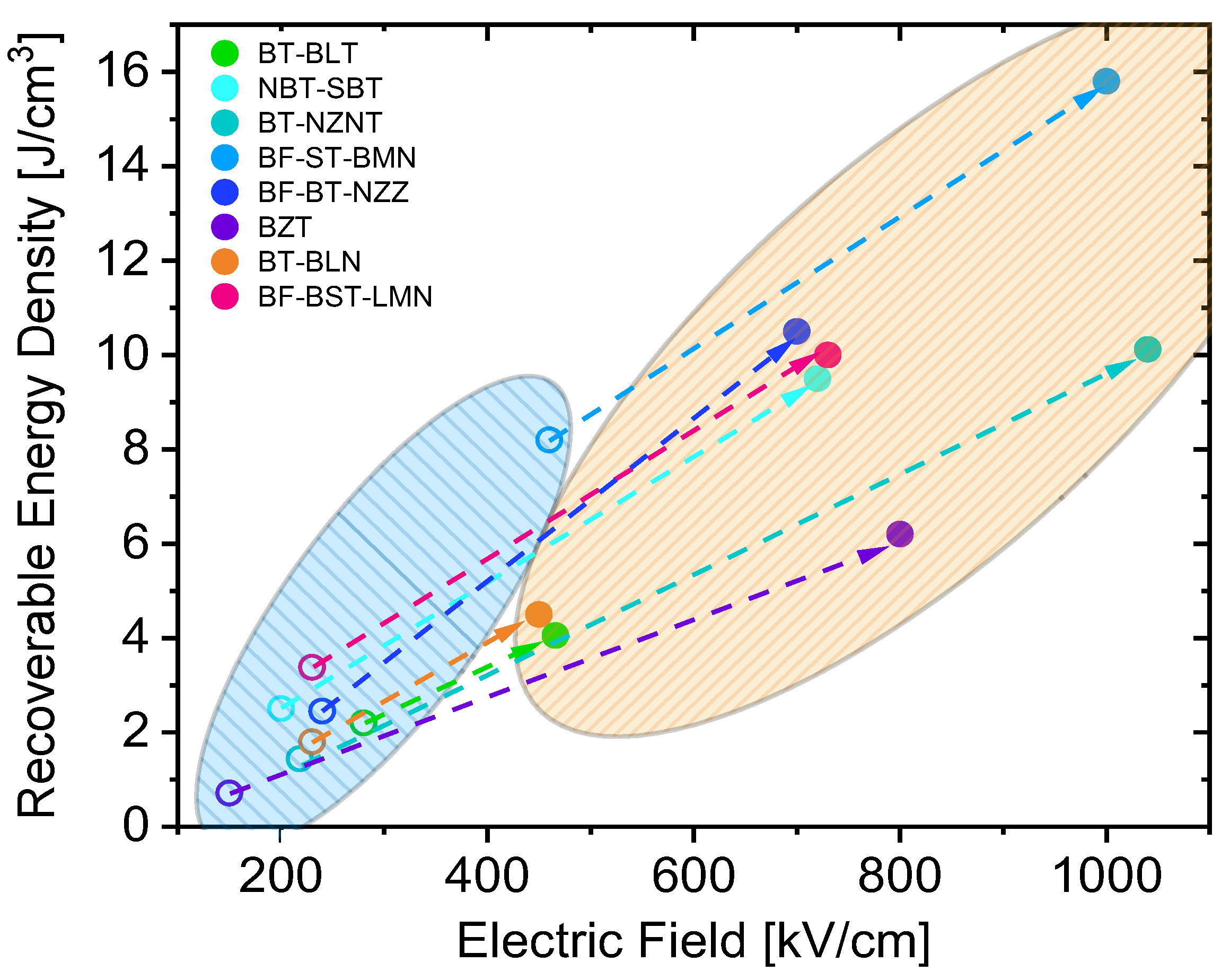
5.4. Final Remarks
6. Guidelines for Selection of Materials and Processing Route
- For high-energy and high-power applications, the thick-film multilayer technology is currently the most attractive because it can realize ED levels much higher than bulk ceramics (and not much lower than thin films), and the processing technology is well established, so that devices storing high amounts of energy (although much less than a battery) can be easily produced.
- For low-energy applications, thin-film devices are still attractive because of their small size and footprint. They can be used in applications where the amount of energy that has to be stored is low (mJ or below), for instance: autonomous sensors for the Internet of Things or small portable microelectronic devices. These applications may also require high-power as well as high-voltage, and need the flexibility in both high power and energy density offered by thin-film relaxor capacitors. If the BDS allows, the higher the voltage, the larger the amount of energy stored so that such thin-film devices can be a suitable energy storage device for these low-energy applications.
7. Future Directions
7.1. Model-Aided Characterization
7.2. Model-Aided Structural Simulation
7.3. Accelerated Materials Search
8. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Whittingham, M.S. History, evolution, and future status of energy storage. Proc. IEEE 2012, 100, 1518–1534. [Google Scholar] [CrossRef]
- Sherrill, S.A.; Banerjee, P.; Rubloff, G.W.; Lee, S.B. High to ultra-high power electrical energy storage. Phys. Chem. Chem. Phys. 2011, 13, 20714–20723. [Google Scholar] [CrossRef] [PubMed]
- Christen, T.; Carlen, M.W. Theory of ragone plots. J. Power Sources 2000, 91, 210–216. [Google Scholar] [CrossRef]
- Fletcher, N.H.; Hilton, A.D.; Ricketts, B.W. Optimization of energy storage density in ceramic capacitors. J. Phys. D. Appl. Phys. 1996, 29, 253–258. [Google Scholar] [CrossRef]
- Moulson, A.J.; Herbert, J.M. Dielectrics and insulators. In Electroceramics; John Wiley & Sons, Ltd.: Chichester, UK, 2003; pp. 243–335. [Google Scholar] [CrossRef]
- Love, G.R. Energy storage in ceramic dielectrics. J. Am. Ceram. Soc. 1990, 73, 323–328. [Google Scholar] [CrossRef]
- Kaliyaperumal Veerapandiyan, V. Inducing Diffuse Phase Transitions in Barium Titanate Using Ga3+-Ta5+ Dipole Pair Substituents. Master’s Thesis, Alfred University, Alfred, NY, USA, June 2017. [Google Scholar]
- Haertling, G. Ferroelectric ceramics: History and technology. J. Am. Ceram. Soc. 1999, 82, 718–818. [Google Scholar] [CrossRef]
- Tilley, R.J.D. Insulating solids. In Understanding Solids: The Science of Materials; John Wiley & Sons, Ltd.: Chichester, UK, 2004. [Google Scholar]
- Jena, A.K.; Kulkarni, A.; Miyasaka, T. Halide Perovskite Photovoltaics: Background, Status, and Future Prospects. Chem. Rev. 2019, 119, 3036–3103. [Google Scholar] [CrossRef]
- Batmunkh, M.; Zhong, Y.L.; Zhao, H. Recent Advances in Perovskite-Based Building-Integrated Photovoltaics. Adv. Mater. 2020, 32, 2000631. [Google Scholar] [CrossRef]
- Hwang, J.; Rao, R.R.; Giordano, L.; Katayama, Y.; Yu, Y.; Shao-Horn, Y. Perovskites in Catalysis and Electrocatalysis. Science 2017, 358, 751–756. [Google Scholar] [CrossRef]
- Bhalla, A.S.; Guo, R.; Roy, R. The Perovskite Structure-a Review of Its Role in Ceramic Science and Technology. Mater. Res. Innov. 2000, 4, 3–26. [Google Scholar] [CrossRef]
- Zhu, X.L.; Zhuang, K.Y.; Wu, S.Y.; Chen, X.M. Energy storage properties in Ba5 LaTi3Ta7O30 Tungsten bronze ceramics. J. Am. Ceram. Soc. 2019, 102, 3438–3447. [Google Scholar] [CrossRef]
- Cao, L.; Yuan, Y.; Tang, B.; Li, E.; Zhang, S. Excellent thermal stability, high efficiency and high power D-density of (Sr0.7Ba0.3)5LaNb7Ti3O30–based Tungsten bronze ceramics. J. Eur. Ceram. Soc. 2020, 40, 2366–2374. [Google Scholar] [CrossRef]
- Jonker, G.H.; Havinga, E.E. The influence of foreign ions on the crystal lattice of barium titanate. Mater. Res. Bull. 1982, 17, 345–350. [Google Scholar] [CrossRef]
- Lemanov, V.V. Barium titanate-based solid solutions. Ferroelectrics 2007, 354, 69–76. [Google Scholar] [CrossRef]
- Goldschmidt, V.M. Die gesetze der krystallochemie. Naturwissenschaften 1926, 14, 477–485. [Google Scholar] [CrossRef]
- Schütz, D.; Deluca, M.; Krauss, W.; Feteira, A.; Jackson, T.; Reichmann, K. Lone-pair-induced covalency as the cause of temperature- and field-induced instabilities in bismuth sodium titanate. Adv. Funct. Mater. 2012, 22, 2285–2294. [Google Scholar] [CrossRef]
- Cohen, R.E. Origin of ferroelectricity in perovskite oxides. Nature 1992, 358, 136–138. [Google Scholar] [CrossRef]
- Bell, A.J.; Deubzer, O. Lead-free piezoelectrics—The environmental and regulatory issues. MRS Bull. 2018, 43, 581–587. [Google Scholar] [CrossRef]
- Megaw, H.D. Origin of ferroelectricity in barium titanate and other perovskite-type crystals. Acta Crystallogr. 1952, 5, 739–749. [Google Scholar] [CrossRef]
- Von Hippel, A. Piezoelectricity, ferroelectricity, and crystal structure. Zeitschrift Für Phys. A Hadron. Nucl. 1952, 133, 158–173. [Google Scholar] [CrossRef]
- Buscaglia, V.; Randall, C.A. Size and scaling effects in barium titanate. An overview. J. Eur. Ceram. Soc. 2020, 40, 3744–3758. [Google Scholar] [CrossRef]
- Acosta, M.; Novak, N.; Rojas, V.; Patel, S.; Vaish, R.; Koruza, J.; Rossetti, G.A.; Rödel, J. BaTiO3-based piezoelectrics: Fundamentals, current status, and perspectives. Appl. Phys. Rev. 2017, 4, 041305. [Google Scholar] [CrossRef]
- Burns, G.; Burstein, E. Index of refraction in “dirty” displacive ferroelectrics. Ferroelectrics 1974, 7, 297–299. [Google Scholar] [CrossRef]
- Smolensky, G. Ferroelectrics with diffuse phase transition. Ferroelectrics 1984, 53, 129–135. [Google Scholar] [CrossRef]
- Cross, L.E. Relaxor ferroelectrics. J. Ceram. Soc. Jpn. 1987, 76, 241–267. [Google Scholar] [CrossRef]
- Cross, L.E. Relaxor ferroelectrics: An overview. Ferroelectrics 1994, 151, 305–320. [Google Scholar] [CrossRef]
- Bokov, A.A.; Ye, Z.-G. Recent progress in relaxor ferroelectrics with perovskite structure. J. Mater. Sci. 2006, 41, 31–52. [Google Scholar] [CrossRef]
- Cowley, R.A.; Gvasaliya, S.N.; Lushnikov, S.G.; Roessli, B.; Rotaru, G.M. Relaxing with relaxors: A review of relaxor ferroelectrics. Adv. Phys. 2011, 60, 229–327. [Google Scholar] [CrossRef]
- Hao, X. A review on the dielectric materials for high energy-storage application. J. Adv. Dielectr. 2013, 3, 1330001. [Google Scholar] [CrossRef]
- Setter, N. What is a ferroelectric—A materials designer perspective. Ferroelectrics 2016, 500, 164–182. [Google Scholar] [CrossRef]
- Ye, Z.G. Relaxor ferroelectric complex perovskites: Structure, properties and phase transitions. Key Eng. Mater. 1998, 155–156, 81–122. [Google Scholar] [CrossRef]
- Ahn, C.W.; Hong, C.H.; Choi, B.Y.; Kim, H.P.; Han, H.S.; Hwang, Y.; Jo, W.; Wang, K.; Li, J.F.; Lee, J.S.; et al. A brief review on relaxor ferroelectrics and selected issues in lead-free relaxors. J. Korean Phys. Soc. 2016, 68, 1481–1494. [Google Scholar] [CrossRef]
- Hlinka, J. Do we need the ether of polar nanoregions? J. Adv. Dielectr. 2012, 02, 1241006. [Google Scholar] [CrossRef]
- Kleemann, W. Random fields in relaxor ferroelectrics—A jubilee review. J. Adv. Dielectr. 2012, 2, 1241001. [Google Scholar] [CrossRef]
- Takenaka, H.; Grinberg, I.; Liu, S.; Rappe, A.M. Slush-like polar structures in single-crystal relaxors. Nature 2017, 546, 391–395. [Google Scholar] [CrossRef] [PubMed]
- Fontana, M.P.; Lambert, M. Linear disorder and temperature dependence of raman scattering in BaTiO3. Solid State Commun. 1972, 10, 1–4. [Google Scholar] [CrossRef]
- Bencan, A.; Oveisi, E.; Hashemizadeh, S.; Veerapandiyan, V.K.; Hoshina, T.; Rojac, T.; Deluca, M.; Drazic, G.; Damjanovic, D. Atomic scale symmetry and polar nanoclusters in the paraelectric phase of ferroelectric materials. arXiv.org 2020, arXiv:2010.10860. [Google Scholar]
- Veerapandiyan, V.K.; Khosravi, H.S.; Canu, G.; Feteira, A.; Buscaglia, V.; Reichmann, K.; Deluca, M. B-Site vacancy induced raman scattering in BaTiO3-based ferroelectric ceramics. J. Eur. Ceram. Soc. 2020, 40, 4684–4688. [Google Scholar] [CrossRef]
- Spear, W.E.; Le Comber, P.G. Substitutional doping of amorphous silicon. Solid State Commun. 1993, 8, 1015–1018. [Google Scholar] [CrossRef]
- Farhi, R.; El Marssi, M.; Simon, A.; Ravez, J. Relaxor-like and spectroscopic properties of niobium modified barium titanate. Eur. Phys. J. B 2000, 18, 605–610. [Google Scholar] [CrossRef]
- Maiti, T.; Guo, R.; Bhalla, A.S. Structure-property phase diagram of BaZrxTi1-xO3 system. J. Am. Ceram. Soc. 2008, 91, 1769–1780. [Google Scholar] [CrossRef]
- Buscaglia, V.; Tripathi, S.; Petkov, V.; Dapiaggi, M.; Deluca, M.; Gajović, A.; Ren, Y. Average and local atomic-scale structure in BaZrxTi1-xO3 (x = 0.10, 0.20, 0.40) ceramics by high-energy X-ray diffraction and raman spectroscopy. J. Phys. Condens. Matter 2014, 26. [Google Scholar] [CrossRef] [PubMed]
- Pramanick, A.; Dmowski, W.; Egami, T.; Budisuharto, A.S.; Weyland, F.; Novak, N.; Christianson, A.D.; Borreguero, J.M.; Abernathy, D.L.; Jørgensen, M.R.V. Stabilization of polar nanoregions in Pb-free ferroelectrics. Phys. Rev. Lett. 2018, 120, 207603. [Google Scholar] [CrossRef]
- Morrison, F.D.; Coats, A.M.; Sinclair, D.C.; West, A.R. Charge compensation mechanisms in La-doped BaTiO3. J. Electroceramics 2001, 6, 219–232. [Google Scholar] [CrossRef]
- Shvartsman, V.V.; Lupascu, D.C. Lead-free relaxor ferroelectrics. J. Am. Ceram. Soc. 2012, 95, 1–26. [Google Scholar] [CrossRef]
- Veerapandiyan, V.K.; Deluca, M.; Misture, S.T.; Schulze, W.A.; Pilgrim, S.M.; Tidrow, S.C. Dielectric and structural studies of ferroelectric phase evolution in dipole-pair substituted barium titanate ceramics. J. Am. Ceram. Soc. 2020, 103, 287–296. [Google Scholar] [CrossRef]
- Ravez, J.; Simon, A. Some solid state chemistry aspects of lead-free relaxor ferroelectrics. J. Solid State Chem. 2001, 162, 260–265. [Google Scholar] [CrossRef]
- Li, W.-B.; Zhou, D.; Pang, L.-X. Enhanced energy storage density by inducing defect dipoles in lead free relaxor ferroelectric BaTiO3-based ceramics. Appl. Phys. Lett. 2017, 110, 132902. [Google Scholar] [CrossRef]
- Ravez, J. Ferroelectricity in solid state chemistry. Comptes Rendus l’Academie des Sciences Ser. IIc Chem. 2000, 3, 267–283. [Google Scholar] [CrossRef]
- Lu, D.Y.; Sun, X.Y.; Liu, B.; Zhang, J.L.; Ogata, T. Structural and dielectric properties, electron paramagnetic resonance, and defect chemistry of Pr-doped BaTiO3 ceramics. J. Alloys Compd. 2014, 615, 25–34. [Google Scholar] [CrossRef]
- Morrison, F.D.; Sinclair, D.C.; West, A.R. Electrical and structural characteristics of lanthanum-doped barium titanate ceramics. J. Appl. Phys. 1999, 86, 6355–6366. [Google Scholar] [CrossRef]
- Anwar, S.; Sagdeo, P.R.; Lalla, N.P. Crossover from classical to relaxor ferroelectrics in BaTi1-xHfxO3 ceramics. J. Phys. Condens. Matter 2006, 18, 3455–3468. [Google Scholar] [CrossRef]
- Canu, G.; Confalonieri, G.; Deluca, M.; Curecheriu, L.; Buscaglia, M.T.; Asandulesa, M.; Horchidan, N.; Dapiaggi, M.; Mitoseriu, L.; Buscaglia, V. Structure-property correlations and origin of relaxor behaviour in BaCexTi1-xO3. Acta Mater. 2018, 152, 258–268. [Google Scholar] [CrossRef]
- Farhi, R.; El Marssi, M.; Simon, A.; Ravez, J. A raman and dielectric study of ferroelectric ceramics. Eur. Phys. J. B 1999, 9, 599–604. [Google Scholar] [CrossRef]
- Lin, J.N.; Wu, T.B. Effects of isovalent substitutions on lattice softening and transition character of BaTiO3 solid solutions. J. Appl. Phys. 1990, 68, 985–993. [Google Scholar] [CrossRef]
- Wei, X.; Yao, X. Preparation, structure and dielectric property of barium stannate titanate ceramics. Mater. Sci. Eng. B Solid State Mater. Adv. Technol. 2007, 137, 184–188. [Google Scholar] [CrossRef]
- Zhou, L.; Vilarinho, P.M.; Baptista, J.L. Dependence of the structural and dielectric properties of Ba1-xSrxTiO3 ceramic solid solutions on raw material processing. J. Eur. Ceram. Soc. 1999, 19, 2015–2020. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Yuan, R.; Tian, Y.; Xue, D.; Xue, D.; Zhou, Y.; Ding, X.; Sun, J.; Lookman, T. Accelerated search for BaTiO3-based ceramics with large energy storage at low fields using machine learning and experimental design. Adv. Sci. 2019, 6. [Google Scholar] [CrossRef]
- Pilgrim, S.M.; Sutherland, A.E.; Winzer, S.R. Diffuseness as a useful parameter for relaxor ceramics. J. Am. Ceram. Soc. 1990, 73, 3122–3125. [Google Scholar] [CrossRef]
- Uchino, K.; Nomura, S. Critical exponents of the dielectric constants in diffused-phase-transition crystals. Ferroelectrics 1982, 44, 55–61. [Google Scholar] [CrossRef]
- Hsiang, H.-I.; Yen, F.-S.; Huang, C.-Y. Effects of porosity on dielectric properties of BaTiO3 ceramics. Jpn. J. Appl. Phys. 1995, 34, 1922–1925. [Google Scholar] [CrossRef]
- Yang, L.; Kong, X.; Li, F.; Hao, H.; Cheng, Z.; Liu, H.; Li, J.F.; Zhang, S. Perovskite lead-free dielectrics for energy storage applications. Prog. Mater. Sci. 2019, 102, 72–108. [Google Scholar] [CrossRef]
- Rahaman, M.N. Grain growth and microstructure control. In Ceramic Processing and Sintering, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 540–619. [Google Scholar]
- Tian, H.Y.; Wang, Y.; Miao, J.; Chan, H.L.W.; Choy, C.L. Preparation and characterization of hafnium doped barium titanate ceramics. J. Alloys Compd. 2007, 431, 197–202. [Google Scholar] [CrossRef]
- Dechakupt, T.; Tangsritrakul, J.; Ketsuwan, P.; Yimnirun, R. Microstructure and electrical properties of niobium doped barium titanate ceramics. Ferroelectrics 2011, 415, 141–148. [Google Scholar] [CrossRef]
- Smyth, D.M. Barium titanate. In The Defect Chemistry of Metal Oxides; Oxford University Press: New York, NY, USA, 2000; pp. 253–282. [Google Scholar]
- Tsur, Y.; Dunbar, T.D.; Randall, C.A. Crystal and Defect Chemistry of Rare Earth Cations in BaTiO3. J. Electroceram. 2001, 7, 25–34. [Google Scholar] [CrossRef]
- Wu, T.-B.; Lin, J.-N. Transition of Compensating Defect Mode in Niobium-Doped Barium Titanate. J. Am. Ceram. Soc. 1994, 77, 759–764. [Google Scholar] [CrossRef]
- Chan, H.M.; Harmer, M.R.; Smyth, D.M. Compensating Defects in Highly Donor-Doped BaTiO3. J. Am. Ceram. Soc. 1986, 69, 507–510. [Google Scholar] [CrossRef]
- Elissalde, C.; Ravez, J. Ferroelectric Ceramics: Defects and Dielectric Relaxations. J. Mater. Chem. 2001, 11, 1957–1967. [Google Scholar] [CrossRef]
- Liu, X.; Shi, J.; Zhu, F.; Du, H.; Li, T.; Liu, X.; Lu, H. Ultrahigh Energy Density and Improved Discharged Efficiency in Bismuth Sodium Titanate Based Relaxor Ferroelectrics with A-Site Vacancy. J. Mater. 2018, 4, 202–207. [Google Scholar] [CrossRef]
- Wang, G.; Li, J.; Zhang, X.; Fan, Z.; Yang, F.; Feteira, A.; Zhou, D.; Sinclair, D.C.; Ma, T.; Tan, X.; et al. Ultrahigh energy storage density lead-free multilayers by controlled electrical homogeneity. Energy Environ. Sci. 2019, 12, 582–588. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, S.; Jiang, W.; Cao, W. Losses in ferroelectric materials. Mater. Sci. Eng. R Rep. 2015, 89, 1–48. [Google Scholar] [CrossRef] [PubMed]
- Guyonnet, J. Ferroelectric Domain Walls; Springer Theses; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Liu, N.; Liang, R.; Zhou, Z.; Dong, X. Designing lead-free bismuth ferrite-based ceramics learning from relaxor ferroelectric behavior for simultaneous high energy density and efficiency under low electric field. J. Mater. Chem. C 2018, 6, 10211–10217. [Google Scholar] [CrossRef]
- Liu, B.; Wu, Y.; Huang, Y.H.; Song, K.X.; Wu, Y.J. Enhanced dielectric strength and energy storage density in BaTi0.7Zr0.3O3 ceramics via spark plasma sintering. J. Mater. Sci. 2019, 54, 4511–4517. [Google Scholar] [CrossRef]
- Seitz, F. On the theory of electron multiplication in crystals. Phys. Rev. 1949, 76, 1376–1393. [Google Scholar] [CrossRef]
- Frohlich, H. On the theory of dielectric breakdown in solids. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1947, 188, 521–532. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, H.; Wu, L.; Chen, L.; Cai, Z.; Li, L.; Wang, X. High-performance relaxor ferroelectric materials for energy storage applications. Adv. Energy Mater. 2019, 9, 1–7. [Google Scholar] [CrossRef]
- Hu, Q.; Wang, T.; Zhao, L.; Jin, L.; Xu, Z.; Wei, X. Dielectric and energy storage properties of BaTiO3–Bi(Mg1/2Ti1/2)O3 ceramic: Influence of glass addition and biasing electric field. Ceram. Int. 2017, 43, 35–39. [Google Scholar] [CrossRef]
- Puli, V.S.; Pradhan, D.K.; Adireddy, S.; Kothakonda, M.; Katiyar, R.S.; Chrisey, D.B. Effect of lead borosilicate glass addition on the crystallization, ferroelectric and dielectric energy storage properties of Ba0.9995La0.0005TiO3 ceramics. J. Alloys Compd. 2016, 688, 721–728. [Google Scholar] [CrossRef]
- Liu, B.; Wang, X.; Zhao, Q.; Li, L. Improved energy storage properties of fine-crystalline BaTiO3 ceramics by coating powders with Al2O3 and SiO2. J. Am. Ceram. Soc. 2015, 98, 2641–2646. [Google Scholar] [CrossRef]
- Chen, K.; Pu, Y.; Xu, N.; Luo, X. Effects of SrO-B2O3-SiO2 Glass additive on densification and energy storage properties of Ba0.4Sr0.6TiO3 ceramics. J. Mater. Sci. Mater. Electron. 2012, 23, 1599–1603. [Google Scholar] [CrossRef]
- Kingery, W.D. Densification during sintering in the presence of a liquid phase I theory. J. Appl. Phys. 1959, 30, 301–306. [Google Scholar] [CrossRef]
- Hsiang, H.I.; Hsi, C.S.; Huang, C.C.; Fu, S.L. Sintering behavior and dielectric properties of BaTiO3 ceramics with glass addition for internal capacitor of LTCC. J. Alloys Compd. 2008, 459, 307–310. [Google Scholar] [CrossRef]
- Jeon, H.P.; Lee, S.K.; Kim, S.W.; Choi, D.K. Effects of BaO-B2O3-SiO2 Glass additive on densification and dielectric properties of BaTiO3 ceramics. Mater. Chem. Phys. 2005, 94, 185–189. [Google Scholar] [CrossRef]
- Lin, J.C.C.; Wei, W.C.J. Low-temperature sintering of BaTiO3 with Mn-Si-O glass. J. Electroceram. 2010, 25, 179–187. [Google Scholar] [CrossRef]
- Yang, H.; Yan, F.; Lin, Y.; Wang, T. Enhanced energy storage properties of Ba0.4Sr0.6TiO3 lead-free ceramics with Bi2O3-B2O3-SiO2 glass addition. J. Eur. Ceram. Soc. 2018, 38, 1367–1373. [Google Scholar] [CrossRef]
- Wang, T.; Jin, L.; Shu, L.; Hu, Q.; Wei, X. Energy storage properties in Ba0.4Sr0.6TiO3 ceramics with addition of semi-conductive BaO-B2O3-SiO2-Na2CO3-K2CO3 glass. J. Alloys Compd. 2014, 617, 399–403. [Google Scholar] [CrossRef]
- Yang, H.; Yan, F.; Zhang, G.; Lin, Y.; Wang, F. Dielectric behavior and impedance spectroscopy of lead-free Ba0.85Ca0.15Zr0.1Ti0.9O3 ceramics with B2O3-Al2O3-SiO2 glass-ceramics addition for enhanced energy storage. J. Alloys Compd. 2017, 720, 116–125. [Google Scholar] [CrossRef]
- Haily, E.; Bih, L.; El bouari, A.; Lahmar, A.; Elmarssi, M.; Manoun, B. Effect of BaO–Bi2O3–P2O5 glass additive on structural, dielectric and energy storage properties of BaTiO3 ceramics. Mater. Chem. Phys. 2020, 241, 122434. [Google Scholar] [CrossRef]
- Wang, S.F.; Yang, T.C.K.; Wang, Y.R.; Kuromitsu, Y. Effect of glass composition on the densification and dielectric properties of BaTiO3 ceramics. Ceram. Int. 2001, 27, 157–162. [Google Scholar] [CrossRef]
- Xiao, S.; Xiu, S.; Zhang, W.; Shen, B.; Zhai, J.; Zhang, Y. Effects of BaxSr1−xTiO3 ceramics additives on structure and energy storage properties of Ba0.4Sr0.6TiO3–BaO–B2O3–Al2O3–SiO2 glass-ceramic. J. Alloys Compd. 2016, 675, 15–21. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, M.; Yao, Z.; Wang, Z.; Song, Z.; Ullah, A.; Hao, H.; Liu, H. Effects of silica coating on the microstructures and energy storage properties of BaTiO3 ceramics. Mater. Res. Bull. 2015, 67, 70–76. [Google Scholar] [CrossRef]
- Dong, G.; Ma, S.; Du, J.; Cui, J. Dielectric properties and energy storage density in ZnO-doped Ba0.3Sr0.7TiO3 ceramics. Ceram. Int. 2009, 35, 2069–2075. [Google Scholar] [CrossRef]
- Ma, W.; Fan, P.; Salamon, D.; Kongparakul, S.; Samart, C.; Zhang, T.; Zhang, G.; Jiang, S.; Chang, J.J.; Zhang, H. Fine-grained BNT-based lead-free composite ceramics with high energy-storage density. Ceram. Int. 2019, 45, 19895–19901. [Google Scholar] [CrossRef]
- Diao, C.; Liu, H.; Hao, H.; Cao, M.; Yao, Z. Effect of SiO2 additive on dielectric response and energy storage performance of Ba0.4Sr0.6TiO3 ceramics. Ceram. Int. 2016, 42, 12639–12643. [Google Scholar] [CrossRef]
- Huang, Y.H.; Wu, Y.J.; Liu, B.; Yang, T.N.; Wang, J.J.; Li, J.; Chen, L.Q.; Chen, X.M. From core-shell Ba0.4Sr0.6TiO3@SiO2 particles to dense ceramics with high energy storage performance by spark plasma sintering. J. Mater. Chem. A 2018, 6, 4477–4484. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, L.; Luo, J.; Tang, Q.; Du, J. Ba0.4Sr0.6TiO3/MgO composites with enhanced energy storage density and low dielectric loss for solid-state pulse-forming line. Int. J. Appl. Ceram. Technol. 2010, 124–128. [Google Scholar] [CrossRef]
- Huang, Y.H.; Wu, Y.J.; Qiu, W.J.; Li, J.; Chen, X.M. Enhanced energy storage density of Ba 0.4 Sr 0.6TiO3-MgO composite prepared by spark plasma sintering. J. Eur. Ceram. Soc. 2015, 35, 1469–1476. [Google Scholar] [CrossRef]
- Ren, P.; Wang, Q.; Li, S.; Zhao, G. Energy storage density and tunable dielectric properties of BaTi0.85Sn0.15O3/MgO composite ceramics prepared by SPS. J. Eur. Ceram. Soc. 2017, 37, 1501–1507. [Google Scholar] [CrossRef]
- Chou, C.S.; Wu, C.Y.; Yang, R.Y.; Ho, C.Y. Preparation and characterization of the bismuth sodium titanate (Na0.5Bi0.5TiO3) ceramic doped with ZnO. Adv. Powder Technol. 2012, 23, 358–365. [Google Scholar] [CrossRef]
- Yao, Y.; Li, Y.; Sun, N.; Du, J.; Li, X.; Zhang, L.; Zhang, Q.; Hao, X. Enhanced dielectric and energy-storage properties in ZnO-doped 0.9(0.94Na0.5Bi0.5TiO3−0.06BaTiO 3)−0.1NaNbO3 ceramics. Ceram. Int. 2018, 44, 5961–5966. [Google Scholar] [CrossRef]
- Tao, C.W.; Geng, X.Y.; Zhang, J.; Wang, R.X.; Gu, Z.B.; Zhang, S.T. Bi0.5Na0.5TiO3-BaTiO3-K0.5Na0.5 NbO3:ZnO relaxor ferroelectric composites with high breakdown electric field and large energy storage properties. J. Eur. Ceram. Soc. 2018, 38, 4946–4952. [Google Scholar] [CrossRef]
- Luo, B.; Wang, X.; Wang, Y.; Li, L. Fabrication, characterization, properties and theoretical analysis of ceramic/PVDF composite flexible films with high dielectric constant and low dielectric loss. J. Mater. Chem. A 2014, 2, 510–519. [Google Scholar] [CrossRef]
- Li, H.; Liu, F.; Fan, B.; Ai, D.; Peng, Z.; Wang, Q. Nanostructured ferroelectric-polymer composites for capacitive energy storage. Small Methods 2018, 2, 1700399. [Google Scholar] [CrossRef]
- Singh, P.; Borkar, H.; Singh, B.P.; Singh, V.N.; Kumar, A. Ferroelectric polymer-ceramic composite thick films for energy storage applications. AIP Adv. 2014, 4. [Google Scholar] [CrossRef]
- Luo, H.; Zhang, D.; Jiang, C.; Yuan, X.; Chen, C.; Zhou, K. Improved dielectric properties and energy storage density of poly(vinylidene fluoride-Co-hexafluoropropylene) nanocomposite with hydantoin epoxy resin coated BaTiO3. ACS Appl. Mater. Interfaces 2015, 7, 8061–8069. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Shen, Y.; Hu, P.; Lin, Y.; Li, M.; Nan, C.W. Significant enhancement in energy density of polymer composites induced by dopamine-modified Ba0.6Sr0.4TiO3 nanofibers. Appl. Phys. Lett. 2012, 101, 1–5. [Google Scholar] [CrossRef]
- Yu, K.; Wang, H.; Zhou, Y.; Bai, Y.; Niu, Y. Enhanced dielectric properties of BaTiO3/Poly(vinylidene fluoride) nanocomposites for energy storage applications. J. Appl. Phys. 2013, 113. [Google Scholar] [CrossRef]
- Rahaman, M.N. Sintering of ceramic: Fundamentals. In Ceramic Processing and Sintering, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 425–468. [Google Scholar]
- Schomann, K.D. Electric breakdown of barium titanate: A model. Appl. Phys. 1975, 6, 89–92. [Google Scholar] [CrossRef]
- Guillon, O.; Gonzalez-Julian, J.; Dargatz, B.; Kessel, T.; Schierning, G.; Räthel, J.; Herrmann, M. Field-assisted sintering technology/spark plasma sintering: Mechanisms, materials, and technology developments. Adv. Eng. Mater. 2014, 16, 830–849. [Google Scholar] [CrossRef]
- Herring, C. Effect of change of scale on sintering phenomena. J. Appl. Phys. 1950, 21, 301–303. [Google Scholar] [CrossRef]
- Chen, I.-W.; Wang, X.-H. Sintering dense nanocrystalline ceramics without final-stage grain growth. Nature 2000, 404, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Lóh, N.J.; Simão, L.; Faller, C.A.; De Noni, A.; Montedo, O.R.K. A review of two-step sintering for ceramics. Ceram. Int. 2016, 42, 12556–12572. [Google Scholar] [CrossRef]
- Wang, X.W.; Zhang, B.H.; Feng, G.; Sun, L.Y.; Hu, Y.C.; Shang, S.Y.; Yin, S.Q.; Shang, J.; Wang, X.E. Enhanced energy storage performance of Ba 0.94 (Bi 0.5 K 0.5) 0.06 Ti 0.85 Zr 0.15 O 3 relaxor ceramics by two-step sintering method. Mater. Res. Bull. 2019, 114, 74–79. [Google Scholar] [CrossRef]
- Ding, J.; Liu, Y.; Lu, Y.; Qian, H.; Gao, H.; Chen, H.; Ma, C. Enhanced energy-storage properties of 0.89Bi0.5Na0.5TiO3–0.06BaTiO3–0.05K0.5Na0.5NbO3 lead-free anti-ferroelectric ceramics by two-step sintering method. Mater. Lett. 2014, 114, 107–110. [Google Scholar] [CrossRef]
- Gao, F.; Dong, X.; Mao, C.; Liu, W.; Zhang, H.; Yang, L.; Cao, F.; Wang, G. Energy-storage properties of 0.89Bi0.5Na0.5TiO3-0.06BaTiO3-0.05K0.5Na0.5NbO3 lead-free anti-ferroelectric ceramics. J. Am. Ceram. Soc. 2011, 94, 4382–4386. [Google Scholar] [CrossRef]
- Vasilos, T.; Spriggs, R.M. Pressure sintering: Mechanisms and microstructures for alumina and magnesia. J. Am. Ceram. Soc. 1963, 46, 493–496. [Google Scholar] [CrossRef]
- Xue, L.A.; Chen, Y.; Gilbart, E.; Brook, R.J. The kinetics of hot-pressing for undoped and donor-doped BaTiO3 ceramics. J. Mater. Sci. 1990, 25, 1423–1428. [Google Scholar] [CrossRef]
- Li, F.; Jiang, T.; Zhai, J.; Shen, B.; Zeng, H. Exploring novel bismuth-based materials for energy storage applications. J. Mater. Chem. C 2018, 6, 7976–7981. [Google Scholar] [CrossRef]
- Li, F.; Hou, X.; Li, T.; Si, R.; Wang, C.; Zhai, J. Fine-grain induced outstanding energy storage performance in novel Bi0.5 K0.5TiO3-Ba(Mg1/3Nb2/3)O3 ceramics: Via a hot-pressing strategy. J. Mater. Chem. C 2019, 7, 12127–12138. [Google Scholar] [CrossRef]
- Gao, X.; Li, Y.; Chen, J.; Yuan, C.; Zeng, M.; Zhang, A.; Gao, X.; Lu, X.; Li, Q.; Liu, J.M. High energy storage performances of Bi 1−x Sm x Fe0.95Sc0.05O3 lead-free ceramics synthesized by rapid hot press sintering. J. Eur. Ceram. Soc. 2019, 39, 2331–2338. [Google Scholar] [CrossRef]
- Becker, M.Z.; Shomrat, N.; Tsur, Y. Recent advances in mechanism research and methods for electric-field-assisted sintering of ceramics. Adv. Mater. 2018, 30, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Langer, J.; Hoffmann, M.J.; Guillon, O. Electric field-assisted sintering and hot pressing of semiconductive zinc oxide: A comparative study. J. Am. Ceram. Soc. 2011, 94, 2344–2353. [Google Scholar] [CrossRef]
- Munir, Z.A.; Anselmi-Tamburini, U.; Ohyanagi, M. The effect of electric field and pressure on the synthesis and consolidation of materials: A review of the spark plasma sintering method. J. Mater. Sci. 2006, 41, 763–777. [Google Scholar] [CrossRef]
- Huang, Y.H.; Wu, Y.J.; Li, J.; Liu, B.; Chen, X.M. Enhanced energy storage properties of barium strontium titanate ceramics prepared by sol-gel method and spark plasma sintering. J. Alloys Compd. 2017, 701, 439–446. [Google Scholar] [CrossRef]
- Qu, B.; Du, H.; Yang, Z. Lead-free relaxor ferroelectric ceramics with high optical transparency and energy storage ability. J. Mater. Chem. C 2016, 4, 1795–1803. [Google Scholar] [CrossRef]
- Pu, Y.; Zhang, L.; Guo, X.; Yao, M. improved energy storage properties of 0.55Bi0.5Na0.5TiO3-0.45Ba0.85Ca0.15Ti0.85Zr0.1Sn0.05O3 ceramics by microwave sintering. Ceram. Int. 2018, 44, S242–S245. [Google Scholar] [CrossRef]
- Randall, C.A. Scientific and engineering issues of the state-of-the-art and future multilayer capacitors. J. Ceram. Soc. Jpn. 2001, 109, S2–S6. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, J.; Li, S.; Zhong, L. Origin of thickness dependent dc electrical breakdown in dielectrics. Appl. Phys. Lett. 2012, 100. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, P.; Chen, L.; Wang, X. Effects of dielectric thickness on energy storage properties of 0.87BaTiO3-0.13Bi(Zn2/3(Nb0.85Ta0.15)1/3)O3 multilayer ceramic capacitors. J. Eur. Ceram. Soc. 2020, 40, 1902–1908. [Google Scholar] [CrossRef]
- Li, W.B.; Zhou, D.; Xu, R.; Pang, L.X.; Reaney, I.M. BaTiO3-Bi(Li0.5Ta0.5)O3, lead-free ceramics, and multilayers with high energy storage density and efficiency. ACS Appl. Energy Mater. 2018, 1, 5016–5023. [Google Scholar] [CrossRef]
- Li, J.; Li, F.; Xu, Z.; Zhang, S. Multilayer lead-free ceramic capacitors with ultrahigh energy density and efficiency. Adv. Mater. 2018, 30, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Xia, W.; Zhang, N.; Yang, H.; Cao, C.; Li, J. Energy storage BaZr0.2Ti 0.8O3 bilayer relaxor ferroelectric ceramic thick films with high discharging efficiency and fatigue resistance. J. Alloys Compd. 2019, 788, 978–983. [Google Scholar] [CrossRef]
- Puli, V.S.; Pradhan, D.K.; Riggs, B.C.; Chrisey, D.B.; Katiyar, R.S. Structure, ferroelectric, dielectric and energy storage studies of Ba0.70Ca0.30TiO3,Ba(Zr0.2Ti0.8)O3 ceramic capacitors. Integr. Ferroelectr. 2014, 157, 139–146. [Google Scholar] [CrossRef]
- Li, W.B.; Zhou, D.; Xu, R.; Wang, D.W.; Su, J.Z.; Pang, L.X.; Liu, W.F.; Chen, G.H. BaTiO3-based multilayers with outstanding energy storage performance for high temperature capacitor applications. ACS Appl. Energy Mater. 2019, 2, 5499–5506. [Google Scholar] [CrossRef]
- Wang, G.; Lu, Z.; Li, J.; Ji, H.; Yang, H.; Li, L.; Sun, S.; Feteira, A.; Yang, H.; Zuo, R.; et al. Lead-free (Ba,Sr)TiO3—BiFeO3 based multilayer ceramic capacitors with high energy density. J. Eur. Ceram. Soc. 2020, 40, 1779–1783. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, G.; Bao, W.; Li, J.; Li, L.; Mostaed, A.; Yang, H.; Ji, H.; Li, D.; Feteira, A.; et al. Superior energy density through tailored dopant strategies in multilayer ceramic capacitors. Energy Environ. Sci. 2020, 13, 2938–2948. [Google Scholar] [CrossRef]
- Kosec, M.; Kuscer, D.; Holc, J. Multifunctional polycrystalline ferroelectric materials. In Springer Series in Materials Science; Springer: Dordrecht, The Netherlands, 2011; Volume 140, pp. 39–61. [Google Scholar]
- Pan, M.-J.; Randall, C.A. A brief introduction to ceramic capacitors. IEEE Electr. Insul. Mag. 2010, 26, 44–50. [Google Scholar] [CrossRef]
- Goossens, D.J.; Weekes, C.J.; Avdeev, M.; Hutchison, W.D. Crystal and magnetic structure of (X = 0.2, 0.3, 0.4 and 0.8). J. Solid State Chem. 2013, 207, 111–116. [Google Scholar] [CrossRef]
- Liu, H.; Yang, X. Structural, dielectric, and magnetic properties of BiFeO3-SrTiO3 solid solution ceramics. Ferroelectrics 2016, 500, 310–317. [Google Scholar] [CrossRef]
- Cai, Z.; Zhu, C.; Wang, H.; Zhao, P.; Chen, L.; Li, L.; Wang, X. High-temperature lead-free multilayer ceramic capacitors with ultrahigh energy density and efficiency fabricated: Via two-step sintering. J. Mater. Chem. A 2019, 7, 14575–14582. [Google Scholar] [CrossRef]
- Li, J.; Shen, Z.; Chen, X.; Yang, S.; Zhou, W.; Wang, M.; Wang, L.; Kou, Q.; Liu, Y.; Li, Q.; et al. Grain-orientation-engineered multilayer ceramic capacitors for energy storage applications. Nat. Mater. 2020, 19, 999–1005. [Google Scholar] [CrossRef] [PubMed]
- Yao, Z.; Song, Z.; Hao, H.; Yu, Z.; Cao, M.; Zhang, S.; Lanagan, M.T.; Liu, H. Homogeneous/inhomogeneous-structured dielectrics and their energy-storage performances. Adv. Mater. 2017, 29. [Google Scholar] [CrossRef] [PubMed]
- Kishi, H.; Mizuno, Y.; Chazono, H. Base-metal electrode-multilayer ceramic capacitors: Past, present and future perspectives. Jpn. J. Appl. Physics Part 1 Regul. Pap. Short Notes Rev. Pap. 2003, 42, 1–5. [Google Scholar] [CrossRef]
- Yoon, J.-R.; Moon, B.H.; Lee, H.Y.; Jeong, D.Y.; Rhie, D.H. Design and analysis of electrical properties of a multilayer ceramic capacitor module for dc-link of hybrid electric vehicles. J. Electr. Eng. Technol. 2013, 8, 808–812. [Google Scholar] [CrossRef][Green Version]
- Cai, Z.; Wang, X.; Luo, B.; Hong, W.; Wu, L.; Li, L. Multiscale design of high-voltage multilayer energy-storage ceramic capacitors. J. Am. Ceram. Soc. 2018, 101, 1607–1615. [Google Scholar] [CrossRef]
- Cai, Z.; Wang, H.; Zhao, P.; Chen, L.; Zhu, C.; Hui, K.; Li, L.; Wang, X. Significantly enhanced dielectric breakdown strength and energy density of multilayer ceramic capacitors with high efficiency by electrodes structure design. Appl. Phys. Lett. 2019, 115. [Google Scholar] [CrossRef]
- Yoon, D.H.; Lee, B.I. Processing of barium titanate tapes with different binders for mlcc applications—Part I: Optimization using design of experiments. J. Eur. Ceram. Soc. 2004, 24, 739–752. [Google Scholar] [CrossRef]
- Yoon, D.H.; Lee, B.I. Processing of barium titanate tapes with different binders for mlcc applications—Part II: Comparison of the properties. J. Eur. Ceram. Soc. 2004, 24, 753–761. [Google Scholar] [CrossRef]
- Haertling, G.H. Ferroelectric thin films for electronic applications. J. Vac. Sci. Technol. A Vac. Surf. Film 1991, 9, 414–420. [Google Scholar] [CrossRef]
- Setter, N.; Damjanovic, D.; Eng, L.; Fox, G.; Gevorgian, S.; Hong, S.; Kingon, A.; Kohlstedt, H.; Park, N.Y.; Stephenson, G.B.; et al. Ferroelectric thin films: Review of materials, properties, and applications. J. Appl. Phys. 2006, 100. [Google Scholar] [CrossRef]
- Xu, Y.; Mackenzie, J.D. Ferroelectric thin films prepared by sol-gel processing. Integr. Ferroelectr. 1992, 1, 17–42. [Google Scholar] [CrossRef]
- Wasa, K. Thin Film Technologies for Manufacturing Piezoelectric Materials; Woodhead Publishing Limited: Cambridge, UK, 2010. [Google Scholar]
- Schneller, T.; Waser, R.; Kosec, M.; Payne, D. Chemical Solution Deposition of Functional Oxide Thin Films; Springer: Vienna, Austria, 2013. [Google Scholar]
- Ulrich, R.; Schaper, L.; Nelms, D.; Leftwich, M. Comparison of paraelectric and ferroelectric materials for applications as dielectrics in thin film integrated capacitors. Int. J. Microcircuits Electron. Packag. 2000, 23, 172–181. [Google Scholar]
- Jeong, Y.S.; Lee, H.U.; Lee, S.A.; Kim, J.P.; Kim, H.G.; Jeong, S.Y.; Cho, C.R. Annealing effect of platinum-based electrodes on physical properties of pzt thin films. Curr. Appl. Phys. 2009, 9, 115–119. [Google Scholar] [CrossRef]
- Fox, G.R.; Trolier-McKinstry, S.; Krupanidhi, S.B.; Casas, L.M. Pt/Ti/SiO2/Si substrates. J. Mater. Res. 1995, 10, 1508–1515. [Google Scholar] [CrossRef]
- Wang, D.Y.; Wang, J.; Chan, H.L.W.; Choy, C.L. Structural and electro-optic properties of Ba0.7Sr0.3TiO3 thin films grown on various substrates using pulsed laser deposition. J. Appl. Phys. 2007, 101. [Google Scholar] [CrossRef]
- Zhang, W.; Cheng, H.; Yang, Q.; Hu, F.; Ouyang, J. Crystallographic orientation dependent dielectric properties of epitaxial batio3 thin films. Ceram. Int. 2016, 42, 4400–4405. [Google Scholar] [CrossRef]
- Nguyen, M.D.; Nguyen, C.T.Q.; Vu, H.N.; Rijnders, G. Controlling microstructure and film growth of relaxor-ferroelectric thin films for high break-down strength and energy-storage performance. J. Eur. Ceram. Soc. 2018, 38, 95–103. [Google Scholar] [CrossRef]
- Zhu, X.; Shi, P.; Lou, X.; Gao, Y.; Guo, X.; Sun, H.; Liu, Q.; Ren, Z. Remarkably enhanced energy storage properties of lead-free Ba0.53Sr0.47TiO3 thin films capacitors by optimizing bottom electrode thickness. J. Eur. Ceram. Soc. 2020, 40, 5475–5482. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, W.; Wang, B.; Zheng, Y. Ultrathin ferroelectric films: Growth, characterization, physics and applications. Materials 2014, 6, 6377–6485. [Google Scholar] [CrossRef]
- Jayadevan, K.P.; Tseng, T.Y. Review composite and multilayer ferroelectric thin films: Processing, properties and applications. J. Mater. Sci. Mater. Electron. 2002, 13, 439–459. [Google Scholar] [CrossRef]
- Mele, P. , Endo, T., Arisawa, S., Li, C., Tsuchiya, T. Oxide Thin Films, Multilayers, and Nanocomposites; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Song, S.; Zhai, J.; Gao, L.; Yao, X.; Lu, S.; Xu, Z. Thickness-dependent dielectric and tunable properties of barium stannate titanate thin films. J. Appl. Phys. 2009, 106, 20–25. [Google Scholar] [CrossRef]
- Ohno, T.; Matsuda, T.; Ishikawa, K.; Suzuki, H. Thickness dependence of residual stress in alkoxide-derived Pb(Zr0.3Ti0.7)O3 thin film by chemical solution deposition. Jpn. J. Appl. Physics Part 1 Regul. Pap. Short Notes Rev. Pap. 2006, 45, 7265–7269. [Google Scholar] [CrossRef]
- Udayakumar, K.R.; Schuele, P.J.; Chen, J.; Krupanidhi, S.B.; Cross, L.E. Thickness-dependent electrical characteristics of lead zirconate titanate thin films. J. Appl. Phys. 1995, 77, 3981–3986. [Google Scholar] [CrossRef]
- Canedy, C.L.; Li, H.; Alpay, S.P.; Salamanca-Riba, L.; Roytburd, A.L.; Ramesh, R. Dielectric properties in heteroepitaxial Ba0.6Sr0.4TiO3 thin films: Effect of internal stresses and dislocation-type defects. Appl. Phys. Lett. 2000, 77, 1695–1697. [Google Scholar] [CrossRef]
- Xu, J.; Menesklou, W.; Ivers-Tiffée, E. Annealing effects on structural and dielectric properties of tunable BZT thin films. J. Electroceramics 2004, 13, 229–233. [Google Scholar] [CrossRef]
- Karan, N.K.; Saavedra-Arias, J.J.; Perez, M.; Thomas, R.; Katiyar, R.S. High energy density metal-insulator-metal capacitors with Ba [(Ni12, W12)0.1 Ti0.9] O3 thin films. Appl. Phys. Lett. 2008, 92, 1–4. [Google Scholar] [CrossRef]
- Kwon, D.K.; Lee, M.H. Temperature-stable high-energy-density capacitors using complex perovskite thin films. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 1894–1899. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, M.; Zhang, Y.; Yu, Z.; Ouyang, J.; Pan, W. Increasing energy storage capabilities of space-charge dominated ferroelectric thin films using interlayer coupling. Acta Mater. 2017, 122, 252–258. [Google Scholar] [CrossRef]
- Yang, B.B.; Guo, M.Y.; Song, D.P.; Tang, X.W.; Wei, R.H.; Hu, L.; Yang, J.; Song, W.H.; Dai, J.M.; Lou, X.J.; et al. Energy storage properties in BaTiO3-Bi3.25La0.75Ti3O12 thin films. Appl. Phys. Lett. 2018, 113. [Google Scholar] [CrossRef]
- Instan, A.A.; Pavunny, S.P.; Bhattarai, M.K.; Katiyar, R.S. Ultrahigh capacitive energy storage in highly oriented Ba(ZrxTi1-x)O3 thin films prepared by pulsed laser deposition. Appl. Phys. Lett. 2017, 111. [Google Scholar] [CrossRef]
- Cheng, H.; Ouyang, J.; Zhang, Y.-X.; Ascienzo, D.; Li, Y.; Zhao, Y.-Y.; Ren, Y. Demonstration of ultra-high recyclable energy densities in domain-engineered ferroelectric films. Nat. Commun. 2017, 8, 1999. [Google Scholar] [CrossRef]
- Fan, Q.; Liu, M.; Ma, C.; Wang, L.; Ren, S.; Lu, L.; Lou, X.; Jia, C.-L. Significantly enhanced energy storage density with superior thermal stability by optimizing Ba(Zr0.15Ti0.85)O3/Ba(Zr0.35Ti0.65)O3 multilayer structure. Nano Energy 2018, 51, 539–545. [Google Scholar] [CrossRef]
- Pan, H.; Kursumovic, A.; Lin, Y.H.; Nan, C.W.; MacManus-Driscoll, J.L. Dielectric films for high performance capacitive energy storage: Multiscale engineering. Nanoscale 2020, 12, 19582–19591. [Google Scholar] [CrossRef] [PubMed]
- Brennecka, G.L.; Parish, C.M.; Tuttle, B.A.; Brewer, L.N. Multilayer thin and ultrathin film capacitors fabricated by chemical solution deposition. J. Mater. Res. 2008, 23, 176–181. [Google Scholar] [CrossRef]
- Brennecka, G.L.; Ihlefeld, J.F.; Maria, J.-P.; Tuttle, B.A.; Clem, P.G. Processing technologies for high-permittivity thin films in capacitor applications. J. Am. Ceram. Soc. 2010, 93, 3935–3954. [Google Scholar] [CrossRef]
- Yoshida, K.; Saita, H.; Kariya, T. Ultra low profile thin film capacitor for high performance electronic packages. In Proceedings of the IEEE 70th Electronic Components and Technology Conference, Orlando, FL, USA, 3–30 June 2020; pp. 414–418. [Google Scholar]
- Nagata, H.; Ko, S.W.; Hong, E.; Randall, C.A.; Trolier-McKinstry, S.; Pinceloup, P.; Skamser, D.; Randall, M.; Tajuddin, A. Microcontact printed BaTiO3 and LaNiO3 thin films for capacitors. J. Am. Ceram. Soc. 2006, 89. [Google Scholar] [CrossRef]
- Wang, P.; Xu, H.; Zhu, G.; Zhao, Y.; Li, J.; Yu, A. An efficient method to achieve MLCC miniaturization and ensure its reliability. J. Mater. Sci. Mater. Electron. 2017, 28, 4102–4106. [Google Scholar] [CrossRef]
- Beauchamp, E.K. Effect of microstructure on pulse electrical strength of MgO. J. Am. Ceram. Soc. 1971, 54, 484–487. [Google Scholar] [CrossRef]
- Song, Z.; Liu, H.; Zhang, S.; Wang, Z.; Shi, Y.; Hao, H.; Cao, M.; Yao, Z.; Yu, Z. Effect of grain size on the energy storage properties of (Ba0.4Sr0.6)TiO3 paraelectric ceramics. J. Eur. Ceram. Soc. 2014, 34, 1209–1217. [Google Scholar] [CrossRef]
- Buscaglia, M.T.; Buscaglia, V.; Viviani, M.; Petzelt, J.; Savinov, M.; Mitoseriu, L.; Testino, A.; Nanni, P.; Harnagea, C.; Zhao, Z.; et al. Ferroelectric properties of dense nanocrystalline BaTiO3 ceramics. Nanotechnology 2004, 15, 1113–1117. [Google Scholar] [CrossRef]
- Pintilie, L.; Vrejoiu, I.; Hesse, D.; Alexe, M. The influence of the top-contact metal on the ferroelectric properties of epitaxial ferroelectric Pb(Zr0.2Ti0.8)O3 thin films. J. Appl. Phys. 2008, 104, 114101. [Google Scholar] [CrossRef]
- Klein, A. Interface properties of dielectric oxides. J. Am. Ceram. Soc. 2016, 99, 369–387. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, D.; Song, K.; Feteira, A.; Randall, C.A.; Reaney, I.M. Cold-sintered C0G multilayer ceramic capacitors. Adv. Electron. Mater. 2019, 5, 1900025. [Google Scholar] [CrossRef]
- Cui, C.; Pu, Y.; Shi, R. High-Energy Storage Performance in Lead-Free (0.8-x)SrTiO3-0.2Na0.5Bi0.5TiO3-XBaTiO3 Relaxor Ferroelectric Ceramics. J. Alloys Compd. 2018, 740, 1180–1187. [Google Scholar] [CrossRef]
- Zheng, D.; Zuo, R.; Zhang, D.; Li, Y. Novel BiFeO3-BaTiO3-Ba(Mg1/3Nb2/3)O3 Lead-Free Relaxor Ferroelectric Ceramics for Energy-Storage Capacitors. J. Am. Ceram. Soc. 2015, 98, 2692–2695. [Google Scholar] [CrossRef]
- Posadas, A.-B.; Lippmaa, M.; Walker, F.J.; Dawber, M.; Ahn, C.H.; Triscone, J.-M. Growth and novel applications of epitaxial oxide thin films. In Physics of Ferroelectrics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 219–304. [Google Scholar]
- Muralt, P. Recent progress in materials issues for piezoelectric MEMS. J. Am. Ceram. Soc. 2008, 91, 1385–1396. [Google Scholar] [CrossRef]
- Yao, K.; Shuting, C.; Rahimabady, M.; Mirshekarloo, M.S.; Shuhui, Y.; Tay, F.E.H.; Sritharan, T.; Li, L. Nonlinear dielectric thin films for high-power electric storage with energy density comparable with electrochemical supercapacitors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1968–1974. [Google Scholar] [CrossRef]
- Hao, X.; Wang, P.; Zhang, X.; Xu, J. Microstructure and energy-storage performance of PbO–B2O3–SiO2–ZnO glass added (Pb0.97La0.02)(Zr0.97Ti0.03)O3 antiferroelectric thick films. Mater. Res. Bull. 2013, 48, 84–88. [Google Scholar] [CrossRef]
- Birnie, D.P. Spin Coating: Art and science. In Chemical Solution Deposition of Functional Oxide Thin Films; Springer: Vienna, Austria, 2013; pp. 263–274. [Google Scholar]
- Bassiri-Gharb, N.; Bastani, Y.; Bernal, A. Chemical solution growth of ferroelectric oxide thin films and nanostructures. Chem. Soc. Rev. 2014, 43, 2125–2140. [Google Scholar] [CrossRef]
- Wang, B.; Luo, L.; Jiang, X.; Li, W.; Chen, H. Energy-storage properties of (1−x)Bi0.47Na0.47Ba0.06TiO3–XKNbO3 lead-free ceramics. J. Alloys Compd. 2014, 585, 14–18. [Google Scholar] [CrossRef]
- Wang, T.; Jin, L.; Li, C.; Hu, Q.; Wei, X. Relaxor ferroelectric BaTiO3-Bi(Mg2/3Nb1/3)O3 ceramics for energy storage application. J. Am. Ceram. Soc. 2014, 9, 559–566. [Google Scholar] [CrossRef]
- Sun, Z.; Li, L.; Yu, S.; Kang, X.; Chen, S. Energy storage properties and relaxor behavior of lead-free Ba1-XSm2x/3Zr0.15Ti0.85O3 Ceramics. Dalt. Trans. 2017, 46, 14341–14347. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Bai, X.; Wang, H.; Du, J.; Bai, W.; Li, L.; Wen, F.; Zheng, P.; Wu, W.; Zheng, L.; et al. Achieving high-energy storage performance in 0.67Bi1-XSmxFeO3-0.33BaTiO3 lead-free relaxor ferroelectric ceramics. Ceram. Int. 2020, 46, 11549–11555. [Google Scholar] [CrossRef]
- Lim, J.B.; Zhang, S.; Shrout, T.R. High temperature capacitors using a BiScO3-BaTiO3-(K1/2Bi1/2)TiO3 ternary system. Electron. Mater. Lett. 2011, 7, 71–75. [Google Scholar] [CrossRef]
- Puli, V.S.; Pradhan, D.K.; Riggs, B.C.; Adireddy, S.; Katiyar, R.S.; Chrisey, D.B. Synthesis and characterization of lead-free ternary component BST–BCT–BZT ceramic capacitors. J. Adv. Dielectr. 2014, 4, 1450014. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhu, H.; Fu, Z.; Zhang, Q. Sintering temperature dependence of dielectric properties and energy-storage properties in (Ba,Zr)TiO3 ceramics. J. Mater. Sci. Mater. Electron. 2017, 28, 514–518. [Google Scholar] [CrossRef]
- Dai, Z.; Xie, J.; Liu, W.; Wang, X.; Zhang, L.; Zhou, Z.; Li, J.; Ren, X. Effective Strategy to achieve excellent energy storage properties in lead-free BaTiO3-based bulk ceramics. ACS Appl. Mater. Interfaces 2020, 12, 30289–30296. [Google Scholar] [CrossRef]
- Yan, B.; Fan, H.; Wang, C.; Zhang, M.; Yadav, A.K.; Zheng, X.; Wang, H.; Du, Z. Giant electro-strain and enhanced energy storage performance of (Y0.5Ta0.5)4 + Co-Doped 0.94(Bi0.5Na0.5)TiO3-0.06BaTiO3 lead-free ceramics. Ceram. Int. 2020, 46, 281–288. [Google Scholar] [CrossRef]
- Li, Q.; Wang, J.; Ma, Y.; Ma, L.; Dong, G.; Fan, H. Enhanced energy-storage performance and dielectric characterization of 0.94Bi0.5Na0.5TiO3–0.06BaTiO3 modified by CaZrO3. J. Alloys Compd. 2016, 663, 701–707. [Google Scholar] [CrossRef]
- Xu, Q.; Xie, J.; He, Z.; Zhang, L.; Cao, M.; Huang, X.; Lanagan, M.T.; Hao, H.; Yao, Z.; Liu, H. Energy-storage properties of Bi0.5Na 0.5TiO3-BaTiO3-KNbO3 ceramics fabricated by wet-chemical method. J. Eur. Ceram. Soc. 2017, 37, 99–106. [Google Scholar] [CrossRef]
- Xu, Q.; Lanagan, M.T.; Huang, X.; Xie, J.; Zhang, L.; Hao, H.; Liu, H. Dielectric behavior and impedance spectroscopy in lead-free BNT–BT–NBN perovskite ceramics for energy storage. Ceram. Int. 2016, 42, 9728–9736. [Google Scholar] [CrossRef]
- Zhao, X.; Bai, W.; Ding, Y.; Wang, L.; Wu, S.; Zheng, P.; Li, P.; Zhai, J. Tailoring high energy density with superior stability under low electric field in novel (Bi0.5Na0.5)TiO3-based relaxor ferroelectric ceramics. J. Eur. Ceram. Soc. 2020, 40, 4475–4486. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Z.; Feng, Y. Temperature-independent dielectric properties of 0.82[0.94Bi0.5Na0.5TiO3–0.06BaTiO3]–0.18K0.5Na0.5NbO3 ceramics. J. Adv. Dielectr. 2012, 2, 1250006. [Google Scholar] [CrossRef]
- Huang, W.; Chen, Y.; Li, X.; Wang, G.; Liu, N.; Li, S.; Zhou, M.; Dong, X. Ultrahigh recoverable energy storage density and efficiency in barium strontium titanate-based lead-free relaxor ferroelectric ceramics. Appl. Phys. Lett. 2018, 113, 203902. [Google Scholar] [CrossRef]
- Puli, V.S.; Kumar, A.; Katiyar, R.S.; Su, X.; Busta, C.M.; Chrisey, D.B.; Tomozawa, M. Dielectric breakdown of BaO–B2O3–ZnO–[(BaZr0.2Ti0.80)O3]0.85 [(Ba0.70Ca0.30)TiO3]0.15 glass-ceramic composites. J. Non. Cryst. Solids 2012, 358, 3510–3516. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhu, H.; Fu, Z.; Zhang, Q. Low dielectric loss of Bi-doped BaZr0.15Ti0.85O3 ceramics for high-voltage capacitor applications. Ceram. Int. 2017, 43, 12186–12190. [Google Scholar] [CrossRef]
- Swain, A.B.; Subramanian, V.; Murugavel, P. The role of precursors on piezoelectric and ferroelectric characteristics of 0.5BCT-0.5BZT ceramic. Ceram. Int. 2018, 44, 6861–6865. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, S.; Wang, T.; Liu, J.; Li, D.; Yang, H.; Hu, G.; Kong, L.; Wang, F.; Liu, G. Structure, dielectric properties of novel Ba(Zr,Ti)O3 based ceramics for energy storage application. Ceram. Int. 2020, 46, 12080–12087. [Google Scholar] [CrossRef]
- Hu, Q.; Jin, L.; Wang, T.; Li, C.; Xing, Z.; Wei, X. Dielectric and temperature stable energy storage properties of 0.88BaTiO3–0.12Bi(Mg1/2Ti1/2)O3 bulk ceramics. J. Alloys Compd. 2015, 640, 416–420. [Google Scholar] [CrossRef]
- Jiang, X.; Hao, H.; Zhang, S.; Lv, J.; Cao, M.; Yao, Z.; Liu, H. Enhanced energy storage and fast discharge properties of BaTiO3 based ceramics modified by Bi(Mg1/2Zr1/2)O3. J. Eur. Ceram. Soc. 2019, 39, 1103–1109. [Google Scholar] [CrossRef]
- Chen, X.; Li, X.; Sun, J.; Sun, C.; Shi, J.; Pang, F.; Zhou, H. Simultaneously achieving ultrahigh energy storage density and energy efficiency in barium titanate based ceramics. Ceram. Int. 2020, 46, 2764–2771. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, C.; Wu, B.; Wu, J. Multifunctional BaTiO3-based relaxor ferroelectrics toward excellent energy storage performance and electrostrictive strain benefiting from crossover region. ACS Appl. Mater. Interfaces 2020, 12, 23885–23895. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Li, Z. Weakly coupled relaxor behavior of BaTiO3-Bi(Mg1/2Ti1/2)O3 lead-free ceramics. J. Adv. Dielectr. 2013, 03, 1320001. [Google Scholar] [CrossRef]
- Li, Y.Q.; Liu, H.X.; Yao, Z.H.; Xu, J.; Cui, Y.J.; Hao, H.; Cao, M.H.; Yu, Z.Y. Characterization and energy storage density of BaTiO3—Ba(Mg1/3Nb2/3)O3 Ceramics. Mater. Sci. Forum 2010, 654–656, 2045–2048. [Google Scholar] [CrossRef]
- Wu, L.; Wang, X.; Li, L. Lead-free BaTiO3–Bi(Zn2/3Nb1/3)O3 weakly coupled relaxor ferroelectric materials for energy storage. RSC Adv. 2016, 6, 14273–14282. [Google Scholar] [CrossRef]
- Chen, P.; Chu, B. Improvement of dielectric and energy storage properties in Bi(Mg1/2Ti1/2)O3-modified (Na1/2Bi1/2)0.92Ba0.08TiO3 ceramics. J. Eur. Ceram. Soc. 2016, 36, 81–88. [Google Scholar] [CrossRef]
- Liu, X.; Du, H.; Liu, X.; Shi, J.; Fan, H. Energy storage properties of BiTi0.5Zn0.5O3-Bi0.5Na0.5TiO3-BaTiO3 relaxor ferroelectrics. Ceram. Int. 2016, 42, 17876–17879. [Google Scholar] [CrossRef]
- Mishra, A.; Majumdar, B.; Ranjan, R. A complex lead-free (Na,Bi,Ba)(Ti,Fe)O3 Single phase perovskite ceramic with a high energy-density and high discharge-efficiency for solid state capacitor applications. J. Eur. Ceram. Soc. 2017, 37, 2379–2384. [Google Scholar] [CrossRef]
- Patel, S.; Chauhan, A.; Vaish, R.; Thomas, P. Enhanced energy storage performance of glass added 0.715Bi0.5Na0.5TiO3-0.065BaTiO3-0.22SrTiO3 ferroelectric ceramics. J. Asian Ceram. Soc. 2015, 3, 383–389. [Google Scholar] [CrossRef][Green Version]
- Ping, W.; Liu, W.; Li, S. Enhanced energy storage property in glass-added Ba(Zr0.2Ti0.8)O3-0.15(Ba 0.7Ca0.3)TiO3 ceramics and the charge relaxation. Ceram. Int. 2019, 45, 11388–11394. [Google Scholar] [CrossRef]
- Li, W.B.; Zhou, D.; Pang, L.X. Structure and energy storage properties of Mn-doped (Ba,Sr)TiO3–MgO composite ceramics. J. Mater. Sci. Mater. Electron. 2017, 28, 8749–8754. [Google Scholar] [CrossRef]
- Zhu, C.; Cai, Z.; Li, L.; Wang, X. High energy density, high efficiency and excellent temperature stability of lead free Mn-doped BaTiO3–Bi(Mg1/2Zr1/2)O3 ceramics sintered in a reducing atmosphere. J. Alloys Compd. 2020, 816, 152498. [Google Scholar] [CrossRef]
- Yang, B.; Guo, M.; Tang, X.; Wei, R.; Hu, L.; Yang, J.; Song, W.; Dai, J.; Lou, X.; Zhu, X.; et al. Lead-free A2Bi4Ti5O18 thin film capacitors (A = Ba and Sr) with large energy storage density, high efficiency, and excellent thermal stability. J. Mater. Chem. C 2019, 7, 1888–1895. [Google Scholar] [CrossRef]
- Xu, Z.; Qiang, H.; Chen, Y. Improved energy storage properties of Mn and Y Co-Doped BST films. Mater. Lett. 2020, 259, 126894. [Google Scholar] [CrossRef]
- Huang, K.; Wang, J.B.; Zhong, X.L.; Liu, B.L.; Chen, T.; Zhou, Y.C. Significant polarization variation near room temperature of Ba0.65Sr0.35TiO3 thin films for pyroelectric energy harvesting. Sens. Actuators B Chem. 2012, 169, 208–212. [Google Scholar] [CrossRef]
- Goodwin, A.L. Opportunities and challenges in understanding complex functional materials. Nat. Commun. 2019, 10, 10–13. [Google Scholar] [CrossRef]
- Paściak, M.; Welberry, T.R.; Kulda, J.; Kempa, M.; Hlinka, J. Polar Nanoregions and diffuse scattering in the relaxor ferroelectric PbMg1/3Nb2/3O3. Phys. Rev. B 2012, 85, 224109. [Google Scholar] [CrossRef]
- Popov, M.N.; Spitaler, J.; Veerapandiyan, V.K.; Bousquet, E.; Hlinka, J.; Deluca, M. Raman spectra of fine-grained materials from first principles. Npj Comput. Mater. 2020, 6, 121. [Google Scholar] [CrossRef]
- Li, L.; Yang, Y.; Zhang, D.; Ye, Z.G.; Jesse, S.; Kalinin, S.V.; Vasudevan, R.K. Machine learning-enabled identification of material phase transitions based on experimental data: Exploring collective dynamics in ferroelectric relaxors. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef]
- Cui, A.; Jiang, K.; Jiang, M.; Shang, L.; Zhu, L.; Hu, Z.; Xu, G.; Chu, J. Decoding Phases of matter by machine-learning raman spectroscopy. Phys. Rev. Appl. 2019, 12, 1. [Google Scholar] [CrossRef]
- Ziatdinov, M.; Nelson, C.; Vasudevan, R.K.; Chen, D.Y.; Kalinin, S.V. Building ferroelectric from the bottom up: The machine learning analysis of the atomic-scale ferroelectric distortions. Appl. Phys. Lett. 2019, 115. [Google Scholar] [CrossRef]
- Kumar, A.; Baker, J.N.; Bowes, P.C.; Cabral, M.J.; Zhang, S.; Dickey, E.C.; Irving, D.L.; LeBeau, J.M. Atomic-resolution electron microscopy of nanoscale local structure in lead-based relaxor ferroelectrics. Nat. Mater. 2020. [Google Scholar] [CrossRef] [PubMed]
- Vorauer, T.; Kumar, P.; Berhaut, C.L.; Chamasemani, F.F.; Jouneau, P.H.; Aradilla, D.; Tardif, S.; Pouget, S.; Fuchsbichler, B.; Helfen, L.; et al. Multi-scale quantification and modeling of aged nanostructured silicon-based composite anodes. Commun. Chem. 2020, 3, 1–11. [Google Scholar] [CrossRef]
- Mentzer, C.; Lisenkov, S.; Fthenakis, Z.G.; Ponomareva, I. Phase evolution in the ferroelectric relaxor Ba(Ti1-x,Zrx) O3 from atomistic simulations. Phys. Rev. B 2019, 99, 1–7. [Google Scholar] [CrossRef]
- Paściak, M.; Welberry, T.R.; Kulda, J.; Leoni, S.; Hlinka, J. Dynamic displacement disorder of cubic BaTiO3. Phys. Rev. Lett. 2018, 120, 167601. [Google Scholar] [CrossRef]
- Wang, B.; Chen, H.N.; Wang, J.J.; Chen, L.Q. Ferroelectric domain structures and temperature-misfit strain phase diagrams of K1-xNaxNbO3 thin films: A phase-field study. Appl. Phys. Lett. 2019, 115, 092902. [Google Scholar] [CrossRef]
- Wang, J.J.; Wang, B.; Chen, L.Q. Understanding, predicting, and designing ferroelectric domain structures and switching guided by the phase-field method. Annu. Rev. Mater. Res. 2019, 49, 127–152. [Google Scholar] [CrossRef]
- Xue, D.; Balachandran, P.V.; Hogden, J.; Theiler, J.; Xue, D.; Lookman, T. Accelerated search for materials with targeted properties by adaptive design. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef]
- Balachandran, P.V.; Kowalski, B.; Sehirlioglu, A.; Lookman, T. Experimental search for high-temperature ferroelectric perovskites guided by two-step machine learning. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef]
- Yuan, R.; Liu, Z.; Balachandran, P.V.; Xue, D.; Zhou, Y.; Ding, X.; Sun, J.; Xue, D.; Lookman, T. Accelerated discovery of large electrostrains in BaTiO3-based piezoelectrics using active learning. Adv. Mater. 2018, 30, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Vuong, L.D.; Gio, P.D. Enhancement in dielectric, ferroelectric, and piezoelectric properties of BaTiO3-modified Bi0.5(Na0.4K0.1)TiO3 lead-free ceramics. J. Alloys Compd. 2020, 817, 152790. [Google Scholar] [CrossRef]
- Hanani, Z.; Mezzane, D.; Amjoud, M.; Razumnaya, A.G.; Fourcade, S.; Gagou, Y.; Hoummada, K.; El Marssi, M.; Gouné, M. Phase transitions, energy storage performances and electrocaloric effect of the lead-free Ba0.85Ca0.15Zr0.10Ti0.90 O3 ceramic relaxor. J. Mater. Sci. Mater. Electron. 2019, 30, 6430–6438. [Google Scholar] [CrossRef]
- Li, F.; Zhai, J.; Shen, B.; Liu, X.; Zeng, H. Simultaneously high-energy storage density and responsivity in quasi-hysteresis-free Mn-doped Bi0.5Na0.5TiO3-BaTiO3-(Sr0.7Bi0.2□0.1)TiO3 ergodic relaxor ceramics. Mater. Res. Lett. 2018, 6, 345–352. [Google Scholar] [CrossRef]
- Wang, S.; Huang, X.; Wang, G.; Wang, Y.; He, J.; Jiang, P. Increasing the energy efficiency and breakdown strength of high-energy-density polymer nanocomposites by engineering the Ba0.7Sr0.3TiO3 nanowire surface via reversible addition–fragmentation chain transfer polymerization. J. Phys. Chem. C 2015, 119, 25307–25318. [Google Scholar] [CrossRef]
- Puli, V.S.; Kumar, A.; Chrisey, D.B.; Tomozawa, M.; Scott, J.F.; Katiyar, R.S. Barium zirconate-titanate/barium calcium-titanate ceramics via sol–gel process: Novel high-energy-density capacitors. J. Phys. D. Appl. Phys. 2011, 44, 395403. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Y.; Wang, X.; Ma, T.; Yuan, Z. Influence of sintering temperature on energy storage properties of BaTiO3–(Sr1−1.5xBix)TiO3 ceramics. Ceram. Int. 2012, 38, 4765–4770. [Google Scholar] [CrossRef]
- Yang, H.; Yan, F.; Lin, Y.; Wang, T.; Wang, F.; Wang, Y.; Guo, L.; Tai, W.; Wei, H. Lead-free BaTiO3-Bi0.5Na0.5TiO3-Na0.73Bi0.09NbO3 relaxor ferroelectric ceramics for high energy storage. J. Eur. Ceram. Soc. 2017, 37, 3303–3311. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Chauhan, V.; Hussain, A.; Rout, S.K. Phase transition and energy storage properties of BaTiO3-modified Bi0.5(Na0.8K0.2)0.5TiO3 ceramics. Ferroelectrics 2017, 517, 97–103. [Google Scholar] [CrossRef]

| Method | Advantages | Disadvantages | |
|---|---|---|---|
| Physical Methods | PLD | Excellent stoichiometry control | Defects formation |
| Good versatility | Poor scalability | ||
| Low substrate temperature | High cost | ||
| MBE | Possibility of epitaxial growth | Sophisticated apparatus | |
| Excellent film thickness control | Precursor unavailability | ||
| Good stoichiometry control | Expensive | ||
| Sputtering | High deposition rates | Poor stoichiometric control | |
| Uniform film | High substrate temperature | ||
| Low impurities | |||
| Ease in scalability | |||
| Chemical Methods | CSD | Excellent stoichiometric control | Crack formation |
| Good uniformity | Delamination | ||
| Affordable | Defects formation | ||
| Easiness | Low deposition rates | ||
| Precursors availability | Poor thickness control | ||
| Ease in scalability | |||
| MOCVD | Good Stoichiometry control | Poor precursors availability | |
| Excellent uniformity | Bad reproducibility | ||
| Texture versatility | High substrate temperatures | ||
| High deposition rates | |||
| MOD | Low temperature | Bad thickness control | |
| High density | Large volume shrinkage | ||
| Good uniformity | Poor precursors availability | ||
| Good stoichiometry control | High annealing temperatures |
| S.No | Composition | Processing Method | Js [J/cm3] | Jr [J/cm3] | η [%] | BDS [kV/cm] | Reference |
|---|---|---|---|---|---|---|---|
| BULK CERAMICS | |||||||
| 1. | 0.9BaTiO3–0.1Bi(Mg2/3 Nb1/3)O3–0.3 wt. % MnCO3 | SSR | - | 1.7 | 90 | >210 | [51] |
| 2. | 0.60BiFeO3–0.34BaTiO3–0.06Ba(Zn1/3Ta2/3)O3 | SSR | - | 2.56 | 80 | >160 | [79] |
| 3. | BaTi0.7Zr0.3O3 | SPS | 0.51 | - | 70–80 | 170 | [80] |
| 4. | Ba0.94(Bi0.5K0.5)0.06Ti0.85Zr0.15O3 | TSS | - | 0.95 | 88 | 76 | [121] |
| 5. | 0.89Bi0.5Na0.5TiO3–0.06Ba TiO3–0.05K0.5Na0.5NbO3 | TSS | 0.9 | - | - | >99 | [122] |
| 6. | 0.89Bi0.5Na0.5TiO3–0.06Ba TiO3–0.05K0.5Na0.5NbO3 | SSR | 0.46 | - | - | >56 | [123] |
| 7. | Bi0.5K0.5TiO3–Ba(Mg1/3Nb2/3)O3 | HP | - | 3.14 | 83.7 | >230 | [127] |
| 8. | Bi1-xSmxFe0.95Sc0.05O3 | HP | - | 2.21 | 76 | >230 | [128] |
| 9. | 0.55Bi0.5Na0.5TiO3–0.45Ba0.85Ca0.15Ti0.85Zr0.1Sn0.05O3 | MW | 1.21 | - | 72.08 | 130.2 | [134] |
| 10. | BaTiO3–Bi(Li0.5Ta0.5)O3 | SSR | - | 2.2 | 89 | 280 | [138] |
| 11. | Ba0.70Ca0.30TiO3–Ba(Zr0.2Ti0.8)O3 | SSR | 1.21 | 0.71 | 150 | [141] | |
| 12. | 0.61BiFeO3–0.33(Ba0.8Sr0.2)TiO3–0.06La(Mg2/3Nb1/3)O3 | SSR | - | 3.38 | 59 | 230 | [143] |
| 13. | 0.45SrTiO3–0.2Na0.5Bi0.5TiO3–0.35BaTiO3 | - | 1.78 | - | >170 | [197] | |
| 14. | 0.85BaTiO3–0.15Bi (Mg2/3Nb1/3)O3 | SSR | 1.18 | 1.13 | >143.5 | [206] | |
| 15. | Ba0.997Sm0.002Zr0.15Ti0.85O3 | SSR | 1.15 | - | 92 | >10 | [207] |
| 16. | 0.67Bi0.9Sm0.1FeO3–0.33BaTiO3 | 2.8 | 55.8 | 200 | [208] | ||
| 17. | BiScO3–BaTiO3 + 20 wt% (K1/2Bi1/2)TiO3 | SSR | 1.28 | - | - | 100 | [209] |
| 18. | 0.89Bi0.5Na0.5TiO3–0.06BaTiO3–0.05K0.5Na0.5NbO3 | TSS | 0.9 | - | - | >100 | [122] |
| 19. | 1/3(Ba0.70Sr0.30TiO3) + 1/3(Ba0.70Ca0.30TiO3) + 1/3(BaZr0.20Ti0.80O3) | SSR | 1.40 | 0.44 | - | >115 | [210] |
| 20. | BaZr0.1Ti0.9O3 | SSR | 0.5 | - | - | 30 | [211] |
| 21. | 0.94Bi0.47Na0.47Ba0.06TiO3–0.06KNbO3 | SSR | 0.89 | - | - | 100 | [205] |
| 22. | 0.61BiFeO3–0.33BaTiO3–0.06Ba(Mg1/3Nb2/3)O3 | SSR | 1.56 | - | 75 | >125 | [198] |
| 23. | 0.9 Ba0.65Sr0.35TiO3–0.1Bi(Mg2/3Nb1/3)O3 | SSR | 3.9 | 3.34 | 85.71 | 400 | [212] |
| 24. | 0.94(Bi0.5Na0.5)[(Y0.5Ta0.5)0.1Ti0.9]O3–0.06BaTiO3 | SSR | 1.215 | - | 68.7 | >98 | [213] |
| 25. | 0.94Bi0.5Na0.5TiO3–0.06BaTiO + 0.03CaZrO3 | SSR | 0.7 | - | - | >70 | [214] |
| 26. | 0.95(0.93Bi0.5Na0.5TiO3–0.07BaTiO3)–0.05 KNbO3 | SG | 1.72 | - | - | >168 | [215] |
| 27. | 0.85[(0.94)Bi0.5Na0.5TiO3–0.06BaTiO3]–0.15Na0.73Bi0.09NbO3 | SSR | 1.4 | - | 66.3 | 142 | [216] |
| 28. | 0.86BaTiO3–0.14Bi(Zn0.5Ti0.5)O3 | SSR | 0.81 | - | 94 | 120 | [217] |
| 29. | 0.82[0.94Bi0.5Na0.5TiO3–0.06BaTiO3]–0.18K0.5Na0.5NbO | 0.616 | - | 94 | >70 | [218] | |
| 30. | 0.93Ba0.55Sr0.45TiO3–0.07BiMg2/3Nb1/3O3 | SSR | - | 4.55 | 81.8 | 450 | [219] |
| 31. | [(BaZr0.2Ti0.80)O3]0.85–[(Ba0.70Ca0.30)TiO3]0.15 | SSR | 7.48 | - | - | 153 | [220] |
| 32. | BaZr0.15Ti0.85O3 + 12 wt% Bi2O3·3TiO2 | SSR | - | - | - | 150.9 | [221] |
| 33. | 0.5(Ba0.7Ca0.3)TiO3-0.5Ba(Ti0.9Zr0.1)O3 | SSR | - | 0.164 | 74 | - | [222] |
| 34. | 0.6 Ba(Zr0.2Ti0.8)O3–0.4Na0.5Bi0.5TiO3 | SSR | - | 3.22 | 91.2 | 241 | [223] |
| 35. | 0.88BaTiO3–0.12Bi(Mg1/2Ti1/2)O3 | SSR | 1.81 | - | 88 | 535.5 | [224] |
| 36. | 0.85BaTiO3–0.15Bi(Mg1/2Zr1/2)O3 | SSR | 1.31 | 1.25 | 95 | 185 | [225] |
| 37. | 0.88BaTiO3–0.12(Mg2/3Ta1/3)O3 | SSR | - | 3.28 | 93 | 395 | [226] |
| 38. | 0.96(1-x)BaTiO3-0.04KNbO3 | SSR | - | 2.03 | 94.5 | 300 | [227] |
| 39. | 0.6Bi(Mg1/2Ti1/2)O3–0.4BaTiO3 @ 120 °C | SSR | 0.7 | - | - | 60 | [228] |
| 40. | 0.9BaTiO3–0.1Ba(Mg1/3Nb2/3)O3 | SSR | 1.01 | - | - | 158 | [229] |
| 41. | 0.85BaTiO3–0.15Bi(Zn2/3Nb1/3)O3 | SSR | 0.79 | - | 93.5 | 131 | [230] |
| 42. | 0.90(Na1/2Bi1/2)0.92Ba0.08TiO3–0.10Bi(Mg1/2Ti1/2)O3 | SSR | 2 | - | - | >135 | [231] |
| 43. | 0.084BiTi0.5Zn0.5O3–0.916(0.935Bi0.5Na0.5TiO3–0.065BaTiO3) | SSR | 1.04 | - | 80 | >95 | [232] |
| 44. | 0.4(Na0.5Bi0.5TiO3)–0.225BaTiO3–0.375BiFeO3 | SPS | 1.4 | - | 90 | - | [233] |
| Ceramic + (Glass/organics) composites | |||||||
| 45. | 0.88BaTiO3–0.12Bi(Mg1/2Ti1/2)O3 + 4% (SiO2–B2O3) | SSR | 1.97 | - | 94.5 | >270 | [84] |
| 46. | Ba0.9995La0.0005TiO3 + 20 wt% 65PbO–20B2O3–15SiO2 | SSR | 0.56 | 0.31 | 54.2 | >300 | [85] |
| 47. | BaTiO3 + 3 wt% Al2O3 + 1 wt% SiO2 | SSR | 0.725 | 80 | 190 | [86] | |
| 48. | Ba0.4Sr0.6TiO3 + 2 wt% (30.8 SrO-58.9B2O3–10.3SiO2) | SSR | 0.44 | 67.4 | [87] | ||
| 49. | Ba0.4Sr0.6TiO3 + 9 wt% (65Bi2O3-20B2O3–15SiO2) | SSR | 2.18 | 1.98 | 90.57 | >279 | [92] |
| 50. | Ba0.4Sr0.6TiO3 + 4 wt% BaO–B2O3–SiO2–Na2CO3–K2CO3 | SSR | - | 0.72 | - | 280.5 | [93] |
| 51. | Ba0.85Ca0.15Zr0.1Ti0.9O3 + 5 wt% B2O3–Al2O3–SiO2 | SSR | 1.153 | - | - | 200 | [94] |
| 52. | BaTiO3 + 2.5 wt% BaO–Bi2O3–P2O5 | SSR | 0.0069 | - | 69.21 | >15 | [95] |
| 53. | Ba0.4Sr0.6TiO3 + 55 wt% BaO–B2O3–Al2O3-SiO2 | SSR | 3.1 | - | - | >405 | [97] |
| 54. | BaTiO3 + 2wt% SiO2 | SSR | 2.23 | 1.2 | 53.8 | 200 | [98] |
| 55. | 0.715Bi0.5Na0.5TiO3–0.065BaTiO3–0.22SrTiO3 + 4 wt% 3BaO-3TiO2–B2O3 | SSR | 0.203 | - | 60 | - | [234] |
| 56. | Ba0.3Sr0.7TiO3 + 1.6 wt% ZnO | SSR | 3.9 | - | - | 400 | [99] |
| 57. | 0.95(0.76Na1/2Bi1/2TiO3–0.24SrTiO3)–0.05AgNbO3:SiO2 | SSR | - | 3.22 | - | 316 | [100] |
| 58. | Ba0.4Sr0.6TiO3 + 0.5 wt% SiO2 | SSR | - | 0.86 | 79 | 134 | [101] |
| 59. | Ba(Zr0.2Ti0.8)O3–0.15(Ba0.7Ca0.3)TiO3 + 11 wt% BaO-SrO-TiO2-Al2O3–SiO2-BaF2 | SSR | 1.45 | - | - | 108 | [235] |
| 60. | Ba0.4Sr0.6TiO3 + 5 wt% MgO | SPS | 1.7 | 1.5 | 88.5 | 300 | [104] |
| 62. | BaTi0.85Sn0.15O3 +10 wt% MgO | SPS | 0.5107 | - | 92.11 | 190 | [105] |
| 63. | 0.55Bi0.5Na0.5TiO3–0.45Ba0.85Ca0.15Ti0.85Zr0.1Sn0.05O3 + 5 wt% MgO | MW | 2.09 | - | 79.51 | 189.7 | [134] |
| 64. | Ba0.4Sr0.6(Ti0.996Mn0.004)O3–2 wt% MgO | - | - | 2.014 | 88.6 | 300 | [236] |
| 65. | 0.9(0.94Na0.5Bi0.5TiO3–0.06BaTiO3)–0.1NaNbO3 + 1 wt% ZnO | SSR | 1.27 | 67 | >100 | [107] | |
| 66. | Bi0.5Na0.5TiO3–BaTiO3–K0.5Na0.5NbO3 + 40 wt% ZnO | SSR | - | 1.03 | 72.7 | 140 | [108] |
| 67. | 0.85BaTiO3–0.15Bi(Mg1/2Zr1/2)O3 + 10 wt% MnCO3 | - | 1.61 | 94.3 | 230 | [237] | |
| Ceramic + Polymer composites | |||||||
| 68. | BTO–(P(VDF-HFP)–20 vol % BTO | SC | 8.13 | - | 57 | 3300 | [112] |
| 69. | Ba0.95Ca0.05Zr0.15Ti0.85O3 + 40% PVDF | SSR-SC | 2.0 | - | - | 600 | [109] |
| 70. | BaTiO3 + 80 wt% PVDF | SSR-SC | 3.54 | - | - | >2000 | [114] |
| THICK FILM MULTILAYERS | |||||||
| 71. | 0.62BiFeO3–0.3BaTiO3–0.08NdZn0.5Zr0.5O3. | SSR-TC | - | 10.5 | 87 | >700 | [76] |
| 72. | 0.87BaTiO3–0.13Bi(Zn2/3(Nb0.85Ta0.15)1/3)O3 | SSR-TC-TSS | - | 10.12 | 90 | >1047 | [83] |
| 73. | 0.87BaTiO3–0.13Bi(Zn2/3(Nb0.85Ta0.15)1/3)O3 | SSR-TSS | - | 10.5 | 93.7 | 1000 | [137] |
| 74. | BaTiO3–Bi(Li0.5Ta0.5)O3 | SSR-TC | - | 4.05 | 95.5 | 466 | [138] |
| 75. | BaZr0.2Ti0.8O3 | SSR-TC | - | 6.2 | 98% | 800 | [140] |
| 76. | 0.90BaTiO3−0.10Bi(Li0.5Nb0.5)O3 | SSR-TC | - | 4.5 | 91.5 | 450 | [142] |
| 77. | 0.61BiFeO3–0.33(Ba0.8Sr0.2)TiO3-0.06La(Mg2/3Nb1/3)O3 | SSR-TC | - | 10 | 72 | >730 | [143] |
| THIN FILM MULTILAYERS | |||||||
| 78. | Ba0.53Sr0.47TiO3 | PLD | 51.2 | 67.3 | 4800 | [169] | |
| 79. | Ba[(Ni1/2,W1/2)0.1Ti0.9]O3 | CSD | 34 | - | - | 3000 | [178] |
| 80. | 0.88BaTiO3–0.12Bi(Mg,Ti)O3 | CSD | 37 | - | - | 1900 | [179] |
| 81. | BaTiO3/BiFeO3 (bilayer) | RFMS | - | 51 | 73 | >2700 | [180] |
| 82. | 0.6BaTiO3–0.4Bi0.25La0.75Ti3O | CSD | 61.1 | 84.2 | 3230 | [181] | |
| 83. | BaZr0.3Ti0.7O3 | PLD | 214 | 156 | 72.8 | 3000 | [182] |
| 84. | Ba(Zr0.15Ti0.85)O3/Ba(Zr0.35Ti0.65)O3 | RFMS | - | 83.9 | 78.4 | 1470 | [184] |
| 85. | Ba2Bi4Ti5O18 | CSD | - | 37.1 | 91.5 | 2340 | [238] |
| 86. | Ba0.664Y0.006Sr0.33Ti0.995Mn0.005O3 | RFMS | - | 9.75 | 77.7 | 450 | [239] |
| 87. | Ba0.65Sr0.35TiO3 | CSD | 0.128 | >100 | [240] | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veerapandiyan, V.; Benes, F.; Gindel, T.; Deluca, M. Strategies to Improve the Energy Storage Properties of Perovskite Lead-Free Relaxor Ferroelectrics: A Review. Materials 2020, 13, 5742. https://doi.org/10.3390/ma13245742
Veerapandiyan V, Benes F, Gindel T, Deluca M. Strategies to Improve the Energy Storage Properties of Perovskite Lead-Free Relaxor Ferroelectrics: A Review. Materials. 2020; 13(24):5742. https://doi.org/10.3390/ma13245742
Chicago/Turabian StyleVeerapandiyan, Vignaswaran, Federica Benes, Theresa Gindel, and Marco Deluca. 2020. "Strategies to Improve the Energy Storage Properties of Perovskite Lead-Free Relaxor Ferroelectrics: A Review" Materials 13, no. 24: 5742. https://doi.org/10.3390/ma13245742
APA StyleVeerapandiyan, V., Benes, F., Gindel, T., & Deluca, M. (2020). Strategies to Improve the Energy Storage Properties of Perovskite Lead-Free Relaxor Ferroelectrics: A Review. Materials, 13(24), 5742. https://doi.org/10.3390/ma13245742







