A Hole Nucleation Method Combining BESO and Topological Sensitivity for Level Set Topology Optimization
Abstract
1. Introduction
2. Level Set Topology Optimization Method
3. Bi-Directional Evolutionary Structural Optimization (BESO) and Topological Sensitivity
3.1. BESO
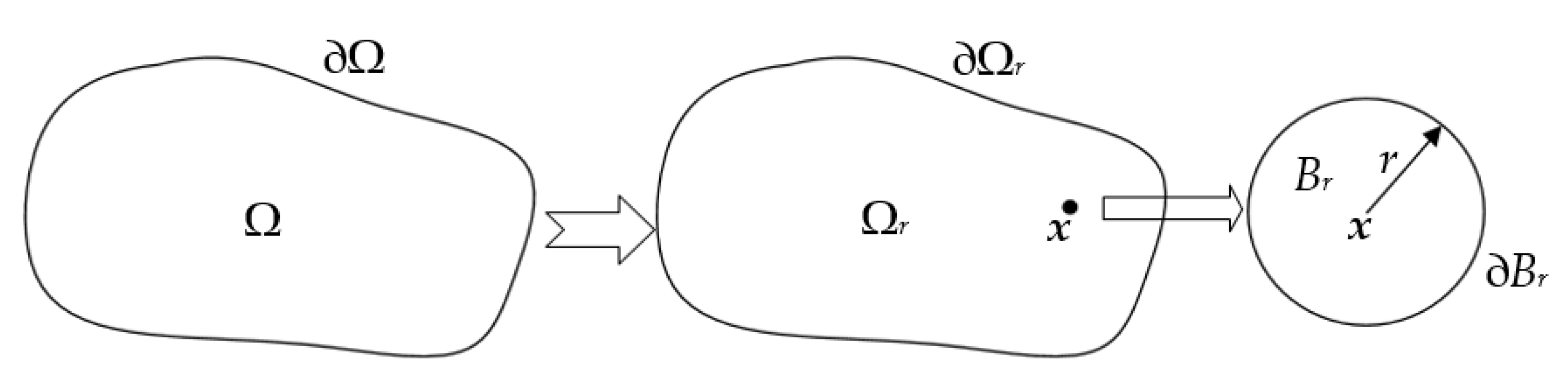
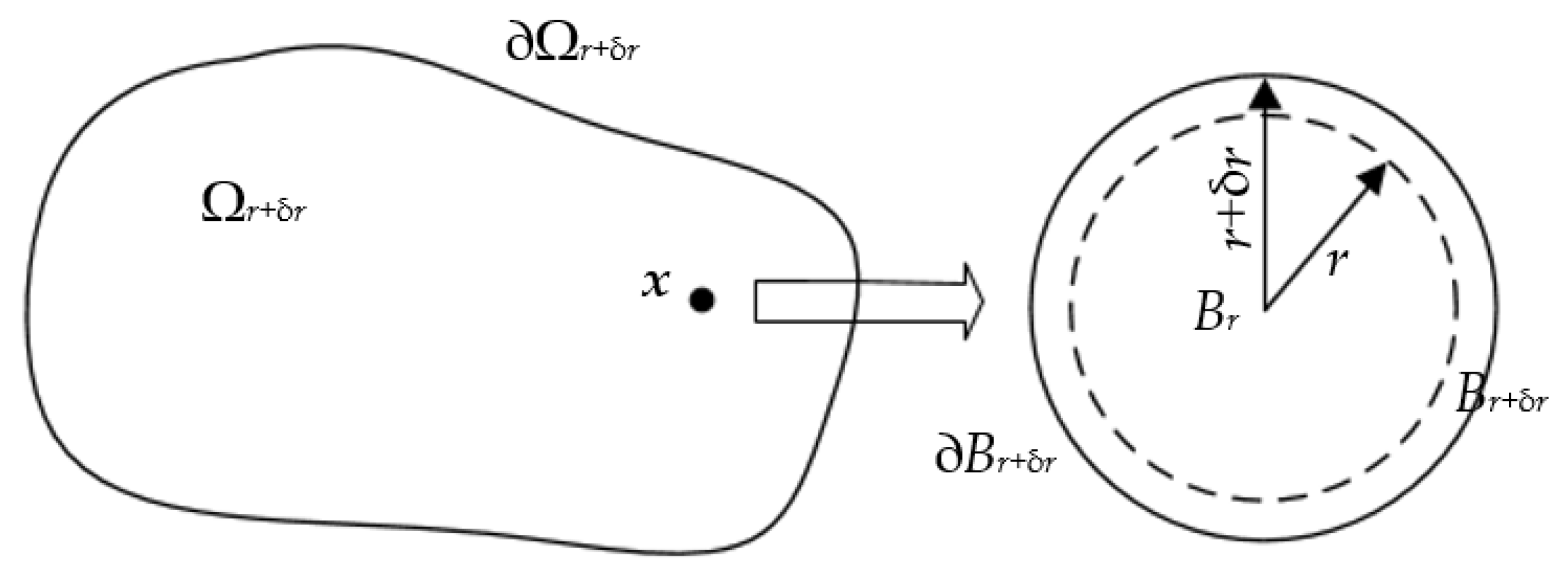
3.2. Topological Sensitivity
- for d = 2
- for d = 3
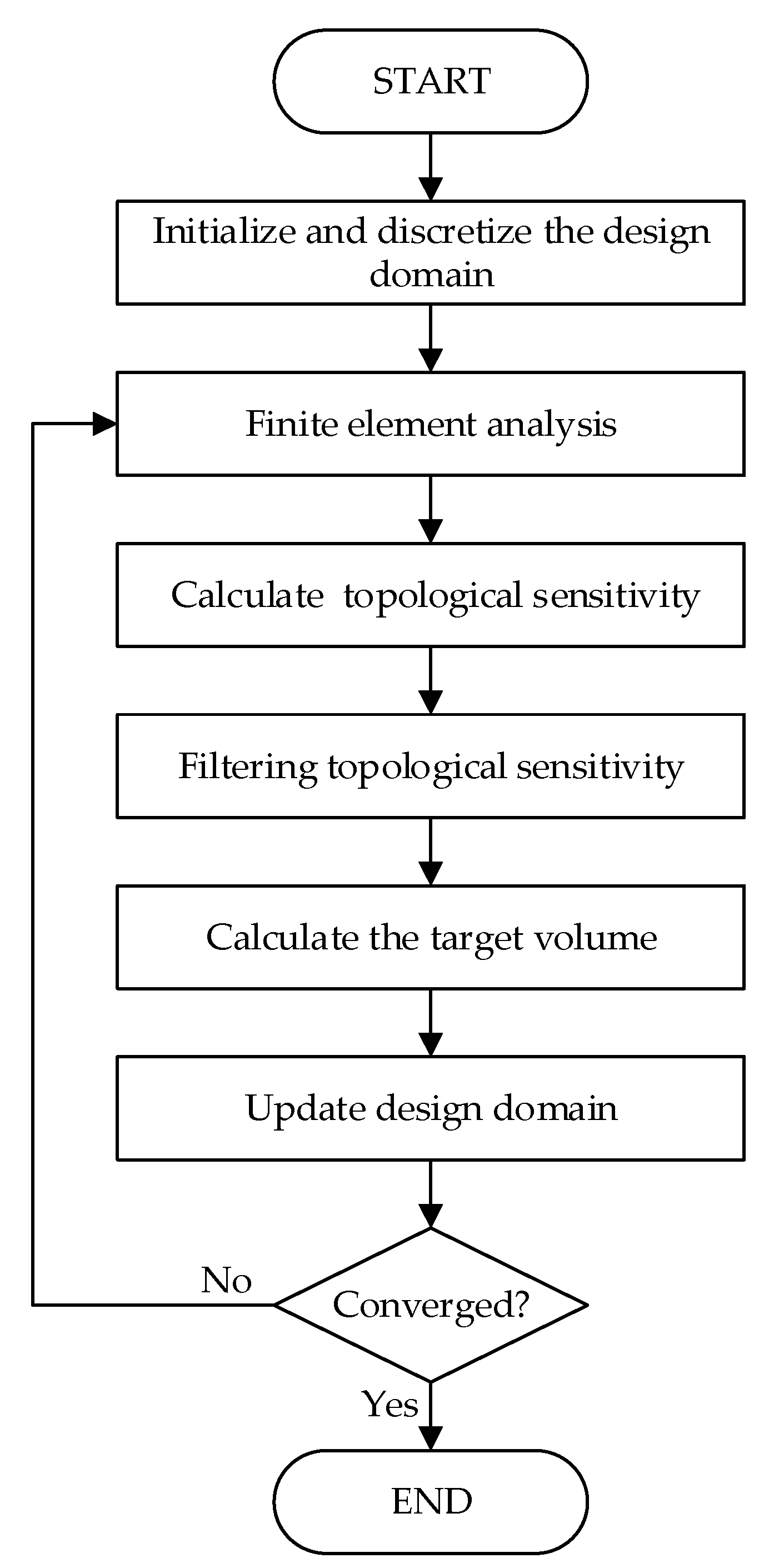
4. BESO Based on Topological Sensitivity
- for d = 2
- for d = 3
- Discretize the design domain and initialize the structure;
- Perform finite element analysis, and calculate the elemental topological sensitivity using Equation (31);
- Filter topological sensitivity using Equations (34) and (35);
- Calculate the target volume using Equation (36);
- Update the structure using Equations (37) and (38);
- Check whether the convergence condition is satisfied. If not, return to step 2 for a new iteration.
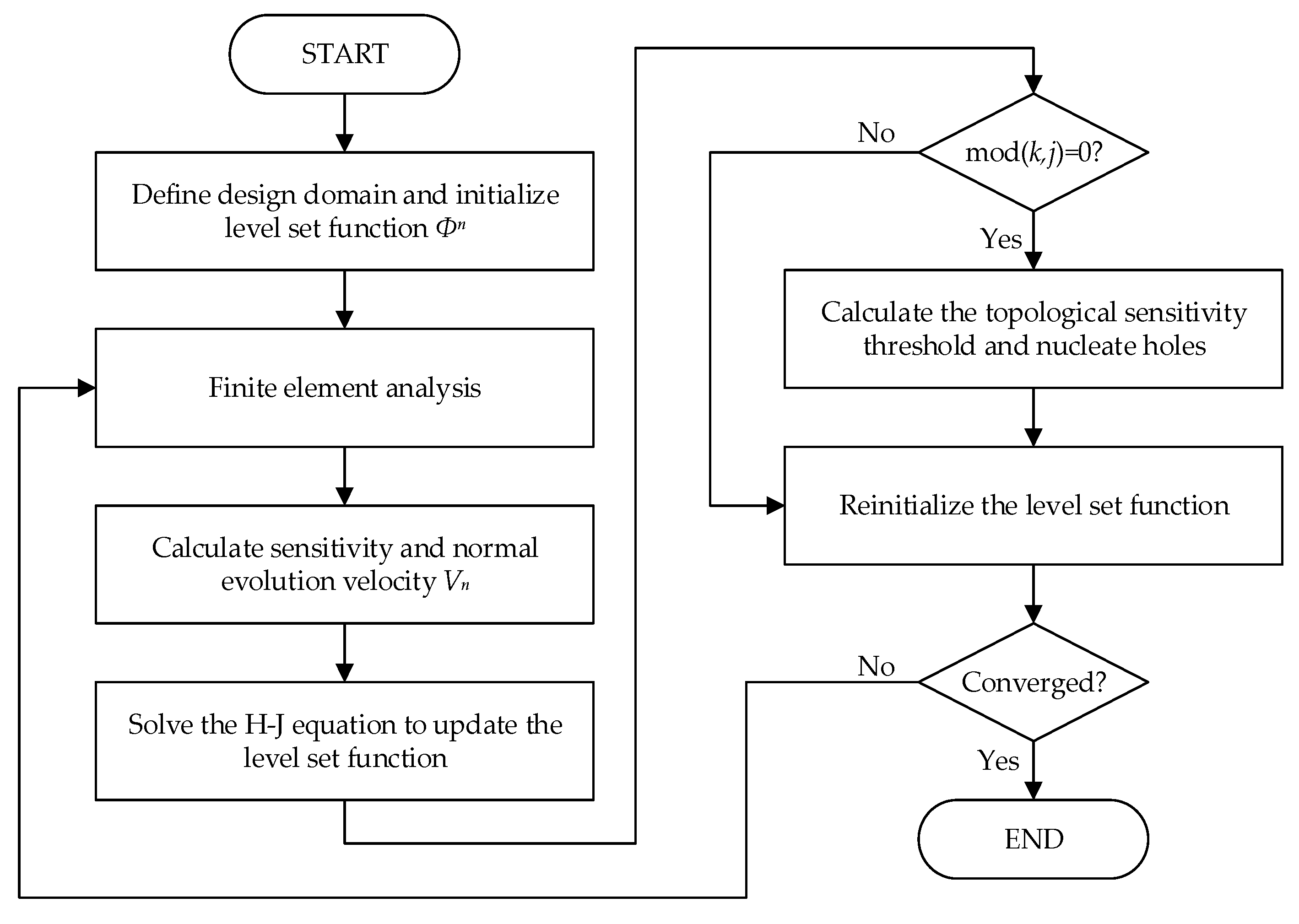
5. Combining BESO and Topological Sensitivity (CBT) Level Set Topology Optimization
- Define the design domain and initialize level set function;
- Solve linear elasticity equation via the finite element method;
- Calculate shape sensitivity, topological sensitivity and the normal evolution velocity ;
- Solve the Hamilton–Jacobi equation to update the level set function;
- If the current iteration number is an integer multiple of j, nucleate hole by Equation (45), then go to step 6. Otherwise, go to step 7;
- Calculate the topological sensitivity threshold ;
- Reinitialize the level set function;
- Check whether the convergence criteria are satisfied. If not, repeat steps 2–8 until convergence.
6. Numerical Examples
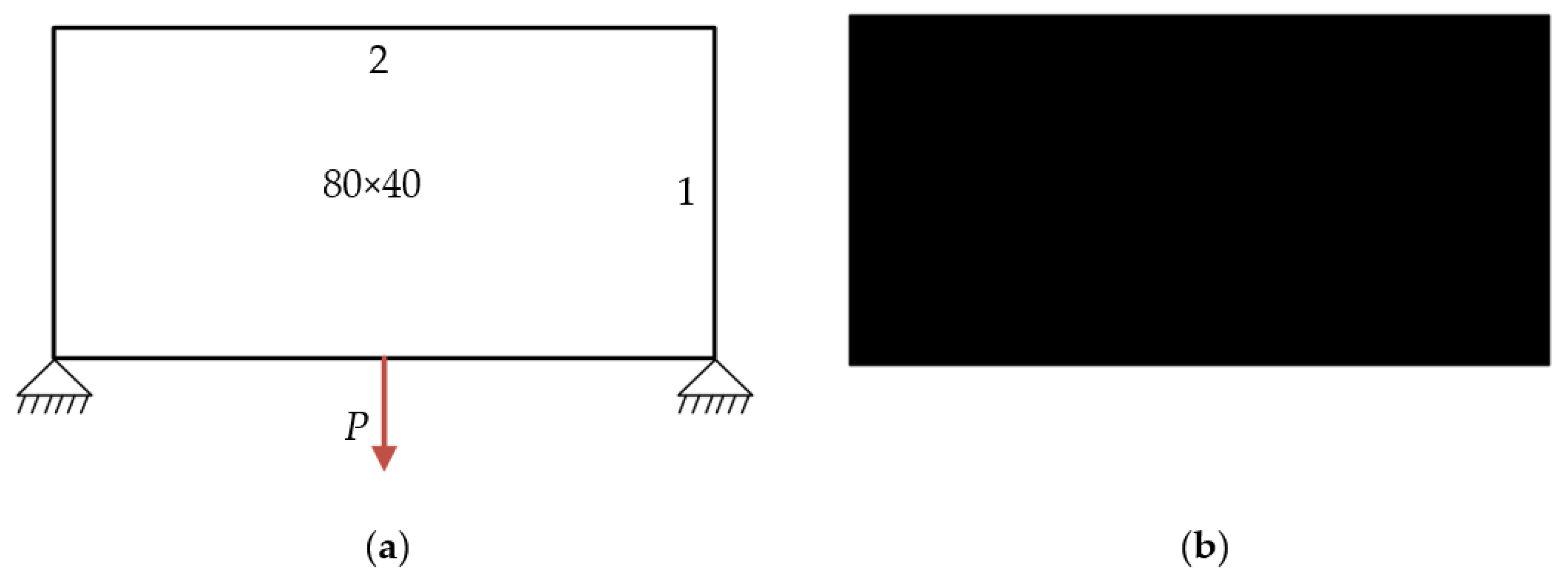
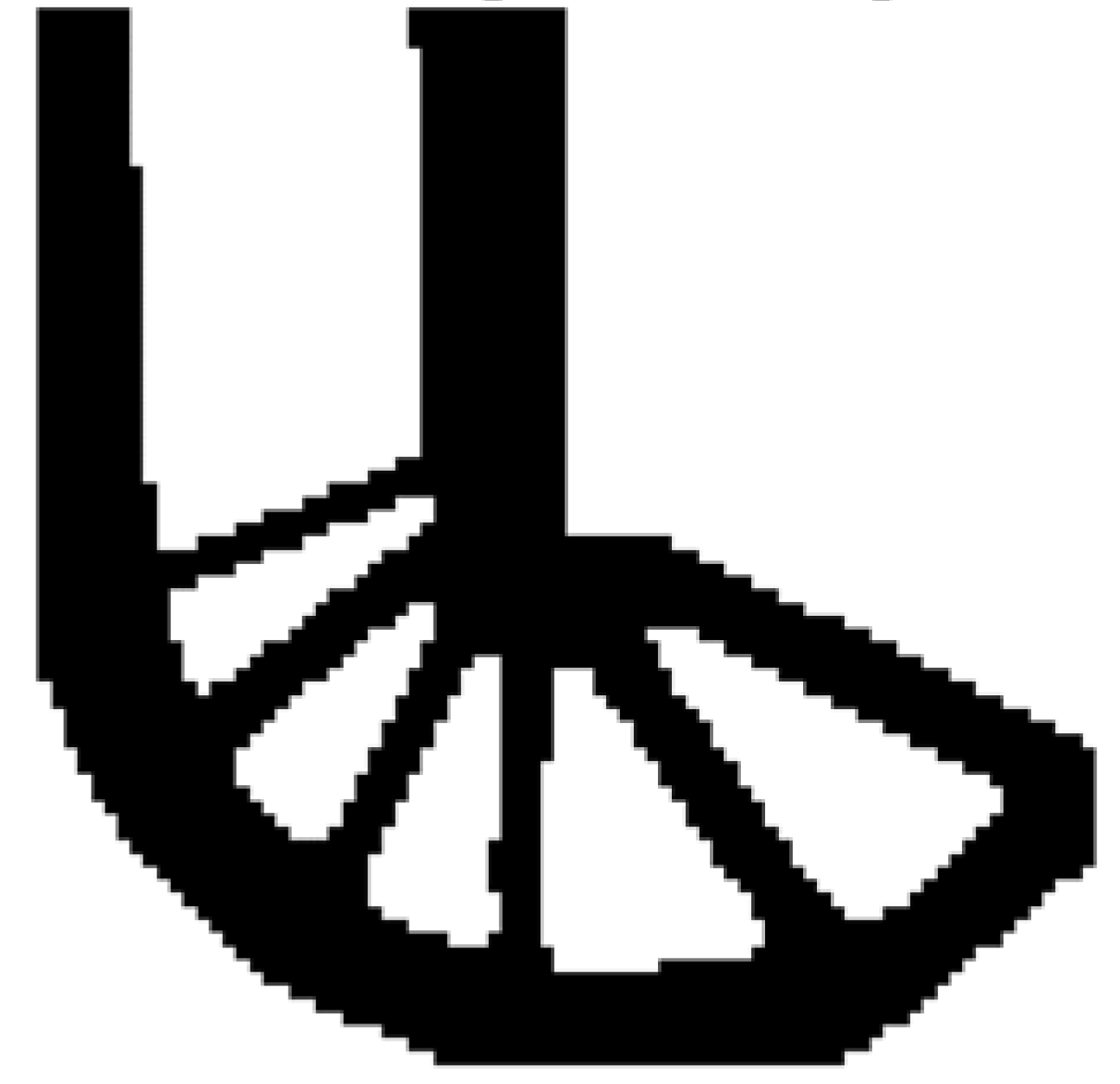
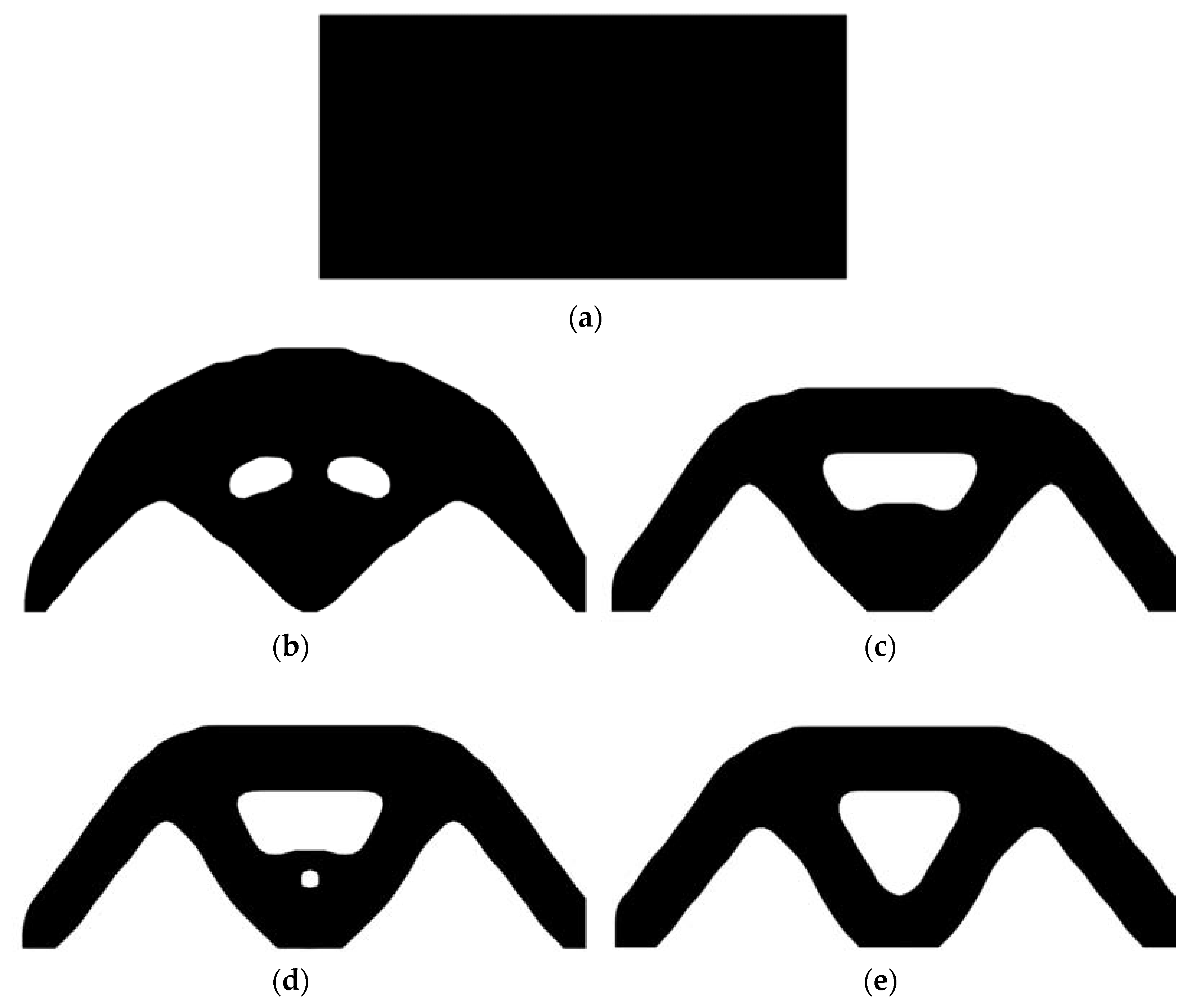
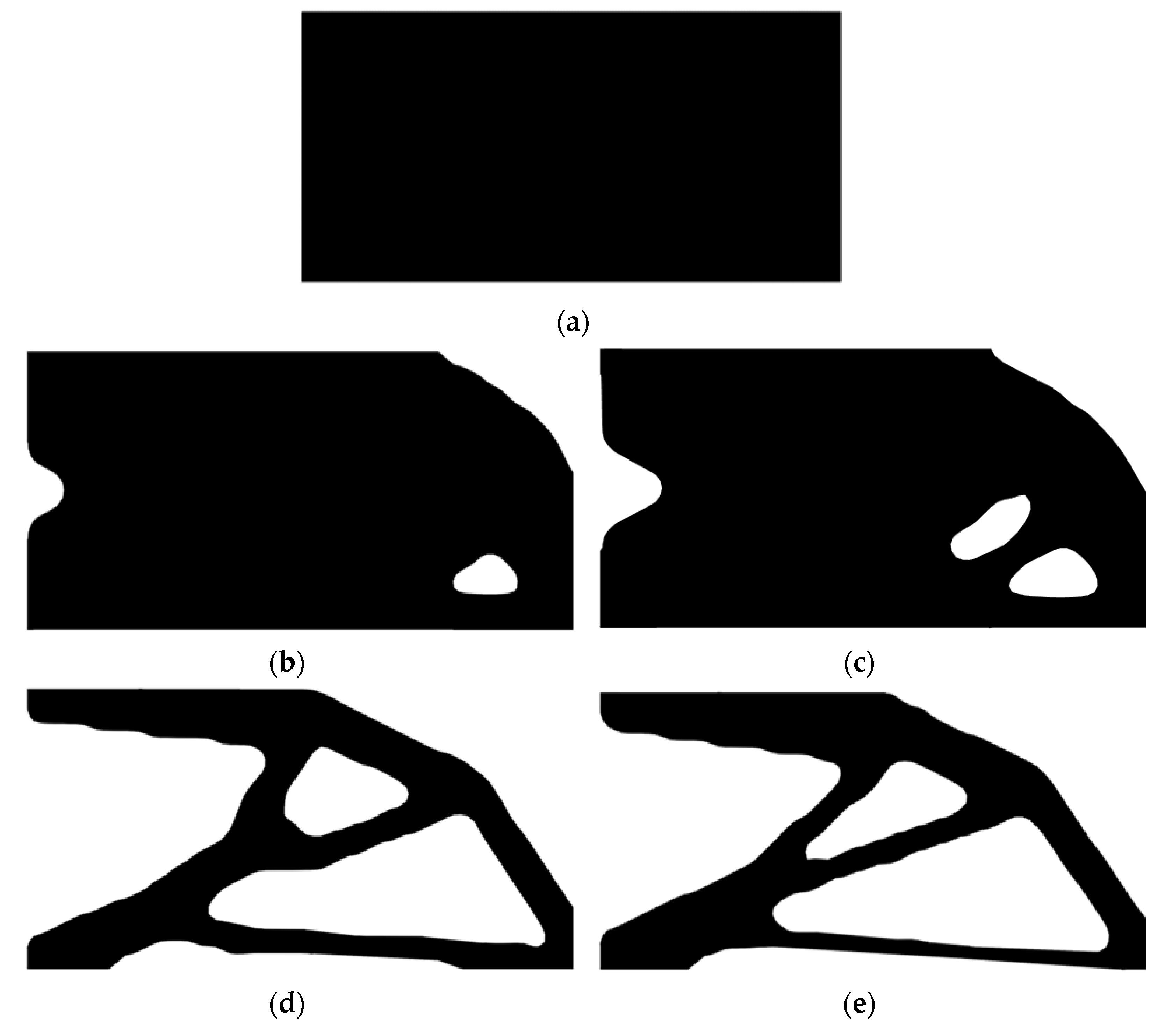
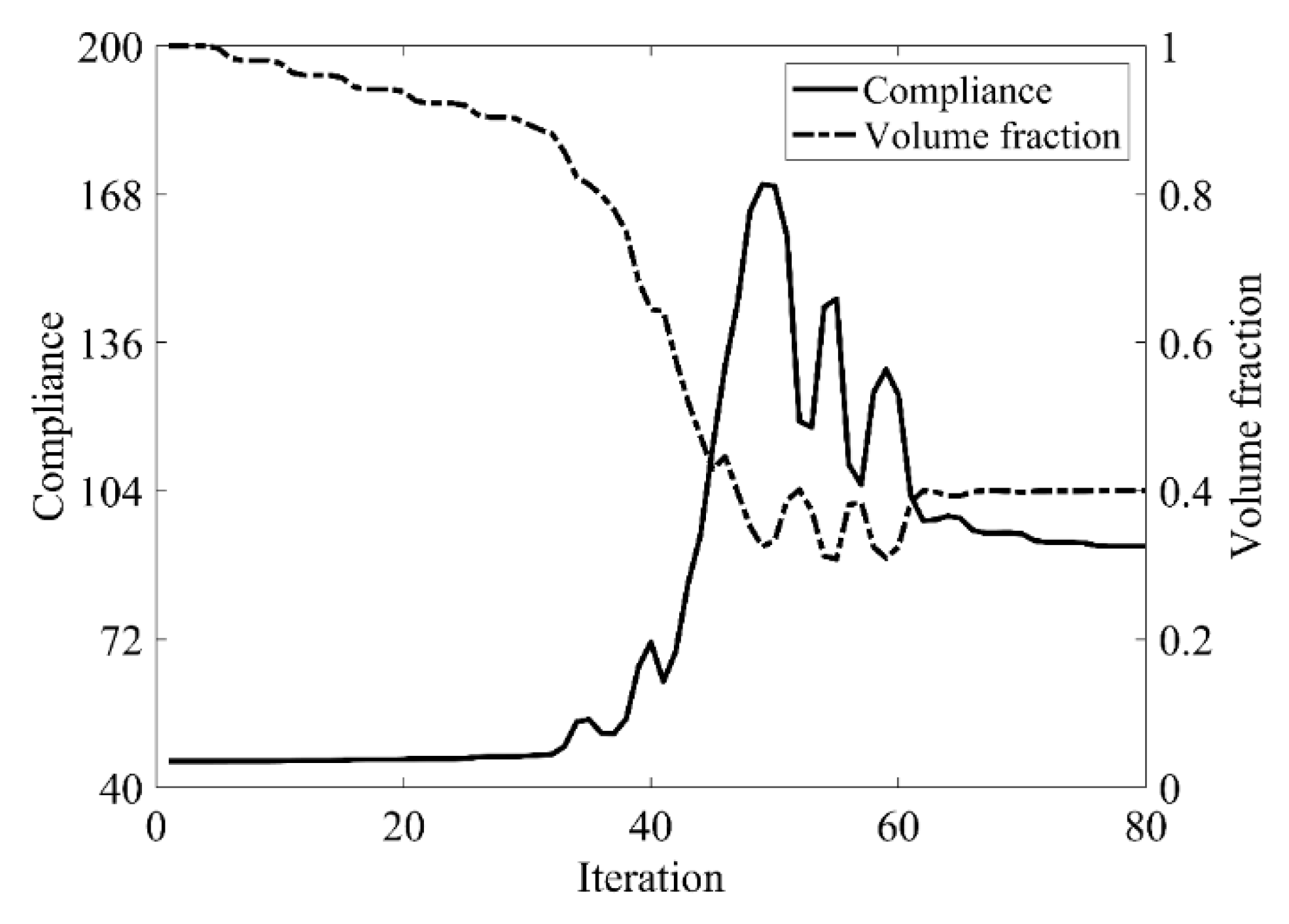
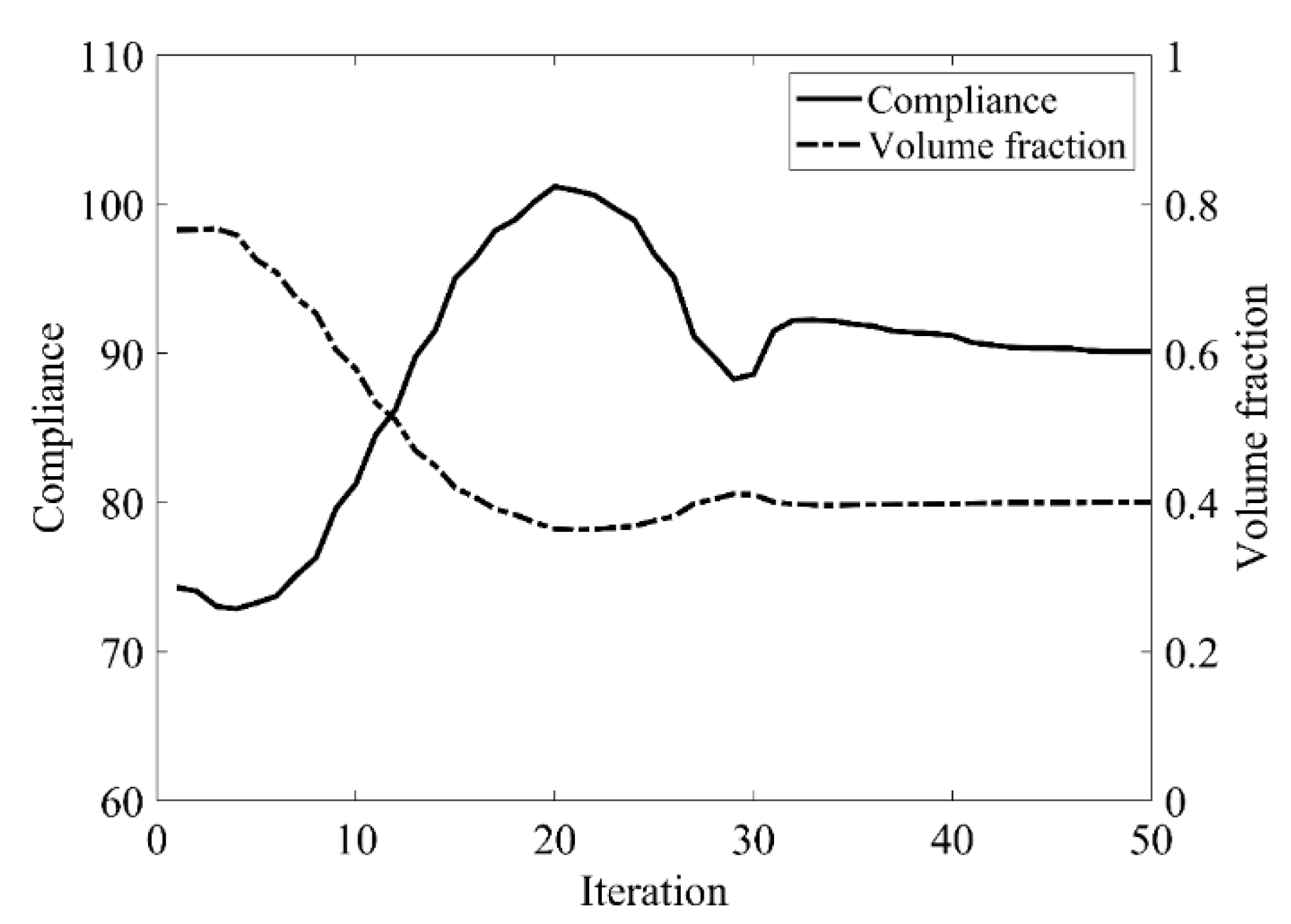
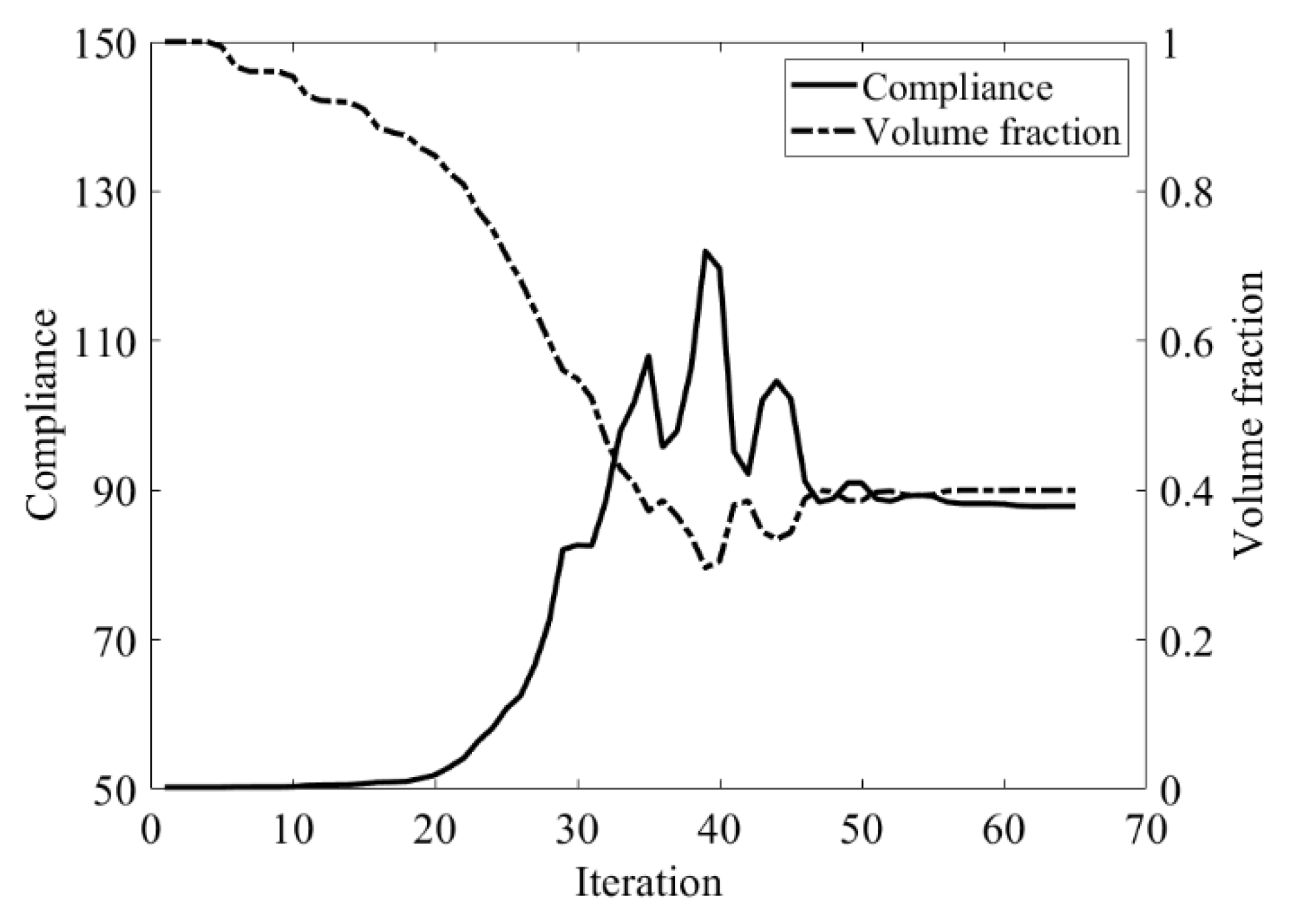
6.1. Simple Bridge Beam
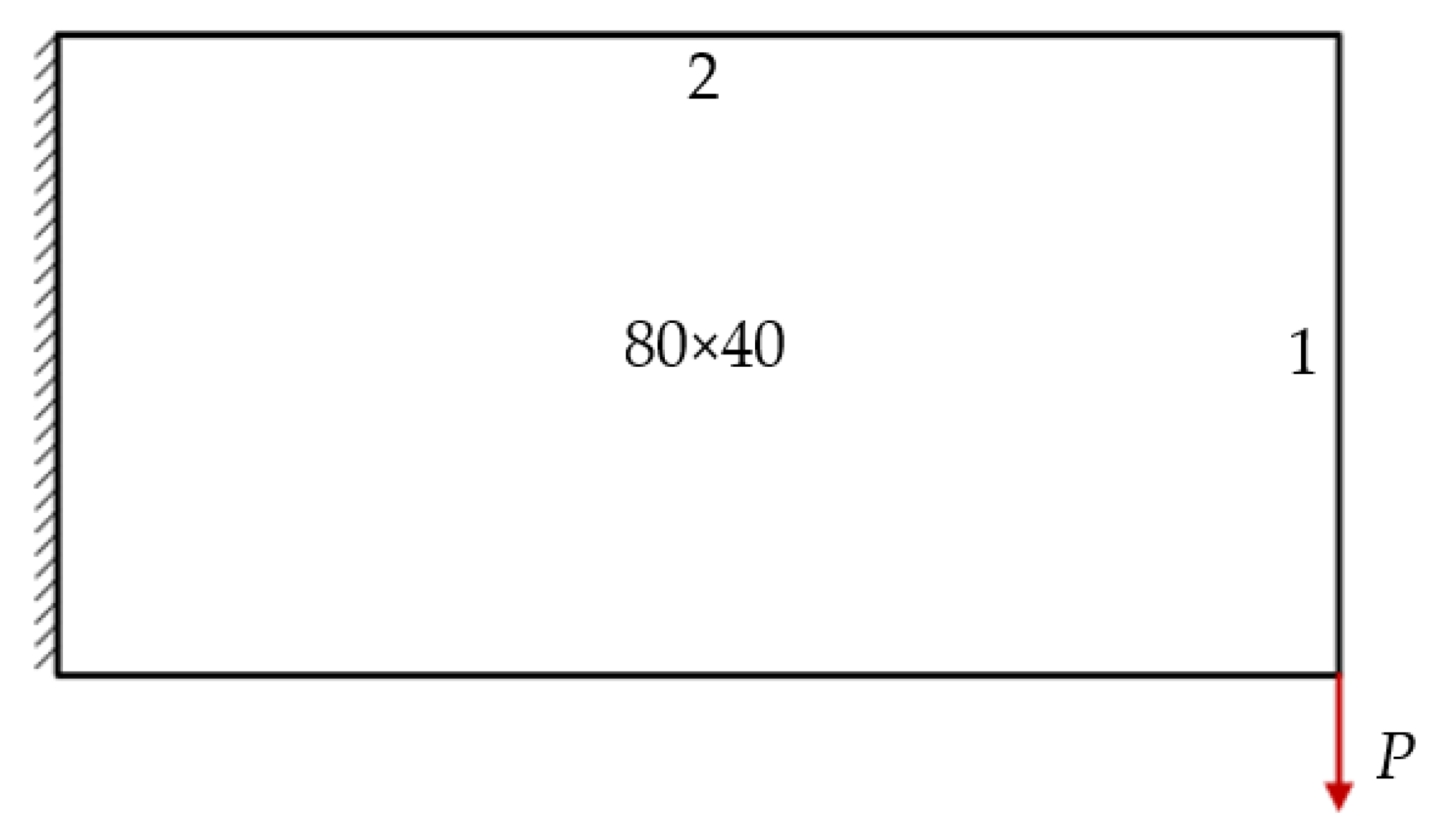
6.2. Cantilever Beam
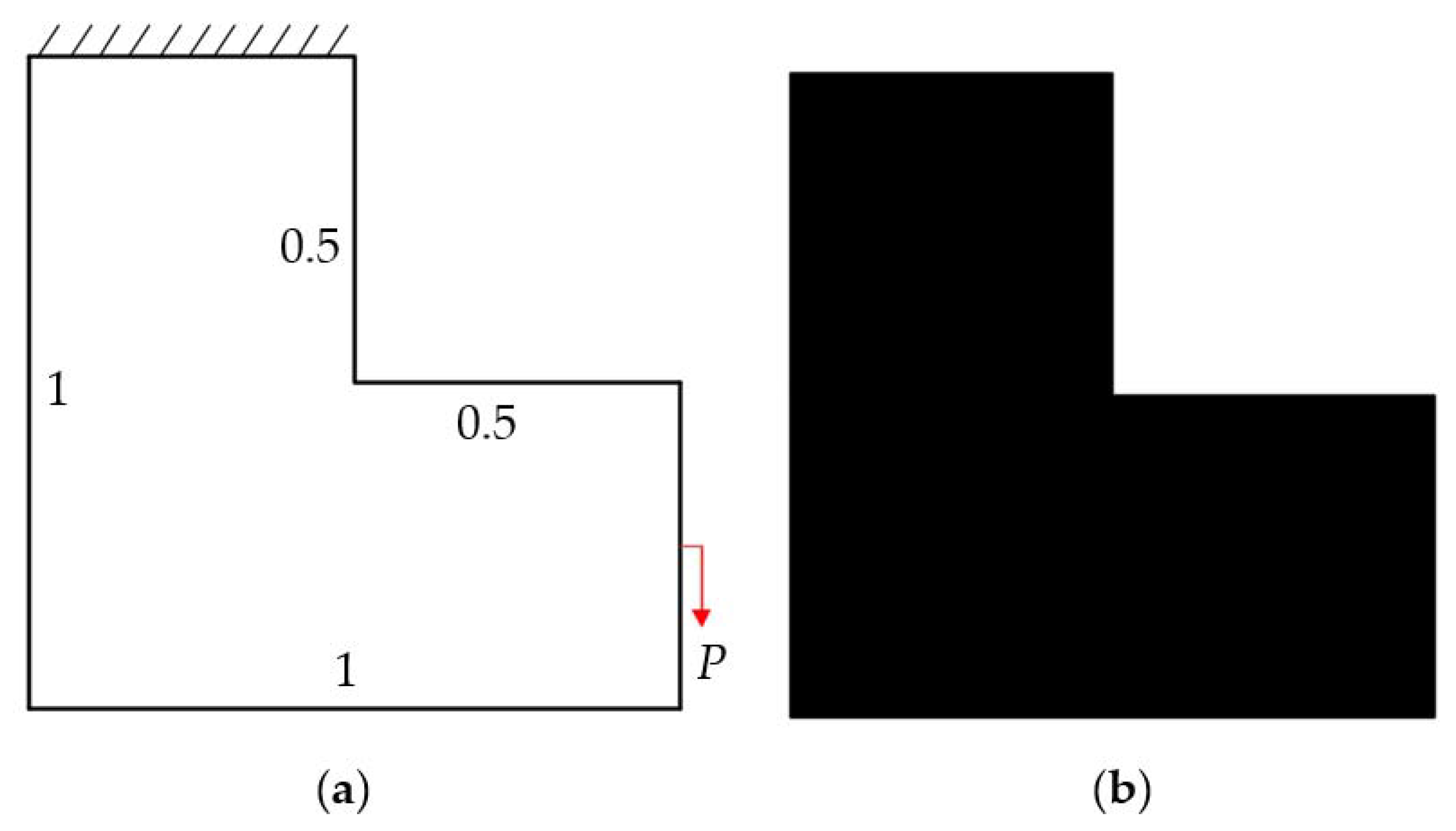
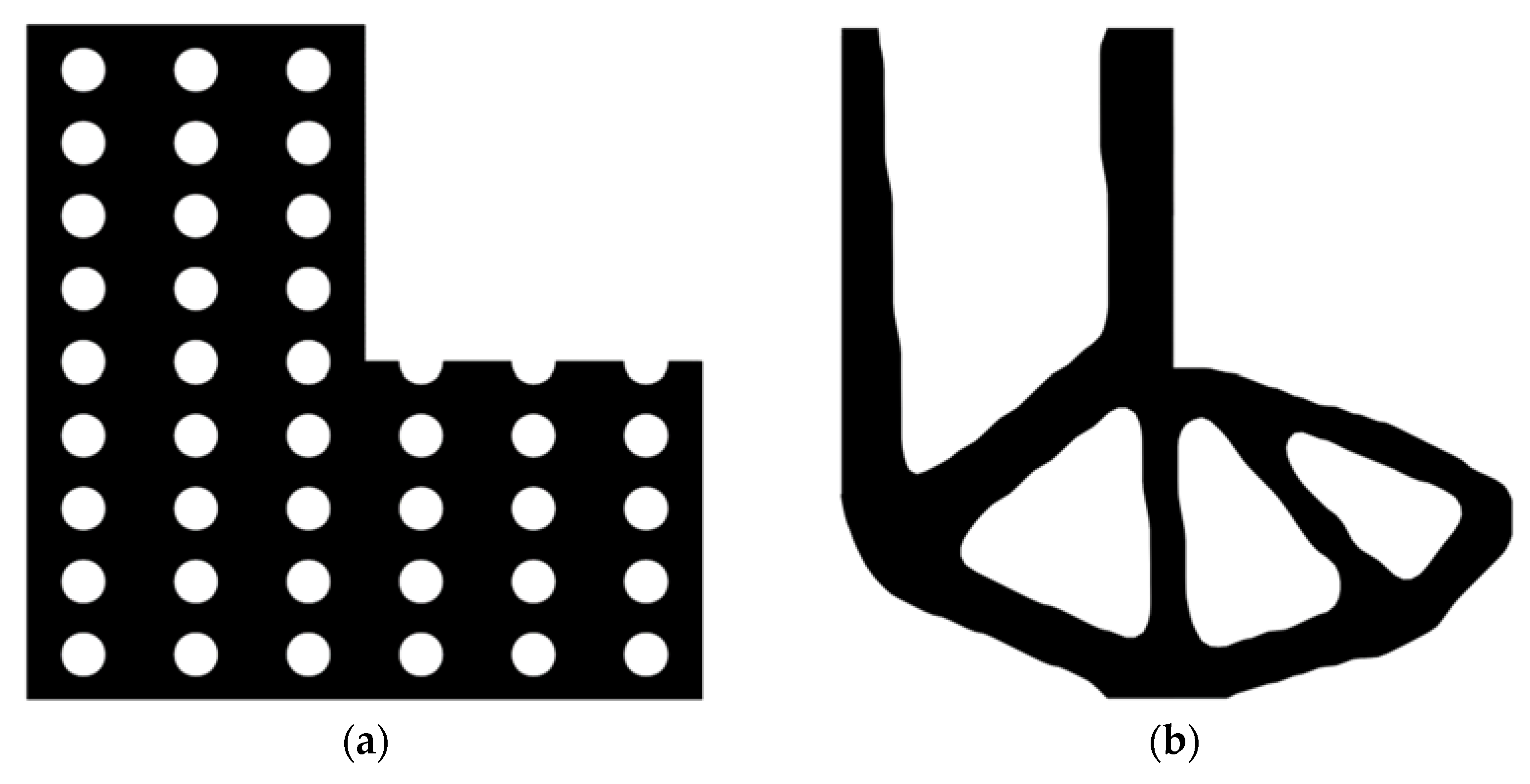
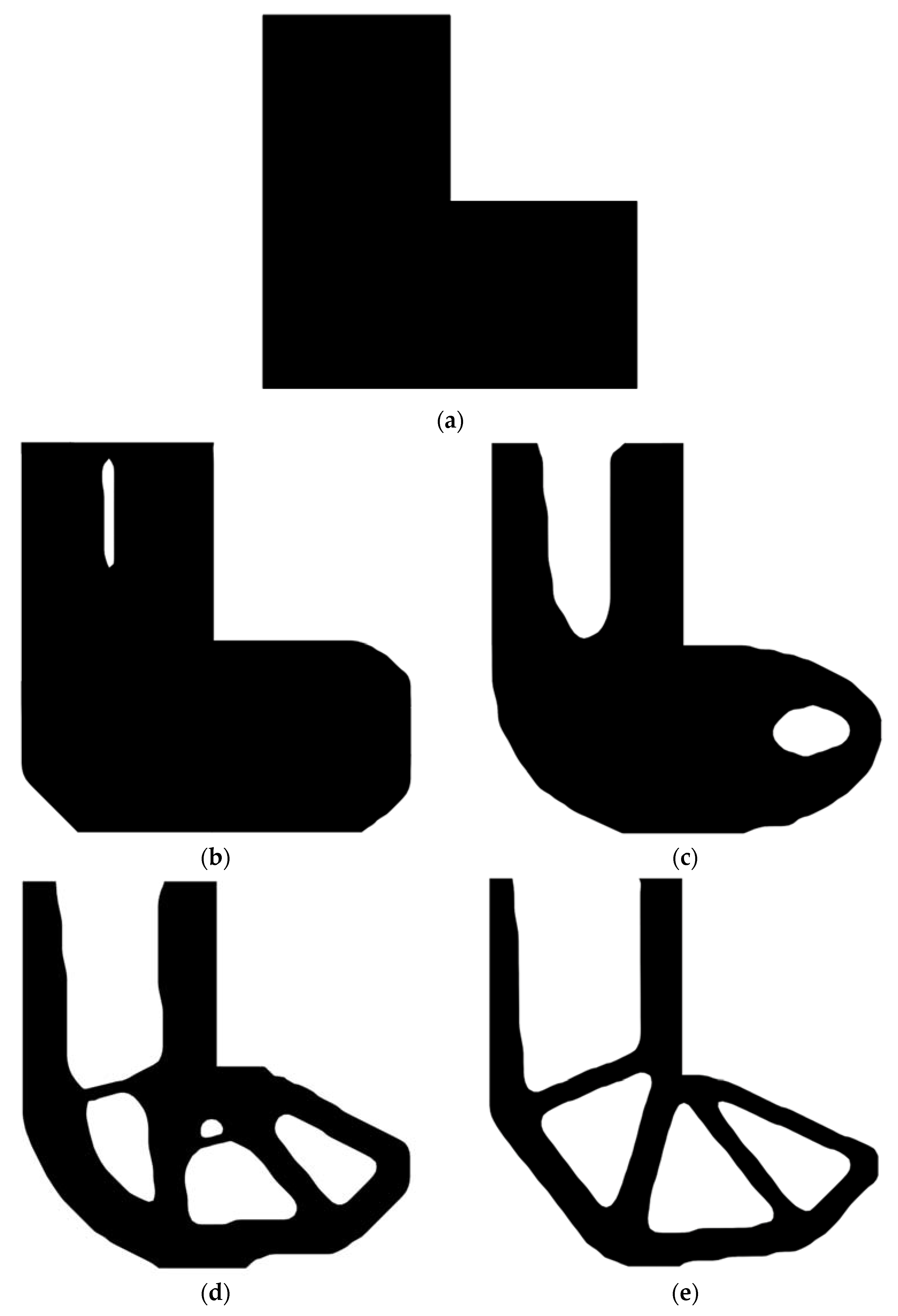
6.3. L-Shaped Beam
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allaire, G.; Jouve, F. Structural Optimization by the Homogenization Method; Springer: Dordrecht, The Netherlands, 1999; pp. 293–300. [Google Scholar]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Díaz, A.R.; Bendsøe, M.P. Shape optimization of structures for multiple loading conditions using a homogenization method. Struct. Optim. 1992, 4, 17–22. [Google Scholar] [CrossRef]
- Suzuki, K.; Kikuchi, N. A homogenization method for shape and topology optimization. Comput. Methods Appl. Mech. Eng. 1991, 93, 291–318. [Google Scholar] [CrossRef]
- Yoo, J.; Kikuchi, N.; Volakis, J.L. Structural optimization in magnetic fields using the homogenization design method—Part I. Arch. Comput. Methods Eng. 2001, 8, 387–406. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Material interpolation schemes in topology optimization. Arch. Appl. Mech. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Rietz, A. Sufficiency of a finite exponent in SIMP (power law) methods. Struct. Multidiscip. Optim. 2001, 21, 159–163. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 line topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Stolpe, M.; Svanberg, K. An alternative interpolation scheme for minimum compliance topology optimization. Struct. Multidiscip. Optim. 2001, 22, 116–124. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elem. Anal. Des. 2007, 43, 1039–1049. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. A new look at ESO and BESO optimization methods. Struct. Multidiscip. Optim. 2008, 35, 89–92. [Google Scholar] [CrossRef]
- Xia, L.; Xia, Q.; Huang, X.; Xie, Y.M. Bi-directional Evolutionary Structural Optimization on Advanced Structures and Materials: A Comprehensive Review. Arch. Comput. Methods Eng. 2018, 25, 437–478. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. A simple evolutionary procedure for structural optimization. Comput. Struct. 1992, 49, 885–896. [Google Scholar] [CrossRef]
- Yang, X.Y.; Xie, Y.M.; Steven, G.P.; Querin, O.M. Bidirectional Evolutionary Method for Stiffness Optimization. AIAA J. 1999, 37, 1483–1488. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.; Zhang, J.; Yuan, J. Explicit structural topology optimization based on moving morphable components (MMC) with curved skeletons. Comput. Methods Appl. Mech. Eng. 2016, 310, 711–748. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.; Zhong, W. Doing Topology Optimization Explicitly and Geometrically—A New Moving Morphable Components Based Framework. J. Appl. Mech. 2014, 81, 081009. [Google Scholar] [CrossRef]
- Zhang, W.; Li, D.; Zhang, J.; Guo, X. Minimum length scale control in structural topology optimization based on the Moving Morphable Components (MMC) approach. Comput. Methods Appl. Mech. Eng. 2016, 311, 327–355. [Google Scholar] [CrossRef]
- Zhang, W.; Yuan, J.; Zhang, J.; Guo, X. A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model. Struct. Multidiscip. Optim. 2016, 53, 1243–1260. [Google Scholar] [CrossRef]
- Allaire, G.; Jouve, F.; Toader, A.-M. Structural optimization using sensitivity analysis and a level-set method. J. Comput. Phys. 2004, 194, 363–393. [Google Scholar] [CrossRef]
- Allaire, G.; Jouve, F.; Toader, A.-M. A level-set method for shape optimization. Comptes Rendus Math. 2002, 334, 1125–1130. [Google Scholar] [CrossRef]
- Challis, V. A discrete level-set topology optimization code written in matlab. Struct. Multidiscip. Optim. 2010, 41, 453–464. [Google Scholar] [CrossRef]
- Otomori, M.; Yamada, T.; Izui, K.; Nishiwaki, S. Matlab code for a level set-based topology optimization method using a reaction diffusion equation. Struct. Multidiscip. Optim. 2015, 51, 1159–1172. [Google Scholar] [CrossRef]
- Sethian, J.A.; Wiegmann, A. Structural Boundary Design via Level Set and Immersed Interface Methods. J. Comput. Phys. 2000, 163, 489–528. [Google Scholar] [CrossRef]
- van Dijk, N.P.; Maute, K.; Langelaar, M.; van Keulen, F. Level-set methods for structural topology optimization: A review. Struct. Multidiscip. Optim. 2013, 48, 437–472. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Yaghmaei, M.; Ghoddosian, A.; Khatibi, M.M. A filter-based level set topology optimization method using a 62-line MATLAB code. Struct. Multidiscip. Optim. 2020, 62, 1001–1018. [Google Scholar] [CrossRef]
- Allaire, G.; de Gournay, F.; Jouve, F.; Toader, A.-M. Structural optimization using topological and shape sensitivity via a level set method. Control Cybern. 2005, 34, 59. [Google Scholar]
- He, L.; Kao, C.-Y.; Osher, S. Incorporating topological derivatives into shape derivatives based level set methods. J. Comput. Phys. 2007, 225, 891–909. [Google Scholar] [CrossRef]
- Xia, Q.; Shi, T.; Xia, L. Stable hole nucleation in level set based topology optimization by using the material removal scheme of BESO. Comput. Methods Appl. Mech. Eng. 2019, 343, 438–452. [Google Scholar] [CrossRef]
- Wang, S.; Wang, M.Y. Radial basis functions and level set method for structural topology optimization. Int. J. Numer. Methods Eng. 2006, 65, 2060–2090. [Google Scholar] [CrossRef]
- Wang, S.Y.; Lim, K.M.; Khoo, B.C.; Wang, M.Y. An extended level set method for shape and topology optimization. J. Comput. Phys. 2007, 221, 395–421. [Google Scholar] [CrossRef]
- Wei, P.; Li, Z.; Li, X.; Wang, M.Y. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions. Struct. Multidiscip. Optim. 2018, 58, 831–849. [Google Scholar] [CrossRef]
- Eschenauer, H.A.; Kobelev, V.V.; Schumacher, A. Bubble method for topology and shape optimization of structures. Struct. Optim. 1994, 8, 42–51. [Google Scholar] [CrossRef]
- Sokolowski, J.; Zochowski, A. On the Topological Derivative in Shape Optimization. Siam J. Control Optim. 1999, 37, 1251–1272. [Google Scholar] [CrossRef]
- Novotny, A.A.; Feijóo, R.; Taroco, E.; Padra, C. Topological Sensitivity Analysis for Three-dimensional Linear Elasticity Problem. Comput. Methods Appl. Mech. Eng. 2007, 196, 4354–4364. [Google Scholar] [CrossRef]
- Novotny, A.A.; Feijóo, R.A.; Taroco, E.; Padra, C. Topological sensitivity analysis. Comput. Methods Appl. Mech. Eng. 2003, 192, 803–829. [Google Scholar] [CrossRef]
- Simon, J. Differentiation with Respect to the Domain in Boundary Value Problems. Numer. Funct. Anal. Optim. 1980, 2, 649–687. [Google Scholar] [CrossRef]
- Giusti, S.M.; Novotny, A.A.; Padra, C. Topological sensitivity analysis of inclusion in two-dimensional linear elasticity. Eng. Anal. Bound. Elem. 2008, 32, 926–935. [Google Scholar] [CrossRef]

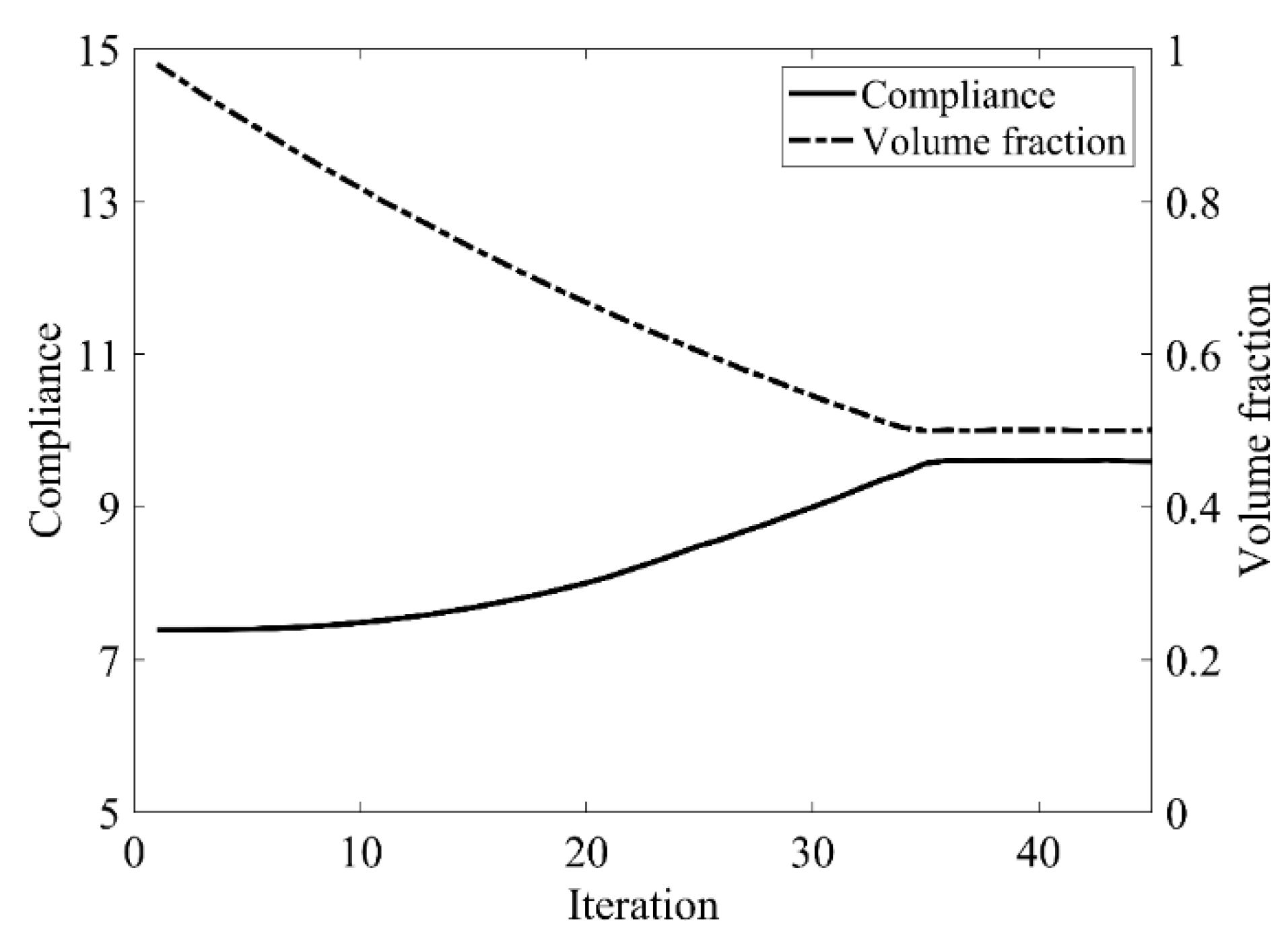

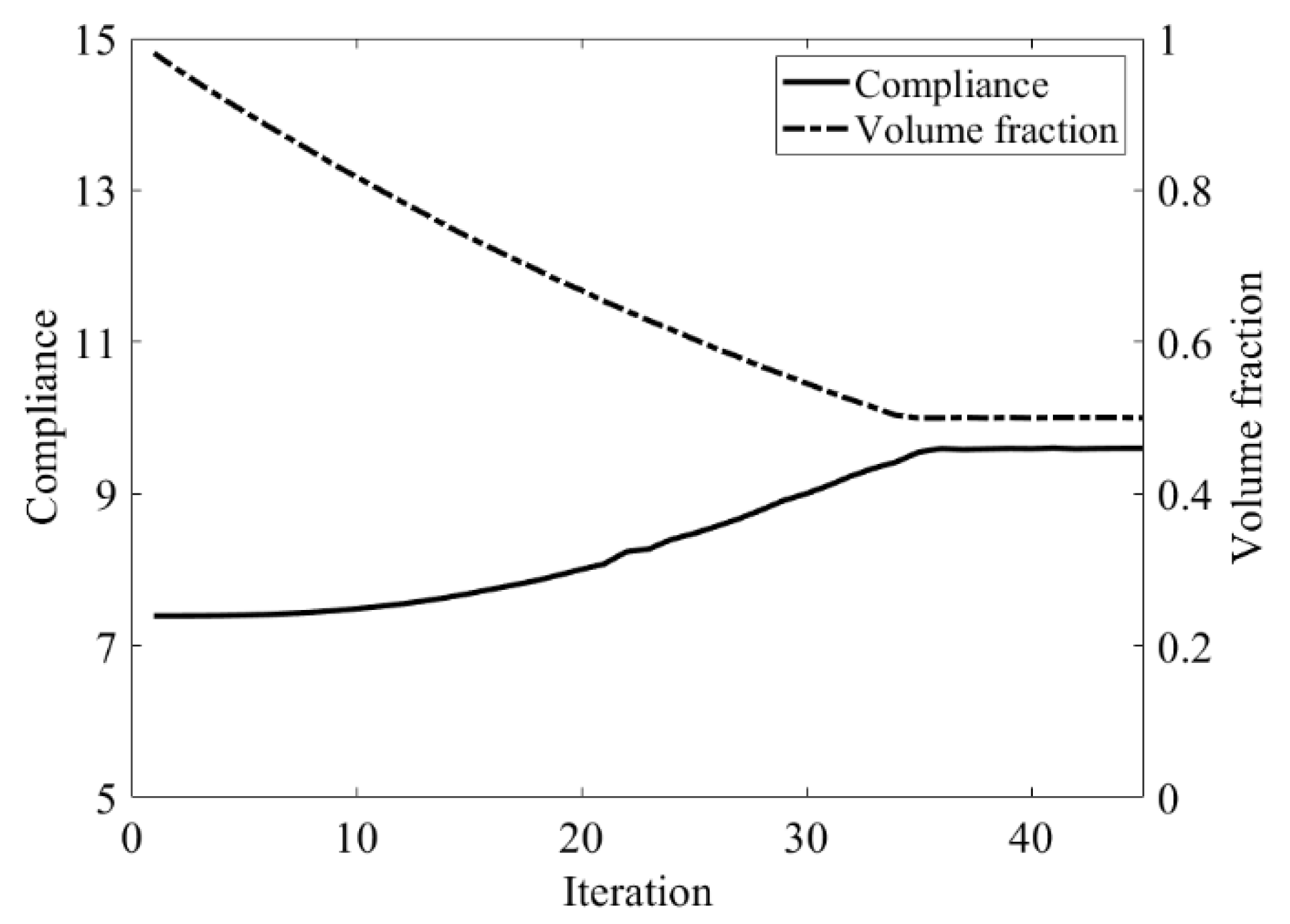

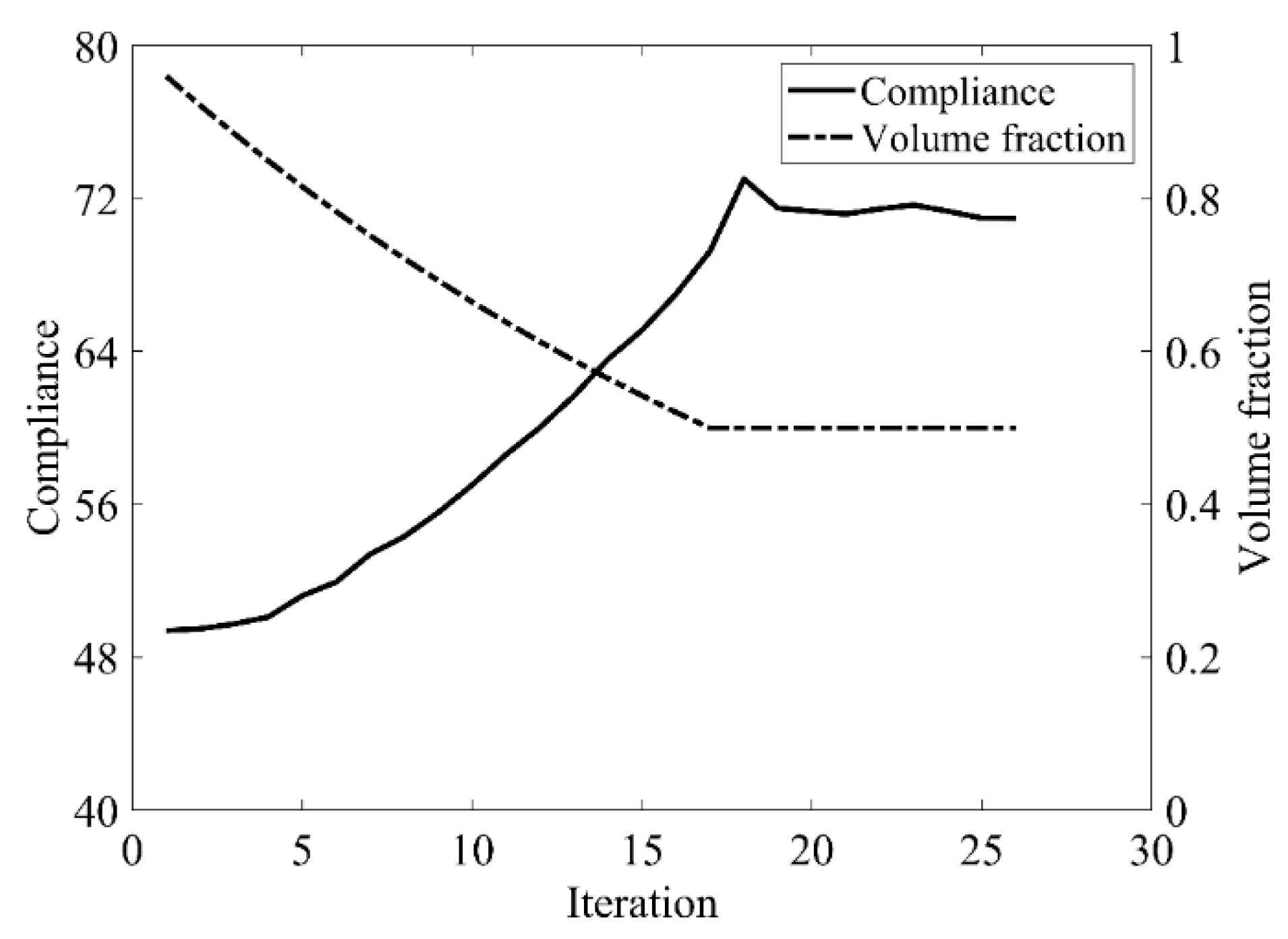





| Traditional BESO | The Improved Method | |
|---|---|---|
| Total element number | 3200 | 3200 |
| Volume fraction | 0.5 | 0.5 |
| Evolutionary volume ratio | 0.02 | 0.02 |
| Filter radius | 3 | 3 |
| Compliance | 9.596 | 9.601 |
| Total iteration | 45 | 45 |
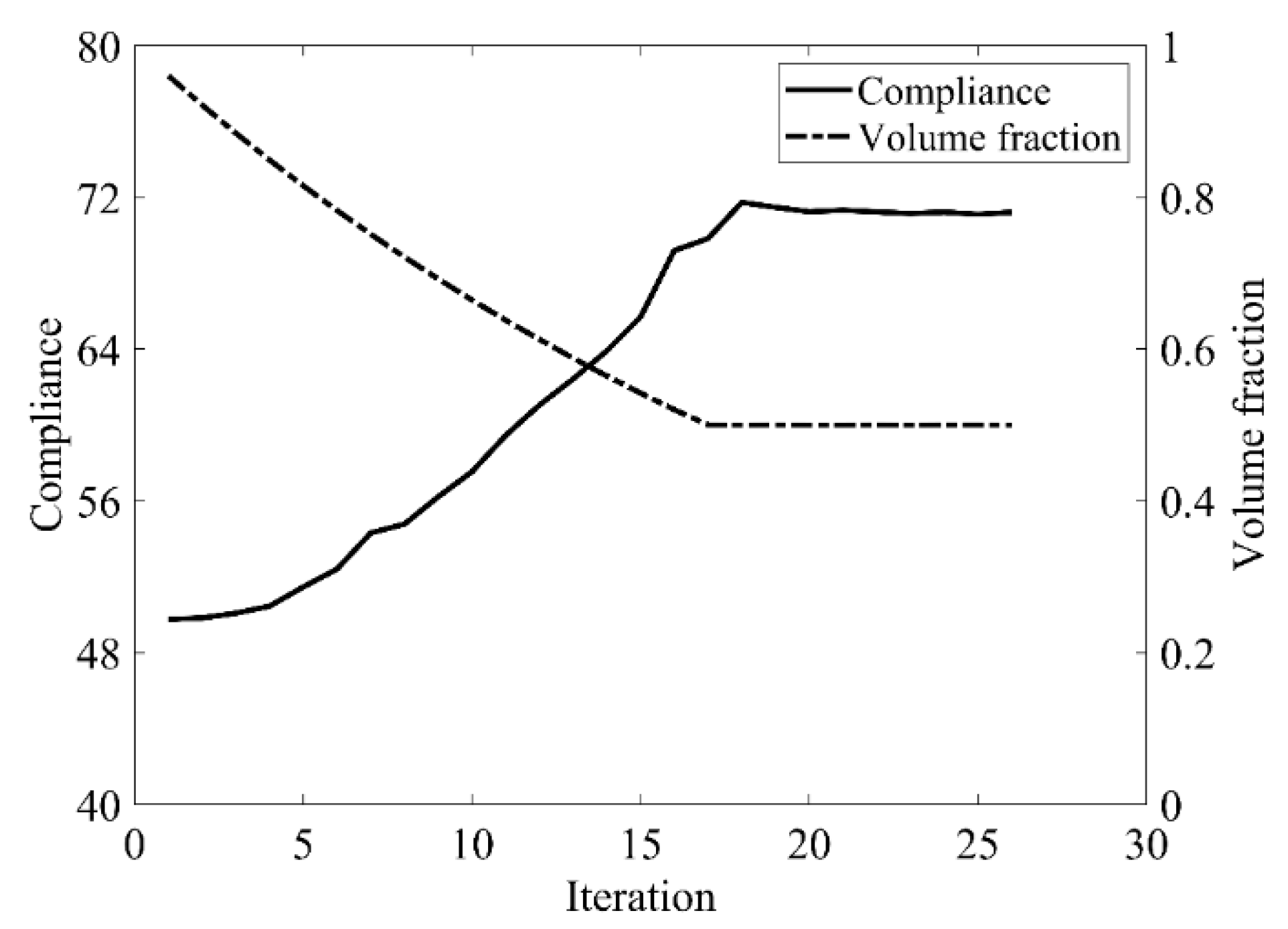
| Traditional BESO | The Improved Method | |
|---|---|---|
| Total element number | 4800 | 4800 |
| Volume fraction | 0.5 | 0.5 |
| Evolutionary volume ratio | 0.04 | 0.04 |
| Filter radius | 3 | 3 |
| Compliance | 70.965 | 71.102 |
| Total iteration | 26 | 26 |
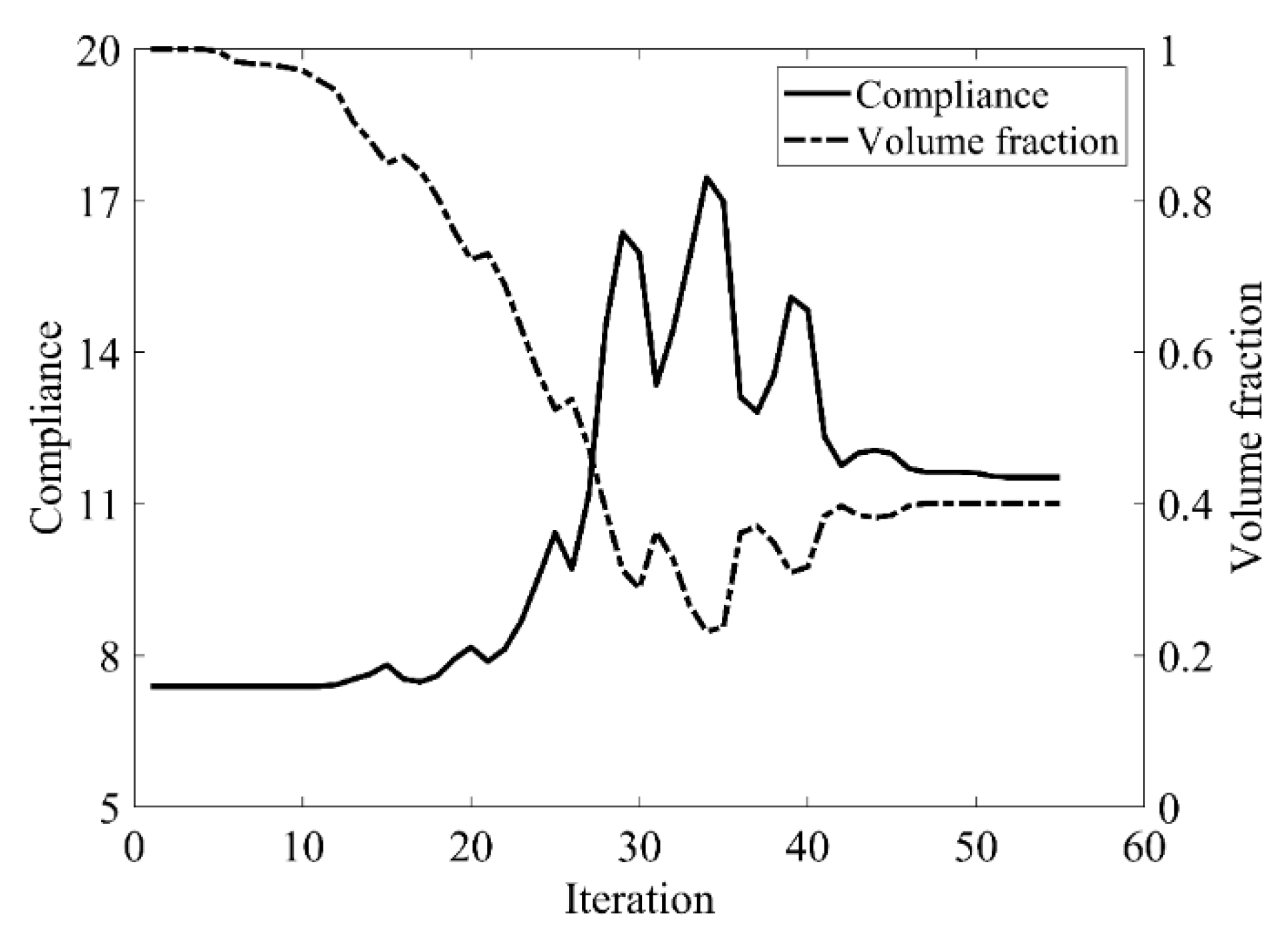
| Classical Level Set Method | CBT Level Set Method | |
|---|---|---|
| Total element number | 3200 | 3200 |
| Volume fraction | 0.4 | 0.4 |
| Evolutionary volume ratio | _ | 0.02 |
| Filter radius | _ | 3 |
| Compliance | 11.399 | 11.526 |
| Total iteration | 58 | 55 |
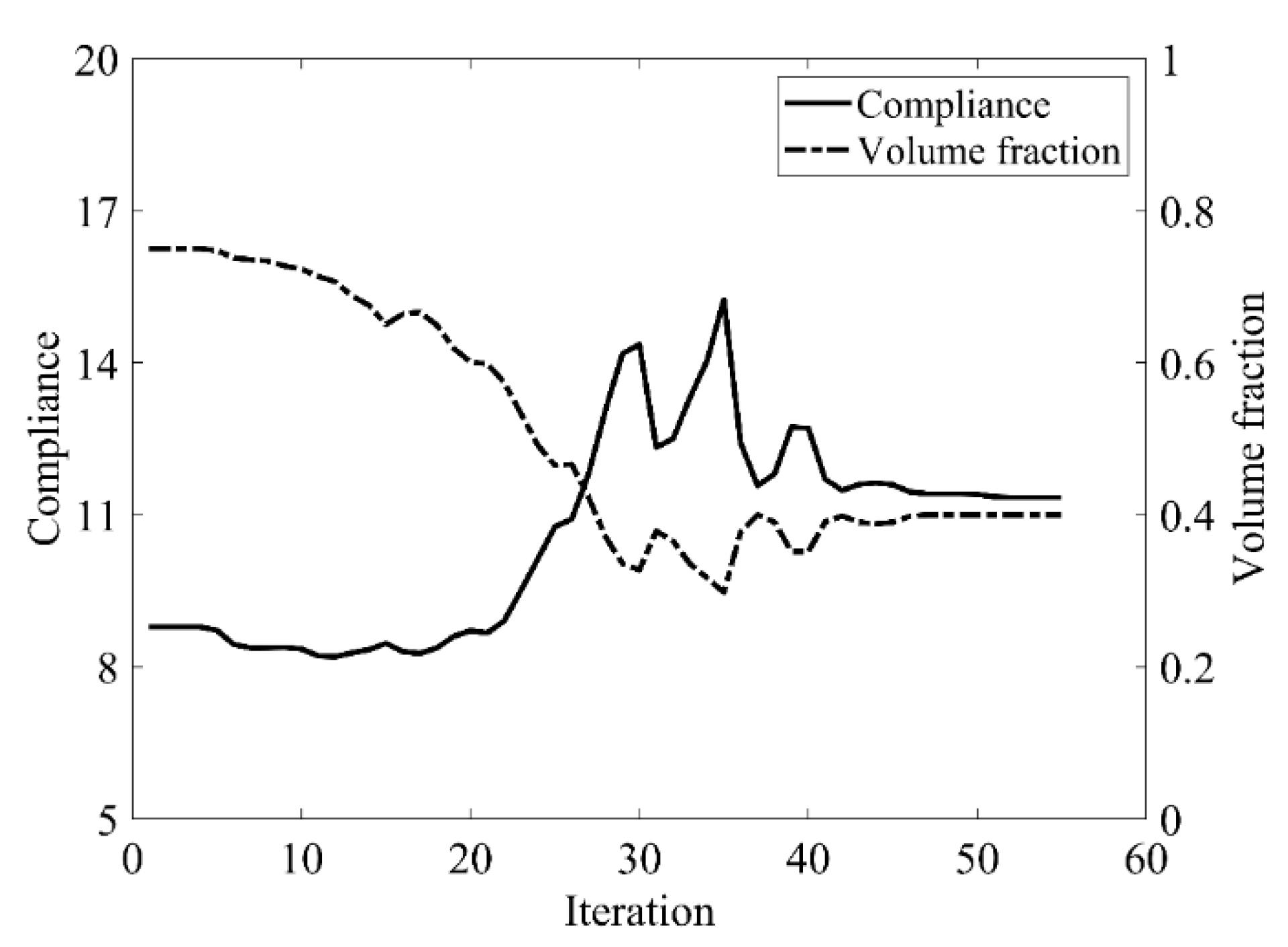
| Classical Level Set Method | CBT Level Set Method | |
|---|---|---|
| Total element number | 3200 | 3200 |
| Volume fraction | 0.4 | 0.4 |
| Evolutionary volume ratio | _ | 0.02 |
| Filter radius | _ | 3 |
| Compliance | 93.150 | 92.064 |
| Total iteration | 96 | 80 |
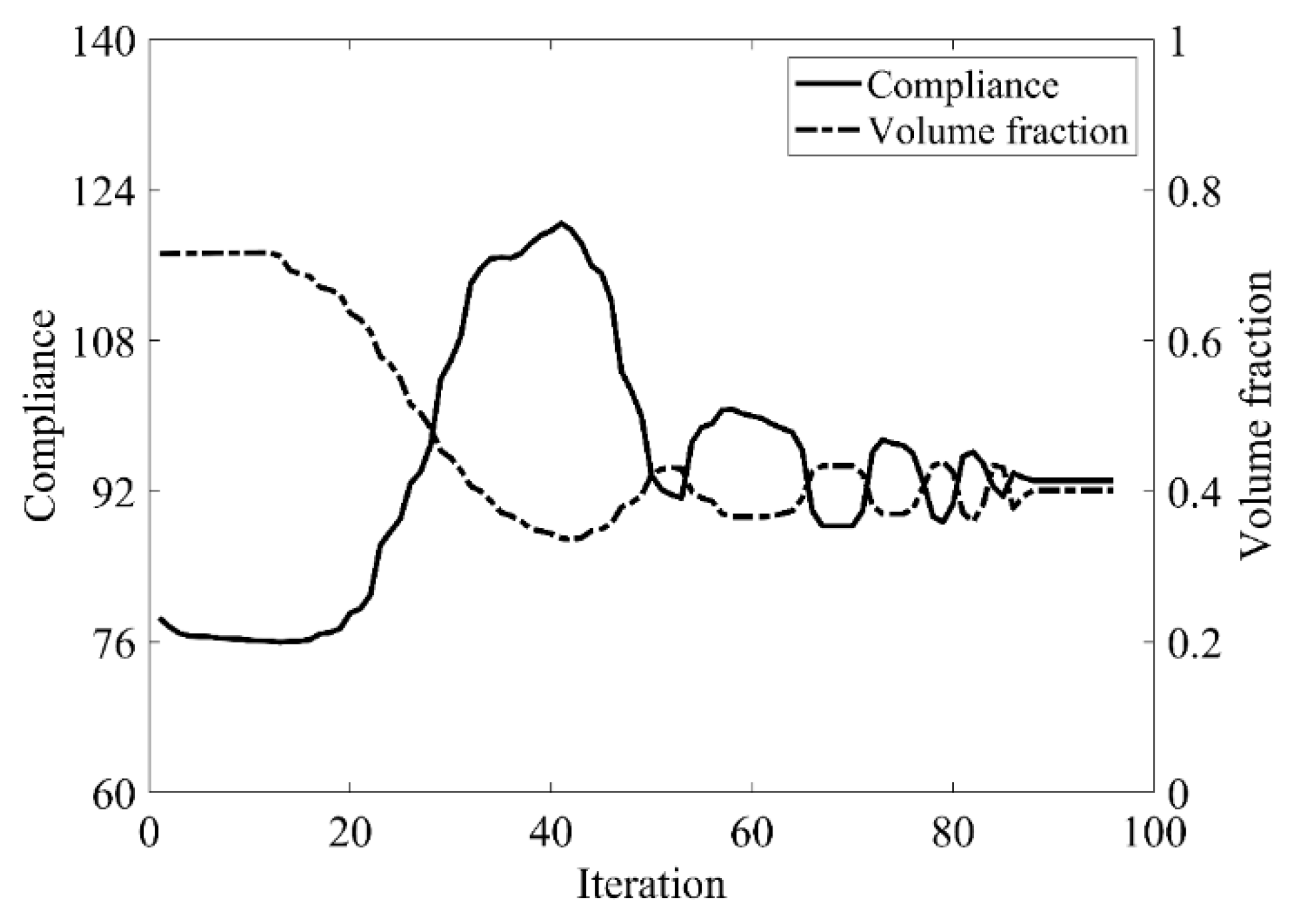
| Classical Level Set Method | CBT Level Set Method | |
|---|---|---|
| Total element number | 4800 | 4800 |
| Volume fraction | 0.4 | 0.4 |
| Evolutionary volume ratio | _ | 0.04 |
| Filter radius | _ | 3 |
| Compliance | 90.126 | 87.835 |
| Total iteration | 50 | 65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, S.; Wang, H.; Tong, J.; Sheng, Z. A Hole Nucleation Method Combining BESO and Topological Sensitivity for Level Set Topology Optimization. Materials 2021, 14, 2119. https://doi.org/10.3390/ma14092119
Cao S, Wang H, Tong J, Sheng Z. A Hole Nucleation Method Combining BESO and Topological Sensitivity for Level Set Topology Optimization. Materials. 2021; 14(9):2119. https://doi.org/10.3390/ma14092119
Chicago/Turabian StyleCao, Shuangyuan, Hanbin Wang, Jianbin Tong, and Zhongqi Sheng. 2021. "A Hole Nucleation Method Combining BESO and Topological Sensitivity for Level Set Topology Optimization" Materials 14, no. 9: 2119. https://doi.org/10.3390/ma14092119
APA StyleCao, S., Wang, H., Tong, J., & Sheng, Z. (2021). A Hole Nucleation Method Combining BESO and Topological Sensitivity for Level Set Topology Optimization. Materials, 14(9), 2119. https://doi.org/10.3390/ma14092119





