Analytical Determination of the Brake Temperature Mode during Repetitive Short-Term Braking
Abstract
1. Introduction
- initial value problem for vehicle motion;
- boundary-value problem of heat conduction, taking into account frictional heat generation (the so-called thermal problem of friction).
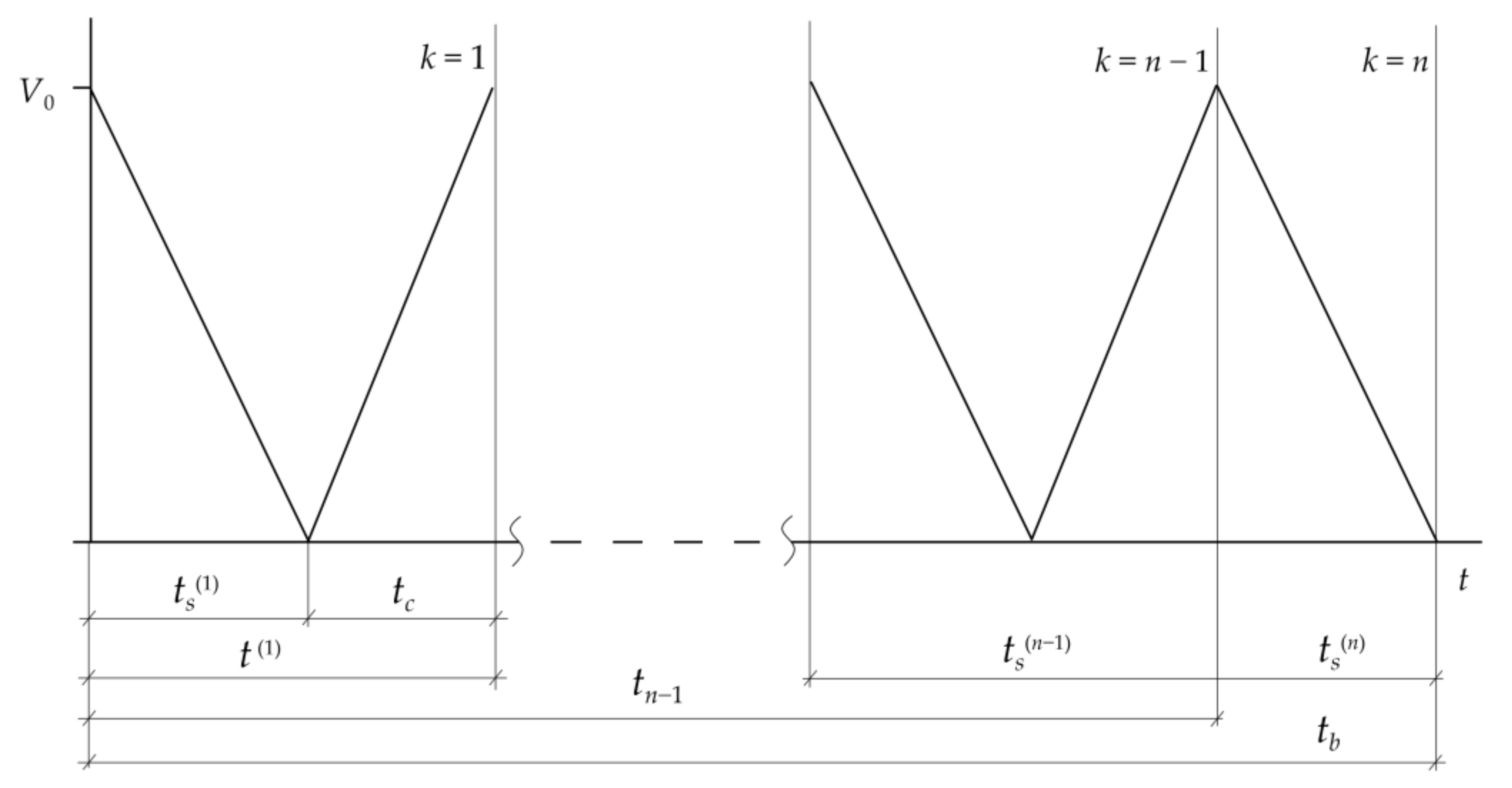
2. Statement of the Problem
- At the initial moment of each braking phase, the friction element is pressed against the primary element contact surface with uniform pressure , which exponentially increases with time , from zero to nominal value , Equation (9):where —time of pressure increase.
- At the initial moment of the cycle of braking, the distribution of temperature in the tribosystem is homogeneous and equal to the averaged volumetric temperature of friction pair ;
- As a result of the friction forces acting on the contact area of friction pair elements, heat is generated and absorbed by these elements in the normal directions of their friction surfaces;
- The thermal contact of friction pair elements is perfect. In other words, the sum of heat flux intensities directed into friction elements, is equal to the specific friction power, and the temperatures of its contact areas are equal.
- During the subsequent braking phases, the free surfaces of the brake system are adiabatic and during the acceleration stages, unforced convection cooling takes place.
3. Solution to the Problem
3.1. Heat Generation on the Nominal Contact Surface
- Based on the experimental data, by means of the approximation formulas (1)–(8), describe the thermal stability of friction and temperature dependencies of thermal , and mechanical , properties of friction materials ;
- Set the operation input parameters: , , , , , , , , , , , , , , , ;
- Begin the first () braking cycle;
- Establish the averaged volumetric temperature of the friction pair from Formulas (25)–(29);
- Taking into account dependencies (1)–(8) calculate the values of friction coefficient and materials properties , , (25) in temperature ;
- Determine braking time and temporal profile of velocity , from Equations (10)–(12) and (22);
- Calculate the evolution of mean temperature on nominal contact surface , (33)–(38);
- Start the subsequent () cycle of braking and repeat the calculations, beginning from point 4). The calculation process ends when condition is met.
3.2. Temperature of the Real Contact Region
- Asperities have the spherical shape and are located on the surface of the harder and stiffer primary element, while the friction lining surface is smooth.
- Plastic roughness deformation mechanism takes place. This means that the contact of a single asperity with the friction lining surface lasts until its material becomes plastic due to a rapid increase in temperature and the appearance of significant thermal stresses.
- Before coming into contact with the friction lining, the temperature of asperity does not change along its height and is equal to the mean temperature of nominal contact area .
- On the basis of the friction surface profiles of the primary friction element, the average values of parameters , , , characterizing the roughness shape and their distribution along the height were calculated in the longitudinal and transverse directions.
- Knowing the temporal profile of mean temperature on nominal contact surface (30)–(37), by means of approximation functions (1)–(8), the evolutions of (39) and , , , , (44) were established.
- Variations of contour contact area (38), (39) and contour pressure (40) during braking were determined, taking into account pressure profile (9).
- Changes of diameter (41) and total area of real contact (42) in time were established.
- Evolution of flash temperature (43) was calculated, taking into account velocity temporal profile (10)–(12).
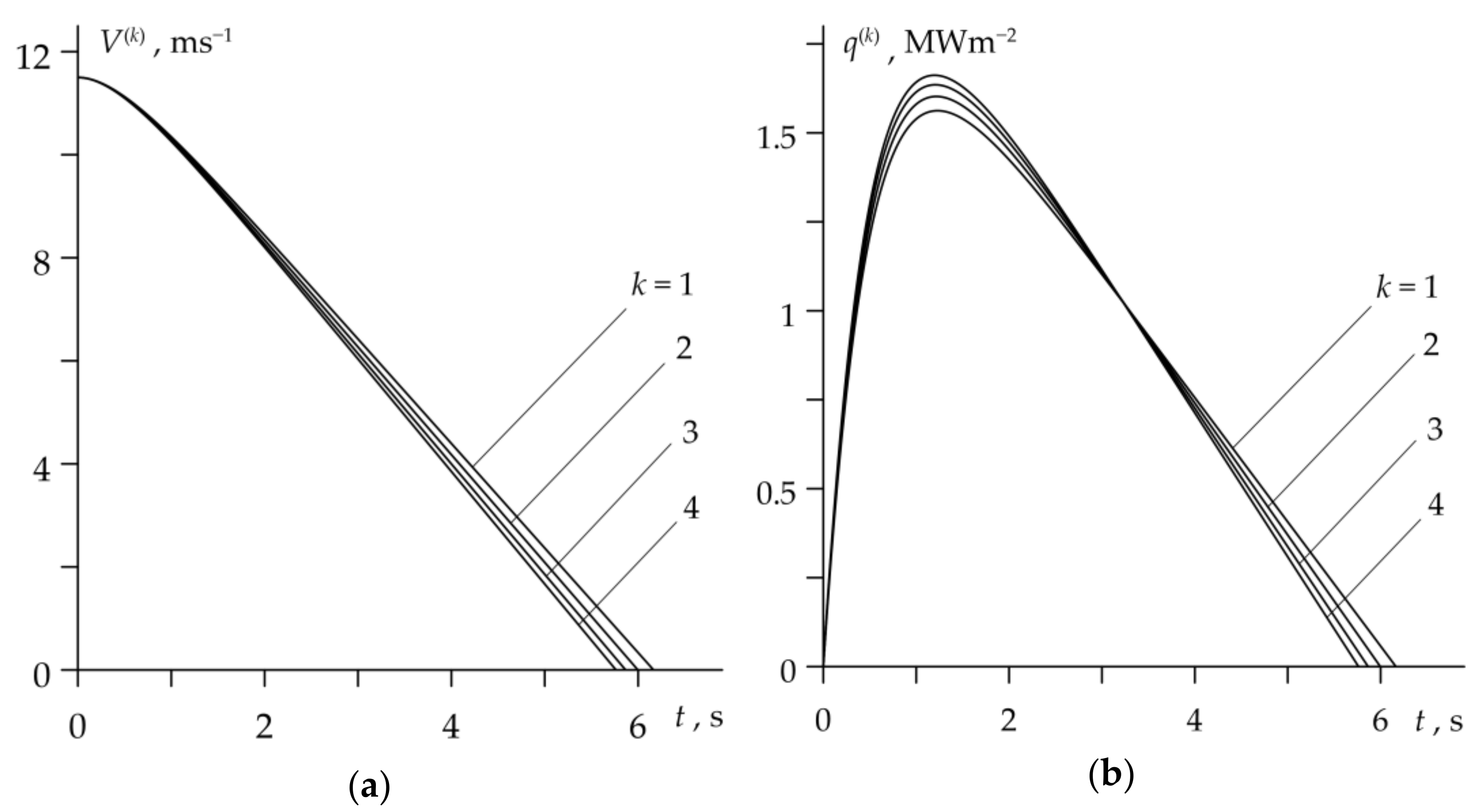
4. Numerical Analysis
4.1. Disc Brake System
4.2. Drum Brake System
5. Summary of the Results and Discussion
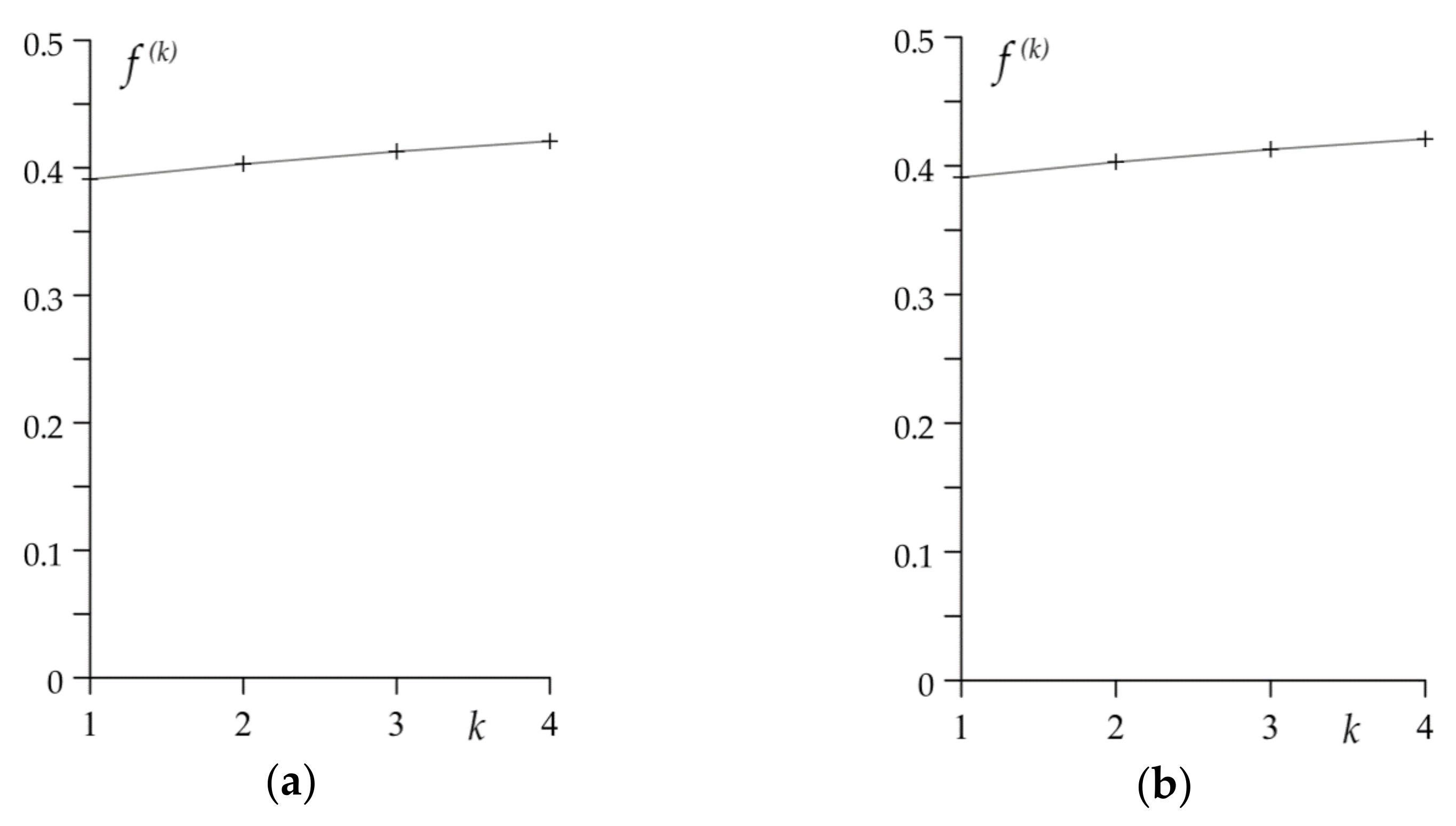
- Dependence of the friction coefficient on temperature (thermal stability curve) shows a significant influence on the time profiles of the velocity, specific friction power and maximum temperature. The coefficient of friction, which decreases with increasing temperature in the disc brake system, results in elongation of each subsequent braking stage and growth of the maximum values of the specific friction power. The effect of the friction coefficient increase, under temperature increase to about 300 °C in the drum brake system, is the reduction of the braking time and the increase of the maximum values of the specific friction power.
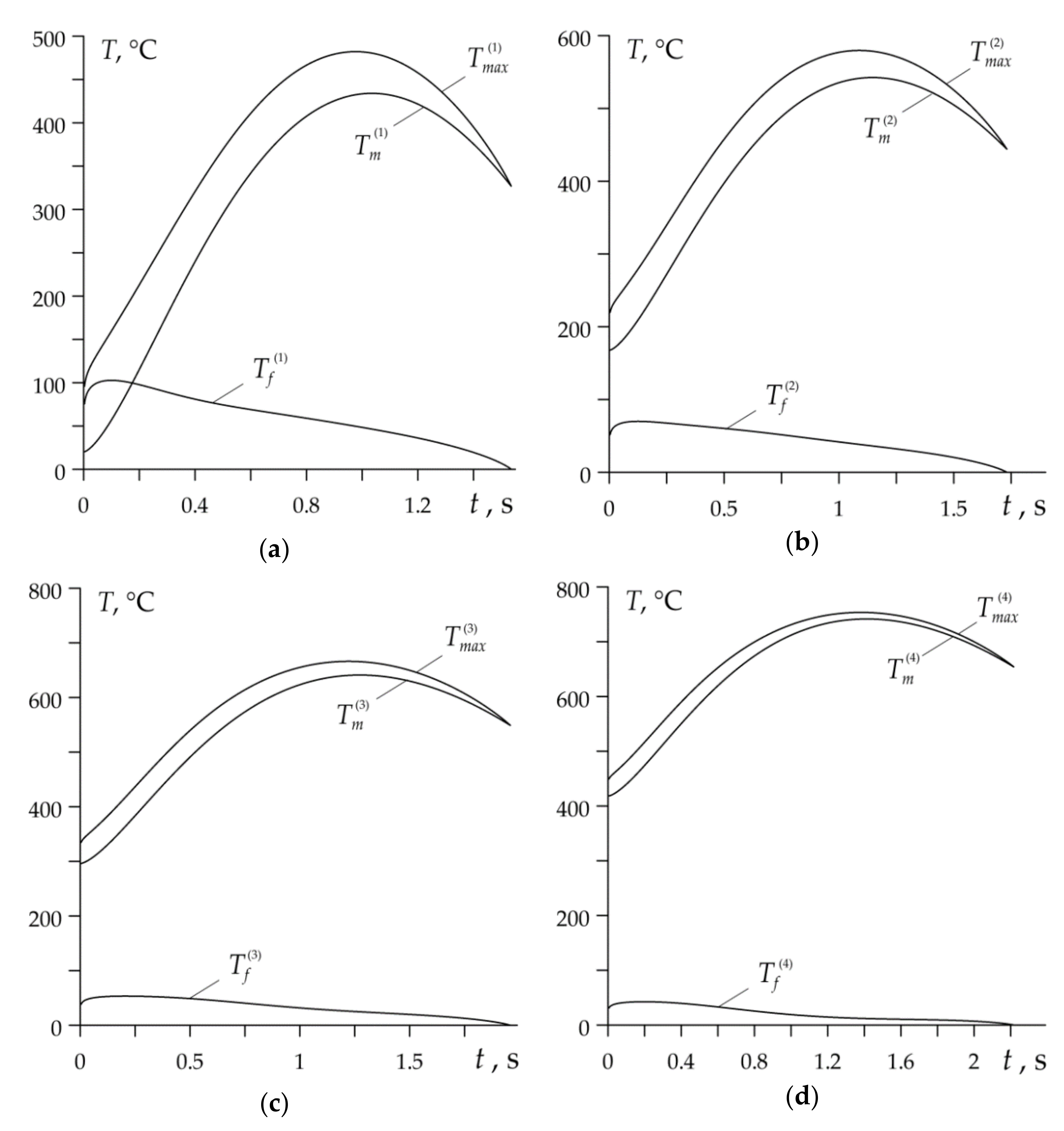
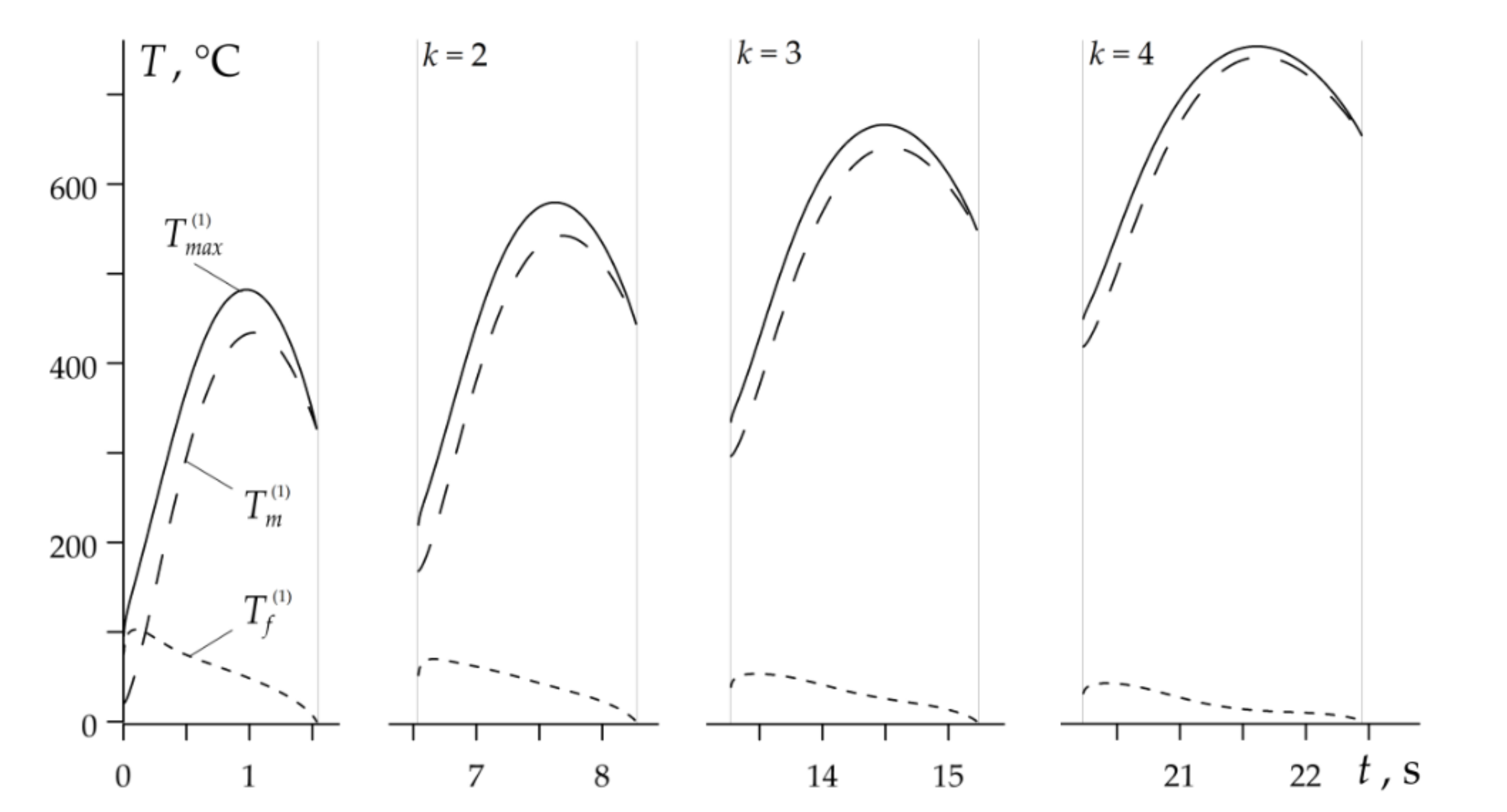
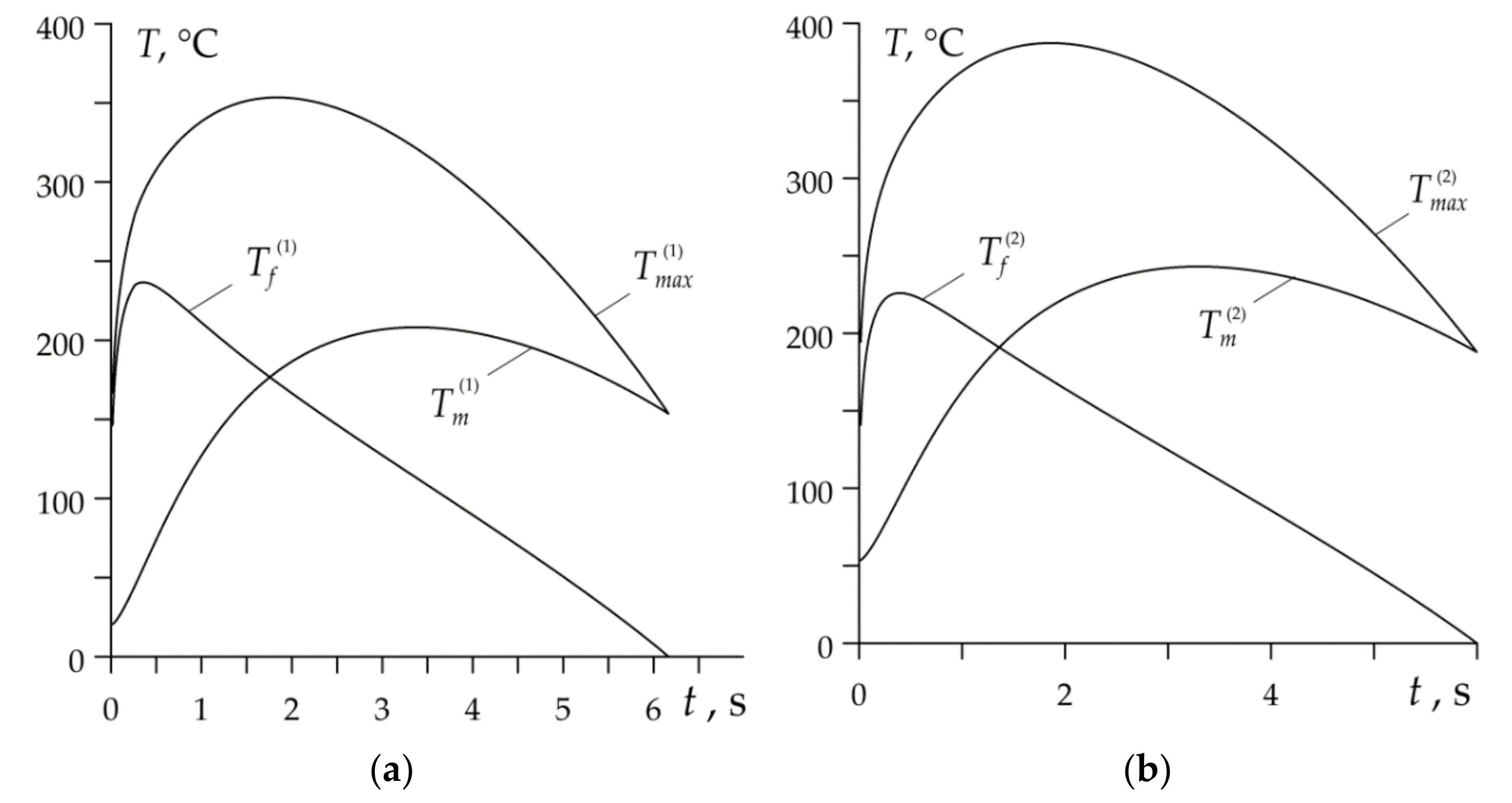
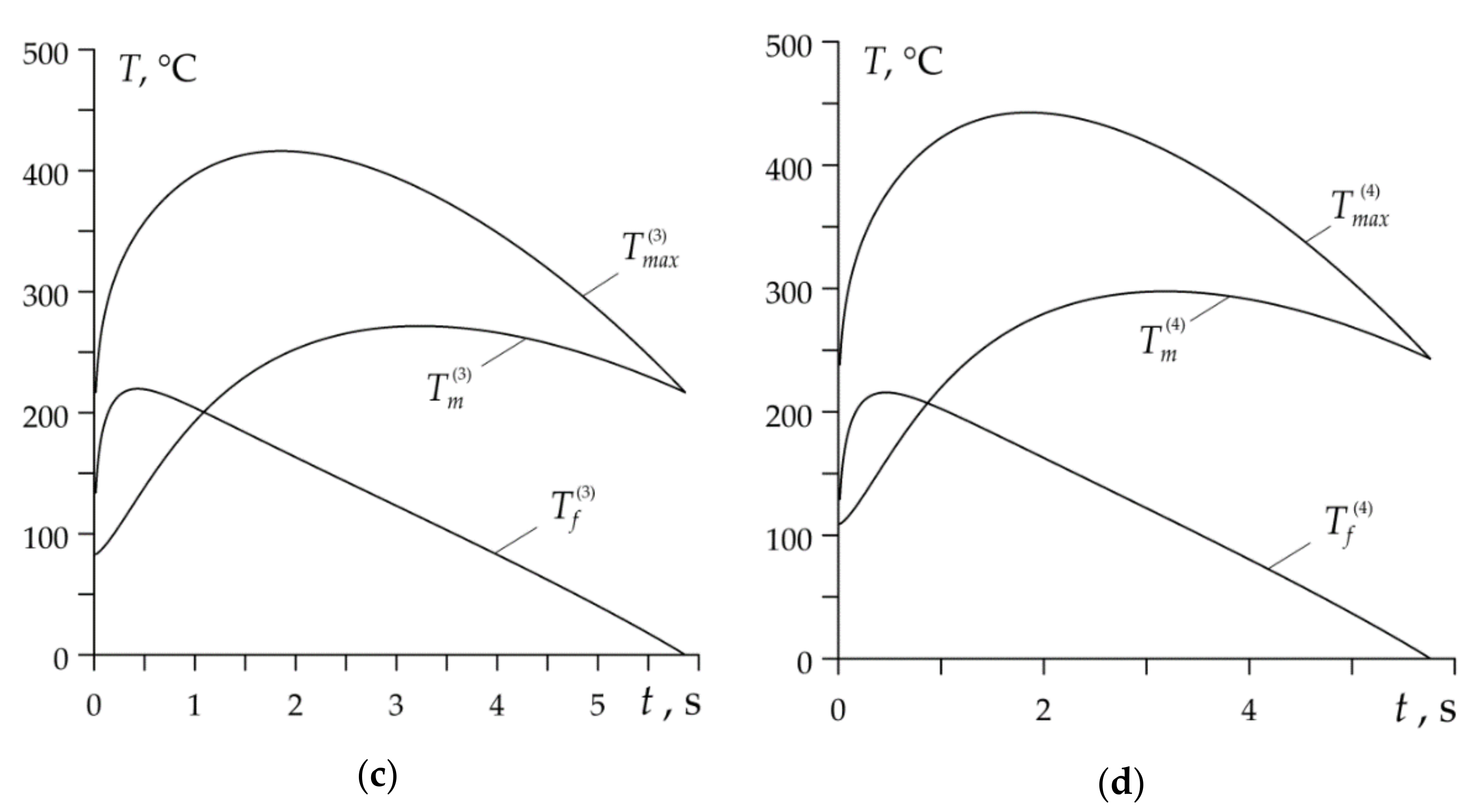
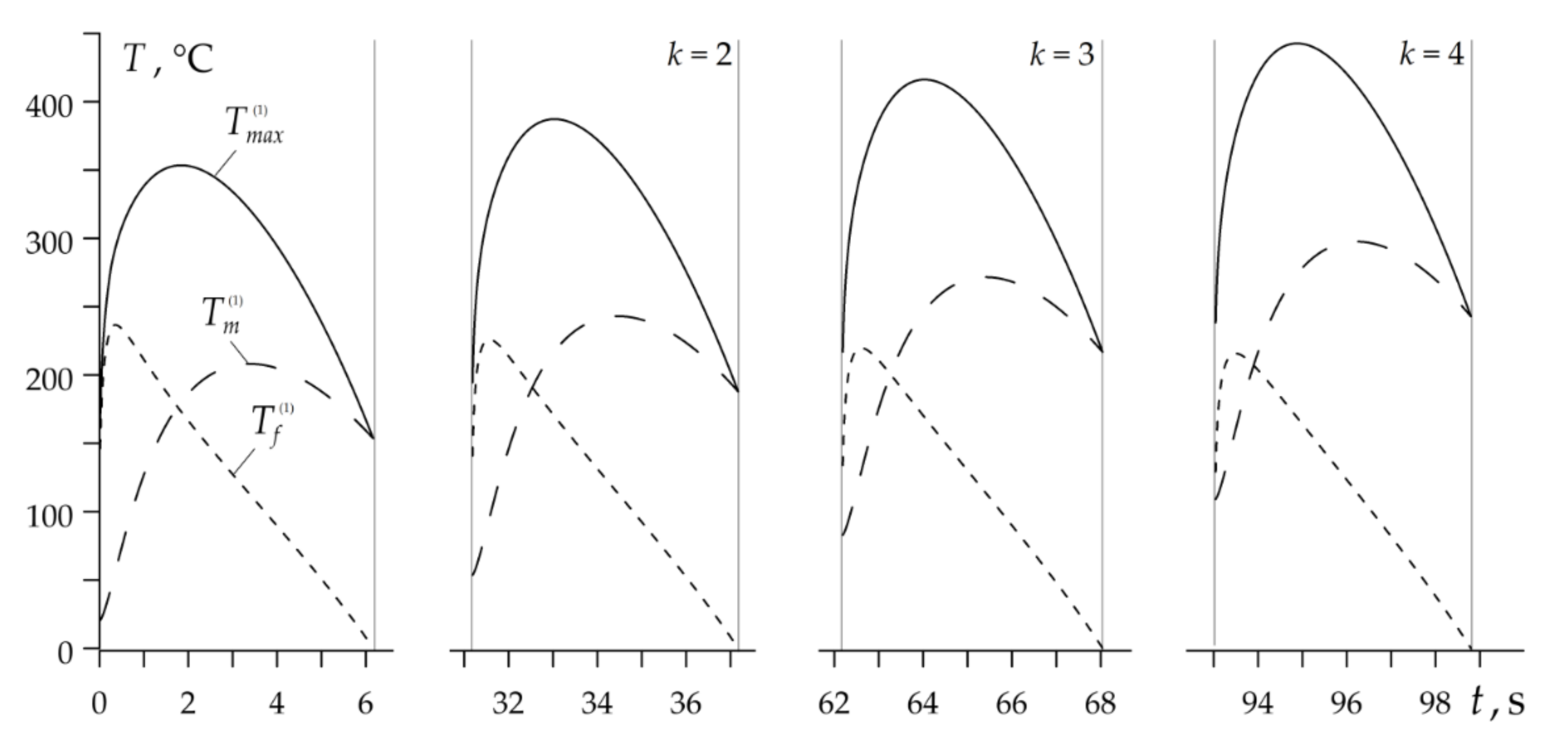
- In the disc brake system operating in heavy mode, the evolution of temperature and its maximum values are determined by the mean temperature on the nominal contact area. The contribution of the flash temperature to the maximum temperature is negligible.
- In the drum brake operating under light conditions, at the beginning of each braking stage, maximum temperature is determined mainly by the flash temperature, while at the end of braking it depends mostly from the mean temperature .
- The results obtained by means of the proposed analytical model show satisfactory compliance with the relevant data obtained with the use of numerical methods, published in the scientific literature. In particular, the highest values of the maximum temperature at the subsequent stages of braking , found as a result of our calculations, are 482 °C, 560 °C, 666 °C and 753 °C (Table 3), and the corresponding data obtained in the article [16] are equal to 491 °C, 615 °C, 720 °C, 847 °C, respectively. The greatest relative percentage difference of the results occurred in the fourth stage and is equal to . In the drum brake the maximum temperatures determined by means of the proposed model, are equal to 353 °C, 387 °C, 416 °C and 443 °C (Table 3), and corresponding results presented in monograph [9] are 295 °C, 330 °C, 400 °C and 440 °C. The highest relative difference in outcomes occurs in the stage one and is equal to . It should be noted that the mean temperature of the selected friction pair drum-brake shoe with similar input parameters during single braking was analyzed with the use of the finite difference method in the article [32]. The highest value of the mean temperature on the nominal contact area of the drum-brake shoe obtained was equal to 210 °C [32], which is in good agreement with the value 280 °C presented in Table 3.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| area of the nominal contact surface () | |
| area of the contour contact region () | |
| area of the real contact region () | |
| area of the ventilated surface of the disc or drum () | |
| parameter of the reference-surface curve (dimensionless) | |
| specific heat () | |
| thickness () | |
| diameter of an average spot of the real contact region () | |
| coefficient of friction (dimensionless) | |
| coefficient of heat transfer () | |
| maximum roughness height on the friction surface of the disc or drum (()) | |
| Brinell hardness () | |
| thermal conductivity () | |
| number of braking in RST brake mode | |
| contact pressure () | |
| nominal value of the contact pressure () | |
| specific power of friction () | |
| nominal value of the specific power of friction () | |
| average rounding radius of roughness on the friction surface () | |
| time () | |
| time of performance of all RST mode of braking (s) | |
| cooling time at acceleration (s) | |
| time of pressure increase (s) | |
| time of braking (s) | |
| temperature () | |
| initial (volumetric) temperature () | |
| flash temperature () | |
| mean temperature () | |
| maximum temperature () | |
| velocity () | |
| initial velocity () | |
| initial kinetic energy () | |
| axial coordinate (()) | |
| Greek Symbols | |
| parameter of the reference-surface curve (dimensionless) | |
| density () | |
| Index | |
| upper | number of a stage of braking |
| lower | number of the main () and frictional () elements of the friction couple |
References
- Chichinadze, A.V.; Eiss, N.S. Polymers in Friction Assembles of Machines and Devices: A Handbook; Allerton Press Inc.: New York, NY, USA, 1984. [Google Scholar]
- Chichinadze, A.V. Processes in heat dynamics and modeling of friction and wear (dry and boundary friction). Tribol. Int. 1995, 28, 55–58. [Google Scholar] [CrossRef]
- Day, A.J. Braking of Road Vehicles; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Adamowicz, A.; Grzes, P. Influence of convective cooling on a disc brake temperature distribution during repetitive braking. Appl. Therm. Eng. 2011, 31, 2177–2185. [Google Scholar] [CrossRef]
- Adamowicz, A. Effect of convective cooling on temperature and thermal stresses in disk during repeated intermittent braking. J. Frict. Wear 2016, 37, 107–112. [Google Scholar] [CrossRef]
- Adamowicz, A. Thermal stressed state of a disk in the process of multiple braking. Mater. Sci. 2016, 51, 814–820. [Google Scholar] [CrossRef]
- Kang, S.S.; Cho, S.K. Thermal deformation and stress analysis of disk brakes by finite element method. J. Mech. Sci. Technol. 2012, 26, 2133–2137. [Google Scholar] [CrossRef]
- Yevtushenko, A.; Kuciej, M.; Grzes, P.; Wasilewski, P. Temperature in the railway disc brake at a repetitive short-term mode of braking. Int. Com. Heat Mass Trans. 2017, 84, 102–109. [Google Scholar] [CrossRef]
- Chichinadze, A.V.; Braun, E.D.; Ginzburg, A.G.; Ignat’eva, Z.V. Calculation, Testing and Selection of Friction Couples; Nauka: Moscow, Russia, 1979. (In Russian) [Google Scholar]
- Ginsburg, A.G.; Romashko, A.M.; Titarenko, V.F. Calculation of temperature regime of a disc rail brake. In Calculation and Modeling of Operation Mode of Breaking and Friction Devices; Nauka: Moscow, Russia, 1974; pp. 21–25. (In Russian) [Google Scholar]
- Lee, K. Numerical Prediction of Brake Fluid Temperature Rise during Braking and Heat Soaking; SAE Technical Paper 1999-01-0483; SAE International: Warrendale, PA, USA, 1999; pp. 1–9. [Google Scholar] [CrossRef]
- Nosko, A.L.; Nosko, A.P. Cooling of braking devices of lifting-and-transport machines. Her. Bauman Mosc. State Tech. Univ. Ser. Mech. Eng. Mach. Sci. 2005, 5, 88–99. (In Russian) [Google Scholar]
- Yevtushenko, A.A.; Grzes, P. The FEM-modeling of the frictional heating phenomenon in the pad/disc tribosystem (a review). Num. Heat Transf. Part A 2010, 58, 207–226. [Google Scholar] [CrossRef]
- Wasilewski, P. Frictional heating in railway brakes: A review of numerical models. Arch. Comput. Methods Eng. 2020, 27, 45–58. [Google Scholar] [CrossRef]
- Grzes, P. Maximum temperature of the disc during repeated braking applications. Adv. Mech. Eng. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Yevtushenko, A.; Kuciej, M. Calculation of friction characteristics of disc brakes used in repetitive short-term braking mode. J. Frict. Wear 2020, 41, 687–697. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Kuciej, M. One-dimensional thermal problem of friction during braking: The history of development and actual state. Int. J. Heat Mass Transf. 2012, 55, 4148–4153. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Kuciej, M.; Topczewska, K. Analytical model for investigation of the effect of friction power on temperature in the disk brake. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Kuciej, M.; Topczewska, K. Effect of the temporal profile of the friction power on temperature of a pad-disc brake system. J. Theoret. Appl. Mech. 2019, 57, 461–473. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Kuciej, M.; Topczewska, K. Frictional heating during braking of the C/C composite disc. Materials 2020, 13, 2691. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Grzes, P. Initial selection of disk brake pads material based on the temperature mode. Materials 2020, 13, 822. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Grzes, P.; Adamowicz, A. The temperature mode of the carbon-carbon multi-disc brake in the view of the interrelations of its operating characteristics. Materials 2020, 13, 1878. [Google Scholar] [CrossRef] [PubMed]
- Chichinadze, A.V.; Kozhemyakina, V.D.; Suvorov, A.V.; Strebezev, M.K.; Serik, A.B. Temperature field under model test of ring specimens at two side contact on new universal friction machine IM-58-T2. Frict. Lubr. Mach. Mech. 2007, 7, 25–33. [Google Scholar]
- Chichinadze, A.V.; Kozhemyakina, V.D.; Suvorov, A.V. Method of temperature-field calculation in model ring specimens during bilateral friction in multidisc aircraft brakes with the IM-58-T2 new multipurpose friction machine. J. Frict. Wear 2010, 31, 23–32. [Google Scholar] [CrossRef]
- Evtushenko, O.; Kuciej, M.; Topczewska, K. Determination of the maximal temperature of a pad–disc tribosystem during one-time braking. Mater. Sci. 2020, 56, 152–159. [Google Scholar] [CrossRef]
- Chichinadze, A.V.; Matveevskii, R.M.; Braun, E.P. Materials in Triboengineering of Unsteady Processes; Nauka: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Topczewska, K. Influence of the time of increase in contact pressure in the course of braking on the temperature of a pad-disc tribosystem. Mater. Sci. 2018, 54, 250–259. [Google Scholar] [CrossRef]
- Demkin, N.B.; Izmailov, V.V.; Korotkov, M.A. Estimation of the deformation of rough spheres and cylinders in compression. Wear 1976, 39, 63–82. [Google Scholar] [CrossRef]
- Demkin, N.B.; Ryzhov, E.V. Surface Quality of Machine Contact Parts; Mashinostroenie: Moscow, Russia, 1981. (in Russian) [Google Scholar]
- Grzes, P. Finite element solution of the three-dimensional system of equations of heat dynamics of friction and wear during single braking. Adv. Mech. Eng. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Grzes, P. Determination of the maximum temperature at single braking from the FE solution of heat dynamics of friction and wear system of equations. Num. Heat Transf. Part A 2017, 71, 737–753. [Google Scholar] [CrossRef]
- Yevtushenko, A.; Kuciej, M.; Och, E.; Yevtushenko, O. Effect of the thermal sensitivity in modeling of the frictional heating during braking. Adv. Mech. Eng. 2016, 8, 1–10. [Google Scholar] [CrossRef]

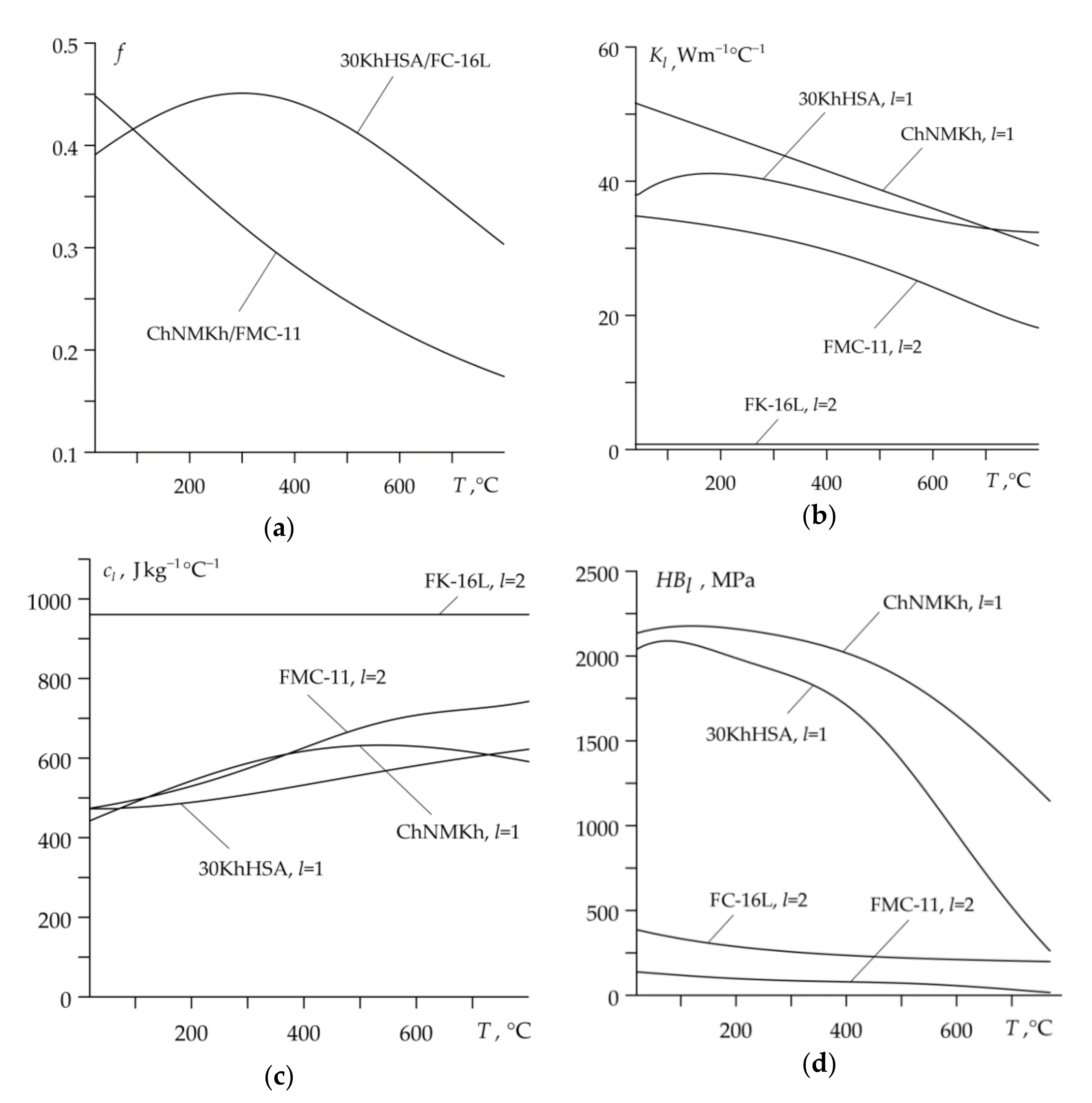


| Material | |||||
|---|---|---|---|---|---|
| ChNMKh | 0.45 | 52.17 | 444.6 | 7100 | 2100 |
| FMC-11 | 35 | 479 | 4700 | 137 | |
| 30KhHSA | 0.39 | 38 | 490 | 7800 | 2050 |
| FC-16L | 0.79 | 961 | 2500 | 392 |
| Coefficients | Material | i = 1 | i = 2 | i = 3, | i = 4, | i = 5 | i = 6, | i = 7, |
|---|---|---|---|---|---|---|---|---|
| ChNMKh/FMC-11 | 0.01 | 1.07 | 1.5 | –250 | 0 | 0 | 0 | |
| 30KhHSA/FC-16L | 0 | 1.1 | 0.0014 | 300 | 0 | 0 | 0 | |
| ChNMKh | –2.37 | 4.22 | 0.196 | –2543 | 0 | 0 | 0 | |
| FMC-11 | 1.125 | –0.64 | 2.3 | 900 | 0 | 0 | 0 | |
| 30KhHSA | 2.455 | –1.58 | 0.86 | 847 | –1.05 | 6.3 | –163 | |
| FC-16L | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| ChNMKh | –0.85 | 6.6 | 0.57 | 4903 | 1.37 | 1.2 | 443 | |
| FMC-11 | 0.78 | 0.74 | 3.5 | 1059 | 0.5 | 2.6 | 573 | |
| 30KhHSA | 2.99 | −1.4 | 859 | –0.59 | 1.36 | 20 | ||
| FC-16L | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| ChNMKh | –0.54 | 1 | 2 | –50 | 1 | 1.7 | 500 | |
| FMC-11 | –0.93 | 0.83 | 2.34 | 546 | 2.02 | 2 | –233 | |
| 30KhHSA | –0.55 | 1 | 3.3 | 0 | 1 | 2.5 | 400 | |
| FC-16L | 0.43 | 1.05 | 3.5 | –250 | 0 | 0 | 0 |
| Characteristic | Brake System | k = 1 | k = 2 | k = 3 | k = 4 |
|---|---|---|---|---|---|
| Disc | 0.45 | 0.38 | 0.32 | 0.28 | |
| Drum | 0.39 | 0.40 | 0.41 | 0.42 | |
| Disc | 1.54 | 1.73 | 1.96 | 2.22 | |
| Drum | 6.17 | 6.00 | 5.87 | 5.77 | |
| Disc | 20 | 168 | 296 | 418 | |
| Drum | 20 | 53 | 83 | 109 | |
| Disc | 434 | 542 | 641 | 741 | |
| Drum | 208 | 243 | 272 | 298 | |
| Disc | 103 | 70 | 53 | 42 | |
| Drum | 237 | 226 | 220 | 216 | |
| Disc | 482 | 560 | 666 | 753 | |
| Drum | 353 | 387 | 416 | 443 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yevtushenko, A.; Topczewska, K.; Kuciej, M. Analytical Determination of the Brake Temperature Mode during Repetitive Short-Term Braking. Materials 2021, 14, 1912. https://doi.org/10.3390/ma14081912
Yevtushenko A, Topczewska K, Kuciej M. Analytical Determination of the Brake Temperature Mode during Repetitive Short-Term Braking. Materials. 2021; 14(8):1912. https://doi.org/10.3390/ma14081912
Chicago/Turabian StyleYevtushenko, Aleksander, Katarzyna Topczewska, and Michal Kuciej. 2021. "Analytical Determination of the Brake Temperature Mode during Repetitive Short-Term Braking" Materials 14, no. 8: 1912. https://doi.org/10.3390/ma14081912
APA StyleYevtushenko, A., Topczewska, K., & Kuciej, M. (2021). Analytical Determination of the Brake Temperature Mode during Repetitive Short-Term Braking. Materials, 14(8), 1912. https://doi.org/10.3390/ma14081912








