Hybrid Modelling by Machine Learning Corrections of Analytical Model Predictions towards High-Fidelity Simulation Solutions
Abstract
1. Introduction
2. Methods and Materials
2.1. Laser Shock Peening
2.2. Physical Models
2.2.1. Pressure Pulse Definition for Physical Models
2.2.2. Low-Fidelity Model — Semi-Analytical Model
2.2.3. High-Fidelity Model — FE Model
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Density | g/cm | 2.8 | |
| Young’s modulus | E | GPa | 74 |
| Poisson’s ratio | – | 0.33 | |
| Quasi-static yield strength | A | MPa | 350 |
| Strengthening coefficient | B | MPa | 972 |
| Strain hardening exponent | n | – | 0.73 |
| Dynamic strain hardening coefficient | C | – | 0.01 |
2.3. Artificial Neural Networks
3. Methodology
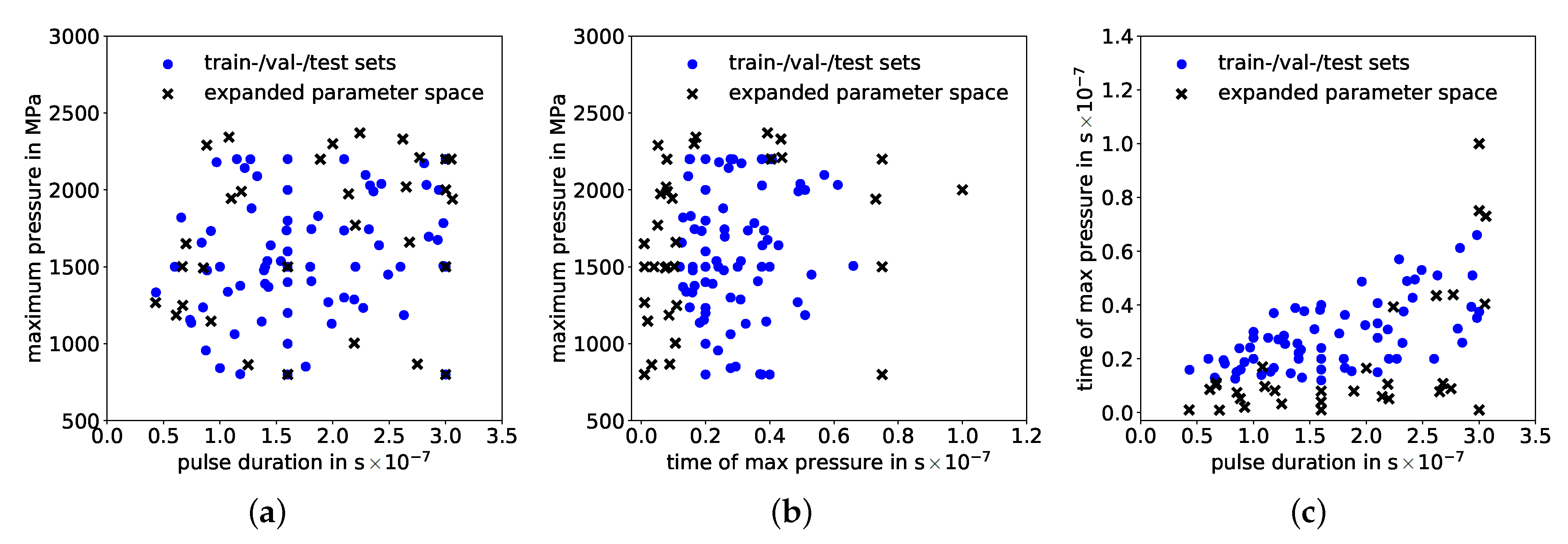
3.1. Data Preparation
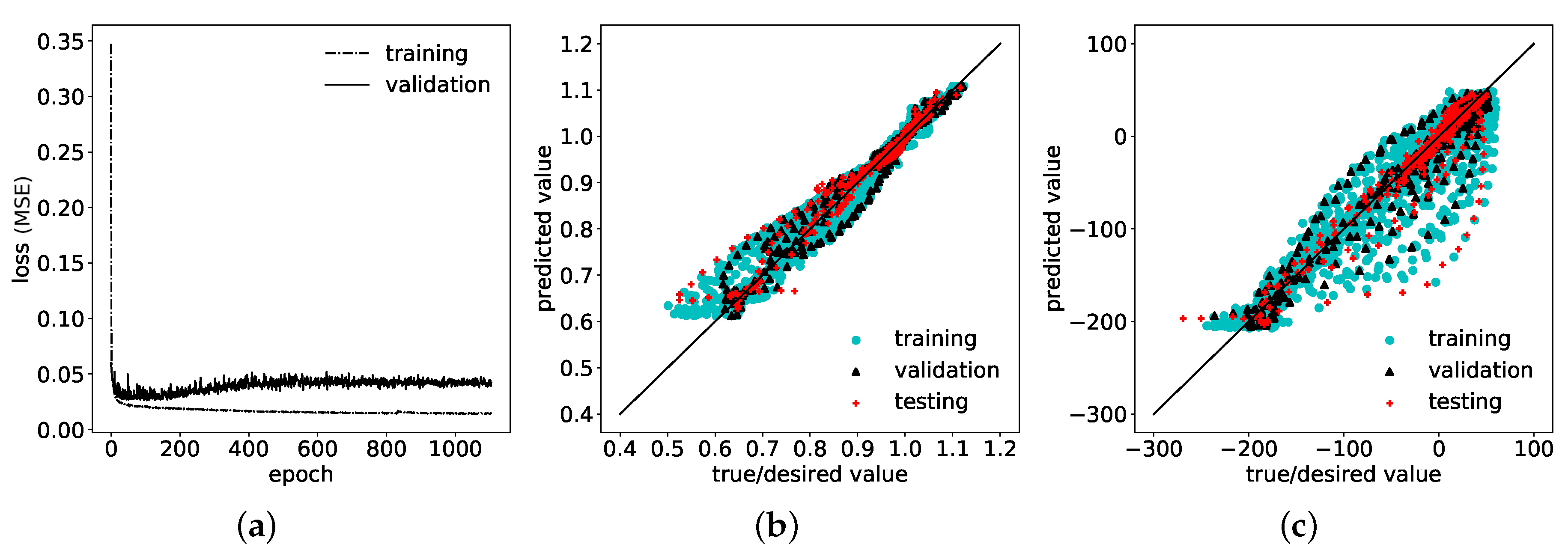
3.2. Hyperparameters of ANN
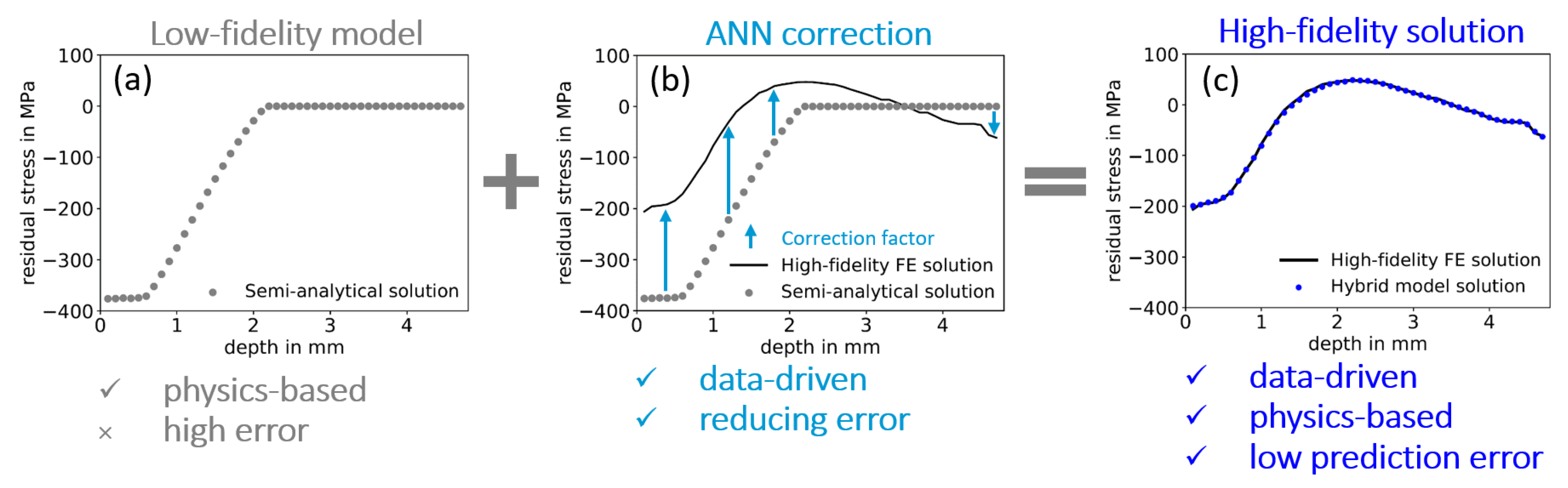
4. Development and Evaluation of ANN-Correction Model
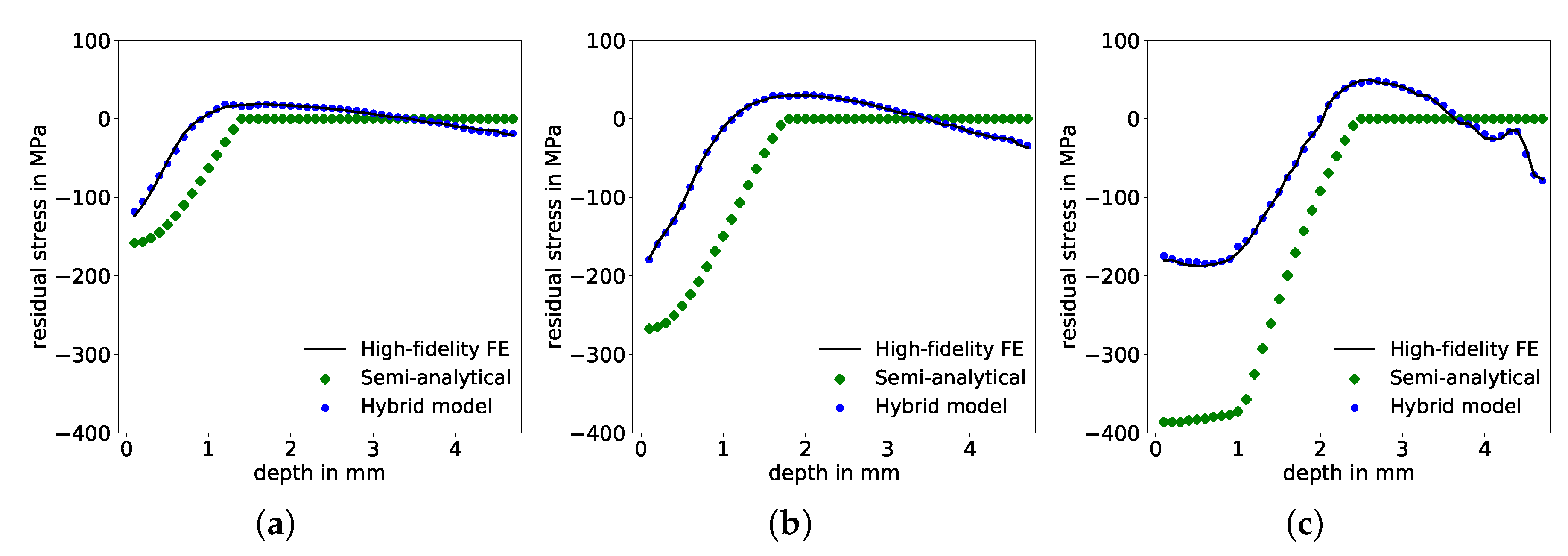
4.1. Approach 1: Consideration of Only Semi-Analytical Residual Stresses as Input
4.2. Approach 2: Adding Salient Features to the Input Space
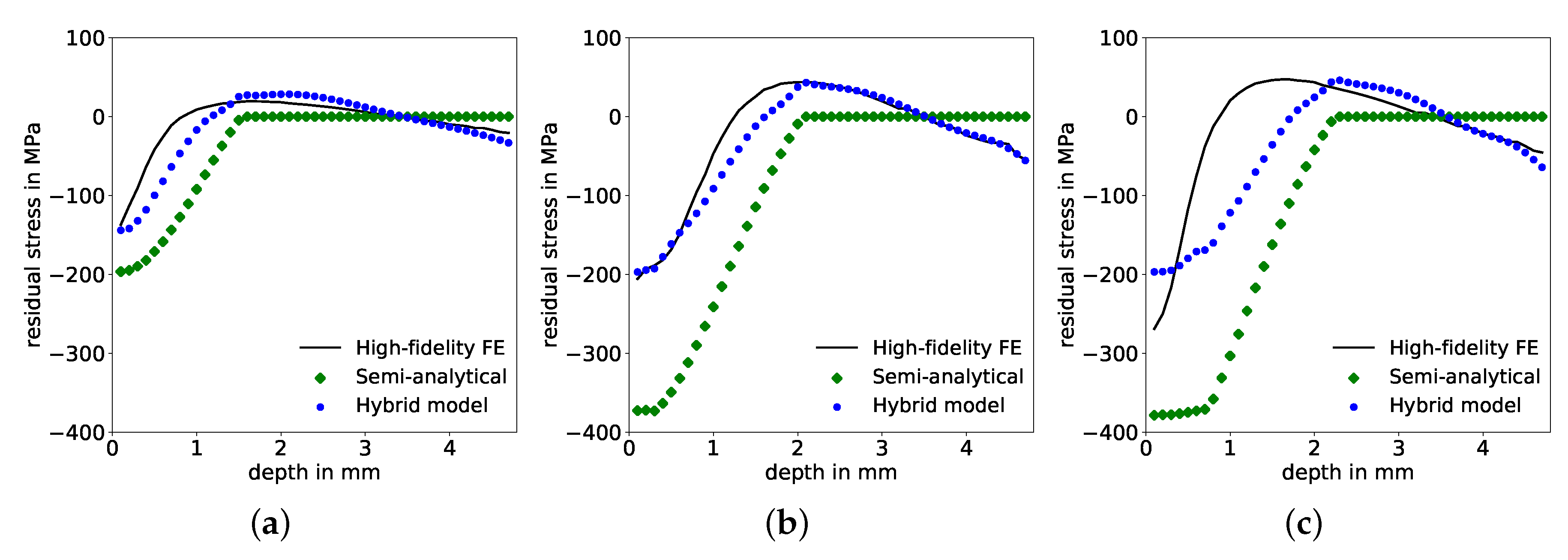
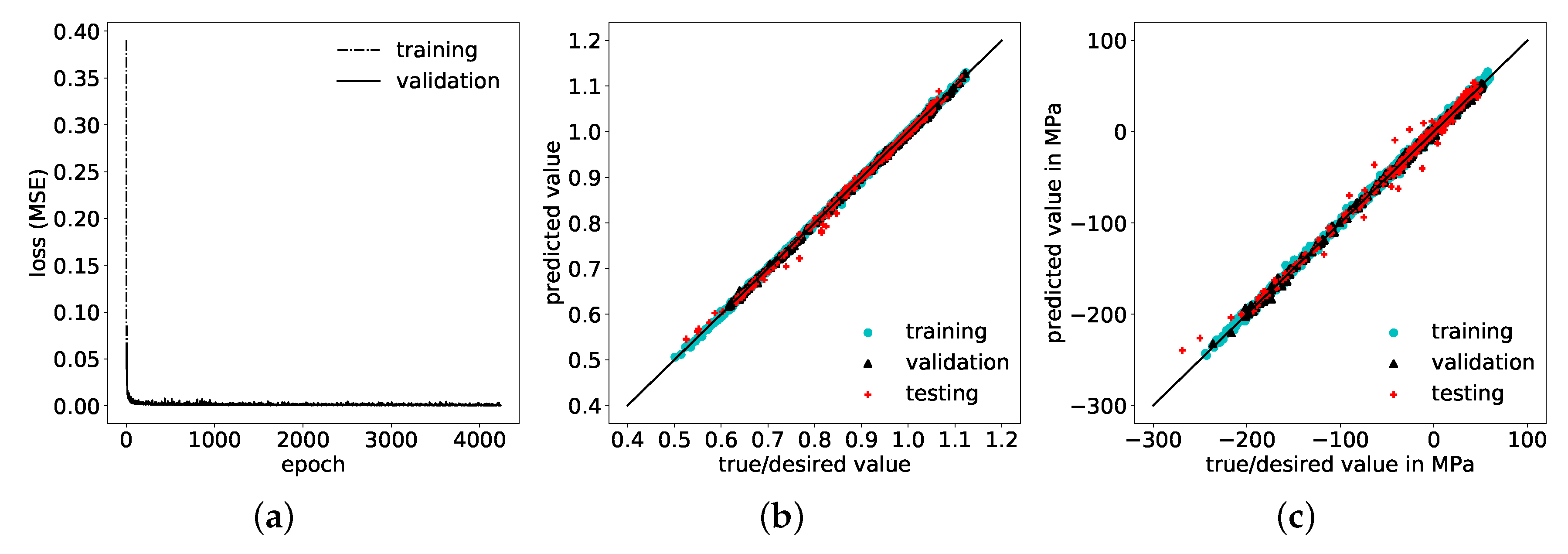
5. Generalization of Hybrid Model
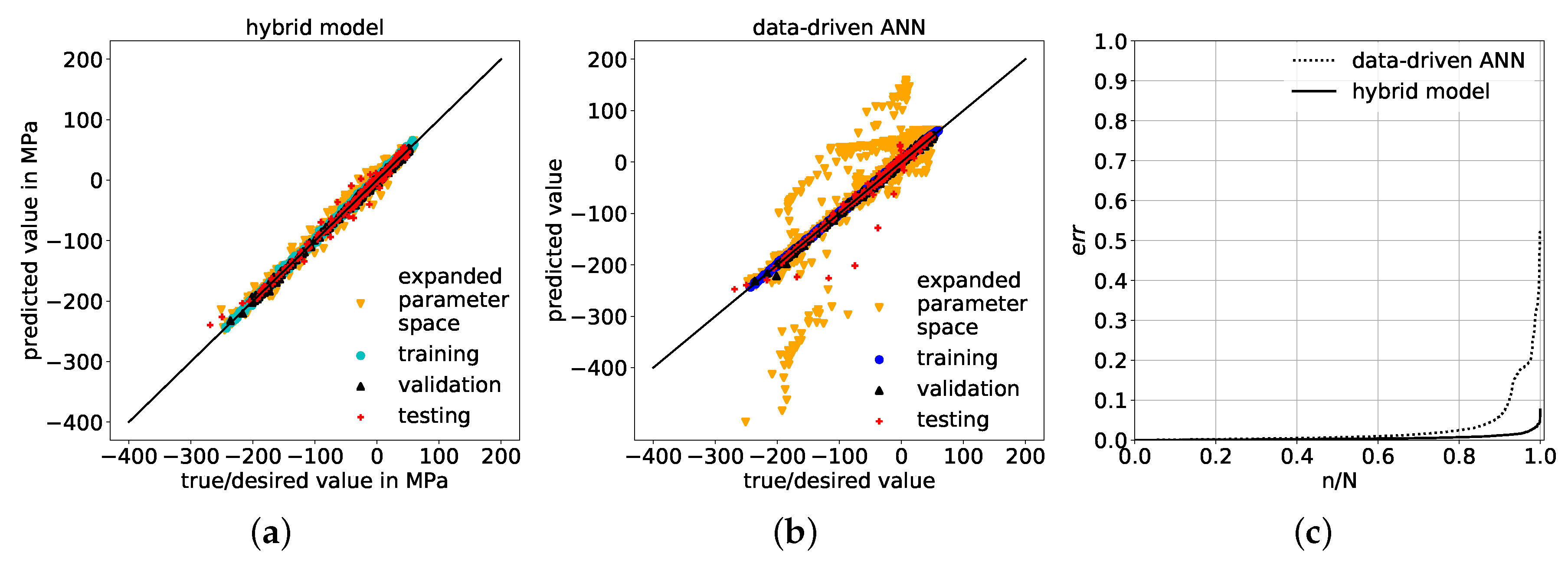
5.1. Setup of Purely Data-Driven ANN as Benchmark
5.2. Comparison of Physics-Based Hybrid Model and Purely Data-Driven ANN
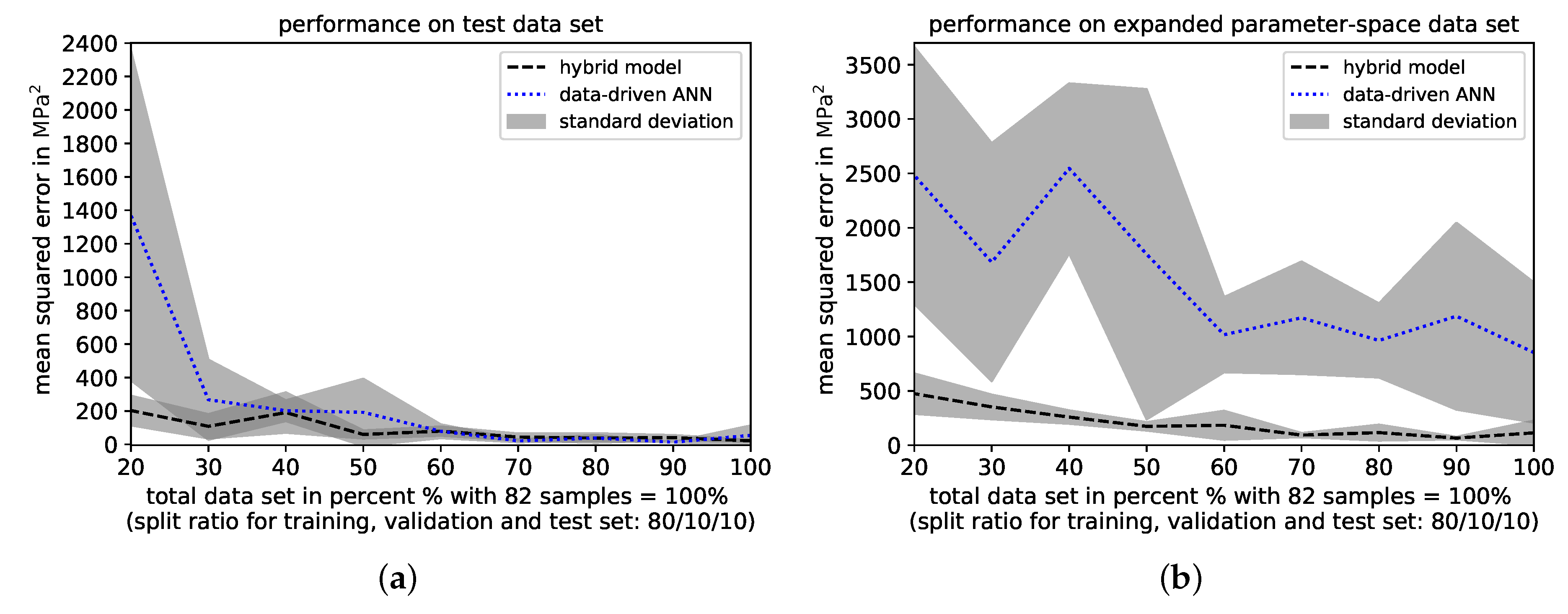
5.3. Data Reduction Effects on Hybrid Model and Data-Driven ANN Predictions
6. Conclusions
- Through the proposed corrective approach of a semi-analytical model, the solution of a high-fidelity numerical simulation is reached very efficiently.
- In particular, trained range of correction factors allows for a maximum adjustments of semi-analytical stresses of up to approximately 50% towards the desired high-fidelity solution.
- Generalized predictions for extended process parameter ranges can be achieved under the condition of correction factor values remaining within the training value range.
- Within the value range of trained correction factors, the generalization of the physics-based corrective approach within an expanded-parameter-space performs with significantly lower prediction errors compared to a purely data-driven generalization.
- When reducing the amount of available data during training, validation and testing, the generalization via the corrective approach demonstrated significantly reduced prediction errors compared to the purely data-driven model on both test set and expanded parameter-space data set, illustrating its ability to handle sparse data.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalidindi, S.R.; Graef, M. Materials Data Science: Current Status and Future Outlook. Annu. Rev. Mater. Res. 2015, 45, 171–193. [Google Scholar] [CrossRef]
- Bock, F.; Aydin, R.; Cyron, C.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A Review of the Application of Machine Learning and Data Mining Approaches in Continuum Materials Mechanics. Front. Mater. 2019, 6, 443. [Google Scholar] [CrossRef]
- Altschuh, P.; Yabansu, Y.C.; Hötzer, J.; Selzer, M.; Nestler, B.; Kalidindi, S.R. Data science approaches for microstructure quantification and feature identification in porous membranes. J. Membr. Sci. 2017, 540, 88–97. [Google Scholar] [CrossRef]
- Brough, D.B.; Kannan, A.; Haaland, B.; Bucknall, D.G.; Kalidindi, S.R. Extraction of Process-Structure Evolution Linkages from X-ray Scattering Measurements Using Dimensionality Reduction and Time Series Analysis. Integr. Mater. Manuf. Innov. 2017, 6, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Yun, M.; Argerich, C.; Cueto, E.; Duval, J.L.; Chinesta, F. Nonlinear Regression Operating on Microstructures Described from Topological Data Analysis for the Real-Time Prediction of Effective Properties. Materials 2020, 13, 2335. [Google Scholar] [CrossRef] [PubMed]
- Adams, B.L.; Kalidindi, S.R.; Fullwood, D.T. Microstructure Sensitive Design for Performance Optimization; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Cecen, A.; Dai, H.; Yabansu, Y.C.; Kalidindi, S.R.; Le, S. Material structure-property linkages using three-dimensional convolutional neural networks. Acta Mater. 2018, 146, 76–84. [Google Scholar] [CrossRef]
- Chupakhin, S.; Kashaev, N.; Klusemann, B.; Huber, N. Artificial neural network for correction of effects of plasticity in equibiaxial residual stress profiles measured by hole drilling. J. Srain. Anal. Eng. 2017, 52, 137–151. [Google Scholar] [CrossRef]
- Bock, F.E.; Blaga, L.A.; Klusemann, B. Mechanical Performance Prediction for Friction Riveting Joints of Dissimilar Materials via Machine Learning. Procedia Manuf. 2020, 47, 615–622. [Google Scholar] [CrossRef]
- Yang, Z.; Yabansu, Y.C.; Al-Bahrani, R.; Liao, W.K.; Choudhary, A.N.; Kalidindi, S.R.; Agrawal, A. Deep learning approaches for mining structure-property linkages in high contrast composites from simulation datasets. Comput. Mater. Sci. 2018, 151, 278–287. [Google Scholar] [CrossRef]
- Raissi, M. Deep Hidden Physics Models: Deep Learning of Nonlinear Partial Differential Equations. J. Mach. Learn. Res. 2018, 18, 1–24. [Google Scholar]
- Lu, L.; Dao, M.; Kumar, P.; Ramamurty, U.; Karniadakis, G.E.; Suresh, S. Extraction of mechanical properties of materials through deep learning from instrumented indentation. Proc. Natl. Acad. Sci. USA 2020, 117, 7052–7062. [Google Scholar] [CrossRef] [PubMed]
- Chinesta, F.; Cueto, E.; Abisset-Chavanne, E.; Duval, J.L.; Khaldi, F.E.B. Virtual, Digital and Hybrid Twins: A New Paradigm in Data-Based Engineering and Engineered Data. Arch. Comput. Methods Eng. 2018, 27, 105–134. [Google Scholar]
- Montáns, F.J.; Chinesta, F.; Gómez-Bombarelli, R.; Kutz, J.N. Data-driven modeling and learning in science and engineering. Comptes Rendus MéCanique 2019, 347, 845–855. [Google Scholar] [CrossRef]
- Kirchdoerfer, T.; Ortiz, M. Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 2016, 304, 81–101. [Google Scholar] [CrossRef]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-Guided Data Science: A New Paradigm for Scientific Discovery from Data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Liu, X.; Athanasiou, C.E.; Padture, N.P.; Sheldon, B.W.; Gao, H. A machine learning approach to fracture mechanics problems. Acta Mater. 2020, 190, 105–112. [Google Scholar] [CrossRef]
- Kapteyn, M.G.; Knezevic, D.J.; Huynh, D.B.P.; Tran, M.; Willcox, K.E. Data-driven physics-based digital twins via a library of component-based reduced-order models. Int. J. Numer. Methods Eng. 2020, 53, 3073. [Google Scholar]
- Moya, B.; Badías, A.; Alfaro, I.; Chinesta, F.; Cueto, E. Digital twins that learn and correct themselves. Int. J. Numer. Methods Eng. 2020, 25, 87. [Google Scholar]
- González, D.; Chinesta, F.; Cueto, E. Learning Corrections for Hyperelastic Models From Data. Front. Mater. 2019, 6, 752. [Google Scholar] [CrossRef]
- Ibáñez, R.; Abisset-Chavanne, E.; González, D.; Duval, J.L.; Cueto, E.; Chinesta, F. Hybrid constitutive modeling: Data-driven learning of corrections to plasticity models. Int. J. Mater. Form. 2019, 12, 717–725. [Google Scholar] [CrossRef]
- Havinga, J.; Mandal, P.K.; van den Boogaard, T. Exploiting data in smart factories: Real-time state estimation and model improvement in metal forming mass production. Int. J. Mater. Form. 2020, 13, 663–673. [Google Scholar] [CrossRef]
- Hu, Y.; Yao, Z.; Hu, J. An Analytical Model to Predict Residual Stress Field Induced by Laser Shock Peening. J. Manuf. Sci. Eng. 2009, 131, 031017. [Google Scholar] [CrossRef]
- Dursun, T.; Soutis, C. Recent developments in advanced aircraft aluminium alloys. Mater. Des. 2014, 56, 862–871. [Google Scholar] [CrossRef]
- Hertwich, E.G.; Ali, S.; Ciacci, L.; Fishman, T.; Heeren, N.; Masanet, E.; Asghari, F.N.; Olivetti, E.; Pauliuk, S.; Tu, Q.; et al. Material efficiency strategies to reducing greenhouse gas emissions associated with buildings, vehicles, and electronics—A review. Environ. Res. Lett. 2019, 14, 043004. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R. Laser shock processing: A review of the physics and applications. J. Mater. Process. Technol. 1995, 27, 1213–1229. [Google Scholar]
- Braisted, W.; Brockman, R.. Finite element simulation of laser shock peening. Int. J. Fatigue 1999, 21, 719–724. [Google Scholar] [CrossRef]
- Brockman, R.A.; Braisted, W.R.; Olson, S.E.; Tenagli, R.D.; Clauer, A.H.; Langer, K.; Shepard, M.J. Prediction and characterization of residual stresses from laser shock peening. Int. J. Fatigue 2012, 36, 96–108. [Google Scholar] [CrossRef]
- Keller, S.; Chupakhin, S.; Staron, P.; Maawad, E.; Kashaev, N.; Klusemann, B. Experimental and numerical investigation of residual stresses in laser shock peened AA2198. J. Mater. Process. Technol. 2018, 255, 294–307. [Google Scholar] [CrossRef]
- Frija, M.; Ayeb, M.; Seddik, R.; Fathallah, R.; Sidhom, H. Optimization of peened-surface laser shock conditions by method of finite element and technique of design of experiments. Int. J. Adv. Manuf. Technol. 2018, 97, 51–69. [Google Scholar] [CrossRef]
- Ayeb, M.; Frija, M.; Fathallah, R. Prediction of residual stress profile and optimization of surface conditions induced by laser shock peening process using artificial neural networks. Int. J. Adv. Manuf. Technol. 2019, 100, 2455–2471. [Google Scholar] [CrossRef]
- Wu, J.; Li, Y.; Zhao, J.; Qiao, H.; Lu, Y.; Sun, B.; Hu, X.; Yang, Y. Prediction of residual stress induced by laser shock processing based on artificial neural networks for FGH4095 superalloy. Mater. Lett. 2021, 286, 129269. [Google Scholar] [CrossRef]
- Mathew, J.; Kshirsagar, R.; Zabeen, S.; Smyth, N.; Kanarachos, S.; Langer, K.; Fitzpatrick, M.E. Machine Learning-Based Prediction and Optimisation System for Laser Shock Peening. Appl. Sci. 2021, 11, 2888. [Google Scholar] [CrossRef]
- Ebert, S.D.; Kenton Musgave, F.; Peachey, D.; Perlin, K.; Worley, S. Texturing & Modeling—A Procedural Approach, 3rd ed.; Morgan Kaufmann Series in Computer Graphics and Geometric Modeling: San Francisco, CA, USA, 2003; pp. 30–31. [Google Scholar]
- Timoshenko, S.; Goodier, J. Theory of Elasticity, 2nd ed.; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Mcdowell, D.L. An Approximate Algorithm for Elastic-Plastic Two-Dimensional Rolling/Sliding Contact. Wear 1997, 211, 237–246. [Google Scholar] [CrossRef]
- Keller, S.; Horstmann, M.; Kashaev, N.; Klusemann, B. Experimentally validated multi-step simulation strategy to predict the fatigue crack propagation rate in residual stress fields after laser shock peening. Int. J. Fatigue 2019, 124, 265–276. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; Volume 21, pp. 541–547. [Google Scholar]
- Sticchi, M.; Staron, P.; Sano, Y.; Meixer, M.; Klaus, M.; Rebelo-Kornmeier, J.; Huber, N.; Kashaev, N. A parametric study of laser spot size and coverage on the laser shock peening induced residual stress in thin aluminium samples. J. Eng. 2015, 13, 97–105. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Haykin, S. Neural Networks. A Comprehensive Foundation, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Qian, N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Mitchell, T. Machine Learning, 2nd ed.; McGraw-Hill: New York, NY, USA, 2010; p. 67. [Google Scholar]
- Huber, N.; Tsakmakis, C. A new loading history for identification of viscoplastic properties by spherical indentation. J. Mater. Res. 2004, 19, 101–113. [Google Scholar] [CrossRef]
- Gibbings, J.C. Dimensional Analysis; Springer: London, UK; New York, NY, USA, 2011. [Google Scholar]
- Huber, N.; Tsakmakis, C. Determination of constitutive properties from spherical indentation data using neural networks. Part I: The case of pure kinematic hardening in plasticity laws. J. Mech. Phys. Solids 1999, 47, 1569–1588. [Google Scholar] [CrossRef]
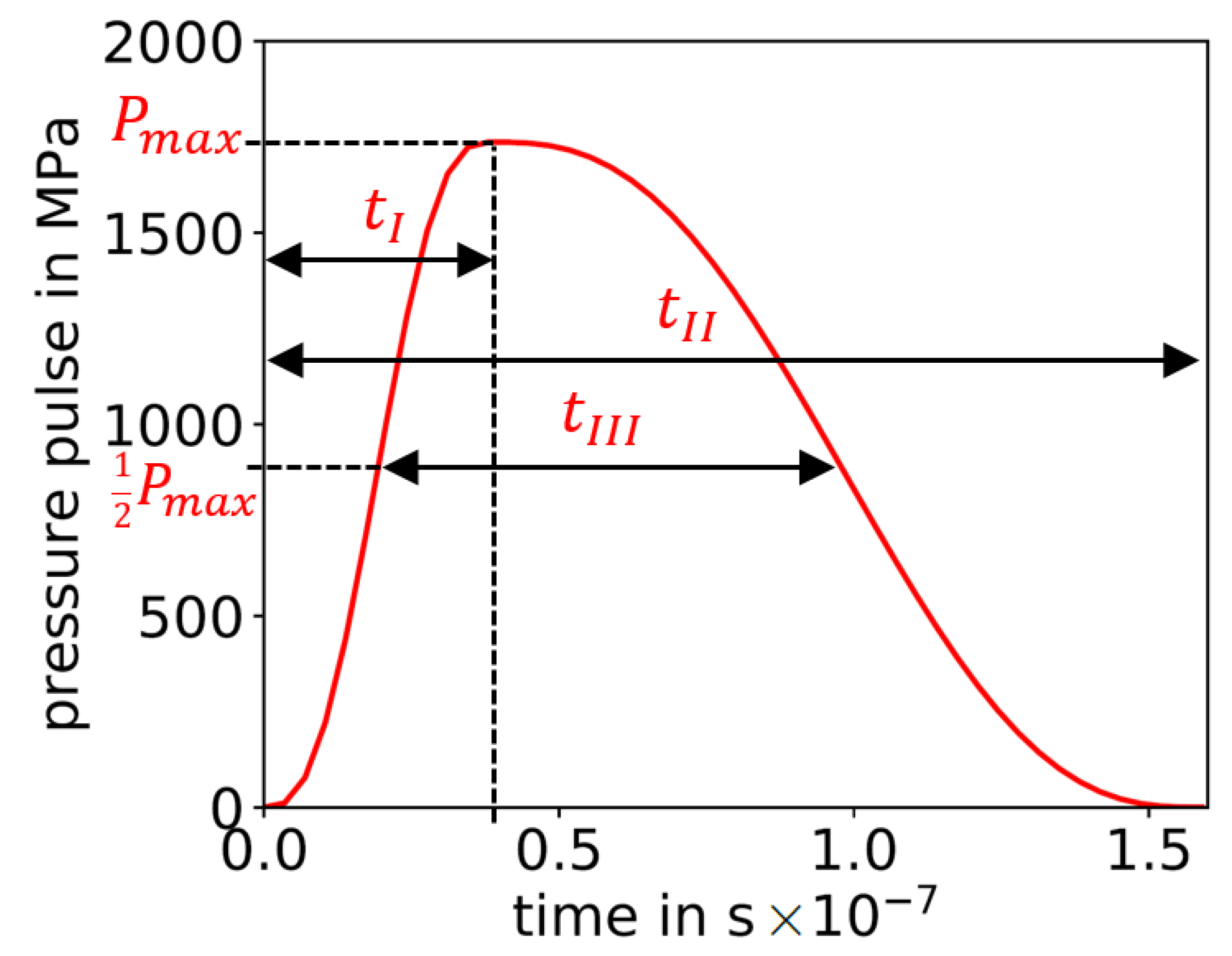
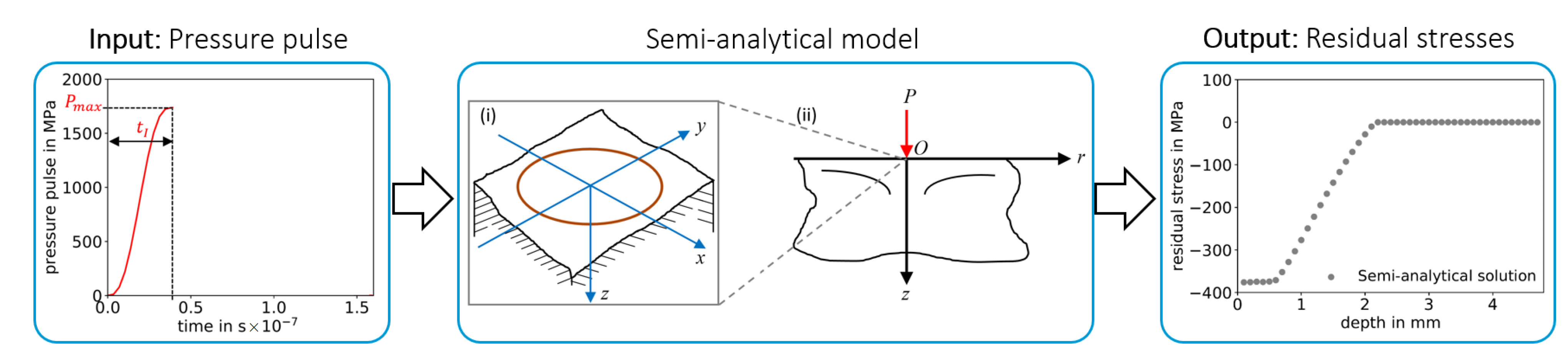
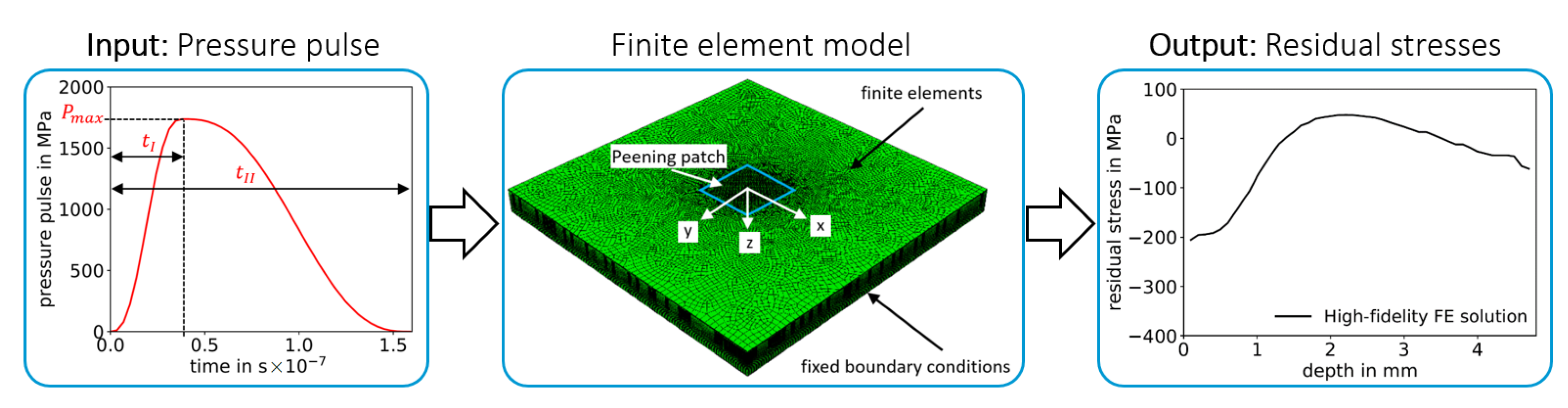
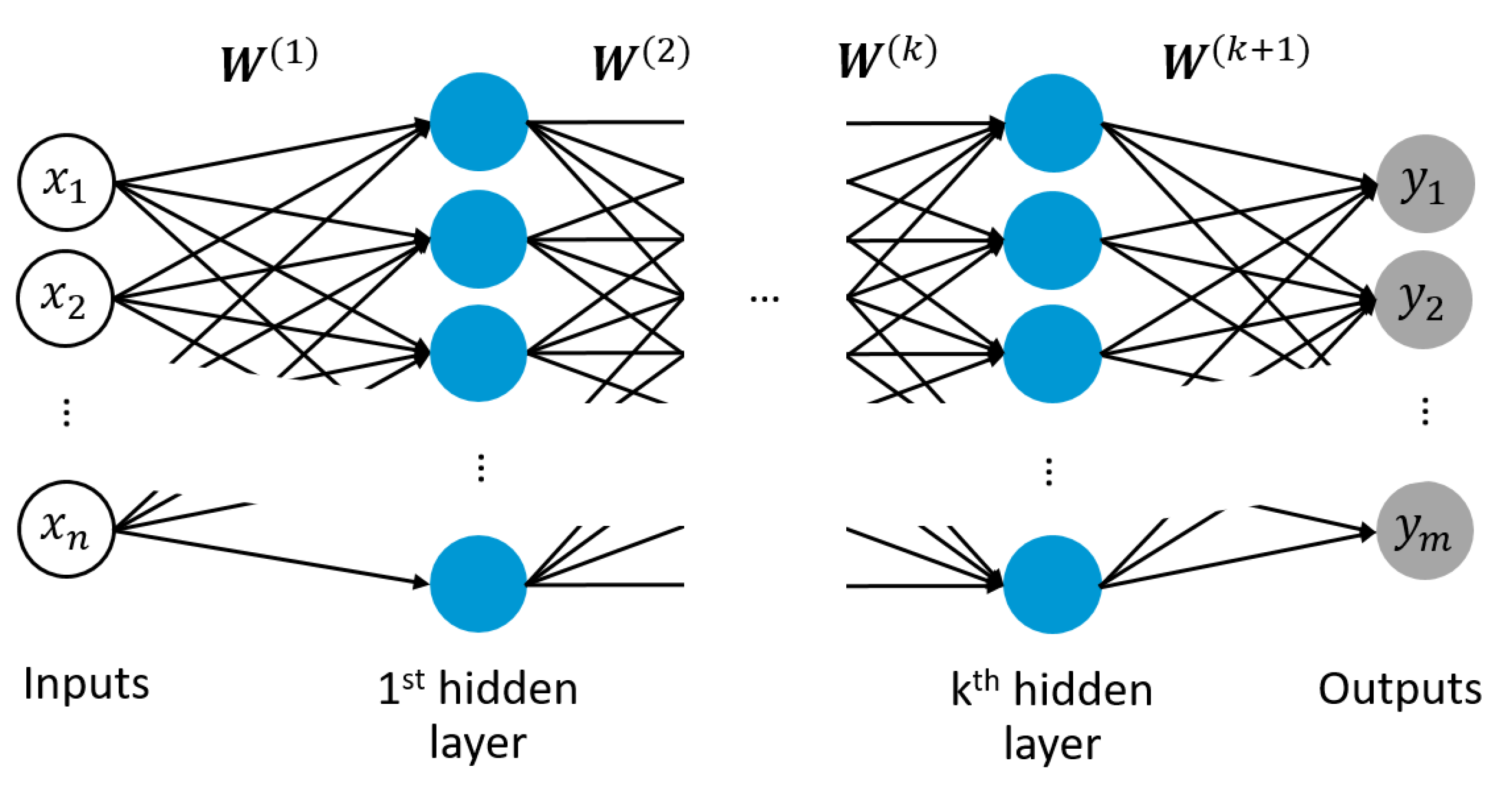

| [MPa] | [ns] | [ns] | |
|---|---|---|---|
| Min. | 800 | 12 | 43 |
| Max. | 2200 | 66 | 300 |
| Correction Factor | Residual Stresses | |||
|---|---|---|---|---|
| Data Set | in % | in % | in MPa | |
| Training | ||||
| Validation | ||||
| Test | ||||
| Correction Factor | Residual Stresses | |||
|---|---|---|---|---|
| Data Set | in % | in % | in MPa | |
| Training | ||||
| Validation | ||||
| Test | ||||
| in MPa | in ns | in ns | ||
|---|---|---|---|---|
| Training, validation, test | Min. | 800 | 12 | 43 |
| Max. | 2200 | 66 | 300 | |
| Expanded parameter space | Min. | 800 | 1 | 43 |
| Max. | 2400 | 100 | 306 |
| Hybrid Model | Data-Driven ANN | |||
|---|---|---|---|---|
| Data Set | in % | in % | in MPa | |
| Training | ||||
| Validation | ||||
| Test | ||||
| Expanded space | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bock, F.E.; Keller, S.; Huber, N.; Klusemann, B. Hybrid Modelling by Machine Learning Corrections of Analytical Model Predictions towards High-Fidelity Simulation Solutions. Materials 2021, 14, 1883. https://doi.org/10.3390/ma14081883
Bock FE, Keller S, Huber N, Klusemann B. Hybrid Modelling by Machine Learning Corrections of Analytical Model Predictions towards High-Fidelity Simulation Solutions. Materials. 2021; 14(8):1883. https://doi.org/10.3390/ma14081883
Chicago/Turabian StyleBock, Frederic E., Sören Keller, Norbert Huber, and Benjamin Klusemann. 2021. "Hybrid Modelling by Machine Learning Corrections of Analytical Model Predictions towards High-Fidelity Simulation Solutions" Materials 14, no. 8: 1883. https://doi.org/10.3390/ma14081883
APA StyleBock, F. E., Keller, S., Huber, N., & Klusemann, B. (2021). Hybrid Modelling by Machine Learning Corrections of Analytical Model Predictions towards High-Fidelity Simulation Solutions. Materials, 14(8), 1883. https://doi.org/10.3390/ma14081883








