Torsional Fatigue Life Prediction of 30CrMnSiNi2A Based on Meso-Inhomogeneous Deformation
Abstract
1. Introduction
2. Experimental Programme
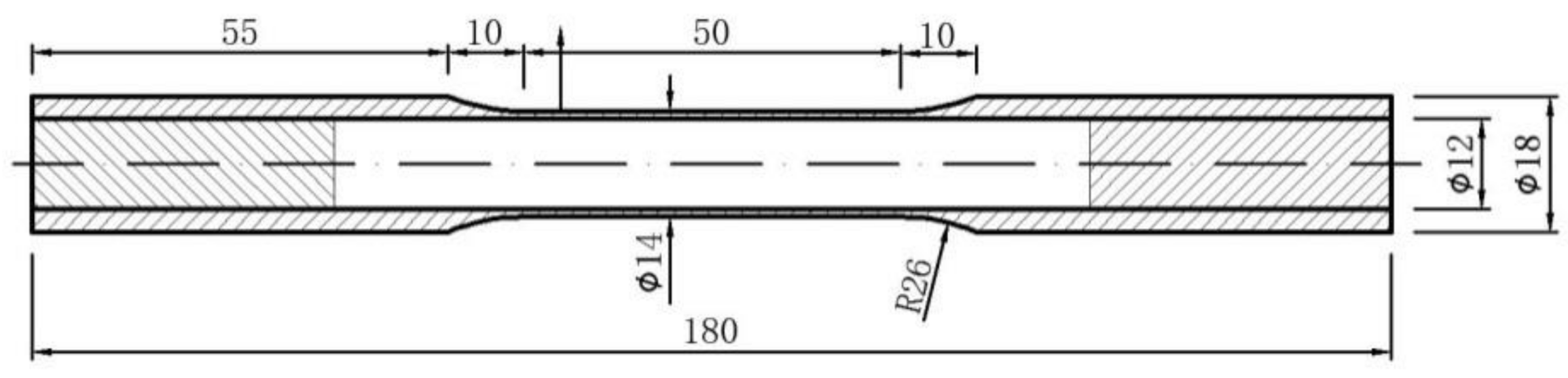
2.1. Materials and Specimen
2.2. Torsional Fatigue Experiment
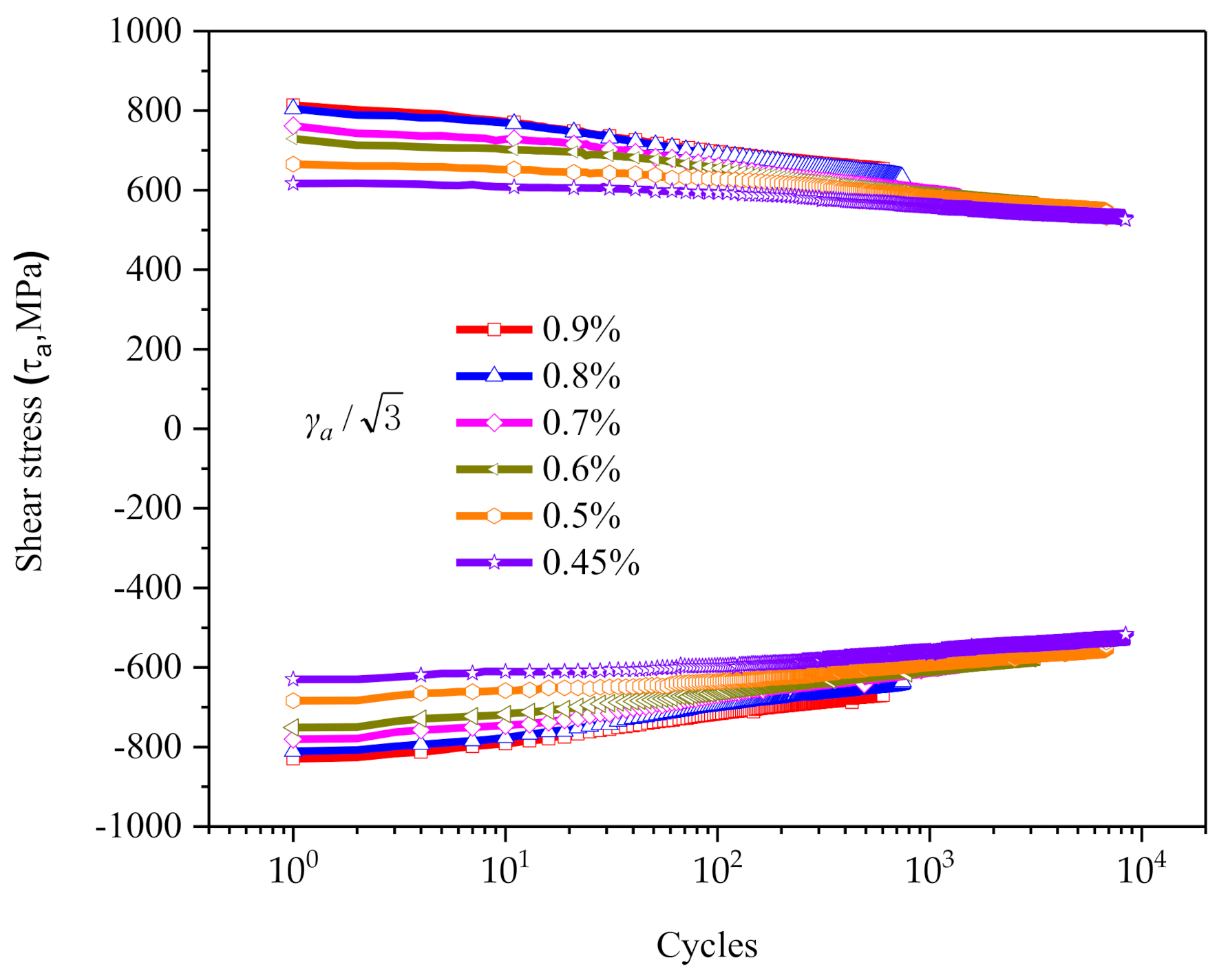
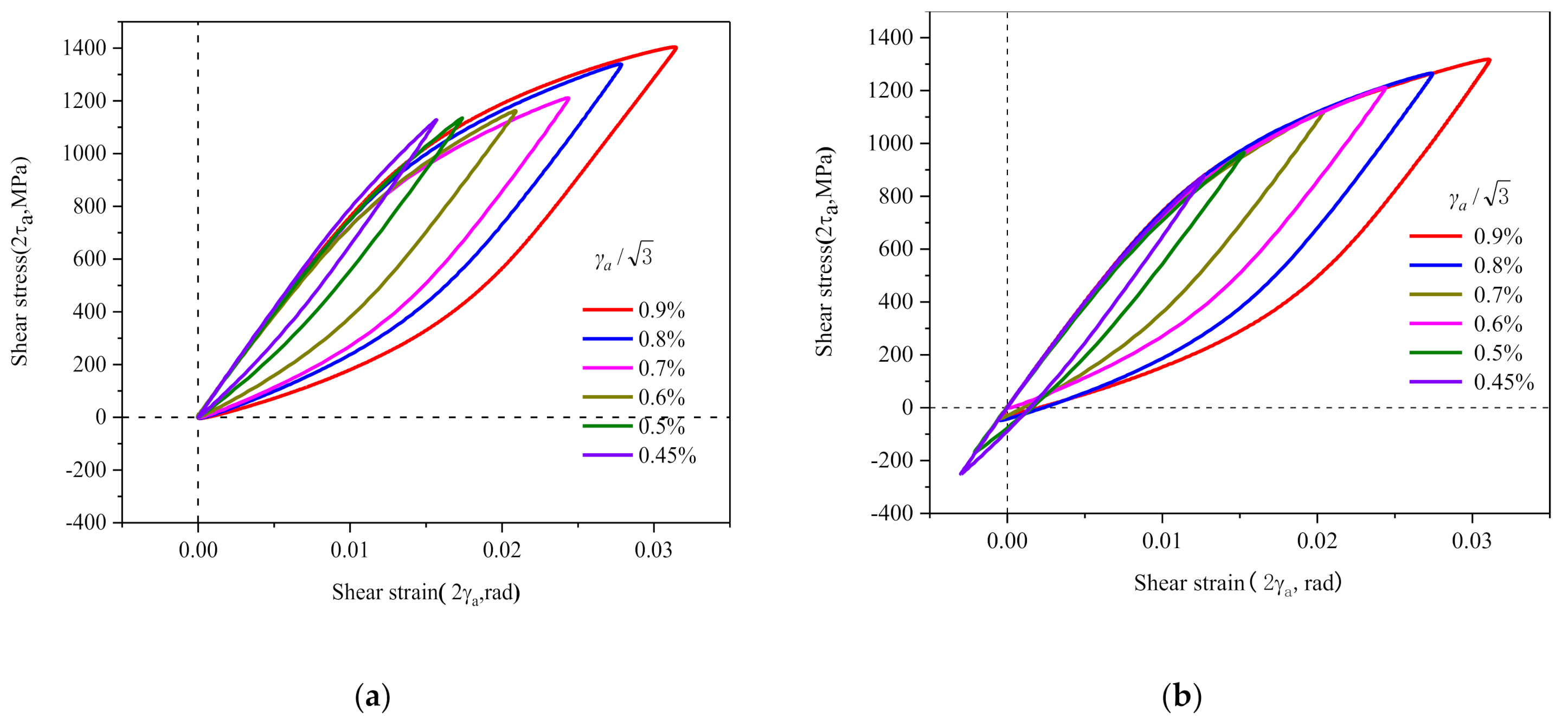
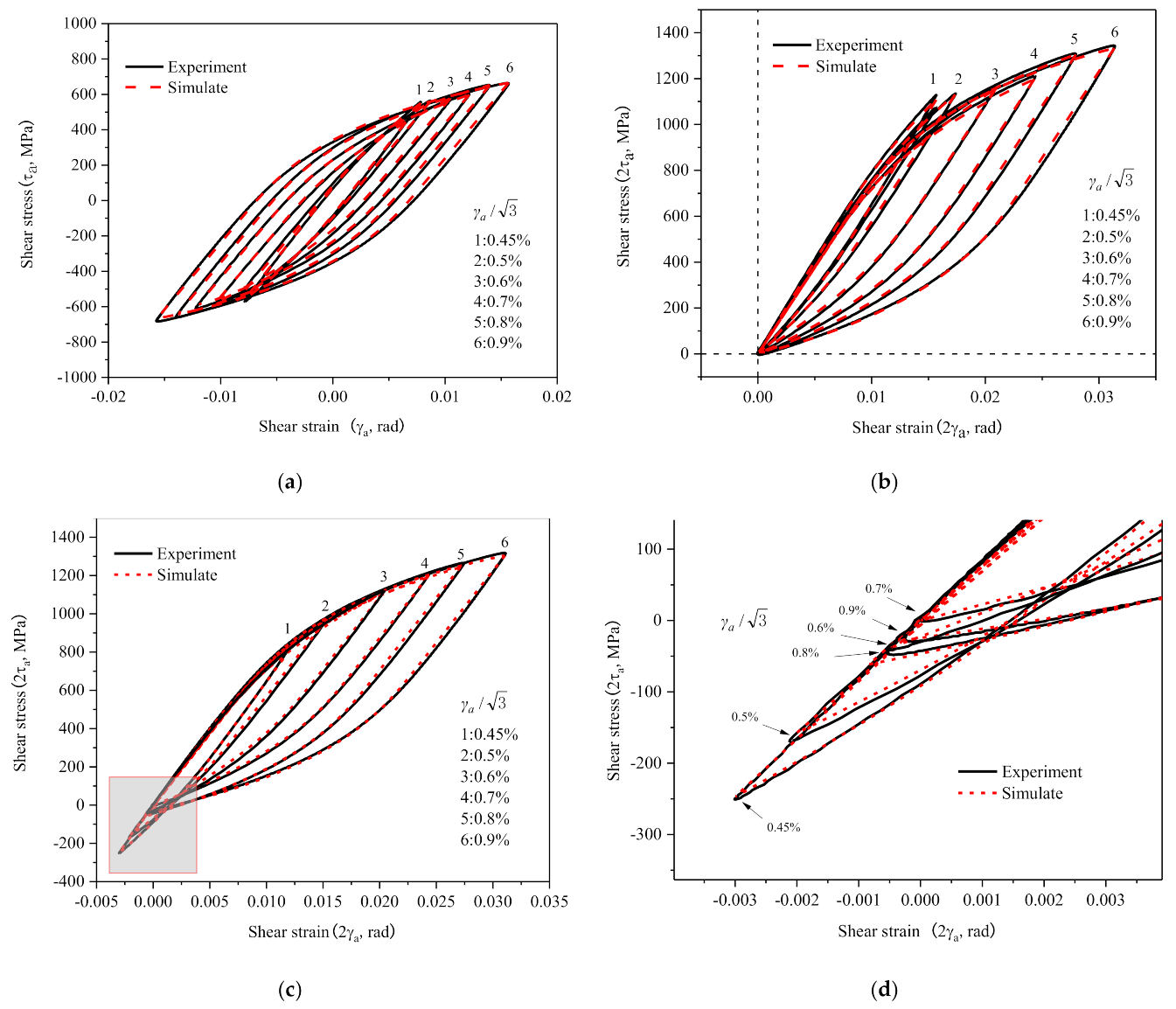
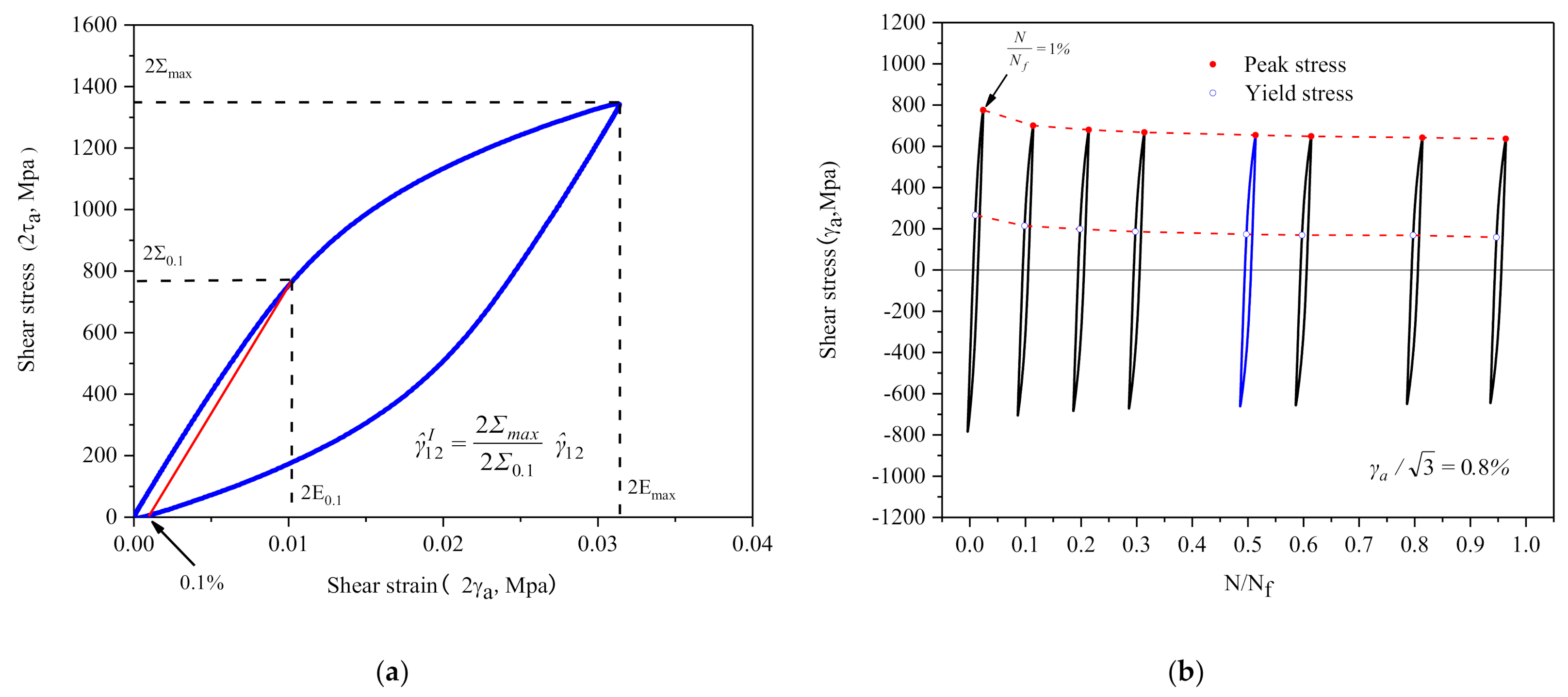
2.3. Cyclic Softening and Non-Masing Behavior
3. Crystal Plastic Constitutive Model and Material Model
3.1. Crystal Plastic Constitutive Model with the Bauschinger Effect
3.2. Material Models
3.3. Material Parameters of Crystal Plasticity Model
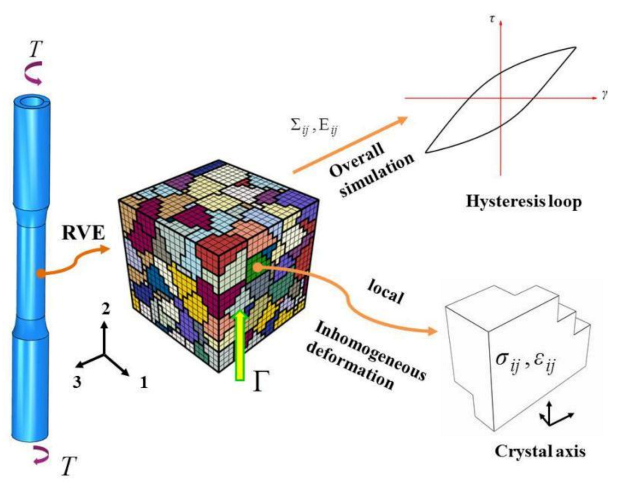
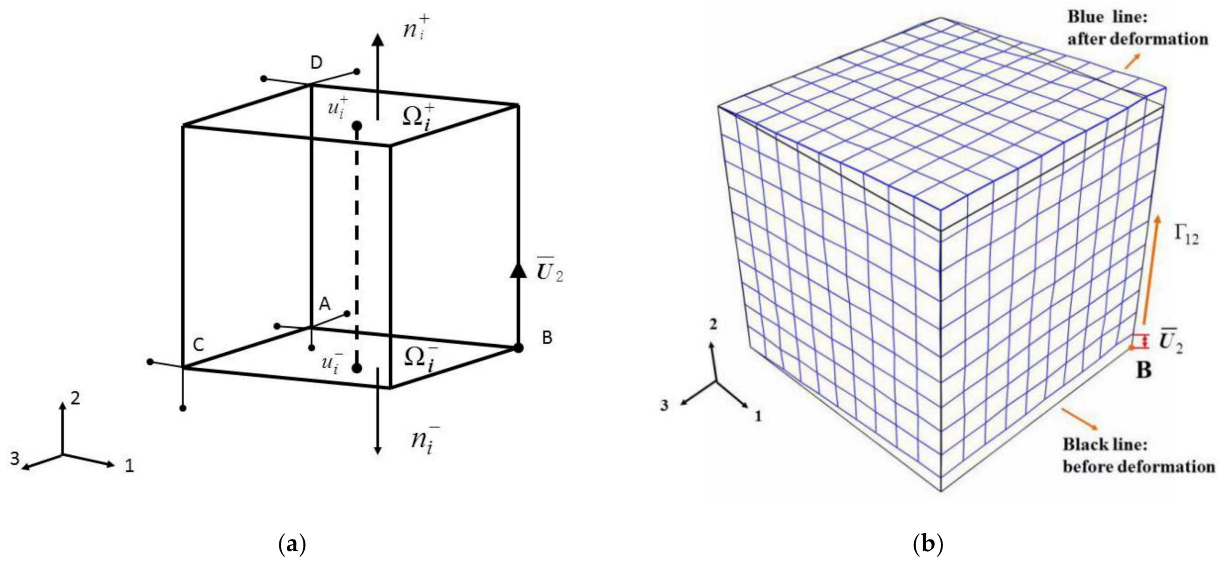
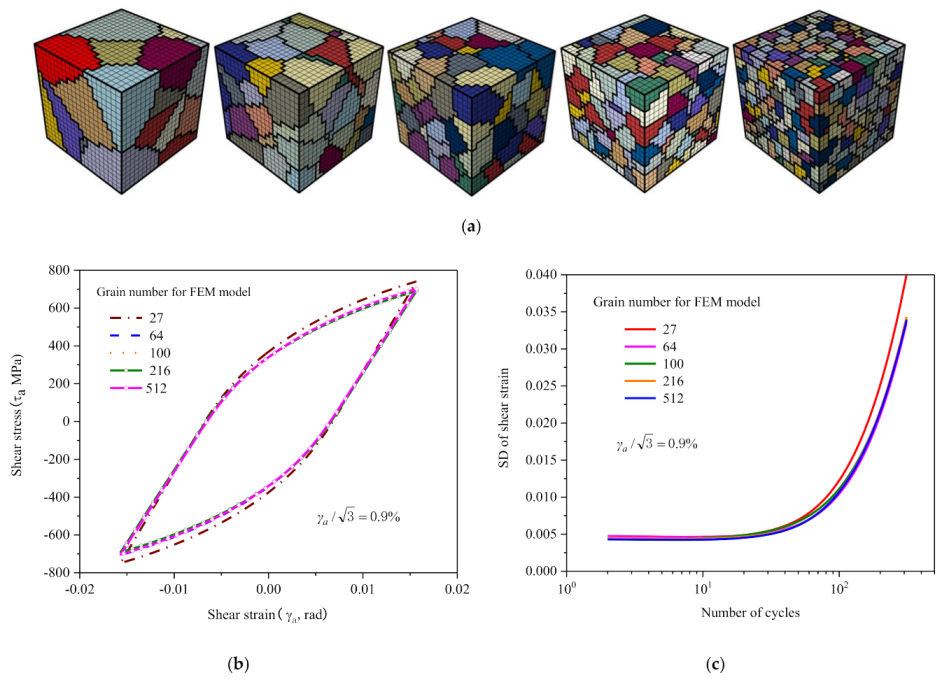
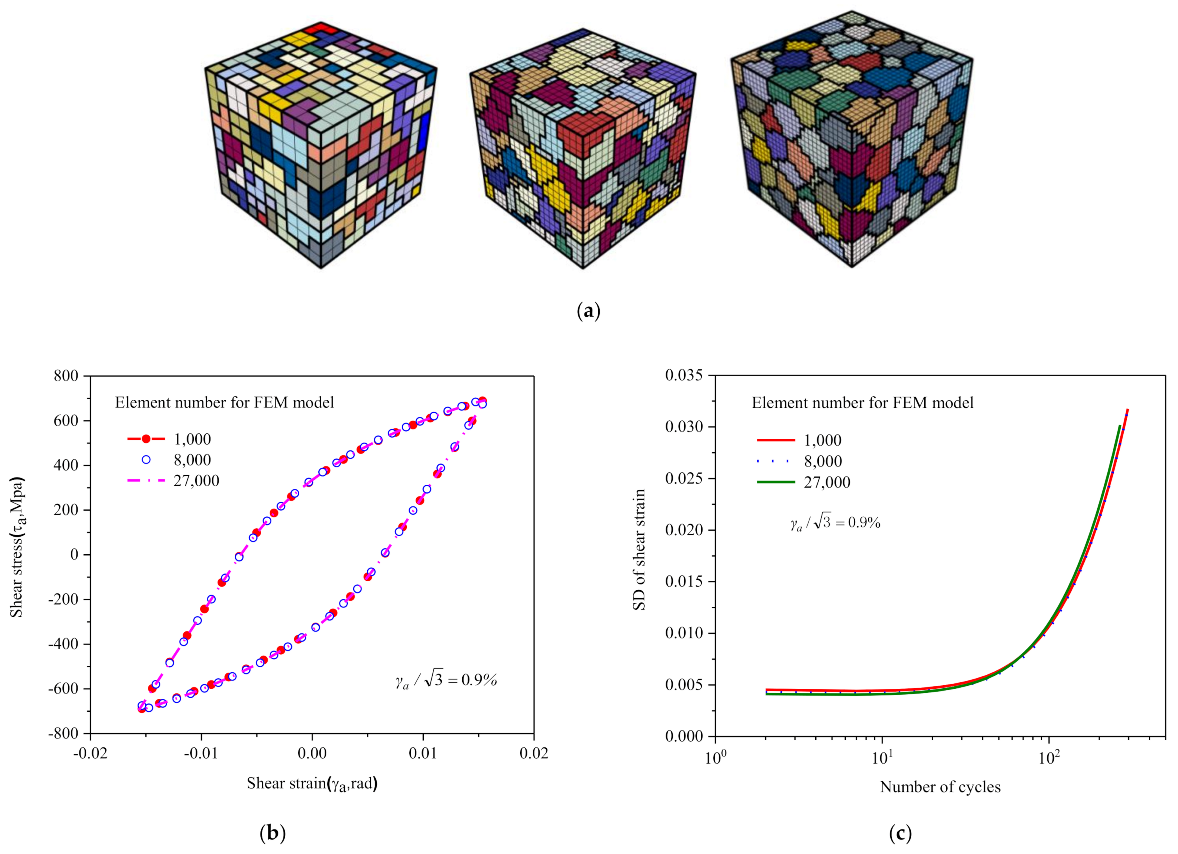
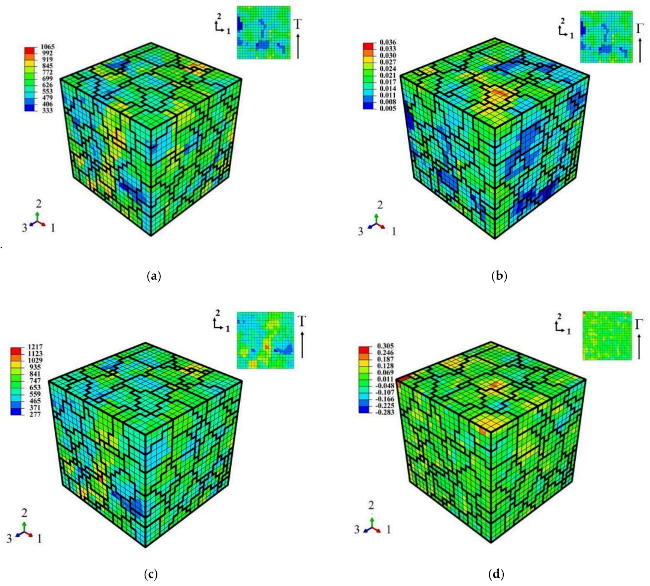
3.4. Validation of the Representative Volume Element (RVE)
4. Prediction of Low Cycle Fatigue Life Based on the Material Deformation Inhomogeneity
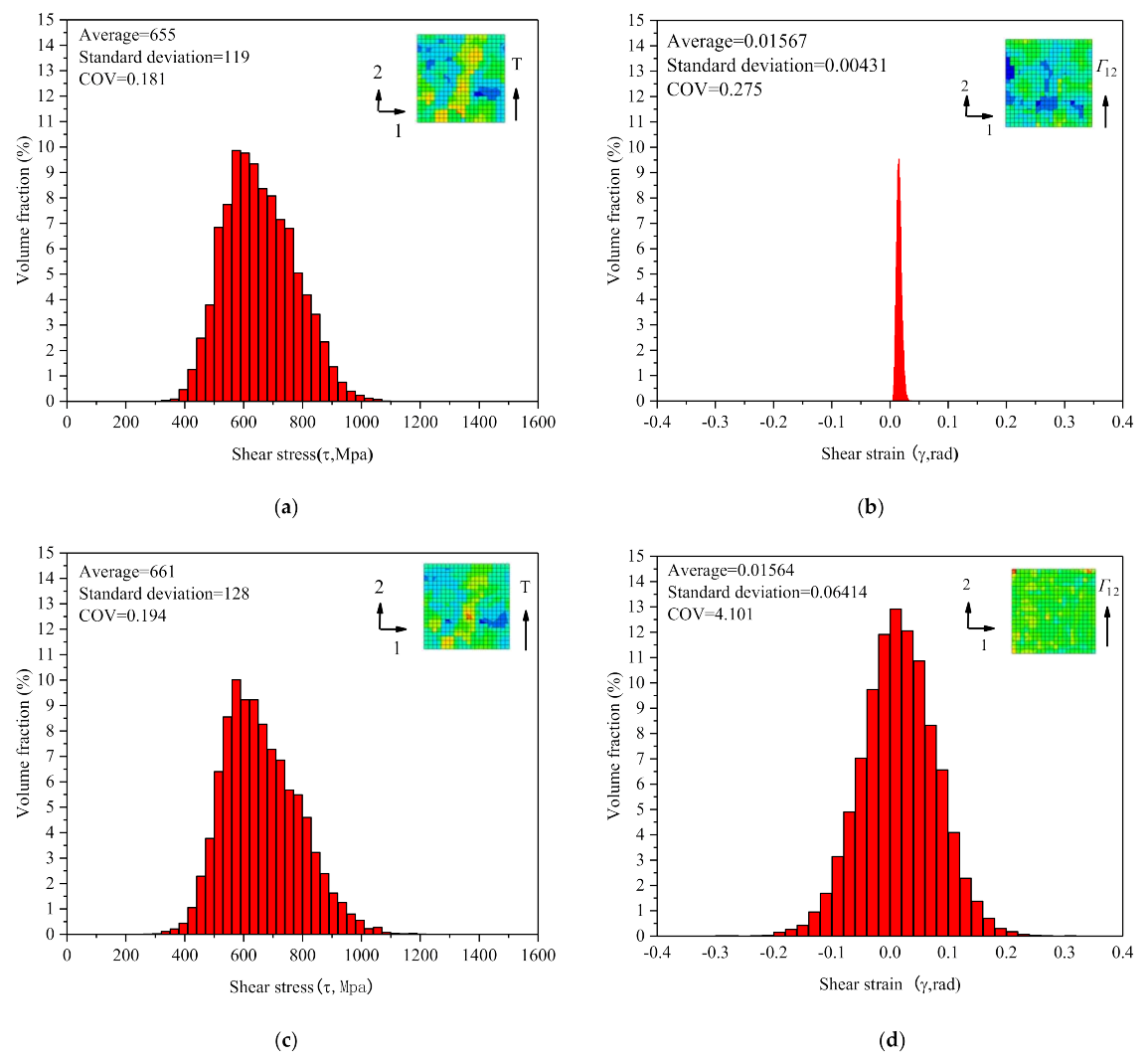
4.1. Analysis of Deformation Inhomogeneity Evolution under Shear Fatigue
4.2. Statistical Analysis of Deformation Inhomogeneity Evolution
4.3. Fatigue Indicator Parameter (FIP) Based on Evolution of Material Deformation Inhomogeneity
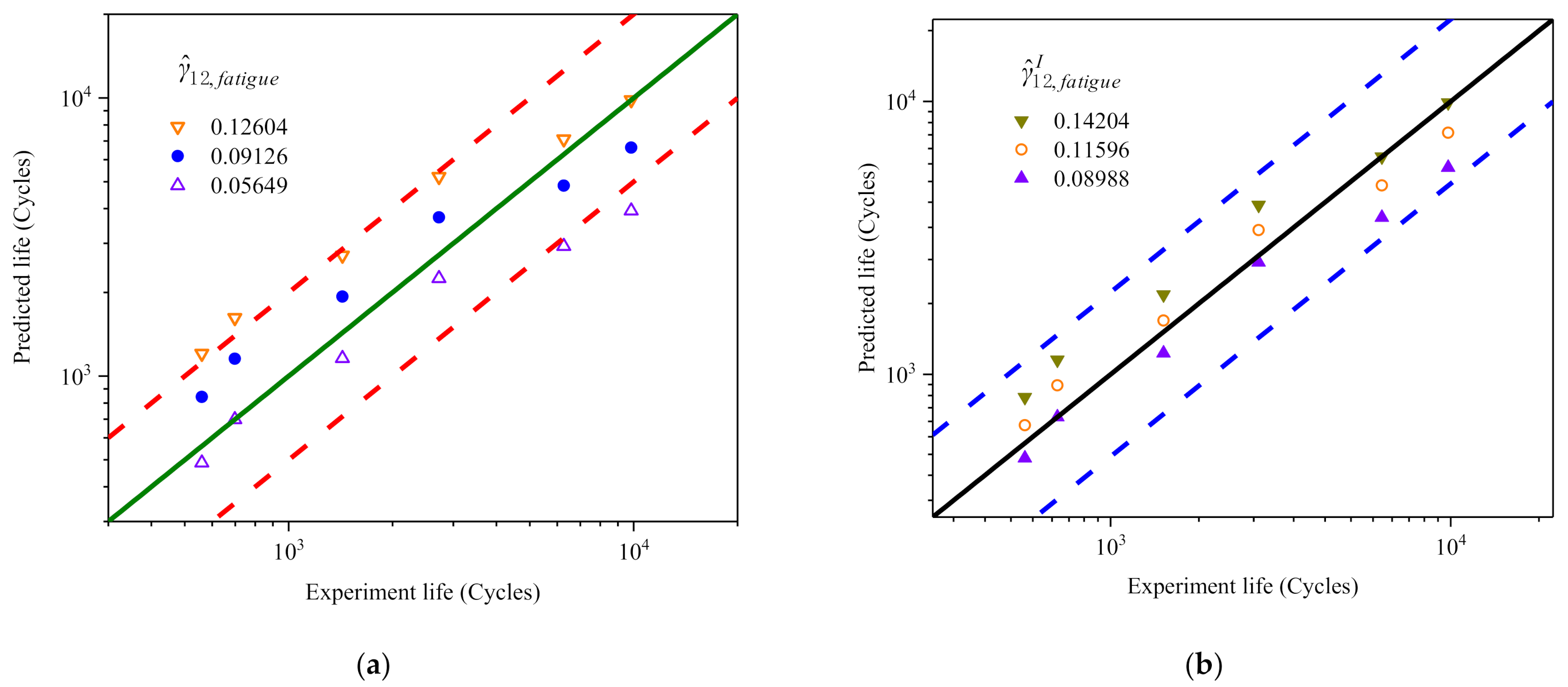
4.4. Prediction and Validation of Shear Fatigue Life Curve
4.5. Verification of Shear Fatigue Life Prediction Error
5. Conclusions
- 30CrMnSiNi2A steel exhibits non-Masing behavior under torsional cycle, its hysteretic behavior is associated with the strain amplitude, and its elastic ranges of different strain amplitudes are different. When the crystal plasticity RVE model is used to numerically simulate the constant amplitude shear cycle process, the correlation between the parameters for RVE and strain amplitude must be taken into account.
- There is a correlation between the evolution of deformation inhomogeneity and the shear fatigue life of material in torsion cycle.
- Using the standard deviation of shear strain () as the FIP, most of the fatigue life predictions fall within the factor of two scatter bands in comparison figures, and the maximum error is not more than 2.5 times compared with the test.
- If using the weighted standard deviation of the shear strain () as the FIP, in which the ratio of peak stress to yield stress is taken into account, all fatigue life predictions fall within the factor of two scatter bands in comparison figures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adinoyi, M.J.; Merah, N.; Albinmousa, J. Shear fatigue behavior of AW2099-T83 aluminum-lithium alloy. Int. J. Fatigue 2018, 117, 101–110. [Google Scholar] [CrossRef]
- Toscano, D.; Behravesh, S.B.; Shaha, S.K.; Jahed, H.; Williams, B. Characterization of closed-die forged AZ31B under pure axial and pure shear loading. Int. J. Fatigue 2020, 139, 105754. [Google Scholar] [CrossRef]
- Li, B.; Zheng, Y.; Shi, S.; Zhang, Z.; Chen, X. Cyclic deformation behavior and failure mechanism of S32205 duplex stainless steel under torsional fatigue loadings. Mater. Sci. Eng. A Struct. 2020, 786, 139443. [Google Scholar] [CrossRef]
- Dey, R.; Tarafder, S.; Sivaprasad, S. Influence of axial and torsional cyclic loading on the fatigue behavior of 304LN stainless steel using solid and hollow specimens. Mech. Mater. 2018, 122, 58–68. [Google Scholar] [CrossRef]
- Sivaprasad, S.; Bar, H.N.; Gupta, S.K.; Arora, P.; Bhasin, V.; Tarafder, S. A comparative assessment of cyclic deformation behaviour in SA333 Gr.6 steel using solid, hollow specimens under axial and shear strain paths. Int. J. Fatigue 2014, 61, 76–86. [Google Scholar] [CrossRef]
- Xu, J.X.; Li, R.H.; Zhang, P.; Zhang, Z.F. Crack propagation behavior and mechanism of coarse-grained copper in cyclic torsion with axial static tension. Int. J. Fatigue 2020, 131, 105304. [Google Scholar] [CrossRef]
- Zhang, W.; Akid, R. Mechanisms and fatigue performance of two steels in cyclic torsion with axial static tension/compression. Fatigue Fract. Eng. Mater. Struct. 1997, 20, 547–557. [Google Scholar] [CrossRef]
- Zhang, W.; Akid, R. Effect of biaxial mean stress on cyclic stress-strain response and behaviour of short fatigue cracks in a high strength spring steel. Fatigue Fract. Eng. Mater. Struct. 1997, 20, 167–177. [Google Scholar] [CrossRef]
- Shiozawa, D.; Nakai, Y.; Murakami, T.; Nosho, H. Observation of fatigue crack propagation behavior under torsional loading by using synchrotron radiation micro-CT imaging. Procedia Eng. 2011, 10, 1479–1484. [Google Scholar] [CrossRef][Green Version]
- Akiniwa, Y.; Stanzltschegg, S.; Mayer, H.; Wakita, M.; Tanaka, K. Fatigue strength of spring steel under axial and torsional loading in the very high cycle regime. Int. J. Fatigue 2008, 30, 2057–2063. [Google Scholar] [CrossRef]
- Fatemi, A.; Molaei, R.; Sharifimehr, S.; Shamsaei, N.; Phan, N. Torsional fatigue behavior of wrought and additive manufactured Ti-6Al-4V by powder bed fusion including surface finish effect. Int. J. Fatigue 2017, 99, 187–201. [Google Scholar] [CrossRef]
- Li, Y.; Retraint, D.; Xue, H.; Gao, T.; Sun, Z. Fatigue properties and cracking mechanisms of a 7075 aluminum alloy under axial and torsional loadings. Procedia Struct. Integr. 2019, 19, 637–644. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, X.; Bao, R.; Fei, B. Tension–torsion high-cycle fatigue failure analysis of 2A12-T4 aluminum alloy with different stress ratios. Int. J. Fatigue 2011, 33, 1066–1074. [Google Scholar] [CrossRef]
- Shamsaei, N.; Fatemi, A. Deformation and fatigue behaviors of case-hardened steels in torsion: Experiments and predictions. Int. J. Fatigue 2009, 31, 1386–1396. [Google Scholar] [CrossRef]
- Wang, J.; Uy, B.; Li, D.; Song, Y. Fatigue behaviour of stainless steel bolts in tension and shear under constant-amplitude loading. Int. J. Fatigue 2020, 133, 105401. [Google Scholar] [CrossRef]
- Sharifimehr, S.; Fatemi, A. Evaluation of methods for estimating shear fatigue properties of steels and titanium alloys. Int. J. Fatigue 2019, 122, 19–34. [Google Scholar] [CrossRef]
- Yuan, G.; Zhang, X.; Chen, B.; Tu, S.; Zhang, C. Low-cycle fatigue life prediction of a polycrystalline nickel-base superalloy uing crystal plasticity modelling approach. J. Mater. Sci. Technol. 2020, 38, 28–38. [Google Scholar] [CrossRef]
- Cruzado, A.; Lucarini, S.; Lorca, J.; Segurado, J. Crystal plasticity simulation of the effect of grain size on the fatigue behavior of polycrystalline inconel 718. Int. J. Fatigue 2018, 113, 236–245. [Google Scholar] [CrossRef]
- Li, Z.S.; Xu, J.; Demartino, C.; Zhang, K.S. Extremely-low cycle fatigue fracture of Q235 steel at different stress triaxialities. J. Constr. Steel Res. 2020, 169, 106060–106074. [Google Scholar] [CrossRef]
- Sweeney, C.A.; Vorster, W.; Leen, S.B.; Sakurada, E.; Mchugh, P.E.; Dunne, F.P.E. The role of elastic anisotropy, length scale and crystallographic slip in fatigue crack nucleation. J. Mech. Phys. Solids 2013, 61, 1224–1240. [Google Scholar] [CrossRef]
- Sadeghi, J.A.R.B. Experimental and numerical investigation of torsion fatigue of bearing steel. J. Tribol. ASME 2013, 135, 31103. [Google Scholar]
- Ahmadi, A.; Sadeghi, F. Experimental and numerical investigation of torsion fatigue of a nickel-based alloy at elevated temperature. Mater. Sci. Eng. A Struct. 2019, 751, 263–270. [Google Scholar] [CrossRef]
- Liu, G.L.; Zhang, K.S.; Zhong, X.C.; Ju, J.W. Analysis of meso-inhomogeneous deformation on a metal material surface under low-cycle fatigue. Acta Mech. Solida Sin. 2017, 30, 557–572. [Google Scholar] [CrossRef]
- Jin, L.L.; Zeng, B.; Lu, D.M.; Gao, Y.J.; Zhang, K.S. Prediction of strain fatigue life of HRB400 steel based on meso-deformation inhomogeneity. Materials 2020, 13, 1464. [Google Scholar] [CrossRef]
- Lefebvre, D.; Ellyin, F. Cyclic response and inelastic strain energy in low cycle fatigue. Int. J. Fatigue 1984, 6, 9–15. [Google Scholar] [CrossRef]
- Numanoglu, O.A.; Musgrove, M.; Harmon, J.A.; Hashans, Y.M.A. Generalized non-Masing hysteresis model for cyclic loading. J. Geotech. Geoenviron. 2018, 144, 6017015. [Google Scholar] [CrossRef]
- Skelton, R.P.; Maier, H.J.; Christ, H.J. The Bauschinger effect, masing model and the Ramberg–Osgood relation for cyclic deformation in metals. Mater. Sci. Eng. A Struct. 1997, 238, 377–390. [Google Scholar] [CrossRef]
- Song, W.; Liu, X.; Berto, F.; Razavi, S.M.J. Low-cycle fatigue behavior of 10CrNi3MoV high strength steel and its undermatched welds. Materials 2018, 11, 661. [Google Scholar] [CrossRef]
- Das, B.; Singh, A. Understanding strain controlled low cycle fatigue response of P91 steel through experiment and cyclic plasticity modeling. Fusion Eng. Des. 2019, 138, 125–137. [Google Scholar] [CrossRef]
- Fatoba, O.; Akid, R. Uniaxial cyclic elasto-plastic deformation and fatigue failure of API-5L X65 steel under various loading conditions. Theor. Appl. Fract. Mech. 2018, 94, 147–159. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J.R. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Needleman, A.; Asaro, R.J.; Lemonds, J.; Peirce, D. Finite element analysis of crystalline solids. Comput. Methods Appl. Mech. 1985, 52, 689–708. [Google Scholar] [CrossRef]
- Asaro, R.J.; Rice, J.R. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R Soc. A Math. Phys. 1976, 348, 101–127. [Google Scholar]
- Feng, L.; Zhang, G.; Zhang, K.S. Discussion of cyclic plasticity and viscoplasticity of single crystal nickel-based superalloy in large strain analysis: Comparison of anisotropic macroscopic model and crystallographic model. Int. J. Mech. Sci. 2004, 46, 1157–1171. [Google Scholar]
- Pan, J. Rate sensitivity of plastic flow and Implications for Yield-Surface Vertices. Int. J. Solids Struct. 1983, 19, 973–987. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Elastic-plastic behaviour of polycrystalline metals and composites. Proc. R. Soc. A Math. Phys. 1970, 319, 247–272. [Google Scholar]
- Chang, Y.W.; Asaro, R.J. An experimental study of shear localization in aluminium-copper single crystals. Acta Metall. 1981, 29, 241–257. [Google Scholar] [CrossRef]
- Zhang, K.S.; Ju, J.W.; Li, Z.H.; Bai, Y.L.; Brocks, W. Micromechanics based fatigue life prediction of a polycrystalline metal applying crystal plasticity. Mech. Mater. 2015, 85, 16–37. [Google Scholar] [CrossRef]
- Zhang, K.S.; Shi, Y.K.; Ju, J.W. Grain-level statistical plasticity analysis on strain cycle fatigue of a FCC metal. Mech. Mater. 2013, 64, 76–90. [Google Scholar] [CrossRef]
- Xia, Z.; Zhang, Y.; Ellyin, F. A unified periodical boundary conditions for representative volume elements of composites and applications. Int. J. Solids Struct. 2003, 40, 1907–1921. [Google Scholar] [CrossRef]



| C | Si | Mn | P | S | Ni | Cr | W | Cu | V | Ti |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.31 | 1 | 1.09 | 0.008 | 0.002 | 1.55 | 1.07 | 0.001 | 0.04 | 0.01 | 0.0058 |
| 0.45% | 0.5% | 0.6% | 0.7% | 0.8% | 0.9% | |
|---|---|---|---|---|---|---|
| 8392/11280 | 6630/5920 | 2306/3095 | 1458/1405 | 647/728 | 590/530 | |
| Average | 9836 | 6275 | 2726 | 1432 | 698 | 560 |
| Elastic Constants | Material Parameters of the Crystal Viscoplastic Model | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GPa | GPa | GPa | MPa | MPa | MPa | GPa | MPa | s−1 | s−1 | |||||
| 0.9% | 276 | 207 | 138 | 320 | 380 | 80 | 3.2 | 30 | 0 | 0 | 0 | 0.001 | 1 | 200 |
| 0.8% | 276 | 207 | 138 | 320 | 345 | 80 | 4.6 | 100 | 0 | 0 | 0 | 0.001 | 1 | 200 |
| 0.7% | 276 | 207 | 138 | 285 | 300 | 80 | 6.3 | 100 | 0 | 0 | 0 | 0.001 | 1 | 200 |
| 0.6% | 276 | 207 | 138 | 270 | 280 | 80 | 9.8 | 90 | 0 | 0 | 0 | 0.001 | 1 | 200 |
| 0.5% | 276 | 207 | 138 | 320 | 340 | 80 | 11.7 | 120 | 0 | 0 | 0 | 0.001 | 1 | 200 |
| 0.45% | 294 | 220 | 147 | 310 | 320 | 80 | 16.6 | 210 | 0 | 0 | 0 | 0.001 | 1 | 200 |
| N/Nf | 0.01 | 0.1 | 0.2 | 0.3 | 0.5 | 0.6 | 0.8 | 0.95 |
| 1.49 | 1.53 | 1.55 | 1.56 | 1.57 | 1.58 | 1.58 | 1.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cen, C.-X.; Lu, D.-M.; Qin, D.-W.; Zhang, K.-S. Torsional Fatigue Life Prediction of 30CrMnSiNi2A Based on Meso-Inhomogeneous Deformation. Materials 2021, 14, 1846. https://doi.org/10.3390/ma14081846
Cen C-X, Lu D-M, Qin D-W, Zhang K-S. Torsional Fatigue Life Prediction of 30CrMnSiNi2A Based on Meso-Inhomogeneous Deformation. Materials. 2021; 14(8):1846. https://doi.org/10.3390/ma14081846
Chicago/Turabian StyleCen, Cheng-Xian, Da-Min Lu, Da-Wei Qin, and Ke-Shi Zhang. 2021. "Torsional Fatigue Life Prediction of 30CrMnSiNi2A Based on Meso-Inhomogeneous Deformation" Materials 14, no. 8: 1846. https://doi.org/10.3390/ma14081846
APA StyleCen, C.-X., Lu, D.-M., Qin, D.-W., & Zhang, K.-S. (2021). Torsional Fatigue Life Prediction of 30CrMnSiNi2A Based on Meso-Inhomogeneous Deformation. Materials, 14(8), 1846. https://doi.org/10.3390/ma14081846






