Linking the Electrical Conductivity and Non-Stoichiometry of Thin Film Ce1−xZrxO2−δ by a Resonant Nanobalance Approach
Abstract
1. Introduction
2. Theoretical Background, Samples Preparation and Experimental Methods
2.1. Defect Interactions in CeO2−δ and Ce1−xZrxO2−δ
2.2. Sample Preparation
2.3. Experimental Methods
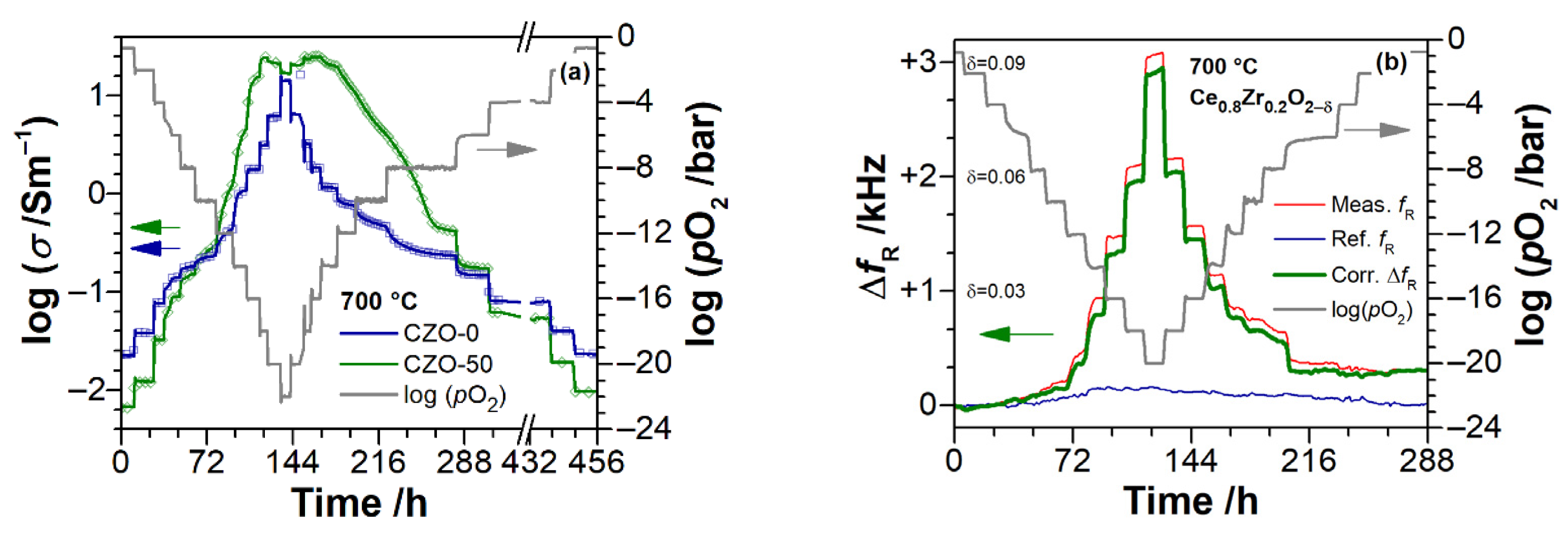
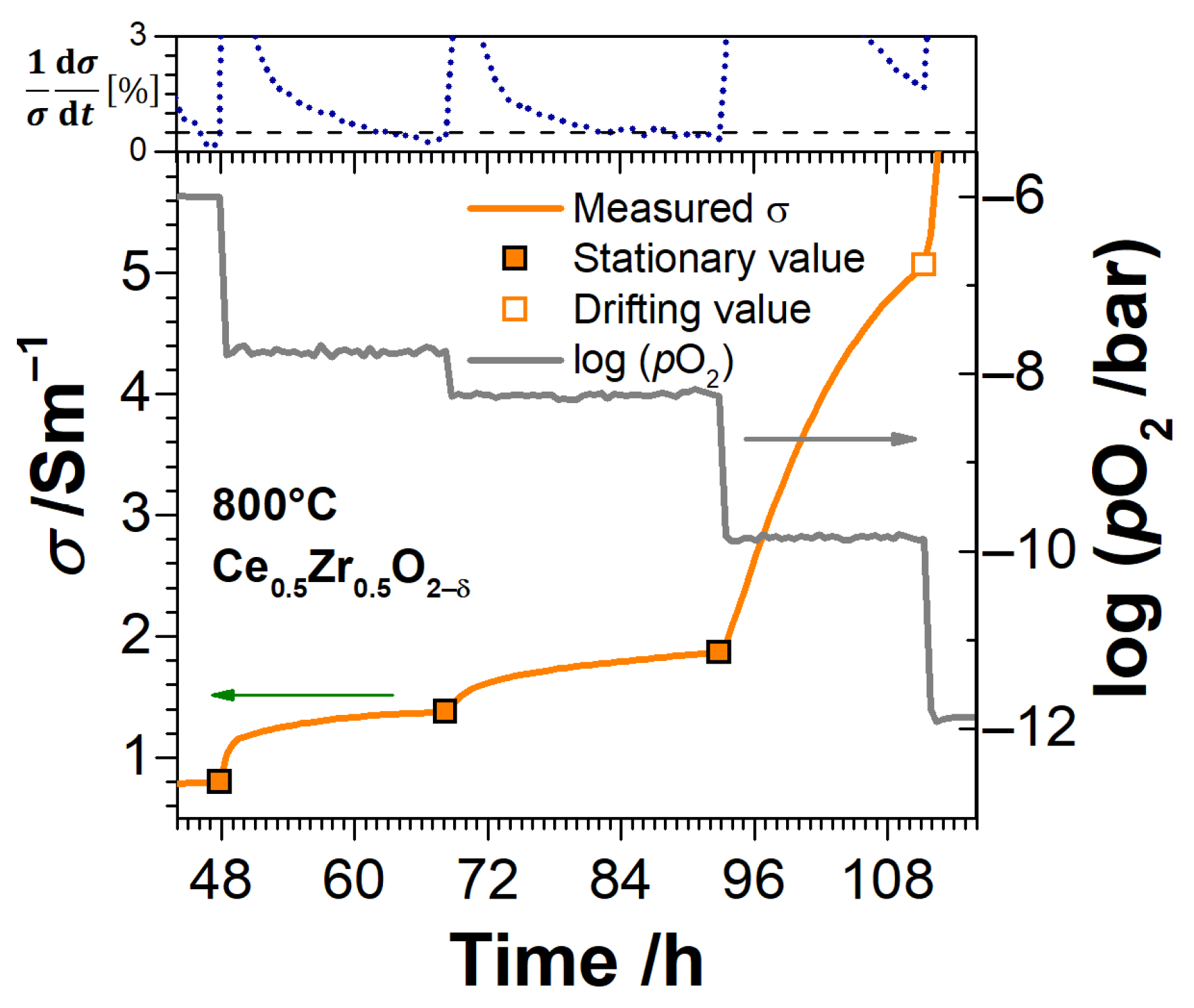
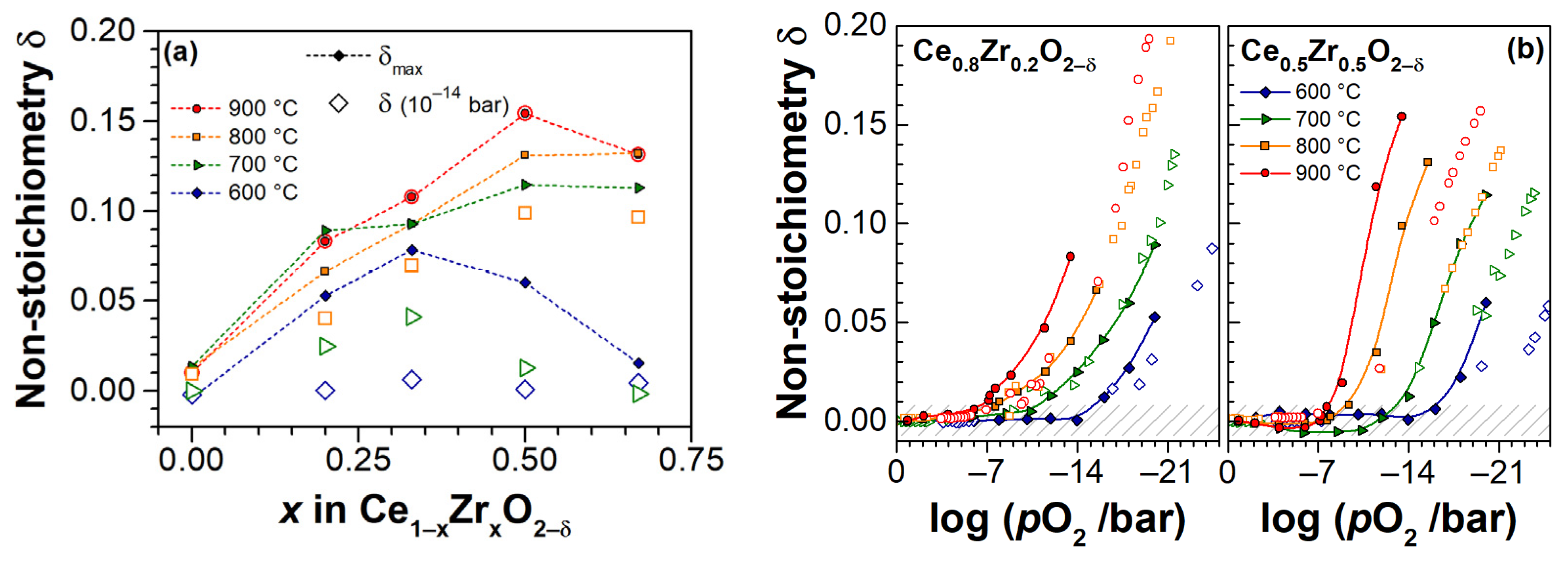
3. Experimental Results
3.1. Characterization of Ce1−xZrxO2 Specimens
3.2. Electrical Conductivity of Ce1−xZrxO2−δ Thin Films as a Function of Temperature
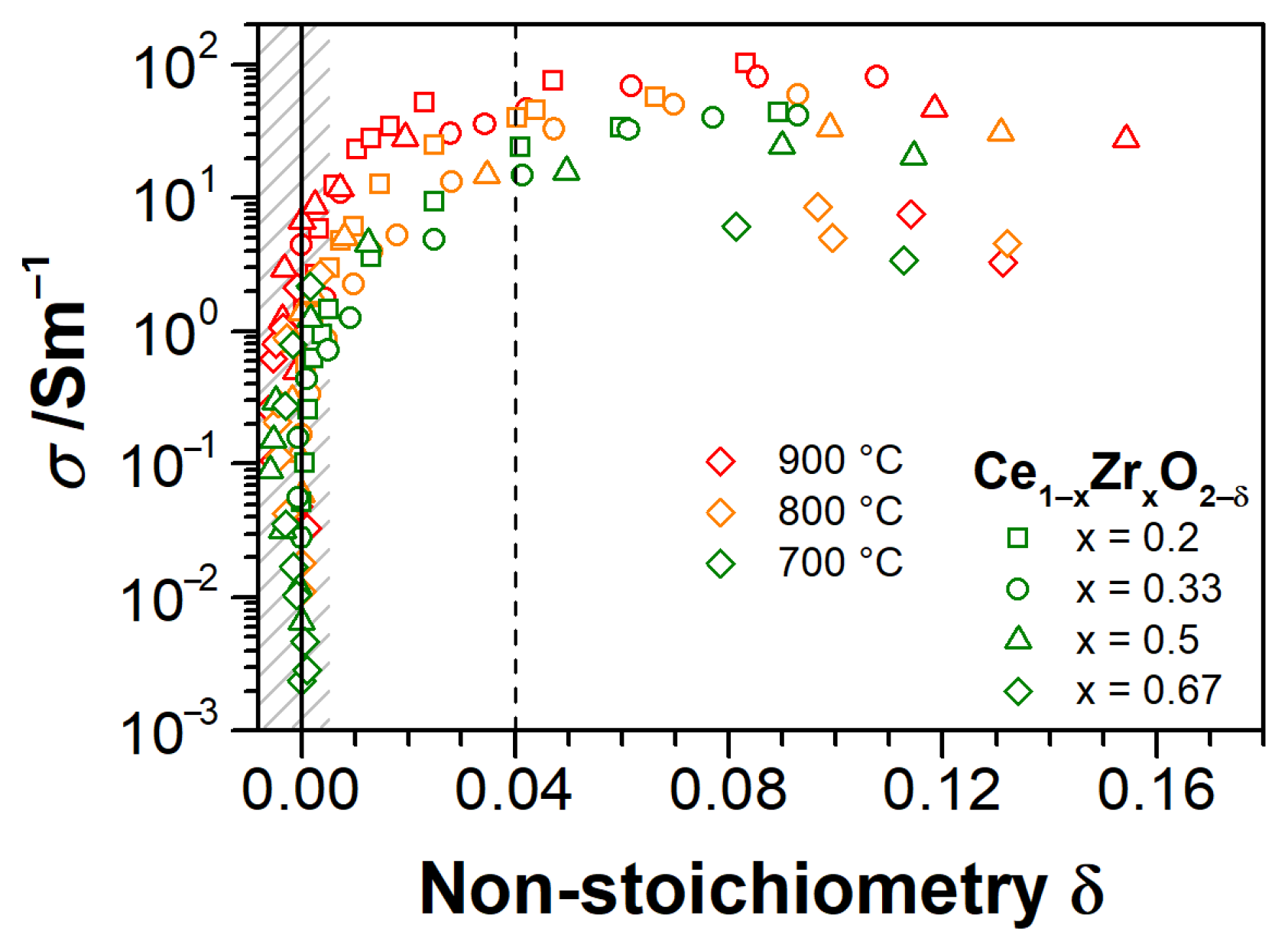
3.3. Electrical Conductivity and Non-Stoichiometry of Ce1−xZrxO2−δ in Reducing Atmosphere
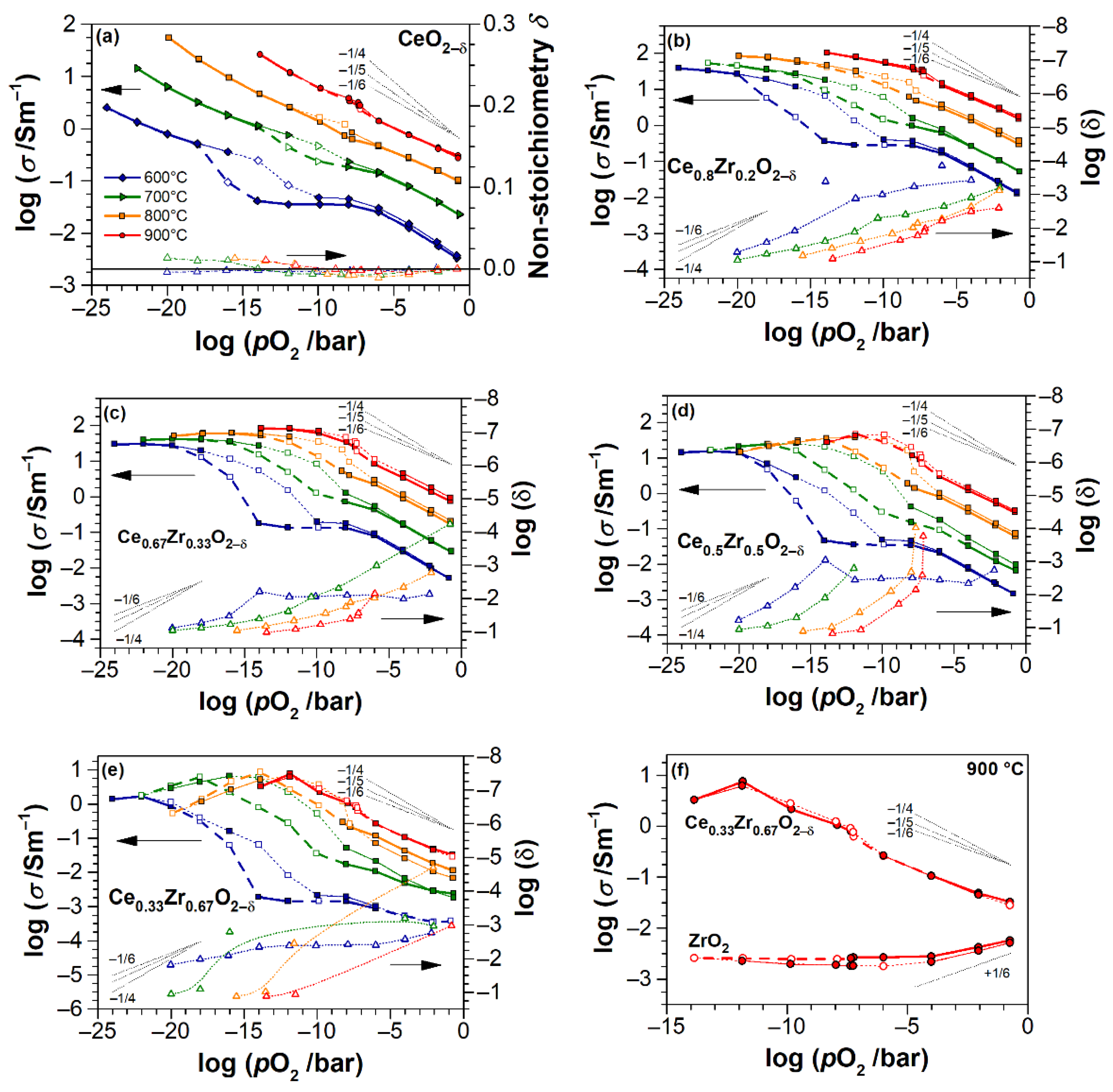
4. Discussion
4.1. Electrical Conductivity of ZrO2 Thin Films
4.2. Electrical Conductivity and Non-Stoichiometry of CeO2−δ Thin Films
4.3. Electrical Conductivity and Non-Stoichiometry of Ce1−xZrxO2−δ Thin Films
- Impurity-mediated conductivity at high pO2 ≥ 10−6 bar and 700 °C, governed by the electroneutrality condition ] = 2[], although with increasing temperature, the conductivity turns closer to a (pO2)−1/6-dependence with the electroneutrality condition [] = 2[].
- At intermediate pO2 (10−12–10−6 bar at 700 °C), the regime transits to [] = 2[], as indicated by the changing slope from −1/4 to −1/6, although the non-stoichiometry is still low (ca. 0.01).
- At further reduced conditions with pO2 between 10−18 and 10−12 bar at 700 °C, strong non-stoichiometry starts and the onset of defect interactions leads to (pO2)−1/4-dependence of conductivity. Complex interactions between Ce3+ cations and oxygen vacancies are assumed. The conductivity transits to [] = [] controlled regime, which is characterized by the formation of either singly ionized oxygen vacancies (Equation (3)) or dimers (Equation (4)).
- At lowest pO2 (<10−18 bar at 700 °C), the oxygen non-stoichiometry rapidly exceeds 0.04 (Figure 9), and [] ≥ [] holds. The saturation of δ and conductivity occurs, inferring complex defect interactions that eventually lead to transit through a maximum of conductivity for CZO with the largest Zr content and a positive slope of ca. +1/6 (p-type conductivity [32]). The latter can be attributed either to strong associations between univalent Ce interstitials and reduced Ce3+ or to a trapping of excess electrons by oxygen vacancies [57] (i.e., essentially the formation of dimer and trimer defect associates), both suppressing the electronic contribution to the conductivity.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taylor, K.C. Automobile Catalytic Converters. In Catalysis—Science and Technology; Anderson, J.R., Boudart, M., Eds.; Springer: Berlin, Germany, 1984; Volume 5, ISBN 978-3-642-69486-8. [Google Scholar]
- Trovarelli, A. Catalytic Properties of Ceria and CeO2-Containing Materials. Catal. Rev. Sci. Eng. 1996, 38, 439–520. [Google Scholar] [CrossRef]
- Di Monte, R.; Kašpar, J. On the role of oxygen storage in three-way catalysis. Top. Catal. 2004, 28, 47–57. [Google Scholar] [CrossRef]
- Lott, P.; Deutschmann, O. Lean-Burn Natural Gas Engines: Challenges and Concepts for an Efficient Exhaust Gas Aftertreatment System. Emiss. Control. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Tuller, H.L.; Nowick, A.S. Defect Structure and Electrical Properties of Nonstoichiometric CeO2 Single Crystals. J. Electrochem. Soc. 1979, 126, 209–217. [Google Scholar] [CrossRef]
- Mogensen, M.; Sammes, N.M.; Tompsett, G.A. Physical, chemical and electrochemical properties of pure and doped ceria. Solid State Ionics 2000, 129, 63–94. [Google Scholar] [CrossRef]
- Seifert, H.J.; Nerikar, P.; Lukas, H.L. Thermodynamic assessment of the Ce-O system in solid state from 60 to 67 mol. % O. Int. J. Mat. Res. 2006, 97, 744–752. [Google Scholar] [CrossRef]
- Tuller, H.L.; Nowick, A.S. Small polaron electron transport in reduced CeO2 single crystals. J. Phys. Chem. Solids 1977, 38, 859–867. [Google Scholar] [CrossRef]
- Kuhn, M.; Bishop, S.R.; Rupp, J.L.M.; Tuller, H.L. Structural characterization and oxygen nonstoichiometry of ceria-zirconia (Ce1-xZrxO2-δ) solid solutions. Acta Mater. 2013, 61, 4277–4288. [Google Scholar] [CrossRef]
- Schneider, D.; Gödickemeier, M.; Gauckler, L.J. Nonstoichiometry and Defect Chemistry of Ceria Solid Solutions. J. Electroceram. 1997, 1, 165–172. [Google Scholar] [CrossRef]
- Otake, T.; Yugami, H.; Yashiro, K.; Nigara, Y.; Kawada, T.; Mizusaki, J. Nonstoichiometry of Ce1-xYxO2-0.5x-δ (x=0.1, 0.2). Solid State Ionics 2003, 161, 181–186. [Google Scholar] [CrossRef]
- Panhans, M.A.; Blumenthal, R.N. A thermodynamic and electrical conductivity study of nonstoichiometric cerium dioxide. Solid State Lonics 1993, 60, 279–298. [Google Scholar] [CrossRef]
- Casselton, R.E.W. Electrical Conductivity of Ceria-Stabilized Zirconia. Phys. Status Solidi A 1970, 1, 787–794. [Google Scholar] [CrossRef]
- Izu, N.; Shin, W.; Matsubara, I.; Murayama, N. Resistive oxygen gas sensors using ceria-zirconia thick films. J. Ceram. Soc. Jpn. 2004, 112, 535–539. [Google Scholar] [CrossRef]
- Izu, N.; Oh-hori, N.; Shin, W.; Matsubara, I.; Murayama, N.; Itou, M. Response of resistive oxygen sensors using Ce1-xZr xO2 (x = 0.05, 0.10) thick films in propane combustion gas. Sens. Actuat. B Chem. 2008, 130, 105–109. [Google Scholar] [CrossRef]
- Izu, N.; Nishizaki, S.; Shin, W.; Itoh, T.; Nishibori, M.; Matsubara, I. Resistive Oxygen Sensor Using Ceria-Zirconia Sensor Material and Ceria-Yttria Temperature Compensating Material for Lean-Burn Engine. Sensors 2009, 9, 8884–8895. [Google Scholar] [CrossRef]
- Devaiah, D.; Reddy, L.H.; Park, S.-E.; Reddy, B.M. Ceria–zirconia mixed oxides: Synthetic methods and applications. Catal. Rev. 2018, 60, 177–277. [Google Scholar] [CrossRef]
- Schmitt, R.; Nenning, A.; Kraynis, O.; Korobko, R.; Frenkel, A.I.; Lubomirsky, I.; Haile, S.M.; Rupp, J.L.M. A review of defect structure and chemistry in ceria and its solid solutions. Chem. Soc. Rev. 2020, 49, 554–592. [Google Scholar] [CrossRef]
- Heinzmann, R.; Issac, I.; Eufinger, J.-P.; Ulbrich, G.; Lerch, M.; Janek, J.; Indris, S. Observing Local Oxygen Interstitial Diffusion in Donor-Doped Ceria by 17O NMR Relaxometry. J. Phys. Chem. C 2016, 120, 8568–8577. [Google Scholar] [CrossRef]
- Bishop, S.R.; Stefanik, T.S.; Tuller, H.L. Electrical conductivity and defect equilibria of Pr0.1Ce0.9O2-δ. Phys. Chem. Chem. Phys. 2011, 13, 10165–10173. [Google Scholar] [CrossRef] [PubMed]
- Sheth, J.; Chen, D.; Kim, J.; Bowman, W.J.; Crozier, P.A.; Tuller, H.L.; Misture, S.T.; Zdzieszynski, S.; Sheldon, B.W.; Bishop, S.R. Coupling of strain, stress, and oxygen non-stoichiometry in thin film Pr0.1Ce0.9O2-δ. Nanoscale 2016, 8, 16499–16510. [Google Scholar] [CrossRef]
- Schröder, S.; Fritze, H.; Bishop, S.; Chen, D.; Tuller, H.L. Thin-film nano-thermogravimetry applied to praseodymium-cerium oxide films at high temperatures. Appl. Phys. Lett. 2018, 112, 213502. [Google Scholar] [CrossRef]
- Aneggi, E.; Boaro, M.; Colussi, S.; De Leitenburg, C.; Trovarelli, A. Ceria-Based Materials in Catalysis: Historical Perspective and Future Trends. In Handbook on the Physics and Chemistry of Rare Earths; Bünzli, J.-C.G., Pecharsky, V.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 50, Chapter 289; pp. 209–242. ISBN 9780444638519. [Google Scholar] [CrossRef]
- Rood, S.; Eslava, S.; Manigrasso, A.; Bannister, C. Recent advances in gasoline three-way catalyst formulation: A review. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 936–949. [Google Scholar] [CrossRef]
- Lucid, A.K.; Keating, P.R.L.; Allen, J.P.; Watson, G.W. Structure and Reducibility of CeO2 Doped with Trivalent Cations. J. Phys. Chem. C 2016, 120, 23430–23440. [Google Scholar] [CrossRef]
- Rushton, M.J.D.; Chroneos, A. Impact of uniaxial strain and doping on oxygen diffusion in CeO2. Sci. Rep. 2014, 4, 6068. [Google Scholar] [CrossRef] [PubMed]
- Sugiura, M.; Ozawa, M.; Suda, A.; Suzuki, T.; Kanazawa, T. Development of Innovative Three-Way Catalysts Containing Ceria–Zirconia Solid Solutions with High Oxygen Storage/Release Capacity. Bull. Chem. Soc. Jpn. 2005, 78, 752–767. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, B.; Li, G.; Zhou, R. Application of Rare Earth Modified Zr-based Ceria-Zirconia Solid Solution in Three-Way Catalyst for Automotive Emission Control. Environ. Sci. Technol. 2010, 44, 3870–3875. [Google Scholar] [CrossRef]
- Liu, S.; Wu, X.; Weng, D.; Ran, R. Ceria-based catalysts for soot oxidation: A review. J. Rare Earths 2015, 33, 567–590. [Google Scholar] [CrossRef]
- Andriopoulou, C.; Harris, D.; Stephenson, H.; Efstathiou, A.M.; Boghosian, S. In Situ Raman Spectroscopy as a Tool for Discerning Subtle Structural Differences between Commercial (Ce,Zr)O2-Based OSC Materials of Identical Composition. Catalysts 2020, 10, 462. [Google Scholar] [CrossRef]
- Call, F.; Roeb, M.; Schmücker, M.; Bru, H.; Curulla-Ferre, D.; Sattler, C.; Pitz-Paal, R. Thermogravimetric Analysis of Zirconia-Doped Ceria for Thermochemical Production of Solar Fuel. Am. J. Anal. Chem. 2013, 4, 37–45. [Google Scholar] [CrossRef]
- Chen, D.; Cao, Y.; Weng, D.; Tuller, H.L. Defect and Transport Model of Ceria–Zirconia Solid Solutions: Ce0.8Zr0.2O2−δ—An Electrical Conductivity Study. Chem. Mater. 2014, 26, 5143–5150. [Google Scholar] [CrossRef]
- Hao, Y.; Yang, C.-K.; Haile, S.M. Ceria−Zirconia Solid Solutions (Ce1−xZrxO2−δ, x ≤ 0.2) for Solar Thermochemical Water Splitting: A Thermodynamic Study. Chem. Mater. 2014, 26, 6073–6082. [Google Scholar] [CrossRef]
- Eufinger, J.-P.; Daniels, M.; Schmale, K.; Berendts, S.; Ulbrich, G.; Lerch, M.; Wiemhöfer, H.-D.; Janek, J. The model case of an oxygen storage catalyst—Non-stoichiometry, point defects and electrical conductivity of single crystalline CeO2-ZrO2-Y2O3 solid solutions. Phys. Chem. Chem. Phys. 2014, 16, 25583–25600. [Google Scholar] [CrossRef]
- Chiodelli, G.; Flora, G.; Scagliotti, M. Electrical properties of the ZrO2–CeO2 system. Solid State Ionics 1996, 91, 109–121. [Google Scholar] [CrossRef]
- Yang, Z.; Woo, T.K.; Hermansson, K. Effects of Zr doping on stoichiometric and reduced ceria: A first-principles study. J. Chem. Phys. 2006, 124, 224704. [Google Scholar] [CrossRef] [PubMed]
- Grieshammer, S. Defect Interactions in the CeO2−ZrO2−Y2O3 Solid Solution. J. Phys. Chem. C 2017, 121, 15078–15084. [Google Scholar] [CrossRef]
- Onn, T.M.; Dai, S.; Chen, J.; Pan, X.; Graham, G.W.; Gorte, R.J. High-Surface Area Ceria-Zirconia Films Prepared by Atomic Layer Deposition. Catal. Lett. 2017, 147, 1464–1470. [Google Scholar] [CrossRef]
- Boyko, Y.I.; Biletskyi, V.I.; Bogdanov, V.V.; Vovk, R.V.; Khadzhai, G.Y.; Goulatis, I.L.; Chroneos, A. Enhanced oxygen diffusion in nano-structured ceria. J. Mater. Sci. Mater. Electron. 2018, 29, 4743–4748. [Google Scholar] [CrossRef]
- Melchionna, M.; Fornasiero, P. The role of ceria-based nanostructured materials in energy applications. Mater. Today 2014, 17, 349–357. [Google Scholar] [CrossRef]
- Gopal, C.B.; Haile, S.M. An electrical conductivity relaxation study of oxygen transport in samarium doped ceria. J. Mater. Chem. A 2014, 2, 2405–2417. [Google Scholar] [CrossRef]
- Bishop, S.R.; Marrocchelli, D.; Fang, W.; Amezawa, K.; Yashirod, K.; Watson, G.W. Reducing the chemical expansion coefficient in ceria by addition of zirconia. Energy Environ. Sci. 2013, 6, 1142–1146. [Google Scholar] [CrossRef]
- Bishop, S.R.; Nakamura, T.; Amezawa, K. Chemically-induced expansion of Zr0.2Ce0.8O2-δ. Solid State Ionics 2014, 261, 1–4. [Google Scholar] [CrossRef]
- Koettgen, J.; Grieshammer, S.; Hein, P.; Grope, B.O.H.; Nakayama, M.; Martin, M. Understanding the ionic conductivity maximum in doped ceria: Trapping and blocking. Phys. Chem. Chem. Phys. 2018, 20, 14291–14321. [Google Scholar] [CrossRef] [PubMed]
- Grieshammer, S.; Martin, M. Influence of defect interactions on the free energy of reduction in pure and doped ceria. J. Mater. Chem. A 2017, 5, 9241–9249. [Google Scholar] [CrossRef]
- De Souza, R.A. Limits to the rate of oxygen transport in mixed conducting oxides. J. Mater. Chem. A 2017, 5, 20334–20350. [Google Scholar] [CrossRef]
- Steiner, C.; Walter, S.; Malashchuk, V.; Hagen, G.; Kogut, I.; Fritze, H.; Moos, R. Determination of the Dielectric Properties of Storage Materials for Exhaust Gas Aftertreatment Using the Microwave Cavity Perturbation Method. Sensors 2020, 20, 6024. [Google Scholar] [CrossRef] [PubMed]
- Moos, R. Catalysts as Sensors—A Promising Novel Approach in Automotive Exhaust Gas Aftertreatment. Sensors 2010, 10, 6773–6787. [Google Scholar] [CrossRef]
- Steiner, C.; Malashchuk, V.; Kubinski, D.; Hagen, G.; Moos, R. Catalyst State Diagnosis of Three-Way Catalytic Converters Using Different Resonance Parameters—A Microwave Cavity Perturbation Study. Sensors 2019, 19, 3559. [Google Scholar] [CrossRef]
- Möller, R.; Votsmeier, M.; Onder, C.; Guzella, L.; Gieshoff, J. Is oxygen storage in three-way catalysts an equilibrium controlled process? Appl. Catal. B 2009, 91, 30–38. [Google Scholar] [CrossRef]
- Porat, O.; Tuller, H.L.; Lavik, E.B.; Chiang, Y.-M. Coulometric Titration Studies of Nonstoicmetric Nanocrystalline Ceria. Mat. Res. Soc. Symp. Proc. 1997, 457, 99–103. [Google Scholar] [CrossRef]
- Chiang, Y.-M.; Lavik, E.B.; Kosacki, I.; Tuller, H.L.; Ying, J.Y. Defect and transport properties of nanocrystalline CeO2-x. Appl. Phys. Lett. 1996, 69, 185–187. [Google Scholar] [CrossRef]
- Knauth, P.; Engel, J.; Bishop, S.R.; Tuller, H.L. Study of compaction and sintering of nanosized oxide powders by in situ electrical measurements and dilatometry: Nano CeO2-case study. J. Electroceram. 2015, 34, 82–90. [Google Scholar] [CrossRef]
- Hartmann, P.; Brezesinski, T.; Sann, J.; Lotnyk, A.; Eufinger, J.-P.; Kienle, L.; Janek, J. Defect Chemistry of Oxide Nanomaterials with High Surface Area: Ordered Mesoporous Thin Films of the Oxygen Storage Catalyst CeO2–ZrO2. ACS Nano 2013, 7, 2999–3013. [Google Scholar] [CrossRef] [PubMed]
- Boaro, M.; Trovarelli, A.; Hwang, J.-H.; Mason, T.O. Electrical and oxygen storage/release properties of nanocrystalline ceria–zirconia solid solutions. Solid State Ionics 2002, 147, 85–95. [Google Scholar] [CrossRef]
- Kosacki, I.; Suzuki, T.; Petrovsky, V.; Anderson, H.U. Electrical conductivity of nanocrystalline ceria and zirconia thin films. Solid State Ionics 2000, 136–137, 1225–1233. [Google Scholar] [CrossRef]
- Reidy, R.F.; Simkovich, G. Electrical conductivity and point defect behavior in ceria-stabilized zirconia. Solid State Ionics 1993, 62, 85–97. [Google Scholar] [CrossRef]
- Takacs, M.; Scheffe, J.R.; Steinfeld, A. Oxygen nonstoichiometry and thermodynamic characterization of Zr doped ceria in the 1573–1773 K temperature range. Phys. Chem. Chem. Phys. 2015, 17, 7813–7822. [Google Scholar] [CrossRef]
- Calès, B.; Baumard, J.F. Transport Properties And Defect Structure Of Nonstoichiometric Yttria Doped Ceria. J. Phys. Chem. Solids 1984, 45, 929–935. [Google Scholar] [CrossRef]
- Schaube, M.; Merkle, R.; Maier, J. Oxygen exchange kinetics on systematically doped ceria: A pulsed isotope exchange study. J. Mater. Chem. A 2019, 7, 21854–21866. [Google Scholar] [CrossRef]
- Shimonosono, T.; Hirata, Y.; Sameshima, S.; Horita, T. Electronic Conductivity of La-Doped Ceria Ceramics. J. Am. Ceram. Soc. 2005, 88, 2114–2120. [Google Scholar] [CrossRef]
- Kumar, A.; Rajdev, D.; Douglass, D.L. Effect of Oxide Defect Structure on the Electrical Properties of ZrO2. J. Am. Ceram. Soc. 1972, 55, 439–445. [Google Scholar] [CrossRef]
- Lee, J.-H.; Yoon, S.M.; Kim, B.-K.; Lee, H.-W.; Song, H.S. Electrical conductivity and defect structure of CeO2-ZrO2 mixed oxide. J. Mater. Sci. 2002, 37, 1165–1171. [Google Scholar] [CrossRef]
- Kwon, O.H.; Jang, C.; Lee, J.; Jeong, H.Y.; Kwon, Y.; Joo, J.H.; Kim, H. Investigation of the electrical conductivity of sintered monoclinic zirconia (ZrO2). Ceram. Int. 2017, 43, 8236–8245. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Hirata, T. Coloration in ceria-doped zirconia induced by reduction heat treatments. Solid State Commun. 1992, 84, 527–529. [Google Scholar] [CrossRef]
- Will, F.G.; DeLorenzi, H.G.; Janora, K.H. Conduction Mechanism of Single-Crystal Alumina. J. Am. Ceram. Soc. 1992, 75, 295–304. [Google Scholar] [CrossRef]
- Özkan, O.T.; Moulson, A.J. The electrical conductivity of single-crystal and polycrystalline aluminium oxide. J. Phys. D Appl. Phys. 1970, 3, 983–987. [Google Scholar] [CrossRef]
- Fritze, H. High-temperature bulk acoustic wave sensors. Meas. Sci. Technol. 2011, 22, 012002. [Google Scholar] [CrossRef]
- Tuller, H.L.; Fritze, H. High-Temperature Balance. U.S. Patent 6,370,955, 16 April 2002. [Google Scholar]
- Schulz, M.; Fritze, H.; Stenzel, C. Measurement and control of oxygen partial pressure at elevated temperatures. Sens. Actuators B Chem. 2013, 187, 503–508. [Google Scholar] [CrossRef]
- Schulz, M.; Brillo, J.; Stenzel, C.; Fritze, H. Oxygen partial pressure control for microgravity experiments. Solid State Ionics 2012, 225, 332–336. [Google Scholar] [CrossRef]
- Schneider, T.; Richter, D.; Doerner, S.; Fritze, H.; Hauptmann, P. Novel impedance interface for resonant high-temperature gas sensors. Sens. Actuators B Chem. 2005, 111–112, 187–192. [Google Scholar] [CrossRef]
- Suhak, Y.; Schulz, M.; Johnson, W.L.; Sotnikov, A.; Schmidt, H.; Fritze, H. Electromechanical properties and charge transport of Ca3TaGa3Si2O14 (CTGS) single crystals at elevated temperatures. Solid State Ionics 2018, 317, 221–228. [Google Scholar] [CrossRef]
- Seh, H.; Fritze, H.; Tuller, H.L. Defect chemistry of langasite III: Predictions of electrical and gravimetric properties and application to operation of high temperature crystal microbalance. J. Electroceram. 2007, 18, 139–147. [Google Scholar] [CrossRef]
- Sauerwald, J.; Richter, D.; Ansorge, E.; Schmidt, B.; Fritze, H. Langasite based miniaturized functional structures: Preparation, high-temperature properties and applications. Phys. Status Solidi A 2011, 208, 390–403. [Google Scholar] [CrossRef]
- Sauerbrey, G. Verwendung von Schwingquarzen zur Wägung dünner Schichten und zur Mikrowägung. Z. Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Varez, A.; Garcia-Gonzalez, E.; Sanz, J. Cation miscibility in CeO2–ZrO2 oxides with fluorite structure. A combined TEM, SAED and XRD Rietveld analysis. J. Mater. Chem. 2006, 16, 4249–4256. [Google Scholar] [CrossRef]
- Lamas, D.G.; Fuentes, R.O.; Fábregas, I.O.; Fernández De Rapp, M.E.; Lascalea, G.E.; Casanova, J.R.; Walsöe De Reca, N.E.; Craievich, A.F. Synchrotron X-ray diffraction study of the tetragonal-cubic phase boundary of nanocrystalline ZrO2-CeO2 synthesized by a gel-combustion process. J. Appl. Crystallogr. 2005, 38, 867–873. [Google Scholar] [CrossRef]
- Varez, A.; Garcia-Gonzalez, E.; Jolly, J.; Sanz, J. Structural characterization of Ce1-xZrxO2 (0 <= x <= 1) samples prepared at 1650 °C by solid state reaction. A combined TEM and XRD study. J. Eur. Ceram. Soc. 2007, 27, 3677–3682. [Google Scholar] [CrossRef]
- Wakita, T.; Yashima, M. In situ observation of the tetragonal-cubic phase transition in the CeZrO4 solid solution—A high-temperature neutron diffraction study. Acta Crystallogr. Sect. B Struct. Sci. 2007, 63, 384–389. [Google Scholar] [CrossRef]
- Jimenez, R.; Bucheli, W.; Varez, A.; Sanz, J. Humidity related low temperature conductivity hysteresis of Ce1-xZrxO2 (0 <= x <= 1) ceramics. Structural disorder relationship. Fuel Cells 2011, 11, 642–653. [Google Scholar] [CrossRef]
- Kishimoto, H.; Omata, T.; Otsuka-Yao-Matsuo, S.; Ueda, K.; Hosono, H.; Kawazoe, H. Crystal structure of metastable κ-CeZrO4 phase possessing an ordered arrangement of Ce and Zr ions. J. Alloys Compd. 2000, 312, 94–103. [Google Scholar] [CrossRef]
- Achary, S.N.; Sali, S.K.; Kulkarni, N.K.; Krishna, P.S.R.; Shinde, A.B.; Tyagi, A.K. Intercalation / Deintercalation of Oxygen: A Sequential Evolution of Phases in Ce2O3/CeO2−ZrO2 Pyrochlores. Chem. Mater. 2009, 21, 5848–5859. [Google Scholar] [CrossRef]
- Wyckoff, R.W.G. Cubic closest packed, ccp, structure. In Crystal Structures, 2nd ed.; Wyckoff, R.W.G., Ed.; Interscience Publishers: New York, NY, USA, 1963; Volume 1, pp. 7–83. ISBN 978-0470968604. [Google Scholar]
- Howard, C.J.; Hill, R.J.; Reichert, B.E. Structures of ZrO2 polymorphs at room temperature by high-resolution neutron powder diffraction. Acta Cryst. 1988, B44, 116–120. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, X.; Wang, X.; Yu, J.; Li, L. A review of zirconia-based solid electrolytes. Ionics 2016, 22, 2249–2262. [Google Scholar] [CrossRef]
- SITUS Technicals—Saphir. Available online: https://www.situs-tec.de/app/download/5812076315/Optischer+Saphir.pdf (accessed on 18 January 2021).
- Sameshima, S.; Kawaminami, M.; Hirata, Y. Thermal Expansion of Rare-Earth-Doped Ceria Ceramics. J. Ceram. Soc. Jpn. 2002, 110, 597–600. [Google Scholar] [CrossRef]
- Scardi, P.; Di Maggio, R.; Lutterotti, L.; Maistrelli, P. Thermal Expansion Anisotropy of Ceria-Stabilized Tetragonal Zirconia. J. Am. Ceram. Soc. 1992, 75, 2828–2832. [Google Scholar] [CrossRef]
- Er, D.; Li, J.; Cargnello, M.; Fornasiero, P.; Gorte, R.J.; Shenoya, V.B. A Model to Determine the Chemical Expansion in Non-Stoichiometric Oxides Based on the Elastic Force Dipole. J. Electrochem. Soc. 2014, 161, F3060–F3064. [Google Scholar] [CrossRef]
- Hwang, J.-H.; McLachlan, D.S.; Mason, T.O. Brick Layer Model Analysis of Nanoscale-to-Microscale Cerium Dioxide. J. Electroceram. 1999, 3, 7–16. [Google Scholar] [CrossRef]
- Migani, A.; Vayssilov, G.N.; Bromley, S.T.; Illas, F.; Neyman, K.M. Greatly facilitated oxygen vacancy formation in ceria nanocrystallites. Chem. Commun. 2010, 46, 5936–5938. [Google Scholar] [CrossRef]
- Rupp, J.L.M.; Gauckler, L.J. Microstructures and electrical conductivity of nanocrystalline ceria-based thin films. Solid State Ionics 2006, 177, 2513–2518. [Google Scholar] [CrossRef]
- Vest, R.W.; Tallan, N.M.; Tripp, W.C. Electrical Properties and Defect Structure of Zirconia: I, Monoclinic Phase. J. Am. Ceram. Soc. 1964, 47, 635–640. [Google Scholar] [CrossRef]
- Elm, M.T.; Hofmann, J.D.; Suchomski, C.; Janek, J.; Brezesinski, T. Ionic Conductivity of Mesostructured Yttria-Stabilized Zirconia Thin Films with Cubic Pore Symmetry—On the Influence of Water on the Surface Oxygen Ion Transport. ACS Appl. Mater. Interfaces 2015, 7, 11792–11801. [Google Scholar] [CrossRef]
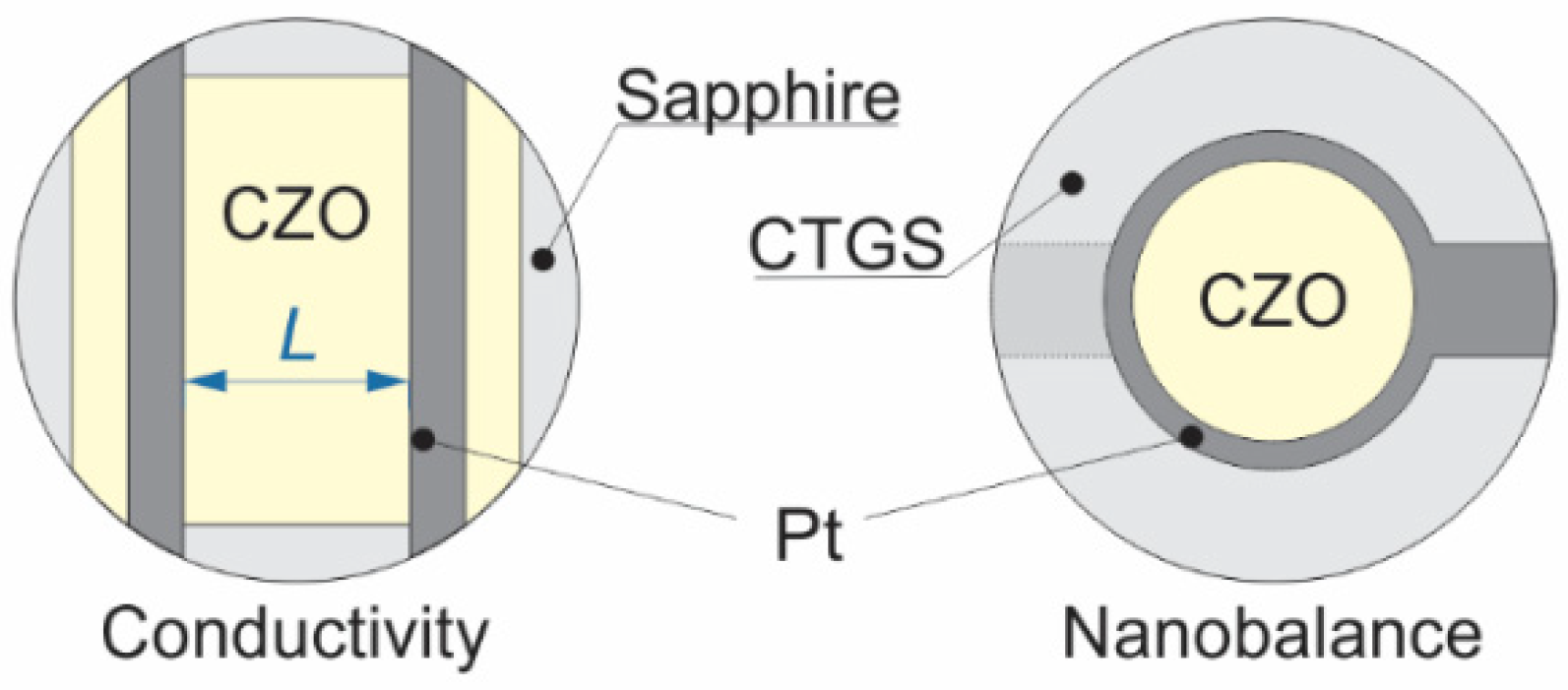
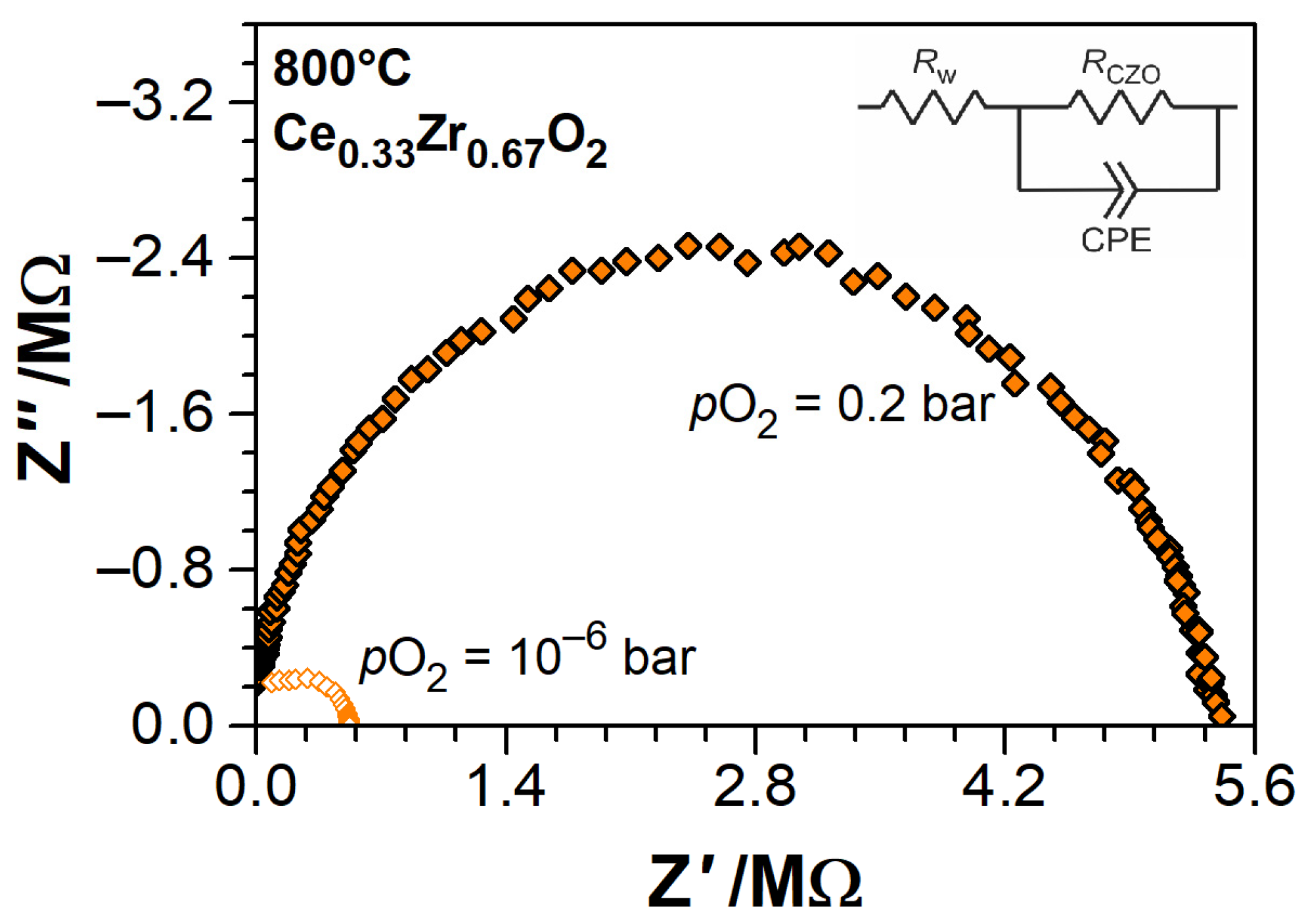
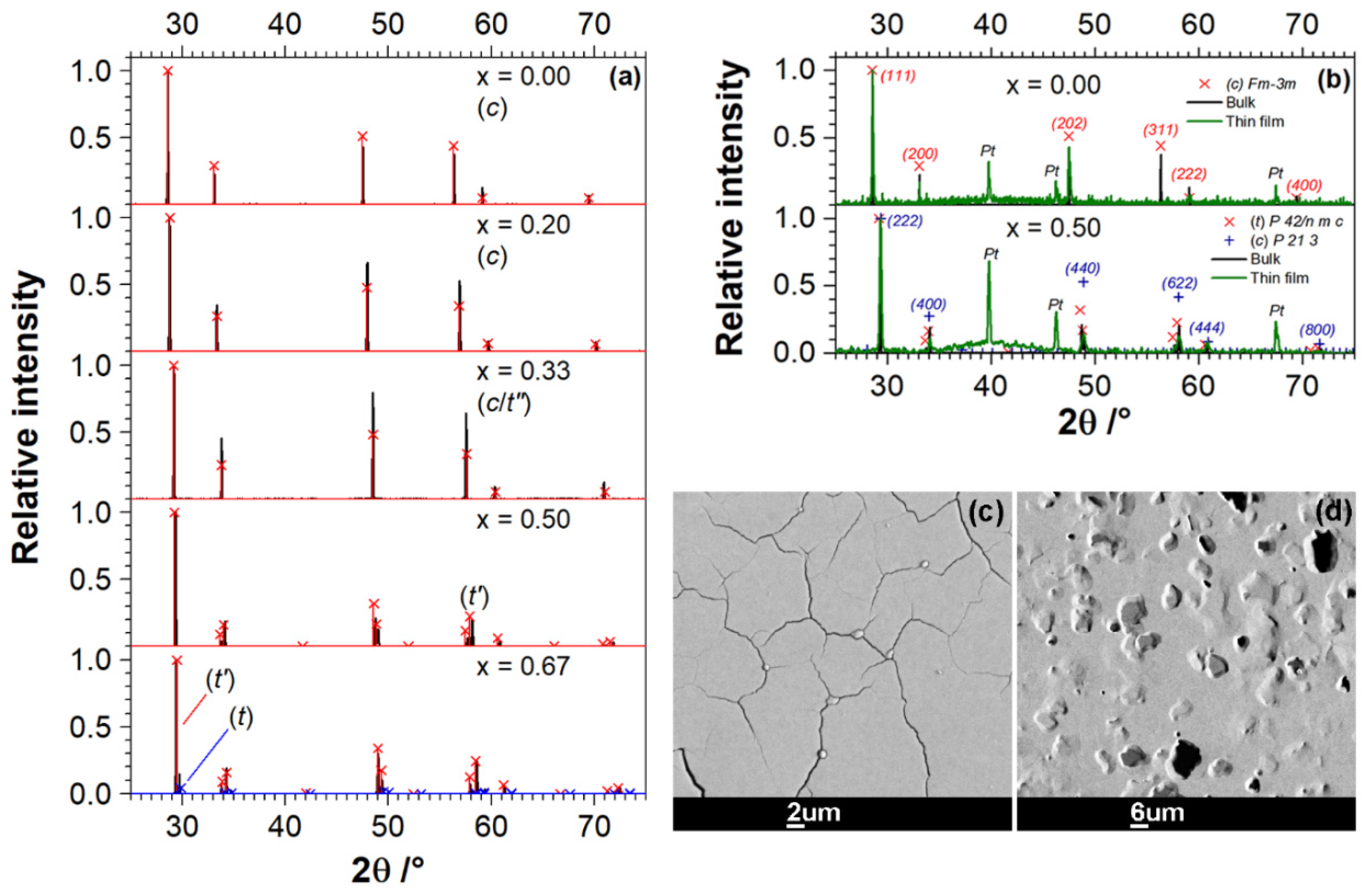
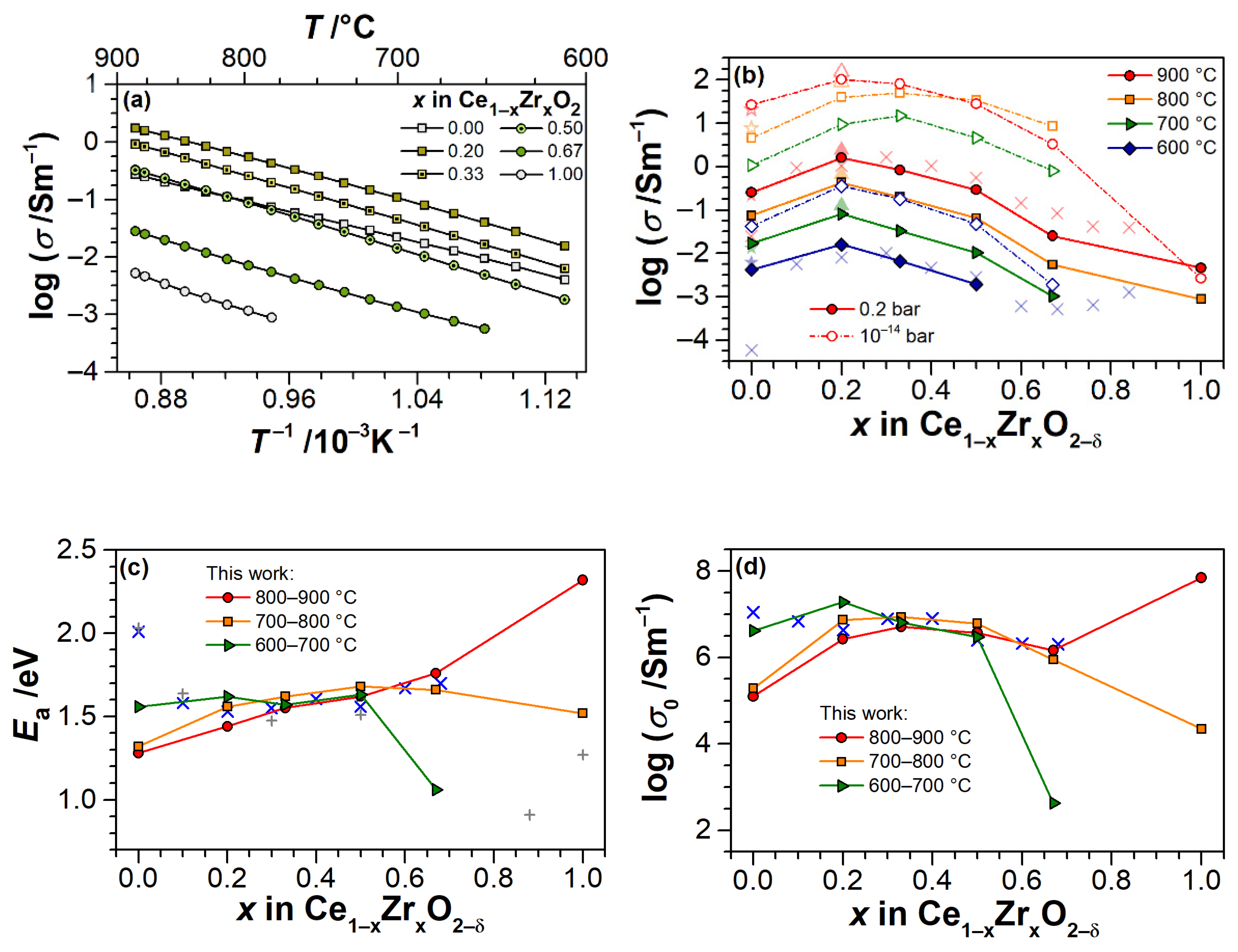
| Nominal ZrO2 Content in mol.% | Actual Composition (EDS) | Electrical Conductivity | Nanobalance Approach | |||
|---|---|---|---|---|---|---|
| t/µm | L/mm | dCTGS/µm | dCZO/µm | m0/µg | ||
| 0 | CeO1.91 * | 1.98 | 3.9 | 274.5 | 3.72 | 461.4 |
| 20 | Ce0.80Zr0.20O1.94 | 1.97 | 3.9 | 246.5 | 6.09 | 834.5 |
| 33 | Ce0.67Zr0.33O1.91 | 2.13 | 3.2 | 283.4 | 2.78 | 369.6 |
| 50 | Ce0.51Zr0.49O1.90 | 5.06 | 3.9 | 255.0 | 3.61 | 461.4 |
| 67 | Ce0.35Zr0.65O2.04 | 3.94 | 1.9 | 257.6 | 4.02 | 491.4 |
| 100 | n/a | 2.67 | 1.9 | n/a | n/a | n/a |
| Ref. CTGS | n/a | n/a | n/a | 294.5 | 0 | 0 |
| Sample | 600–700 °C (Air) | 600–700 °C (Argon) | 700–800 °C (Air) | 800–900 °C (Air) | 900–750 °C (Air, Cool.) | 750–600 °C (Air, Cool.) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ea | σ0 | Ea | σ0 | Ea | σ0 | Ea | σ0 | Ea | σ0 | Ea | σ0 | |
| CZO-0 | 1.56 | 4.2 | 1.33 | 0.53 | 1.32 | 0.191 | 1.28 | 0.125 | 1.32 | 0.151 | 1.42 | 0.5 |
| CZO-20 | 1.62 | 19 | 1.56 | 25.7 | 1.56 | 7.35 | 1.44 | 2.64 | 1.43 | 3.01 | 1.59 | 19 |
| CZO-33 | 1.57 | 6.42 | 1.60 | 22.8 | 1.62 | 8.62 | 1.55 | 5.12 | 1.57 | 6.2 | 1.63 | 12.6 |
| CZO-50 | 1.63 | 2.96 | 1.69 | 21.6 | 1.68 | 6.18 | 1.62 | 3.74 | 1.63 | 4.18 | 1.69 | 7.94 |
| CZO-67 | 1.06 * | 0.0004 * | 1.68 | 2.36 | 1.66 | 0.88 | 1.76 | 1.46 | 1.64 | 0.381 | 1.43 | 0.0368 |
| CZO-100 | - | - | - | - | 1.52 | 0.022 | 2.32 | 70.6 | 1.82 | 0.441 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kogut, I.; Wollbrink, A.; Steiner, C.; Wulfmeier, H.; El Azzouzi, F.-E.; Moos, R.; Fritze, H. Linking the Electrical Conductivity and Non-Stoichiometry of Thin Film Ce1−xZrxO2−δ by a Resonant Nanobalance Approach. Materials 2021, 14, 748. https://doi.org/10.3390/ma14040748
Kogut I, Wollbrink A, Steiner C, Wulfmeier H, El Azzouzi F-E, Moos R, Fritze H. Linking the Electrical Conductivity and Non-Stoichiometry of Thin Film Ce1−xZrxO2−δ by a Resonant Nanobalance Approach. Materials. 2021; 14(4):748. https://doi.org/10.3390/ma14040748
Chicago/Turabian StyleKogut, Iurii, Alexander Wollbrink, Carsten Steiner, Hendrik Wulfmeier, Fatima-Ezzahrae El Azzouzi, Ralf Moos, and Holger Fritze. 2021. "Linking the Electrical Conductivity and Non-Stoichiometry of Thin Film Ce1−xZrxO2−δ by a Resonant Nanobalance Approach" Materials 14, no. 4: 748. https://doi.org/10.3390/ma14040748
APA StyleKogut, I., Wollbrink, A., Steiner, C., Wulfmeier, H., El Azzouzi, F.-E., Moos, R., & Fritze, H. (2021). Linking the Electrical Conductivity and Non-Stoichiometry of Thin Film Ce1−xZrxO2−δ by a Resonant Nanobalance Approach. Materials, 14(4), 748. https://doi.org/10.3390/ma14040748






