Glass Transition Behavior of Wet Polymers
Abstract
1. Introduction
2. Experimental Methods
2.1. Material Synthesis
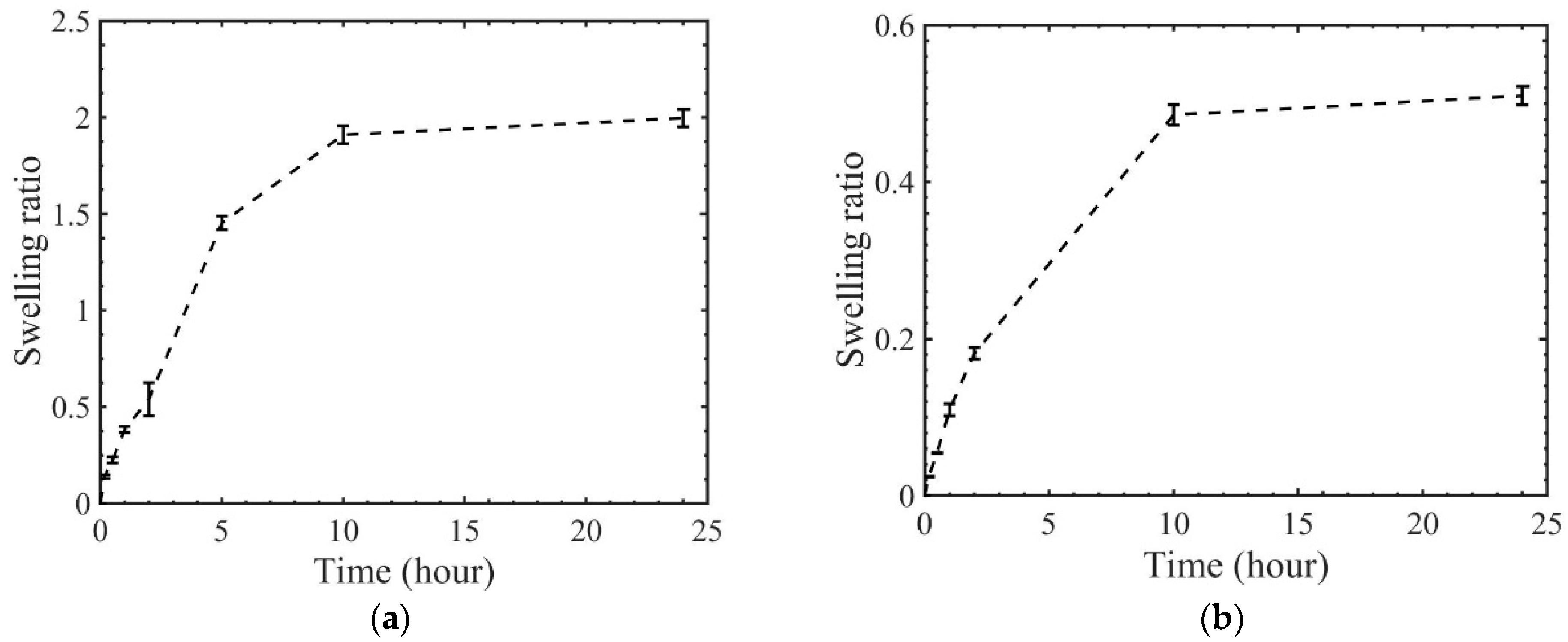
2.2. Treatment by IPA
2.3. Dynamic Temperature Sweep Tests
2.4. Dynamic Frequency Sweep Tests
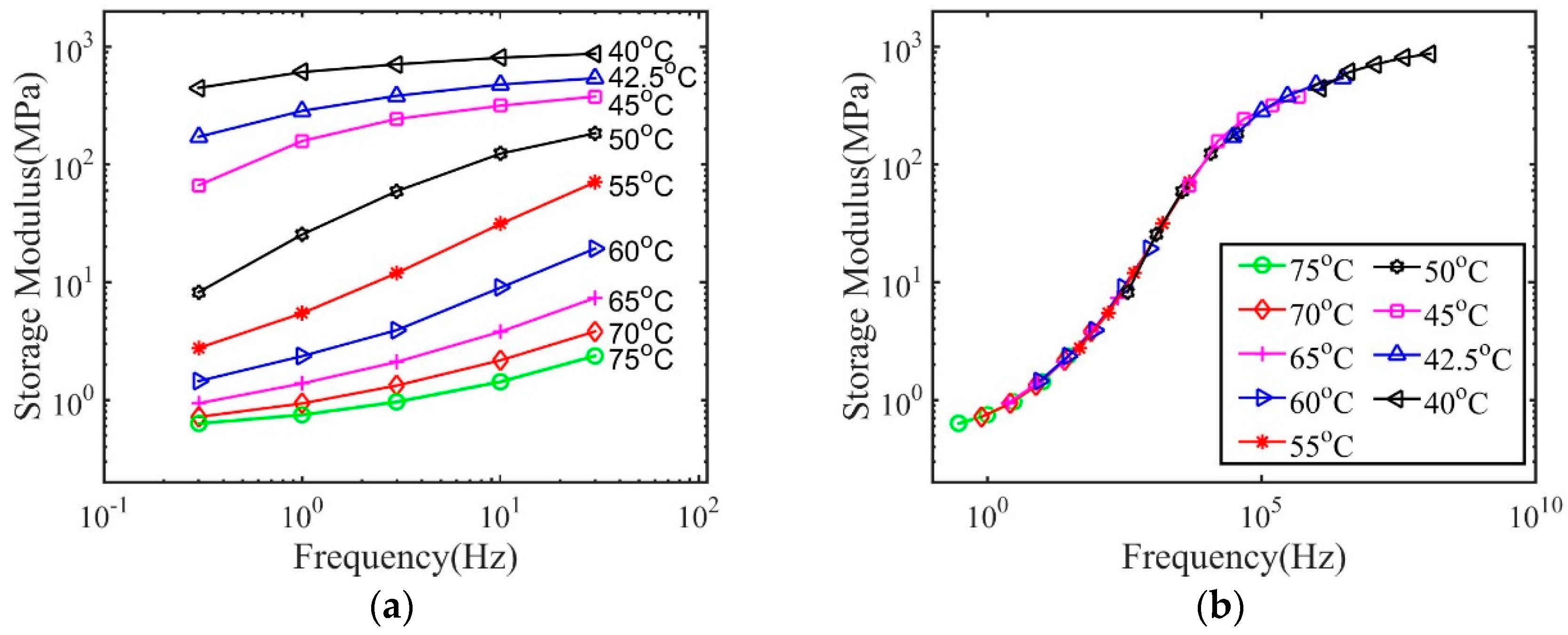
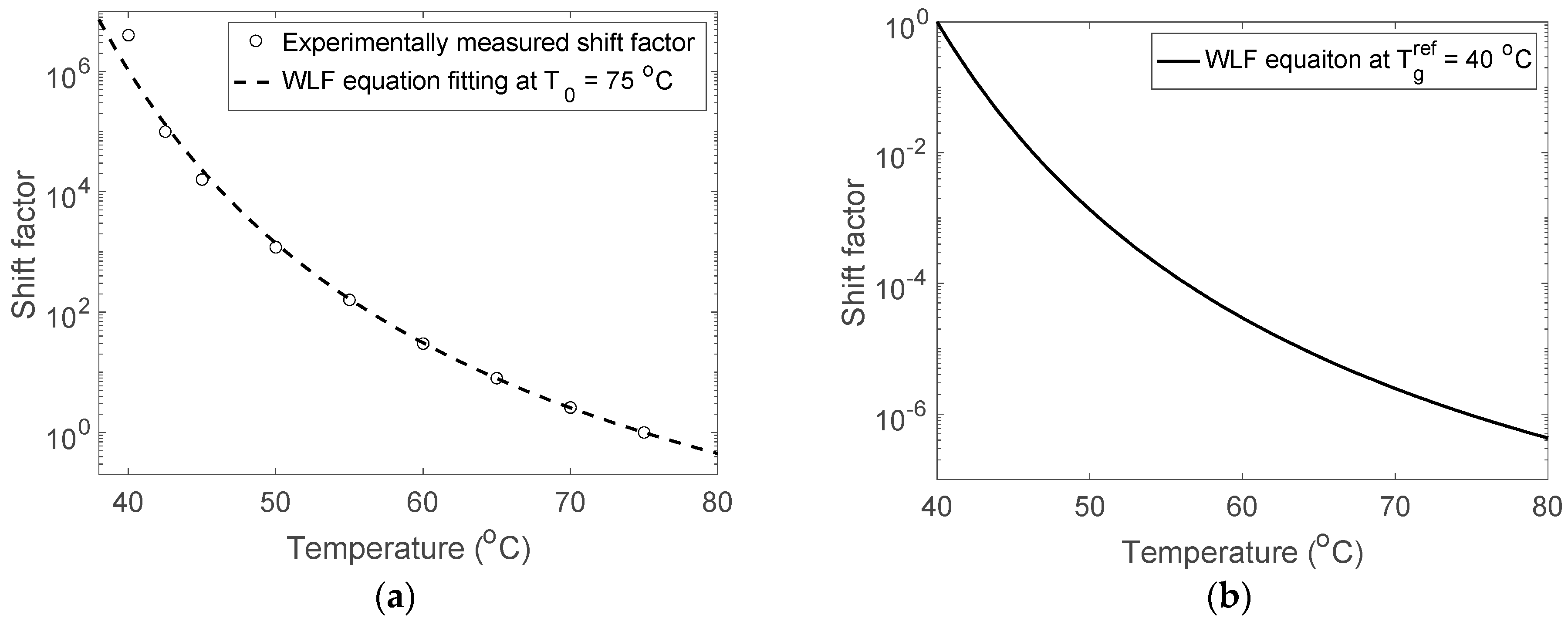
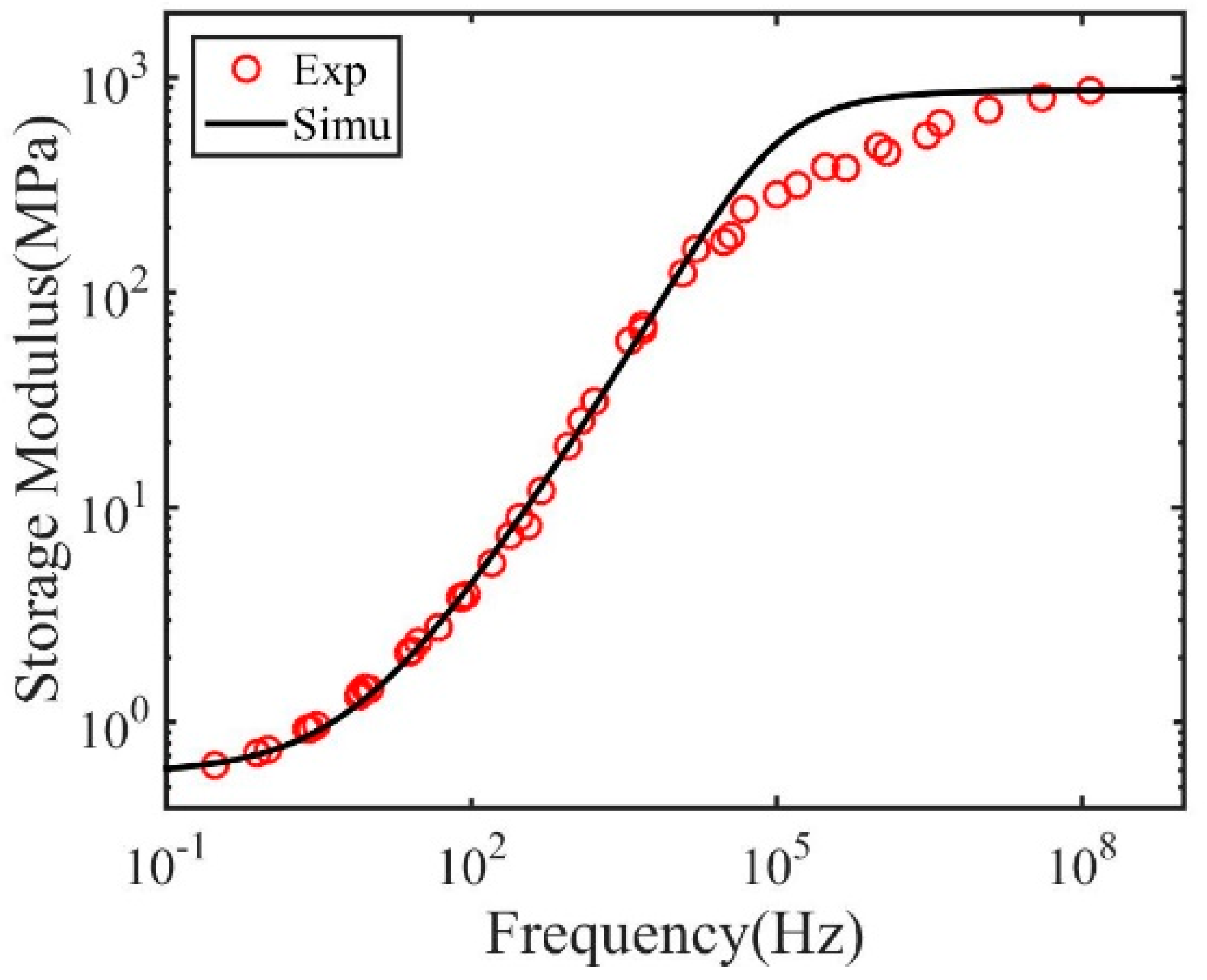
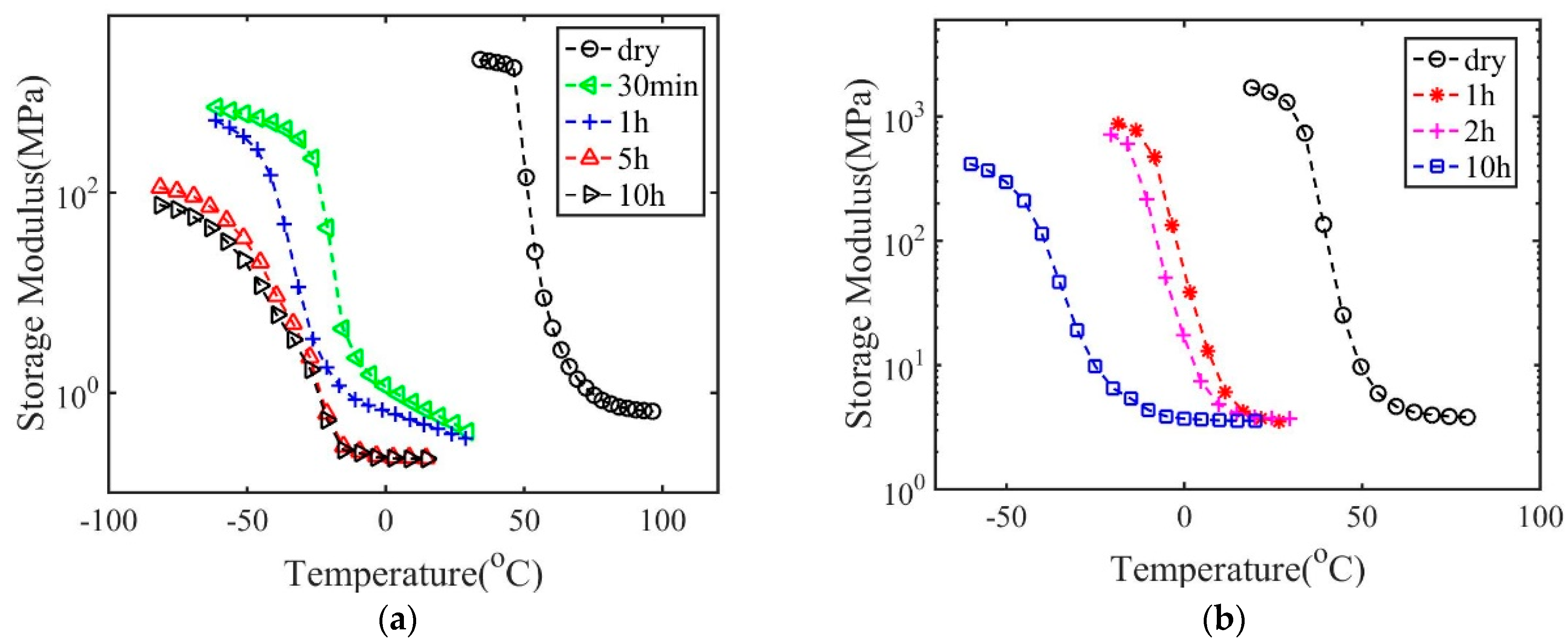
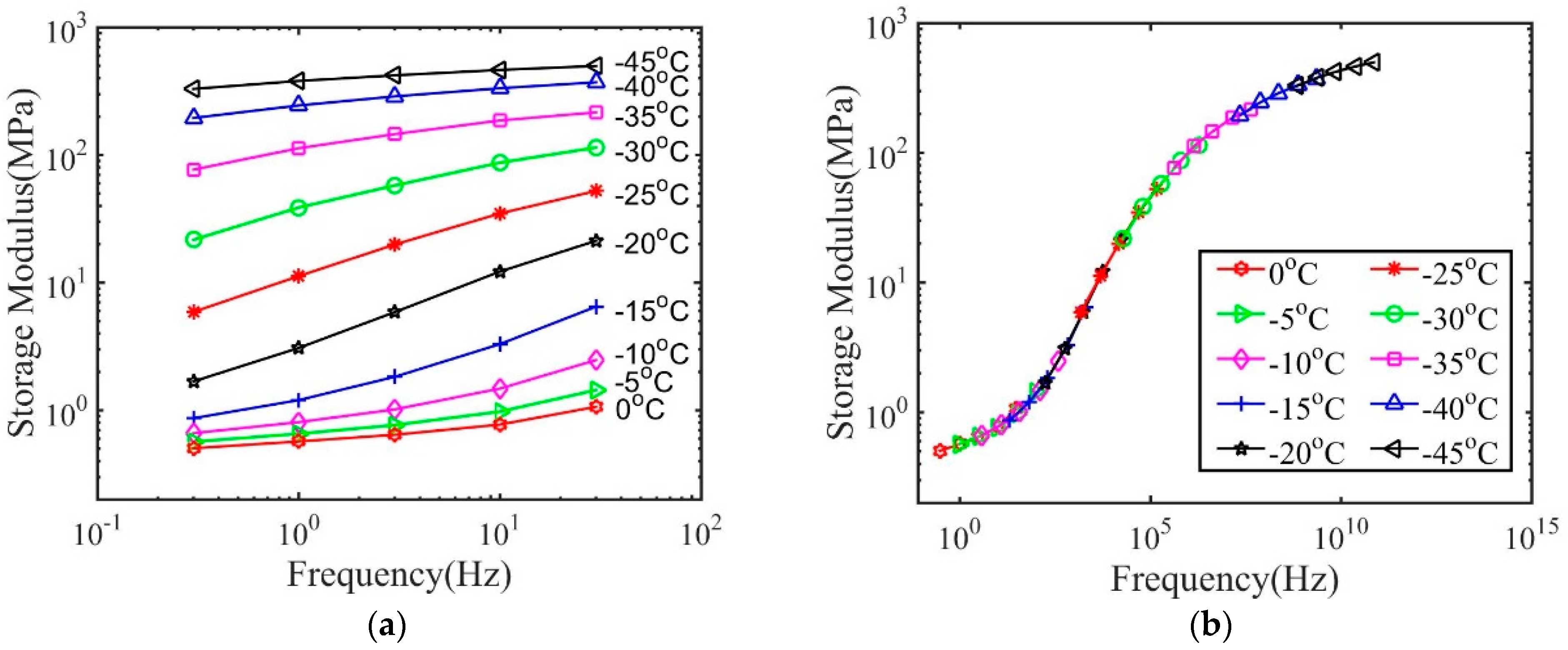
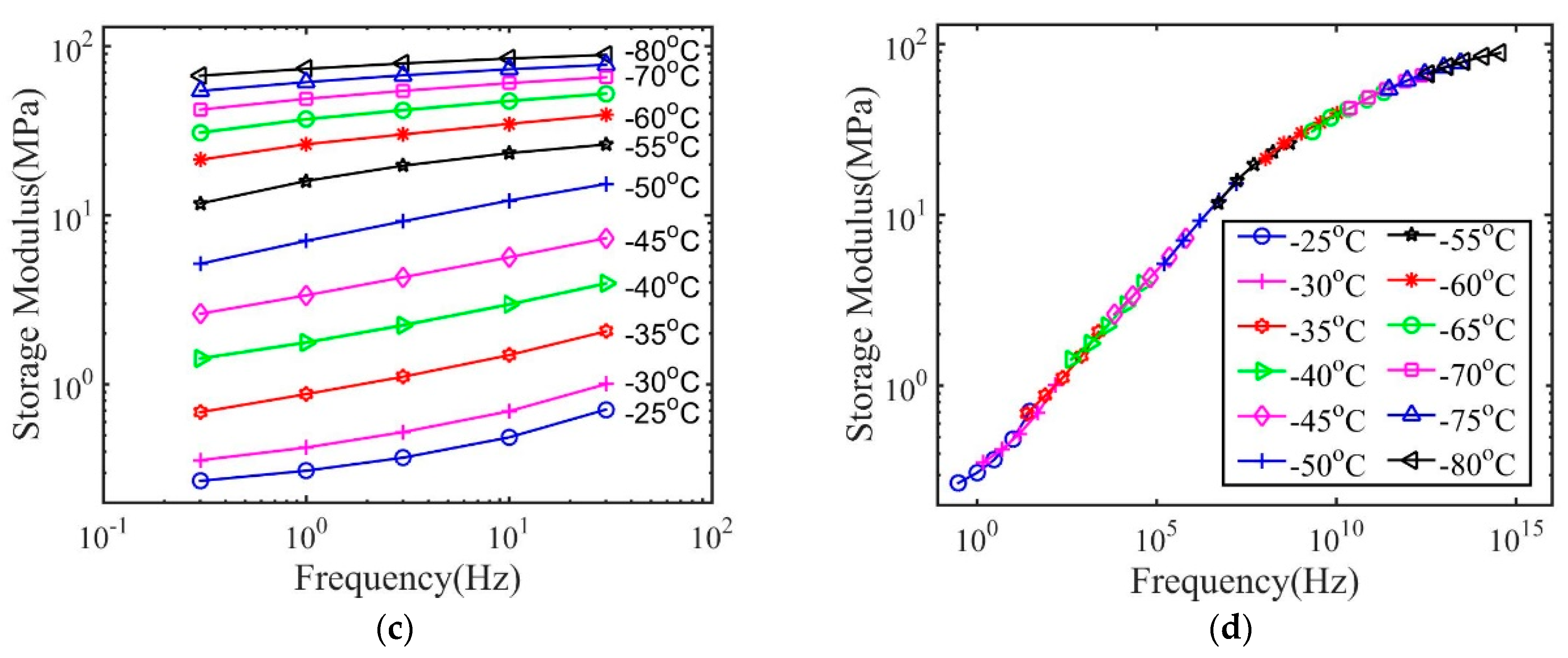
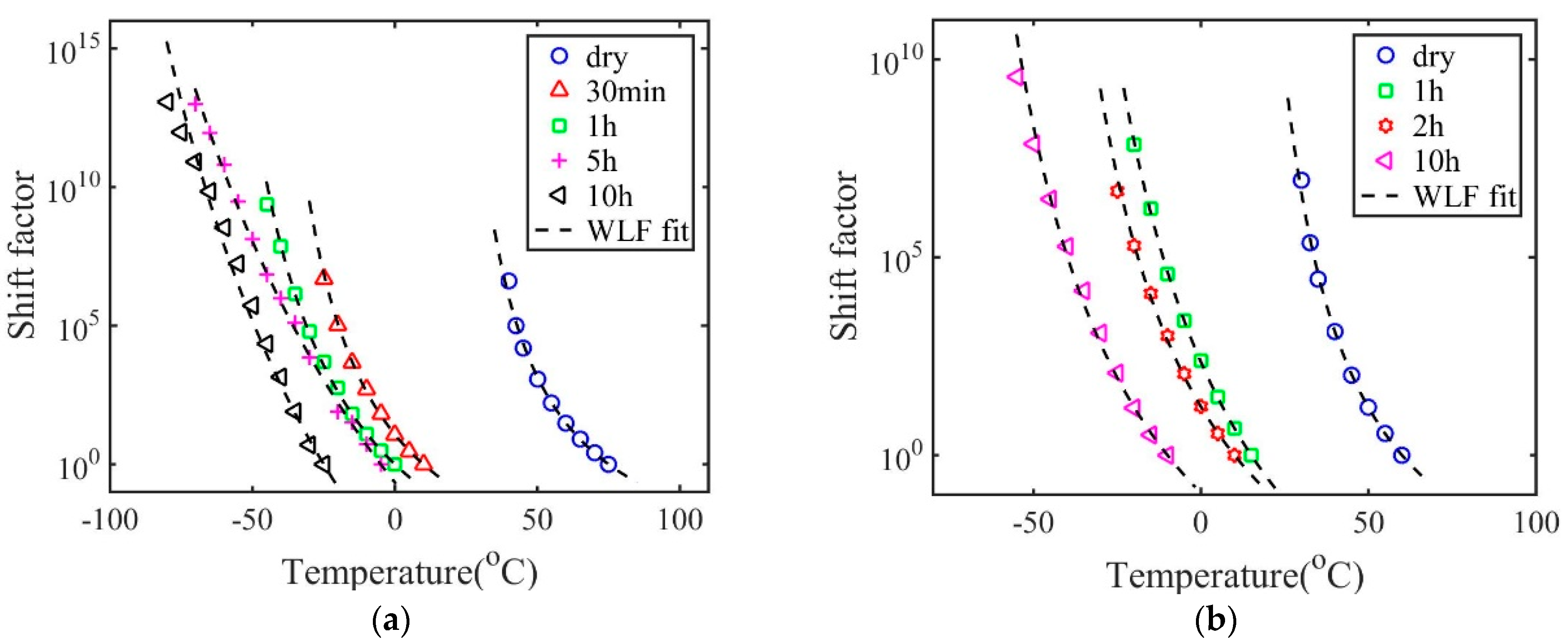
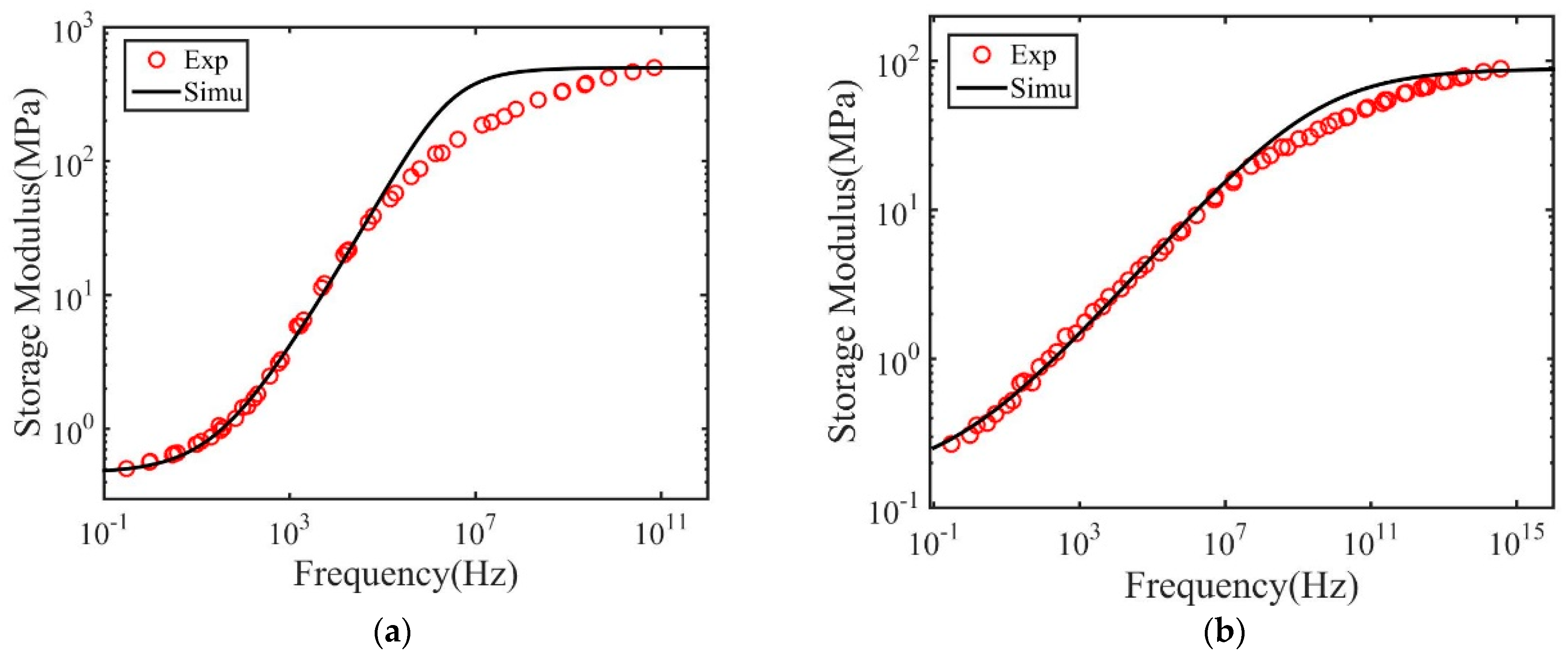
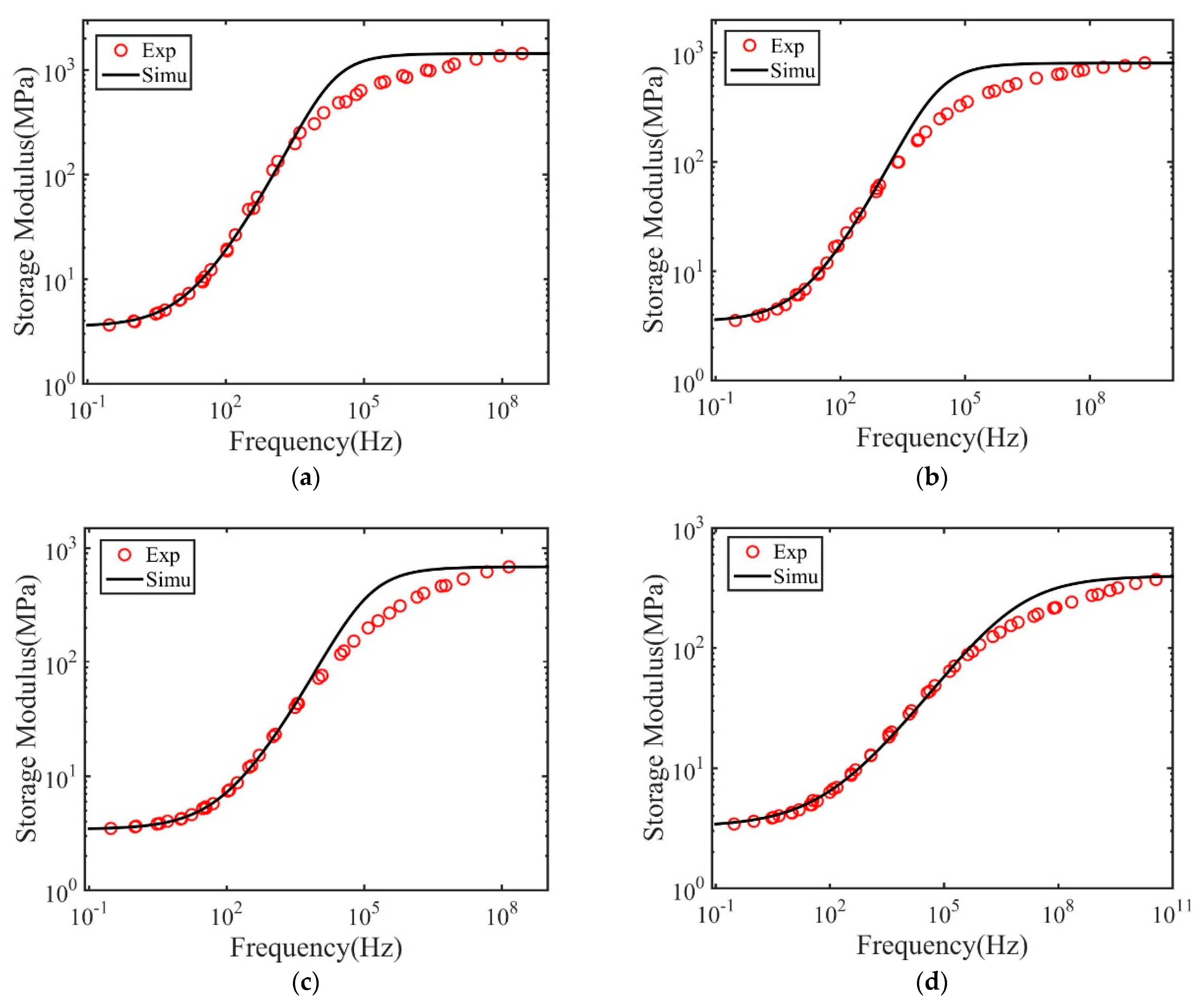
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luis de la Fuente, J. An analysis of the thermal aging behaviour in high-performance energetic composites through the glass transition temperature. Polym. Degrad. Stabil. 2009, 94, 664–669. [Google Scholar] [CrossRef]
- Guo, Y.F.; Lv, Z.Y.; Huo, Y.R.; Sun, L.J.; Chen, S.; Liu, Z.H.; He, C.L.; Bi, X.P.; Fan, X.Q.; You, Z.W. A biodegradable functional water-responsive shape memory polymer for biomedical applications. J. Mat. Chem. B 2019, 7, 123–132. [Google Scholar] [CrossRef]
- Yang, B.; Huang, W.M.; Li, C.; Lee, C.M.; Li, L. On the effects of moisture in a polyurethane shape memory polymer. Smart Mater. Struct. 2004, 13, 191–195. [Google Scholar] [CrossRef]
- Huang, W.M.; Yang, B.; An, L.; Li, C.; Chan, Y.S. Water-driven programmable polyurethane shape memory polymer: Demonstration and mechanism. Appl. Phys. Lett. 2005, 86, 114105. [Google Scholar] [CrossRef]
- Xiao, R.; Zhang, C.; Gou, X.; Huang, W.M. Tunable shape-memory behaviors in amorphous polymers through bound solvent. Mater. Lett. 2017, 209, 131–133. [Google Scholar] [CrossRef]
- Zhang, H.; Düring, L.; Kovacs, G.; Yuan, W.; Niu, X.; Pei, Q. Interpenetrating polymer networks based on acrylic elastomers and plasticizers with improved actuation temperature range. Polym. Int. 2010, 59, 384–390. [Google Scholar] [CrossRef]
- Simon, P.P.; Ploehn, H.J. Modeling the effect of plasticizer on the viscoelastic response of crosslinked polymers using the tube-junction model. J. Rheol. 2000, 44, 169–183. [Google Scholar] [CrossRef][Green Version]
- Dimarzio, E.A.; Gibbs, H.J. Molecular interpretation of glass temperature depression by plasticizers. J. Polym. Sci. 1963, 1, 1417–1428. [Google Scholar] [CrossRef]
- Vieira, M.G.A.; da Silva, M.A.; dos Santos, L.O.; Beppu, M.M. Natural-based plasticizers and biopolymer films: A review. Eur. Polym. J. 2011, 47, 254–263. [Google Scholar] [CrossRef]
- Da Silva, M.A.; Vieira, M.G.A.; Macumoto, A.C.G.; Beppu, M.M. Polyvinylchloride (PVC) and natural rubber films plasticized with a natural polymeric plasticizer obtained through polyesterification of rice fatty acid. Polym. Test. 2011, 30, 478–484. [Google Scholar] [CrossRef]
- Kawai, K.; Hagura, Y. Discontinuous and heterogeneous glass transition behavior of carbohydrate polymer-plasticizer systems. Carbohydr. Polym. 2012, 89, 836–841. [Google Scholar] [CrossRef] [PubMed]
- Xiao, R.; Guo, J.; Nguyen, T.D. Modeling the multiple shape memory effect and temperature memory effect in amorphous polymers. RSC Adv. 2015, 5, 416–423. [Google Scholar] [CrossRef]
- Lv, H.; Leng, J.; Liu, Y.; Du, S. Shape-memory polymer in response to solution. Adv. Eng. Mater. 2008, 10, 592–595. [Google Scholar] [CrossRef]
- Boyle, A.J.; Weems, A.C.; Hasan, S.M.; Nash, L.D.; Monroe, M.B.B.; Maitland, D.J. Solvent stimulated actuation of polyurethane-based shape memory polymer foams using dimethyl sulfoxide and ethanol. Smart Mater. Struct. 2016, 25, 075014. [Google Scholar] [CrossRef] [PubMed]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley and Sons: New York, NY, USA, 1980. [Google Scholar]
- Xiao, R.; Choi, J.; Lakhera, N.; Yakacki, C.M.; Frick, C.P.; Nguyen, T.D. Modeling the glass transition of amorphous networks for shape-memory behavior. J. Mech. Phys. Solids 2013, 61, 1612–1635. [Google Scholar] [CrossRef]
- Xiao, R.; Sun, H.G.; Chen, W. An equivalence between generalized Maxwell model and fractional Zener model. Mech. Mater. 2016, 100, 148–153. [Google Scholar] [CrossRef]
- Haupt, P.; Lion, A.; Backhaus, E. On the dynamic behaviour of polymers under finite strains: Constitutive modelling and identification of parameters. Int. J. Solids Struct. 2000, 37, 3633–3646. [Google Scholar] [CrossRef]
- Zielinski, J.M.; Duda, J.L. Predicting polymer solvent diffusion-coefficients using free-volume theory. AIChE J. 1992, 38, 405–415. [Google Scholar] [CrossRef]
- Vrentas, J.S.; Duda, J.L. A free-volume interpretation of influence of glass-transition on diffusion in amorphous polymers. J. Appl. Polym. Sci. 1978, 22, 2325–2339. [Google Scholar] [CrossRef]
- Yildiz, M.E.; Kokini, J.L. Determination of Williams-Landel-Ferry constants for a food polymer system: Effect of water activity and moisture content. J. Rheol. 2001, 45, 903–912. [Google Scholar] [CrossRef]
- Kelley, F.N.; Bueche, F. Viscosity and glass temperature relations for polymer-diluent systems. J. Polym. Sci. 1961, 50, 549–556. [Google Scholar] [CrossRef]
- Losi, G.U.; Knauss, W.G. Free volume theory and nonlinear thermoviscoelasticity. Polym. Eng. Sci. 1992, 32, 542–557. [Google Scholar] [CrossRef]
- Chang, F.C.; Lam, F.; Kadla, J.F. Application of time–temperature–stress superposition on creep of wood–plastic composites. Mech. Time Depend. Mater. 2013, 17, 427–437. [Google Scholar] [CrossRef]
- Maidannyk, V.A.; Roos, Y.H. Modification of the WLF model for characterization of the relaxation time-temperature relationship in trehalose-whey protein isolate systems. J. Food Eng. 2016, 188, 21–31. [Google Scholar] [CrossRef]
- Okumura, D.; Kawabata, H.; Chester, S.A. A general expression for linearized properties of swollen elastomers undergoing large deformations. J. Mech. Phys. Solids 2020, 135, 103805. [Google Scholar] [CrossRef]
- Wu, C.; Wei, C.; Guo, W.; Wu, C. Dynamic mechanical properties of acrylic rubber blended with phenolic resin. J. Appl. Polym. Sci. 2008, 109, 2065–2070. [Google Scholar] [CrossRef]
- Lee, H.N.; Riggleman, R.A.; de Pablo, J.J.; Ediger, M.D. Deformation-induced mobility in polymer glasses during multistep creep experiments and simulations. Macromolecules 2009, 42, 4328–4336. [Google Scholar] [CrossRef]
- Dai, L.; Tian, C.; Xiao, R. Modeling the thermo-mechanical behavior and constrained recovery performance of cold-programmed amorphous shape-memory polymers. Int. J. Plast. 2020, 127, 102654. [Google Scholar] [CrossRef]
- Guo, J.; Li, Z.; Long, J.; Xiao, R. Modeling the effect of physical aging on the stress response of amorphous polymers based on a two-temperature continuum theory. Mech. Mater. 2020, 143, 103335. [Google Scholar] [CrossRef]
- Shi, Q.; Xiao, R.; Yang, H.; Lei, D. Effects of physical aging on thermomechanical behaviors of poly (ethylene terephthalate)-glycol (PETG). Polym. Plast. Technol. Mater. 2020, 59, 835–846. [Google Scholar] [CrossRef]
- Lu, H.B.; Wang, X.D.; Hossain, M.; Fu, Y.Q. A Methodology of Hydrodynamic Complexity in Topologically Hyper-Branched Polymers Undergoing Hierarchical Multiple Relaxations. Macromol. Chem. Phys. 2020, 15, 2000052. [Google Scholar] [CrossRef]
- Liao, Z.S.; Hossain, M.; Yao, X.H.; Navaratne, R.; Chagnon, G. A comprehensive thermo-viscoelastic experimental investigation of Ecoflex polymer. Polym. Test. 2020, 86, 106478. [Google Scholar] [CrossRef]

| Name of Samples | The Mass Ratio (tBA:PEGDMA:DMPA) |
|---|---|
| Acrylate-based polymer with 2 wt.% crosslink density | 98:2:0.2 |
| Acrylate-based polymer with 20 wt.% crosslink density | 80:20:0.2 |
| Parameter | Dry | 30 min | 1 h | 5 h | 10 h | Physical Significance |
|---|---|---|---|---|---|---|
| () | 75 | 10 | 0 | −5 | −25 | The reference temperature |
| 4.70 | 5.90 | 7.78 | 25.52 | 24.62 | First WLF constant at | |
| () | 62.34 | 64.92 | 79.47 | 187.80 | 144.08 | Second WLF constant at |
| () | 40 | −25 | −45 | −70 | −80 | Glass transition temperature |
| 10.72 | 12.80 | 17.94 | 39.03 | 39.82 | First WLF constant at | |
| () | 27.34 | 29.92 | 34.47 | 122.80 | 89.08 | Second WLF constant at |
| Parameter | Dry | 1 h | 2 h | 10 h | Physical Significance |
|---|---|---|---|---|---|
| () | 60 | 15 | 10 | −10 | The reference temperature |
| 5.31 | 10.14 | 7.81 | 8.80 | First WLF constant at | |
| () | 54.06 | 79.69 | 73.84 | 82.33 | Second WLF constant at |
| () | 30 | −20 | −25 | −55 | Glass transition temperature |
| 11.93 | 18.08 | 14.85 | 19.41 | First WLF constant at | |
| () | 24.06 | 44.69 | 38.84 | 37.33 | Second WLF constant at |
| Parameter | Dry | 30 min | 1 h | 5 h | 10 h | Physical Significance |
|---|---|---|---|---|---|---|
| (MPa) | 872 | 527 | 498 | 170 | 89 | The glassy moduli |
| (MPa) | 0.58 | 0.51 | 0.47 | 0.20 | 0.15 | The rubbery moduli |
| 2100 | 2150 | 80 | 0.010 | 0.074 | Stress relaxation time at | |
| 0.7 | 0.68 | 0.58 | 0.26 | 0.28 | Breadth of relaxation spectrum |
| Parameter | Dry | 1 h | 2 h | 10 h | Physical Significance |
|---|---|---|---|---|---|
| (MPa) | 1438 | 805 | 686 | 399 | The glassy moduli |
| (MPa) | 3.53 | 3.46 | 3.43 | 3.25 | The rubbery moduli |
| 9270 | 9200 | 1690 | 30 | Stress relaxation time at | |
| 0.72 | 0.66 | 0.66 | 0.42 | Breadth of relaxation spectrum |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xiao, R. Glass Transition Behavior of Wet Polymers. Materials 2021, 14, 730. https://doi.org/10.3390/ma14040730
Li H, Xiao R. Glass Transition Behavior of Wet Polymers. Materials. 2021; 14(4):730. https://doi.org/10.3390/ma14040730
Chicago/Turabian StyleLi, Hai, and Rui Xiao. 2021. "Glass Transition Behavior of Wet Polymers" Materials 14, no. 4: 730. https://doi.org/10.3390/ma14040730
APA StyleLi, H., & Xiao, R. (2021). Glass Transition Behavior of Wet Polymers. Materials, 14(4), 730. https://doi.org/10.3390/ma14040730






