An Ab Initio Study of Pressure-Induced Changes of Magnetism in Austenitic Stoichiometric Ni2MnSn
Abstract
1. Introduction
2. Methods
2.1. Quantum-Mechanical Calculations
2.2. Experiments
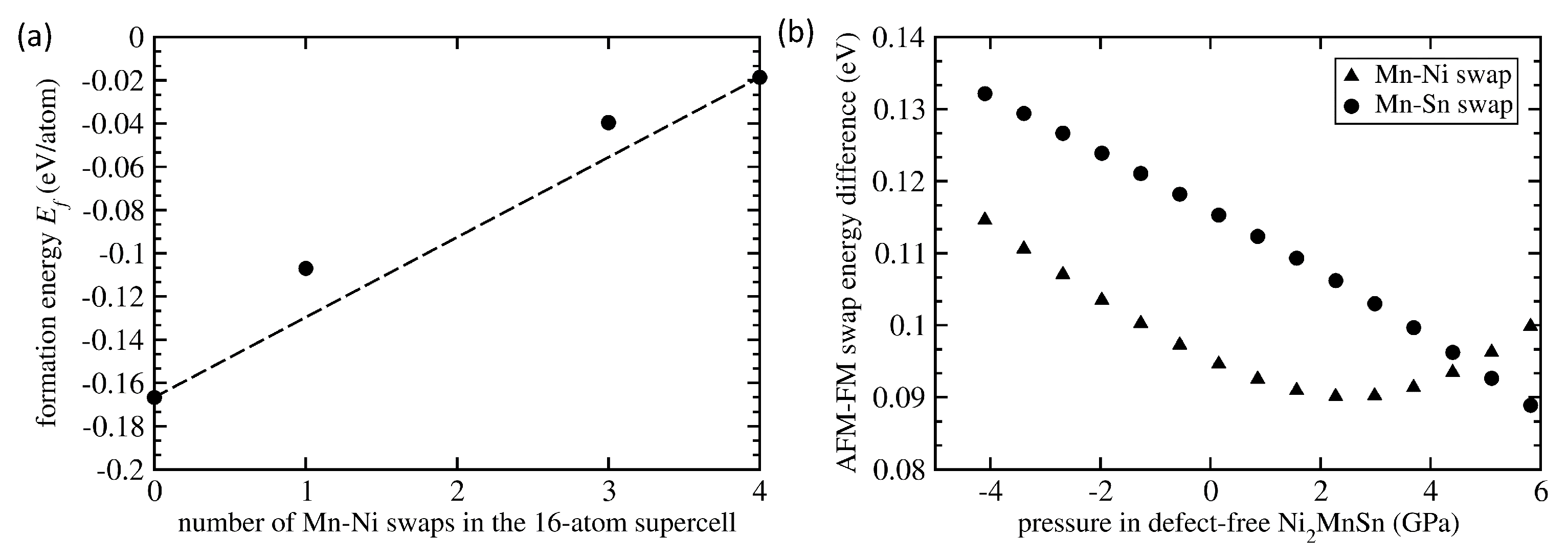
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Graf, T.; Felser, C.; Parkin, S.S. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Recarte, V.; Pérez-Landazábal, J.I.; Sánchez-Alarcos, V.; Cesari, E.; Jiménez-Ruiz, M.; Schmalzl, K.; Chernenko, V.A. Direct evidence of the magnetoelastic interaction in Ni2MnGa magnetic shape memory system. Appl. Phys. Lett. 2013, 102, 201906. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, Y.P.; Hyun, Y.H.; Kudryavtsev, Y.V. Magnetic, magneto-optical, and transport properties of ferromagnetic shape-memory Ni2MnGa alloy. J. Appl. Phys. 2003, 93, 6975–6977. [Google Scholar] [CrossRef]
- Brown, P.J.; Crangle, J.; Kanomata, T.; Matsumoto, M.; Neumann, K.U.; Ouladdiaf, B.; Ziebeck, K.R.A. The crystal structure and phase transitions of the magnetic shape memory compound Ni2MnGa. J. Phys. Condens. Matter 2002, 14, 10159–10171. [Google Scholar] [CrossRef]
- Entel, P.; Siewert, M.; Gruner, M.E.; Herper, H.C.; Comtesse, D.; Arróyave, R.; Singh, N.; Talapatra, A.; Sokolovskiy, V.V.; Buchelnikov, V.D.; et al. Complex magnetic ordering as a driving mechanism of multifunctional properties of Heusler alloys from first principles. Eur. Phys. J. B 2013, 86, 65. [Google Scholar] [CrossRef]
- Kaštil, J.; Kamarád, J.; Isnard, O.; Skourski, Y.; Míšek, M.; Arnold, Z. Effect of pressure and high magnetic field on phase transitions and magnetic properties of Ni1.92Mn1.56Sn0.52 and Ni2MnSn Heusler compounds. J. Alloys Compd. 2015, 650, 248–255. [Google Scholar] [CrossRef]
- Sutou, Y.; Imano, Y.; Koeda, N.; Omori, T.; Kainuma, R.; Ishida, K.; Oikawa, K. Magnetic and martensitic transformations of NiMnX(X=In,Sn,Sb) ferromagnetic shape memory alloys. Appl. Phys. Lett. 2004, 85, 4358–4360. [Google Scholar] [CrossRef]
- Brown, P.J.; Gandy, A.P.; Ishida, K.; Kainuma, R.; Kanomata, T.; Neumann, K.U.; Oikawa, K.; Ouladdiaf, B.; Ziebeck, K.R.A. The magnetic and structural properties of the magnetic shape memory compound Ni2Mn1.44Sn0.56. J. Phys. Condens. Matter 2006, 18, 2249–2259. [Google Scholar] [CrossRef]
- Çakır, A.; Righi, L.; Albertini, F.; Acet, M.; Farle, M. Intermartensitic transitions and phase stability in Ni50Mn50-xSnx Heusler alloys. Acta Mater. 2015, 99, 140–149. [Google Scholar] [CrossRef]
- Khan, M.; Pathak, A.K.; Paudel, M.R.; Dubenko, I.; Stadler, S.; Ali, N. Magnetoresistance and field-induced structural transitions in Ni50Mn50-xSnx Heusler alloys. J. Magn. Magn. Mater. 2008, 320, L21–L25. [Google Scholar] [CrossRef]
- Maheswar Repaka, D.V.; Chen, X.; Ramanujan, R.V.; Mahendiran, R. Magnetic field dependence of electrical resistivity and thermopower in Ni50Mn37Sn13 ribbons. AIP Adv. 2015, 5, 097116. [Google Scholar] [CrossRef]
- Kaštil, J.; Kamarád, J.; Míšek, M.; Hejtmánek, J.; Arnold, Z. Complex transport properties of the Ni1.92Mn1.56Sn0.52 Heusler alloy and its magnetic behavior. J. Magn. Magn. Mater. 2018, 466, 260–266. [Google Scholar] [CrossRef]
- Aksoy, S.; Acet, M.; Deen, P.P.; Mañosa, L.; Planes, A. Magnetic correlations in martensitic Ni-Mn-based Heusler shape-memory alloys: Neutron polarization analysis. Phys. Rev. B 2009, 79, 212401. [Google Scholar] [CrossRef]
- Khan, M.; Dubenko, I.; Stadler, S.; Ali, N. Exchange bias in bulk Mn rich Ni-Mn-Sn Heusler alloys. J. Appl. Phys. 2007, 102, 113914. [Google Scholar] [CrossRef]
- Webster, P.J. Heusler alloys. Contemp. Phys. 1969, 10, 559–577. [Google Scholar] [CrossRef]
- Alves, A.L.; Magnus Gomes Carvalho, A.; Cápua Proveti, J.R.; Nascimento, V.P.; Passamani, E.C. EXAFS studies of enhancement of L21-B2 chemical disorder induced by ball milling in martensitic Ni50Mn36Sn14 pseudo-Heusler alloy. Mater. Charact. 2019, 158, 109972. [Google Scholar] [CrossRef]
- Kuzmin, R.N.; Ibraimov, N.S.; Zhdano, G.S. Mössbauer effect in Heusler alloys. Sov. Phys. JETP 1966, 23, 219. [Google Scholar]
- Leiper, W.; Geldart, D.J.W.; Pothier, P.J. Hyperfine field at the tin sites in the Heusler alloy Ni2MnSn. Phys. Rev. B 1971, 3, 1637–1640. [Google Scholar] [CrossRef]
- Williams, J.M.; Danson, D.P. A Mössbauer study of the Heusler alloys series Ni2MnxTi1-xSn. Le J. Phys. Colloq. 1979, 40, C2-169–C2-171. [Google Scholar] [CrossRef]
- Gavriliuk, A.G.; Stepanov, G.N.; Sidorov, V.A.; Irkaev, S.M. Hyperfine magnetic fields and Curie temperature in the Heusler alloy Ni2MnSn at high pressure. J. Appl. Phys. 1996, 79, 2609–2612. [Google Scholar] [CrossRef]
- Şaşıoğlu, E.; Sandratskii, L.M.; Bruno, P. Pressure dependence of the Curie temperature in Ni2MnSn Heusler alloy: A first-principles study. Phys. Rev. B 2005, 71, 214412. [Google Scholar] [CrossRef]
- Bose, S.K.; Kudrnovský, J.; Drchal, V.; Turek, I. Magnetism of mixed quaternary Heusler alloys: (Ni,T)2MnSn(T=Cu,Pd) as a case study. Phys. Rev. B 2010, 82, 174402. [Google Scholar] [CrossRef]
- Bose, S.K.; Kudrnovský, J.; Drchal, V.; Turek, I. Pressure dependence of Curie temperature and resistivity in complex Heusler alloys. Phys. Rev. B 2011, 84, 174422. [Google Scholar] [CrossRef]
- Fichtner, T.; Kreiner, G.; Chadov, S.; Fecher, G.H.; Schnelle, W.; Hoser, A.; Felser, C. Magnetic and transport properties in the Heusler series Ni2-xMn1+xSn affected by chemical disorder. Intermetallics 2015, 57, 101–112. [Google Scholar] [CrossRef]
- Comtesse, D.; Gruner, M.E.; Ogura, M.; Sokolovskiy, V.V.; Buchelnikov, V.D.; Grünebohm, A.; Arróyave, R.; Singh, N.; Gottschall, T.; Gutfleisch, O.; et al. First-principles calculation of the instability leading to giant inverse magnetocaloric effects. Phys. Rev. B 2014, 89, 184403. [Google Scholar] [CrossRef]
- Jezierski, A. Electronic structure, magnetic, optical and thermodynamic properties of Ni2Mn1-xRexSn and NiMn1-xRexSn Heusler alloys-ab-initio study. J. Alloys Compd. 2019, 803, 153–164. [Google Scholar] [CrossRef]
- Saunders, N.; Miodownik, A. CALPHAD (Calculation of Phase Diagrams): A Comprehensive Guide; Elsevier Ltd.: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Lukas, H.; Fries, S.; Sundman, B. Computational Thermodynamics (The Calphad Method), 1st ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Guo, C.; Du, Z. Thermodynamic optimization of the Mn–Ni system. Intermetallics 2005, 13, 525–534. [Google Scholar] [CrossRef]
- Miettinen, J. Thermodynamic solution phase data for binary Mn-based systems. Calphad 2001, 25, 43–58. [Google Scholar] [CrossRef]
- Walnsch, A.; Kriegel, M.J.; Rudolph, M.; Motylenko, M.; Fabrichnaya, O.; Leineweber, A. Thermodynamic assessment and experimental investigation of the Al–Mn–Ni system. Calphad 2019, 64, 78–89. [Google Scholar] [CrossRef]
- Miettinen, J. Thermodynamic description of the Cu–Mn–Sn system in the copper-rich corner. Calphad 2004, 28, 71–77. [Google Scholar] [CrossRef]
- Rababah, M.; Itradat, A.; Almagableh, A.; Aljarrah, M.; Obeidat, S.; Al-Hadeethi, R. Thermodynamic calculations of the Mn–Sn, Mn–Sr and Mg–Mn–{Sn, Sr} systems. IET Sci. Meas. Technol. 2015, 9, 681–692. [Google Scholar] [CrossRef]
- Zemanová, A.; Kroupa, A.; Dinsdale, A. Theoretical assessment of the Ni–Sn system. Monatshefte Chem. Chem. Mon. 2012, 143, 1255–1261. [Google Scholar] [CrossRef]
- Liu, H.S.; Wang, J.; Jin, Z.P. Thermodynamic optimization of the Ni–Sn binary system. Calphad 2004, 28, 363–370. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Sun, Y.; Zhang, J.; Zhou, G.; Luo, H.; Liu, G. The thermodynamic, electronic and magnetic properties of Ni2MnX (X=Ge, Sn, Sb) Heusler alloys: A quasi-hormonic Debye model and first principles study. Phys. B Condens. Matter 2013, 409, 35–41. [Google Scholar] [CrossRef]
- Podgornykh, S.; Streltsov, S.; Kazantsev, V.; Shreder, E. Heat capacity of Heusler alloys: Ferromagnetic Ni2MnSb, Ni2MnSn, NiMnSb and antiferromagnetic CuMnSb. J. Magn. Magn. Mater. 2007, 311, 530–534. [Google Scholar] [CrossRef]
- Vřešťál, J. Recent progress in modelling of sigma-phase. Arch. Metall. 2001, 46, 239–247. [Google Scholar]
- Havránková, J.; Vřešťál, J.; Wang, L.G.; Šob, M. Ab initio analysis of energetics of σ-phase formation in Cr-based systems. Phys. Rev. B 2001, 63, 174104. [Google Scholar] [CrossRef]
- Burton, P.; Dupin, N.; Fries, S.; Grimvall, G.; Guillermet, A.F.; Miodownik, P.; Oates, W.A.; Vinograd, V. Using ab Iiitio calculations in the CALPHAD environment. Z. Für Met. 2001, 92, 514–537. [Google Scholar]
- Kaufman, L.; Turchi, P.; Huang, W.; Liu, Z.K. Thermodynamics of the Cr-Ta-W system by combining the ab initio and CALPHAD methods. Calphad 2001, 25, 419–433. [Google Scholar] [CrossRef]
- Dutta, B.; Opahle, I.; Hickel, T. Interface effects on the magnetic properties of layered Ni2MnGa/Ni2MnSn alloys: A first-principles investigation. Funct. Mater. Lett. 2016, 9, 1642010. [Google Scholar] [CrossRef]
- Entel, P.; Gruner, M.E.; Acet, M.; Çakır, A.; Arróyave, R.; Duong, T.; Sahoo, S.; Fähler, S.; Sokolovskiy, V.V. Properties and decomposition of Heusler alloys. Energy Technol. 2018, 6, 1478–1490. [Google Scholar] [CrossRef]
- Waske, A.; Dutta, B.; Teichert, N.; Weise, B.; Shayanfar, N.; Becker, A.; Hütten, A.; Hickel, T. Coupling phenomena in magnetocaloric materials. Energy Technol. 2018, 6, 1429–1447. [Google Scholar] [CrossRef]
- Zhang, K.; Tian, X.; Tan, C.; Guo, E.; Zhao, W.; Cai, W. Designing a new Ni-Mn-Sn ferromagnetic shape memory alloy with excellent performance by Cu addition. Metals 2018, 8, 152. [Google Scholar] [CrossRef]
- Buchelnikov, V.D.; Sokolovskiy, V.V.; Miroshkina, O.N.; Zagrebin, M.A.; Nokelainen, J.; Pulkkinen, A.; Barbiellini, B.; Lähderanta, E. Correlation effects on ground-state properties of ternary Heusler alloys: First-principles study. Phys. Rev. B 2019, 99, 014426. [Google Scholar] [CrossRef]
- Benguerine, O.; Nabi, Z.; Benichou, B.; Bouabdallah, B.; Bouchenafa, H.; Maachou, M.; Ahuja, R. Structural, elastic, electronic, and magnetic properties of Ni2MnSb, Ni2MnSn, and Ni2MnSb0.5Sn0.5 magnetic shape memory alloys. Rev. Mex. Fis. 2020, 66, 121–126. [Google Scholar] [CrossRef]
- Zagrebin, M.A.; Sokolovskiy, V.V.; Buchelnikov, V.D. Ab initio calculations of structural and magnetic properties of Ni-Co-Mn-Cr-Sn supercell. Intermetallics 2017, 87, 55–60. [Google Scholar] [CrossRef]
- Pramanick, S.; Dutta, P.; Chatterjee, S.; Majumdar, S.; Chatterjee, S. Anomalous pressure effect on the magnetic properties of Ni-Mn based shape memory alloys. J. Appl. Phys. 2018, 124, 133901. [Google Scholar] [CrossRef]
- Sokolovskiy, V.V.; Zagrebin, M.A.; Buchelnikov, V.D.; Entel, P. The effect of anti-site disorder on structural and magnetic properties of Ni-Co-Mn-In alloys: Ab initio and Monte Carlo studies. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Sokolovskiy, V.; Zagrebin, M.; Buchelnikov, V.D. First-principles study of Ni-Co-Mn-Sn alloys with regular and inverse Heusler structure. J. Magn. Magn. Mater. 2019, 476, 546–550. [Google Scholar] [CrossRef]
- Sokolovskiy, V.; Miroshkina, O.; Zagrebin, M.; Buchelnikov, V. Prediction of giant magnetocaloric effect in Ni40Co10Mn36Al14 Heusler alloys: An insight from ab initio and Monte Carlo calculations. J. Appl. Phys. 2020, 127, 163901. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kamarád, J.; Machátová, Z.; Arnold, Z. High pressure cells for magnetic measurements - Destruction and functional tests. Rev. Sci. Instrum. 2004, 75, 5022–5025. [Google Scholar] [CrossRef]
- Sokolovskiy, V.V.; Buchelnikov, V.D.; Zagrebin, M.A.; Entel, P.; Sahoo, S.; Ogura, M. First-principles investigation of chemical and structural disorder in magnetic Ni2Mn1+xSn1-x Heusler alloys. Phys. Rev. B 2012, 86, 134418. [Google Scholar] [CrossRef]
- Szytuła, A.; Kołodziejczyk, A.; Rżany, H.; Todorović, J.; Wanic, A. Atomic and magnetic structure of the Heusler alloys Ni2MnSb, Ni2MnSn, and Co2MnSn. Phys. Status Solidi (a) 1972, 11, 57–65. [Google Scholar] [CrossRef]
- Chen, X.Q.; Wolf, W.; Podloucky, R.; Rogl, P.; Marsman, M. Ab initio study of ground-state properties of the Laves-phase compound ZrMn2. Phys. Rev. B 2005, 72, 054440. [Google Scholar] [CrossRef]
- Unzueta, I.; Sánchez-Alarcos, V.; Recarte, V.; Pérez-Landazábal, J.I.; Zabala, N.; García, J.A.; Plazaola, F. Identification of a Ni-vacancy defect in Ni-Mn-Z (Z = Ga, Sn, In): An experimental and DFT positron-annihilation study. Phys. Rev. B 2019, 99, 064108. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
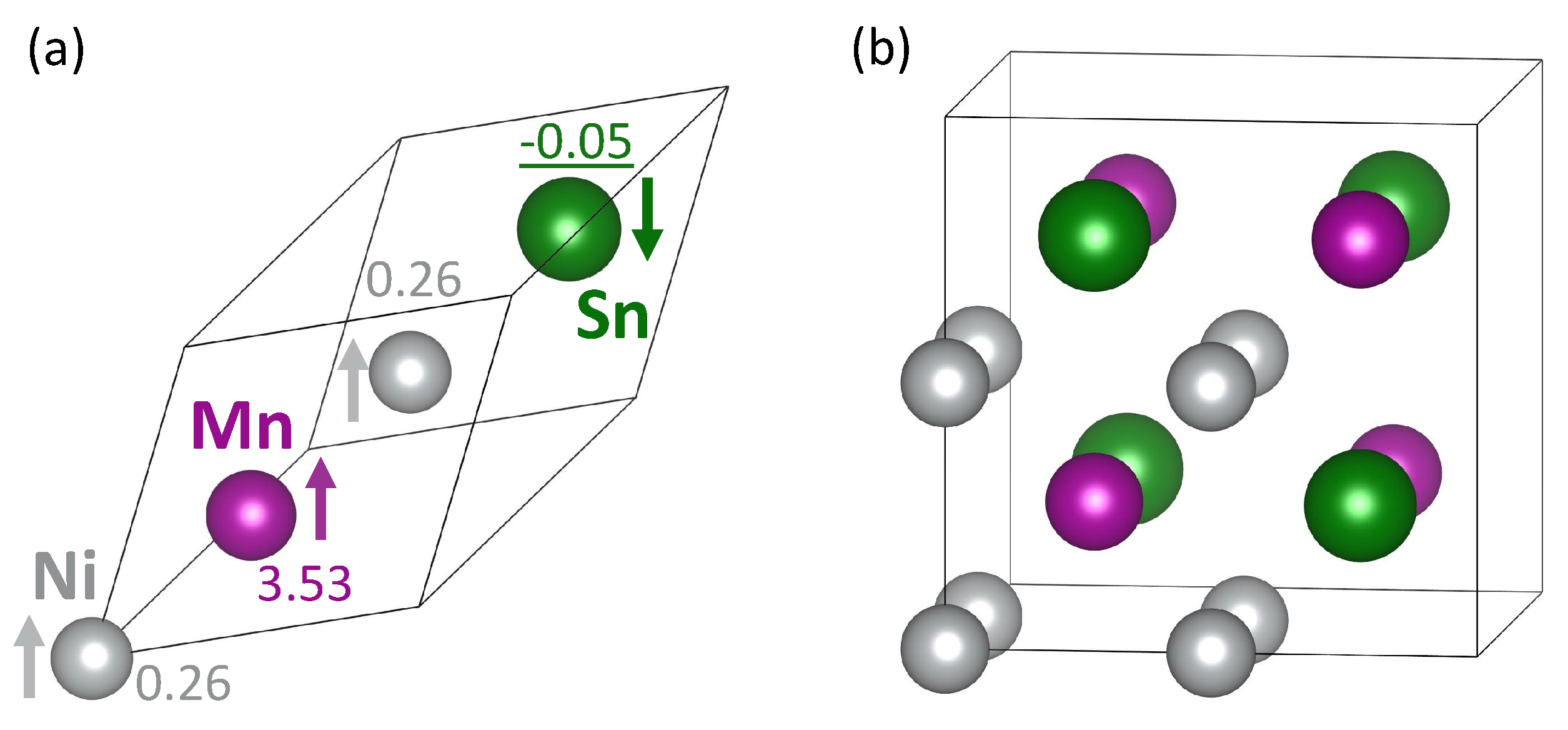
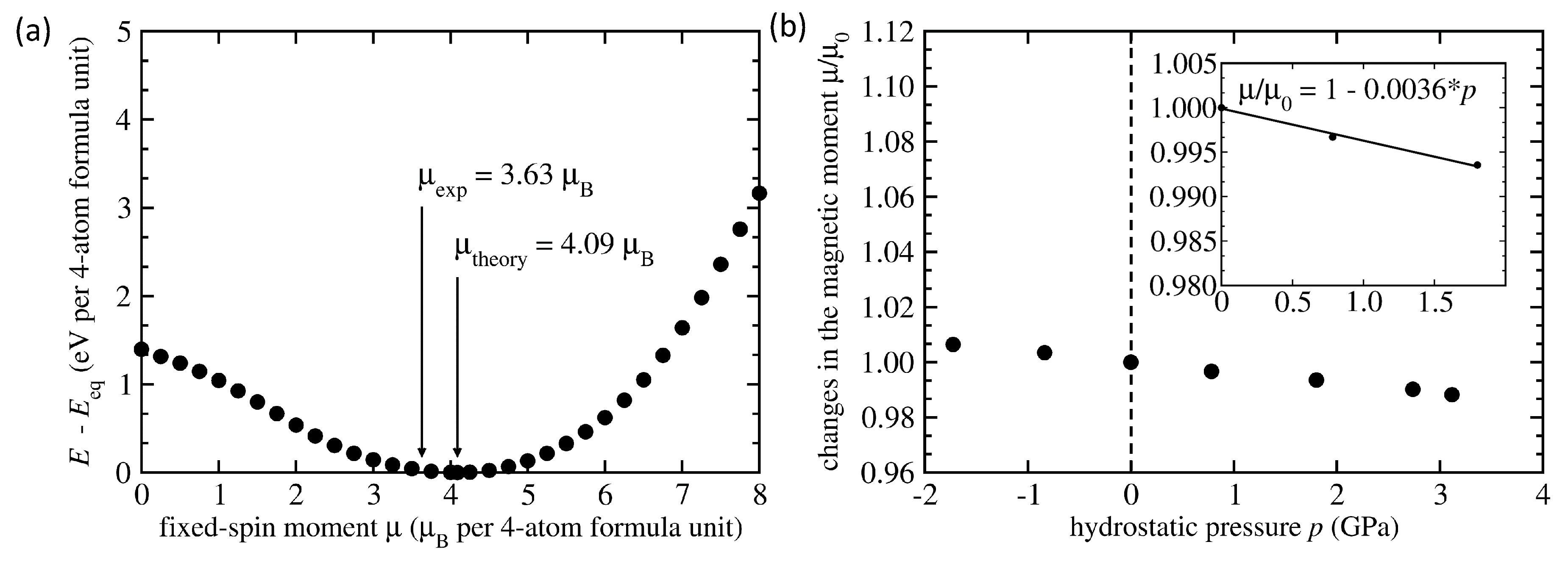
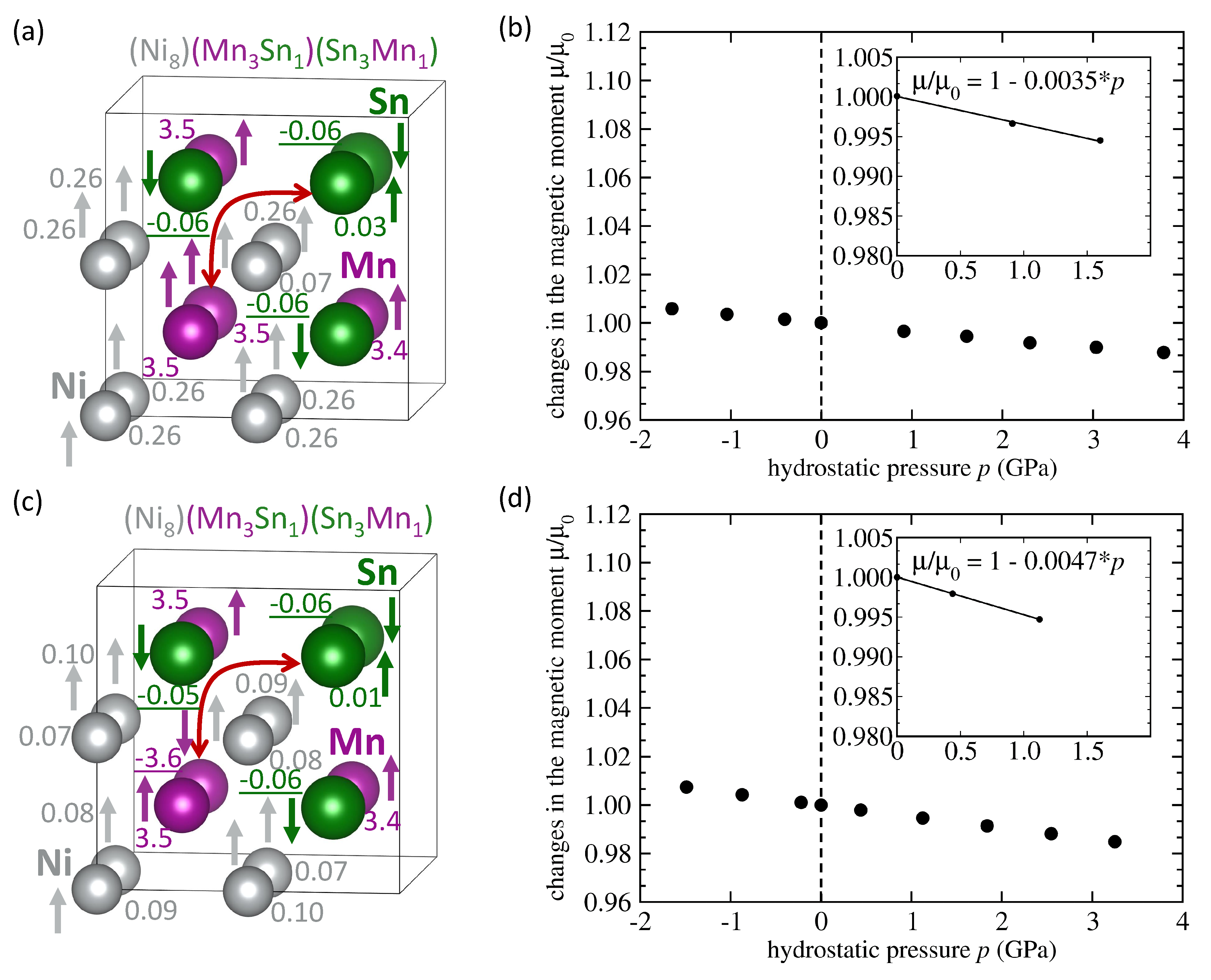
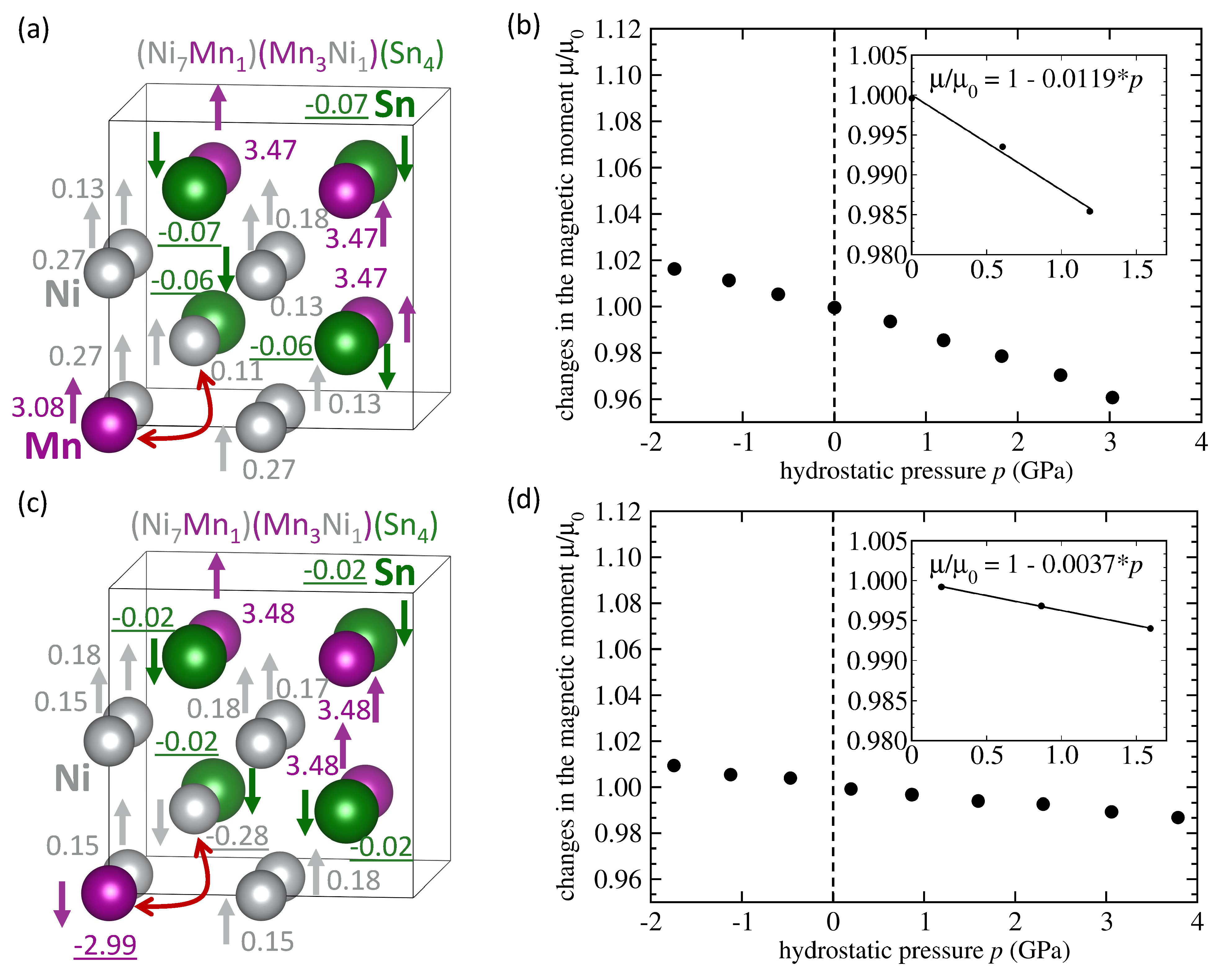
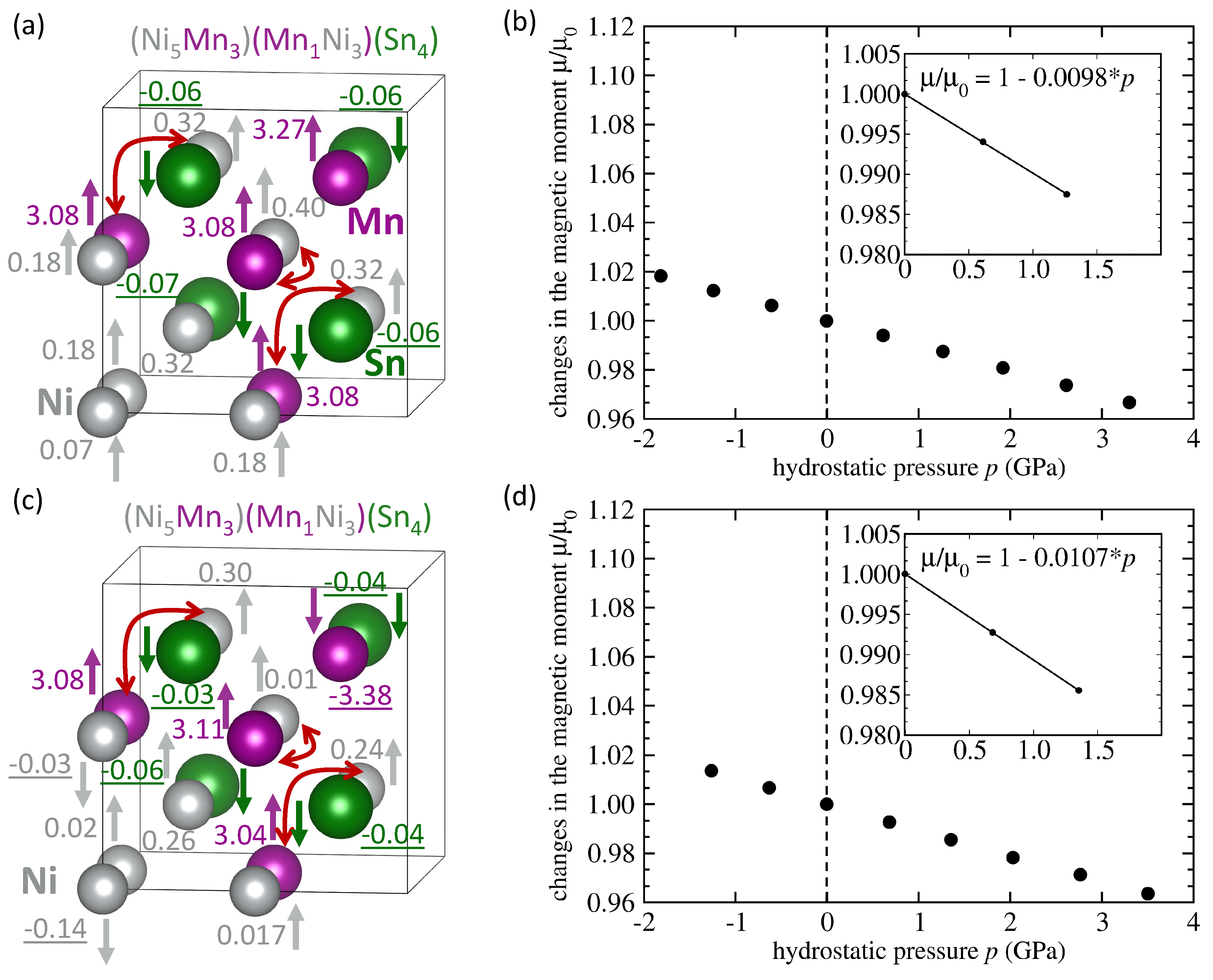
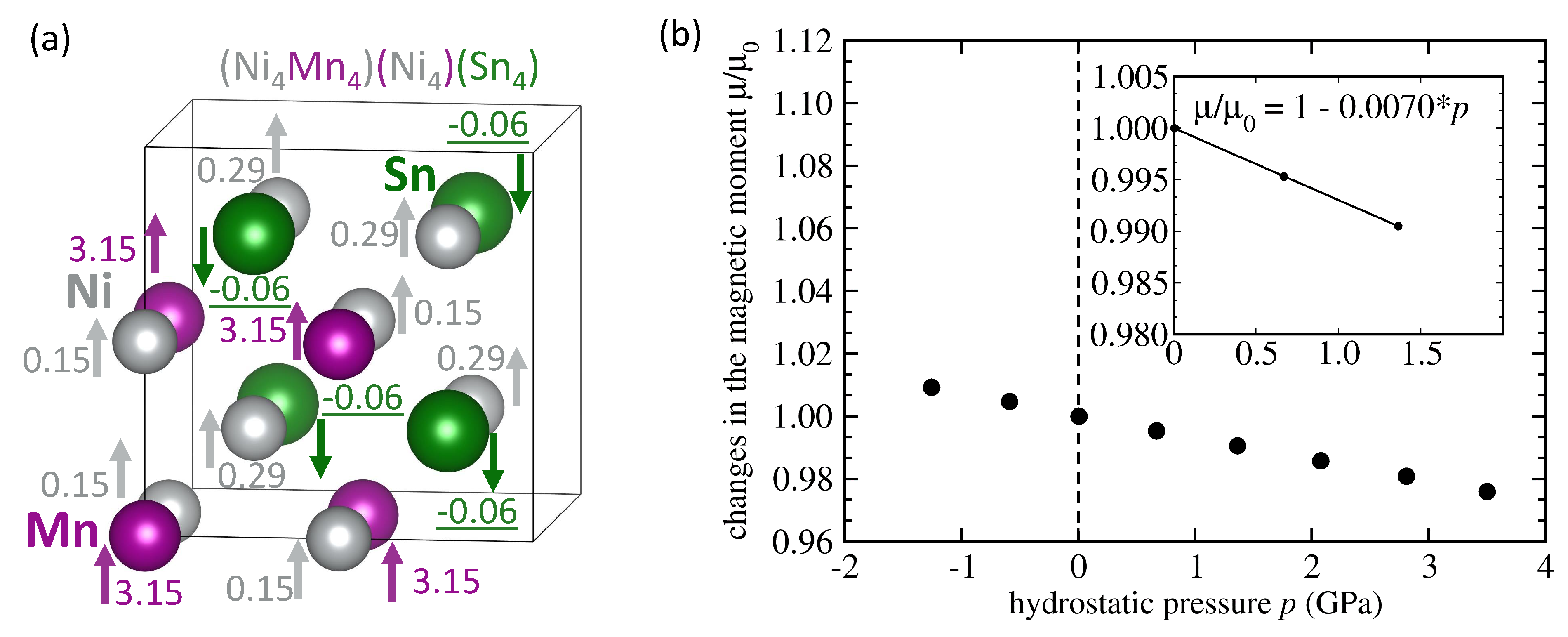
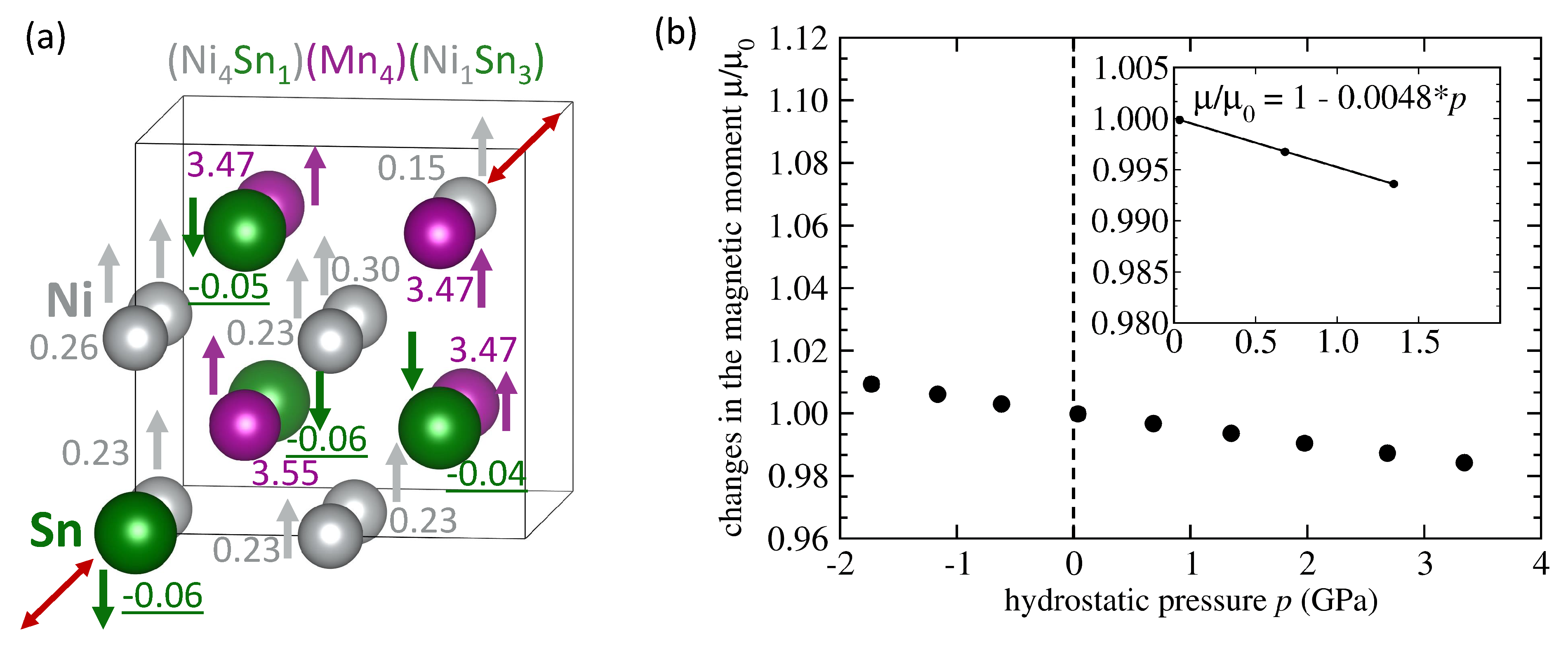
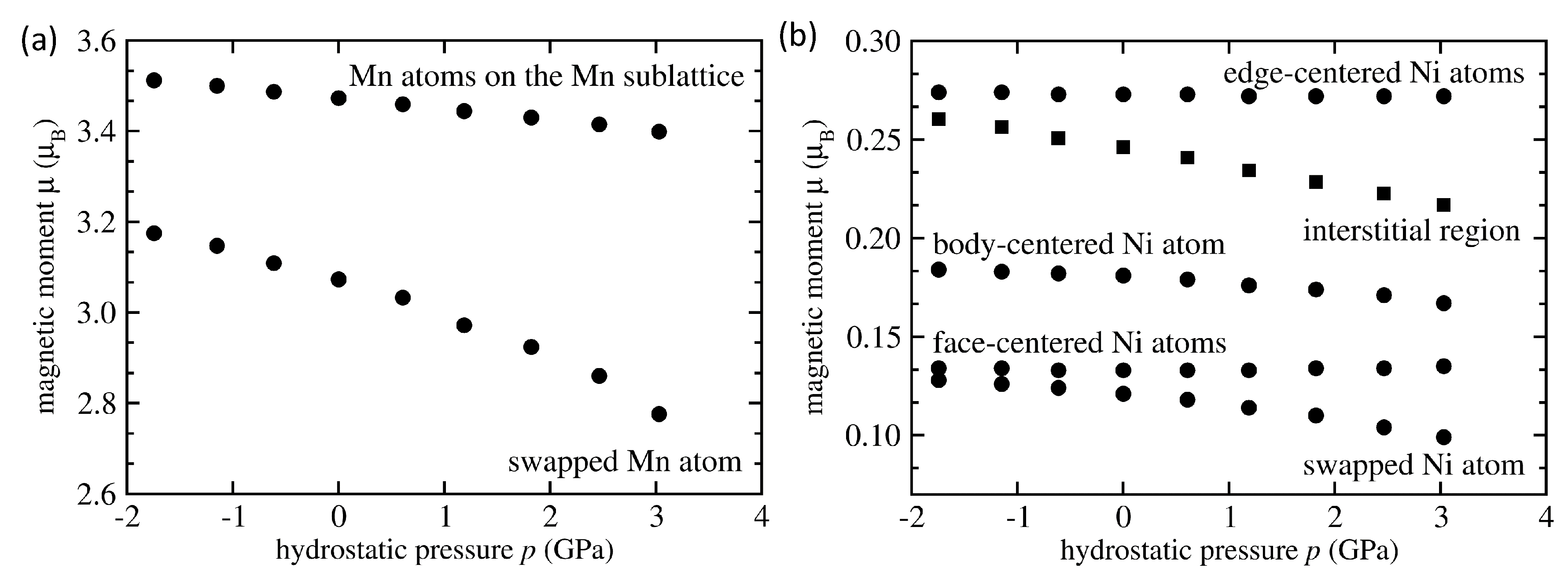
| System | Mn-Mn Coupling | Lattice Parameter | |||
|---|---|---|---|---|---|
| (Å) | (/f.u.) | (eV/atom) | (GPa) | ||
| NiMnSn L2 full Heusler | FM | 6.059 | 4.09 | −0.167 | −0.0036 |
| NiMnSn Mn swaps Sn | FM | 6.083 | 4.03 | −0.074 | −0.0035 |
| NiMnSn Mn swaps Sn | AFM | 6.076 | 1.87 | −0.066 | −0.0047 |
| NiMnSn Mn swaps Ni | FM | 6.058 | 3.75 | −0.113 | -0.0119 |
| NiMnSn Mn swaps Ni | AFM | 6.053 | 2.09 | −0.107 | −0.0037 |
| NiMnSn 3 Mn swap 3 Ni | FM | 6.054 | 3.58 | −0.029 | −0.0098 |
| NiMnSn 3 Mn swap 3 Ni | AFM | 6.049 | 1.57 | −0.040 | −0.0107 |
| NiMnSn inverse Heusler | FM | 6.048 | 3.51 | −0.019 | −0.0070 |
| NiMnSn Ni swaps Sn | FM | 6.106 | 4.04 | −0.012 | −0.0048 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friák, M.; Mazalová, M.; Turek, I.; Zemanová, A.; Kaštil, J.; Kamarád, J.; Míšek, M.; Arnold, Z.; Schneeweiss, O.; Všianská, M.; et al. An Ab Initio Study of Pressure-Induced Changes of Magnetism in Austenitic Stoichiometric Ni2MnSn. Materials 2021, 14, 523. https://doi.org/10.3390/ma14030523
Friák M, Mazalová M, Turek I, Zemanová A, Kaštil J, Kamarád J, Míšek M, Arnold Z, Schneeweiss O, Všianská M, et al. An Ab Initio Study of Pressure-Induced Changes of Magnetism in Austenitic Stoichiometric Ni2MnSn. Materials. 2021; 14(3):523. https://doi.org/10.3390/ma14030523
Chicago/Turabian StyleFriák, Martin, Martina Mazalová, Ilja Turek, Adéla Zemanová, Jiří Kaštil, Jiří Kamarád, Martin Míšek, Zdeněk Arnold, Oldřich Schneeweiss, Monika Všianská, and et al. 2021. "An Ab Initio Study of Pressure-Induced Changes of Magnetism in Austenitic Stoichiometric Ni2MnSn" Materials 14, no. 3: 523. https://doi.org/10.3390/ma14030523
APA StyleFriák, M., Mazalová, M., Turek, I., Zemanová, A., Kaštil, J., Kamarád, J., Míšek, M., Arnold, Z., Schneeweiss, O., Všianská, M., Zelený, M., Kroupa, A., Pavlů, J., & Šob, M. (2021). An Ab Initio Study of Pressure-Induced Changes of Magnetism in Austenitic Stoichiometric Ni2MnSn. Materials, 14(3), 523. https://doi.org/10.3390/ma14030523








